Experimental and Numerical Evaluation of an HCCI Engine Fueled with Biogas for Power Generation under Sub-Atmospheric Conditions
Abstract
:1. Introduction
2. Materials and Methods
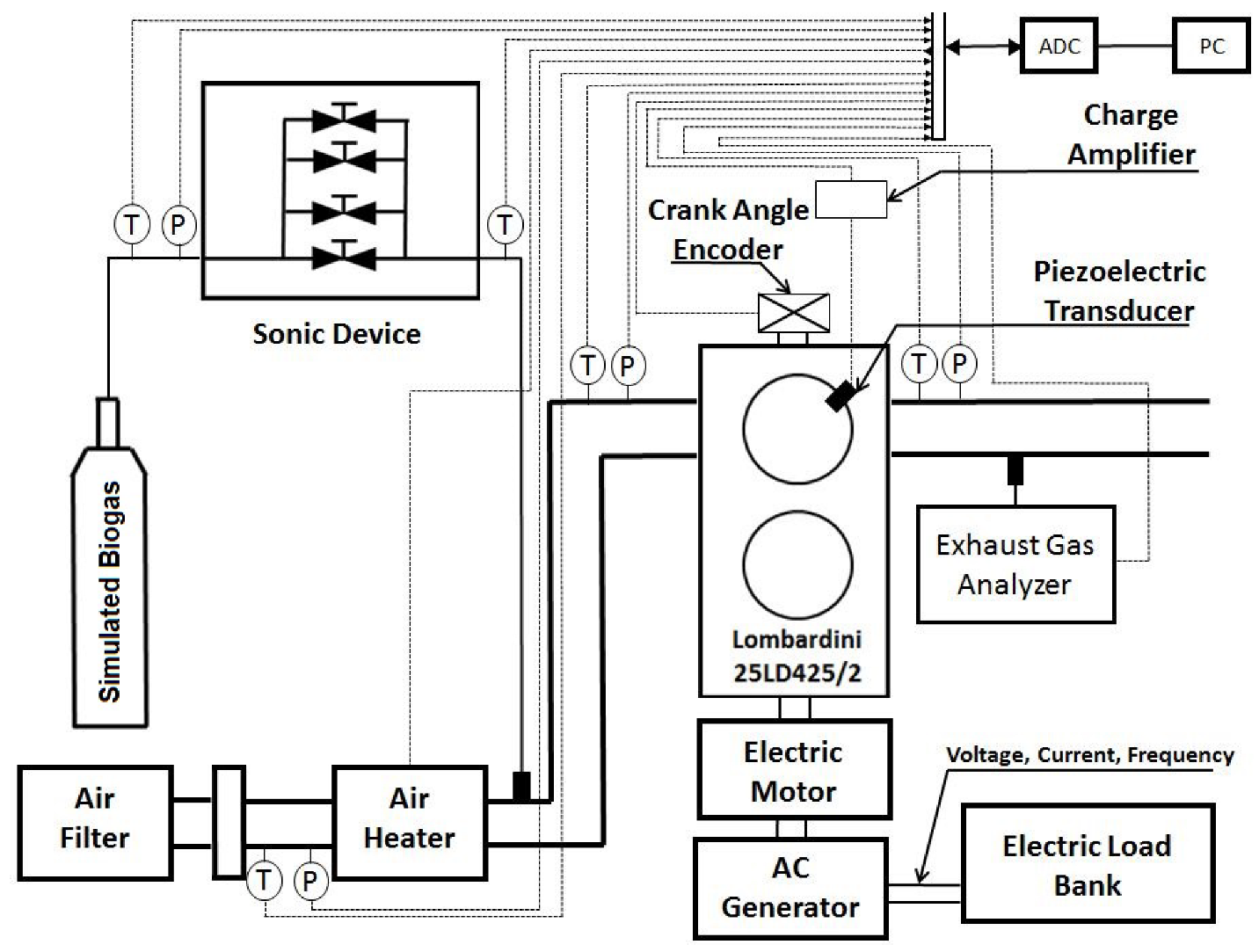
2.1. Experimental Setup
2.1.1. Experimental Procedure
2.1.2. Rate of Heat Release Calculations
2.2. Numerical Methodology: Single-Zone Model Approach
2.3. Wall Temperature Estimation
3. Results and Discussions
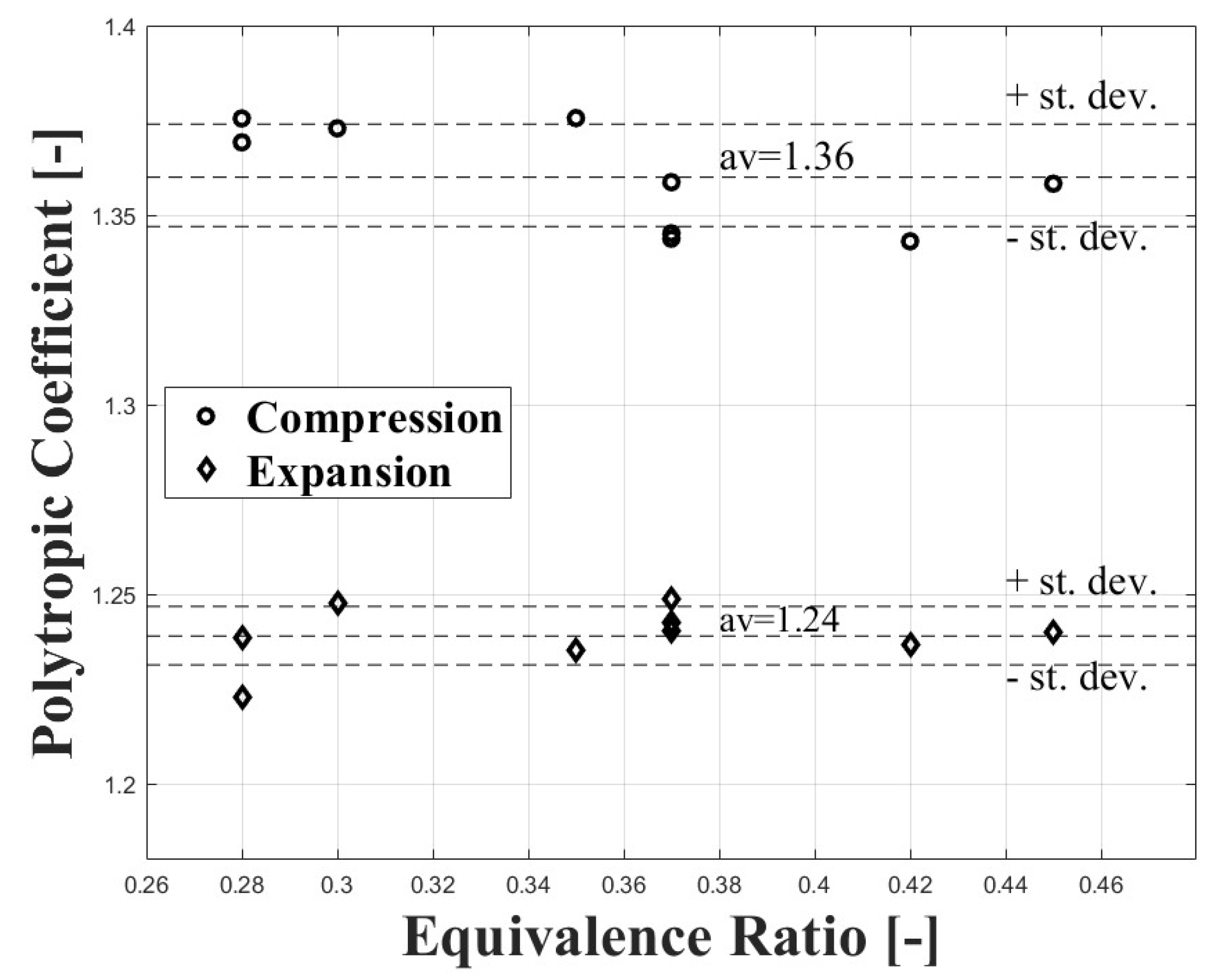
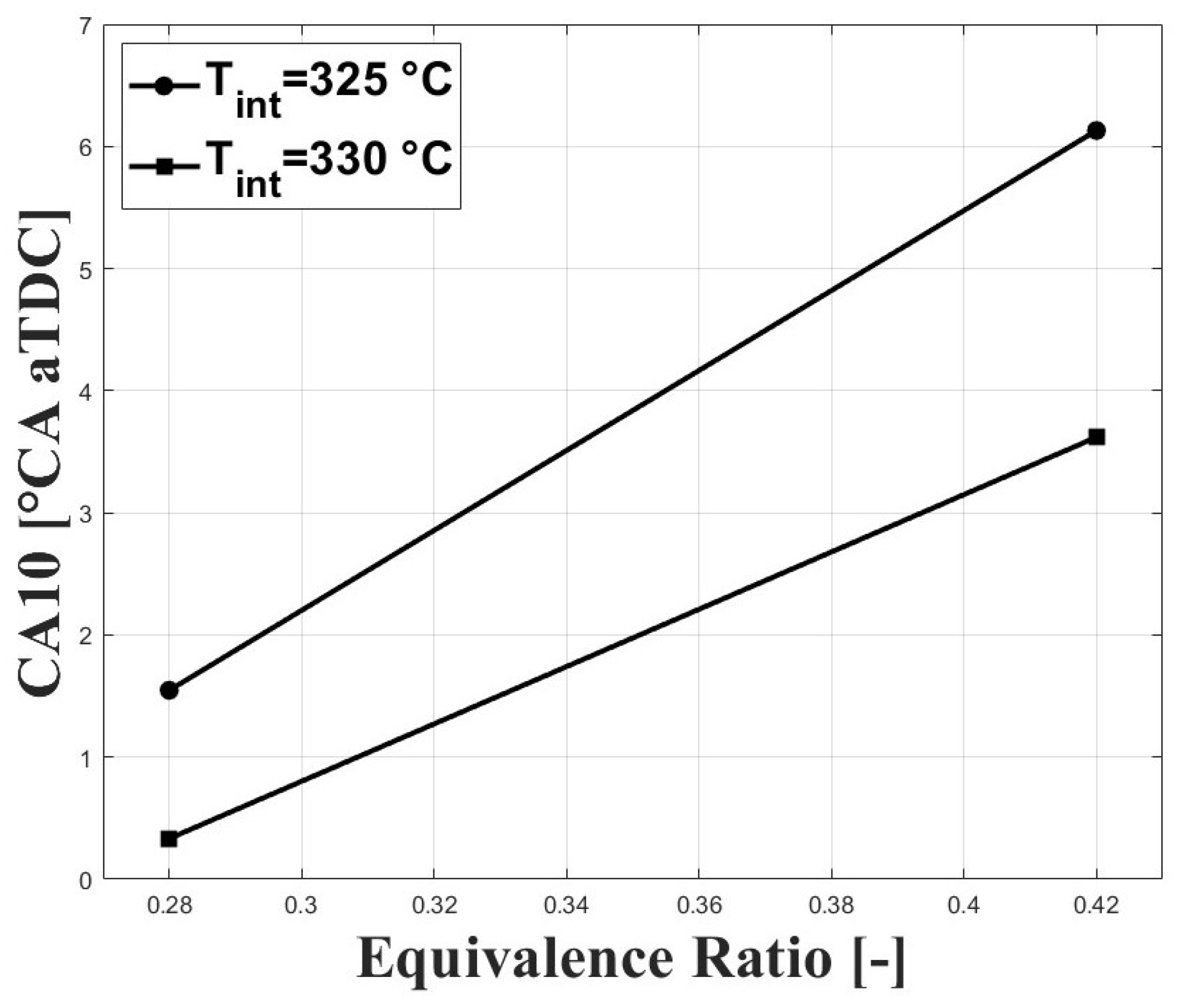
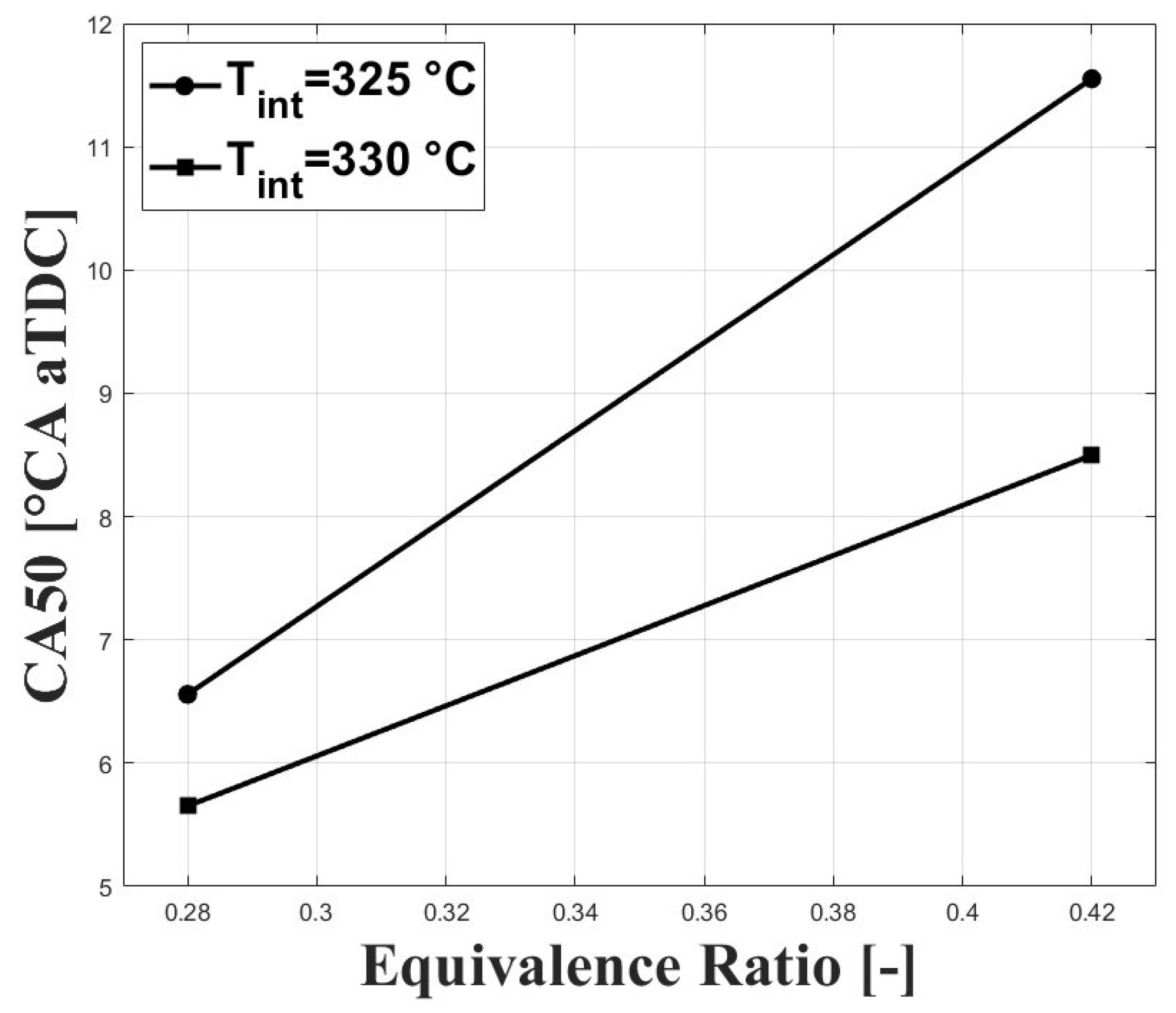
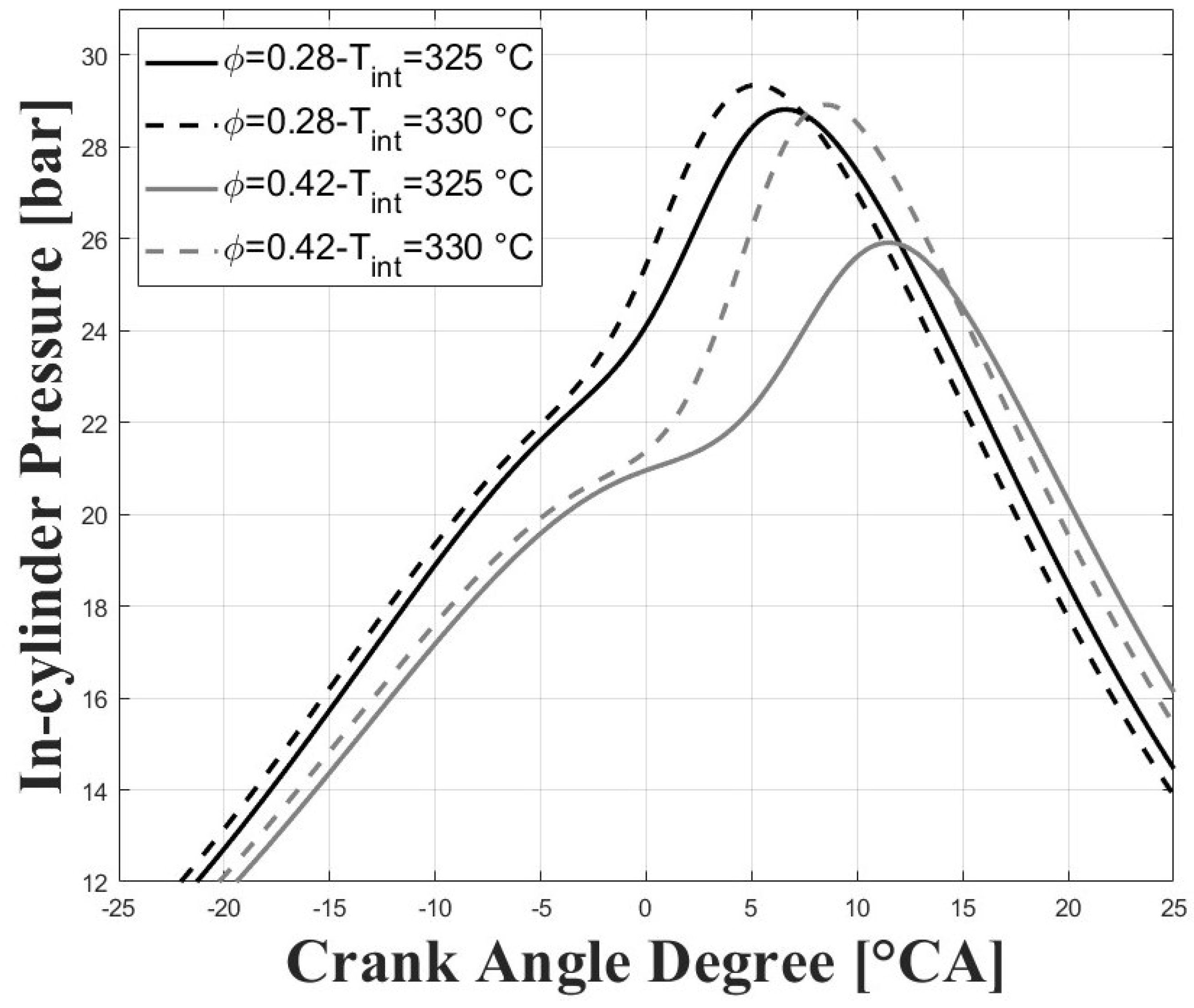
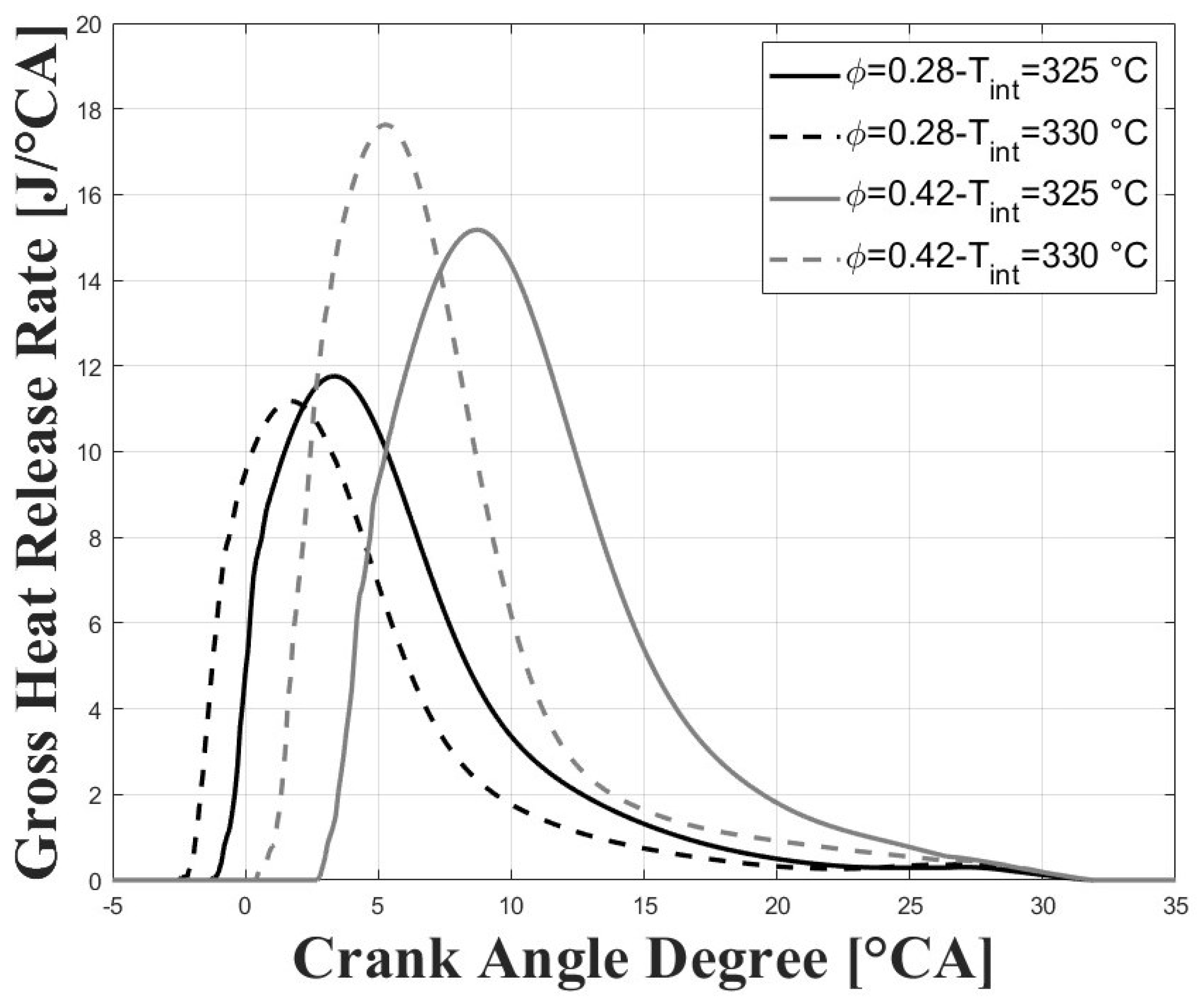
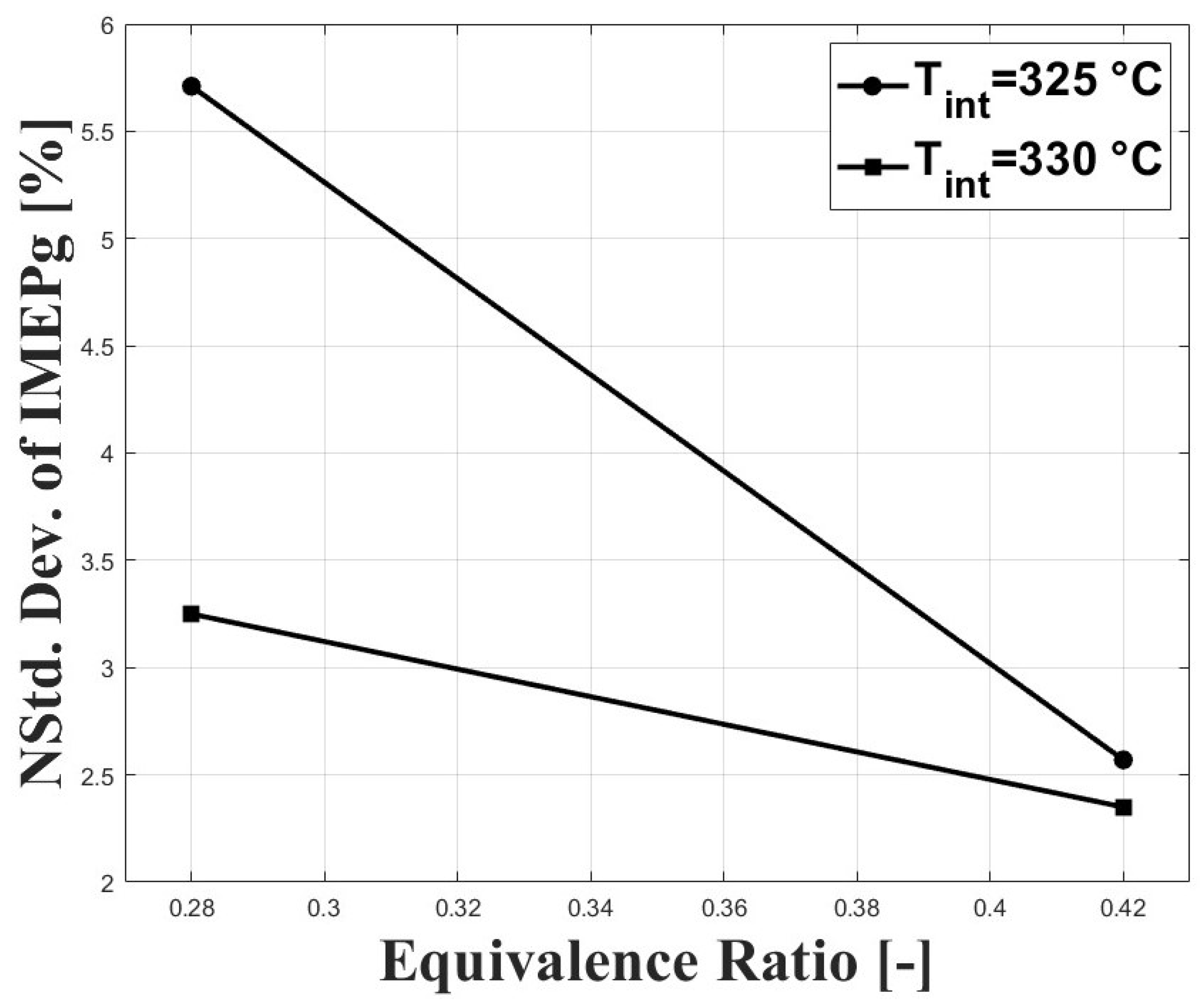
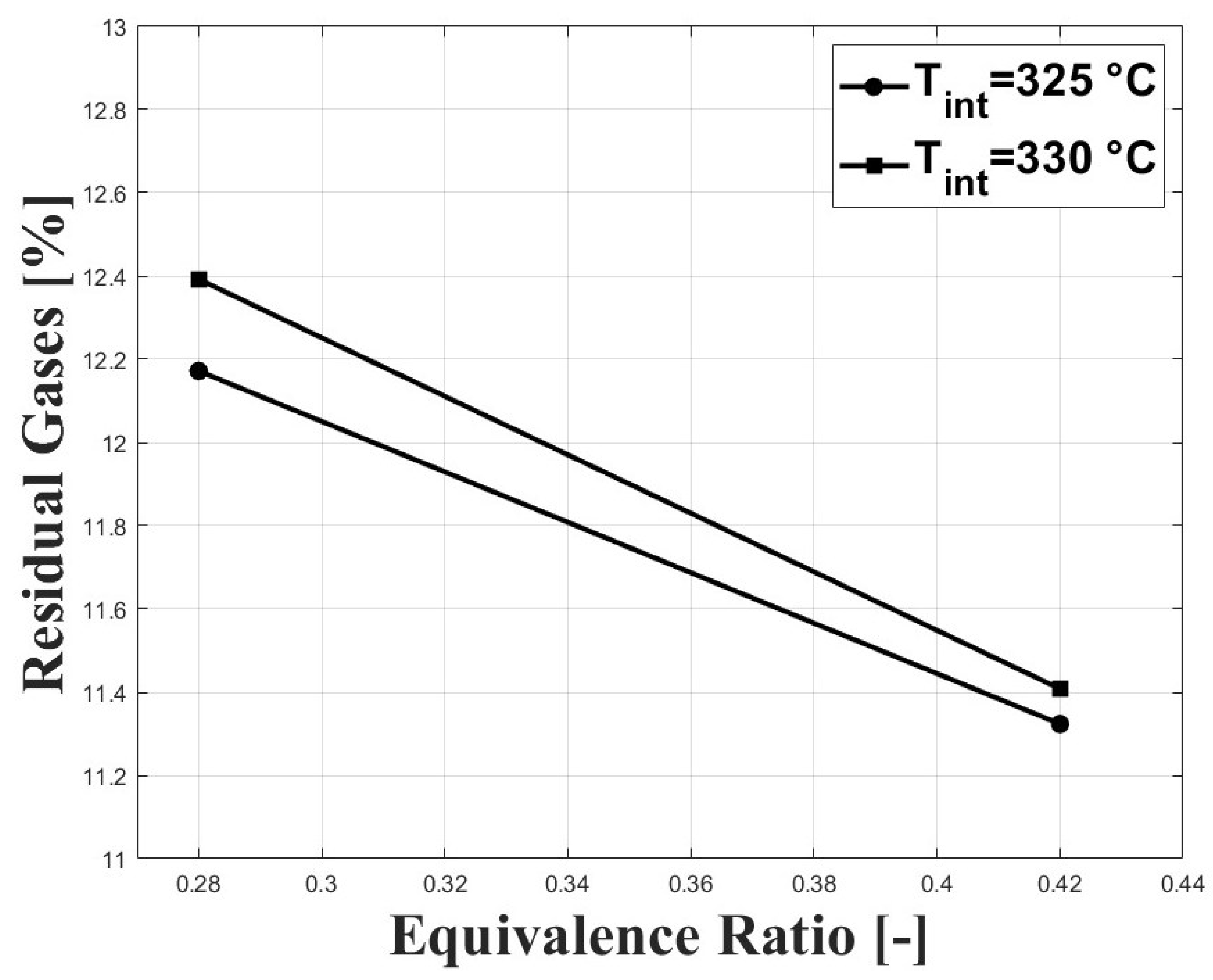
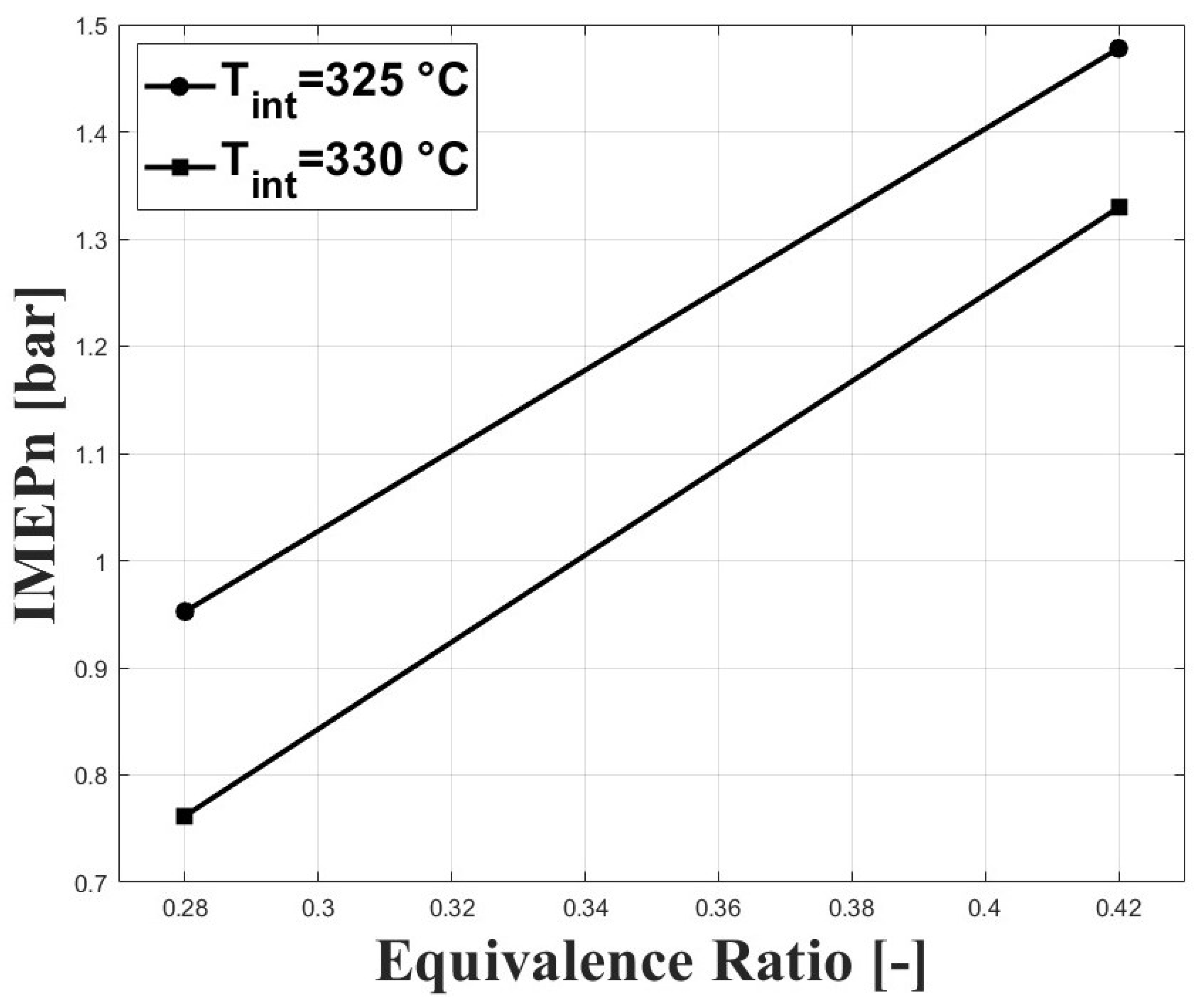
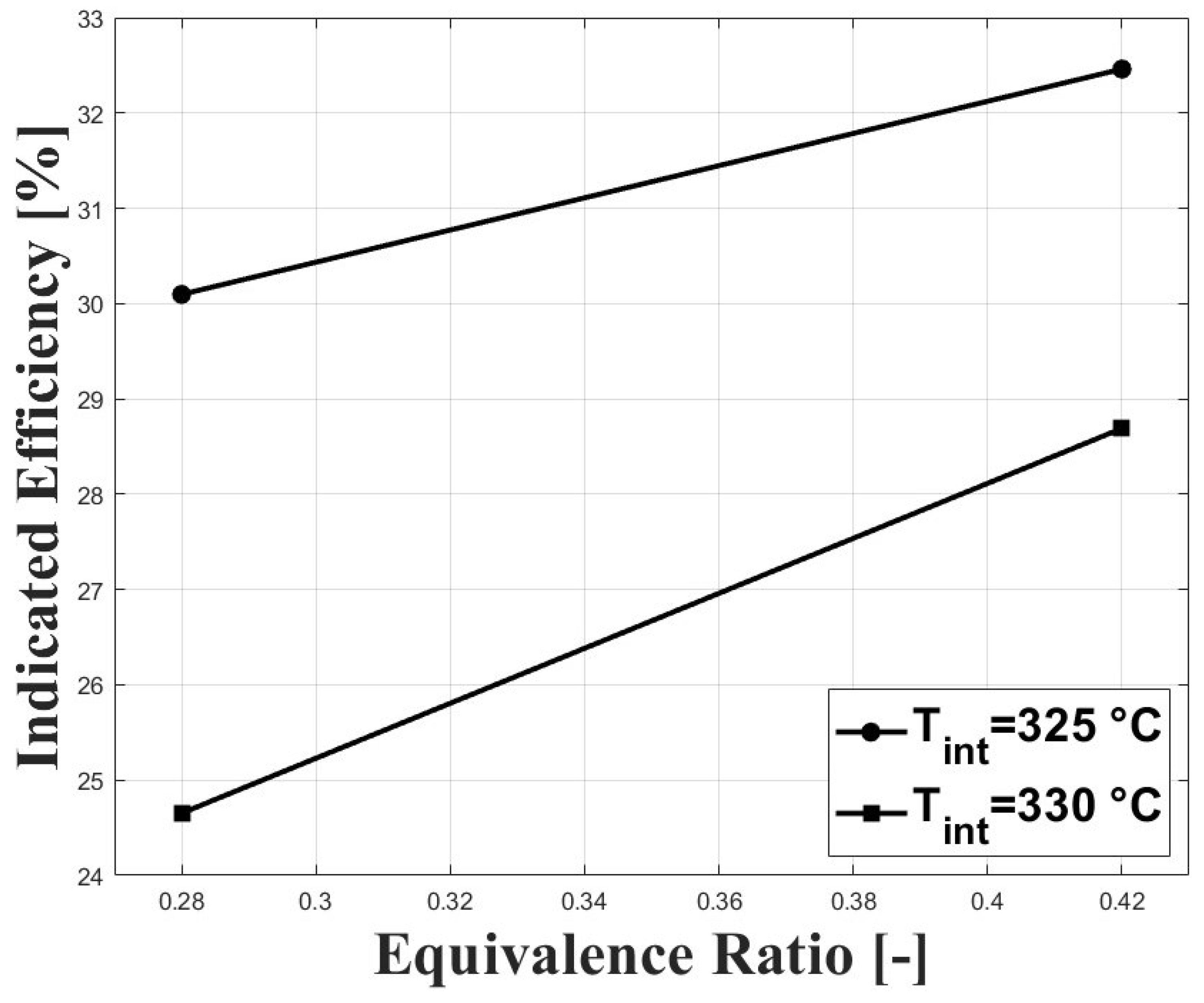
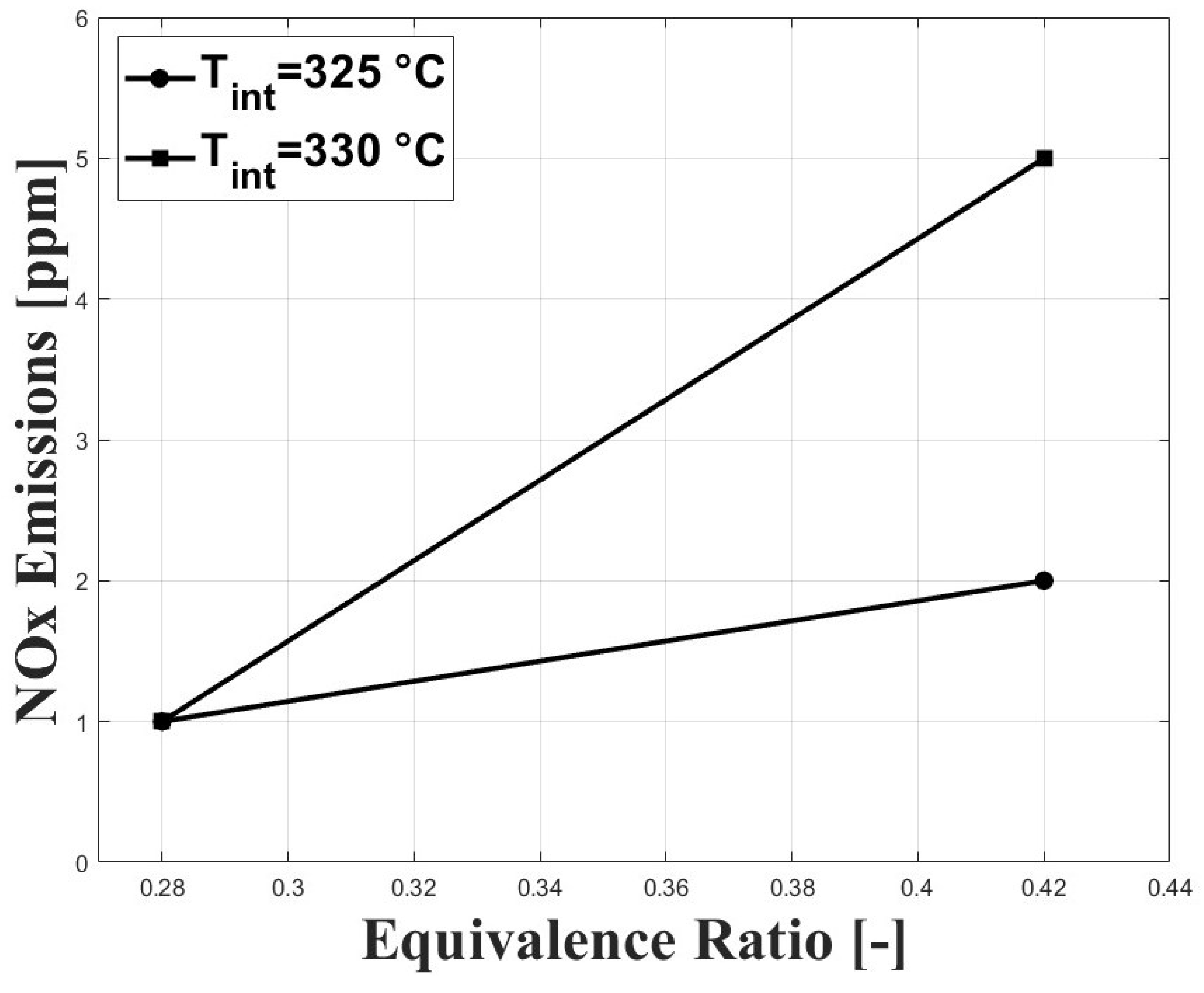
3.1. Experimental Results
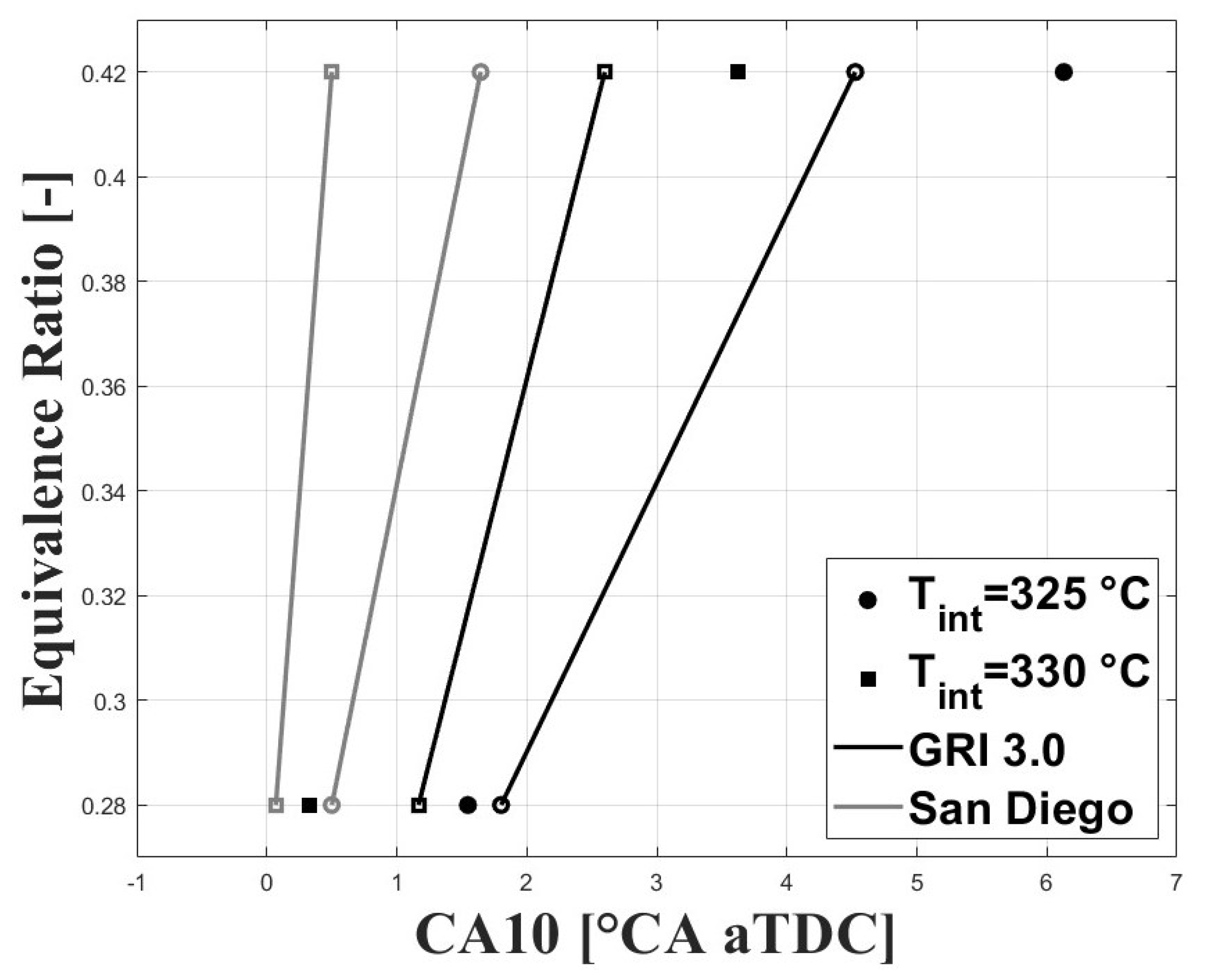
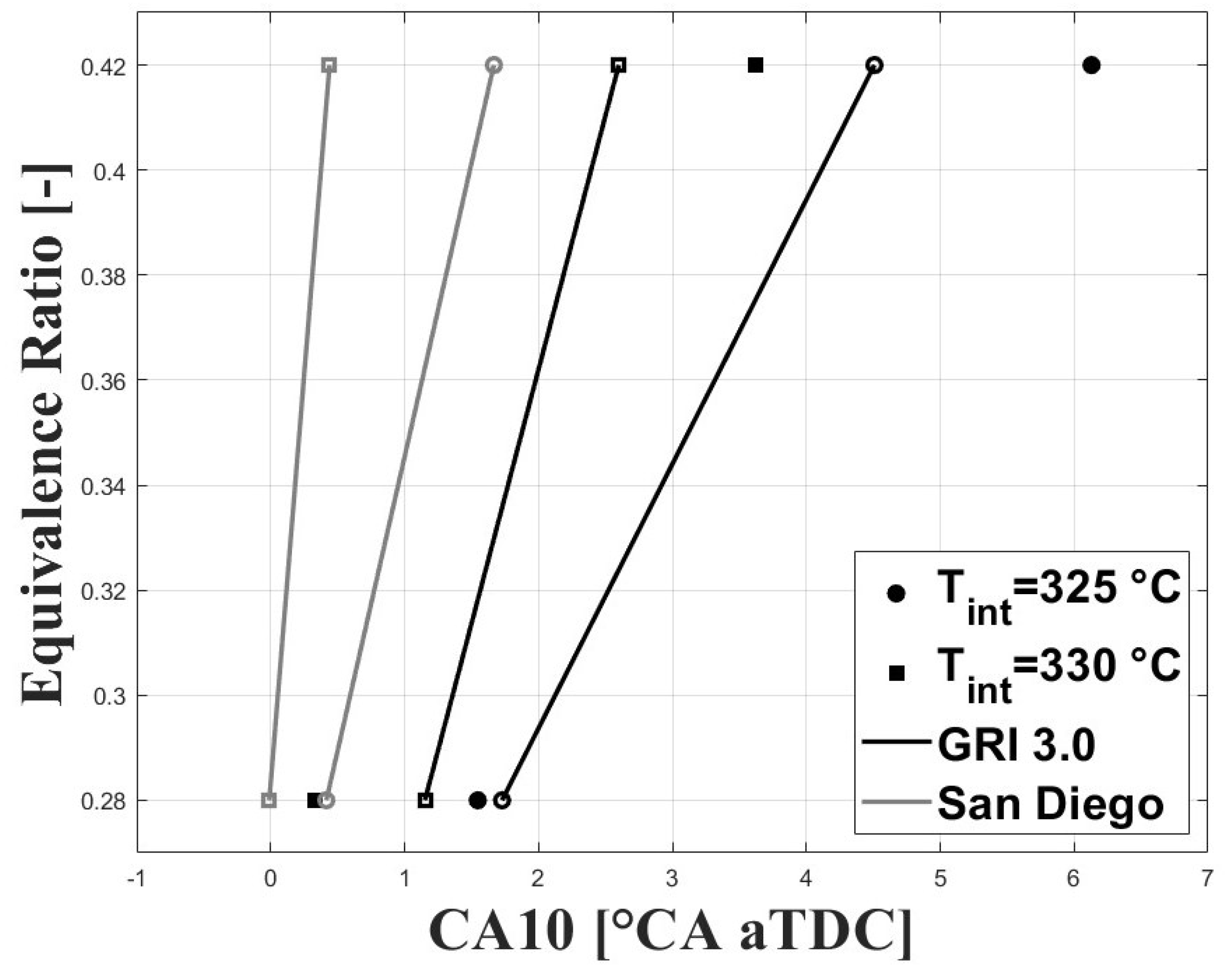
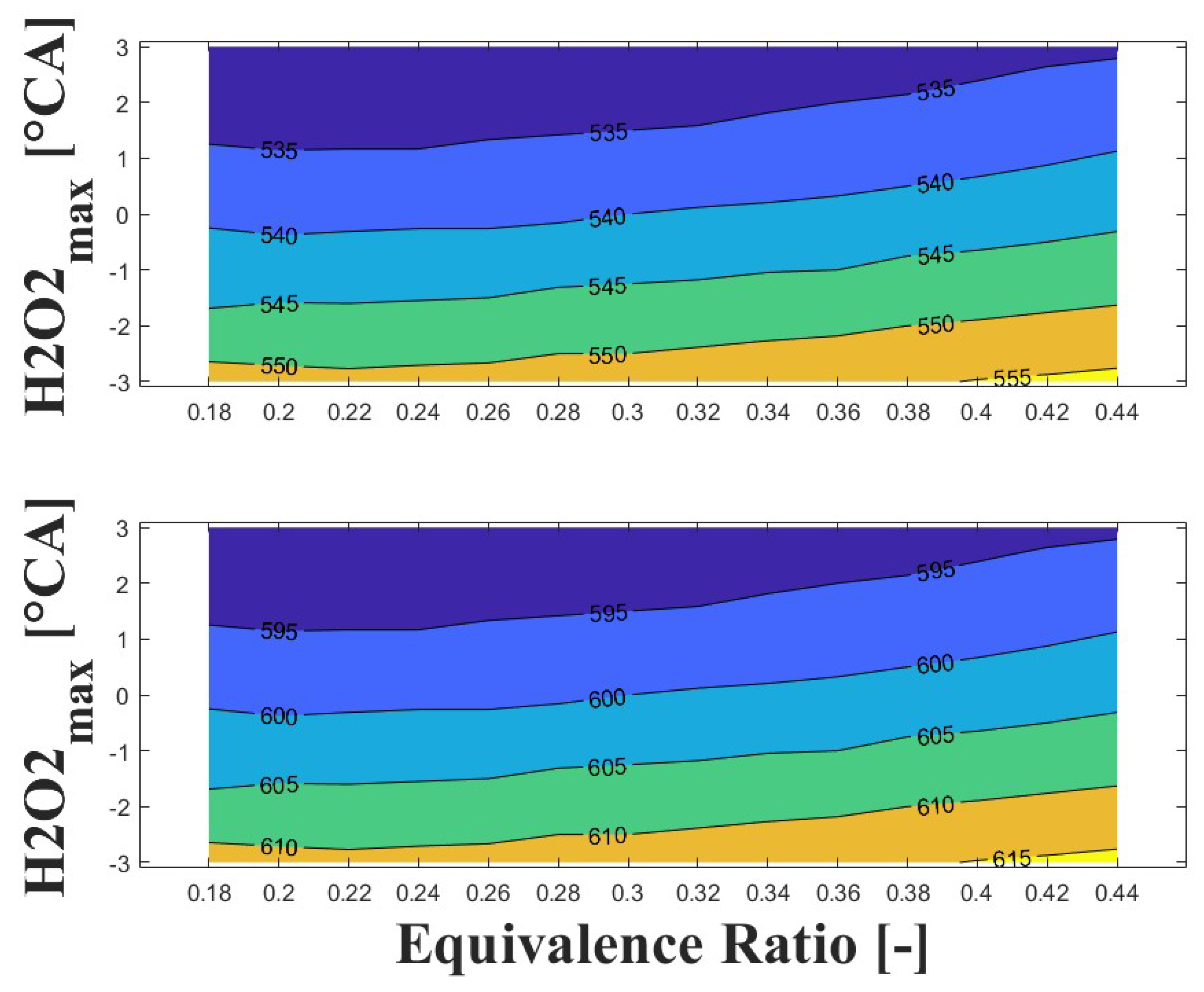
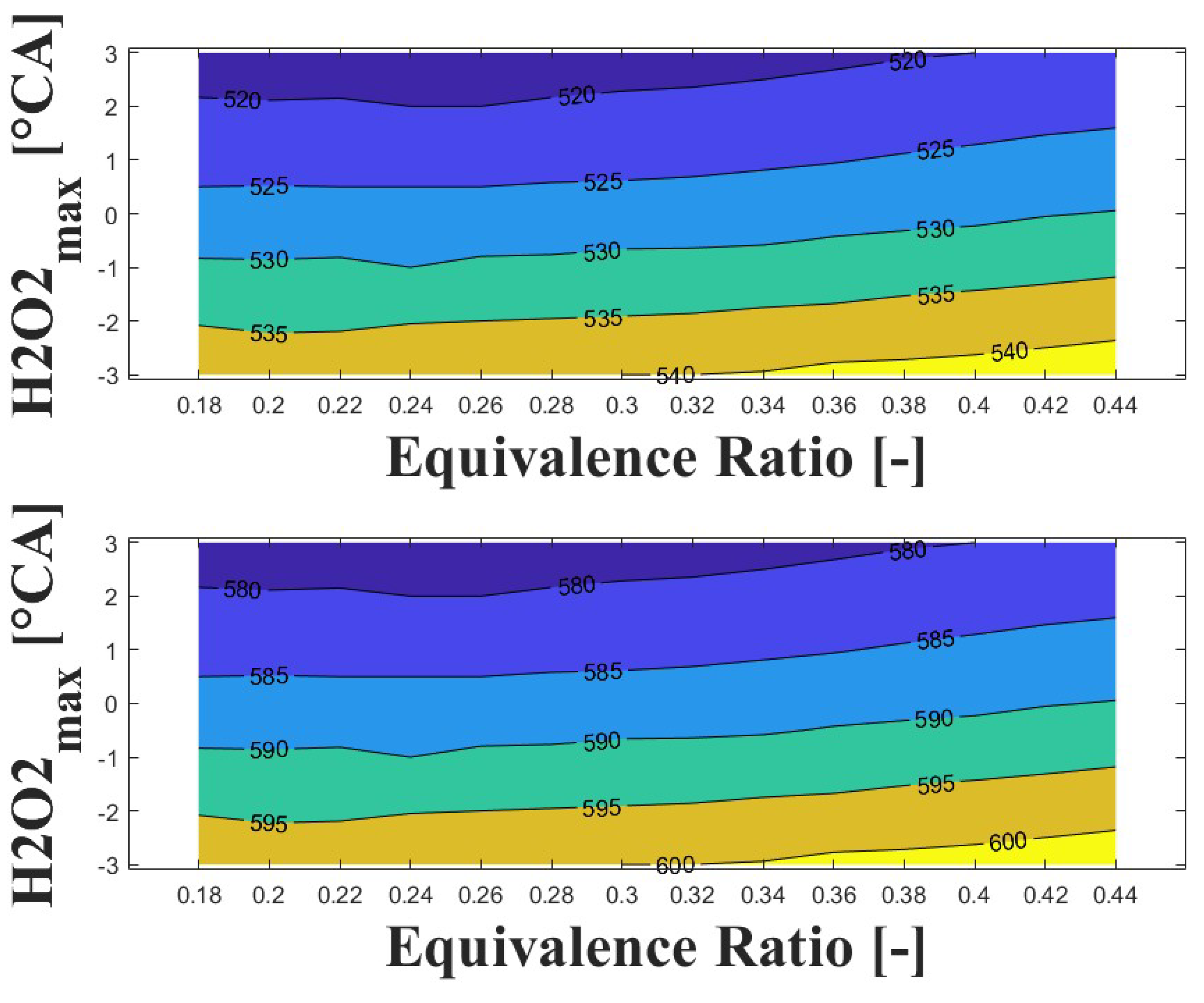
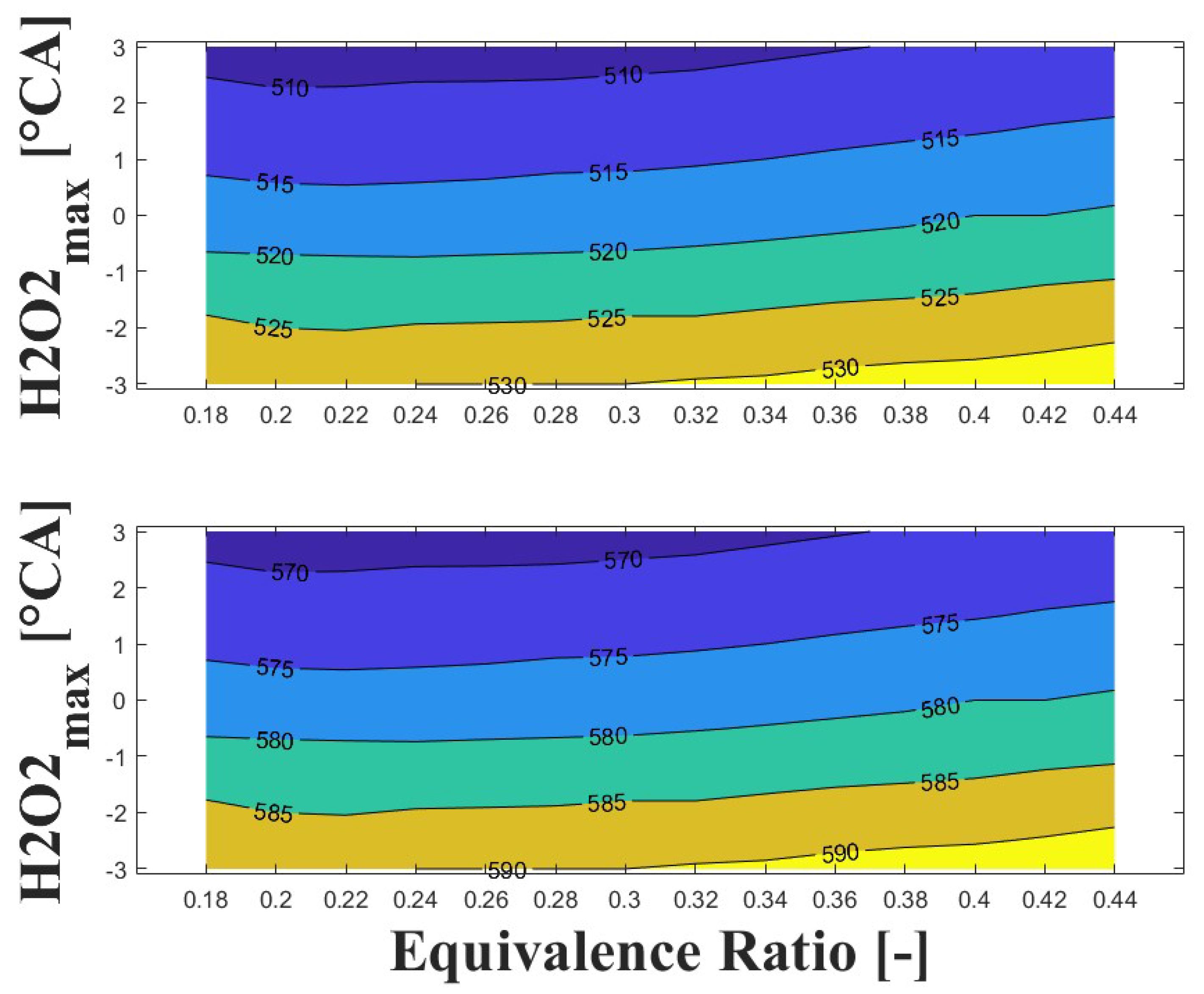
3.2. Numerical Results
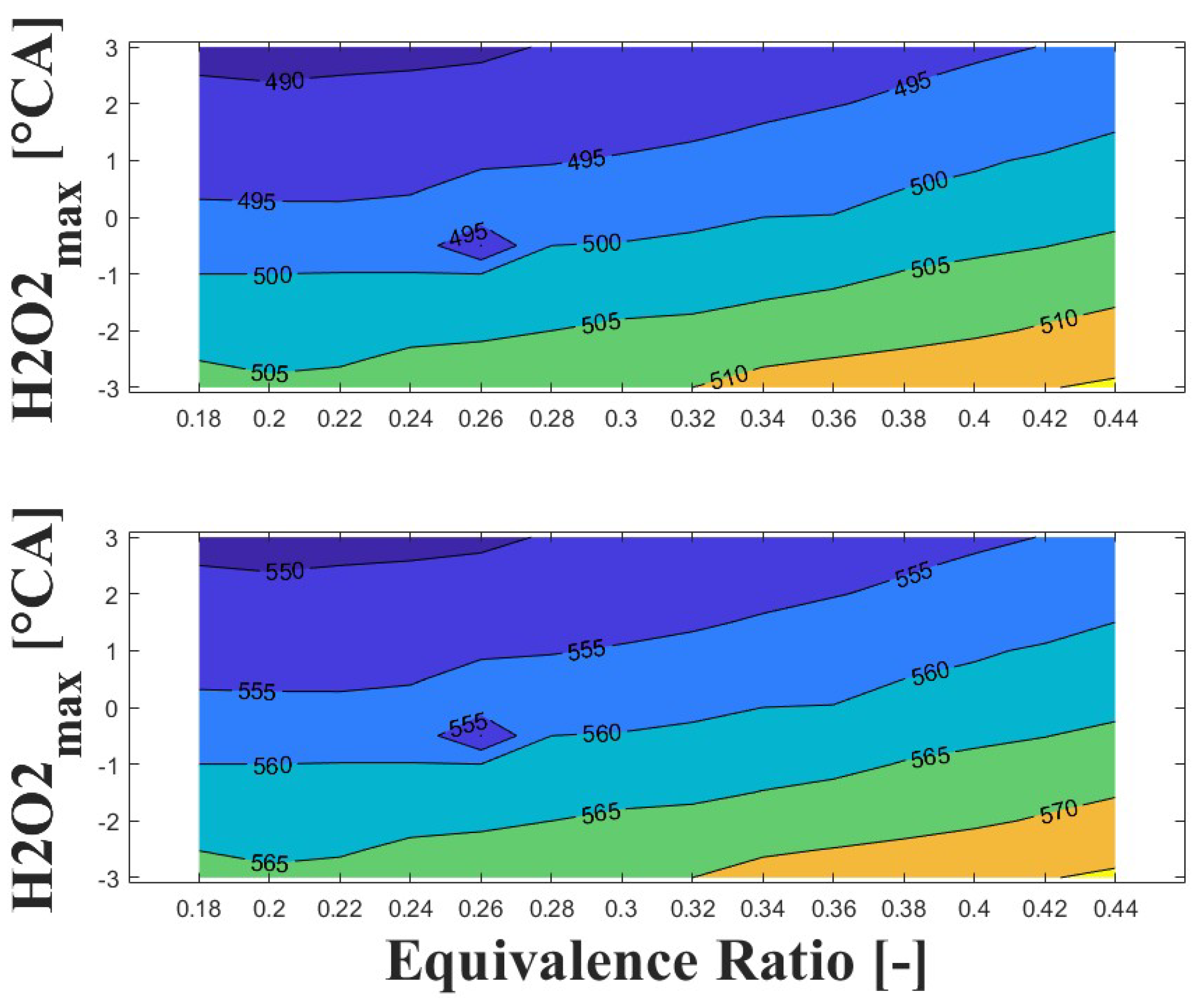
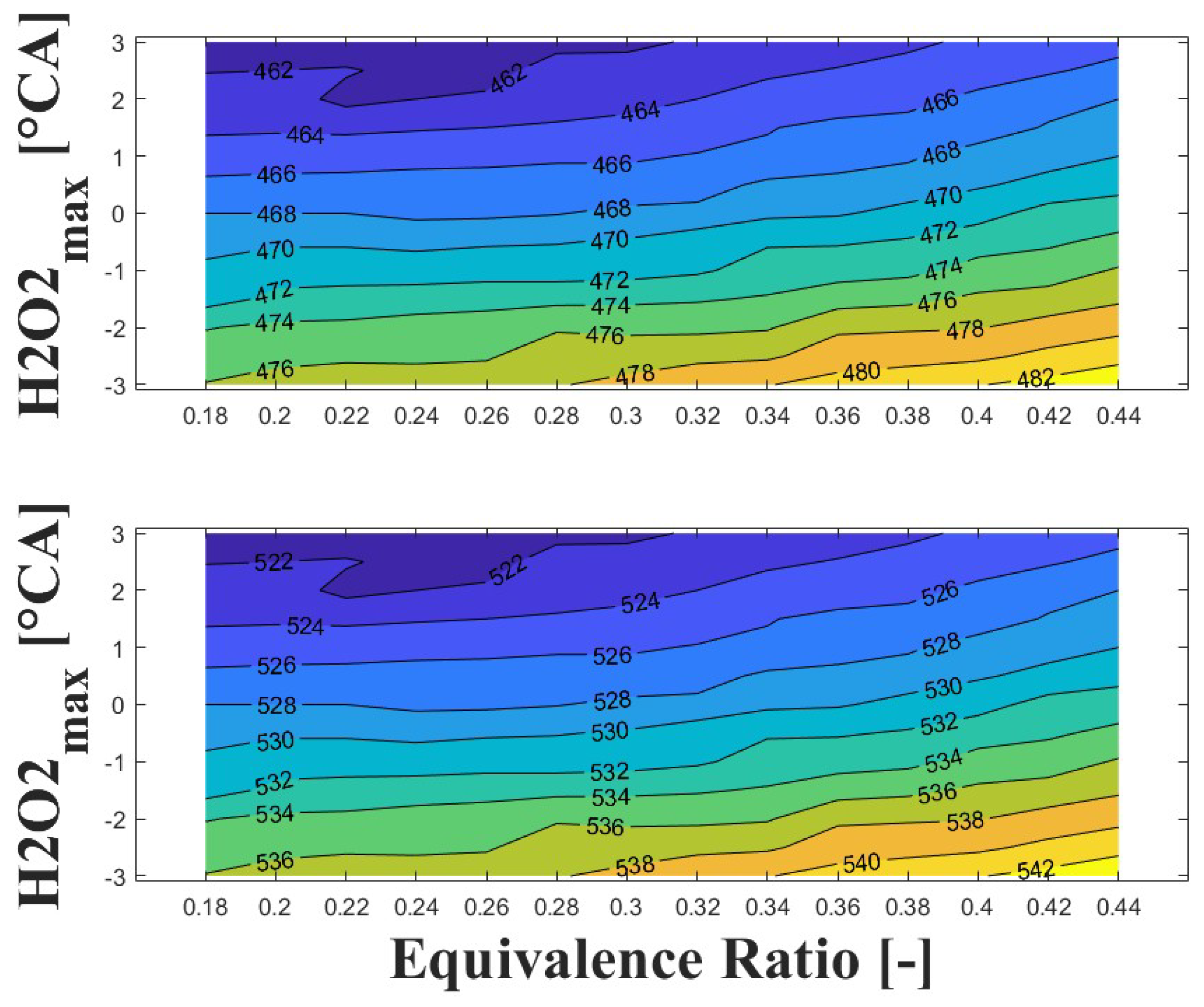
3.3. Effect of Boosted Intake Pressure on Intake Temperature
3.4. Effect of Ozone Addition on Intake Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| aTDC | After top dead centre |
| bcme | Billion cubic metres equivalent |
| bTDC | Before top dead centre |
| int | Intake |
| rpm | Revolutions per minute |
| AFR | Air fuel ratio |
| BTE | Brake Thermal Efficiency |
| CA10 | Crank angle of of cumulative heat release |
| CA50 | Crank angle of of cumulative heat release |
| CAD | Crank angle degree |
| CNG | Compressed natural gas |
| CO | Carbon monoxide |
| CO | Carbon dioxide |
| EVO | Exhaust valve opening |
| GHG | Greenhouse gases |
| H | Hydrogen |
| HC | unburned hydrocarbons |
| HCCI | Homogeneous Charge Compression Ignition |
| HRR | Heat release rate |
| ICE | Internal combustion engine |
| IMEP | Indicated Mean Effective Pressure |
| IMEPg | Gross indicated mean effective pressure |
| IMEPn | Net indicated mean effective pressure |
| IVC | Intake valve closure |
| LHV | Low heating value |
| NO | Nitrogen oxides |
| NVO | Negative valve overlap |
| PM | Particulate matter |
| PV | Photovoltaic |
| RGF | Residual gas fraction |
| TDC | Top dead center |
References
- IEA. World Energy Outlook 2022; IEA: Paris, France, 2022.
- Kapoor, R.; Ghosh, P.; Tyagi, B.; Vijay, V.K.; Vijay, V.; Thakur, I.S.; Kamyab, H.; Nguyen, D.D.; Kumar, A. Advances in biogas valorization and utilization systems: A comprehensive review. J. Clean. Prod. 2020, 273, 123052. [Google Scholar] [CrossRef]
- Sun, Q.; Li, H.; Yan, J.; Liu, L.; Yu, Z.; Yu, X. Selection of appropriate biogas upgrading technology-a review of biogas cleaning, upgrading and utilisation. Renew. Sustain. Energy Rev. 2015, 51, 521–532. [Google Scholar] [CrossRef]
- Paolini, V.; Petracchini, F.; Segreto, M.; Tomassetti, L.; Naja, N.; Cecinato, A. Environmental impact of biogas: A short review of current knowledge. J. Environ. Sci. Health Part A 2018, 53, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Dec, J.E. Advanced compression-ignition engines—Understanding the in-cylinder processes. Proc. Combust. Inst. 2009, 32, 2727–2742. [Google Scholar] [CrossRef]
- Blizman, B.J.; Makel, D.B.; Mack, J.H.; Dibble, R.W. Landfill gas fueled hcci demonstration system. In Proceedings of the Internal Combustion Engine Division Fall Technical Conference, Aachen, Germany, 7–10 May 2006; Volume 42606, pp. 327–347. [Google Scholar]
- Bedoya, I.D.; Saxena, S.; Cadavid, F.J.; Dibble, R.W.; Wissink, M. Experimental study of biogas combustion in an HCCI engine for power generation with high indicated efficiency and ultra-low NOx emissions. Energy Convers. Manag. 2012, 53, 154–162. [Google Scholar] [CrossRef]
- Bedoya, I.D.; Saxena, S.; Cadavid, F.J.; Dibble, R.W.; Wissink, M. Experimental evaluation of strategies to increase the operating range of a biogas-fueled HCCI engine for power generation. Appl. Energy 2012, 97, 618–629. [Google Scholar] [CrossRef]
- Kozarac, D.; Vuilleumier, D.; Saxena, S.; Dibble, R.W. Analysis of benefits of using internal exhaust gas recirculation in biogas-fueled HCCI engines. Energy Convers. Manag. 2014, 87, 1186–1194. [Google Scholar] [CrossRef]
- Depcik, C.; Mangus, M.; Ragone, C. Ozone-assisted combustion—Part I: Literature review and kinetic study using detailed n-heptane kinetic mechanism. J. Eng. Gas Turbines Power 2014, 136, 091507. [Google Scholar] [CrossRef]
- Nishida, H.; Tachibana, T. Homogeneous charge compression ignition of natural gas/air mixture with ozone addition. J. Propuls. Power 2006, 22, 151–157. [Google Scholar] [CrossRef]
- Kubesh, J.; King, S.R.; Liss, W.E. Effect of Gas Composition on Octane Number of Natural Gas Fuels; Technical Report; SAE Technical Paper; SAE: Warrendale, PA, USA, 1992. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Chang, J.; Güralp, O.; Filipi, Z.; Assanis, D.; Kuo, T.W.; Najt, P.; Rask, R. New heat transfer correlation for an HCCI engine derived from measurements of instantaneous surface heat flux. SAE Trans. 2004, 113, 1576–1593. [Google Scholar]
- Namazian, M.; Heywood, J.B. Flow in the piston-cylinder-ring crevices of a spark-ignition engine: Effect on hydrocarbon emissions, efficiency and power. SAE Trans. 1982, 91, 261–288. [Google Scholar]
- Ortiz-Soto, E.A.; Vavra, J.; Babajimopoulos, A. Assessment of residual mass estimation methods for cylinder pressure heat release analysis of HCCI engines with negative valve overlap. J. Eng. Gas Turbines Power 2012, 134, 082802. [Google Scholar] [CrossRef]
- Sjöberg, M.; Dec, J.E.; Babajimopoulos, A.; Assanis, D. Comparing enhanced natural thermal stratification against retarded combustion phasing for smoothing of HCCI heat-release rates. SAE Trans. 2004, 113, 1557–1575. [Google Scholar]
- Aceves, S.M.; Smith, J.R.; Westbrook, C.K.; Pitz, W. Compression ratio effect on methane HCCI combustion. J. Eng. Gas Turbines Power. 1999, 121, 569–574. [Google Scholar] [CrossRef]
- Bedoya, I.D.; Cadavid, F.; Saxena, S.; Dibble, R.; Aceves, S.; Flowers, D. A Sequential Chemical Kinetics-CFD-Chemical Kinetics Methodology to Predict HCCI Combustion and Main Emissions; Technical Report; SAE Technical Paper; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Bedoya, I.; Saxena, S.; Dibble, R.; Cadavid, F. Exploring Optimal Operating Conditions for Stationary Power Generation from a Biogas-Fueled HCCI Engine. In Proceedings of the 7th US National Technical Meeting of the Combustion Institute, Georgia Institute of Technology, Atlanta, GA, USA, 20–23 March 2011; pp. 2172–2177. [Google Scholar]
- Halter, F.; Higelin, P.; Dagaut, P. Experimental and detailed kinetic modeling study of the effect of ozone on the combustion of methane. Energy Fuels 2011, 25, 2909–2916. [Google Scholar] [CrossRef]
- Quintana, S.H.; Castano-Mesa, E.S.; Bedoya, I.D. Experimental Study of the Polytropic Coefficient for an Air-Cooled, High-Compression-Ratio, Spark-Ignition Engine Fueled with Natural Gas, Biogas, and a Propane–Syngas Blend. Energy Fuels 2018, 32, 2376–2384. [Google Scholar] [CrossRef]
- Zhao, F.; Asmus, T.N.; Assanis, D.N.; Dec, J.E.; Eng, J.A.; Najt, P.M. Homogeneous Charge Compression Ignition (HCCI) Engines; SAE: Warrendale, PA, USA, 2003. [Google Scholar]
- Saxena, S.; Bedoya, I.D. Fundamental phenomena affecting low temperature combustion and HCCI engines, high load limits and strategies for extending these limits. Prog. Energy Combust. Sci. 2013, 39, 457–488. [Google Scholar] [CrossRef]
- Duan, X.; Lai, M.C.; Jansons, M.; Guo, G.; Liu, J. A review of controlling strategies of the ignition timing and combustion phase in homogeneous charge compression ignition (HCCI) engine. Fuel 2021, 285, 119142. [Google Scholar] [CrossRef]
| Designation | Lombardini 25LD425/2 Direct-Injection Four Stroke Two-Cylinder Air-Cooled Diesel Engine |
|---|---|
| Charge aspiration | Naturally aspirated |
| Displacement | 851 |
| Original compression ratio | 19:1 |
| Modified compression ratio | 17.4:1 |
| Bore × stroke (mm) | 85 × 75 |
| Connecting rod length (mm) | |
| Valves (intake, exhaust) | 1, 1 |
| Intake Valve Open, IVO (CAD ATDC) | 350 |
| Intake Valve Close, IVC (CAD ATDC) | |
| Exhaust Valve Open, EVO (CAD ATDC) | 95 |
| Exhaust Valve Close, EVC (CAD ATDC) | |
| Original rated power | 14 kW @ 3600 rpm |
| Original maximum torque | Nm @ 2400 rpm |
| Original combustion chamber | Bowl |
| Modified combustion chamber | Flat head |
| Property | Natural Gas | Biogas |
|---|---|---|
| Low heating value (MJ/kg) | ||
| Simplified chemical composition | CHON | - |
| Stoichiometric air fuel ratio (AFR) | ||
| Lower Woobe index (kWh/Nm) | ||
| Methane number [12] | - |
| Measurement | Accuracy | Uncertainty |
|---|---|---|
| Fuel flow rate (mg/s) | ||
| Air flow rate (g/s) | ||
| Temperature (C) | ||
| Intake manifold pressure (bar) | ||
| In-cylinder pressure (bar) | ||
| Crank angle position | ||
| Engine speed (rpm) |
| Factor | Level Description | Level Designation |
|---|---|---|
| Intake temperature | 1 | 325 C |
| 2 | 330 C | |
| Equivalence ratio | 1 | |
| 2 | ||
| Engine speed | 1 | 1800 rpm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintana, S.H.; Morales Rojas, A.D.; Bedoya, I.D. Experimental and Numerical Evaluation of an HCCI Engine Fueled with Biogas for Power Generation under Sub-Atmospheric Conditions. Energies 2023, 16, 6267. https://doi.org/10.3390/en16176267
Quintana SH, Morales Rojas AD, Bedoya ID. Experimental and Numerical Evaluation of an HCCI Engine Fueled with Biogas for Power Generation under Sub-Atmospheric Conditions. Energies. 2023; 16(17):6267. https://doi.org/10.3390/en16176267
Chicago/Turabian StyleQuintana, Sebastián H., Andrés D. Morales Rojas, and Iván D. Bedoya. 2023. "Experimental and Numerical Evaluation of an HCCI Engine Fueled with Biogas for Power Generation under Sub-Atmospheric Conditions" Energies 16, no. 17: 6267. https://doi.org/10.3390/en16176267
APA StyleQuintana, S. H., Morales Rojas, A. D., & Bedoya, I. D. (2023). Experimental and Numerical Evaluation of an HCCI Engine Fueled with Biogas for Power Generation under Sub-Atmospheric Conditions. Energies, 16(17), 6267. https://doi.org/10.3390/en16176267





