The Blasting Vibration Characteristics of Layered Rock Mass under High-Pressure Gas Impact
Abstract
:1. Introduction
2. Experimental Study on Blasting Vibration of Layered Rock Mass under High-Pressure Gas Impact
2.1. Experimental Test of Blasting Vibration of Layered Rock Mass
2.2. Experimental Test Results and Analysis
- (1)
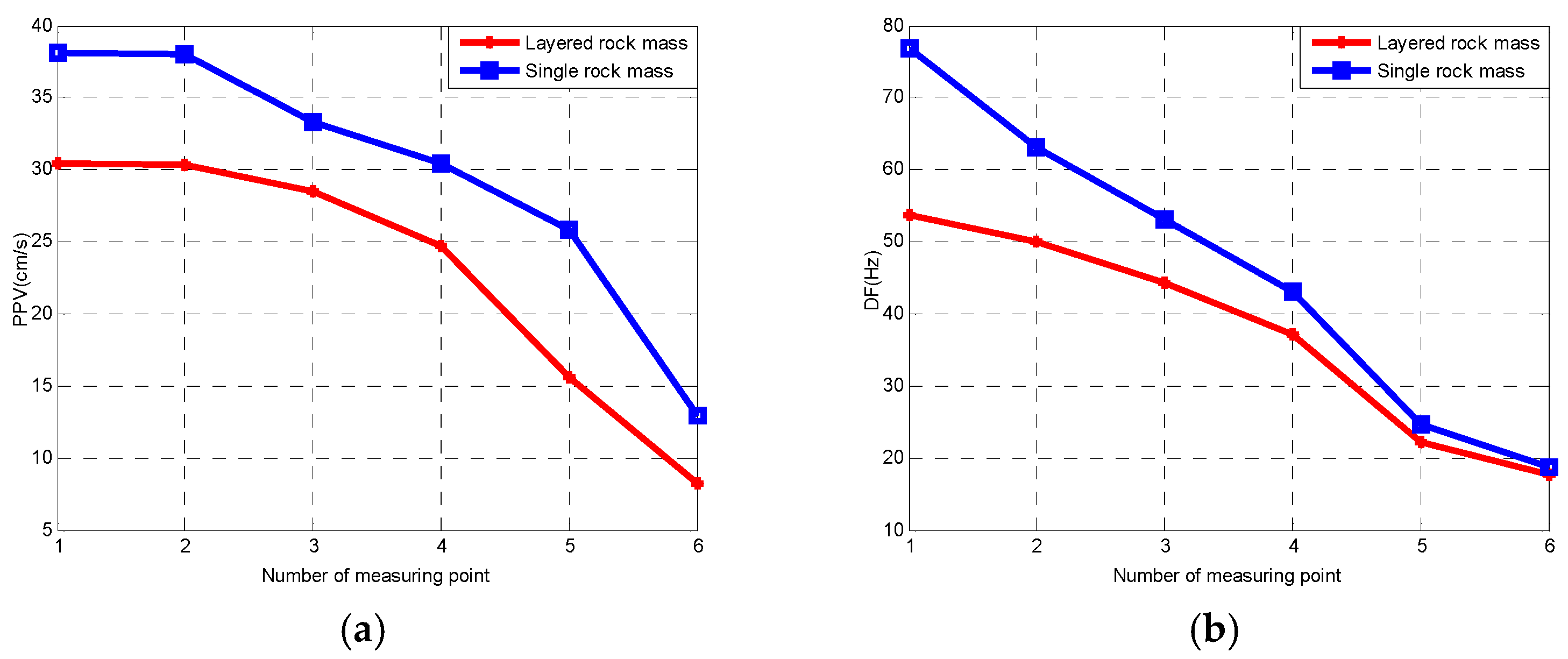
- Under high-pressure gas impact, the PPV and DF of blasting vibration of layered and single rock masses decrease gradually with the increase in distance from the explosion source. From measuring point CZ1 to measuring point CZ6, the PPV of blasting vibration decreases from 30.45 cm/s to 8.24 cm/s, and the DF of blasting vibration decreases from 53.69 Hz to 17.60 Hz. This is because the impact energy from the high-pressure gas is continuously consumed during the propagation process in the medium, ultimately leading to a continuous decrease in the PPV and DF of blasting vibration.
- (2)
- Under the same impact pressure of high-pressure gas, the PPV of blasting vibration of layered rock mass is lower than that of single rock mass at each measuring point, which is mainly due to the vibration-amplitude reduction effect of layered rock mass at the interface of soft and hard rock.
- (3)
- Under the same impact pressure of high-pressure gas, the DF of blasting vibration of layered rock mass is lower than that of single rock mass at each measuring point, which is mainly due to the vibration-frequency reduction effect of layered rock mass at the interface of soft and hard rock.
- (4)
- Whether the layered rock sample or the single rock sample, there is little difference between the PPV of blasting vibration at the measuring point C(D)Z1 and measuring point C(D)Z2, which is mainly due to the equal distance between the two measuring points and the bottom of the blast hole.
3. Blasting Vibration Models of Layered Rock Mass by Dimensional Analysis Method
3.1. PPV Model of Blasting Vibration by Dimensional Analysis Method
- (1)
- Define the scaled distance: ; then the PPV of blasting vibration is inversely proportional to the scaled distance. If the blast hole radius (r) remains unchanged, the PPV of blasting vibration is inversely proportional to the distance from the explosion source (R). That is, the farther the measuring point is from the explosion source, the smaller the PPV of blasting vibration;
- (2)
- The PPV of blasting vibration is directly proportional to the initial pressure of high-pressure gas (P) and inversely proportional to the product ()of the wave impedance () and P-wave velocity of soft rock () and that of hard rock ();
- (3)
- The PPV of blasting vibration is linearly proportional to the P-wave velocity of soft rock () and nonlinearly exponential to the P-wave velocity ratio of hard and soft rock ();
- (4)
- When the explosion source factors, including the initial pressure of high-pressure gas (P) and the blast hole radius (r), and the rock mass factors, including the density of soft rock (), P-wave velocity of soft rock (), density of hard rock () and P-wave velocity of hard rock (), remain unchanged, Equation (7) can be further simplified into the following formula:
3.2. DF Model of Blasting Vibration by Dimensional Analysis Method
- (1)
- The DF of blasting vibration is inversely proportional to the scaled distance. If the blast hole radius (r) remains unchanged, the DF of blasting vibration is inversely proportional to the distance from the explosion source (R); that is, the farther the measuring point is from the explosion source, the smaller the DF of blasting vibration;
- (2)
- The DF of blasting vibration is directly proportional to the initial pressure of high-pressure gas (P) and inversely proportional to the product of the wave impedance and P-wave velocity of soft rock () and that of hard rock ();
- (3)
- The DF of blasting vibration is inversely linearly proportional to the blast hole radius (r), directly linearly proportional to the P-wave velocity of soft rock () and nonlinearly exponential to the P-wave velocity ratio of hard and soft rock ();
- (4)
- When the explosion source factors, including the initial pressure of high-pressure gas (P) and the blast hole radius (r), and the rock mass factors, including the density of soft rock (), P-wave velocity of soft rock (), density of hard rock () and P-wave velocity of hard rock (), remain unchanged, Equation (14) can be further simplified into the following formula:
4. Numerical Simulation Study on the Blasting Vibration of Layered Rock Mass under High-Pressure Gas Impact
4.1. Feasibility Analysis on Numerical Simulation Test of Blasting Vibration of Layered Rock Mass
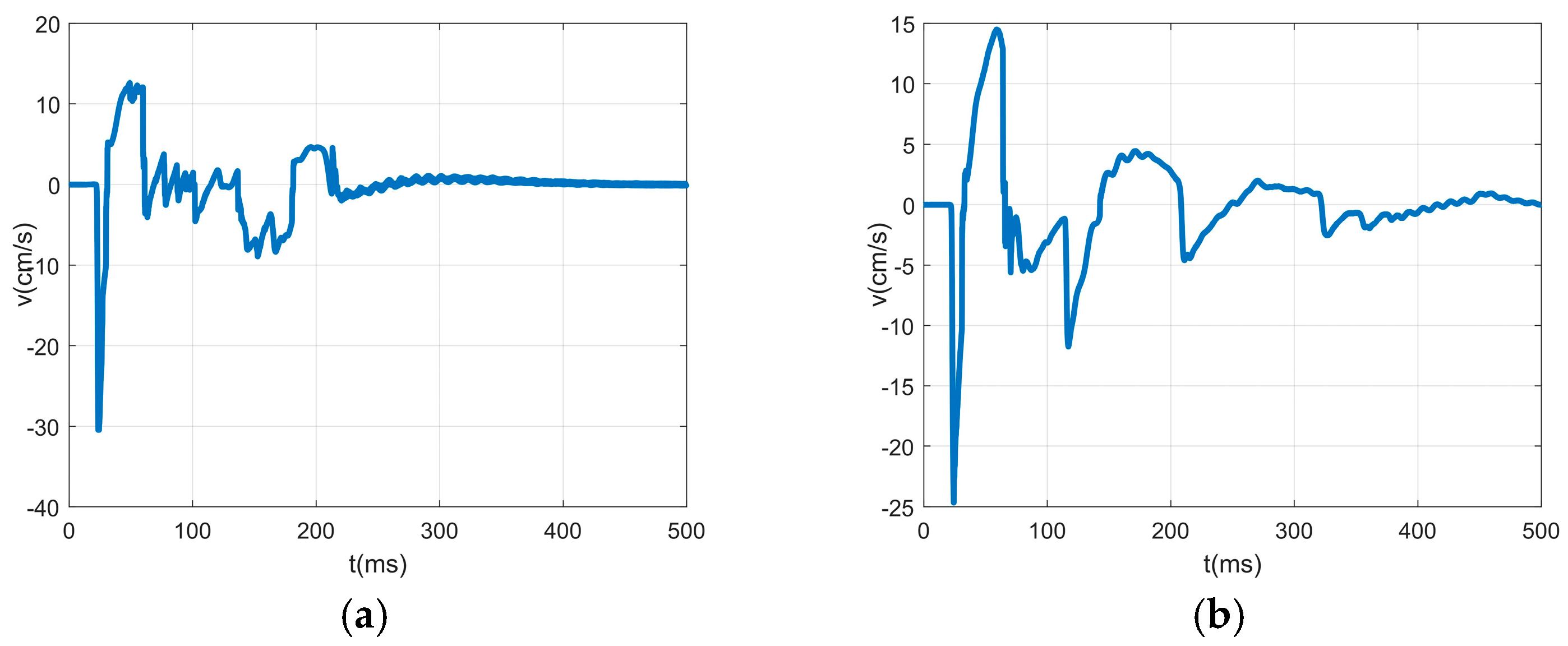
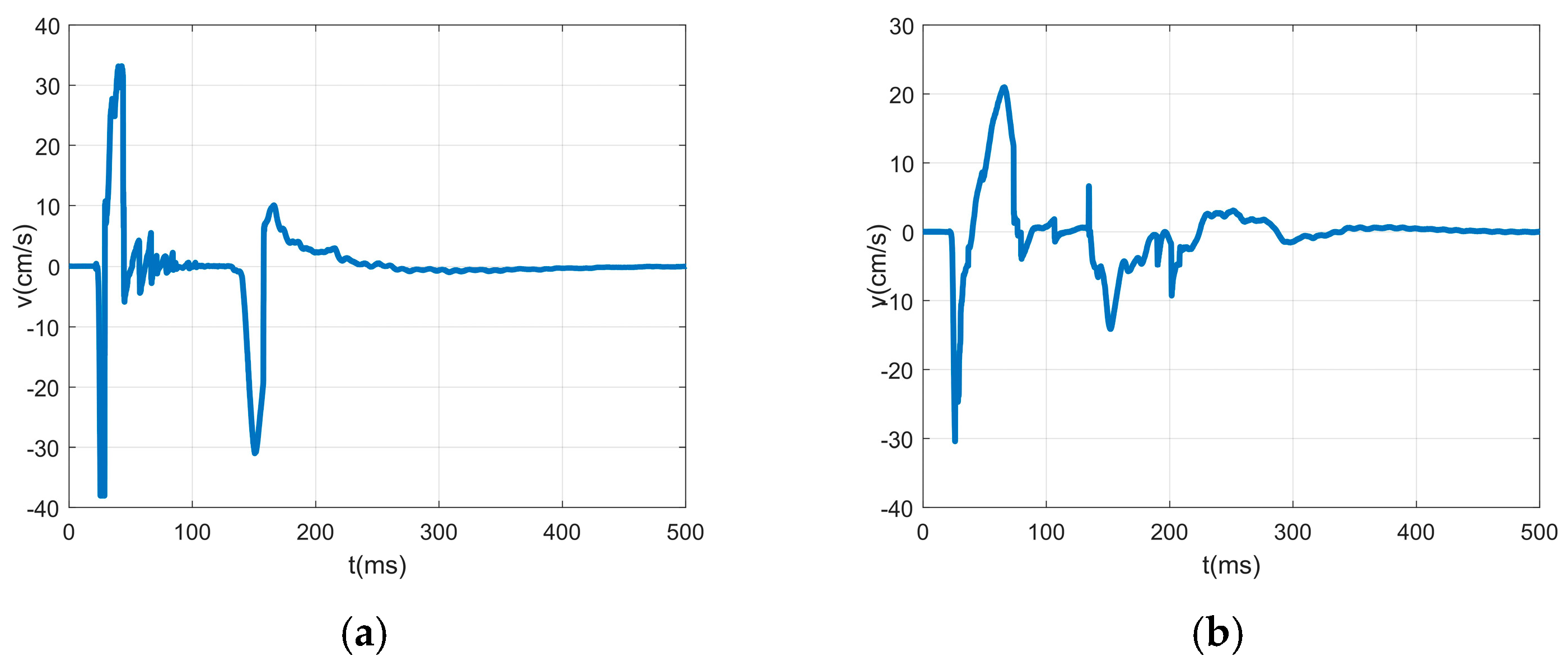
4.2. Analysis of the Blasting Vibration Characteristics of Layered Rock Mass
4.3. Influence of Hole Spacing on Characteristics of Blasting Vibration
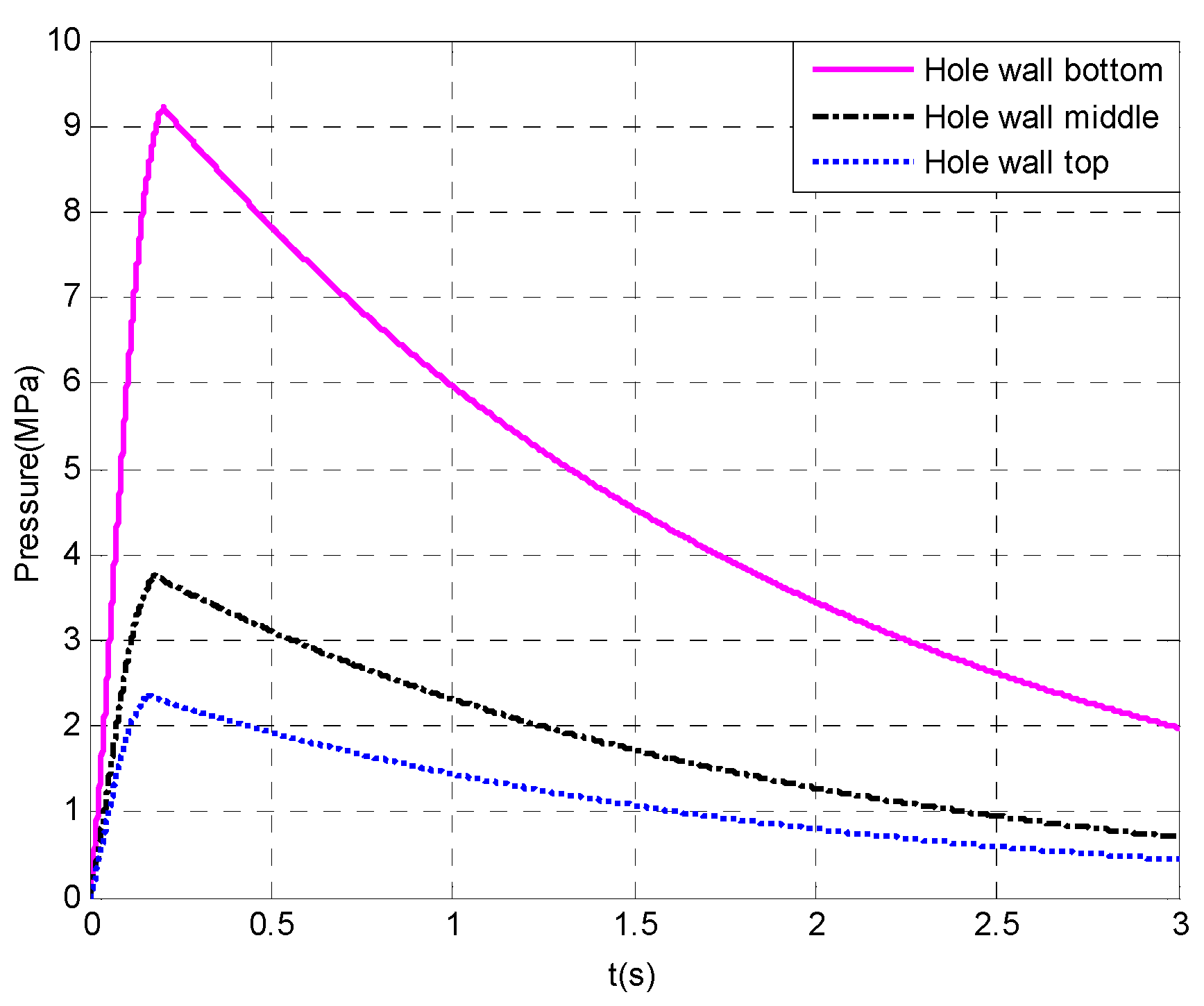
5. Comparison of Blasting Vibration Effects under High-Pressure Gas Impact and Explosive Blasting
6. Conclusions
- (1)
- Under high-pressure gas impact, the PPV and DF of blasting vibration of layered rock mass decrease gradually with the increase in distance from the explosion source;
- (2)
- Under the same impact pressure of high-pressure gas, the PPV and DF of blasting vibration of layered rock mass are lower than those of single rock mass at the same measuring points due to the amplitude reduction and high-frequency filtering at the interface of soft and hard rock of layered rock mass. This can provide ideas for further research and utilization of the reducing effect of rock joints with different quantities and parameters on the amplitude and frequency of blasting vibration;
- (3)
- The relationship models between the PPV and DF of blasting vibration of layered rock mass under high-pressure gas blasting and their influencing factors were deduced by the dimensional analysis method. And the feasibility of the two proposed models was verified by the results of the experimental and numerical simulation tests;
- (4)
- With the increase in hole spacing, the blasting effect first becomes better and then worse, and the PPV and DF of blasting vibration become smaller. Considering the allowable standard of blasting vibration and blasting effect at the same time, the optimal hole spacing recommended in the engineering example in this paper is 100 cm;
- (5)
- Due to the lower peak pressure and longer duration of the hole wall pressure caused by high-pressure gas impact, high-pressure gas impact causes smaller PPV and larger DF compared with explosive blasting. Therefore, compared with explosive blasting, high-pressure gas impact can significantly reduce the blasting vibration effect of layered rock mass under the premise of the same cutting blasting effect;
- (6)
- Due to the limited experimental conditions, urgent time and other factors, this paper has some shortcomings that need to be further studied. Only the small-scale model test of horizontal layered rock mass with upper soft rock and lower hard rock under single-hole high-pressure gas impact is carried out in this paper. This will result in certain errors between the experimental results and the actual results, which, to some extent, affects the generalizability of the conclusions drawn based on the experimental results. More large-scale model tests of layered rock mass with different mix-proportion materials, different layered dip angles and more layers need to be further carried out to obtain experimental results that are closer to the actual results in engineering. The PPV and DF models of blasting vibration deduced by the dimensional analysis method, which contains more influencing factors, need to be further verified and applied. Numerical simulation tests of blasting vibration of layered rock mass under high-pressure gas blasting with multi-hole and millisecond conditions need to be carried out to obtain more and better blasting parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khandelwal, M.; Monjezi, M. Prediction of flyrock in open pit blasting operation using machine learning method. Int. J. Min. Sci. Technol. 2013, 23, 313–316. [Google Scholar] [CrossRef]
- Wei, H.X.; Chen, J.F.; Zhu, J.; Yang, X.L.; Chu, H.B. A novel algorithm of Nested-ELM for predicting blasting vibration. Eng. Comput. 2022, 38, 1241–1256. [Google Scholar] [CrossRef]
- Cardu, M.; Coragliotto, D.; Oreste, P. Analysis of predictor equations for determining the blast-induced vibration in rock blasting. Int. J. Min. Sci. Technol. 2019, 29, 905–915. [Google Scholar] [CrossRef]
- Xu, S.D.; Li, Y.H.; Liu, J.P.; Zhang, F.P. Optimization of blasting parameters for an underground mine through prediction of blasting vibration. J. Vib. Control 2019, 25, 1585–1595. [Google Scholar] [CrossRef]
- Mohamed, M.T. Performance of fuzzy logic and artificial neural network in prediction of ground and air vibrations. Int. J. Rock Mech. Min. Sci. 2011, 48, 845–851. [Google Scholar] [CrossRef]
- Ghasemi, E.; Ataei, M.; Hashemolhosseini, H. Development of a fuzzy model for predicting ground vibration caused by rock blasting in surface mining. J. Vib. Control 2012, 19, 755–770. [Google Scholar] [CrossRef]
- Monjezi, M.; Hasanipanah, M.; Khandelwal, M. Evaluation and prediction of blast-induced ground vibration at Shur River Dam, Iran, by artificial neural network. Neural Comput. Appl. 2013, 22, 1637–1643. [Google Scholar] [CrossRef]
- Amiri, M.; Amnieh, H.B.; Hasanipanah, M.; Khanli, L.M. A new combination of artificial neural network and K-nearest neighbors models to predict blast-induced ground vibration and air-overpressure. Eng. Comput. 2016, 32, 631–644. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Hasanipanah, M.; Amnieh, H.B.; Mohamad, E.T. Feasibility of ICA in approximating ground vibration resulting from mine blasting. Neural Comput. Appl. 2018, 29, 457–465. [Google Scholar] [CrossRef]
- Chen, S.H.; Wu, J.; Zhang, Z.H. Blasting vibration characteristics and PPV calculation formula considering cylindrical charge length. Environ. Earth Sci. 2017, 76, 674. [Google Scholar] [CrossRef]
- Zhao, K.; Zhao, D.F.; Zhang, D.; Zhuang, H.Y.; Chen, G.X. Characteristics of environmental vibration induced by millisecond-delay blasting in metro tunnel excavation. Explos. Shock Waves 2020, 40, 105201. [Google Scholar] [CrossRef]
- Gorgulu, K.; Arpaz, E.; Uysal, O.; Duruturk, Y.S.; Yuksek, A.G.; Kocaslan, A.; Dilmac, M.K. Investigation of the effects of blasting design parameters and rock properties on blast-induced ground vibrations. Arab. J. Geosci. 2015, 8, 4269–4278. [Google Scholar] [CrossRef]
- Uysal, O.; Arpaz, E.; Berber, M. Studies on the effect of burden width on blast-induced vibration in open-pit mines. Environ. Geol. 2007, 53, 643–650. [Google Scholar] [CrossRef]
- You, Y.Y.; Cui, Z.R.; Li, E.B. Numerical simulation on variation characteristics of blasting vibration particle peak velocity under high in-situ stress. Blasting 2020, 37, 36–42. [Google Scholar] [CrossRef]
- Zhu, J.B.; Zhao, R.; Li, Y.S.; Ma, Y.K.; Wang, J.X.; Peng, Q.; Guo, J. Experimental study of vibration reduction effect of barrier holes under blasting. Rock Mech. Rock Eng. 2023, 56, 1185–1198. [Google Scholar] [CrossRef]
- Zhou, J.R.; Lu, W.B.; Zhong, D.W.; Wu, L.; Leng, Z.D.; Yang, W.G. Attenuation characteristics of vibration frequency induced by vertical borehole blasting. Blasting 2019, 36, 14–20. [Google Scholar] [CrossRef]
- Alvarez-Vigil, A.E.; Gonzalez-Nicieza, C.; Lopez Gayarre, F.; Alvarez-Fernandez, M.I. Predicting blasting propagation velocity and vibration frequency using artificial neural networks. Int. J. Rock Mech. Min. Sci. 2012, 55, 108–116. [Google Scholar] [CrossRef]
- Shi, X.Z.; Chen, S.R. Explosive blasted per delay and burden effects on the time frequency characteristic of vibration induced by blast. J. China Coal Soc. 2009, 34, 345–349. [Google Scholar] [CrossRef]
- Zhao, M.S.; Liang, K.S.; Yu, D.Y.; Ren, S.F. Effect of segments on time frequency characteristics of blasting vibration signals. J. China Coal Soc. 2012, 37, 55–61. [Google Scholar] [CrossRef]
- Trivino, L.F.; Mohanty, B.; Milkereit, B. Seismic waveforms from explosive sources located in boreholes and initiated in different directions. J. Appl. Geophys. 2012, 87, 81–93. [Google Scholar] [CrossRef]
- Yang, J.H.; Lu, W.B.; Yan, P.; Jiang, Q.H.; Zhou, C.B. Influences of blast-created free surfaces on blasting vibration frequencies during full-face excavation. J. Vib. Shock 2016, 35, 192–197. [Google Scholar] [CrossRef]
- Sun, P.C.; Lu, W.B.; Zhou, J.R.; Huang, X.C.; Chen, M.; Li, Q. Comparison of dominant frequency attenuation of blasting vibration for different charge structures. J. Rock Mech. Geotech. Eng. 2022, 14, 448–459. [Google Scholar] [CrossRef]
- Chen, S.; Pang, H. Prediction and Control of Blasting Disasters; China Coal Industry Publishing House: Beijing, China, 2006. [Google Scholar]
- Yuan, Z.S.; Xu, Z.Y.; Pan, B.; Li, G.S. Discrete element simulation of blasting damage characteristics of granite under different decoupling coefficients. Chin. J. High Press. Phys. 2022, 36, 015301. [Google Scholar]
- Tan, Q. Dimensional Analysis; Press of University of Science and Technology of China: Hefei, China, 2005. [Google Scholar]
- Li, H.C.; Chen, Y.; Liu, D.S.; Huang, Y.H.; Zhao, L. Sensitivity analysis determination and optimization of rock RHT parameter. Trans. Beijing Inst. Technol. 2018, 38, 779–785. [Google Scholar] [CrossRef]
- Liu, X.L.; Li, Y.; Wang, X.Y.; Gurkalo, F. Anti-explosion performance of different anti-explosion structures under gas explosion in pipe gallery. Chin. J. High Press. Phys. 2019, 33, 195–204. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, C.B.; Lu, S.W.; Cai, J.Y.; Wang, C. Numerical simulation on cylindrical charged explosives with different initiation. Blasting 2016, 33, 74–77, 91. [Google Scholar] [CrossRef]









| Rock Type | Density (g/cm3) | Elasticity Modulus (GPa) | Poisson’s Ratio | S-Wave Velocity (km/s) | P-Wave Velocity (km/s) | Compressive Strength (MPa) | Tensile Strength (MPa) | Cohesive Strength (MPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|---|---|---|
| Soft rock | 1.91 | 5.69 | 0.16 | 3.17 | 3.39 | 15.93 | 1.56 | 4.66 | 34.22 |
| Hard rock | 2.01 | 9.54 | 0.21 | 3.28 | 3.82 | 23.07 | 2.15 | 4.02 | 41.67 |
| Rock Type | C(D)Z1 | C(D)Z2 | C(D)Z3 | C(D)Z4 | C(D)Z5 | C(D)Z6 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PPV (cm/s) | DF (Hz) | PPV (cm/s) | DF (Hz) | PPV (cm/s) | DF (Hz) | PPV (cm/s) | DF (Hz) | PPV (cm/s) | DF (Hz) | PPV (cm/s) | DF (Hz) | |
| Layered rock mass | 30.45 | 53.69 | 30.37 | 50.02 | 28.46 | 44.19 | 24.66 | 37.03 | 15.61 | 22.10 | 8.24 | 17.60 |
| Single rock mass | 38.06 | 76.92 | 37.96 | 63.19 | 33.32 | 53.00 | 30.41 | 43.12 | 25.87 | 24.62 | 12.94 | 18.60 |
| Variable Type | Parameter | Symbol | Unit | Dimension |
|---|---|---|---|---|
| Dependent variable | PPV | Vmax | m/s | [L·T−1] |
| DF | f | s−1 | [T−1] | |
| Independent variable | Initial impact pressure of high-pressure gas | P | kg/m/s2 (Pa) | [M·L−1·T−2] |
| Distance from explosion source | R | m | [L] | |
| Blast hole radius | r | m | [L] | |
| Density of soft rock | kg/m3 | [M·L−3] | ||
| P-wave velocity of soft rock | Cp1 | m/s | [L·T−1] | |
| Density of hard rock | kg/m3 | [M·L−3] | ||
| P-wave velocity of hard rock | Cp2 | m/s | [L·T−1] |
| ro | shear | onempa | epsf | b0 | b1 | t1 | |
| 1.91 | 0.033002 | −6 | 2 | 1.12 | 1.12 | 0.219499 | |
| a | n | fc | fs* | ft* | q0 | b | t2 |
| 1.6 | 0.61 | 0.0001593 | 0.05273 | 0.097928 | 0.6805 | 0.0105 | 0 |
| e0c | e0t | ec | et | betac | betat | ptf | |
| 3.00 × 10−12 | 3.00 × 10−13 | 3.00 × 1018 | 3.00 × 1018 | 0.199995 | 0.0999992 | 0.001 | |
| gc* | gt* | xi | d1 | d2 | epm | af | nf |
| 0.53 | 0.7 | 0.5 | 0.04 | 1 | 0.01 | 1.6 | 0.61 |
| gamma | a1 | a2 | a3 | pel | pco | np | alpha |
| 0 | 0.219499 | 0.245839 | 0.02871 | 0.0000531 | 0.6 | 3 | 1.1 |
| ro | shear | onempa | epsf | b0 | b1 | t1 | |
| 2.009 | 0.0577 | −6 | 2 | 1.12 | 1.12 | 0.2931613 | |
| a | n | fc | fs* | ft* | q0 | b | t2 |
| 1.6 | 0.61 | 0.0002307 | 0.17035 | 0.0931946 | 0.6805 | 0.0105 | 0 |
| e0c | e0t | ec | et | betac | betat | ptf | |
| 3.00 × 10−12 | 3.00 × 10−13 | 3.00 × 1018 | 3.00 × 1018 | 0.199993 | 0.0999988 | 0.001 | |
| gc* | gt* | xi | d1 | d2 | epm | af | nf |
| 0.53 | 0.7 | 0.5 | 0.04 | 1 | 0.01 | 1.6 | 0.61 |
| gamma | a1 | a2 | a3 | pel | pco | np | alpha |
| 0 | 0.29316 | 0.32834 | 0.038345 | 0.0000769 | 0.6 | 3 | 1.1 |
| Material | ρ (kg/m3) | C0 | C1 | C2 | C3 | C4 | C5 | C6 | V0 | E0 (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| Air | 1.293 | 0 | 0 | 0 | 0 | 0.4 | 0.4 | 0 | 1 | 0.25 |
| Blasting Vibration | Number of Measuring Points | ||||||
|---|---|---|---|---|---|---|---|
| (M)CZ1 | (M)CZ2 | (M)CZ3 | (M)CZ4 | (M)CZ5 | (M)CZ6 | ||
| PPV | Experimental values/(cm/s) | 30.45 | 30.37 | 28.46 | 24.66 | 15.61 | 8.24 |
| Simulation values/(cm/s) | 41.11 | 40.39 | 36.71 | 30.09 | 18.42 | 9.15 | |
| Relative error | 35% | 33% | 29% | 22% | 18% | 11% | |
| DF | Experimental values/(Hz) | 53.69 | 50.02 | 44.19 | 37.03 | 22.10 | 17.60 |
| Simulation values/(Hz) | 79.46 | 70.53 | 60.54 | 48.88 | 27.40 | 20.24 | |
| Relative error | 48% | 41% | 37% | 32% | 24% | 15% | |
| Rock Type | Density (kg/m3) | Cohesive Strength (kPa) | Internal Friction Angle (°) | Elasticity Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| Completely weathered granite | 1900 | 20 | 25 | 0.02 | 0.24 |
| Sandy strongly weathered granite | 2000 | 30 | 32 | 54 | 0.21 |
| Number of Measuring Points | Distance from Explosion Source (m) | Scaled Distance | Blasting Vibration | |
|---|---|---|---|---|
| PPV (cm/s) | DF (Hz) | |||
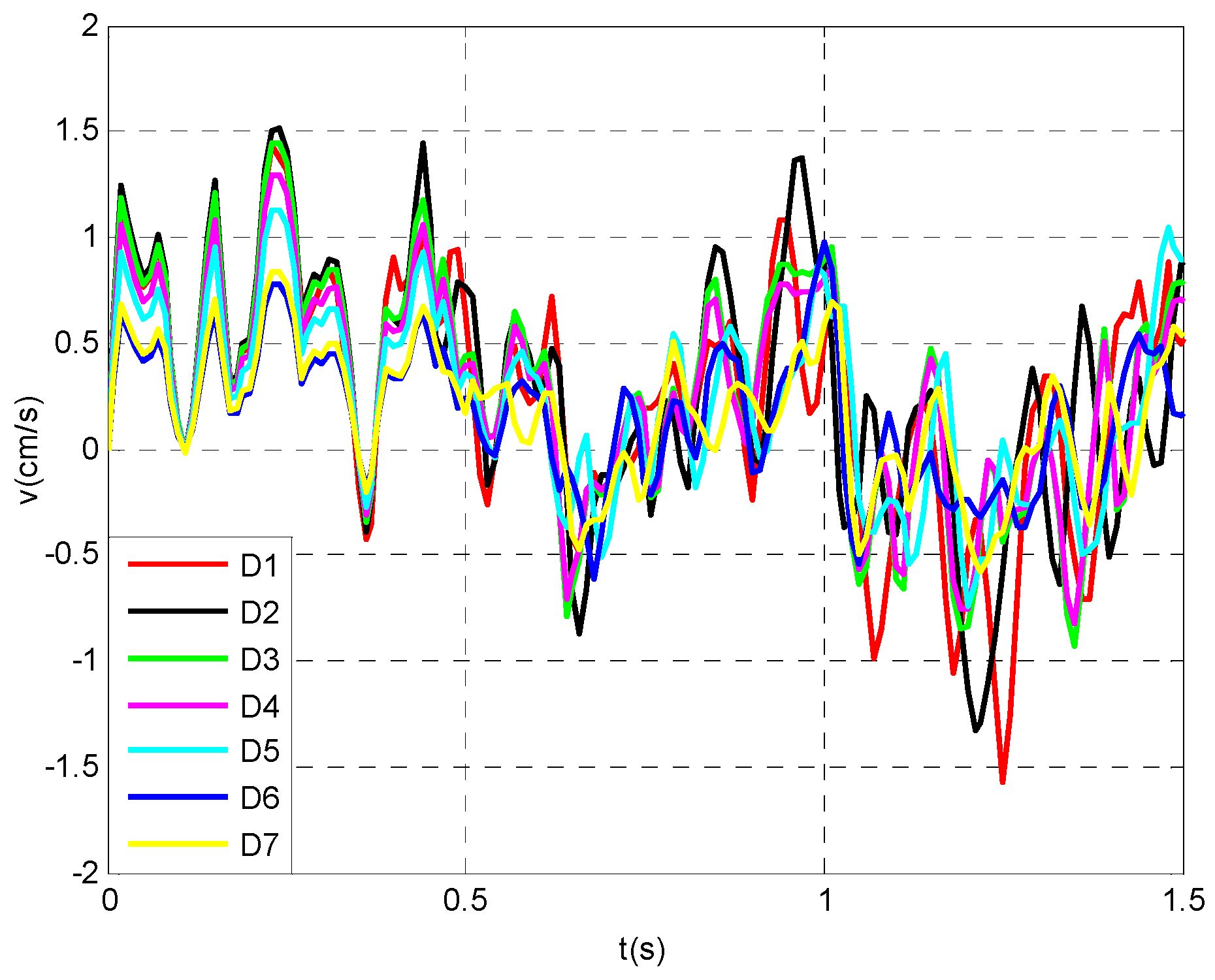
| D1 | 7.02 | 127.63 | 1.57 | 125.3 |
| D2 | 7.16 | 130.18 | 1.45 | 124.4 |
| D3 | 7.43 | 135.09 | 1.40 | 123.1 |
| D4 | 7.83 | 142.36 | 1.29 | 121.8 |
| D5 | 8.32 | 151.27 | 1.13 | 120.1 |
| D6 | 8.90 | 161.82 | 0.98 | 116.3 |
| D7 | 9.55 | 173.64 | 0.84 | 112.9 |
| Number of Measuring Point | D1 | D2 | D3 | D4 | D5 | D6 | D7 | |
|---|---|---|---|---|---|---|---|---|
| Hole spacing | 60 cm | 1.57 | 1.45 | 1.40 | 1.29 | 1.13 | 0.98 | 0.84 |
| 80 cm | 1.00 | 0.96 | 0.93 | 0.84 | 0.71 | 0.62 | 0.54 | |
| 100 cm | 0.58 | 0.55 | 0.51 | 0.46 | 0.40 | 0.35 | 0.30 | |
| 120 cm | 0.19 | 0.18 | 0.17 | 0.14 | 0.13 | 0.10 | 0.09 | |
| Number of Measuring Point | D1 | D2 | D3 | D4 | D5 | D6 | D7 | |
|---|---|---|---|---|---|---|---|---|
| Hole spacing | 60 cm | 125.3 | 124.4 | 123.1 | 121.8 | 120.1 | 116.3 | 112.9 |
| 80 cm | 119.3 | 118.5 | 117.3 | 113.9 | 111.9 | 108.5 | 106.2 | |
| 100 cm | 108.7 | 107.8 | 105.9 | 104.1 | 101.0 | 98.4 | 94.6 | |
| 120 cm | 99.8 | 98.7 | 96.9 | 93.8 | 91.7 | 89.5 | 86.0 | |
| ρ (kg/m3) | D (m/s) | PCJ GPa | A GPa | B GPa | R1 | R2 | ω | E0 GPa |
|---|---|---|---|---|---|---|---|---|
| 1000 | 3200 | 4.36 | 0.182 | 1.01 | 4.2 | 0.9 | 0.15 | 4.192 |
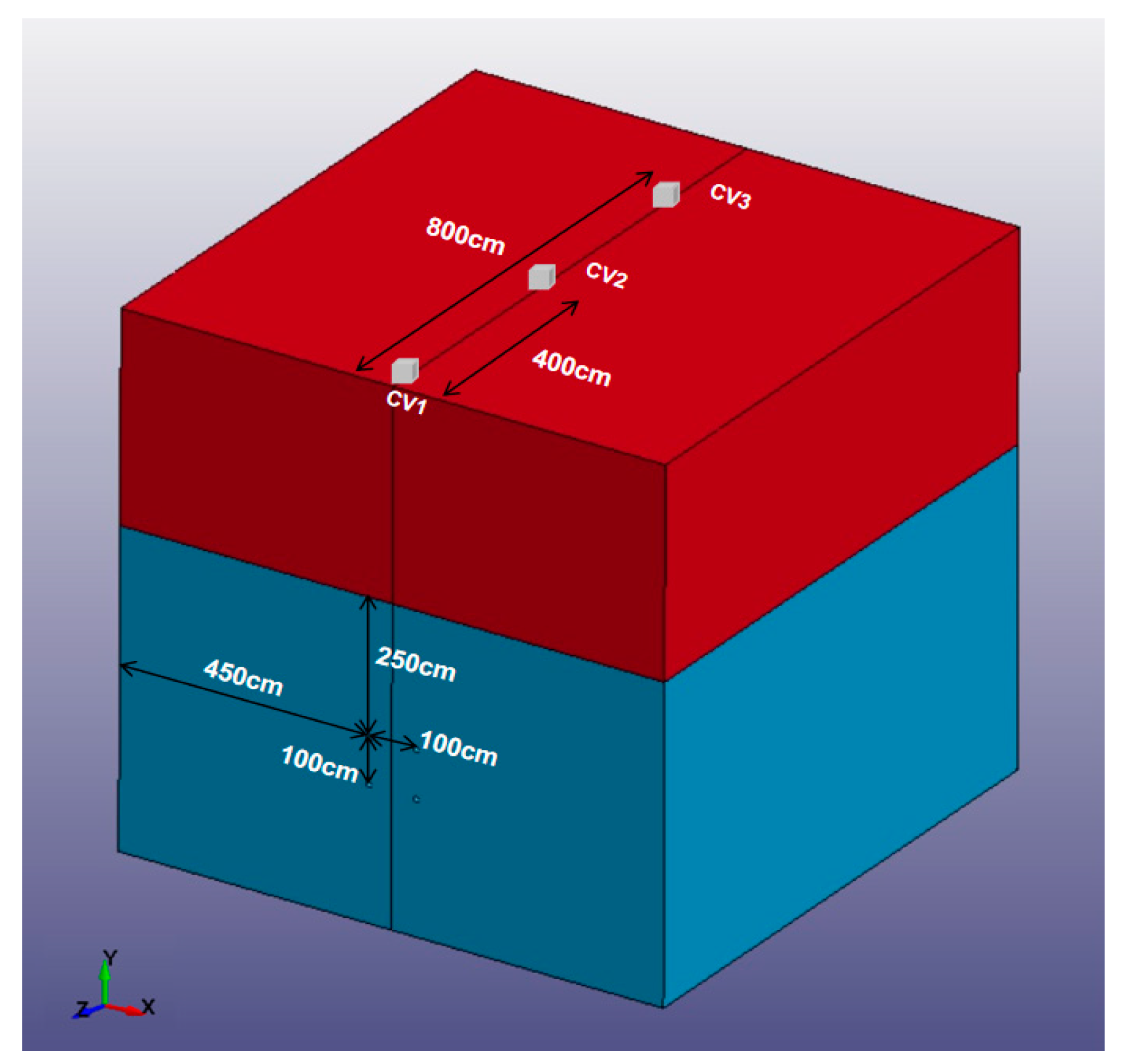
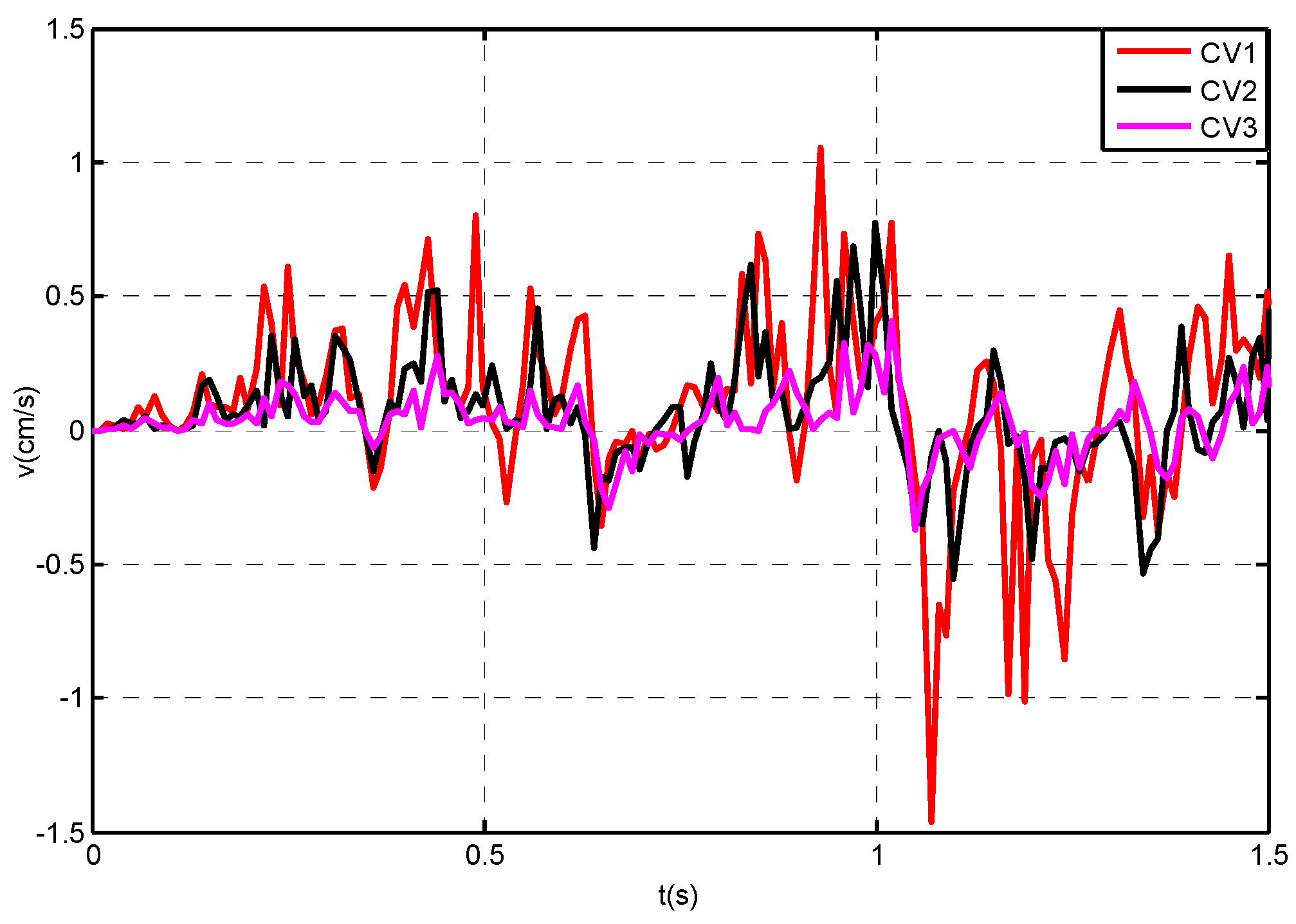
| Numerical Model | CV1 | CV2 | CV3 | |||
|---|---|---|---|---|---|---|
| PPV (cm/s) | DF (Hz) | PPV (cm/s) | DF (Hz) | PPV (cm/s) | DF (Hz) | |
| Under high-pressure gas impact | 1.46 | 107.3 | 0.77 | 99.7 | 0.41 | 95.6 |
| Under explosive blasting | 5.34 | 68.8 | 4.11 | 52.6 | 1.63 | 48.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Li, D.; Zhu, J.; Yang, X.; Chu, H. The Blasting Vibration Characteristics of Layered Rock Mass under High-Pressure Gas Impact. Energies 2023, 16, 6454. https://doi.org/10.3390/en16186454
Wei H, Li D, Zhu J, Yang X, Chu H. The Blasting Vibration Characteristics of Layered Rock Mass under High-Pressure Gas Impact. Energies. 2023; 16(18):6454. https://doi.org/10.3390/en16186454
Chicago/Turabian StyleWei, Haixia, Dongbing Li, Jie Zhu, Xiaolin Yang, and Huaibao Chu. 2023. "The Blasting Vibration Characteristics of Layered Rock Mass under High-Pressure Gas Impact" Energies 16, no. 18: 6454. https://doi.org/10.3390/en16186454







