Simulation and Experimental Study on Harmonic Optimization of Magnetically Controlled Reactor Based on Multistage Saturated Magnetic Valve Structure
Abstract
:1. Introduction
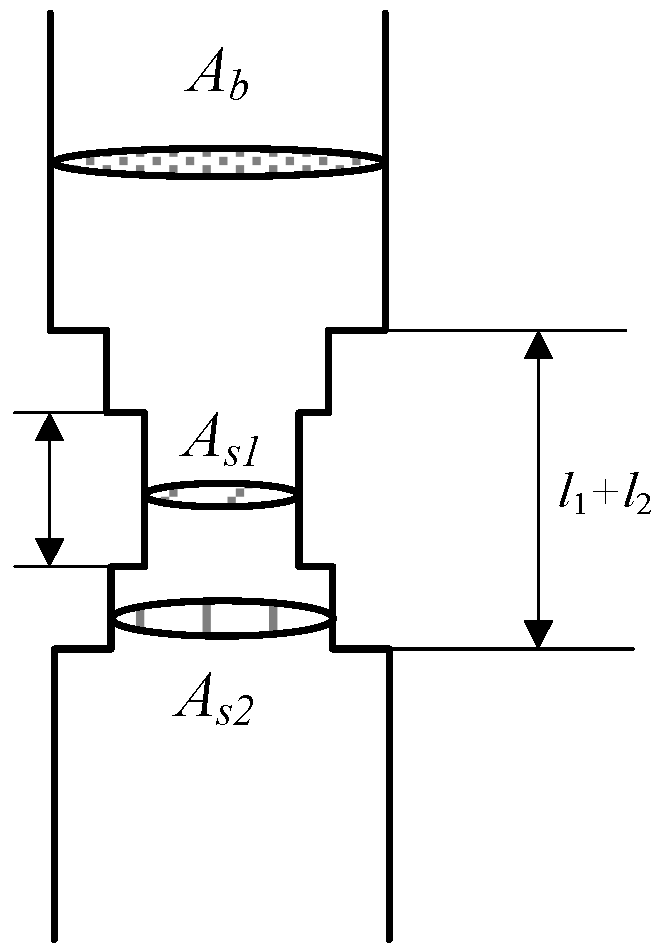
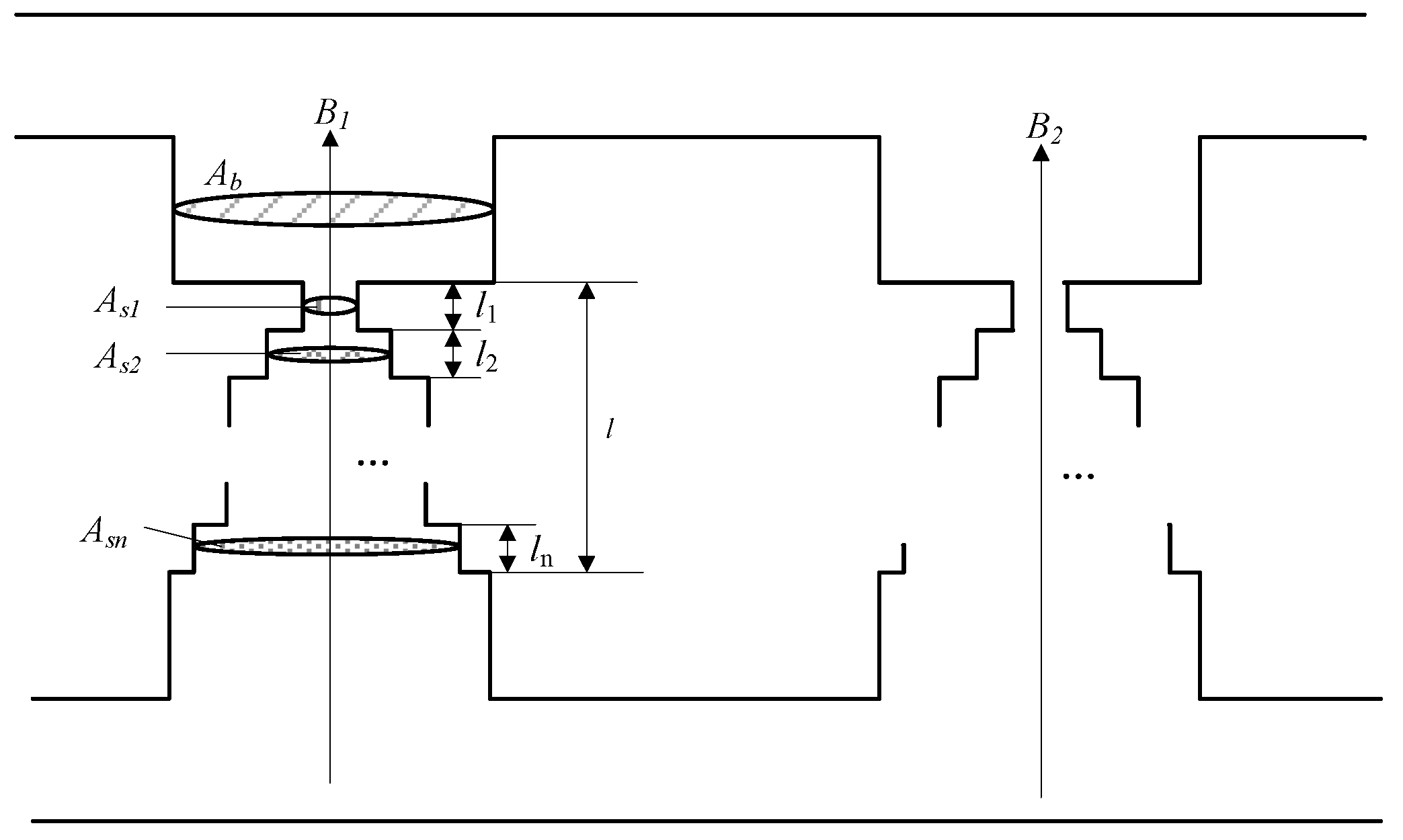
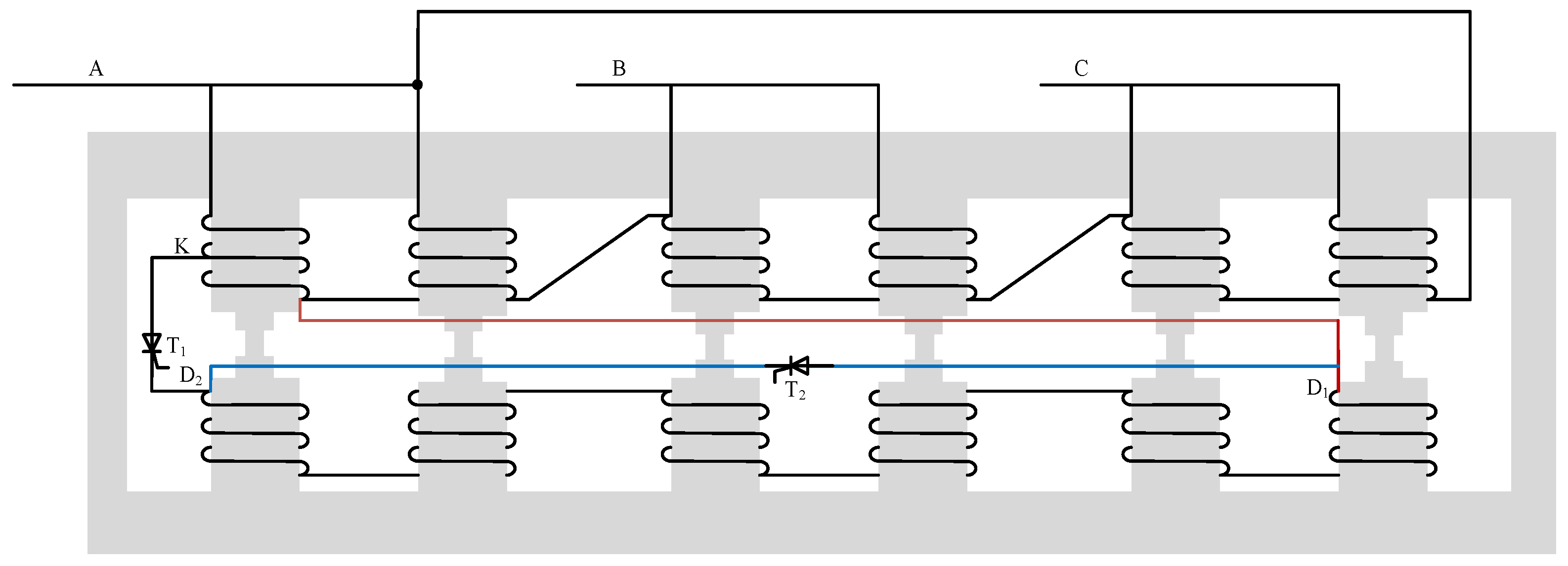
2. Study on Harmonic Mathematical Model of Three-Phase Magnetically Controlled Reactor
3. Simulation Analysis
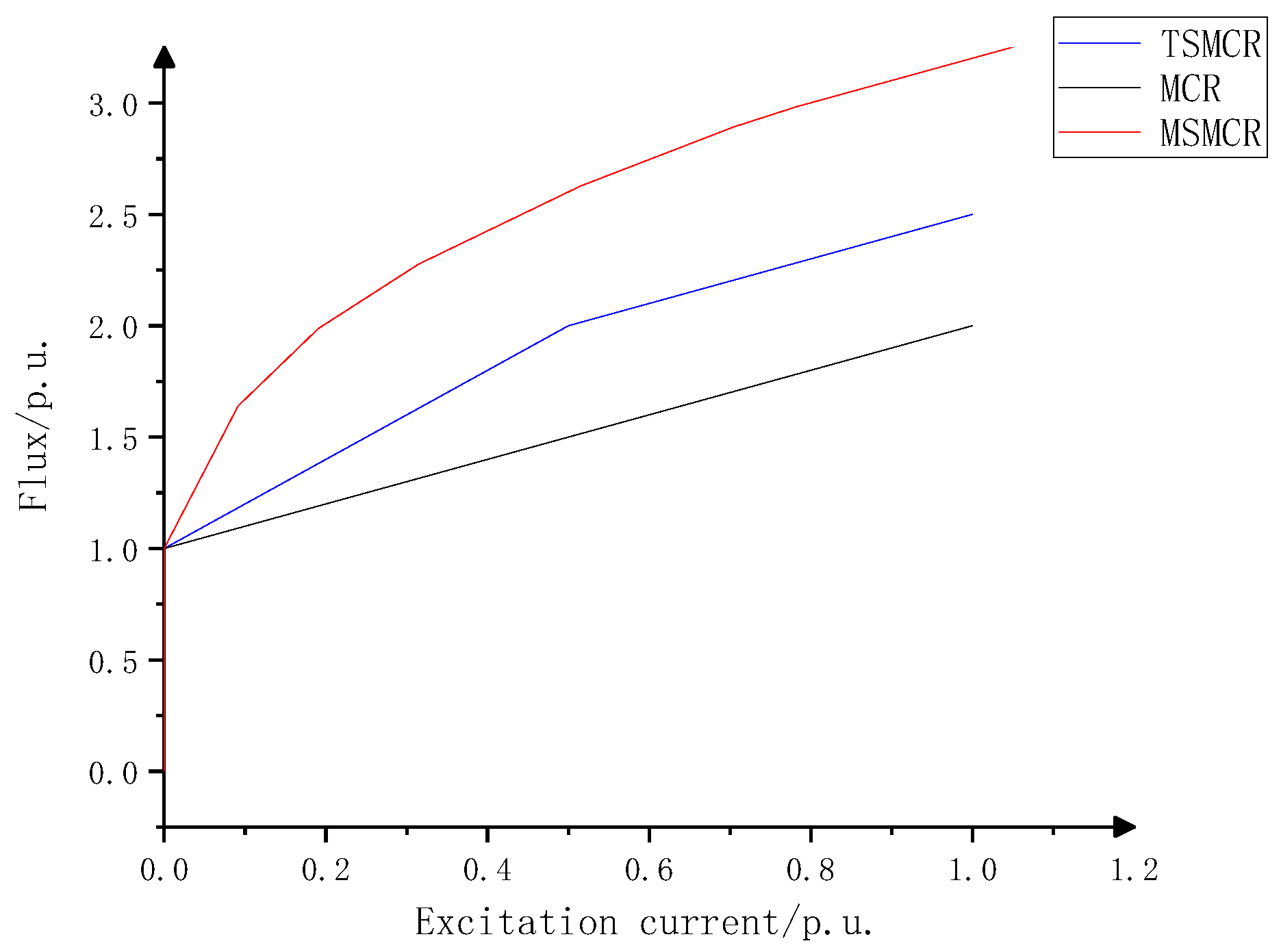
3.1. Magnetization Curve of Magnetically Controlled Reactor
3.2. Simulation Results
4. Test Verification
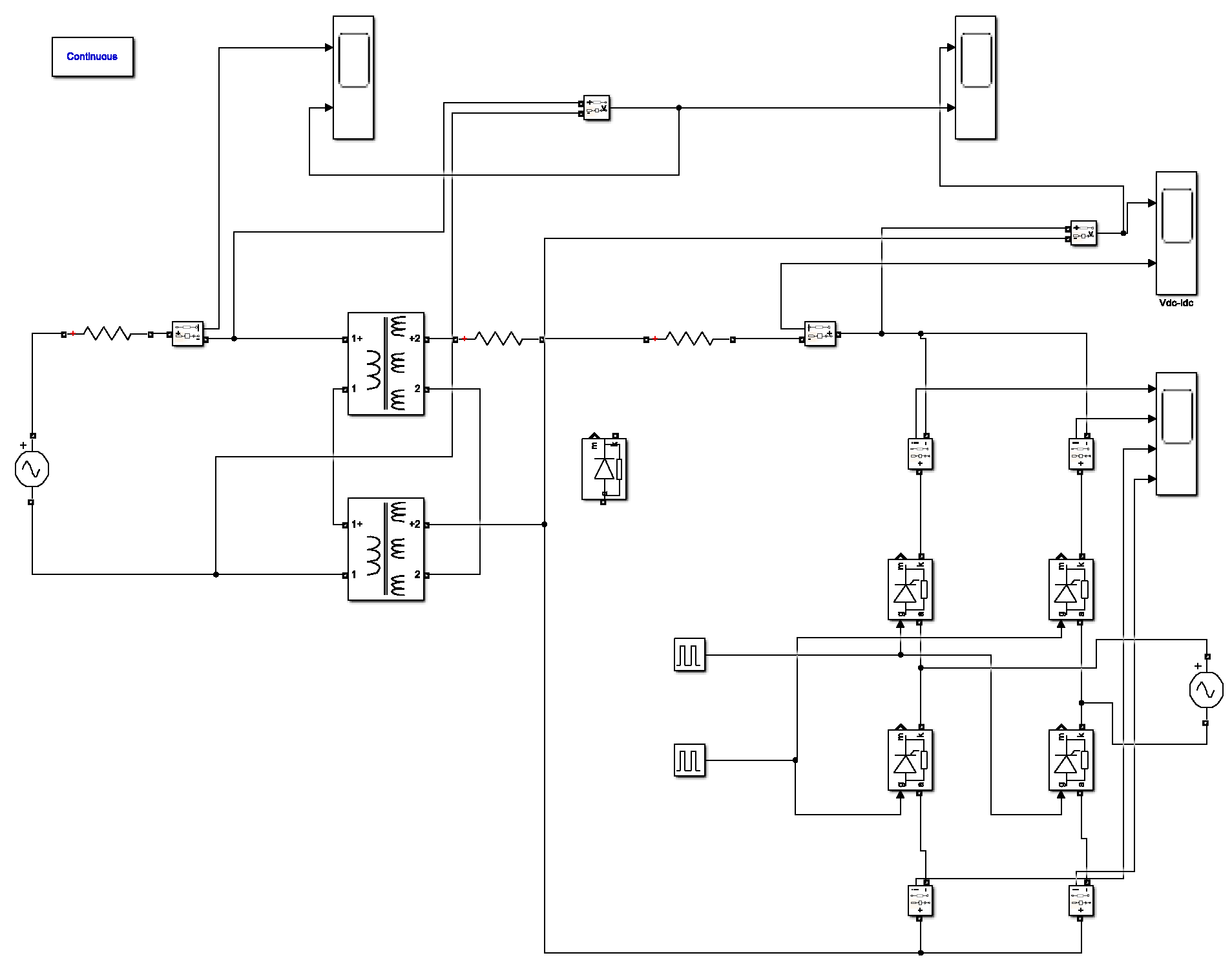
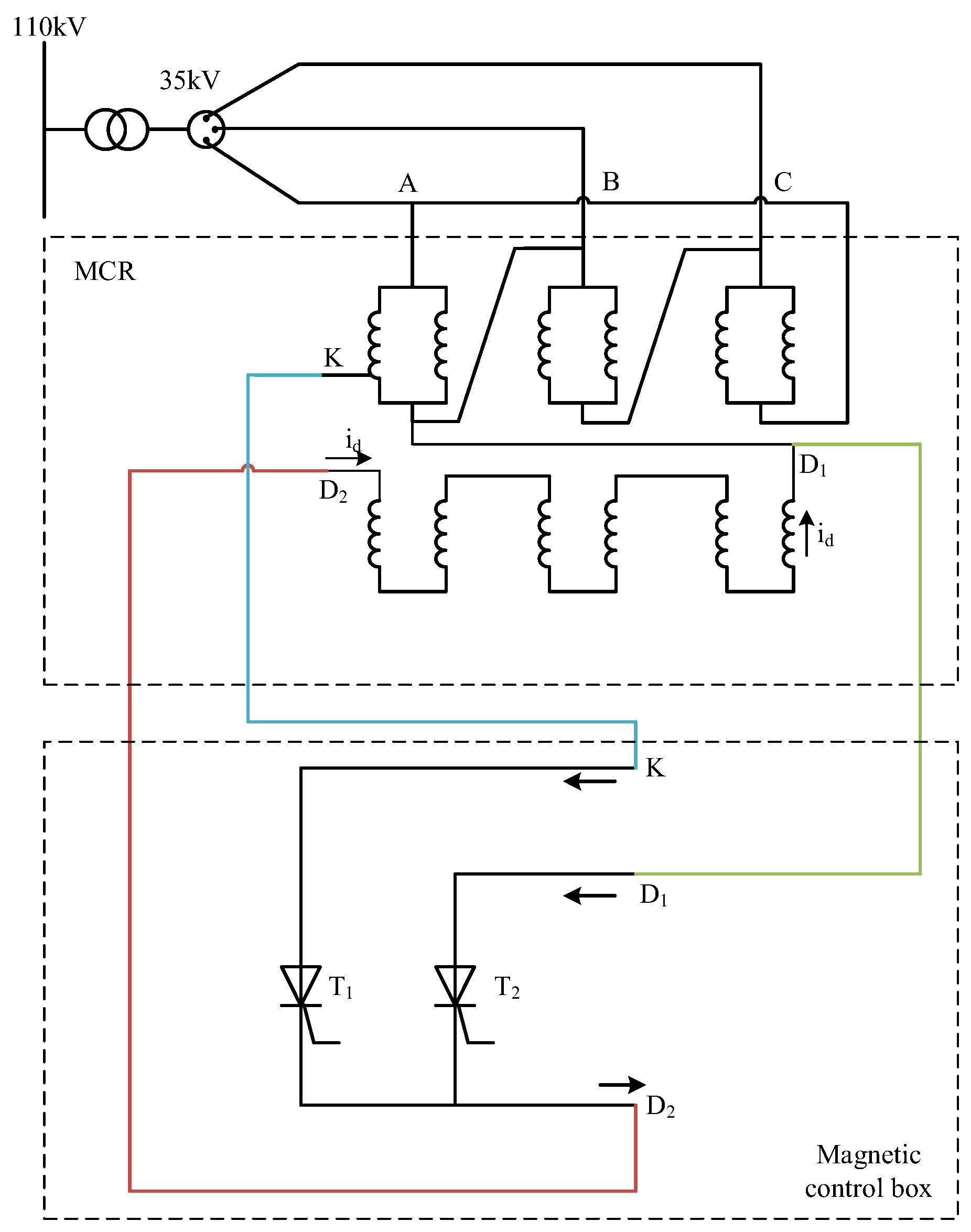
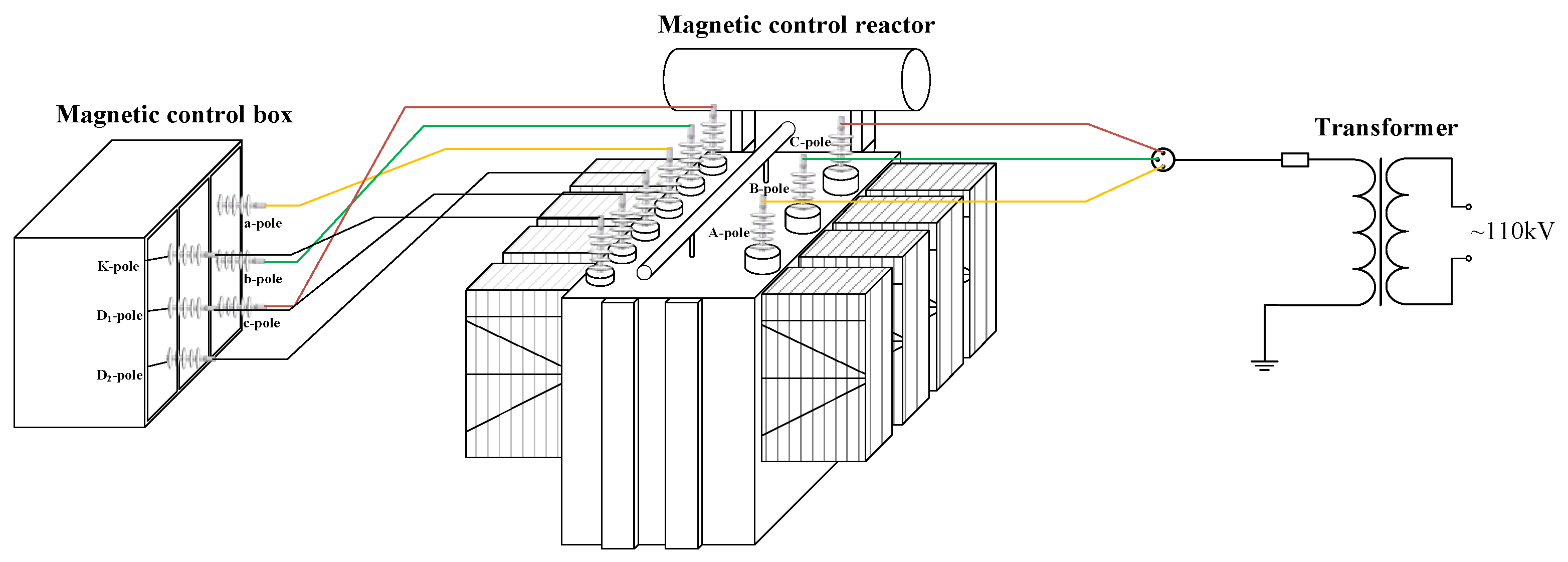
4.1. Test Principle and Wiring
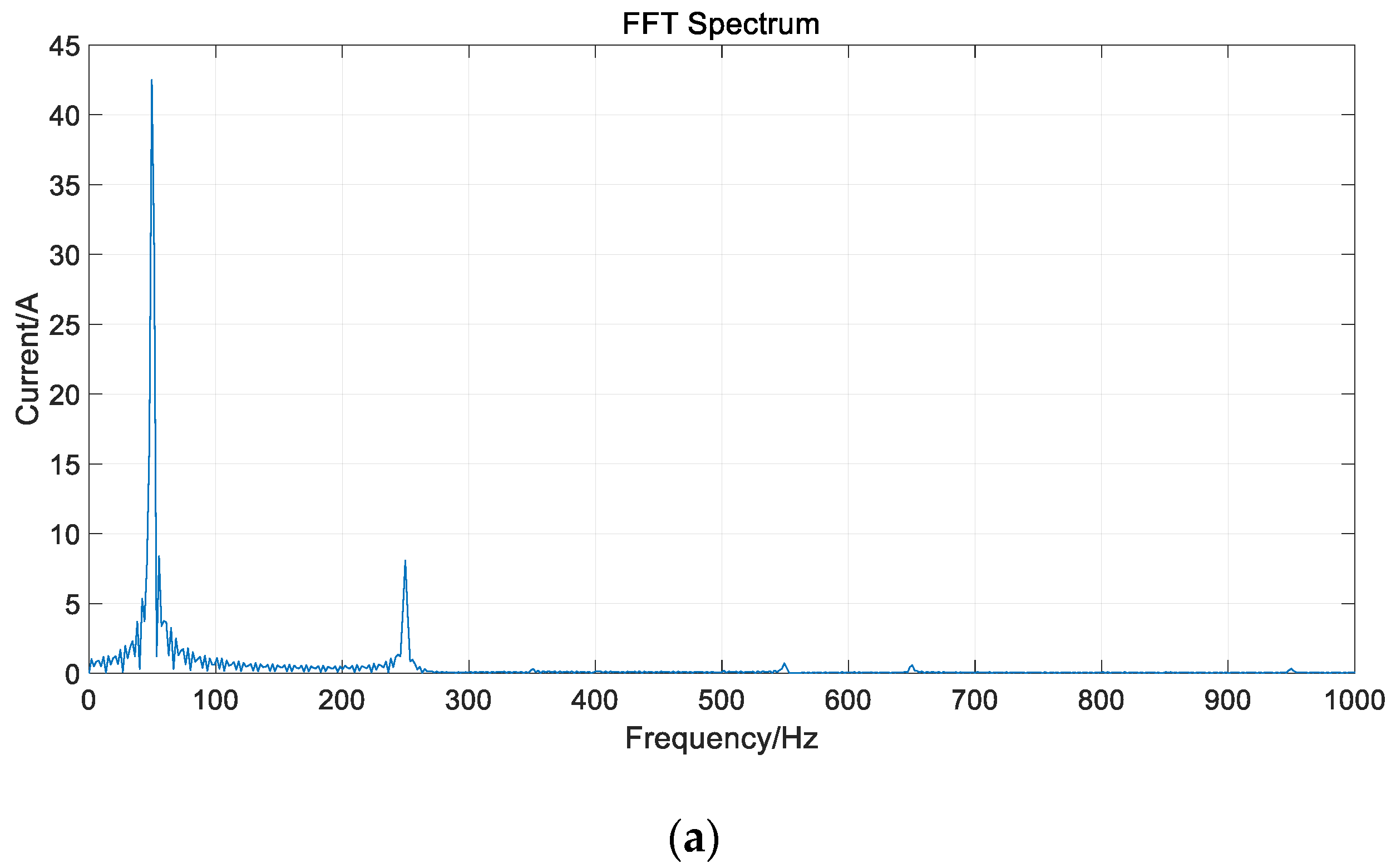
4.2. Analysis of Test Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, B.; Kokernak, J. Thyristor Controlled Two-Stage Magnetic-Valve Reactor for Dynamic Var-Compensation in Electric Railway Power Supply Systems. In Proceedings of the APEC 2000, New Orleans, LA, USA, 6–10 February 2000; pp. 1066–1072. [Google Scholar]
- Li, G.; Li, G.; Yan, S. Analysis of 4th harmonic amplification of 10 kV series reactor. Electrotech. Electr. 2021, 6, 33–37. [Google Scholar]
- GB/T 14549-1993; Quality of Electric Energy Supply-Harmonics in Public Supply. Standards Press of China: Beijing, China, 1993.
- Zhang, R.; Deng, G. Discussion on the problems in the Practical Application of GB/T 14549-93 Power Quality Power System Harmonics. China Electr. Power Educ. 2010, S1, 289–291. [Google Scholar]
- Wang, Z. Harmonic Suppression and Reactive Power Compensation; China Machine Press: Beijing, China, 2016. [Google Scholar]
- Zhan, Y.; Cheng, H.Z.; Ge, N.C.; Huang, G. Generalized growing and pruning RBF neural network based harmonic source modeling. Proceeding CSEE 2005, 25, 42–46. [Google Scholar]
- Wu, D.; Xu, Z. Harmonic modeling of electric loads. Power Syst. Technol. 2004, 28, 20–24. [Google Scholar]
- Zhao, C. Research on Multiphysical Fields of Power Capacitor and Its Series Reactor under the Influence of Harmonics. Master’s Thesis, South China University of Technology, Guangzhou, China, 2021. [Google Scholar]
- Tian, M.; An, X.; Gu, S. Voltage-controlling methods and simulation analysis of magnetically saturated and transformer-type controllable reactors. High Volt. Eng. 2013, 39, 791–796. [Google Scholar]
- Gao, G.; Chen, H.; Tian, M. Design and simulation of voltage control system for magnetic saturation type controllable reactor. Transformer 2013, 50, 39–42. [Google Scholar]
- Liu, H.; Yin, Z.; Dong, X.; Xu, J.; Li, H. A method of harmonic excitation based on magnetically controlled reactor. Autom. Electr. Power Syst. 2015, 39, 120–125+154. [Google Scholar]
- Zhou, L.; Yin, Z.; Xiao, X. Harmonic suppression in the electric propulsive shipping system based on phase-shifting reactor. Trans. China Electrotech. Soc. 2007, 22, 90–94. [Google Scholar]
- Chen, X.; Chen, B.; Tian, C.; Yuan, J. Optimization technique of harmonic suppression for TSMCR. Electr. Power Autom. Equip. 2011, 31, 71–75. [Google Scholar]
- Chen, X.; Tian, C.; Chen, B.; Liu, Y.; Yuan, J. Mathematical Model for Harmonics Analysis of the Multi-Stage Saturable Magnetic-Valve Controllable Reactor. Trans. China Electrotech. Soc. 2011, 26, 57–64. [Google Scholar] [CrossRef]
- Gao, D.; Yuan, H.; Zhang, Y. Novel three-phase multi-stage magnetically controlled reactor for harmonic suppression. High Volt. Appar. 2008, 44, 389–391. [Google Scholar]
- Zhang, G. Research and Analysis on the Characteristics of New Magnetic Control Reactor. Master’s Thesis, Zheng Zhou University, Zhengzhou, China, 2020. [Google Scholar]
- Jiang, P.; Li, Z.; Wei, L.; Li, F.; Li, F.; Liu, T. Research on fast response of magnetically controlled reactor based on IGBT full control bridge. Transformer 2021, 58, 27–32. [Google Scholar]
- Chen, B. Theory and Application of New Type Controllable Saturable Reactor; Wuhan University of Water Resources and Electric Power Press: Wuhan, China, 1999. [Google Scholar]
- Chen, B.; Tian, C.; Liang, B.; Wang, Q. Principle and implementation of a harmonic depression approach for single phase controlled saturable reacor. Proc. CSEE 2002, 22, 64–68. [Google Scholar]
- Karymov, R.R.; Ebadian, M. Comparison of Magnetically Controlled Reactor (MCR) and Thyristor Controlled Reactor (TCR) from harmonics point of view. Int. J. Electr. Power Energy Syst. 2007, 29, 191–198. [Google Scholar] [CrossRef]
- Chen, B.; Chen, W. Voltage restraining characteristic and harmonic analysis of high-voltage controller reactor. Proc. CSEE 1997, 17, 122–125. [Google Scholar]
- Tian, M.; Li, Q.; Wang, S. An equivalent physical model and a mathematical model of the controlled saturable reactor. Trans. China Electrotech. Soc. 2002, 17, 18–21. [Google Scholar]


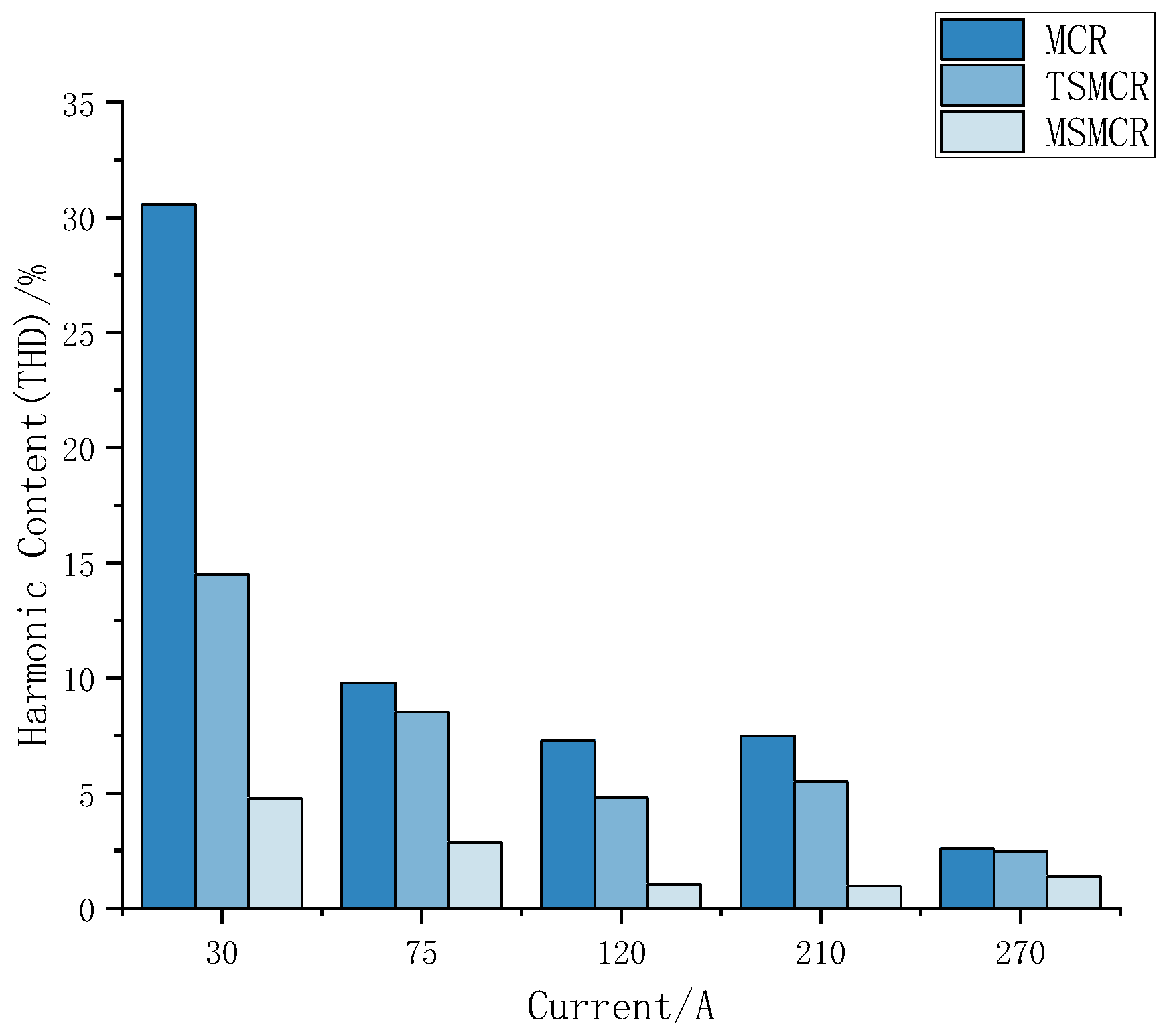
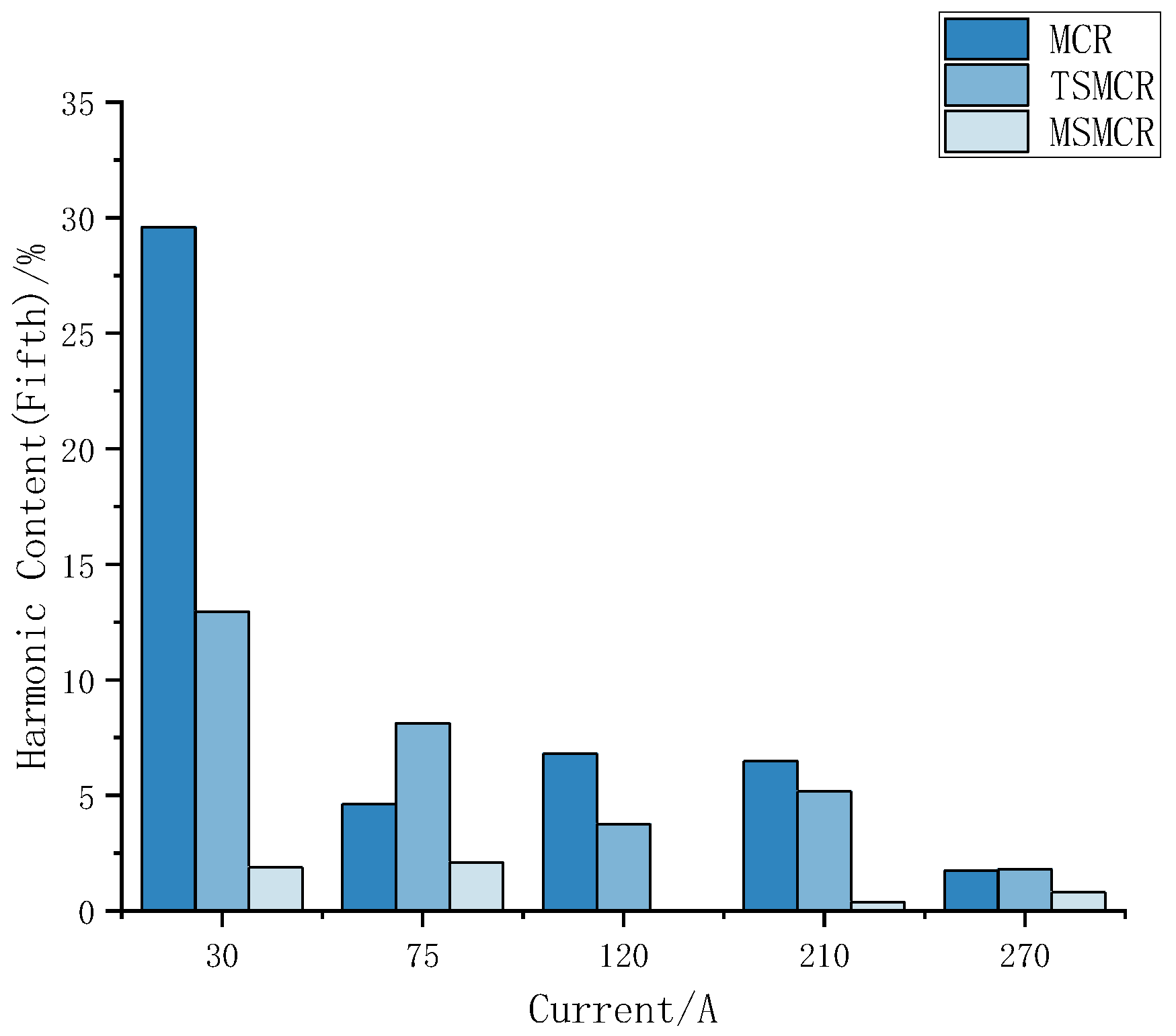
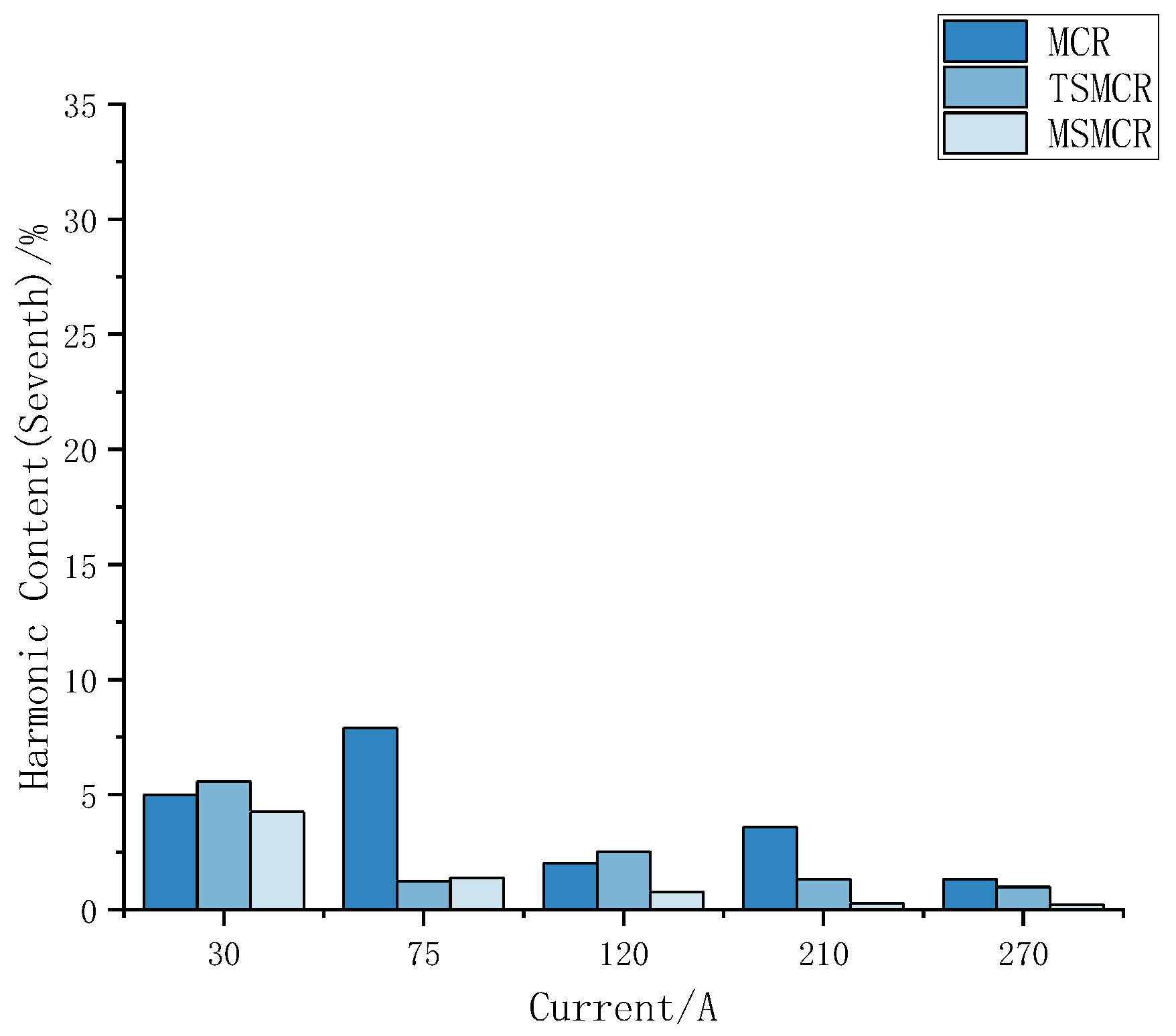

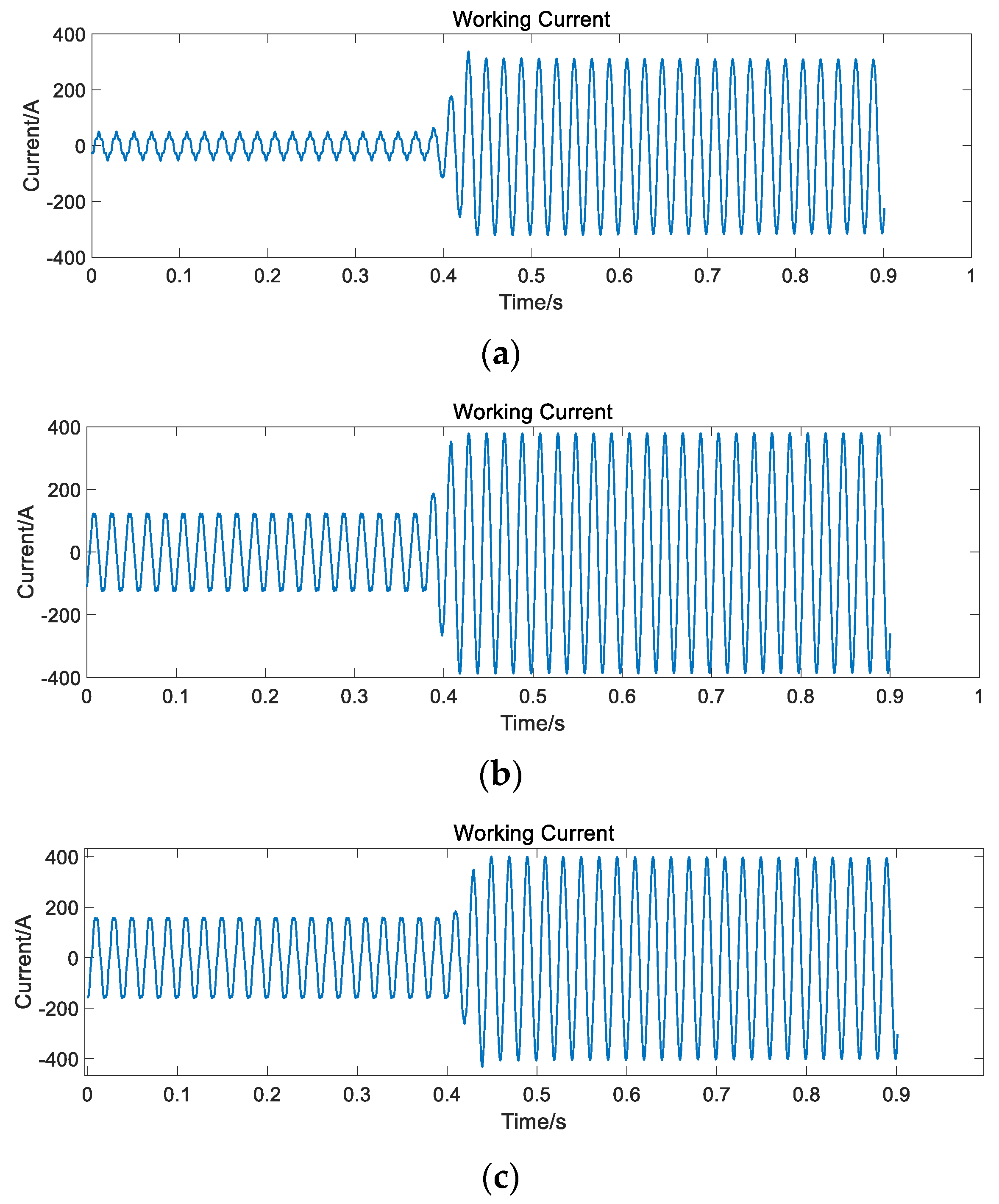

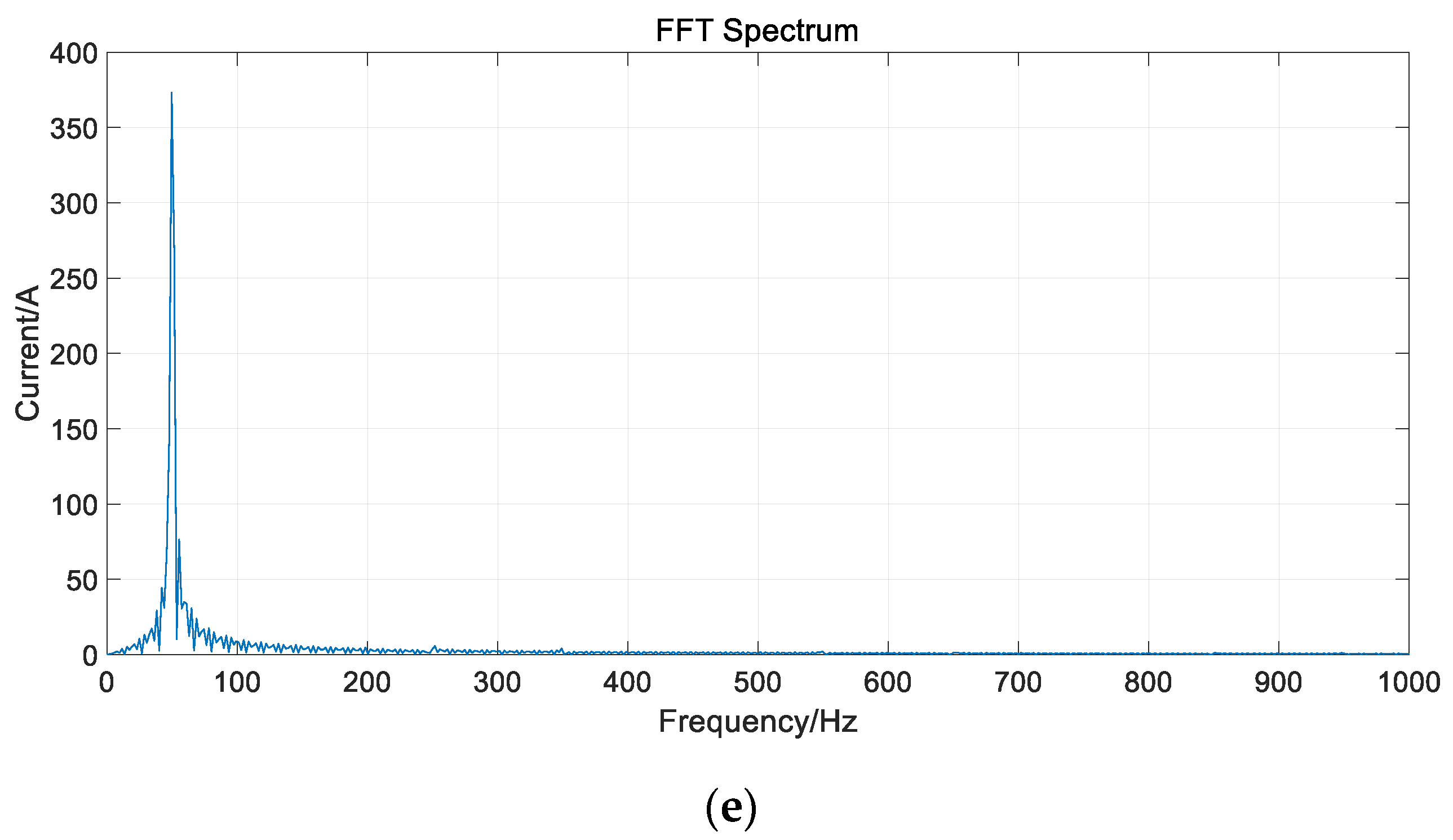
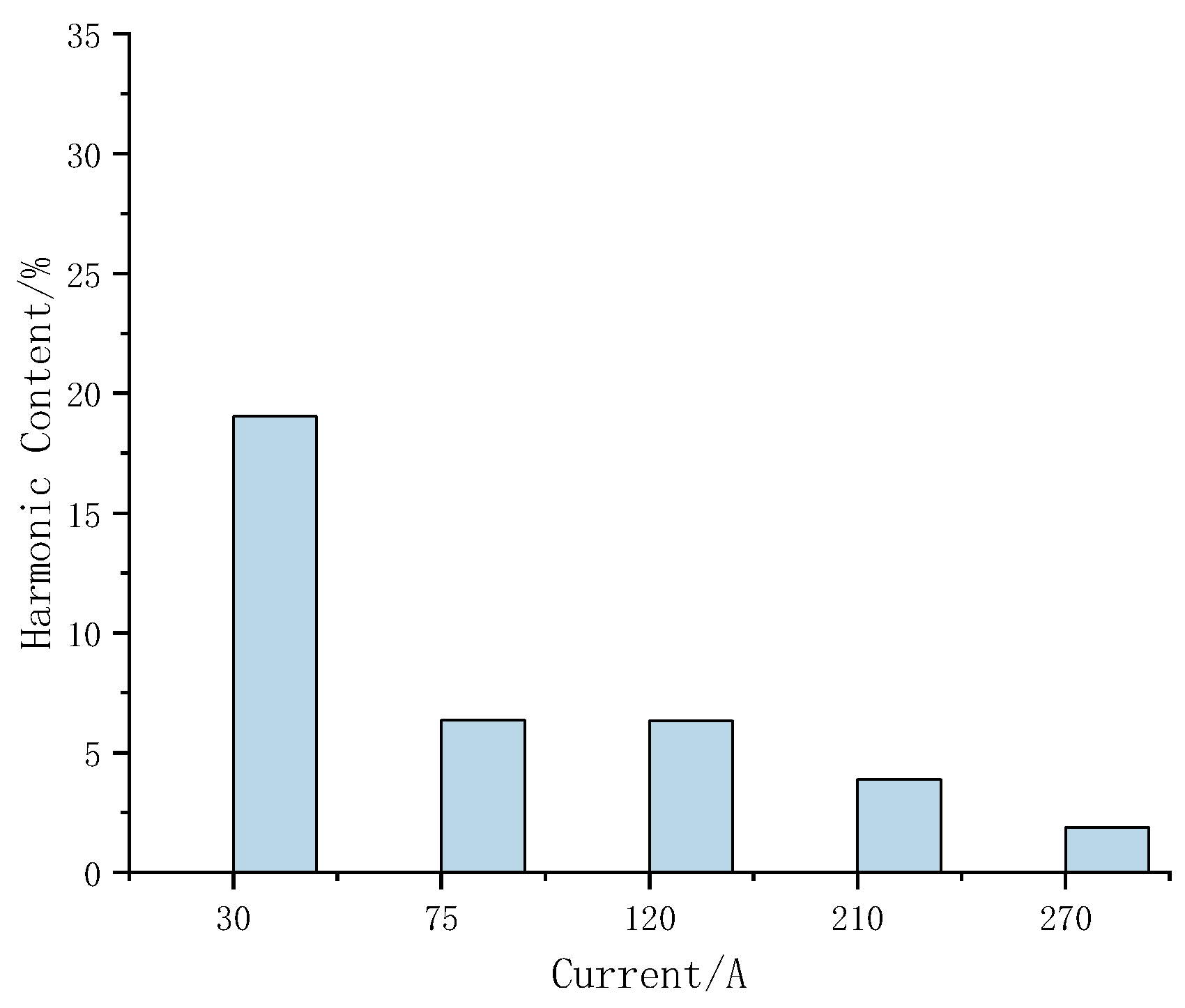
| (a) | |||||
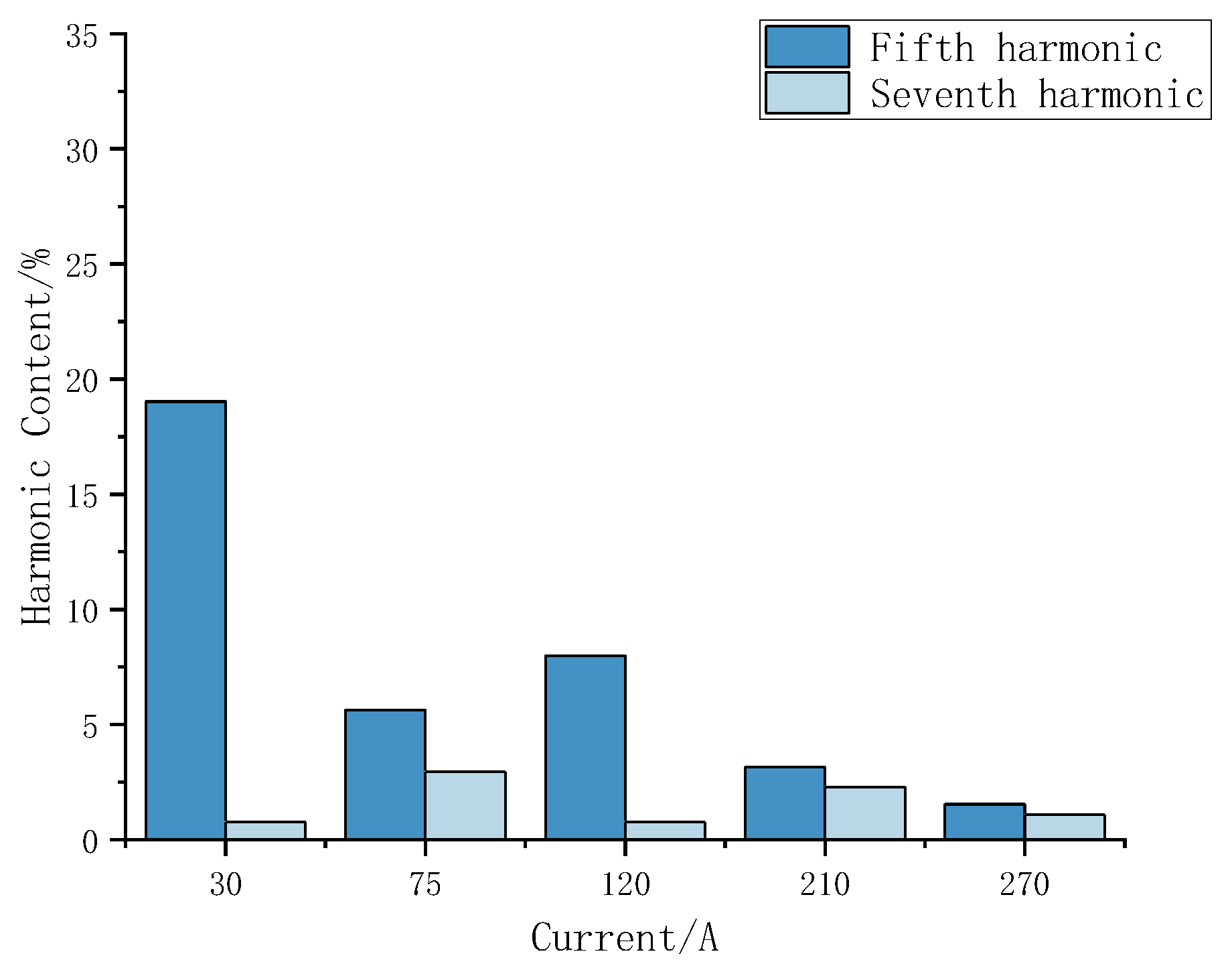
| Working Current/A | 30 | 75 | 120 | 210 | 270 |
| THD | 30.58% | 9.79% | 7.28% | 7.49% | 2.58% |
| 5th harmonic | 29.59% | 4.61% | 6.8% | 6.47% | 1.73% |
| 7th harmonic | 4.98% | 7.89% | 2.01% | 3.58% | 1.33% |
| (b) | |||||
| Working current/A | 30 | 75 | 120 | 210 | 270 |
| THD | 14.5% | 8.52% | 4.8% | 5.49% | 2.49% |
| 5th harmonic | 12.95% | 8.13% | 3.76% | 5.17% | 1.8% |
| 7th harmonic | 5.57% | 1.25% | 2.52% | 1.33% | 0.99% |
| (c) | |||||
| Working current/A | 30 | 75 | 120 | 210 | 270 |
| THD | 4.78% | 2.87% | 1.03% | 0.96% | 1.38% |
| 5th harmonic | 1.88% | 2.1% | 0.04% | 0.39% | 0.8% |
| 7th harmonic | 4.26% | 1.39% | 0.78% | 0.29% | 0.23% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Yin, X.; Bao, Y.; Lan, Y.; Wang, C.; Chen, B.; Chen, X.; Wang, Y. Simulation and Experimental Study on Harmonic Optimization of Magnetically Controlled Reactor Based on Multistage Saturated Magnetic Valve Structure. Energies 2023, 16, 6457. https://doi.org/10.3390/en16186457
Liu C, Yin X, Bao Y, Lan Y, Wang C, Chen B, Chen X, Wang Y. Simulation and Experimental Study on Harmonic Optimization of Magnetically Controlled Reactor Based on Multistage Saturated Magnetic Valve Structure. Energies. 2023; 16(18):6457. https://doi.org/10.3390/en16186457
Chicago/Turabian StyleLiu, Chunhui, Xiyu Yin, Yinfu Bao, Yue Lan, Chun Wang, Baichao Chen, Xiaoyue Chen, and Yu Wang. 2023. "Simulation and Experimental Study on Harmonic Optimization of Magnetically Controlled Reactor Based on Multistage Saturated Magnetic Valve Structure" Energies 16, no. 18: 6457. https://doi.org/10.3390/en16186457
APA StyleLiu, C., Yin, X., Bao, Y., Lan, Y., Wang, C., Chen, B., Chen, X., & Wang, Y. (2023). Simulation and Experimental Study on Harmonic Optimization of Magnetically Controlled Reactor Based on Multistage Saturated Magnetic Valve Structure. Energies, 16(18), 6457. https://doi.org/10.3390/en16186457






