Data Augmentation and Feature Selection for the Prediction of the State of Charge of Lithium-Ion Batteries Using Artificial Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
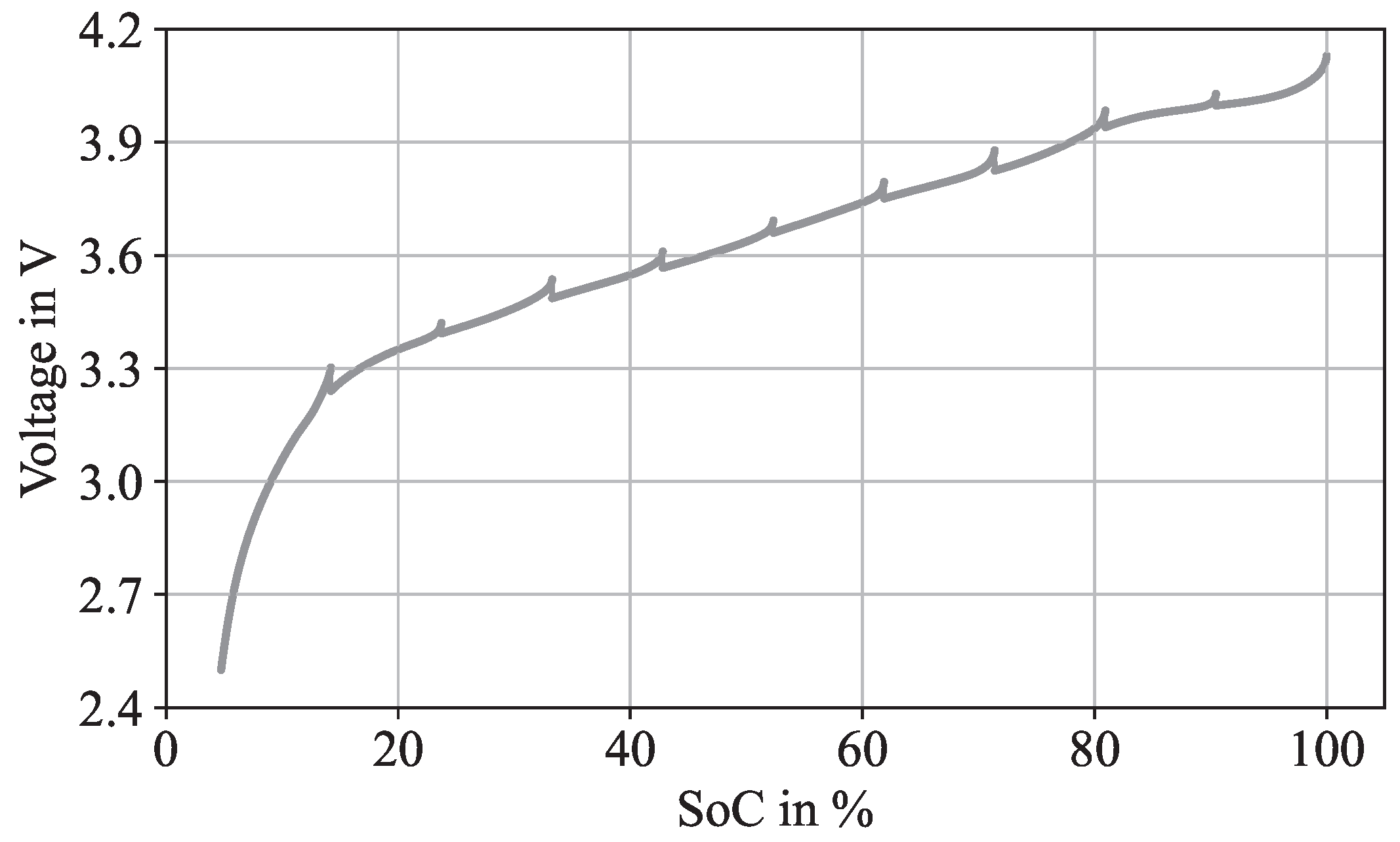
2.1. Data Origin and Data Augmentation
2.2. Machine Learning Models
2.2.1. Linear Regression
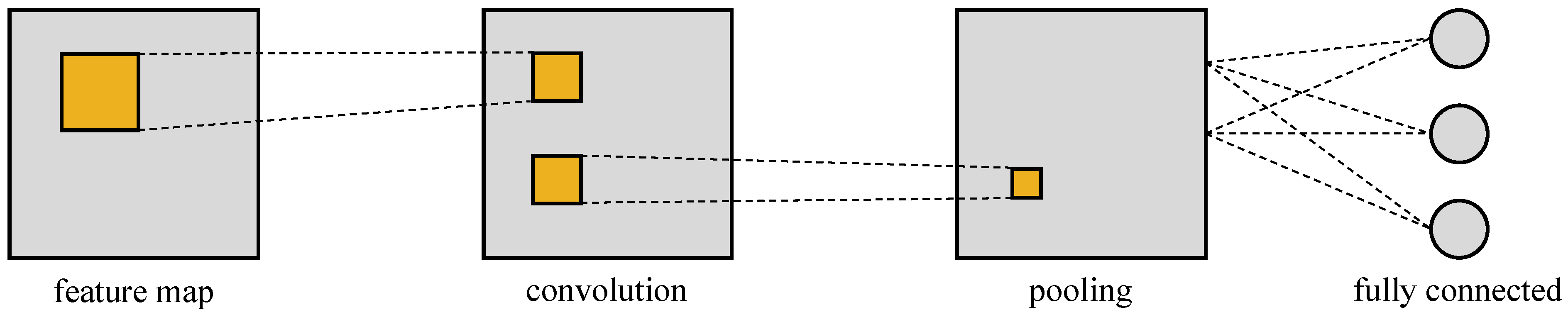
2.2.2. Artificial Neural Networks
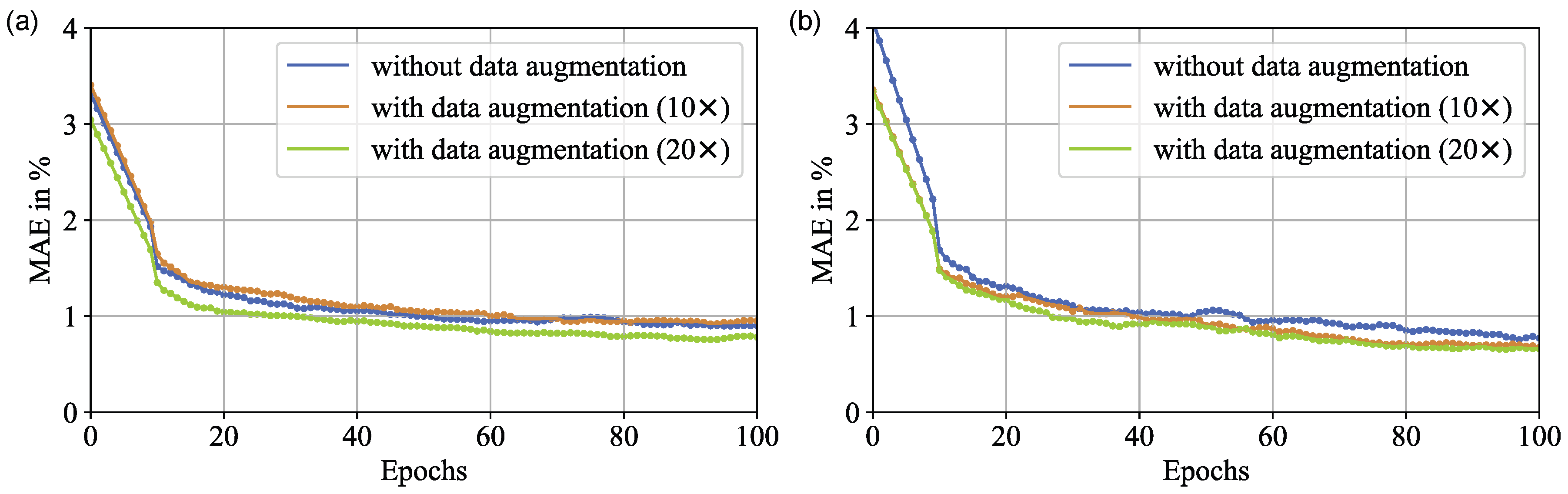
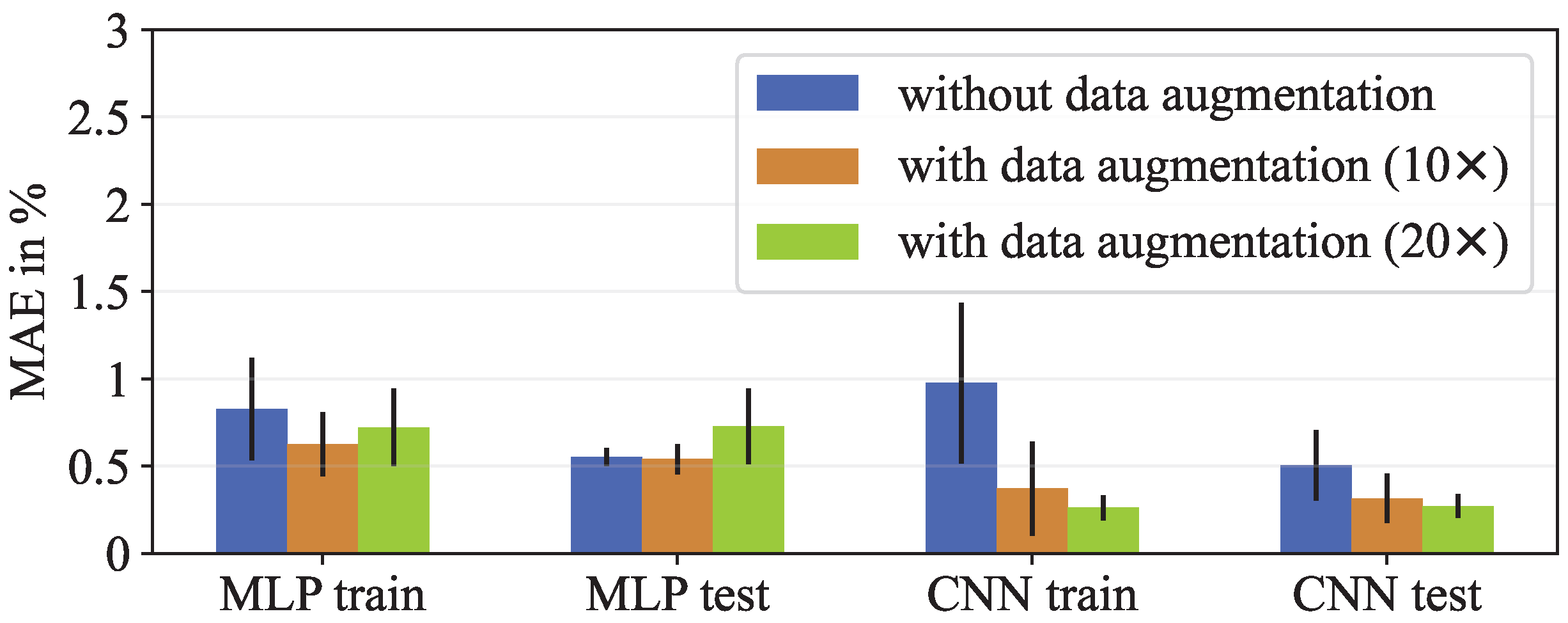
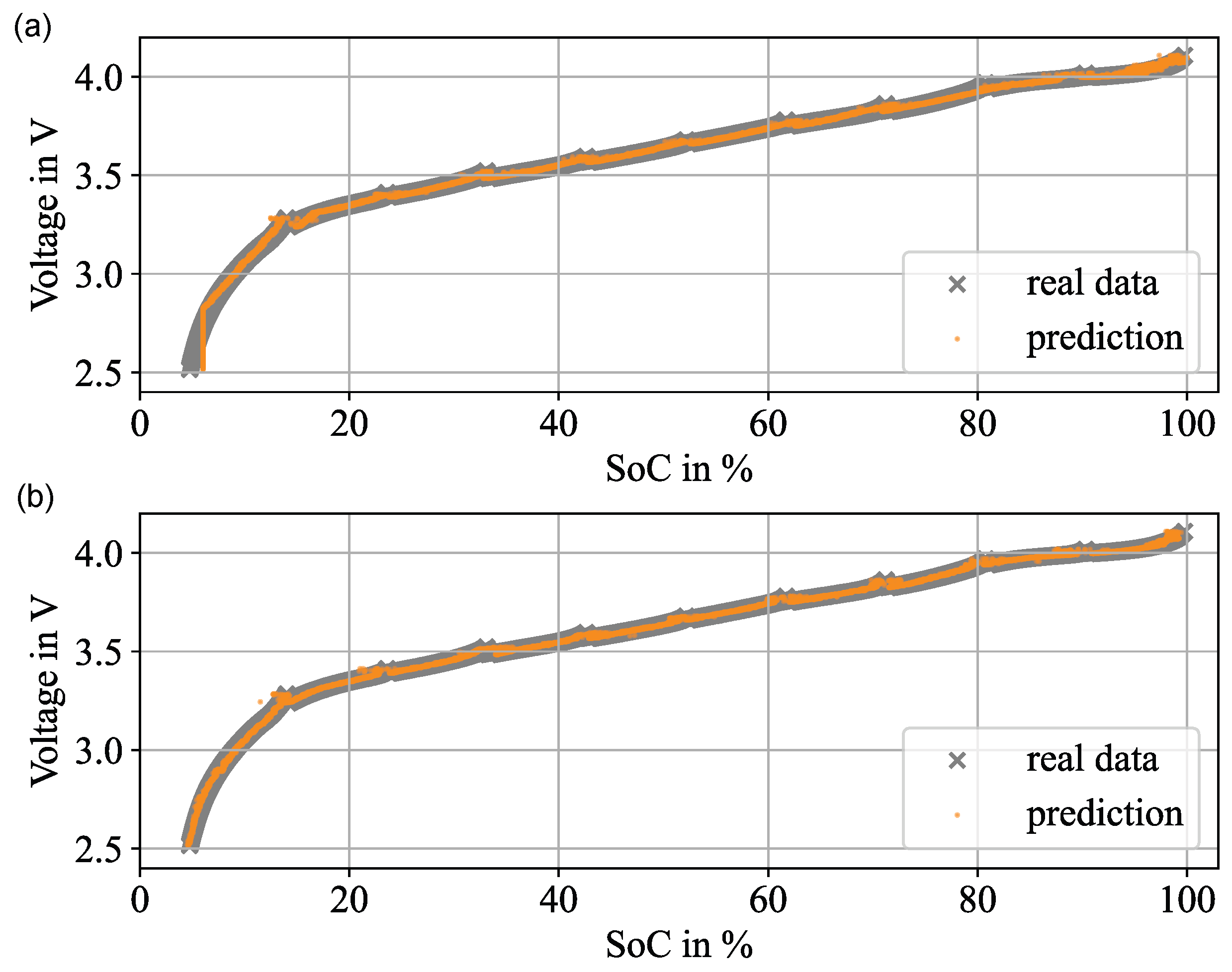
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| BEV | Battery electric vehicle |
| BMS | Battery management system |
| CNN | Convolutional neural network |
| LIB | Lithium-ion battery |
| MAE | Mean absolute error |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| PCA | Principal component analysis |
| RMSE | Root mean square error |
| RNN | Recurrent neural network |
| SoC | State-of-Charge |
| SVD | Singular value decomposition |
| SVM | Support vector machine |
References
- Buberger, J.; Kersten, A.; Kuder, M.; Eckerle, R.; Weyh, T.; Thiringer, T. Total CO2-equivalent life-cycle emissions from commercially available passenger cars. Renew. Sustain. Energy Rev. 2022, 159, 112158. [Google Scholar] [CrossRef]
- Bernhart, W. Challenges and Opportunities in Lithium-ion Battery Supply. In Future Lithium-Ion Batteries; The Royal Society of Chemistry: London, UK, 2019; pp. 316–334. [Google Scholar] [CrossRef]
- Schulte, J.; Figgener, J.; Woerner, P.; Broering, H.; Sauer, D.U. Forecast-based charging strategy to prolong the lifetime of lithium-ion batteries in standalone PV battery systems in Sub-Saharan Africa. Sol. Energy 2023, 258, 130–142. [Google Scholar] [CrossRef]
- Stock, S.; Pohlmann, S.; Günter, F.J.; Hille, L.; Hagemeister, J.; Reinhart, G. Early Quality Classification and Prediction of Battery Cycle Life in Production Using Machine Learning. J. Energy Storage 2022, 50, 104144. [Google Scholar] [CrossRef]
- Castro, F.D.; Cutaia, L.; Vaccari, M. End-of-life automotive lithium-ion batteries (LIBs) in Brazil: Prediction of flows and revenues by 2030. Resour. Conserv. Recycl. 2021, 169, 105522. [Google Scholar] [CrossRef]
- Boxall, N.J.; King, S.; Cheng, K.Y.; Gumulya, Y.; Bruckard, W.; Kaksonen, A.H. Urban mining of lithium-ion batteries in Australia: Current state and future trends. Miner. Eng. 2018, 128, 45–55. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, I.S. Lithium Battery SOH Monitoring and an SOC Estimation Algorithm Based on the SOH Result. Energies 2021, 14, 4506. [Google Scholar] [CrossRef]
- Shchurov, N.I.; Dedov, S.I.; Malozyomov, B.V.; Shtang, A.A.; Martyushev, N.V.; Klyuev, R.V.; Andriashin, S.N. Degradation of Lithium-Ion Batteries in an Electric Transport Complex. Energies 2021, 14, 8072. [Google Scholar] [CrossRef]
- Bonfitto, A. A Method for the Combined Estimation of Battery State of Charge and State of Health Based on Artificial Neural Networks. Energies 2020, 13, 2548. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Chaoui, H.; Mandalapu, S. Comparative Study of Online Open Circuit Voltage Estimation Techniques for State of Charge Estimation of Lithium-Ion Batteries. Batteries 2017, 3, 12. [Google Scholar] [CrossRef]
- Marcicki, J.; Canova, M.; Conlisk, A.T.; Rizzoni, G. Design and parametrization analysis of a reduced-order electrochemical model of graphite/LiFePO4 cells for SOC/SOH estimation. J. Power Sources 2013, 237, 310–324. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.E.; Arif, M.T. Kalman filtering techniques for the online model parameters and state of charge estimation of the Li-ion batteries: A comparative analysis. J. Energy Storage 2022, 51, 104174. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Luo, Y.; Qi, P.; Kan, Y.; Huang, J.; Huang, H.; Luo, J.; Wang, J.; Wei, Y.; Xiao, R.; Zhao, S. State of charge estimation method based on the extended Kalman filter algorithm with consideration of time–varying battery parameters. Int. J. Energy Res. 2020, 44, 10538–10550. [Google Scholar] [CrossRef]
- Sharma, P.; Bora, B.J. A Review of Modern Machine Learning Techniques in the Prediction of Remaining Useful Life of Lithium-Ion Batteries. Batteries 2023, 9, 13. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Ker, P.J.; Mahlia, T.M.I.; Mansor, M.; Ayob, A.; Saad, M.H.; Dong, Z.Y. Toward Enhanced State of Charge Estimation of Lithium-ion Batteries Using Optimized Machine Learning Techniques. Sci. Rep. 2020, 10, 4687. [Google Scholar] [CrossRef]
- Basia, A.; Simeu-Abazi, Z.; Gascard, E.; Zwolinski, P. Review on State of Health estimation methodologies for lithium-ion batteries in the context of circular economy. CIRP J. Manuf. Sci. Technol. 2021, 32, 517–528. [Google Scholar] [CrossRef]
- Álvarez Antón, J.C.; García Nieto, P.J.; Blanco Viejo, C.; Vilán Vilán, J.A. Support Vector Machines Used to Estimate the Battery State of Charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Che, Y.; Xu, L.; Guo, W. Data-driven state of charge estimation for lithium-ion battery packs based on Gaussian process regression. Energy 2020, 205, 118000. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, L.; Li, Q.; Wang, K. A comprehensive review on the state of charge estimation for lithium-ion battery based on neural network. Int. J. Energy Res. 2022, 46, 5423–5440. [Google Scholar] [CrossRef]
- Li, X.; Jiang, H.; Guo, S.; Xu, J.; Li, M.; Liu, X.; Zhang, X.; Bhardwaj, A. SOC Estimation of Lithium-Ion Battery for Electric Vehicle Based on Deep Multilayer Perceptron. Comput. Intell. Neurosci. 2022, 2022, 3920317. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Ju, C.; Li, J.; Fang, R.; Tao, Z.; Li, B.; Zhang, T. State-of-Charge Estimation of Lithium-Ion Batteries in the Battery Degradation Process Based on Recurrent Neural Network. Energies 2021, 14, 306. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Qiu, J. A GRU-RNN based momentum optimized algorithm for SOC estimation. J. Power Sources 2020, 459, 228051. [Google Scholar] [CrossRef]
- Qian, C.; Xu, B.; Chang, L.; Sun, B.; Feng, Q.; Yang, D.; Wang, Z. Convolutional neural network based capacity estimation using random segments of the charging curves for lithium-ion batteries. Energy 2021, 227, 120333. [Google Scholar] [CrossRef]
- Bian, C.; Yang, S.; Liu, J.; Zio, E. Robust state-of-charge estimation of Li-ion batteries based on multichannel convolutional and bidirectional recurrent neural networks. Appl. Soft Comput. 2022, 116, 108401. [Google Scholar] [CrossRef]
- Hu, W.; Peng, Y.; Wei, Y.; Yang, Y. Application of Electrochemical Impedance Spectroscopy to Degradation and Aging Research of Lithium-Ion Batteries. J. Phys. Chem. C 2023, 127, 4465–4495. [Google Scholar] [CrossRef]
- Naaz, F.; Herle, A.; Channegowda, J.; Raj, A.; Lakshminarayanan, M. A generative adversarial network-based synthetic data augmentation technique for battery condition evaluation. Int. J. Energy Res. 2021, 45, 19120–19135. [Google Scholar] [CrossRef]
- Qiu, X.; Wang, S.; Chen, K. A conditional generative adversarial network-based synthetic data augmentation technique for battery state-of-charge estimation. Appl. Soft Comput. 2023, 142, 110281. [Google Scholar] [CrossRef]
- Channegowda, J.; Maiya, V.; Joshi, N.; Raj Urs, V.; Lingaraj, C. An attention-based synthetic battery data augmentation technique to overcome limited dataset challenges. Energy Storage 2022, 4, e354. [Google Scholar] [CrossRef]
- Fayyad, U.; Piatetsky-Shapiro, G.; Smyth, P. From Data Mining to Knowledge Discovery in Databases. AI Mag. 1996, 17, 37. [Google Scholar] [CrossRef]
- Zhang, F.; Lai, T.L.; Rajaratnam, B.; Zhang, N.R. Cross-Validation and Regression Analysis in High-Dimensional Sparse Linear Models; Stanford University: Stanford, CA, USA, 2011. [Google Scholar]
- Kondo, M.; Bezemer, C.P.; Kamei, Y.; Hassan, A.E.; Mizuno, O. The impact of feature reduction techniques on defect prediction models. Empir. Softw. Eng. 2019, 24, 1925–1963. [Google Scholar] [CrossRef]
- Debie, E.; Shafi, K. Implications of the curse of dimensionality for supervised learning classifier systems: Theoretical and empirical analyses. Pattern Anal. Appl. 2019, 22, 519–536. [Google Scholar] [CrossRef]
- Gruosso, G.; Storti Gajani, G.; Ruiz, F.; Valladolid, J.D.; Patino, D. A Virtual Sensor for Electric Vehicles’ State of Charge Estimation. Electronics 2020, 9, 278. [Google Scholar] [CrossRef]
- Yanai, H.; Takeuchi, K.; Takane, Y. Projection Matrices, Generalized Inverse Matrices, and Singular Value Decomposition, 1st ed.; Statistics for Social and Behavioral Sciences; Springer: New York, NY, USA, 2011. [Google Scholar]
- Tipping, M.E.; Bishop, C.M. Mixtures of Probabilistic Principal Component Analyzers. Neural Comput. 1999, 11, 443–482. [Google Scholar] [CrossRef] [PubMed]
- Zhou, N.; Zhao, X.; Han, B.; Li, P.; Wang, Z.; Fan, J. A novel quick and robust capacity estimation method for Li-ion battery cell combining information energy and singular value decomposition. J. Energy Storage 2022, 50, 104263. [Google Scholar] [CrossRef]
- Joshi, A.V. Machine Learning and Artificial Intelligence; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Yu, Y.; Feng, Y. Modified Cross-Validation for Penalized High-Dimensional Linear Regression Models. J. Comput. Graph. Stat. 2013, 23, 1009–1027. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural Network Approach for Estimating State of Charge of Lithium-Ion Battery Using Backtracking Search Algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Pedrycz, W.; Chen, S.M. Interpretable Artificial Intelligence: A Perspective of Granular Computing, 1st ed.; Studies in Computational Intelligence; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Hu, C.; Ma, L.; Guo, S.; Guo, G.; Han, Z. Deep learning enabled state-of-charge estimation of LiFePO4 batteries: A systematic validation on state-of-the-art charging protocols. Energy 2022, 246, 123404. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A hybrid neural network model with improved input for state of charge estimation of lithium-ion battery at low temperatures. Renew. Energy 2022, 198, 1328–1340. [Google Scholar] [CrossRef]
- Hannan, M.A.; How, D.N.T.; Lipu, M.S.H.; Ker, P.J.; Dong, Z.Y.; Mansur, M.; Blaabjerg, F. SOC Estimation of Li-ion Batteries With Learning Rate-Optimized Deep Fully Convolutional Network. IEEE Trans. Power Electron. 2021, 36, 7349–7353. [Google Scholar] [CrossRef]
- Rebala, G.; Ravi, A.; Churiwala, S. An Introduction to Machine Learning; Springer International Publishing: San Ramon, CA, USA; San Jose, CA, USA; Hyderabad, India, 2019. [Google Scholar] [CrossRef]
- Zhang, D.; Zhong, C.; Xu, P.; Tian, Y. Deep Learning in the State of Charge Estimation for Li-Ion Batteries of Electric Vehicles: A Review. Machines 2022, 10, 912. [Google Scholar] [CrossRef]
- Tian, Y.; Xia, B.; Sun, W.; Xu, Z.; Zheng, W. A modified model based state of charge estimation of power lithium-ion batteries using unscented Kalman filter. J. Power Sources 2014, 270, 619–626. [Google Scholar] [CrossRef]
- Li, X.; Huang, Z.; Tian, J.; Tian, Y. State-of-charge estimation tolerant of battery aging based on a physics-based model and an adaptive cubature Kalman filter. Energy 2021, 220, 119767. [Google Scholar] [CrossRef]
- Wang, L.; Lu, D.; Liu, Q.; Liu, L.; Zhao, X. State of charge estimation for LiFePO4 battery via dual extended kalman filter and charging voltage curve. Electrochim. Acta 2019, 296, 1009–1017. [Google Scholar] [CrossRef]

| Linear | Training | Test | ||
|---|---|---|---|---|
| Regression | MAE | RMSE | MAE | RMSE |
| Without augmented data | 3.874 (±0.021)% | 4.941 (±0.012)% | 4.089 (±0.205)% | 4.999 (±0.095)% |
| With augmented data (10×) | 3.914 (±0.029)% | 4.970 (±0.018)% | 4.041 (±0.220)% | 4.980 (±0.100)% |
| With augmented data (20×) | 4.004 (±0.027)% | 5.066 (±0.036)% | 3.977 (±0.050)% | 5.044 (±0.052)% |
| MLP | Training | Test | ||
|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |
| Without augmented data | 0.828 (±0.292)% | 1.072 (±0.329)% | 0.553 (±0.051)% | 0.805 (±0.072)% |
| With augmented data (10×) | 0.626 (±0.184)% | 0.848 (±0.190)% | 0.539 (±0.087)% | 0.758 (±0.109)% |
| With augmented data (20×) | 0.722 (±0.222)% | 0.977 (±0.242)% | 0.727 (±0.217)% | 0.978 (±0.246)% |
| CNN | Training | Test | ||
|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | |
| Without augmented data | 0.975 (±0.459)% | 1.173 (±0.531)% | 0.505 (±0.201)% | 0.723 (±0.249)% |
| With augmented data (10×) | 0.371 (±0.269)% | 0.494 (±0.315)% | 0.315 (±0.140)% | 0.478 (±0.124)% |
| With augmented data (20×) | 0.261 (±0.071)% | 0.392 (±0.102)% | 0.270 (±0.068)% | 0.437 (±0.101)% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pohlmann, S.; Mashayekh, A.; Kuder, M.; Neve, A.; Weyh, T. Data Augmentation and Feature Selection for the Prediction of the State of Charge of Lithium-Ion Batteries Using Artificial Neural Networks. Energies 2023, 16, 6750. https://doi.org/10.3390/en16186750
Pohlmann S, Mashayekh A, Kuder M, Neve A, Weyh T. Data Augmentation and Feature Selection for the Prediction of the State of Charge of Lithium-Ion Batteries Using Artificial Neural Networks. Energies. 2023; 16(18):6750. https://doi.org/10.3390/en16186750
Chicago/Turabian StylePohlmann, Sebastian, Ali Mashayekh, Manuel Kuder, Antje Neve, and Thomas Weyh. 2023. "Data Augmentation and Feature Selection for the Prediction of the State of Charge of Lithium-Ion Batteries Using Artificial Neural Networks" Energies 16, no. 18: 6750. https://doi.org/10.3390/en16186750
APA StylePohlmann, S., Mashayekh, A., Kuder, M., Neve, A., & Weyh, T. (2023). Data Augmentation and Feature Selection for the Prediction of the State of Charge of Lithium-Ion Batteries Using Artificial Neural Networks. Energies, 16(18), 6750. https://doi.org/10.3390/en16186750






