Experimental and Numerical Analysis of the Efficacy of a Real Downhole Heat Exchanger
Abstract
:1. Introduction
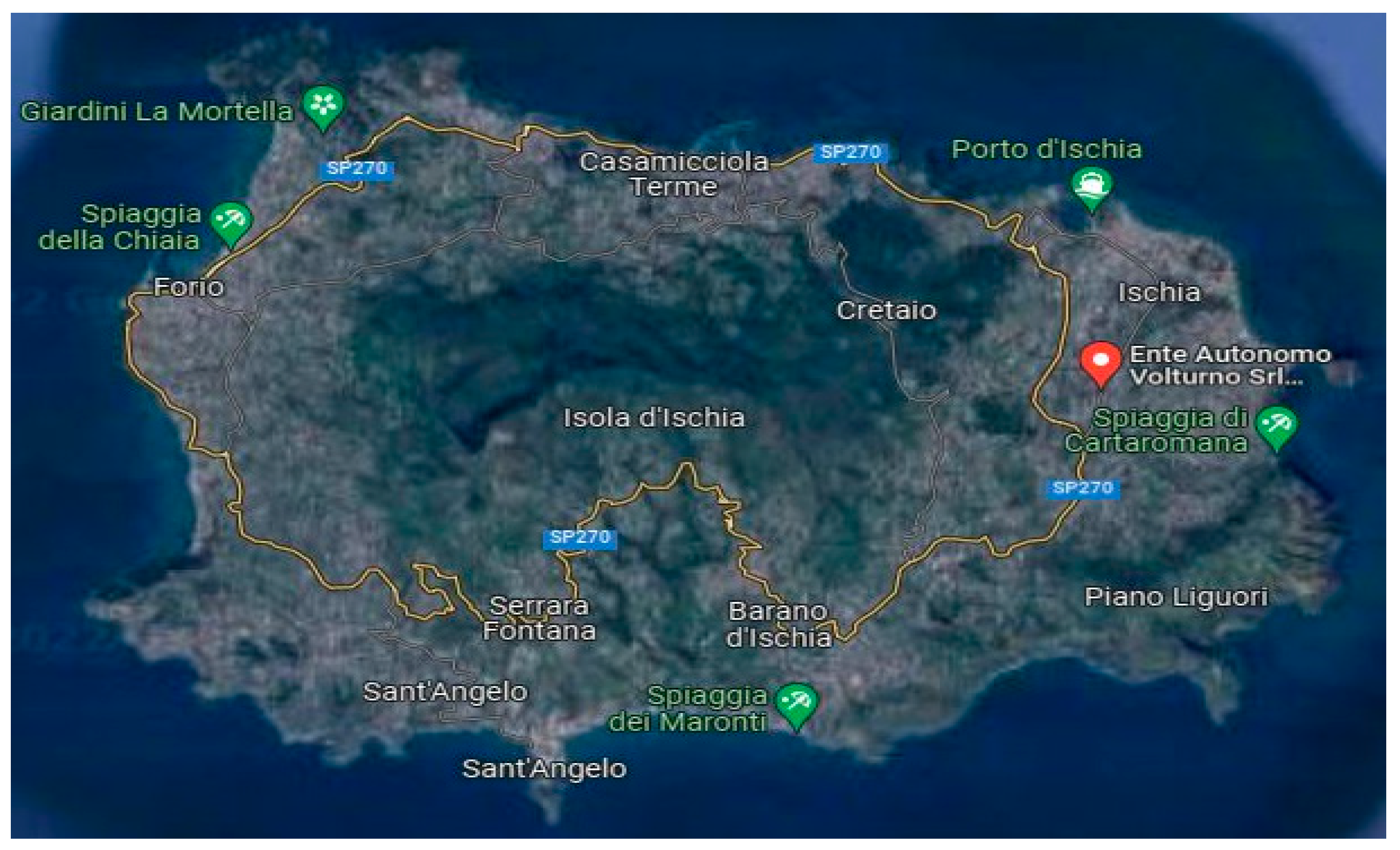
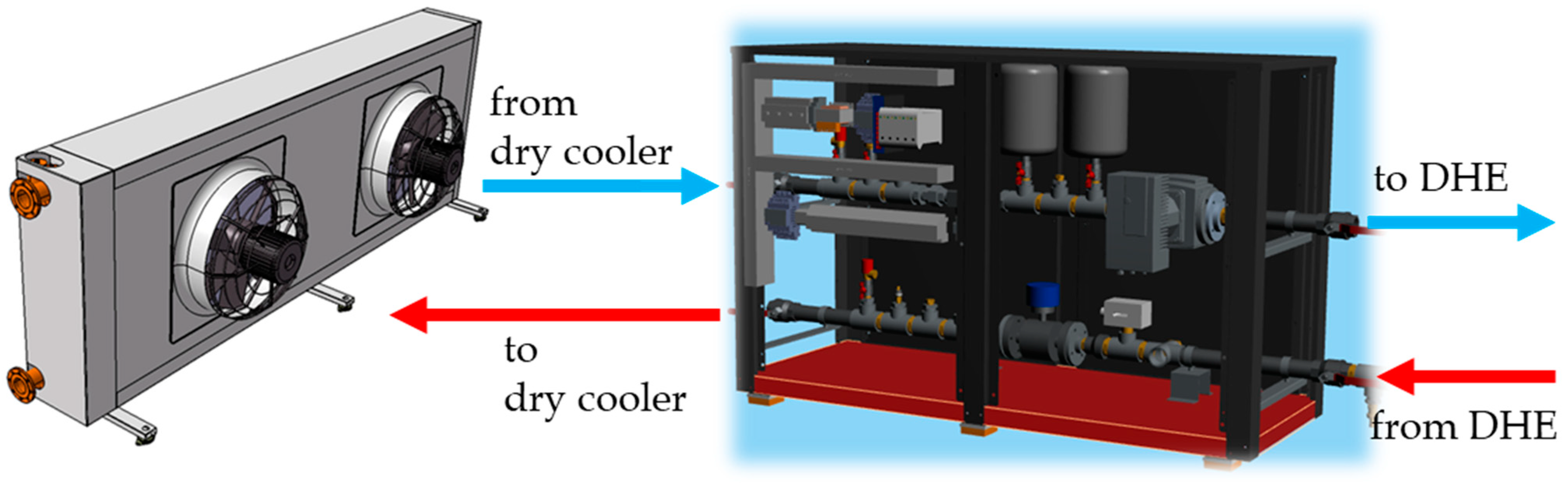
2. Experimental Setup
3. Description of Numerical Model
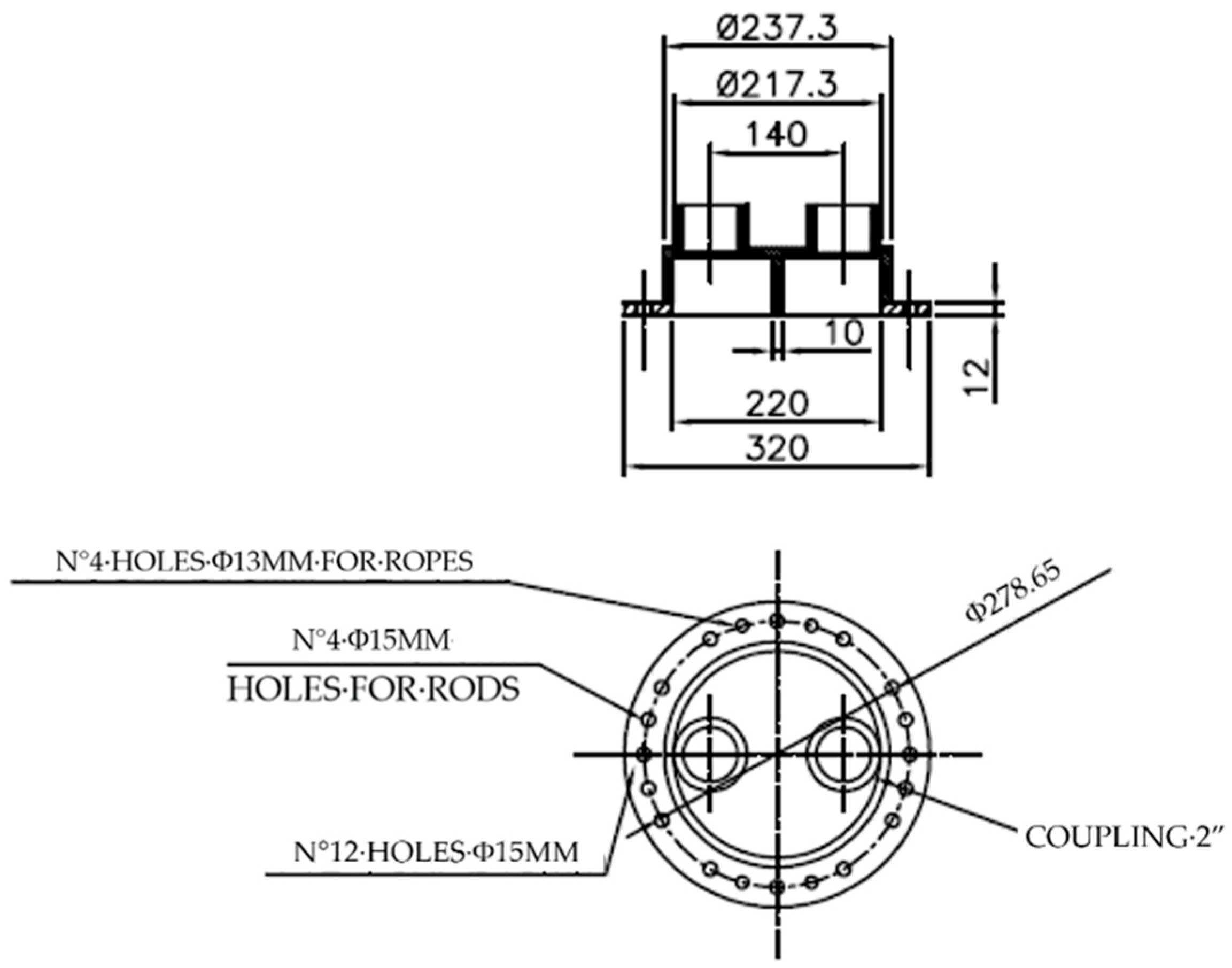
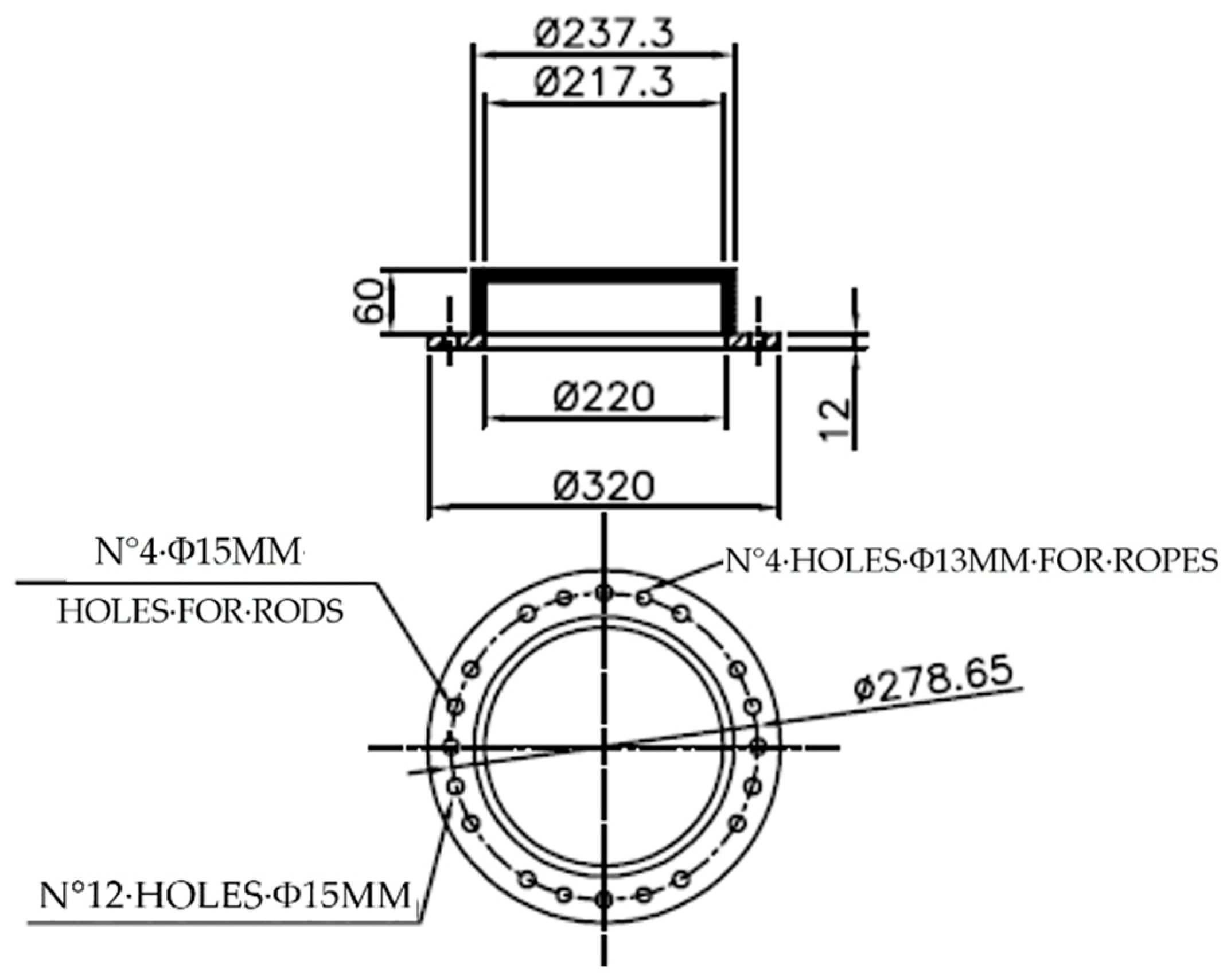
3.1. DHE Geometry
3.2. Fluid Flow and Heat Transfer Model of the DHE
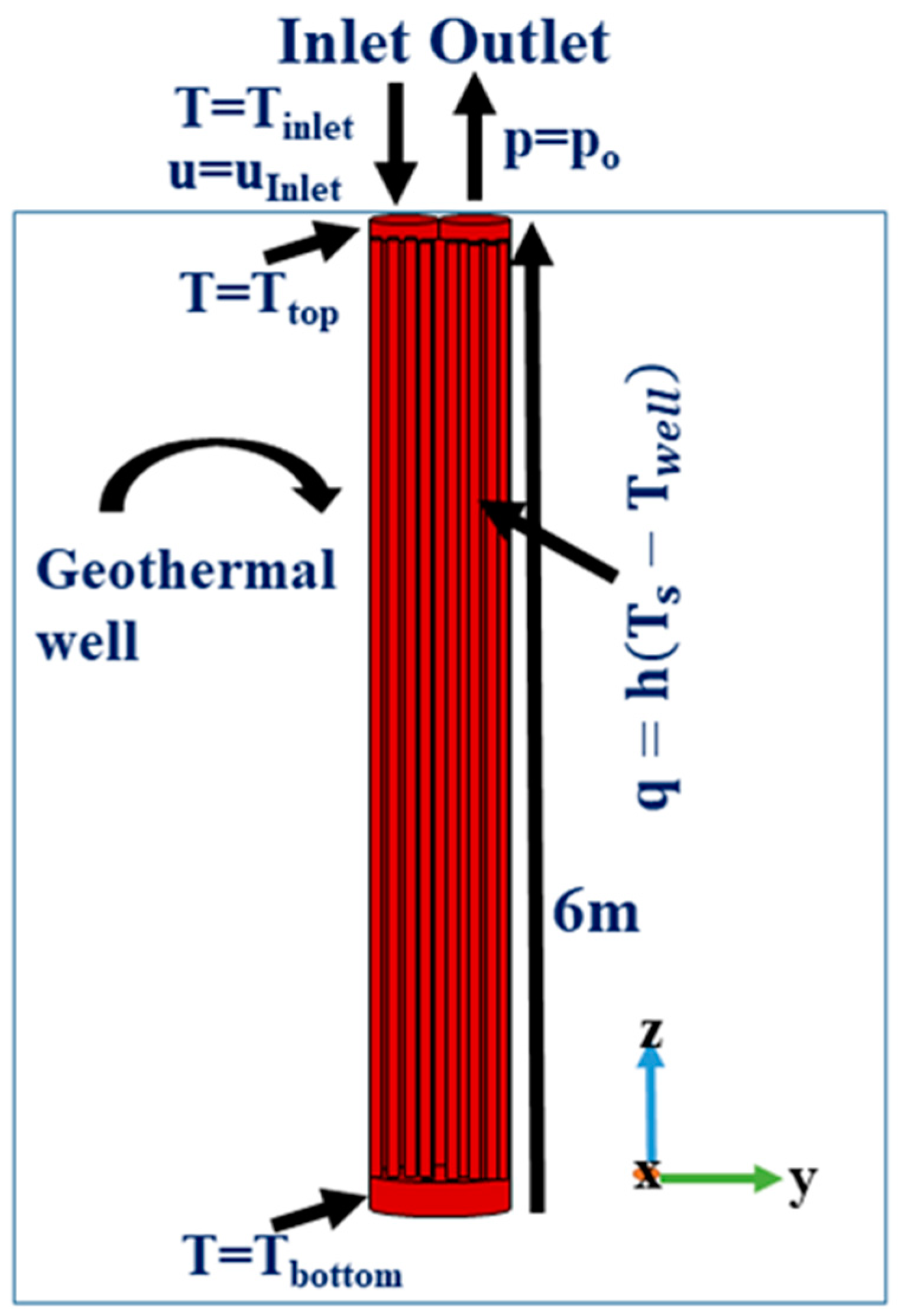
3.3. Domain and Boundary Conditions
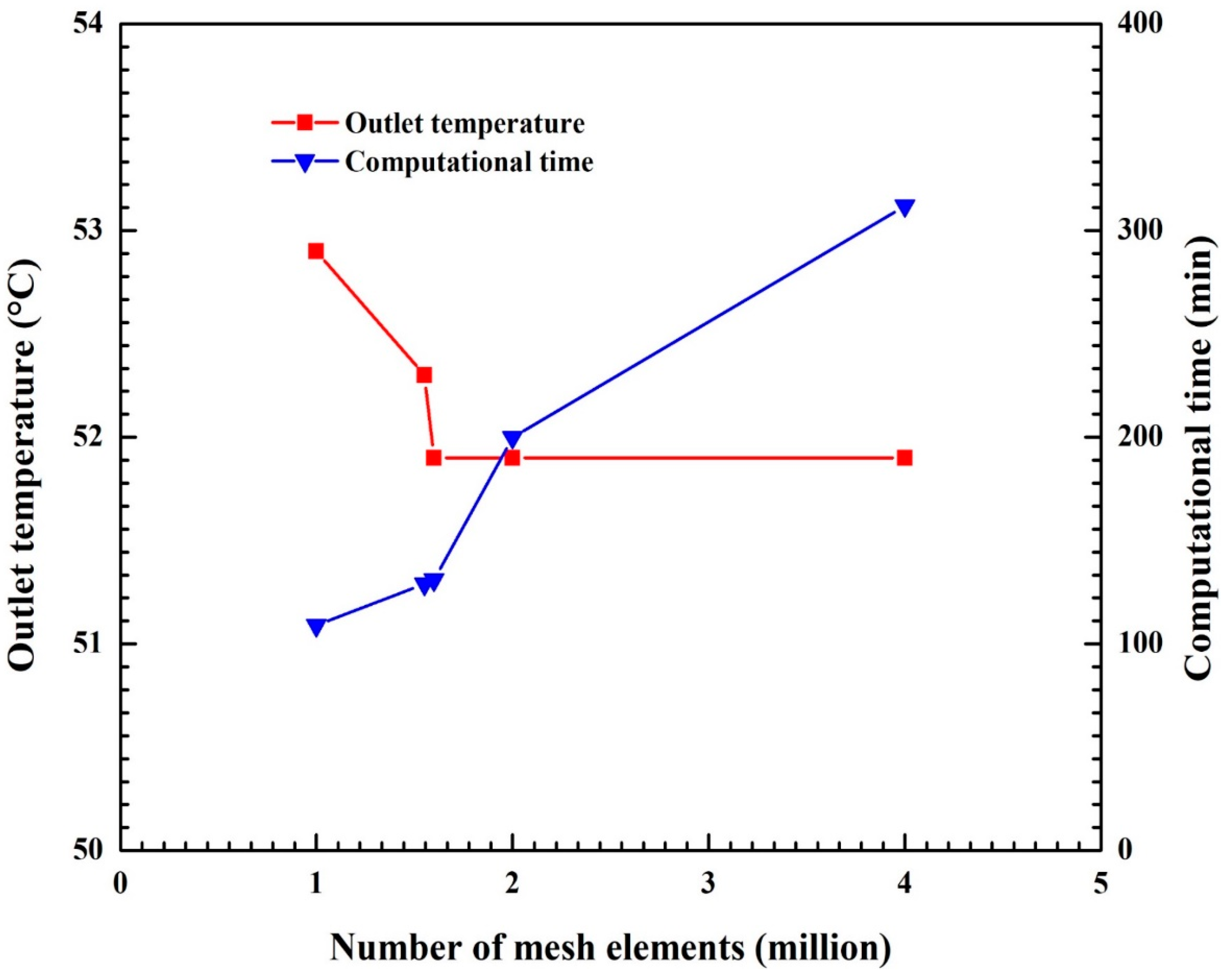
3.4. Mesh Sensitivity Analysis
3.5. Model Assumptions
4. Results and Discussion
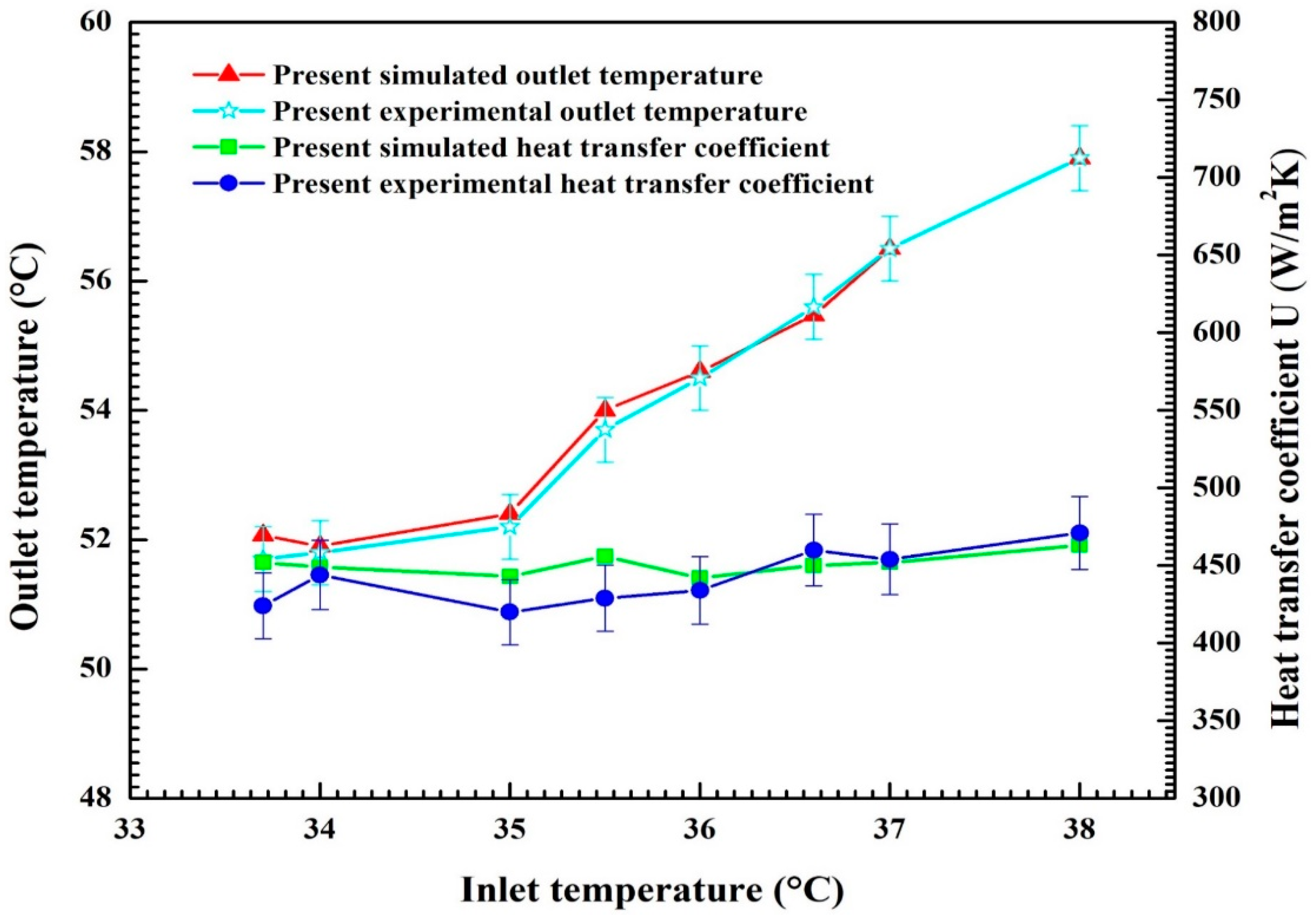
4.1. Verification and Validation
4.2. Outlet Temperature and Heat Transfer Coefficient
4.3. Thermal Power and Efficiency
4.4. Effects of Degree of Salinity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| cp | specific heat capacity: J/kg K |
| Tinlet | inlet temperature, °C |
| Toutlet | outlet temperature, °C |
| Twell | temperature of the well, °C |
| m | molality, parts per thousand |
| U | overall heat transfer coefficient, W/m2 K |
| surface temperature of DHE, °C | |
| logarithmic mean temperature, °C | |
| L | characteristic length, m |
| thermal conductivity, W/m K | |
| q | heat flux, W/m2 |
| heat transfer, W | |
| convective heat transfer coefficient, W/m2 K | |
| Ra | Rayleigh number |
| Pr | Prandtl number |
| Gr | Grashof number |
| D | diameter of tube, m |
| mass flow rate, kg/s | |
| gravitational acceleration, m/s2 | |
| u | velocity, m/s |
| p | fluid pressure, Pa |
| I | identity matrix |
| ∇ | del operator |
| T | stress tensor |
| Greek symbols | |
| kinematic viscosity, m2/s | |
| thermal expansion coefficient, 1/K | |
| density, kg/m3 | |
| µ | dynamic viscosity, Ns/m2 |
| turbulent viscosity, Ns/m2 | |
| efficiency | |
| Acronyms | |
| HEX | heat exchanger |
| DHE | downhole heat exchanger |
| GCHP | ground coupled heat pump |
| FEM | finite element method |
References
- Sarkar, J.; Bhattacharyya, S. Application of Graphene and Graphene-Based Materials in Clean Energy-Related Devices Minghui. Arch. Thermodyn. 2012, 33, 23–40. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Statistics 2021. Stat. Focus-Eurostat 2021, 56, 460. [Google Scholar]
- EU Action to Address the Energy Crisis. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal/eu-action-address-energy-crisis_en (accessed on 27 January 2023).
- Ceglia, F.; Marrasso, E.; Roselli, C.; Sasso, M. Effect of Layout and Working Fluid on Heat Transfer of Polymeric Shell and Tube Heat Exchangers for Small Size Geothermal ORC via 1-D Numerical Analysis. Geothermics 2021, 95, 102118. [Google Scholar] [CrossRef]
- Watson, S. Quantifying the Variability of Wind Energy. Wiley Interdiscip. Rev. Energy Environ. 2014, 3, 330–342. [Google Scholar] [CrossRef]
- Bett, P.E.; Thornton, H.E. The Climatological Relationships between Wind and Solar Energy Supply in Britain. Renew. Energy 2016, 87, 96–110. [Google Scholar] [CrossRef]
- Calise, F.; D’Accadia, M.D.; MacAluso, A.; Piacentino, A.; Vanoli, L. Exergetic and Exergoeconomic Analysis of a Novel Hybrid Solar–Geothermal Polygeneration System Producing Energy and Water. Energy Convers. Manag. 2016, 115, 200–220. [Google Scholar] [CrossRef]
- Crainz, M.; Curto, D.; Franzitta, V.; Longo, S.; Montana, F.; Musca, R.; Sanseverino, E.R.; Telaretti, E. Flexibility Services to Minimize the Electricity Production from Fossil Fuels. A Case Study in a Mediterranean Small Island. Energies 2019, 12, 3492. [Google Scholar] [CrossRef]
- Yildirim, N.; Parmanto, S.; Akkurt, G.G. Thermodynamic Assessment of Downhole Heat Exchangers for Geothermal Power Generation. Renew. Energy 2019, 141, 1080–1091. [Google Scholar] [CrossRef]
- van der Zwaan, B.; Dalla Longa, F. Integrated Assessment Projections for Global Geothermal Energy Use. Geothermics 2019, 82, 203–211. [Google Scholar] [CrossRef]
- Martirosyan, A.V.; Martirosyan, K.V.; Grudyaeva, E.K.; Chernyshev, A.B. Calculation of the Temperature Maximum Value Access Time at the Observation Point. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering, ElConRus 2021, Moscow, Russia, 26 January 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2021; pp. 1014–1018. [Google Scholar]
- Ilyushin, Y.; Golovina, E. Stability of Temperature Field of The Distributed Control System. ARPN J. Eng. Appl. Sci. 2020, 15, 664–668. [Google Scholar]
- Application of Ground Heat Exchangers|Encyclopedia MDPI. Available online: https://encyclopedia.pub/entry/10048 (accessed on 14 July 2022).
- Pouloupatis, P.D.; Florides, G.; Tassou, S. Measurements of Ground Temperatures in Cyprus for Ground Thermal Applications. Renew. Energy 2011, 36, 804–814. [Google Scholar] [CrossRef]
- Zeng, H.; Diao, N.; Fang, Z. Heat Transfer Analysis of Boreholes in Vertical Ground Heat Exchangers. Int. J. Heat Mass. Transf. 2003, 46, 4467–4481. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, H.; Meggers, F.; Zhang, L. Deep Coaxial Borehole Heat Exchanger: Analytical Modeling and Thermal Analysis. Energy 2019, 185, 1298–1313. [Google Scholar] [CrossRef]
- Lund, J.W. The Use of Downhole Heat Exchangers. Geothermics 2003, 32, 535–543. [Google Scholar] [CrossRef]
- Aresti, L.; Christodoulides, P.; Florides, G. A Review of the Design Aspects of Ground Heat Exchangers. Renew. Sustain. Energy Rev. 2018, 92, 757–773. [Google Scholar] [CrossRef]
- Zeng, H.Y.; Diao, N.R.; Fang, Z.H. A Finite Line-Source Model for Boreholes in Geothermal Heat Exchangers. Heat Trans. Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
- Li, M.; Lai, A.C.K. New Temperature Response Functions (G Functions) for Pile and Borehole Ground Heat Exchangers Based on Composite-Medium Line-Source Theory. Energy 2012, 38, 255–263. [Google Scholar] [CrossRef]
- Cui, P.; Li, X.; Man, Y.; Fang, Z. Heat Transfer Analysis of Pile Geothermal Heat Exchangers with Spiral Coils. Appl. Energy 2011, 88, 4113–4119. [Google Scholar] [CrossRef]
- Leroy, A.; Bernier, M. Development of a Novel Spiral Coil Ground Heat Exchanger Model Considering Axial Effects. Appl. Therm. Eng. 2015, 84, 409–419. [Google Scholar] [CrossRef]
- Man, Y.; Yang, H.; Diao, N.; Liu, J.; Fang, Z. A New Model and Analytical Solutions for Borehole and Pile Ground Heat Exchangers. Int. J. Heat Mass. Transf. 2010, 53, 2593–2601. [Google Scholar] [CrossRef]
- Morchio, S.; Fossa, M. Thermal Modeling of Deep Borehole Heat Exchangers for Geothermal Applications in Densely Populated Urban Areas. Therm. Sci. Eng. Prog. 2019, 13, 100363. [Google Scholar] [CrossRef]
- Akhmadullin, I.; Kartushinsky, A. CFD Simulation of Bubbly Flow in a Long Coaxial Heat Exchanger. Therm. Sci. Eng. Prog. 2021, 25, 100991. [Google Scholar] [CrossRef]
- Al-Zyoud, S.; Rühaak, W.; Sass, I. Dynamic Numerical Modeling of the Usage of Groundwater for Cooling in North East Jordan –A Geothermal Case Study. Renew. Energy 2014, 62, 63–72. [Google Scholar] [CrossRef]
- Han, C.; Yu, X. Sensitivity Analysis of a Vertical Geothermal Heat Pump System. Appl. Energy 2016, 170, 148–160. [Google Scholar] [CrossRef]
- Go, G.H.; Lee, S.R.; Nikhil, N.V.; Yoon, S. A New Performance Evaluation Algorithm for Horizontal GCHPs (Ground Coupled Heat Pump Systems) That Considers Rainfall Infiltration. Energy 2015, 83, 766–777. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.R.; Xue, J.; Zosseder, K.; Go, G.H.; Park, H. Evaluation of the Thermal Efficiency and a Cost Analysis of Different Types of Ground Heat Exchangers in Energy Piles. Energy Convers. Manag. 2015, 105, 393–402. [Google Scholar] [CrossRef]
- Carotenuto, A.; Casarosa, C.; Martorano, L. The Geothermal Convector: Experimental and Numerical Results. Appl. Therm. Eng. 1999, 19, 349–374. [Google Scholar] [CrossRef]
- Carotenuto, A.; Casarosa, C.; Dell’isola, M.; Martorano, L. An Aquifer-Well Thermal and Fluid Dynamic Model for Downhole Heat Exchangers with a Natural Convection Promoter. Int. J. Heat Mass. Transf. 1997, 40, 4461–4472. [Google Scholar] [CrossRef]
- Carotenuto, A.; Casarosa, C. A Lumped Parameter Model of the Operating Limits of One-Well Geothermal Plant with down Hole Heat Exchangers. Int. J. Heat Mass. Transf. 2000, 43, 2931–2948. [Google Scholar] [CrossRef]
- Galgaro, A.; Farina, Z.; Emmi, G.; De Carli, M. Feasibility Analysis of a Borehole Heat Exchanger (BHE) Array to Be Installed in High Geothermal Flux Area: The Case of the Euganean Thermal Basin, Italy. Renew. Energy 2015, 78, 93–104. [Google Scholar] [CrossRef]
- Gustafsson, A.M.; Westerlund, L.; Hellström, G. CFD-Modelling of Natural Convection in a Groundwater-Filled Borehole Heat Exchanger. Appl. Therm. Eng. 2010, 30, 683–691. [Google Scholar] [CrossRef]
- Lyu, Z.; Song, X.; Li, G.; Hu, X.; Shi, Y.; Xu, Z. Numerical Analysis of Characteristics of a Single U-Tube Downhole Heat Exchanger in the Borehole for Geothermal Wells. Energy 2017, 125, 186–196. [Google Scholar] [CrossRef]
- Carotenuto, A.; Massarotti, N.; Mauro, A. A New Methodology for Numerical Simulation of Geothermal Down-Hole Heat Exchangers. Appl. Therm. Eng. 2012, 48, 225–236. [Google Scholar] [CrossRef]
- Walsh, S.D.C.; Garapati, N.; Leal, A.M.M.; Saar, M.O. Calculating Thermophysical Fluid Properties during Geothermal Energy Production with NESS and Reaktoro. Geothermics 2017, 70, 146–154. [Google Scholar] [CrossRef]
- Klyukin, Y.I.; Driesner, T.; Steele-Macinnis, M.; Lowell, R.P.; Bodnar, R.J. Effect of Salinity on Mass and Energy Transport by Hydrothermal Fluids Based on the Physical and Thermodynamic Properties of H2O-NaCl. Geofluids 2016, 16, 585–603. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998. [Google Scholar]
- Shi, Y.; Song, X.; Li, G.; Li, R.; Zhang, Y.; Wang, G.; Zheng, R.; Lyu, Z. Numerical Investigation on Heat Extraction Performance of a Downhole Heat Exchanger Geothermal System. Appl. Therm. Eng. 2018, 134, 513–526. [Google Scholar] [CrossRef]
- Lynn, B.; Medved, A.; Griggs, T. A Comparative Analysis on the Impact of Salinity on the Heat Generation of OTEC Plants to Determine the Most Plausible Geographical Location. PAM Rev. Energy Sci. Technol. 2018, 5, 119–130. [Google Scholar] [CrossRef]










| Property Description | Value | Unit |
|---|---|---|
| Tubes’ diameter | 0.020 | m |
| Tubes’ interior diameter | 0.018 | m |
| Tubes’ exterior diameter | 0.022 | m |
| DHE’s length | 6.0 | m |
| Number of tubes | 24 | - |
| Case Number | Tinlet (°C) | Twell (°C) | h (W/m2 K) | Ttop (°C) | Tbottom (°C) |
|---|---|---|---|---|---|
| Case 1 | 33.7 | 54.7 | 206.5 | 65.5 | 47.4 |
| Case 2 | 34.0 | 54.5 | 205.3 | 65.9 | 49.4 |
| Case 3 | 35.0 | 55.0 | 204.0 | 65.2 | 49.9 |
| Case 4 | 35.5 | 56.6 | 208.4 | 65.9 | 54.2 |
| Case 5 | 36.0 | 57.4 | 207.3 | 65.7 | 55.2 |
| Case 6 | 36.6 | 58.2 | 207.8 | 65.5 | 56.3 |
| Case 7 | 37.0 | 59.3 | 209.3 | 65.9 | 57.6 |
| Case 8 | 38.0 | 60.5 | 209.7 | 65.9 | 59.3 |
| Property | Value |
|---|---|
| Thermal conductivity, | 0.598 W/m K |
| Thermal expansion coefficient, | 0.000210 1/K |
| Kinematic viscosity, | 0.0000010023 m2/s |
| Dynamic viscosity, | 0.0010005 Ns/m2 |
| Specific heat capacity, cp | 4183 J/kg K |
| Case Number | Re (−) | Gr (−) | Ra (−) |
|---|---|---|---|
| Case 1 | 3043.5 | 251,062.2 | 1,760,215.1 |
| Case 2 | 3041.8 | 245,483.1 | 1,721,099.1 |
| Case 3 | 3038.6 | 239,106.9 | 1,676,395.3 |
| Case 4 | 3035.3 | 244,287.5 | 1,712,717.2 |
| Case 5 | 3038.6 | 255,844.3 | 1,793,742.9 |
| Case 6 | 3040.2 | 258,235.4 | 1,810,506.9 |
| Case 7 | 3041.8 | 266,205.6 | 1,866,386.8 |
| Case 8 | 3050.1 | 268,995.2 | 1,885,944.7 |
| Property\Degree of Salinity | m = 0 (ppt) | m = 60 (ppt) | m = 120 (ppt) | m = 180 (ppt) |
|---|---|---|---|---|
| Dynamic viscosity, Ns/m2 | 0.001001 | 0.00189 | 0.0028 | 0.00365 |
| Specific Heat capacity, J/(kg K) | 4183 | 4000 | 3860 | 3620 |
| Density, kg/m3 | 1000 | 1028 | 1060 | 1098 |
| Thermal conductivity, W/(m K) | 0.6562 | 0.676 | 0.751 | 0.826 |
| U (W/m2 K) | Q (kW) | Efficiency (−) | Tout (°C) |
|---|---|---|---|
| 424 | 39.0 | 0.75 | 51.7 |
| 444 | 38.7 | 0.76 | 51.8 |
| 420 | 36.6 | 0.75 | 52.5 |
| 429 | 39.3 | 0.58 | 53.7 |
| 434 | 40.0 | 0.55 | 54.5 |
| 460 | 41.1 | 0.51 | 55.6 |
| 454 | 42.2 | 0.46 | 56.5 |
| 471 | 43.2 | 0.39 | 50.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asad, M.; Guida, V.; Mauro, A. Experimental and Numerical Analysis of the Efficacy of a Real Downhole Heat Exchanger. Energies 2023, 16, 6783. https://doi.org/10.3390/en16196783
Asad M, Guida V, Mauro A. Experimental and Numerical Analysis of the Efficacy of a Real Downhole Heat Exchanger. Energies. 2023; 16(19):6783. https://doi.org/10.3390/en16196783
Chicago/Turabian StyleAsad, Muhammad, Vincenzo Guida, and Alessandro Mauro. 2023. "Experimental and Numerical Analysis of the Efficacy of a Real Downhole Heat Exchanger" Energies 16, no. 19: 6783. https://doi.org/10.3390/en16196783
APA StyleAsad, M., Guida, V., & Mauro, A. (2023). Experimental and Numerical Analysis of the Efficacy of a Real Downhole Heat Exchanger. Energies, 16(19), 6783. https://doi.org/10.3390/en16196783







