Influence of Fluidised Bed Inventory on the Performance of Limestone Sorbent in Calcium Looping for Thermochemical Energy Storage
Abstract
:1. Overview
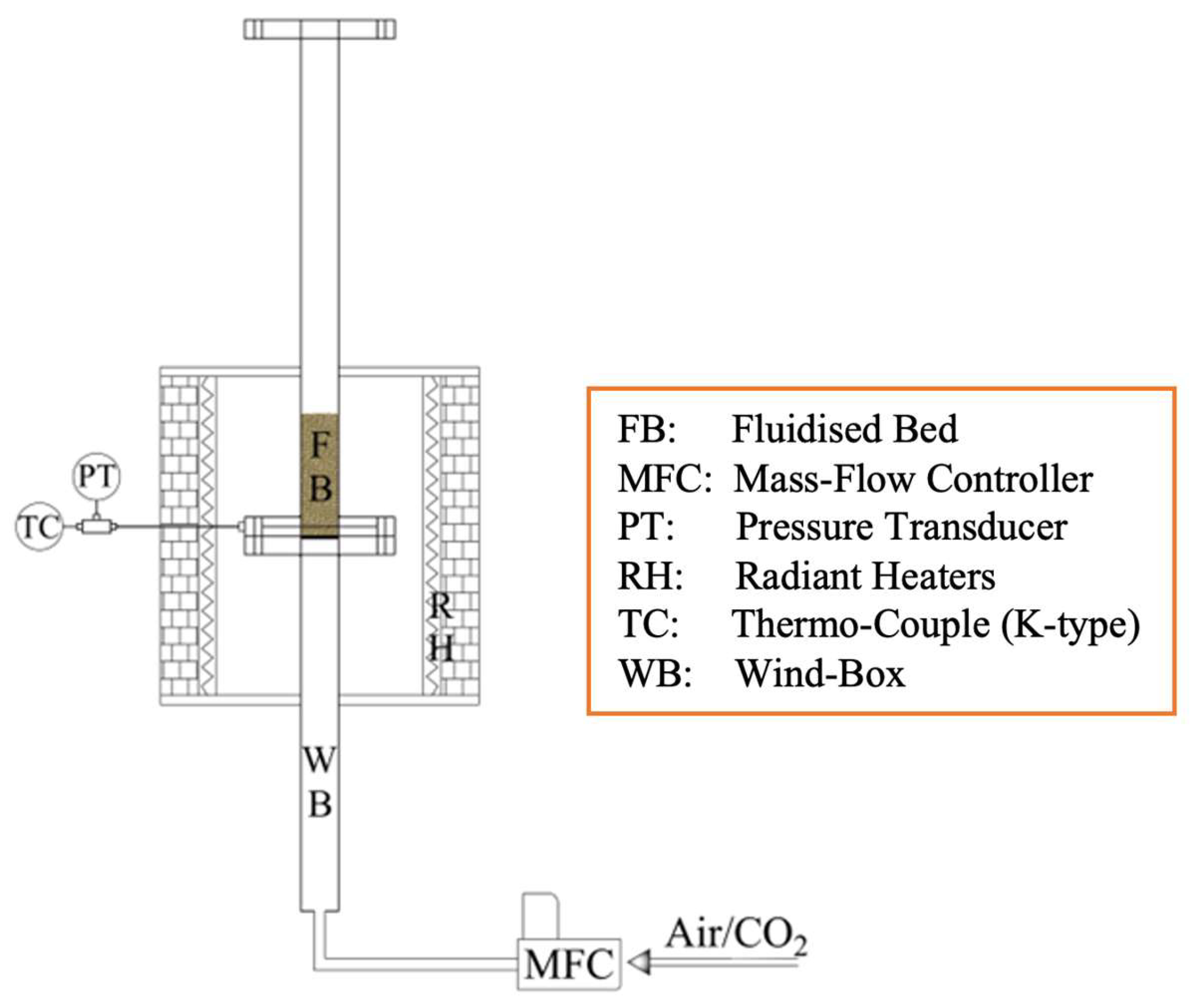
2. Materials, Methods, Equipment, and Operating Conditions
- ○
- Limestone from Sardinia (Italy)—very rich in CaCO3 (98.5%wt.), with initial particle size range between 420 and 590 μm;
- ○
- Silica sand from the Ticino River (Italy), mostly silico-aluminous, initial size range 850–1000 μm;
- ○
- Reagent grade silicon carbide (purity in SiC = 98.80%wt.; size range 600–850 μm). This material was chosen due to its high emissivity/absorption in the solar spectrum [40], making it a very good candidate to improve the opto-thermal properties of the limestone bed.
| Material | Size Range [μm] | umf @ 850–950 °C [m/s] | Main Chemical Composition [%wt.] |
|---|---|---|---|
| Limestone (Sardinia, Italy) | 420–590 | 0.12–0.11 | 98.5% CaCO3 |
| Sand (Ticino River, Italy) | 850–1000 | 0.35–0.33 | 83.9% SiO2; 8.4% Al2O3; 2.4% K2O; 1.8% Na2O |
| Silicon carbide (r.g.) | 600–850 | 0.32–0.30 | 98.80% SiC; 0.20% C; 0.19% Fe |
- ○
- A bed consisting of limestone only (under both calcination and carbonation, superficial gas velocity ug = 0.6 m/s);
- ○
- A bed consisting of a 1:1 mixture of silica sand and limestone (under both calcination and carbonation, ug = 0.7 m/s);
- ○
- A bed consisting of a 1:1 mixture of silicon carbide and limestone (under both calcination and carbonation, ug = 0.7 m/s).
- ○
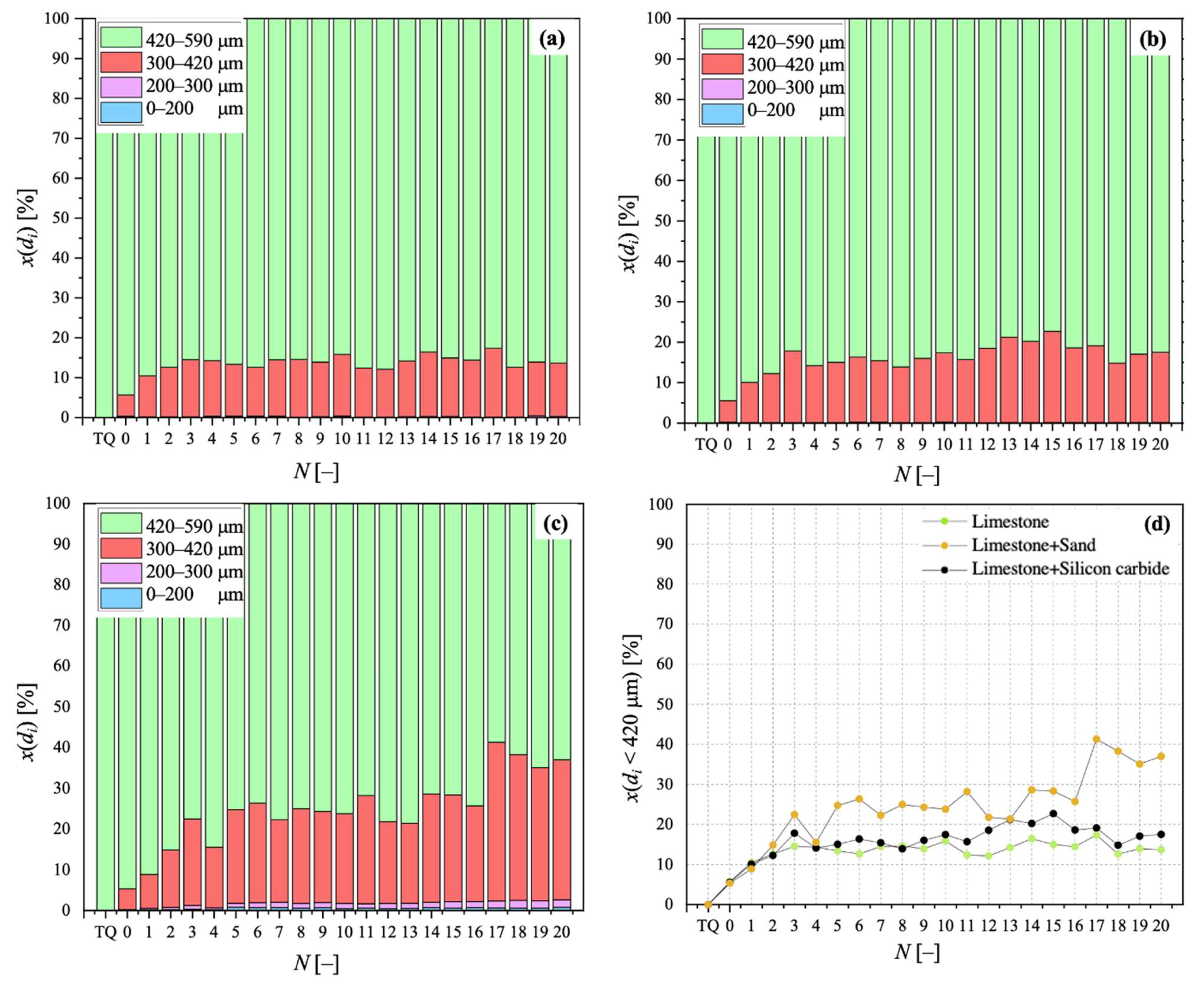
- For its Particle Size Distribution (PSD), via sieving in the size ranges of 0–100, 100–200, 300–420, and 420–590 μm, so as to obtain the mass fraction for particles falling in a size bin with mean diameter di, x(di). PSD data reported in this work refer, in particular, to sorbent samples after calcination stages. PSD characterisation served as a means to analyse particle fragmentation, which is related to FB fluid dynamics;
- ○
- For its bulk density, ρ, by pouring the material into a 50 mL graduated cylinder and measuring the mass and the occupied volume.
3. Results and Discussion
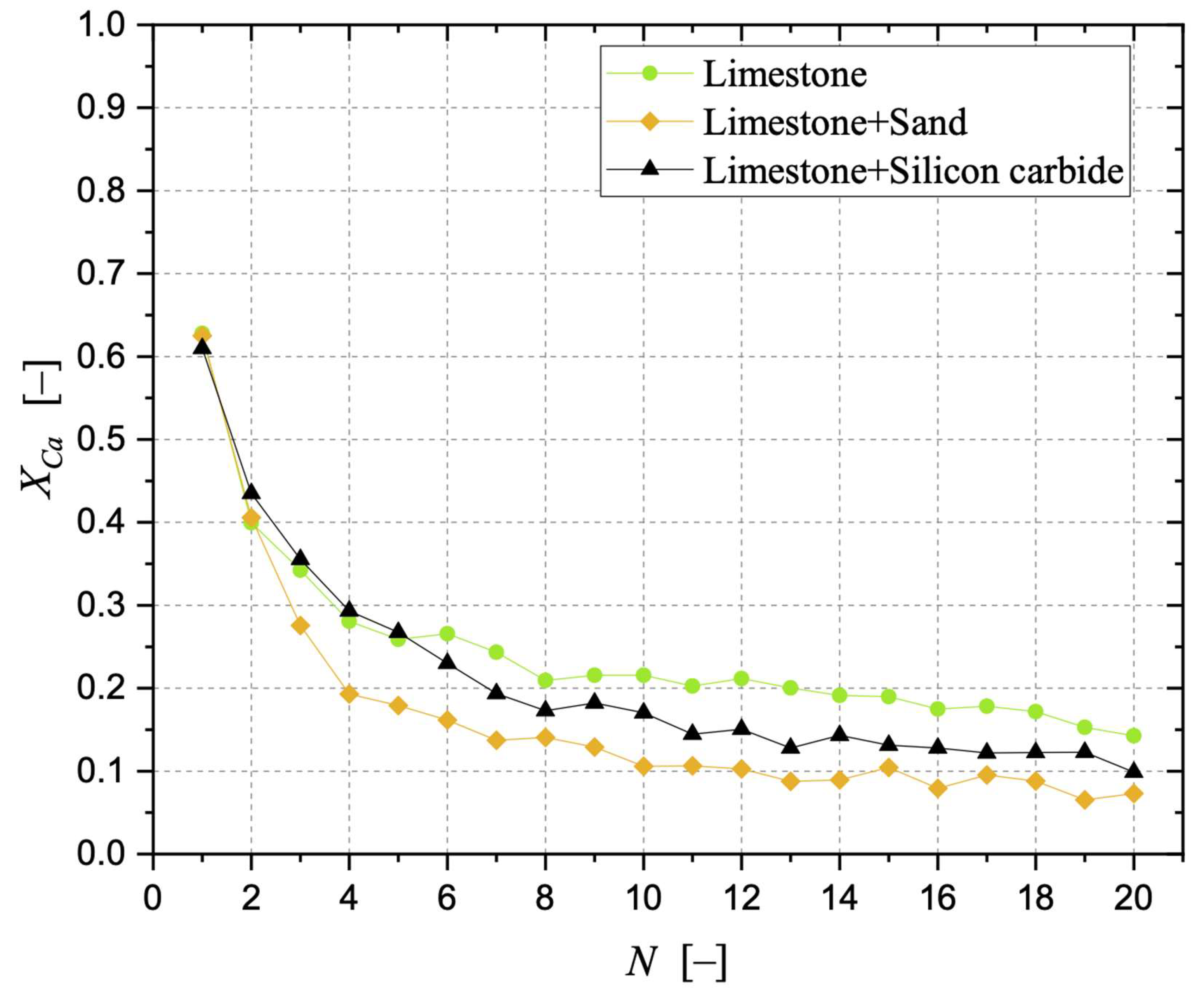
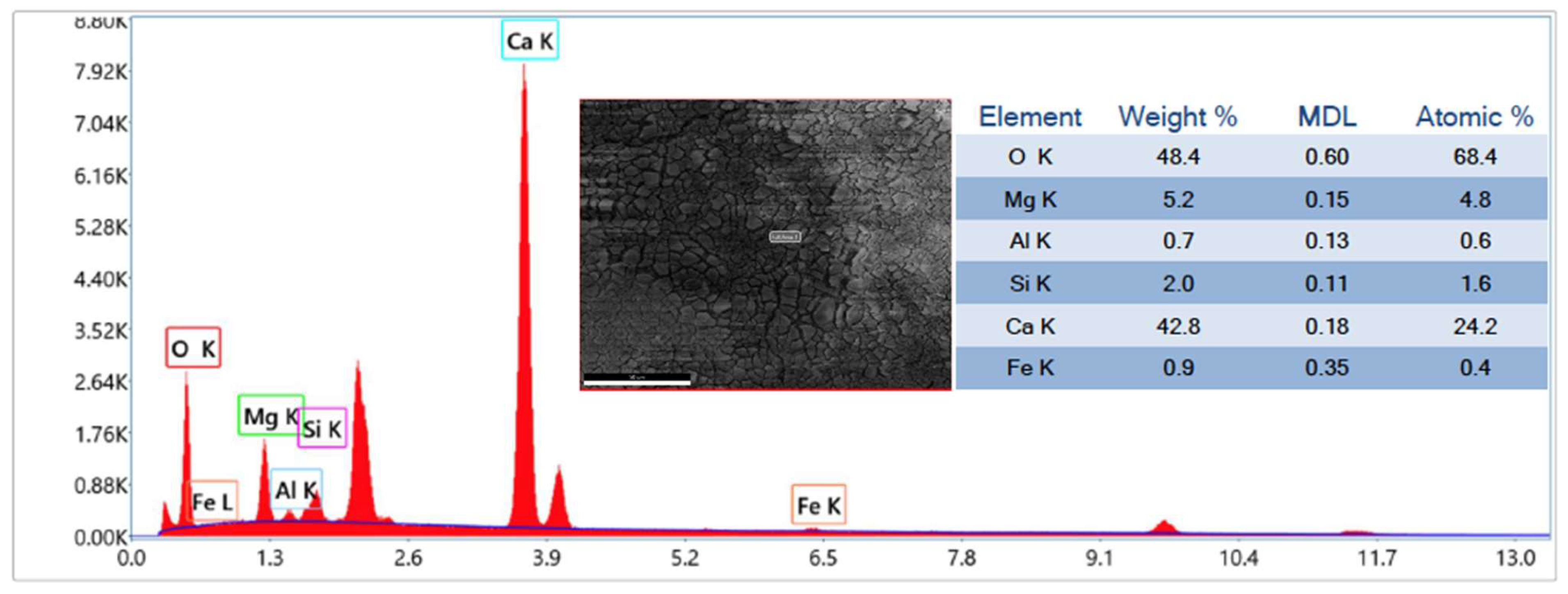
3.1. CaO Carbonation Degree and Interaction of Sorbent with Sand and Silicon Carbide
| CaO(S) + CO2(G) → CaCO3(S) |
| (R1: carbonation) |
| 2CaO(S) + SiO2(S) → 2CaO·SiO2(S) |
| (R2: formation of dicalcium silicate from CaO) |
| 2CaCO3(S) + SiO2(S) → 2CaO·SiO2(S) + 2CO2(G) |
| (R3: formation of dicalcium silicate from CaCO3) |
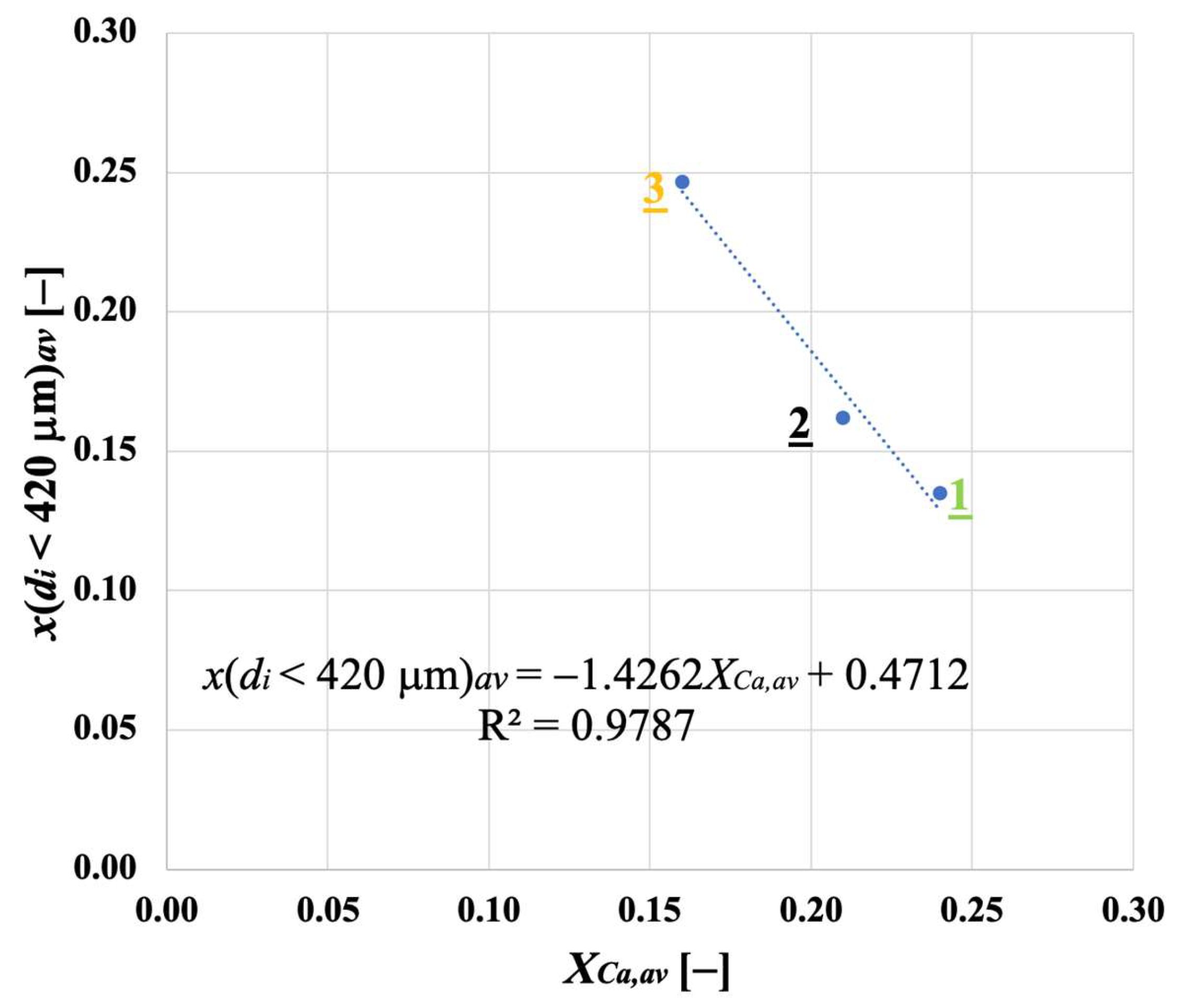
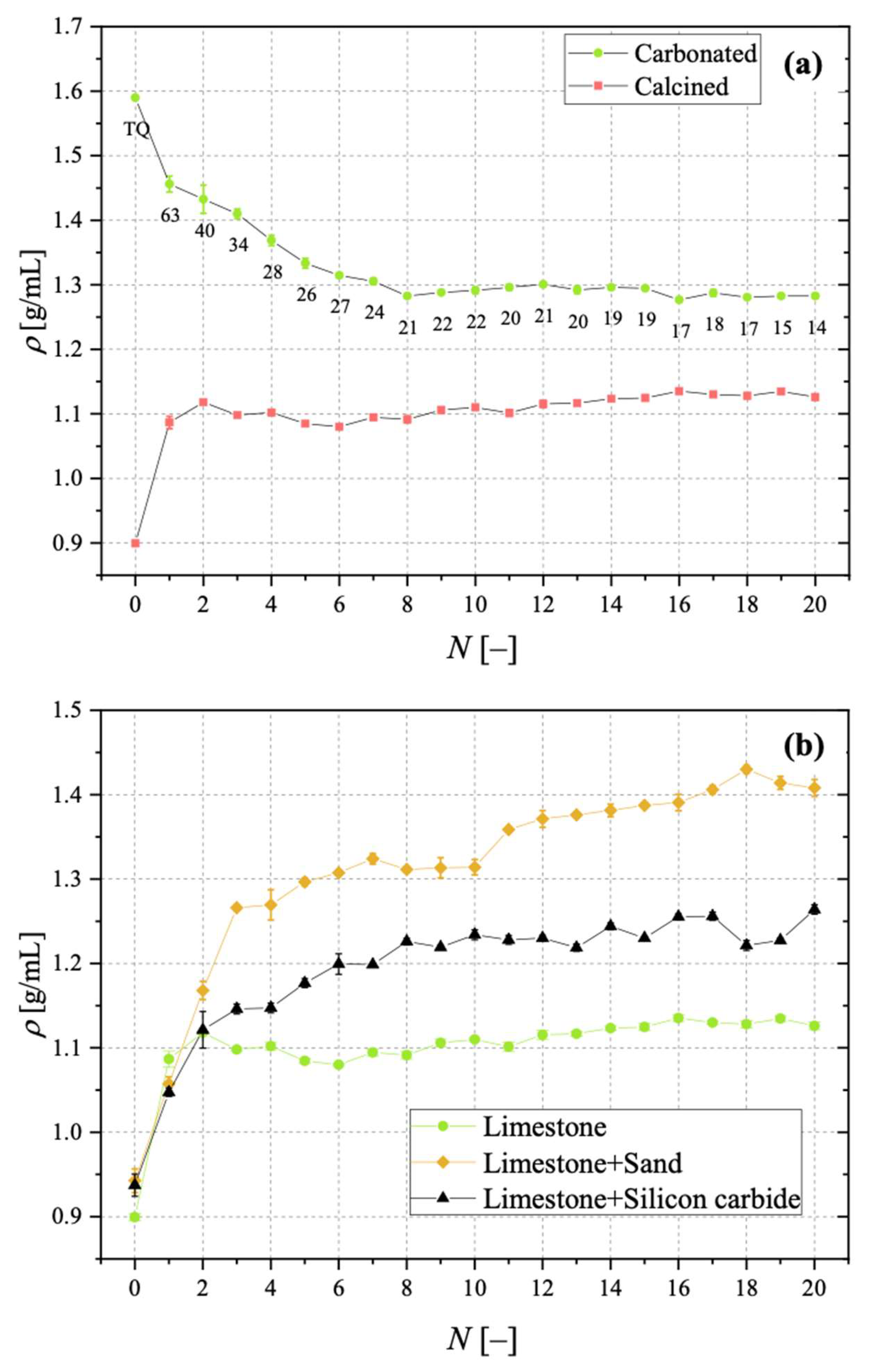
3.2. Particle Size Distribution for Calcined Sorbent
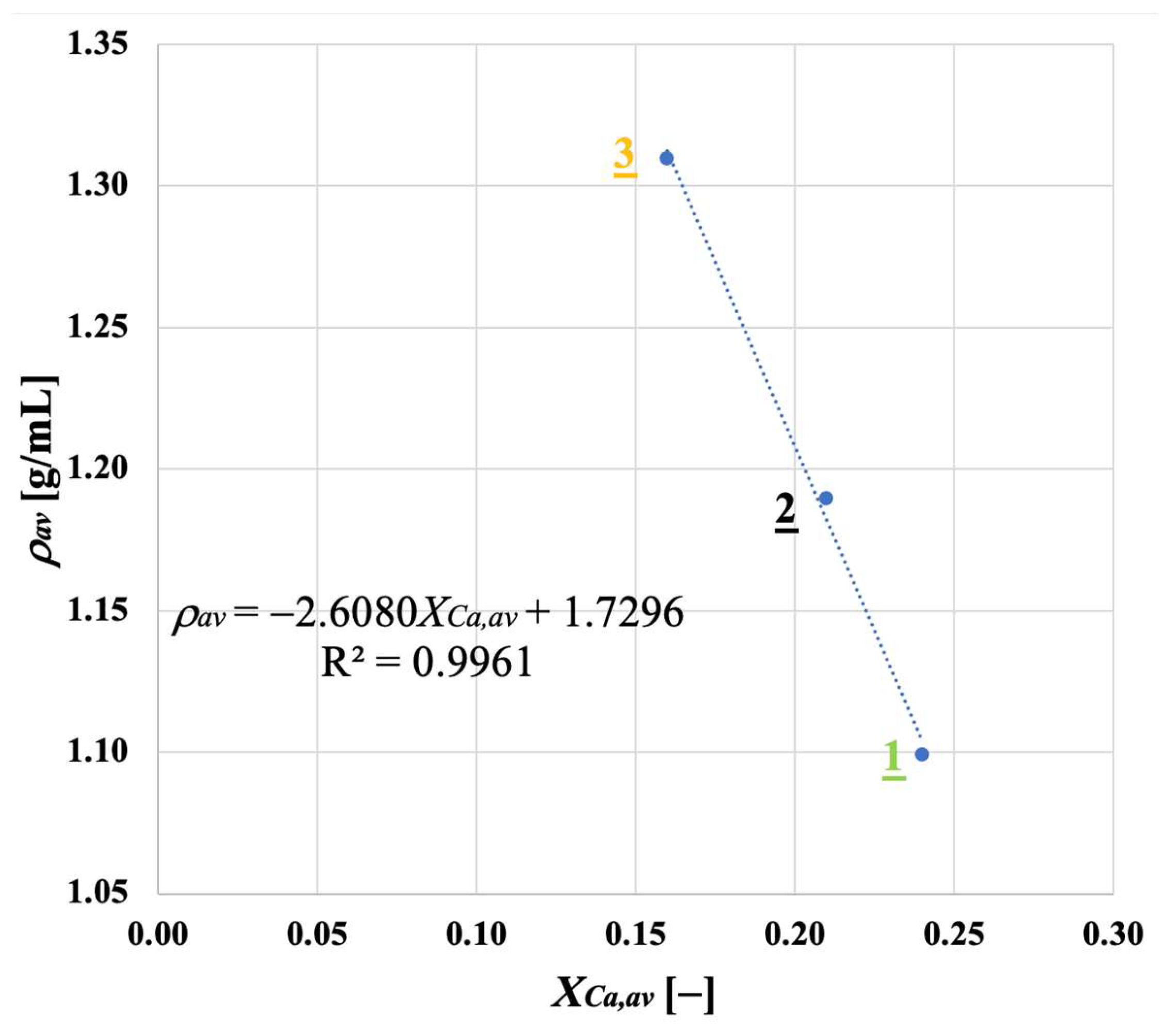
3.3. Bulk Density for Calcined and Carbonated Sorbent
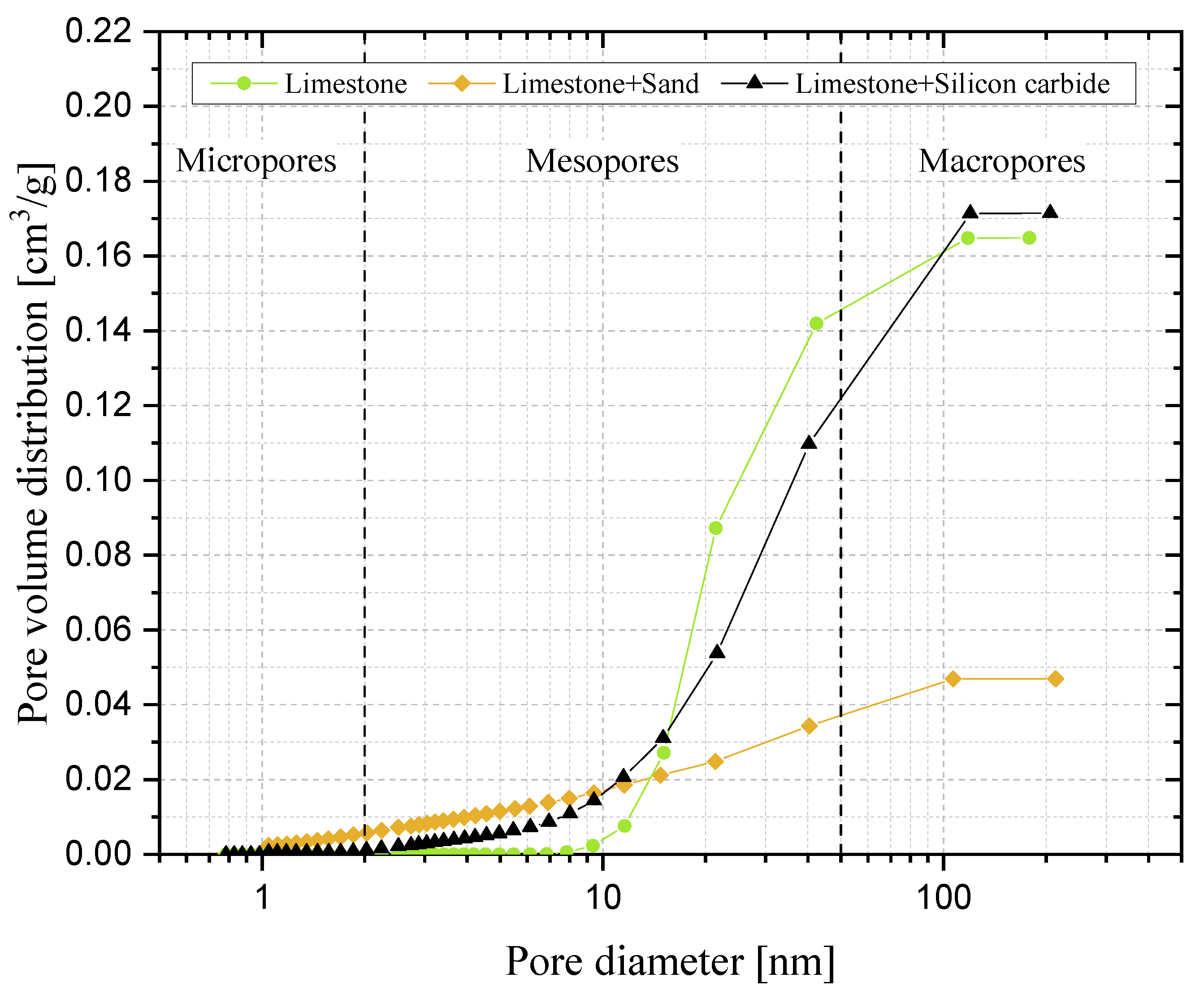
3.4. Reactive Porosity and Porosimetric Analysis
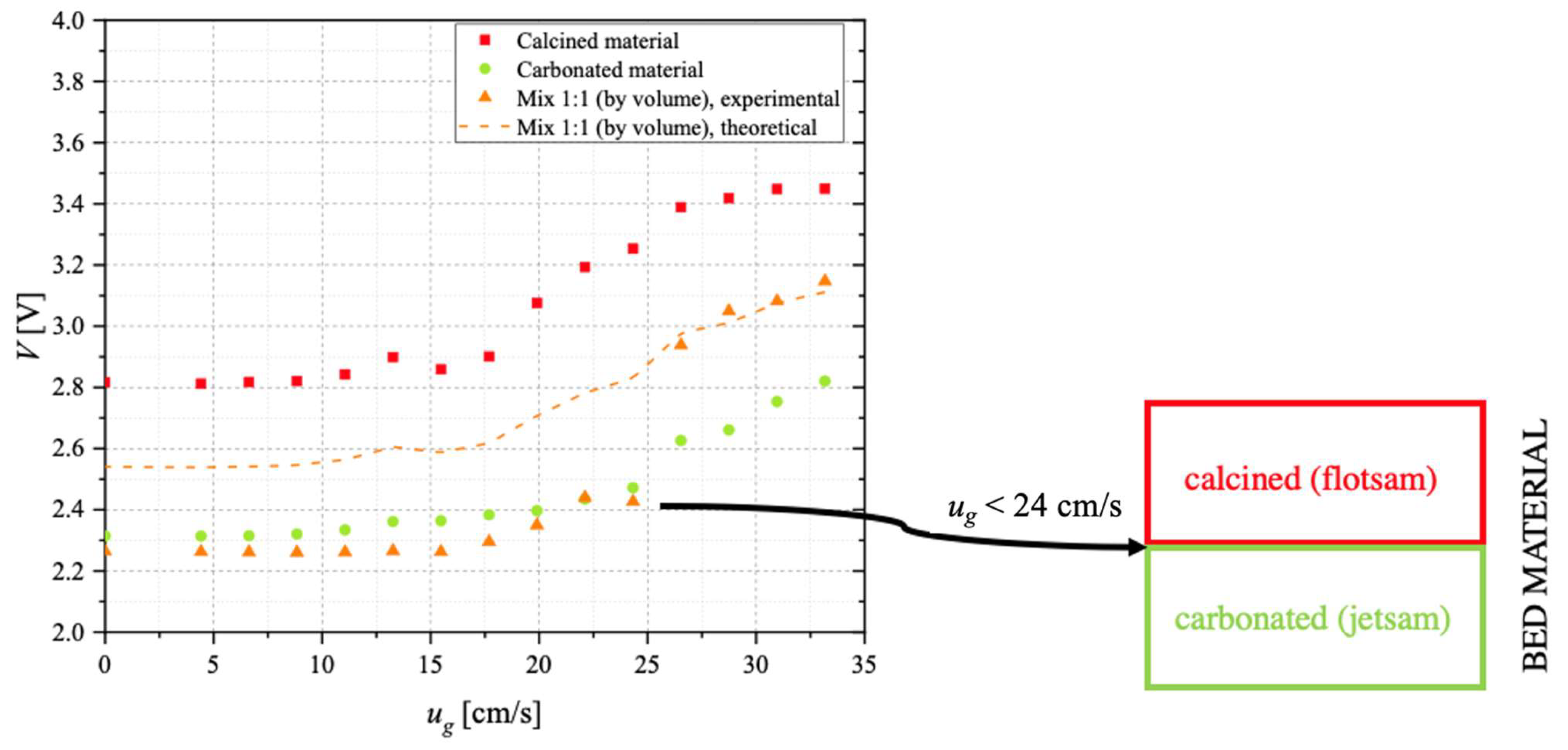
3.5. Segregation Tests
- ○
- V increases with ug, starting from the onset of minimum fluidisation, that is, under fluidised conditions; the larger the gas velocity, the lower the solid concentration;
- ○
- V for the calcined material is larger than for the carbonated sorbent; this reflects the circumstance that calcined particles are more porous and, therefore, material concentration is lower.
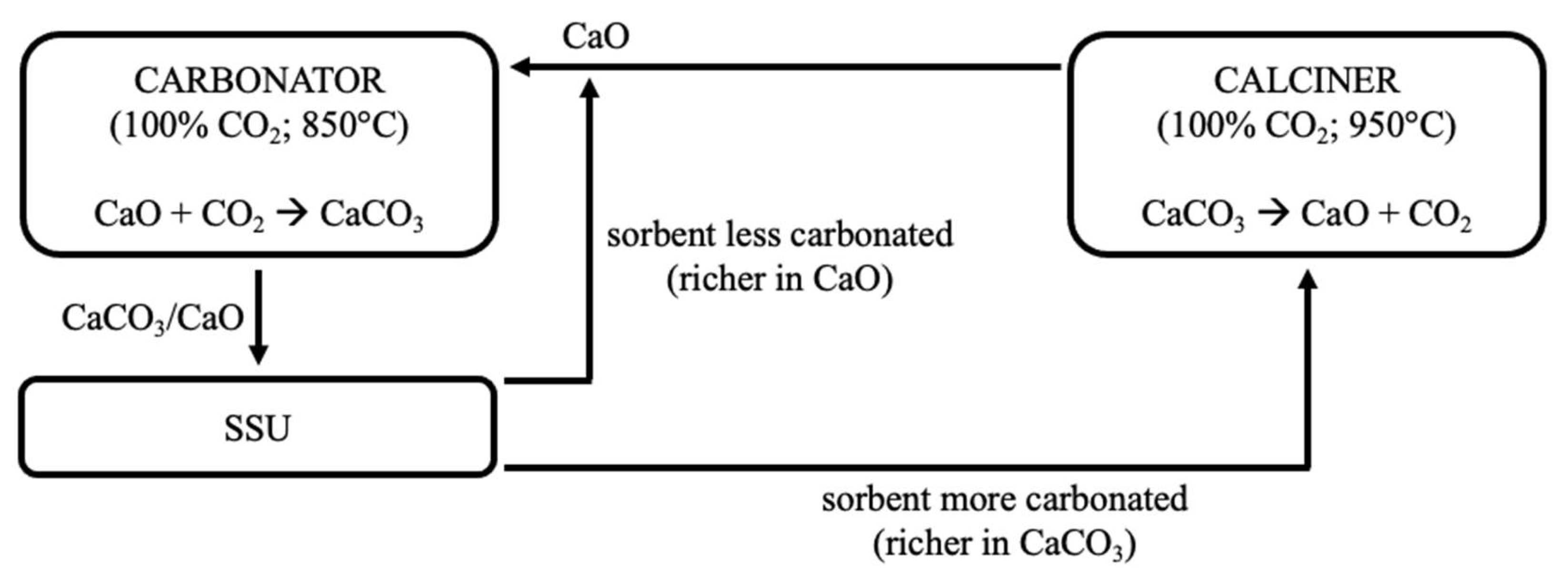
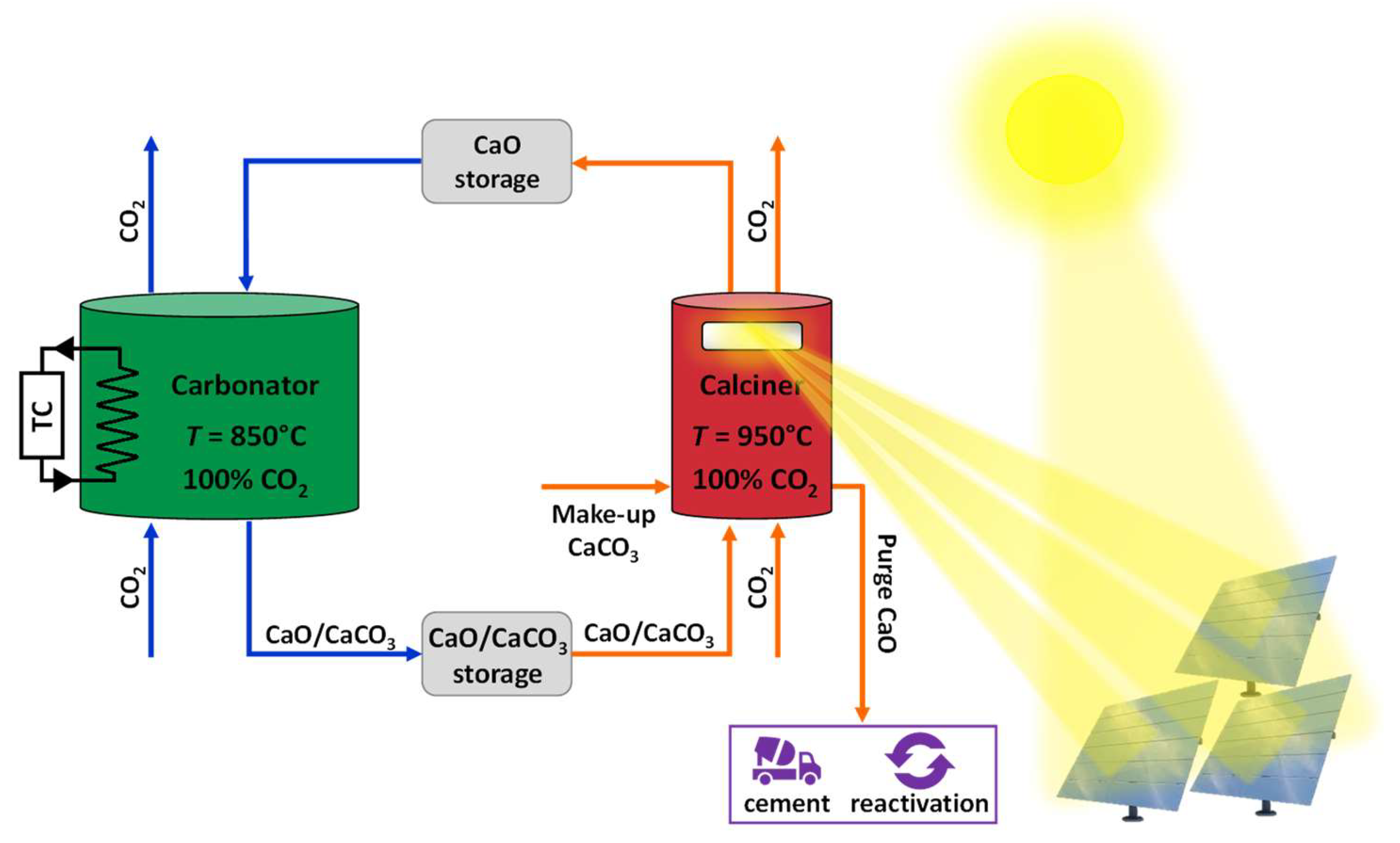
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| di | Particle diameter | [length] |
| k1 | Initial activity constant | [−] |
| k2 | Decay constant | [−] |
| Kcalcined | Relative dielectric constant for the calcined material | [−] |
| Kcarbonated | Relative dielectric constant for the carbonated material | [−] |
| Relative dielectric constant for a bed of calcined material | [−] | |
| Relative dielectric constant for a bed of carbonated material | [−] | |
| Relative dielectric constant of the emulsion phase in fluidised bed | [−] | |
| Kfixed bed | Relative dielectric constant under fixed bed conditions | [−] |
| mcalc | Overall mass of the calcined sample | [mass] |
| mcarb | Overall mass of the carbonated sample | [mass] |
| MW | Molecular weight | [mass/mole] |
| N | Cycles of carbonation/calcination | [−] |
| Partial pressure of CO2 | [pressure] | |
| R2 | Coefficient of determination | [−] |
| T | Temperature | [temperature] |
| ug | Superficial gas velocity | [length/time] |
| umf | Minimum fluidisation velocity | [length/time] |
| V | Voltage | [electric potential] |
| Vcalcined | Voltage for a bed of calcined material | [electric potential] |
| Vcarbonated | Voltage for a bed of carbonated material | [electric potential] |
| Theoretical voltage for a mix of calcined/carbonated material | [electric potential] | |
| Voltage in absence of solid | [electric potential] | |
| x | Absolute granulometric fraction | [−] |
| xav | Average absolute granulometric fraction | [−] |
| xCaO | Mass fraction of CaO in the calcined sorbent | [−] |
| XCa | Degree of carbonation | [−] |
| XCa,av | Average degree of carbonation | [−] |
| ΔHr° | Reaction enthalpy | [energy/mole] |
| ε | Voidage degree for a bed of limestone | [−] |
| εcalcined | Voidage degree for the calcined material | [−] |
| εcarbonated | Voidage degree for the carbonated material | [−] |
| εmix | Voidage degree for a mix of calcined/carbonated material | [−] |
| Porosity of particle in its calcined form at stage N − 1 | [−] | |
| Porosity of particle in its carbonated form at stage N | [−] | |
| Reactive porosity of particle at stage N | [−] | |
| ρ | Bulk density | [mass/volume] |
| ρav | Average bulk density | [mass/volume] |
References
- Ortiz, C.; Chacartegui, R.; Valverde, J.M.; Carro, A.; Tejada, C.; Valverde, J. Increasing the solar share in combined cycles through thermochemical energy storage. Energy Convers. Manag. 2021, 229, 113730. [Google Scholar] [CrossRef]
- Baigorri, J.; Zaversky, F.; Astrain, D. Massive grid-scale energy storage for next-generation concentrated solar power: A review of the potential emerging concepts. Renew. Sustain. Energy Rev. 2023, 185, 113633. [Google Scholar] [CrossRef]
- Xu, D.; Gu, X.; Dai, Y. Concentrating solar assisted biomass-to-fuel conversion through gasification: A review. Front. Energy Res. 2023, 10, 1029477. [Google Scholar] [CrossRef]
- Romero, M.; González-Aguilar, J. Solar thermal CSP technology. Wiley Interdiscip. Rev. Energy Environ. 2014, 3, 42–59. [Google Scholar] [CrossRef]
- Kiefer, C.P.; Caldés, N.; Del Río, P. Will dispatchability be a main driver to the European Union cooperation mechanisms for concentrated solar power? Energy Sources B Econ. Plan. Policy 2021, 16, 42–54. [Google Scholar] [CrossRef]
- Bayon, A.; Bader, R.; Jafarian, M.; Fedunik-Hofman, L.; Sun, Y.; Hinkley, J.; Miller, S.; Lipiński, W. Techno-economic assessment of solid–gas thermochemical energy storage systems for solar thermal power applications. Energy 2018, 149, 473–484. [Google Scholar] [CrossRef]
- Carrillo, A.J.; González-Aguilar, J.; Romero, M.; Coronado, J.M. Solar energy on demand: A review on high temperature thermochemical heat storage systems and materials. Chem. Rev. 2019, 119, 4777–4816. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.I.; Asfand, F.; Al-Ghamdi, S.G. Progress in research and technological advancements of thermal energy storage systems for concentrated solar power. J. Energy Storage 2022, 55, 105860. [Google Scholar] [CrossRef]
- Guo, S.J.; Tian, X.K.; Xu, Y.X.; Yan, J.; Ju, S.H.; Zhao, C.Y. Ca/Co-based composites with improved cyclic stability and optical absorption for advanced thermochemical energy storage systems. Chem. Eng. J. 2023, 468, 143691. [Google Scholar] [CrossRef]
- Nabil, A.; Sánchez Jiménez, P.E.; Pérez Maqueda, L.A.; Perejón, A. Thermochemical energy storage using calcium magnesium acetates under low CO2 pressure conditions. J. Energy Storage 2023, 63, 106958. [Google Scholar] [CrossRef]
- Zhao, C.; Yan, J.; Tian, X.; Xue, X.; Zhao, Y. Progress in thermal energy storage technologies for achieving carbon neutrality. Carb. Neutrality 2023, 2, 10. [Google Scholar] [CrossRef]
- Zhang, H.; Benoit, H.; Perez-Lopèz, I.; Flamant, G.; Tan, T.; Baeyens, J. High-efficiency solar power towers using particle suspensions as heat carrier in the receiver and in the thermal energy storage. Renew. Energy 2017, 111, 438–446. [Google Scholar] [CrossRef]
- Flamant, G.; Grange, B.; Wheeldon, J.; Siros, F.; Valentin, B.; Bataille, F.; Zhang, H.; Deng, Y.; Baeyens, J. Opportunities and challenges in using particle circulation loops for concentrated solar power applications. Prog. Energy Combust. Sci. 2023, 94, 101056. [Google Scholar] [CrossRef]
- Tregambi, C.; Troiano, M.; Montagnaro, F.; Solimene, R.; Salatino, P. Fluidized beds for concentrated solar thermal technologies—A review. Front. Energy Res. 2021, 9, 618421. [Google Scholar] [CrossRef]
- Jiang, K.; Kong, Y.; Xu, C.; Ge, Z.; Du, X. Experimental performance of gas-solid countercurrent fluidized bed particle solar receiver with high-density suspension. Appl. Therm. Eng. 2022, 213, 118661. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, S.; Kim, S.W. Heat absorption characteristics of gas in a directly irradiated solar fluidized bed receiver with tube shaped immersed transmission window. Sol. Energy 2022, 232, 388–397. [Google Scholar] [CrossRef]
- Alvarez Rivero, M.; Rodrigues, D.; Pinheiro, C.I.C.; Cardoso, J.P.; Mendes, L.F. Solid–gas reactors driven by concentrated solar energy with potential application to calcium looping: A comparative review. Renew. Sustain. Energy Rev. 2022, 158, 112048. [Google Scholar] [CrossRef]
- Wang, F.; Deng, S.; Zhao, J.; Wang, J.; Sun, T.; Yan, J. Performance and economic assessments of integrating geothermal energy into coal-fired power plant with CO2 capture. Energy 2017, 119, 278–287. [Google Scholar] [CrossRef]
- Yang, N.; Zhou, Y.; Ge, X. A flexible CO2 capture operation scheme design and evaluation of a coal-fired power plant integrated with a novel DCP and retrofitted solar system. Energy 2019, 170, 73–84. [Google Scholar] [CrossRef]
- Tregambi, C.; Bareschino, P.; Mancusi, E.; Pepe, F.; Montagnaro, F.; Solimene, R.; Salatino, P. Modelling of a concentrated solar power—Photovoltaics hybrid plant for carbon dioxide capture and utilization via calcium looping and methanation. Energy Convers. Manag. 2021, 230, 113792. [Google Scholar] [CrossRef]
- Tregambi, C.; Bareschino, P.; Hanak, D.P.; Montagnaro, F.; Pepe, F.; Mancusi, E. Modelling of an integrated process for atmospheric carbon dioxide capture and methanation. J. Clean. Prod. 2022, 356, 131827. [Google Scholar] [CrossRef]
- Atkinson, K.; Hughes, R.; Macchi, A. Application of the calcium looping process for thermochemical storage of variable energy. Energies 2023, 16, 3299. [Google Scholar] [CrossRef]
- Choi, D.; Noh, S.; Park, Y. Enhancing solar absorption and reversibility in calcium looping-based energy storage via salt-promoted CaO. Chem. Eng. J. 2023, 470, 144036. [Google Scholar] [CrossRef]
- Desage, L.; McCabe, E.; Vieira, A.P.; Humphries, T.D.; Paskevicius, M.; Buckley, C.E. Thermochemical batteries using metal carbonates: A review of heat storage and extraction. J. Energy Storage 2023, 71, 107901. [Google Scholar] [CrossRef]
- Li, L.; Rahbari, A.; Taheri, M.; Pottas, R.; Wang, B.; Hangi, M.; Matthews, L.; Yue, L.; Zapata, J.; Kreider, P.; et al. Experimental evaluation of an indirectly-irradiated packed-bed solar thermochemical reactor for calcination–carbonation chemical looping. Chem. Eng. J. 2023, 468, 143543. [Google Scholar] [CrossRef]
- Pascual, S.; Romeo, L.M.; Lisbona, P. Optimized Ca-looping thermochemical energy storage under dynamic operation for concentrated solar power. J. Energy Storage 2023, 68, 107587. [Google Scholar] [CrossRef]
- Quang, D.V.; Milani, D.; Zahra, M.A. A review of potential routes to zero and negative emission technologies via the integration of renewable energies with CO2 capture processes. Int. J. Greenh. Gas Control 2023, 124, 103862. [Google Scholar] [CrossRef]
- Sun, M.; Liu, T.; Wang, X.; Liu, T.; Li, M.; Chen, G.; Jiang, D. Roles of thermal energy storage technology for carbon neutrality. Carb. Neutrality 2023, 2, 12. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, l.; Li, Z.; Shi, L. A calcium looping system powered by renewable electricity for long-term thermochemical energy storage, residential heat supply and carbon capture. Energy Convers. Manag. 2023, 276, 116592. [Google Scholar] [CrossRef]
- Benitez-Guerrero, M.; Valverde, J.M.; Sanchez-Jimenez, P.E.; Perejon, A.; Perez-Maqueda, L.A. Multicycle activity of natural CaCO3 minerals for thermochemical energy storage in concentrated solar power plants. Sol. Energy 2017, 153, 188–199. [Google Scholar] [CrossRef]
- Tregambi, C.; Di Lauro, F.; Montagnaro, F.; Salatino, P.; Solimene, R. 110th anniversary: Calcium looping coupled with concentrated solar power for carbon capture and thermochemical energy storage. Ind. Eng. Chem. Res. 2019, 58, 21262–21272. [Google Scholar] [CrossRef]
- Colelli, G.; Chacartegui, R.; Ortiz, C.; Carro, A.; Arena, A.P.; Verda, V. Life cycle and environmental assessment of calcium looping (CaL) in solar thermochemical energy storage. Energy Convers. Manag. 2022, 257, 115428. [Google Scholar] [CrossRef]
- Sayyah, M.; Lu, Y.; Masel, R.I.; Suslick, K.S. Mechanical activation of CaO-based adsorbents for CO2 capture. ChemSusChem 2013, 6, 193–198. [Google Scholar] [CrossRef]
- Di Lauro, F.; Tregambi, C.; Montagnaro, F.; Salatino, P.; Chirone, R.; Solimene, R. Improving the performance of calcium looping for solar thermochemical energy storage and CO2 capture. Fuel 2021, 298, 120791. [Google Scholar] [CrossRef]
- Antzara, A.; Heracleous, E.; Lemonidou, A.A. Improving the stability of synthetic CaO-based CO2 sorbents by structural promoters. Appl. Energy 2015, 156, 331–343. [Google Scholar] [CrossRef]
- Benitez-Guerrero, M.; Valverde, J.M.; Sanchez-Jimenez, P.E.; Perejon, A.; Perez-Maqueda, L.A. Calcium-looping performance of mechanically modified Al2O3-CaO composites for energy storage and CO2 capture. Chem. Eng. J. 2018, 334, 2343–2355. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Yan, X.; Wang, Z.; Liu, W. CaO/CaCO3 thermochemical heat storage performance of CaO-based micrometre-sized tubular composite. Energy Convers. Manag. 2020, 222, 113222. [Google Scholar] [CrossRef]
- García-Plaza, J.; Díaz-Heras, M.; Mondragón, R.; Hernández, L.; Calderón, A.; Barreneche, C.; Canales-Vázquez, J.; Fernández, A.I.; Almendros-Ibáñez, J.A. Experimental study of different coatings on silica sand in a directly irradiated fludised bed: Thermal behaviour and cycling analysis. Appl. Therm. Eng. 2022, 217, 119169. [Google Scholar] [CrossRef]
- Da, Y.; Xuan, Y.; Teng, L.; Zhang, K.; Liu, X.; Ding, Y. Calcium-based composites for direct solar-thermal conversion and thermochemical energy storage. Chem. Eng. J. 2020, 382, 122815. [Google Scholar] [CrossRef]
- Zheng, H.; Song, C.; Bao, C.; Liu, X.; Xuan, Y.; Li, Y.; Ding, Y. Dark calcium carbonate particles for simultaneous full-spectrum solar thermal conversion and large-capacity thermochemical energy storage. Sol. Energy Mater. Sol. Cells 2020, 207, 110364. [Google Scholar] [CrossRef]
- Teixeira, P.; Afonso, E.; Pinheiro, C.I.C. Tailoring waste-derived materials for Calcium-Looping application in thermochemical energy storage systems. J. CO2 Util. 2022, 65, 102180. [Google Scholar] [CrossRef]
- Champagne, V.K., III; Pisaturo, G.; Clarke, D.R. High temperature oxides for selective absorption of thermal radiation. J. Eur. Ceram. Soc. 2023, 43, 7656–7667. [Google Scholar] [CrossRef]
- Da, Y.; Zhou, J.; Zeng, F. Calcium-based composites directly irradiated by solar spectrum for thermochemical energy storage. Chem. Eng. J. 2023, 456, 140986. [Google Scholar] [CrossRef]
- Pascual, S.; Lisbona, P.; Bailera, M.; Romeo, L.M. Design and operational performance maps of calcium looping thermochemical energy storage for concentrating solar power plants. Energy 2021, 220, 119715. [Google Scholar] [CrossRef]
- Pascual, S.; Lisbona, P.; Romeo, L.M. Operation maps in calcium looping thermochemical energy storage for concentrating solar power plants. J. Energy Storage 2022, 55, 105771. [Google Scholar] [CrossRef]
- Sarrión, B.; Perejón, A.; Sánchez-Jiménez, P.E.; Pérez-Maqueda, L.A.; Valverde, J.M. Role of calcium looping conditions on the performance of natural and synthetic Ca-based materials for energy storage. J. CO2 Util. 2018, 28, 374–384. [Google Scholar] [CrossRef]
- Xu, T.X.; Tian, X.K.; Khosa, A.A.; Yan, J.; Ye, Q.; Zhao, C.Y. Reaction performance of CaCO3/CaO thermochemical energy storage with TiO2 dopant and experimental study in a fixed-bed reactor. Energy 2021, 236, 121451. [Google Scholar] [CrossRef]
- Han, R.; Xing, S.; Wu, X.; Pang, C.; Lu, S.; Su, Y.; Liu, Q.; Song, C.; Gao, J. Relevant influence of alkali carbonate doping on the thermochemical energy storage of Ca-based natural minerals during CaO/CaCO3 cycles. Renew. Energy 2022, 181, 267–277. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, Y.; Liu, X. Enhancing direct solar thermochemical performance of modified CaCO3 with thermal transport networks composed of tetrapod-shaped ZnO whiskers. Sol. Energy Mater. Sol. Cells 2022, 248, 111981. [Google Scholar] [CrossRef]
- Carro, A.; Chacartegui, R.; Ortiz, C.; Arcenegui-Troya, J.; Pérez-Maqueda, L.A.; Becerra, J.A. Integration of calcium looping and calcium hydroxide thermochemical systems for energy storage and power production in concentrating solar power plants. Energy 2023, 283, 128388. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, X.; Xuan, Y.; Song, C.; Liu, D.; Zhu, Q.; Zhu, Z.; Gao, K.; Li, Y.; Ding, Y. Thermochemical heat storage performances of fluidized black CaCO3 pellets under direct concentrated solar irradiation. Renew. Energy 2021, 178, 1353–1369. [Google Scholar] [CrossRef]
- Tregambi, C.; Di Lauro, F.; Pascual, S.; Lisbona, P.; Romeo, L.M.; Solimene, R.; Salatino, P.; Montagnaro, F. Solar-driven calcium looping in fluidized beds for solar thermochemical energy storage. Chem. Eng. J. 2023, 466, 142708. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, X.; Xuan, Y.; Ding, Y.; Flamant, G. Efficient direct solar-driven thermochemical energy storage of (AlMgFeMn)OxCaCO3 pellets in a fluidized bed reactor. Energy Convers. Manag. 2023, 285, 116990. [Google Scholar] [CrossRef]
- Gravina, T.; Lirer, L.; Marzocchella, A.; Petrosino, P.; Salatino, P. Fluidization and attrition of pyroclastic granular solids. J. Volcanol. Geotherm. Res. 2004, 138, 27–42. [Google Scholar] [CrossRef]
- Olivieri, G.; Marzocchella, A.; Salatino, P. Segregation of fluidized binary mixtures of granular solids. AIChE J. 2004, 50, 3095–3106. [Google Scholar] [CrossRef]
- Alonso, M.; Fernández, J.R.; Abanades, J.C. Kinetic study of belite formation in cement raw meals used in the calcium looping CO2 capture process. Ind. Eng. Chem. Res. 2019, 58, 5445–5454. [Google Scholar] [CrossRef]
- Gazulla, M.F.; Gómez, M.P.; Orduña, M.; Barba, A. Physico-chemical characterisation of silicon carbide refractories. J. Eur. Ceram. Soc. 2006, 26, 3451–3458. [Google Scholar] [CrossRef]
- Coppola, A.; Sattari, A.; Montagnaro, F.; Scala, F.; Salatino, P. Performance of limestone-based sorbent for sorption-enhanced gasification in dual interconnected fluidized bed reactors. AIChE J. 2023, 69, e17588. [Google Scholar] [CrossRef]




| Bed | Calcination Temperature and Atmosphere | Carbonation Temperature and Atmosphere | Value of ug for Calcination and Carbonation at Reaction Temperature |
|---|---|---|---|
| Limestone | 950 °C; 100% CO2 | 850 °C; 100% CO2 | 0.6 m/s |
| Limestone + Sand (1:1) | 0.7 m/s | ||
| Limestone + Silicon carbide (1:1) | 0.7 m/s |
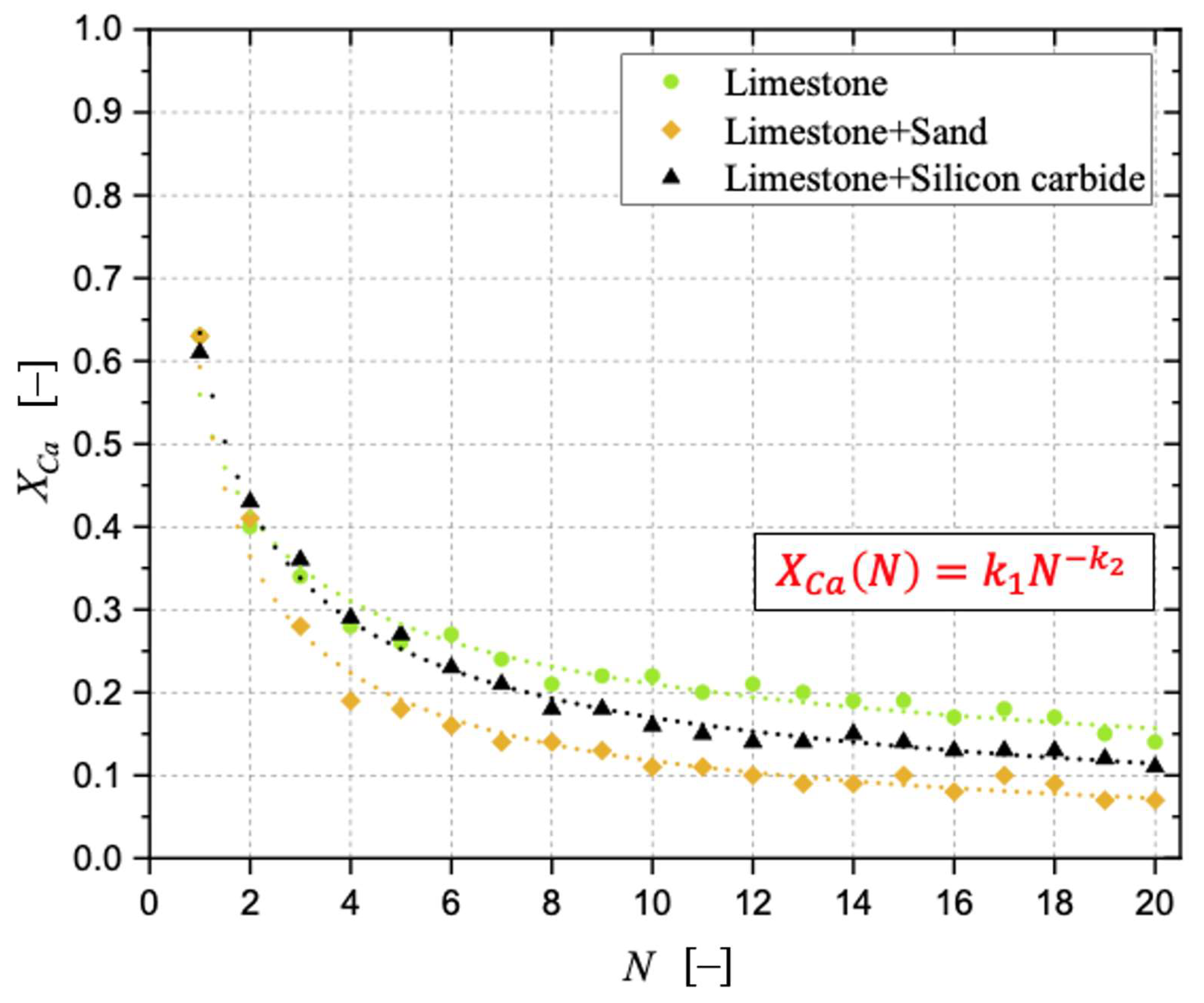
| k2 [–] | R2 [–] | |
|---|---|---|
| Limestone | 0.425 | 0.967 |
| Limestone + Silicon carbide | 0.572 | 0.993 |
| Limestone + Sand | 0.703 | 0.988 |
| Carbonation Reactivity | Fragmentation Propensity | Bulk Density for Calcined Material | |
|---|---|---|---|
| Limestone | Higher | Lower | Lower |
| Limestone + Silicon carbide | Intermediate | Intermediate | Intermediate |
| Limestone + Sand | Lower | Higher | Higher |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Lauro, F.; Tregambi, C.; Montagnaro, F.; Molignano, L.; Salatino, P.; Solimene, R. Influence of Fluidised Bed Inventory on the Performance of Limestone Sorbent in Calcium Looping for Thermochemical Energy Storage. Energies 2023, 16, 6942. https://doi.org/10.3390/en16196942
Di Lauro F, Tregambi C, Montagnaro F, Molignano L, Salatino P, Solimene R. Influence of Fluidised Bed Inventory on the Performance of Limestone Sorbent in Calcium Looping for Thermochemical Energy Storage. Energies. 2023; 16(19):6942. https://doi.org/10.3390/en16196942
Chicago/Turabian StyleDi Lauro, Francesca, Claudio Tregambi, Fabio Montagnaro, Laura Molignano, Piero Salatino, and Roberto Solimene. 2023. "Influence of Fluidised Bed Inventory on the Performance of Limestone Sorbent in Calcium Looping for Thermochemical Energy Storage" Energies 16, no. 19: 6942. https://doi.org/10.3390/en16196942
APA StyleDi Lauro, F., Tregambi, C., Montagnaro, F., Molignano, L., Salatino, P., & Solimene, R. (2023). Influence of Fluidised Bed Inventory on the Performance of Limestone Sorbent in Calcium Looping for Thermochemical Energy Storage. Energies, 16(19), 6942. https://doi.org/10.3390/en16196942









