Impact of Superconducting Cables on a DC Railway Network
Abstract
:1. Introduction
2. Objective and Methodology
2.1. Objective
2.2. Methodology
3. Design and Modeling of DC Superconducting Cable and Its Auxiliary Systems
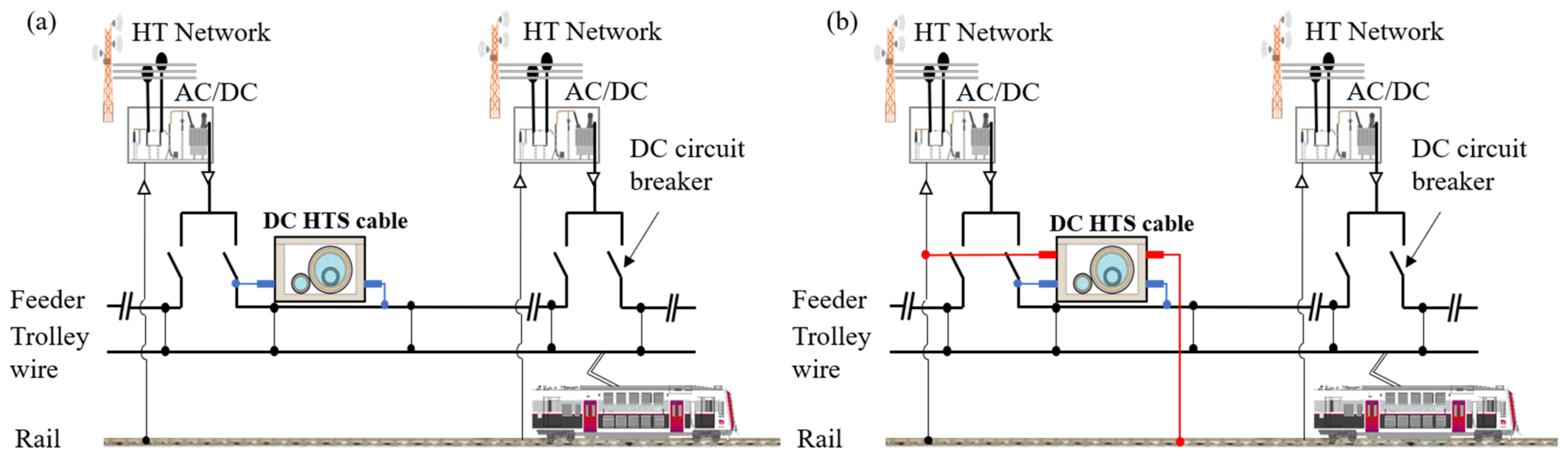
3.1. Cable Topologies
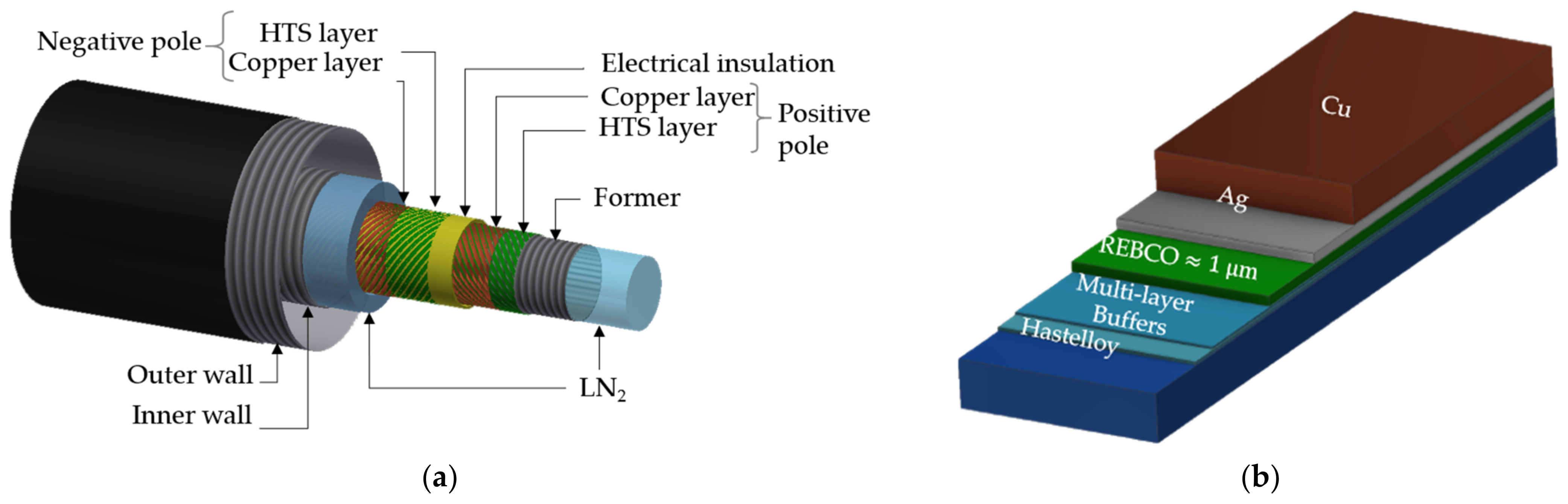
3.2. Design of the DC HTS Cables
3.3. Design of the Cooling System
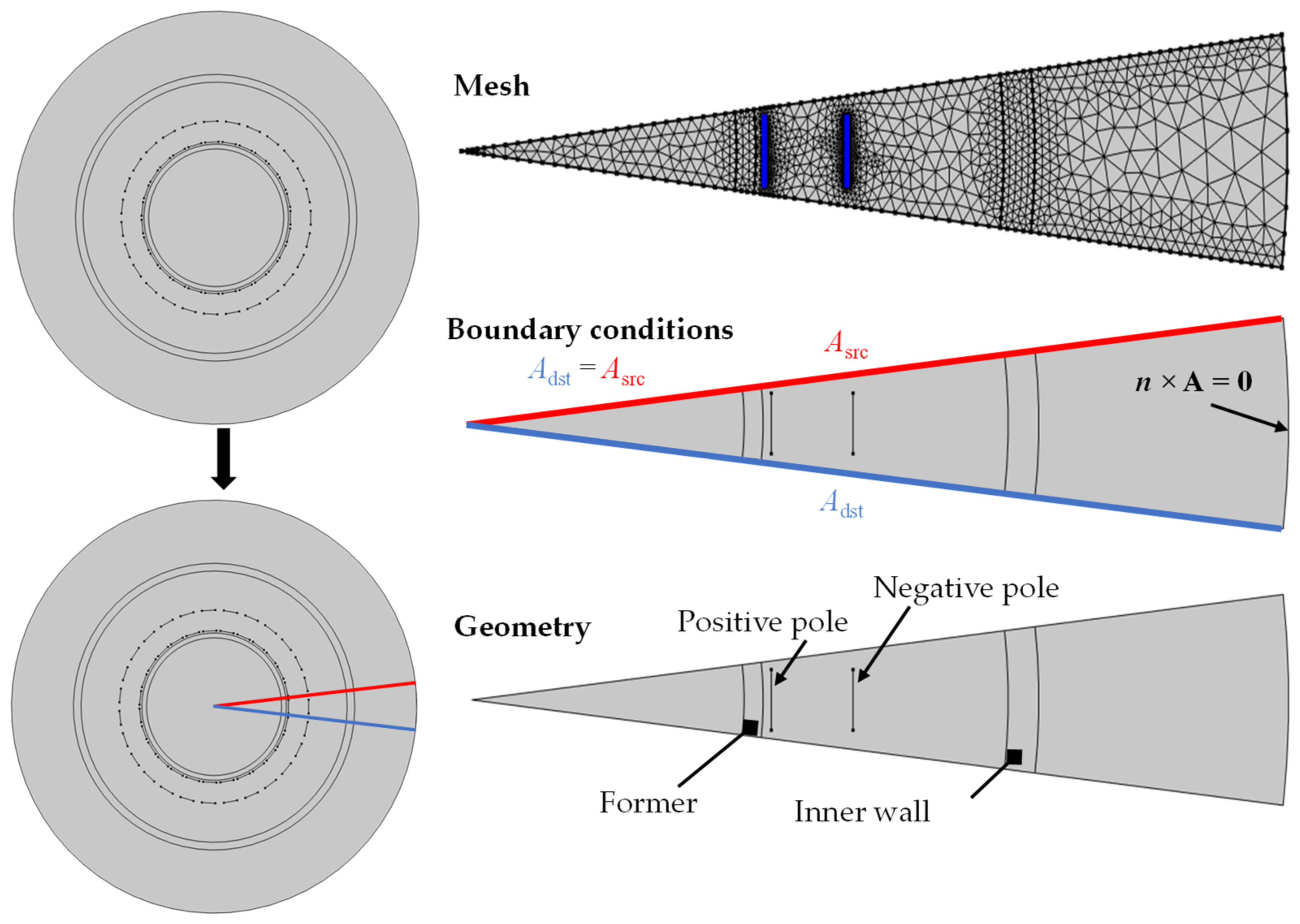
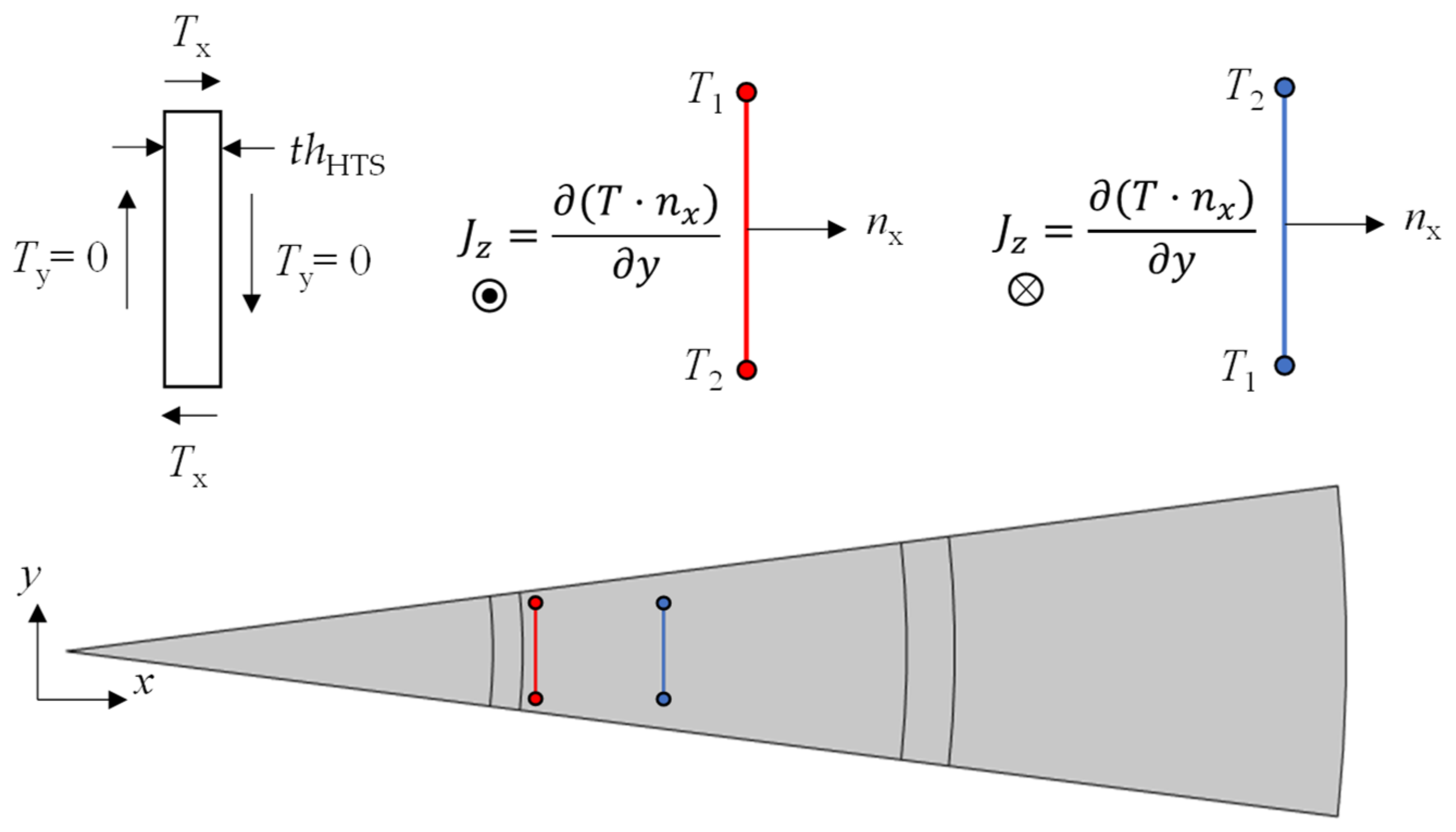
3.4. Modeling of the DC HTS Cable
4. Modeling of an Electrical Traction Network
4.1. Modeling of the Substation (SS)
4.2. Modeling of the Train
4.3. Modeling of the Traction Line
5. Co-Simulation: FEM (Cable) and Circuit (Traction Network)
6. Results and Discussion with Constant Speed Trains
- A railway network without a superconducting cable (referred to as “conventional”);
- A railway network with a unipolar superconducting cable (referred to as “UniHTSC”). The cable connects the substation 1 to the injection point pHTS of the overhead line and the return of the current through the rails;
- A railway network with a bipolar superconducting cable (referred to as “BiHTSC”). The cable connects substation 1 to the overhead traction line at pHTS and the return of the current to substation 1 is also guaranteed by the same cable.
6.1. Influence of the Insertion of a HTSC on the Voltage Drop of Traction Lines
6.2. Influence of the Length of the HTSC on the Voltage Drop of the Traction Lines
6.3. Influence of HTSC Length on Energy Consumption
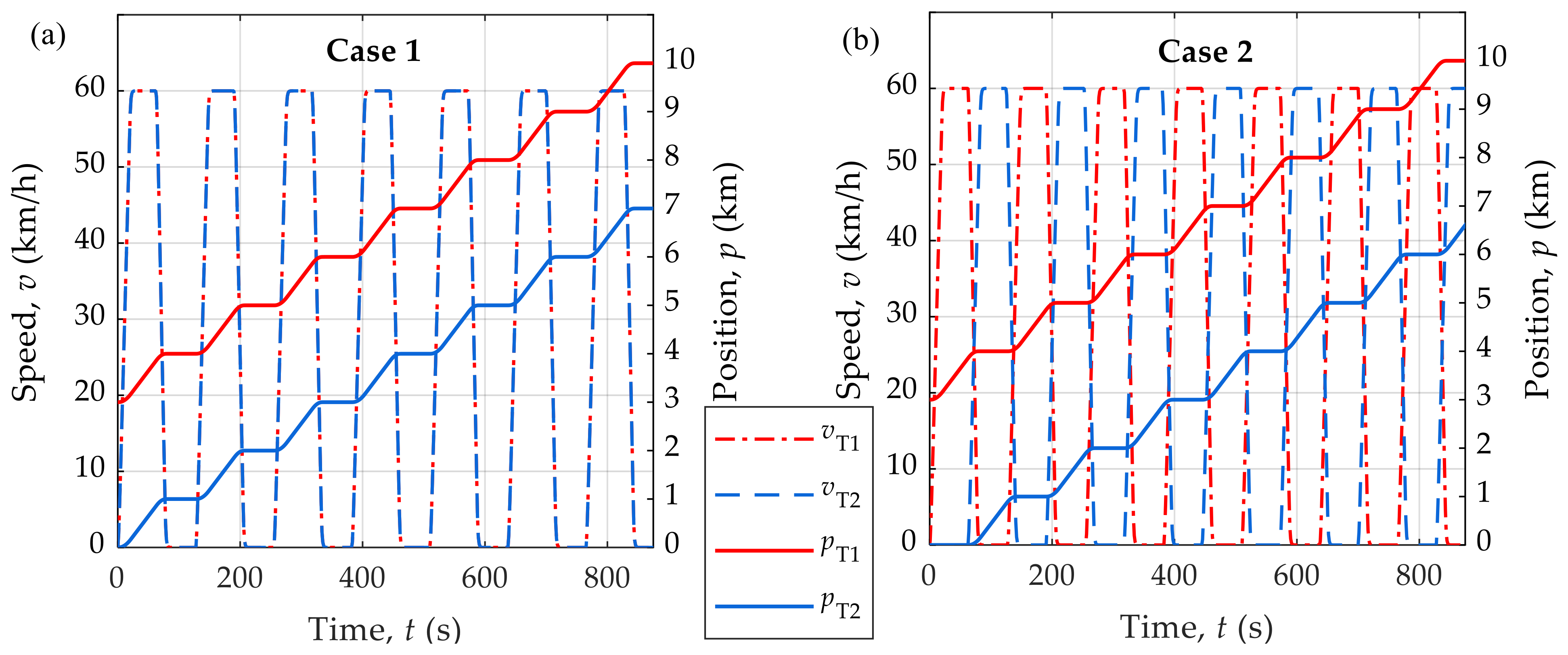
7. Results and Discussion with Variable Speed Trains
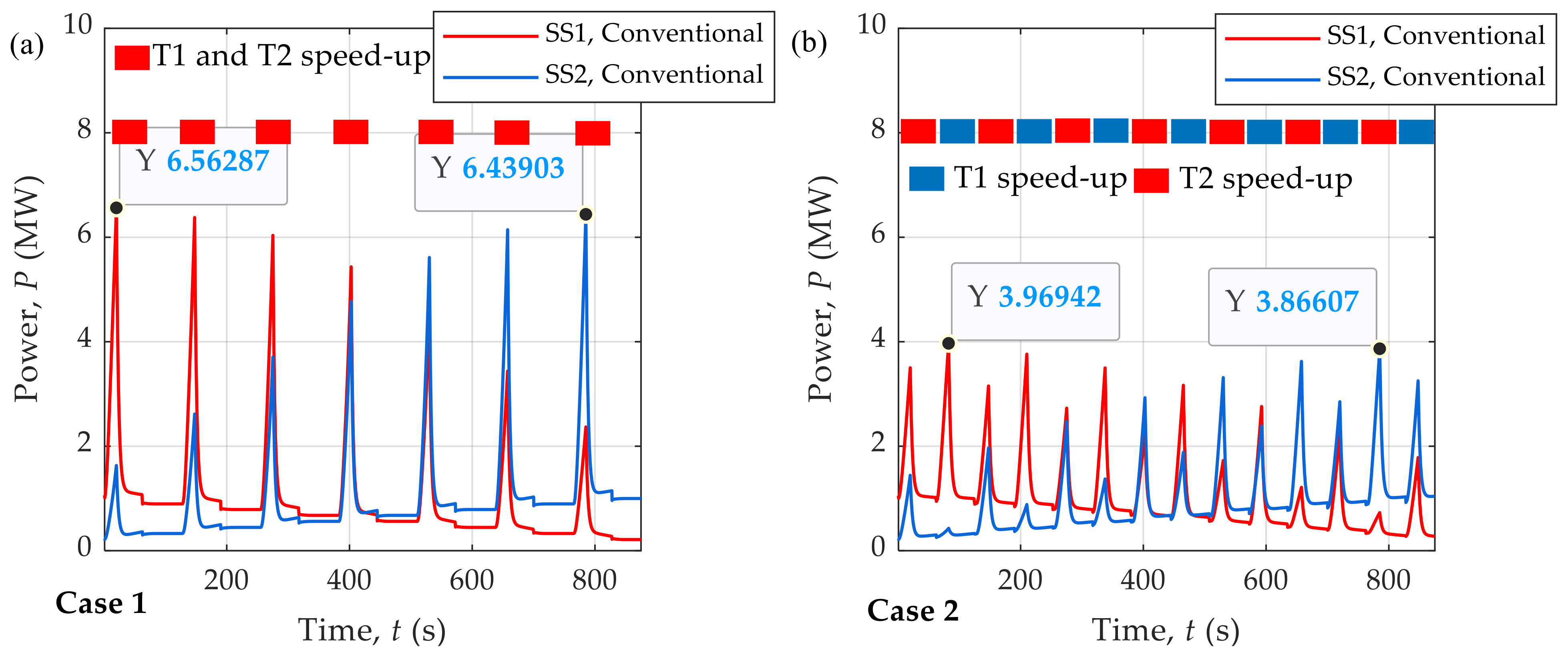
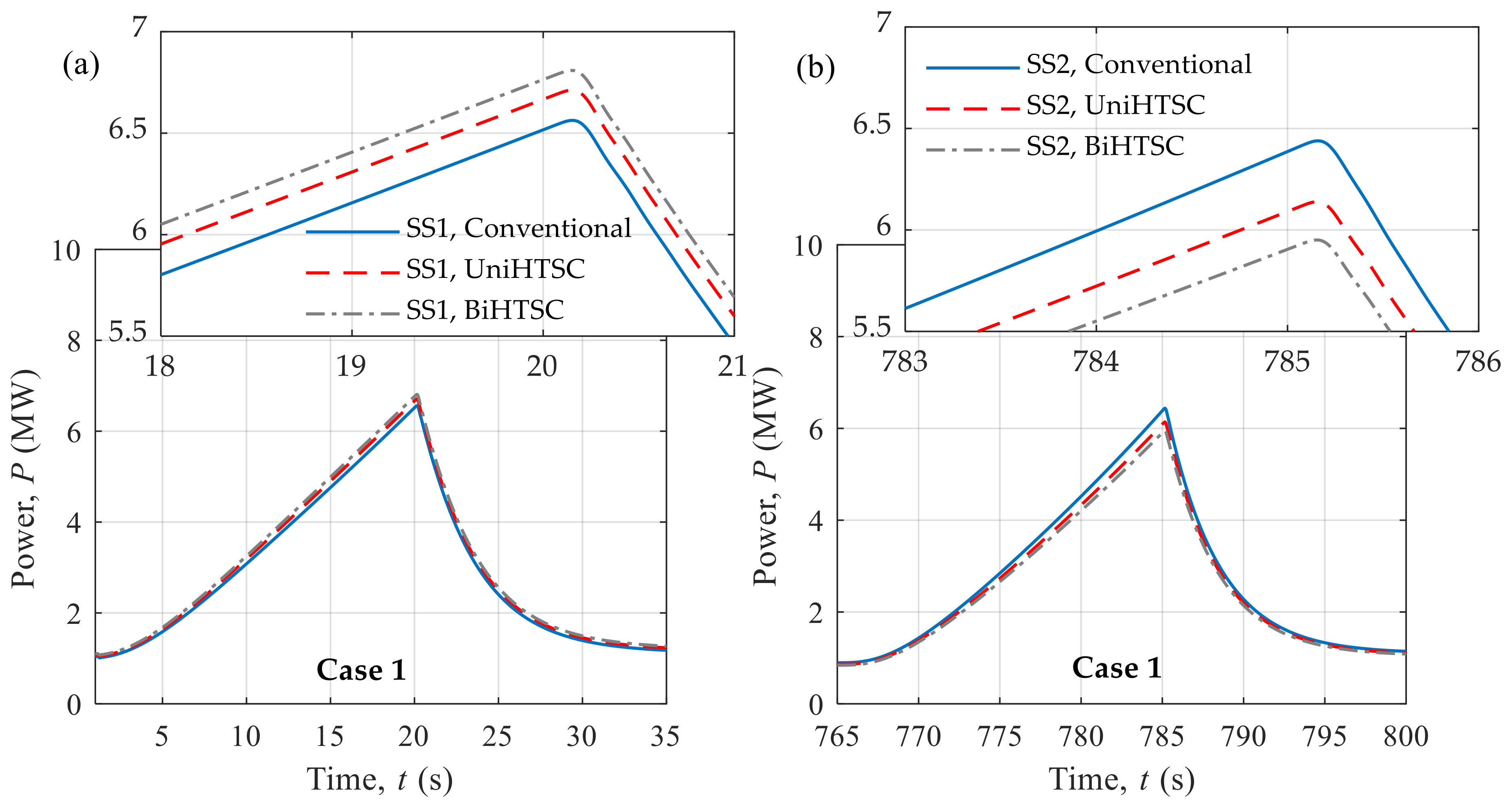
7.1. Influence of HTSC on the Substations
7.2. Influence of HTSC on the Traction Line
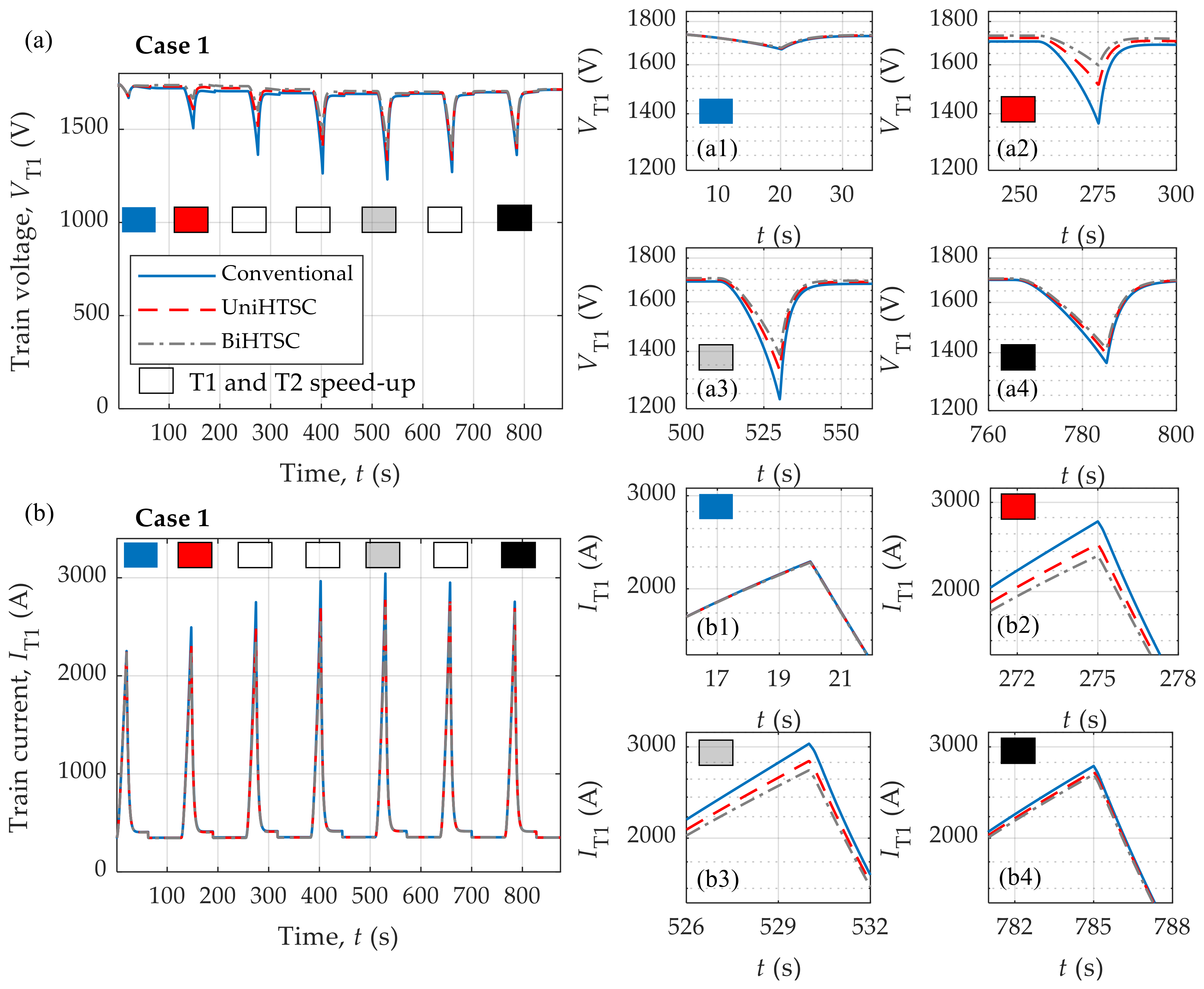
7.3. Influence of HTSC on the Trains
7.4. Electrical Losses in HTSC
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, C.; Ma, Y. Superconducting materials: Challenges and opportunities for large-scale applications. iScience 2021, 24, 102541. [Google Scholar] [CrossRef] [PubMed]
- Yazdani-Asrami, M.; Seyyedbarzegar, S.M.; Sadeghi, A.; de Sousa, W.T.B.; Kottonau, D. High temperature superconducting cables and their performance against short circuit faults: Current development, challenges, solutions, and future trends. Supercond. Sci. Technol. 2022, 35, 083002. [Google Scholar] [CrossRef]
- Uglietti, D. A review of commercial high temperature superconducting materials for large magnets: From wires and tapes to cables and conductors. Supercond. Sci. Technol. 2019, 32, 053001. [Google Scholar] [CrossRef]
- Dorget, R.; Nouailhetas, Q.; Colle, A.; Berger, K.; Sudo, K.; Ayat, S.; Lévêque, J.; Koblischka, M.; Sakai, N.; Oka, T.; et al. Review on the Use of Superconducting Bulks for Magnetic Screening in Electrical Machines for Aircraft Applications. Materials 2021, 14, 2847. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Izumi, M.; Miki, M.; Felder, B.; Ida, T.; Kitano, M. An overview of rotating machine systems with high-temperature bulk superconductors. Supercond. Sci. Technol. 2012, 25, 103001. [Google Scholar] [CrossRef]
- Xiao, L.; Dai, S.; Lin, L.; Zhang, J.; Guo, W.; Zhang, D.; Gao, Z.; Song, N.; Teng, Y.; Zhu, Z.; et al. Development of the World’s First HTS Power Substation. IEEE Trans. Appl. Supercond. 2012, 22, 5000104. [Google Scholar] [CrossRef]
- Leghissa, M.; Gromoll, B.; Rieger, J.; Oomen, M.; Neumüller, H.-W.; Schlosser, R.; Schmidt, H.; Knorr, W.; Meinert, M.; Henning, U. Development and application of superconducting transformers. Phys. C Supercond. Appl. 2002, 372–376, 1688–1693. [Google Scholar] [CrossRef]
- Tsutsumi, T.; Tomioka, A.; Iwakuma, M.; Okamoto, H.; Gosho, Y.; Hayashi, H.; Iijima, Y.; Saito, T.; Ohkuma, T.; Tagomori, A.; et al. Development of REBCO Superconducting Transformers with Current Limiting Function. Phys. Procedia 2012, 36, 1115–1120. [Google Scholar] [CrossRef] [Green Version]
- Mimeur, C.; Queyroi, F.; Banos, A.; Thévenin, T. Revisiting the structuring effect of transportation infrastructure: An empirical approach with the French railway network from 1860 to 1910. Hist. Methods J. Quant. Interdiscip. Hist. 2018, 51, 65–81. [Google Scholar] [CrossRef]
- Femine, A.D.; Gallo, D.; Landi, C.; Luiso, M. Discussion on DC and AC Power Quality Assessment in Railway Traction Supply Systems. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; pp. 1–6. [Google Scholar]
- Pietzcker, R.C.; Longden, T.; Chen, W.; Fu, S.; Kriegler, E.; Kyle, P.; Luderer, G. Long-term transport energy demand and climate policy: Alternative visions on transport decarbonization in energy-economy models. Energy 2014, 64, 95–108. [Google Scholar] [CrossRef]
- Steimel, A. Under Europe’s Incompatible Catenary Voltages a Review of Multi-System Traction Technology. In Proceedings of the Railway and Ship Propulsion 2012 Electrical Systems for Aircraft, Bologna, Italy, 16–18 October 2012; pp. 1–8. [Google Scholar]
- Fabre, J.; Ladoux, P.; Caron, H.; Verdicchio, A.; Blaquiere, J.-M.; Flumian, D.; Sanchez, S. Characterization and Implementation of Resonant Isolated DC/DC Converters for Future MVdc Railway Electrification Systems. IEEE Trans. Transp. Electrification 2021, 7, 854–869. [Google Scholar] [CrossRef]
- Wimbush, S.C.; Strickland, N.M. A Public Database of High-Temperature Superconductor Critical Current Data. IEEE Trans. Appl. Supercond. 2017, 27, 1–5. [Google Scholar] [CrossRef]
- Hamabe, M.; Sugino, M.; Watanabe, H.; Kawahara, T.; Yamaguchi, S.; Ishiguro, Y.; Kawamura, K. Critical Current and Its Magnetic Field Effect Measurement of HTS Tapes Forming DC Superconducting Cable. IEEE Trans. Appl. Supercond. 2011, 21, 1038–1041. [Google Scholar] [CrossRef]
- Sun, J.; Watanabe, H.; Hamabe, M.; Yamamoto, N.; Kawahara, T.; Yamaguchi, S. Critical current behavior of a BSCCO tape in the stacked conductors under different current feeding mode. Phys. C Supercond. Appl. 2013, 494, 297–301. [Google Scholar] [CrossRef]
- Zhang, D.; Dai, S.; Zhang, F.; Zhu, Z.; Xu, X.; Zhou, W.; Teng, Y.; Lin, L. Stability Analysis of the Cable Core of a 10 kA HTS DC Power Cable Used in the Electrolytic Aluminum Industry. IEEE Trans. Appl. Supercond. 2015, 25, 1–4. [Google Scholar] [CrossRef]
- Bruzek, C.E.; Ballarino, A.; Escamez, G.; Giannelli, S.; Grasso, G.; Grilli, F.; Haberstroh, C.; Holé, S.; Koeppel, S.; Lesur, F.; et al. Status of the MgB2-Based High-Power DC Cable Demonstrator within BEST PATHS; Research Institute for Sustainability Helmholtz Centre Potsdam: Potsdam, Germany, 2017. [Google Scholar]
- Ballarino, A.; Flükiger, R. Status of MgB2 wire and cable applications in Europe. J. Phys. Conf. Ser. 2017, 871, 012098. [Google Scholar] [CrossRef] [Green Version]
- Sytnikov, V.E.; Bemert, S.E.; Kopylov, S.I.; Romashov, M.A.; Ryabin, T.V.; Shakaryan, Y.G.; Lobyntsev, V.V. Status of HTS Cable Link Project for St. Petersburg Grid. IEEE Trans. Appl. Supercond. 2015, 25, 1–4. [Google Scholar] [CrossRef]
- Elschner, S.; Brand, J.; Goldacker, W.; Hollik, M.; Kudymow, A.; Strauss, S.; Zermeno, V.M.R.; Hanebeck, C.; Huwer, S.; Reiser, W.; et al. 3S–Superconducting DC-Busbar for High Current Applications. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Chikumoto, N.; Watanabe, H.; Ivanov, Y.V.; Takano, H.; Yamaguchi, S.; Koshizuka, H.; Hayashi, K.; Sawamura, T. Construction and the Circulation Test of the 500-m and 1000-m DC Superconducting Power Cables in Ishikari. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar] [CrossRef]
- Yang, B.; Kang, J.; Lee, S.; Choi, C.; Moon, Y. Qualification Test of a 80 kV 500 MW HTS DC Cable for Applying Into Real Grid. IEEE Trans. Appl. Supercond. 2015, 25, 5402705. [Google Scholar] [CrossRef]
- Tomita, M.; Akasaka, T.; Fukumoto, Y.; Ishihara, A.; Suzuki, K.; Kobayashi, Y. Laying method for superconducting feeder cable along railway line. Cryogenics 2018, 89, 125–130. [Google Scholar] [CrossRef]
- SuperRail: Une Solution Innovante Pour Alimenter Le Réseau Ferré En Énergie | Actualité | SNCF RÉSEAU. Available online: https://www.sncf-reseau.com/fr/entreprise/newsroom/actualite/superrail-solution-innovante-alimenter-reseau-ferre-en-energie (accessed on 30 September 2022).
- Graber, G.; Calderaro, V.; Galdi, V.; Ippolito, L.; Massa, G. Impact Assessment of Energy Storage Systems Supporting DC Railways on AC Power Grids. IEEE Access 2022, 10, 10783–10798. [Google Scholar] [CrossRef]
- Mohamed, B.; El-Sayed, I.; Arboleya, P. DC Railway Infrastructure Simulation Including Energy Storage and Controllable Substations. In Proceedings of the 2018 IEEE Vehicle Power and Propulsion Conference (VPPC), Chicago, IL, USA, 27–30 August 2018; pp. 1–6. [Google Scholar]
- Arboleya, P.; Mohamed, B.; El-Sayed, I. DC Railway Simulation Including Controllable Power Electronic and Energy Storage Devices. IEEE Trans. Power Syst. 2018, 33, 5319–5329. [Google Scholar] [CrossRef] [Green Version]
- Khodaparastan, M.; Mohamed, A.A.; Brandauer, W. Recuperation of Regenerative Braking Energy in Electric Rail Transit Systems. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2831–2847. [Google Scholar] [CrossRef] [Green Version]
- Yao, P.; Wang, H.; Liu, Y.; Niu, J.; Zhu, Z.; Lin, L. Integrated railway smart grid architecture based on energy routers. Chin. J. Electr. Eng. 2021, 7, 93–106. [Google Scholar] [CrossRef]
- Yan, Y.; Qu, T.; Grilli, F. Numerical Modeling of AC Loss in HTS Coated Conductors and Roebel Cable Using T-A Formulation and Comparison with H Formulation. IEEE Access 2021, 9, 49649–49659. [Google Scholar] [CrossRef]
- Li, X.; Ren, L.; Xu, Y.; Shi, J.; Chen, X.; Chen, G.; Tang, Y.; Li, J. Calculation of CORC Cable Loss Using a Coupled Electromagnetic-Thermal T-A Formulation Model. IEEE Trans. Appl. Supercond. 2021, 31, 1–7. [Google Scholar] [CrossRef]
- Fetisov, S.S.; Zubko, V.V.; Zanegin, S.Y.; Nosov, A.A.; Vysotsky, V.S. Numerical Simulation and Cold Test of a Compact 2G HTS Power Cable. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Zubko, V.V.; Fetisov, S.; Vysotsky, V.S. Hysteresis Losses Analysis in 2G HTS Cables. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Tomita, M.; Fukumoto, Y.; Ishihara, A.; Suzuki, K.; Akasaka, T.; Kobayashi, Y.; Onji, T.; Arai, Y. Energy analysis of superconducting power transmission installed on the commercial railway line. Energy 2020, 209, 118318. [Google Scholar] [CrossRef]
- Nishihara, T.; Hoshino, T.; Tomita, M. FCL Effect of DC Superconducting Cables in Unsteady State. IEEE Trans. Appl. Supercond. 2017, 27, 1–4. [Google Scholar] [CrossRef]
- Voccio, J.; Kim, J.-H.; Pamidi, S. Study of AC Losses in a 1-m Long, HTS Power Cable Made from Wide 2G Tapes. IEEE Trans. Appl. Supercond. 2012, 22, 5800304. [Google Scholar] [CrossRef]
- Hajiri, G.; Berger, K.; Dorget, R.; Leveque, J.; Caron, H. Thermal and Electromagnetic Design of DC HTS Cables for the Future French Railway Network. IEEE Trans. Appl. Supercond. 2021, 31, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, G.; Qiu, R.; Liu, Z.; Yao, N. Distribution Correction Model of Urban Rail Return System Considering Rail Skin Effect. IEEE Trans. Transp. Electrif. 2021, 7, 883–891. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, G.; Tian, Z.; Qiu, R.; Liu, Z. An Online Thermal Deicing Method for Urban Rail Transit Catenary. IEEE Trans. Transp. Electrif. 2021, 7, 870–882. [Google Scholar] [CrossRef]
- Baskys, A.; Patel, A.; Hopkins, S.C.; Kalitka, V.; Molodyk, A.; Glowacki, B.A. Self-Supporting Stacks of Commercial Superconducting Tape Trapping Fields up to 1.6 T Using Pulsed Field Magnetization. IEEE Trans. Appl. Supercond. 2015, 25, 1–4. [Google Scholar] [CrossRef]
- Gromoll, D.; Schumacher, R.; Humpert, C. Dielectric strength of insulating material in LN2 with thermally induced bubbles. J. Phys. Conf. Ser. 2020, 1559, 012087. [Google Scholar] [CrossRef]
- Kwag, D.; Cheon, H.; Choi, J.; Kim, H.; Cho, J.; Yun, M.; Kim, S. The Electrical Insulation Characteristics for a HTS Cable Termination. IEEE Trans. Appl. Supercond. 2006, 16, 1618–1621. [Google Scholar] [CrossRef]
- Bulinski, A.; Densley, J. High voltage insulation for power cables utilizing high temperature superconductivity. IEEE Electr. Insul. Mag. 1999, 15, 14–22. [Google Scholar] [CrossRef]
- Rigby, S.J.; Weedy, B.M. Liquid Nitrogen-Impregnated Tape Insulation for Cryoresistive Cable. IEEE Trans. Electr. Insul. 1975, EI-10, 1–9. [Google Scholar] [CrossRef]
- De Sousa, W.T.B.; Shabagin, E.; Kottonau, D.; Noe, M. An open-source 2D finite difference based transient electro-thermal simulation model for three-phase concentric superconducting power cables. Supercond. Sci. Technol. 2021, 34, 015014. [Google Scholar] [CrossRef]
- Stemmle, M.; Merschel, F.; Noe, M.; Hobl, A. AmpaCity—Installation of Advanced Superconducting 10 KV System in City Center Replaces Conventional 110 KV Cables. In Proceedings of the 2013 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices, Beijing, China, 25–27 October 2013; pp. 323–326. [Google Scholar]
- Jacob, T.; Buchholz, A.; Noe, M.; Weil, M. Comparative Life Cycle Assessment of Different Cooling Systems for High-Temperature Superconducting Power Cables. IEEE Trans. Appl. Supercond. 2022, 32, 1–5. [Google Scholar] [CrossRef]
- Herzog, F.; Kutz, T.; Stemmle, M.; Kugel, T. Cooling unit for the AmpaCity project—One year successful operation. Cryogenics 2016, 80, 204–209. [Google Scholar] [CrossRef]
- Tang, T.; Zong, X.H.; Yu, Z.G.; Lu, X.H.; Han, Y.W. Design and Operation of Cryogenic System for 35kV/2000A HTS Power Cables. In Proceedings of the 2015 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD), Shanghai, China, 20–23 November 2015; pp. 573–575. [Google Scholar]
- Ren, L.; Tang, Y.; Shi, J.; Jiao, F. Design of a Termination for the HTS Power Cable. IEEE Trans. Appl. Supercond. 2012, 22, 5800504. [Google Scholar] [CrossRef]
- Morandi, A. HTS dc transmission and distribution: Concepts, applications and benefits. Supercond. Sci. Technol. 2015, 28, 123001. [Google Scholar] [CrossRef]
- Maguire, J.F.; Schmidt, F.; Bratt, S.; Welsh, T.E.; Yuan, J.; Allais, A.; Hamber, F. Development and Demonstration of a HTS Power Cable to Operate in the Long Island Power Authority Transmission Grid. IEEE Trans. Appl. Supercond. 2007, 17, 2034–2037. [Google Scholar] [CrossRef]
- Cho, J.; Bae, J.-H.; Kim, H.-J.; Sim, K.-D.; Seong, K.-C.; Jang, H.-M.; Kim, D.-W. Development and Testing of 30 m HTS Power Transmission Cable. IEEE Trans. Appl. Supercond. 2005, 15, 1719–1722. [Google Scholar] [CrossRef]
- Maguire, J.F.; Yuan, J.; Romanosky, W.; Schmidt, F.; Soika, R.; Bratt, S.; Durand, F.; King, C.; McNamara, J.; Welsh, T.E. Progress and Status of a 2G HTS Power Cable to Be Installed in the Long Island Power Authority (LIPA) Grid. IEEE Trans. Appl. Supercond. 2011, 21, 961–966. [Google Scholar] [CrossRef]
- Gouge, M.; Lindsay, D.; Demko, J.; Duckworth, R.; Ellis, A.; Fisher, P.; James, D.; Lue, J.; Roden, M.; Sauers, I.; et al. Tests of Tri-Axial HTS Cables. IEEE Trans. Appl. Supercond. 2005, 15, 1827–1830. [Google Scholar] [CrossRef]
- Lee, C.; Kim, D.; Kim, S.; Won, D.Y.; Yang, H.S. Thermo-hydraulic analysis on long three-phase coaxial HTS power cable of several kilometers. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Prikhna, T.; Kasatkin, A.; Eisterer, M.; Moshchil, V.; Shapovalov, A.; Rabier, J.; Jouline, A.; Chaud, X.; Rindfleisch, M.; Tomsic, M.; et al. Critical Current Density, Pinning and Nanostructure of MT-YBCO and MgB2-based Materials. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Laborde, O.; Tholence, J.L.; Lejay, P.; Sulpice, A.; Tournier, R.; Capponi, J.J.; Michel, C.; Provost, J. Critical field, Hc2, and critical current in YBa2Cu3O7, up to 20 Tesla. Solid State Commun. 1987, 63, 877–880. [Google Scholar] [CrossRef]
- Turrioni, D.; Barzi, E.; Lamm, M.J.; Yamada, R.; Zlobin, A.V.; Kikuchi, A. Study of HTS Wires at High Magnetic Fields. IEEE Trans. Appl. Supercond. 2009, 19, 3057–3060. [Google Scholar] [CrossRef] [Green Version]
- De Sousa, W.T.B.; Kottonau, D.; Bock, J.; Noe, M. Investigation of a Concentric Three-Phase HTS Cable Connected to an SFCL Device. IEEE Trans. Appl. Supercond. 2018, 28, 1–5. [Google Scholar] [CrossRef]
- Kojima, H.; Kato, F.; Hayakawa, N.; Hanai, M.; Okubo, H. Superconducting Fault Current Limiting Cable (SFCLC) with Current Limitation and Recovery Function. Phys. Procedia 2012, 36, 1296–1300. [Google Scholar] [CrossRef] [Green Version]
- Berrospe-Juarez, E.; Trillaud, F.; Zermeño, V.M.R.; Grilli, F. Advanced electromagnetic modeling of large-scale high-temperature superconductor systems based on H and T-A formulations. Supercond. Sci. Technol. 2021, 34, 044002. [Google Scholar] [CrossRef]
- Huber, F.; Song, W.; Zhang, M.; Grilli, F. The T-A formulation: An efficient approach to model the macroscopic electromagnetic behaviour of HTS coated conductor applications. Supercond. Sci. Technol. 2022, 35, 043003. [Google Scholar] [CrossRef]
- Berrospe-Juarez, E.; Zermeño, V.M.R.; Trillaud, F.; Grilli, F. Real-time simulation of large-scale HTS systems: Multi-scale and homogeneous models using the T–A formulation. Supercond. Sci. Technol. 2019, 32, 065003. [Google Scholar] [CrossRef] [Green Version]
- Fetisov, S.S.; Zubko, V.V.; Zanegin, S.Y.; Nosov, A.A.; Vysotsky, V.S.; Kario, A.; Kling, A.; Goldacker, W.; Molodyk, A.; Mankevich, A.; et al. Development and Characterization of a 2G HTS Roebel Cable for Aircraft Power Systems. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar] [CrossRef]
- Hajiri, G.; Berger, K.; Dorget, R.; Lévêque, J.; Caron, H. Design and modelling tools for DC HTS cables for the future railway network in France. Supercond. Sci. Technol. 2022, 35, 024003. [Google Scholar] [CrossRef]
- Leys, P.M.; Klaeser, M.; Schleissinger, F.; Schneider, T. Angle-Dependent U(I) Measurements of HTS Coated Conductors. IEEE Trans. Appl. Supercond. 2013, 23, 8000604. [Google Scholar] [CrossRef]
- Strickland, N. A High-Temperature Superconducting (HTS) Wire Critical Current Database. IEEE Trans. Appl. Supercond. 2022, 27, 2861821. [Google Scholar] [CrossRef]
- Lee, J.-D.; Kwon, Y.-K.; Baik, S.-K.; Lee, E.-Y.; Kim, Y.-C.; Moon, T.-S.; Park, H.-J.; Kwon, W.-S.; Hong, J.-P.; Park, M.; et al. Thermal Quench in HTS Double Pancake Race Track Coil. IEEE Trans. Appl. Supercond. 2007, 17, 1603–1606. [Google Scholar] [CrossRef]




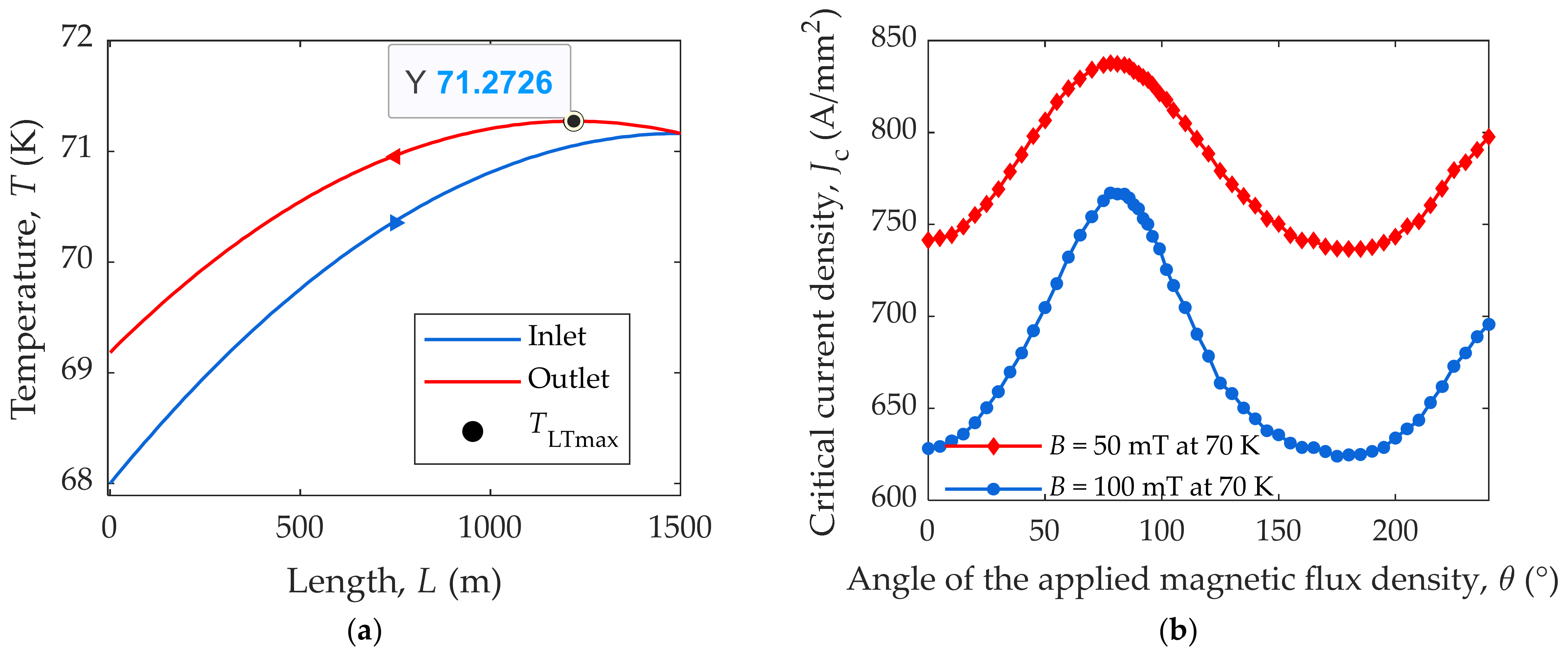



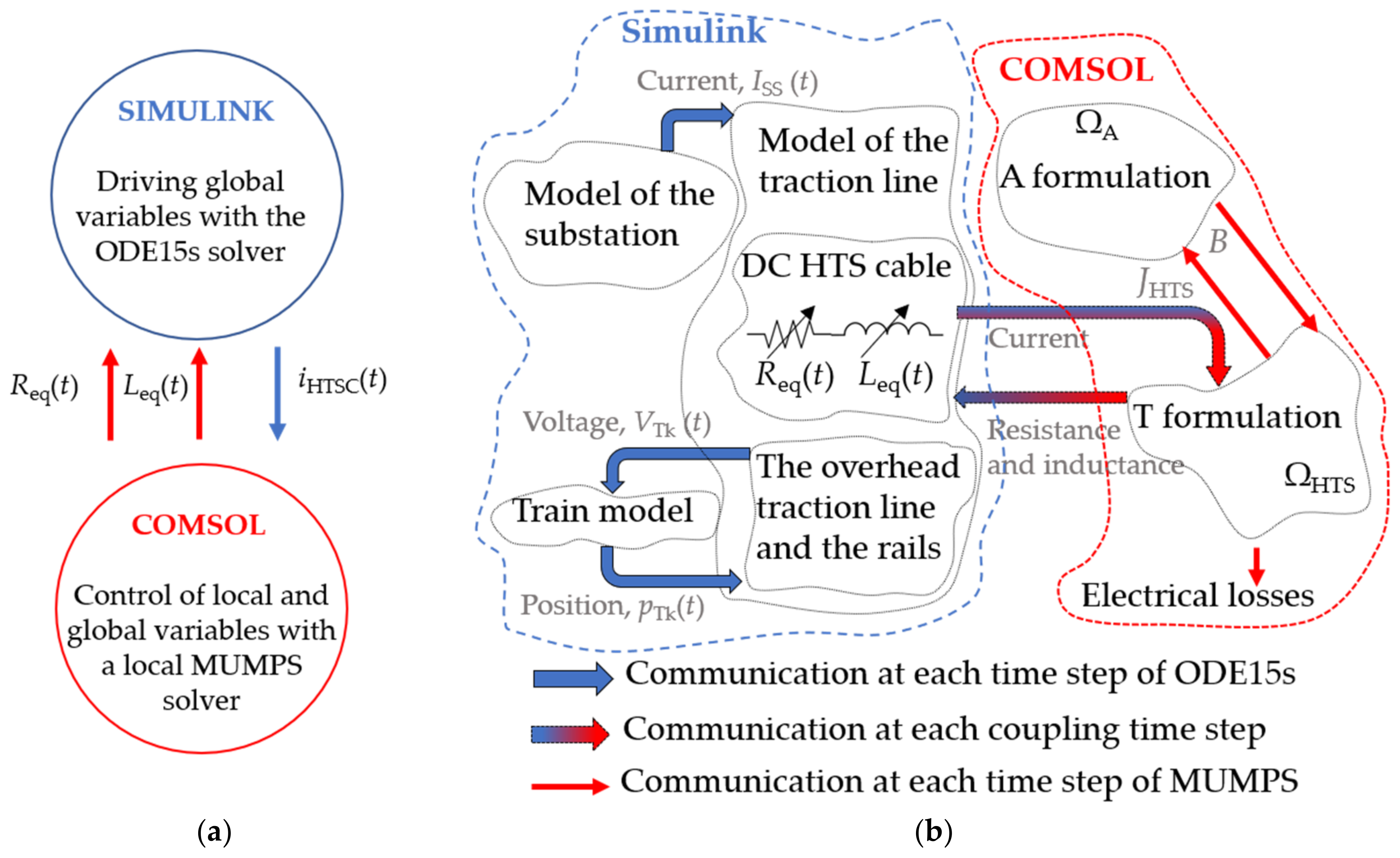

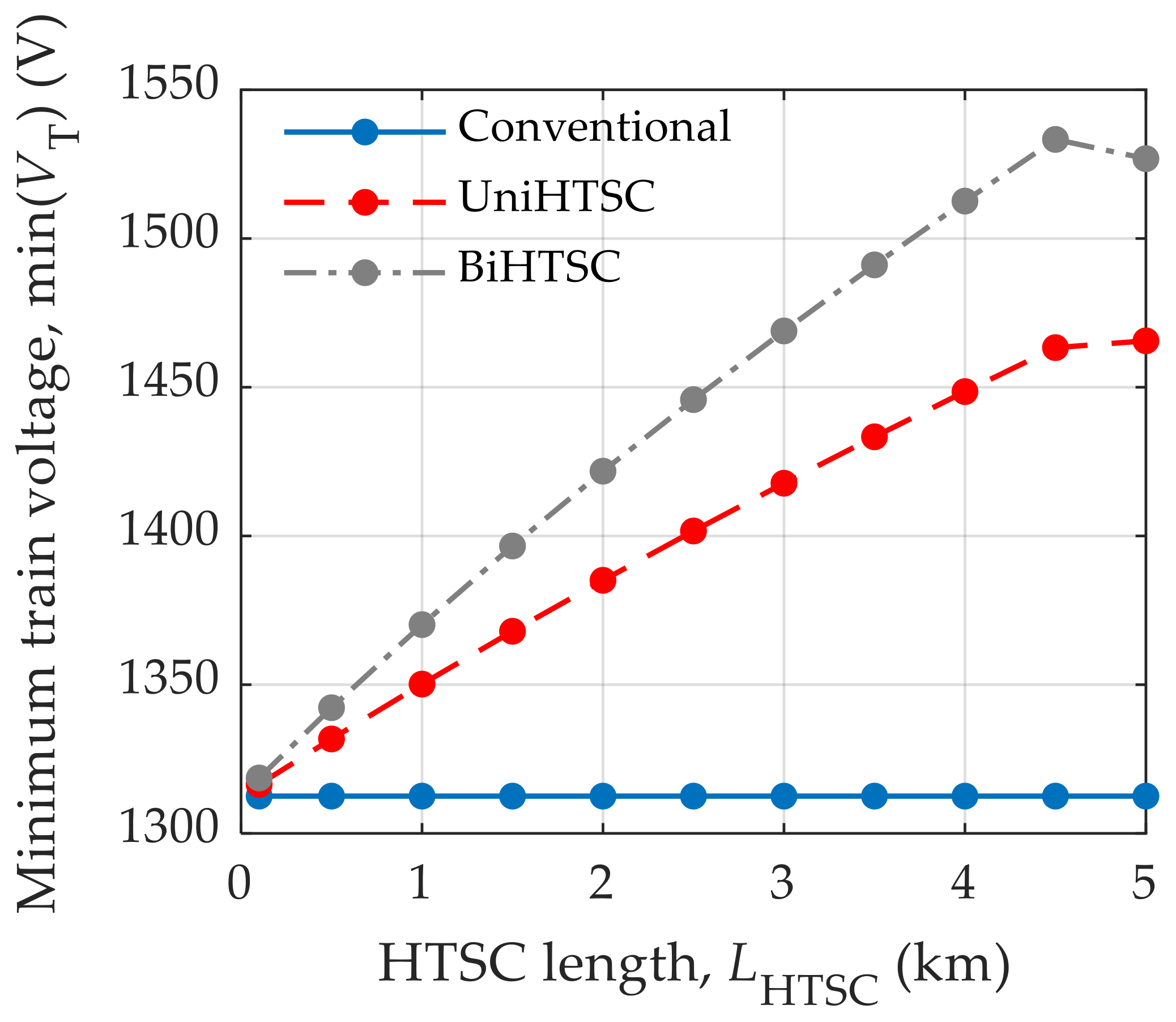
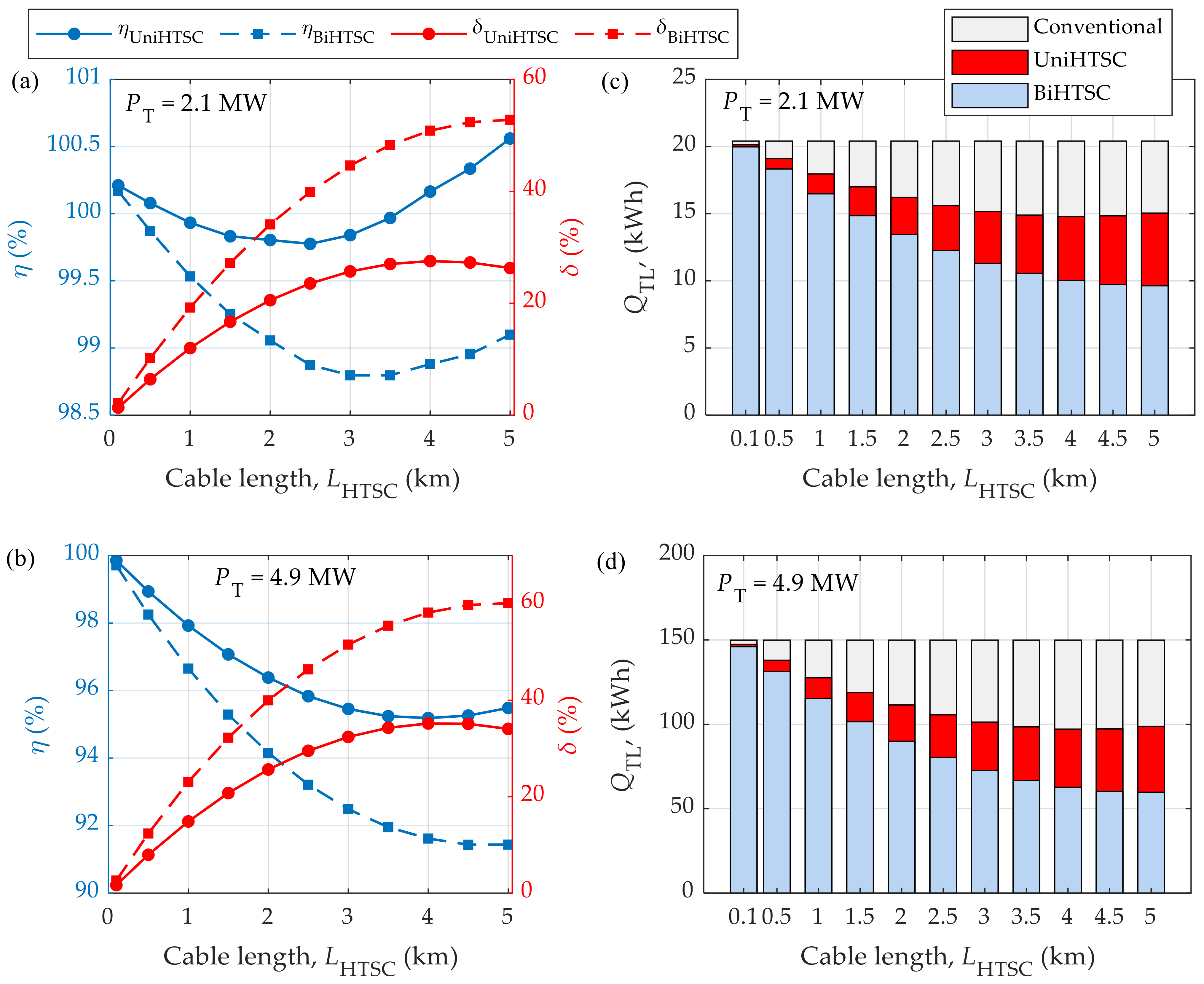




| Parameter | Unit | Value |
|---|---|---|
| kg m−3 | 808 | |
| J kg−1 K−1 | 1048 | |
| K | 68 | |
| K | <78 |
| Position | |||
|---|---|---|---|
| Zl1(t) | Bipolar HTSC | ||
| Unipolar HTSC | |||
| Zl2(t) | Bipolar HTSC | 0 | |
| Unipolar HTSC | 0 | ||
| Zl3(t) | Bipolar HTSC | 0 | |
| Unipolar HTSC | 0 | ||
| Zl4(t) | Bipolar HTSC | ||
| Unipolar HTSC | |||
| Zr1(t) | Bipolar HTSC | ||
| Unipolar HTSC | |||
| Zr2(t) | Bipolar HTSC | 0 | |
| Unipolar HTSC | |||
| Zr3(t) | Bipolar HTSC | 0 | |
| Unipolar HTSC | NA | NA | |
| Zr4(t) | Bipolar HTSC | ||
| Unipolar HTSC | NA | NA | |
| Parameter | Unit | Value |
|---|---|---|
| Rated voltage | kV | 1.5 |
| Rated power | MW | 3.464 |
| Traction force | kN | 310 |
| Mass | T | 245 |
| Length | M | 103.508 |
| Width | M | 2.280 |
| Height | M | 4.320 |
| Capacity | Passengers | 1598 |
| Maximum speed | km/h | 140 |
| Parameter | Unit | Value | ||
|---|---|---|---|---|
| Nominal voltage\at no load | kV | 1.5\1.75 | ||
| Nominal\Maximum current | kA | 4.4\6.75 | ||
| Nominal\Maximum power | MW | 6.6\10.125 | ||
| Number of layers per pole 1 | -- | 1 or 2 | ||
| Critical current at 70 K\78 K | A | 285\210 | ||
| Number of tapes per layer | -- | UniHTSC | Pole (+) | 27 |
| BiHTSC | Pole (+) | 27 | ||
| Pole (−) | 28 | |||
| Parameter | Unit | Value |
|---|---|---|
| Input temperature (LN2) | K | 68 |
| Initial pressure (LN2) | bar | 15 |
| Output temperature (LN2) 1 | K | <78 |
| Mass flow rate | kg/s | [0.1; 2] |
| Pressure drop1 | bar | <10 |
| Parameter | Unit | UniHTSC | BiHTSC | |
|---|---|---|---|---|
| Number of layers per pole | -- | 1 | 1 | |
| Standard former (inside\outside) | mm | 40 (40\42.8) | 40 (40\42.8) | |
| Diameter of the superconducting layers | mm | 42.8\43.1 | Pole (+) | 42.8\43.1 |
| Pole (−) | 49.1\51.1 | |||
| Insulating layer between the poles | mm | NA | 6 | |
| Number of tapes per layer | -- | 27 | Pole (+) | 27 |
| Pole (−) | 28 | |||
| Minimum critical current at 72 K | A | 251 | 248 | |
| Standard diameter of inner pipe (inside\outside) | mm | 100 (79.8\83.8) | 120 (99.8\104.4) | |
| Standard diameter of outer pipe (inside\outside) | mm | 120 (125.6\130.8) | 150 (151.9\157.9) | |
| Length | km | 1.5 | ||
| Mass flow rate | kg/s | 0.5 | 0.6 | |
| Pressure drop | bar | 3.2 | 4.5 | |
| Maximum temperature | K | 72.5 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajiri, G.; Berger, K.; Trillaud, F.; Lévêque, J.; Caron, H. Impact of Superconducting Cables on a DC Railway Network. Energies 2023, 16, 776. https://doi.org/10.3390/en16020776
Hajiri G, Berger K, Trillaud F, Lévêque J, Caron H. Impact of Superconducting Cables on a DC Railway Network. Energies. 2023; 16(2):776. https://doi.org/10.3390/en16020776
Chicago/Turabian StyleHajiri, Ghazi, Kévin Berger, Frederic Trillaud, Jean Lévêque, and Hervé Caron. 2023. "Impact of Superconducting Cables on a DC Railway Network" Energies 16, no. 2: 776. https://doi.org/10.3390/en16020776
APA StyleHajiri, G., Berger, K., Trillaud, F., Lévêque, J., & Caron, H. (2023). Impact of Superconducting Cables on a DC Railway Network. Energies, 16(2), 776. https://doi.org/10.3390/en16020776








