An Experimental Investigation on the Performance of a Water Storage Tank with Sodium Acetate Trihydrate
Abstract
:1. Introduction
2. Experimental System and Uncertainty Analysis
2.1. Apparatus Introduction
2.2. Uncertainty Analysis
3. Thermal Properties
3.1. Dimensionless Time
3.2. Water Tank Capacity
3.3. Fill Efficiency
3.4. MIX
3.5. Exergy Efficiency
4. Experimental Result Analysis
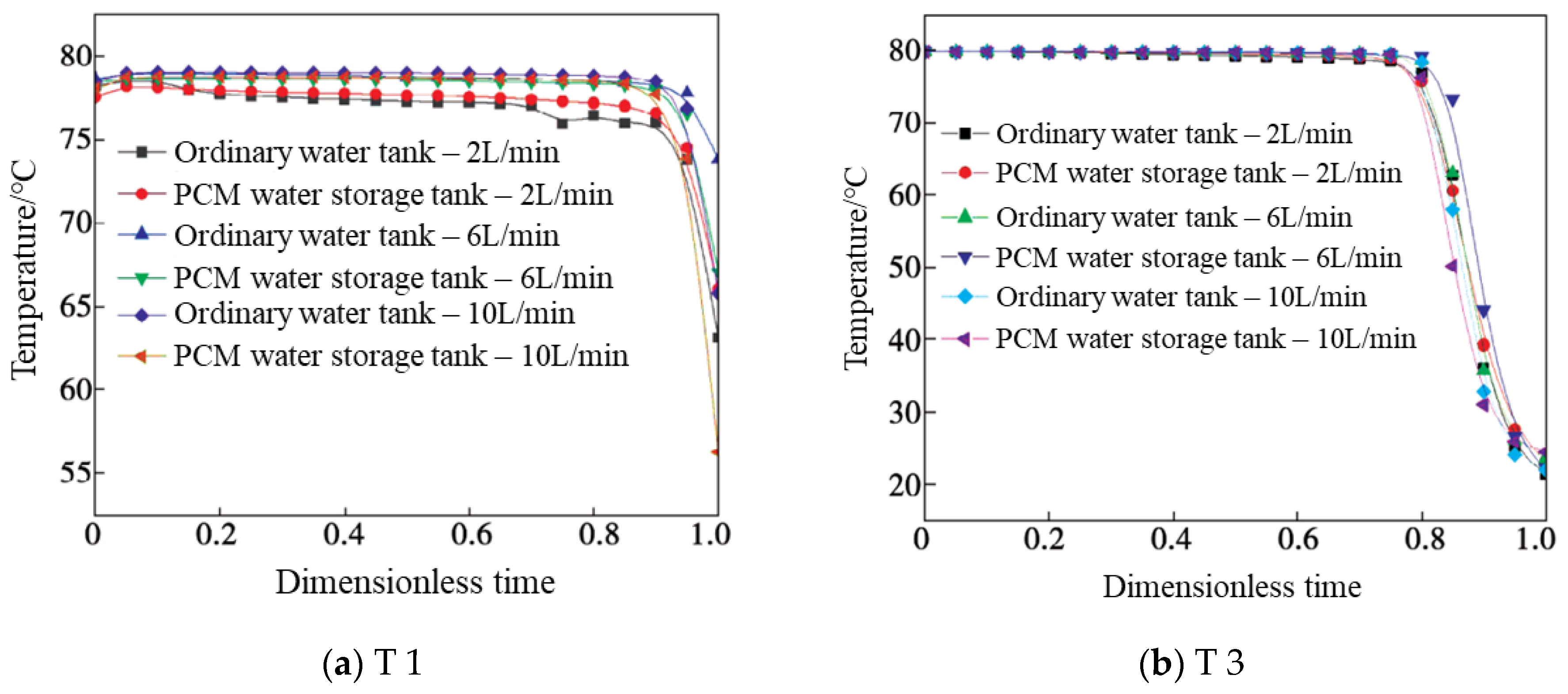
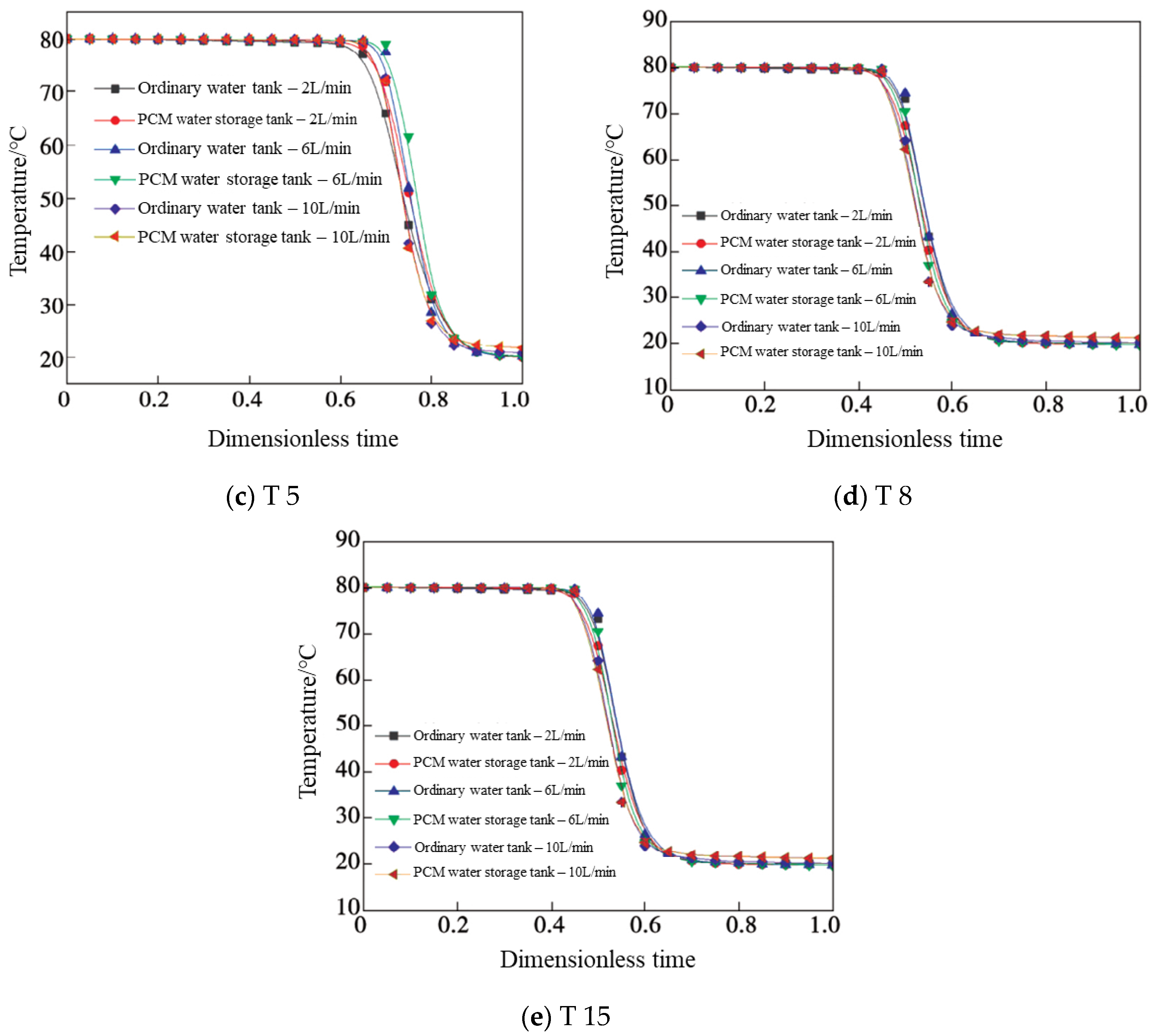
4.1. Temperature
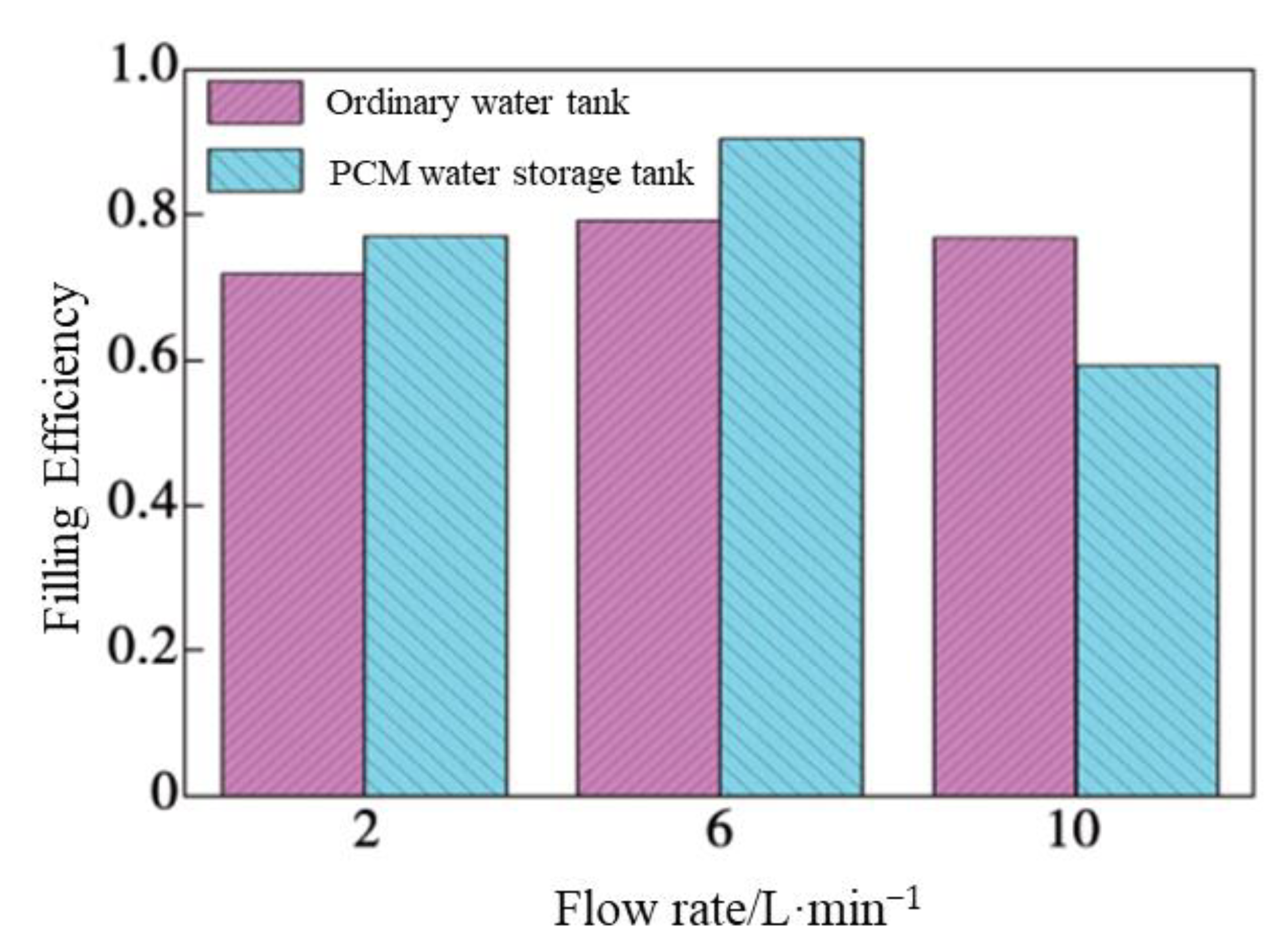
4.2. Filling Efficiencye
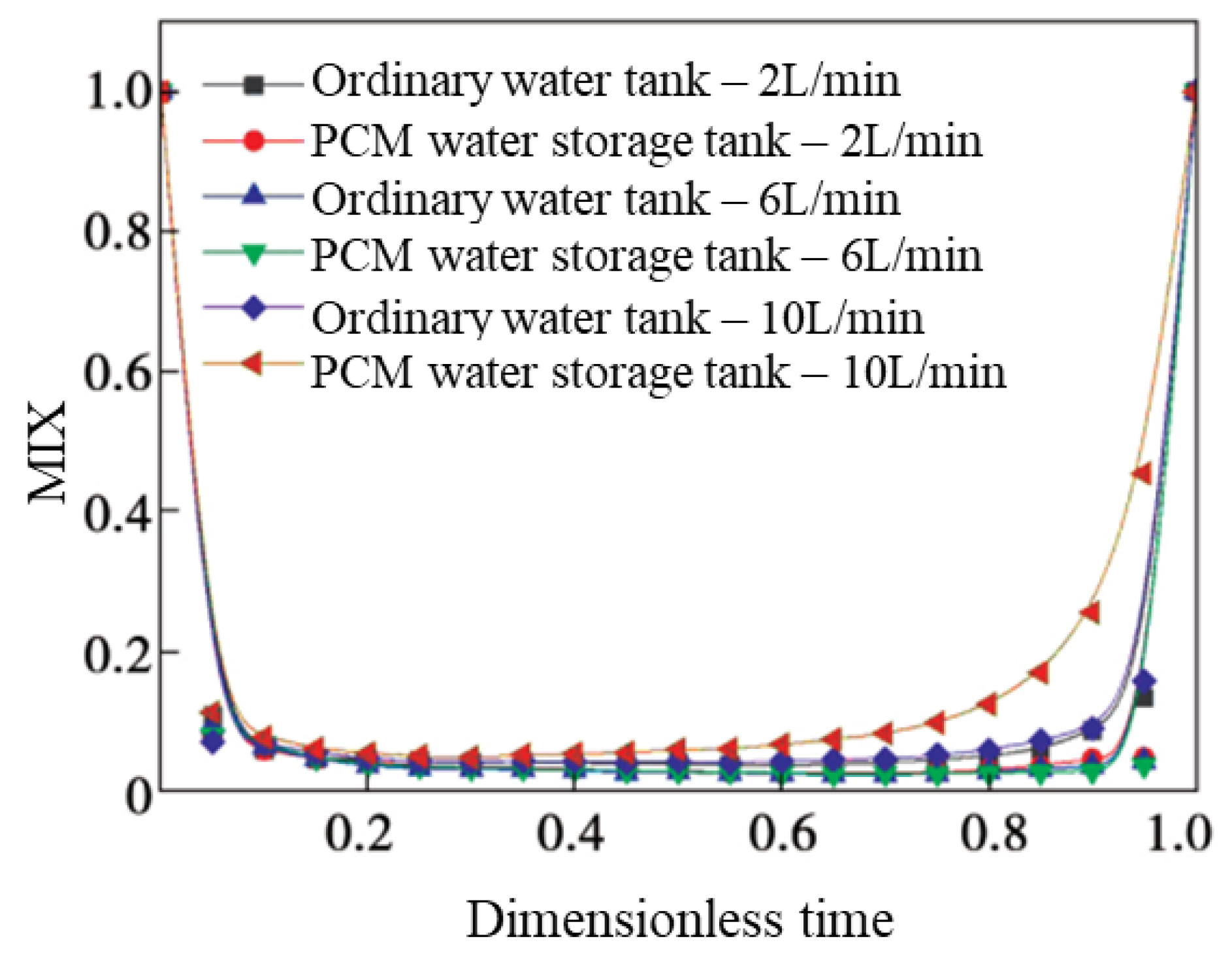
4.3. MIX Number
4.4. Exergy Efficiency
5. Conclusions
- A new water inlet structure was designed, which reduces the water inlet speed, weakens the mutual immersion of high- and low-temperature water, and improves the heat stratification efficiency of the water storage tank. As the flow rates were less than or equal to 6 L/min, the PCMs provided additional heat to and reheat of the water temperature layer, which effectively ameliorated the stratification of the tanks. When the water flow increased to 10 L/min, the PCM balls were unable to release latent heat in time, and stratification effect was poor.
- The filling efficiency as a new performance assessment criterion of tanks was defined. This value is colligated with the influence of the initial temperature of the storage tank, the intake temperature, the exit temperature, and the inlet flow on the performance. This is a relatively comprehensive measurement parameter. The FE of the tank containing PCM whose thermal stratification effect was better than the other tanks in the tests would reach 0.905 with a 6 L/min flow inlet.
- The studied provided research of the influencing mechanisms of SAT heat storage followed by an emphasis on thermal stratification in tanks. The test results showed that the temperature change trend in each layer of the water tank was similar when the dimensionless time kept increasing. The higher the flow rate, the earlier the inflection points appears and the worse the stratification effect. In the meantime, the EE gradually decreased, and the FE increased first and then decreased. When the dimensionless time was 0.95, its EE was about 1.404 times that of the ordinary tank with the same flow rate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| τ | Dimensionless time |
| t | Water inlet time of the tank(s) |
| θ | Time to completely replace the whole box of water at the current flow |
| Qw | Energy of ordinary hot water storage tank (J) |
| CP | Constant pressure specific heat capacity of the water (J/(kg·K)) |
| ρw | Density of the water (kg/m) |
| VT | Volume of the water tank (m) |
| Thot | Temperature of the hot water (K) |
| Tcold | Temperature of the cold water (K) |
| QPCM | Energy of the PCM water tank (J) |
| VP | Volume of the PCM storage ball (m3) |
| ρPCM | Density of the PCM storage ball (kg /m3) |
| Cpl | Liquid specific heat capacity of the PCM (J/(kg·K)) |
| Tl | Liquid temperature of PCM (K) |
| L | Latent heat of the PCM (J/kg) |
| Cps | Solid specific heat capacity of the PCM (J/(kg·K)) |
| Ts | Solid state temperature of the PCM (K) |
| MIX | MIX number |
| Me | Momentum of the experimental water tank (J·m) |
| Ms | Momentum of the perfectly stratified tank (J·m) |
| Vi | Volume of water tank layer i (m3) |
| yi | Vertical distance from the center of gravity of the first floor of the tank to the bottom of the tank (m) |
| Ei | Energy of layer i of the water tank (J) |
| Ee | Energy of the experimental water tank (J) |
| Es | Energy of the perfectly stratified water tank (J) |
| Vh | Perfectly stratified tank’s hot water volume (m3) |
| Vc | Perfectly stratified tank’s cold water volume (m3) |
| D | Diameter of the water tank (m) |
| H | Height of the water tank (m) |
| ys | Vertical distance from the thermocline center to the tank bottom (m) |
| Es,i | Energy of layer I of the perfectly stratified water tank (J) |
| mi | Quality of water tank layer I (kg) |
| Ti | Temperature of water tank layer I (K) |
| Te | Water tank outlet temperature (K) |
| Tin | Water tank inlet temperature (K) |
| ξe | Exergy value of the experimental water tank (J) |
| ξs | Exergy value of the perfectly stratified water tank (J) |
References
- Mao, Q.J.; Liu, N.; Peng, L. Preparation and characterization of a novel composite phase change heat storage material. Renew. Energy 2018, 36, 1574–1580. [Google Scholar]
- Kurşun, B. Effect of rectangular hot water tank position and aspect ratio on thermal stratification enhancement. Renew. Energy 2018, 16, 639–646. [Google Scholar] [CrossRef]
- Zhang, H.T.; Zhao, Y.J.; Zhang, P.; Shi, L.J.; Li, J.L. Research progress of heat storage materials of molten nitrate in solar energy utilization. Mater. Rev. 2015, 29, 54–60. [Google Scholar]
- Zhu, M.S.; Wang, Z.L.; Zhang, H.; Sun, X.X. Experimental investigation of the comprehensive heat transfer performance of PCMs filled with CMF in a heat storage device. Int. J. Heat Mass Transf. 2022, 188, 122582. [Google Scholar] [CrossRef]
- Wang, Z.L.; Zhang, H.; Dou, B.L.; Wu, W.D. Effect of copper metal foam proportion on heat transfer enhancement in the melting process of phase change materials. Appl. Therm. Eng. 2022, 201, 117778. [Google Scholar] [CrossRef]
- Turski, M.; Jachura, A. Life cycle assessment of dispersed phase change material heat accumulators for cooperation with buildings in the district heating system. Energies 2022, 15, 5771. [Google Scholar] [CrossRef]
- Hua, W.S.; Zhang, X.L.; Ding, J.H.; Liu, F. Design and research of compound heat storage tank. Build. Energy Effic. 2016, 44, 108–113. [Google Scholar]
- Zhou, Y.K.; Yu, Z.; He, J.A. Model and Application of a Domestic Hot-Water Tank with a Novel Structure Comprising a Phase-Change Material. Build. Sci. 2017, 33, 27–33. [Google Scholar]
- Brumleve, T.D. Sensible Heat Storage in Liquids; Report No. SLL-73-0263; Sandia National Laboratories: Albuquerque, NM, USA, 1974.
- Frazzica, A.; Manzan, M.; Sapienza, A. Experimental testing of a hybrid sensible-latent heat storage system for domestic hot water applications. Appl. Energy 2016, 18, 1157–1167. [Google Scholar] [CrossRef]
- Ramana, A.S.; Venkatesh, R.; Antony, A.R.V. Experimental investigation of the LHS system and comparison of the stratification performance with the SHS system using CFD simulation. Sol. Energy 2014, 103, 378–389. [Google Scholar] [CrossRef]
- Bellan, S.; Alam, T.E.; Gonzalez-Aguilar, J. Numerical and experimental studies on heat transfer characteristics of thermal energy storage system packed with molten salt PCM capsules. Appl. Therm. Eng. 2015, 90, 970–979. [Google Scholar] [CrossRef]
- Kumar, G.S.; Nagarajan, D.; Chidambaram, L.A. Role of PCM addition on stratification behaviour in a thermal storage tank—An experimental study. Energy 2016, 15, 1168–1178. [Google Scholar] [CrossRef]
- Panchabikesan, K.; Antony Aroul Raj, V.; Ding, Y. Enhancement in free cooling potential through PCM based storage system integrated with Direct Evaporative Cooling (DEC) unit. Energy 2017, 144, 443–455. [Google Scholar] [CrossRef] [Green Version]
- Koca, A.; Oztop, H.F.; Koyun, T. Energy and exergy analysis of a latent heat storage system with phase change material for a solar collector. Renewable Energy 2008, 33, 567–574. [Google Scholar] [CrossRef]
- Bony, J.; Citherlet, S. Numerical model and experimental validation of heat storage with phase change materials. Energy Build. 2007, 39, 1065–1072. [Google Scholar] [CrossRef]
- Abdelsalam, M.Y.; Sarafraz, P.; Cotton, J.S. Heat transfer characteristics of a hybrid thermal energy storage tank with Phase Change Materials (PCMs) during indirect charging using isothermal coil heat exchanger. Solar Energy 2017, 157, 462–476. [Google Scholar] [CrossRef]
- Navarro, L.; Barreneche, C.; Castell, A. High density polyethylene spheres with PCM for domestic hot water applications: Water tank and laboratory scale study. J. Energy Storage 2017, 13, 262–267. [Google Scholar] [CrossRef] [Green Version]
- Prieto, M.M.; González, B.; Granado, E. Thermal performance of a heating system working with a PCM plate heat exchanger and comparison with a water tank. Energy Build. 2016, 122, 89–97. [Google Scholar] [CrossRef]
- Najafian, A.; Haghighat, F.; Moreau, A. Integration of PCM in domestic hot water tanks: Optimization for shifting peak demand. Energy Build. 2015, 5, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.; Furbo, S.; Kong, W. Thermal performance assessment and improvement of a solar domestic hot water tank with PCM in the mantle. Energy Build. 2018, 172, 10–21. [Google Scholar] [CrossRef]
- Kicsiny, R. Black-box model for solar storage tanks based on multiple linear regression. Renew. Energy 2018, 125, 857–865. [Google Scholar] [CrossRef]
- Afshan, M.E.; Selvakumar, A.S.; Velraj, R.; Rajaraman, R. Effect of aspect ratio and dispersed PCM balls on the charging performance of a latent heat thermal storage unit for solar thermal applications. Renew. Energy 2019, 148, 876–888. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Ibanez, M.; Sole, C. Experimentation with a water tank including a PCM module. Sol. Energy Mater. Sol. Cells 2006, 9, 1273–1282. [Google Scholar] [CrossRef]
- Zalba, B.; Marín, J.M.; Cabeza, L.F. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Sharma, S.D.; Sagara, K. Latent heat storage materials and systems: A review. Int. J. Green Energy 2005, 2, 51–56. [Google Scholar] [CrossRef]
- Ibáñez, M.; Cabeza, L.F.; Solè, C. Modelization of a water tank including a PCM module. Appl. Therm. Eng. 2006, 26, 1328–1333. [Google Scholar] [CrossRef]
- Berkel, J.V. Mixing in thermally stratified energy stores. Solar Energy 1996, 58, 203–211. [Google Scholar] [CrossRef] [Green Version]
- Ievers, S.; Lin, W. Numerical simulation of three-dimensional flow dynamics in a hot water storage tank. Appl. Energy 2009, 86, 2604–2614. [Google Scholar] [CrossRef] [Green Version]
- Altuntop, N.; Arslan, M.; Ozceyhan, V. Effect of obstacles on thermal stratification in hot water storage tanks. Appl. Therm. Eng. 2005, 25, 2285–2298. [Google Scholar] [CrossRef]
- Allouche, Y.; Varga, S.; Bouden, C. Validation of a CFD model for the simulation of heat transfer in a tubes-in-tank PCM storage unit. Renew. Energy 2016, 89, 371–379. [Google Scholar] [CrossRef]
- Wang, Z.L.; Zhang, H.; Dou, B.L.; Huang, H.J.; Wu, W.D.; Wang, Z.Y. Experimental and numerical research of thermal stratification with a novel inlet in a dynamic hot water storage tank. Renew. Energy 2017, 111, 353–371. [Google Scholar] [CrossRef]
- Davidson, J.H.; Adams, D.A. Fabric stratification manifolds for solar water heating. J. Sol. Energy Eng. 1994, 3, 130–136. [Google Scholar] [CrossRef]
- Njoku, H.O.; Ekechukwu, O.V.; Onyegegbu, S.O. Analysis of stratified thermal storage systems: An overview. Heat Mass Transf. 2014, 50, 1017–1030. [Google Scholar] [CrossRef]


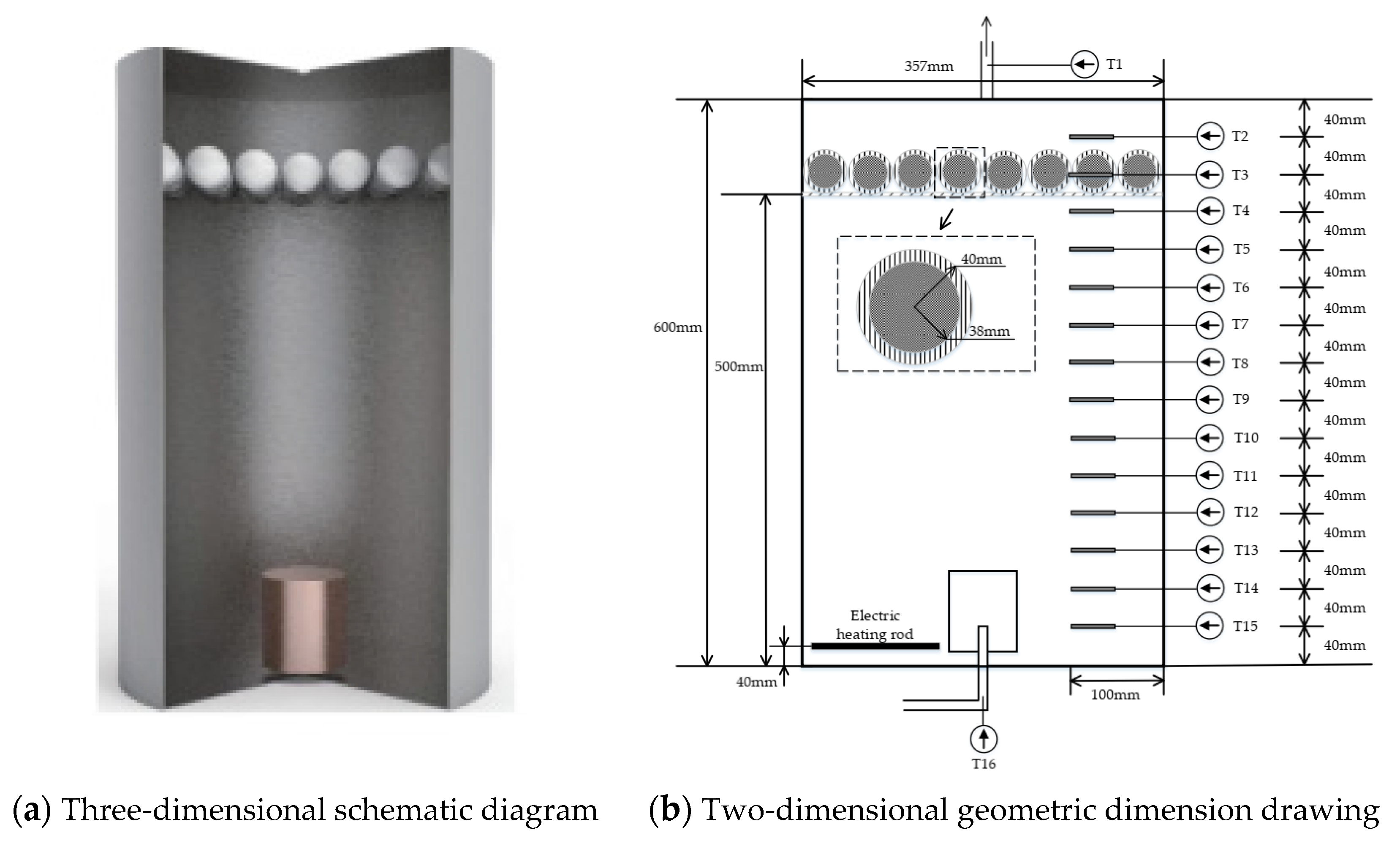



| Thermophysical Property | Unite | Value |
|---|---|---|
| Latent heat | kJ·kg−1 | 250 |
| Specific heat capacity | kJ·(kg K)−1 | 2.719 |
| Thermal conductivity | W·(m·K)−1 | 0.8 |
| Density | kg·m−3 | 1520 |
| Phase transition temperature | °C | 58/62 |
| Latent heat | kJ·kg−1 | 250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Xu, F.; Wang, Z.; Zhang, H. An Experimental Investigation on the Performance of a Water Storage Tank with Sodium Acetate Trihydrate. Energies 2023, 16, 777. https://doi.org/10.3390/en16020777
Huang J, Xu F, Wang Z, Zhang H. An Experimental Investigation on the Performance of a Water Storage Tank with Sodium Acetate Trihydrate. Energies. 2023; 16(2):777. https://doi.org/10.3390/en16020777
Chicago/Turabian StyleHuang, Jie, Fei Xu, Zilong Wang, and Hua Zhang. 2023. "An Experimental Investigation on the Performance of a Water Storage Tank with Sodium Acetate Trihydrate" Energies 16, no. 2: 777. https://doi.org/10.3390/en16020777
APA StyleHuang, J., Xu, F., Wang, Z., & Zhang, H. (2023). An Experimental Investigation on the Performance of a Water Storage Tank with Sodium Acetate Trihydrate. Energies, 16(2), 777. https://doi.org/10.3390/en16020777







