A Comprehensive Multi-Factor Method for Identifying Overflow Fluid Type
Abstract
:1. Introduction
2. Traditional Overflow Fluid Identification Method and Its Deficiencies
2.1. Empirical Method
2.2. Classical Density Model
2.3. Gas Logging Interpretation Methods
3. Comprehensive Multi-Factor Method
3.1. Calculation Correction Method of Overflow Fluid Density
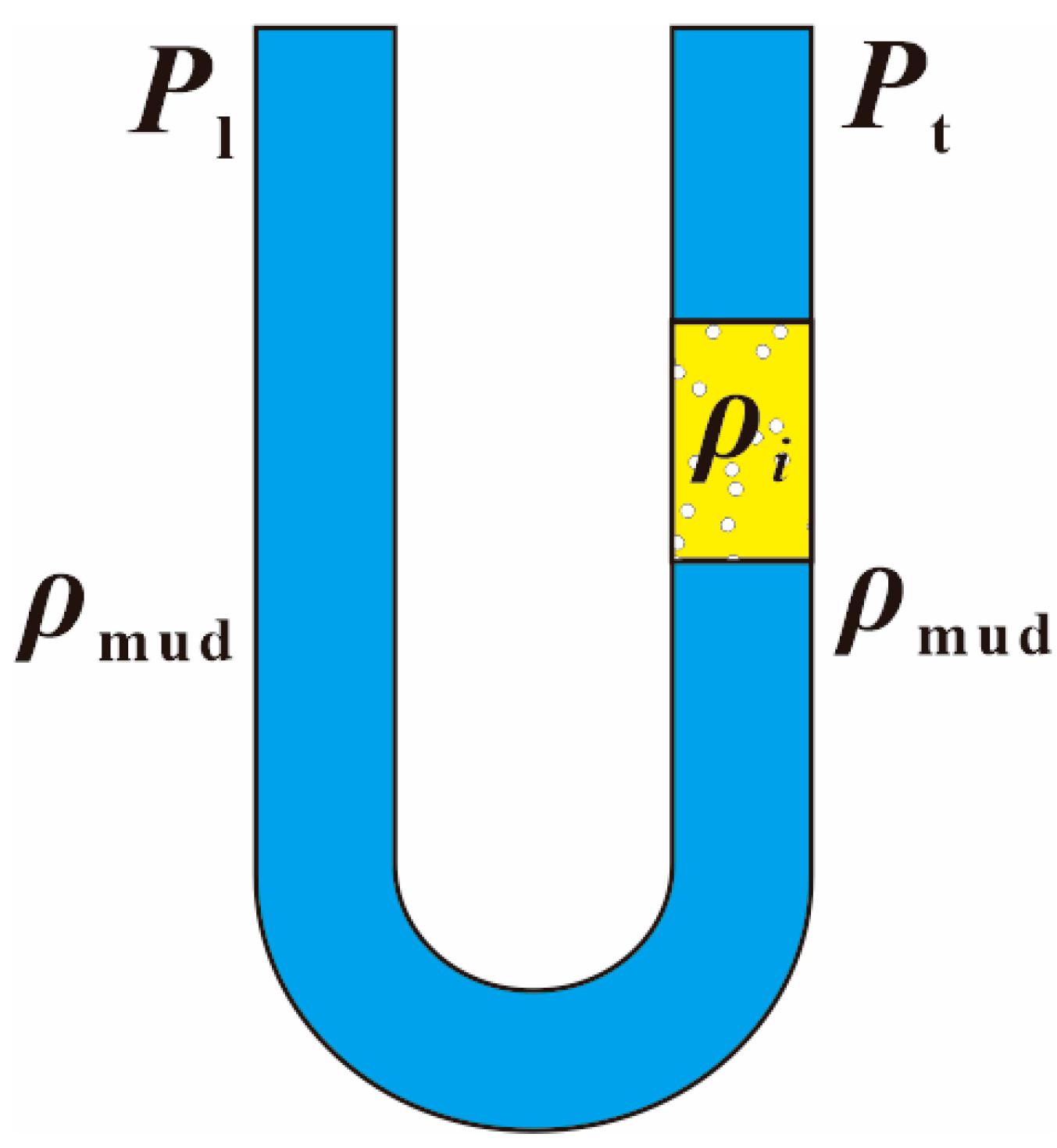
3.1.1. The Influence of Temperature and Pressure
- (1)
- Empirical density model
- (2)
- Composite density model
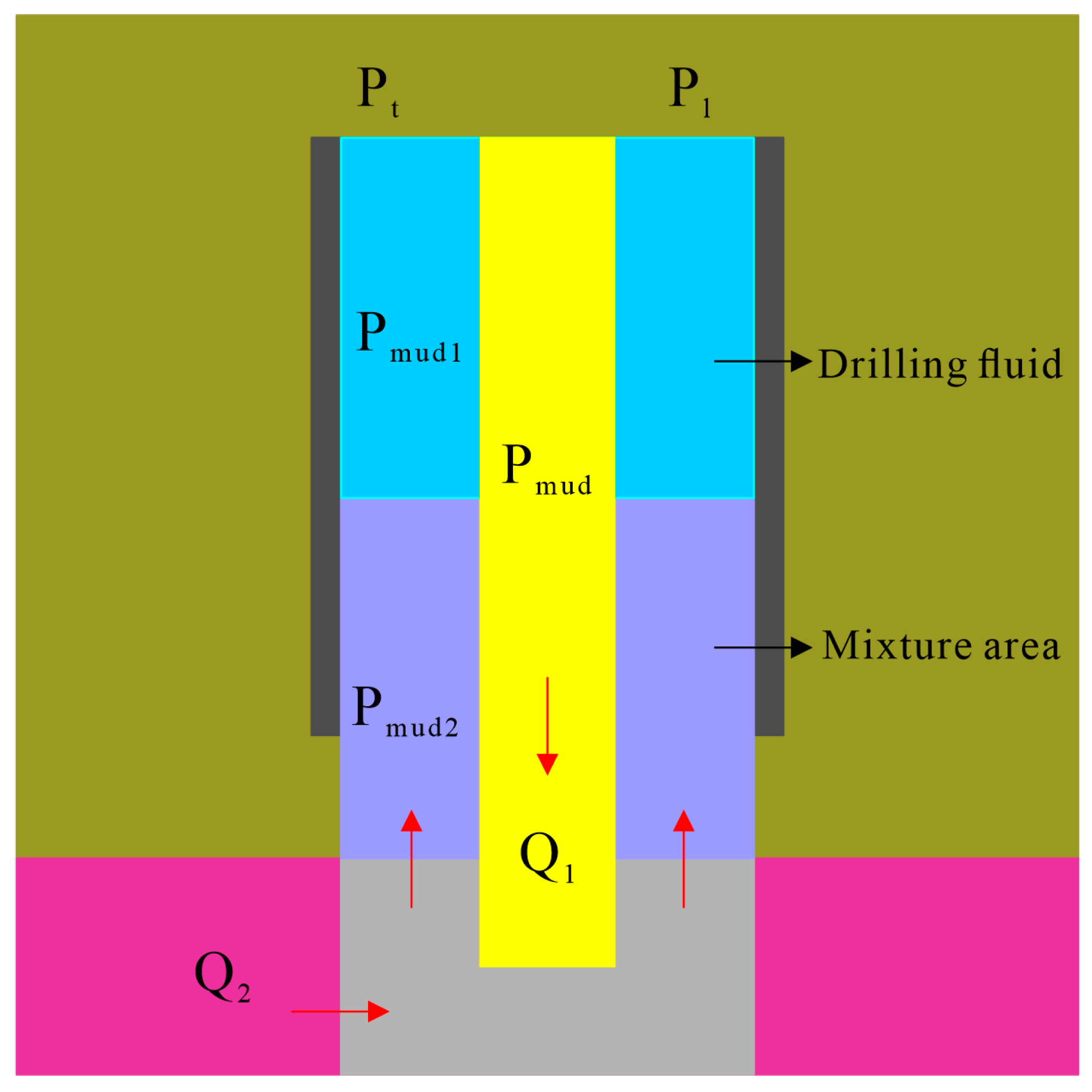
3.1.2. The Influence of the Two-Phase Flow Model
3.2. The Gas Logging Comprehensive Analysis Method
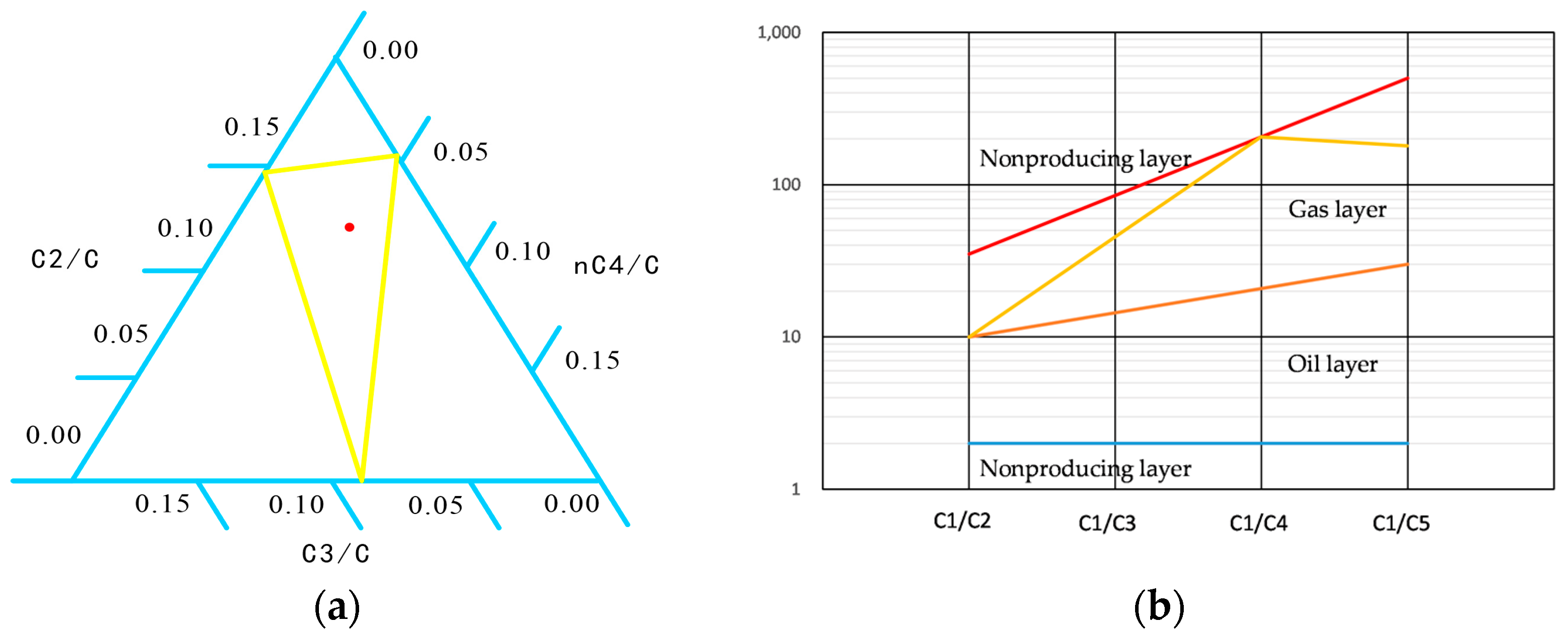
3.2.1. The Triangle Diagram Method
3.2.2. The Pixler Method
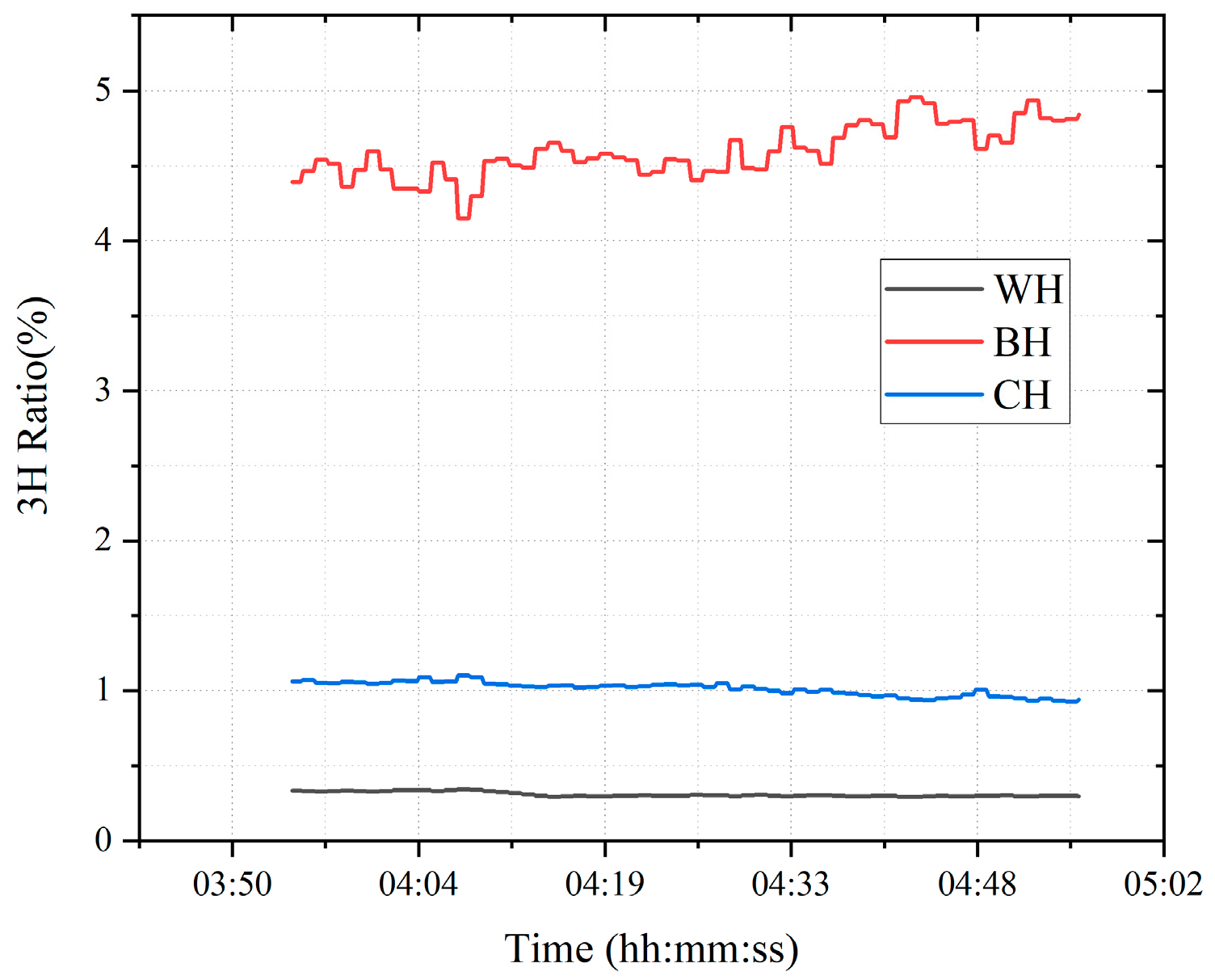
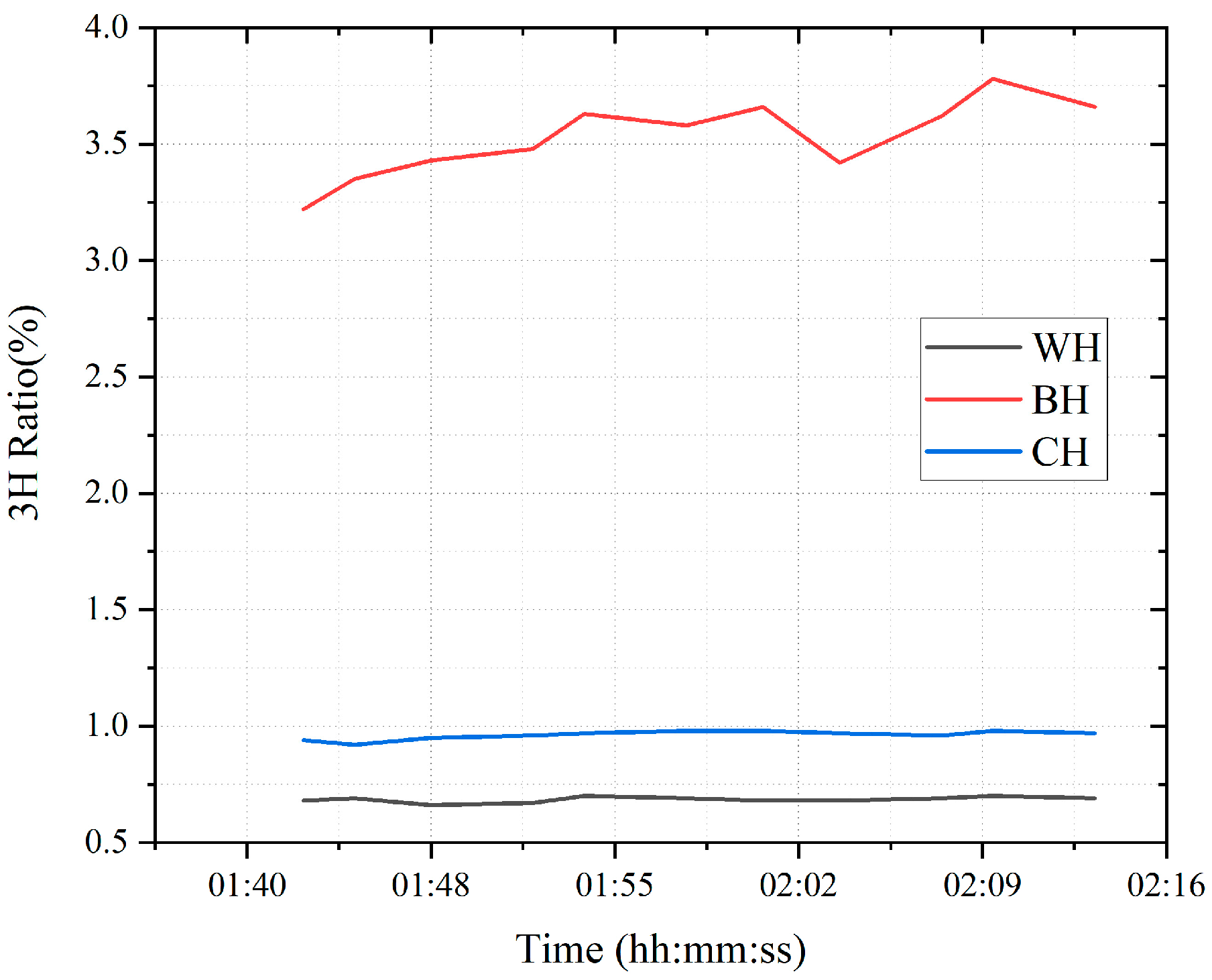
3.2.3. 3H Ratio Method
3.2.4. Comprehensive Analysis Method of Overflow Fluid Types Based on Gas Logging Interpretation
- (1)
- Identification of water and saltwater layers
- (2)
- Identification of oil and gas layers
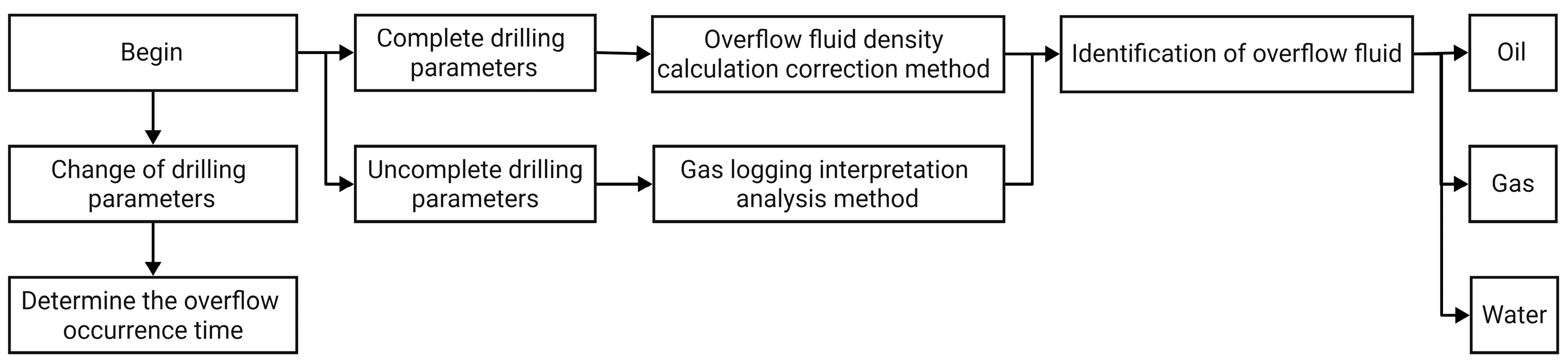
3.3. Identification Process of Overflow Fluid Type
- (1)
- Determine the overflow occurrence time according to the change in drilling parameters;
- (2)
- If the drilling parameters during the overflow period are complete and normal without error, extract the drilling parameters during the overflow period, use the overflow fluid density calculation correction method to obtain the overflow fluid density, and identify the type of overflow fluid according to Table 1;
- (3)
- If there are no real-time drilling parameters or if the drilling parameters are abnormal, extract the gas logging at the time of the overflow and use the comprehensive analysis method of gas logging data to identify the type of overflow fluid;
- (4)
- If both drilling parameters and gas logging data can be used, compare the results obtained by the two methods and combine them with the field analysis to obtain the final identification result.
4. Example Calculation and Validation
4.1. OnSite Example Calculation
4.2. Validation of Overflow Fluid Density Model
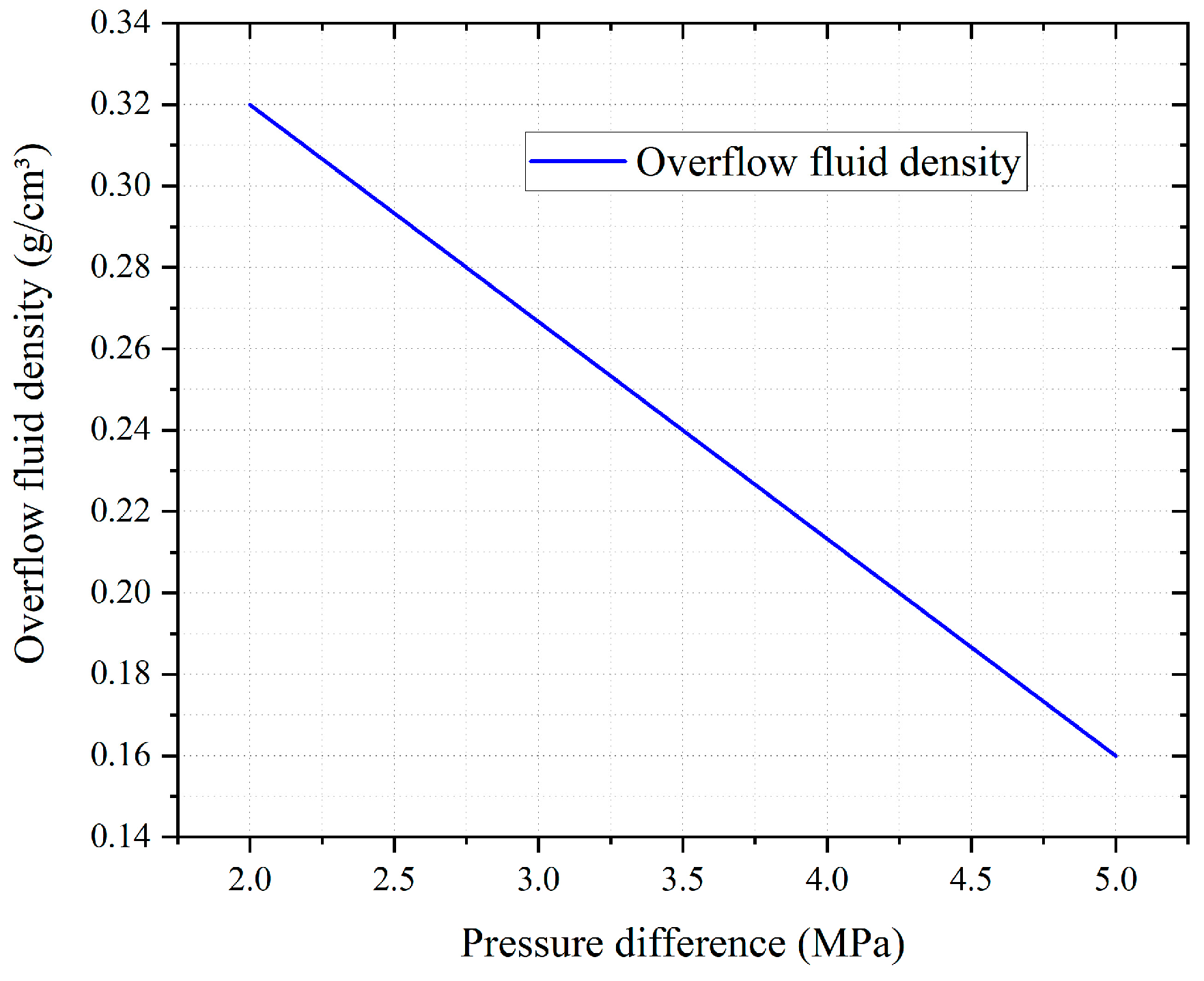
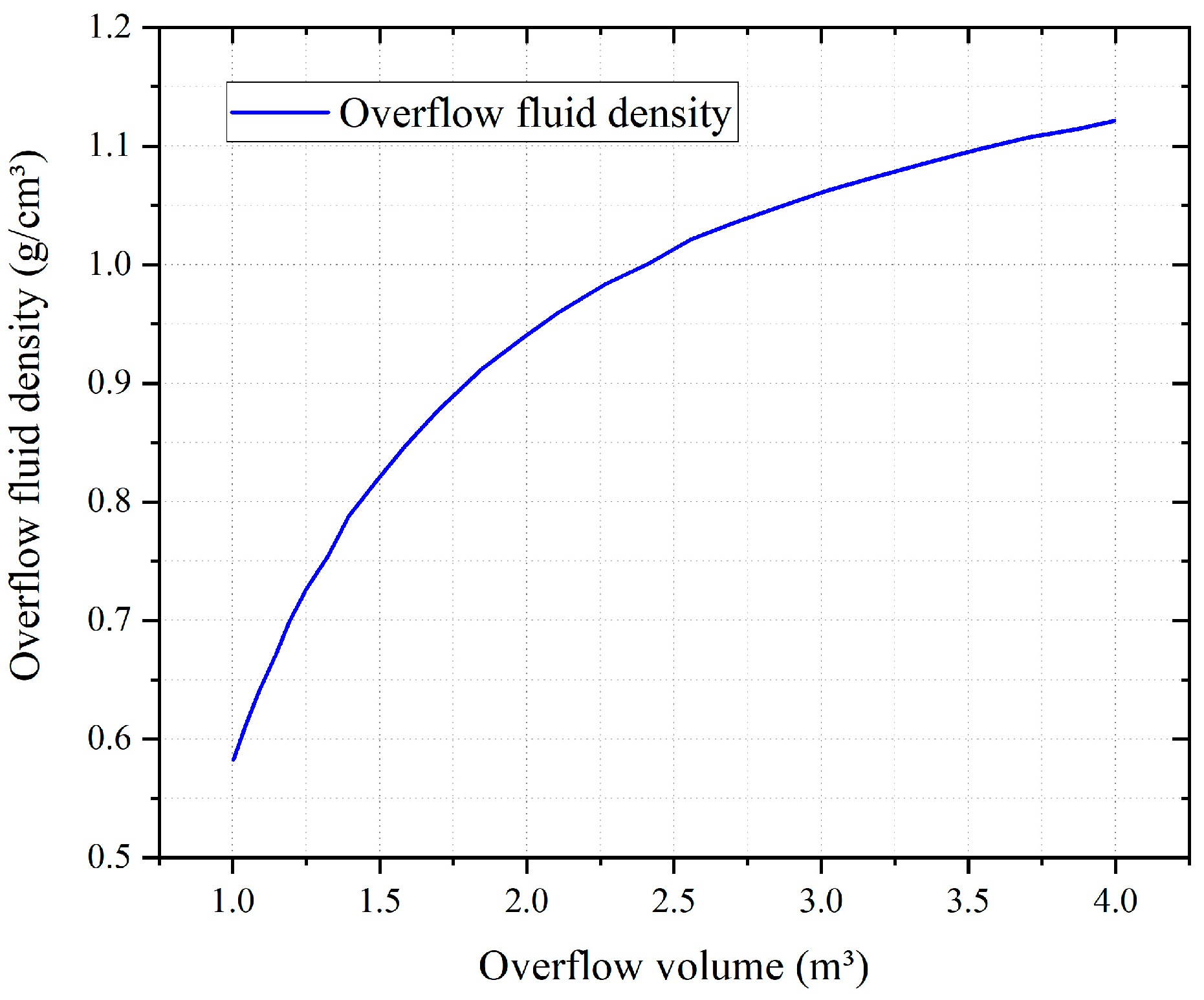
5. Analysis of Influencing Factors for Overflow Fluid Density
- (1)
- The geothermal gradient
- (2)
- The pressure difference between standpipe pressure and casing pressure
- (3)
- The amount of overflow fluid
6. Summary and Conclusions
- (1)
- In this paper, a comprehensive multi-factor method for identifying the types of overflow fluid is established, which includes a comprehensive analysis of the method of gas logging and the method of the correction of the overflow fluid density calculation. When comparing this method with field test results from more than 20 overflow wells onsite, the discriminant accuracy of this method was over 90% and the density calculation accuracy was higher than that of the traditional model.
- (2)
- In this paper, the effects of geothermal gradient, vertical casing pressure difference after well shut-in, and formation fluid kick-on of the overflow fluid density were analyzed. It was found that as the geothermal gradient increases, the overflow fluid density decreases; when the kick amount is constant, an increase in the pressure difference gradually decreases the overflow fluid density. When other conditions remain unchanged, the kick amount increases, and the growth rate of overflow fluid density gradually slows down.
- (3)
- The comprehensive method presented in this paper can be used to provide guidance for handling overflow accidents in the field and ensure that drilling operations are carried out safely.
- (4)
- In further research based on this paper, the density model can be improved by considering different working conditions, and a new gas logging analysis method with greater accuracy may be proposed.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Xue, Z.; Cheng, Z.; Jiang, H.; Wang, R. Progress and Development directions of deep oil and gas exploration and development in China. China Pet. Explor. 2020, 25, 45–57. [Google Scholar]
- Zhang, G.; Ma, F.; Liang, Y.; Zhao, J.; Qin, Y.; Liu, X.; Zhang, K.; Ke, W. Domain and theory-technology progress of global deep oil & gas exploration. Acta Pet. Sin. 2015, 36, 1156–1166. [Google Scholar]
- Guan, Z.; Chen, T. Drilling Engineering Theory and Technology; Petroleum University Press: Beijing, China, 2000. [Google Scholar]
- Compilation of Blowout Accident Cases of China National Petroleum Corporation; Petroleum Industry Press: Beijing, China, 2006.
- Wang, P.; Luo, P.; Nie, X.; Zhang, X.; Yang, L. Treatment of complicated well conditions with blowout and leakage in Well Shuangmiao 1. Nat. Gas Ind. 2007, 27, 4. [Google Scholar]
- Zhang, G. Analysis of Overflow Killing in Well Qingxi 1. Pet. Drill. Tech. 2009, 37, 5. [Google Scholar]
- Zhang, G. Oil Drilling Technology about One-cycle Killing Technology from Typical Blowout Cases. Pet. Drill. Tech. 2018, 46, 6. [Google Scholar]
- Bi, W. On-Site Killing Method Optimization and Well Killing Process Simulation Research; China University of Petroleum: Beijing, China, 2006. [Google Scholar]
- Drilling Manual; Petroleum Industry Press: Beijing, China, 1990.
- Li, J.; Lei, J.; Hou, X. Discussion about the application of comprehensive interpretation method of gas logging in Tarim Basin. Logging Eng. 2003, 14, 18–24. [Google Scholar]
- Huang, X. Gas logging and logging methane correction method and gas logging interpretation method selection principle. Logging Eng. 2007, 18, 1–5. [Google Scholar]
- Hou, P. A method for comprehensively discriminating oil and gas water layers using logging data. Logging Eng. 2008, 19, 1–8. [Google Scholar]
- Hou, P. A simple parameter method of gas logging to identify oil, gas and water layers. Logging Eng. 2009, 20, 21–24. [Google Scholar]
- Duan, Y.; Zhang, J. Application of Light Hydrocarbon Triangle Method in Oil and Gas Reservoir Evaluation in Mahuangshan Area. Pet. Geol. Eng. 2010, 24, 43–46. [Google Scholar]
- Yu, M.; Bian, H.; Zhuang, W.; Zhu, D.; Ye, X.; Xue, Z. Analysis of applicability of Pixler chart interpretation method for gas logging. Logging Eng. 2013, 24, 14–19, 85–86. [Google Scholar]
- Li, Z.; Hu, W.; Xia, Y.; Chen, X.; Wei, F. Studies about the method for identification of the oil gas layer types with gas logging data. Offshore Oil 2015, 35, 78–85. [Google Scholar]
- Su, Y.; Lu, B.; Liu, Y.; Zhou, Y.; Liu, X.; Liu, W.; Zang, Y. Status and research suggestions on the drilling and completion technologies for onshore deep and ultra-deep wells in China. Oil Drill. Prod. Technol. 2020, 42, 527–542. [Google Scholar]
- Wang, Z.; Hao, X.; Wang, X.; Xue, L.; Guo, X. Numerical Simulation on Deepwater Drilling Wellbore Temperature and Pressure Distribution. Pet. Sci. Technol. 2010, 28, 911–919. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, J.; Wang, X. Predicting temperature and pressure in high-temperature–high-pressure gas wells. Petrol. Sci. Technol. 2011, 2, 132–148. [Google Scholar] [CrossRef]
- Yan, J.; Li, Y. Mathematical model for predicting mud density at high temperature and pressure. Oil Drill. Prod. Technol. 1990, 12, 27–34. [Google Scholar]
- Wang, E.; Fan, H.; Ma, L. Simple method for calculating the down-hole drilling fluid density. Sci. Technol. Rev. 2015, 33, 54–58. [Google Scholar] [CrossRef]
- Fan, H. Practical Drilling Fluid Mechanics; Petroleum Industry Press: Beijing, China, 2014. [Google Scholar]
- Chen, J. Petroleum Gas-Liquid Two-Phase Pipe Flow; Petroleum Industry Press: Beijing, China, 1989. [Google Scholar]
- He, H.; Tong, J.; An, Y. Research on triangle illustration to gas logging hydrocarbon component. J. Tianjin Inst. Technol. 2004, 20, 30–33. [Google Scholar]
- Zhou, B. Research on Complex Process Treatment Technology under MPD Conditions in Tazhong Area; China University of Petroleum: Beijing, China, 2017. [Google Scholar]
- Hu, J. A new method to calculate the Z factor of natural gases. Acta Pet. Sin. 2011, 32, 862–865. [Google Scholar]




| Overflow Fluid Density | Overflow Fluid Type |
|---|---|
| ρ < 0.36 g/cm3 | Gas |
| ρ = 0.37–0.60 g/cm3 | Gas and oil mixture |
| ρ = 0.61–0.92 g/cm3 | Oil or water and oil mixture |
| ρ > 0.92 g/cm3 | Water or saltwater |
| The Internal Triangle Type | Reservoir Properties |
|---|---|
| An equilateral triangle | Gas layer |
| An inverted triangle | Oil layer |
| A large triangle (the border length ratio is greater than 100%) | Dry gas or the oil and gas ratio is very low |
| A small triangle (the border length ratio is less than 25%) | Wet gas or the oil and gas ratio is very high |
| The intersection of the inner triangle vertex and the vertex of the outer triangle is distributed in the internal triangle | Production capacity |
| The intersection of the inner triangle vertex and the vertex of the outer triangle is distributed outside the internal triangle | No production capacity |
| 3H Ratio | Type of the Fluid |
|---|---|
| < 0.5 | Light-associated gas, basically no productivity |
| > 40 | Heavy oil or residual oil, and low productivity |
| < 0.5 and > 100 | Extremely light dry gas, unprofitable |
| 0.5 < < 17.5, < < 100 | Recoverable gas |
| 0.5 < < 17.5, < | Recoverable oil with a high gas–oil ratio |
| 17.5 < < 40, < | Recoverable oil |
| 0.5 < < 17.5, < , < 0.5 | Recoverable wet gas or condensate oil |
| 0.5 < < 17.5, < , > 0.5 | Recoverable oil with a high gas–oil ratio |
| Formation Fluid Properties | Overflow Fluid Density Range (g/cm3) |
|---|---|
| Light associated gas | 0–0.15 |
| Recoverable gas | 0.15–0.34 |
| Recoverable oil with a high gas–oil ratio | 0.34–0.50 |
| Oil | 0.50–0.62 |
| Heavy oil | 0.62–0.85 |
| Well Name | Well Depth | Shut-In Standpipe Pressure | Shut-In Casing Pressure | Overflow Volume | ρmud | ρi | Identification Result | Test Result |
|---|---|---|---|---|---|---|---|---|
| Y | 8547.72 | 5.04 | 5.82 | 0.6 | 1.29 | 0.29 | Gas | Gas |
| Traditional Method Density (g/cm3) | Correction Method Density (g/cm3) | Overflow Fluid Density (g/cm3) |
|---|---|---|
| 0.282 | 0.269 | 0.272 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Z.; Fan, H.; Liu, Y.; Ye, Y. A Comprehensive Multi-Factor Method for Identifying Overflow Fluid Type. Energies 2023, 16, 922. https://doi.org/10.3390/en16020922
Tao Z, Fan H, Liu Y, Ye Y. A Comprehensive Multi-Factor Method for Identifying Overflow Fluid Type. Energies. 2023; 16(2):922. https://doi.org/10.3390/en16020922
Chicago/Turabian StyleTao, Zhenyu, Honghai Fan, Yuhan Liu, and Yuguang Ye. 2023. "A Comprehensive Multi-Factor Method for Identifying Overflow Fluid Type" Energies 16, no. 2: 922. https://doi.org/10.3390/en16020922
APA StyleTao, Z., Fan, H., Liu, Y., & Ye, Y. (2023). A Comprehensive Multi-Factor Method for Identifying Overflow Fluid Type. Energies, 16(2), 922. https://doi.org/10.3390/en16020922











