Reliable Tools to Forecast Sludge Settling Behavior: Empirical Modeling
Abstract
:1. Introduction
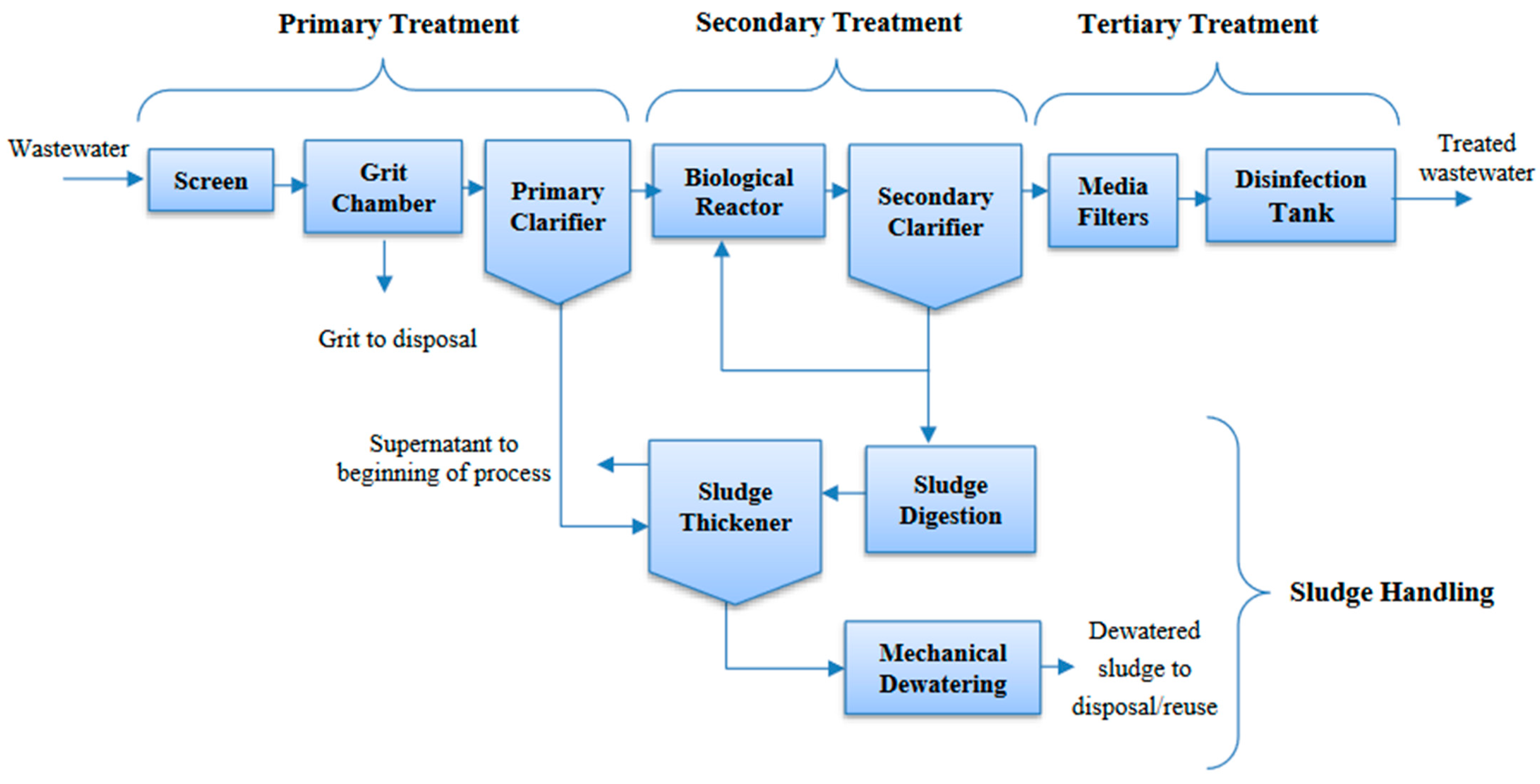
2. Description of the Sedimentation Process
- -
- Preliminary treatment: Grit removal (i.e., sedimentation of inorganic particles of large dimensions);
- -
- Primary sedimentation: Sedimentation of suspended solids from the raw sewage;
- -
- Secondary treatment: Secondary sedimentation (i.e., removal of mainly biological solids);
- -
- Sludge treatment: Thickening (i.e., settling and thickening of primary sludge and/or excess biological sludge), and;
- -
- Physical–chemical treatment: Solid particle settling after chemical-induced precipitation.
3. Materials and Methods
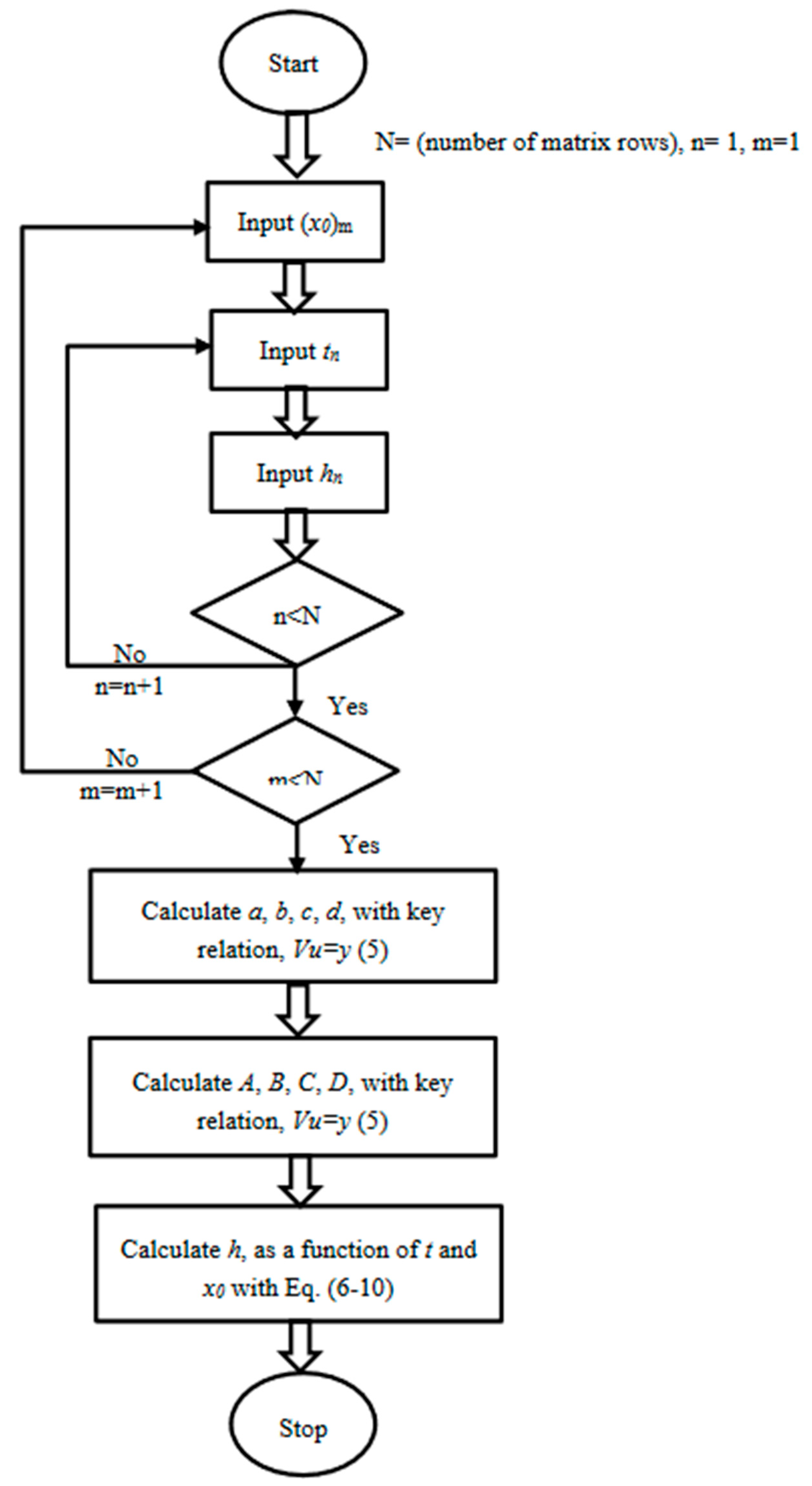
3.1. Correlation Based on the Vandermonde Matrix (VM)
- (1)
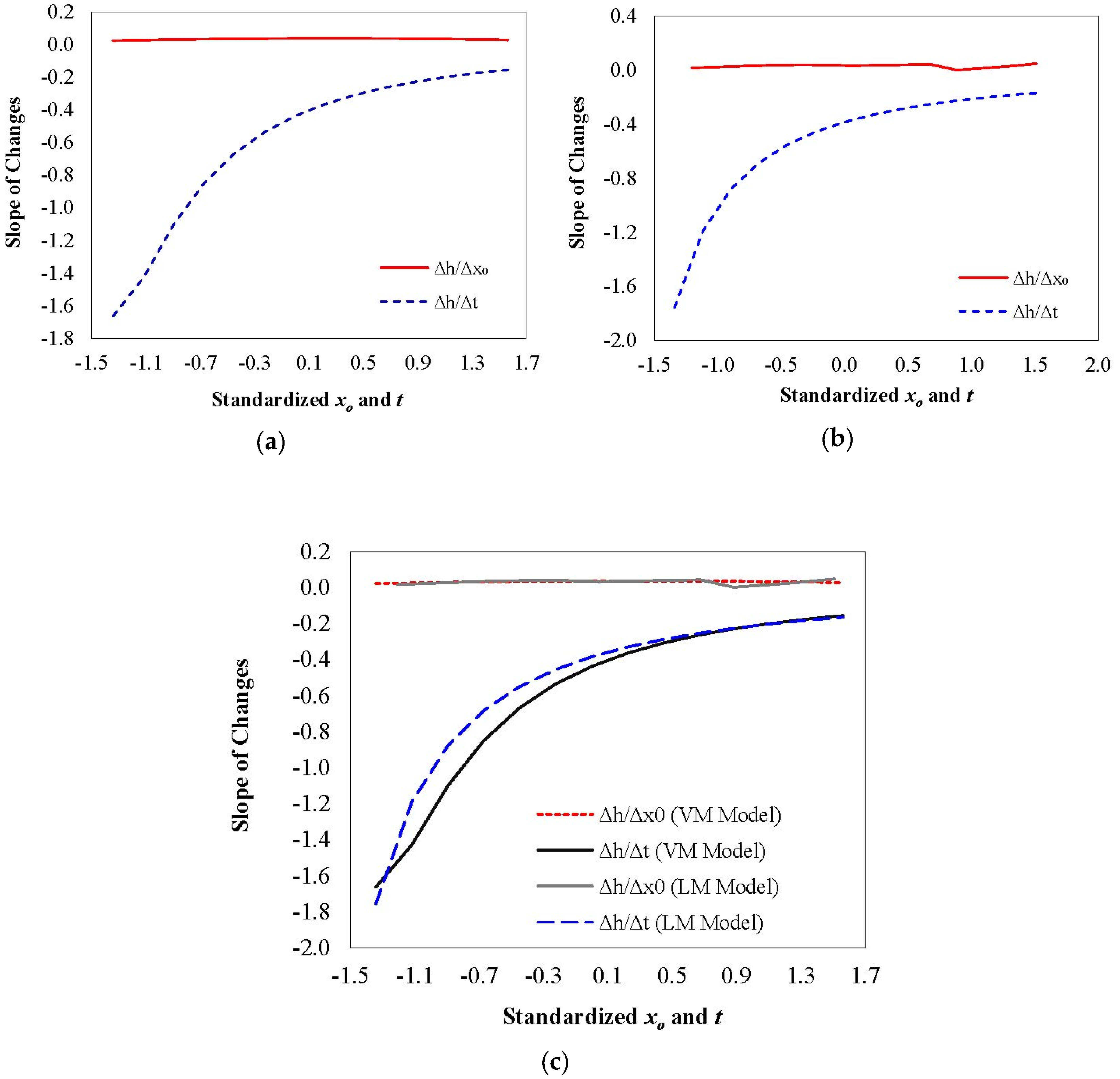
- At a given initial sludge concentration (x0) and relevant height data (h), Equation (6) was applied and the coefficients a, b, c, and d were determined so that the interface height variations were correct function of the settling time using Equation (4).
- (2)
- The coefficients for Equation (6) were recalculated at each subsequent initial sludge concentration using step 1.
- (3)
- According to Equations (7)–(10), the coefficients A1–A3, B1–B3, C1–C3, and D1–D3 are dependent on the initial solid concentration. Therefore, these coefficients should be found so that the coefficients of the previous step in Equation (6), i.e., a, b, c, and d represent the correct functionality of the initial concentration. The different coefficients obtained from the previous steps (i.e., a, b, c, and d) were correlated to the initial concentration, and the new coefficients (i.e., A1–A3, B1–B3, C1–C3, and D1–D3) for Equations (7)–(10) were obtained in a similar way using Equation (4).
3.2. Correlation Based on the Levenberg–Marquardt (LM) Algorithm
3.3. Error Analysis
- -
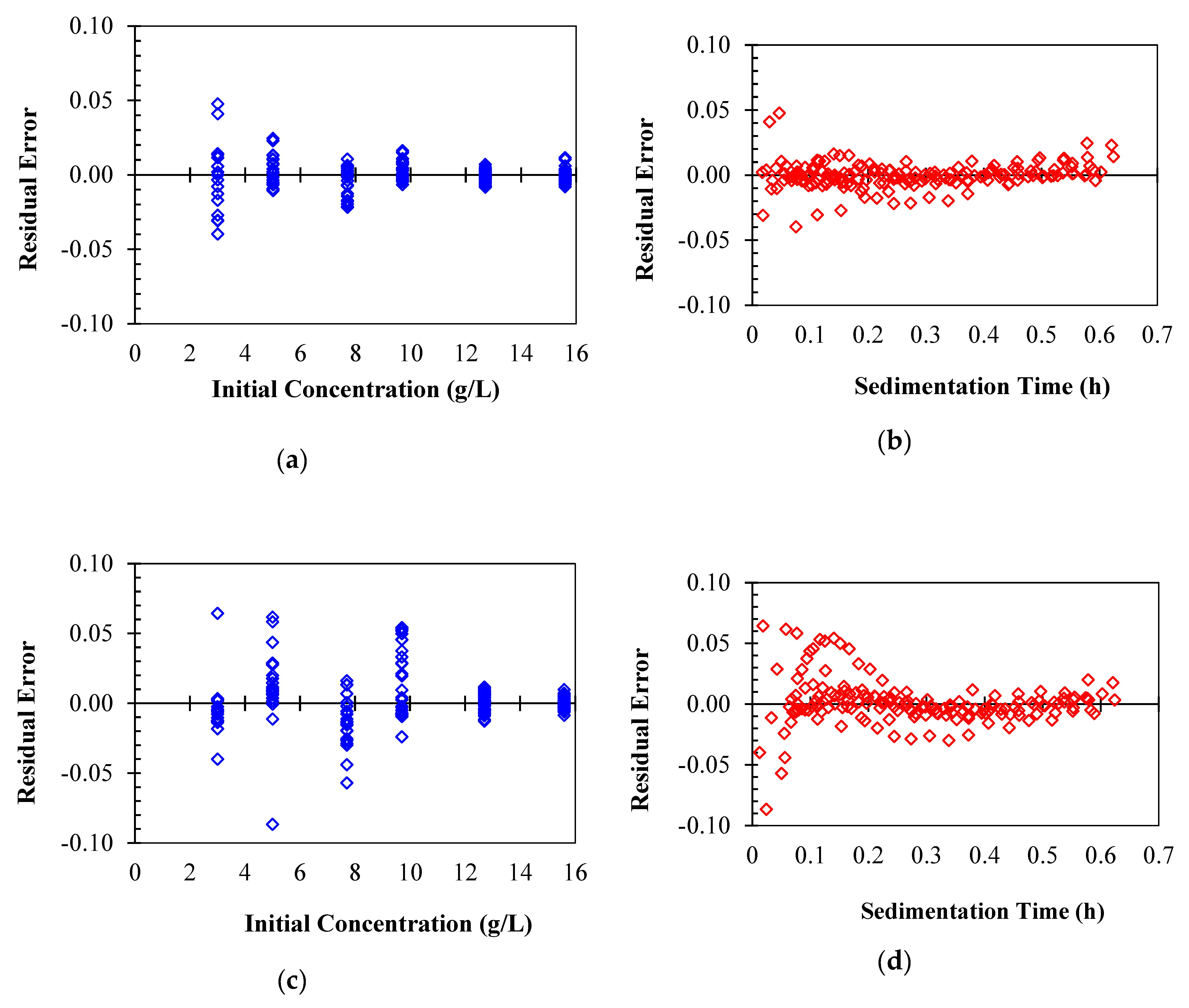
- The experimental data of interface height versus time could be subject to measurement error.
- -
- The interface height versus time curve has various sections with different curvatures. The temporal slopes associated with each particular settling time as well as the changes between the phases can occur at steeper or gentler slopes. In addition, modeling the hindered settling period is a very challenging task.
- -
- Another source of uncertainty comes from the model’s ability to predict the behavior associated with the experimental data. There is no universal model that could completely capture different behaviors associated with the solid settling phenomenon. If the tuning parameters are not optimally adjusted or insufficient experimental data are utilized, modeling error would increase.
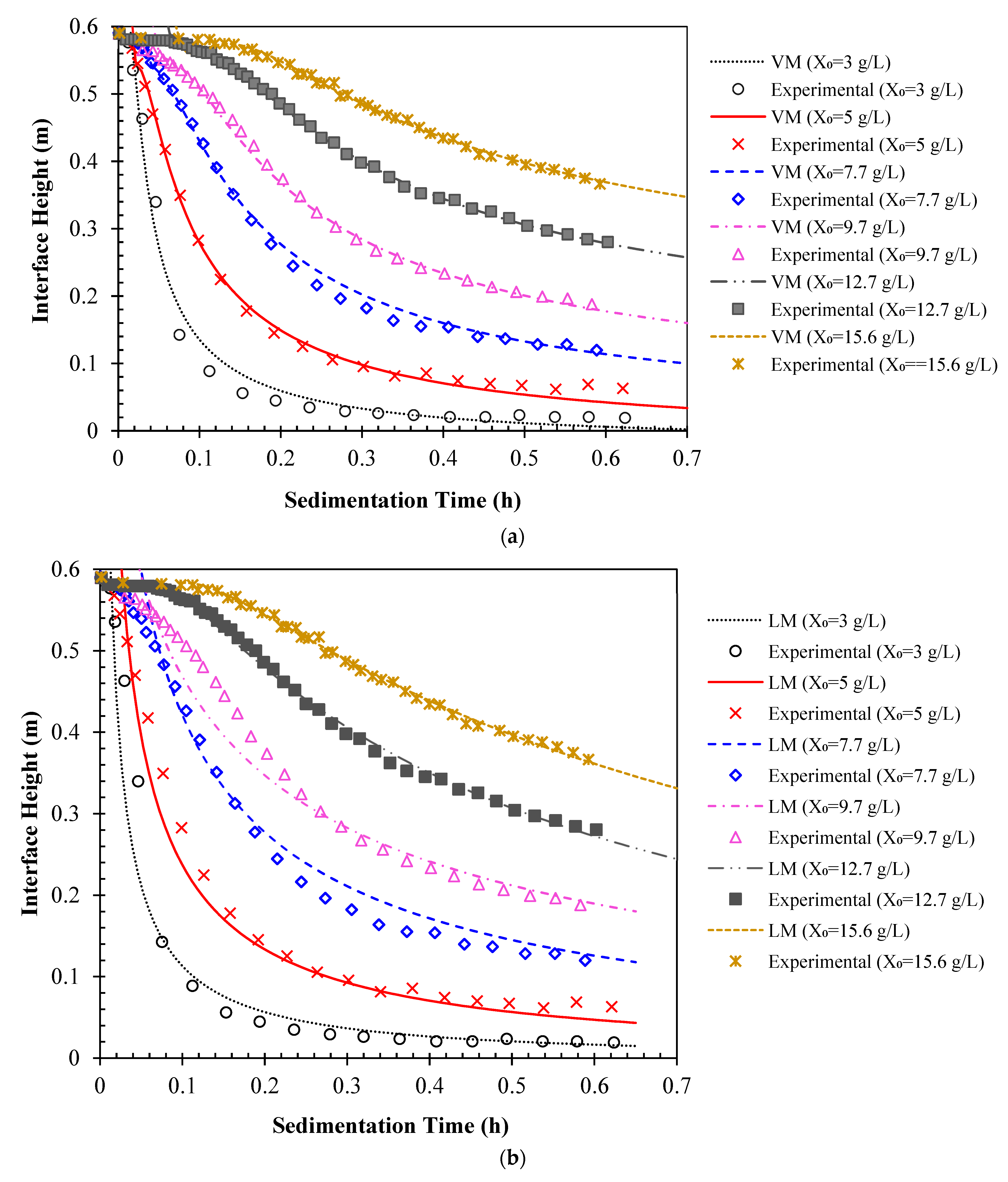
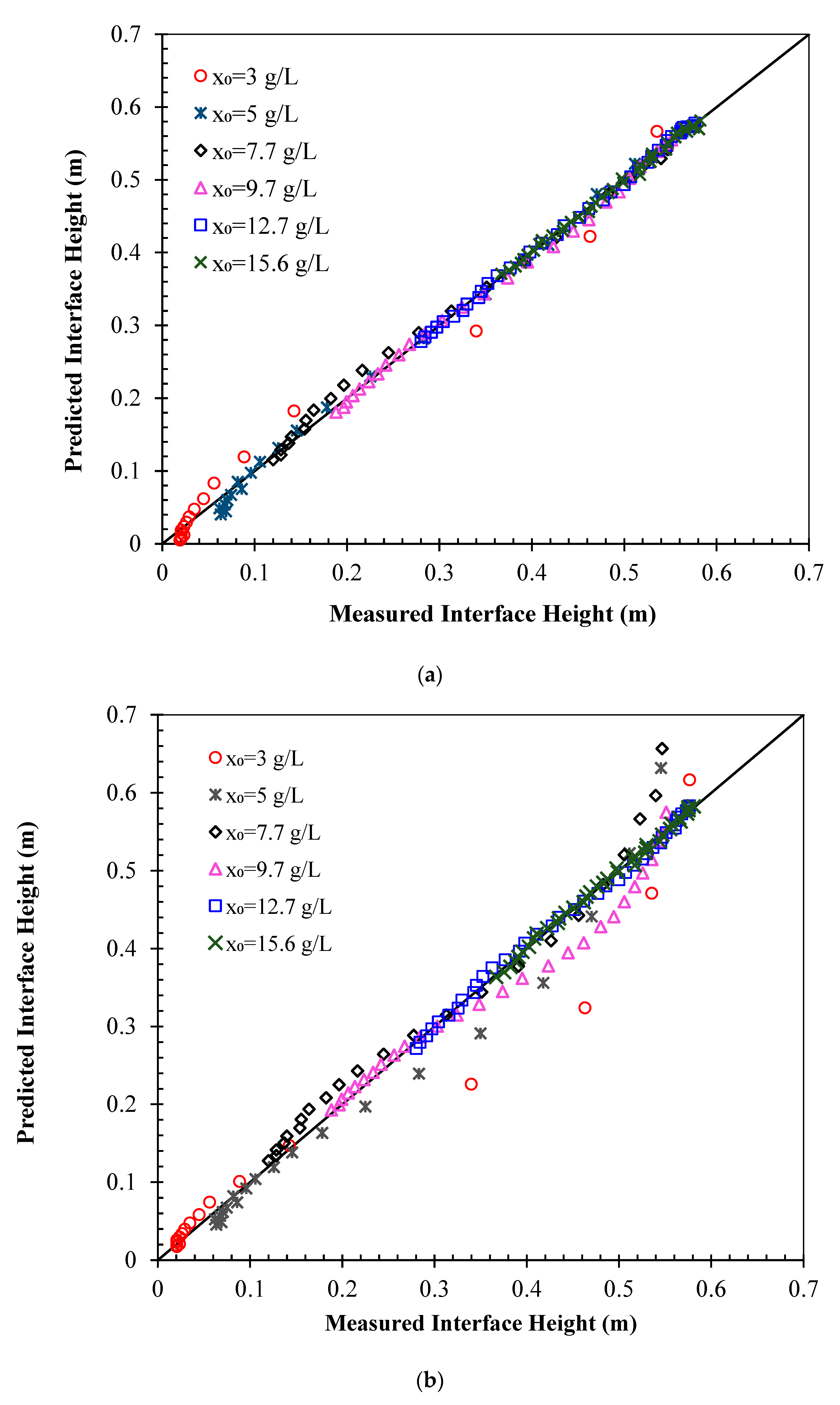
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Acronyms | Greek Letters | ||
| LM | Levenberg–Marquardt | α | Tuned coefficient for Equation (11) |
| MAPE | Mean absolute percentage error | β | Tuned coefficient for Equation (11) |
| ODE | Ordinary differential equation | γ | Tuned coefficient for Equation (11) |
| PDE | Partial differential equation | δ | Tuned coefficient for Equation (11) |
| PE | Percentage error | ε | Tuned coefficient for Equation (11) |
| R2 | Coefficient of determination | θ | Tuned coefficient for Equation (11) |
| RMSE | Root mean square error | ||
| VM | Vandermonde model | ||
| Variables/Letters | Subscripts | ||
| A | Tuned coefficient for Equations (7)–(10) | 0 | Initial value |
| a | Coefficient of Equation (6) | Exp | Experimental data |
| B | Tuned coefficient for Equations (7)–(10) | i | ith value |
| b | Coefficient of Equation (6) | j | jth value |
| C | Tuned coefficient for Equations (7)–(10) | Mean | Average value |
| c | Coefficient of Equation (6) | Predict | Predicted by model |
| D | Tuned coefficient for Equations (7)–(10) | s | Standardized |
| d | Coefficient of Equation (6) | ||
| h | Solid–liquid interface (m) | ||
| n, m | Number of rows and columns of VM | ||
| N | Number of experimental data | ||
| x | Concentration (g/L) | ||
| std | Standard deviation | ||
| u | Unknown coefficients in Equations (4) and (5) | ||
| t | Sedimentation time (h) | ||
| V | Vandermonde matrix | ||
| y | Unknown coefficients in Equation (5) | ||
References
- Rasouli, S.; Rezaei, N.; Hamedi, H.; Zendehboudi, S.; Duan, X. Superhydrophobic and superoleophilic membranes for oil-water separation application: A comprehensive review. Mater. Des. 2021, 204, 109599. [Google Scholar] [CrossRef]
- Hamedi, H.; Ehteshami, M.; Mirbagheri, S.A.; Rasouli, S.A.; Zendehboudi, S. Current Status and Future Prospects of Membrane Bioreactors (MBRs) and Fouling Phenomena: A Systematic Review. Can. J. Chem. Eng. 2018, 97, 32–58. [Google Scholar] [CrossRef] [Green Version]
- Metcalf, W.; Eddy, C. Wastewater Engineering, 4th ed.; Mcgraw-Hill Inc.: New York, NY, USA, 2003. [Google Scholar]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Li, B.; Stenstrom, M.K. Dynamic one-dimensional modeling of secondary settling tanks and design impacts of sizing decisions. Water Res. 2014, 50, 160–170. [Google Scholar] [CrossRef]
- Li, B.; Stenstrom, M.K. Construction of analytical solutions and numerical methods comparison of the ideal continuous settling model. Comput. Chem. Eng. 2015, 80, 211–222. [Google Scholar] [CrossRef]
- Li, B.; Stenstrom, M. Research advances and challenges in one-dimensional modeling of secondary settling Tanks—A critical review. Water Res. 2014, 65, 40–63. [Google Scholar] [CrossRef] [PubMed]
- Plósz, B.G.; Weiss, M.; Printemps, C.; Essemiani, K.; Meinhold, J. One-dimensional modelling of the secondary clarifier-factors affecting simulation in the clarification zone and the assessment of the thickening flow dependence. Water Res. 2007, 41, 3359–3371. [Google Scholar] [CrossRef] [PubMed]
- Bürger, R.; Diehl, S.; Nopens, I. A Consistent Modelling Methodology for Secondary Settling Tanks in Wastewater Treatment. Water Res. 2011, 45, 2247–2260. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Farås, S.; Nopens, I.; Torfs, E. A consistent modelling methodology for secondary settling tanks: A reliable numerical method. Water Sci. Technol. 2013, 68, 192–208. [Google Scholar] [CrossRef] [Green Version]
- Bürger, R.; Diehl, S.; Mejías, C. On time discretizations for the simulation of the batch settling–compression process in one dimension. Water Sci. Technol. 2015, 73, 1010–1017. [Google Scholar] [CrossRef]
- Torfs, E.; Maere, T.; Bürger, R.; Diehl, S.; Nopens, I. Impact on Sludge Inventory and Control Strategies Using the Bench-mark Simulation Model No. 1 with the Bürger-Diehl Settler Model. Water Sci. Technol. 2015, 71, 1524–1535. [Google Scholar] [CrossRef] [Green Version]
- Coe, H.; Clevenger, G. Methods for Determining the Capacities of Slime Settling Tanks. Trans. Am. Inst. Min. Eng. 1916, 55, 356–384. [Google Scholar]
- Hassett, N.J. Design and Operation of Continuous Thickeners. Ind. Chem. 1958, 34, 116–120. [Google Scholar]
- Talmage, W.P.; Fitch, E.B. Determining Thickener Unit Areas. Ind. Eng. Chem. 1955, 47, 38–41. [Google Scholar] [CrossRef]
- Yoshioka, N.; Hotta, Y.; Tanaka, S.; Naito, S.; Tsugami, S. Continuous Thickening of Homogeneous Flocculated Slurries. Chem. Eng. 1957, 21, 66–74. [Google Scholar] [CrossRef] [Green Version]
- Diehl, S. Estimation of the batch-settling flux function for an ideal suspension from only two experiments. Chem. Eng. Sci. 2007, 62, 4589–4601. [Google Scholar] [CrossRef]
- Vesilind, P.A. Design of Prototype Thickeners from Batch Settling Tests. Water Sew. Work. 1968, 115, 302–307. [Google Scholar]
- Zhang, D.; Li, Z.; Lu, P.; Zhang, T.; Xu, D. A method for characterizing the complete settling process of activated sludge. Water Res. 2006, 40, 2637–2644. [Google Scholar] [CrossRef]
- Cho, S.; Colin, F.; Sardin, M.; Prost, C. Settling velocity model of activated sludge. Water Res. 1993, 27, 1237–1242. [Google Scholar] [CrossRef]
- Vanderhasselt, A.; Vanrolleghem, P.A. Estimation of Sludge Sedimentation Parameters from Single Batch Settling Curves. Water Res. 2000, 34, 395–406. [Google Scholar] [CrossRef]
- Turlej, T. Automation of sedimentation test. Water Sci. Technol. 2018, 77, 1960–1966. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.M.P.; Udayabhanu, G.; Gouricharan, T. Comparative Studies on The Settling Behavior of Indian Noncoking Coal Fines by Standard Jar Test and Instrument Au. Int. L. J. Coal. Prep. Util. 2014, 34, 65–74. [Google Scholar] [CrossRef]
- Guerin, M.; Seaman, J.C. Characterizing Clay Mineral Suspensions Using Acoustic and Electroacoustic Spectroscopy—A Review. Clays Clay Miner. 2004, 52, 145–157. [Google Scholar] [CrossRef]
- Vergouw, J.; Anson, J.; Dalhke, R.; Xu, Z.; Gomez, C.; Finch, J. An automated data acquisition technique for settling tests. Miner. Eng. 1997, 10, 1095–1105. [Google Scholar] [CrossRef]
- Hunter, T.; Peakall, J.; Biggs, S. Ultrasonic velocimetry for the in situ characterisation of particulate settling and sedimentation. Miner. Eng. 2011, 24, 416–423. [Google Scholar] [CrossRef]
- Kaushal, D.; Tomita, Y. Experimental investigation for near-wall lift of coarser particles in slurry pipeline using γ-ray densitometer. Powder Technol. 2007, 172, 177–187. [Google Scholar] [CrossRef]
- Hoffman, D.L.; Brooks, D.R.; Dolez, P.I.; Love, B.J. Design of A Z-Axis Translating Laser Light Scattering Device For Par-ticulate Settling Measurement In Dispersed Fluids. Rev. Sci. Instrum. 2002, 73, 2479–2482. [Google Scholar] [CrossRef] [Green Version]
- Hernando, L.; Omari, A.; Reungoat, D. Experimental study of sedimentation of concentrated mono-disperse suspensions: Determination of sedimentation modes. Powder Technol. 2014, 258, 265–271. [Google Scholar] [CrossRef]
- Lu, X.; Liao, Z.; Li, X.; Wang, M.; Wu, L.; Li, H.; York, P.; Xu, X.; Yin, X.; Zhang, J. Automatic monitoring and quantitative characterization of sedimentation dynamics for non-homogenous systems based on image profile analysis. Powder Technol. 2015, 281, 49–56. [Google Scholar] [CrossRef]
- Kołodziejczyk, K. Numerical simulation of polydispersed suspension sedimentation under flow conditions Symulacja numeryczna procesu sedymentacji zawiesiny polidyspersyjnej w układzie przepływowym. Przem. Chem. 2016, 1, 66–69. [Google Scholar] [CrossRef]
- Nocoń, W. Quantitative monitoring of batch sedimentation based on fractional density changes. Powder Technol. 2016, 292, 1–6. [Google Scholar] [CrossRef]
- Acosta-Cabronero, J.; Hall, L.D. Measurements by Mri of The Settling and Packing of Solid Particles from Aqueous Suspensions. Aiche J. 2009, 55, 1426–1433. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, J.; Shepherd, I.; Coghill, M.; Vagias, N.; Elkin, K. An automated measurement technique for slurry settling tests. Miner. Eng. 2000, 13, 765–772. [Google Scholar] [CrossRef]
- Hubner, T.; Will, S.; Leipertz, A. Sedimentation Image Analysis (SIA) for the Simultaneous Determination of Particle Mass Density and Particle Size. Part. Part. Syst. Charact. 2001, 18, 70–78. [Google Scholar] [CrossRef]
- Zheng, Y.; Bagley, D.M. Numerical Simulation of Batch Settling Process. J. Environ. Eng. 1999, 125, 1007–1013. [Google Scholar] [CrossRef]
- Wu, C.-H.; Chern, J.-M. Experiment and Simulation of Sludge Batch Settling Curves: A Wave Approach. Ind. Eng. Chem. Res. 2006, 45, 2026–2031. [Google Scholar] [CrossRef]
- Grassia, P.; Usher, S.; Scales, P. A simplified parameter extraction technique using batch settling data to estimate suspension material properties in dewatering applications. Chem. Eng. Sci. 2008, 63, 1971–1986. [Google Scholar] [CrossRef]
- Lester, D.R.; Usher, S.P.; Scales, P.J. Estimation of The Hindered Settling Function R (Φ) From Batch-Settling Tests. Aiche J. 2005, 51, 1158–1168. [Google Scholar] [CrossRef]
- Grassia, P.; Usher, S.; Scales, P. Closed-form solutions for batch settling height from model settling flux functions. Chem. Eng. Sci. 2011, 66, 964–972. [Google Scholar] [CrossRef]
- Van Deventer, B.B.; Usher, S.P.; Kumar, A.; Rudman, M.; Scales, P.J. Aggregate densification and batch settling. Chem. Eng. J. 2011, 171, 141–151. [Google Scholar] [CrossRef]
- Betancourt, F.; Bürger, R.; Diehl, S.; Mejías, C. Advanced methods of flux identification for clarifier–thickener simulation models. Miner. Eng. 2014, 63, 2–15. [Google Scholar] [CrossRef]
- Van Deventer, B.B.G. Aggregate Densification Behaviour in Sheared Suspensions. Ph.D. Thesis, University of Melbourne, Melbourne, Austrailia, 2012. [Google Scholar]
- Banisi, S.; Yahyaei, M. Feed Dilution-Based Design of a Thickener for Refuse Slurry of a Coal Preparation Plant. Int. J. Coal Prep. Util. 2008, 28, 201–223. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, A.; Wang, H.; Wang, L. Representation of batch settling via fitting a logistic function. Miner. Eng. 2018, 128, 160–167. [Google Scholar] [CrossRef]
- Kang, X.; Xia, Z.; Wang, J.; Yang, W. A Novel Approach to Model the Batch Sedimentation and Estimate the Settling Velocity, Solid Volume Fraction, and Floc Size of Kaolinite in Concentrated Solutions. Colloids Surf. A Physicochem. Eng. Asp. 2019, 579, 123647. [Google Scholar] [CrossRef]
- Von Sperling, M. Basic Principles of Wastewater Treatment; IWA Publishing: London, UK, 2017. [Google Scholar]
- Barrott, L.; Ersoz, M. Best Practice Guide on Metals Removal from Drinking Water by Treatment; IWA Publishing: London, UK, 2012. [Google Scholar]
- Spellman, F.R. Mathematics Manual for Water and Wastewater Treatment Plant Operators: Wastewater Treatment Operations: Math Concepts and Calculations; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Lundengård, K. Generalized Vandermonde Matrices and Determinants. In Electromagnetic Compatibility; Mälardalen University: Västerås, Sweden, 2017. [Google Scholar]
- Bahadori, A.; Zahedi, G.; Zendehboudi, S.; Bahadori, M. Estimation of Air Concentration in Dissolved Air Flotation (Daf) Sys-Tems Using A Simple Predictive Tool. Chem. Eng. Res. Des. 2013, 91, 184–190. [Google Scholar] [CrossRef]
- Ghiasi, M.M.; Bahadori, A.; Zendehboudi, S. Estimation of The Water Content of Natural Gas Dried By Solid Calcium Chloride Dehydrator Units. Fuel 2014, 117, 33–42. [Google Scholar] [CrossRef]
- Ghiasi, M.M.; Bahadori, A.; Zendehboudi, S.; Jamili, A.; Rezaei-Gomari, S. Novel Methods Predict Equilibrium Vapor Metha-Nol Content During Gas Hydrate Inhibition. J. Nat. Gas Sci. Eng. 2013, 15, 69–75. [Google Scholar] [CrossRef]
- Fulton, W.; Harris, J. Representation Theory: A First Course, Graduate Texts in Mathematics, Readings in Mathematics; Springer: New York, NY, USA, 1991; Volume 129. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Topics in Matrix Analysis; Cambridge University Press: London, UK, 1991; Volume Section 6.1. [Google Scholar]
- Bahadori, A.; Zahedi, G.; Zendehboudi, S.; Jamili, A. Estimation of the effect of biomass moisture content on the direct combustion of sugarcane bagasse in boilers. Int. J. Sustain. Energy 2011, 33, 349–356. [Google Scholar] [CrossRef]
- Amin, J.S.; Alimohammadi, S.; Zendehboudi, S. Systematic investigation of asphaltene precipitation by experimental and reliable deterministic tools. Can. J. Chem. Eng. 2017, 95, 1388–1398. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Ghiasi, M.M. Initial Estimation of Hydrate Formation Temperature of Sweet Natural Gases Based on New Empirical Correlation. J. Nat. Gas Chem. 2012, 21, 508–512. [Google Scholar] [CrossRef]
- Vanrolleghem, P.A. Modelling Aspects of Water Framework Directive Implementation; IWA Publishing: London, UK, 2010; Volume 1, 260p. [Google Scholar]
- Chiulli, R.M. Quantitative Analysis: An Introduction; CRC Press: Boca Raton, FL, USA, 1999; Volume 2. [Google Scholar]
- Millard, S.P.; Neerchal, N.K. Environmental Statistics with S-PLUS; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Bozdogan, H. Statistical Data Mining and Knowledge Discovery; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Everitt, B.; Skrondal, A. The Cambridge Dictionary of Statistics; Cambridge University Press: Cambridge, UK, 2002; ISBN 0-521-81099-X. [Google Scholar]
- Haan, C.T.; Barfield, B.J.; Hayes, J.C. 7—Sediment Properties and Transport. In Design Hydrology and Sedimentology for Small Catchments; Haan, C.T., Barfield, B.J., Hayes, J.C., Eds.; Academic Press: San Diego, CA, USA, 1994; pp. 204–237. [Google Scholar]
- Yetilmezsoy, K. A New Empirical Model for The Determination of The Required Retention Time in Hindered Settling. Frese-Nius Environ. Bull. 2007, 16, 674–684. [Google Scholar]
- Downing, D.J.; Gardner, R.H.; Hoffman, F.O. An Examination of Response-Surface Methodologies for Uncertainty Analysis in Assessment Models. Technometrics 1985, 27, 151–163. [Google Scholar] [CrossRef]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]


| Coefficient | Value |
|---|---|
| A1 | 8.077 × 10−3 |
| B1 | −0.0176 |
| C1 | 2.785 × 10−3 |
| D1 | −5.99 × 10−5 |
| A2 | −0.0103 |
| B2 | 7.672 × 10−3 |
| C2 | 5.043 × 10−4 |
| D2 | −2.55 × 10−5 |
| A3 | −3.659 × 10−4 |
| B3 | 3.897 × 10−4 |
| C3 | −1.025 × 10−4 |
| D3 | 1.07 × 10−6 |
| A4 | 3.30 × 10−6 |
| B4 | −1.22 × 10−6 |
| C4 | −5.41 × 10−7 |
| D4 | 1.82 × 10−7 |
| Coefficient | Value | |
|---|---|---|
| x0 < 10.5 g/L | x0 > 10.5 g/L | |
| α | −6.930 | 0.765 |
| β | 0.836 | −0.450 |
| γ | −0.0337 | 0.0202 |
| δ | −1.513 | −1.453 |
| ε | −0.0667 | −0.152 |
| θ | 0.0846 | 0.0486 |
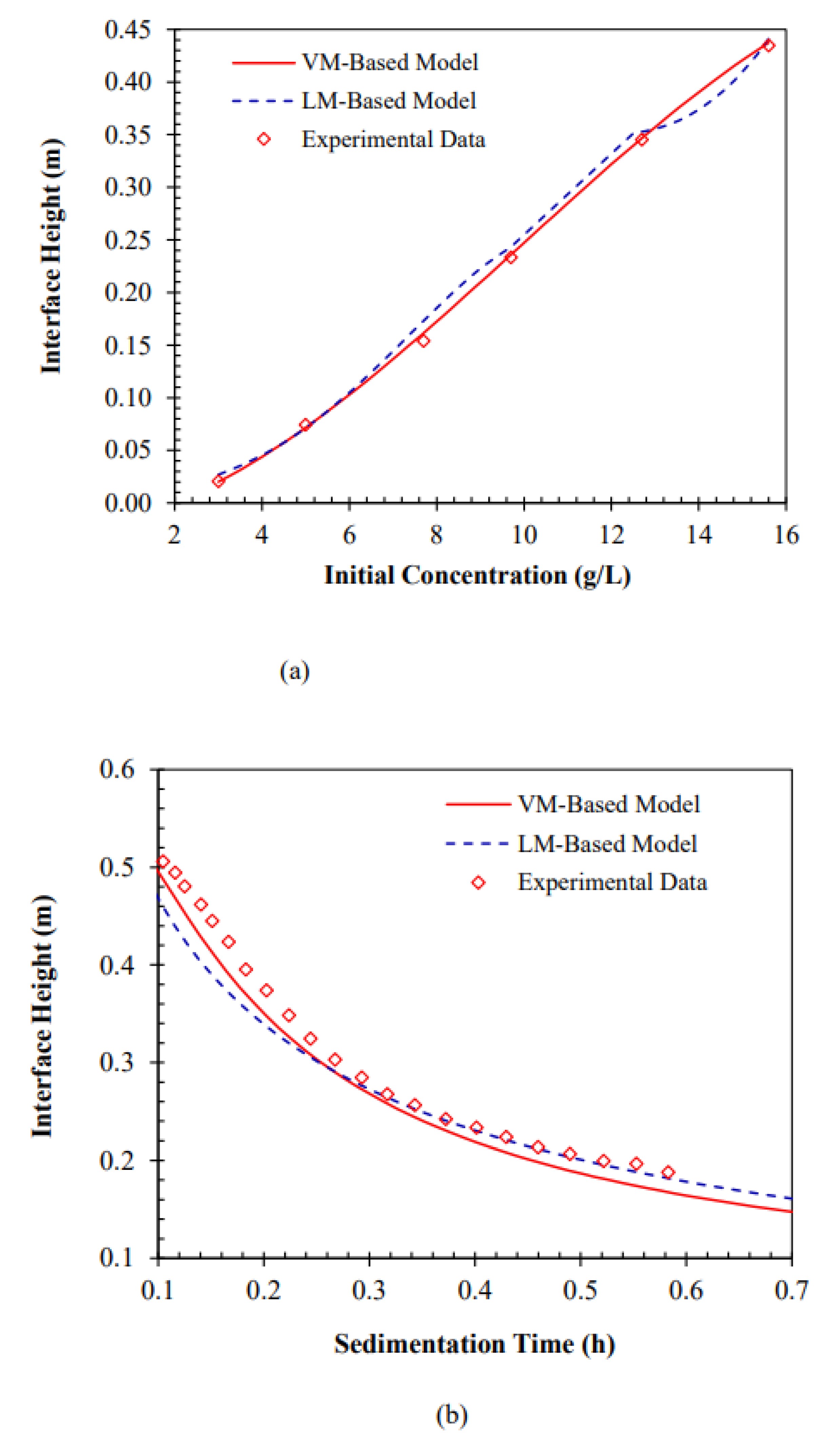
| Model | R2 | RMSE | Minimum Percentage Error | Maximum Percentage Error | % MAPE |
|---|---|---|---|---|---|
| VM-based model | 0.997 | 0.132 | 4.869 × 10−4 | 74.077 | 5.413 |
| LM-based model | 0.969 | 0.107 | 0.026 | 36.59 | 6.433 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasanzadeh, R.; Sayyad Amin, J.; Abbasi Souraki, B.; Mohammadzadeh, O.; Zendehboudi, S. Reliable Tools to Forecast Sludge Settling Behavior: Empirical Modeling. Energies 2023, 16, 963. https://doi.org/10.3390/en16020963
Hasanzadeh R, Sayyad Amin J, Abbasi Souraki B, Mohammadzadeh O, Zendehboudi S. Reliable Tools to Forecast Sludge Settling Behavior: Empirical Modeling. Energies. 2023; 16(2):963. https://doi.org/10.3390/en16020963
Chicago/Turabian StyleHasanzadeh, Reyhaneh, Javad Sayyad Amin, Behrooz Abbasi Souraki, Omid Mohammadzadeh, and Sohrab Zendehboudi. 2023. "Reliable Tools to Forecast Sludge Settling Behavior: Empirical Modeling" Energies 16, no. 2: 963. https://doi.org/10.3390/en16020963







