On the Sublimation of Dry-Ice: Experimental Investigation and Thermal Modelling of Low-Temperatures on a Sandy Soil
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Measurements and Test Cases
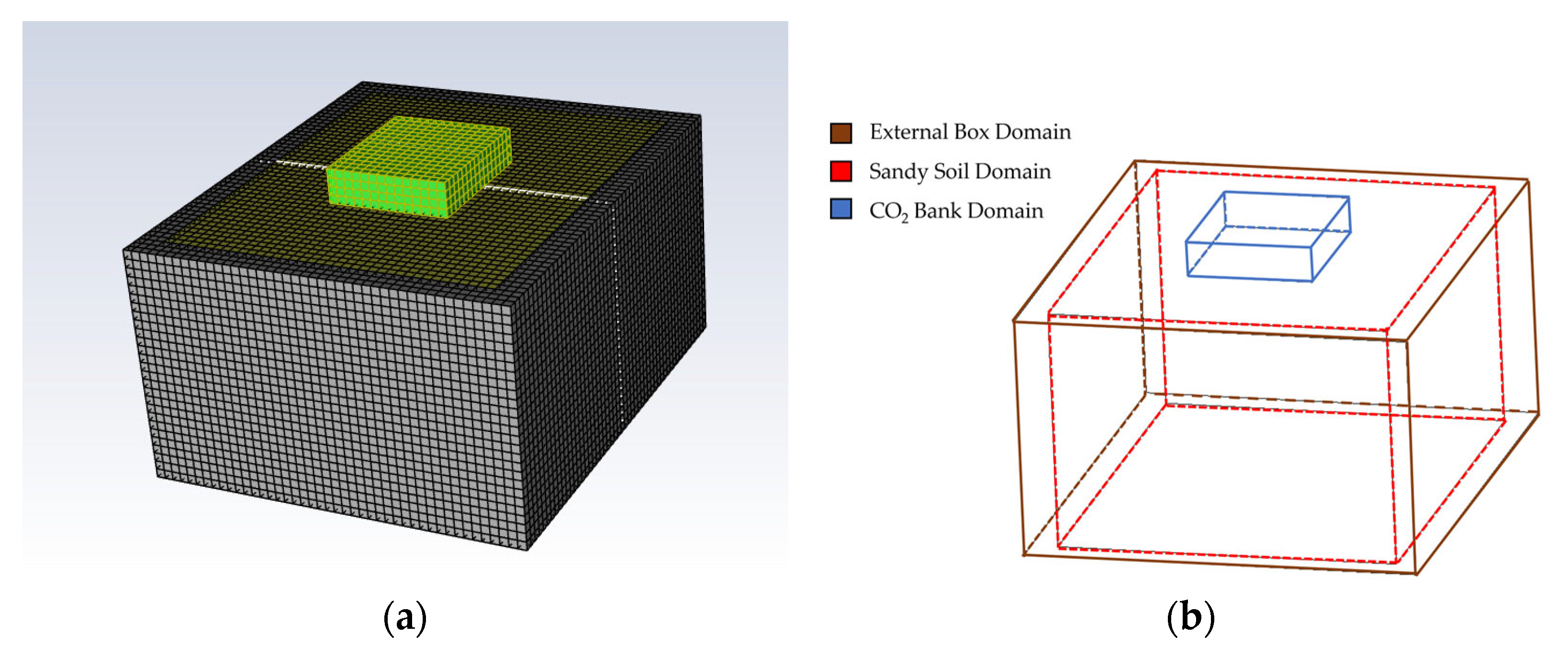
3. Numerical Model
4. Results
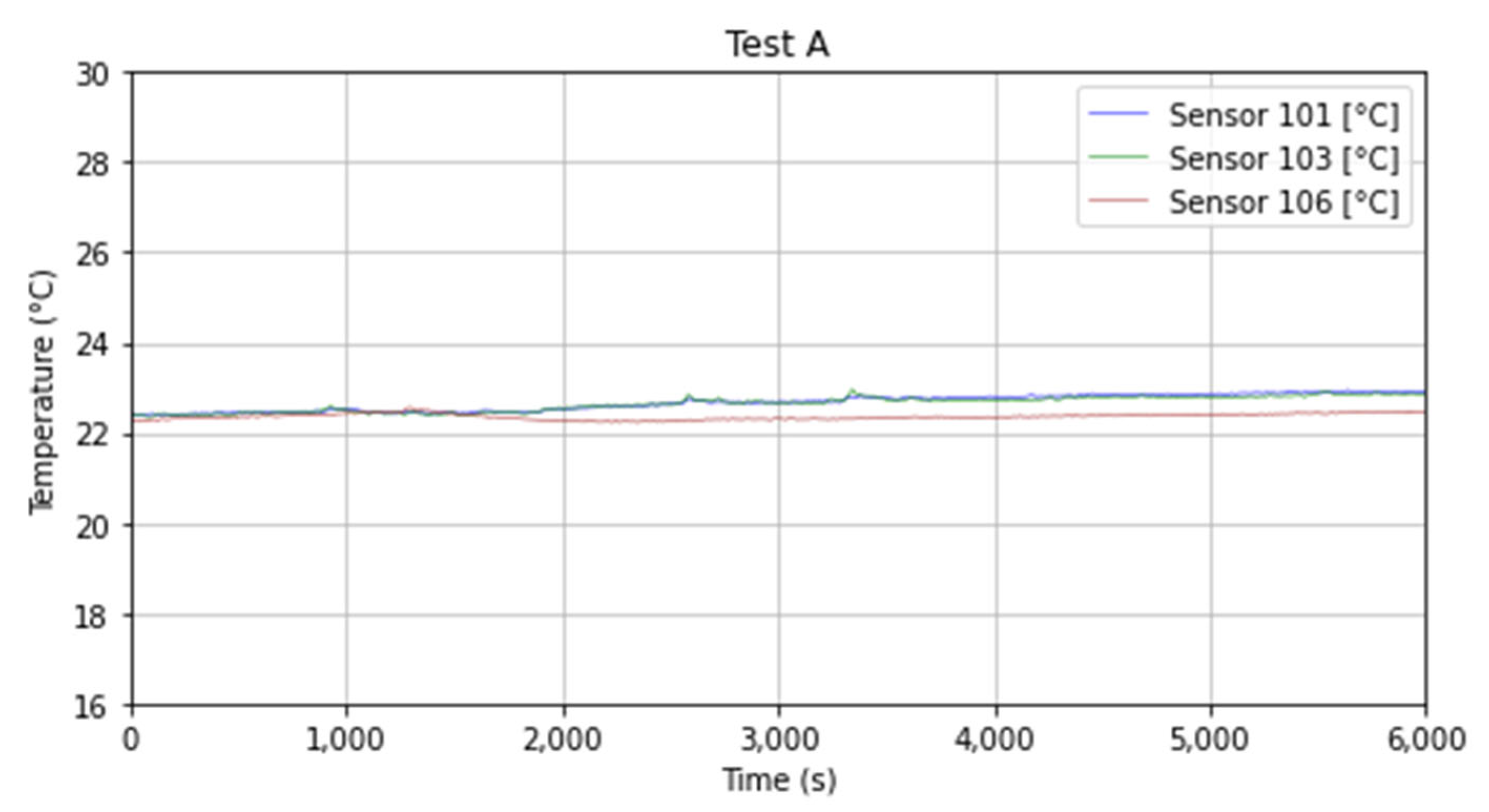
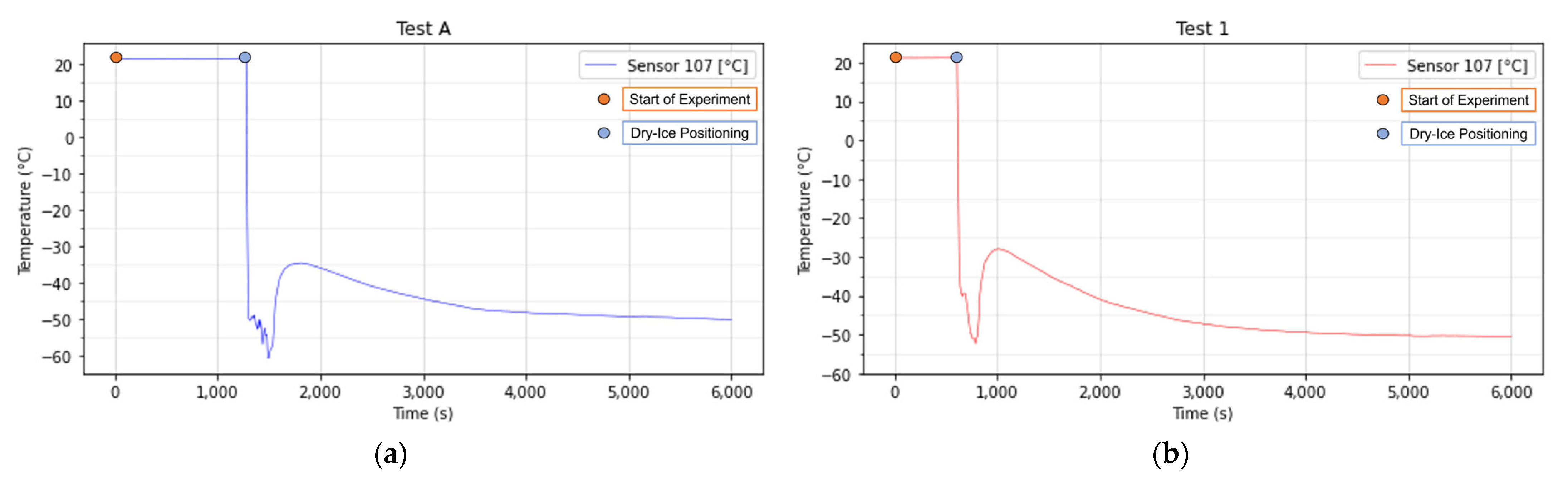
4.1. Experimental Results
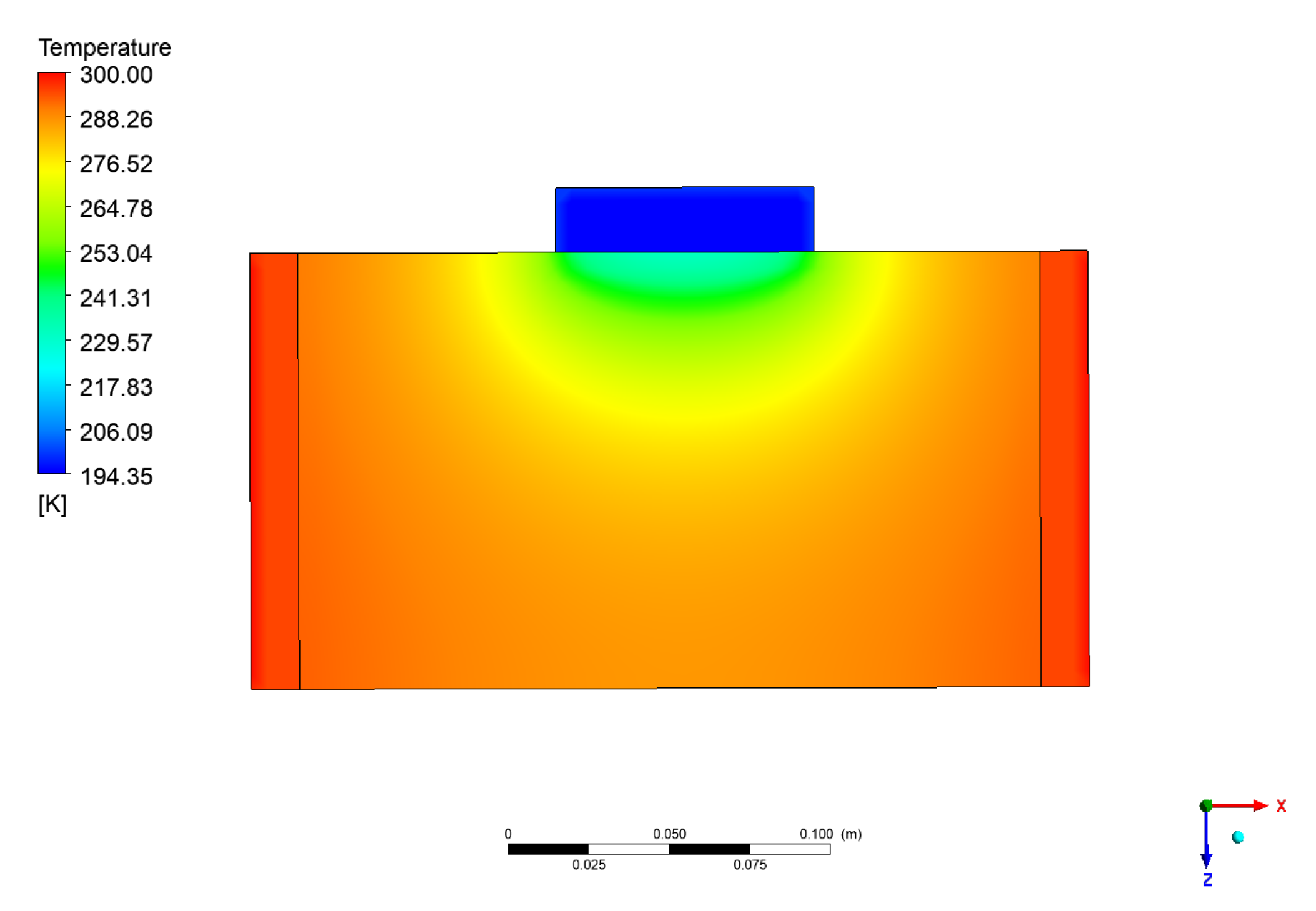
4.2. Numerical Results
5. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arias, P.; Bellouin, N.; Coppola, E.; Jones, R.; Krinner, G.; Marotzke, J.; Naik, V.; Palmer, M.; Plattner, G.-K.; Rogelj, J. Climate Change 2021: The Physical Science Basis. In Proceedings of the Contribution of Working Group14 I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Technical Summary, Weßling, Germany, 8–26 July 2021. [Google Scholar]
- IEA. Energy Technology Perspectives 2020—Special Report on Carbon Capture Utilisation and Storage; OECD Publishing: Paris, France, 2020. [Google Scholar] [CrossRef]
- International Energy Agency. Transforming Industry through CCUS; OECD Publishing: Paris, France, 2019. [Google Scholar] [CrossRef]
- Vitali, M.; Corvaro, F.; Marchetti, B.; Terenzi, A. Thermodynamic challenges for CO2 pipelines design: A critical review on the effects of impurities, water content, and low temperature. Int. J. Greenh. Gas Control 2022, 114, 103605. [Google Scholar] [CrossRef]
- Lee, U.; Lim, Y.; Lee, S.; Jung, J.; Han, C. CO2 Storage Terminal for Ship Transportation. Ind. Eng. Chem. Res. 2012, 51, 389–397. [Google Scholar] [CrossRef]
- Bjerketvedt, V.S.; Tomasgard, A.; Roussanaly, S. Deploying a Shipping Infrastructure to Enable Carbon Cap-ture and Storage from Norwegian Industries. J. Clean. Prod. 2022, 333, 129586. [Google Scholar] [CrossRef]
- Compressed Gas Association. Carbon Dioxide & Dry Ice Fact Sheet; Compressed Gas Association: Chantilly, VA, USA, 2022. [Google Scholar]
- Wang, C.; Li, Y.; Teng, L.; Gu, S.; Hu, Q.; Zhang, D.; Ye, X.; Wang, J. Experimental study on dispersion behavior during the leakage of high pressure CO2 pipelines. Exp. Therm. Fluid Sci. 2019, 105, 77–84. [Google Scholar] [CrossRef]
- Fan, X.; Wang, Y.; Zhou, Y.; Chen, J.; Huang, Y.; Wang, J. Experimental study of supercritical CO2 leakage behavior from pressurized vessels. Energy 2018, 150, 342–350. [Google Scholar] [CrossRef]
- Mazzoldi, A.; Hill, T.; Colls, J.J. CO2 transportation for carbon capture and storage: Sublimation of carbon dioxide from a dry ice bank. Int. J. Greenh. Gas Control 2008, 2, 210–218. [Google Scholar] [CrossRef]
- Vianello, C.; Mocellin, P.; Maschioa, G. Study of Formation, Sublimation and Deposition of Dry Ice from Carbon Capture and Storage Pipelines. Chem. Eng. 2014, 36, 613–618. [Google Scholar]
- Mocellin, P.; Carboni, M.; Pio, G.; Vianello, C.; Salzano, E. Investigation of Sublimating Dry-Ice Bank due to Accidental Release in the Framework of CCS Risk Analysis. Chem. Eng. Trans. 2022, 90, 193–198. [Google Scholar]
- Feliu, J.A.; Manzulli, M.; Alós, M.A. Determination of Dry-Ice Formation during the Depressurization of a CO2 Re-Injection System. In Cutting-Edge Technology for Carbon Capture, Utilization, and Storage; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 135–146. [Google Scholar]
- Vitali, M.; Zuliani, C.; Corvaro, F.; Marchetti, B.; Terenzi, A.; Tallone, F. Risks and Safety of CO2 Transport via Pipeline: A Review of Risk Analysis and Modeling Approaches for Accidental Releases. Energies 2021, 14, 4601. [Google Scholar] [CrossRef]
- Vitali, M.; Zuliani, C.; Corvaro, F.; Marchetti, B.; Tallone, F. Statistical analysis of incidents on onshore CO2 pipelines based on PHMSA database. J. Loss Prev. Process. Ind. 2022, 77, 104799. [Google Scholar] [CrossRef]
- Mocellin, P.; Vianello, C.; Maschio, G. Carbon Capture and Storage Hazard Investigation: Numerical Analy-sis of Hazards Related to Dry Ice Bank Sublimation Following Accidental Carbon Dioxide Releases. Chem. Eng. Trans. 2015, 43, 1892–1902. [Google Scholar]
- d’Amore, F.; Mocellin, P.; Vianello, C.; Maschio, G.; Bezzo, F. Economic Optimisation of European Supply Chains for CO2 Capture, Transport and Sequestration, including Societal Risk Analysis and Risk Mitigation Measures. Appl. Energy 2018, 223, 401–415. [Google Scholar] [CrossRef]
- Baxter, P.J.; Kapila, M.; Mfonfu, D. Lake Nyos Disaster, Cameroon, 1986: The Medical Effects of Large Scale Emission of Carbon Dioxide? Br. Med. J. 1989, 298, 1437–1441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmad, M.; Lowesmith, B.; De Koeijer, G.; Nilsen, S.; Tonda, H.; Spinelli, C.; Cooper, R.; Clausen, S.; Mendes, R.; Florisson, O. COSHER joint industry project: Large scale pipeline rupture tests to study CO2 release and dispersion. Int. J. Greenh. Gas Control 2015, 37, 340–353. [Google Scholar] [CrossRef]
- Godbole, A.; Liu, X.; Michal, G.; Davis, B.; Lu, C.; Armstrong, K.; Medina, C.H. Atmospheric Dispersion of CO2 Following Full-Scale Burst Tests. In Proceedings of the 14th Greenhouse Gas Control Technologies Conference, Melbourne, Australia, 21–26 October 2018. [Google Scholar]
- Gant, S.; Narasimhamurthy, V.; Skjold, T.; Jamois, D.; Proust, C. Evaluation of multi-phase atmospheric dispersion models for application to Carbon Capture and Storage. J. Loss Prev. Process. Ind. 2014, 32, 286–298. [Google Scholar] [CrossRef] [Green Version]
- Zegart, D. The Gassing of Satartia. Huffington Post. 2021. Available online: https://www.huffpost.com/entry/gassing-satartia-mississippi-co2-pipeline_n_60ddea9fe4b0ddef8b0ddc8f (accessed on 20 November 2022).
- Agilent. Agilent 34970A—Data Acquisition Unit Switch Manual Agilent Technologies; Agilent Technologies: Santa Clara, CA, USA, 2003. [Google Scholar]
- ANSYS, Inc. ANSYS CFX-Fluent 14.0 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2011. [Google Scholar]
- Nikolaev, P.; Sedighi, M.; Rajabi, H.; Pankratenko, A. Artificial ground freezing by solid carbon dioxide—Analysis of thermal performance. Tunn. Undergr. Space Technol. 2022, 130, 104741. [Google Scholar] [CrossRef]


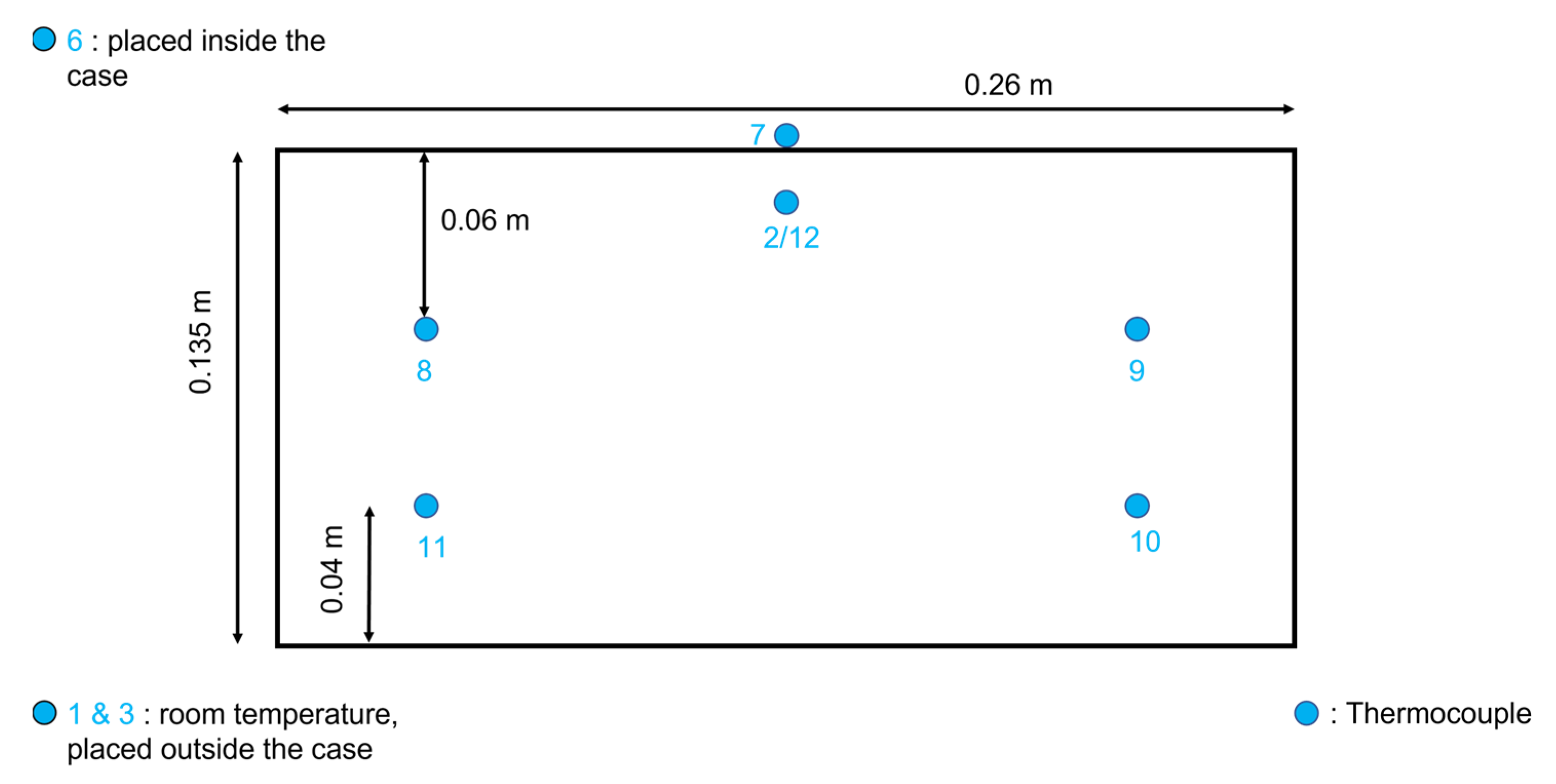



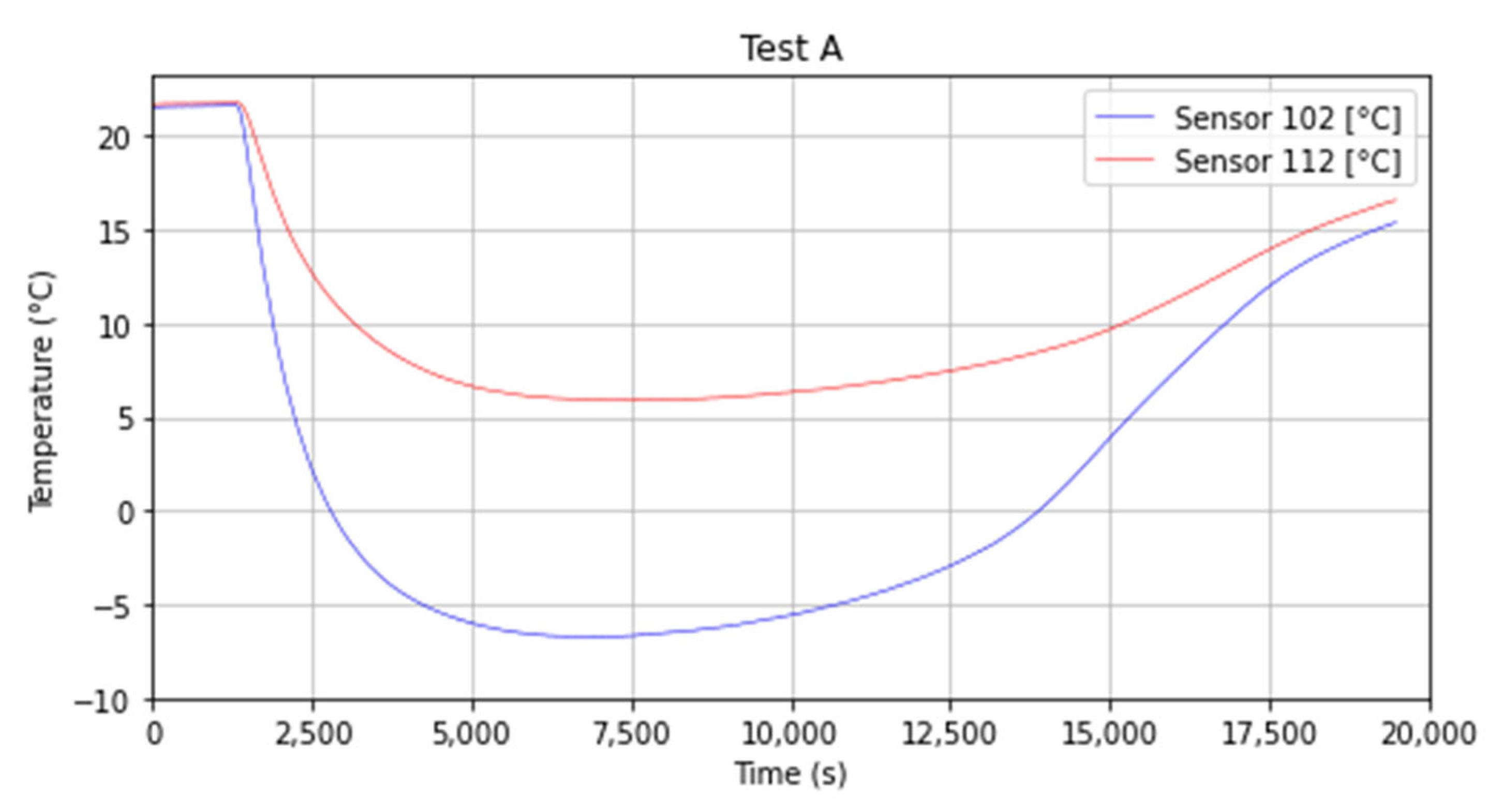
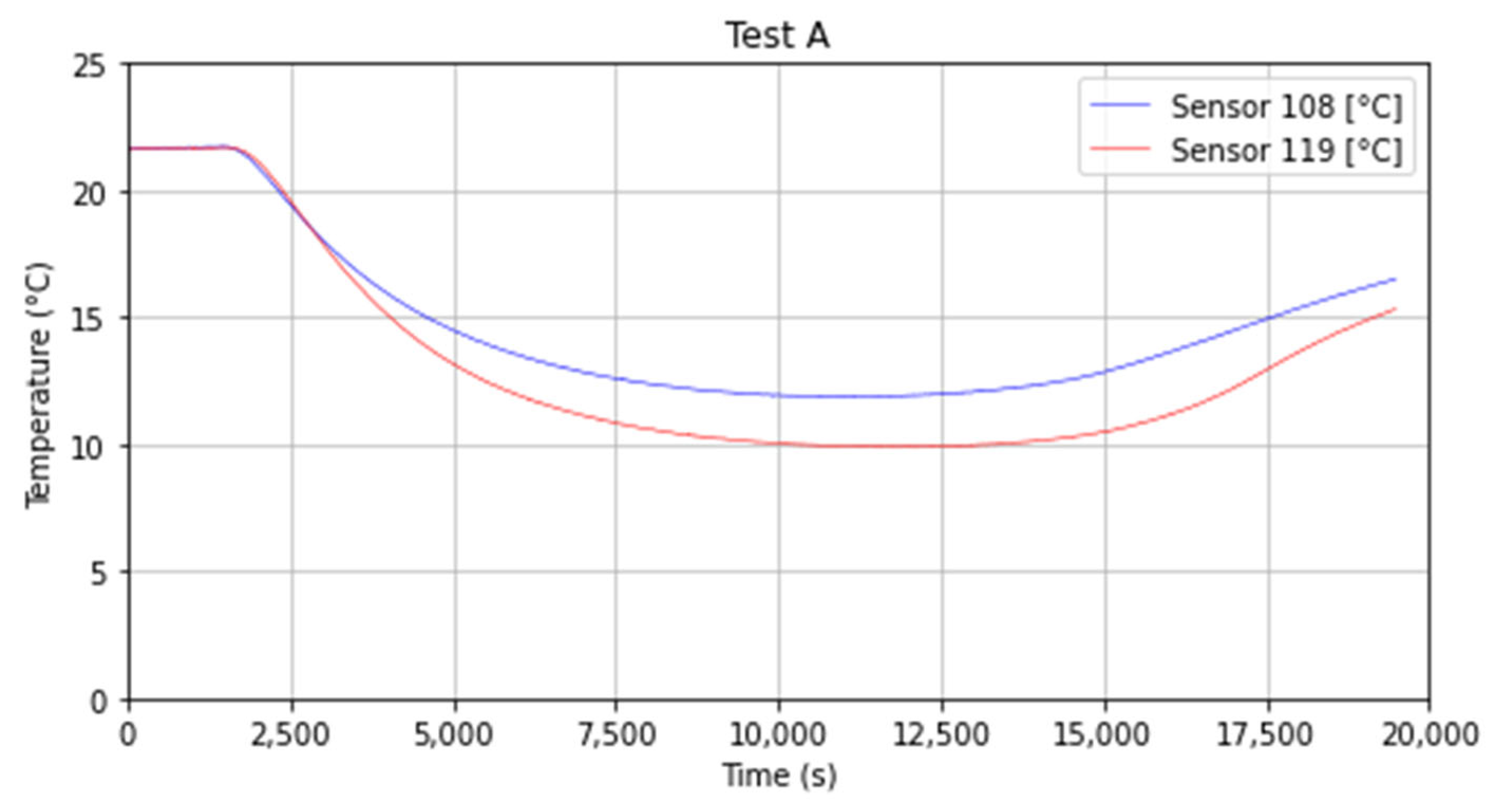

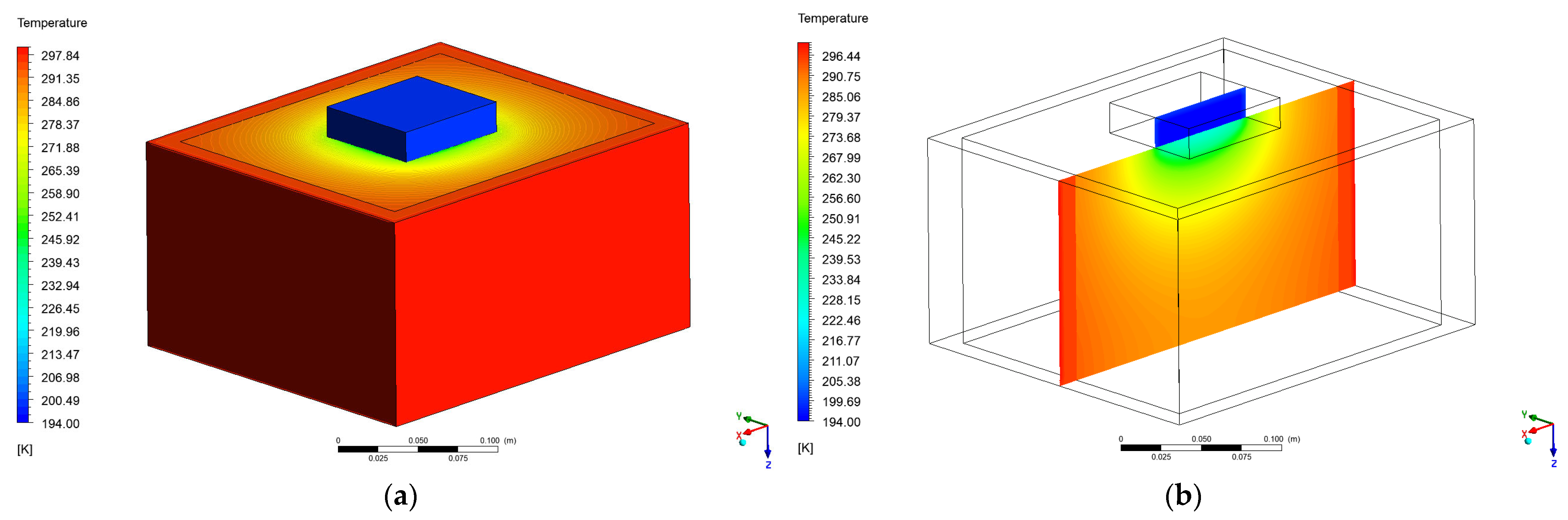
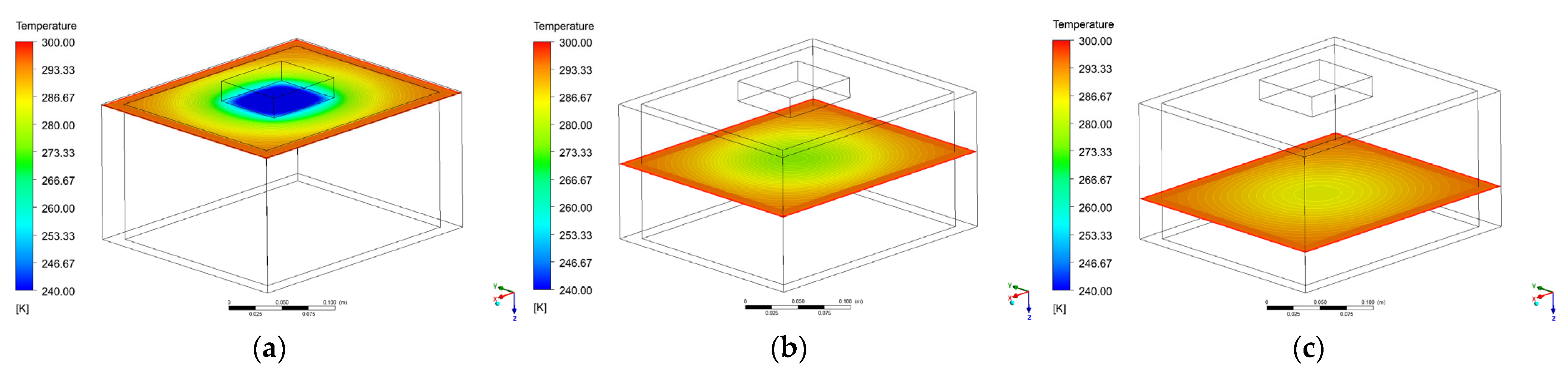
| Number | Channel | Description | Relative Position “x” (m) | Depth (m) |
|---|---|---|---|---|
| 1 | 101 | TROOM | Not applicable | Not applicable |
| 2 | 102 | TSOIL_high | 0.065 | 0.01 |
| 3 | 103 | TROOM | Not applicable | Not applicable |
| 6 | 106 | TAIR_CASE | Not applicable | Not applicable |
| 7 | 107 | TDRY-ICE | 0.105 | 0 |
| 8 | 108 | TSOIL | 0.105 | 0.06 |
| 9 | 109 | TSOIL | 0.105 | 0.06 |
| 10 | 110 | TSOIL_deep | 0.105 | 0.095 |
| 11 | 111 | TSOIL_deep | 0.105 | 0.095 |
| 12 | 112 | TSOIL_high | 0.155 | 0.01 |
| Test | Size (m) | Weight (kg) | Shape |
|---|---|---|---|
| 0 | Not applicable | Not applicable | Not applicable |
| 1 | 0.07 × 0.08 | 0.175 | Bank |
| A | 0.07 × 0.08 | 0.170 | Bank |
| B | 0.09 × 0.06 | 0.167 | Bank |
| C | Not applicable | 0.165 | Irregular |
| Materials | Mass Density (kg m−3) | Specific Heat Capacity (J kg−1 K−1) | Thermal Conductivity (W m−1 K−1) |
|---|---|---|---|
| Dry-ice [10] | 1511 | 849 | 0.05 ÷ 0.30 * |
| Coarse Sand [25] | 2530 | 1760 | 2.02 |
| Wood | 700 | 2310 | 0.173 |
| Sensor N° | TAVG | TMIN | TSTEADY | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test -> | 1 | A | B | C | 1 | A | B | C | 1 | A | B | C |
| 1 | 21.38 | 23.04 | 23.32 | 23.42 | 20.77 | 22.40 | 23.10 | 23.06 | 21.59 | 22.95 | 23.48 | 23.33 |
| 2 | −6.46 | 1.93 | 3.24 | 7.33 | −16.49 | −6.77 | −16.71 | −15.06 | −15.60 | −5.71 | −15.58 | −5.76 |
| 3 | 21.14 | 22.99 | 23.29 | 23.37 | 20.20 | 22.35 | 23.09 | 23.11 | 21.41 | 22.89 | 23.44 | 23.28 |
| 6 | 20.95 | 22.64 | 22.80 | 22.85 | 20.43 | 22.23 | 22.47 | 22.30 | 21.07 | 22.50 | 22.78 | 22.51 |
| 7 | −31.18 | −29.33 | −11.45 | −5.38 | −52.40 | −60.81 | −53.24 | −58.67 | −50.33 | −49.88 | −50.18 | −26.46 |
| 8 | 11.03 | 14.63 | 14.59 | 14.34 | 8.04 | 11.85 | 9.56 | 6.94 | 9.57 | 13.49 | 10.26 | 8.66 |
| 9 | 11.98 | 13.13 | 14.98 | 15.15 | 9.09 | 9.87 | 10.64 | 8.70 | 11.42 | 11.98 | 11.73 | 10.41 |
| 10 | 17.41 | 18.80 | 17.57 | 18.97 | 14.79 | 16.49 | 15.94 | 17.23 | 18.83 | 19.74 | 17.76 | 18.95 |
| 11 | 17.83 | 19.62 | 17.99 | 19.22 | 15.38 | 17.73 | 16.59 | 17.57 | 19.19 | 20.45 | 18.34 | 19.52 |
| 12 | 9.92 | 10.24 | 14.39 | 11.69 | 6.90 | 5.88 | 8.65 | −3.43 | 7.63 | 6.65 | 9.05 | 4.58 |
| Sensor n° | Tests Deviation (DEV) | |||
|---|---|---|---|---|
| 1 | A | B | C | |
| 2 | 12.34% | −0.56% | 11.90% | −1.98% |
| 7 | 6.15% | 5.88% | 8.91% | −33.87% |
| 8 | 4.37% | −0.65% | 3.19% | 5.71% |
| 9 | 2.11% | 1.64% | 1.31% | 3.46% |
| 10 | −4.85% | −6.07% | −3.59% | −4.67% |
| 11 | −5.41% | −7.19% | −4.39% | −5.57% |
| 12 | −18.49% | −17.06% | −20.69% | −16.74% |
| Sensor n° | Tests Deviation (DEV) | |||
|---|---|---|---|---|
| 1 | A | B | C | |
| 2 | 9.56% | −3.34% | 9.12% | −4.76% |
| 7 | 0.57% | 0.30% | 3.33% | −39.45% |
| 8 | 3.42% | −1.59% | 2.24% | 4.77% |
| 9 | 1.16% | 0.70% | 0.37% | 2.51% |
| 10 | −5.54% | −6.75% | −4.27% | −5.35% |
| 11 | −6.10% | −7.87% | −5.08% | −6.26% |
| 12 | −21.27% | −19.84% | −23.47% | −19.52% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitali, M.; Biancini, G.; Marchetti, B.; Corvaro, F. On the Sublimation of Dry-Ice: Experimental Investigation and Thermal Modelling of Low-Temperatures on a Sandy Soil. Energies 2023, 16, 987. https://doi.org/10.3390/en16020987
Vitali M, Biancini G, Marchetti B, Corvaro F. On the Sublimation of Dry-Ice: Experimental Investigation and Thermal Modelling of Low-Temperatures on a Sandy Soil. Energies. 2023; 16(2):987. https://doi.org/10.3390/en16020987
Chicago/Turabian StyleVitali, Matteo, Giovanni Biancini, Barbara Marchetti, and Francesco Corvaro. 2023. "On the Sublimation of Dry-Ice: Experimental Investigation and Thermal Modelling of Low-Temperatures on a Sandy Soil" Energies 16, no. 2: 987. https://doi.org/10.3390/en16020987
APA StyleVitali, M., Biancini, G., Marchetti, B., & Corvaro, F. (2023). On the Sublimation of Dry-Ice: Experimental Investigation and Thermal Modelling of Low-Temperatures on a Sandy Soil. Energies, 16(2), 987. https://doi.org/10.3390/en16020987







