Power Grid Structure Performance Evaluation Based on Complex Network Cascade Failure Analysis
Abstract
:1. Introduction
- The comprehensive evaluation index of a power grid structure performance proposed in this paper can analyze the grid operation status more comprehensively than previous indices;
- With the cascading failure analysis on the network, we find out that the performance loss of the grid structure is not directly related to the number of failed nodes of the network;
- The functional weighted integrated evaluation index proposed in this paper can better reflect the changes in network structure performance in the case of node failure than the unweighted topology evaluation index.
2. Grid Modeling Based on Complex Network Theory
2.1. Construction of Complex Network Models for Power Grids
2.2. Grid Complex Network Model Characteristics Indicators
2.2.1. Degree
2.2.2. Clustering Coefficient
2.2.3. Betweenness
3. Grid Structure Performance Evaluation Index
3.1. Grid Structure Performance Indicators
3.1.1. Grid Invulnerability
3.1.2. Grid Reliability
3.1.3. Grid Vulnerability
3.2. Objective Empowerment Method
3.3. Comprehensive Assessment Index of Grid Structure Performance
4. Comprehensive Grid Structure Performance Assessment Process
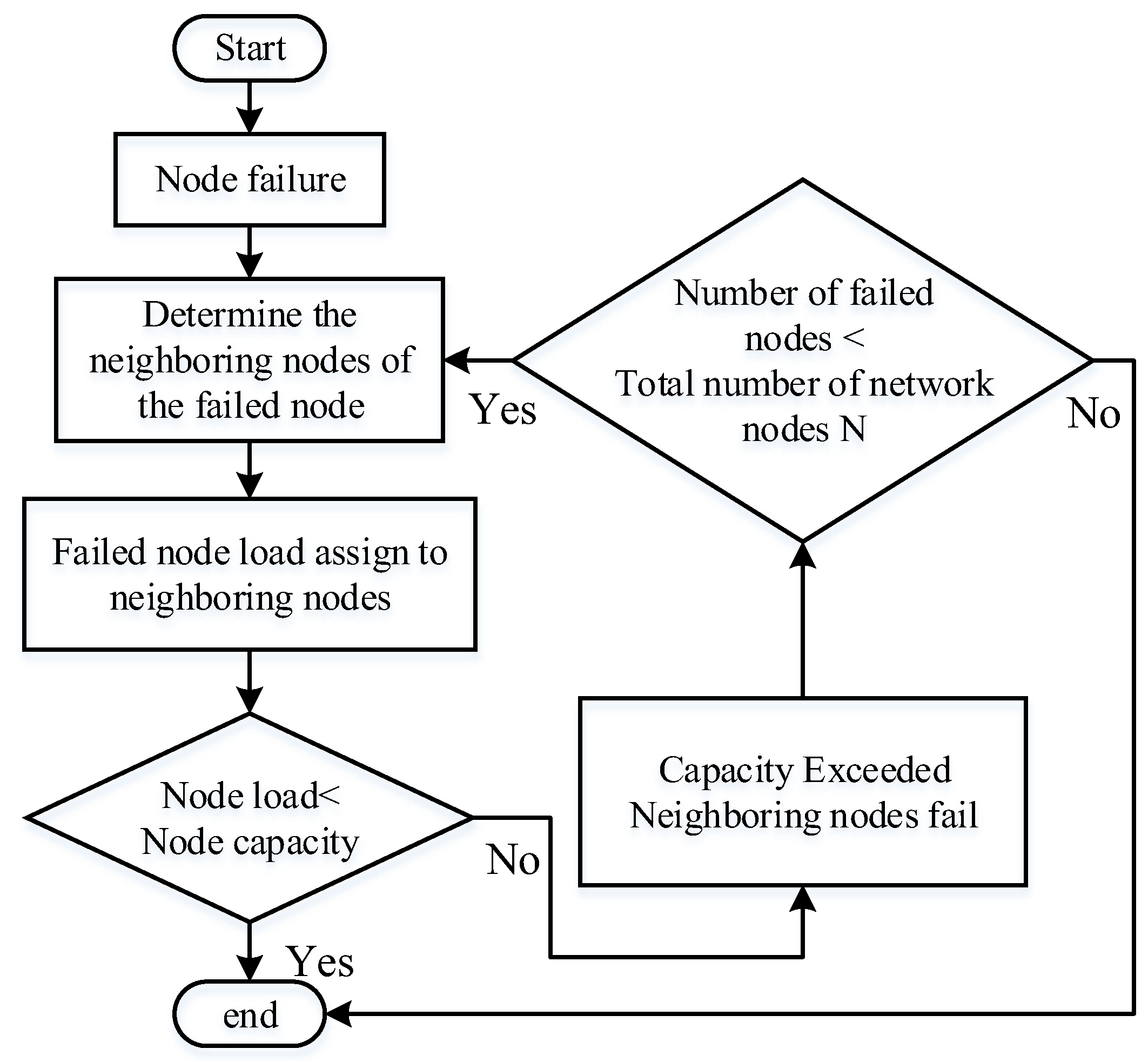
4.1. Grid Cascade Failure Process
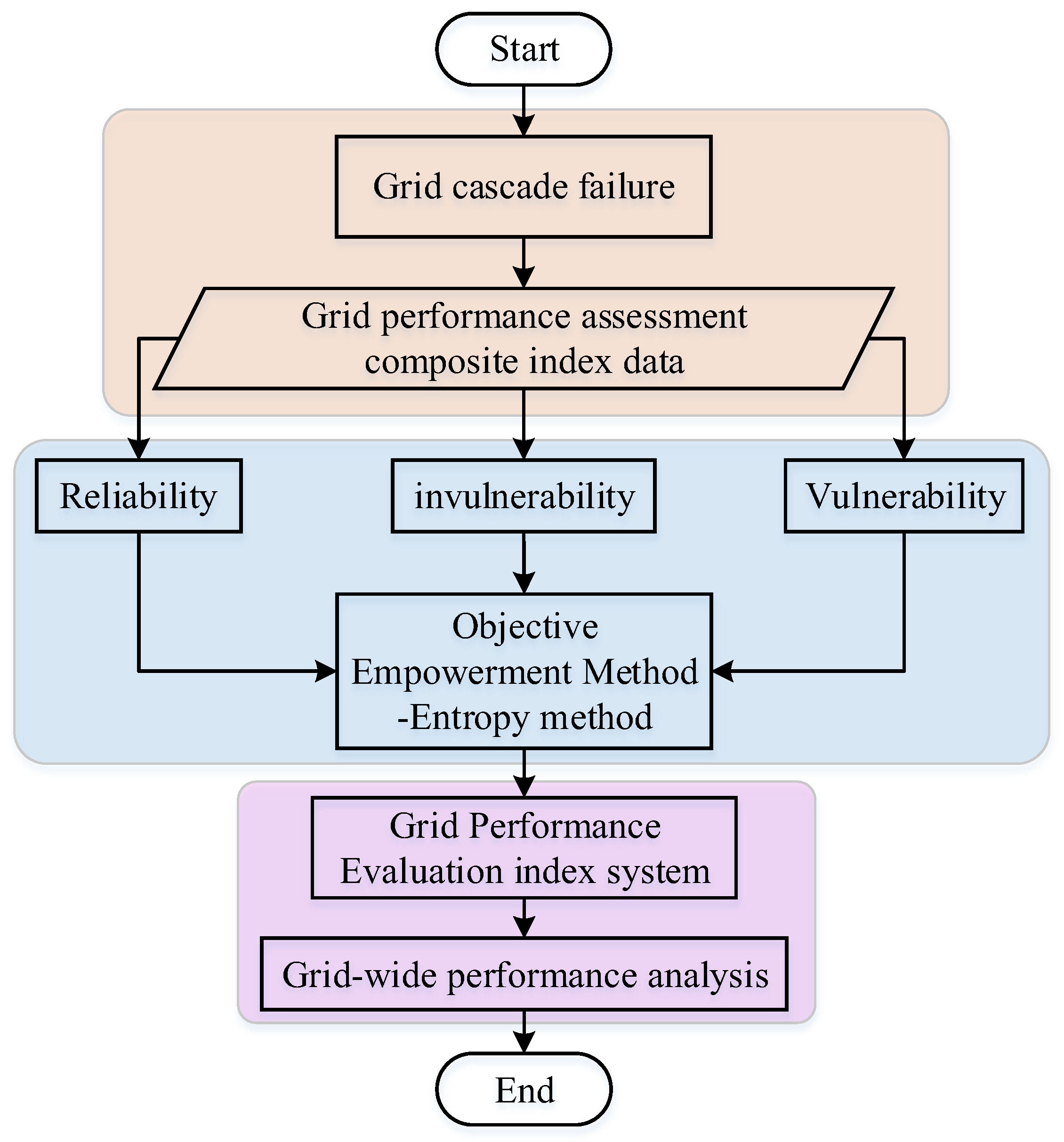
4.2. Comprehensive Evaluation Process of Grid Structure Performance
- Calculate the grid characteristics indicators. Construct the weighted network of grid functional attributes according to Formulas (1)–(3), and then calculate the weighted network measures before and after node failure happened, respectively, according to Formulas (4)–(6) and the cascade failure model;
- Calculate the network structure performance indicators. Calculate the network invulnerability according to Formula (7), the network reliability according to Formula (8), and the network vulnerability according to Formula (9);
- Combine performance indicators by the entropy method to obtain the comprehensive indicators. Combine the calculated invulnerability, reliability, and vulnerability by the entropy method into the comprehensive evaluation index of grid performance;
- Apply the comprehensive index to analyze the current network’s structure performance, and provide reference suggestions for future grid-expanding planning. The process is shown in Figure 2.
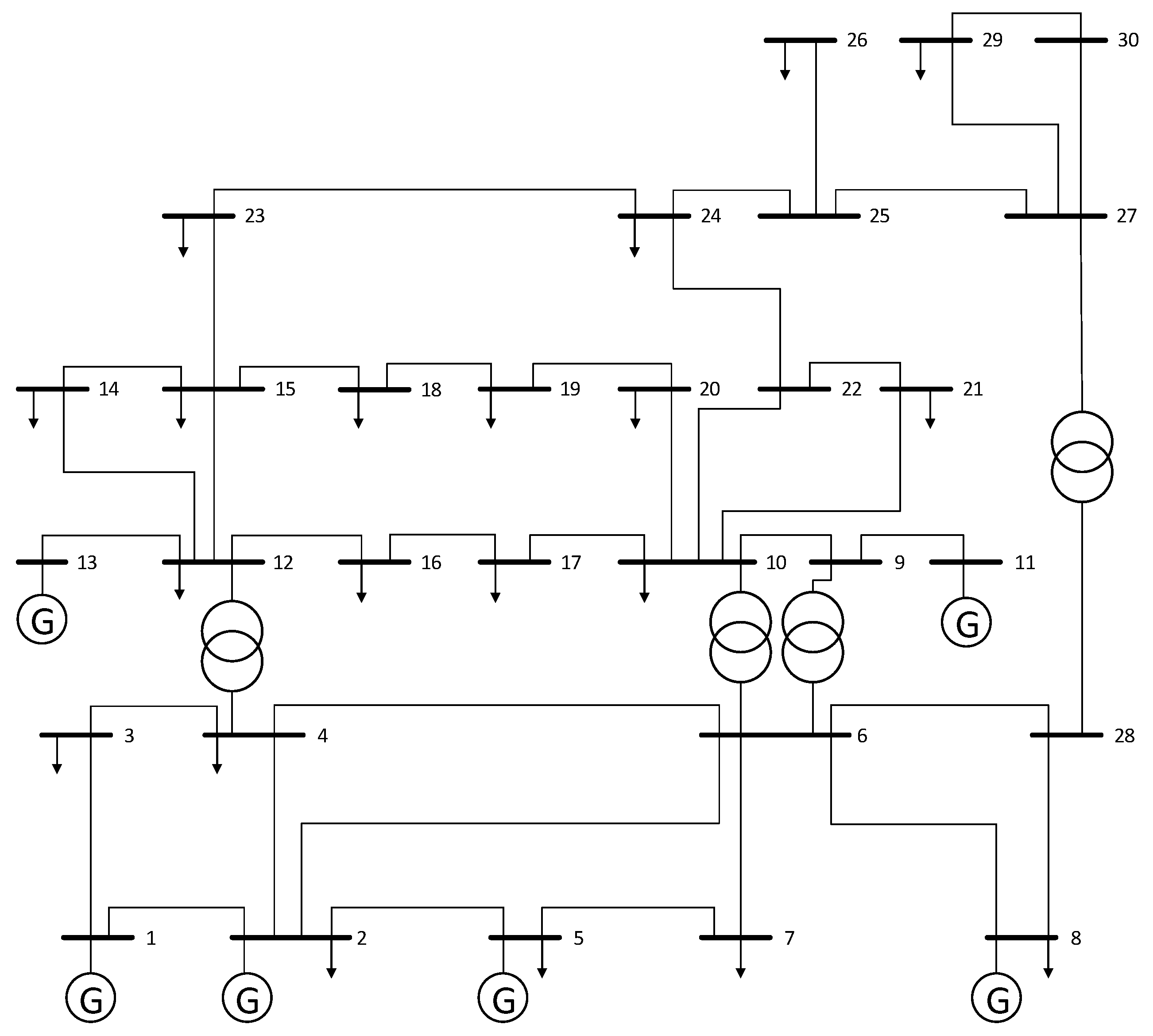
5. Case Study
5.1. Problem Description
5.2. Experimental Schemes
5.3. Results Analysis
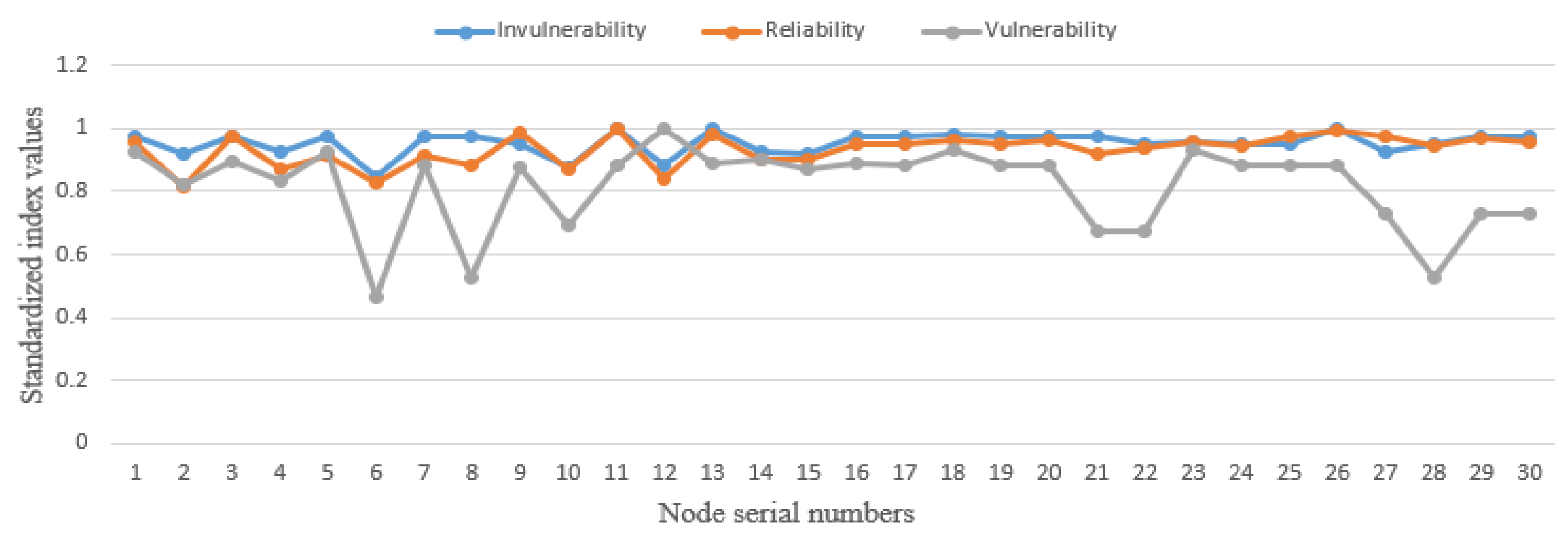
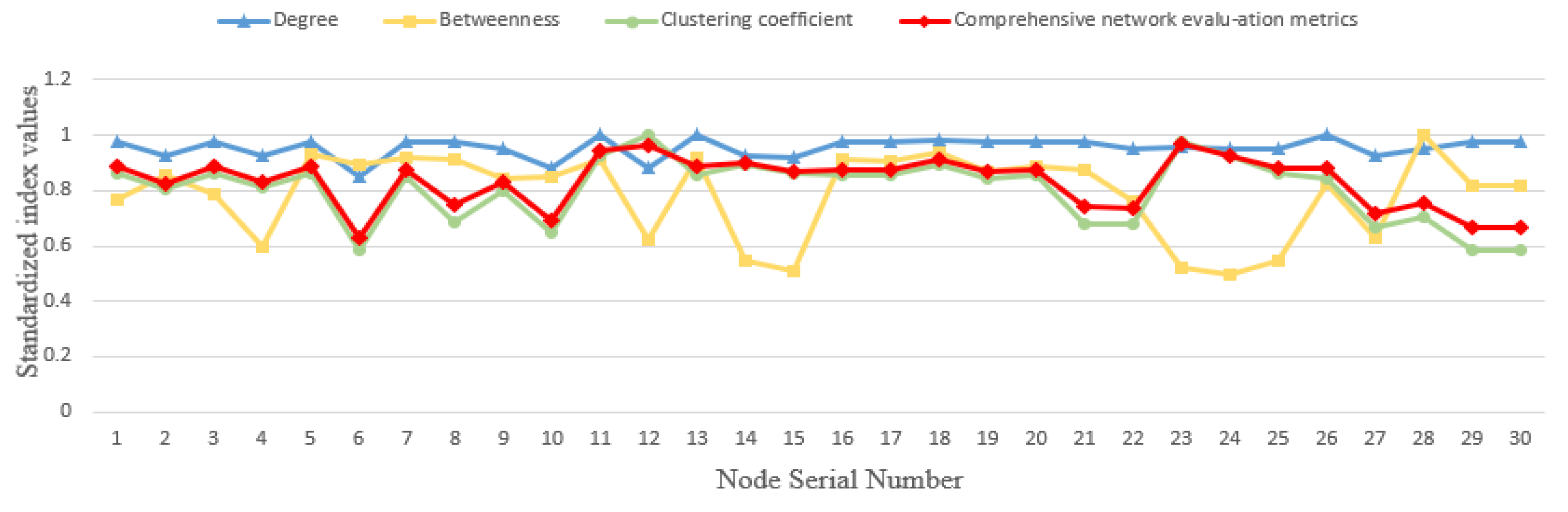
5.3.1. Experiment 1: Comparing Topological Eigenvalues with Unweighted Composite Evaluation Metrics
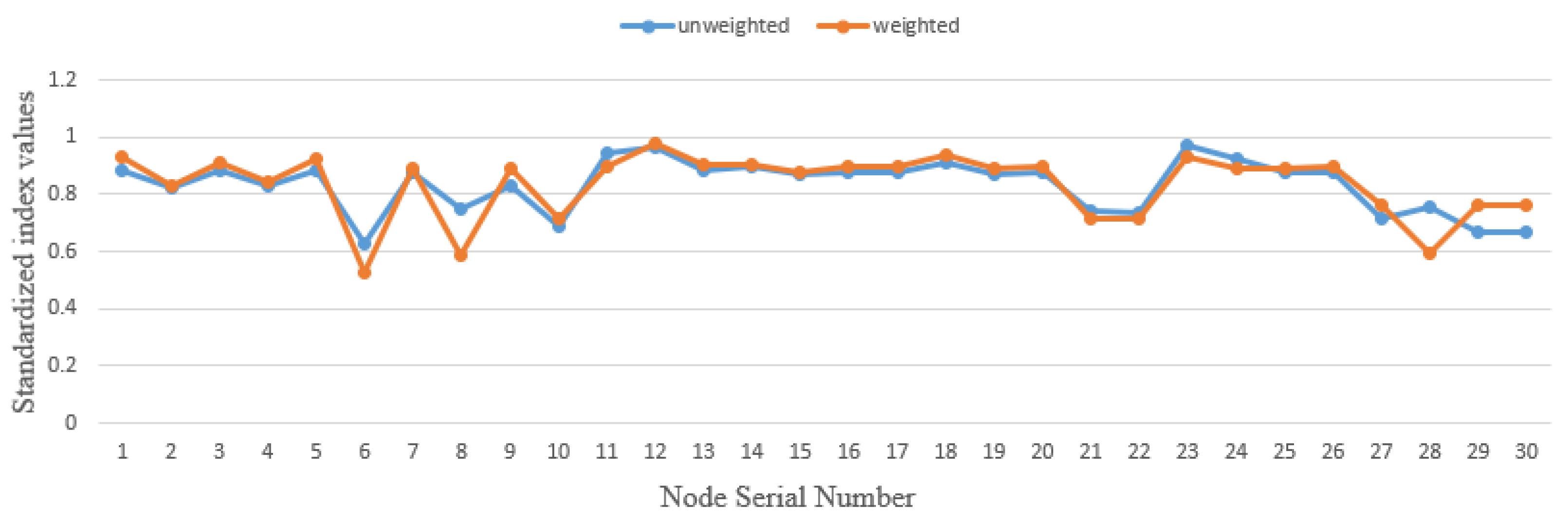
5.3.2. Experiment 2: Comparison Study of Unweighted Composite Assessment Metrics with Power-Weighted Composite Assessment Metrics
- The cascade failure model in this paper only considers the mode of node overload failure removal; the actual grid may be a mixture of node and line failure modes simultaneously, which should be taken into consideration in the system attack strategy analysis;
- The model in this paper is not pilot-run in the real grid, and the results obtained in the real grid may vary from the simulation results. Further real application studies need to be carried out to make the model better for application;
- The entropy method applied in this paper assigns weights according to the data characteristics, and the weights obtained by this indicator become larger when there are large fluctuations in the data types of individual indicators, which makes the influence of the indicator on the comprehensive performance assessment of the network larger, and the limitations of this assignment method can be improved in the future study.
6. Conclusions
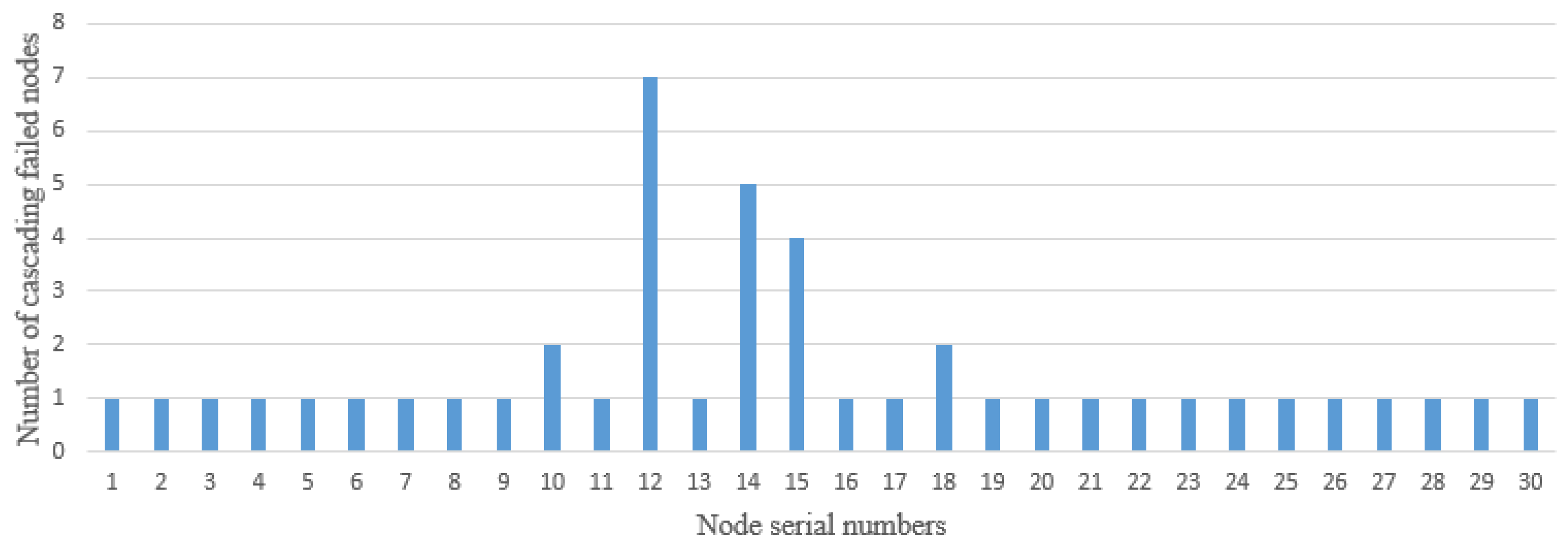
- The cascading failure of the grid to individual nodes has a good overall performance, but there are still individual weak nodes that exist;
- The number of failed nodes in the network does not have a direct effect on the comprehensive performance loss of the network. Topology is not a direct factor affecting the network performance
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, W.; Liao, Y. Wide area measurements based fault detection and location method for transmission lines. Prot. Control. Mod. Power Syst. 2019, 4, 53–64. [Google Scholar] [CrossRef]
- Chu, C.C.; Iu, H.H.C. Complex networks theory for modern smart grid applications: A survey. IEEE J. Emerg. Sel. Top. Circuits Syst. 2017, 7, 177–191. [Google Scholar] [CrossRef]
- Xiao, F.; Li, J.; Wei, B. Cascading failure analysis and critical node identification in complex networks. Phys. A Stat. Mech. Its Appl. 2022, 596, 127117. [Google Scholar] [CrossRef]
- Wu, Y.P.; Chen, Z.L.; Zhao, X.D.; Liu, Y.; Zhang, P.; Liu, Y. Robust analysis of cascading failures in complex networks. Phys. A Stat. Mech. Its Appl. 2021, 583, 126320. [Google Scholar] [CrossRef]
- Lee, L.; Hu, P. Vulnerability analysis of cascading dynamics in smart grids under load redistribution attacks. Int. J. Electr. Power Energy Syst. 2019, 111, 182–190. [Google Scholar] [CrossRef]
- Guo, J.; Feng, T.; Cai, Z.L.; Lian, X.L.; Tang, W.H. Vulnerability Assessment for power transmission lines under typhoon weather based on a cascading failure state transition diagram. Energies 2020, 13, 3681. [Google Scholar] [CrossRef]
- Rahnamay-Naeini, M.; Wang, Z.; Ghani, N.; Mammoli, A.; Hayat, M.M. Stochastic analysis of cascading-failure dynamics in power grids. IEEE Trans. Power Syst. 2014, 29, 1767–1779. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.L.; Liu, Z.G.; Hu, P.; Mei, S.W. Cascading failure model in power grids using the complex network theory. IET Gener. Transm. Distrib. 2016, 10, 3940–3949. [Google Scholar]
- Peng, X.Z.; Yao, H.; Du, J.; Wang, Z.; Ding, C. Invulnerability of scale-free network against critical node failures based on a renewed cascading failure model. Phys. A 2015, 421, 69–77. [Google Scholar] [CrossRef]
- Fan, X.K.; Dudkina, E.; Gambuzza, L.V.; Frasca, M.; Crisostomi, E. A network-based structure-preserving dynamical model for the study of cascading failures in power grids. Electr. Power Syst. Res. 2022, 209, 107987. [Google Scholar] [CrossRef]
- Li, J.; Sun, C.W.; Su, Q.Y. Analysis of cascading failures of power cyber-physical systems considering false data injection attacks. Glob. Energy Interconnect. 2021, 4, 204–213. [Google Scholar] [CrossRef]
- Dai, Y.T.; Preece, R.; Panteli, M. Risk assessment of cascading failures in power systems with increasing wind penetration. Electr. Power Syst. Res. 2022, 211, 108392. [Google Scholar] [CrossRef]
- Gao, X.X.; Li, X.J.; Yang, X.Y. Robustness assessment of the cyber-physical system against cascading failure in a virtual power plant based on complex network theory. Int. Trans. Electr. Energy Syst. 2021, 31, e13039. [Google Scholar] [CrossRef]
- Guo, W.Z.; Wang, H.; Wu, Z.P. Robustness analysis of complex networks with power decentralization strategy via flow-sensitive centrality against cascading failures. Phys. A Stat. Mech. Its Appl. 2018, 494, 186–199. [Google Scholar] [CrossRef]
- Sun, Y.S.; Tang, X.S.; Zhang, G.W.; Miao, F.F.; Wang, P. Dynamic power flow cascading failure analysis of wind power integration with complex network theory. Energies 2017, 11, 63. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Tang, Y.F.; He, H.B.; Sun, Y. Cascading failure analysis with DC power flow model and transient stability analysis. IEEE Trans. Power Syst. 2014, 30, 285–297. [Google Scholar] [CrossRef]
- Alberto, A.; Dueñas-Osorio, L.; Cadini, F.; Zio, E. Electrical and topological drivers of the cascading failure dynamics in power transmission networks. Reliab. Eng. Syst. Saf. 2018, 175, 196–206. [Google Scholar]
- Li, J.; Shi, C.L.; Chen, C.K.; Dueñas-Osorio, L. A cascading failure model based on AC optimal power flow: Case study. Phys. A Stat. Mech. Its Appl. 2018, 508, 313–323. [Google Scholar] [CrossRef]
- Noebels, M.; Preece, R.; Panteli, M. AC cascading failure model for resilience analysis in power networks. IEEE Syst. J. 2022, 16, 374–385. [Google Scholar] [CrossRef]
- Peng, H.; Kan, Z.; Zhao, D.D.; Han, J.M.; Lu, J.F.; Hu, Z.L. Reliability analysis in interdependent smart grid systems. Phys. A Stat. Mech. Its Appl. 2018, 500, 50–59. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Liu, Z.Q.; He, X.; Ma, J.F. Cascade phenomenon against subsequent failures in complex networks. Phys. A Stat. Mech. Its Appl. 2018, 499, 472–480. [Google Scholar] [CrossRef]
- Fan, W.L.; He, X.F.; Xiao, Y.Q.; Li, Q.Y. Vulnerability analysis of power system by modified H-index method on cascading failure state transition graph. Electr. Power Syst. Res. 2022, 209, 107986. [Google Scholar] [CrossRef]
- Li, K.W.; Liu, K.; Wang, M. Robustness of the Chinese power grid to cascading failures under attack and defense strategies. Int. J. Crit. Infrastruct. Prot. 2021, 33, 100432. [Google Scholar] [CrossRef]
- Guo, J.K.; Wang, S.B.; Wang, D.D.; Liu, T.B. Spatial structural pattern and vulnerability of China-Japan-Korea shipping network. Chin. Geogr. Sci. 2017, 27, 697–708. [Google Scholar] [CrossRef]
- Gull, S.F.; Skilling, J. Maximum entropy method in image processing. Commun. Radar Signal Process. 2008, 131, 646–659. [Google Scholar] [CrossRef]
- Hu, F.N.; Chen, L.J.; Chen, J. Robustness evaluation of complex power grids containing renewable energy. Int. J. Electr. Power Energy Syst. 2021, 132, 107187. [Google Scholar] [CrossRef]
- Zhou, D.Y.; Hu, F.N.; Wang, S.L.; Chen, J. Power network robustness analysis based on electrical engineering and complex network theory. Phys. A Stat. Mech. Its Appl. 2020, 564, 125540. [Google Scholar] [CrossRef]


| The Work in Existing Literature | The Work Conducted in This Paper | |
|---|---|---|
| Research Focus | 1. The study on power system cascade failure propagation mechanism modeling; 2. The dynamic cascade failure study using power flow information. | 1. No need to take the power flow characteristics into consideration; 2. A variety of evaluation indices are proposed for different grid characteristics; 3. Objective weighting method is employed to synthesize the indices so that a comprehensive evaluation of the grid characteristics can be made in a proper manner. |
| Characteristic Indicators | Maximum Value | Minimum Value | Average Value | 0.25 Quantile |
|---|---|---|---|---|
| Degree | 17.7724 | 14.5172 | 16.5719 | 16.0308 |
| Betweenness | 0.1199 | 0.0549 | 0.0893 | 0.0707 |
| Clustering coefficient | 1.4657 | 0.6856 | 1.1956 | 1.0663 |
| Indicators | Maximum Value | Minimum Value | Average Value | 0.25 Quantile |
|---|---|---|---|---|
| Invulnerability | 1.0239 | 0.8669 | 0.9761 | 0.9489 |
| Reliability | 1.0491 | 0.8569 | 0.9782 | 0.9462 |
| Vulnerability | 1.0835 | 0.5068 | 0.8838 | 0.7882 |
| Characteristic Indicators | Maximum Value | Minimum Value | Average Value | 0.25 Quantile |
|---|---|---|---|---|
| Degree | 2.7586 | 2.3448 | 2.6325 | 2.5600 |
| Betweenness | 0.0220 | 0.0109 | 0.0174 | 0.0138 |
| Clustering coefficient | 0.1437 | 0.0839 | 0.1156 | 0.0983 |
| Indicators | Maximum Value | Minimum Value | Average Value | 0.25 Quantile |
|---|---|---|---|---|
| Comprehensive network evaluation metrics | 0.9705 | 0.6297 | 0.8335 | 0.7458 |
| Indicators | Maximum Value | Minimum Value | Average Value | 0.25 Quantile |
|---|---|---|---|---|
| Comprehensive network evaluation metrics | 0.9773 | 0.5244 | 0.8348 | 0.7635 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Jia, L.; Ning, J.; Ye, Y.; Sun, H.; Shi, R. Power Grid Structure Performance Evaluation Based on Complex Network Cascade Failure Analysis. Energies 2023, 16, 990. https://doi.org/10.3390/en16020990
Zhang D, Jia L, Ning J, Ye Y, Sun H, Shi R. Power Grid Structure Performance Evaluation Based on Complex Network Cascade Failure Analysis. Energies. 2023; 16(2):990. https://doi.org/10.3390/en16020990
Chicago/Turabian StyleZhang, Di, Limin Jia, Jin Ning, Yujiang Ye, Hao Sun, and Ruifeng Shi. 2023. "Power Grid Structure Performance Evaluation Based on Complex Network Cascade Failure Analysis" Energies 16, no. 2: 990. https://doi.org/10.3390/en16020990
APA StyleZhang, D., Jia, L., Ning, J., Ye, Y., Sun, H., & Shi, R. (2023). Power Grid Structure Performance Evaluation Based on Complex Network Cascade Failure Analysis. Energies, 16(2), 990. https://doi.org/10.3390/en16020990







