A Decentralized Control Strategy for Series-Connected Single-Phase Two-Stage Photovoltaic Grid-Connected Inverters

Abstract

Currently, most of the series inverter control methods rely on communication, which greatly reduces the reliability of the system and increases the cost. To address the above problems, this paper proposes a decentralized control strategy for series-connected single-phase two-stage grid-connected photovoltaic (PV) inverters. By improving the traditional droop control, the frequency and phase of the output voltage of each inverter unit are consistent and self-synchronized with the power grid while relying only on local independent control, and each unit realizes maximum power point tracking (MPPT). At different light intensities, each series-connected unit can quickly track the new maximum power point while still maintaining self-synchronization between the units. The system stability is analyzed via the small signal method, and sufficient conditions for system stability are obtained. Finally, the simulation results verify the correctness and effectiveness of the proposed control strategy.

1. Introduction

Fossil energy such as oil, coal, and natural gas is irrecoverable and will eventually be consumed, while also causing many environmental pollution problems. Therefore, the development of renewable energy such as marine energy, wind energy, and solar energy has received extensive attention from the international community, and its development has been highly valued by all countries. Solar energy has developed more rapidly than other renewable energy sources due to its advantages of large supply, universal distribution, and economic feasibility, thereby promoting the development of the photovoltaic power generation industry, so the structure and control method of the PV grid-connected power generation system has become a research hotspot [1,2,3].

At present, the inverter clusters in most photovoltaic power plants are connected to the AC bus in parallel, and then accessed by medium- or high-voltage transmission lines through the power-frequency step-up transformer. This system structure has the advantages of high reliability, plug-and-play, and high flexibility. However, step-up transformers increase the cost and complexity of the system. Moreover, it is difficult for a single inverter to further increase power and voltage levels. Compared to the parallel-connected inverter structure, the output voltage of each inverter in the series-connected structure is superimposed, which enables the cluster of low-voltage PV inverters to be directly connected into the medium-high voltage power network without the need for a step-up transformer. Therefore, researchers have proposed a lot of series-connected inverter structures, such as the Cascaded H-Bridge (CHB), quasi-Z-source cascade inverter, hybrid cascade inverter, and other topologies [4,5,6,7,8,9]. Due to their modular, easily extensible structural layouts, they have been widely used in PV power generation systems.

Currently, most series-connected inverters use centralized control methods [10,11,12]. However, centralized control relies on a real-time communication network and a powerful central controller. If a communication failure occurs, it can cause the system to be paralyzed and unable to work properly. In addition, when the amount of series-connected inverters is large and the distance between the units is far, its implementation will become more difficult.

Therefore, researchers developed some interest in the distributed control strategies based on weak communications [13,14,15,16,17]. Study [13] proposes a distributed autonomous control method for series photovoltaic inverters. It designs a fast output active power control loop and a slow voltage control loop, which can enable all PV modules to achieve MPPT. Study [16] proposes an improved distributed power control strategy in which all series-connected inverter units are controlled as voltage sources to regulate the output active and reactive power. In addition, study [17] proposes a current-voltage hybrid control scheme for a series-connected inverter, in which the main inverter is controlled as a current source to regulate the common current of the line, and the other inverters are controlled as voltage sources to establish voltage at the common coupling point (PCC). In this way, the MPPT operation of all series-connected inverter units can be well ensured. The common feature of studies [14,15,16,17,18] is the need for low-bandwidth communication links to transmit grid synchronization signals to each inverter. To save costs and avoid the adverse effects of communication failures, studies [18,19,20,21,22,23] propose decentralized control methods without communication for series-connected inverters. Study [18] uses a P-ω droop control strategy to self-synchronize the output voltage of all series-connected inverter units, but it can only be applied when the line impedance is inductive. Furthermore, the previous work [19] proposes a φ-ω power factor angle droop control strategy, which can be applied to any line impedance characteristics. However, [18,19] are implemented on the premise that all inverter units are the same, and the output voltage amplitude of all units is fixed, so it is not suitable for inverters with different capacities. In study [22], the improved ω-p droop control requires simultaneous active power and inverter DC side voltage, and is influenced by the droop coefficient and PI controller parameters, making the entire system relatively complex. In the same way, the output voltage amplitude of all the units are equal, meaning that the output apparent power of all units is the same. Furthermore, study [23] proposes a decentralized control strategy for cascaded single-stage PV inverters with a MPPT capability, which can realize the series connection of inverter units with different power generation capabilities. It can only be used in single-stage PV inverter series systems.

According to the above analysis, to get rid of the dependence on communication, reduce the complexity and cost of the system, and realize the series connection of inverters with different capacities, this paper proposes a decentralized control strategy for series-connected single-phase two-stage PV grid-connected inverters. This strategy enables the frequency and phase of the output voltages of all series-connected units to be consistent and self-synchronized to the grid, and the amplitude of the output voltage is adjustable and proportional to their output active power. The stability of the decentralized control strategy proposed in this paper is proved via small signal analysis, and the system stability conditions are obtained. The simulation results verify the correctness and effectiveness of the control strategy. The control strategy proposed in this paper offers great potential for the application of series PV inverters in large-scale medium or high voltage grid-connected PV power generation; it is possible that this strategy could be applied to utility-scale solar farms in the future.

The following parts of this article are structured as follows. In Section 2, the configuration of the series-connected single-phase two-stage PV inverters grid-connected system is introduced, and the output power characteristic of any inverter unit is formulated. Then, in Section 3, a decentralized control strategy with MPPT ability is proposed. In Section 4, the steady-state analysis of the proposed strategy is carried out, and the possible steady points are calculated. In Section 5, the system stability is verified via the small signal analysis method. In Section 6, the simulation results are provided. In Section 7, the contributions of this paper are concluded.

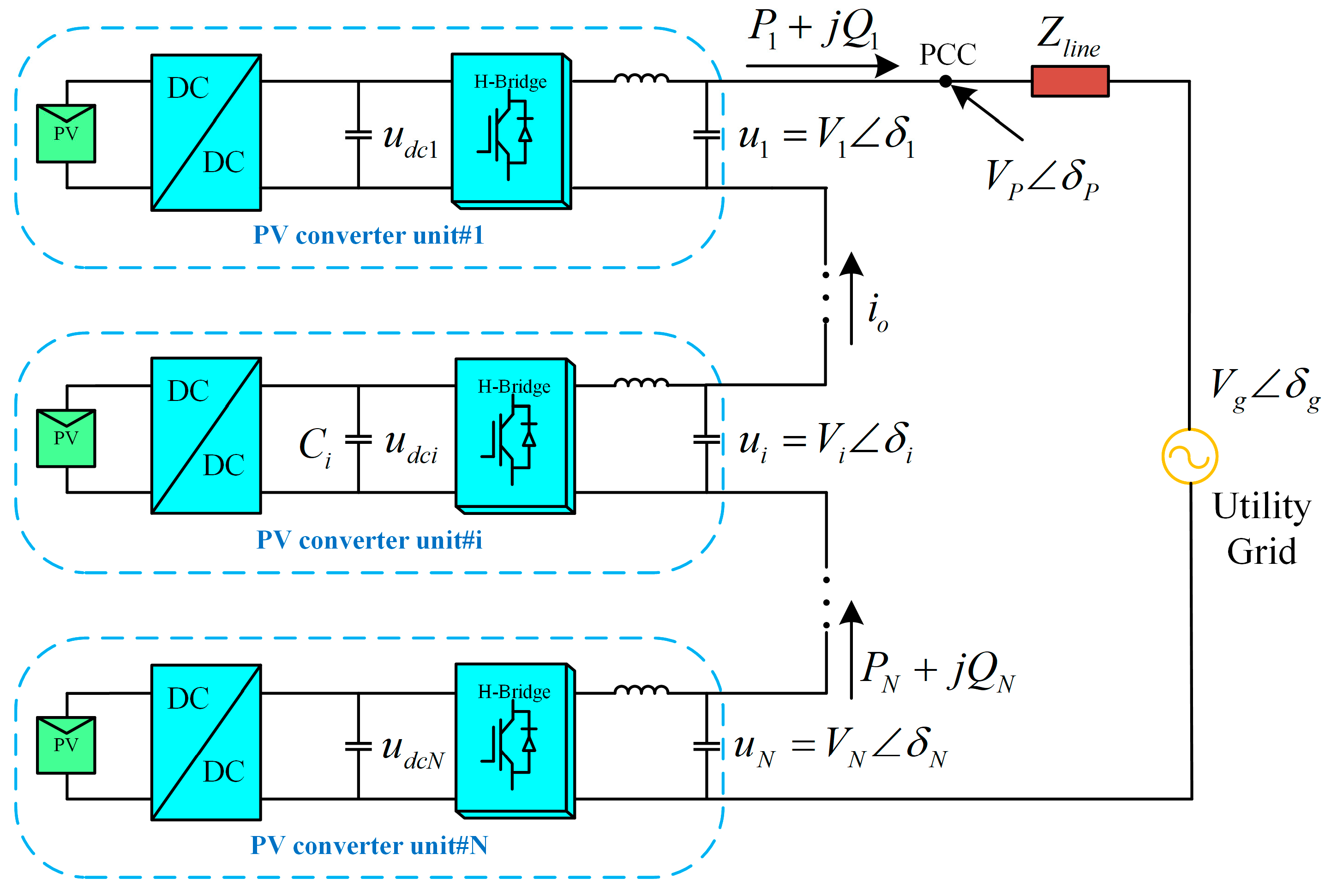
2. Equivalent Model of Series-Connected PV Inverters Grid-Connected System

The structure of the single-phase two-stage PV inverters grid-connected system is shown in Figure 1, where N PV inverter units are series-connected. The DC pre-stage of each unit is composed of an independent PV array and a DC/DC converter, which is used to boost the PV voltage and realize MPPT control; the AC post-stage is composed of an H-Bridge inverter module and a LC filter. These PV inverters are expected to transmit their maximum active power to the power grid.

From Figure 1, the output power expression of the i-th PV inverter unit is obtained as follows:

$$P_i+j{Q}_i=V_i{e}^{j{\delta }_i}{\left(\frac{V_P{e}^{j{\delta }_P}-V_g{e}^{j{\delta }_g}}{\left|Z_{line}\right|e^{j{\theta }_{line}}}\right)}^{\ast }$$

(1)

where P_i and Q_i represent the active and reactive power output of the i-th unit, respectively; V_i and δ_i represent the amplitude and phase angle of the output voltage, respectively; V_g and δ_g represent the amplitude and phase angle of the grid voltage, respectively; |Z_line| and θ_line represent the amplitude and phase angle of the grid-tied line impedance, respectively, and |Z_line| is usually inductive, with θ_line ≈ π/2; and V_P and δ_P represent the amplitude and phase angle of the common coupling point (PCC) voltage, respectively. The PCC voltage is the sum of the output voltages of the N units, which can be expressed as follows:

$$V_P{e}^{j{\delta }_P}={\displaystyle \sum _{j=1}^N{V}_j{e}^{j{\delta }_j}}$$

(2)

where N is the number of series-connected PV inverter units.

From Equations (1)–(2), the expressions of P_i and Q_i are derived as follows:

$$P_i=\frac{V_i{V}_g}{\left|Z_{line}\right|}\sin \left({\delta }_i-{\delta }_g\right)-{\displaystyle \sum _{j=1}^N\frac{V_i{V}_j}{\left|Z_{line}\right|}}\sin \left({\delta }_i-{\delta }_j\right)$$

(3)

$$Q_i={\displaystyle \sum _{j=1}^N\frac{V_i{V}_j}{\left|Z_{line}\right|}}\cos \left({\delta }_i-{\delta }_j\right)-\frac{V_i{V}_g}{\left|Z_{line}\right|}\cos \left({\delta }_i-{\delta }_g\right)$$

(4)

3. Design of the Decentralized Control Strategy for Series-Connected PV Inverters

To make the frequency and phase of the output voltage of each unit consistent and synchronized with the power grid, and to realize the MPPT function, this paper improves the traditional ω-P and V-Q droop controls and proposes a new droop control strategy. The principle analysis is as follows. Because the DC side voltage of the inverter $u_{dc}$ can reflect the power balance of the system, if $u_{dc}$ is greater than its reference value $u_{dc}^{\ast }$, it means that the inverter output power is less than the PV array output power $P_{MPPT}$. On the contrary, if $u_{dc}$ is less than the reference value $u_{dc}^{\ast }$, it means that the inverter output power is greater than $P_{MPPT}$. Therefore, the ω-$u_{dc}$ droop control law can be designed as shown in Equation (5). Entering the steady state, there is ω = ω*, thus $u_{dc}$ = $u_{dc}^{\ast }$. As a consequence, the frequency self-synchronization, MPPT, and stable DC side voltage functions are achieved. To keep the phase of the output voltage consistent when each unit outputs different active powers, the V-$P_{MPPT}$ control law is designed as shown in Equation (6). It can be seen that the output voltage amplitude of each unit is adjustable and is proportional to its output active power. Because the output current of each unit is the same, their output voltage phases are also the same.

$${\omega }_i={\omega }^{\ast }+m\left(u_{dci}-u_{dc}^{\ast }\right)$$

(5)

$$V_i=V^{\ast }\frac{P_{MPPT-i}}{P_{max}}=\frac{V_g\cdot P_{MPPT-i}}{M\cdot P_{max}}$$

(6)

where ω_i and V_i represent the angular frequency and amplitude of the output voltage of the i-th unit, respectively; ω* is the angular frequency reference and is set to equal to the normal grid angular frequency, that is, ω* = ω_g; $u_{dc}$ and $u_{dc}^{\ast }$ indicate the amplitude and amplitude reference of the DC side voltage of the inverter, respectively; m is the droop control coefficient; V* indicates the amplitude reference of the AC side output voltage; $P_{MPPT-i}$ is the maximum power provided by the PV array in real-time, and its value is given by the MPPT algorithm; $P_{max}$ is the maximum output power of the PV array under standard test conditions (irradiance of 1000 W/m², PV cell temperature of 25 °C), and its value is given by the manufacturer. Obviously, $P_{MPPT-i}\le P_{max}$; M is a parameter related to system stability and the power factor, which is discussed later in Section 5.

The control block diagram of the i-th unit in the series-connected PV inverters is shown in Figure 2. The output voltage $u_{PVi}$ and output current $i_{PVi}$ of the PV array are sampled, and the driving pulse signal $d_{DC-i}$ of the DC/DC converter is obtained according to the MPPT algorithm and PWM modulation, to realize the real-time MPPT of the PV array. Meanwhile, the voltage on the DC side of the inverter, $u_{dci}$, is sampled, and through the proposed decentralized control strategy, the output voltage reference $V_i\angle {\delta }_i$ is generated while $u_{dci}$ is stabilized. Also, the output voltage $u_i$ and current $i_i$ are sampled, then the driving pulse signal $d_i$ of the H-Bridge inverter is obtained through voltage and current dual closed-loop control and PWM modulation, to make sure that $u_i$ tracks $V_i\angle {\delta }_i$ well. Finally, the goal of MPPT, frequency and phase self-synchronization, is achieved.

4. Steady-State Analysis

Since the output current of these series units is the same, the ratio of the apparent power of any two units is equal to the ratio of their output voltage amplitude, i.e.,

$$\frac{S_i}{S_j}=\frac{V_i}{V_j}$$

(7)

where $i,j\in \left\{1,2,\cdots ,N\right\}$.

At the steady state, since ${\omega }_i={\omega }^{\ast }$, it can be seen from Equation (5) that the DC side voltage of any unit is equal to the given DC side voltage reference:

$$u_{dci}=u_{dc}^{\ast }$$

(8)

At this point, the output active power of each unit is equal to the real-time power of the PV array, i.e.,

$$P_i=P_{MPPT-i}$$

(9)

From Equation (6), it can be seen that the ratio of the output voltage amplitude of any two units is equal to the ratio of the maximum power output of the respective photovoltaic array, i.e.,

$$\frac{V_i}{V_j}=\frac{P_{MPPT-i}}{P_{MPPT-j}}$$

(10)

From Equations (7)–(10), it can be obtained that the ratio of the apparent power of any two units is equal to the ratio of their output active power, i.e.,

$$\frac{S_i}{S_j}=\frac{P_i}{P_j}=\frac{Q_i}{Q_j}$$

(11)

From Equation (11), there comes the conclusion that the output voltage phase of each cell is identical, i.e.,

$${\delta }_i={\delta }_j$$

(12)

From Equations (3)–(12), the steady-state power transfer expression for each unit can be obtained:

$${\overline{P}}_i=S_c\sin \overline{\delta };{\overline{Q}}_i=S_c\left(\frac{{\displaystyle \sum _{j=1}^N{P}_{MPPT-i}}}{M\cdot P_{max}}-\cos \overline{\delta }\right)$$

(13)

where $S_c=\frac{V_g^2\cdot P_{MPPT-i}}{(P_{max}\cdot M\cdot \left|Z_{line}\right|)}$ represents the power transfer capacity and $\overline{\delta }$ represents the steady-state power angle ($\overline{\delta }={\delta }_i-{\delta }_g$). From Equation (13), it can be seen that the system has two stable operating points: $\overline{\delta }=\arcsin \left({\overline{P}}_i/S_c\right)$ and $\overline{\delta }=\pi -\arcsin \left({\overline{P}}_i/S_c\right)$.

5. Stability Analysis

To verify the stability of the proposed control strategy, a small signal analysis is carried out. First, the small-signal model of the system in Figure 2 is established. Then, an eigenvalue analysis is performed to assess the stability of the system. Finally, reasonable design rules of the system parameters are discussed to obtain a satisfactory stability margin and dynamic performance.

5.1. Small Signal Modeling

The mathematical model of the i-th unit is given as follows:

$$\{\begin{array}{l}{C}_i{u}_{dci}{\dot{u}}_{dci}=P_{PVi}-P_i\\ {\dot{\delta }}_i={\omega }_i={\omega }^{\ast }+m\left(u_{dci}-u_{dc}^{*}\right)\end{array}$$

(14)

where $C_i$ is the DC side capacitance; $P_{PVi}$ is the output power of the PV array. In the steady state there are $P_{PVi}$ = $P_{MPPT-i}$ and $u_{dci}$ = $u_{dc}^{\ast }$; by linearizing Equation (14) near the steady-state operating point, the small signal model is derived as:

$$\{\begin{array}{l}{C}_i{\dot{u}}_{dci}{|}_{u_{dci}=u_{dc}^{*}}\mathsf{\Delta }{u}_{dci}+C_i{u}_{dc}^{*}\mathsf{\Delta }{\dot{u}}_{dci}=-\mathsf{\Delta }{P}_i\\ \mathsf{\Delta }{\dot{\delta }}_i=m\mathsf{\Delta }{u}_{dci}\end{array}$$

(15)

Simplifying Equation (15) yields

$$\{\begin{array}{l}\mathsf{\Delta }{\dot{u}}_{dci}=-k\mathsf{\Delta }{P}_i\\ \mathsf{\Delta }{\dot{\delta }}_i=m\mathsf{\Delta }{u}_{dci}\end{array}$$

(16)

where $k=\frac{1}{C_i{u}_{dc}^{*}}$.

Substituting Equation (6) into Equation (3) yields

$$P_i=\frac{V^{\ast 2}{P}_{MPPT-i}}{\left|Z_{line}\right|P_{max}^2}\left[P_{max}M\sin \left({\delta }_i-{\delta }_g\right)-{\displaystyle \sum _{j=1}^N{P}_{MPPT-j}}\sin \left({\delta }_i-{\delta }_j\right)\right]$$

(17)

Then, linearizing Equation (17) yields

$$\mathsf{\Delta }{P}_i=\frac{V^{\ast 2}{P}_{MPPT-i}}{\left|Z_{line}\right|P_{max}^2}\left[P_{max}M\cos \overline{\delta }\left(\mathsf{\Delta }{\delta }_i-\mathsf{\Delta }{\delta }_g\right)-{\displaystyle \sum _{j=1}^N{P}_{MPPT-j}}\left(\mathsf{\Delta }{\delta }_i-\mathsf{\Delta }{\delta }_j\right)\right]$$

(18)

Substituting Equation (18) into Equation (16) yields

$$\{\begin{array}{l}\mathsf{\Delta }{\dot{u}}_{dci}=-k^{\prime }\left(P_{max}M\cos \overline{\delta }-{\displaystyle \sum _{j=1}^N{P}_{MPPT-j}}\right)\mathsf{\Delta }{\delta }_i\\ \mathsf{\Delta }{\dot{\delta }}_i=m\mathsf{\Delta }{u}_{dci}\end{array}$$

(19)

where $k^{\prime }=\frac{1}{C_i{u}_{dc}^{*}}\cdot \frac{V^{\ast 2}{P}_{MPPT-i}}{\left|Z_{line}\right|P_{max}^2}$.

The complete small signal model is as follows:

$$\{\begin{array}{l}\mathsf{\Delta }{\dot{u}}_{dc}=-k^{\prime }{T}_1\mathsf{\Delta }\delta \\ \mathsf{\Delta }\dot{\delta }=T_2\mathsf{\Delta }{u}_{dc}\end{array}$$

(20)

where $\mathsf{\Delta }{u}_{dc}={\left[\mathsf{\Delta }{u}_{dc1} \mathsf{\Delta }{u}_{dc2} \cdots \mathsf{\Delta }{u}_{dcN}\right]}^T$, $\mathsf{\Delta }\delta ={\left[\mathsf{\Delta }{\delta }_1 \mathsf{\Delta }{\delta }_2 \cdots \mathsf{\Delta }{\delta }_N\right]}^T$, $T_1=\left[\begin{array}{cccc}{P}_{max}M\cos \overline{\delta }-{\displaystyle \sum _{j=1,j\ne i}^N{P}_{MPPT-j}}& P_{MPPT-2}& \cdots & P_{MPPT-N}\\ P_{MPPT-1}& P_{max}M\cos \overline{\delta }-{\displaystyle \sum _{j=1,j\ne i}^N{P}_{MPPT-j}}& \cdots & P_{MPPT-N}\\ ⋮& ⋮& \ddots & ⋮\\ P_{MPPT-1}& P_{MPPT-2}& \cdots & P_{max}M\cos \overline{\delta }-{\displaystyle \sum _{j=1,j\ne i}^N{P}_{MPPT-j}}\end{array}\right]$, $T_2={\left[\begin{array}{cccc}m& 0& \cdots & 0\\ 0& m& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & m\end{array}\right]}_{N\times N}=m{I}_{N\times N}$, $I_{N\times N}$ is a unity matrix.

5.2. System Stabilization Conditions

Rewriting Equation (20) into the following uniform matrix forms

$$\mathsf{\Delta }\dot{x}=A\mathsf{\Delta }x$$

(21)

where

$$\{\begin{array}{l}\mathsf{\Delta }x={\left[\mathsf{\Delta }{u}_{dc} \mathsf{\Delta }\delta \right]}^T\\ A=\left(\begin{array}{cc}{0}_{N\times N}& -k^{\prime }{T}_1\\ T_2& 0_{N\times N}\end{array}\right)\end{array}$$

(22)

The eigenvalues of the system matrix A are

$$\{\begin{array}{l}{\lambda }_1\left(A\right)=-k^{\prime }{P}_{max}M\cos \overline{\delta }\\ {\lambda }_2\left(A\right)=\cdots ={\lambda }_N\left(A\right)=-k^{\prime }(P_{max}M\cos \overline{\delta }-{\displaystyle \sum _{j=1}^N{P}_{MPPT-j}})\\ {\lambda }_{N+1}\left(A\right)=\cdots ={\lambda }_{2N}\left(A\right)=-m\end{array}$$

(23)

Therefore, the sufficient non-essential condition for system stability is derived as follows:

$$\mathsf{\Delta }=P_{max}M\cos \overline{\delta }-{\displaystyle \sum _{j=1}^N{P}_{MPPT-j}}>0$$

(24)

To make the stability condition (24) true, $\cos \overline{\delta }$ > 0 (i.e., $\overline{\delta }\in (-\pi /2,\pi /2)$) must be satisfied, and M > N. According to the steady-state analysis above, only the stable point $\overline{\delta }=\arcsin \left({\overline{P}}_i/S_c\right)$ meets the requirement. It can be seen from Equation (24) that to make the system stability range larger $\mathsf{\Delta }$ should be as large as possible, so that the eigenvalues of the system matrix A will be far away from the imaginary axis. Since the power angle $\overline{\delta }$ is generally small, i.e., $\cos \overline{\delta }\approx 1$, considering the extreme case $P_{MPPT-i}=P_{max}$, M >> N is required to make $\mathsf{\Delta }$ as large as possible. However, it can be seen from (13) that M >> N will make ${\overline{Q}}_i$ << 0, causing the system to absorb more reactive power and reduce the power factor. Thus, the design of the M value is a compromise between system stability and power factor.

6. Simulation Verification

6.1. Simulation Settings

To verify the correctness and effectiveness of the proposed control strategy, simulation tests are carried out in MATLAB/SIMULINK. Based on Figure 1, a PV grid-connected system with the number of series units N = 3 is built, and the corresponding system parameters are shown in

Table 1. Simulation parameters.

Symbol	Value	Symbol	Value
$V_g$	311 V	$u_{dc}^{\ast }$	200 V
$f_g$	50 Hz	$Z_{line}$	0.1 + j2 Ω
$V^{\ast }$	97.2 V	M	3.2
${\omega }^{\ast }$	100π rad/s	N	3
m	5 × 10−3	$N_p$	2
$f_c$	10 kHz	$N_s$	4

, where $N_p$ and $N_s$ represent the number of modules connected in parallel and series of the photovoltaic array, respectively, and $f_c$ is the switching frequency of the inverter.

The PV module cells used in the simulation are modeled according to the commercial PV panel 1Soltech-1STH-215-P, and its parameters under standard test conditions (illuminance of 1000 W/m², ambient temperature of 25 °C) are shown in

Table 2. PV panel parameters.

Symbol	Value	Symbol	Value
$P_N$	213.15 W	$V_{mp}$	29 V
$V_{oc}$	36.3 V	$I_{mp}$	7.35 A
$I_{sc}$	7.84 A

.

The P-V characteristic curve of the PV module is obtained from the Matlab simulation component model and shown in Figure 3, which as can be seen from the figure is $P_{\max }$ = 1705 W.

6.2. Simulation Results

During the simulation process, only the light intensity parameters are changed, while the temperature remains unchanged at 25 °C, and the initial value of the light intensity of each unit is 1000 W/m². The system simulation duration is set to 10 s, and the whole process is divided into three stages: In the first stage (0~3 s), the light intensity of the three units remains unchanged at 1000 W/m². In the second stage (3~6 s), when t = 3 s, the light intensity of unit 2 and unit 3 drops from 1000 W/m² to 800 W/m² and 700 W/m², respectively, and the light intensity of unit 1 remains unchanged at 1000 W/m². In the third stage (6~10 s), when t = 6s, the light intensity of unit 1 drops from 1000 W/m² to 900 W/m², and the light intensity of unit 2 and unit 3 remains unchanged at 800 W/m² and 700 W/m².

The simulation experiment results are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, and the relative analysis is given as follows:

(1)

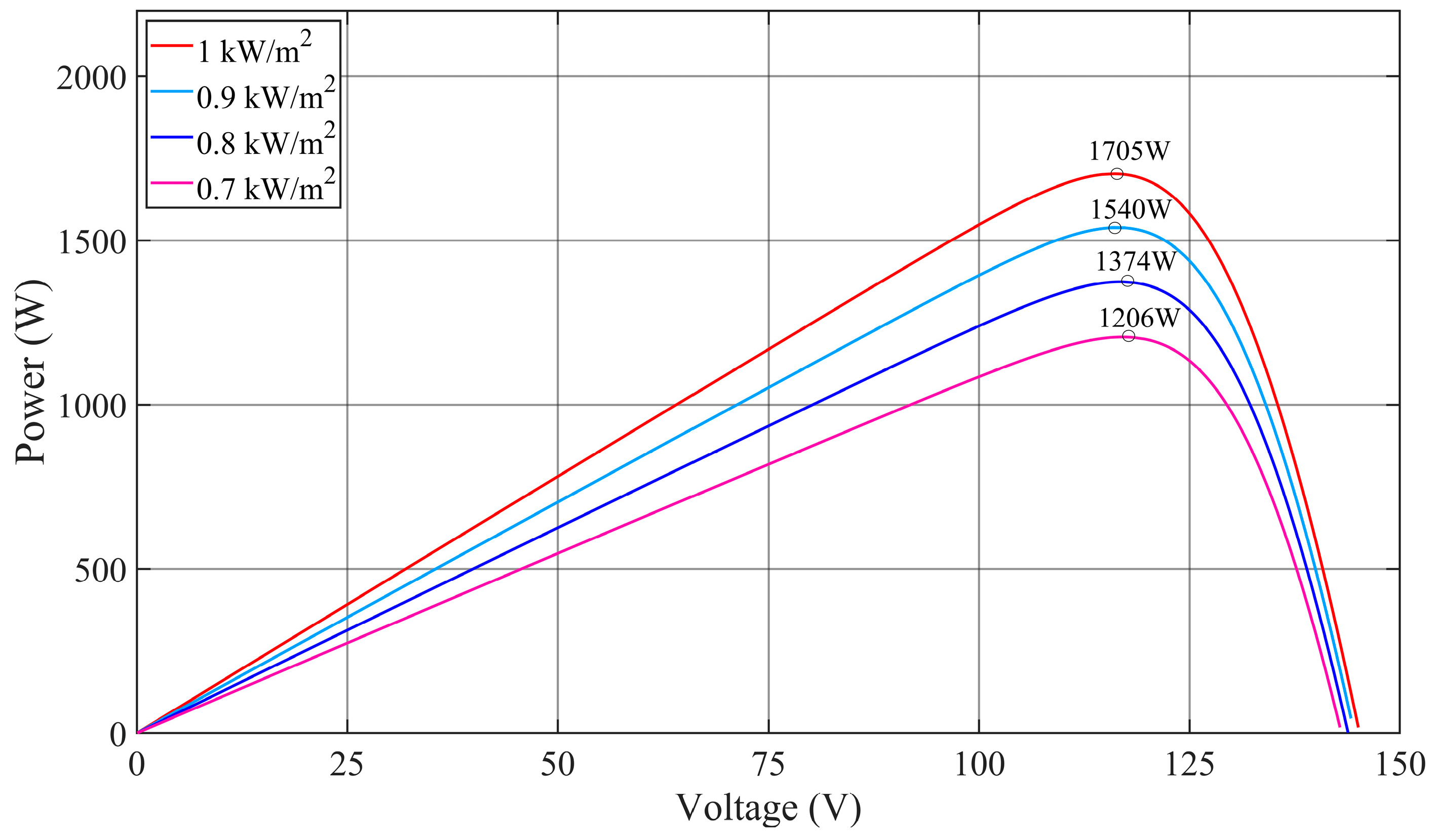
Output active power. It can be seen from Figure 4 that, in the first stage, the light intensity of the three units is the same (1000 W/m²), therefore, the output active power of each unit is the same, given as $P_1$ = $P_2$ = $P_3$ = 1681 W. In the second stage, when t = 3 s, $P_2$ and $P_3$ immediately decrease, and finally reach a new steady state, there, $P_2$ = 1356W, $P_3$ = 1186 W, and the steady-state value of $P_1$ is not affected by unit 2 and unit 3 and does not change; $P_1$ = 1681 W still. In the third stage, when t = 6 s, $P_1$ immediately drops and eventually reaches a new steady state, with $P_1$ = 1534 W. The steady-state values of $P_2$ and $P_3$ are not affected by unit 1 and are the same as the steady-state values in the second stage, which are $P_2$ = 1356 W and $P_3$ = 1186 W. It can be seen from Figure 3 that the maximum output power of the PV modules at 1000 W/m², 900 W/m², 800 W/m², and 700 W/m² is 1705 W, 1540 W, 1374 W, and 1206 W, respectively. Considering the power loss in the inverters and lines, it can be considered that the active power output of these units realize the real-time tracking of the maximum power of PV arrays, and each unit does not affect each other.

Figure 4. Output active power of the three series-connected units.

Figure 4. Output active power of the three series-connected units.

(2)

Output reactive power. It can be seen from Figure 5 that in the first stage, the reactive power output of each unit is the same, with $Q_1=Q_2=Q_3$ = −620 Var, which realizes the reactive power sharing between these units. In the second stage, at steady state, $Q_1$ = −2283 Var, $Q_2$ = −1888 Var, and $Q_3$ = −1677 Var. In the third stage, at steady state, $Q_1$ = −2382 Var, $Q_2$ = −2152 Var, and $Q_3$ = −1911 Var. The above results agree with Equation (11).

Figure 5. Reactive power of the three series-connected units.

Figure 5. Reactive power of the three series-connected units.

(3)

Frequency. As can be seen from Figure 6, the output frequencies of all series units converge to the grid frequency (50 Hz) in steady state with a deviation range of no more than 0.05 Hz. The output voltage frequency is self-synchronized with the grid frequency.

Figure 6. Frequency of the three series-connected units.

Figure 6. Frequency of the three series-connected units.

(4)

DC side voltage of the inverter. It can be seen from Figure 7 that despite the change in light intensity, the DC side voltage $u_{dc1}~u_{dc3}$ of all series inverters can converge to the reference value (200 V) quickly, and the voltage ripple does not exceed 2 V, which verifies the effectiveness of Equation (5) for the DC side voltage regulation of the inverter.

Figure 7. DC side voltage of the three series-connected units.

Figure 7. DC side voltage of the three series-connected units.

(5)

Output voltage and current. The common output current and inverter output voltages at different stages are shown in Figure 8. It can be seen from Figure 8a that in the first stage, because the light intensity is the same, the amplitude (V₁ = V₂ = V₃ = 95.8 V) and phase of the output voltages u₁, u₂, and u₃ are the same. In the second stage, only the light intensity of units 2 and 3 change. It can be seen from Figure 8b that the phase of u₁, u₂, and u₃ is still the same, the amplitude V₁ remains unchanged, but V₂ and V₃ have changed, which are given by V₁ = 95.8 V, V₂ = 77.3 V, and V₃ = 67.6 V. In the third stage, only the light intensity of unit 1 changes. It can be seen from Figure 8c that the phases of u₁, u₂, and u₃ are still the same, and the output voltage amplitudes are V₁ = 87.5 V, V₂ = 77.3 V, and V₃ = 67.6 V. The result data above satisfy Equations (6) and (10), which are consistent with the analytical conclusions of Section 3. As the output voltage amplitude of each unit decreases, the power factor of the system also decreases, which is reflected in Figure 8 as the phase difference between the output current i_o and voltage u₁ (or u₂, u₃) becomes larger.

Figure 8. Steady-state output current and voltage under different operating conditions.

Figure 8. Steady-state output current and voltage under different operating conditions.

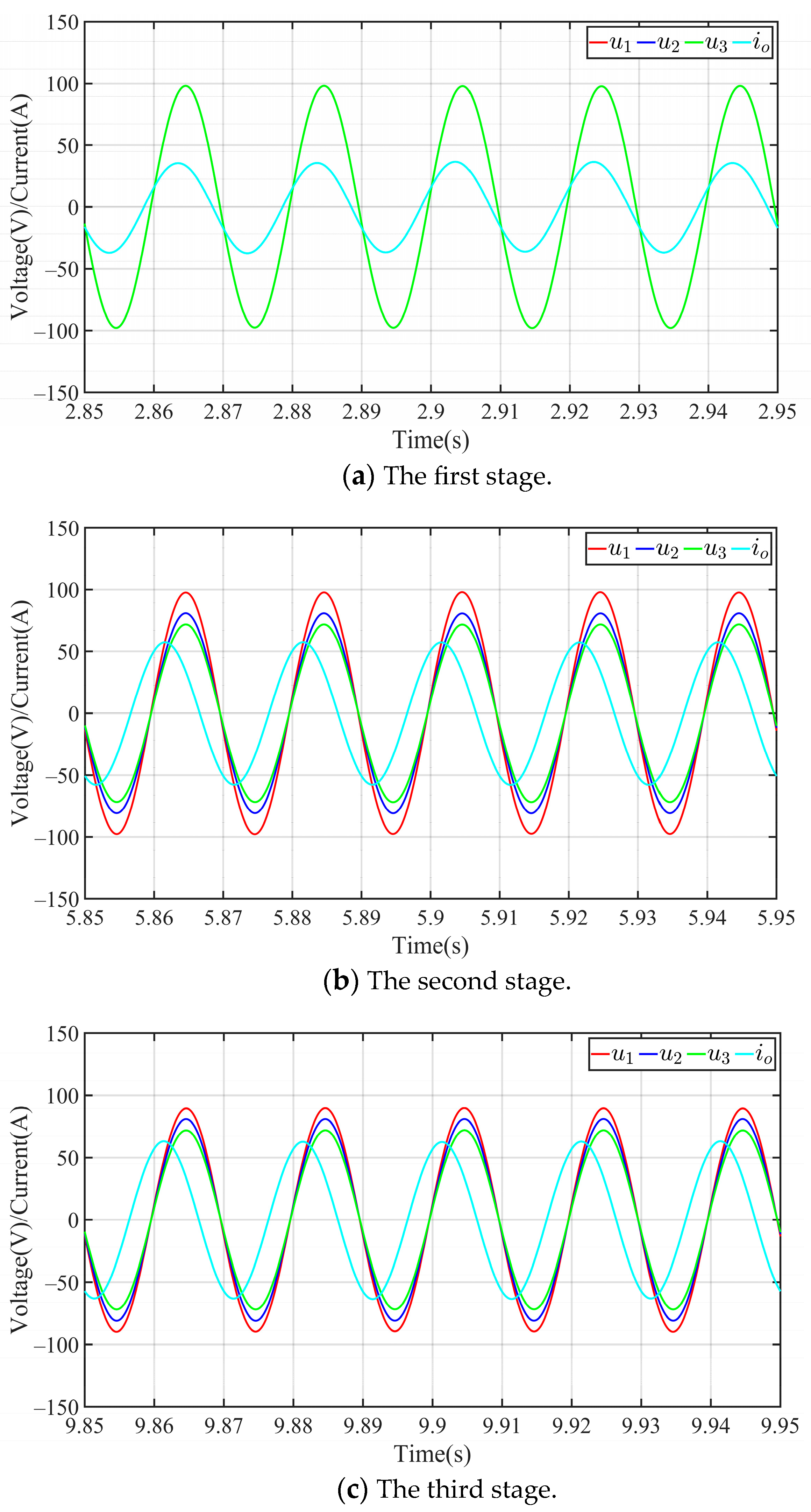
(6)

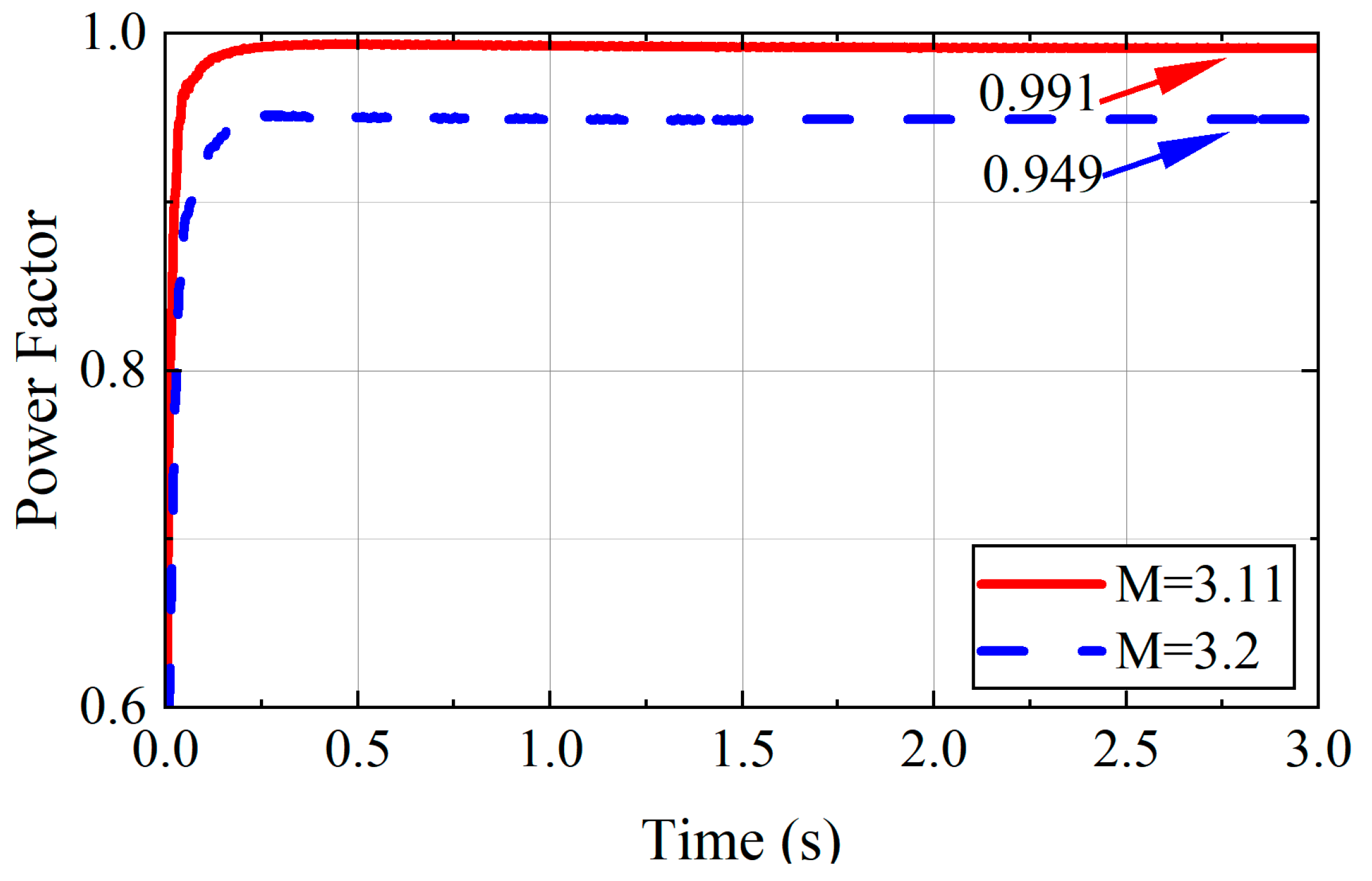
Power factor. To verify the relationship between the power factor of the system and the M value, a comparative test is carried out in the first stage of simulation. It can be seen from Figure 9 that when M decreases from 3.2 to 3.11, the power factor increases from 0.949 to 0.991. It shows that the value of M affects the size of the power factor, and the relationship is inversely proportional, which is consistent with the analysis conclusion in Section 5 of this paper.

Figure 9. Power factor in the first stage with M = 3.11 and 3.2.

Figure 9. Power factor in the first stage with M = 3.11 and 3.2.

In summary, the simulation results are consistent with the previous analysis in this paper, which verifies the correctness and effectiveness of the proposed decentralized control strategy for series-connected inverters.

7. Conclusions

In this paper, a decentralized control strategy for series-connected single-phase two-stage grid-connected PV inverters is proposed, which only requires local information to achieve a consistent phase and frequency of the output voltage of each unit and self-synchronization with the power grid. Each unit independently implements MPPT with efficiencies ($P_i/P_{max}$) up to 98.6%. Since the output voltage amplitude of each unit is proportional to the actual output power, inverters with different generating capacities can be connected in series.

However, the disadvantage of this strategy is that the power factor of the system decreases when the light intensity is low, because the PV output power reduces at this time, and the inverter output voltage amplitude drops according to Equation (6). Similarly, another restriction is that the amplitude of the power grid cannot change too much, which also brings power factor and stability issues. As M is a constant, when the grid amplitude increases, the power factor becomes lower; when the grid amplitude decreases, the stability decreases. The next step is to study the adaptive adjustment method of the M value based on power factor feedback, and improve the system power factor by reasonably adjusting the value of M.