Development of an Electric All-Wheel-Drive Simulation Model Used to Test Torque Distribution Algorithms

Abstract

The paper describes the developed curvilinear motion simulation model for a vehicle with two traction electric motors moving on a solid surface used to study the dynamic properties of a wheeled vehicle and to subject the developed methods to virtual testing. The simulation model of the electric all-wheel drive vehicle is carried out in the Simcenter Amesim environment to account for the dynamic characteristics and features of the vehicle. The simulation model was developed based on the drawn requirements while the assumptions were justified. Inertia characteristics, tire characteristics, suspension elements, grip characteristics, and surface and air resistance were considered, as these factors affect the vehicle longitudinal and transverse dynamics. The article presents the model implemented in the “Labcar” system and confirms its adequacy by comparing it with the data obtained during the full-scale prototype tests. The bench and range tests of a test vehicle with electric transmission equipped with a measuring complex confirmed the adequacy of the developed model. The results of comparative tests allow for the conclusion that the developed model complex is suitable for modeling purposes, including studying, debugging and initial calibrations of the algorithm of torque distribution on the driving axles of all-wheel drive electric vehicle.

1. Introduction

Four-wheel drive electric vehicles and vehicles with combined electric powertrains are currently gaining popularity. Most of them have schemes where torque is independently generated by electric motors on the front and rear axles or on each wheel. In this case the front and rear axles of the electric vehicle are not mechanically connected to each other, except through a support surface. The automatic torque distribution to the axles or wheels in this case becomes a necessity, rather than an additional system to improve the performance.

Active torque distribution plays an important role in maximizing dynamic performance, especially in challenging road situations such as cornering on the verge of drifting or driving on surfaces with low or variable adhesion coefficient. Therefore, the influence of active distribution on stability and controllability is being actively investigated.

The distribution of the requested torque over the electric motors has been studied by Leonardo De Novellis [1,2,3,4,5,6,7], Perdo Antunez [8,9] Mattis Klomp [10,11,12] and others. Despite extensive research performed, most of the studies concentrate on the power distribution control with mechanical transmission mechanisms. Therefore, the methods of controlling power distribution between the driving axles of the vehicle with electric drivetrain are currently under-investigated.

A simulation model is required to investigate the peculiar dynamic properties, stability and controllability of the vehicle, as well as to verify, debug and pre-tune the algorithm of torque distribution over the driving axles of the vehicle [13].

In [14,15] an analysis of field-oriented torque control (FOC) and prediction (MPC) methods is presented. In [16], virtual vectors and duty cycle control are added to MPC to achieve steady-state performance equivalent to FOC while maintaining fast dynamic response.

The developed control functions are tested using full-scale test benches or a prototype vehicle. The complexity of building full-scale test bench depends on the peculiarities of system tested and can be associated with significant time and financial costs. An error in the algorithm can break down both the test object and the test bench and, in certain cases, poses a threat to the operator himself. Prototype testing increases the possible adverse effects during the approbation of the developed control functions. In addition, certain tests, such as system failure tests, tests of long-term operation at the extreme characteristics of object performance, intentional emergency modes of operation that cannot be performed on a full-scale object due to the potential failure of the system under test.

Such consequences can be minimized by performing a preliminary verification of the developed algorithm. Such a verification is usually performed in several stages [17]:

• MiL-testing (model in the loop)—Testing the control algorithm in a simulation environment, in which a model of the controlled object interacts with the algorithm. It is used to verify the control logic of the object.
• SiL-testing (software in the loop)—Interaction of the controlled object model with the program code including the logic of controlling this object. It is used to check the program code development and the possibility of hardware implementation.
• PiL-testing (processor in the loop)—Interaction of the controlled object model with the simulation of the processor, in which the program code including the object control algorithm is implemented. It is used to verify the processor’s ability to execute the developed control logic.
• HiL-testing (hardware-in-the-loop)—Interaction of the control unit with the controlled object model. It is used to verify the development of the control unit that includes the control logic of the tested system, so-called hardware-software modeling.

The present research features the MiL and HiL testing stages, describes the methodology of development and the composition of the simulation model as well as the structure of the hardware and software stand, and provides the results confirming the adequacy of the model.

The requirements to the simulation model are set out with regards to the specifics of the problem being solved. The developed model of the wheeled vehicle dynamics should consider the joint dynamics of the body, power plant and the chassis with sufficient accuracy to conduct virtual runs on non-deformable soils. The model of interaction between the wheel and the supporting base should ensure the absence of restriction, consider the surface traction and resistance characteristics, as these factors significantly impact the vehicle movement.

The advantages of using simulation modeling methods lie in their greater accessibility compared to in-situ tests and in the perfect repeatability of maneuvers, which eliminates the human factor impact. However, none of the models replicates the real-world conditions with sufficient accuracy to eliminate the necessity for in-situ testing.

The scientific novelty of the study lies in the applicability of the developed simulation model for debugging, testing and calibration of the developed new algorithms of torque distribution between the axles of a two-motor electric car, which will improve the directional stability of the electric car and effectively counteract slipping of the driving wheels.

2. Development of the Electric All-Wheel Drive Vehicle Simulation Model

Simcenter Amesim 2019.1 software [17] was used as the model development environment as it features a wide array of elements describing the vehicle motion and allows combining elements of different physical nature (mechanical, electrical, thermodynamic).

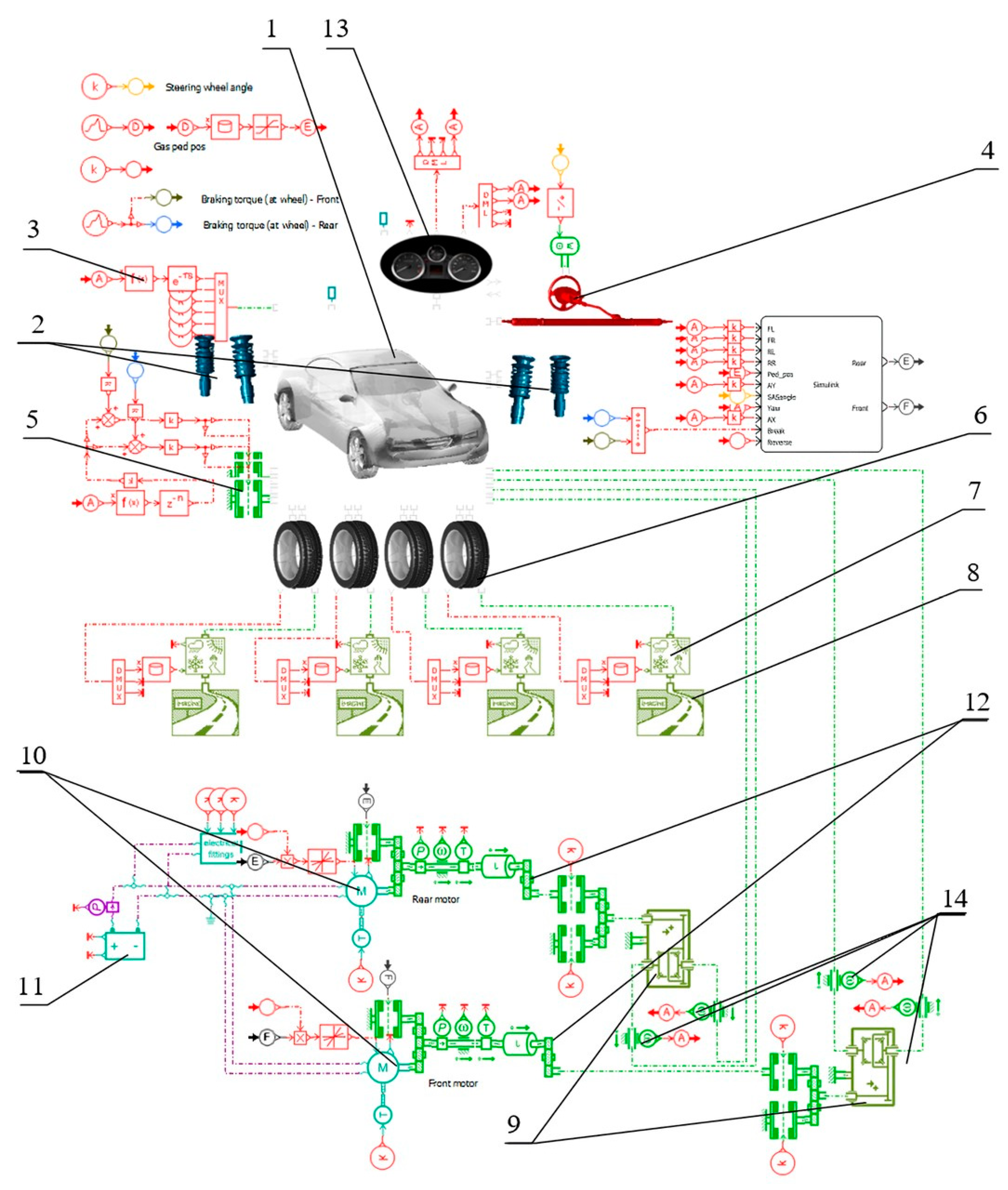
The model is a closed system of elements, each of which contains a mathematical description with the equations of motion. The structure of the model presented in Figure 1 contains:

(1)

a block describing the inertial characteristics of the sprung part of the vehicle and the suspension kinematics;

(2)

a block describing the elastic-damping characteristics of the suspension;

(3)

a block accounting for the aerodynamic drag;

(4)

a steering mechanism;

(5)

a sub-model of braking elements;

(6)

a sub-model of the wheel and the wheel contact with road surface;

(7)

a block that accounts for the traction properties of the road surface;

(8)

a road surface profile block;

(9)

a differentials submodel;

(10)

an electric motors submodel;

(11)

a high voltage battery submodel;

(12)

a gearbox submodel;

(13)

vehicle center of mass velocity and acceleration sensors;

(14)

wheel speed and rotation sensors.

The central element of the model is a block describing the kinematic relationships of angular and linear velocities with angular and spatial coordinates derived from the equations of relationships between different coordinate systems. It accounts for the inertial characteristics of the sprung part and suspension kinematics. The block describes 15 degrees of freedom that determine the state of the car. These, as shown in Figure 2 [17], are yaw angle, longitudinal angle, roll angle, displacement of the center of mass relative to the three axes (longitudinal, transverse, vertical), vertical displacement of the rotation axes of the four wheels, rotation of the four wheels relative to their own rotation axes, and displacement of the steering rack relative to the body along the transverse axis.

The displacement of the vehicle’s sprung mass is calculated using the basic equation of motion:

$$M\ast \overline{\ddot{x}}=\overline{Q}+\overline{C}$$

(1)

where: M—generalized inertial characteristics matrix [15 × 15]; $\overline{x}$—generalized vector of accelerations by degrees of freedom [1 × 15]; $\overline{Q}$—generalized external and internal forces; $\overline{C}$—generalized inertial forces.

The mathematical description of the suspension is based on the simplified scheme shown in Figure 3 [5], the movement of the wheel axis of rotation relative to the body is described in a coordinate system referenced to the car body (x₁, y₁, z₁).

A₁ is a fixed point on the body, A₁′ is the point moving along the z₁ axis in the body coordinate system, A₂ is the point corresponding to the real wheel center.

The total linear displacement of the wheel rotation axis relative to the body is determined using the empirical relationships, depending on the relative vertical displacement:

$$z_{\mathrm{OT}}=A_1-A_1^{\prime }$$

(2)

and the transverse displacement of the steering rack $y_{\mathrm{pp}}$. The angular displacement of the rotation axis of the relative body wheel is also described using the empirical relationships:

$$\delta =f\left(z_{\mathrm{OT}},y_{\mathrm{pp}}\right)$$

(3)

The steering mechanism model represents the conversion of the rotary motion of the steering column to the translational motion of the steering rack. At the heart of this element is a rack-and-pinion with three input and three output variables related by expressions:

$$y_{\mathrm{pp}}=\left({\theta }_2-offset\right)·r$$

(4)

$$v_{\mathrm{pp}}=w_2·r$$

(5)

$$T_2=F_1·r$$

(6)

where: $y_{\mathrm{pp}}$—translational movement of the steering rack, (м); $v_{\mathrm{pp}}$—translational speed of the rack (m/s); ${\theta }_2$—angular displacement of the steering column, (°); offset—pinion angle at zero rack displacement, (°); $w_2$—angular speed of the pinion, (r/min); r—the radius of the dividing circle of the pinion, (mm); $F_1$—force on the rack (N), $T_2$—torque on the pinion (Nm).

The block describing the elastic-damping characteristics of the suspension generates a vertical force calculated from the displacement and velocity of point A1′ relative to point A1 according to the scheme in Figure 3.

$$F=F_{spr}+F_{dmp}$$

(7)

where:

$$F_{spr}=f\left(A,A1\right)$$

(8)

The elastic force, which is determined by two coefficients—spring stiffness and baffle stiffness (N/m).

$$F_{dmp}=f\left(V_{z1}\right)$$

(9)

Damping force is determined by the empirical characteristics of the target prototype shock absorbers. The aerodynamic drag is applied to the center of mass and is calculated as follows:

$$F_{aero}=\frac{1}{2}\rho S{C}_I{V}^2$$

(10)

where: V—current air velocity relative to the car, (m/s); $\rho$—air density, (kg*m³); S—frontal surface area, (m²); C—air resistance coefficient.

Braking is performed in the model by an element generating a rotational dry friction torque. The dry friction torque is calculated by the speed controller. The braking torque is the same for all wheels, ABS and ESC are not considered.

Since the wheel model does not take the rolling resistance into account, the rolling resistance torque is implemented by means of an additional friction torque. Thus, the total torque on the brake pads is:

$$M_{bp}=M_{brake}+M_{res}$$

(11)

where: $M_{brake}$—braking torque requested by the speed controller, (Nm); $M_{res}$—rolling resistance torque, (Nm).

$$M_{res}=0.01+(5·{10}^{-6}·V^2)·M·g·R_D \#$$

(12)

where: V—current vehicle speed, (m/s); M—vehicle mass, (kg); g—acceleration of free fall, (m/s²); $R_D$—dynamic radius of the wheel, (m).

To mathematically describe the dynamics of the interaction between the tire and the road, the Magic Formula by Pasejka [18] was used, which is generally described by the following expression:

$$R_i\left(x\right)=D_i\ast \sin \left(C_i\ast arctg\left(B_i-E_i\left(B_i-\arctan \left(B_i\right)\right)\right)\right)+S_v$$

(13)

where B, C, D, E, S are empirical coefficients.

A typical characteristic described by the Pasejka’s formula is presented in Figure 4 [19].

This expression defines the dependence of the longitudinal reaction on the longitudinal slip $R_x\left(S_x\right)$ and the transverse reaction on the lateral drift angle $R_x\left(\alpha \right)$. The drift angle of each wheel $a_i$ is calculated according to the kinematic scheme of the turn shown in Figure 5 by the following expression:

$$a_i={\delta }_i-arctg\left(\frac{V_{CoGy }\pm {\omega }_z\ast l_i}{V_{CoGx }\pm {\omega }_z\ast \frac{b}{2}}\right)$$

(14)

where: ${\delta }_i$—steering angles of the steered wheels; $l_i$—longitudinal distance from the center of mass of the car to the wheel axis; and $b$—axle track (equal value for front and rear axle is assumed here.

Despite the disadvantages of the formula, i.e., its complexity and the need for many empirical coefficients, the Magic Formula provides the most accurate description of how the tire behaves when in contact with the road surface. The coefficient D is determined by the tire traction, so this formula allows simulating the motion with variable traction depending on the simulation time or contact patch coordinate using a signal library.

The differential model describes the relationship between the angular velocities of the input shaft and the half axles as follows:

$$w=\frac{1}{2}\left(w_1-w_2\right)$$

(15)

where: $w$ is the angular velocity of the input shaft, (rpm); and $w_1$ and $w_2$—angular velocity of semi-axes, (rpm).

The mathematical model of a permanent magnet synchronous electric motor with vector control of the actuators is used as a model of the electric drives [18].

The battery model is based on a lithium battery cell model. The charge and discharge characteristic of the cell are obtained experimentally. The insulation control model is included in the battery model [20].

The model described above and implemented in Amesim after its validation can be used to conduct the MIL test of the developed moment distribution modes implemented in Matlab Simulink. For this, Amesim provides a co-simulation mode. In this mode, the simulation of the car model is performed in Amesim solver with a variable step, and the control model is performed in Simulink solver with a fixed step corresponding to the frequency of the target control unit.

3. Experimental Setup

Testing of the compiled software based on the developed algorithms in the HIL mode was carried out on the LabCar hardware-programming complex. The LabCar real-time bench (Figure 6) allows testing and validation of a wide range of automotive ECUs using numerical simulation models that mimic the physical behavior of the system under test [21].

To test the algorithms being developed as part of the control unit on the bench in HIL mode, it is necessary to assemble the project on the experimental setup, which includes:

(1)

a vehicle model;

(2)

a script simulating the start-up logic of the high-voltage system components (battery, inverters, converters), C-code;

(3)

CAN-bus simulator, realized with the help of LabCar V 4.1 software;

(4)

a block of settings of the HPC hardware I/O modules;

(5)

a Simulink constraint calculation model for the drive and battery models;

(6)

a Simulink driver model (control of gas and brake pedals, a steering pad, power and ignition terminals, a selector, as well as the possibility of the vehicle movement according to one of the selected driving cycle—WLTC, NEDC, FTP, ECE.

The HPC scheme for HIL testing is presented in Figure 7. The compiled project is integrated into the real-time test bench. The communication with control unit containing the implemented tested algorithm, is performed by an electrical harness. Its response part is connected to the Breakout Box, which is a hub of electrical wiring. It allows the user to perform the necessary electrical breaks and measurements by communicating with the front part of the device. The Breakout Box is connected to the hardware pins of the bench—I/O modules capable of receiving and generating digital-to-analog and analog-to-digital signals, high-frequency PWM signals (up to 100 kHz), simulate and process CAN messages. The experiment is controlled through the interaction with the graphical environment (i.e., the experiment environment).

The Figure 8 shows the general structure of the developed function of torque distribution, which allows by active redistribution of torque between the axles of the electric car to counteract the occurrence of slippage of the leading wheels, to ensure the target character of turning and reduce the risk of loss of directional stability in a turn, including the basic distribution of torque between the driving axles of the electric car, yaw and slippage rate control, and the final formation of torque for the electric motors of the front and rear axle of the car.

The base distribution unit 2 includes direct-coupled regulators 3 and 4 to divide the requested torque $M_{in}$ into the base torque request values for the front and rear axle $M_{i{n}_{front}}$ and $M_{i{n}_{rear}}$ in order to solve the tasks of reducing the probability of slipping of the drive wheels and loss of directional stability and reducing the probability of lateral drift in case of loss of directional stability. Also, the base distribution controller 4 adjusts the target character of the vehicle’s turning character. The task of the yaw rate control unit is to determine the state of the curvilinear motion of the vehicle: drift, skid or countersteer, and generate a torque shift request according to the determined state. The yaw rate control unit 5 includes a drift/skid detection function and two controllers: a yaw rate error feedback controller 6 and a steering position direct feedback controller 7, which calculate the corrective values of $M_{Y{C}_{front}}$ and $M_{Y{C}_{rear}}$. The slip control unit 8 includes a drive wheel slip detection function and a wheel speed difference error feedback controller 9, which calculates the corrective values of $M_{S{D}_{front}}$ and $M_{S{D}_{rear}}$. The total torque requests for the front and rear axle are checked by the external constraints unit 10, which includes TCS and ESC constraints, after which the final torque request for the front and rear electric motor $M_{Front}$ and $M_{Rear}$ is generated.

The method of reducing the likelihood of slipping is implemented using a direct linkage controller that distributes torque in proportion to the vertical reactions at the front and rear axles, which are estimated from the longitudinal acceleration of the vehicle’s center of mass. This method is based on the fact that with unknown traction coefficients under the front and rear axle, the probability of slip occurring on the front or rear axle will be inversely proportional to the corresponding vertical reactions.

The method for detecting drive wheel slip is based on a comparison of the expected $∆V\_exp$ and measured $∆V\_m$ axle velocity differences. The expected axle speed difference in a turn is determined using an empirically derived response surface. When slipping of one of the active axles is detected, the torque is redistributed to the non-slipping axle by means of a PID controller, which is characterized by the inclusion of a correction link in the control scheme to counteract auto oscillations. A method for detecting auto oscillations, based on determining the levels of oscillations at the input and output of the PID controller.

The method of reducing the probability of loss of directional stability is based on the use of a regulator with a direct link on lateral acceleration, which, with the help of an empirically obtained characteristic, generates a request for the distribution of torque which provides the target neutral character of the turning character.

The method for determining the directional stability state of the vehicle is based on a comparison between the expected ${\omega }_{z\_exp}$ and the measured ${\omega }_{z_m}$ yaw rate. The expected yaw rate is calculated from the wheel speed and steering position signals according to the expression:

$${\omega }_{z_{\exp }}=V_x·{\theta }_{\mathrm{steer}}·i_{\mathrm{steer}}·\frac{1}{1+K_{\mathrm{s}}·V_x^2}$$

(16)

where: $K_{\mathrm{s}}$—constant determining the character of vehicle turning character; $i_{\mathrm{steer}}$—steering gear ratio; ${\theta }_{\mathrm{steer}}$—steering angle; $V_x$—longitudinal velocity of the car, which is determined by bringing the measured value of the velocity of the slowest wheel to the center of mass of the car.

Steady motion condition:

$$\left|{\omega }_{z\_exp}-{\omega }_{z_m}\right|<{\omega }_{z_{to{l}_{ust}}}\hspace{1em}and\hspace{1em}\left|{\omega }_{z\_exp}-{\omega }_{z_m}\right|<{\omega }_{z_{to{l}_{ost}}}$$

(17)

where: ${\omega }_{z_{to{l}_{ust}}}$—is the allowable excess of the expected yaw rate over the measured yaw rate, ${\omega }_{z_{to{l}_{ost}}}$—permissible excess of the measured yaw rate over the expected yaw rate.

The condition of drift registration:

$$\left|{\omega }_{z\_exp}\right|-\left|{\omega }_{z_m}\right|>{\omega }_{z_{to{l}_{ust}}}$$

(18)

Skid registration condition:

$$\left|{\omega }_{z\_exp}\right|-\left|{\omega }_{z_m}\right|<{\omega }_{z_{to{l}_{ost}}}$$

(19)

Countersteering registration condition:

$$\left|{\omega }_{z\_exp}\right|-\left|{\omega }_{z_m}\right|>{\omega }_{z_{cst}}$$

$${\omega }_{z_{exp}}·{\omega }_{z_m}<0$$

(20)

where ${\omega }_{z_{cst}}$—is the threshold value of counter-rotation registration.

4. Validation

Field tests were conducted to prove the consistency between the real and simulation results. The in-test control signals, i.e., the selector position, brake and accelerator pedal position, steering wheel position, and the driving parameter signals were recorded: vehicle speed, torque of each drive, rotor speed, lateral acceleration of the vehicle, yaw rate.

Further on, the recorded control signals are set as input signals for the simulation model. Its results become the output signals of the motion parameters, which are compared to the motion parameters during field tests.

The standard deviation calculated by the formula [22] is used as an accuracy criterion for the results:

$$S_0=\sqrt{\frac{1}{N-1}{\displaystyle \sum }_{t=1}^n{\left(x_i-\stackrel{=}{x}\right)}^2}$$

(21)

where: N—sample volume; i is the sample number; x_i—sample element or numerical value at the step:

$$x_i=a_{xmodeli}-a_{xexperti}$$

(22)

$\overline{x}$—normalized mean arithmetic error.

The modelling outcomes are compared to those of the field tests by reproducing the signals recorded during the Amesim tests. The structural scheme of reproduction and comparison of the results of virtual and real races is presented in Figure 9: (1) the source of the recorded experimental data; (2) the recorded control signals, which are used as inputs for the simulation model; (3) the motion parameters signals obtained as a result of modeling; (4) calculation of the standard deviation.

The test runs verifying the operation of the developed modeling system were recorded with the target prototype on a drum stand at the test ground.

The test vehicle is a prototype car with the electric propulsion system, the main characteristics of which are presented in

Table 1. The test object main characteristics.

Motor Type	electric drive
Location	one on the front axle and one on the rear axle
Total power	380 kW
Curb weight	3943 kg

.

4.1. Measurement Equipment

The following control measuring equipment was used during the prototype testing: ADMA Speed satellite navigation system, laser speed sensors ISD5, inertial sensors IMU, strain gauge wheel hubs. Figure 10 shows the installation scheme for the ADMA Speed SNS antenna and the ISD5 and IMU sensors with plotted dimensions (mm) that allow positioning the measurement points relative to the center of gravity (“CoG”) of the vehicle, its longitudinal axis of symmetry and the wheel axles.

4.2. WLTC Race

Standardized driving cycle tests provide valuable information on the vehicle performance as well as the performance of the prototype systems [23,24]. The Worldwide harmonized Light vehicles Test Cycle (WLTC) is divided with short stops into 4 phases: acceleration of the vehicle to 56.5 km/h, to 76.6 km/h, to 97.4 km/h, to 131.6 km/h. The races in this cycle are recorded on a drum stand. The prototype mounted on drums is shown in Figure 11.

The test results and simulation results compared are shown in Figure 12. The calculated errors relative to the simulation and in-situ test results were:

(1)

TC speed = 2.1%;

(2)

Torque on the front motor 0.6%;

(3)

Rear motor torque 1.05%.

4.3. Lane Change Maneuver on Dry Asphalt

The lane change maneuver was performed on the dry asphalt road. The results of the run and the simulation results compared are shown in Figure 13.

The calculated error relative to the results of modeling and field tests was:

(1)

Vehicle speed = 2.4%;

(2)

Lateral acceleration of the vehicle 9.8%;

(3)

Vehicle yaw rate 9.1%.

4.4. Lane Change Maneuver on Wet Polymer Pavement

The “lane change” was performed on a wet road surface covered with polymer compound, coefficient of adhesion 0.45...0.55. The maneuver in action is presented in Figure 14. The results of the run and simulation results are compared in Figure 15.

The calculated error relative to the simulation and field test results were:

(1)

Vehicle speed = 2.2%;

(2)

Lateral acceleration of the vehicle 11.9%;

(3)

Vehicle yaw rate 12.8%.

4.5. Follow a Trajectory with Variable Speed Up to 80 km/h

The test run is performed on dry asphalt, at speeds that do not result in drifting/skidding. The test runs trajectory curves are presented in Figure 16. The comparison of the test run and the simulation results is presented in Figure 17.

The calculated error relative to the simulation and field test results were:

(1)

Vehicle speed = 2.5%;

(2)

Lateral acceleration of the vehicle 10.3%;

(3)

Vehicle yaw rate 5.4%.

5. Conclusions

The developed model considers the design features of the vehicle electric transmission and the inertial and geometric characteristics of the target prototype. It also allows exploring the dynamic properties, stability, and controllability of the all-wheel drive electric vehicle, as well as checking, debugging, making preliminary adjustments to the algorithm of torque distribution on the driving axles of the electric vehicle, and determining the primary empirical characteristics.

The field tests have proved the adequacy of the developed model of the prototype all-wheel drive vehicle with an electric transmission equipped with a measuring complex. The adequacy of the model was assessed with bench and range tests. The results support the conclusion that the developed model complex is suitable to achieve the modeling purposes, including the research, debugging, and initial calibrations of the algorithm of torque distribution on the driving axles of all-wheel drive electric vehicle. Modeling errors depending on test conditions are presented in

Table 2. RMS relative error of the simulation results.

	CoG Velocity	Transverse Acceleration	Yaw Velocity
WLTC cycle (Bench)	2.1%	-	-
Trajectory	2.5%	10.3%	5.4%
Oversteer on dry asphalt	2.4%	9.8%	9.1%
Oversteer on wet polymer	2.2%	11.9%	12.8%

.

Hence, the developed mathematical model is proven adequate. The achieved accuracy allows conducting the performance analysis and debugging the active torque distribution algorithms using the developed simulation model.