Efficient Allocation and Sizing the PV-STATCOMs in Electrical Distribution Grids Using Mixed-Integer Convex Approximation

Abstract

Photovoltaic (PV) systems are a clean energy source that allows for power generation integration into electrical networks without destructive environmental effects. PV systems are usually integrated into electrical networks only to provide active power during the day, without taking full advantage of power electronics devices, which can compensate for the reactive power at any moment during their operation. These systems can also generate dynamic reactive power by means of voltage source converters, which are called PV-STATCOM devices. This paper presents a convex formulation for the optimal integration (placement and sizing) of PV-STATCOM devices in electrical distribution systems. The proposed model considers reducing the costs of the annual energy losses and installing PV-STATCOM devices. A convex formulation was obtained to transform the hyperbolic relation between the products of the voltage into a second-order constraint via relaxation. Two simulation cases in the two IEEE test systems (33- and 69-node) with radial and meshed topologies were implemented to demonstrate the effectiveness of the proposed mixed-integer convex model. The results show that PV-STATCOM devices reduce the annual cost of energy losses of electrical networks in a more significant proportion than PV systems alone.

1. Introduction

1.1. General Context

Improving the operating performance of electrical distribution systems (EDSs) poses a permanent challenge that the operators (i.e., utilities) must address to guarantee efficiency, quality, safety, and reliability for all end-user in medium- and low-voltage applications related to the electricity service [1,2]. EDSs are particularly complex networks due to their extension (from tens to hundreds of kilometers) in different zones, such as urban and rural zones. They are typically constructed using tree topologies (i.e., radial configurations) [3], as this reduces complexities regarding the coordination of protective devices [4], as well as the costs of investment in distribution lines [5]. However, even though they are cheaper than meshed networks, they produce significantly higher energy losses in comparison [6], which implies that EDS companies must resort to efficient approaches in order to improve their electrical performance, using compensation technologies and grid reconfiguration alternatives [7,8].

Different alternatives to enhance the electrical operation of distribution grids are available in the scientific literature. The improvement alternatives applicable to distribution networks include grid reconfiguration and optimal load balancing [9,10], the optimal integration of distributed generators [11,12], the efficient integration and operation of energy storage devices [13,14], and the effective integration of reactive power compensators [15,16,17]. Considering these options, EDS companies must select the best subset of options for implementation as a function of their budget and planning, operation, and maintenance projections.

1.2. Motivation

To contribute to efficient alternatives for improving performance in EDSs and allow these systems to deal with the new operation paradigm in the context of active EDSs, the subject of this study was the compensation of apparent power (i.e., active and reactive power simultaneously) in EDSs. As previously mentioned, there are multiple alternatives to improve the performance of EDSs, which include the integration (i.e., placement and dimension) of renewable energy generations (mainly photovoltaic (PV) sources) [18] and shunt compensators of the reactive power [19]. The primary idea of this study is to explore the possibility of dynamically apparent power (i.e., active and reactive power simultaneously) in EDSs, considering PV generation sources. The main advantage is that the power electronic converters of said sources can be redesigned to inject reactive power with variable power factors without the need for additional compensation systems, as the forced commutation switches within the power electronic converters that interface the PV generating plants with the AC network can decouple the active and reactive power variables [20].

This research’s primary motivation consists of presenting a new mathematical modeling alternative for compensating active and reactive power in EDSs. This is achieved by incorporating the concept of static distribution compensators (STATCOMs) into PV generation units. These are known in the specialized literature as PV-STATCOM devices [21]. This dynamic active and reactive power compensation alternative is an excellent opportunity for distribution companies to address the significant integration of renewable generation systems. A controlled injection of reactive power can help improve voltage profiles, reduce expected energy losses, and enhance the feasibility of connecting new users to the existing grid infrastructure [22].

1.3. Literature Review

The specialized literature has extensively explored the simultaneous compensation of active and reactive power in EDSs using PV-STATCOM devices. This section analyzes the main references in this research topic. The authors [23] presented the integration and design of PV-STATCOM devices in electrical transmission systems in Northern Cyprus. This network consists of 23 substations that provide 345 MW. At the same time, the system contains two different voltage levels, i.e., 132 kV and 66 kV. To design the PV-STATCOM systems, empirical information about the network is used. The authors consider two objective functions: minimizing energy losses and minimizing investment costs. The problem is decoupled into location and sizing issues. A power loss index is implemented to define the allocation of PV-STATCOM devices, while the sizing of these devices is calculated using an adaptive particle swarm optimizer. Comparative results with two algorithms, namely bee colony optimization and lightning search, demonstrate the effectiveness of this solution methodology.

Ref. [24] proposed the optimal location of PV generation plants and STATCOMs in a specific section of an EDS in South Kerman. The network in question operates with a capacity of 20 kV with 61 nodes. The objective functions considered are improving the voltage profile and minimizing the total power losses in the grid. Analytical voltage and loss-sensitive indices are used to identify the best placements for the PV generators and the STATCOM devices. A particle swarm optimization (PSO) approach is utilized to determine the compensation devices’ sizes optimally, aided by probabilistic power flow and Monte Carlo simulations. The results are interesting in terms of improving voltage profiles and reducing power losses. However, no validations and comparisons with different optimization approaches are provided to confirm these achievements.

Ref. [22] proposed applying the hunter-prey-based algorithm to define the optimal placement and dimensioning of PV-STATCOM devices in two EDSs, which are IEEE 33-node and 69-node distribution networks. The study aims to reduce grid power losses and enhance grid voltage profiles. According to their numerical results in two grids, there is a reduction in expected power losses of more than 55%, and the voltage profiles report improvements higher than 42% compared to benchmark cases. The effectiveness of this optimization algorithm is tested against different combinatorial optimizers.

Ref. [25] presented a combination of the PSO algorithm and the optimal power flow problem to determine the optimal integration of PV plants and STATCOM devices in power systems. The test system used was the IEEE 30-bus system, which contains 132 or 33 kV buses. The work presents a multi-objective analysis that considers the simultaneous minimization of overall losses and voltage deviation, which works as a voltage stability index. This work presented numerical results on the IEEE 30-bus network using the MATPOWER tool 7.1 for MATLAB 2020a. The proposed optimizer validated its effectiveness compared to the reference case. However, no comparisons with other optimization tools are provided.

Additional works related to implementing PV-STATCOMs and PV plants and STATCOMs include various approaches such as an exhaustive search algorithm [26] and the artificial rabbit optimization approach [27], which were evaluated in the 33-bus system, while the tabu search algorithm used to locate and size STATCOM presented in [28] was tested in a version modified of the IEEE 300-bus test system. A mix of differential evolution and harmonic search for the optimum location of STATCOM in the IEEE 30-bus system was described in [29].

The literature mentioned above has two main characteristics. Firstly, it deals with the issue of determining the best location and size of PV-STATCOM devices using combinatorial optimization methods. Secondly, the most common goals are to minimize power losses and investment costs and enhance voltage profiles. Currently, the focus is on combining combinatorial optimizers with power flow and optimal power flow tools. This approach allows for creating accurate mixed-integer nonlinear programming (MINLP) models through sequential programming. However, efficient solutions to this optimization problem require convex approximations, the research gap this study aims to address. Unlike some solvers that can directly solve MINLP problems (non-convex), they have problems since they cannot guarantee the global optimum. For this reason, we focus on convex formulations that can ensure the global optimum in any convex problem.

1.4. Contributions and Scope

Based on the review provided above, this research adds the following contributions:

i.

This study presents a reformulation of the exact MINLP model that represents the problem of optimally integrating PV-STATCOM devices in EDSs. The model uses a mixed-integer second-order cone programming approach, which offers the main advantage of analyzing radial and meshed grids. This eliminates the need for heuristic algorithms to decrease the size of the feasible region.

ii.

An analysis of the operation of the PV-STATCOM devices against PV sources that operate with a unitary power factor is presented. This analysis shows that PV-STATCOM devices minimize network operating costs by a higher percentage. This is because these devices dynamically inject active and reactive power based on grid requirements.

It is essential to mention that the work by [30] has presented the optimal integration of PV-STATCOM devices in EDSs using a MINLP model relaxed as a second-order cone programming equivalent run using a commercial optimization tool. However, they reduced the mixed-integer component of the optimization problem by incorporating a sensitive index factor that accounts for power losses. The proposed second-order cone programming model only applies to EDSs with purely radial structures. Considering these aspects, our contribution can be regarded as an improvement in the field of convex optimization. It can be applied to radial and meshed EDSs, eliminating the need for heuristic algorithms to reduce the solution space size.

On the other hand, it is also important to mention that the proposed method can only be applied to distribution network systems since, if it is to be applied to the power system, it is necessary to include the capacitive shunt effect of the transmission lines in the power balance equations.

Regarding the scope of this research, it is important to note the following points:

(i)

The research assumes that the information on constant power load behaviors (i.e., demand–load curves) and the expected behavior of PV generation plants is constant, without any uncertainties. The utility company in the area provides these curves that represent average behaviors based on multiple measurements taken throughout the year.

(ii)

In order to assess the feasibility of the proposed mixed-integer convex approximation on the exact MINLP model, the placement and sizing of PV-STATCOM devices were evaluated using the GAMS software 24.3.3 r48116. This evaluation was performed by treating the binary variables as constants, which transforms the MINLP programming into a nonlinear model equivalent that represents the daily operation of the network.

1.5. Document Structure

This study is organized as follows: Section 2 presents the problem formulation for the efficient allocation and sizing of PV-STATCOM devices in EDSs using a MINLP model in the complex domain. Section 3 outlines the procedure used to transform the MINLP model into an MI convex approximation by representing the product between complex voltages using a second-order cone equivalent representation. Section 4 provides an overview of the IEEE 33- and 69-bus networks used for simulation purposes. Section 5 presents the numerical validations of the proposed mixed-integer convex formulation in both test feeders, considering three cases: a benchmark case without compensation devices, the integration of PV plants with unity power factor, and the implementation of PV-STATCOMs. Additionally, simulations use the meshed configuration for the IEEE 33-bus grid are included. Finally, Section 6 summarizes the main conclusions obtained from this investigation and suggests new possible contributions.

2. Mathematical Problem Formulation

The objective of the research is to minimize the yearly expenses linked to energy losses and the installation of PV-STATCOMs. This involves developing an optimization model in the form of a MINLP model, as it includes binary/integer variables that determine the placement of PV-STATCOM devices. The model consists of continuous variables that represent power flows, nodal voltages, and the size of the PV-STATCOM devices. Figure 1 illustrates a schematic diagram of an EDS with PV-STATCOM devices installed. This can serve as a basis for future studies.

2.1. Objective Function

The primary goal of this research is to incorporate PV-STATCOM systems into EDSs in order to reduce the equivalent annual operating costs z. These costs encompass the decrease in energy losses and the expenses associated with installing PV-STATCOM devices [30]. In order to achieve this, the following objective function is used:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill min& z=z_1+z_2\hfill \\ \hfill z_1& =CT\sum _{t\in \mathcal{T}}\sum _{l\in \mathcal{B}}\left(p_{lt}^s+p_{lt}^r\right)\Delta t\hfill \\ \hfill z_2& =C_{PV-STATCOM}\sum _{m\in \mathcal{N}}{s}_k^{PV-STATCOM}\hfill \end{array}\end{array}$$

(1)

where $z_1$ and $z_2$ represent the annual energy loss costs and the investment costs of the PV-STATCOM devices, respectively; C denotes the average energy loss costs; T is the number of days in a year; $p_{lt}^s$ and $p_{lt}^r$ represent the sending and receiving active power flows in the line connected between nodes k and m at time t, respectively; $\Delta t$ represents the daily time interval analyzed (0.5 h); $\mathcal{T}$, $\mathcal{B}$, and $\mathcal{N}$ are sets that contain all periods of analysis, all network branches, and all network nodes, respectively; $s_k^{PV-STATCOM}$ is the rated size of the PV-STATCOM devices at node m; and $C_{PV-STATCOM}$ represents the installation costs for the PV-STATCOM devices, which can be represented as

$$\begin{array}{c}\hfill C_{PV-STATCOM}=C_{PV}+C_{STATCOM},\end{array}$$

(2)

where $C_{PV}$ is the cost of only installing a PV system, while $C_{STATCOM}$ represents the increase in installation costs of the PV-STATCOM devices with respect to the previous alternative.

One issue that may arise regarding the objective function (1) is that the possible values of $z_1$ and $z_2$ are unequal (i.e., not well-conditioned objective functions). This does not allow for a proper balance in optimization. Therefore, the objective function is normalized with respect to the benchmark case (i.e., no PV-STATCOM devices) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}min& z={\displaystyle \frac{z_1}{C_{Loss}^{base}}}+{\displaystyle \frac{z_2}{C_{PV-STATCOM}^{max}}}\hfill \end{array}\end{array}$$

(3)

where $C_{Loss}^{base}$ denotes the costs of the total energy losses in the electrical network without PV-STATCOM devices, and $C_{PV-STATCOM}^{max}$ represents the maximum possible costs of installing said devices.

2.2. Set of Constraints

The problem being studied involves a set of constraints. These constraints include maintaining a balance of active and reactive power at each node, limiting the power flow on each line to a maximum and minimum value, setting bounds on voltage regulation, determining the number of PV-STATCOM devices to be installed, and specifying their capacity for injecting or absorbing reactive power, among other factors.

2.2.1. Active and Reactive Energy Balance Equations

The node power balance equations for node m regarding active and reactive power are computed as the sum of the active and reactive power generated/demanded, which must be equal to the power flow (active/reactive) for distribution lines, as follows:

$$\begin{array}{c}{p}_{mt}^g-p_{mt}^d+p_{mt}^{PV-STATCOM}=\sum _{l\in L}\left(A_{ml}^{+}{p}_{lt}^s+A_{ml}^{-}{p}_{lt}^r\right),\forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(4)

$$\begin{array}{c}{q}_{mt}^g-q_{mt}^d+q_{mt}^{PV-STATCOM}=\sum _{l\in L}\left(A_{ml}^{+}{q}_{lt}^s+A_{ml}^{-}{q}_{lt}^r\right),\forall m\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(5)

where $p_{mt}^g$ and $q_{mt}^g$ denote the active and reactive power generated at node m, at time t; $p_{mt}^d$ and $q_{mt}^d$ are the active and reactive power demanded at node m and time t; the variables $q_{lt}^s$ and $q_{lt}^r$ represent the sending and receiving reactive power flows of the line connected between nodes k and m at time t, respectively; $p_{mt}^{PV-STATCOM}$ and $q_{mt}^{PV-STATCOM}$ are the active and reactive power injected by the PV-STATCOM device at node m and time t; and $A^{+}$ and $A^{-}$ represent the positive and negative values of the node-to-branch incidence matrix A, which can be expressed as the sum of $A^{+}$ and $A^{-}$.

2.2.2. Active and Reactive Energy Flow Equations

The distribution line’s active and reactive power flow, as well as its maximum capacities, are indicated as

$$\begin{array}{c}{p}_{lt}^s=real\left(v_{mt}{y}_l^{*}{\left(v_{mt}-v_{kt}\right)}^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(6)

$$\begin{array}{c}{p}_{lt}^r=real\left(v_{kt}{y}_l^{*}{\left(v_{kt}-v_{mt}\right)}^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(7)

$$\begin{array}{c}{q}_{lt}^s=imag\left(v_{mt}{y}_l^{*}{\left(v_{mt}-v_{kt}\right)}^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(8)

$$\begin{array}{c}{q}_{lt}^r=imag\left(v_{kt}{y}_l^{*}{\left(v_{kt}-v_{kt}\right)}^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(9)

$$\begin{array}{c}∥p_{lt}^s+j{q}_{lt}^s∥\le s_l^{max},\forall l\in \mathcal{B},\forall t\in \mathcal{T}\end{array}$$

(10)

$$\begin{array}{c}∥p_{lt}^r+j{q}_{lt}^r∥\le s_l^{max},\forall l\in \mathcal{B},\forall t\in \mathcal{T}\end{array}$$

(11)

where $v_{mt}$ denotes the voltage at node m (or k) and time t in complex form; $y_l$ represent the admittance of the distribution line (branch l); ${(·)}^{*}$ is the conjugate of the argument; $s_l^{max}$ is the maximum limit of the apparent power flow through the distribution line; the operators $real\left(·\right)$ and $imag\left(·\right)$ take only the real and imaginary parts of a complex number, respectively; and the operator $∥·∥$ corresponds to the Euclidean norm.

2.2.3. Operating Regulations

For an EDS to function correctly, all nodal voltage profiles must adhere to the limits established by regulatory policies. These limits are essential for ensuring satisfactory operation and are defined as

$$\begin{array}{cc}{v}_{0h}=v^{\mathrm{nom}}{e}^{j0},& \forall t\in \mathcal{T},\end{array}$$

(12)

$$\begin{array}{cc}∥v_{mt}∥\ge v^{min},& \forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(13)

$$\begin{array}{cc}∥v_{mt}∥\le v^{max},& \forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(14)

where $v_{0h}$ is the rated voltage at the substation bus (well known as the slack bus) at time t, whose rated value is $v^{\mathrm{nom}}$, which is usually equal to 1.0 (per-unit); $v^{min}$ and $v^{max}$ denotes the minimum and maximum voltage profiles permitted in an EDS.

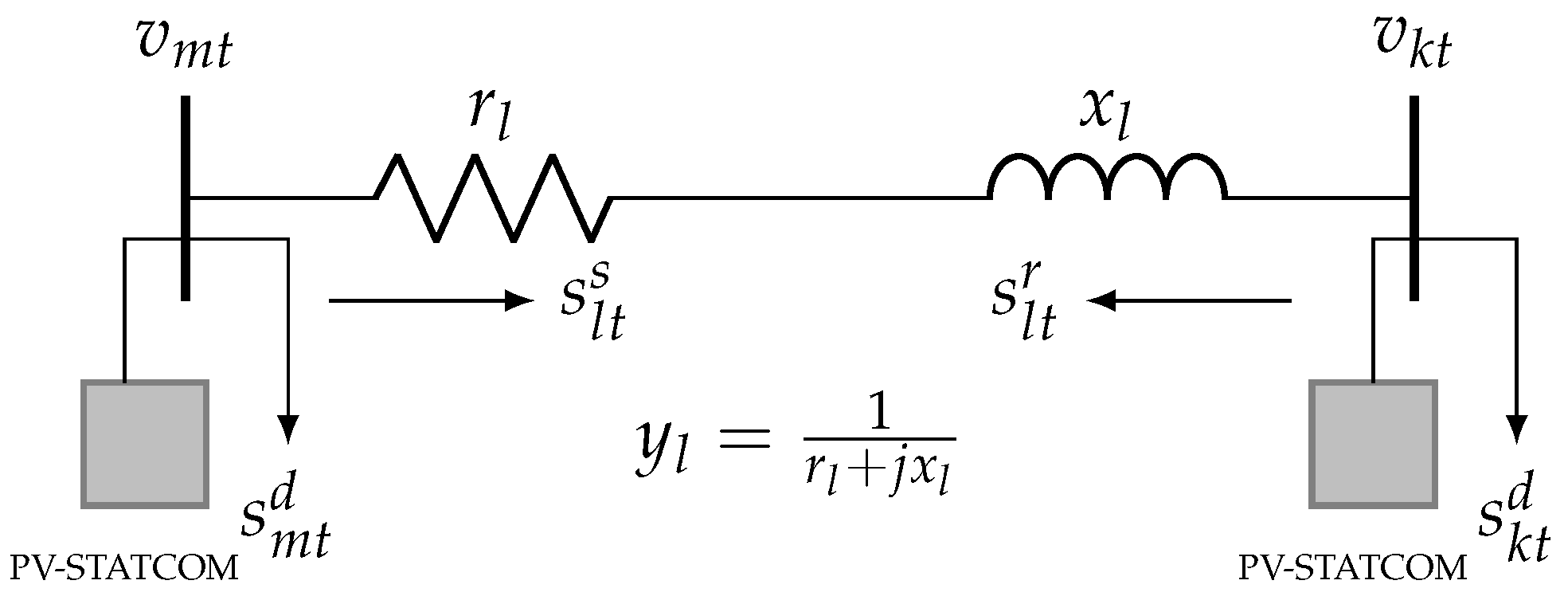
2.2.4. Incorporation of PV-STATCOM Devices

For a proper integration of PV-STATCOM devices in electrical grids, it is necessary to establish the optimal location and the available nominal operating sizes. The location and size of the PV-STATCOM devices are defined as

$$\begin{array}{c}0\le s_k^{PV-STATCOM}\le z_m{s}_{max}^{PV-STATCOM},\forall m\in \mathcal{N},\end{array}$$

(15)

$$\begin{array}{c}0\le p_{mt}^{PV-STATCOM}\le s_k^{PV-STATCOM},\forall m\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(16)

$$\begin{array}{c}-s_k^{PV-STATCOM}\le q_{mt}^{PV-STATCOM}\le s_k^{PV-STATCOM},\forall m\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(17)

$$\begin{array}{c}∥p_{mt}^{PV-STATCOM}+j{q}_{mt}^{PV-STATCOM}∥\le s_k^{PV-STATCOM},\forall m\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(18)

$$\begin{array}{c}\sum _{m\in \mathcal{N}}{z}_m\le \eta ,\end{array}$$

(19)

$$\begin{array}{c}{z}_m\in \left\{0,1\right\},\forall m\in \mathcal{N},\end{array}$$

(20)

where $s_k^{PV-STATCOM}$ is a variable employed to compute the optimal size of the PV-STATCOM devices at node m; $s_{max}^{PV-STATCOM}$ is the maximum capacity allowed for the devices to be installed in the electrical network (this capacity typically ranges from 0 MVA to 2 MVA at the distribution level) [26]; $z_m$ is the binary variable that denotes the PV-STATCOM device’s location at node m, i.e., $z_m=1$ indicates that a PV-STATCOM device will be installed at node m (otherwise, $z_m=0$); and $\eta$ is the maximum number of PV-STATCOM devices to be located in the network.

2.3. Interpretation of the Optimization Model

The optimization model for integrating the PV-STATCOM devices optimally in EDSs presented from (1)–(20) involves the binary variable related to the optimal placement of PV-STATCOM devices in EDSs, as well as the continuous variables related to the distribution line’s active and reactive power flow, the complex nodal voltages, and the apparent power provided by generators, among others. The model considers the following: Equation (1) denotes the annual equivalent operating costs z, which is made up of two terms: the first one represents the annual energy losses costs $z_2$ of the electrical grid, and the second term determines the investment costs of the PV-STATCOM devices $z_2$. Equations (4) and (5) correspond to the nodal balance of the active and reactive power in time t. Equations (6) and (7) are the active power flows transported by the transmission lines for each branch l and each time t, while the reactive power flows are denoted by Equations (8) and (9). Inequalities (10) and (11) define the maximum capacities of apparent power to be transported in transmission lines for each branch l in any period. Equation (12) sets the voltage value at the slack bus, and inequalities (13) and (14) work to limit the voltage profiles in each node to their minimum and maximum values any each time t. Inequality (15) determines the maximum possible value of the PV-STATCOM devices, while inequalities (16) and (17) define the limits regarding the maximum active and reactive power that the PV-STATCOM devices can deliver/absorb for each node. Inequality (18) is the maximum value of the apparent power that can flow through the PV-STATCOM devices at node m and time t, and, finally, inequality (19) defines the maximum number of PV-STATCOM devices that will be located into the network.

3. Convex Reformulation

The MINLP model presented in Equations (1)–(20) is challenging to solve and falls into the category of problems with a problematic computational complexity. Hence, this problem type is typically solved using metaheuristic algorithms [22,23,24,26]. Nevertheless, no metaheuristic algorithm can guarantee that it will reach the global optimum of the MINLP model. Furthermore, these algorithms often need parameter tuning, indicating that they cannot always perform similarly. Another possible solution to solve this problem is to relax the model, transforming it into an MI–convex model. This method ensures finding the global optimum and does not require parameter tuning.

3.1. Convex Representation of the Active and Reactive Power Flow Equations

The active and reactive power flow equations presented in Equations (6)–(9) are equality constraints with products between voltages, which makes them non-convex constraints. To transform these equations into convex constraints, two auxiliary variables are proposed [31]:

$$\begin{array}{c}{u}_{mt}=v_{mt}{v}_{mt}^{*}={∥v_{mt}∥}^2,\end{array}$$

(21)

$$\begin{array}{c}{w}_{lt}=v_{mt}{v}_{kt}^{*},\end{array}$$

(22)

where $u_{mt}\in \mathcal{R}$ corresponds to the square of the voltage at node m, time t; $w_{lt}\in \mathcal{C}$ is the cross product of the voltages in branch l at time t; and $\mathcal{R}$ refer to the set of real numbers, while $\mathcal{C}$ denotes the set of complex numbers.

Now, by replacing these two auxiliary variables $u_{mt}$ and $w_{lt}$ in (6)–(9), the following is obtained:

$$\begin{array}{cc}{p}_{lt}^s& =real\left(\left(u_{mt}-w_{lt}\right)y_l^{*}\right),\end{array}$$

(23)

$$\begin{array}{cc}{p}_{lt}^r& =real\left(\left(u_{kt}-w_{lt}^{*}\right)y_l^{*}\right),\end{array}$$

(24)

$$\begin{array}{cc}{q}_{lt}^s& =imag\left(\left(u_{mt}-w_{lt}\right)y_l^{*}\right),\end{array}$$

(25)

$$\begin{array}{cc}{q}_{lt}^r& =imag\left(\left(u_{kt}-w_{lt}^{*}\right)y_l^{*}\right).\end{array}$$

(26)

The new active and reactive power flow Equations (23)–(26) are represented as a function of the auxiliary variables (21) and (22), and these equations are non-convex. Hence, they can be relaxed using a hyperbolic shape, as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w_{lt}& =v_{mt}{v}_{kt}^{*}\hfill \\ \hfill w_{lt}{w}_{lt}^{*}& =v_{mt}{v}_{mt}^{*}{v}_{kt}{v}_{kt}^{*}\hfill \\ \hfill {∥w_{lt}∥}^2& ={∥v_{mt}∥}^2{∥v_{kt}∥}^2=u_{mt}{u}_{kt}\hfill \\ \hfill {∥w_{lt}∥}^2& =\frac{1}{4}{\left(u_{mt}+u_{kt}\right)}^2-\frac{1}{4}{\left(u_{mt}-u_{kt}\right)}^2\hfill \\ \hfill {\left(u_{mt}-u_{kt}\right)}^2+{∥2w_{lt}∥}^2& ={\left(u_{mt}+u_{kt}\right)}^2\hfill \\ \hfill ∥\begin{array}{c}2w_{lt}\\ u_{mt}-u_{kt}\end{array}∥& =u_{mt}+u_{kt}\hfill \\ \hfill ∥\begin{array}{c}2w_{lt}\\ u_{mt}-u_{kt}\end{array}∥& \le u_{mt}+u_{kt}.\hfill \end{array}\end{array}$$

(27)

3.2. Proposed MI Convex Model

The MINLP model presented in Equations (1) to (20) is transformed into an MI convex one invoking the above relaxations:

$$\begin{array}{cc}minz& ={\displaystyle \frac{z_1}{C_{Loss}^{base}}}+{\displaystyle \frac{z_2}{C_{PV-STATCOM}^{max}}},\end{array}$$

(28)

$$\begin{array}{cc}& z_1=CT\sum _{t\in \mathcal{T}}\sum _{l\in \mathcal{B}}\left(p_{lt}^s+p_{lt}^r\right)\Delta t,\end{array}$$

(29)

$$\begin{array}{cc}& z_2=C_{PV-STATCOM}\sum _{m\in \mathcal{N}}{s}_k^{PV-STATCOM},\end{array}$$

(30)

$$\begin{array}{cc}& p_{mt}^g-p_{mt}^d+p_{mt}^{PV-STATCOM}=\sum _{l\in L}\left(A_{ml}^{+}{p}_{lt}^s+A_{ml}^{-}{p}_{lt}^r\right),\forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(31)

$$\begin{array}{cc}& q_{mt}^g-q_{mt}^d+q_{kk}^{PV-STATCOM}=\sum _{l\in L}\left(A_{ml}^{+}{q}_{lt}^s+A_{ml}^{-}{q}_{lt}^r\right),\forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(32)

$$\begin{array}{cc}& p_{lt}^s=real\left(\left(u_{mt}-w_{lt}\right)y_l^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(33)

$$\begin{array}{cc}& p_{lt}^r=real\left(\left(u_{mt}-w_{lt}^{*}\right)y_l^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(34)

$$\begin{array}{cc}& q_{lt}^s=imag\left(\left(u_{mt}-w_{lt}\right)y_l^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(35)

$$\begin{array}{cc}& q_{lt}^r=imag\left(\left(u_{mt}-w_{lt}^{*}\right)y_l^{*}\right),\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(36)

$$\begin{array}{cc}& ∥p_{lt}^s+j{q}_{lt}^s∥\le s_l^{max},\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(37)

$$\begin{array}{cc}& ∥p_{lt}^r+j{q}_{lt}^r∥\le s_l^{max},\forall l\in \mathcal{B},\forall t\in \mathcal{T},\end{array}$$

(38)

$$\begin{array}{cc}& u_{0t}={\left(v^{\mathrm{nom}}\right)}^2,\forall t\in \mathcal{T},\end{array}$$

(39)

$$\begin{array}{cc}& ∥\begin{array}{c}2w_{lt}\\ u_{mt}-u_{mt}\end{array}∥\le u_{mt}+u_{mt},\forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(40)

$$\begin{array}{cc}& {\left(v^{\min }\right)}^2\le u_{mt}\le {\left(v^{\max }\right)}^2,\forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(41)

$$\begin{array}{cc}& 0\le s_k^{PV-STATCOM}\le z_m{s}_{max}^{\mathrm{FACT}},\forall m\in \mathcal{N},\end{array}$$

(42)

$$\begin{array}{cc}& 0\le p_{mt}^{PV-STATCOM}\le s_k^{PV-STATCOM},\forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(43)

$$\begin{array}{cc}& -s_k^{PV-STATCOM}\le q_{mt}^{PV-STATCOM}\le s_k^{PV-STATCOM},\forall m\in \mathcal{N},\forall t\in \mathcal{T},\end{array}$$

(44)

$$\begin{array}{cc}& ∥p_{mt}^{PV-STATCOM}+j{q}_{mt}^{PV-STATCOM}∥\le s_k^{PV-STATCOM},\forall m\in \mathcal{N},\forall t\in \mathcal{T}\end{array}$$

(45)

$$\begin{array}{cc}& \sum _{m\in \mathcal{N}}{z}_m\le \eta ,\end{array}$$

(46)

$$\begin{array}{cc}& z_m\in \left\{0,1\right\},\forall m\in \mathcal{N}.\end{array}$$

(47)

The MI convex model shown in Equations (28)–(47) can find the best solution of the exact mixed-integer model (1)–(20); in other words, it can obtain the global optimum. This is possible if the conditions of the set of hyperbolic constraints (40) are well defined, as presented in [32].

4. Test Systems

This section describes the test systems that were used to evaluate the proposed mixed-integer optimization model for the optimal allocation and sizing of PV-STATCOM devices, namely the IEEE 33-EDS with radial and meshed topologies and the IEEE 69-EDS with radial topology. Figure 2 illustrates both topologies of the IEEE 33-EDS. This grid comprises 33 nodes and 32 distribution lines in its radial topology, while the meshed topology contains three additional distribution lines to form the system meshes (Figure 2b). The IEEE 33-EDS features a slack bus at node 1 operating at 12.66 kV. It has peak active and reactive demands of 3715 + j2300 kVA, respectively. This operating condition generates active and reactive power losses of $210.9876$ kW and $143.1283$ kvar, respectively. The test system’s peak demand, resistance, and reactance values can be found in

Table 1. Branch and load information for the IEEE 33-test system for both radial and meshed topologies.

Node		${\mathit{R}}_{\mathit{km}}$	${\mathit{X}}_{\mathit{km}}$	${\mathit{P}}_{\mathit{m}}$	${\mathit{Q}}_{\mathit{m}}$	Node		${\mathit{R}}_{\mathit{km}}$	${\mathit{X}}_{\mathit{km}}$	${\mathit{P}}_{\mathit{m}}$	${\mathit{Q}}_{\mathit{m}}$
$\mathit{k}$	$\mathit{m}$	($\Omega$)	($\Omega$)	(kW)	(kvar)	$\mathit{k}$	$\mathit{m}$	($\Omega$)	($\Omega$)	(kW)	(kvar)
1	2	0.0922	0.0477	100	60	17	18	0.7320	0.5740	90	40
2	3	0.4930	0.2511	90	40	2	19	0.1640	0.1565	90	40
3	4	0.3660	0.1864	120	80	19	20	1.5042	1.3554	90	40
4	5	0.3811	0.1941	60	30	20	21	0.4095	0.4784	90	40
5	6	0.8190	0.7070	60	20	21	22	0.7089	0.9373	90	40
6	7	0.1872	0.6188	200	100	3	23	0.4512	0.3083	90	50
7	8	1.7114	1.2351	200	100	23	24	0.8980	0.7091	420	200
8	9	1.0300	0.7400	60	20	24	25	0.8960	0.7011	420	200
9	10	1.0400	0.7400	60	20	6	26	0.2030	0.1034	60	25
10	11	0.1966	0.0650	45	30	26	27	0.2842	0.1447	60	25
11	12	0.3744	0.1238	60	35	27	28	1.0590	0.9337	60	20
12	13	1.4680	1.1550	60	35	28	29	0.8042	0.7006	120	70
13	14	0.5416	0.7129	120	80	29	30	0.5075	0.2585	200	600
14	15	0.5910	0.5260	60	10	30	31	0.9744	0.9630	150	70
15	16	0.7463	0.5450	60	20	31	32	0.3105	0.3619	210	100
16	17	1.2860	1.7210	60	20	32	33	0.3410	0.5302	60	40
12	22	2.0000	2.0000	-	-	18	33	0.5000	0.5000	-	-
25	29	0.5000	0.5000	-	-	-	-	-	-	-	-

and were sourced from [33].

Figure 3 illustrates the radial topology of the IEEE 69-EDS. This EDS has 69 nodes and 68 distribution lines, and its main power source is at node 1, providing a voltage output of 12.66 kV. This test system’s peak apparent power is 3890.7 + j2693.6 kVA. This operating condition generates apparent power losses of 224.9520 + j102.3559 kVA, respectively. The maximum power consumption and the branch impedance parameters for the IEEE 69-EDS can be found in

Table 2. Branch and load information for the IEEE 69-bus grid.

Node		${\mathit{R}}_{\mathit{km}}$	${\mathit{X}}_{\mathit{km}}$	${\mathit{P}}_{\mathit{m}}$	${\mathit{Q}}_{\mathit{m}}$	Node		${\mathit{R}}_{\mathit{km}}$	${\mathit{X}}_{\mathit{km}}$	${\mathit{P}}_{\mathit{m}}$	${\mathit{Q}}_{\mathit{m}}$
$\mathit{k}$	$\mathit{m}$	($\Omega$)	($\Omega$)	(kW)	(kvar)	$\mathit{k}$	$\mathit{m}$	($\Omega$)	($\Omega$)	(kW)	(kvar)
1	2	0.0005	000012	0.00	0.00	3	36	0.0044	0.0108	26.00	18.55
2	3	0.0005	0.0012	0.00	0.00	36	37	0.0640	0.1565	26.00	18.55
3	4	0.0015	0.0036	0.00	0.00	37	38	0.1053	0.1230	0.00	0.00
4	5	0.0251	0.0294	0.00	0.00	38	39	0.0304	0.0355	24.00	17.00
5	6	0.3660	0.1864	2.60	2.20	39	40	0.0018	0.0021	24.00	17.00
6	7	0.3810	0.1941	40.40	30.00	40	41	0.7283	0.8509	1.20	1.00
7	8	0.0922	0.0470	75.00	54.00	41	42	0.3100	0.3623	0.00	0.00
8	9	0.0493	0.0251	30.00	22.00	42	43	0.0410	0.0478	6.00	4.30
9	10	0.8190	0.2707	28.00	19.00	43	44	0.0092	0.0116	0.00	0.00
10	11	0.1872	0.0619	145.00	104.00	44	45	0.1089	0.1373	39.22	26.30
11	12	0.7114	0.2351	145.00	104.00	45	46	0.0009	0.0012	29.22	26.30
12	13	1.0300	0.3400	8.00	5.00	4	47	0.0034	0.0084	0.00	0.00
13	14	1.0440	0.3450	8.00	5.50	47	48	0.0851	0.2083	79.00	56.40
14	15	1.0580	0.3496	0.00	0.00	48	49	0.2898	0.7091	384.70	274.50
15	16	0.1966	0.0650	45.50	30.00	49	50	0.0822	0.2011	384.70	274.50
16	17	0.3744	0.1238	60.00	35.00	8	51	0.0928	0.0473	40.50	28.30
17	18	0.0047	0.0016	60.00	35.00	51	52	0.3319	0.1114	3.60	2.70
18	19	0.3276	0.1083	0.00	0.00	9	53	0.1740	0.0886	4.35	3.50
19	20	0.2106	0.0690	1.00	0.60	53	54	0.2030	0.1034	26.40	19.00
20	21	0.3416	0.1129	114.00	81.00	54	55	0.2842	0.1447	24.00	17.20
21	22	0.0140	0.0046	5.00	3.50	55	56	0.2813	0.1433	0.00	0.00
22	23	0.1591	0.0526	0.00	0.00	56	57	1.5900	0.5337	0.00	0.00
23	24	0.3463	0.1145	28.00	20.00	57	58	0.7837	0.2630	0.00	0.00
24	25	0.7488	0.2475	0.00	0.00	58	59	0.3042	0.1006	100.00	72.00
25	26	0.3089	0.1021	14.00	10.00	59	60	0.3861	0.1172	0.00	0.00
26	27	0.1732	0.0572	14.00	10.00	60	61	0.5075	0.2585	1244.00	888.00
3	28	0.0044	0.0108	26.00	18.60	61	62	0.0974	0.0496	32.00	23.00
28	29	0.0640	0.1565	26.00	18.60	62	63	0.1450	0.0738	0.00	0.00
29	30	0.3978	0.1315	0.00	0.00	63	64	0.7105	0.3619	227.00	162.00
30	31	0.0702	0.0232	0.00	0.00	64	65	1.0410	0.5302	59.00	42.00
31	32	0.3510	0.1160	0.00	0.00	11	66	0.2012	0.0611	18.00	13.00
32	33	0.8390	0.2816	14.00	10.00	66	67	0.0470	0.0140	18.00	13.00
33	34	1.7080	0.5646	19.50	14.00	12	68	0.7394	0.2444	28.00	20.00
34	35	1.4740	0.4873	6.00	4.00	68	69	0.0047	0.0016	28.00	20.00

and were sourced from [33].

EDSs typically experience daily load variations. The active and reactive power demand curves are depicted in Figure 4, which showcases the typical patterns observed in an EDS in Colombia [34].

Figure 5 depicts the power available for the optimal integration of the PV-STATCOM devices.

The data for the objective function parameter z in Equation (1) can be found in

Table 3. Data of the objective function parameters (1).

Parameter	Value	Unit	Parameter	Value	Unit
C	0.1390	USD/kWh	T	365	Days
${\Delta }_h$	0.50	h	$C_{PV}$	1.0365	USD/MVA
$C_{STATCOM}$	2.457	USD/kVA	-	-	-

. The values of the costs for the PV-STATCOM devices were taken from [33,35], respectively.

5. Numerical Implementation

The proposed optimization model for the optimal integration (placement and sizing) of PV-STATCOM devices was executed in the MATLAB 2021a interface with Yalmip toolbox R20230609 [36], employing the Gurobi solver 9.5.1 [37]. Two cases were conducted to assess the effectiveness of the proposed model (28)–(47). In both cases, it is assumed that a maximum of three PV-STATCOM devices can be installed. The details of these cases are as follows:

S1:

The proposed optimization model was analyzed in the IEEE 33- and 69-EDSs with radial configurations.

S2:

The optimal integration of the PV-STATCOM devices was analyzed in the IEEE 33-EDS with a meshed topology.

5.1. Analysis of Case 1 (S1)

This case compares the optimal integration of PV-STATCOM systems against the benchmark case and PV systems with unit power factor. This case considers up to three devices to be installed (i.e., $\eta =3$). The base total energy loss costs $C_{Loss}^{base}$ for the IEEE 33- and 69-bus test systems are USD 112,740.90 and 119,715.63 per year, respectively.

Table 4. Comparison between the optimal integration of PV and PV-STATCOM devices for the radial test systems.

Device	Location	Size (MVA)	z (Per-Unit/Year)	Reduction (%)	Loss Reduction (%)
IEEE 33-EDS
Benchmark case	-	-	1	-	-
PV	[14, 17, 32]	[0.3657, 0.2089, 0.5091]	0.8697	13.03	31.05
PV-STATCOM	[14, 30, 32]	[0.5491, 0.5001, 0.2948]	0.6684	33.16	55.56
IEEE 69-EDS
Benchmark case	-	-	1	-	-
PV	[61, 64, 65]	[0.8544, 0.2504, 0.0641]	0.8407	15.92	35.80
PV-STATCOM	[21, 61, 61]	[0.1479, 0.9590, 0.3136]	0.6219	37.81	61.53

lists the results obtained for the objective function in the two test systems with a radial configuration and without the PV or PV-STATCOM systems. Table 4 also displays the decrease in the objective function values compared to the benchmark case, as well as the reduction in power loss costs.

Based on the findings presented in Table 4, it can be concluded that:

i.

Installing PV-STATCOM devices generates a greater reduction in the objective function values when compared to only installing PV systems, even though the investment costs are higher.

ii.

There is a more significant loss reduction with the installation of PV-STATCOMs in comparison with the exclusive use of PV devices. These reductions occur because PV-STATCOM devices can compensate for reactive power during utility operations.

iii.

For the IEEE 33-EDS, the costs of energy losses are reduced by USD 35,006.05 and 62,638.84 per year when PV and PV-STATCOM devices are installed, respectively. This indicates that the latter outperforms the PV systems by 24.87%, saving about USD 27,632.79 more in energy loss costs per year.

iv.

The energy loss costs for the IEEE 69-bus test system are reduced by USD 42,858.18 and 73,661.01 per year when the PV and PV-STATCOM devices are installed, respectively. This demonstrates that it is more efficient to install PV-STATCOM devices since they save USD 30,802.82 more per year than PV systems.

A comparison of the voltage profiles for the test systems (with PV systems, PV-STATCOMs, and no devices) is illustrated in Figure 6. The voltage profiles shown in this figure are the worst case for each node. To compare these results, the voltage deviation index was used, which determines the deviation from the amplitude of the rated voltage at each node and time. The voltage deviation index ($L_v$) is computed as follows:

$$\begin{array}{c}\hfill L_v=\sqrt{\sum _{t\in \mathcal{T}}\sum _{k\in \mathcal{N}}{\left(\frac{v^{\mathrm{nom}}-v_{ht}}{v^{\mathrm{nom}}}\right)}^2}.\end{array}$$

(48)

Based on the worst cases regarding the voltage profiles (Figure 6), it can be noted that PV-STATCOM devices report the best improvements. These devices allow the voltage profiles to be brought ≈ 1 pu closer in both test systems. In Figure 6a, the worst voltage profile when PV-STATCOM devices are located is 0.9351 pu at node 18, whereas, without these devices, the worst value is 0.9095 pu at the same node. Thus, PV-STATCOMs reduce the voltage deviation by 3.0%. For the IEEE 69-EDS (Figure 6b), the voltage deviation is reduced by 2.0% (the worst voltage profiles with and without PV-STATCOMs are 0.9310 and 0.9136 at node 65, respectively). The voltage deviation indices for the IEEE 33- and 69-EDSs in the benchmark case are 1.6735 and 1.4621, respectively. When PV devices are installed, these indices are reduced to 1.3089 and 1.1643 for the IEEE 33- and 69-EDSs. In comparison, the PV-STATCOM devices reduce these indices to 0.8834 and 0.9564. These results demonstrate that installing PV-STATCOM devices significantly improves the voltages of the test systems, as the part that operates as the STATCOM compensates for the reactive power during a large part of the day.

5.2. Analysis of Case 2 (S2)

This case studies the optimal integration of PV-STATCOMs in test systems with meshed configurations, considering up to three devices to be installed (i.e., $\eta =3$). In this case, the base total energy losses cost $C_{Loss}^{base}$ is USD 72,732.50 per year for the IEEE 33-EDS. According to the results, the radial configuration constitutes the worst case. Therefore, the meshed configuration was only analyzed for the IEEE 33-EDS. The simulation results obtained in this case can be found in

Table 5. Comparison of the optimal integration of PV and PV-STATCOM devices in the meshed test system.

Device	Location	Size (MVA)	z (Per-Unit/Year)	Reduction (%)	Loss Reduction (%)
IEEE 33-EDS
Benchmark case	-	-	1	-	-
PV	[15, 30, 32]	[0.2671, 0.3407, 0.5343]	0.9084	13.31	31.37
PV-STATCOM	[14, 30, 32]	[0.2867, 0.7058, 0.4530]	0.7225	27.74	51.83

, which contains the normalized objective function results for the two meshed test systems without the PV or PV-STATCOM devices. This table also presents the reduction in the objective function concerning the benchmark case and the reduction in power loss cost.

From Table 5, it can be stated that:

i.

The installation of PV-STATCOM devices reduces the objective function in meshed topologies to a greater extent than the exclusive use of PV devices. PV-STATCOMs improve the objective function by 27.74%. Meanwhile, PV devices improve the objective function by 13.31%. This means that PV-STATCOM devices can reduce the objective function by 14.43% more than PV systems.

ii.

The optimal integration of PV-STATCOMs significantly reduces the costs of energy losses in the IEEE 33-EDS with a meshed configuration compared to PV devices. The values reported for this reduction are USD 22,816.18 and 37,697.25 per year for the PV and PV-STATCOM devices, respectively. Therefore, PV-STATCOMs can save USD 14,881.07 more per year.

The worst cases regarding voltage profiles in the IEEE 33-EDS with a meshed configuration are depicted in Figure 7. Here, the lowest voltage profiles for the PV and PV-STATCOM devices are 0.9527 pu and 0.9668 pu, respectively, both at node 18. This shows that PV-STATCOMs improve the lower voltage by 1.47%. The voltage deviation indices are 0.7899 and 0.5588 for the PV and PV-STATCOM devices, respectively. Thus, PV-STATCOMs improve the overall voltages of the electrical networks, as they can inject/absorb reactive power throughout the day, unlike PV systems alone.

5.3. Comparative Analysis

This section compares the proposed method with the exact MINLP model implemented in the GAMS software. This comparison is performed only for PV-STATCOM devices because they exhibit better performance and have a more complex model, as they contain more variables than PV devices alone.

Table 6. Comparison of the optimal integration of PV-STATCOM devices.

Method	Location	Size (MVA)	z (Per-Unit/Year)	Reduction (%)	Loss Reduction (%)
IEEE 33-EDS
Benchmark case	-	-	1	-	-
DICOPT	[16, 25, 29]	[0.5039, 0.4781, 0.81175]	0.6884	33.16	53.89
PV-STATCOM	[14, 30, 32]	[0.5491, 0.5001, 0.2948]	0.6684	31.16	55.56
IEEE 33-EDS with meshed topology
Benchmark case	-	-	1	-	-
DICOPT	[8, 17, 30]	[0.3029, 0.2082, 0.9531]	0.7651	23.49	47.89
PV-STATCOM	[14, 30, 32]	[0.2867, 0.7058, 0.4530]	0.7225	27.74	51.83

presents the results obtained for the objective function in the two test systems with radial and meshed configurations. It is essential to mention that solvers such as BONMIN, SCIP, and Couenne failed to solve the exact MINLP model. In contrast, the DICOPT solver can only find solutions in the IEEE 33-EDS, whereas in the IEEE 69-EDS it was unable to reach certain solutions.

The results shown in Table 6 indicate that solving the exact MINLP model is challenging. Even widely used software like GAMS presents difficulties in solving it. For the IEEE 33-EDS with radial topology, the DICOPT solver finds a worse solution than the proposed model. This solution can be considered locally optimal; however, the placement and size of the PV-STATCOM differ from the solution reached by the proposed model. For the IEEE 33-EDS with a meshed topology, the DICOPT solver achieves a solution (local optimum) that is 5.89% higher than the proposed model. These results confirm that the proposed model can achieve the best solutions in any test system or configuration. Furthermore, it does not present convergence problems in large test systems.

6. Conclusions and Future Works

This study analyzed the problem of optimizing the integration of PV-STATCOMs in EDSs. The objective function considered minimizing costs for two components: energy losses per year and investments in installing PV-STATCOM devices. Furthermore, the objective function was normalized to assign equal weight to both objectives. The optimization model for the problem under study is a mixed-integer nonlinear model, which is why it cannot ensure a global optimum. This study transformed the exact optimization model into a mixed-integer convex one by employing second-order constraint relaxations in the product of the voltages. The proposed convex model was evaluated in two test systems with radial and meshed configurations. Likewise, the optimal integration of PV-STATCOM devices was compared to a benchmark case (no devices) and the exclusive installation of PV devices.

The results showed that PV-STATCOMs reduce annual energy loss costs by a more significant percentage than only allocating PV devices. The latter saved USD 35,006.05 and 42,858.18 per year for the IEEE 33- and 69-bus test systems with radial configurations. In contrast, PV-STATCOM devices increased these savings, i.e., USD 62,638.84 and 73,661.01 per year for the test systems with radial topologies. PV-STATCOMs can save USD 27,632.79 and 30,802.82 more per year, which confirms the positive improvements for distribution companies when efficient active and reactive power management strategies are considered in the distribution system operation cases. In addition, these systems improved all voltage profiles in both test systems with radial and meshed configurations. PV-STATCOM devices can inject or absorb reactive power continuously, leading to this improvement.

The following future works could be conducted: (i) comparing the effectiveness of using PV-STATCOM devices in EDSs against locating PV plants and STATCOMs independently; (ii) combining PV-STATCOMs with battery energy storage systems; and (iii) extending the proposed formulation to large scale transmission systems while including new objectives, loadability, and voltage profile improvements.