Research on Heat Generation Law and Cooling System Performance of Hydraulic System of Combined Machine Tool
Abstract
:1. Introduction
2. Heat Generation Mechanism of Hydraulic System
2.1. Working Mode
2.2. Mathematical Model of Hydraulic System
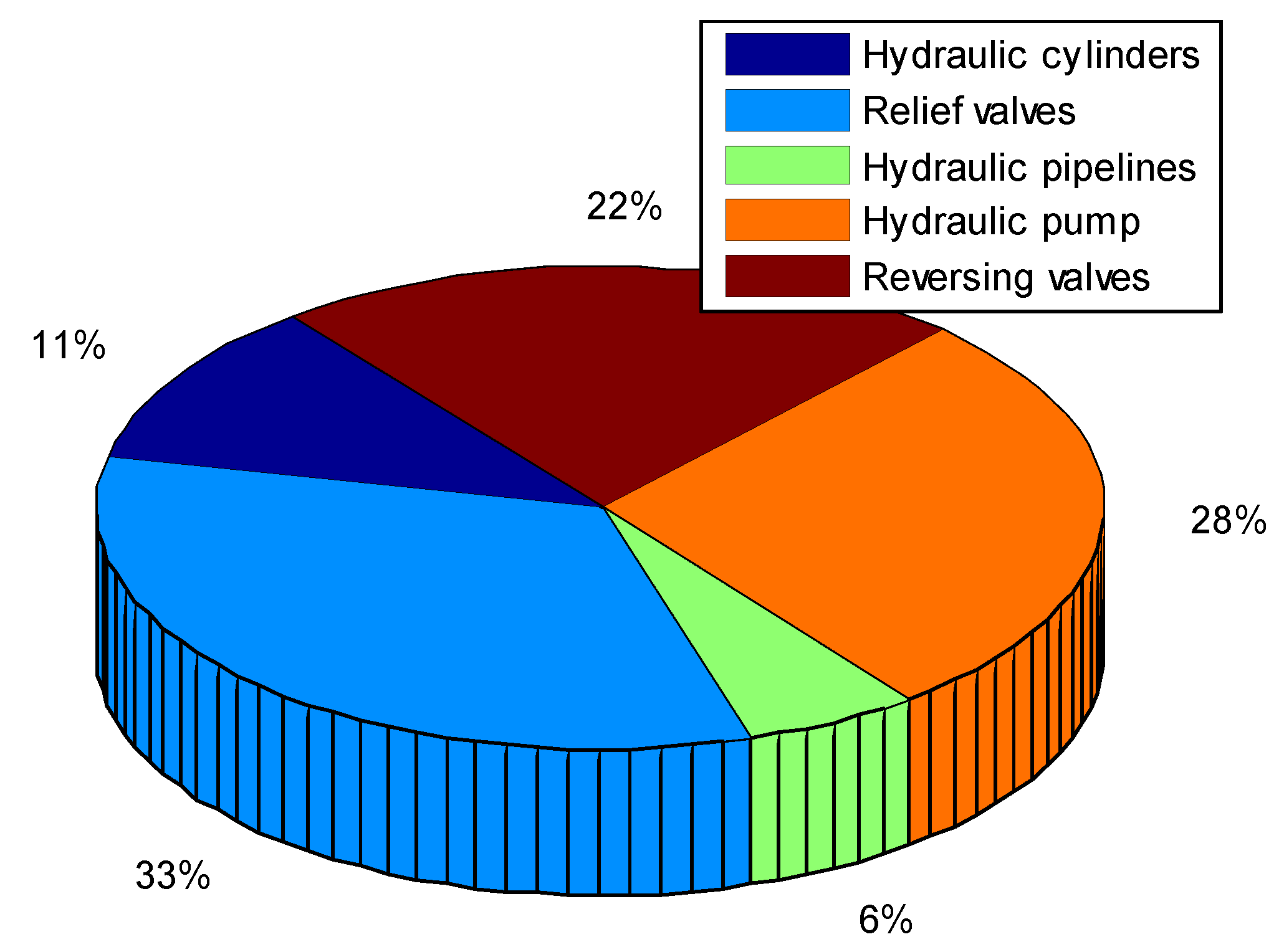
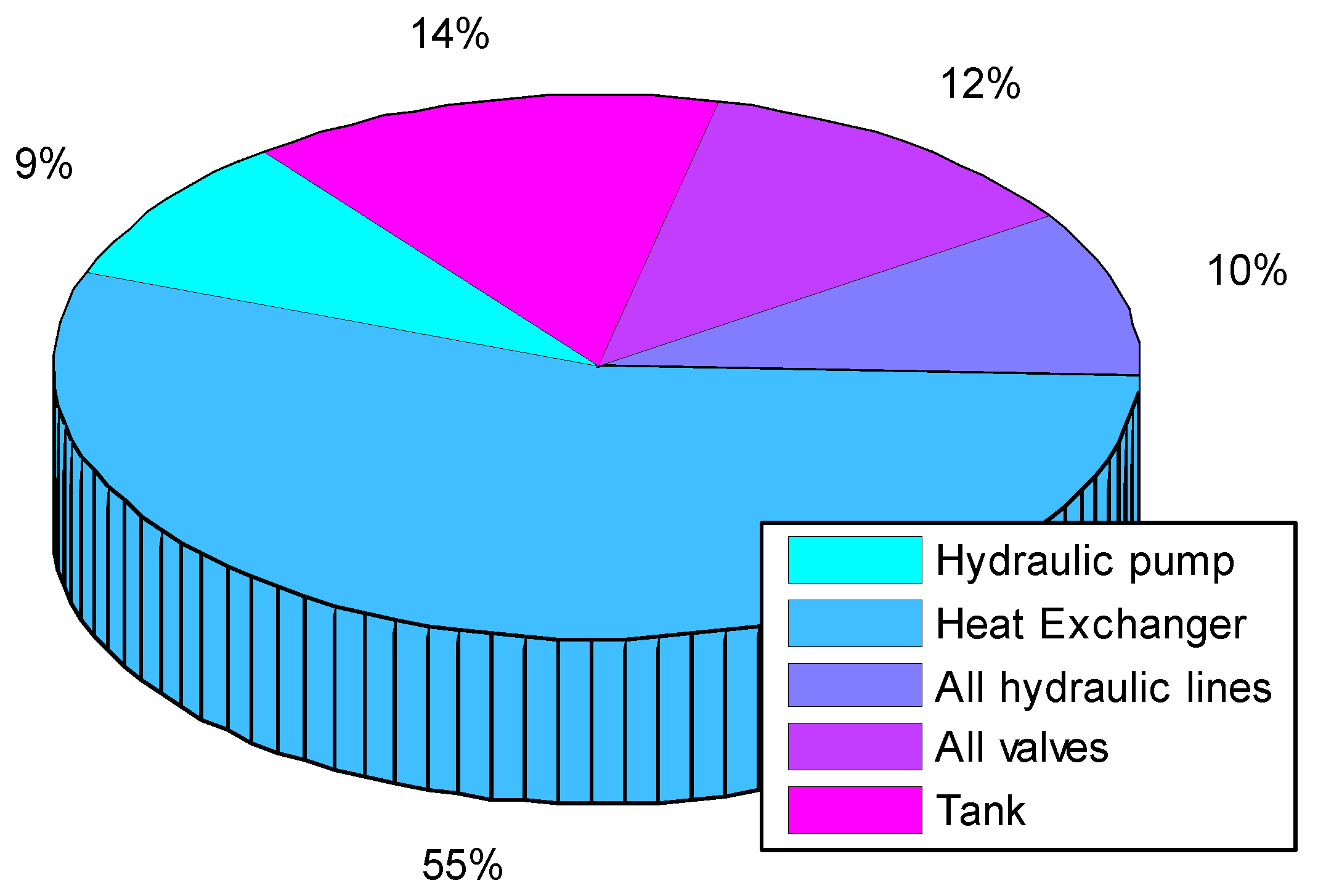
2.3. Heat Generation Mechanism of Hydraulic System
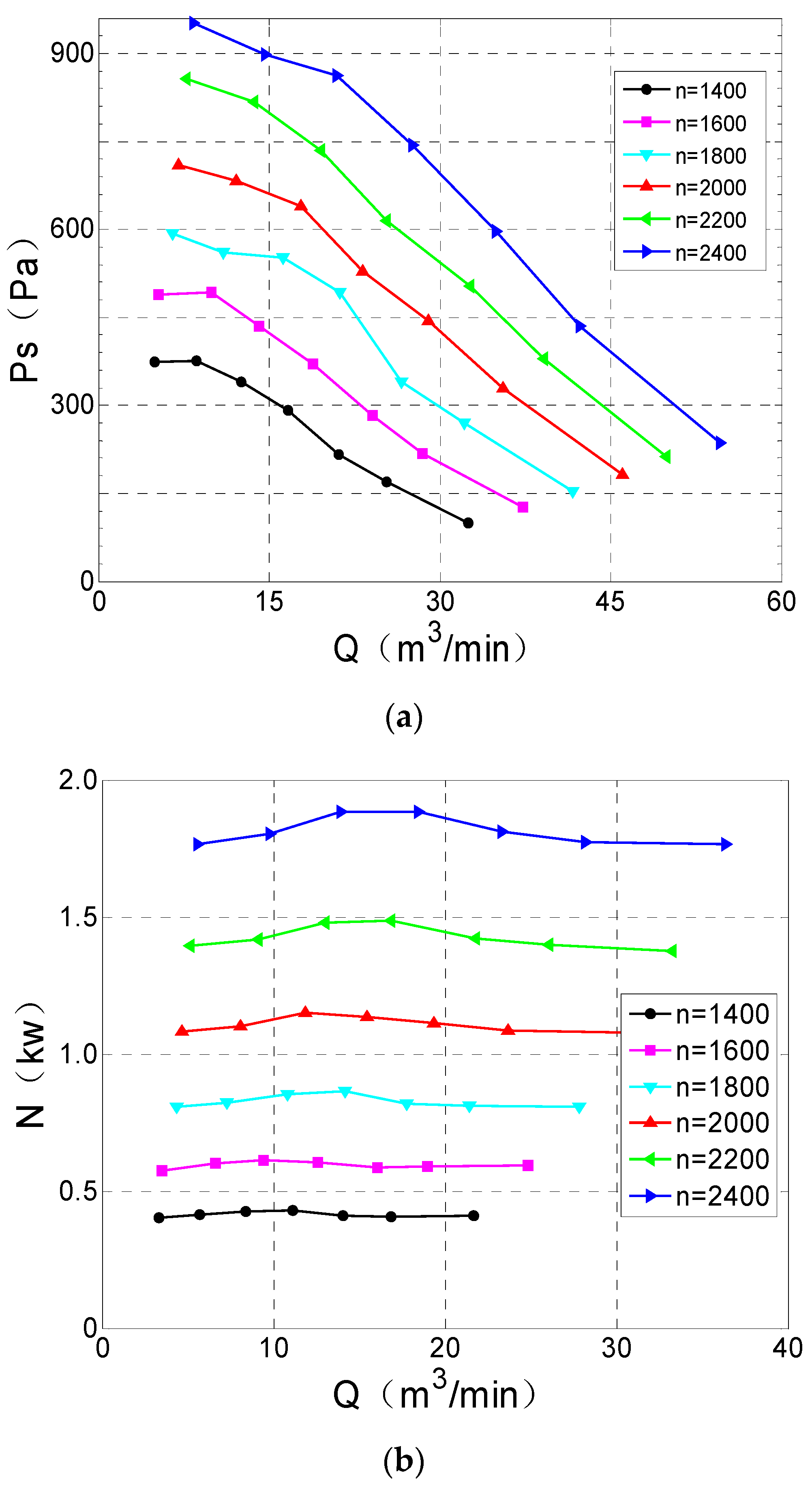
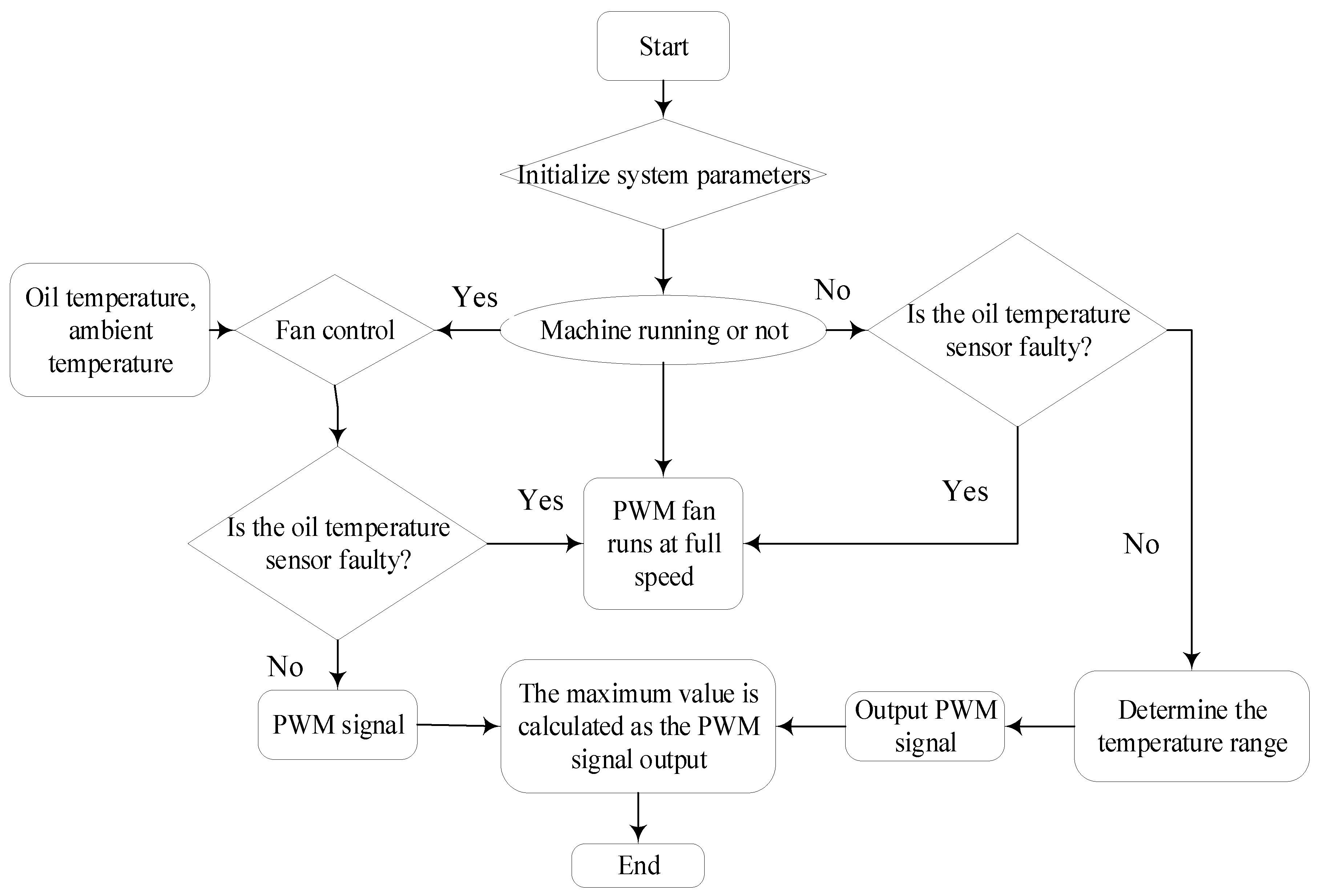
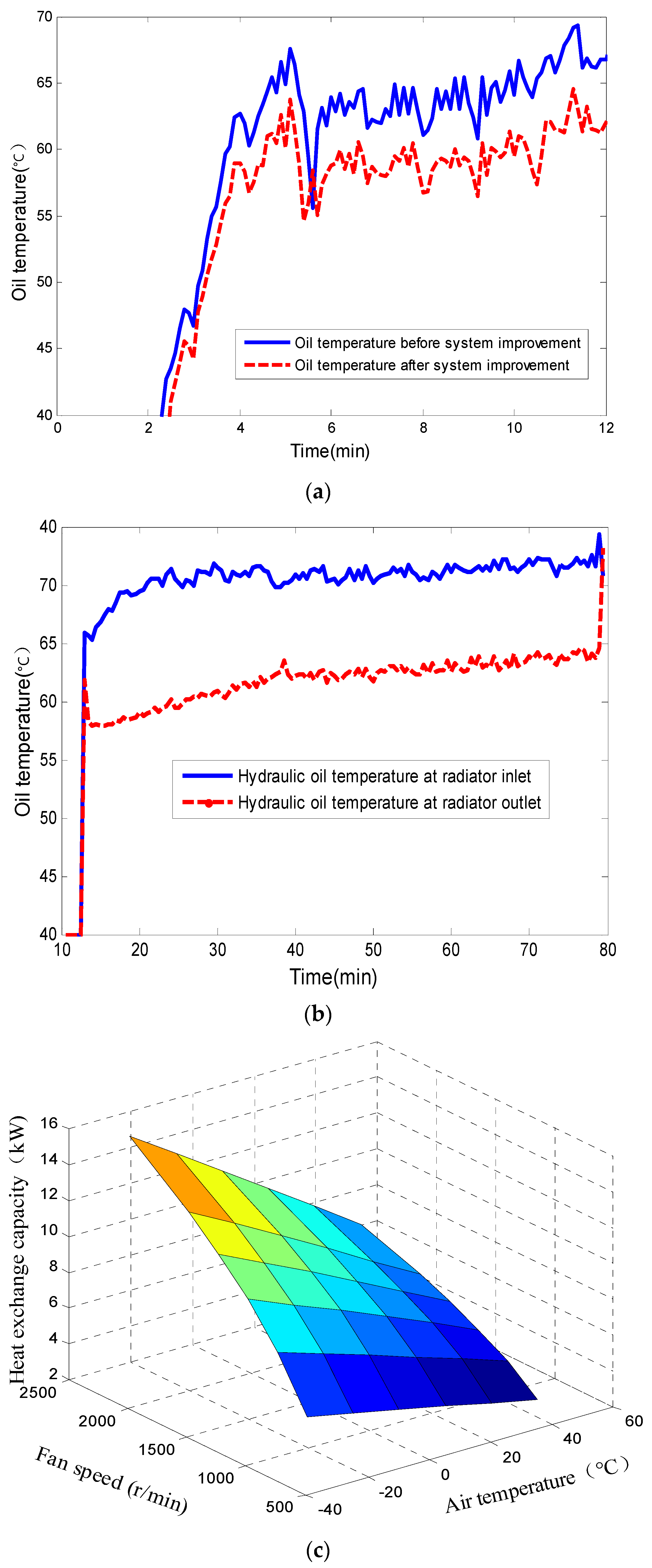
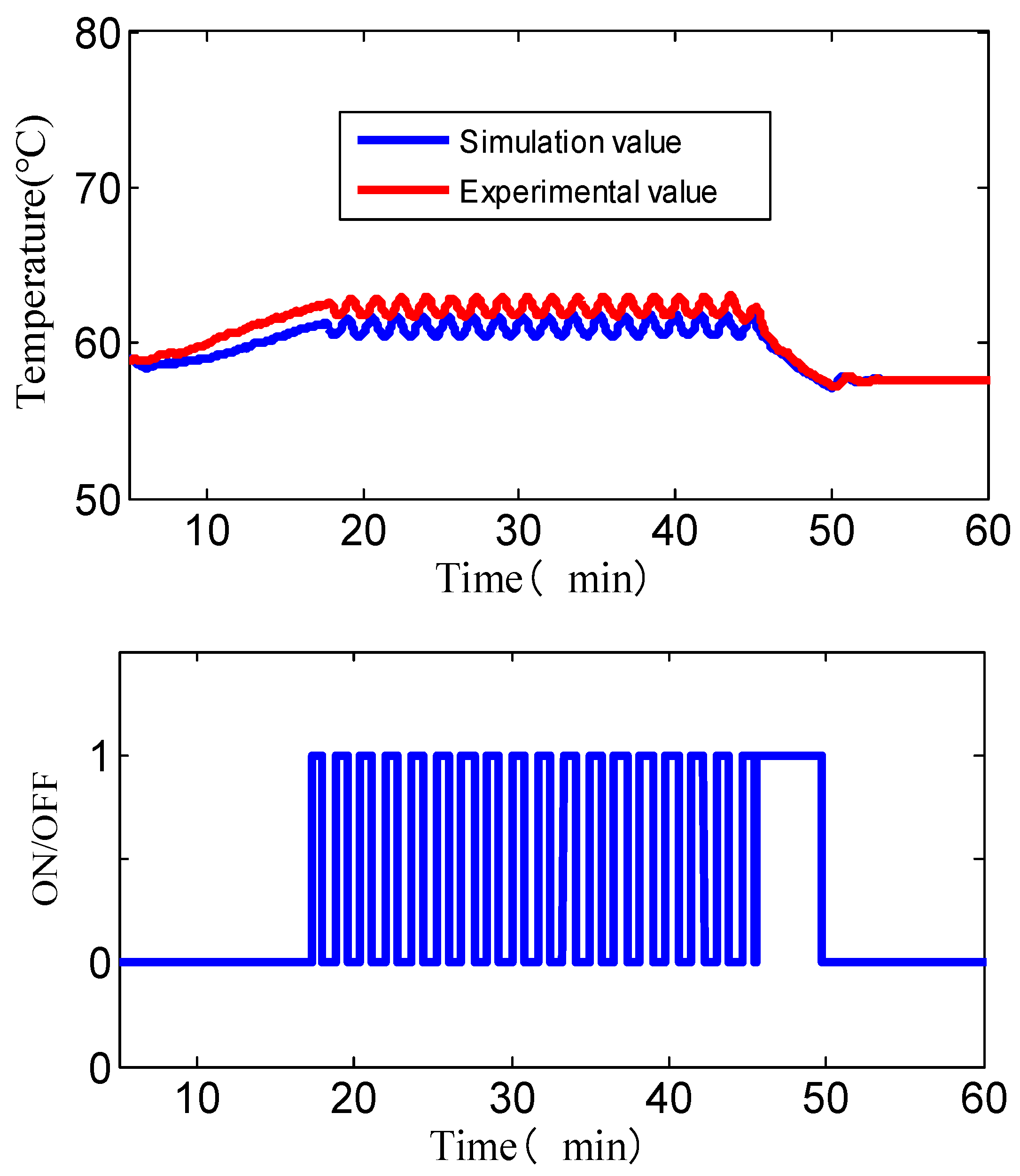
2.4. Cooling System Optimization
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | ld | Length of damping hole [m] | |
| A | Heat transfer area [m2] | Pin | Inlet pressure [Pa] |
| Cp | Specific heat capacity [J/kg.K] | Pout | Outlet pressure [Pa] |
| W | Thermal power[kW] | Fd | Output force [N] |
| Qf | Volume flow [m3·s−1] | A1 | Cross-sectional area [m2] |
| Temperature difference [°C] | A2 | Cross-sectional area [m2] | |
| P | Fan drive power [kW] | Abbreviation | |
| Tf | Fan torque [N·m] | min | Minimum value |
| U | Heat transfer coefficient [J kg−1K−1] | max | Maximum value |
| Mass flow rate [kg s−1] | NTU | Number of heat transfer units | |
| n | Percentage of heat in the fuel heat | exp | Exponential |
| g | fuel consumption rate [g/kW·h] | Superscripts and subscripts | |
| N | Calibrated power of the engine | Out | Outlet |
| h | Low calorific value of fuel | In | Inlet |
| Vm | Flow rate of motor [mL·r−1] | m | Motor |
| Pp | Pump power [kW] | p | Pump |
| qp | Pump flow rate [mL·r−1] | f | Fan |
| np | Pump speed [r·min−1] | p | Pressure |
| P1 | pressure of the main valve cavity | h | Hot |
| P2 | Pressure of the pilot valve cavity [N] | c | Cool |
| Fs | Steady-state hydrodynamic force [N] | V | Valve |
| kD1 | current-force gain factor | s | Steady-state |
| Current [A] | d | Damping hole | |
| k1 | Current-force gain | Greek Symbols | |
| k2 | Displacement-force gain | Transmission efficiency | |
| Displacement [m] | Emissivity | ||
| x | Displacement of valve spool [m] | Spool half-cone angle [°] | |
| dd | Diameter of damping hole [m] | Density [kg·m−3] | |
| Ad | Flow area [m2] | Viscosity (m2/s) | |
References
- Tong, Z.; Miao, J.; Li, Y.; Tong, S.-G.; Zhang, Q.; Tan, G.-R. Development of electric construction machinery in China: A review of key technologies and future directions. J. Zhejiang Univ.-Sci. A 2021, 22, 245–264. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, Z.; Li, K.; Liu, J.; Zhang, Y.; Dan, D.; Wu, C.; Wang, P.; Wang, X. An improved intelligent model predictive controller for cooling system of electric vehicle. Appl. Therm. Eng. 2021, 182, 116084. [Google Scholar] [CrossRef]
- Fan, R.; Zheng, N.; Sun, Z. Evaluation of fin intensified phase change material systems for thermal management of Li-ion battery modules. Int. J. Heat Mass Transf. 2021, 166, 120753. [Google Scholar] [CrossRef]
- Wang, S.; Ji, S.; Zhu, Y. A comparative study of cooling schemes for laminated lithium-ion batteries. Appl. Therm. Eng. 2021, 182, 116040. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, F.; Liu, Y.; Xu, S.; Chen, X. Thermal performance of honeycomb-like battery thermal management system with bionic liquid mini-channel and phase change materials for cylindrical lithium-ion battery. Appl. Therm. Eng. 2021, 188, 116649. [Google Scholar] [CrossRef]
- Akbarzadeh, M.; Jaguemont, J.; Kalogiannis, T.; Karimi, D.; He, J.; Jin, L.; Xie, P.; Van Mierlo, J.; Berecibar, M. A novel liquid cooling plate concept for thermal management of lithium-ion batteries in electric vehicles. Energy Convers. Manag. 2021, 231, 113862. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Liu, X.; Wang, Y.; Wu, X.; Zhou, D. Experiment investigation on a novel composite silica gel plate coupled with liquid-cooling system for square battery thermal management. Appl. Therm. Eng. 2021, 184, 116217. [Google Scholar] [CrossRef]
- Samudre, P.; Kailas, S.V. Thermal performance enhancement in open-pore metal foam and foam-fin heat sinks for electronics cooling. Appl. Therm. Eng. 2022, 205, 117885. [Google Scholar] [CrossRef]
- Jin, Q.; Wen, J.T.; Narayan, S. Oscillatory valve effect on temperature synchronization in microchannel cooling systems. Appl. Therm. Eng. 2022, 204, 117999. [Google Scholar] [CrossRef]
- Guo, Z.M.; Pfotenhauer, J.M.; Miller, F.K.; Zhu, S.W. A research of micro-pulse tube cryocooler with displacer phase shifter. Appl. Therm. Eng. 2022, 205, 117995. [Google Scholar] [CrossRef]
- Alzahrani, S.; Islam, M.S.; Sah, S.C. Heat transfer enhancement of modified flat plate heat exchanger. Appl. Therm. Eng. 2021, 186, 116533. [Google Scholar] [CrossRef]
- Al-Turki, Y.A.; Mori, H.; Shawabkeh, A. Thermal, frictional and exergetic analysis of non-parallel configurations for plate heat exchangers. Chem. Eng. Process. Process Intensif. 2021, 161, 108319. [Google Scholar] [CrossRef]
- Arsenyeva, O.; Tran, J.; Piper, M.; Kenig, E. An approach for pillow plate heat exchangers design for single-phase applications. Appl. Therm. Eng. 2019, 147, 579–591. [Google Scholar] [CrossRef]
- Khalil, I.; Hayes, R.; Pratt, Q.; Spitler, C.; Codd, D. Experimental and numerical modeling of heat transfer in directed thermoplates. Int. J. Heat Mass Transf. 2018, 123, 89–96. [Google Scholar] [CrossRef]
- Feng, S.Z.; Cheng, Y.H. An element decomposition method for heat transfer analysis. Int. J. Heat Mass Transf. 2018, 123, 437–444. [Google Scholar] [CrossRef]
- Mayo, I.; Arts, T.; Gicquel, L.Y.M. The three-dimensional flow field and heat transfer in a rib-roughened channel at large rotation numbers. Int. J. Heat Mass Transf. 2018, 123, 848–866. [Google Scholar] [CrossRef]
- Gong, C.; Du, Y.; Yu, Y.; Chang, H.; Luo, X.; Tu, Z. Numerical and experimental investigation of enhanced heat transfer radiator through air deflection used in fuel cell vehicles. Int. J. Heat Mass Transf. 2022, 183, 122205. [Google Scholar] [CrossRef]
- Zhang, B.; Qu, Z.; Guo, T.; Sheng, M.; Chen, M. Coupled thermal-hydraulic investigation on the heat extraction performance considering a fractal-like tree fracture network in a multilateral well enhanced geothermal system. Appl. Therm. Eng. 2022, 208, 118221. [Google Scholar] [CrossRef]
- Lu, Q.; Yuan, Y.; Li, F.; Yang, B.; Li, Z. Prediction method for thermal-hydraulic parameters of nuclear reactor system based on deep learning algorithm. Appl. Therm. Eng. 2021, 196, 117272. [Google Scholar] [CrossRef]
- Xie, Y.; Guo, H.; Li, W.; Zhang, Y.; Chen, B.; Zhang, K. Improving battery thermal behavior and consistency by optimizing structure and working parameter. Appl. Therm. Eng. 2021, 196, 117281. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Xiao, Y. Research on influence of high and low temperature heat sources for heat transfer characteristics of pulsating heat pipe cold storage device. Heat Mass Transf. 2022, 58, 233–246. [Google Scholar] [CrossRef]
- Zheng, S.; Feng, Z.; Lin, Q.; Hu, Z.; Lan, Y.; Guo, F.; Huang, K. Numerical investigation on thermal–hydraulic characteristics in a mini-channel with trapezoidal cross-section longitudinal vortex generators. Appl. Therm. Eng. 2021, 199, 117542. [Google Scholar] [CrossRef]
- Chen, S.R.; Lin, W.C.; Ferng, Y.M.; Chieng, C.C.; Pei, B.S. CFD simulating the transient thermal–hydraulic characteristics in a 17 × 17 bundle for a spent fuel pool under the loss of external cooling system accident. Ann. Nucl. Energy 2014, 73, 241–249. [Google Scholar] [CrossRef]
- Zhou, Y.; Yin, D.; Guo, X.; Dong, C. Numerical analysis of the thermal and hydraulic characteristics of CO2/propane mixtures in printed circuit heat exchangers. Int. J. Heat Mass Transf. 2022, 185, 122434. [Google Scholar] [CrossRef]
- Kwon, H.; Ivantysynova, M. Experimental and theoretical studies on energy characteristics of hydraulic hybrids for thermal management. Energy 2021, 223, 120033. [Google Scholar] [CrossRef]
- Hui, K.; Chen, W.; Li, S.; Zhao, Q.; Yan, J. Experimental study on transient thermal–hydraulic characteristics of an open natural circulation for the passive containment cooling system. Int. J. Heat Mass Transf. 2021, 179, 121680. [Google Scholar] [CrossRef]
- Kaood, A.; Hassan, M.A. Thermo-hydraulic performance of nanofluids flow in various internally corrugated tubes. Chem. Eng. Process. Process Intensif. 2020, 154, 108043. [Google Scholar] [CrossRef]
- Khalil, E.E.; Kaood, A. Numerical Investigation of Thermal-Hydraulic Characteristics for Turbulent Nanofluid Flow in Various Conical Double Pipe Heat Exchangers. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021. [Google Scholar]
- Sun, P.; Li, Q.; He, H.; Chen, H.; Zhang, J.; Li, H.; Liu, D. Design and optimization investigation on hydraulic transmission and energy storage system for a floating-array-buoys wave energy converter. Energy Convers. Manag. 2021, 235, 113998. [Google Scholar] [CrossRef]
- Tan, K.; Hu, Y.; He, Y. Effect of wettability on flow boiling heat transfer in a microtube. Case Stud. Therm. Eng. 2021, 26, 101108. [Google Scholar] [CrossRef]
- Yao, P.; Zhai, Y.; Li, Z.; Shen, X.; Wang, H. Thermal performance analysis of multi-objective optimized microchannels with triangular cavity and rib based on field synergy principle. Case Stud. Therm. Eng. 2021, 5, 100963. [Google Scholar]
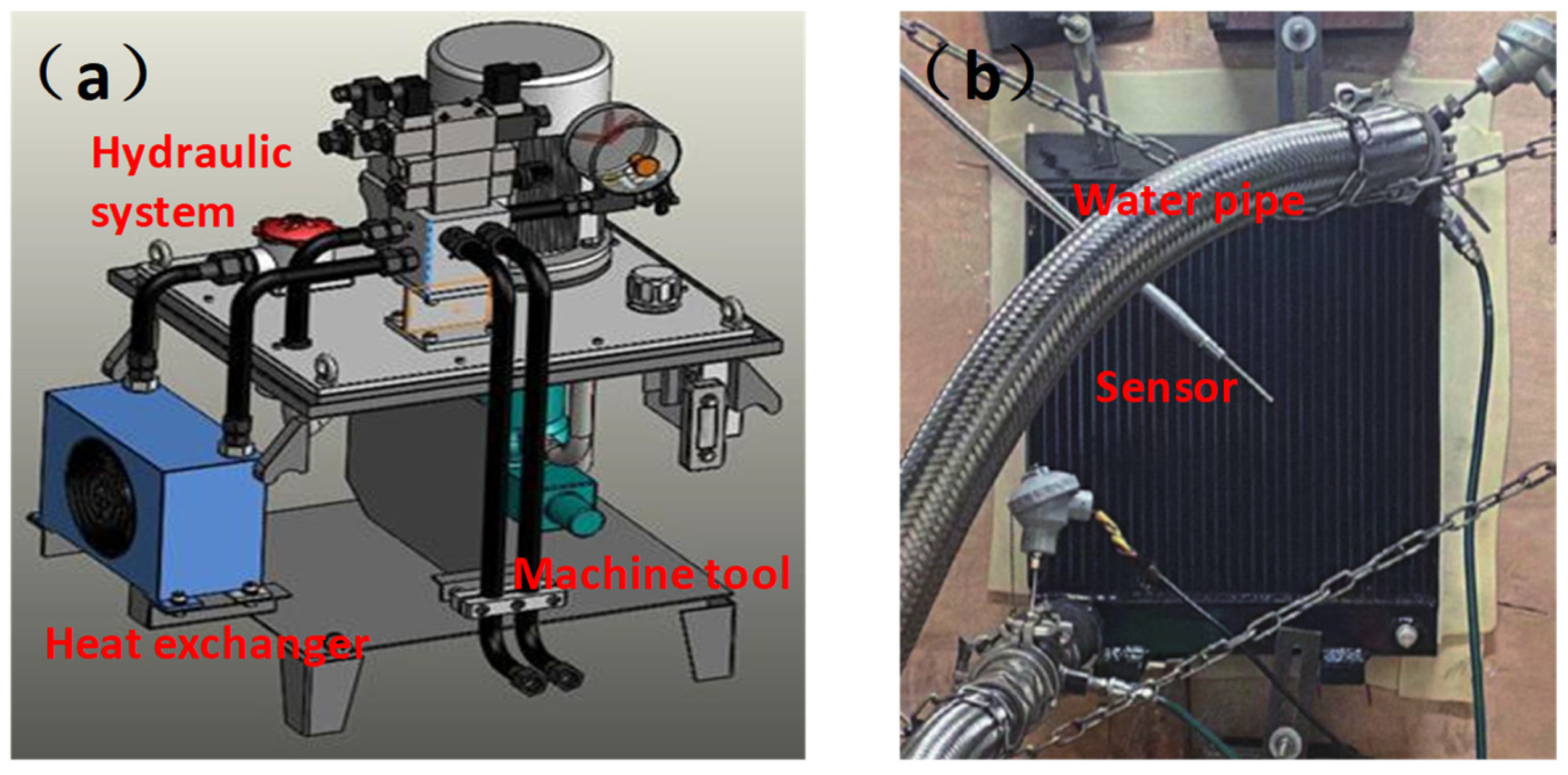

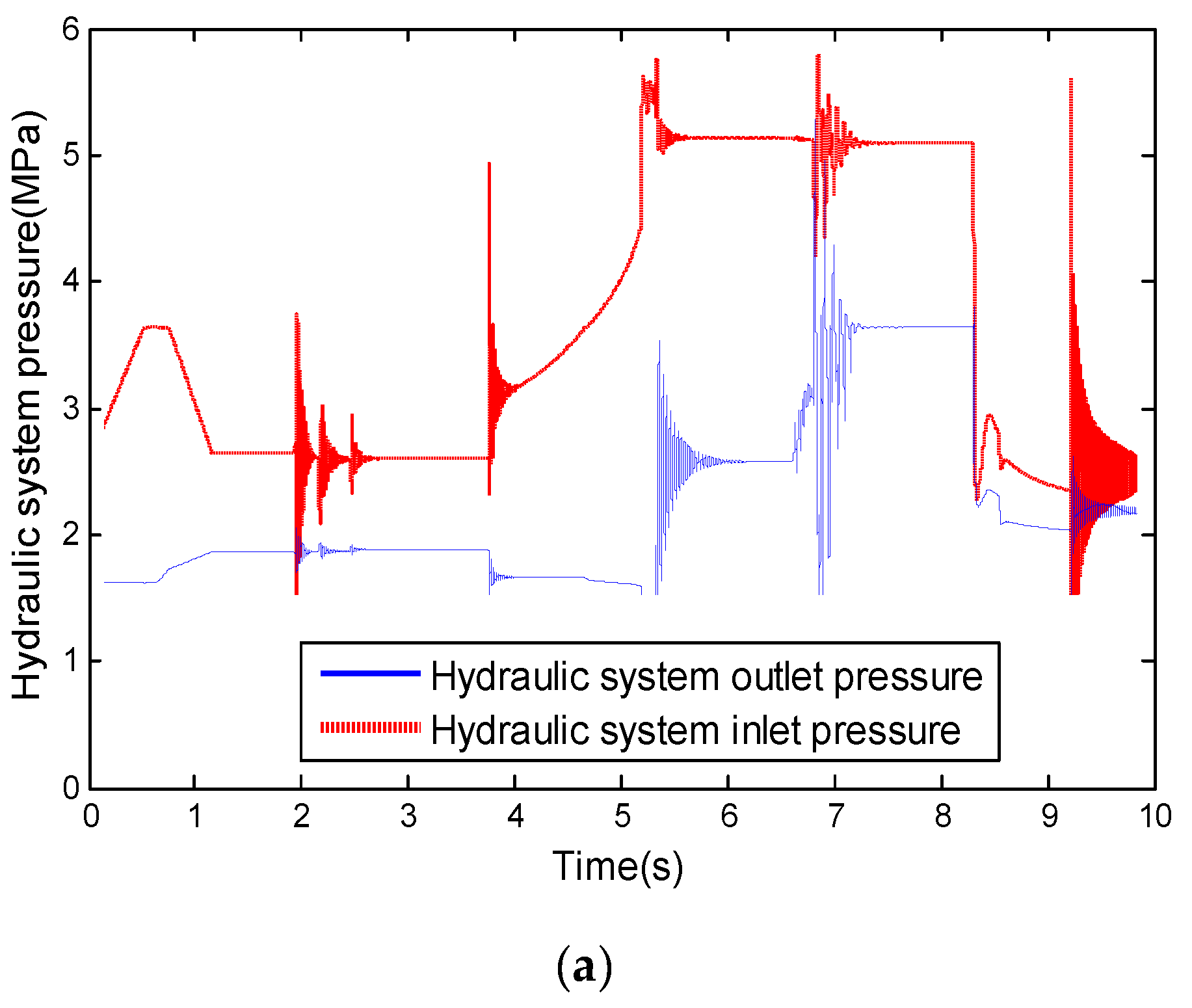
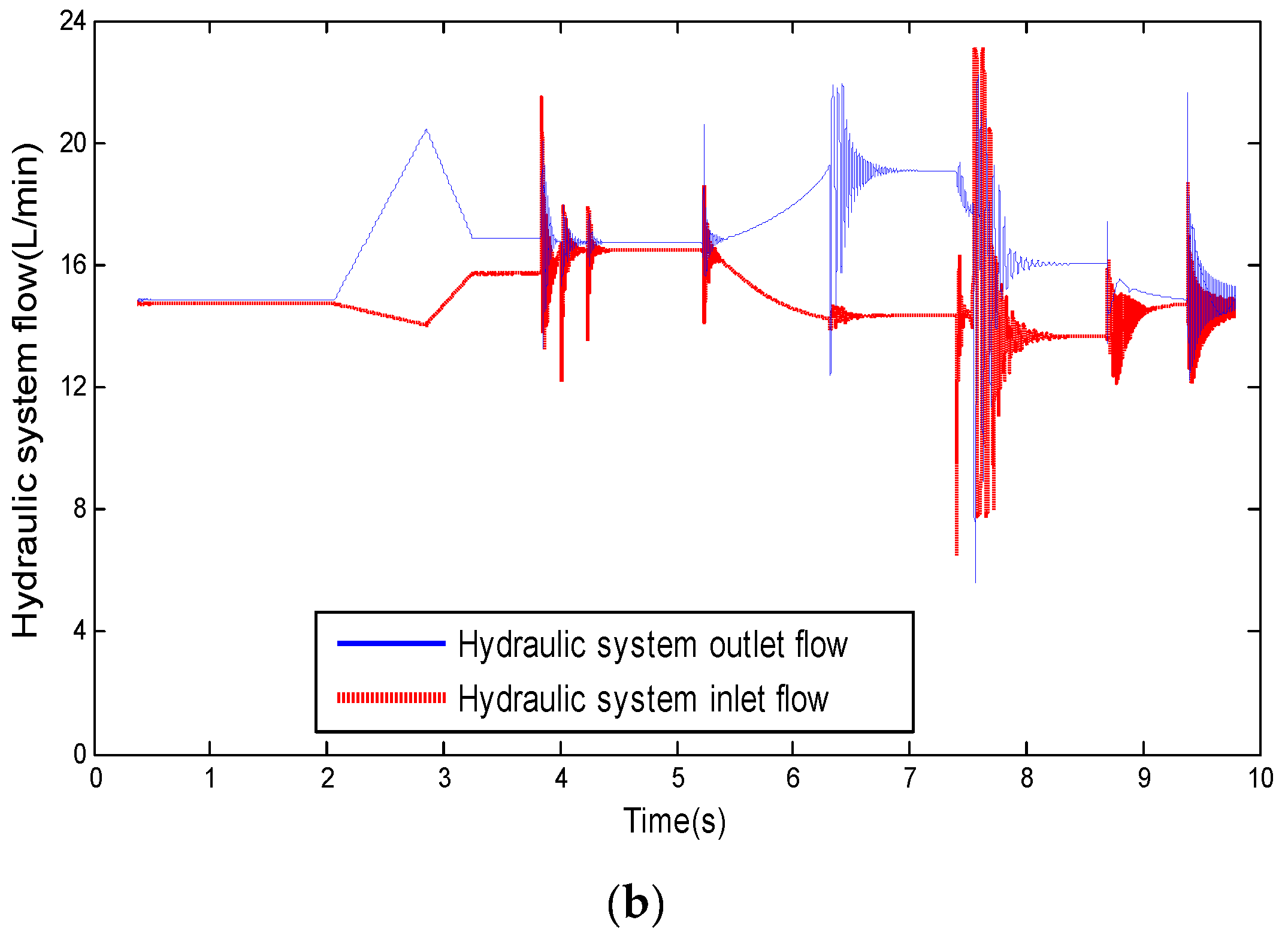
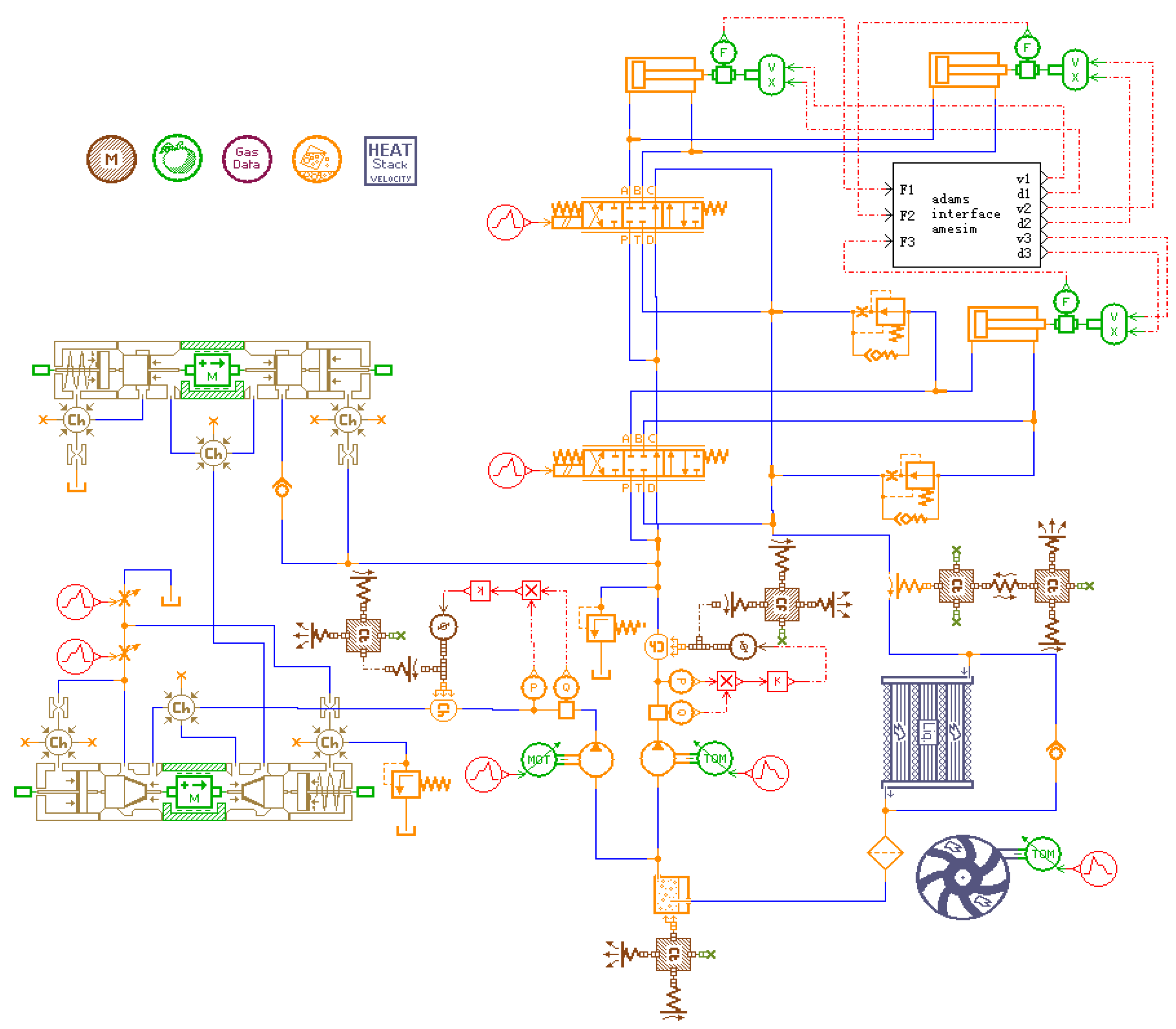
| Parameter | Relational Formula |
|---|---|
| Density (kg/m3) | |
| Specific heat capacity (kJ/kg °C) | |
| Dynamic viscosity (Pa·s) | |
| Thermal conductivity (kW/m °C) |
| Parameter | Relational Formula |
|---|---|
| Density (kg/m3) | |
| Specific heat capacity (kJ/kg °C) | |
| Dynamic viscosity (Pa·s) | |
| Thermal conductivity (kW/m °C) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Liu, X.; Tong, Z.; Cheng, Z. Research on Heat Generation Law and Cooling System Performance of Hydraulic System of Combined Machine Tool. Energies 2023, 16, 7322. https://doi.org/10.3390/en16217322
Zhang Q, Liu X, Tong Z, Cheng Z. Research on Heat Generation Law and Cooling System Performance of Hydraulic System of Combined Machine Tool. Energies. 2023; 16(21):7322. https://doi.org/10.3390/en16217322
Chicago/Turabian StyleZhang, Qinguo, Xiaojian Liu, Zheming Tong, and Zhewu Cheng. 2023. "Research on Heat Generation Law and Cooling System Performance of Hydraulic System of Combined Machine Tool" Energies 16, no. 21: 7322. https://doi.org/10.3390/en16217322
APA StyleZhang, Q., Liu, X., Tong, Z., & Cheng, Z. (2023). Research on Heat Generation Law and Cooling System Performance of Hydraulic System of Combined Machine Tool. Energies, 16(21), 7322. https://doi.org/10.3390/en16217322







