Optimizing Instrument Transformer Performance through Adaptive Blind Equalization and Genetic Algorithms
Abstract
:1. Introduction
2. Overview of Applied Techniques
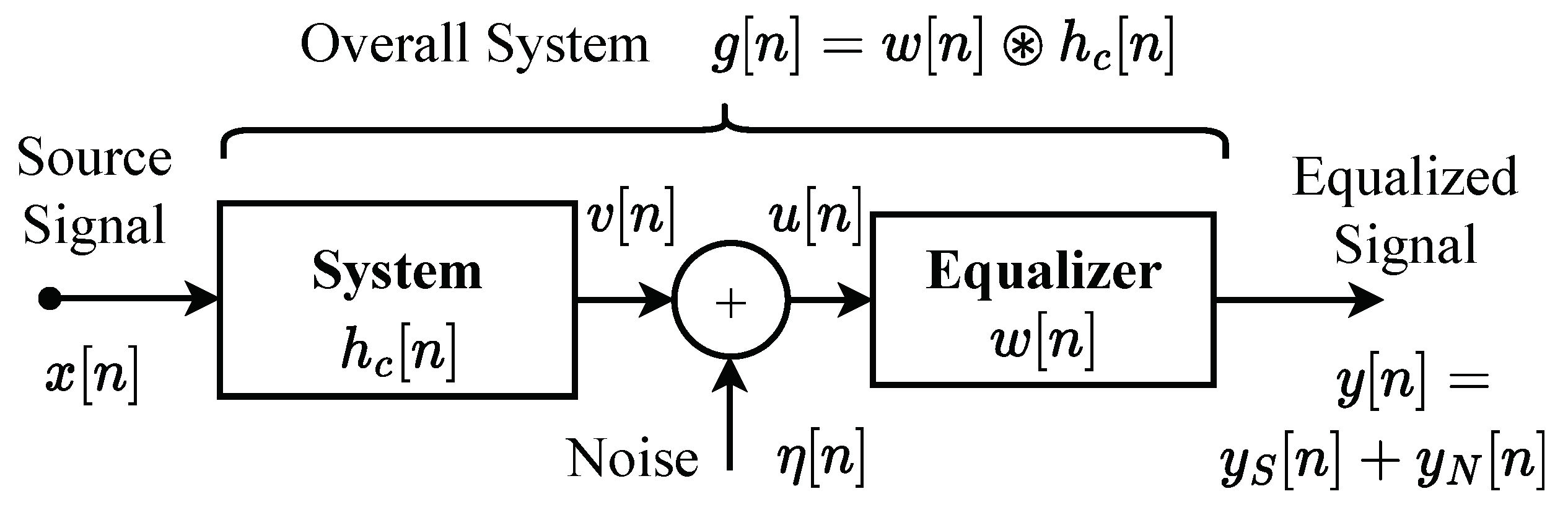
2.1. Blind Equalization
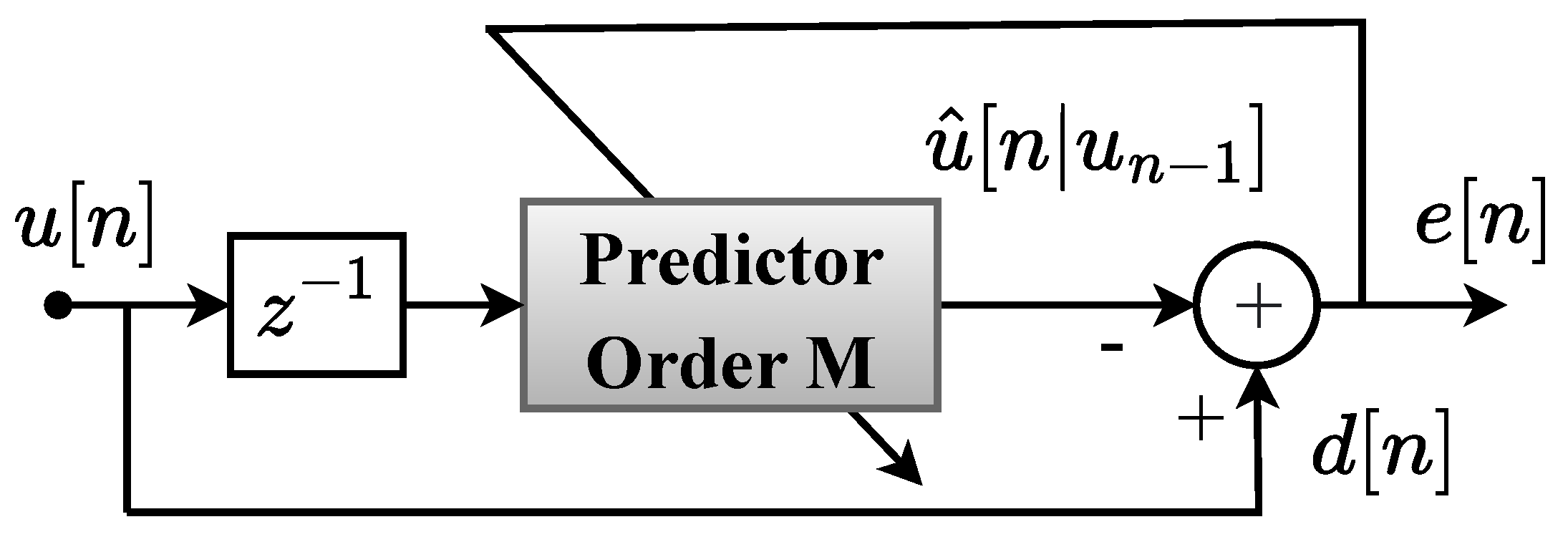
2.2. Linear Prediction Error (LPE) Filter
- The SISO LTI system represented by must be stable and have a minimum phase.
- The source signal is a Wide Sense Stationary (WSS) white process with a variance of .
- The noise is a zero-mean WSS white process with a variance of .
- The source signal is statistically independent of the noise .
2.3. Genetic Algorithm
3. Proposed Methodology
4. Discussion and Results
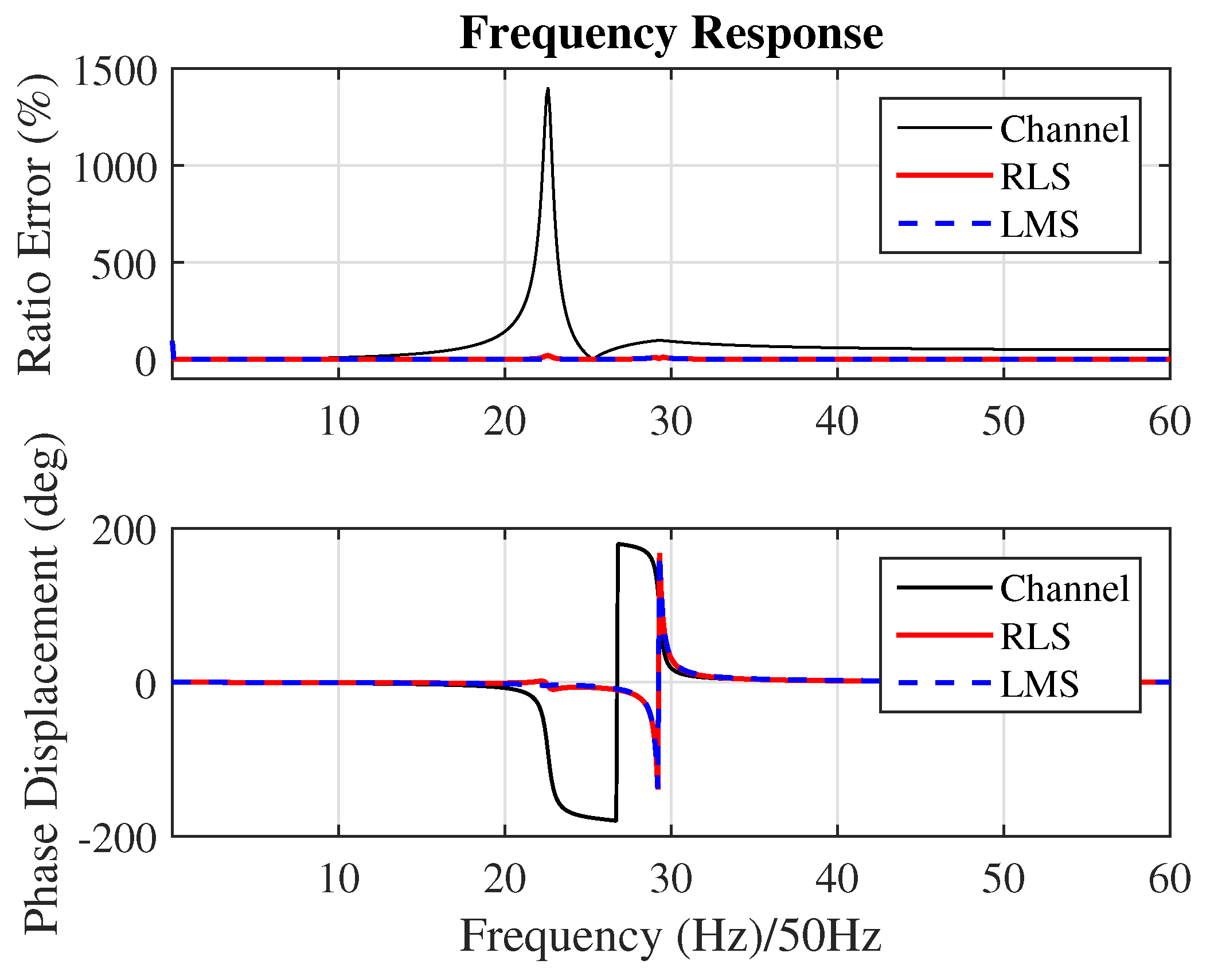
4.1. Synthetic Experiments
4.2. Real Experimental
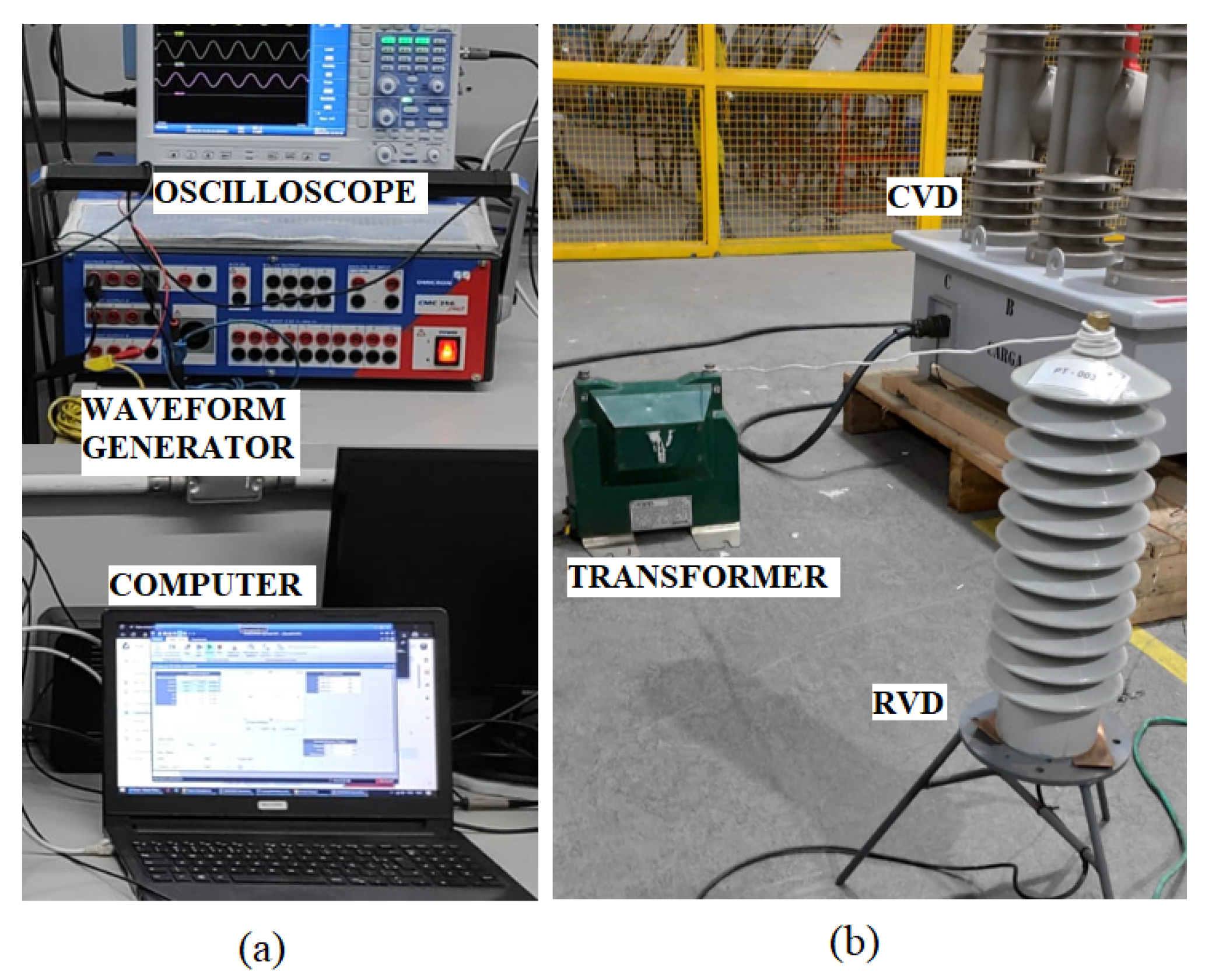
4.2.1. Laboratory Implementation
4.2.2. Results for Real Experimental
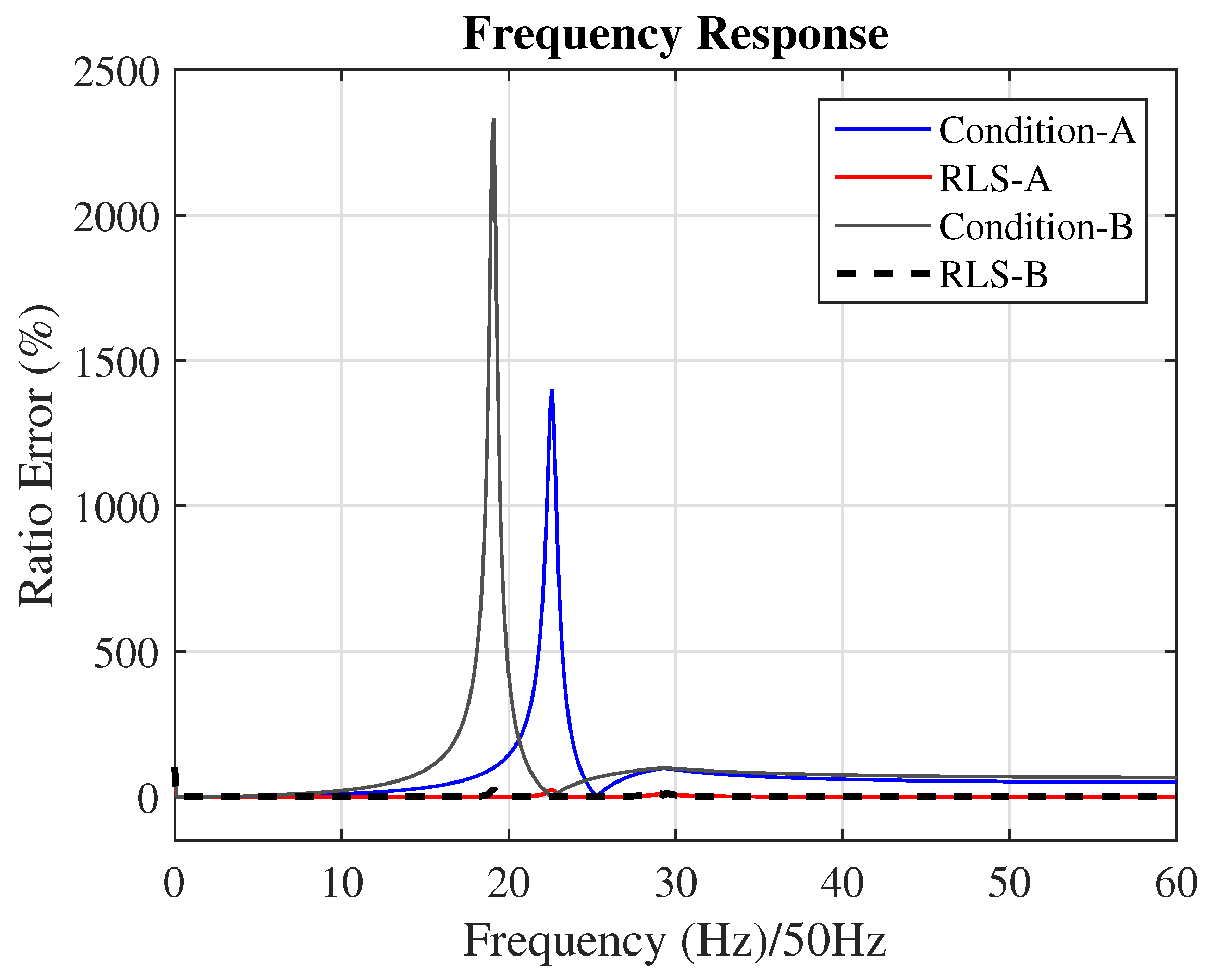
4.3. Online Equalization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Castello, P.; Laurano, C.; Muscas, C.; Pegoraro, P.A.; Toscani, S.; Zanoni, M. Harmonic Synchrophasors Measurement Algorithms with Embedded Compensation of Voltage Transformer Frequency Response. IEEE Trans. Instrum. Meas. 2021, 70, 9001310. [Google Scholar] [CrossRef]
- Verhelst, B.; Rens, S.; Rens, J.; Knockaert, J.; Desmet, J. On the Remote Calibration of Instrumentation Transformers: Influence of Temperature. Energies 2023, 16, 4744. [Google Scholar] [CrossRef]
- Artale, G.; Caravello, G.; Cataliotti, A.; Cosentino, V.; Cara, D.D.; Guaiana, S.; Panzavecchia, N.; Tine, G. Measurement of Simplified Single- And Three-Phase Parameters for Harmonic Emission Assessment Based on IEEE 1459–2010. IEEE Trans. Instrum. Meas. 2021, 70, 9000910. [Google Scholar] [CrossRef]
- D’Avanzo, G.; Faifer, M.; Landi, C.; Laurano, C.; Letizia, P.S.; Luiso, M.; Ottoboni, R.; Toscani, S. Improving Harmonic Measurements with Instrument Transformers: A Comparison among Two Techniques. In Proceedings of the Conference Record—IEEE Instrumentation and Measurement Technology Conference, Glasgow, UK, 17–20 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S. Adaptive Polynomial Harmonic Distortion Compensation in Current and Voltage Transformers Through Iteratively Updated QR Factorization. IEEE Trans. Instrum. Meas. 2023, 72, 9001810. [Google Scholar] [CrossRef]
- Faifer, M.; Ferrero, A.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. An Innovative Approach to Express Uncertainty Introduced by Voltage Transformers. IEEE Trans. Instrum. Meas. 2020, 69, 6696–6703. [Google Scholar] [CrossRef]
- Crotti, G.; D’Avanzo, G.; Landi, C.; Letizia, P.S.; Luiso, M. Evaluation of Voltage Transformers’ Accuracy in Harmonic and Interharmonic Measurement. IEEE Open J. Instrum. Meas. 2022, 1, 9000310. [Google Scholar] [CrossRef]
- Stiegler, R.; Freiburg, M.; von Zyl, J.; Meyer, J.; Feustel, F.; German, C. Methods for on-site qualification and calibration of inductive instrument voltage transformers for harmonic measurements. In Proceedings of the CIRED 2021—The 26th International Conference and Exhibition on Electricity Distribution. Institution of Engineering and Technology, Online Conference, 20–23 September 2021; pp. 752–756. [Google Scholar] [CrossRef]
- Beug, M.F.; Kolling, A.; Moser, H. A New Calibration Transformer and Measurement Setup for Bridge Standard Calibrations Up To 5 kHz. IEEE Trans. Instrum. Meas. 2017, 66, 1531–1538. [Google Scholar] [CrossRef]
- Jaschke, C.; Schegner, P. A measuring system to identify the frequency response of high current instrument transformers. In Proceedings of the 2015 Modern Electric Power Systems (MEPS), Wroclaw, Poland, 6–9 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Hu, H.; Xu, Y.; Wu, X.; Lin, F.; Xiao, X.; Lei, M. Passive-compensation clamp-on two-stage current transformer for online calibration. IET Sci. Meas. Technol. 2021, 15, 730–737. [Google Scholar] [CrossRef]
- Letizia, P.S.; Crotti, G.; Mingotti, A.; Tinarelli, R.; Chen, Y.; Mohns, E.; Agazar, M.; Istrate, D.; Ayhan, B.; Çayci, H.; et al. Characterization of Instrument Transformers under Realistic Conditions: Impact of Single and Combined Influence Quantities on Their Wideband Behavior. Sensors 2023, 23, 7833. [Google Scholar] [CrossRef] [PubMed]
- Agazar, M.; Istrate, D.; Pradayrol, P. Evaluation of the Accuracy and Frequency Response of Medium-Voltage Instrument Transformers under the Combined Influence Factors of Temperature and Vibration. Energies 2023, 16, 5012. [Google Scholar] [CrossRef]
- Stiegler, R.; Meyer, J. Impact of external influences on the frequency dependent transfer ratio of resin cast MV voltage instrument transformers. In Proceedings of the International Conference on Harmonics and Quality of Power, ICHQP, Naples, Italy, 29 May–1 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Mingotti, A.; Costa, F.; Peretto, L.; Tinarelli, R. Effects on the Accuracy Performance of Rogowski Coils Due to Temperature and Humidity. In Proceedings of the Conference Record—IEEE Instrumentation and Measurement Technology Conference, Ottawa, ON, Canada, 16–19 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Cesky, L.; Janicek, F.; Kubica, J.; Skudrik, F. Overheating of primary and secondary coils of voltage instrument transformers. In Proceedings of the 2017 18th International Scientific Conference on Electric Power Engineering, EPE 2017, Kouty nad Desnou, Czech Republic, 17–19 May 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Gopp, D.; Sperling, E.; Bischof, T.; Krüger, M. Temperature dependency of the frequency response characteristic of high voltage inductive instrument transformers and RC dividers. In Proceedings of the 22nd International Symposium on High Voltage Engineering (ISH 2021), Institution of Engineering and Technology, Xi’an, China, 21–26 November 2021; pp. 1664–1669. [Google Scholar] [CrossRef]
- Dadić, M.; Župan, T.; Kolar, G. FIR modeling of voltage instrument transformers from frequency response data. In Proceedings of the 2018 1st International Colloquium on Smart Grid Metrology, SmaGriMet 2018, Split, Croatia, 24–27 April 2018; Number 3; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, H.; Zhang, P.; Bi, T.; Qian, C. Instrument Transformer Calibration Method Based on Synchrophasor Measurement. In Proceedings of the I and CPS Asia 2022—2022 IEEE IAS Industrial and Commercial Power System Asia, Shanghai, China, 8–11 July 2022; pp. 179–184. [Google Scholar] [CrossRef]
- Vaytelenok, L. Operation of relay protection digital elements at saturation of current transformers: Modeling and analysis. In Proceedings of the 2019 International Conference on Industrial Engineering, Applications and Manufacturing, ICIEAM 2019, Sochi, Russia, 25–29 March 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Cui, B.; Srivastava, A.K.; Banerjee, P. Synchrophasor-Based Condition Monitoring of Instrument Transformers Using Clustering Approach. IEEE Trans. Smart Grid 2020, 11, 2688–2698. [Google Scholar] [CrossRef]
- Sidorova, A.; Litvinov, I.; Kornilovich, D.; Fedorova, V.; Tanfilev, O.; Titov, V. Development and Verification of an Advanced Method for Diagnosing Measuring Transformers. In Proceedings of the 2021 Ural-Siberian Smart Energy Conference, USSEC 2021, Novosibirsk, Russia, 13–15 November 2021; pp. 57–61. [Google Scholar] [CrossRef]
- Kaczmarek, M.; Stano, E. Challenges of Accurate Measurement of Distorted Current and Voltage in the Power Grid by Conventional Instrument Transformers. Energies 2023, 16, 2648. [Google Scholar] [CrossRef]
- Toscani, S.; Faifer, M.; Ferrero, A.; Laurano, C.; Ottoboni, R.; Zanoni, M. Compensating Nonlinearities in Voltage Transformers for Enhanced Harmonic Measurements: The Simplified Volterra Approach. IEEE Trans. Power Deliv. 2021, 36, 362–370. [Google Scholar] [CrossRef]
- Collin, A.J.; Femine, A.D.; Gallo, D.; Langella, R.; Luiso, M. Compensation of Current Transformers’ Nonlinearities by Tensor Linearization. IEEE Trans. Instrum. Meas. 2019, 68, 3841–3849. [Google Scholar] [CrossRef]
- D’Avanzo, G.; Faifer, M.; Landi, C.; Laurano, C.; Letizia, P.S.; Luiso, M.; Ottoboni, R.; Toscani, S. Theory and Experimental Validation of Two Techniques for Compensating VT Nonlinearities. IEEE Trans. Instrum. Meas. 2022, 71, 9001312. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Harmonic Distortion Compensation in Voltage Transformers for Improved Power Quality Measurements. IEEE Trans. Instrum. Meas. 2019, 68, 3823–3830. [Google Scholar] [CrossRef]
- Cataliotti, A.; Cosentino, V.; Crotti, G.; Femine, A.D.; Di Cara, D.; Gallo, D.; Giordano, D.; Landi, C.; Luiso, M.; Modarres, M.; et al. Compensation of Nonlinearity of Voltage and Current Instrument Transformers. IEEE Trans. Instrum. Meas. 2019, 68, 1322–1332. [Google Scholar] [CrossRef]
- Resende, D.F.; Duque, C.A.; Nepomuceno, E.G.; Lima, M.A.A.; Silva, L.R.M. Adaptive Channel Equalization for Frequency Response Correction of Instrument Transformers. In Proceedings of the 20th International Conference on Harmonics and Quality of Power—ICHQP, Naples, Italy, 29 May–1 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Chi, C.Y.; Feng, C.C.; Chen, C.H.; Chen, C.Y. Blind Equalization and System Identification: Batch Processing Algorithms, Performance and Applications; Springer Science & Business Media: London, UK, 2006; p. 478. [Google Scholar] [CrossRef]
- Zhan, Z.H.; Shi, L.; Tan, K.C.; Zhang, J. A survey on evolutionary computation for complex continuous optimization. Artif. Intell. Rev. 2022, 55, 59–110. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1976; p. 529. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989; p. 412. [Google Scholar]
- Raj, A.; Kumar, A.; Sharma, V.; Rani, S.; Shanu, A.K.; Singh, T. Applications of Genetic Algorithm with Integrated Machine Learning. In Proceedings of the 2023 3rd International Conference on Innovative Practices in Technology and Management, ICIPTM 2023, Uttar Pradesh, India, 22–24 February 2023; pp. 1–6. [Google Scholar] [CrossRef]
- IEC 61869-1; Instrument Transformers—Part 1: General Requirements. Technical report; IEC—International Electrotechnical Commission: Geneva, Switzerland, 2007.
- TR 61869-103; Instrument Transformers—The Use of Instrument Transformers for Power Quality Measurement. Technical report; IEC—International Eectrotechnical Commission: Geneva, Switzerland, 2012.





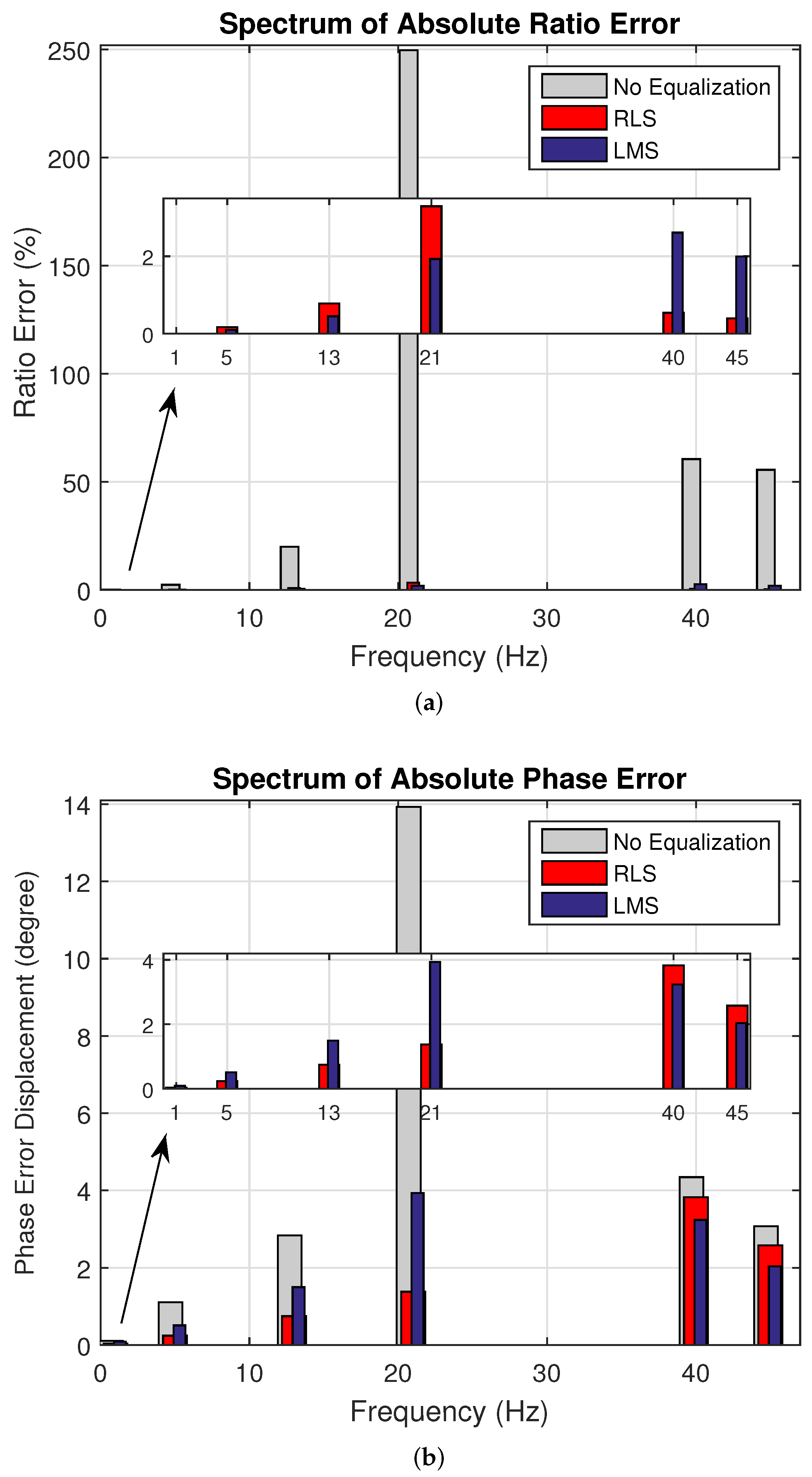

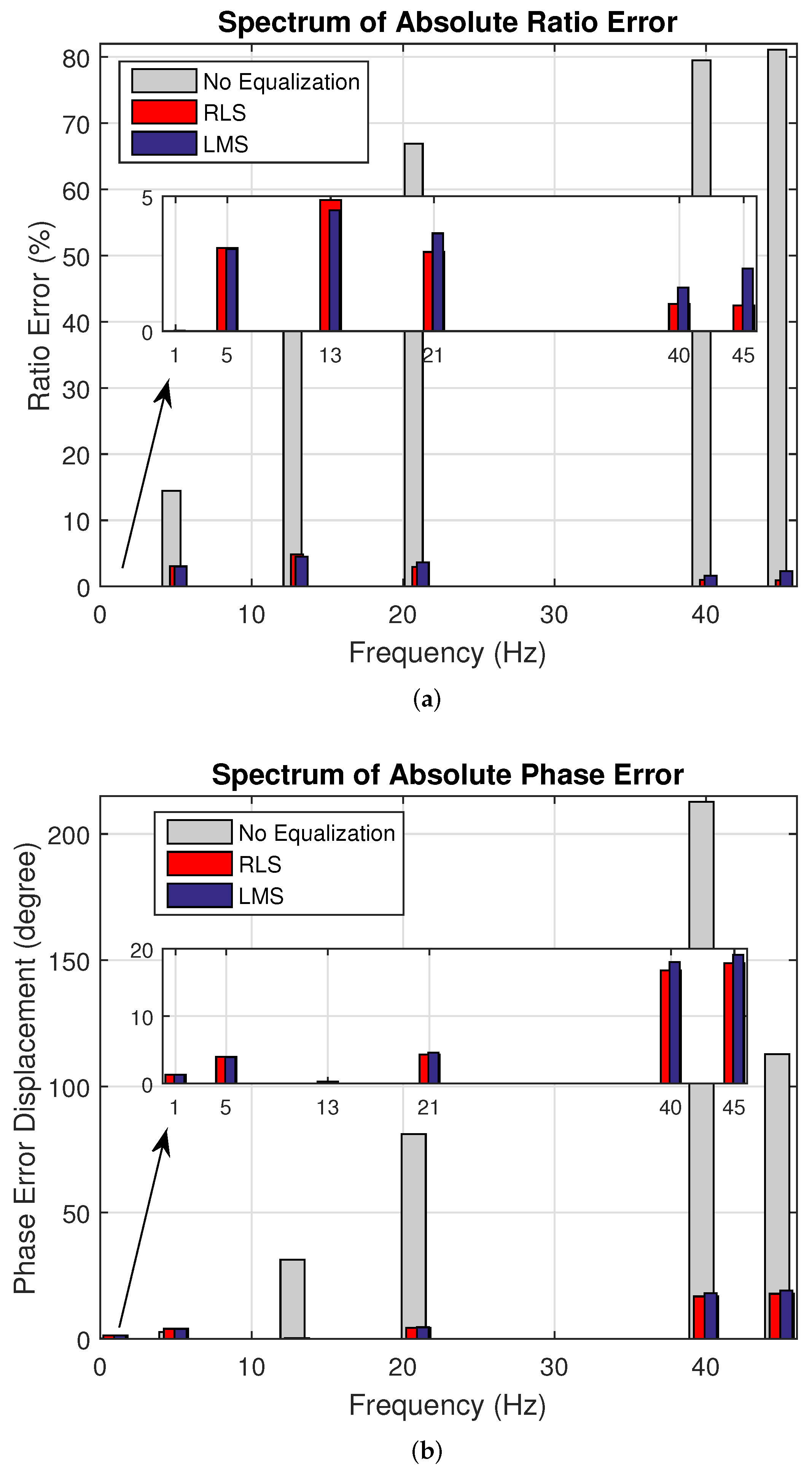
| Spectrum | Absolute Ratio Error (%) | |||||||
|---|---|---|---|---|---|---|---|---|
| Harmonic Index | 1 | 5 | 13 | 21 | 40 | 45 | ||
| Blind Synthetic Experiments | Case 1 | No Equalization | 0.17 | 5.00 | 27.93 | 290.64 | 61.18 | 55.29 |
| RLS | 0.00 | 0.03 | 0.24 | 2.15 | 0.12 | 0.14 | ||
| LMS | 0.00 | 0.09 | 0.58 | 3.82 | 0.78 | 1.27 | ||
| Case 2 | No Equalization | 0.08 | 2.23 | 19.79 | 248.99 | 60.38 | 55.50 | |
| RLS | 0.00 | 0.01 | 0.07 | 1.46 | 0.55 | 0.44 | ||
| LMS | 0.00 | 0.01 | 0.13 | 0.84 | 0.09 | 0.30 | ||
| Case 3 | No Equalization | 0.07 | 2.35 | 20.48 | 253.08 | 60.44 | 55.38 | |
| RLS | 0.00 | 0.03 | 0.26 | 2.25 | 0.05 | 0.21 | ||
| LMS | 0.00 | 0.06 | 0.52 | 3.64 | 0.70 | 1.16 | ||
| Case 4 | No Equalization | 0.16 | 3.23 | 20.26 | 245.42 | 59.15 | 55.85 | |
| RLS | 0.00 | 0.40 | 1.53 | 4.87 | 2.87 | 1.30 | ||
| LMS | 0.00 | 0.29 | 0.97 | 2.52 | 3.84 | 2.58 | ||
| Case 5 | No Equalization | 0.09 | 2.39 | 19.96 | 249.63 | 60.51 | 55.56 | |
| RLS | 0.00 | 0.16 | 0.78 | 3.29 | 0.54 | 0.39 | ||
| LMS | 0.00 | 0.10 | 0.45 | 1.93 | 2.61 | 1.99 | ||
| Case 6 | No Equalization | 0.06 | 1.93 | 19.50 | 247.55 | 60.22 | 55.33 | |
| RLS | 0.00 | 0.04 | 0.43 | 2.13 | 1.55 | 0.78 | ||
| LMS | 0.00 | 0.03 | 0.31 | 0.24 | 1.57 | 0.85 | ||
| Blind Real Experiments | Case 7 | No Equalization | 0.04 | 14.43 | 50.00 | 66.46 | 79.27 | 80.79 |
| RLS | 0.00 | 1.30 | 1.03 | 1.93 | 4.44 | 9.13 | ||
| LMS | 0.04 | 0.39 | 2.04 | 4.52 | 4.24 | 9.52 | ||
| Case 8 | No Equalization | 0.01 | 14.44 | 49.72 | 66.88 | 79.50 | 81.10 | |
| RLS | 0.00 | 3.08 | 4.86 | 2.93 | 1.00 | 0.95 | ||
| LMS | 0.01 | 3.04 | 4.48 | 3.62 | 1.61 | 2.32 | ||
| Case 9 | No Equalization | 0.05 | 14.38 | 49.46 | 66.97 | 79.70 | 80.98 | |
| RLS | 0.00 | 3.65 | 4.02 | 4.31 | 3.70 | 5.44 | ||
| LMS | 0.05 | 4.55 | 3.67 | 0.52 | 3.62 | 8.77 | ||
| Spectrum | Absolute Phase Error (Degree) | |||||||
|---|---|---|---|---|---|---|---|---|
| Harmonic Index | 1 | 5 | 13 | 21 | 40 | 45 | ||
| Blind Synthetic Experiments | Case 1 | No Equalization | 0.10 | 1.61 | 1.51 | 9.22 | 6.79 | 5.21 |
| RLS | 0.02 | 0.17 | 0.51 | 0.24 | 2.34 | 1.52 | ||
| LMS | 0.00 | 0.09 | 0.32 | 0.16 | 2.83 | 1.94 | ||
| Case 2 | No Equalization | 0.10 | 0.91 | 2.53 | 13.12 | 3.62 | 2.43 | |
| RLS | 0.04 | 0.23 | 0.70 | 0.61 | 2.06 | 1.28 | ||
| LMS | 0.04 | 0.23 | 0.84 | 2.56 | 2.53 | 1.65 | ||
| Case 3 | No Equalization | 0.10 | 0.67 | 1.91 | 11.48 | 1.23 | 0.70 | |
| RLS | 0.02 | 0.15 | 0.47 | 0.07 | 2.15 | 1.38 | ||
| LMS | 0.01 | 0.07 | 0.30 | 0.33 | 2.60 | 1.77 | ||
| Case 4 | No Equalization | 0.11 | 2.54 | 5.33 | 18.28 | 12.89 | 10.18 | |
| RLS | 0.03 | 0.35 | 0.90 | 0.38 | 4.05 | 2.69 | ||
| LMS | 0.08 | 0.54 | 1.47 | 4.02 | 3.51 | 2.21 | ||
| Case 5 | No Equalization | 0.10 | 1.10 | 2.84 | 13.93 | 4.34 | 3.07 | |
| RLS | 0.03 | 0.24 | 0.74 | 1.37 | 3.82 | 2.57 | ||
| LMS | 0.09 | 0.50 | 1.49 | 3.93 | 3.23 | 2.03 | ||
| Case 6 | No Equalization | 0.10 | 0.56 | 2.03 | 12.19 | 2.55 | 1.73 | |
| RLS | 0.10 | 0.51 | 1.63 | 3.14 | 4.71 | 3.01 | ||
| LMS | 0.12 | 0.64 | 2.07 | 5.96 | 4.89 | 3.12 | ||
| Blind Real Experiments | Case 7 | No Equalization | 0.15 | 2.61 | 31.90 | 278.51 | 147.56 | 112.69 |
| RLS | 0.21 | 2.60 | 3.51 | 12.40 | 12.23 | 20.55 | ||
| LMS | 0.24 | 1.14 | 1.82 | 4.97 | 11.98 | 20.72 | ||
| Case 8 | No Equalization | 0.18 | 2.64 | 31.33 | 81.07 | 212.77 | 112.80 | |
| RLS | 1.30 | 3.97 | 0.26 | 4.31 | 16.79 | 17.86 | ||
| LMS | 1.30 | 3.93 | 0.24 | 4.58 | 18.02 | 19.09 | ||
| Case 9 | No Equalization | 0.15 | 2.30 | 31.57 | 80.73 | 212.16 | 112.77 | |
| RLS | 0.91 | 0.30 | 4.16 | 1.49 | 13.34 | 13.09 | ||
| LMS | 1.29 | 1.01 | 3.72 | 2.06 | 14.28 | 11.82 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Resende, D.F.; Silva, L.R.M.; Nepomuceno, E.G.; Duque, C.A. Optimizing Instrument Transformer Performance through Adaptive Blind Equalization and Genetic Algorithms. Energies 2023, 16, 7354. https://doi.org/10.3390/en16217354
Resende DF, Silva LRM, Nepomuceno EG, Duque CA. Optimizing Instrument Transformer Performance through Adaptive Blind Equalization and Genetic Algorithms. Energies. 2023; 16(21):7354. https://doi.org/10.3390/en16217354
Chicago/Turabian StyleResende, Denise Fonseca, Leandro Rodrigues Manso Silva, Erivelton Geraldo Nepomuceno, and Carlos Augusto Duque. 2023. "Optimizing Instrument Transformer Performance through Adaptive Blind Equalization and Genetic Algorithms" Energies 16, no. 21: 7354. https://doi.org/10.3390/en16217354
APA StyleResende, D. F., Silva, L. R. M., Nepomuceno, E. G., & Duque, C. A. (2023). Optimizing Instrument Transformer Performance through Adaptive Blind Equalization and Genetic Algorithms. Energies, 16(21), 7354. https://doi.org/10.3390/en16217354








