Battery Energy Storage System Damper Design for a Microgrid with Wind Generators Participating in Frequency Regulation
Abstract
:1. Introduction
1.1. Background and Literature Review
1.2. Research Gap and Motivation
1.3. Contributions
- (1)
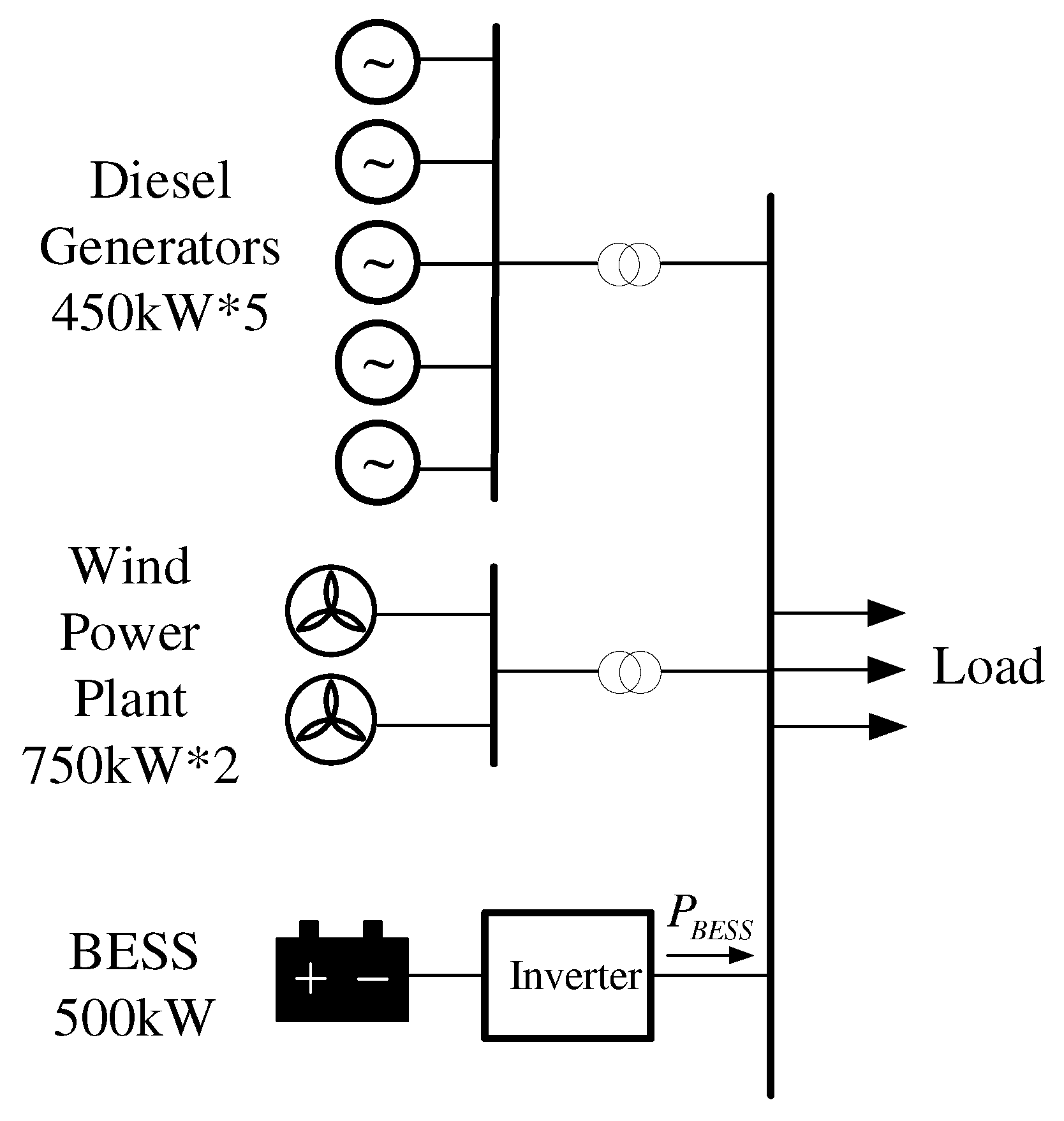
- We present a complete model for a microgrid comprising diesel generators, wind generators with droop control, and a BESS.
- (2)
- We derived a transfer function that relates the BESS damping signal to the DFIG damping torque. We also designed a feedforward compensator for the BESS damper based on the phase lag computed using the transfer function.
- (3)
- To improve the damping ratio for the torsional mode, we use the pole assignment method to shift the eigenvalues of poorly damped modes leftward to desired locations. The eigenvalue location with minimal damper gain is chosen in order to minimize power output from the BESS.
1.4. Structure of Paper
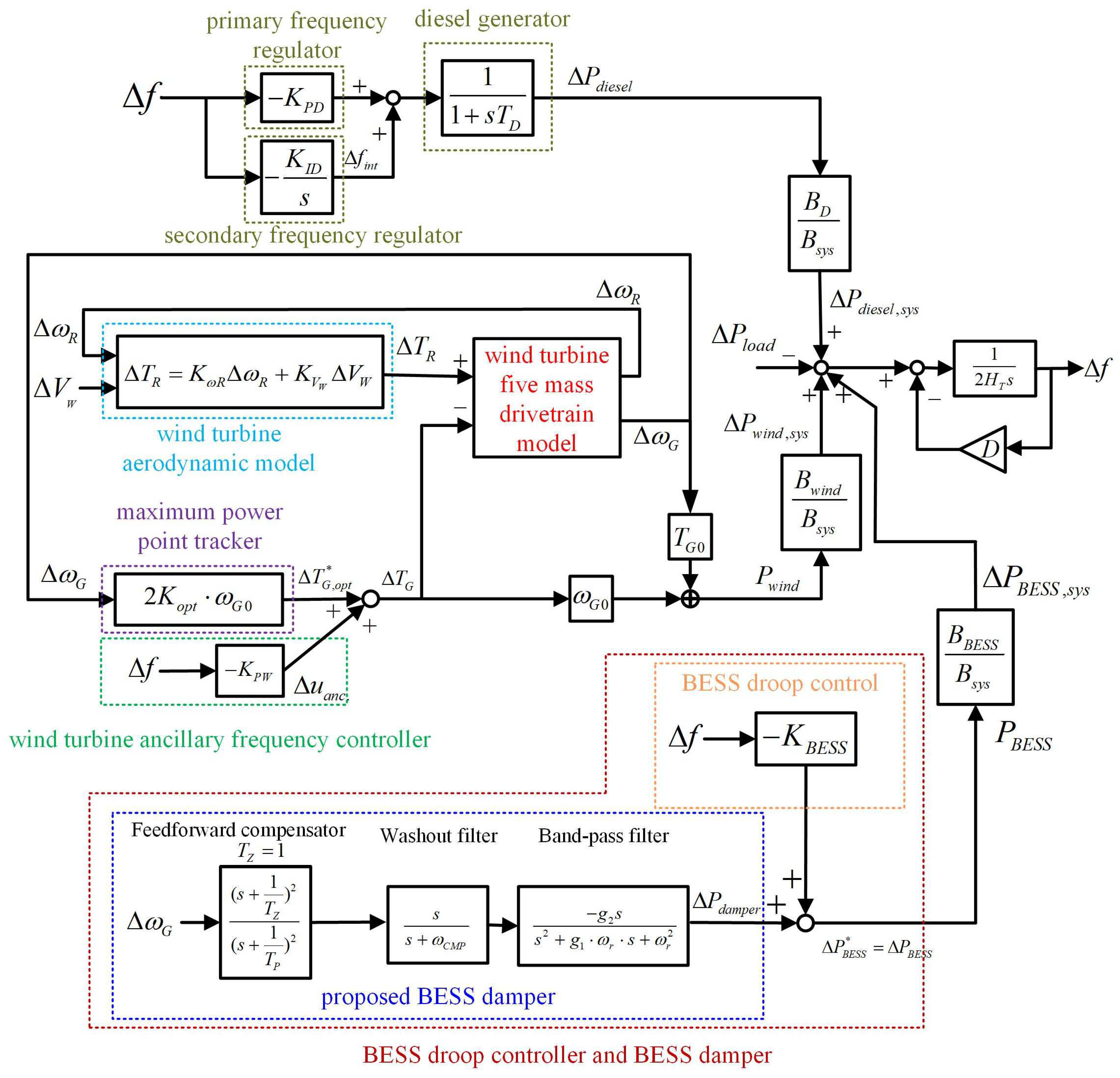
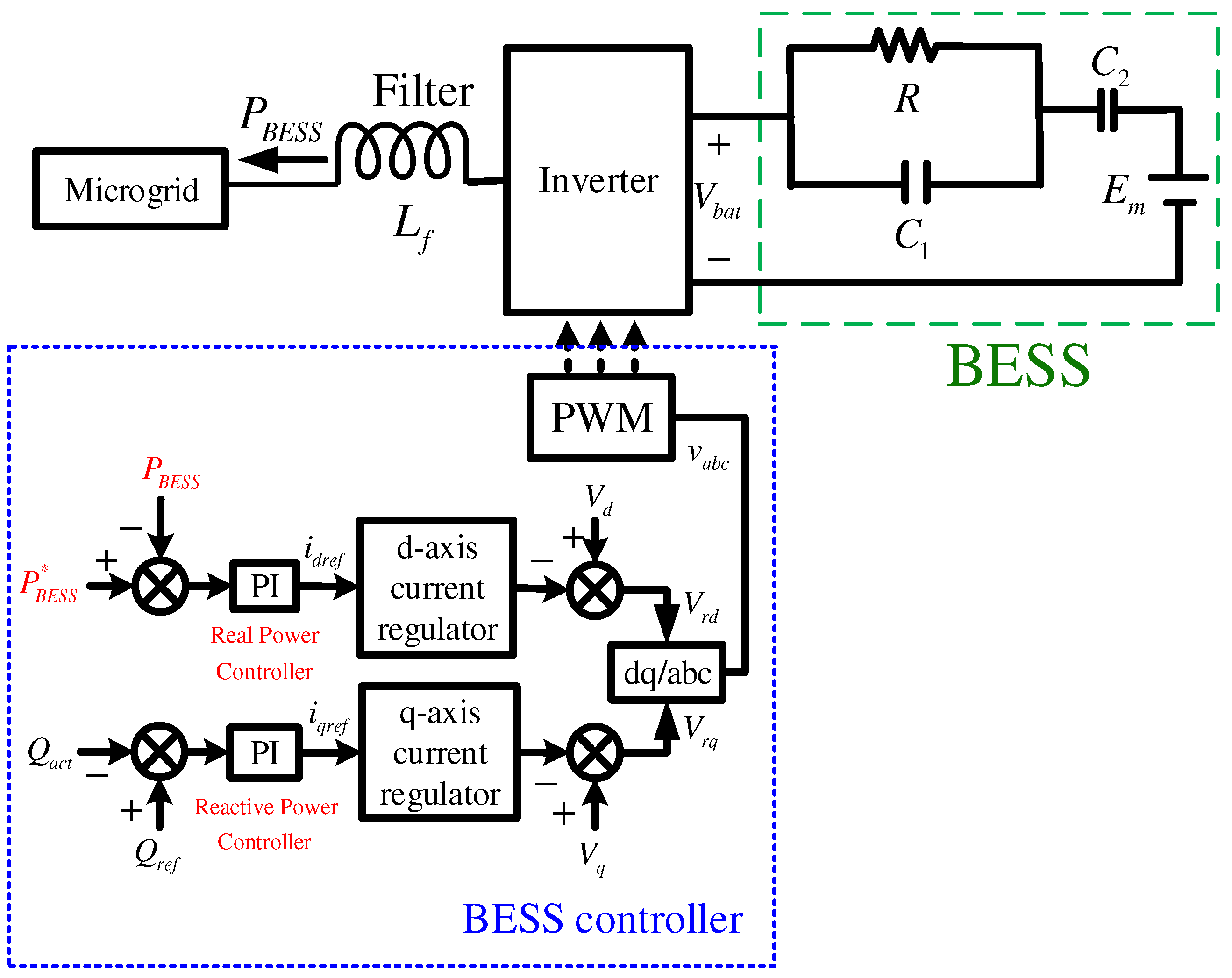
2. System Model
3. Modal Analysis of Microgrid with Wind Generator and BESS
3.1. Modal Analysis of Microgrid without BESS
3.2. Modal Analysis of Microgrid with BESS but without BESS Damper
4. BESS Damper Design Based on Modal Control Theory
4.1. Design of Feedforward Compensator
4.2. Design of Bandpass Filter
5. Simulation Results
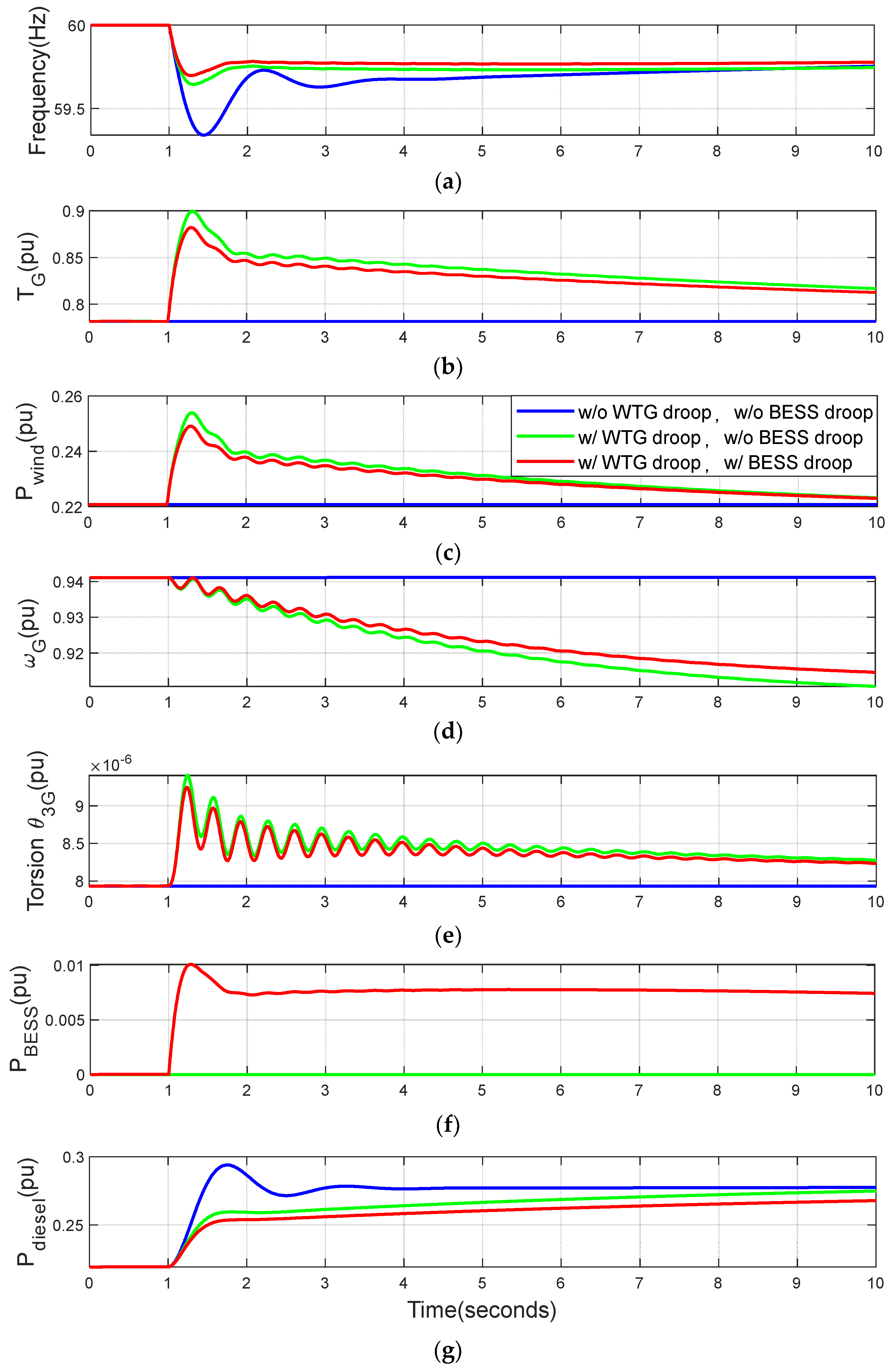
5.1. Effects of Wind Turbine Generator (WTG) Droop Control on Torsional Mode Oscillations: Microgrid without BESS Damper
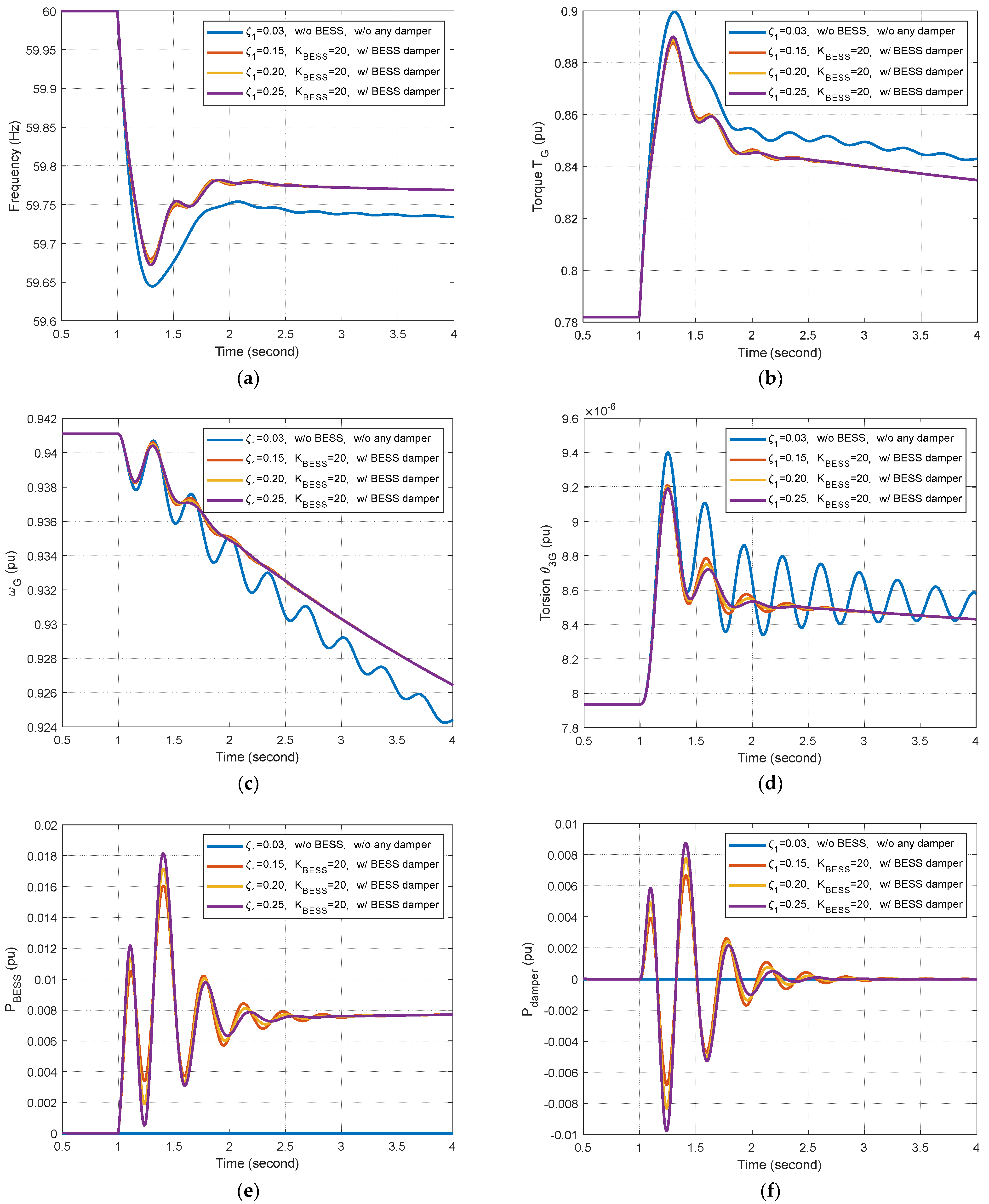
5.2. Effects of BESS Damper on Torsional Oscillation: Microgrid with a BESS Damper
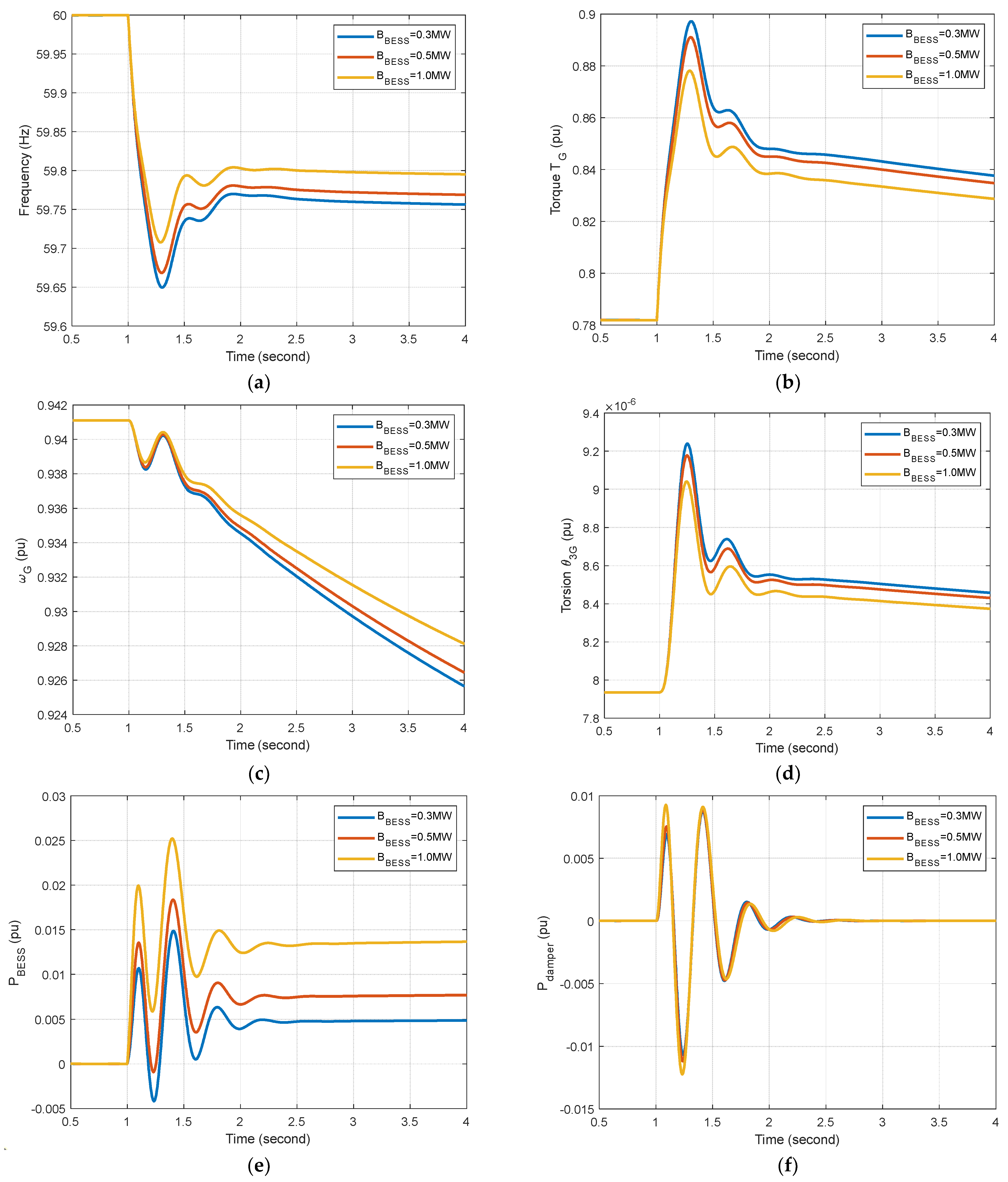
5.3. Effects of BESS Capacity on Dynamic Performance
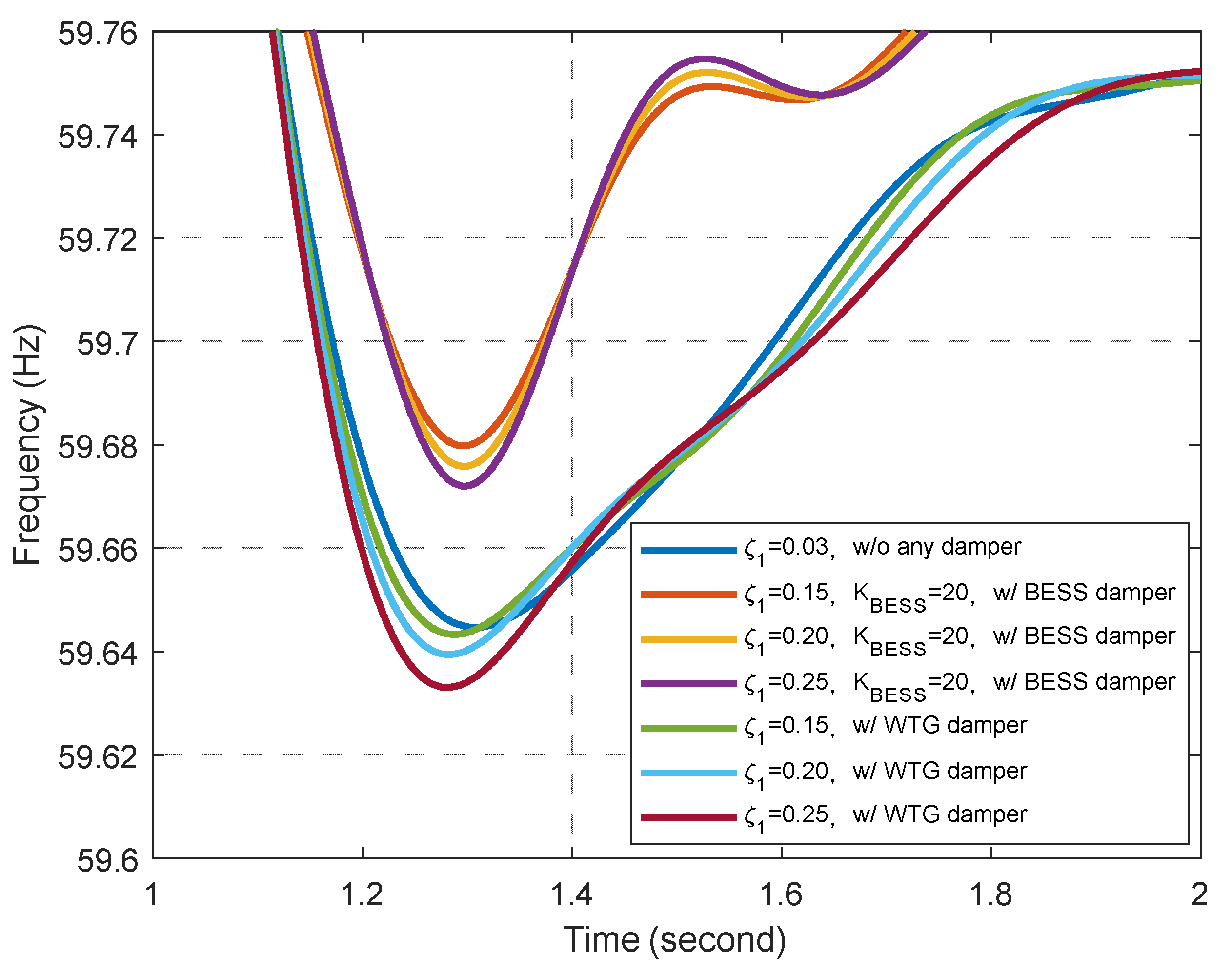
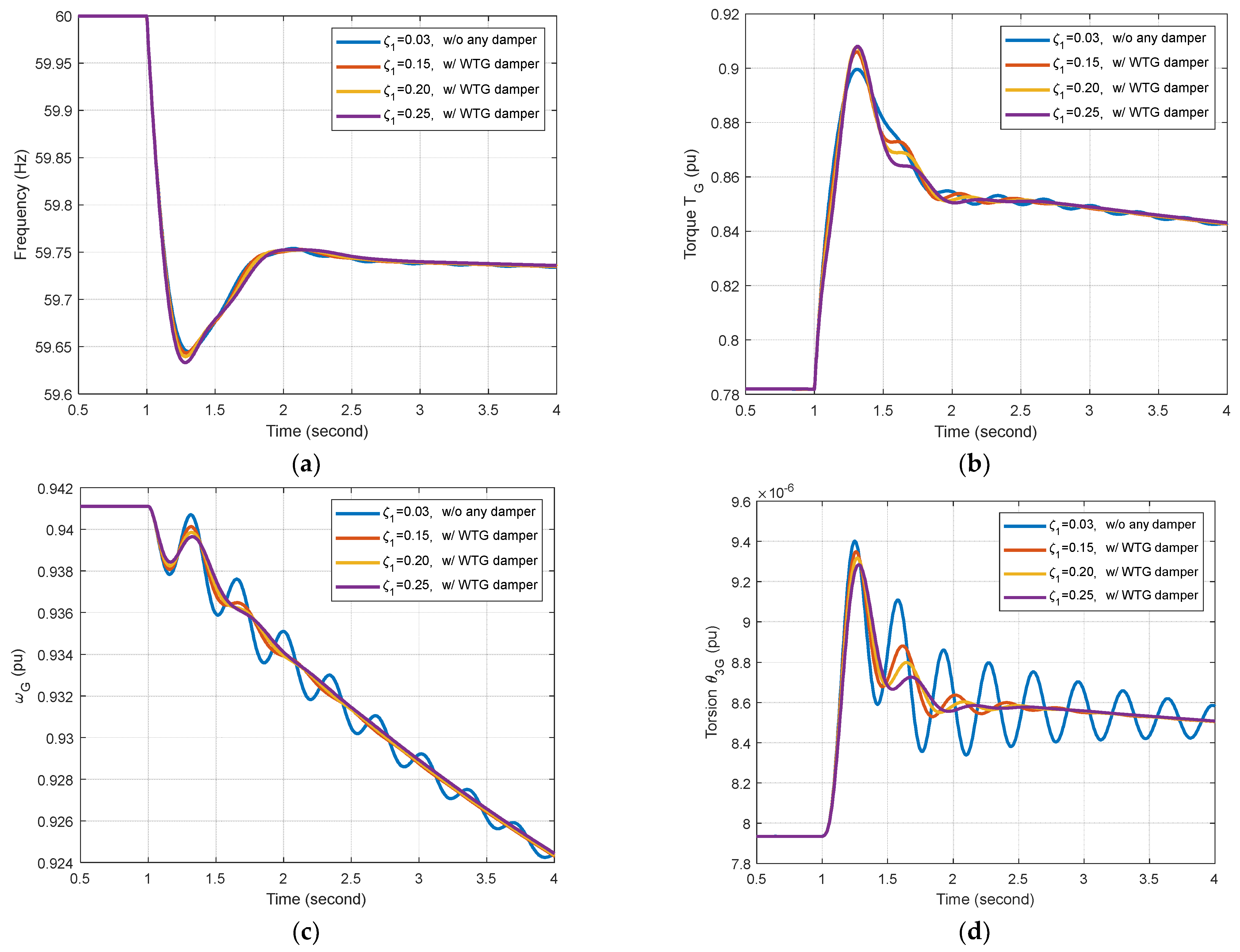
5.4. Comparison with Wind Turbine Generator (WTG) Damper
5.5. Wind Speed Step Change
6. Conclusions
- (1)
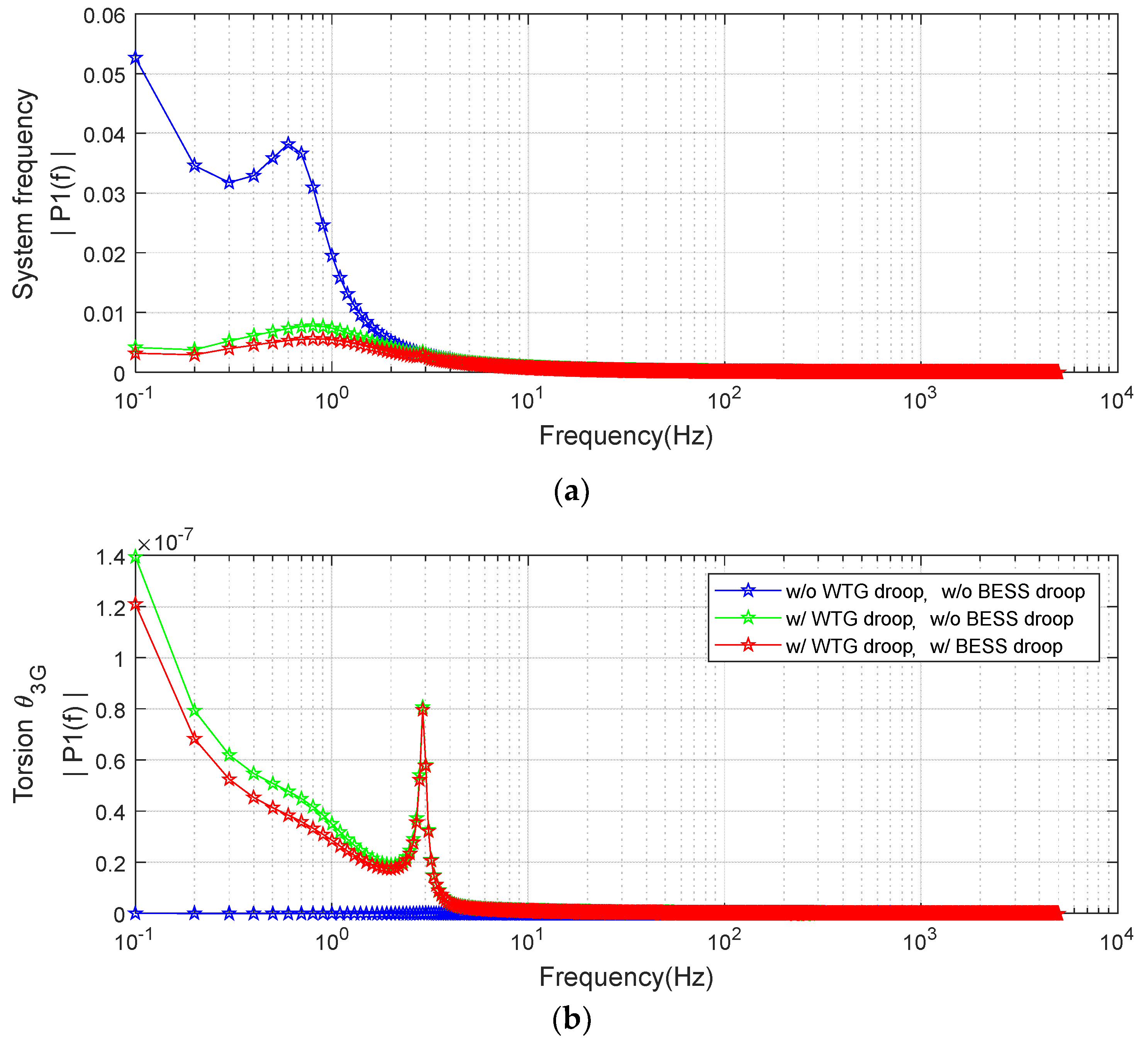
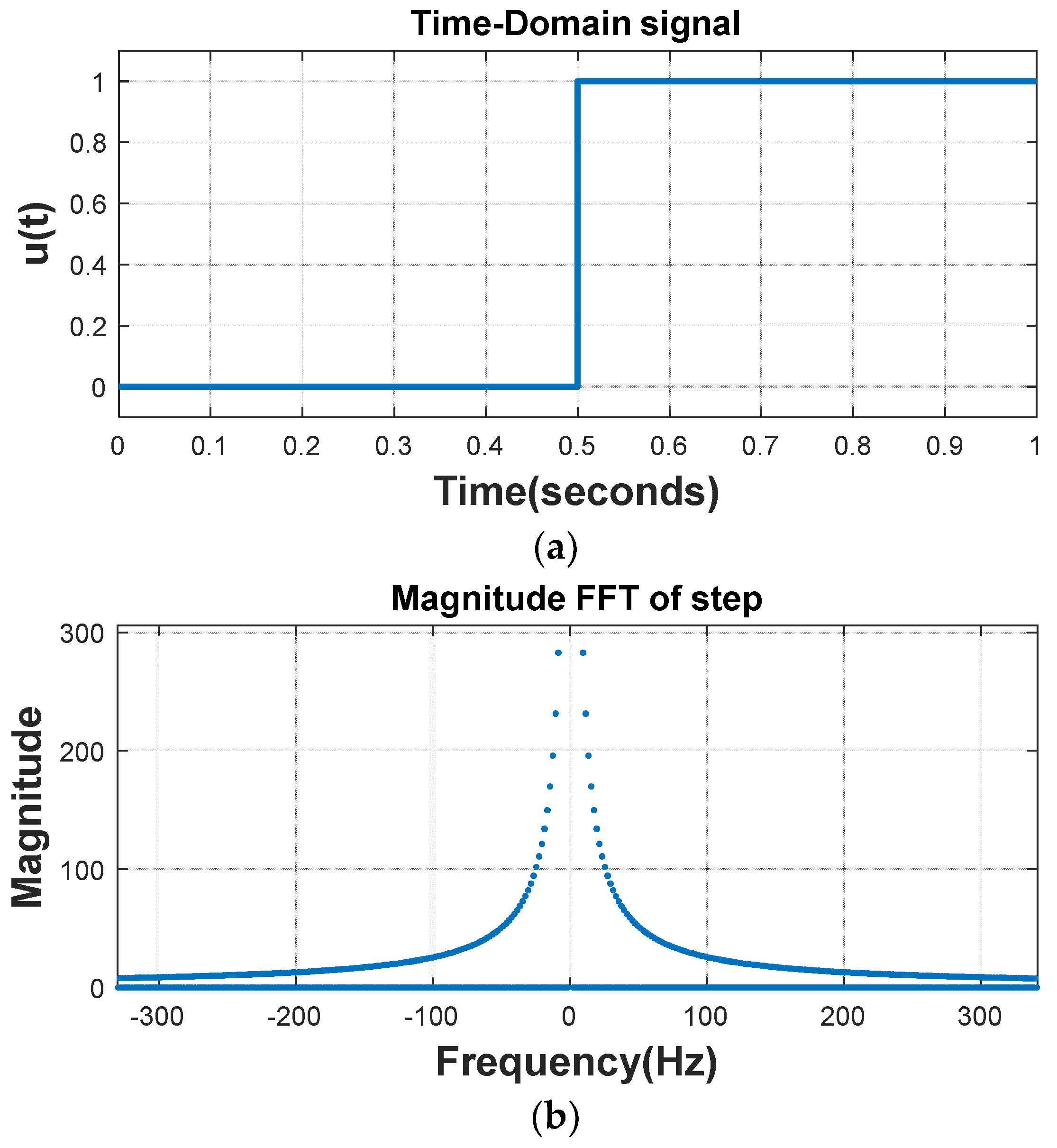
- Based on FFT spectra of step responses, we determined that only torsional mode 1 (2.92 Hz) was excited by step load changes in the microgrid. Thus, this study focused exclusively on mode 1 in the design of the BESS damper.
- (2)
- Providing suitable compensation for the phase lag between the BESS damping signal and DFIG torque made it possible for the BESS damper to provide a damping signal capable of generating damping torque in phase with DFIG speed.
- (3)
- The proposed BESS damper improved the damping ratio for torsional mode 1 from 0.0319 to 0.25.
- (4)
- When using the feedforward compensator to deal with phase lag, the damping characteristics of the BESS damper were similar to those obtained using a DFIG damper. Note, however, that the frequency nadir obtained using the BESS damper (59.6726 Hz) exceeded that obtained using the DFIG damper (59.6331 Hz), due to the fact that the damping power was from a BESS instead of a DFIG.
- (5)
- The proposed BESS damper improved torsional mode damping in situations involving changes in wind speed, as well as stepped changes in load.
- (6)
- In microgrids with low system inertia, frequency deviations are relatively large and the torsional mode damping ratio is relatively small.
- (7)
- The proposed feedforward compensator proved effective in dealing with the phase lag between BESS power output and DFIG torque. As a result, the proposed BESS damper provided essentially the same damping effects as those reported in previous works, in which the damper was installed on rotor-side converters (RSCs) while avoiding the degradation of frequency response associated with dampers on the RSC.
- (8)
- BESS damper constants have been designed based on a specific operating condition. Future work will focus on the adaptation of BESS damper constants in accordance with system operating conditions, such as the number of diesel units and wind generators.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| battery energy voltage system | |
| , , , | bases for BESS, diesel generators, system, and wind generators, respectively |
| load damping | |
| system frequency | |
| integral of system frequency | |
| , | bandpass filter parameters |
| , , , , | inertia constants for 5-mass drivetrain of the wind turbine generator |
| inertia constants for diesel generator | |
| , , , | stiffness coefficients for 5-mass drivetrain of the wind generator |
| , , | droop gains of diesel generators, wind generators, and BESS |
| MPPT gain parameter | |
| , , , | output powers of BESS, diesel generators, and wind generators, respectively, and load power |
| diesel generator time constants | |
| , | electromagnetic and mechanical torque of the wind generator |
| , | lead-lag compensator parameters |
| wind velocity | |
| wind generator speed | |
| pitch angle | |
| , , , | 5-mass drivetrain torsion |
| tip speed ratio | |
| ζ | damping ratio |
| linearized incremental quantity |
Appendix A
- 5 MVA
- 0.675 s
- 0.5 p.u.
- 20 p.u.
- 0.1 p.u.
- 0.35 s
- 2.25 MVA
- 1.5 MVA
- 20 p.u.
- 387 p.u.
- 5708 p.u.
- 799,438 p.u.
- 98,537 p.u.
- 5.2322 s
- 0.0007 s
- 0.0042 s
- 0.0069 s
- 0.5684 s
- = 0.5 MVA
- 20 p.u.
References
- Manaz, M.A.M.; Lu, C.-N. Design of resonance damper for wind energy conversion system providing frequency support service to low inertia power systems. IEEE Trans. Power Syst. 2020, 35, 4297–4306. [Google Scholar] [CrossRef]
- Mandic, G.; Nasiri, A.; Muljadi, E.; Oyague, F. Active torque control for gearbox load reduction in a variable-speed wind turbine. IEEE Trans. Ind. Appl. 2012, 48, 2424–2432. [Google Scholar] [CrossRef]
- Fateh, F.; White, W.N.; Gruenbacher, D. Torsional vibrations mitigation in the drivetrain of DFIG-based grid-connected wind turbine. IEEE Trans. Ind. Appl. 2017, 53, 5760–5767. [Google Scholar] [CrossRef]
- Bian, X.; Zhang, J.; Ding, Y.; Zhao, J.; Zhou, Q.; Lin, S. Microgrid Frequency Regulation Involving Low-wind-speed Wind Turbine Generators Based on Deep Belief Network. IET Gener. Transm. Distrib. 2020, 14, 2046–2054. [Google Scholar] [CrossRef]
- Van de Vyver, J.; De Kooning, J.D.M.; Meersman, B.; Vandevelde, L.; Vandoorn, T.L. Droop control as an alternative inertial response strategy for the synthetic inertia on wind turbines. IEEE Trans. Power Syst. 2016, 31, 1129–1138. [Google Scholar] [CrossRef]
- Hwang, M.; Muljadi, E.; Park, J.W.; Sørensen, P.; Kang, Y.C. Dynamic droop–based inertial control of a doubly-fed induction generator. IEEE Trans. Sustain. Energy 2016, 7, 924–933. [Google Scholar] [CrossRef]
- Lee, J.; Jang, G.; Muljadi, E.; Blaabjerg, F.; Chen, Z.; Kang, Y.C. Stable short-term frequency support using adaptive gains for a DFIG-based wind power plant. IEEE Trans. Energy Convers. 2016, 31, 1068–1079. [Google Scholar] [CrossRef]
- Lee, J.; Muljadi, E.; Srensen, P.; Kang, Y.C. Releasable Kinetic Energy-Based Inertial Control of a DFIG Wind Power Plant. IEEE Trans. Sustain. Energy 2016, 7, 279–288. [Google Scholar] [CrossRef]
- Abouzeid, S.I.; Guo, Y.; Zhang, H.C.; Ma, X. Improvements in primary frequency regulation of the grid-connected variable speed wind turbine. IET Renew. Power Gener. 2019, 13, 491–499. [Google Scholar] [CrossRef]
- Yang, P.; He, B.; Wang, B.; Dong, X.; Liu, W.; Zhang, J.; Wu, Z.; Liu, J.; Qin, Z. Coordinated control of rotor kinetic energy and pitch angle for large-scale doubly fed induction generators participating in system primary frequency regulation. IET Renew. Power Gener. 2021, 15, 1836–1847. [Google Scholar] [CrossRef]
- Roozbehani, S.; Hagh, M.T.; Zadeh, S.G. Frequency control of islanded wind-powered microgrid based on coordinated robust dynamic droop power sharing. IET Gener. Transm. Distrib. 2019, 13, 4968–4977. [Google Scholar] [CrossRef]
- Garmroodi, M.; Verbič, G.; Hill, D.J. Frequency support from wind turbine generators with a time-variable droop characteristic. IEEE Trans. Sustain. Energy 2018, 9, 676–684. [Google Scholar] [CrossRef]
- Wu, Y.K.; Yang, W.H.; Hu, Y.L.; Dzung, P.Q. Frequency regulation at a wind farm using time-varying inertia and droop controls. IEEE Trans. Ind. Appl. 2019, 55, 213–224. [Google Scholar] [CrossRef]
- Kumar, A. Primary frequency regulation support through deloaded offshore renewable power generators with HVDC-link. IET Renew. Power Gener. 2021, 15, 1693–1705. [Google Scholar] [CrossRef]
- Persson, M.; Chen, P. Frequency control by variable speed wind turbines in islanded power systems with various generation mix. IET Renew. Power Gener. 2017, 11, 1101–1109. [Google Scholar] [CrossRef]
- De Oliveira, J.D.A.; de Araújo Lima, F.K.; Tofoli, F.L.; Branco, C.G.C. Synchronverter-based frequency control technique applied in wind energy conversion systems based on the doubly-fed induction generator. Electr. Power Syst. Res. 2023, 214, 108820. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Babu, T.S.; Pouryekta, A. Synchronverter: A comprehensive review of modifications, stability assessment, applications, and future perspectives. IEEE Access 2020, 8, 131565–131589. [Google Scholar] [CrossRef]
- Din, Z.; Zhang, J.; Xu, Z.; Zhang, Y.; Milyani, A.H.; Cheema, K.M.; Nawaz, A.; Song, Y. Recent development and future trends of resonance in doubly fed induction generator system under weak grid. IET Renew. Power Gener. 2022, 16, 807–834. [Google Scholar] [CrossRef]
- Gu, K.; Wu, F.; Zhang, X.P. Sub-synchronous interactions in power systems with wind turbines: A review. IET Renew. Power Gener. 2019, 13, 4–15. [Google Scholar] [CrossRef]
- Bu, S.; Zhang, J.; Chung, C.Y. Damping torque analysis for open-loop modal resonance as a cause of torsional sub-synchronous oscillations excited by grid-connected wind farms. IET Renew. Power Gener. 2023, 17, 604–616. [Google Scholar] [CrossRef]
- Li, Y.; Fan, L.; Miao, Z. Replicating real-world wind farm SSR events. IEEE Trans. Power Del. 2020, 35, 339–348. [Google Scholar] [CrossRef]
- Leon, A.E. Integration of DFIG-based wind farms into series-compensated transmission systems. IEEE Trans. Sustain. Energy 2016, 7, 451–460. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, J.; Green, T.C.; Li, W.; He, X. Motion-induction compensation to mitigate sub-synchronous oscillation in wind farms. IEEE Trans. Sustain. Energy 2020, 11, 1247–1256. [Google Scholar] [CrossRef]
- Leon, A.E.; Amodeo, S.J.; Mauricio, J.M. Enhanced compensation filter to mitigate subsynchronous oscillations in series-compensated DFIG-based wind farms. IEEE Trans. Power Deliv. 2021, 36, 3805–3814. [Google Scholar] [CrossRef]
- Karunanayake, C.; Ravishankar, J.; Dong, Z.Y. Nonlinear SSR damping controller for DFIG based wind generators interfaced to series compensated transmission systems. IEEE Trans. Power Syst. 2020, 35, 1156–1165. [Google Scholar] [CrossRef]
- Baesmat, H.J.; Bodson, M. Suppression of sub-synchronous resonances through excitation control of doubly fed induction generators. IEEE Trans. Power Syst. 2019, 34, 4329–4340. [Google Scholar] [CrossRef]
- Ghafouri, M.; Karaagac, U.; Karimi, H.; Jensen, S.; Mahseredjian, J.; Faried, S.O. An LQR controller for damping of subsynchronous interaction in DFIG-based wind farms. IEEE Trans. Power Syst. 2017, 32, 4934–4942. [Google Scholar] [CrossRef]
- Ghaffarzdeh, H.; Mehrizi-Sani, A. Mitigation of subsynchronous resonance induced by a type III wind system. IEEE Trans. Sustain. Energy 2020, 11, 1717–1727. [Google Scholar] [CrossRef]
- Ali, M.T.; Zhou, D.; Song, Y.; Ghandhari, M.; Harnefors, L.; Blaabjerg, F. Analysis and mitigation of SSCI in DFIG systems with experimental validation. IEEE Trans. Energy Convers. 2020, 35, 714–723. [Google Scholar] [CrossRef]
- Karaagac, U.; Mahseredjian, J.; Jensen, S.; Gagnon, R.; Fecteau, M.; Kocar, I. Safe operation of DFIG-based wind parks in series-compensated systems. IEEE Trans. Power Deliv. 2018, 33, 709–718. [Google Scholar] [CrossRef]
- Licari, J.; Ugalde-Loo, C.E.; Ekanayake, J.B.; Jenkins, N. Damping of torsional vibrations in a variable-speed wind turbine. IEEE Trans. Energy Convers. 2013, 28, 172–180. [Google Scholar] [CrossRef]
- Teleke, S.; Baran, M.E.; Bhattacharya, S.; Huang, A.Q. Optimal control of battery energy storage for wind farm dispatching. IEEE Trans. Energy Convers. 2010, 25, 787–794. [Google Scholar] [CrossRef]
- Zhang, S.; Mishra, Y.; Shahidehpour, M. Fuzzy-logic based frequency controller for wind farms augmented with energy storage systems. IEEE Trans. Power Syst. 2016, 31, 1595–1603. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, D.W.; Zhang, H.; Yan, S.; Wang, X. Coordinated control strategy of battery energy storage system and PMSG-WTG to enhance system frequency regulation capability. IEEE Trans. Sustain. Energy 2017, 8, 1330–1343. [Google Scholar] [CrossRef]
- Datta, U.; Kalam, A.; Shi, J. Battery energy storage system to stabilize transient voltage and frequency and enhance power export capability. IEEE Trans. Power Syst. 2019, 34, 1845–1857. [Google Scholar] [CrossRef]
- Choi, J.W.; Heo, S.Y.; Kim, K.K. Hybrid operation strategy of wind energy storage system for power grid frequency regulation. IET Gener. Transm. Distrib. 2016, 10, 736–749. [Google Scholar] [CrossRef]
- Cao, J.; Du, W.; Wang, H.; McCulloch, M. Optimal Sizing and Control Strategies for Hybrid Storage System as Limited by Grid Frequency Deviations. IEEE Trans. Power Syst. 2018, 33, 5486–5495. [Google Scholar] [CrossRef]
- Kurian, S.; Krishnan, S.T.; Cheriyan, E.P. Real-time implementation of artificial neural networks-based controller for battery storage supported wind electric generation. IET Gener. Transm. Distrib. 2015, 9, 937–946. [Google Scholar] [CrossRef]
- Shim, J.W.; Verbič, G.; Zhang, N.; Hur, K. Harmonious integration of faster-acting energy storage systems into frequency control reserves in the power grid with high renewable generation. IEEE Trans. Power Syst. 2018, 33, 6193–6205. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, X.; Zhou, Z.; Harnefors, L.; Svensson, J.R.; Kocewiak, L.H.; Gryning, M.P.S. Control interaction modeling and analysis of grid-forming battery energy storage system for offshore wind power plant. IEEE Trans. Power Syst. 2022, 37, 497–507. [Google Scholar] [CrossRef]
- Sebastián, R. Battery energy storage for increasing stability and reliability of an isolated wind-diesel power system. IET Renew. Power Gener. 2017, 11, 296–303. [Google Scholar] [CrossRef]
- Daraiseh, F. Frequency response of energy storage systems in grids with a high level of wind power penetration—Gotland case study. IET Renew. Power Gener. 2020, 14, 1282–1287. [Google Scholar] [CrossRef]
- Gu, F.C.; Chen, H.C. Modeling and control of vanadium redox flow battery for smoothing wind power fluctuation. IET Renew. Power Gener. 2021, 15, 3552–3563. [Google Scholar] [CrossRef]
- Pradhan, C.; Bhende, C.N.; Srivastava, A.K. Frequency sensitivity analysis of dynamic demand response in a wind farm integrated power system. IET Renew. Power Gener. 2019, 13, 905–919. [Google Scholar] [CrossRef]
- Krishan, O.; Suhag, S. Power management control strategy for a hybrid energy storage system in a grid-independent hybrid renewable energy system: A hardware-in-loop real-time verification. IET Renew. Power Gener. 2020, 14, 454–465. [Google Scholar] [CrossRef]
- Parthasarathy, C.; Sirviö, K.; Hafezi, H.; Laaksonen, H. Modeling battery energy storage systems for active network management—Coordinated control design and validation. IET Renew. Power Gener. 2021, 15, 2426–2437. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Quynh, N.V.; Bianchi, N. Performance dynamics improvement of a hybrid wind/fuel cell/battery system for standalone operation. IET Renew. Power Gener. 2023, 17, 349–375. [Google Scholar] [CrossRef]
- Teodorescu, R.; Sui, X.; Vilsen, S.B.; Bharadwaj, P.; Kulkarni, A.; Stroe, D.-I. Smart battery technology for lifetime improvement. Batteries 2022, 8, 169. [Google Scholar] [CrossRef]
- Martyushev, N.V.; Malozyomov, B.V.; Khalikov, I.H.; Kukartsev, V.A.; Kukartsev, V.V.; Tynchenko, V.S.; Tynchenko, Y.A.; Qi, M. Review of Methods for Improving the Energy Efficiency of Electrified Ground Transport by Optimizing Battery Consumption. Energies 2023, 16, 729. [Google Scholar] [CrossRef]
- Park, J.; Choi, J.; Jo, H.; Kodaira, D.; Han, S.; Acquah, M.A. Life Evaluation of Battery Energy System for Frequency Regulation Using Wear Density Function. Energies 2022, 15, 8071. [Google Scholar] [CrossRef]
- Papakonstantinou, A.G.; Papathanassiou, S.A. Battery Energy Storage Participation in Automatic Generation Control of Island Systems, Coordinated with State of Charge Regulation. Appl. Sci. 2022, 12, 596. [Google Scholar] [CrossRef]
- Rancilio, G.; Rossi, A.; Di Profio, C.; Alborghetti, M.; Galliani, A.; Merlo, M. Grid-Scale BESS for Ancillary Services Provision: SoC Restoration Strategies. Appl. Sci. 2020, 10, 4121. [Google Scholar] [CrossRef]
- Shahabi, M.; Haghifam, M.R.; Mohamadian, M.; Nabavi-Niaki, S.A. Microgrid dynamic performance improvement using a doubly fed induction wind generator. IEEE Trans. Energy Convers. 2009, 24, 137–145. [Google Scholar] [CrossRef]
- Vidyanandan, K.V.; Senroy, N. Primary frequency regulation by deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 2013, 28, 837–846. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]





| Mode | Torsional Modes | Frequency Mode | ||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | ||
| Eigenvalues | −0.104 | −0.586 ± j18.58 | −9.1 × 10−3 ± j1834 | −5.74 × 10−3 ± j2334 | −7.61 × 10−6 ± j12405 | −3.79 ± j4.23 |
| Oscillation frequency (Hz) | 0 | 2.921 | 291.97 | 371.52 | 1974.27 | 0.673 |
| Damping ratio (ζ) | 1 | 0.0319 | 4.9 × 10−6 | 2.4 × 10−6 | 6.1 × 10−10 | 0.667 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
() | () | () | ||
| Eigenvalue | −0.586 ± j18.58 | −0.57 ± j18.36 | −0.568 ± j18.365 | −0.564 ± j18.368 |
| Frequency | 2.921 | 2.922 | 2.923 | 2.923 |
| Damping ratio | 0.0319 | 0.0310 | 0.0309 | 0.0307 |
| Case 1 | Case 2 | Case 3 | Case 4 | |
|---|---|---|---|---|
() | () | () | ||
| Eigenvalue | −3.79 ± j4.230 | −4.544 ± j3.992 | −4.733 ± j3.908 | −4.921 ± j3.812 |
| Frequency | 0.673 | 0.635 | 0.622 | 0.607 |
| Damping ratio | 0.667 | 0.751 | 0.771 | 0.791 |
| 0.25 | 4518.08 | 2.0129 | 2244.58 | −4.09 | 15.85 |
| 0.20 | 3877.37 | 2.0907 | 1854.59 | −3.52 | 17.25 |
| 0.15 | 3019.89 | 2.0396 | 1480.62 | −2.69 | 17.75 |
| 0.3 MW | 10485.57 | 2.5939 | 4042.36 | 59.650 |
| 0.5 MW | 7971.39 | 3.0574 | 2607.23 | 59.669 |
| 1.0 MW | 8285.95 | 5.3148 | 1559.05 | 59.708 |
| Frequency Nadir (Hz) | ||
|---|---|---|
| Without any damper | 0.03 | 59.6447 |
| With BESS damper | 0.15 | 59.6803 |
| 0.20 | 59.6764 | |
| 0.25 | 59.6726 | |
| With WTG damper | 0.15 | 59.6434 |
| 0.20 | 59.6395 | |
| 0.25 | 59.6331 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, B.-K.; Lee, K.-Y.; Hsu, Y.-Y. Battery Energy Storage System Damper Design for a Microgrid with Wind Generators Participating in Frequency Regulation. Energies 2023, 16, 7439. https://doi.org/10.3390/en16217439
Chiu B-K, Lee K-Y, Hsu Y-Y. Battery Energy Storage System Damper Design for a Microgrid with Wind Generators Participating in Frequency Regulation. Energies. 2023; 16(21):7439. https://doi.org/10.3390/en16217439
Chicago/Turabian StyleChiu, Bing-Kuei, Kuei-Yen Lee, and Yuan-Yih Hsu. 2023. "Battery Energy Storage System Damper Design for a Microgrid with Wind Generators Participating in Frequency Regulation" Energies 16, no. 21: 7439. https://doi.org/10.3390/en16217439
APA StyleChiu, B.-K., Lee, K.-Y., & Hsu, Y.-Y. (2023). Battery Energy Storage System Damper Design for a Microgrid with Wind Generators Participating in Frequency Regulation. Energies, 16(21), 7439. https://doi.org/10.3390/en16217439