High-Resistance Connection Diagnosis of Doubly Fed Induction Generators
Abstract
:1. Introduction
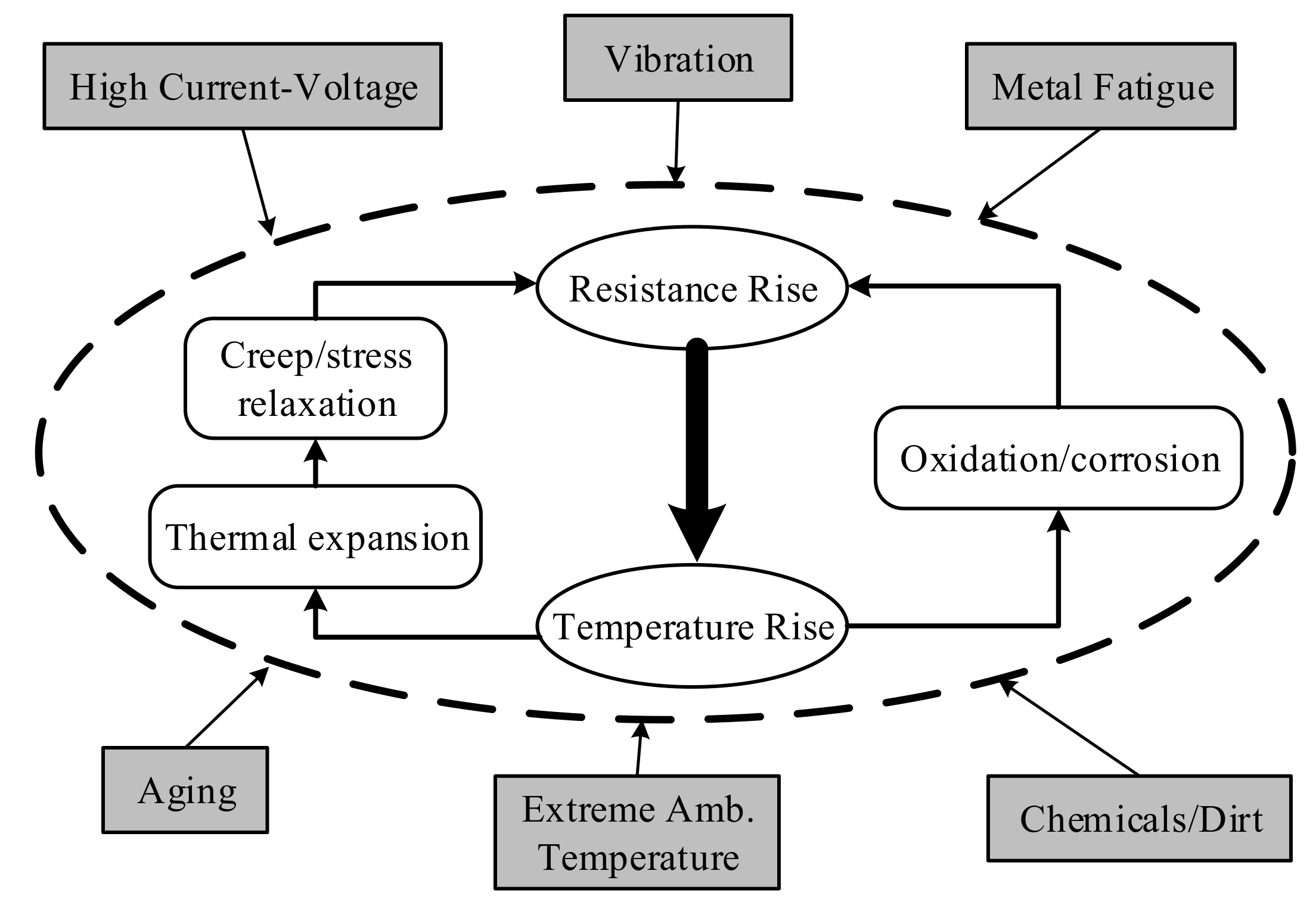
1.1. Motivations
1.2. Related Works
1.3. Contributions
1.4. Paper Organization
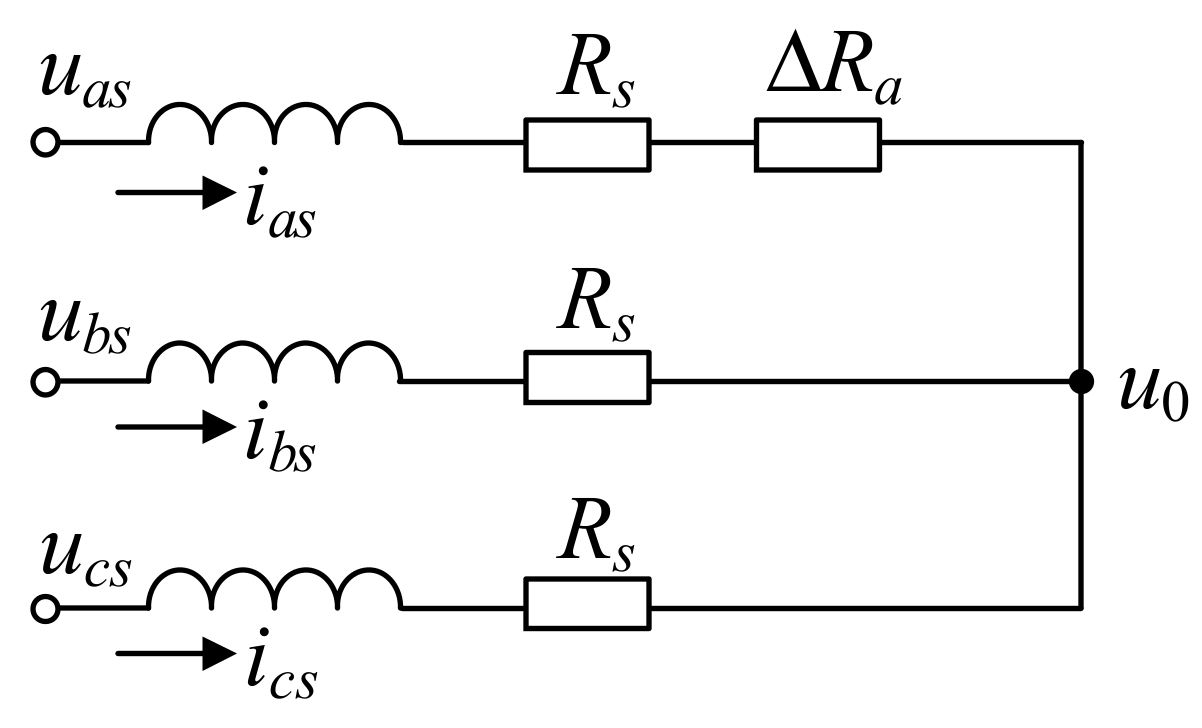
2. DFIG Model with HRC
3. Diagnostic Method
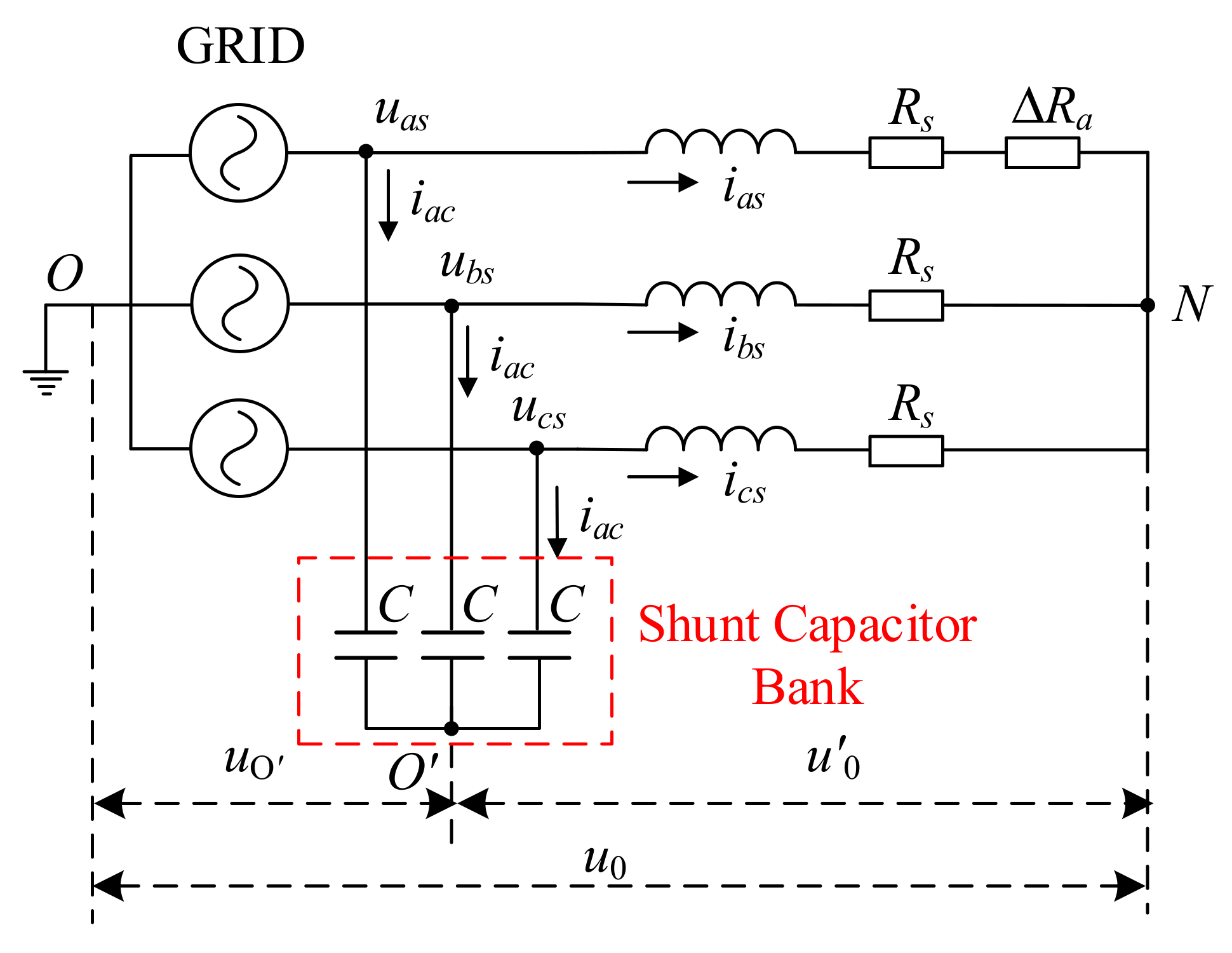
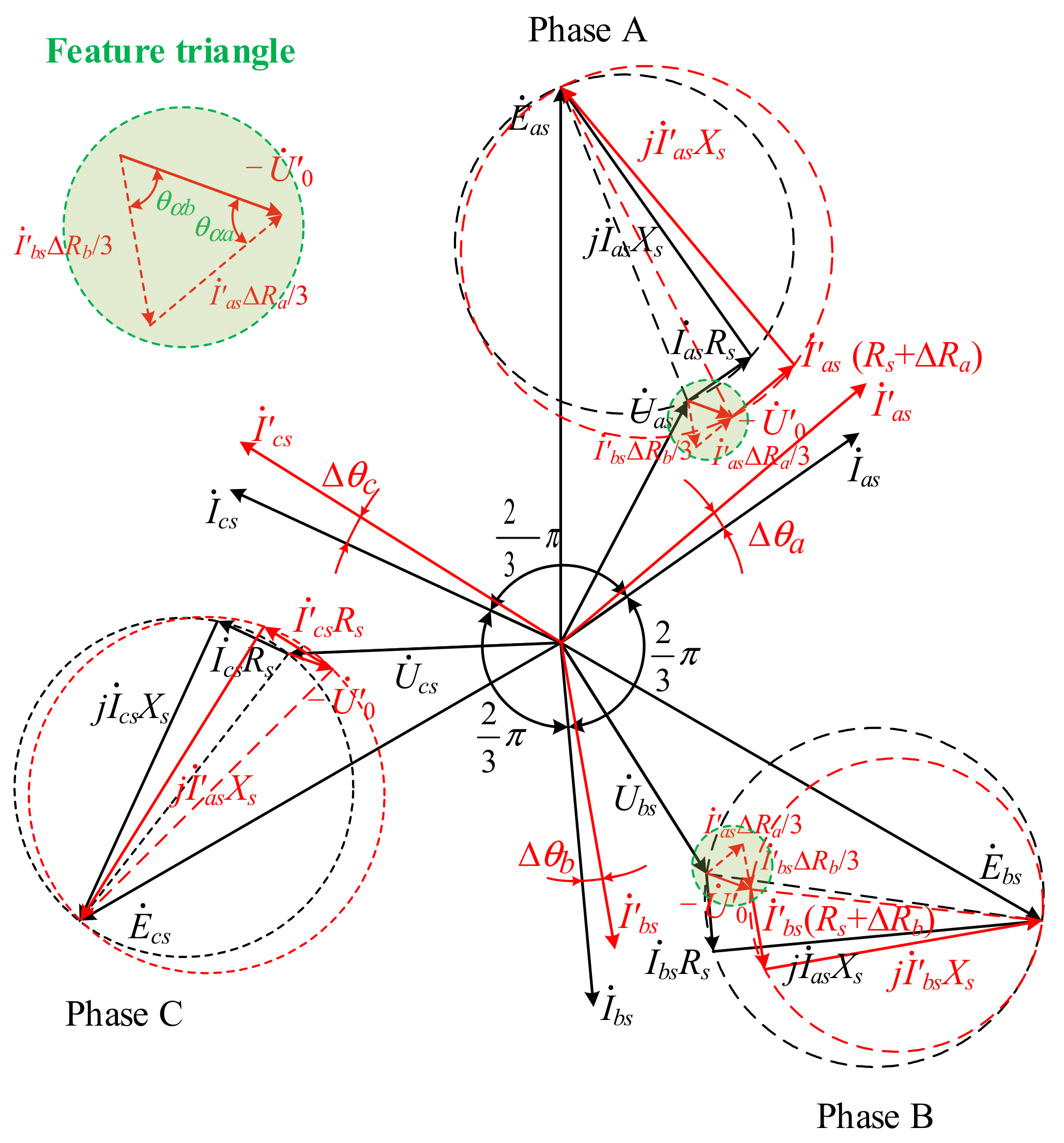
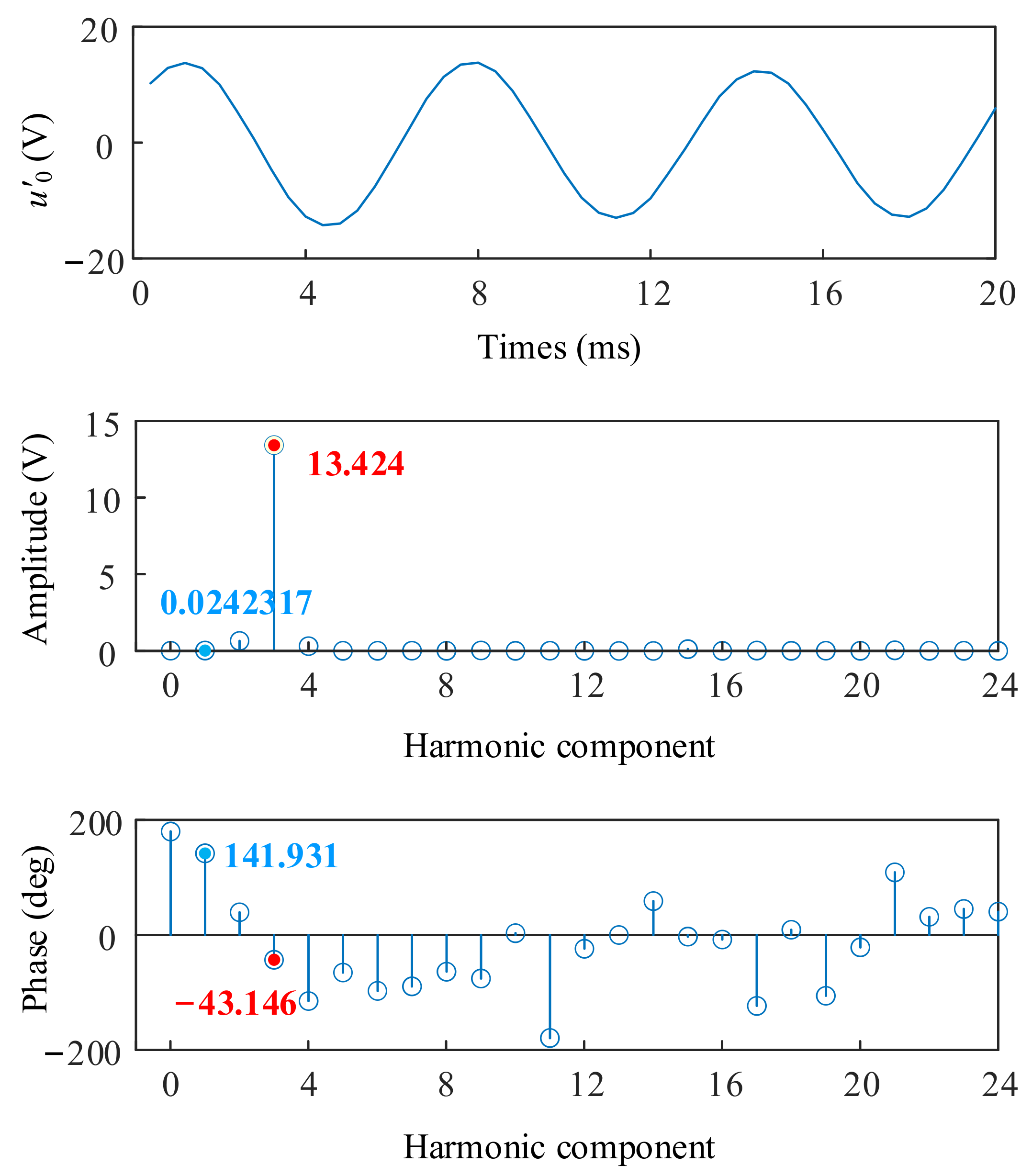
3.1. Potential Drift of Stator Winding Neutral Point
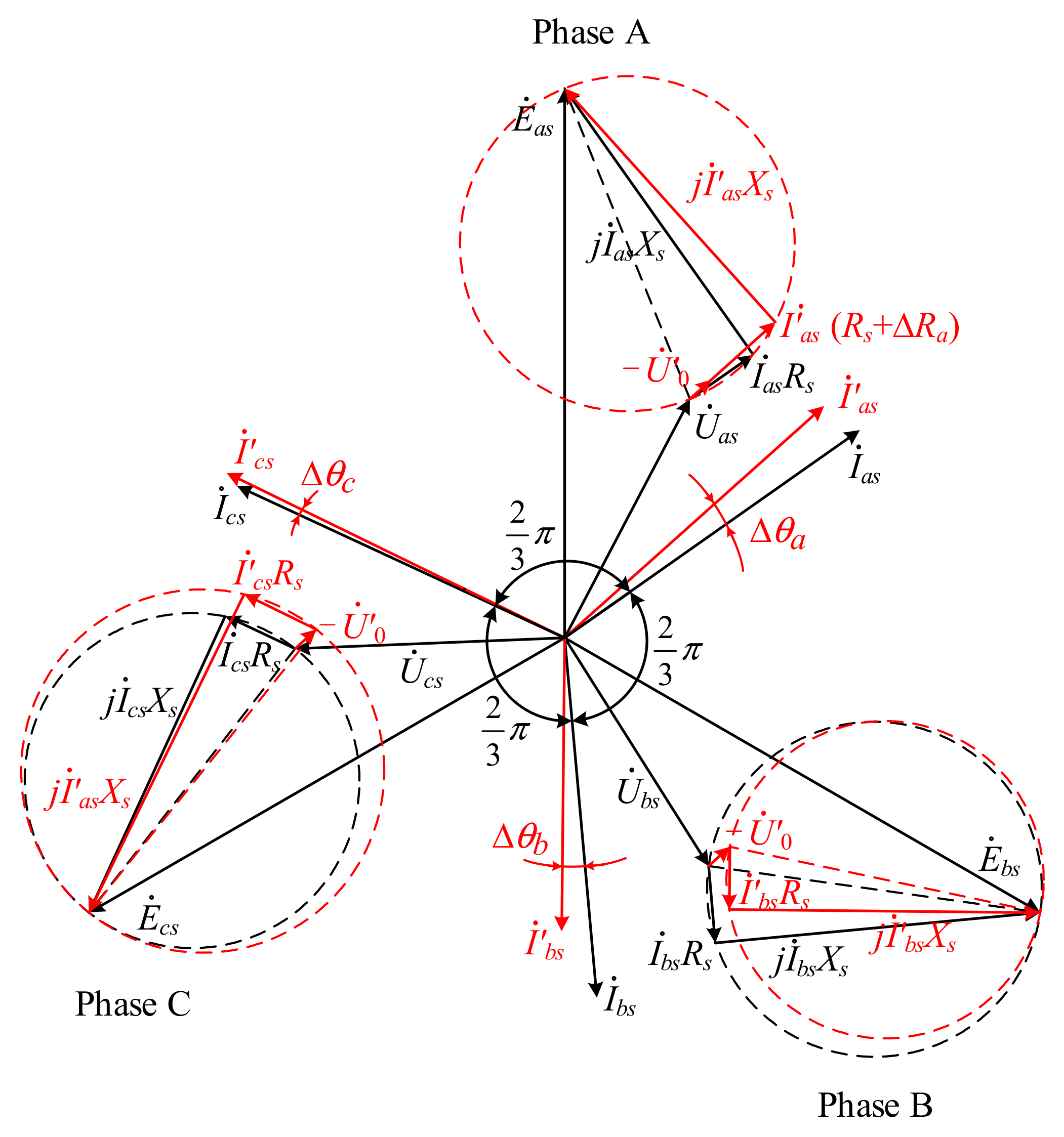
3.2. HRC Diagnosis under Balanced Grid
3.3. Artificial Neutral Point
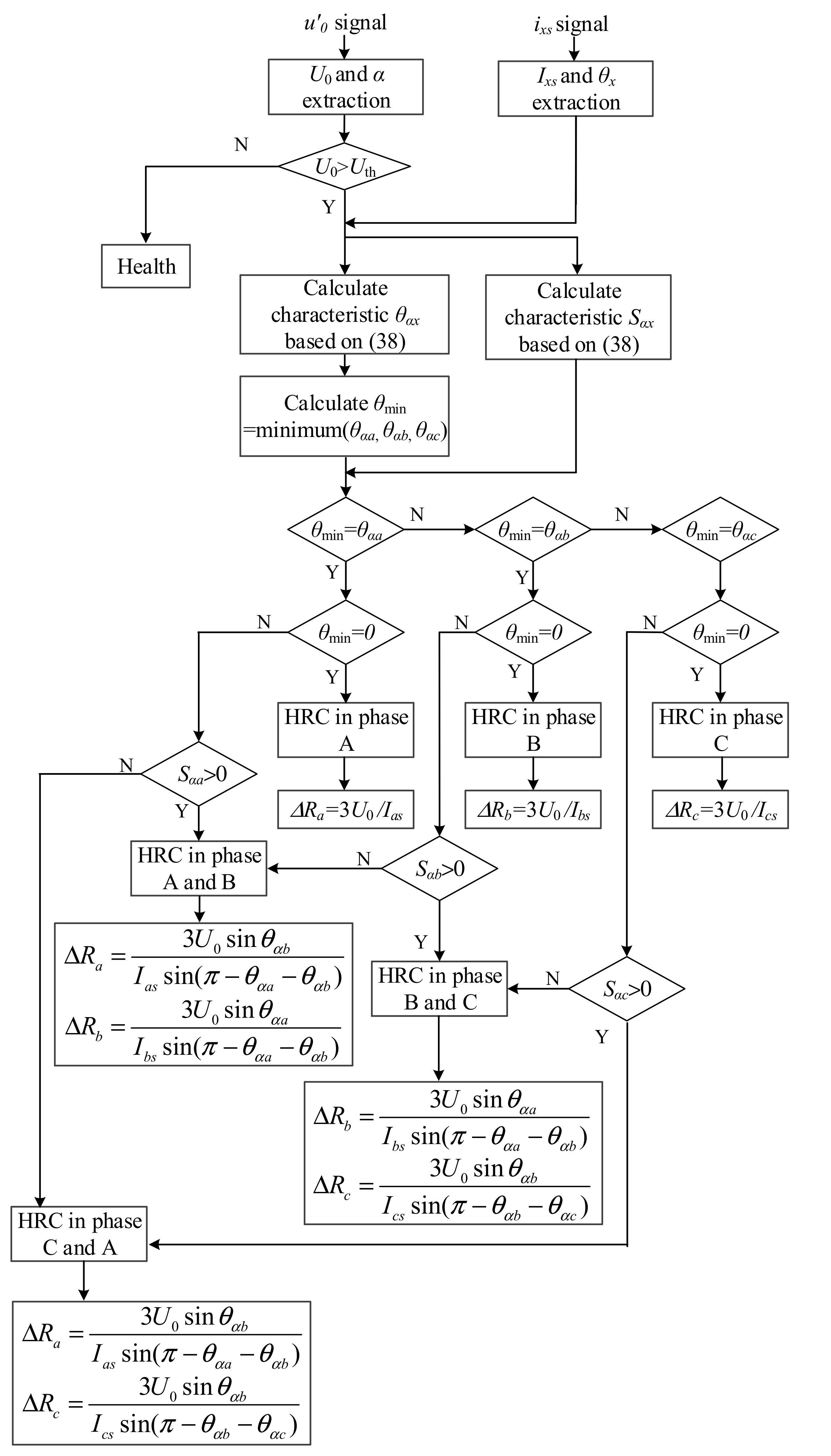
3.4. Fault Location and Degree Estimation
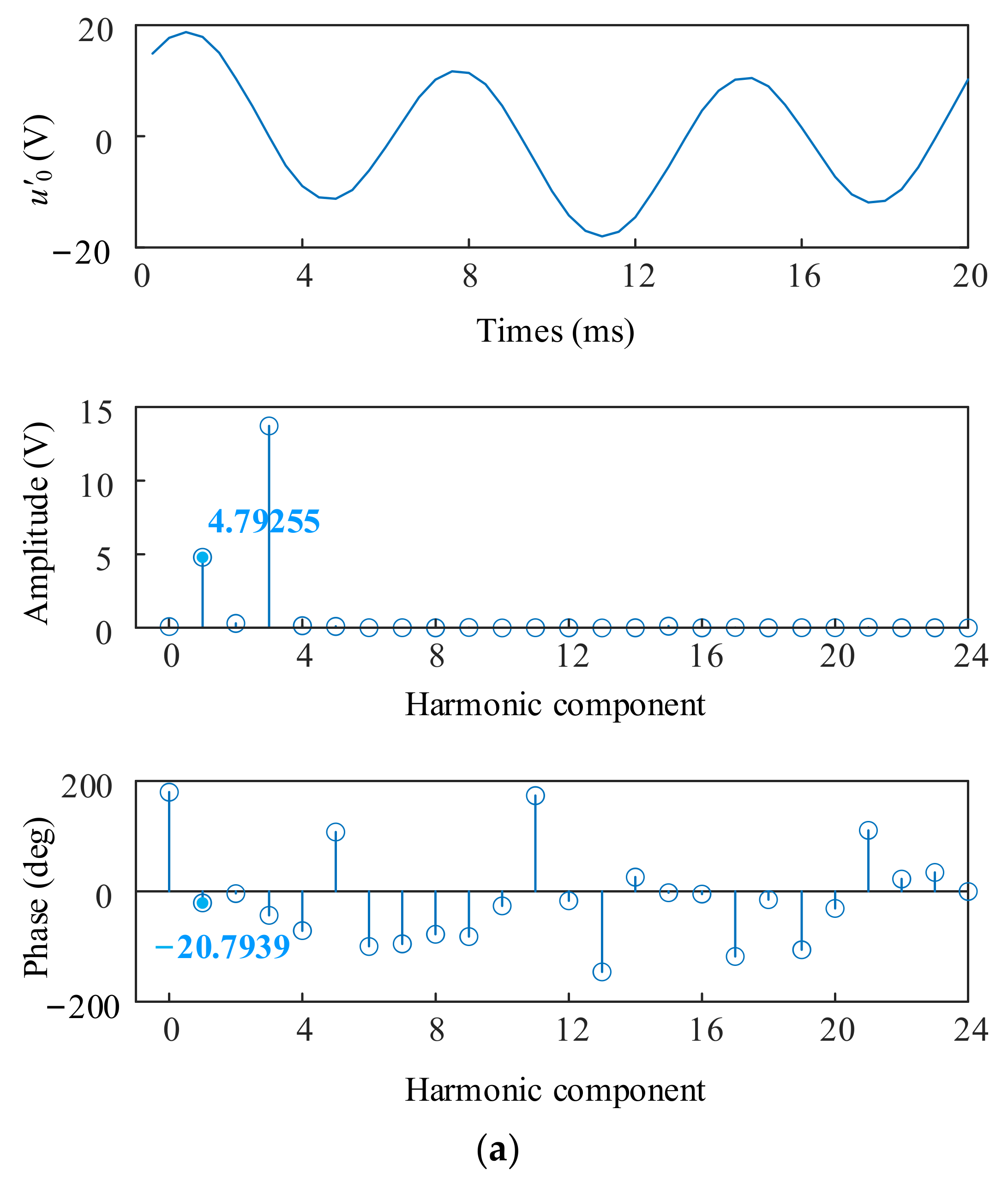
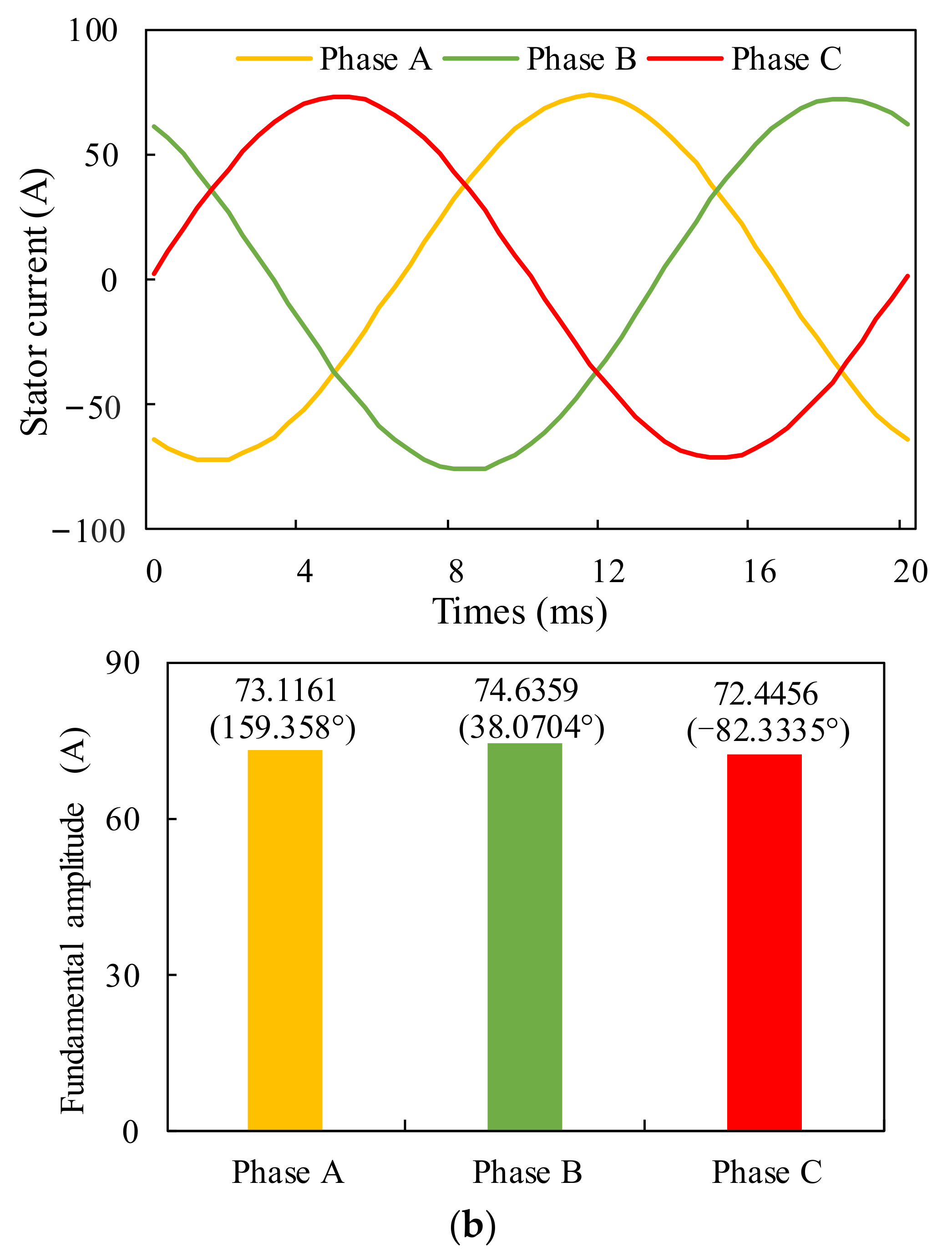
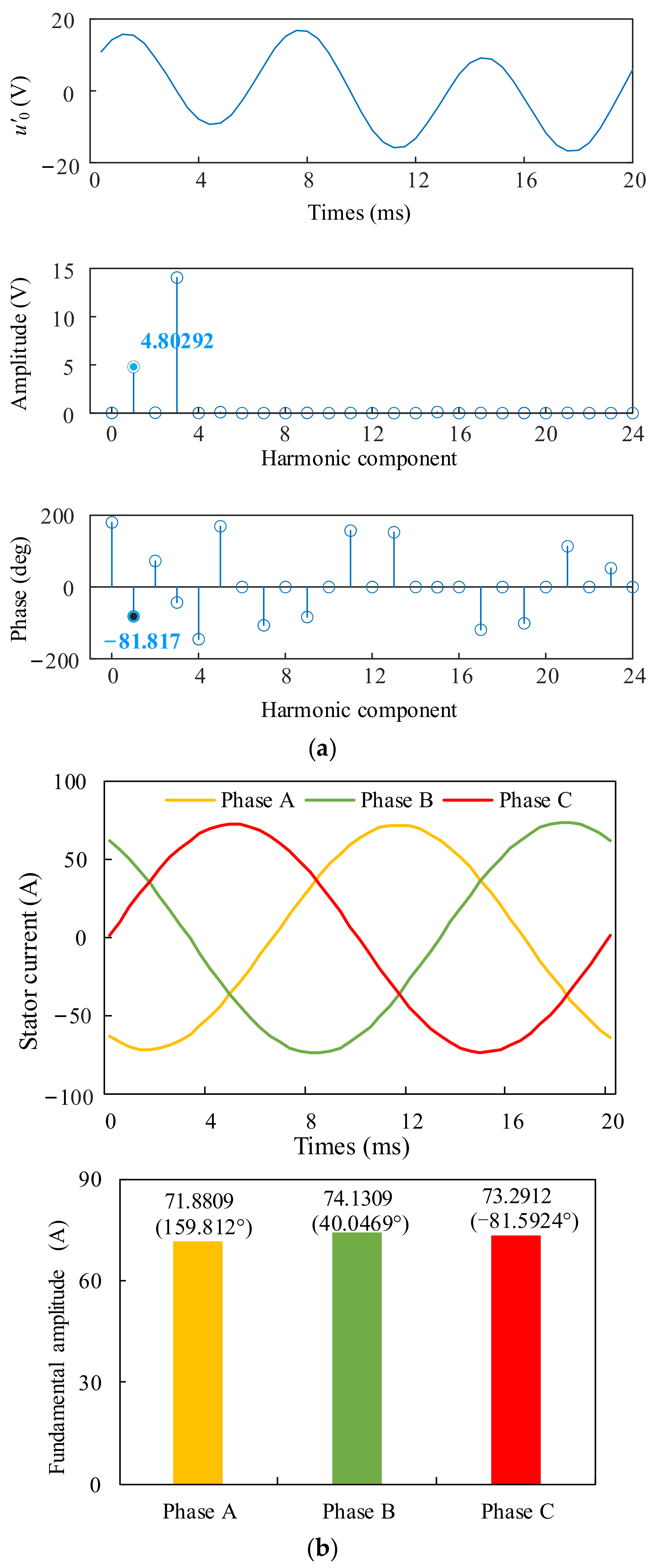
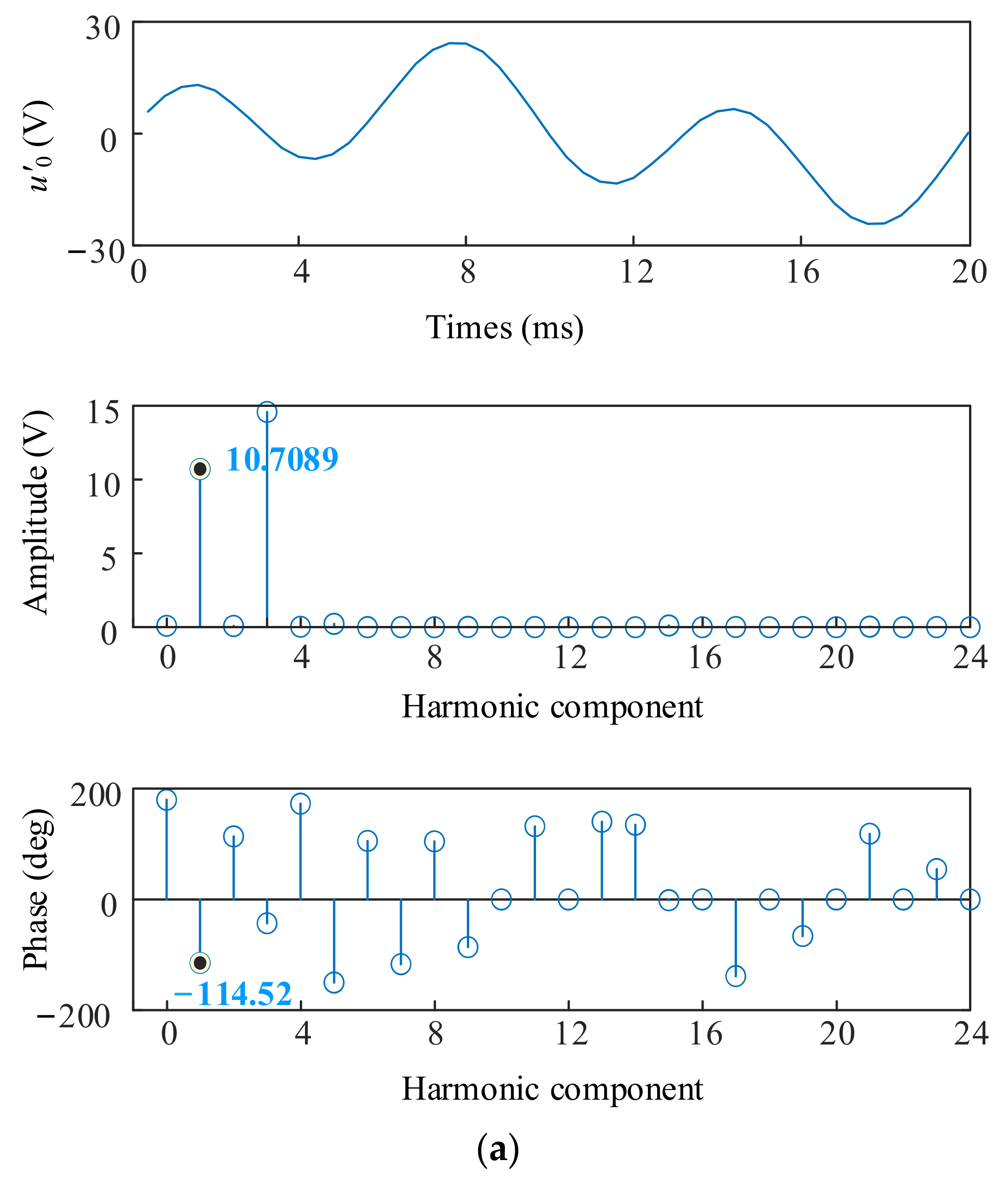
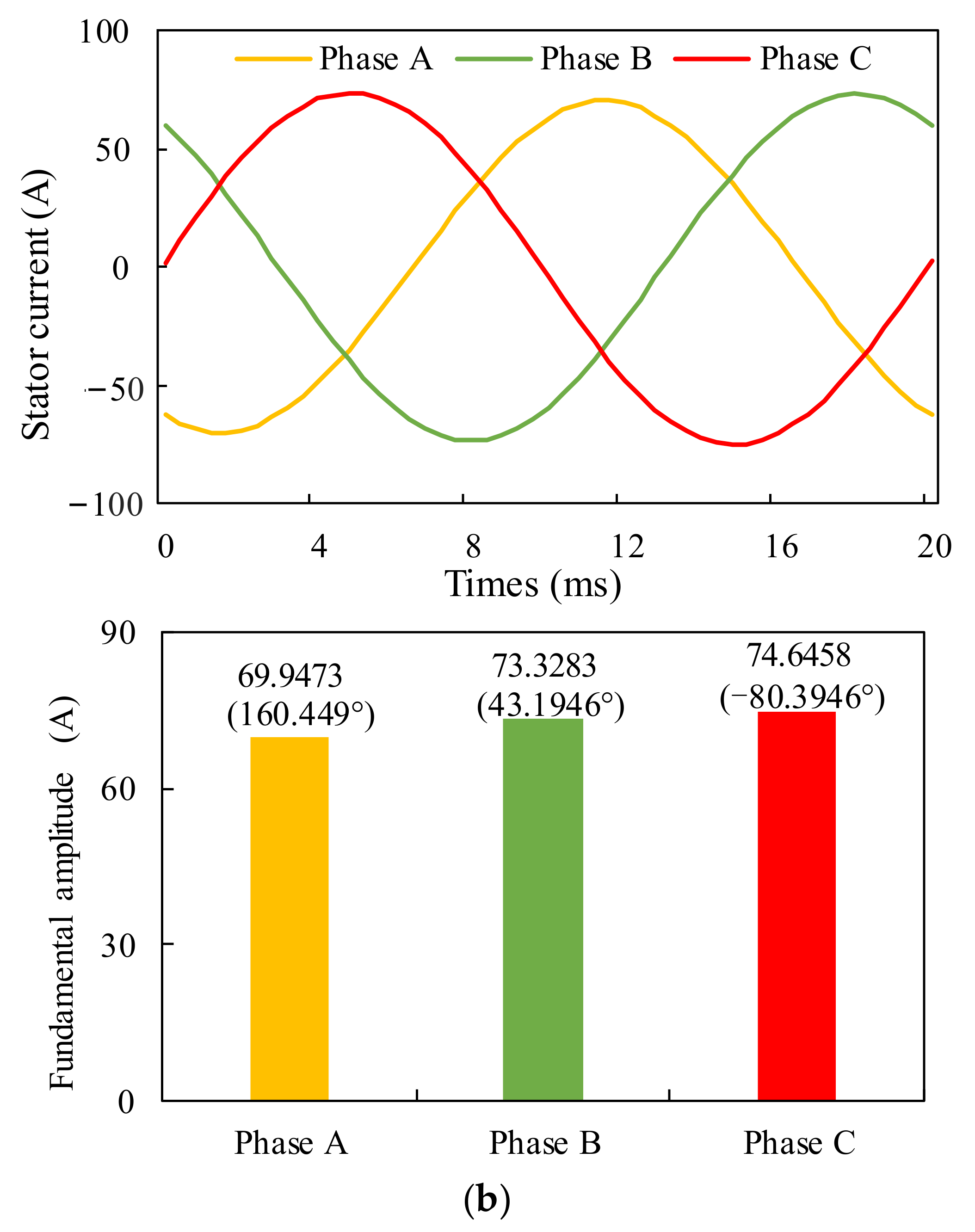
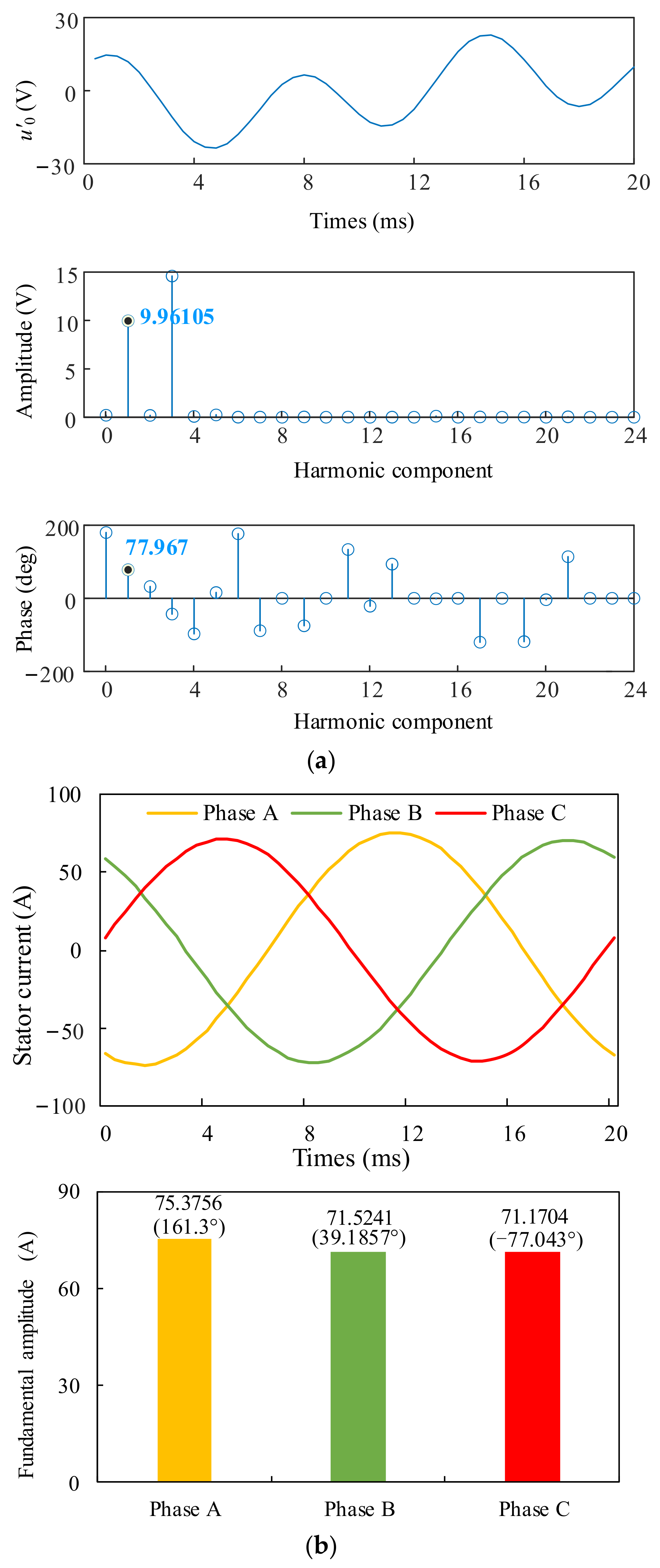
4. Simulations
5. Discussion of Results
6. Conclusions and Future Work
- (1)
- The interference and false alarms caused by power grid imbalance can be eliminated through the method of constructing an artificial neutral point, as proposed in this paper.
- (2)
- The proposed method can accurately locate the faulty phase and evaluate the degree of the fault in the case of single-phase faults, with an evaluation accuracy of over 98%.
- (3)
- In the case of faults occurring in two phases, regardless of whether the faults are the same or not, the proposed method can accurately locate the faulty phase and evaluate the degree of fault in each phase, with an evaluation accuracy of over 97%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hang, J.; Xia, M.; Ding, S.; Li, Y.; Sun, L. Research on vector control strategy of surface-mounted permanent magnet synchronous machine drive system with high-resistance connection. IEEE Trans. Power Electron. 2020, 35, 2023–2033. [Google Scholar] [CrossRef]
- Hang, J.; Ren, X.; Tang, C.; Tong, M. Fault-tolerant control strategy for five-phase PMSM drive system with high-resistance connection. IEEE Trans. Transp. Electrific. 2021, 7, 1390–1400. [Google Scholar] [CrossRef]
- Xu, Z.; Din, Z.; Jiang, Y.; Cheema, K.M.; Milyani, A.H.; Alghamdi, S. High-resistance connection diagnosis considering current closed-loop effect for permanent magnet machine. Front. Energy Res. 2022, 10, 933246. [Google Scholar] [CrossRef]
- Gonçalves, P.F.C.; Cruz, S.M.A.; Mendes, A.M.S. Online diagnostic method for the detection of high-resistance connections and open-phase faults in six-phase PMSM drives. IEEE Trans. Ind. Appl. 2022, 58, 345–355. [Google Scholar] [CrossRef]
- Rossi, C.; Gritli, Y.; Pilati, A.; Rizzoli, G.; Tani, A.; Casadei, D. High resistance fault-detection and fault-tolerance for asymmetrical six-phase surface-mounted AC permanent magnet synchronous motor drives. Energies 2020, 13, 3089. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Antonino-Daviu, J.A.; Osornio-Rios, R.A.; de Jesus Romero-Troncoso, R.; Razik, H. Detection of winding asymmetries in wound-rotor induction motors via transient analysis of the external magnetic field. IEEE Trans. Ind. Electron. 2020, 67, 5050–5059. [Google Scholar]
- Zamudio-Ramirez, I.; Antonino-Daviu, J.A.; Osornio-Rios, R.A.; Dunai, L. Tracking of high-order stray-flux harmonics under starting for the detection of winding asymmetries in wound-rotor induction motors. IEEE Trans. Ind. Electron. 2022, 69, 8463–8471. [Google Scholar] [CrossRef]
- Zamudio-Ramirez, I.; Antonino-Daviu, J.; Osornio-Rios, R.A.; Dunai, L.; Quijano-Lopez, A.; Fuster-Roig, V. Detection of stator asymmetries in wound rotor induction motors through the advanced analysis of rotor currents. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022. [Google Scholar]
- Martínez, M.E.I.; Antonino-Daviu, J.A.; de Córdoba, P.F.; Conejero, J.A.; Dunai, L. Automatic classification of winding asymmetries in wound rotor induction motors based on bicoherence and fuzzy c-means algorithms of stray flux signals. IEEE Trans. Ind. Appl. 2021, 57, 5876–5886. [Google Scholar] [CrossRef]
- Wang, H.; Lu, S.; Qian, G.; Ding, J.; Liu, Y.; Wang, Q. A two-step strategy for online fault detection of high-resistance connection in bldc motor. IEEE Trans. Power Electron. 2020, 35, 3043–3053. [Google Scholar] [CrossRef]
- Hang, J.; Yan, D.; Xia, M.; Ding, S.; Wang, Q. Quantitative fault severity estimation for high-resistance connection in PMSM drive system. IEEE Access 2019, 7, 26855–26866. [Google Scholar] [CrossRef]
- Hu, R.; Wang, J.; Mills, A.R.; Chong, E.; Sun, Z. Detection and classification of turn fault and high resistance connection fault in permanent magnet machines based on zero sequence voltage. IEEE Trans. Power Electron. 2020, 35, 1922–1933. [Google Scholar] [CrossRef]
- Hang, J.; Wu, H.; Ding, S.; Hua, W.; Wang, Q. A DC-flux-injection method for fault diagnosis of high-resistance connection in direct-torque-controlled PMSM drive system. IEEE Trans. Power Electron. 2020, 35, 3029–3042. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Ding, S.; Huang, Y.; Wang, Q. A model-based strategy with robust parameter mismatch for online HRC diagnosis and location in PMSM drive system. IEEE Trans. Power Electron. 2020, 35, 10917–10929. [Google Scholar] [CrossRef]
- Kommuri, S.K.; Park, Y.; Bin Lee, S. High-resistance fault control in permanent magnet synchronous motors. IEEE/ASME Trans. Mech. 2019, 25, 271–281. [Google Scholar] [CrossRef]
- Lee, H.; Jeong, H.; Koo, G.; Ban, J.; Kim, S.W. Attention Recurrent Neural Network-Based Severity Estimation Method for Interturn Short-Circuit Fault in Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2021, 68, 3445–3453. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.; Mao, R.; Zhang, Y.; Zhu, K.; Li, Y.; Zhang, J. A Fault Diagnosis Method Based on an Improved Deep Q-Network for the Inter-Turn Short Circuits of a Permanent Magnet Synchronous Motor. IEEE Trans. Ind. Electron. 2023, in press. [Google Scholar] [CrossRef]
- Faiz, J.; Abadi, M.B.; Cruz, S.M.; Moosavi, S.M.M. Comparison of rotor electrical fault indices owing to inter-turn short circuit and unbalanced resistance in doubly-fed induction generator. IET Electr. Power App. 2019, 13, 235–242. [Google Scholar]
- Battulga, B.; Shaikh, M.F.; Bin Lee, S.; Osama, M. Automated identification of failures in doubly-fed induction generators for wind turbine applications. IEEE Trans. Ind. Appl. 2023, 59, 4454–4463. [Google Scholar] [CrossRef]
- Ibrahim, R.K.; Watson, S.J.; Djurović, S.; Crabtree, C.J. An effective approach for rotor electrical asymmetry detection in wind turbine DFIGs. IEEE Trans. Ind. Electron. 2018, 65, 8872–8881. [Google Scholar] [CrossRef]
- Fu, Y.; Ren, Z.; Wei, S.; Xu, Y.; Li, F. Using flux linkage difference vector in early inter-turn short circuit detection for the windings of offshore wind DFIGs. IEEE Trans. Energy Convers. 2021, 36, 3007–3015. [Google Scholar] [CrossRef]
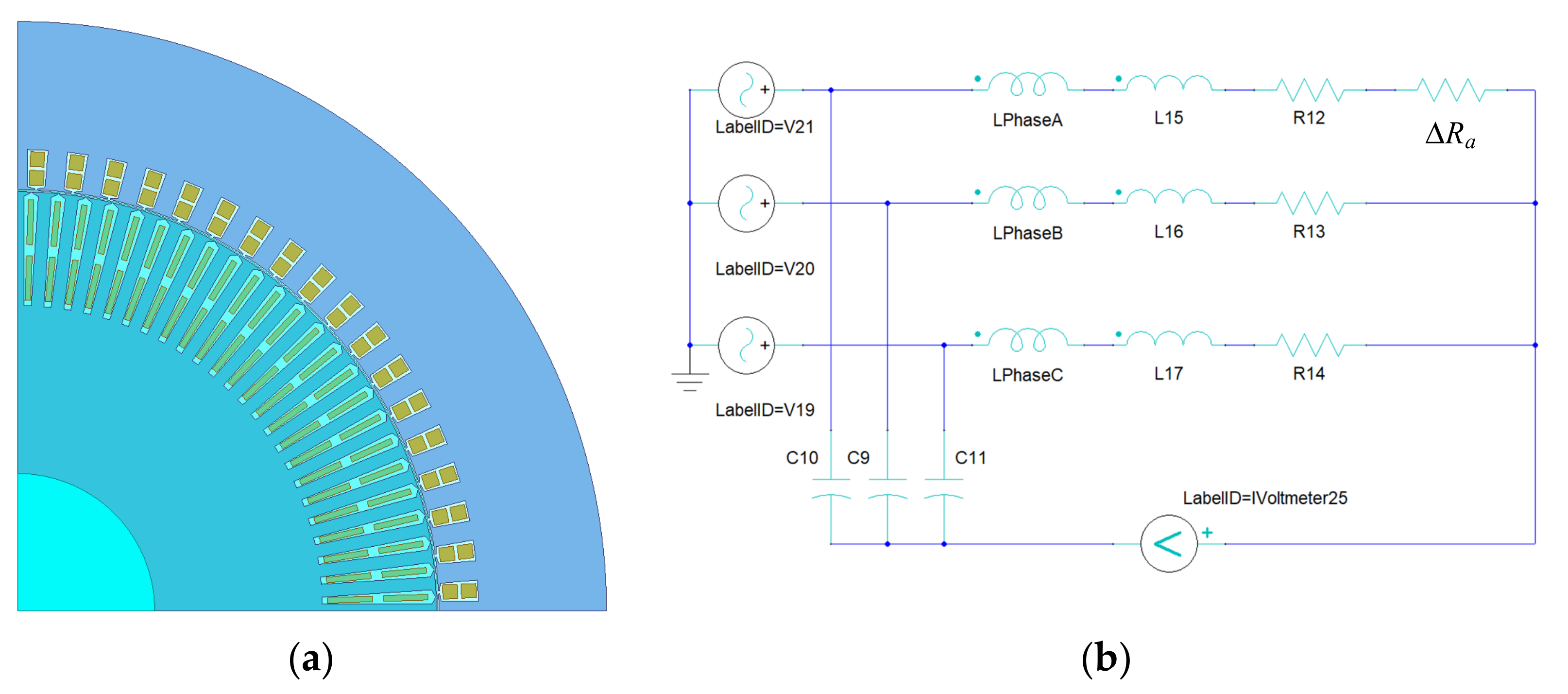
| Item | Value | Item | Value |
|---|---|---|---|
| Rated power [kW] | 1500 | Rated speed [rpm] | 1750 |
| Stator outer diameter [mm] | 860 | Stack length [mm] | 780 |
| Stator inner diameter [mm] | 615 | Pole-pair number | 2 |
| Thickness of stator yoke [mm] | 93.5 | Number of stator slot | 72 |
| Tooth width of stator [mm] | 14 | Number of rotor slot | 96 |
| Rotor outer diameter [mm] | 611.4 | Number of stator winding layers | 2 |
| Rotor inner diameter [mm] | 200 | Number of rotor winding layers | 2 |
| Thickness of rotor yoke [mm] | 122.5 | Stator coil pitch | 16 |
| Tooth width of rotor [mm] | 9.3 | Rotor coil pitch | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, W.; Jin, Y.; Wu, X.; Yang, Y.; Jiang, Y. High-Resistance Connection Diagnosis of Doubly Fed Induction Generators. Energies 2023, 16, 7516. https://doi.org/10.3390/en16227516
Ding W, Jin Y, Wu X, Yang Y, Jiang Y. High-Resistance Connection Diagnosis of Doubly Fed Induction Generators. Energies. 2023; 16(22):7516. https://doi.org/10.3390/en16227516
Chicago/Turabian StyleDing, Wei, Yulong Jin, Xijin Wu, Yufeng Yang, and Yongjiang Jiang. 2023. "High-Resistance Connection Diagnosis of Doubly Fed Induction Generators" Energies 16, no. 22: 7516. https://doi.org/10.3390/en16227516
APA StyleDing, W., Jin, Y., Wu, X., Yang, Y., & Jiang, Y. (2023). High-Resistance Connection Diagnosis of Doubly Fed Induction Generators. Energies, 16(22), 7516. https://doi.org/10.3390/en16227516






