Parameter-Free Model Predictive Current Control for PMSM Based on Current Variation Estimation without Position Sensor
Abstract
:1. Introduction
- Taking the current variations as the estimation target, a parameter-free MPCC is designed on the basis of RLS, where the natural attenuation and forced response of current variations are estimated accurately. It successfully avoids the effects of lost initial data in [25] and the problem of current variation renewal stagnates in [23].
- To estimate the rotor position through the known current variations, the forced response value is analyzed together with the active voltage vector, after which an accurate rotor position angle can be obtained by the built arc tangent function. Parameter dependence in [24,26] is successfully overcome.
- Both simulated and experimental results verify the correctness and effectiveness of the proposed method.
2. Model of PMSM Drive System
2.1. Mathematical Model of Motor
2.2. Model of Current Variations
3. Proposed Sensorless Parameter-Free MPCC Strategy
3.1. Parameter-Free MPCC
3.2. Estimation of Current Variation
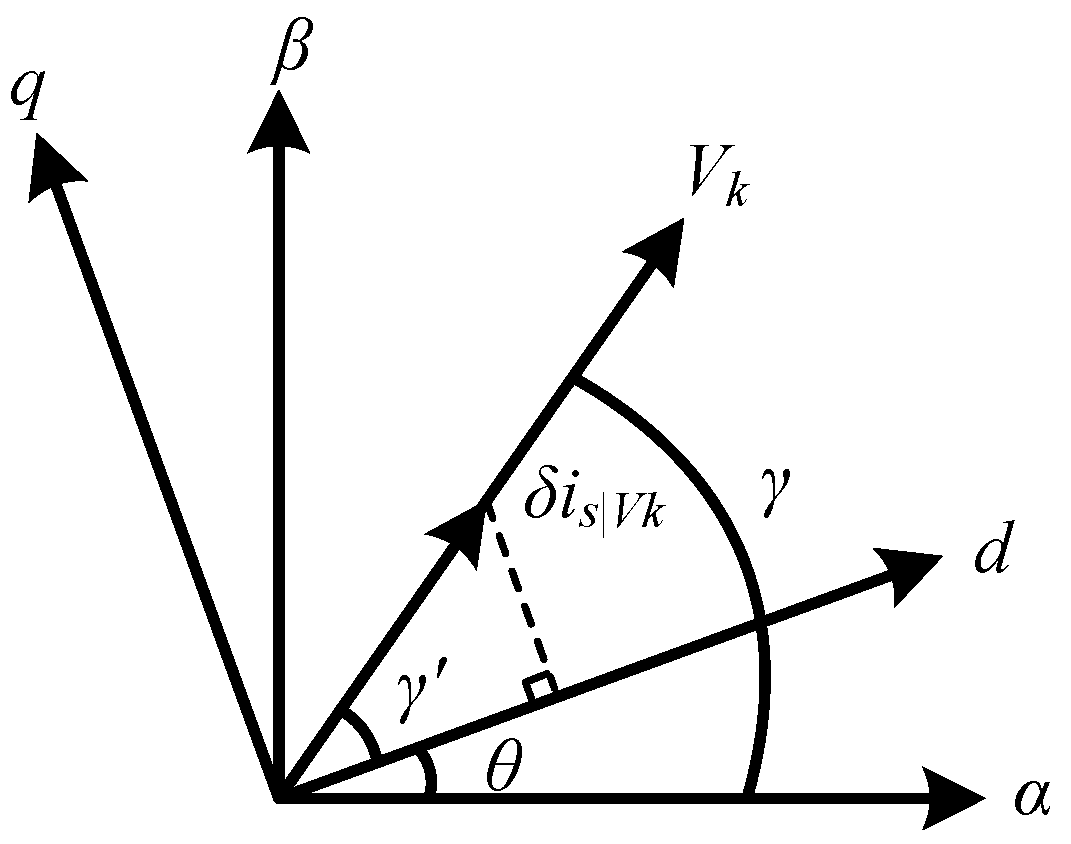
3.3. Rotor Position Estimation
3.4. Summary
- Collection and storage of the phase currents and applied voltage vectors and obtention of Ψx(x = d,q) and yx according to (15) and (16). Also, current reference iqref(k + 1) needs to be achieved through the speed controller.
- Relying on the applied voltage vector at (k − 1)th, vector position angle γ can be decided. Meanwhile, the angle between the voltage vector and the d-axis of the rotating coordinate system, namely γ′, needs to be achieved via the forced response of current variations through (26). Then, the rotor position angle θ can be estimated by (27).
- The current variations need to be estimated through the RLS based on (23) and (24). Then, the future current can be predicted by (25).
- The cost function gj (10) can be evaluated and the optimal voltage vector corresponding to the minimal gj needs to be selected to drive the inverter.
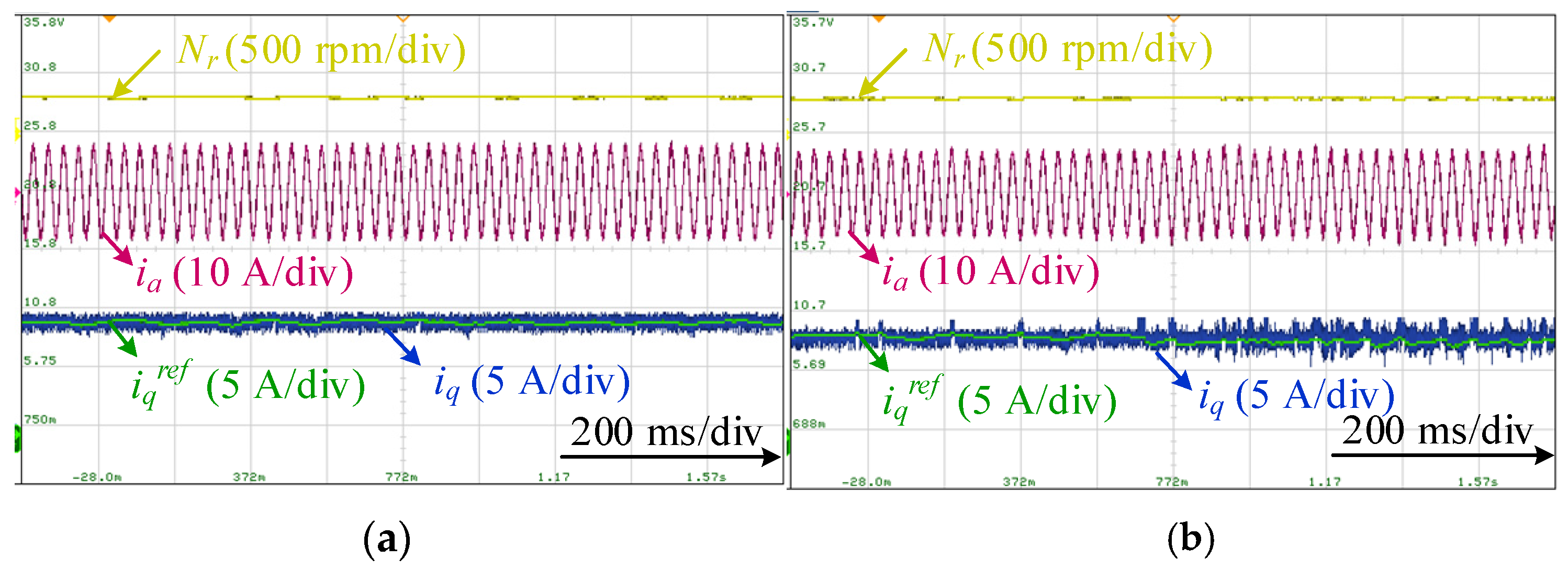
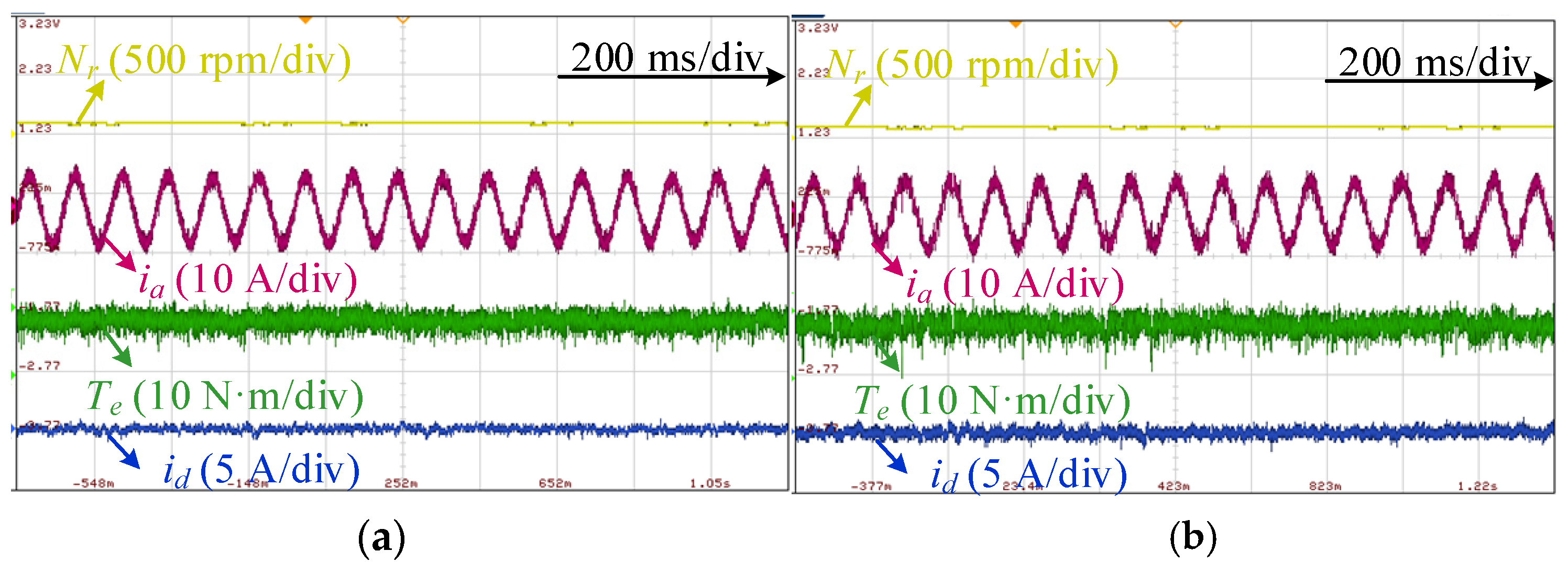
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, D.K.; Hwang, W.; Lee, J.Y.; Woo, B.C. Design, Analysis, and Experimental Validation of a Permanent Magnet Synchronous Motor for Articulated Robot Applications. IEEE Trans. Magn. 2018, 54, 8201304. [Google Scholar] [CrossRef]
- Li, X.; Xue, Z.; Yan, X.; Zhang, L.; Ma, W.; Hua, W. Low-Complexity Multivector-Based Model Predictive Torque Control for PMSM with Voltage Preselection. IEEE Trans. Power Electron. 2021, 36, 11726–11738. [Google Scholar] [CrossRef]
- Huang, W.; Hua, W.; Yin, F. Model Predictive Thrust Force Control of a Linear Flux-Switching Permanent Magnet Machine with Voltage Vectors Selection and Synthesis. IEEE Trans. Ind. Electron. 2019, 66, 4956–4967. [Google Scholar] [CrossRef]
- Wang, W.; Liu, C.; Liu, S.; Zhao, H. Model Predictive Torque Control for Dual Three-Phase PMSMs with Simplified Deadbeat Solution and Discrete Space-Vector Modulation. IEEE Trans. Energy Convers. 2021, 36, 1491–1499. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J. Model Predictive Switching Control for PMSM Drives. IEEE J. Emerg. Sel. Topics Power Electron. 2023, 11, 942–951. [Google Scholar] [CrossRef]
- Yu, F.; Li, K.; Zhu, Z.; Liu, X. An Over-Modulated Model Predictive Current Control for Permanent Magnet Synchronous Motors. IEEE Access 2022, 10, 40391–40401. [Google Scholar] [CrossRef]
- Im, J.; Kim, R. Improved Saliency-Based Position Sensorless Control of Interior Permanent-Magnet Synchronous Machines with Single DC-Link Current Sensor Using Current Prediction Method. IEEE Trans. Ind. Electron. 2018, 65, 5335–5343. [Google Scholar] [CrossRef]
- Tang, Q.; Shen, A.; Luo, P. IPMSMs Sensorless MTPA Control Based on Virtual q-Axis Inductance by Using Virtual High-Frequency Signal Injection. IEEE Trans. Ind. Electron. 2020, 67, 136–146. [Google Scholar] [CrossRef]
- Xiao, D.; Nalakath, S.; Filho, S. Universal Full-Speed Sensorless Control Scheme for Interior Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2021, 36, 4723–4737. [Google Scholar] [CrossRef]
- Teymoori, V.; Kamper, M.; Wang, R.-J.; Kennel, R. Sensorless Control of Dual Three-Phase Permanent Magnet Synchronous Machines—A Review. Energies 2023, 16, 1326. [Google Scholar] [CrossRef]
- Fadi, A.; Ahmad, A.; Rabia, S.; Cristina, M.; Ibrahim, K. Velocity Sensor Fault-Tolerant Controller for Induction Machine using Intelligent Voting Algorithm. Energies 2022, 15, 3084. [Google Scholar]
- Jiang, Y.; Xu, W.; Mu, C.; Zhu, J.; Dian, R. An Improved Third-Order Generalized Integral Flux Observer for Sensorless Drive of PMSMs. IEEE Trans. Ind. Electron. 2019, 66, 9149–9160. [Google Scholar] [CrossRef]
- Chen, S.; Ding, W.; Wu, X.; Huo, L.; Hu, R.; Shi, S. Sensorless Control of IPMSM Drives Using High-Frequency Pulse Voltage Injection with Random Pulse Sequence for Audible Noise Reduction. IEEE Trans. Power Electron. 2023, 38, 9395–9408. [Google Scholar] [CrossRef]
- Wang, G.; Yang, L.; Yuan, B.; Wang, B.; Zhang, G.; Xu, D. Pseudo-Random High-Frequency Square-Wave Voltage Injection Based Sensorless Control of IPMSM Drives for Audible Noise Reduction. IEEE Trans. Ind. Electron. 2016, 63, 7423–7433. [Google Scholar] [CrossRef]
- Gao, S.; Yuan, L.; Dai, Y.; Mou, D.; Chen, K.; Zhao, Z. High-Frequency Current Predictive Control Method for Multiactive-Bridge Converter. IEEE Trans. Power Electron. 2022, 37, 10144–10148. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Walker, P.D.; Liang, J.; Zhang, N.; Xia, B. Speed Sensorless Model Predictive Current Control with Ability to Start a Free Running Induction Motor. IET Electr. Power Appl. 2017, 11, 893–901. [Google Scholar] [CrossRef]
- Kumar, P.; Bhaskar, D.V.; Muduli, U.R.; Beig, A.R.; Behera, R.K. Iron-Loss Modeling with Sensorless Predictive Control of PMBLDC Motor Drive for Electric Vehicle Application. IEEE Trans. Transp. Electr. 2021, 7, 1506–1515. [Google Scholar] [CrossRef]
- Liu, K.; Wang, X.; Wang, R.; Sun, G.; Wang, X. Antisaturation Finite-Time Attitude Tracking Control Based Observer for a Quadrotor. IEEE Trans. Circuits-II 2021, 68, 2047–2051. [Google Scholar] [CrossRef]
- Liu, J.; Cao, J.; Li, L. A Novel Method for Estimating the Position and Speed of a Winding Segmented Permanent Magnet Linear Motor. Energies 2023, 16, 3361. [Google Scholar] [CrossRef]
- Wang, H.; Wu, T.; Guo, Y.; Lei, G.; Wang, X. Predictive Current Control of Sensorless Linear Permanent Magnet Synchronous Motor. Energies 2023, 16, 628. [Google Scholar] [CrossRef]
- Eid, M.A.E.; Elbaset, A.A.; Ibrahim, H.A.; Abdelwahab, S.A.M. Modelling, Simulation of MPPT Using Perturb and Observe and Incremental Conductance techniques For Stand-Alone PV Systems. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 429–434. [Google Scholar]
- Eid, M.A.E.; Abdelwahab, S.A.M.; Ibrahim, H.A.; Alaboudy, A.H.K. Improving the Resiliency of a PV Standalone System under Variable Solar Radiation and Load Profile. In Proceedings of the 2018 Twentieth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 18–20 December 2018; pp. 570–576. [Google Scholar]
- Yu, F.; Zhou, C.; Liu, X.; Zhu, C. Model-Free Predictive Current Control for Three-Level Inverter-Fed IPMSM with an Improved Current Difference Updating Technique. IEEE Trans. Energy Convers. 2021, 36, 3334–3343. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Z.; Freire, N.M.A. High Frequency Signal Injection Sensorless Control of Finite-Control-Set Model Predictive Control with Deadbeat Solution. IEEE Trans. Ind. Appl. 2022, 58, 3685–3695. [Google Scholar] [CrossRef]
- Wei, Y.; Xie, H.; Ke, D.; Wang, F. Sensorless Model-Free Predictive Current Control with Variable Prediction Horizon by Estimated Position for PMSM. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–5. [Google Scholar]
- Zhu, X.; Zhang, L.; Xiao, X.; Lee, C.H.T.; Que, H. Adjustable-Flux Permanent Magnet Synchronous Motor Sensorless Drive System Based on Parameter-Sensitive Adaptive Online Decoupling Control Strategy. IEEE Trans. Transp. Electr. 2023, 9, 501–511. [Google Scholar] [CrossRef]








| Voltage Vector | Sabc | Vector Position Angle γ | Voltage Vector | Sabc | Vector Position Angle γ |
|---|---|---|---|---|---|
| V1 | 100 | 0 | V2 | 110 | π/3 |
| V3 | 010 | 2π/3 | V4 | 011 | π |
| V5 | 001 | 4π/3 | V6 | 101 | 5π/3 |
| V7 | 000 | 0 | V8 | 111 | 0 |
| Reference | [14] | [17] | [18] | [26] | Proposed |
|---|---|---|---|---|---|
| Requires gain tuning | No | Yes | Yes | Yes | No |
| Estimation errors | Middle | Low | Low | Middle | Low |
| Parameter robustness | Low | Low | Low | High | High |
| Relative Simplicity of algorithm | Low | High | Middle | Middle | Middle |
| Parameters | Values |
|---|---|
| Rated power | 1.2 kW |
| Rated voltage | 380 V |
| Rated current | 5 A |
| Rated torque | 8 N∙m |
| Rated speed | 1500 rpm |
| Inductance of direct axis | 24 mH |
| Inductance of quadrature axis | 36 mH |
| Stator resistance | 5.25 Ω |
| Moment of inertia | 0.001 kg·m2 |
| Pole pairs | 2 |
| Permanent magnet flux linkage | 0.8 Wb |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Yu, F.; Ren, L.; Lu, C. Parameter-Free Model Predictive Current Control for PMSM Based on Current Variation Estimation without Position Sensor. Energies 2023, 16, 6792. https://doi.org/10.3390/en16196792
Luo L, Yu F, Ren L, Lu C. Parameter-Free Model Predictive Current Control for PMSM Based on Current Variation Estimation without Position Sensor. Energies. 2023; 16(19):6792. https://doi.org/10.3390/en16196792
Chicago/Turabian StyleLuo, Laiwu, Feng Yu, Lei Ren, and Cheng Lu. 2023. "Parameter-Free Model Predictive Current Control for PMSM Based on Current Variation Estimation without Position Sensor" Energies 16, no. 19: 6792. https://doi.org/10.3390/en16196792
APA StyleLuo, L., Yu, F., Ren, L., & Lu, C. (2023). Parameter-Free Model Predictive Current Control for PMSM Based on Current Variation Estimation without Position Sensor. Energies, 16(19), 6792. https://doi.org/10.3390/en16196792








