A Fuzzy Logic Concept for Predicting the Seasonal Thermal Performance of Building Envelopes Based on Structural and Geographical Parameters
Abstract
:1. Introduction
2. Materials and Methods
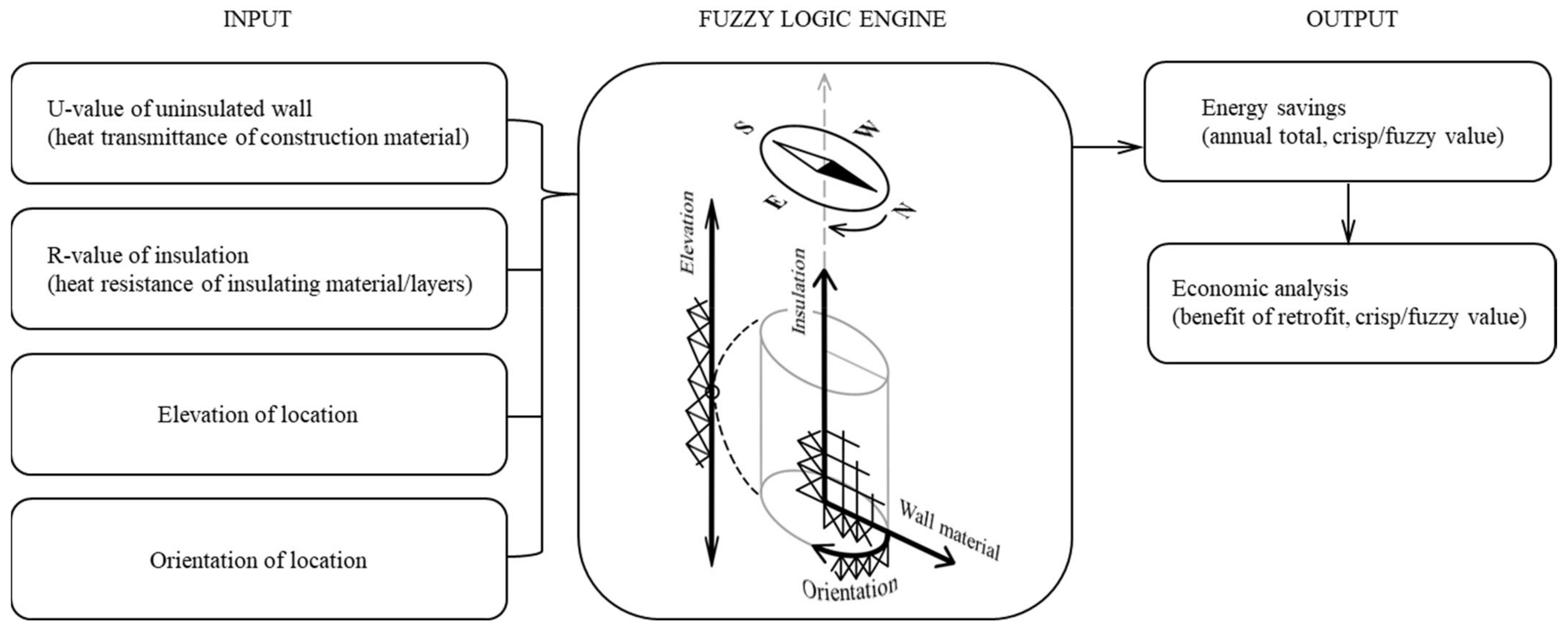
2.1. Implementation Strategy
2.2. Fuzzy Logic Model
2.3. Computational Model
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Office of Energy Efficiency & Renewable Energy. Buildings Energy Data Book. Available online: https://data.openei.org/submissions/144 (accessed on 13 September 2023).
- Albatici, R.; Passerini, F.; Tonelli, A.M.; Gialanella, S. Assessment of the Thermal Emissivity Value of Building Materials Using an Infrared Thermovision Technique Emissometer. Energy Build. 2013, 66, 33–40. [Google Scholar] [CrossRef]
- Blanusa, P.; Goss, W.P.; Roth, H.; Weitzmannn, P.; Jensen, C.F.; Svendsen, S.; Elmahdy, H. Comparison between ASHRAE and ISO Thermal Transmittance Calculation Methods. Energy Build. 2007, 39, 374–384. [Google Scholar] [CrossRef]
- Lu, X.; Memari, A.M. Comparison of the Experimental Measurement Methods for Building Envelope Thermal Transmittance. Buildings 2022, 12, 282. [Google Scholar] [CrossRef]
- Catalina, T.; Virgone, J.; Blanco, E. Development and Validation of Regression Models to Predict Monthly Heating Demand for Residential Buildings. Energy Build. 2008, 40, 1825–1832. [Google Scholar] [CrossRef]
- Cansino, J.M.; Pablo-Romero, M.d.P.; Román, R.; Yñiguez, R. Promoting Renewable Energy Sources for Heating and Cooling in EU-27 Countries. Energy Policy 2011, 39, 3803–3812. [Google Scholar] [CrossRef]
- Pokharel, T.R.; Rijal, H.B.; Shukuya, M. A Field Investigation on Indoor Thermal Environment and Its Associated Energy Use in Three Climatic Regions in Nepal. Energy Build 2020, 222, 110073. [Google Scholar] [CrossRef]
- Perez, Y.V.; Capeluto, I.G. Climatic Considerations in School Building Design in the Hot-Humid Climate for Reducing Energy Consumption. Appl. Energy 2009, 86, 340–348. [Google Scholar] [CrossRef]
- Budaiwi, I.M. Envelope Thermal Design for Energy Savings in Mosques in Hot-Humid Climate. J. Build. Perform. Simul. 2011, 4, 49–61. [Google Scholar] [CrossRef]
- De Masi, R.F.; Gigante, A.; Ruggiero, S.; Vanoli, G.P. The Impact of Weather Data Sources on Building Energy Retrofit Design: Case Study in Heating-Dominated Climate of Italian Backcountry. J. Build. Perform. Simul. 2020, 13, 264–284. [Google Scholar] [CrossRef]
- Cao, Y.; Pourrostam, T.; Zandi, Y.; Denić, N.; Ćirković, B.; Agdas, A.S.; Selmi, A.; Vujović, V.; Jermsittiparsert, K.; Milic, M. Analyzing the Energy Performance of Buildings by Neuro-Fuzzy Logic Based on Different Factors. In Environment, Development and Sustainability: A Multidisciplinary Approach to the Theory and Practice of Sustainable Development; Springer: Berlin/Heidelberg, Germany, 2021; Volume 23, pp. 17349–17373. [Google Scholar] [CrossRef]
- Kajl, S.; Roberge, M.A.; Lamarche, L.; Malinowski, P. Evaluation of Building Energy Consumption Based on Fuzzy Logic and Neural Networks Applications. In Proceedings of the Clima 2000 Conference, Brussels, Belgium, 30 August–2 September 1997. [Google Scholar]
- Biks, Y.; Lyalyuk, O.; Ratushnyak, G.; Ratushnyak, O.; Lyalyuk, A. Energy Efficiency Assessment of Heat Insulation Building Products: Fuzzy-Probabilistic Approach. Archit. Civ. Eng. Environ. 2021, 14, 59–68. [Google Scholar] [CrossRef]
- He, T.; Ukil, A. Design of Fuzzy Logic Based Controller for Energy Efficient Operation in Building. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 90–95. [Google Scholar] [CrossRef]
- Mpelogianni, V.; Groumpos, P.P.; Tsipianitis, D.; Papagiannaki, A.; Gionas, J. Proactive Building Energy Management Based on Fuzzy Logic and Expert Intelligence. Inf. Intell. Syst. Appl. 2020, 1, 56–58. [Google Scholar] [CrossRef]
- Zhang, H.; Davigny, A.; Colas, F.; Poste, Y.; Robyns, B. Fuzzy Logic Based Energy Management Strategy for Commercial Buildings Integrating Photovoltaic and Storage Systems. Energy Build. 2012, 54, 196–206. [Google Scholar] [CrossRef]
- Paris, B.; Eynard, J.; Salvador, M.; Grieu, S. Fuzzy Logic as a Useful Tool for Managing Resources in Multi-Energy Buildings. In Proceedings of the 7th Conference of the European Society for Fuzzy Logic and Technology, EUSFLAT 2011 and French Days on Fuzzy Logic and Applications, LFA 2011, Aix-Les-Bains, France, 18–22 July 2011; Volume 1, pp. 712–719. [Google Scholar] [CrossRef]
- Mehta, R. Optimal Design and Modeling of Sustainable Buildings Based on Multivariate Fuzzy Logic. Int. J. Sustain. Dev. Plan. 2021, 16, 195–206. [Google Scholar] [CrossRef]
- Nie, P.; Roccotelli, M.; Fanti, M.P.; Li, Z. Fuzzy Rule-Based Models for Home Energy Consumption Prediction. Energy Rep. 2022, 8, 9279–9289. [Google Scholar] [CrossRef]
- Al-Shanableh, F.; Evcil, A. Prediction of Energy Consumption of Residential Buildings in Northern Cyprus Using Fuzzy Interference System. Energy Build. 2022, 256, 111555. [Google Scholar] [CrossRef]
- Li, Y.; Tong, Z.; Tong, S.; Westerdahl, D. A Data-Driven Interval Forecasting Model for Building Energy Prediction Using Attention-Based LSTM and Fuzzy Information Granulation. Sustain. Cities Soc. 2022, 76, 103481. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Kočí, V.; Kočí, J.; Maděra, J.; Pavlík, Z.; Gu, X.; Zhang, W.; Černý, R. Thermal and Hygric Assessment of an Inside-Insulated Brick Wall: 2D Critical Experiment and Computational Analysis. J. Build. Phys. 2018, 41, 497–520. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy Identification of Systems and Its Applications to Modeling and Control. IEEE Trans. Syst. Man. Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Kočí, V.; Maděra, J.; Krejčí, T.; Kruis, J.; Černý, R. Efficient Techniques for Solution of Complex Computational Tasks in Building Physics. Adv. Civ. Eng. 2019, 2019, 3529360. [Google Scholar] [CrossRef]
- Krejčí, T.; Kruis, J.; Šejnoha, M.; Koudelka, T. Hybrid Parallel Approach to Homogenization of Transport Processes in Masonry. Adv. Eng. Softw. 2017, 113, 25–33. [Google Scholar] [CrossRef]
- Maděra, J.; Kočí, J.; Kočí, V.; Kruis, J. Parallel Modeling of Hygrothermal Performance of External Wall Made of Highly Perforated Bricks. Adv. Eng. Softw. 2017, 113, 47–53. [Google Scholar] [CrossRef]





| Load-Bearing Material | Wall Thickness | Bulk Density | U-Value Estimation | Additional Insulation |
|---|---|---|---|---|
| Stone/brick | 750 mm | 2244 kg·m−3 | 2.06 W·m−2·K−1 | 0 mm |
| 100 mm | ||||
| 200 mm | ||||
| Stone/brick | 1000 mm | 2244 kg·m−3 | 1.74 W·m−2·K−1 | 0 mm |
| 100 mm | ||||
| 200 mm | ||||
| AAC | 300 mm | 500 kg·m−3 | 0.37 W·m−2·K−1 | 0 mm |
| 100 mm | ||||
| 200 mm | ||||
| AAC | 500 mm | 500 kg·m−3 | 0.23 W·m−2·K−1 | 0 mm |
| 100 mm | ||||
| 200 mm |
| Parameter | Value |
|---|---|
| Room width (m) | 5.0 |
| Interior heat capacity (per 1 m2 of the wall) (J·m−2·K−1) | 2.6·105 |
| Solar radiation (W·m2) | data from TRY |
| Glazing ratio (-) | 0.3 |
| SHGC of the windows (-) | 0.6 |
| Air infiltration rate (h−1) | 0.6 |
| Heating setpoint (°C) | 20.0 |
| U (W·m−2·K−1) | γ (°) | e (m a.s.l.) | i (mm) | Value (kWh·m−2·Year−1) |
|---|---|---|---|---|
| 0.5 | 90 | 235 | 0 | 80.26 |
| 0.6 | 120 | 405 | 80 | 93.75 |
| 1.3 | 45 | 390 | 150 | 81.34 |
| 0.8 | 275 | 390 | 50 | 93.29 |
| 1.9 | 145 | 250 | 190 | 81.87 |
| 1.8 | 50 | 290 | 100 | 77.27 |
| 1.2 | 80 | 330 | 40 | 88.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kočí, J.; Maděra, J.; Khmurovska, Y.; Štemberk, P.; Černý, R. A Fuzzy Logic Concept for Predicting the Seasonal Thermal Performance of Building Envelopes Based on Structural and Geographical Parameters. Energies 2023, 16, 7719. https://doi.org/10.3390/en16237719
Kočí J, Maděra J, Khmurovska Y, Štemberk P, Černý R. A Fuzzy Logic Concept for Predicting the Seasonal Thermal Performance of Building Envelopes Based on Structural and Geographical Parameters. Energies. 2023; 16(23):7719. https://doi.org/10.3390/en16237719
Chicago/Turabian StyleKočí, Jan, Jiří Maděra, Yulia Khmurovska, Petr Štemberk, and Robert Černý. 2023. "A Fuzzy Logic Concept for Predicting the Seasonal Thermal Performance of Building Envelopes Based on Structural and Geographical Parameters" Energies 16, no. 23: 7719. https://doi.org/10.3390/en16237719
APA StyleKočí, J., Maděra, J., Khmurovska, Y., Štemberk, P., & Černý, R. (2023). A Fuzzy Logic Concept for Predicting the Seasonal Thermal Performance of Building Envelopes Based on Structural and Geographical Parameters. Energies, 16(23), 7719. https://doi.org/10.3390/en16237719







