A Communication Encryption-Based Distributed Cooperative Control for Distributed Generators in Microgrids under FDI Attacks
Abstract
:1. Introduction
- (1)
- A new cooperative control algorithm, which can eliminate the impact of FDI attacks to microgrids, is proposed. The frequency of each DGs in the microgrid can be restored to track the reference.
- (2)
- An enhanced second-order control based on the finite-time control theory is proposed. The new higher-order control can restore the stability of the system faster.
- (3)
- The proposed control algorithm is designed based on simple algorithm rather than conventional trust or confidential-based protocol, which can be implemented using inexpensive digital controllers.
- (4)
- The communication protection algorithm used in this paper is based on the Paillier homomorphic encryption strategy, which has never been used for DGs in microgrids.
2. Theoretical Basis
2.1. Priliminary of Graph Theory
2.2. Priliminary of Lyapunov Stabiliy of DG Frequencies
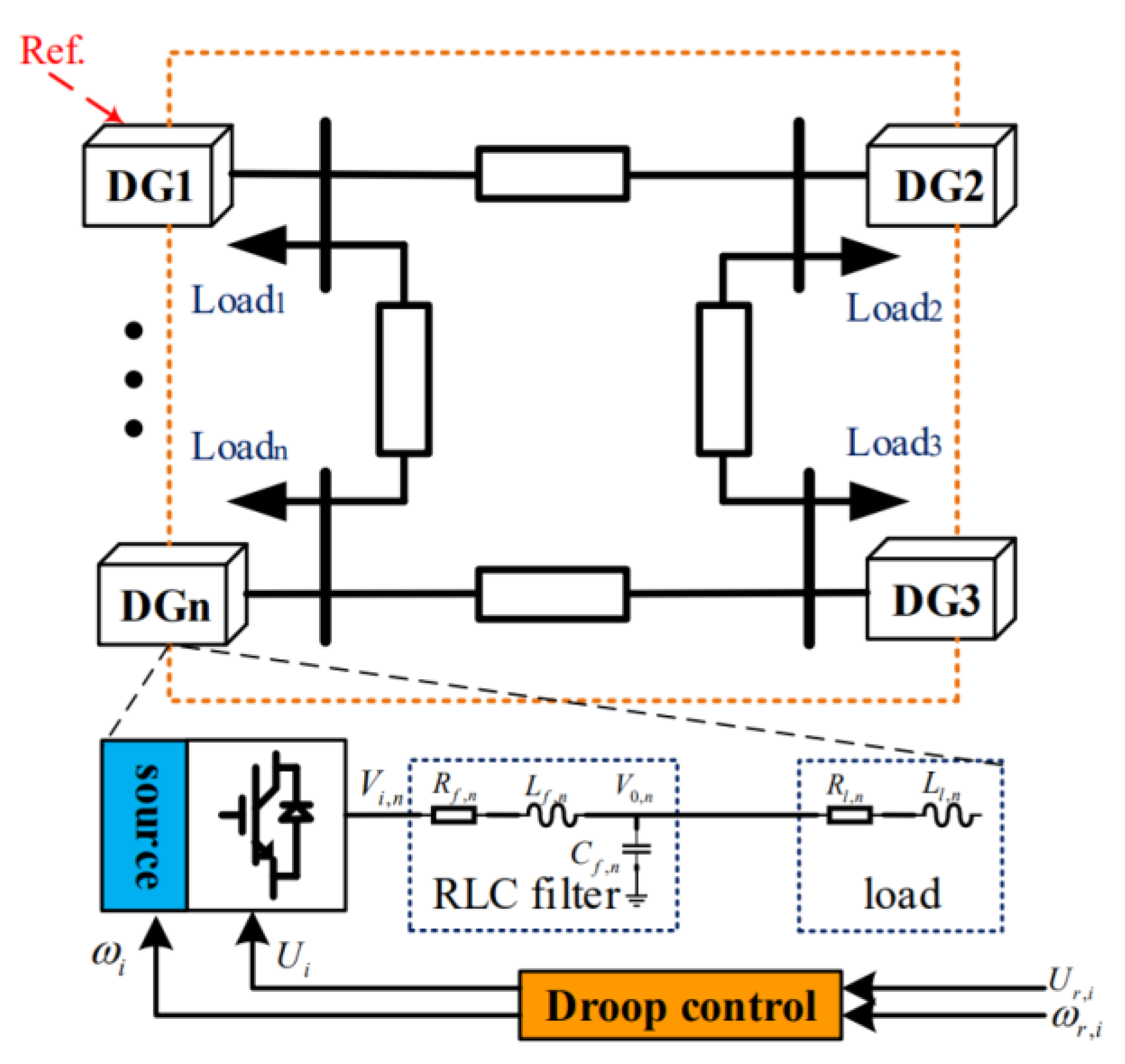
3. Cooperative Control of DGs in Microgrids
3.1. Primary Droop Control
3.2. Secondary Cooperative Control
4. Distributed Cooperative Control for DGs in Microgrids under FDI Attacks
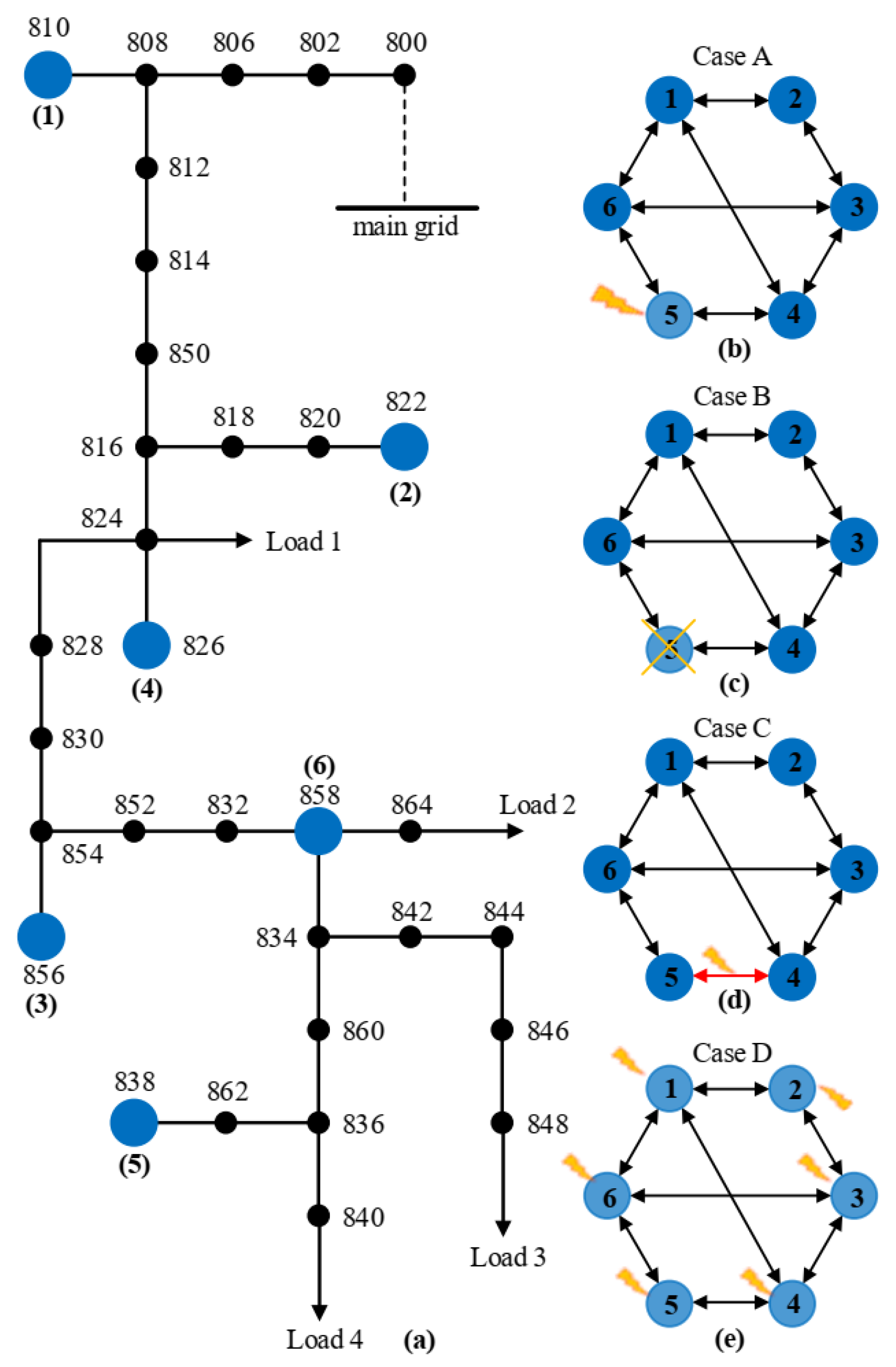
4.1. Attack Models
4.2. Distributed Cooperative Control Algorithm Design and Stability Analysis under an FDI Attack
4.3. Paillier Encryption Algorithm
| Algorithm 1: Information Exchange in Networks |
| Preparation (node i) to all its neighbors (including node j). Encryption and Transmission (node i) , to the neighbor: node j. Calculation, and Transmission (node j) Step 1: Decrypt after the out-of-limit judgment, obtain the plaintext , Step 2: Encrypt the kth calculation results of (10) as , Step 3: Transmit to node i. Decryption (node i) Repeat the above process and ensure the security of data during communication. |
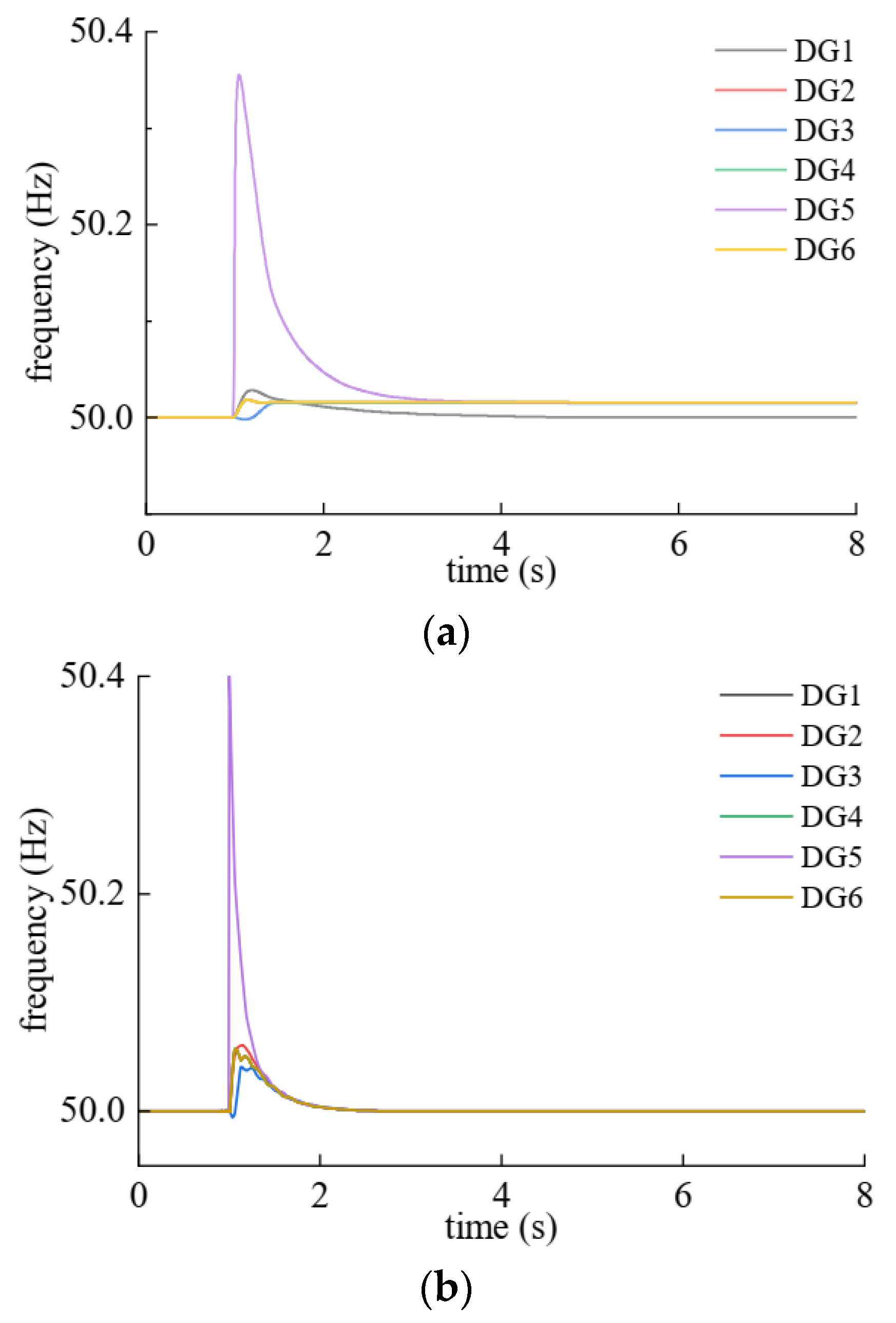
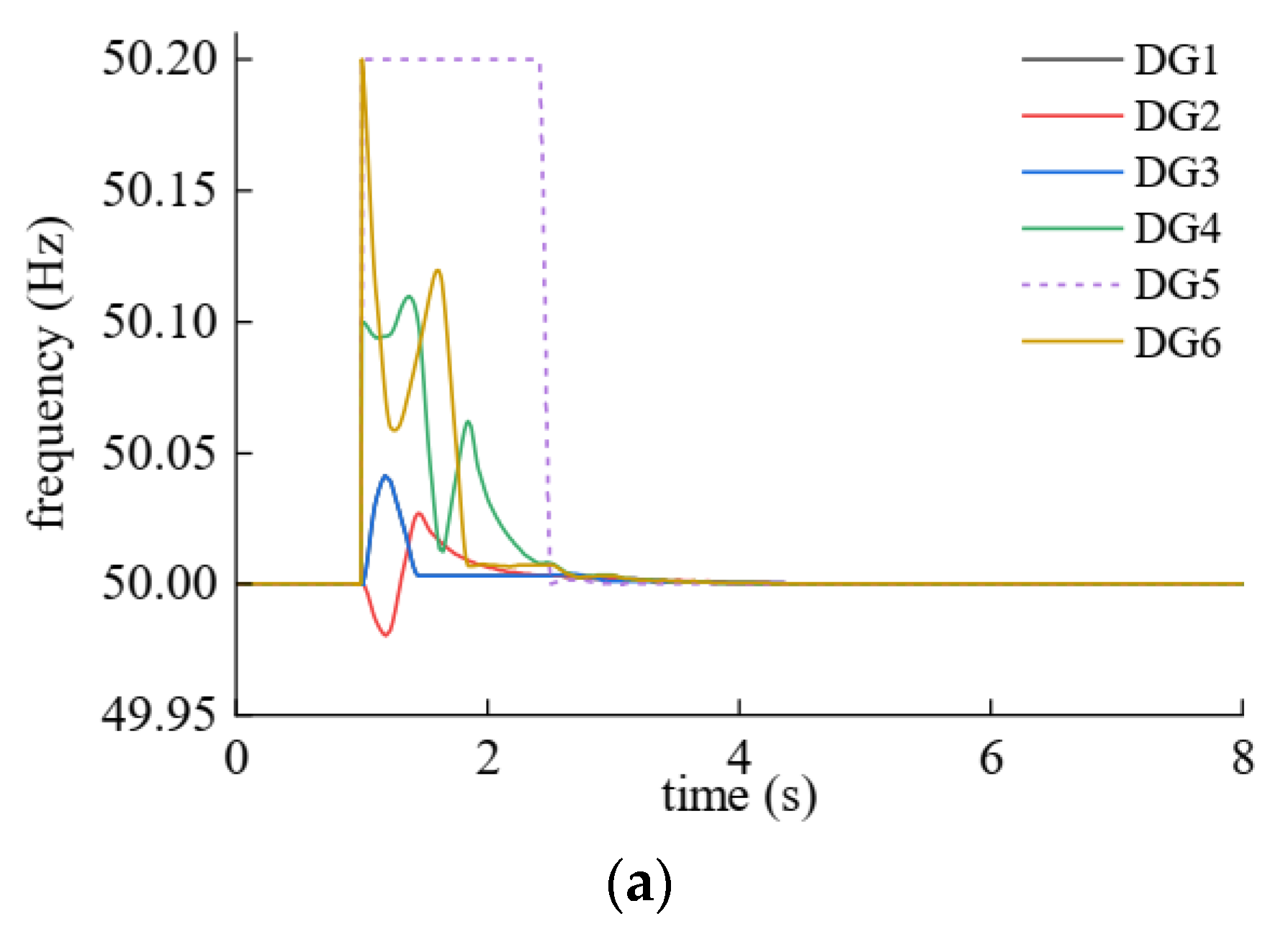
5. Simulation Study
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, G.; Gu, W.; Li, P.; Sheng, W.; Liu, K.; Sun, L.; Cao, Z.; Pan, J. Operational Risk Evaluation of Active Distribution Networks Considering Cyber Contingencies. IEEE Trans. Ind. Inform. 2020, 16, 3849–3861. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, S.-C.; Hui, S.Y.R. Mitigating Distribution Power Loss of DC Microgrids with DC Electric Springs. IEEE Trans. Smart Grid 2018, 9, 5897–5906. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.-L.; Ge, X.; Wang, J. Secure State Estimation and Control of Cyber-Physical Systems: A Survey. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 176–190. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, Y.; Tan, S.-C.; Hui, S.Y.R. Reducing Distribution Power Loss of Islanded AC Microgrids Using Distributed Electric Springs with Predictive Control. IEEE Trans. Ind. Electron. 2020, 67, 9001–9011. [Google Scholar] [CrossRef]
- Abdi, F.; Chen, C.-Y.; Hasan, M.; Liu, S.; Mohan, S.; Caccamo, M. Preserving Physical Safety under Cyber Attacks. IEEE Internet Things J. 2019, 6, 6285–6300. [Google Scholar] [CrossRef]
- Lu, X.; Yu, X.; Lai, J.; Wang, Y.; Guerrero, J.M. A Novel Distributed Secondary Coordination Control Approach for Islanded Microgrids. IEEE Trans. Smart Grid 2018, 9, 2726–2740. [Google Scholar] [CrossRef]
- Yang, Y.; Ho, S.-S.; Tan, S.-C.; Hui, S.-Y.R. Small-Signal Model and Stability of Electric Springs in Power Grids. IEEE Trans. Smart Grid 2018, 9, 857–865. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.-L.; Wang, Z.; Ge, X. A Survey on Model-Based Distributed Control and Filtering for Industrial Cyber-Physical Systems. IEEE Trans. Ind. Inform. 2019, 15, 2483–2499. [Google Scholar] [CrossRef]
- Bidram, A.; Davoudi, A. Hierarchical Structure of Microgrids Control System. IEEE Trans. Smart Grid 2012, 3, 1963–1976. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, S.-C.; Hui, S.Y.R. Adaptive Reference Model Predictive Control with Improved Performance for Voltage-Source Inverters. IEEE Trans. Control. Syst. Technol. 2018, 26, 724–731. [Google Scholar] [CrossRef]
- Shafiee, Q.; Guerrero, J.M.; Vasquez, J.C. Distributed Secondary Control for Islanded Microgrids—A Novel Approach. IEEE Trans. Power Electron. 2014, 29, 1018–1031. [Google Scholar] [CrossRef]
- Yang, Y.; Mok, K.-T.; Tan, S.-C.; Hui, S.Y. Nonlinear dynamic power tracking of low-power wind energy conversion system. IEEE Trans. Power Electron. 2015, 30, 5223–5236. [Google Scholar] [CrossRef]
- Zhang, G.; Li, C.; Qi, D.; Xin, H. Distributed Estimation and Secondary Control of Autonomous Microgrid. IEEE Trans. Power Syst. 2017, 32, 989–998. [Google Scholar] [CrossRef]
- Chen, Y.; Qi, D.; Dong, H.; Li, C.; Li, Z.; Zhang, J. A FDI Attack-Resilient Distributed Secondary Control Strategy for Islanded Microgrids. IEEE Trans. Smart Grid 2021, 12, 1929–1938. [Google Scholar] [CrossRef]
- Zhao, Z.; Huang, Y.; Zhen, Z.; Li, Y. Data-Driven False Data-Injection Attack Design and Detection in Cyber-Physical Systems. IEEE Trans. Cybern. 2021, 51, 6179–6187. [Google Scholar] [CrossRef]
- Yang, Y.; Qin, Y.; Tan, S.-C.; Hui, S.Y.R. Efficient Improvement of Photovoltaic-Battery Systems in Standalone DC Microgrids Using a Local Hierarchical Control for the Battery System. IEEE Trans. Power Electron. 2019, 34, 10796–10807. [Google Scholar] [CrossRef]
- Jiao, Q.; Modares, H.; Lewis, F.L.; Xu, S.; Xie, L. Distributed L2-gain output-feedback control of homogeneous and heterogeneous systems. Automatica 2016, 71, 361–368. [Google Scholar] [CrossRef]
- Shafiee, Q.; Nasirian, V.; Vasquez, J.C.; Guerrero, J.M.; Davoudi, A. A Multi-Functional Fully Distributed Control Framework for AC Microgrids. IEEE Trans. Smart Grid 2018, 9, 3247–3258. [Google Scholar] [CrossRef]
- Abhinav, S.; Schizas, I.D.; Lewis, F.L.; Davoudi, A. Distributed Noise-Resilient Networked Synchrony of Active Distribution Systems. IEEE Trans. Smart Grid 2018, 9, 836–846. [Google Scholar] [CrossRef]
- Abhinav, S.; Modares, H.; Lewis, F.L.; Ferrese, F.; Davoudi, A. Synchrony in Networked Microgrids under Attacks. IEEE Trans. Smart Grid 2018, 9, 6731–6741. [Google Scholar] [CrossRef]
- El-Yahyaoui, A.; El Kettani, M.D.E.-C. A verifiable fully homomorphic encryption scheme to secure big data in cloud computing. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications (WINCOM), Rabat, Morocco, 1–4 November 2017; pp. 1–5. [Google Scholar]
- Wu, W.; Liu, J.; Wang, H.; Hao, J.; Xian, M. Secure and Efficient Outsourced k-Means Clustering using Fully Homomorphic Encryption with Ciphertext Packing Technique. IEEE Trans. Knowl. Data Eng. 2021, 33, 3424–3437. [Google Scholar] [CrossRef]
- Sutisna, N.; Jonatan, G.; Syafalni, I.; Mulyawan, R.; Adiono, T. Polynomial multiplication systolic array for homomorphic encryption in secure network communications. In Proceedings of the 2020 IEEE International Conference on Communication, Networks and Satellite (Comnetsat), Batam, Indonesia, 17–18 December 2020; pp. 390–394. [Google Scholar]
- Wang, L.; Xiao, F. Finite-Time Consensus Problems for Networks of Dynamic Agents. IEEE Trans. Autom. Control. 2010, 55, 950–955. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Bicchi, A.; Bullo, F. Consensus Computation in Unreliable Networks: A System Theoretic Approach. IEEE Trans. Autom. Control. 2012, 57, 90–104. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Dorfler, F.; Bullo, F. Attack Detection and Identification in Cyber-Physical Systems. IEEE Trans. Autom. Control. 2013, 58, 2715–2729. [Google Scholar] [CrossRef]
- Rong-Bing, W.; Ya-Nan, L.; Hong-Yan, X.; Yong, F.; Yong-Gang, Z. Electronic Scoring Scheme Based on Real Paillier Encryption Algorithms. IEEE Access 2019, 7, 128043–128053. [Google Scholar] [CrossRef]
- Chen, W.; Liu, L.; Liu, G.-P. Privacy-Preserving Distributed Economic Dispatch of Microgrids: A Dynamic Quantization-Based Consensus Scheme with Homomorphic Encryption. IEEE Trans. Smart Grid 2023, 14, 701–713. [Google Scholar] [CrossRef]
- Ogunseyi, T.B.; Tang, B. Fast Decryption algorithm for paillier homomorphic cryptosystem. In Proceedings of the IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 28–30 July 2020; pp. 803–806. [Google Scholar]
- Mwakabuta, N.; Sekar, A. Comparative study of the IEEE 34 node test feeder under practical simplifications. In Proceedings of the Presented at 39th American Power Symposium, Las Cruces, NM, USA, 30 September–2 October 2007; pp. 484–491. [Google Scholar]
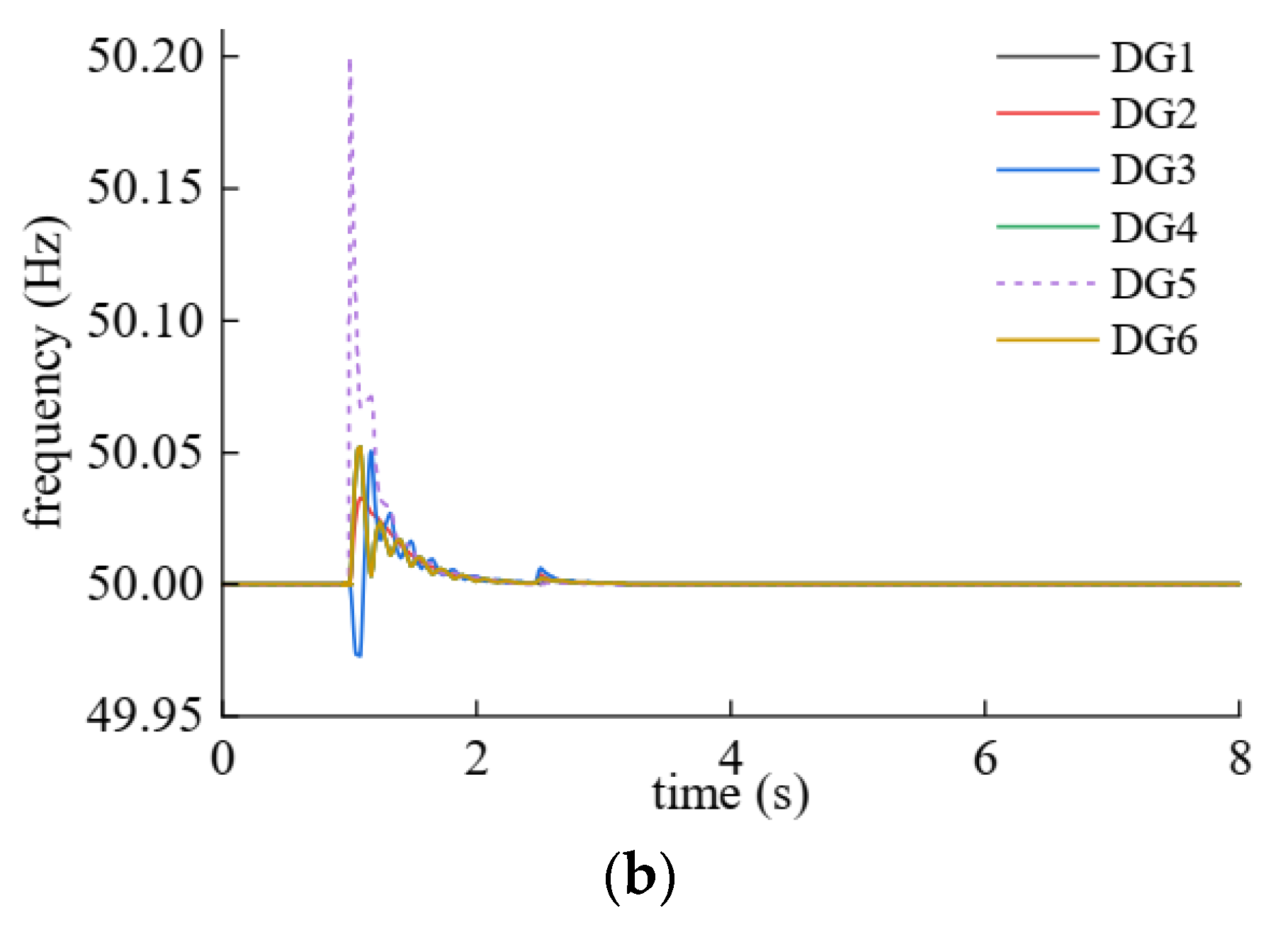
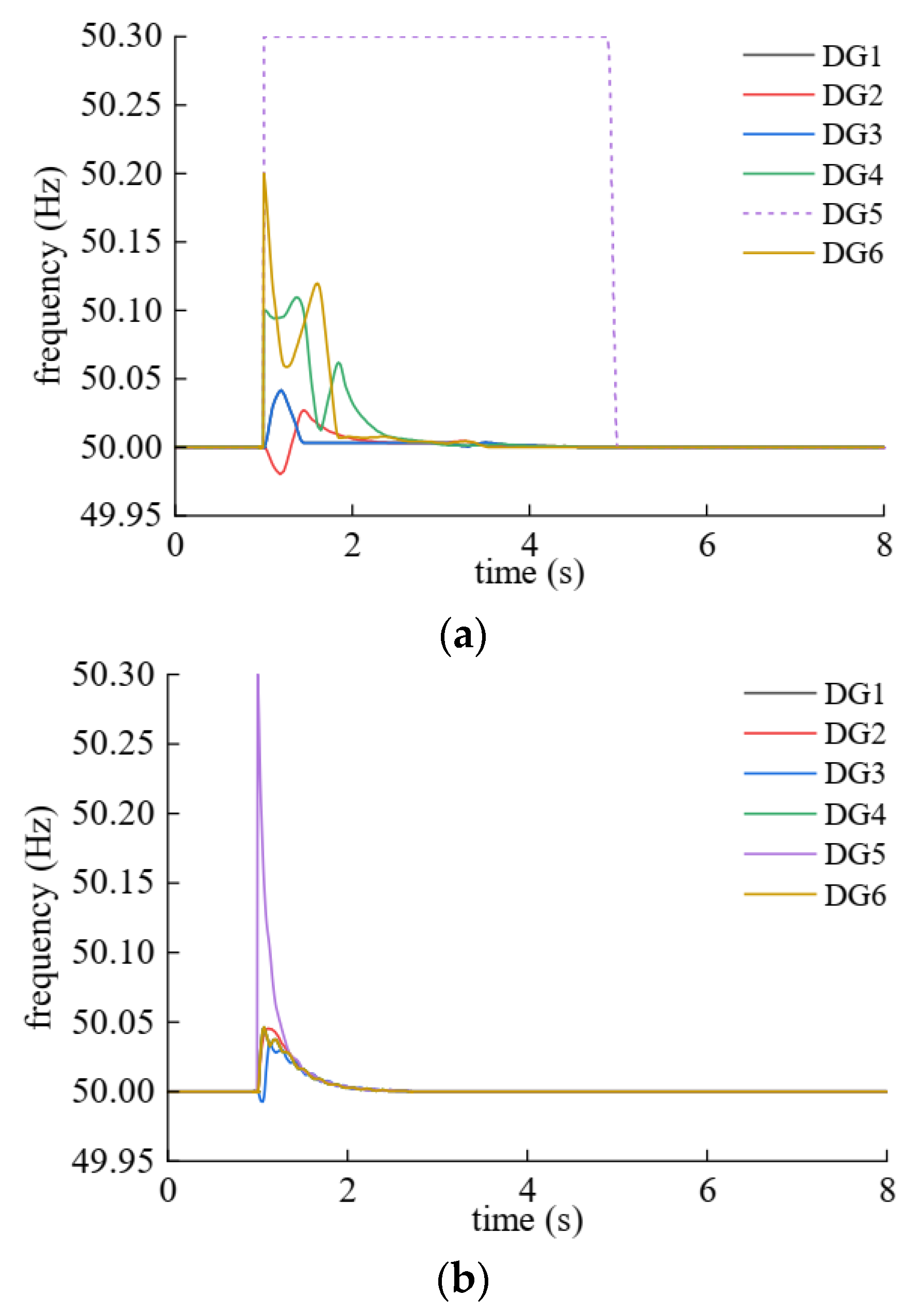
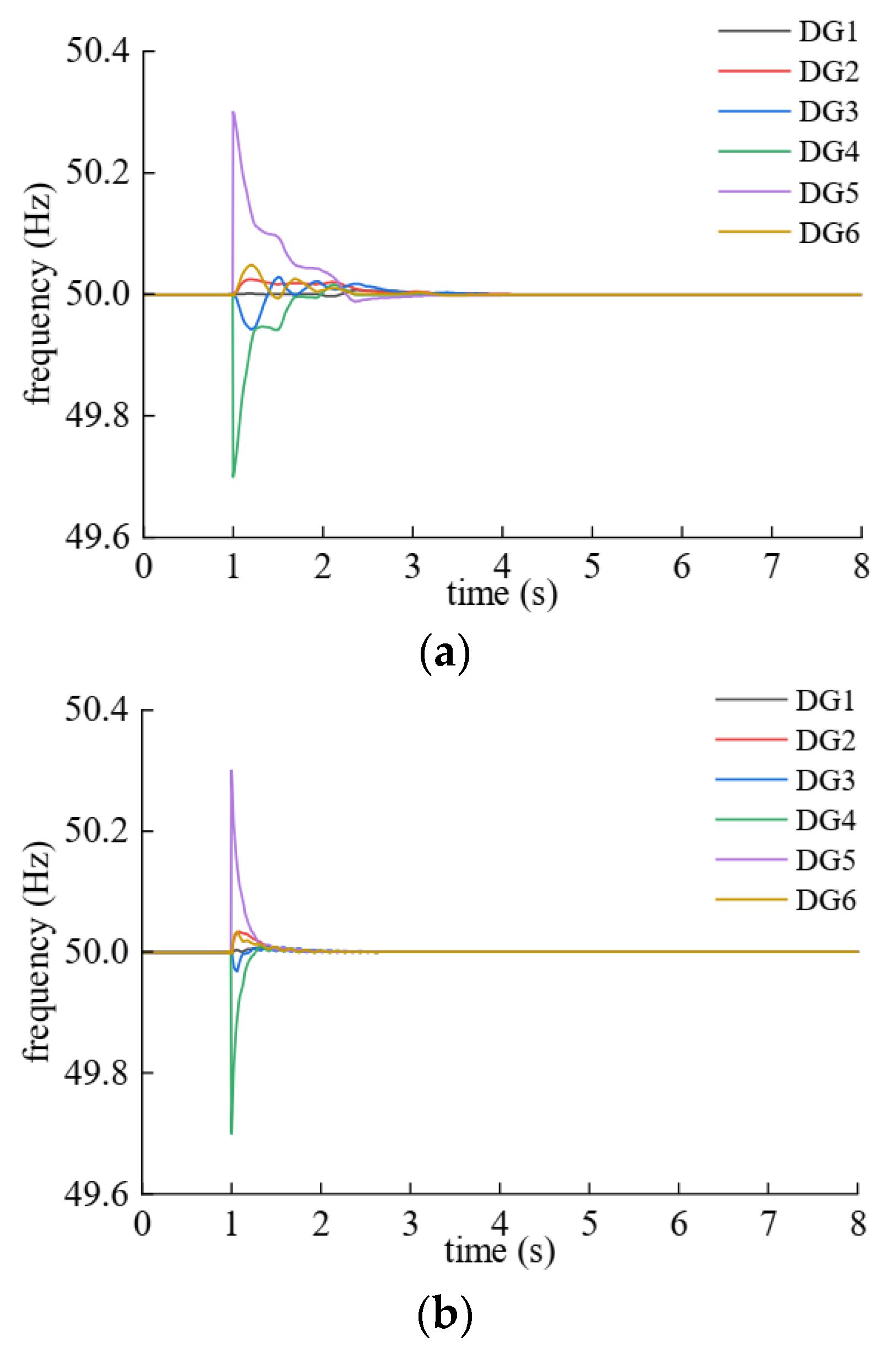
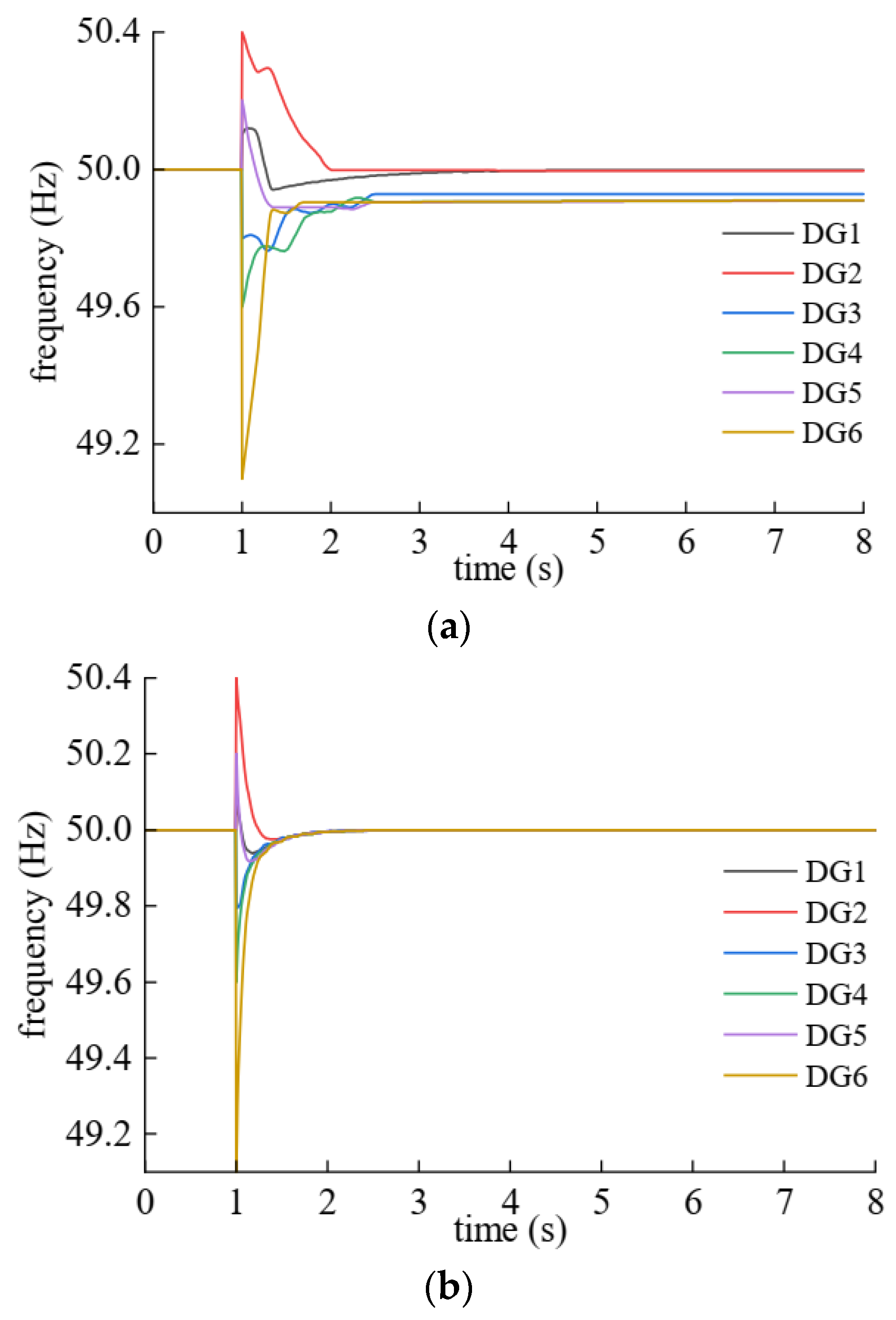
| DG | Plaintext | Ciphertext |
|---|---|---|
| DG1 | 50.0032355670135 | 13962878293123695743 9242239157272820843 |
| DG2 | 50.0026633037715 | 14406571166828568720 953973516366529545 |
| DG3 | 50.0018906850775 | 60862867060801566833 099386705657357782 |
| DG4 | 50.0032355670135 | 11225137299717172167 5466582369177460666 |
| DG5 | 50.0022263829894 | 14023597620684394011 1984608615102968414 |
| DG6 | 50.0032355670135 | 15775176166453180300 5257059011426352748 |
| DG | Plaintext | Ciphertext |
|---|---|---|
| DG1 | 50.0020935573353 | 95041175951322109463 733745365162478020 |
| DG2 | 50.0023534232178 | 17620672608558025515 504011146357424466 |
| DG3 | 50.0026884404735 | 20223420227290324722 718693972073728424 |
| DG4 | 50.0020935573353 | 40584764380985213406 764078574284625510 |
| DG5 | 50.0025465624365 | 14635744288036751950 4011498137737930240 |
| DG6 | 50.0020935573353 | 15924659508651567860 86017854118045541375257059 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Li, W.; Qiu, L.; Ai, Y.; Liu, Z. A Communication Encryption-Based Distributed Cooperative Control for Distributed Generators in Microgrids under FDI Attacks. Energies 2023, 16, 7754. https://doi.org/10.3390/en16237754
Fu H, Li W, Qiu L, Ai Y, Liu Z. A Communication Encryption-Based Distributed Cooperative Control for Distributed Generators in Microgrids under FDI Attacks. Energies. 2023; 16(23):7754. https://doi.org/10.3390/en16237754
Chicago/Turabian StyleFu, Han, Wenpei Li, Long Qiu, Yongheng Ai, and Zhixiong Liu. 2023. "A Communication Encryption-Based Distributed Cooperative Control for Distributed Generators in Microgrids under FDI Attacks" Energies 16, no. 23: 7754. https://doi.org/10.3390/en16237754
APA StyleFu, H., Li, W., Qiu, L., Ai, Y., & Liu, Z. (2023). A Communication Encryption-Based Distributed Cooperative Control for Distributed Generators in Microgrids under FDI Attacks. Energies, 16(23), 7754. https://doi.org/10.3390/en16237754








