Performance Evaluation of a Steam Ejector Considering Non-Equilibrium Condensation in Supersonic Flows
Abstract
1. Introduction
- (1)
- We established an experimental system for the steam ejector refrigeration cycle to provide an experimental reference for numerical calculation and analysis;
- (2)
- We developed a numerical model of the ejector under wet steam conditions and verified the veracity and validity of the numerical model by comparing it with experimental data;
- (3)
- We studied the flow of the effective area, expansion nuclei, and excitation waves inside the ejector under the flow of choking flow and the effect on the induced coefficient of the ejector and then discussed the law of the influence of the choked flow on the priming coefficient at different operating and pumped gas pressures;
- (4)
- We investigated the importance of choked flow in preventing backflow at the outlet, improved and optimized the operating conditions of the ejector, and analyzed the performance improvement of the ejector under different choking flows.
2. Experimental Systems
2.1. Experimental Setup
- (1)
- The expansion process of working steam ejected from the nozzle;
- (2)
- The mixing process between the working steam and the induced steam in the ejector;
- (3)
- The process of mixed steam being compressed at the throat of the diffuser.
2.2. Physical Model and Operating Conditions of Ejectors
3. Mathematical Models
3.1. Governing Equations
3.2. Wet Steam Flow Transport Equations
3.3. Wet Steam State Equations
3.4. Numerical Methods and Validation
4. Results and Discussion
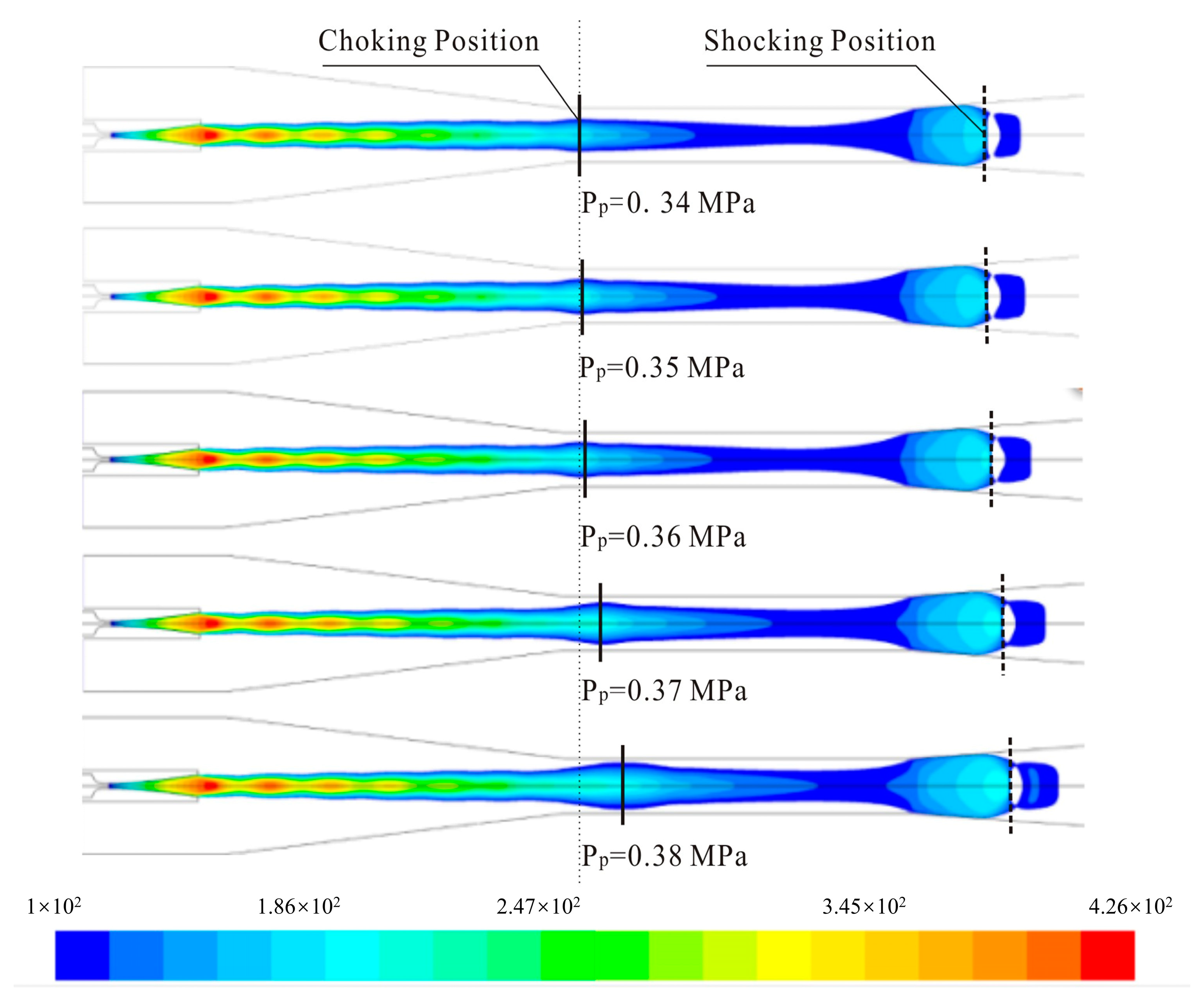
4.1. Effect of Primary Fluid Pressure on Entrainment Ratios
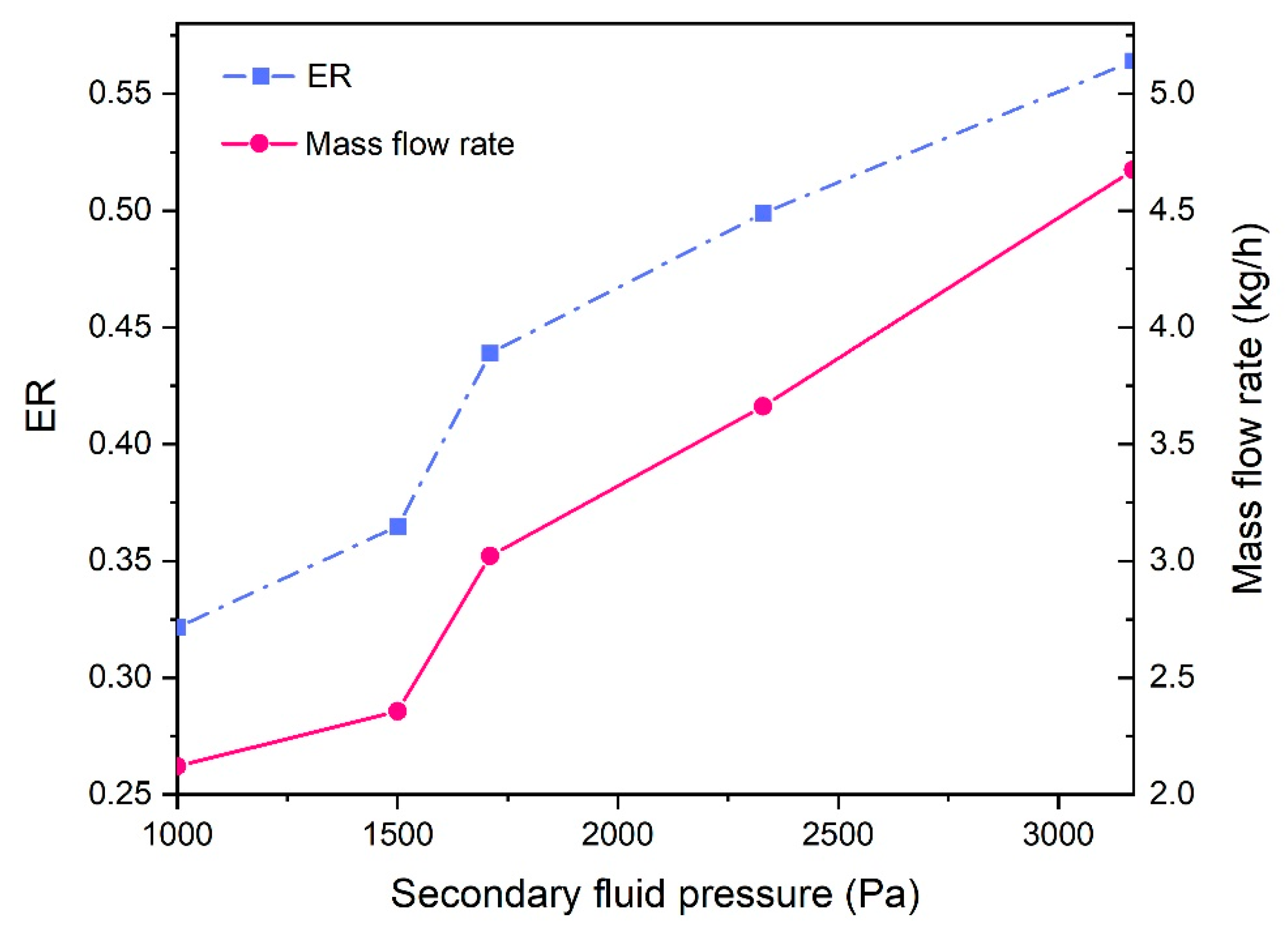
4.2. Effect of Secondary Fluid Pressure on Entrainment Ratios
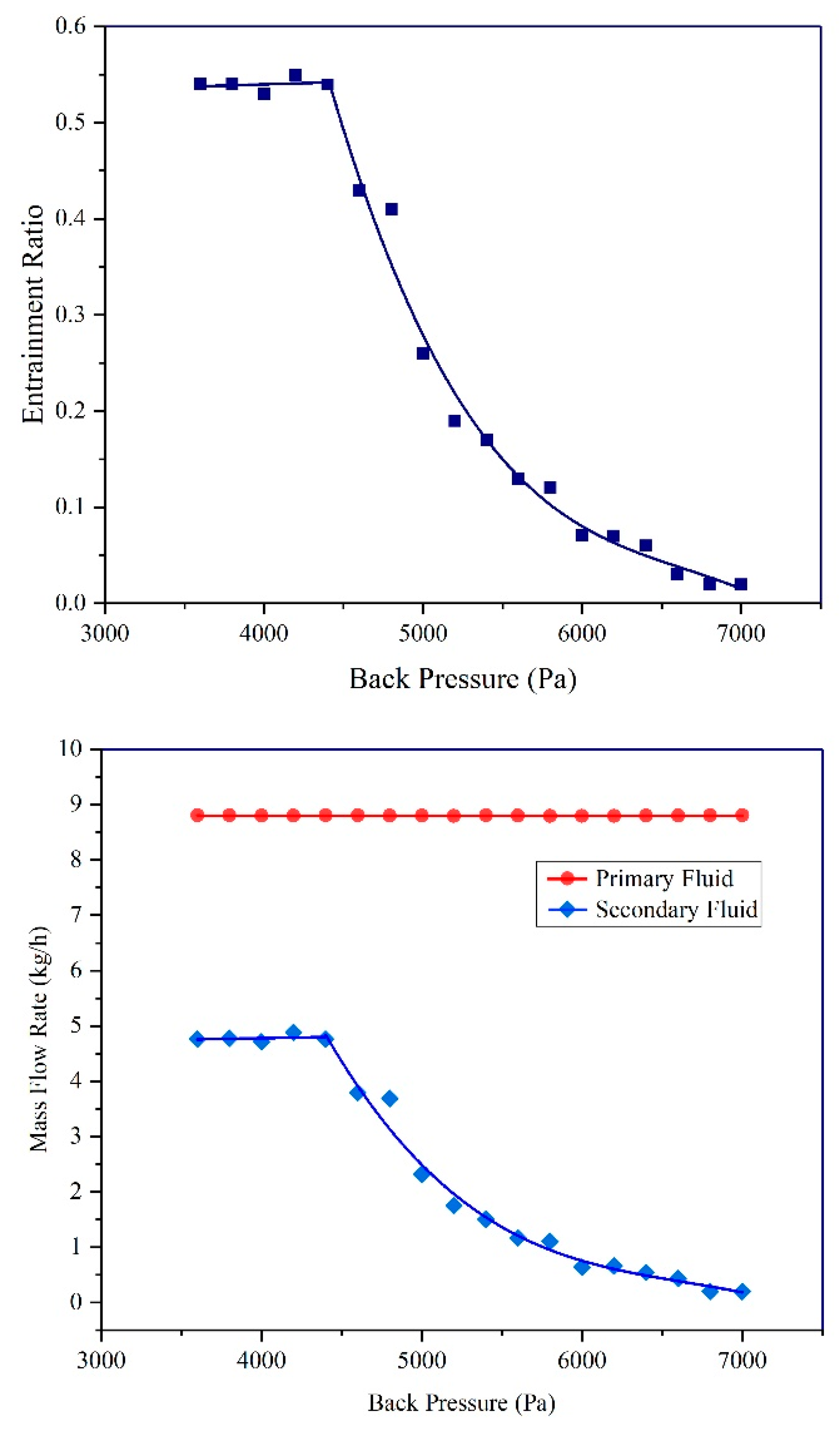
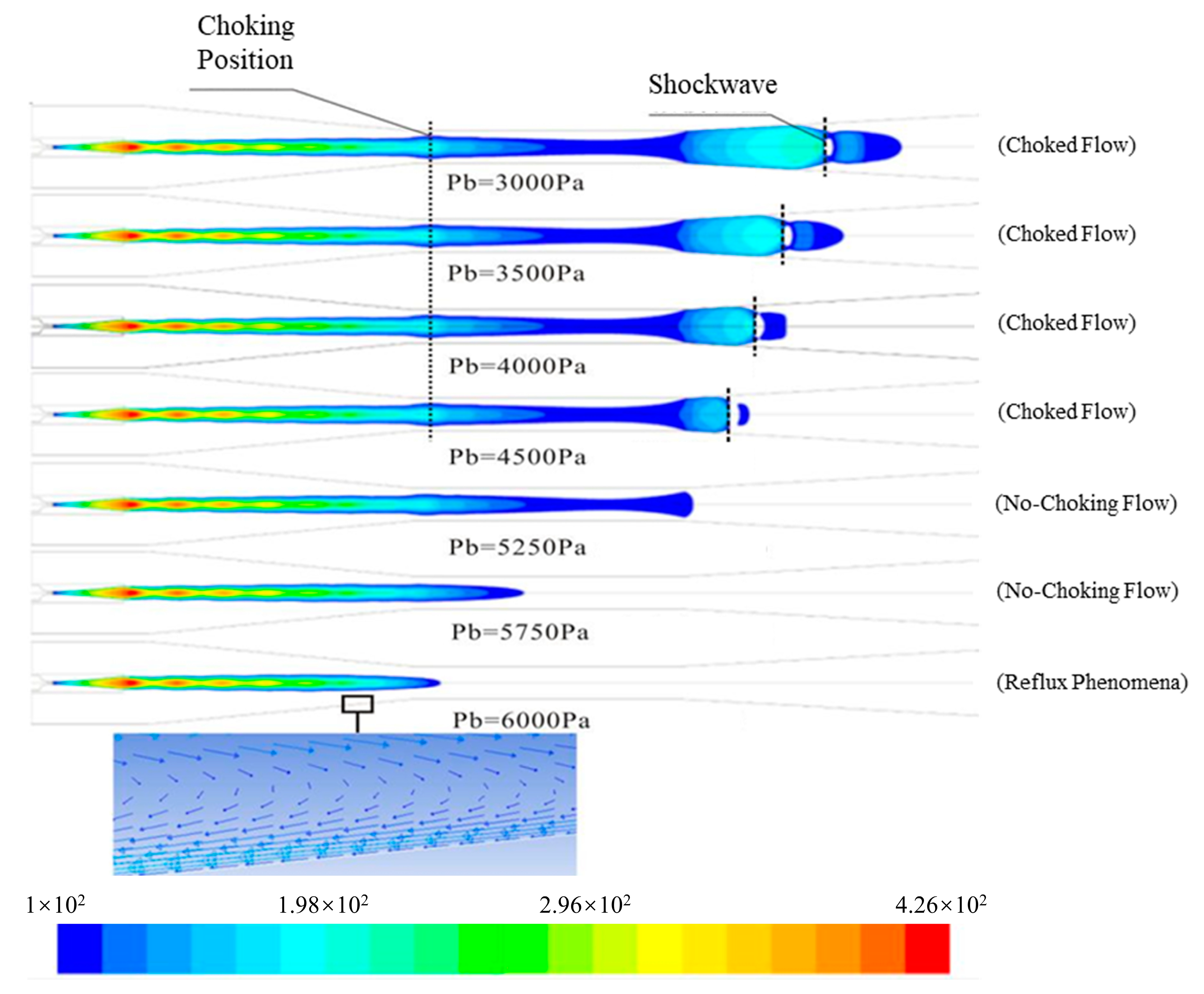
4.3. Effect of Back Pressure on Entrainment Ratios
5. Conclusions
- (1)
- The experimental system of ejector cooling was established, and the relevant experimental data were obtained. The comparison between the experimental and simulated values showed that the relevant data of the ejector were closer to the experimental values under the non-equilibrium spontaneous condensation conditions and were more effective and realistic.
- (2)
- The results indicated that the excessive primary fluid pressure enlarged its expansion core, thereby reducing the effective flow area of the secondary fluid and the entrainment ratio.
- (3)
- As the mass flow rate and pressure of the primary fluid remained unchanged, the increased secondary fluid pressure elevated the entrainment ratio due to the reduction in the expansion angle after passing the Laval nozzle.
- (4)
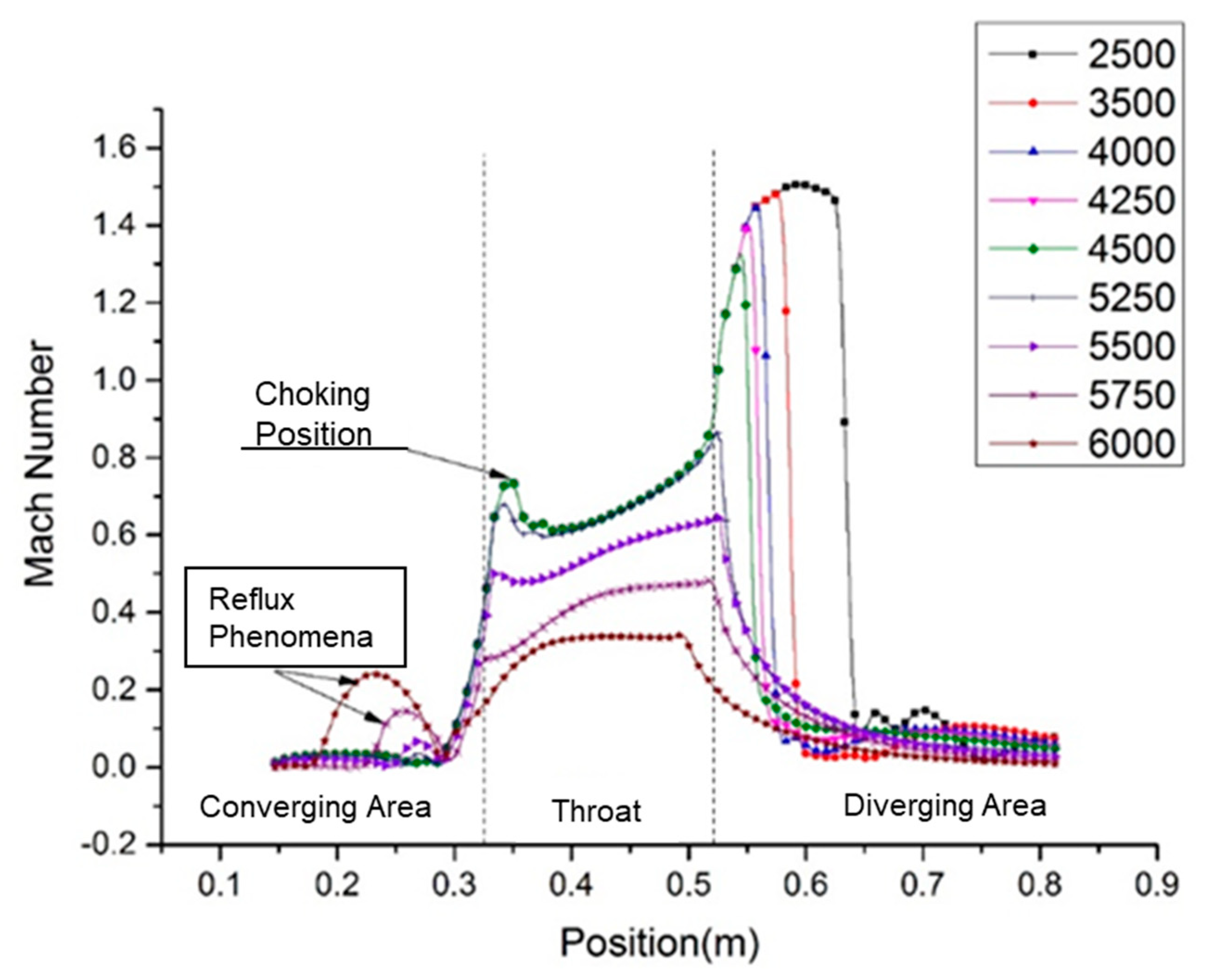
- When the back pressure was lower than the critical back pressure of 4500 Pa, the entrainment ratio remained unchanged; however, when the back pressure exceeded its critical value, the entrainment ratio gradually reduced. The entrainment ratio approached 0 when back pressure consistently increased.
- (5)
- The location of the choking is a major flow characteristic that affects ejector performance and ejector failure. Mastering the flow of the choke helps us improve ejector efficiency, reduce and minimize the risk of ejector failure, and provides an important reference for optimizing the geometry and improving the efficiency of the ejector.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ρ, ρl, ρv | Density, liquid density, and vapor density (kg/m3). |
| u | Velocity (m/s). |
| u’ | Fluctuation velocity (m/s). |
| P | Pressure (Pa). |
| τij | Stress tensor. |
| E | Total energy. |
| αeff | Effective thermal conductivity. |
| β | Mass fraction. |
| Γ | Mass generation rate (kg/s). |
| Droplet average radius (m). | |
| r* | Critical droplet radius (m). |
| I | Nucleation rate (1/s). |
| η | Droplet number density (1/m3). |
| qc | Evaporation coefficient. |
| θ | Non-isothermal correction factor. |
| σ | Droplet surface tension (kg/m). |
| T | Thermal temperature (K). |
| K | Boltzmann constant. |
| M | Molecular mass (kg). |
| γ | Specific heat capacities ratio. |
| hv | Vapor-specific enthalpy (J/kg). |
| R | Gas law constant. |
| S | Super saturation ratio. |
| Cp | Isobaric heat capacity (J/(kgK)). |
| T0 | Droplet temperature (K). |
| Vd | Average droplet volume (m3). |
| B, C | Virial coefficients (m3/kg, m6/kg2). |
| αv | Volume fraction. |
| h | Specific enthalpy (J/kg). |
| s | Specific entropy (J/(kg.mol.K)). |
| k | Turbulent kinetic energy. |
| μt | Eddy viscosity. |
| ε | Turbulence kinetic energy dissipation. |
| Sij | Strain rate. |
| C2, C1ε, C3ε, σk, σε | Model coefficients. |
| V | Kinematic viscosity. |
| Sk, Sε | Source terms. |
References
- Hamzaoui, M.; Nesreddine, H.; Aidoun, Z.; Balistrou, M. Experimental study of a low grade heat driven ejector cooling system using the working fluid R245fa. Int. J. Refrig. 2018, 86, 388–400. [Google Scholar] [CrossRef]
- Sharifi, N. Numerical study of non-equilibrium condensing supersonic steam flow in a jet-pump based on supersaturation theory. Int. J. Mech. Sci. 2020, 165, 105221. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F. Computational fluid-dynamics modeling of supersonic ejectors: Screening of turbulence modeling approaches. Appl. Therm. Eng. 2017, 117, 122–144. [Google Scholar] [CrossRef]
- Croquer, S.; Fang, Y.; Metsue, A.; Bartosiewicz, Y.; Poncet, S. Compound-choking theory for supersonic ejectors working with real gas. Energy 2021, 227, 120396. [Google Scholar] [CrossRef]
- Li, A.; Yuen, A.C.Y.; Chen, T.B.Y.; Wang, C.; Liu, H.; Cao, R.; Yang, W.; Yeoh, G.H.; Timchenko, V. Computational Study of Wet Steam Flow to Optimize Steam Ejector Efficiency for Potential Fire Suppression Application. Appl. Sci. 2019, 9, 1486. [Google Scholar] [CrossRef]
- Desevaux, P.; Mellal, A.; Alves de Sousa, Y. Visualization of Secondary Flow Choking Phenomena in a Supersonic Air Ejector. J. Vis. 2004, 7, 249–256. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Li, A.; AF, A.E.; Wen, C. Optimum Efficiency of a Steam Ejector for Fire Suppression Based on the Variable Mixing Section Diameter. Entropy 2022, 24, 1625. [Google Scholar] [CrossRef] [PubMed]
- Kracik, J.; Dvorak, V. Secondary flow choking in axisymmetric supersonic air ejector with adjustable motive nozzle. Appl. Therm. Eng. 2022, 204, 117936. [Google Scholar] [CrossRef]
- DeBonis, J.R. Full Navier-Stokes analysis of a two-dimensional mixer/ejector nozzle for noise suppression. In Proceedings of the 28th Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar]
- Kim, H.-D.; Setoguchi, T.; Yu, S.; Raghunathan, S. Navier-Stokes computations of the supersonic ejector-diffuser system with a second throat. J. Therm. Sci. 1999, 8, 79–83. [Google Scholar] [CrossRef]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 2. Flow structure of a steam ejector influenced by operating pressures and geometries. Int. J. Therm. Sci. 2007, 46, 823–833. [Google Scholar] [CrossRef]
- Pianthong, K.; Seehanam, W.; Behnia, M.; Sriveerakul, T.; Aphornratana, S. Investigation and improvement of ejector refrigeration system using computational fluid dynamics technique. Energy Convers. Manag. 2007, 48, 2556–2564. [Google Scholar] [CrossRef]
- Wang, X.D.; Dong, J.L. Numerical study on the performances of steam-jet vacuum pump at different operating conditions. Vacuum 2010, 84, 1341–1346. [Google Scholar] [CrossRef]
- Sharifi, N.; Boroomand, M. An investigation of thermo-compressor design by analysis and experiment: Part 1. Validation of the numerical method. Energy Convers. Manag. 2013, 69, 217–227. [Google Scholar] [CrossRef]
- Lei, Y.; Li, S.; Lu, J.; Xu, Y.; Yong, Y.; Xing, D. Numerical Analysis of Steam Ejector Performance with Non-Equilibrium Condensation for Refrigeration Applications. Buildings 2023, 13, 1672. [Google Scholar] [CrossRef]
- Chen, J.; Jarall, S.; Havtun, H.; Palm, B. A review on versatile ejector applications in refrigeration systems. Renew. Sustain. Energy Rev. 2015, 49, 67–90. [Google Scholar] [CrossRef]
- Wang, X.; Dong, J.; Li, A.; Lei, H.; Tu, J. Numerical study of primary steam superheating effects on steam ejector flow and its pumping performance. Energy 2014, 78, 205–211. [Google Scholar] [CrossRef]
- Chunnanond, K.; Aphornratana, S. An experimental investigation of a steam ejector refrigerator: The analysis of the pressure profile along the ejector. Appl. Therm. Eng. 2004, 24, 311–322. [Google Scholar] [CrossRef]
- Rusly, E.; Aye, L.; Charters, W.W.S.; Ooi, A. CFD analysis of ejector in a combined ejector cooling system. Int. J. Refrig. 2005, 28, 1092–1101. [Google Scholar] [CrossRef]
- Lamberts, O.; Chatelain, P.; Bourgeois, N.; Bartosiewicz, Y. The compound-choking theory as an explanation of the entrainment limitation in supersonic ejectors. Energy 2018, 158, 524–536. [Google Scholar] [CrossRef]
- Besagni, G. Ejectors on the cutting edge: The past, the present and the perspective. Energy 2019, 170, 998–1003. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Z.; Li, Y.; Wu, H.; Zhang, X.; Yang, N. Visualization experimental study of the condensing flow regime in the transonic mixing process of desalination-oriented steam ejector. Energy Convers. Manag. 2019, 197, 111849. [Google Scholar] [CrossRef]
- Zhu, Y.; Cai, W.; Wen, C.; Li, Y. Numerical investigation of geometry parameters for design of high performance ejectors. Appl. Therm. Eng. 2009, 29, 898–905. [Google Scholar] [CrossRef]
- Rand, C.P.; Croquer, S.; Poirier, M.; Poncet, S. Optimal nozzle exit position for a single-phase ejector (Experimental, numerical and thermodynamic modelling). Int. J. Refrig. 2022, 144, 108–117. [Google Scholar] [CrossRef]
- Kang, S.H.; Kim, J.G.; Namkoung, H.-J. Effects of component geometries and inflow conditions on ejector operational mode. J. Mech. Sci. Technol. 2019, 33, 5003–5008. [Google Scholar] [CrossRef]
- Huang, B.J.; Jiang, C.B.; Hu, F.L. Ejector Performance Characteristics and Design Analysis of Jet Refrigeration System. J. Eng. Gas Turbines Power 1985, 107, 792–802. [Google Scholar] [CrossRef]
- Munday, J.T.; Bagster, D.F. New ejector theory applied to steam jet refrigeration. Ind. Eng. Chem. Process Des. Dev. 1977, 16, 442–449. [Google Scholar] [CrossRef]
- Tang, Y.; Liu, Z.; Li, Y.; Yang, N.; Wan, Y.; Chua, K.J. A double-choking theory as an explanation of the evolution laws of ejector performance with various operational and geometrical parameters. Energy Convers. Manag. 2020, 206, 112499. [Google Scholar] [CrossRef]
- Besagni, G.; Mereu, R.; Inzoli, F. Ejector refrigeration: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 53, 373–407. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Yuen, A.C.Y.; Li, A.; Guo, L.; Yeoh, G.H.; Tu, J. Characterization of choking flow behaviors inside steam ejectors based on the ejector refrigeration system. Int. J. Refrig. 2020, 113, 296–307. [Google Scholar] [CrossRef]
- Fu, W.; Liu, Z.; Li, Y.; Wu, H.; Tang, Y. Numerical study for the influences of primary steam nozzle distance and mixing chamber throat diameter on steam ejector performance. Int. J. Therm. Sci. 2018, 132, 509–516. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X.; Sun, H.; Zhang, G.; Guo, L.; Tu, J. CFD simulation on the boundary layer separation in the steam ejector and its influence on the pumping performance. Energy 2019, 167, 469–483. [Google Scholar] [CrossRef]
- Ishazaki, K.; Ikohagi, T.; Daiguii, H. A High-Resolution Numerical Method for Transonic Non-Equilibrium Condensation Flows through a Steam Turbine Cascade. In Proceedings of the 6th International Symposium on Computational Fluid Dynamics, Lake Tahoe, NV, USA, 4–8 September 1995; pp. 479–484. [Google Scholar]
- Young, J.B. An Equation of State for Steam for Turbomachinery and Other Flow Calculations. J. Eng. Gas Turbines Power 1988, 110, 1–7. [Google Scholar] [CrossRef]
- Young, J.B. Two-Dimensional, Nonequilibrium, Wet-Steam Calculations for Nozzles and Turbine Cascades. J. Turbomach. 1992, 114, 569–579. [Google Scholar] [CrossRef]
- Varga, S.; Soares, J.; Lima, R.; Oliveira, A.C. On the selection of a turbulence model for the simulation of steam ejectors using CFD. Int. J. Low-Carbon Technol. 2017, 12, 233–243. [Google Scholar] [CrossRef][Green Version]
- Jeong, H.; Utomo, T.; Ji, M.; Lee, Y.; Lee, G.; Chung, H. CFD analysis of flow phenomena inside thermo vapor compressor influenced by operating conditions and converging duct angles. J. Mech. Sci. Technol. 2009, 23, 2366–2375. [Google Scholar] [CrossRef]
- Da-Wen, S. Variable geometry ejectors and their applications in ejector refrigeration systems. Energy 1995, 21, 919–929. [Google Scholar]
- Sriveerakul, T.; Aphornratana, S.; Chunnanond, K. Performance prediction of steam ejector using computational fluid dynamics: Part 1. Validation of the CFD results. Int. J. Therm. Sci. 2007, 46, 812–822. [Google Scholar] [CrossRef]

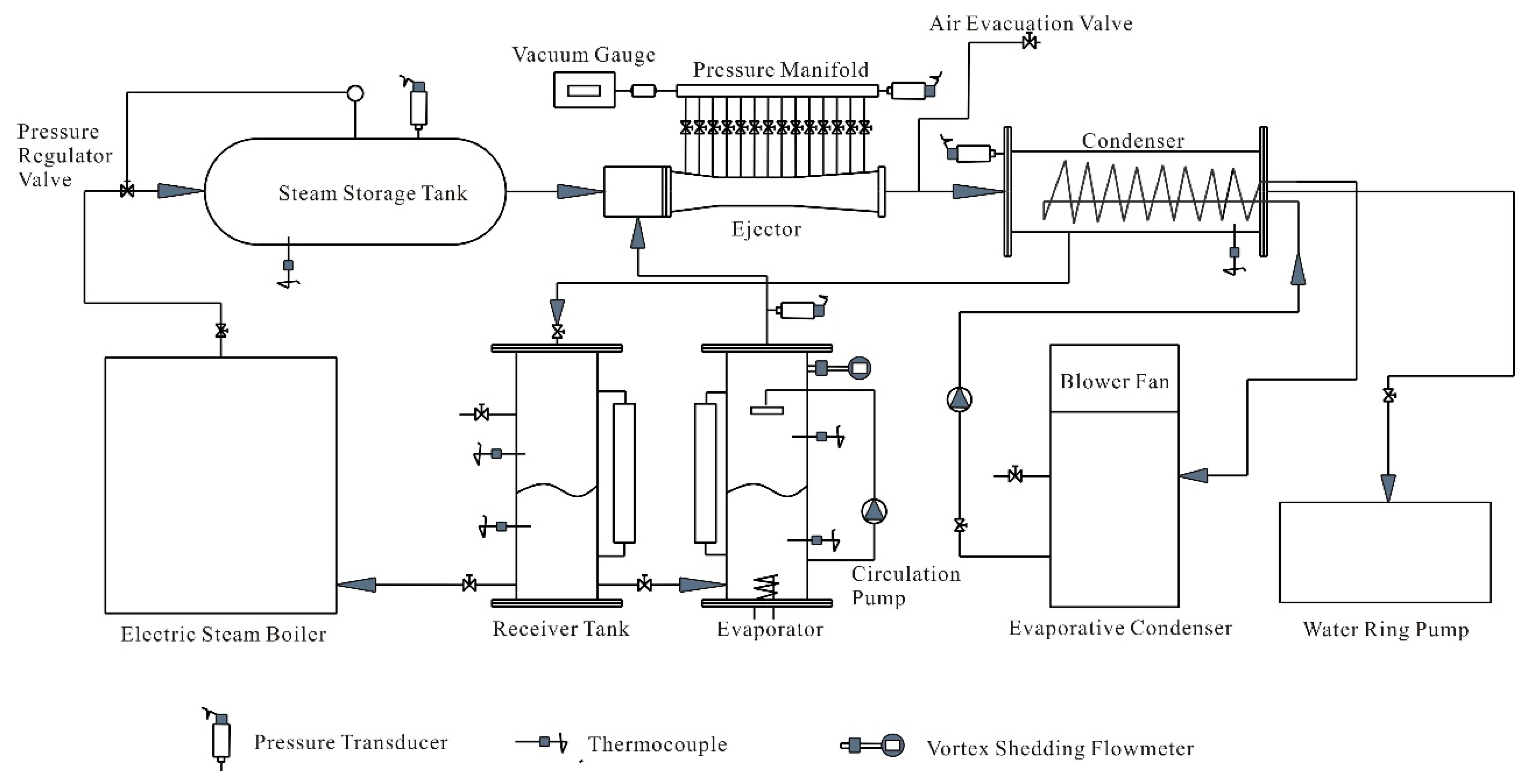
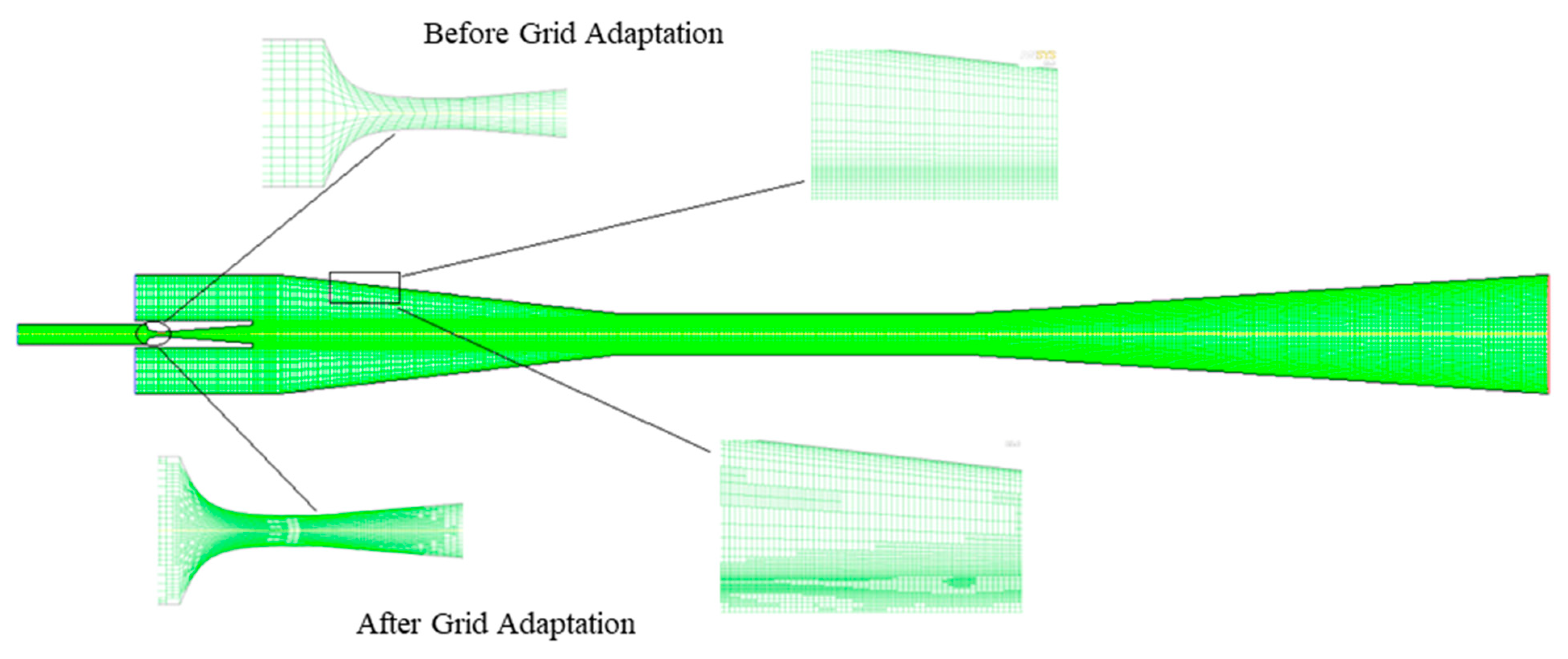
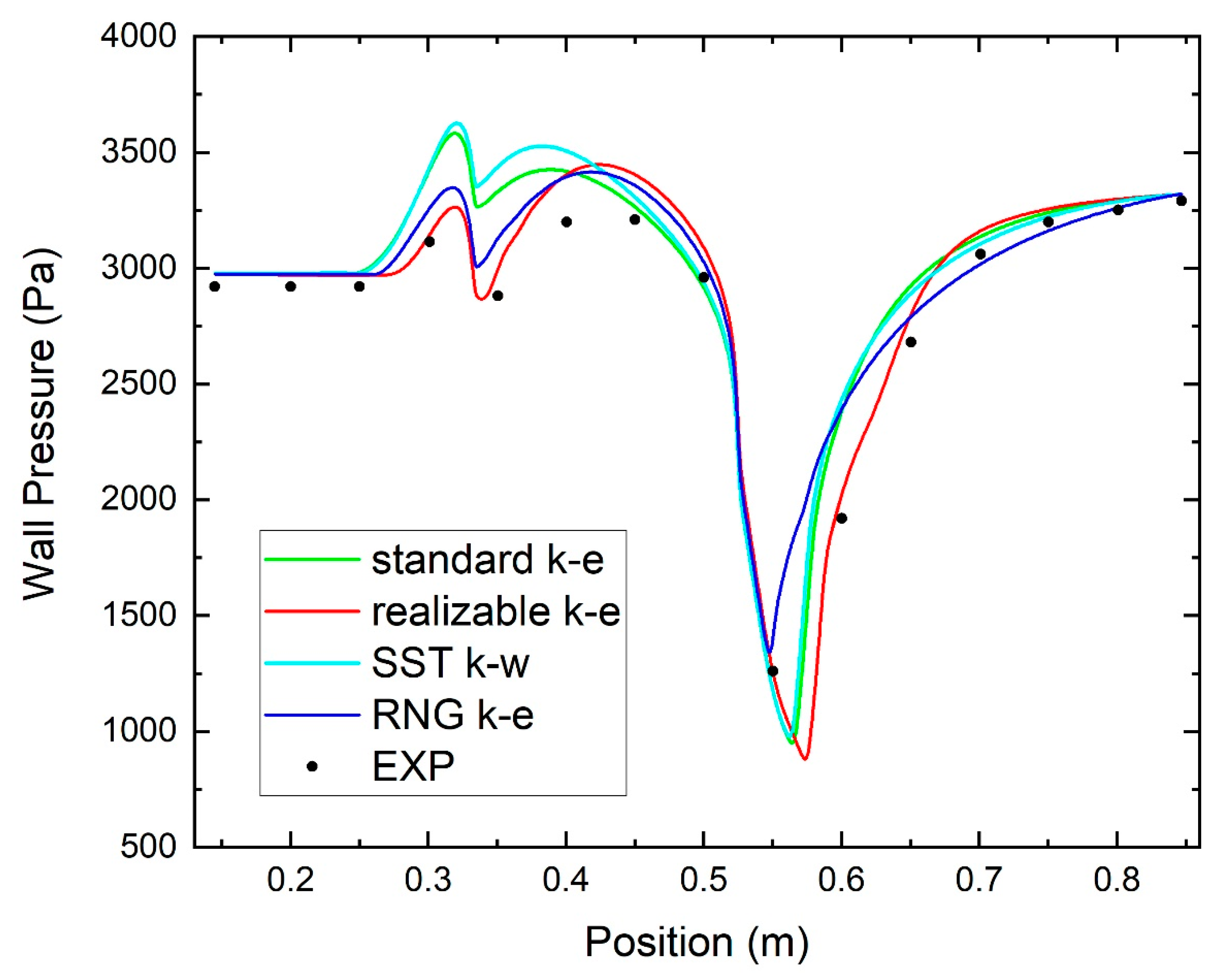
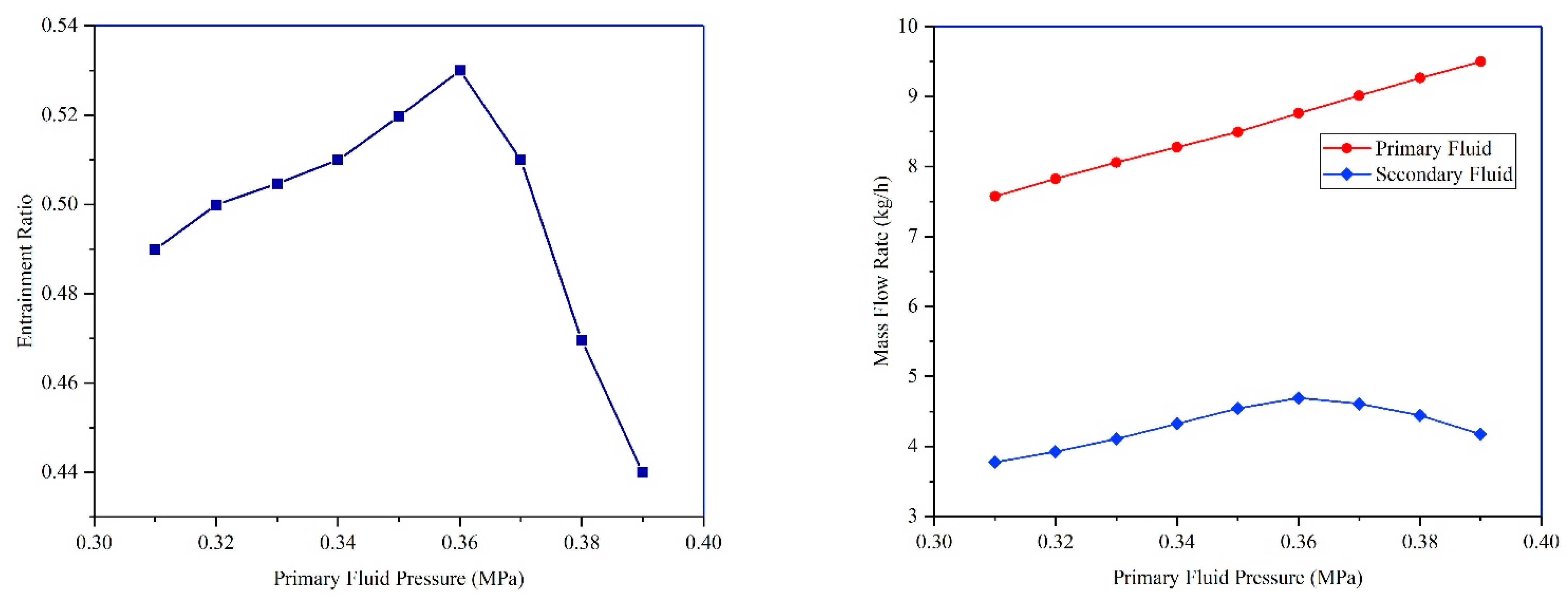

| Component | Aspect | Size (mm) |
|---|---|---|
| Nozzle Throat | Diameter | 2.5 |
| Nozzle Outlet | Diameter | 11 |
| Nozzle Throat to Outlet | Length | 48 |
| Diffuser Throat | Diameter | 24 |
| Diffuser Throat | Length | 192 |
| Diffuser Inlet | Diameter | 70 |
| Diffuser Outlet | Diameter | 70 |
| Diffuser Inlet Reducer | Length | 188 |
| Diffuser Outlet | Length | 322 |
| Ejector Suction Port | Diameter | 54 |
| Discrete Format | The control equations are discretized into algebraic equation systems that can be numerically solved using the finite volume method. The coupled implicit solver is employed to solve these equations. The diffusion was discretized using the central difference scheme in the Coupled Implicit Model. The second-order upwind scheme was used to discretely solve the convective terms. |
| Meshing | The mesh element in certain areas of the nozzle wall was refined to cope with the Enhanced Wall Treatment near-wall modeling method. The initial generated mesh number was 53,463. After the mesh fining with the aid of an adaptive technique, the final mesh number was 62,796. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Han, Y.; Wang, X.; Wen, C.; Yang, Y. Performance Evaluation of a Steam Ejector Considering Non-Equilibrium Condensation in Supersonic Flows. Energies 2023, 16, 7755. https://doi.org/10.3390/en16237755
Xie Y, Han Y, Wang X, Wen C, Yang Y. Performance Evaluation of a Steam Ejector Considering Non-Equilibrium Condensation in Supersonic Flows. Energies. 2023; 16(23):7755. https://doi.org/10.3390/en16237755
Chicago/Turabian StyleXie, Youhao, Yu Han, Xiaodong Wang, Chuang Wen, and Yan Yang. 2023. "Performance Evaluation of a Steam Ejector Considering Non-Equilibrium Condensation in Supersonic Flows" Energies 16, no. 23: 7755. https://doi.org/10.3390/en16237755
APA StyleXie, Y., Han, Y., Wang, X., Wen, C., & Yang, Y. (2023). Performance Evaluation of a Steam Ejector Considering Non-Equilibrium Condensation in Supersonic Flows. Energies, 16(23), 7755. https://doi.org/10.3390/en16237755










