Study on Market-Based Trading Strategies for Biomass Power Generation Participation in Microgrid Systems
Abstract
:1. Introduction
2. Transaction Participants and Protective Regulations
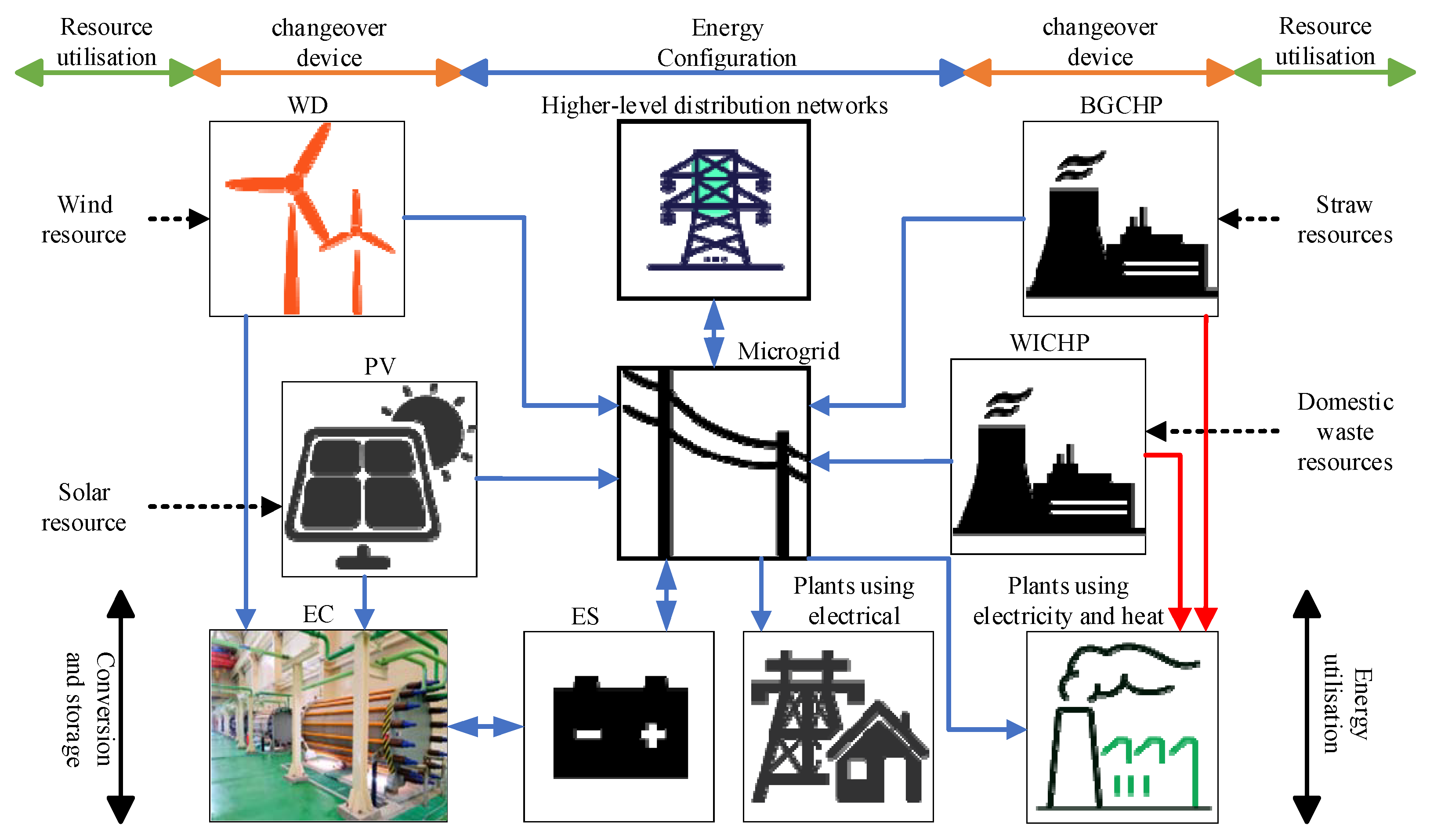
2.1. Modeling of Microgrid Systems
2.2. A Model of Quoting Strategies for Market-Based Trading Entities
2.2.1. Modelling of Cogeneration Units and Their Bidding Strategies
2.2.2. Modelling Bidding Strategies for WD and PV Power
2.2.3. Model for the Operator’s Bidding Strategy
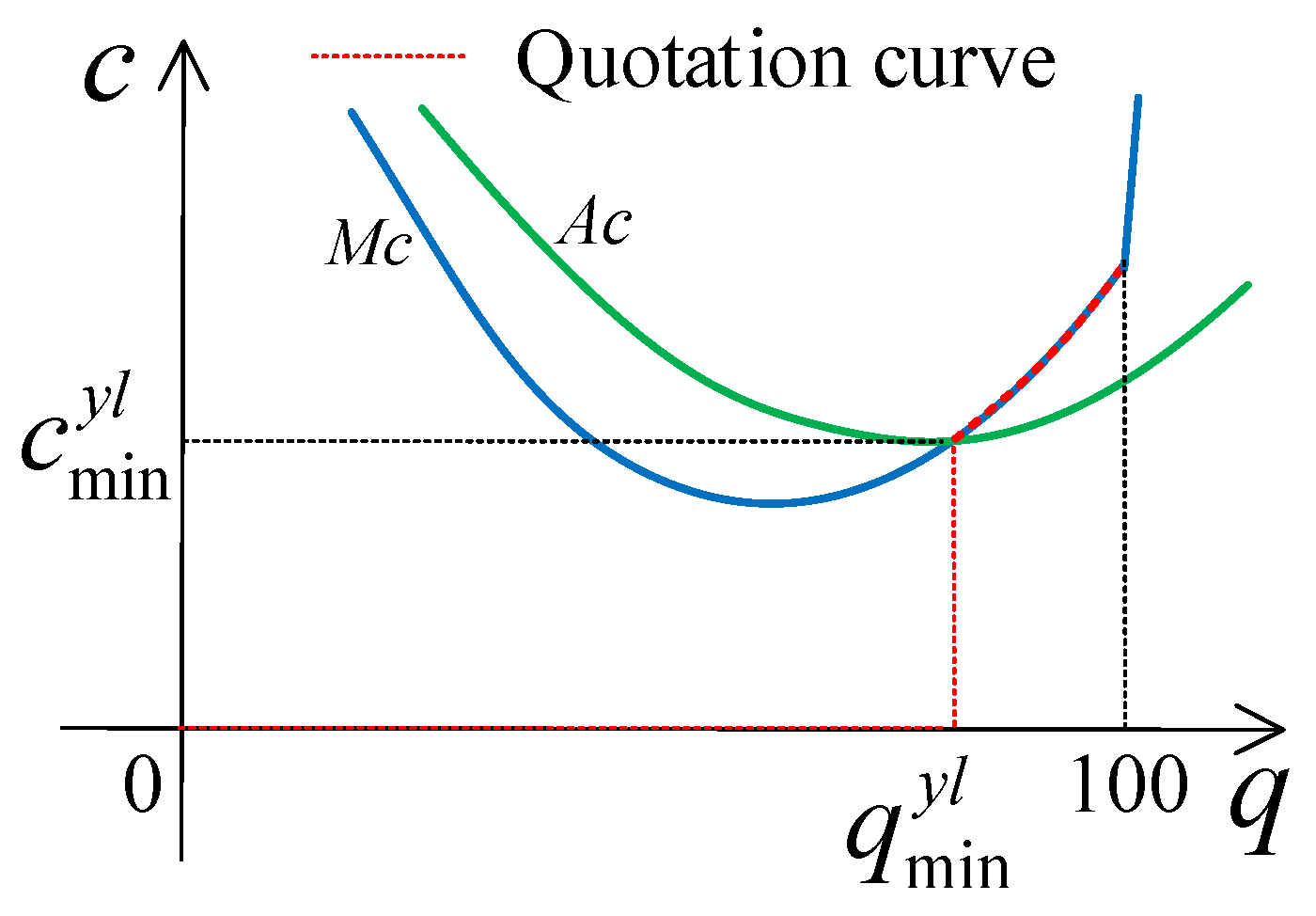
2.3. Marginal Price and Guaranteed Output
3. Market-Based Trading Strategy Model
3.1. Day-Ahead Market Trading Strategy Model
3.1.1. Operator Trading Strategy Model
3.1.2. Capacity Provider Trading Strategy Model
3.1.3. Consumption of EL Power under WD and PV Power Output Constraints
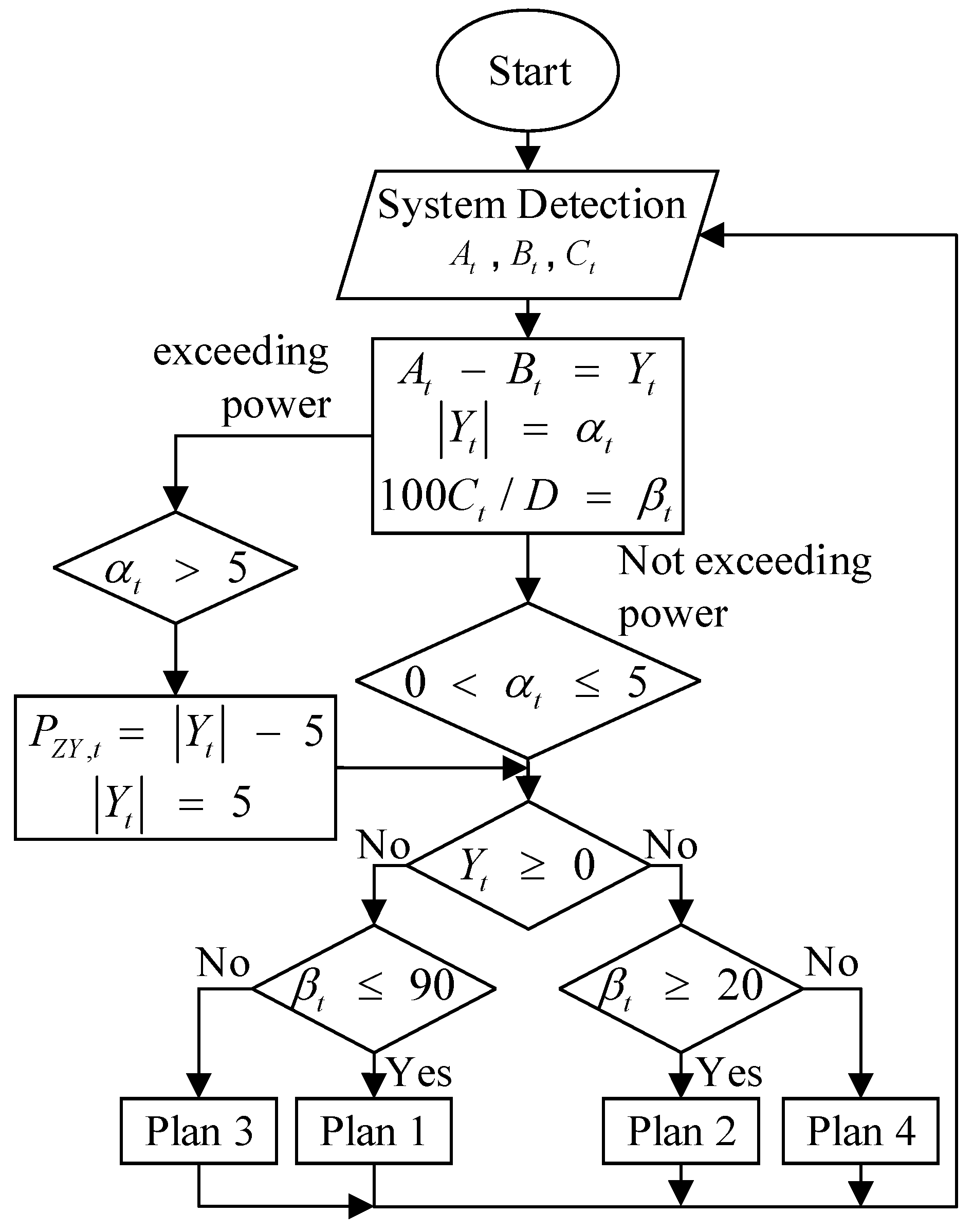
3.2. Intraday Market Adjustment Strategy Model
3.2.1. ES Adjustment Strategy Model
3.2.2. EL Power Redistribution
3.2.3. Incentive for Reserve Capacity Selling
4. Model Solving and Simulation Analysis
4.1. Construction and Solving of Electricity Trading Model
4.2. Trading Results and Analysis
4.2.1. Results and Analysis of Electricity Trading
- (1)
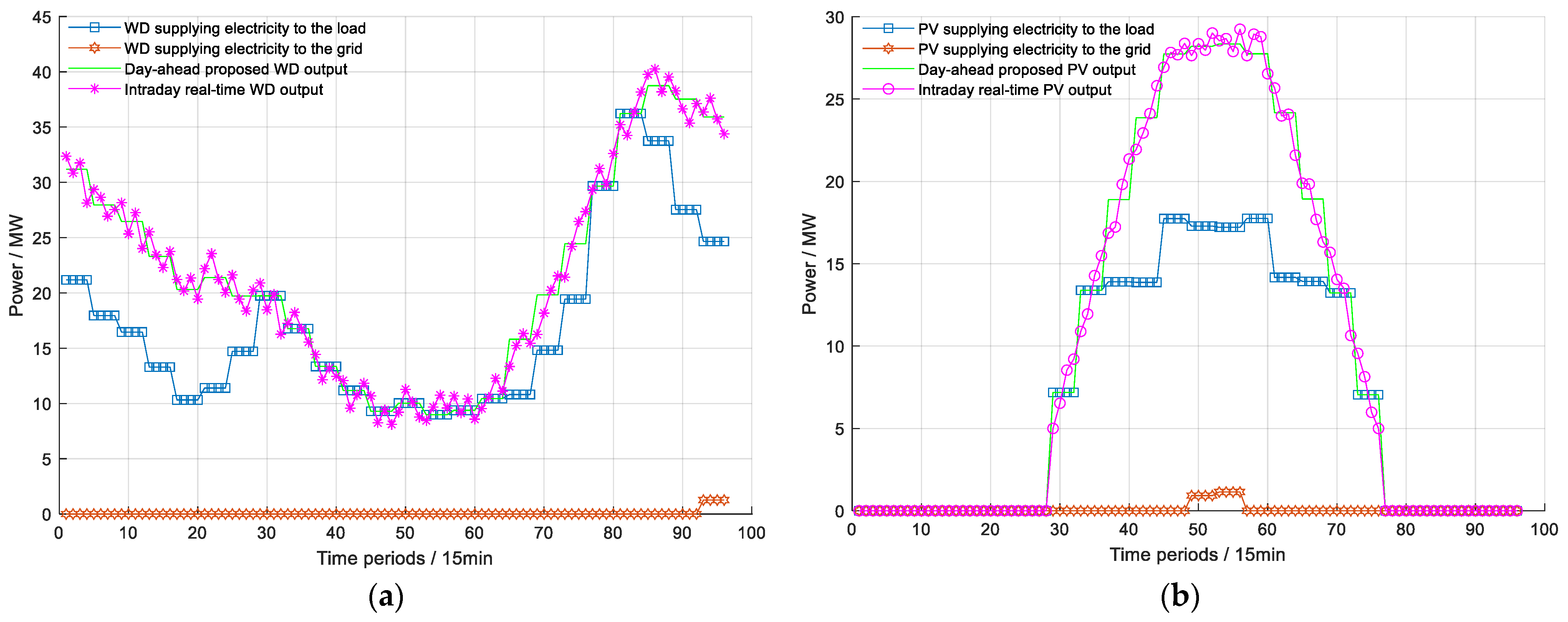
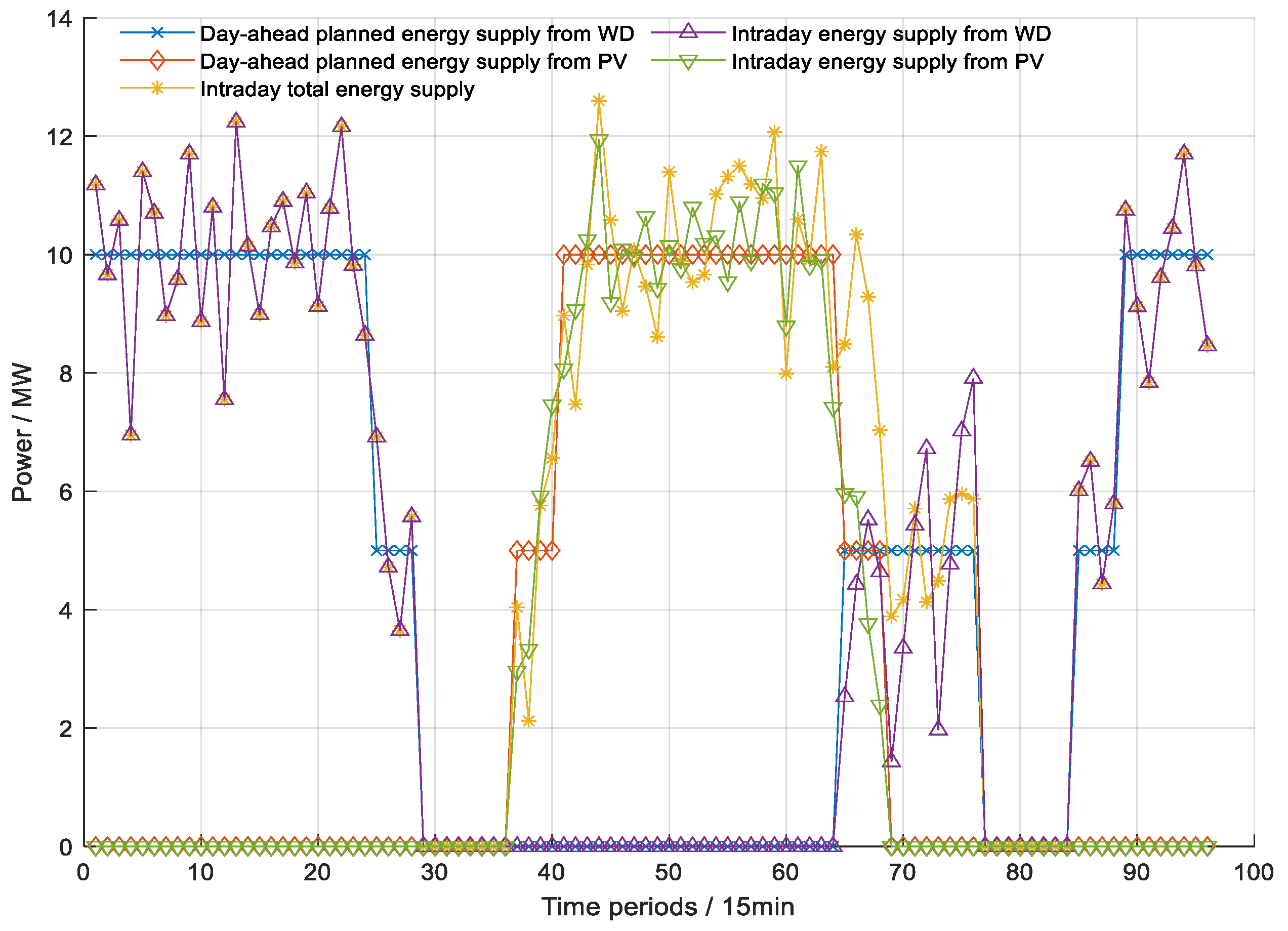
- Analysis of WD and PV trading results.
- (2)
- Analysis of BGCHP and WICHP transaction results.
- (3)
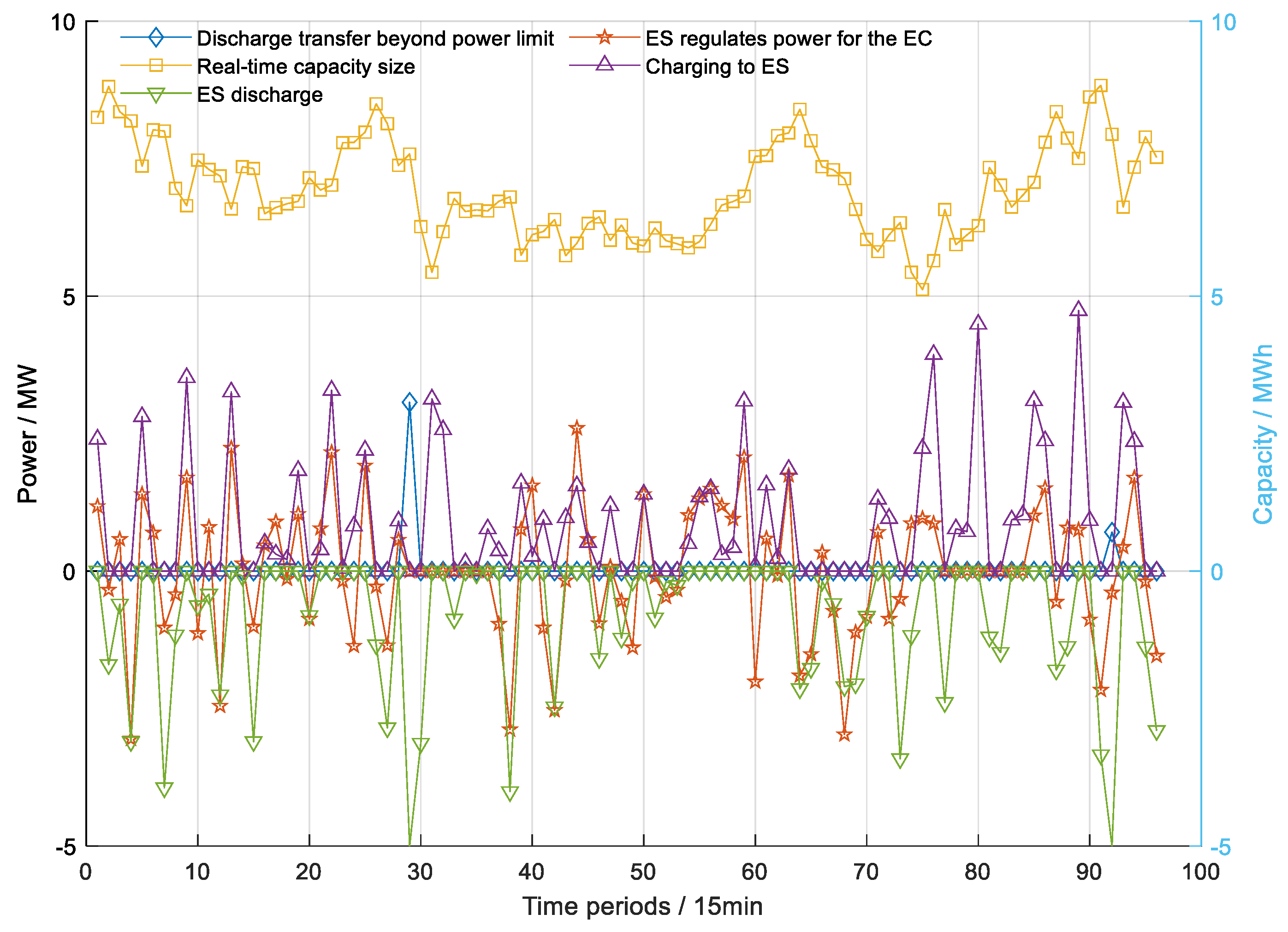
- Analysis of ES transaction results.
- (4)
- Analysis of EL trading results.
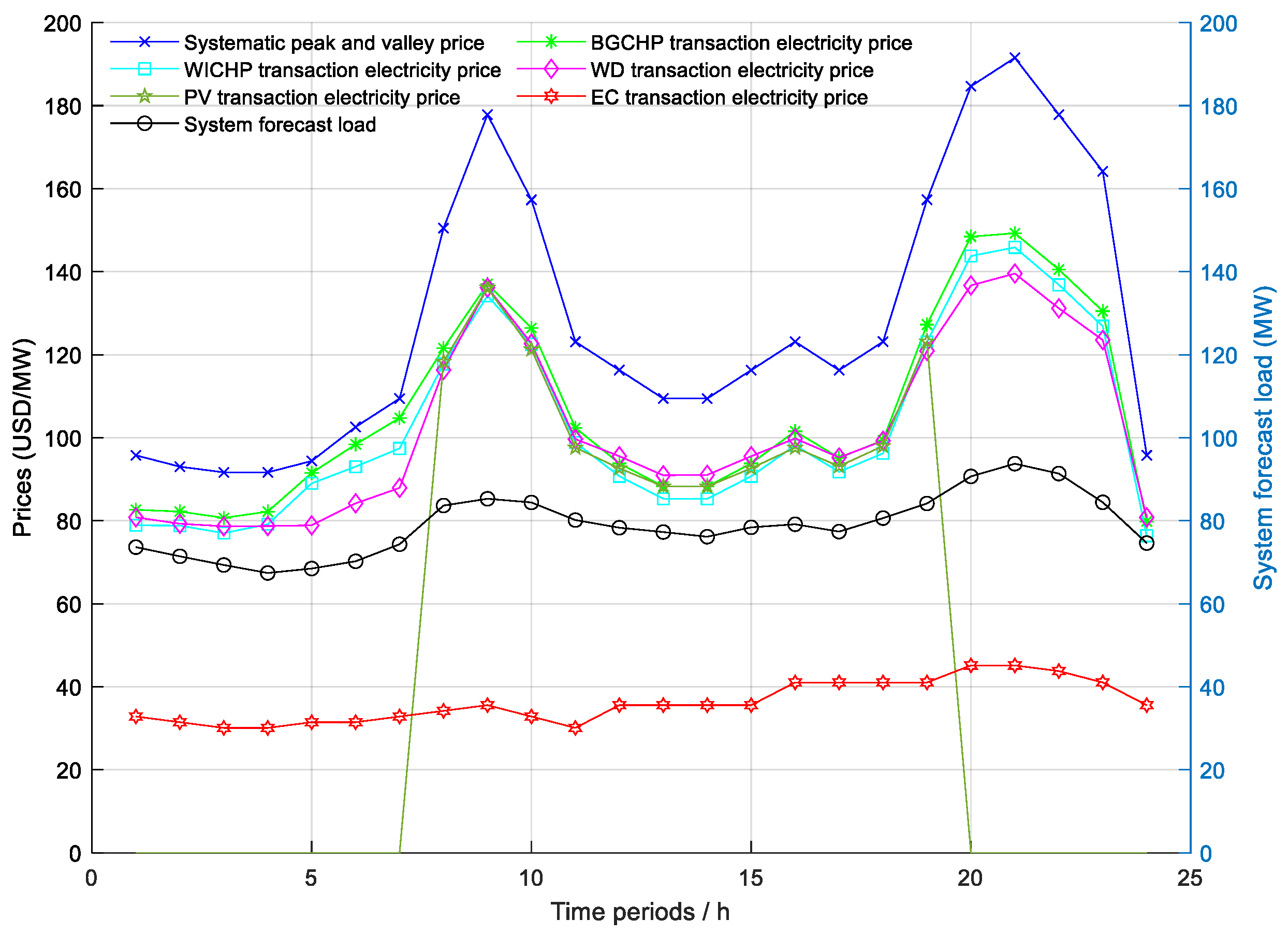
4.2.2. Analysis of Electricity Transaction Price
4.2.3. Analysis of Revenue Generated from Electrical Energy
- (1)
- Analysis of trading volume and revenue.
- (2)
- Comparative analysis.
5. Conclusions
- In this study, the microgrid system, comprised completely of renewable energy sources, operates in a mode of “self-generation and self-consumption, electricity surplus sales, electricity shortfall purchase”. There is an exceptional situation that energy is purchased from the higher grid once, power is generated at full capacity twice, and operation is conducted under the minimum guaranteed power three times. Additionally, the power generated by WD and PVs is rarely supplied to the grid. Instead, the excess capacity is efficiently incorporated by the EL, thus eliminating the possibility of any excess capacity being wasted due to wind and sunlight. It is demonstrated that the capacity configuration proposed in this paper satisfies the requirements on system load, which ensures that BGCHP and WICHP can generate power within a reasonable range. Meanwhile, the utilization of all electricity generated by WD and PVs is maximized.
- The trading strategy proposed in this paper aligns with the trend of market-oriented reforms, ensuring that significantly higher economic returns are generated for all capacity units involved in market-based trading. For instance, BGCHP and WICHP guarantee a daily net profit that is USD 2864.592 and USD 9415.944 higher than in Scenario 3, respectively. WD and PVs can also generate an additional USD 17,763.480 and USD 7082.136 per day in revenue, respectively, when compared to Scenario 3. Additionally, the operator records substantial daily net profits of USD 13,313.376.
- The ES system introduced in this paper enables the prompt adjustment made by the systems to load supply and demand, which facilitates system operations. Moreover, it enhances the stability of electrical energy supply for EL. Although a lower ES capacity has the potential to boost revenues for the operator, it may not be conducive to ensuring system stability.
- An innovative market-based trading concept is introduced for the microgrids comprised entirely of renewable energy sources. It aims to create a multi-energy complementary energy supply portfolio that improves the capacity and profitability of the power supply.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WD | wind power |
| PV | photovoltaic |
| BGCHP | biomass gasification cogeneration |
| WICHP | waste incineration cogeneration |
| EL | electrolysis |
| ES | energy in storage |
| CHP | combined heat and power |
Appendix A

Appendix B
- (1)
- 10 MW Levels
- (2)
- 5 MW or 0 MW Levels
Appendix C
| Parameters | Items | Numerical Value/Unit |
|---|---|---|
| Biomass gasification cogeneration | Rated electric power | 30 MW |
| Rated thermal power | 55 MW | |
| Electrical efficiency | 23.37% | |
| Thermal efficiency | 42.84% | |
| Average calorific value of corn stover | 15.407 MJ/kg | |
| Straw costs | 41.040 USD/t | |
| Unit O&M costs | 4.788 USD/MW | |
| Unit construction cost | 1.778 million USD/MW | |
| service life | 30 year | |
| Waste incineration cogeneration | Rated electric power | 30 MW |
| Rated thermal power | 36 MW | |
| Electrical efficiency | 23.14% | |
| Thermal efficiency | 27.77% | |
| Average calorific value of domestic waste | 7.063 MJ/kg | |
| Rubbish disposal charge | 13.133 USD/t | |
| Unit O&M costs | 4.651 USD/MW | |
| Unit construction cost | 4.966 million USD/MW | |
| service life | 30 year | |
| Wind power generation | Rated power | 50 MW |
| Unit O&M costs | 4.104 USD/MW | |
| Unit construction cost | 0.889 million USD/MW | |
| service life | 25 year | |
| Photovoltaic power generation | Rated power | 30 MW |
| Unit O&M costs | 3.557 USD/MW | |
| Unit construction cost | 0.4378 million USD/MW | |
| service life | 30 year | |
| Electrolytic cell | Rated power | 10 MW |
| Integrated efficiency | 60% | |
| Start-up costs | USD 20.520 | |
| Downtime costs | USD 13.680 | |
| Electricity storage (Lithium iron phosphate) | Rated power/capacity | 5 MW/15 MW·h |
| Unit maintenance cost | 0.821 million USD/MW | |
| service life | 15 year | |
| Charging efficiency | 95% | |
| Discharge efficiency | 95% | |
| wastage rate | 0.10% |
References
- Han, G.; Zhou, Z. Summary of Development Status of Incremental Distribution Network and Research on Development Trend. China Water Power Electrif. 2022, 204, 46–50. [Google Scholar]
- Wang, X. New power system to build a new ecology of source-grid-load-storage. Energy 2021, 7, 28–30. [Google Scholar]
- Yu, D.; Zhang, C.; Wang, S.; Zhang, L. Evolutionary Game and Simulation Analysis of Power Plant and Government Behavior Strategies in the Coupled Power Generation Industry of Agricultural and Forestry Biomass and Coal. Energies 2023, 16, 1553. [Google Scholar] [CrossRef]
- Fu, P.; Xu, G.; Li, X.; Zhu, T.; Zhang, Z. Analysis of the Development Status and Trends of China’s Biomass Power Industry and Carbon Emission Reduction Potential. Ind. Saf. Environ. Prot. 2021, 47, 48–52. [Google Scholar]
- Zhu, X.; Dou, K.; Wang, Z. Economic Analysis of China’ s Agricultural and Forestry Biomass Power Generation Projects. J. Glob. Energy Interconnect. 2022, 5, 182–187. [Google Scholar]
- Illankoon, W.A.M.A.N.; Milanese, C.; Girella, A.; Rathnasiri, P.G.; Sudesh, K.H.M.; Llamas, M.M.; Collivignarelli, M.C.; Sorlini, S. Agricultural Biomass-Based Power Generation Potential in Sri Lanka: A Techno-Economic Analysis. Energies 2022, 15, 8984. [Google Scholar] [CrossRef]
- Lin, X.; Wu, Y. Thermodynamic Simulation and Analysis of Biomass Gasification Cogeneration System. J. Eng. Therm. Energy Power 2019, 34, 15–22. [Google Scholar]
- Li, S.; Liu, Z.; Wang, J.; Liu, W.; Guo, H. Two-stage operation optimization of rural biomass energy integrated energy system considering heat network loss. Electr. Power Autom. Equip. 2021, 41, 24–32. [Google Scholar]
- Bagherian, M.A.; Mehranzamir, K.; Rezania, S.; Abdul-Malek, Z.; Pour, A.B.; Alizadeh, S.M. Analyzing Utilization of Biomass in Combined Heat and Power and Combined Cooling, Heating, and Power Systems. Processes 2021, 9, 1002. [Google Scholar] [CrossRef]
- Indrawan, N.; Simkins, B.; Kumar, A.; Huhnke, R.L. Economics of Distributed Power Generation via Gasification of Biomass and Municipal Solid Waste. Energies 2020, 13, 3703. [Google Scholar] [CrossRef]
- Baeyens, E.; Bitar, E.Y.; Khargonekar, P.P.; Poolla, K. Coalitional aggregation of wind power. IEEE Trans. Power Syst. 2013, 28, 3774–3784. [Google Scholar] [CrossRef]
- Smale, R.; Spaargaren, G.; van Vliet, B. Householders co-managing energy systems: Space for collaboration. Build. Res. Inf. 2019, 47, 585–597. [Google Scholar] [CrossRef]
- Huang, W.; Ge, W.; Ren, H.; Zhu, Y.; Chen, H. Exploration of optimal configuration and operation for all-renewable multi-energy complementary systems. J. Acta Energiae Solaris Sin. 2023, 11–25. [Google Scholar]
- Wang, X.; Ren, H.; Wu, Q.; Li, Q. Research on Optimal Planning Method of Multi-source Heterogeneous All-renewable Energy System facing Carbon Neutrality. J. Eng. Therm. Energy Power 2022, 37, 136–145. [Google Scholar]
- Zhong, W.; Pan, X.; Fan, W.; Zhang, J.; Zhou, R. Energy Efficiency Optimization of Waste Incineration Power Plant with Waste Heat Recovery Device and Compression Heat Pump. Proc. CSU-EPSA 2021, 33, 117–124. [Google Scholar]
- Zhang, Y.; Zhao, N.; Huang, J.; Bu, G. Two-level coordinated operation optimization model of the source-storage-load in microgrid considering demand response. Energy Res. Inf. 2020, 36, 216–221. [Google Scholar]
- Zhao, R.; Tan, Z.; Degjirif, U. A two-level coordinated operation optimisation model of microgrid “source-storage-load” taking into account demand response. Renew. Energy Resour. 2019, 37, 1630–1636. [Google Scholar]
- Qian, C.; Bao, H. Unscrambling of marginal cost algorithm in power market. Power Syst. Prot. Control. 2010, 38, 7–10+15. [Google Scholar]
- Yu, J. Study on Competitive Bidding Strategy of Power Plant Based on Marginal Generating Cost Analysis; Shandong University: Jinan, China, 2015. [Google Scholar]
- Wang, Y.; Wang, X.; Sun, Q.; Zhang, Y.; Liu, J.; Jinghan, H.E. Multi-agent Real-time Collaborative Optimization Strategy for Integrated Energy System Group Based on Energy Sharing. Autom. Electr. Power Syst. 2022, 46, 56–65. [Google Scholar]
- Lin, X.; Zhang, Y.; Chen, B.; Fan, S.; Chen, Z. Bi-level Optimal Configuration of Park Energy Internet Considering Multiple Evaluation Indicators. Autom. Electr. Power Syst. 2019, 43, 8–15+30. [Google Scholar]
- Kumar, P.P.; Nuvvula, R.S.S.; Hossain, M.A.; Shezan, S.A.; Suresh, V.; Jasinski, M.; Gono, R.; Leonowicz, Z. Optimal Operation of an Integrated Hybrid Renewable Energy System with Demand-Side Management in a Rural Context. Energies 2022, 15, 5176. [Google Scholar] [CrossRef]


| Project Title | Scenarios | Electricity Traded (MWh) | Energy Gains (USD) | Fuel Costs (USD) | O&M Cost (USD) | Heat Traded (t/h) |
|---|---|---|---|---|---|---|
| BGCHP | 1 | 720.000 | 73,872.000 | 29,548.800 | 3447.360 | |
| 2 | 655.489 | 70,118.208 | 26,897.616 | 3138.192 | 1716.580 | |
| 3 | 655.489 | 67,253.616 | 26,897.616 | 3138.192 | ||
| WICHP | 1 | 720.000 | 64,022.400 | 20,827.800 | 3348.864 | |
| 2 | 660.132 | 68,114.088 | 19,095.912 | 3069.792 | 1131.736 | |
| 3 | 660.132 | 58,698.144 | 19,095.912 | 3069.792 | ||
| WD | 1 | 517.443 | 33,269.760 | 0 | 2123.136 | |
| 2 | 411.390 | 44,213.760 | 0 | 2123.136 | ||
| 3 | 411.390 | 26,450.280 | 0 | 2123.136 | ||
| PV | 1 | 238.140 | 14,008.320 | 0 | 846.792 | |
| 2 | 166.700 | 16,887.960 | 0 | 846.792 | ||
| 3 | 166.700 | 9805.824 | 0 | 846.792 | ||
| Operator | 2 | 1894.700 | 47,044.152 | 0 | 33,732.144 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Wang, W.; Li, X. Study on Market-Based Trading Strategies for Biomass Power Generation Participation in Microgrid Systems. Energies 2023, 16, 7830. https://doi.org/10.3390/en16237830
Yu W, Wang W, Li X. Study on Market-Based Trading Strategies for Biomass Power Generation Participation in Microgrid Systems. Energies. 2023; 16(23):7830. https://doi.org/10.3390/en16237830
Chicago/Turabian StyleYu, Weiwei, Weiqing Wang, and Xiaozhu Li. 2023. "Study on Market-Based Trading Strategies for Biomass Power Generation Participation in Microgrid Systems" Energies 16, no. 23: 7830. https://doi.org/10.3390/en16237830
APA StyleYu, W., Wang, W., & Li, X. (2023). Study on Market-Based Trading Strategies for Biomass Power Generation Participation in Microgrid Systems. Energies, 16(23), 7830. https://doi.org/10.3390/en16237830




