A Three-Dimensional Time-Dependent Model of the Degradation Caused by Chromium Poisoning in a Solid Oxide Fuel Cell Stack
Abstract
:1. Introduction
2. Geometry of the Model
3. Numerical Model
3.1. Assumptions
- Only CrO2(OH)2 is considered for chromium poisoning. Thermodynamic calculations [25] showed that even in the case of a low water partial pressure (e.g., ∼0.1% atm), the molar concentration of CrO2(OH)2 is two orders of magnitude higher than that of CrO3 at the operation temperature of the SOFC stacks considered here (∼700 C).
- The degradation only arises from the decreasing reactive area of LSCF due to chromium deposition processes. Other factors that can also lead to degradation, such as material fractures and lowered conductivity due to the formation of secondary phases, are currently not considered in the model.
3.2. Mass Transport of CrO2(OH)2
3.3. The Kinetic Model of Chromium Poisoning
4. Numerical Setting
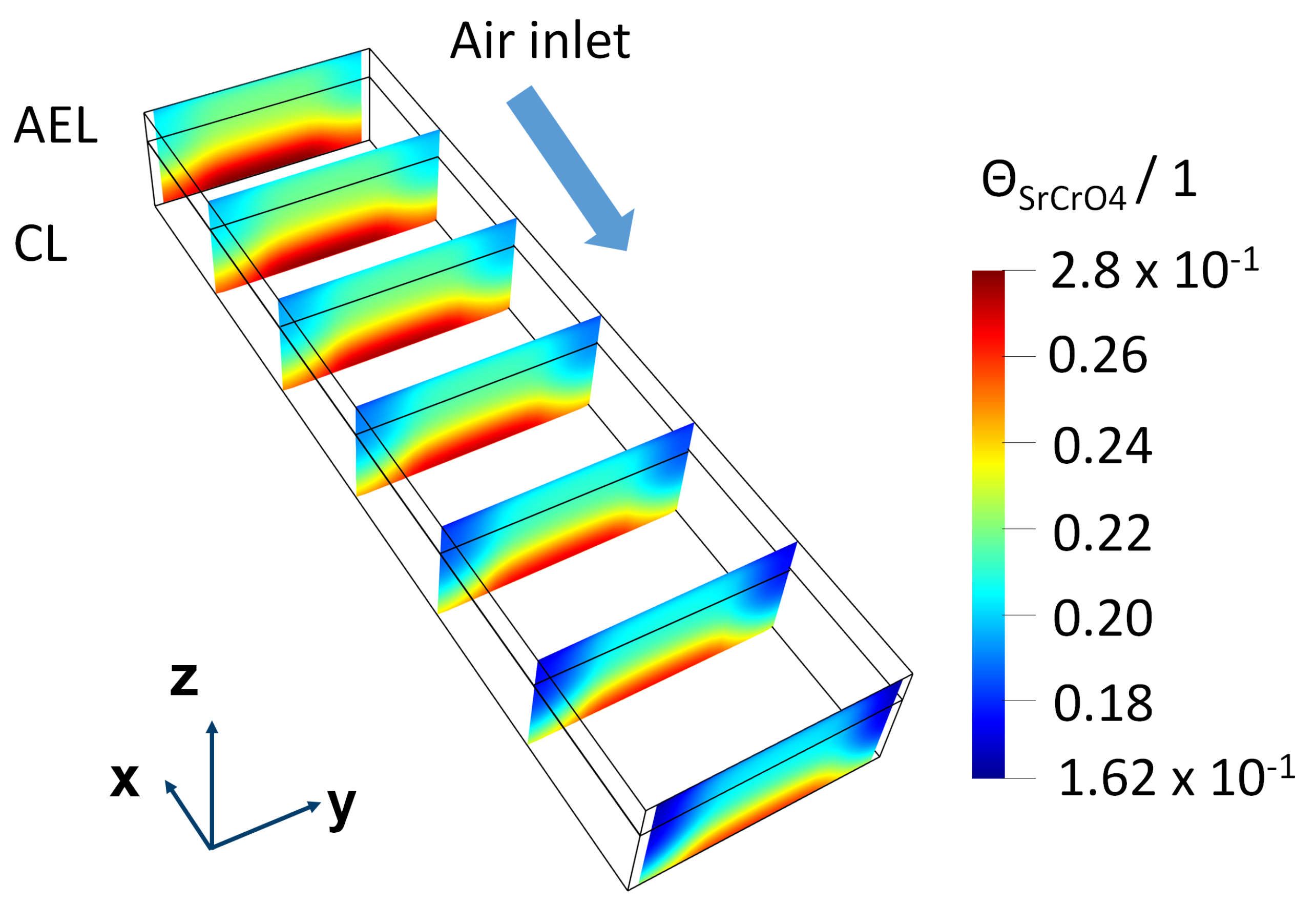
5. Results
5.1. Simulation Results of F1002-97
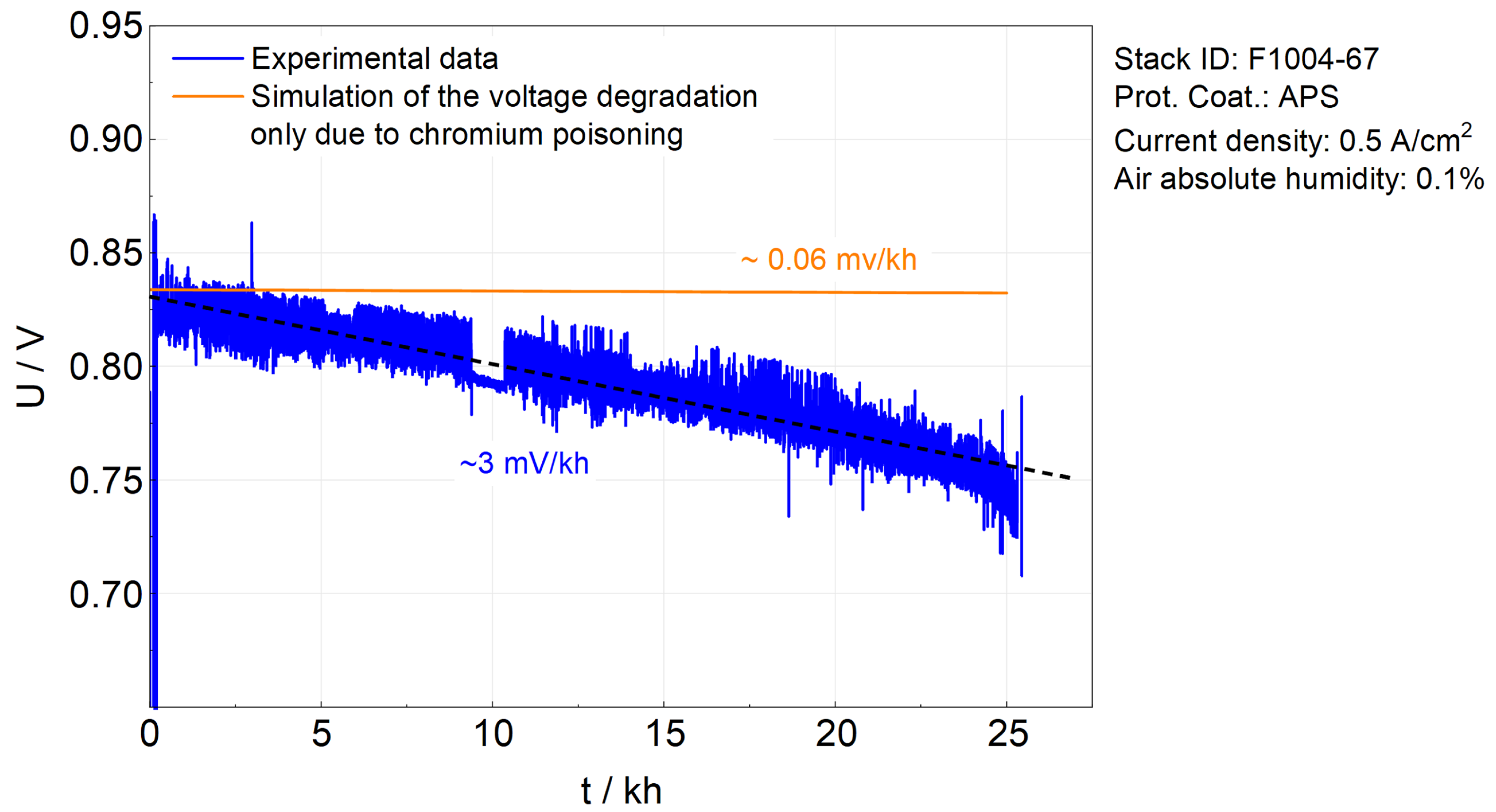
5.2. Simulation Results of F1004-67
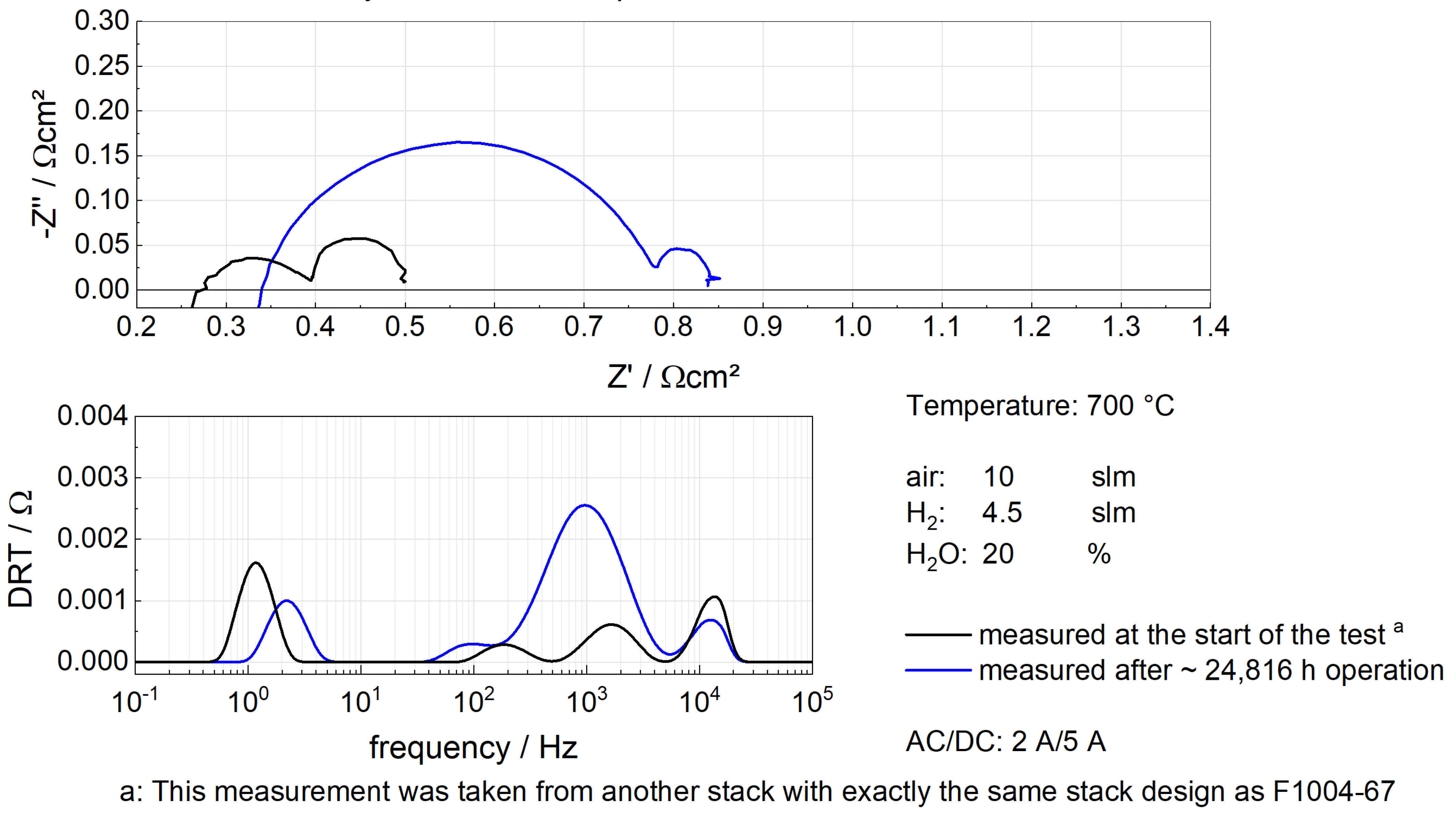
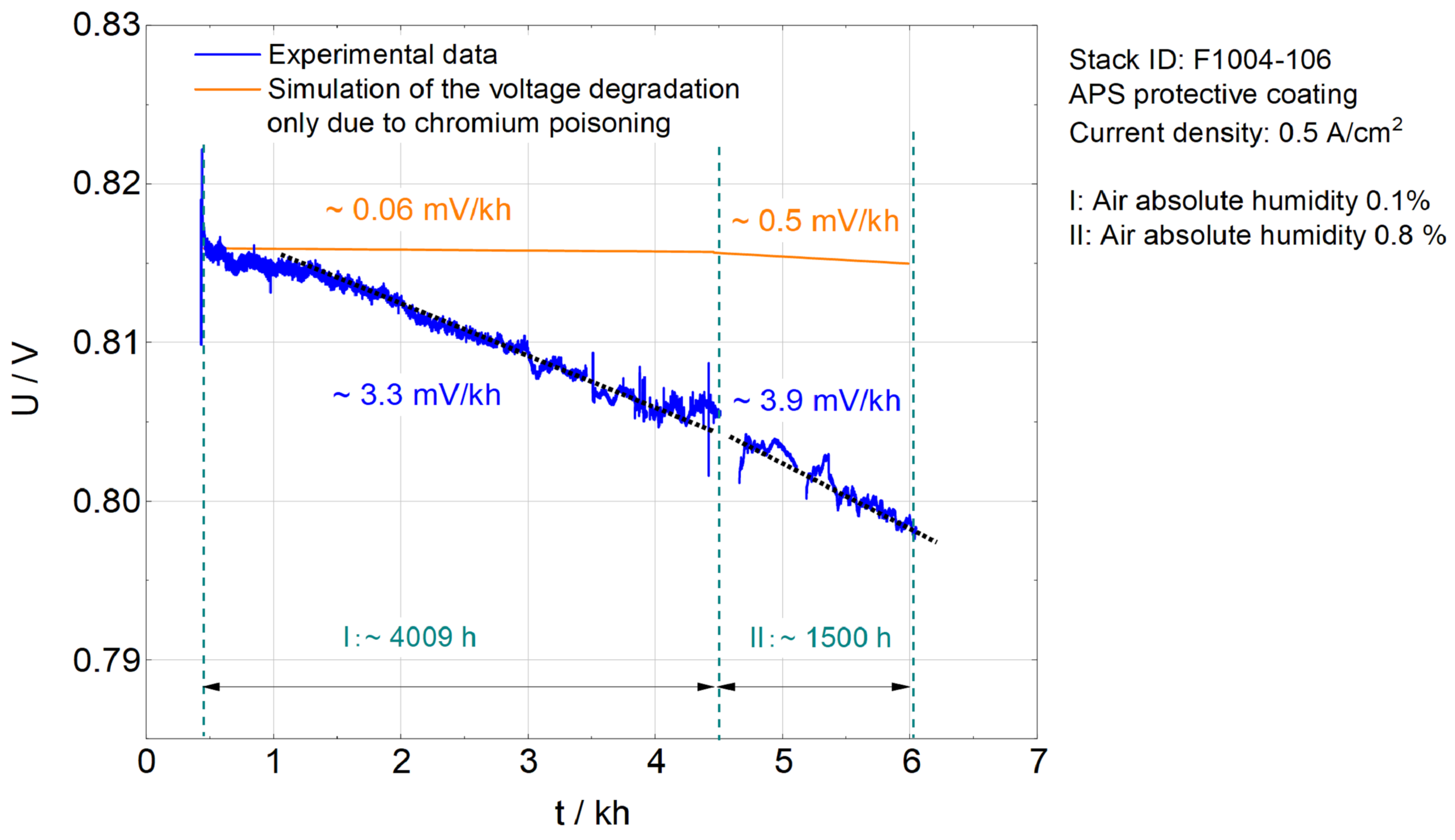
5.3. Simulation Results of F1004-106
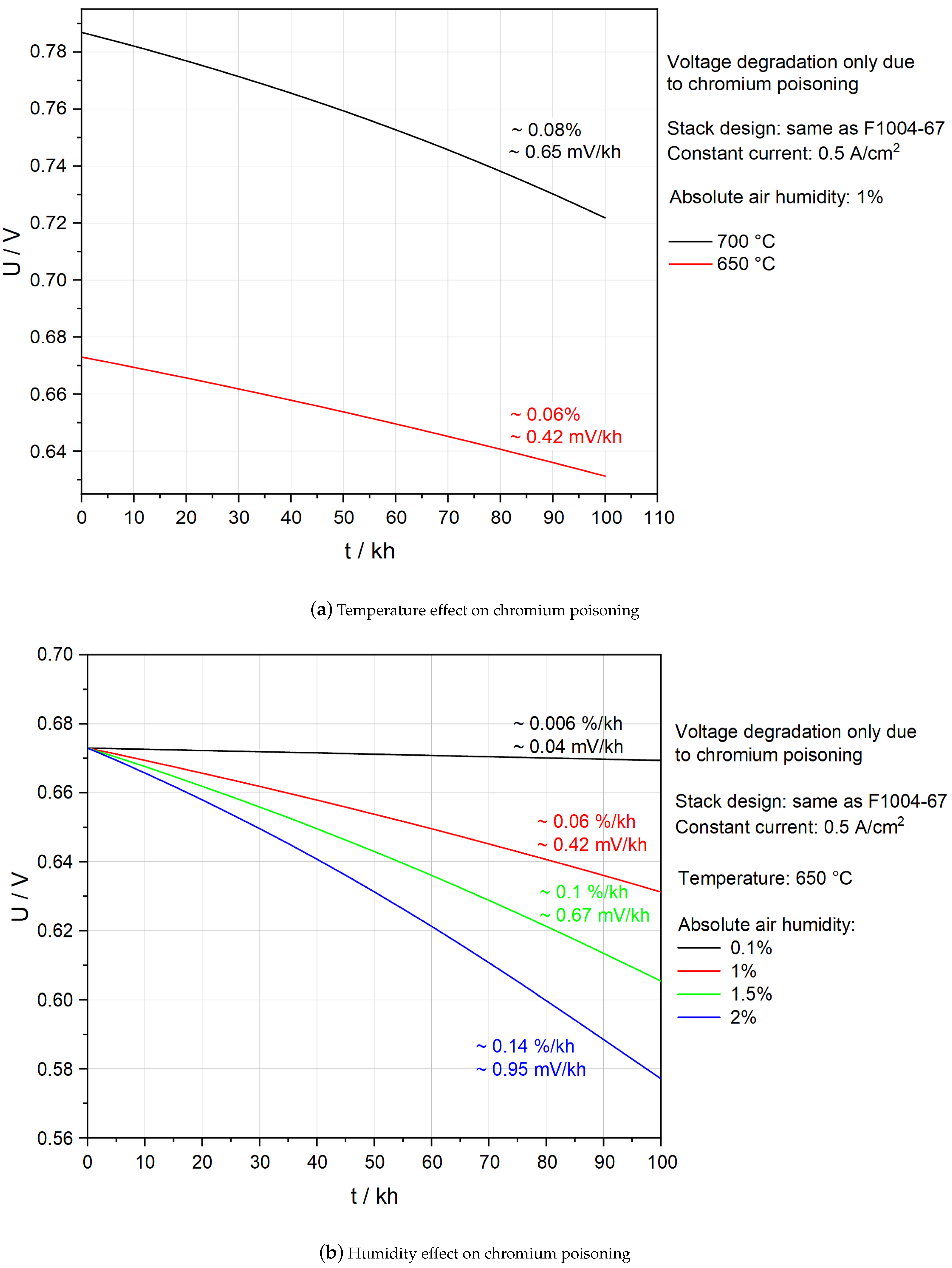
5.4. Effects of Temperature and Humidity on Chromium Poisoning
6. Discussion
6.1. One-Channel Model Representing the Chromium Poisoning in the Whole SOFC Stack
- The SOFC stacks considered in this work were tested inside ovens. Thanks to the heat radiation, based on the temperature measured from thermocouples in the stack [22], it was found that the spatial variation in temperature across the whole stack during the steady operation was slight (10∼15 C). Additionally, a simulation considering the single-cell stack shows a uniform temperature distribution on the reactive part, where the total temperature variation is ∼14.1 C (please see Figure S1 in the Supplementary Materials). Hence, the temperature profile in the single channel is expected to be similar to that of the whole stack.
- Regarding the origin of CrO2(OH)2, the current model assumes the formation of CrO2(OH)2 only originates from the internal surface of the air channel and the rib. In principle CrO2(OH)2 could be released from the metal frames’ surfaces. However, internal experiments indicate the impact of the metal frames is negligible.
6.2. The Stack Design
6.3. Operation under Higher Air Absolute Humidity and Lower Temperature
7. Conclusions
- With an APS protective coating, the chromium poisoning issue in the SOFC stack is almost resolved.
- Lower temperatures and less moisture in the inlet air mitigate chromium poisoning.
- It should be possible to operate an SOFC stack with 1% humidified air at 650 C if APS protective coating is applied.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Surface coverage of species i | |
| Density of adsorption sites on LSCF surface | |
| Overpotential in the air electrode | |
| Porosity of the coating made using the i technique | |
| Velocity | |
| Partial pressure of gaseous species i in air | |
| c | Molar density of the air |
| Molar fraction of gaseous species i in air | |
| Molar diffusion flux of CrO2(OH)2 | |
| T | Temperature |
| Molar mass of species i | |
| Diffusion coefficient of CrO2(OH)2 in air | |
| Source term of CrO2(OH)2 in the mass transport equation | |
| Rate of the surface coverage change due to the electrochemical reaction | |
| Rate of the surface coverage change due to the chemical reaction | |
| K | Thermal equilibrium constant |
| Sticking coefficient of gaseous species i | |
| AEL/ELEC | The interface between the air electrode and the electrolyte |
| AEL | Air electrode |
| CL | Contact layer |
| SOFC | Solid oxide fuel cell |
| 8YSZ | 8 mol% yttria-stabilized zirconia |
| LSCF | La0.58Sr0.4Co0.2Fe0.8O3- |
| LSM | (La,Sr)MnO3 |
| MIC | Metal interconnect |
| APS | Atmospheric plasma spraying |
| WPS | Wet powder spraying |
| ITM | Intermediate temperature metal |
| MIC | Metal interconnect |
| FZJ | Forschungszentrum Jülich GmbH |
| CFD | Computational fluid dynamics |
| TPB | Triple-phase boundary |
| LCC12 | La0.97Mn0.4Co0.3Cu0.3O3- |
| ASR | Area-specific-resistance |
| EIS | Electrochemical impedance spectroscopy |
| DRT | Distribution of relaxation times |
Appendix A. Definition of
Appendix B. Calculation of
- Adsorption of CrO2(OH)2 on the LSCF surface ();
- SrO segregation on the LSCF surface ();
- Formation of SrCrO4 ();
- Desorption of H2O from the LSCF surface ().
Appendix C. Parameters Used in the Model
| Property | Value |
|---|---|
| Porosity of the AEL (εael) | 0.45 [51] |
| Specific area of the LSCF particles (a) | 2.84 × 10 m [51] |
| Porosity of WPS protective coating () | 0.45 [52] |
| Porosity of APS protective coating () | 0.03 [20] |
| Diffusion coefficient of CrO2(OH)2 () | 1 × 10 m s [53] |
| Density of adsorption sites () | 1.1 × 10 mol m [54] |
| Sticking coefficient of CrO2(OH)2 () | 1 |
| Sticking coefficient of H2O () | 0 2 [55] |
Appendix D. Initial Values of in the Model
| Stack Design | Boundary Value | Distribution |
|---|---|---|
| Function 1 | ||
| LSCF as the CL | ||
| LCC12 as the CL |
Appendix E. Initial Values of , , and in the Model
| Initial Value/1 | Comment | |
|---|---|---|
| 5 | Assumed value | |
| 5 | Assumed value | |
| 1 | Assumed value | |
| 1 | Obtained according to the thermal equilibrium |
References
- Zhou, J.; Feng, C.; Su, Q.; Jiang, S.; Fan, Z.; Ruan, J.; Sun, S.; Hu, L. The Multi-Objective Optimization of Powertrain Design and Energy Management Strategy for Fuel Cell–Battery Electric Vehicle. Sustainability 2022, 14, 6320. [Google Scholar] [CrossRef]
- Jia, C.; Zhou, J.; He, H.; Li, J.; Wei, Z.; Li, K.; Shi, M. A novel energy management strategy for hybrid electric bus with fuel cell health and battery thermal- and health-constrained awareness. Energy 2023, 271, 127105. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Z.; Jiang, J. Fuel Cell Technology for Distributed Generation: An Overview. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; Volume 2, pp. 1613–1618. [Google Scholar] [CrossRef]
- Zarabi Golkhatmi, S.; Asghar, M.I.; Lund, P.D. A review on solid oxide fuel cell durability: Latest progress, mechanisms, and study tools. Renew. Sustain. Energy Rev. 2022, 161, 112339. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Liu, W. A review of solid oxide fuel cell application. IOP Conf. Ser. Earth Environ. Sci. 2020, 619, 012012. [Google Scholar] [CrossRef]
- Zhou, L.; Mason, J.H.; Li, W.; Liu, X. Comprehensive review of chromium deposition and poisoning of solid oxide fuel cells (SOFCs) cathode materials. Renew. Sustain. Energy Rev. 2020, 134, 110320. [Google Scholar] [CrossRef]
- Horita, T. Chromium poisoning for prolonged lifetime of electrodes in solid oxide fuel cells—Review. Ceram. Int. 2021, 47, 7293–7306. [Google Scholar] [CrossRef]
- Fang, Q.; Blum, L.; Stolten, D. Electrochemical Performance and Degradation Analysis of an SOFC Short Stack Following Operation of More than 100,000 Hours. J. Electrochem. Soc. 2019, 166, F1320–F1325. [Google Scholar] [CrossRef]
- Vora, S.D.; Lundberg, W.L.; Pierre, J.F. Overview of U.S. Department of Energy Office of Fossil Energy’s Solid Oxide Fuel Cell Program. ECS Trans. 2017, 78, 3. [Google Scholar] [CrossRef]
- Nakajo, A.; Tanasini, P.; Diethelm, S.; Herle, J.V.; Favrat, D. Electrochemical Model of Solid Oxide Fuel Cell for Simulation at the Stack Scale II: Implementation of Degradation Processes. J. Electrochem. Soc. 2011, 158, B1102. [Google Scholar] [CrossRef]
- Miyoshi, K.; Iwai, H.; Kishimoto, M.; Saito, M.; Yoshida, H. Chromium poisoning in (La,Sr)MnO3 cathode: Three-dimensional simulation of a solid oxide fuel cell. J. Power Sources 2016, 326, 331–340. [Google Scholar] [CrossRef]
- Babaie Rizvandi, O.; Miao, X.Y.; Frandsen, H.L. Multiscale modeling of degradation of full solid oxide fuel cell stacks. Int. J. Hydrogen Energy 2021, 46, 27709–27730. [Google Scholar] [CrossRef]
- Menzler, N.H.; Sebold, D.; Sohn, Y.J.; Zischke, S. Post-test characterization of a solid oxide fuel cell after more than 10 years of stack testing. J. Power Sources 2020, 478, 228770. [Google Scholar] [CrossRef]
- Jiang, S.P.; Chen, X. Chromium deposition and poisoning of cathodes of solid oxide fuel cells—A review. Int. J. Hydrogen Energy 2014, 39, 505–531. [Google Scholar] [CrossRef]
- Koo, B.; Kim, K.; Kim, J.K.; Kwon, H.; Han, J.W.; Jung, W. Sr Segregation in Perovskite Oxides: Why It Happens and How It Exists. Joule 2018, 2, 1476–1499. [Google Scholar] [CrossRef]
- Türk, H.; Götsch, T.; Schmidt, F.P.; Hammud, A.; Ivanov, D.; de Haart, L.G.J.B.; Vinke, I.C.; Eichel, R.A.; Schlögl, R.; Reuter, K.; et al. Sr Surface Enrichment in Solid Oxide Cells—Approaching the Limits of EDX Analysis by Multivariate Statistical Analysis and Simulations. ChemCatChem 2022, 14, e202200300. [Google Scholar] [CrossRef]
- Yin, X.; Bencze, L.; Motalov, V.; Spatschek, R.; Singheiser, L. Thermodynamic perspective of Sr-related degradation issues in SOFCs. Int. J. Appl. Ceram. Technol. 2018, 15, 380–390. [Google Scholar] [CrossRef]
- Blum, L.; Fang, Q.; Groß-Barsnick, S.M.; de Haart, L.B.; Malzbender, J.; Menzler, N.H.; Quadakkers, W.J. Long-term operation of solid oxide fuel cells and preliminary findings on accelerated testing. Int. J. Hydrogen Energy 2020, 45, 8955–8964. [Google Scholar] [CrossRef]
- Menzler, N.H.; Sebold, D.; Guillon, O. Post-test characterization of a solid oxide fuel cell stack operated for more than 30,000 hours: The cell. J. Power Sources 2018, 374, 69–76. [Google Scholar] [CrossRef]
- Grünwald, N.; Lhuissier, P.; Salvo, L.; Villanova, J.; Menzler, N.H.; Guillon, O.; Martin, C.L.; Vaßen, R. In situ investigation of atmospheric plasma-sprayed Mn–Co–Fe–O by synchrotron X-ray nano-tomography. J. Mater. Sci. 2020, 55, 12725–12736. [Google Scholar] [CrossRef]
- Steinberger-Wilckens, R.; De Haart, L.; Vinke, I.; Blum, L.; Cramer, A.; Remmel, J.; Blass, G.; Tietz, F.; Quadakkers, W. Recent results of stack development at forschungszentrum jülich. In Proceedings of the Fuel Cell Technologies: State and Perspectives; Sammes, N., Smirnova, A., Vasylyev, O., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 123–134. [Google Scholar]
- Yu, S.; Zhang, S.; Schäfer, D.; Peters, R.; Kunz, F.; Eichel, R.A. Numerical Modeling and Simulation of the Solid Oxide Cell Stacks and Metal Interconnect Oxidation with OpenFOAM. Energies 2023, 16, 3827. [Google Scholar] [CrossRef]
- Zhang, S.; Hess, S.; Marschall, H.; Reimer, U.; Beale, S.B.; Lehnert, W. openFuelCell2: A New Computational Tool for Fuel Cells, Electrolyzers, and other Electrochemical Devices and Processes. Comput. Phys. Commun. 2023; in press. [Google Scholar]
- Hilpert, K.; Das, D.; Miller, M.; Peck, D.H.; Weiß, R. Chromium Vapor Species over Solid Oxide Fuel Cell Interconnect Materials and Their Potential for Degradation Processes. J. Electrochem. Soc. 1996, 143, 3642. [Google Scholar] [CrossRef]
- Ebbinghaus, B.B. Thermodynamics of gas phase chromium species: The chromium oxides, the chromium oxyhydroxides, and volatility calculations in waste incineration processes. Combust. Flame 1993, 93, 119–137. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C. A modeling study on concentration overpotentials of a reversible solid oxide fuel cell. J. Power Sources 2006, 163, 460–466. [Google Scholar] [CrossRef]
- Ni, M. Computational fluid dynamics modeling of a solid oxide electrolyzer cell for hydrogen production. Int. J. Hydrogen Energy 2009, 34, 7795–7806. [Google Scholar] [CrossRef]
- Opila, E.J. Volatility of common protective oxides in high-temperature water vapor: Current understanding and unanswered questions. In Proceedings of the High Temperature Corrosion and Protection of Materials 6; Materials Science Forum; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2004; Volume 461, pp. 765–774. [Google Scholar] [CrossRef]
- Wuillemin, Z. Experimental and Modeling Investigations on Local Performance and Local Degradation in Solid Oxide Fuel Cells. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2009. [Google Scholar]
- Foo, K.; Hameed, B. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Chorkendorff, I.; Niemantsverdriet, J. Concepts of Modern Catalysis and Kinetics, 3rd ed.; Wiley-VCH: Hoboken, NJ, USA, 2017. [Google Scholar]
- Kröll, L.; de Haart, L.G.J.; Vinke, I.; Eichel, R.A. Degradation Mechanisms in Solid-Oxide Fuel and Electrolyzer Cells: Analytical Description of Nickel Agglomeration in a Ni/YSZ Electrode. Phys. Rev. Appl. 2017, 7, 044007. [Google Scholar] [CrossRef]
- Beez, A.; Schiemann, K.; Menzler, N.H.; Bram, M. Accelerated Testing of Chromium Poisoning of Sr-Containing Mixed Conducting Solid Oxide Cell Air Electrodes. Front. Energy Res. 2018, 6, 70. [Google Scholar] [CrossRef]
- Motagamwala, A.H.; Dumesic, J.A. Microkinetic Modeling: A Tool for Rational Catalyst Design. Chem. Rev. 2021, 121, 1049–1076. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Gardner, D.J.; Reynolds, D.R.; Woodward, C.S.; Balos, C.J. Enabling new flexibility in the SUNDIALS suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. (TOMS) 2022, 48, 1–24. [Google Scholar] [CrossRef]
- Fang, Q.; Menzler, N.H.; Blum, L. Degradation Analysis of Long-Term Solid Oxide Fuel Cell Stacks with Respect to Chromium Poisoning in La0.58Sr0.4Co0.2Fe0.8O3−δ and La0.6Sr0.4CoO3−δ in Cathodes. J. Electrochem. Soc. 2021, 168, 104505. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Yan, Y.; Fang, Q.; Blum, L.; Lehnert, W. Performance and degradation of an SOEC stack with different cell components. Electrochim. Acta 2017, 258, 1254–1261. [Google Scholar] [CrossRef]
- Caliandro, P.; Nakajo, A.; Diethelm, S.; Van herle, J. Model-assisted identification of solid oxide cell elementary processes by electrochemical impedance spectroscopy measurements. J. Power Sources 2019, 436, 226838. [Google Scholar] [CrossRef]
- Weather Data in Jülich from December 2019 to February 2020. Available online: https://www.timeanddate.com/weather/germany/juelich/historic?month=3&year=2020 (accessed on 1 February 2023).
- Calculator of the Absolute Humidity. Available online: https://www.omnicalculator.com/physics/absolute-humidity (accessed on 1 February 2023).
- Whiston, M.M.; Azevedo, I.M.; Litster, S.; Samaras, C.; Whitefoot, K.S.; Whitacre, J.F. Meeting U.S. Solid Oxide Fuel Cell Targets. Joule 2019, 3, 2060–2065. [Google Scholar] [CrossRef]
- Menzler, N.H.; Sebold, D.; Zischke, S. SOC Degradation: Long-Term and Small-Scale Effects. ECS Trans. 2019, 91, 719. [Google Scholar] [CrossRef]
- Haart, L.G.J.B.D.; Beale, S.B.; Deja, R.; Dittrich, L.; Duyster, T.; Fang, Q.; Foit, S.; Gross-Barsnick, S.; Margaritis, N.; de Haart, U.; et al. Forschungszentrum Jülich—Current Activities in SOC Development. ECS Trans. 2021, 103, 299. [Google Scholar] [CrossRef]
- Hui, R.; Wang, Z.; Kesler, O.; Rose, L.; Jankovic, J.; Yick, S.; Maric, R.; Ghosh, D. Thermal plasma spraying for SOFCs: Applications, potential advantages, and challenges. J. Power Sources 2007, 170, 308–323. [Google Scholar] [CrossRef]
- Qiu, P.; Lin, J.; Lei, L.; Yuan, Z.; Jia, L.; Li, J.; Chen, F. Evaluation of Cr-Tolerance of the Sr2Fe1.5Mo0.5O63−δ Cathode for Solid Oxide Fuel Cells. ACS Appl. Energy Mater. 2019, 2, 7619–7627. [Google Scholar] [CrossRef]
- Niu, Y.; Zhou, Y.; Lv, W.; Chen, Y.; Zhang, Y.; Zhang, W.; Luo, Z.; Kane, N.; Ding, Y.; Soule, L.; et al. Enhancing Oxygen Reduction Activity and Cr Tolerance of Solid Oxide Fuel Cell Cathodes by a Multiphase Catalyst Coating. Adv. Funct. Mater. 2021, 31, 2100034. [Google Scholar] [CrossRef]
- Yang, J.; Polfus, J.M.; Li, Z.; Tuller, H.L.; Yildiz, B. Role of Adsorbate Coverage on the Oxygen Dissociation Rate on Sr-Doped LaMnO3 Surfaces in the Presence of H2O and CO2. Chem. Mater. 2020, 32, 5483–5492. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, W.; Kane, N.; Luo, Z.; Pei, K.; Sasaki, K.; Choi, Y.; Chen, Y.; Ding, D.; Liu, M. An Efficient Bifunctional Air Electrode for Reversible Protonic Ceramic Electrochemical Cells. Adv. Funct. Mater. 2021, 31, 2105386. [Google Scholar] [CrossRef]
- Joos, J. Microstructural Characterisation, Modelling and Simulation of Solid Oxide Fuel Cell Cathodes. Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruher, Germany, 2017. [Google Scholar] [CrossRef]
- Ruder, A.; Buchkremer, H.P.; Jansen, H.; Malléner, W.; Stöver, D. Wet powder spraying—A process for the production of coatings. Surf. Coatings Technol. 1992, 53, 71–74. [Google Scholar] [CrossRef]
- Stenzel, A.; Fähsing, D.; Schütze, M.; Galetz, M.C. Volatilization kinetics of chromium oxide, manganese oxide, and manganese chromium spinel at high temperatures in environments containing water vapor. Mater. Corros. 2019, 70, 1426–1438. [Google Scholar] [CrossRef]
- Effori, E.; Laurencin, J.; Silva, E.D.R.; Hubert, M.; David, T.; Petitjean, M.; Geneste, G.; Dessemond, L.; Siebert, E. An Elementary Kinetic Model for the LSCF and LSCF-CGO Electrodes of Solid Oxide Cells: Impact of Operating Conditions and Degradation on the Electrode Response. J. Electrochem. Soc. 2021, 168, 044520. [Google Scholar] [CrossRef]
- Huang, Y.L.; Pellegrinelli, C.; Wachsman, E.D. Fundamental Impact of Humidity on SOFC Cathode ORR. J. Electrochem. Soc. 2015, 163, F171. [Google Scholar] [CrossRef]
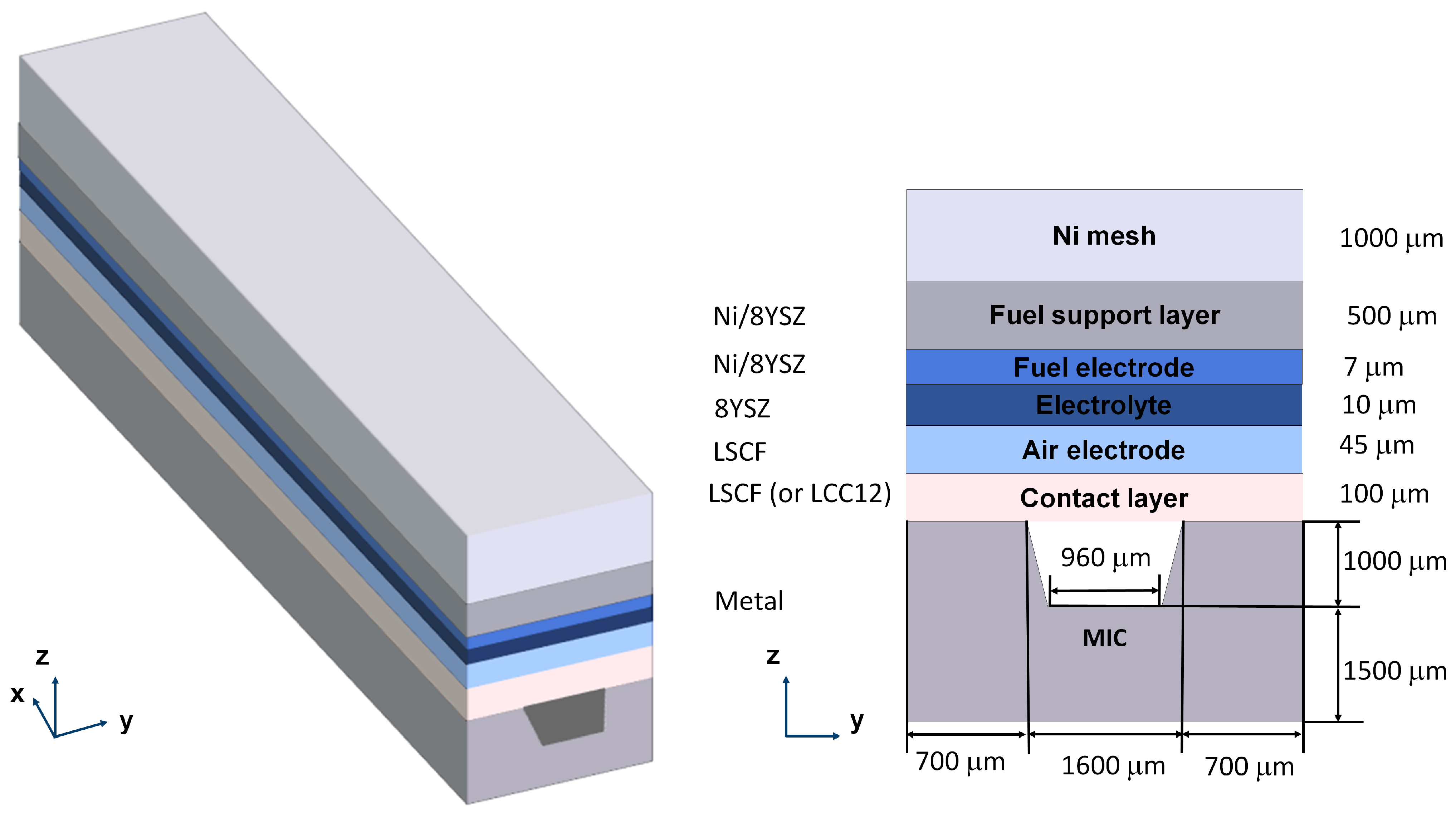
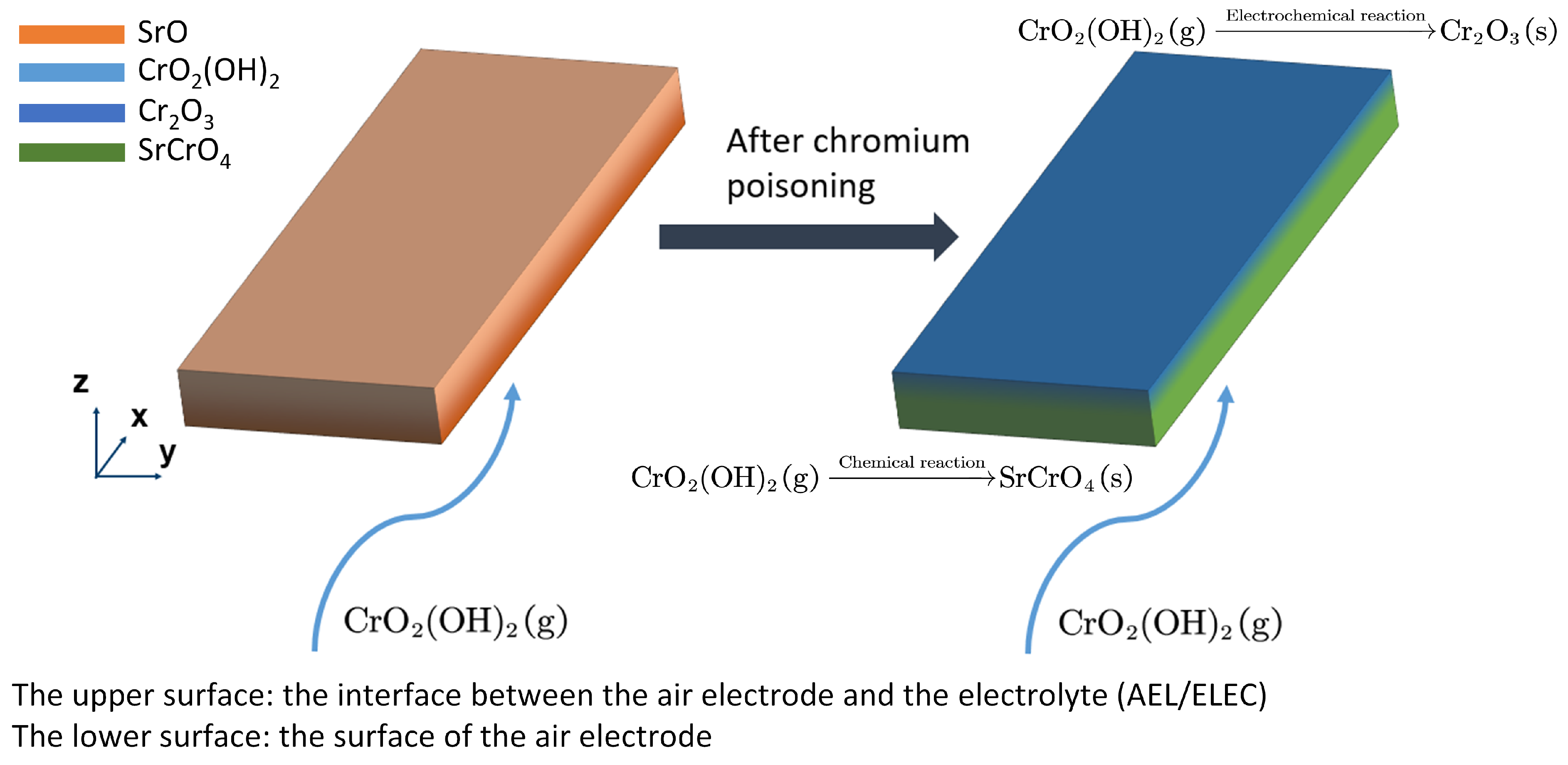
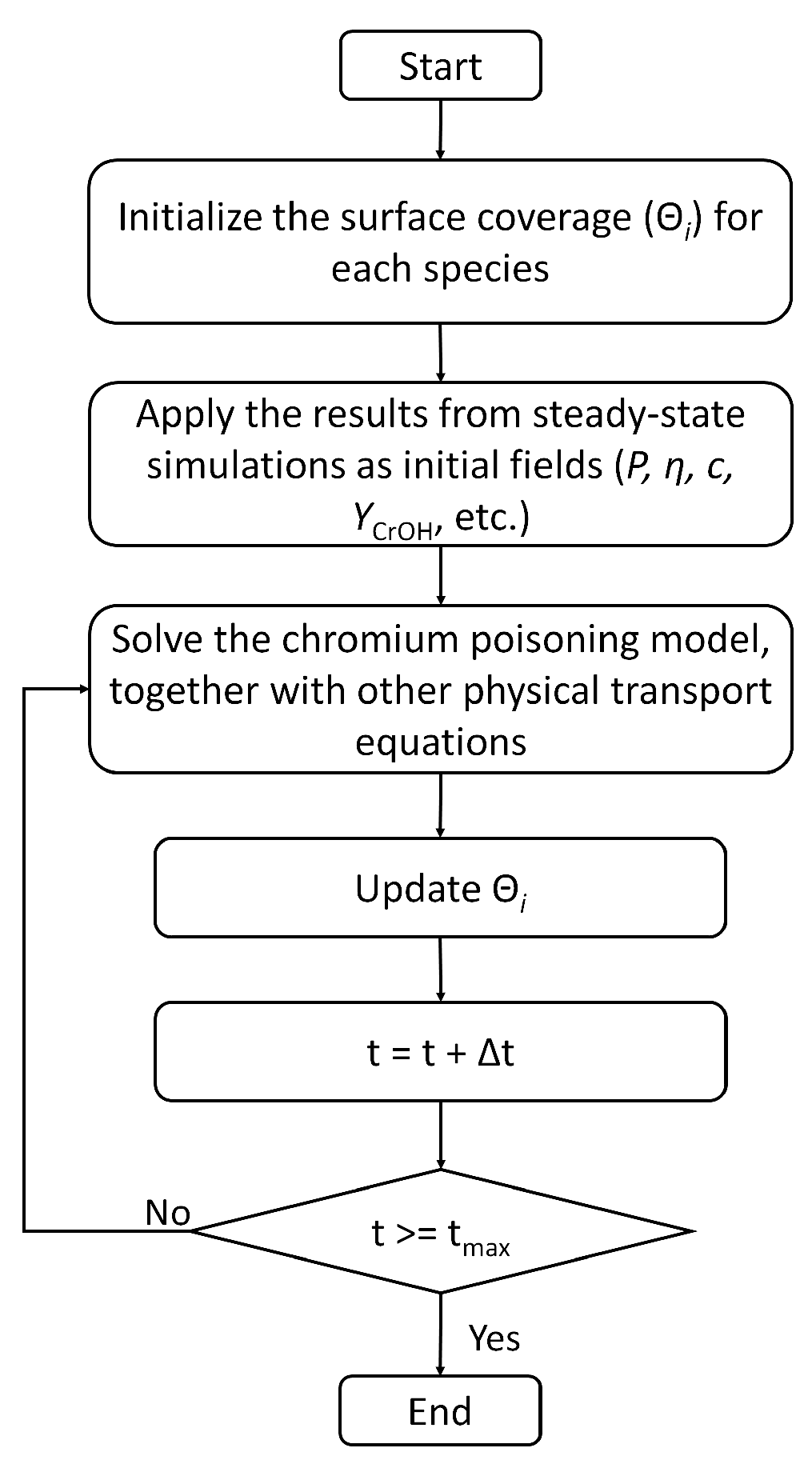


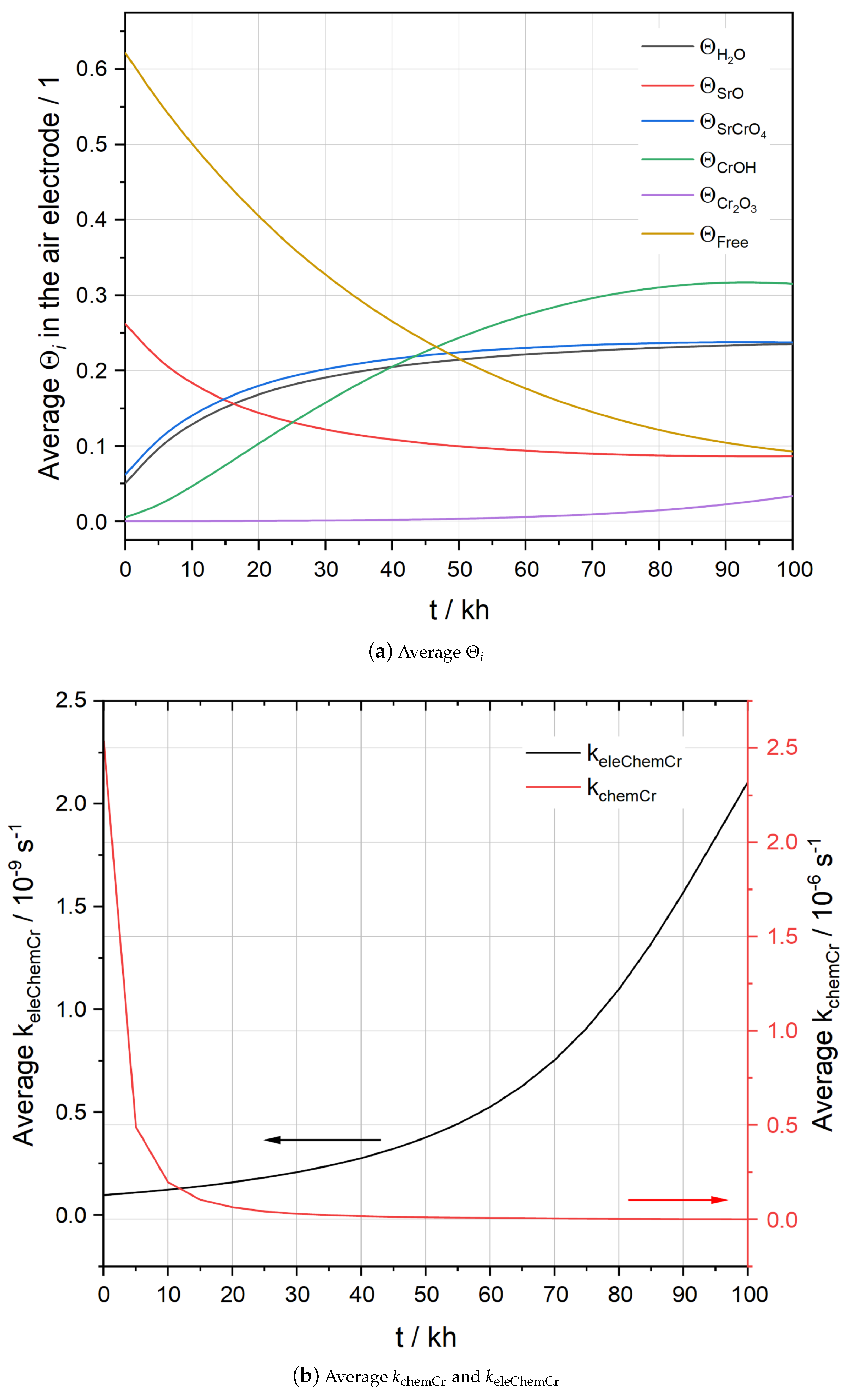
| Physical Process | Governing Equation | Computational Domain |
|---|---|---|
| Mass transport, CrO2(OH)2 | Equation (3) | Air channel, CL and AEL |
| Chromium deposition | Equations (14)–(19) and (23) | Domain made of LSCF |
| Stack ID 1 | F1002-97 | F1004-67 | F1004-106 | |
|---|---|---|---|---|
| Stack design | CL | LCC12 | LSCF | LSCF |
| Protective coating | WPS | APS | APS | |
| Operation conditions | Temperature 2 | 720 C | 730 C | 720 C |
| Current density | 0.5 Acm | 0.5 Acm | 0.5 Acm | |
| Time | 100 kh | 25 kh | 5509 h | |
| Fuel mass flow | 1.18 kg/s | 1.15 × 10−7 kg/s | 1.15 × 10−7 kg/s | |
| Molar ratio in fuel H2/H2O | 79/21 | 80/20 | 80/20 | |
| Air mass flow | 1.9 × 10−6 kg/s | 1.18 kg/s | 1.18 × 10−6 kg/s | |
| Molar ratio in air O2/N2 | 21/79 | 21/79 | 21/79 | |
| Absolute humidity | 0.1% | 0.1% | ∼4009 h 0.1% | |
| in inlet air | ∼1500 h 0.8% | |||
| References | [8] | [18] | [37] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Schäfer, D.; Zhang, S.; Peters, R.; Kunz, F.; Eichel, R.-A. A Three-Dimensional Time-Dependent Model of the Degradation Caused by Chromium Poisoning in a Solid Oxide Fuel Cell Stack. Energies 2023, 16, 7841. https://doi.org/10.3390/en16237841
Yu S, Schäfer D, Zhang S, Peters R, Kunz F, Eichel R-A. A Three-Dimensional Time-Dependent Model of the Degradation Caused by Chromium Poisoning in a Solid Oxide Fuel Cell Stack. Energies. 2023; 16(23):7841. https://doi.org/10.3390/en16237841
Chicago/Turabian StyleYu, Shangzhe, Dominik Schäfer, Shidong Zhang, Roland Peters, Felix Kunz, and Rüdiger-A. Eichel. 2023. "A Three-Dimensional Time-Dependent Model of the Degradation Caused by Chromium Poisoning in a Solid Oxide Fuel Cell Stack" Energies 16, no. 23: 7841. https://doi.org/10.3390/en16237841
APA StyleYu, S., Schäfer, D., Zhang, S., Peters, R., Kunz, F., & Eichel, R.-A. (2023). A Three-Dimensional Time-Dependent Model of the Degradation Caused by Chromium Poisoning in a Solid Oxide Fuel Cell Stack. Energies, 16(23), 7841. https://doi.org/10.3390/en16237841








