Numerical Study of the Influence of Different Bending Shapes on the Heat Transfer Characteristics of Annular Cross Wavy Primary Surface Recuperator (CW-PSR)
Abstract
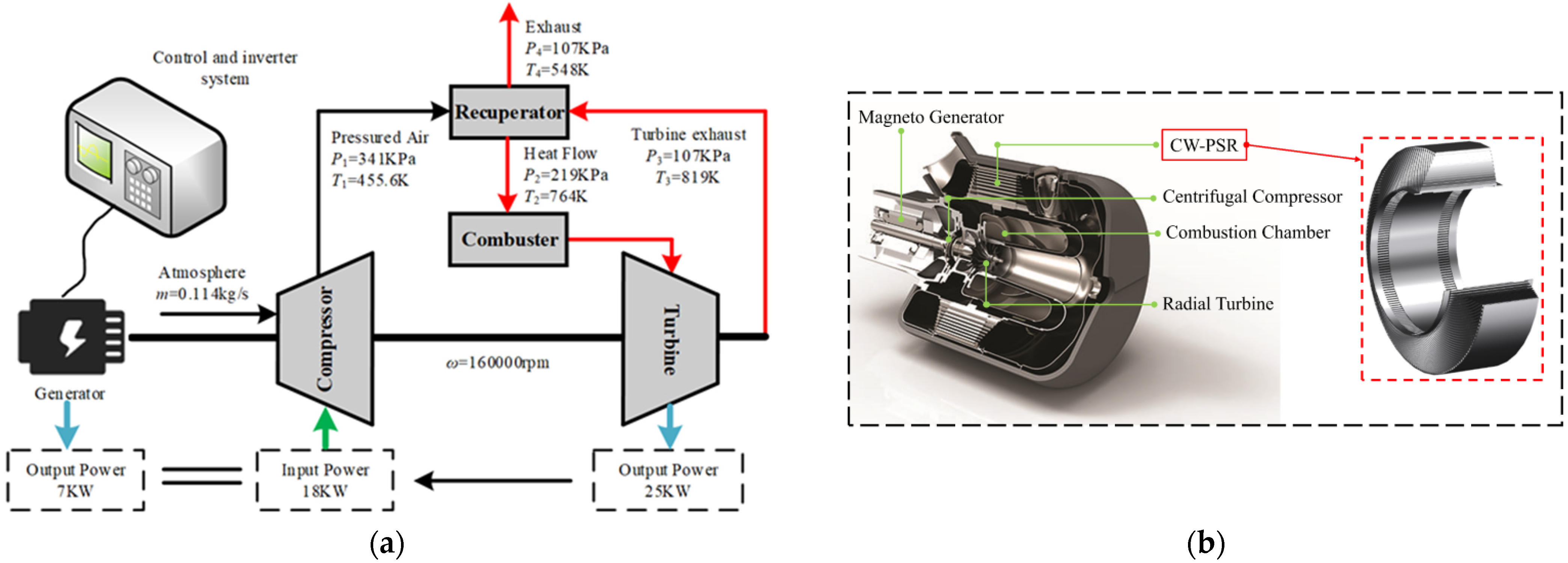
:1. Introduction
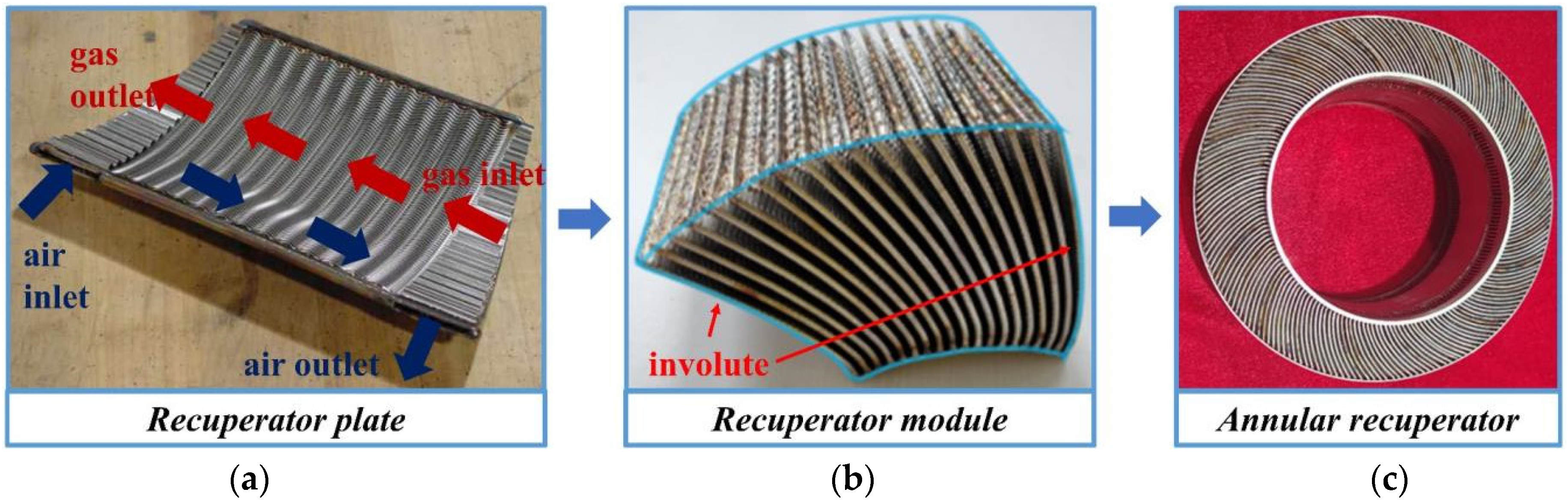
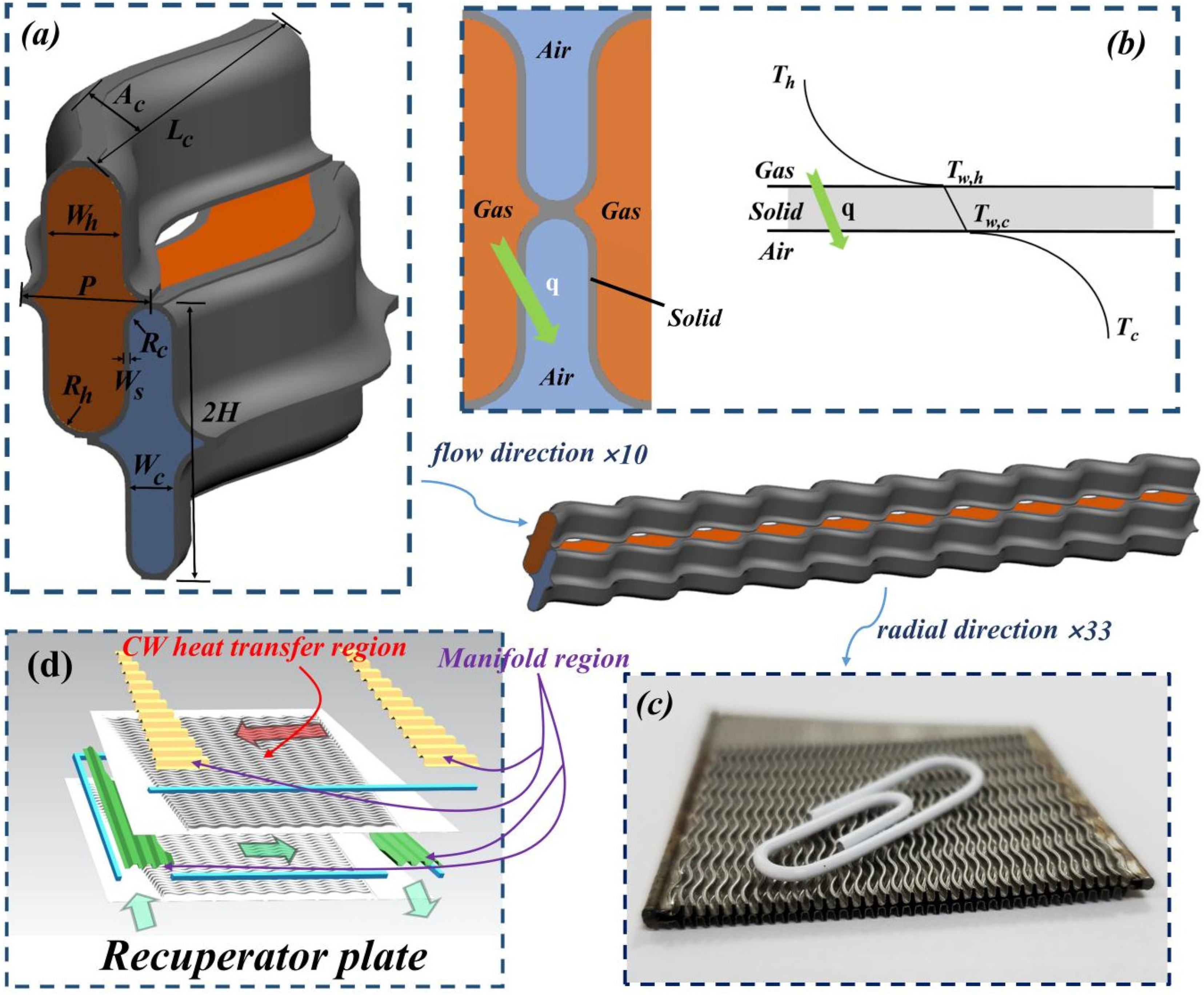
2. The Physical Model of CW-PSR
3. Numerical Method
3.1. Governing Equations
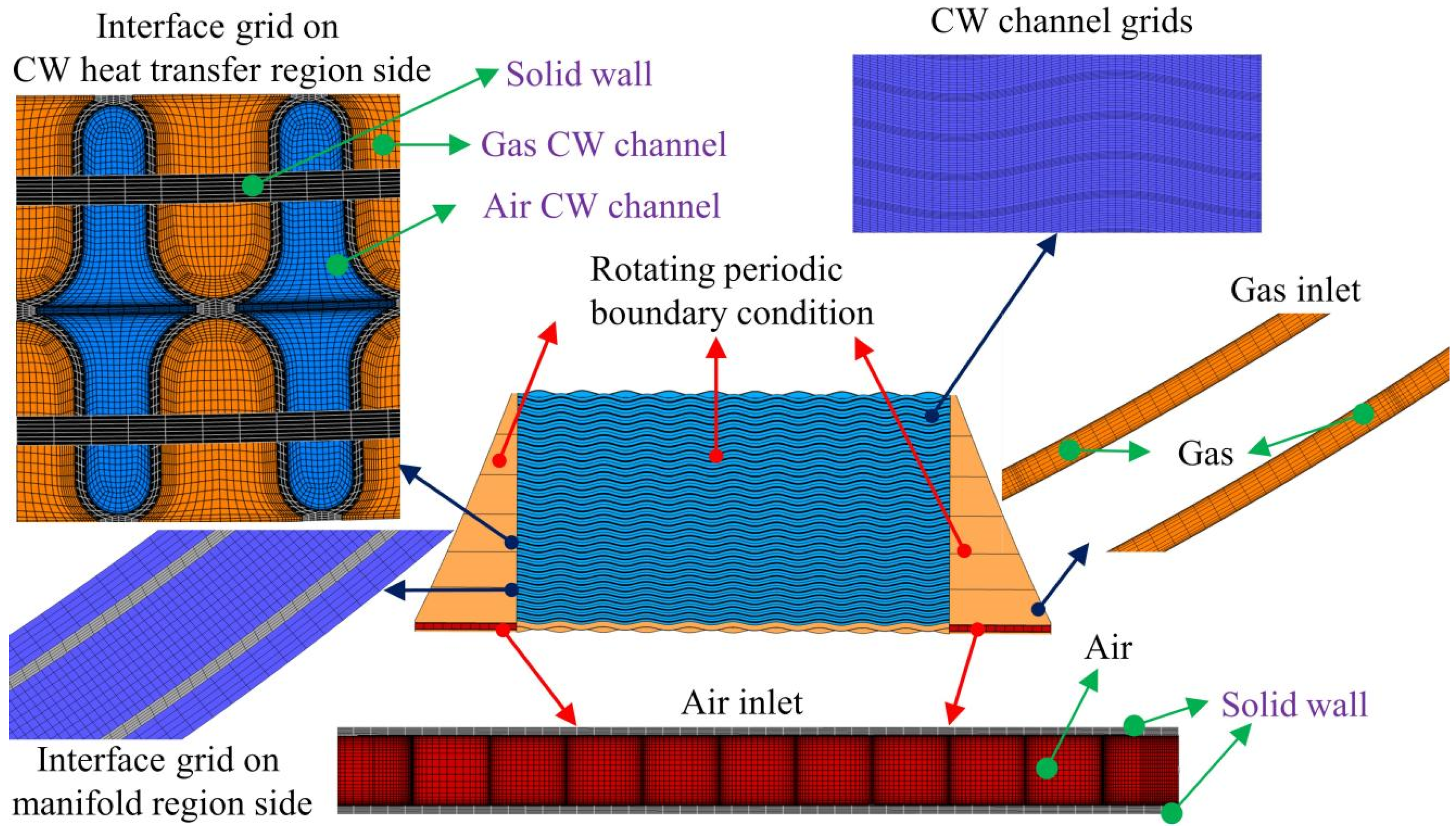
3.2. Boundary Conditions
3.3. Solver Setup
3.4. Principle of Vorticity Field Synergy
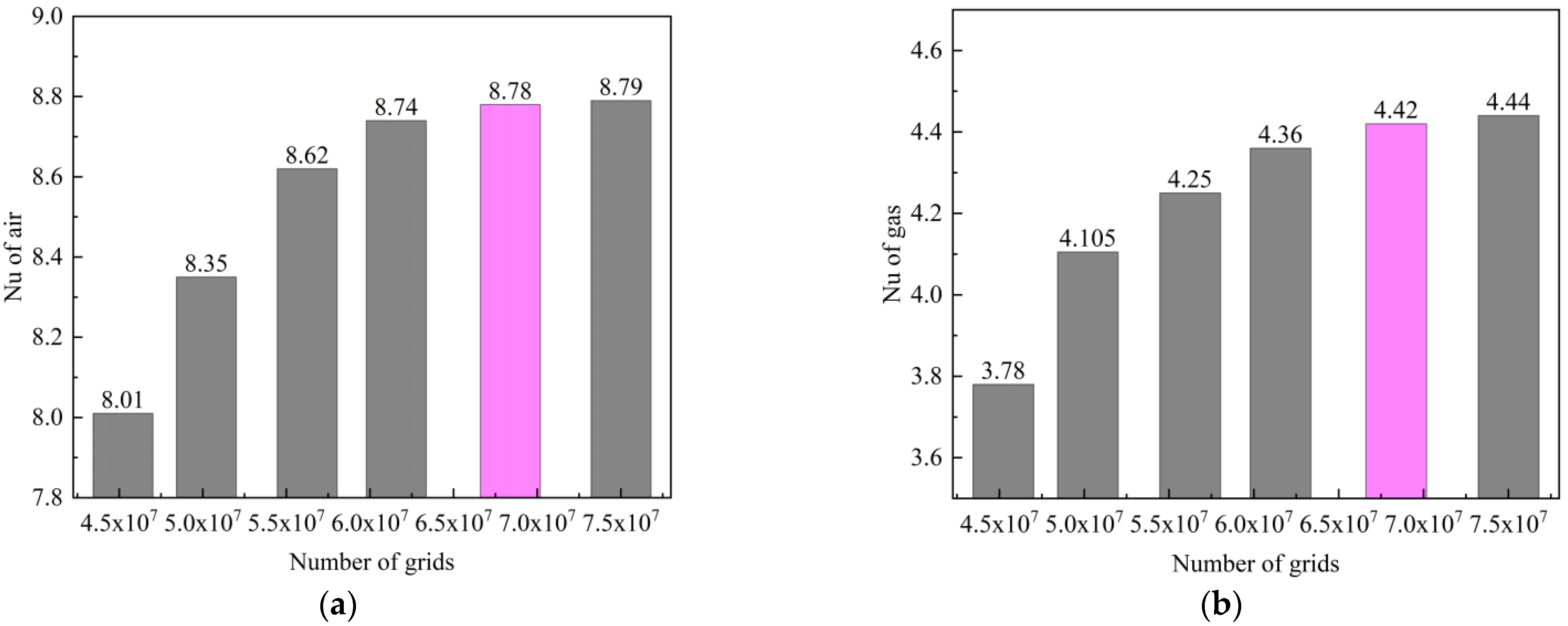
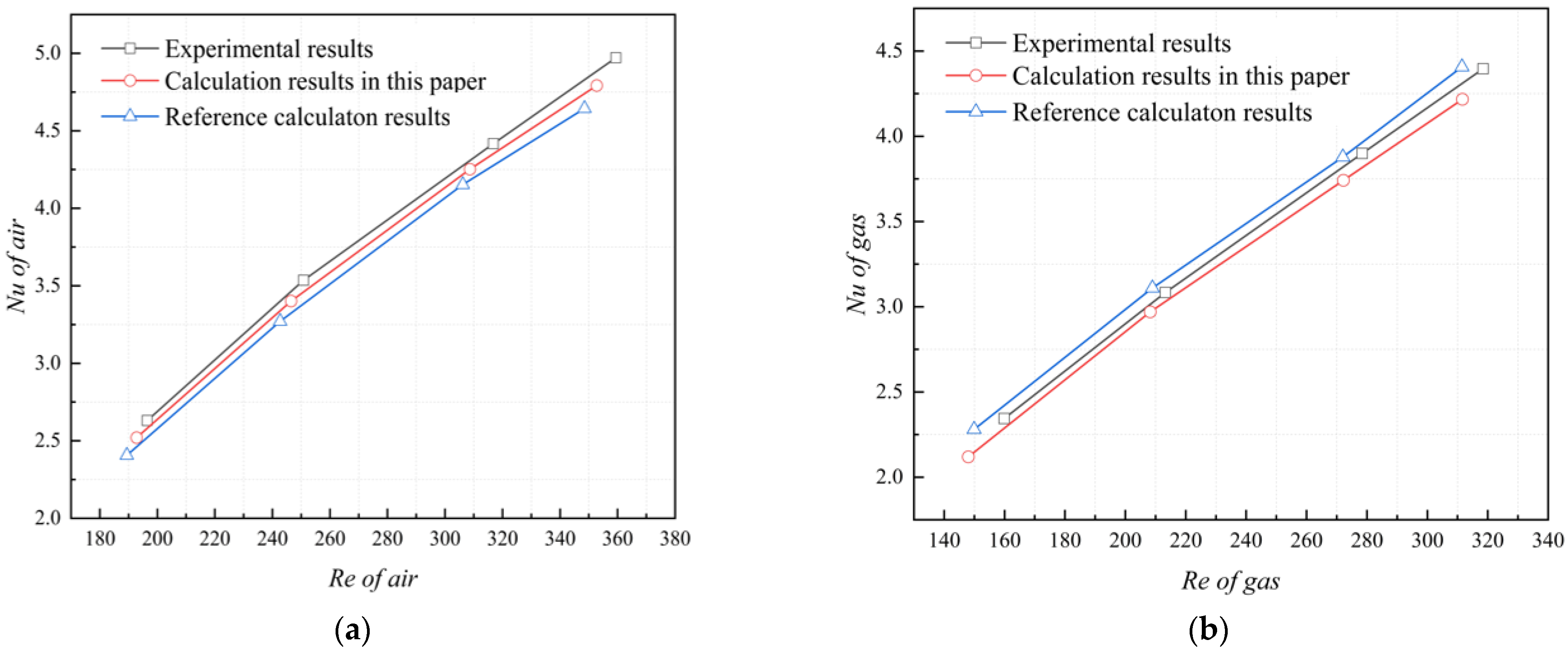
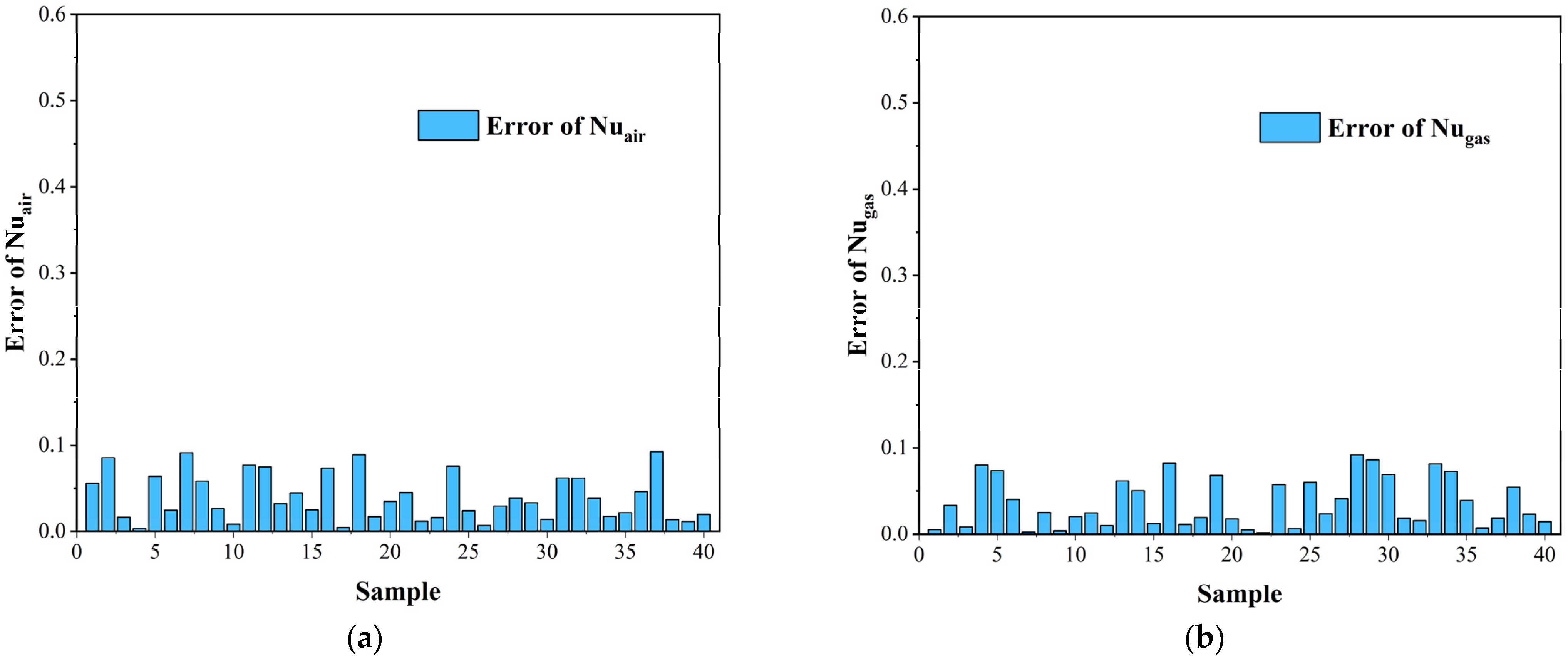
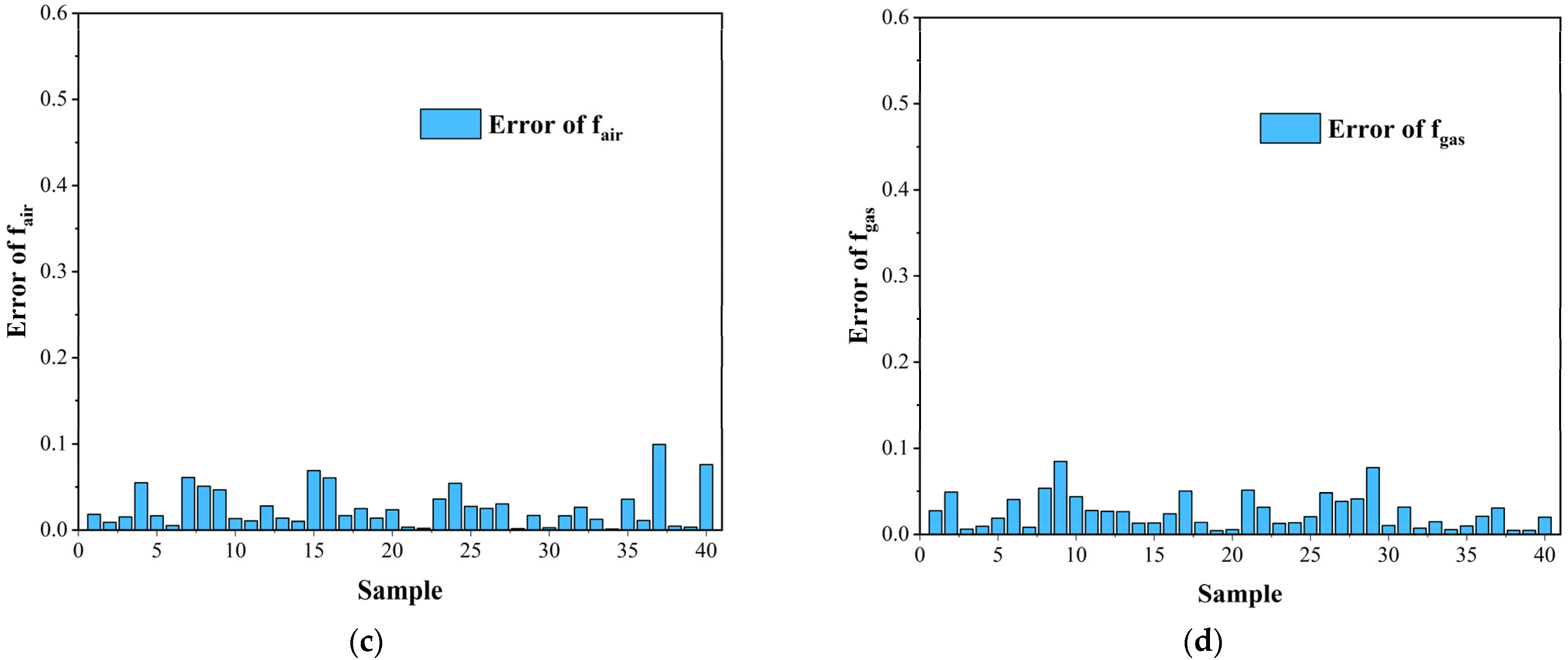
3.5. Grid Independence and Numerical Verification
4. Results and Discussion
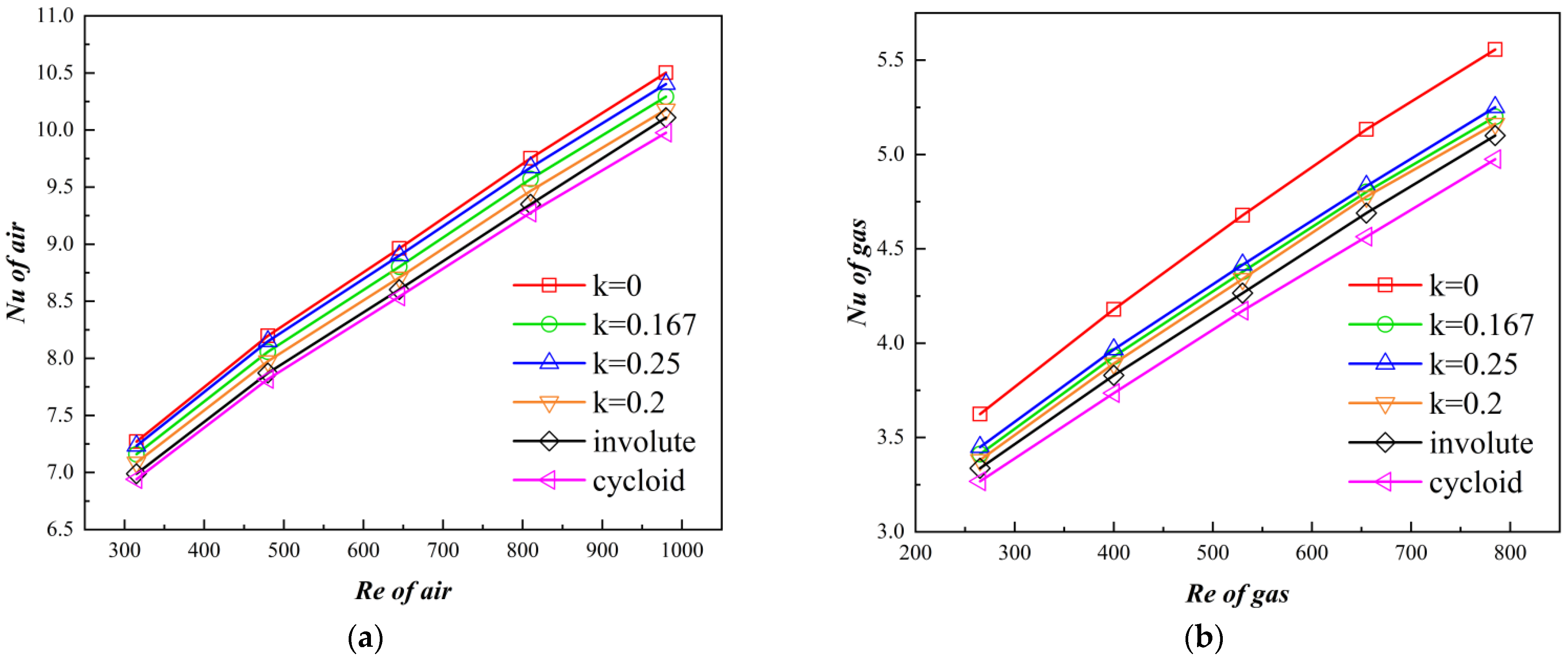
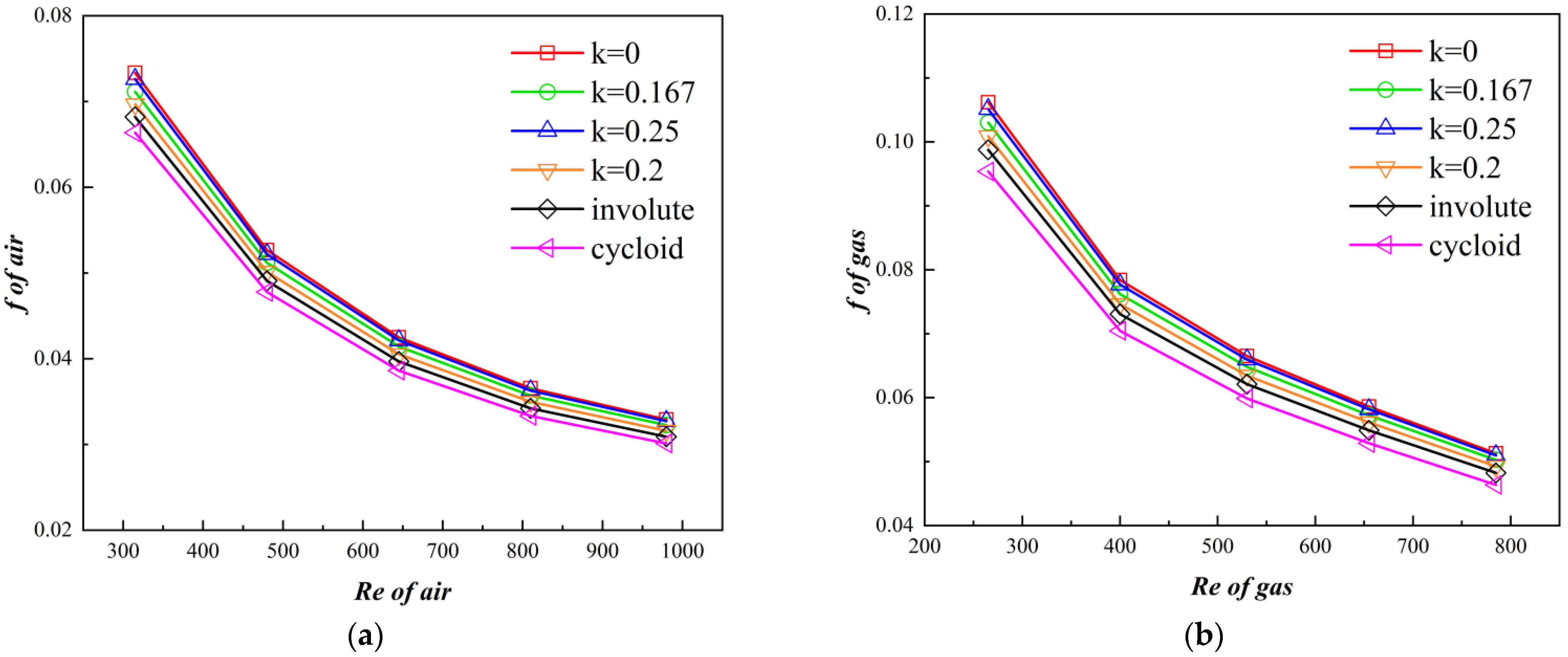
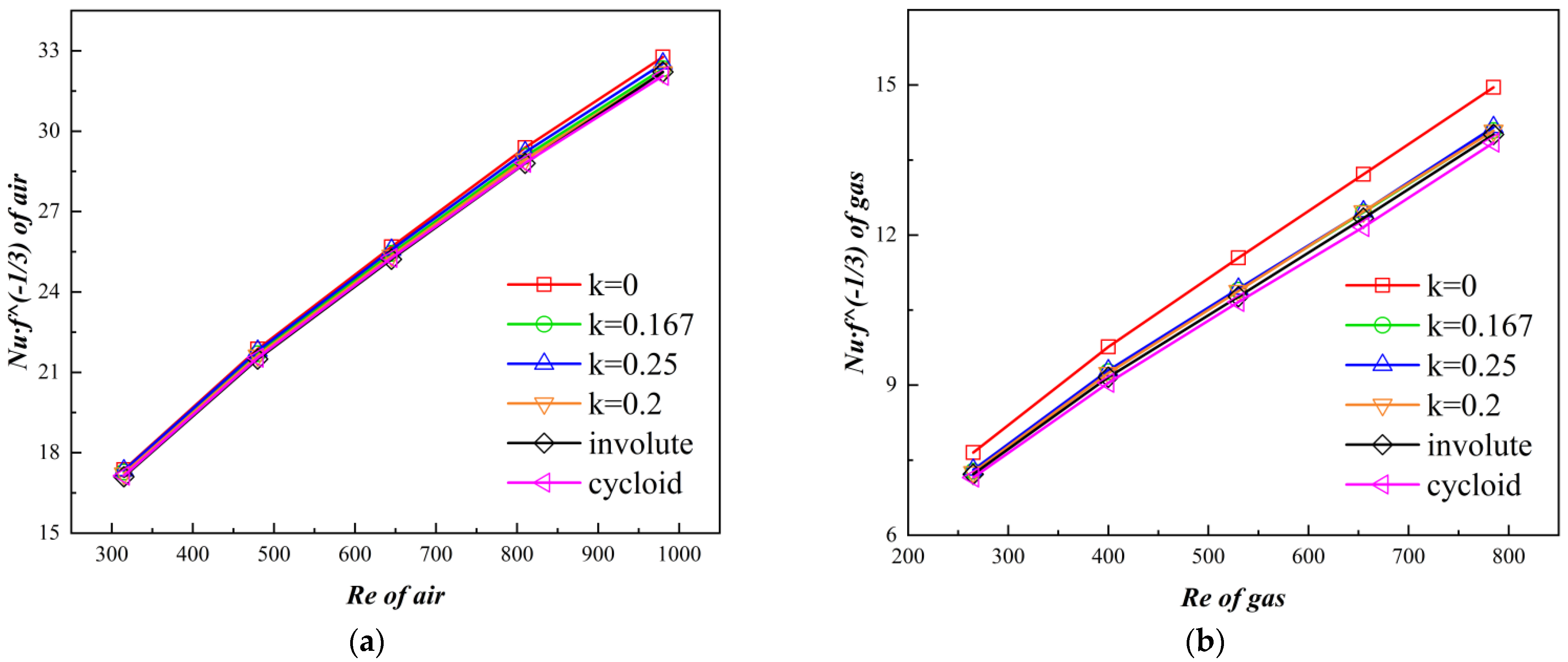
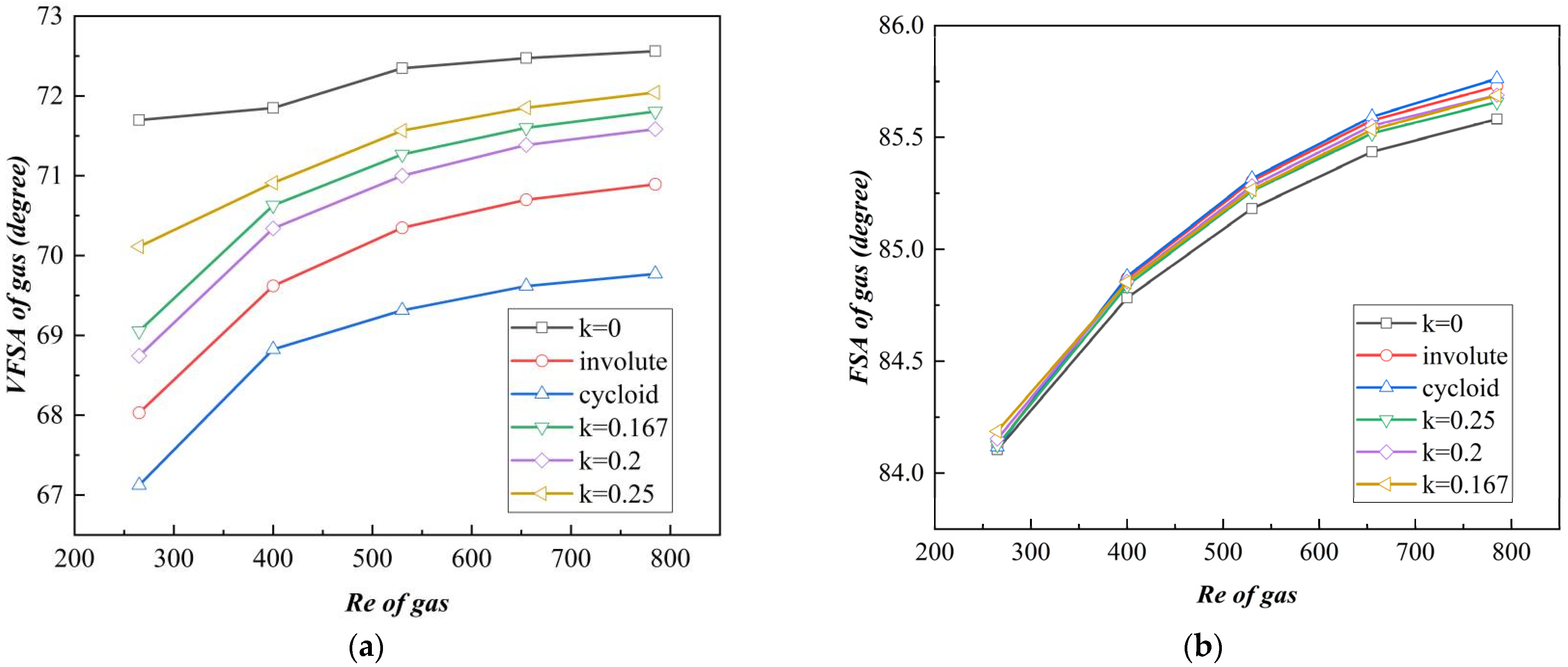
4.1. Comparison of Heat Transfer Performance
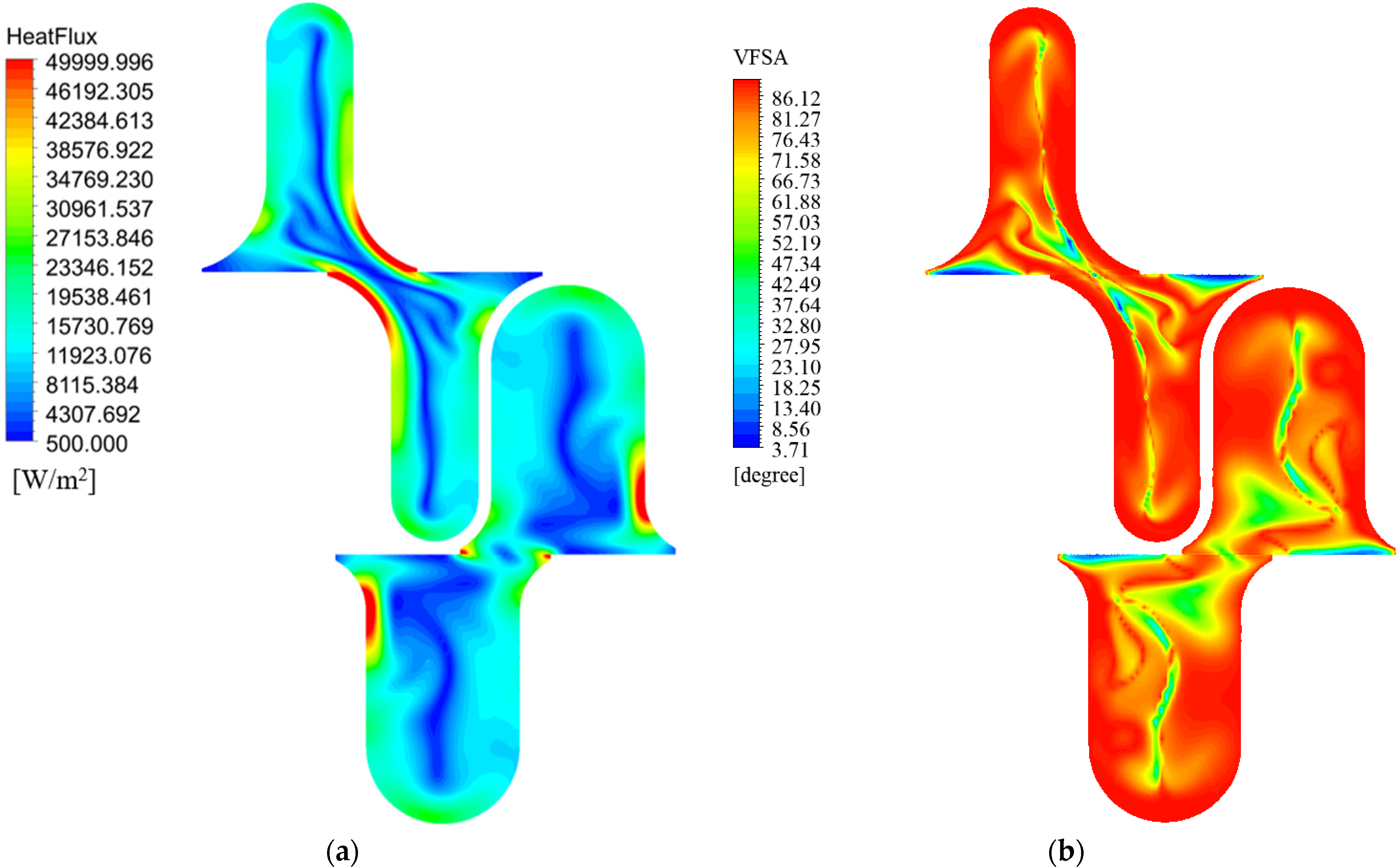
4.2. Analysis of the Effect of VSFA on Heat Transfer Performance
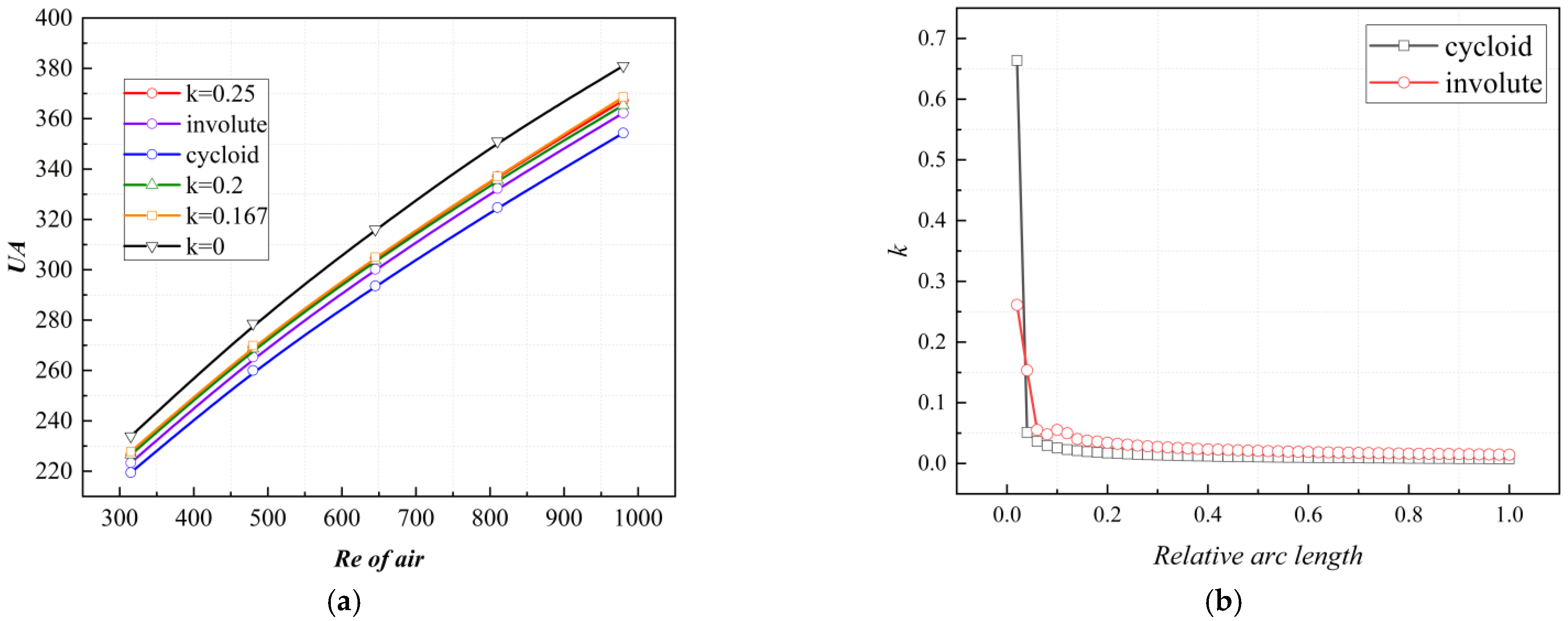
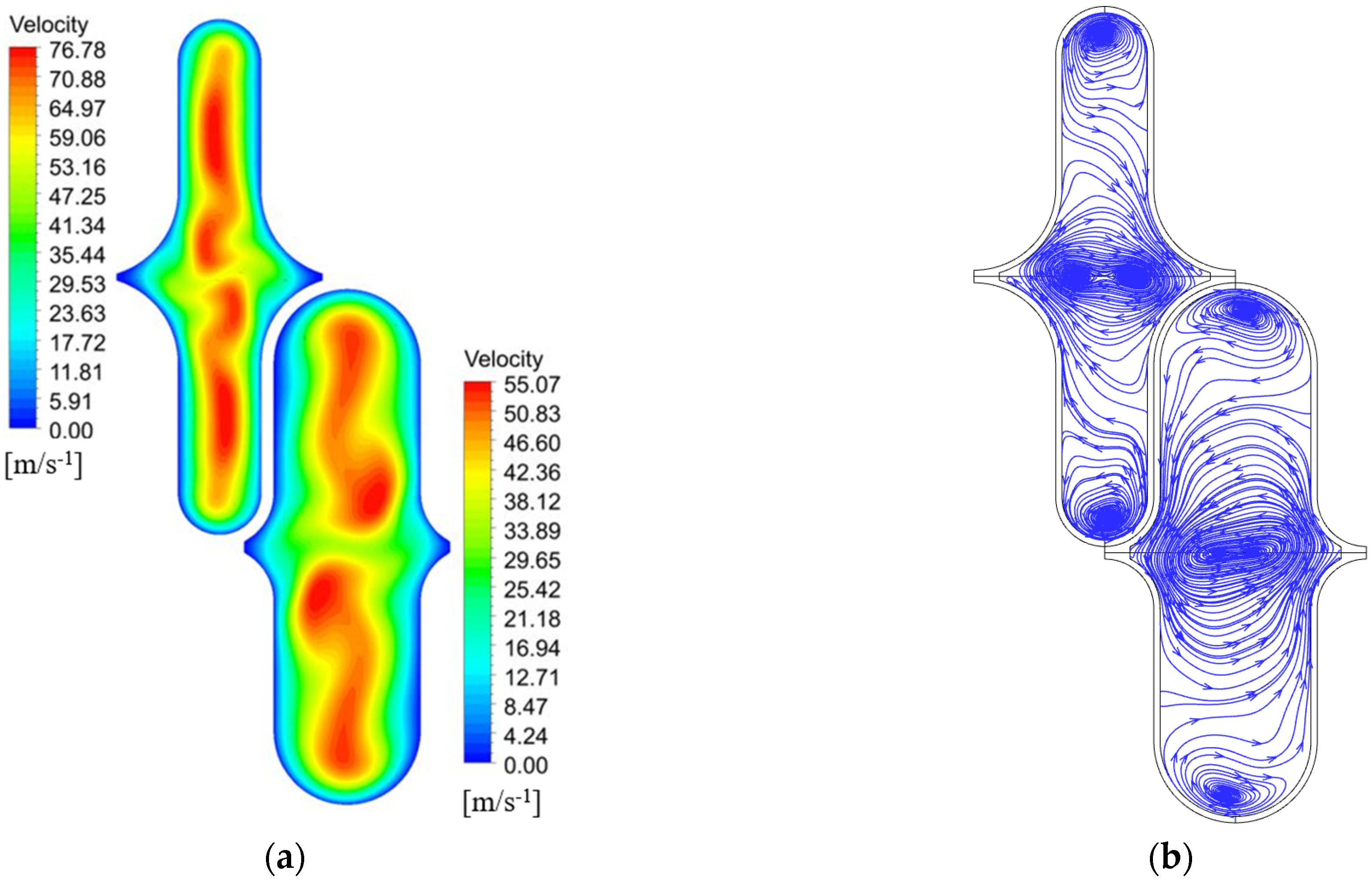
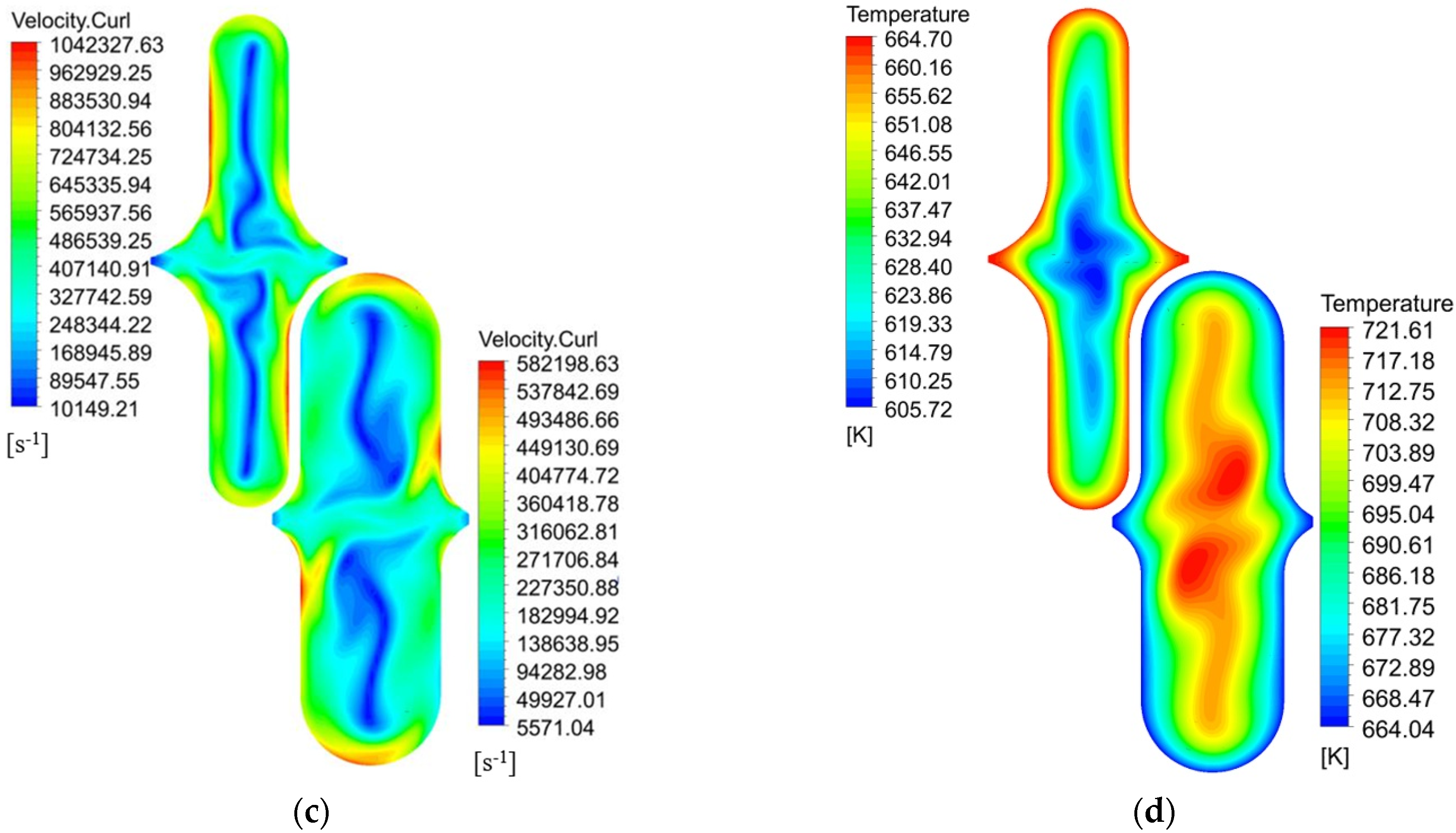
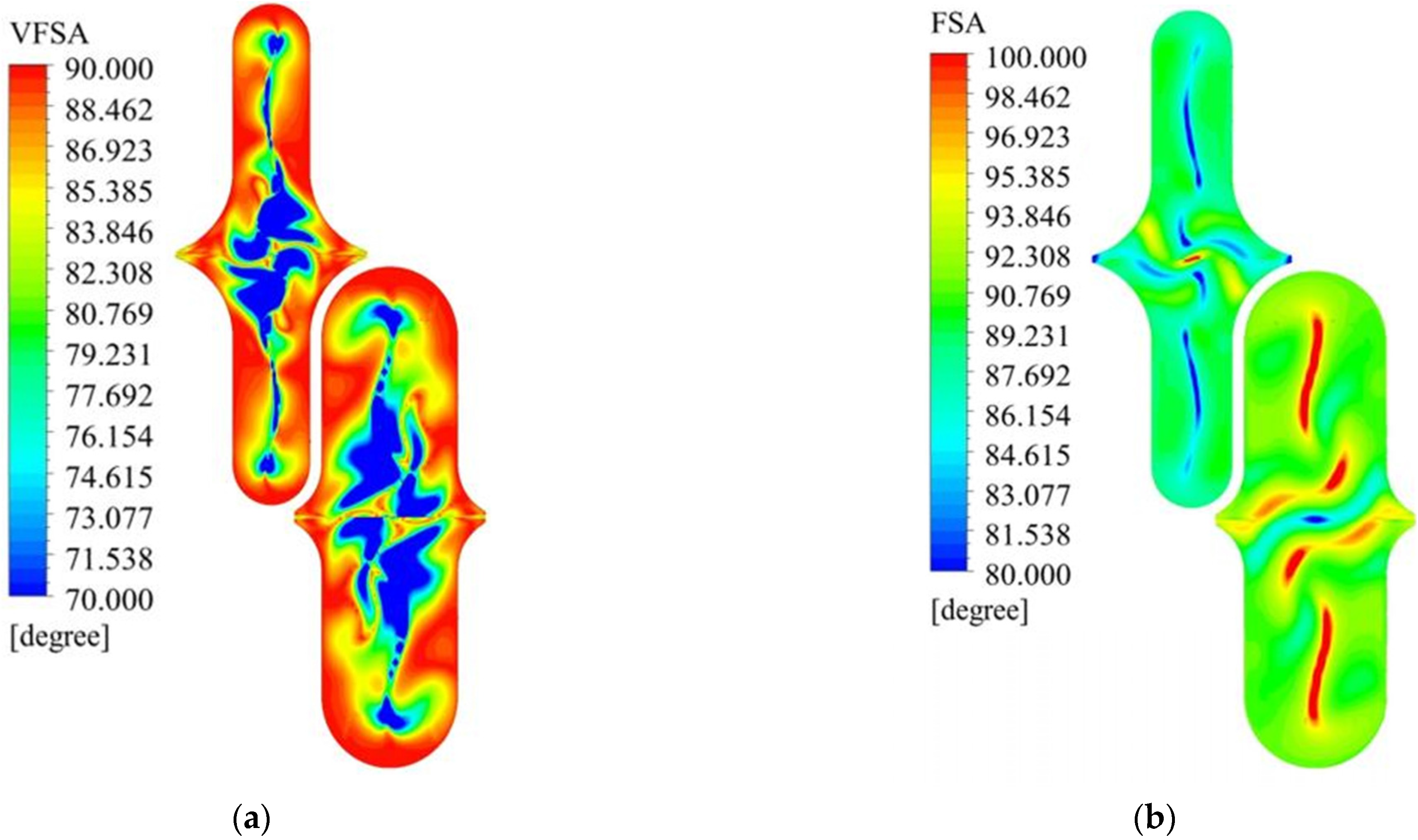
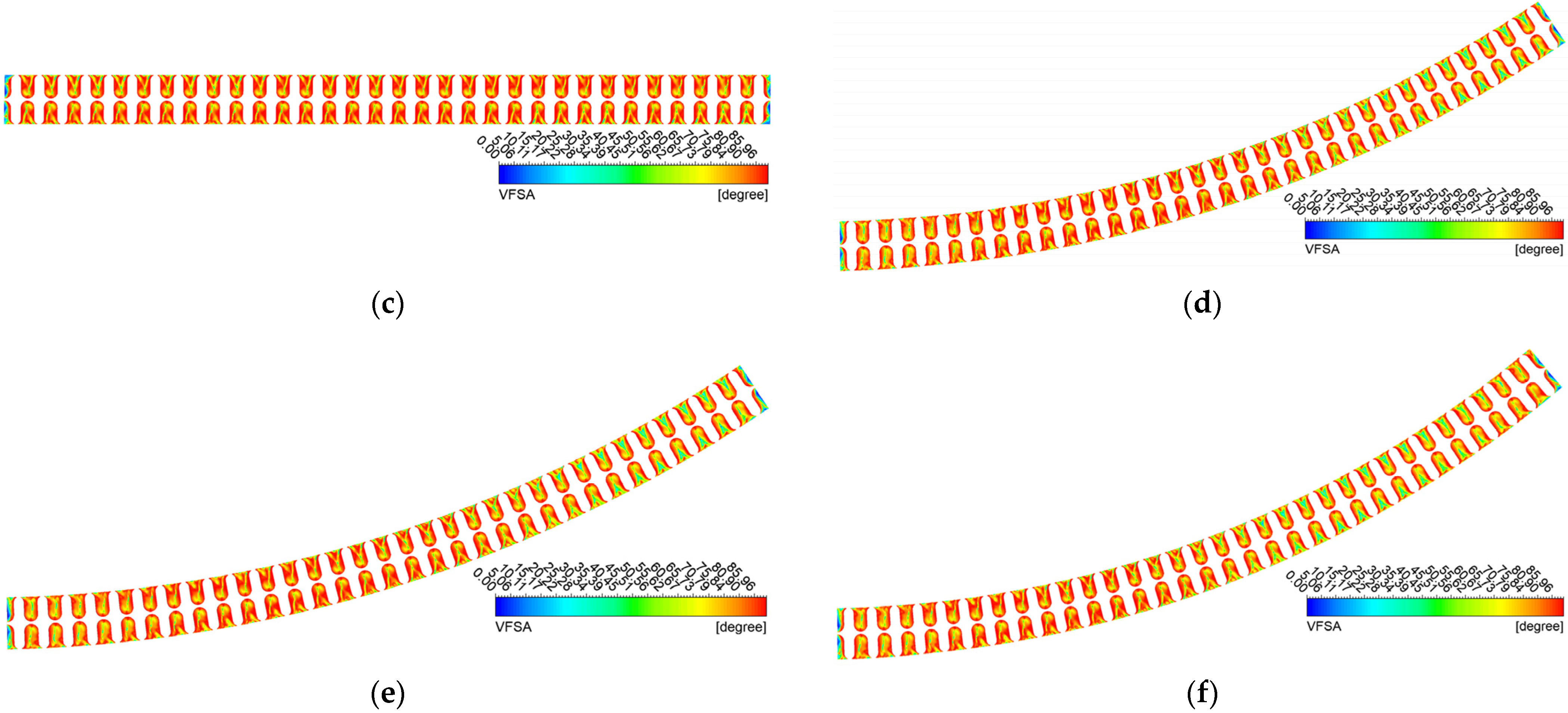
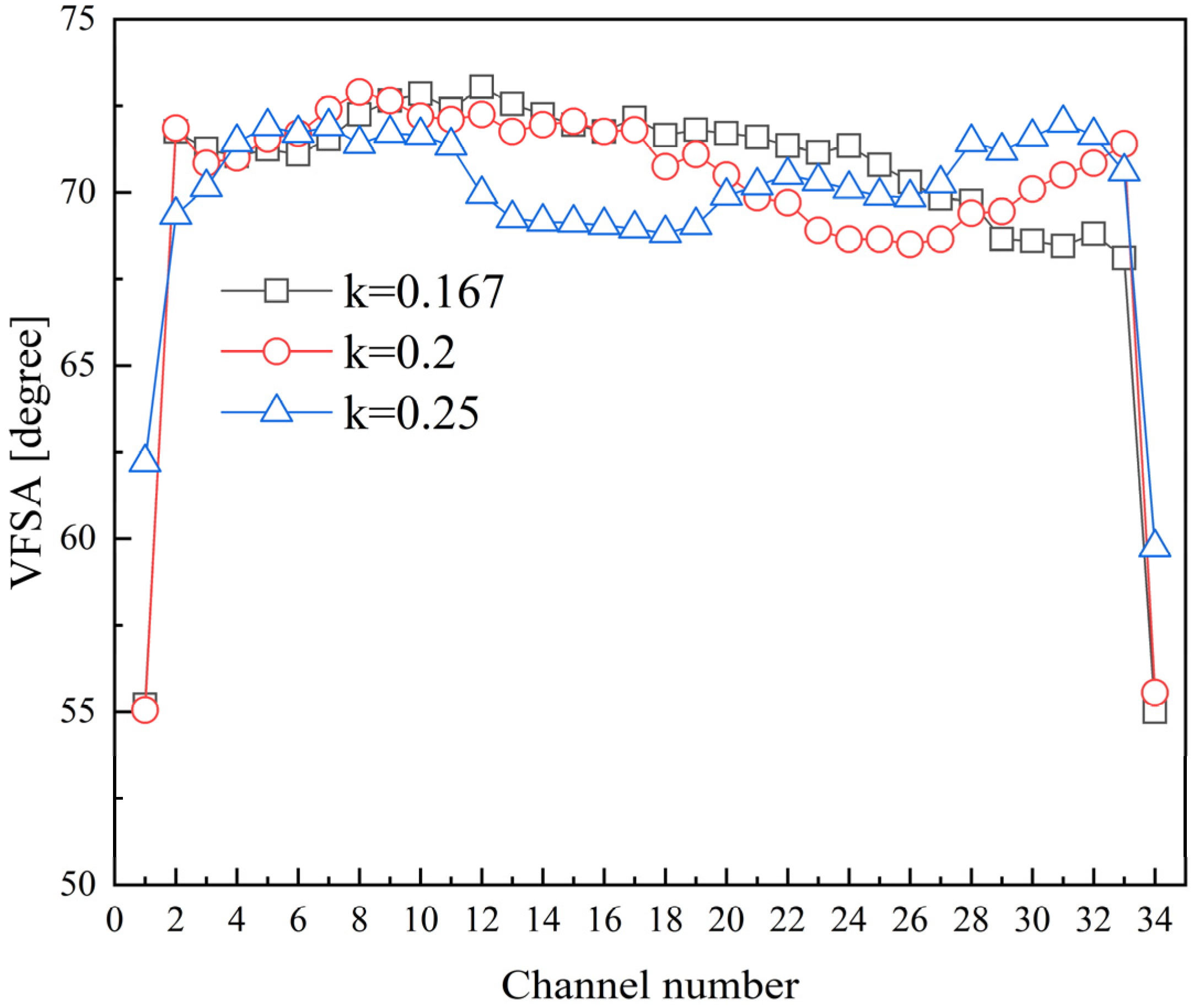
4.3. The Effect of Different Curvature on the Distribution of VFSA
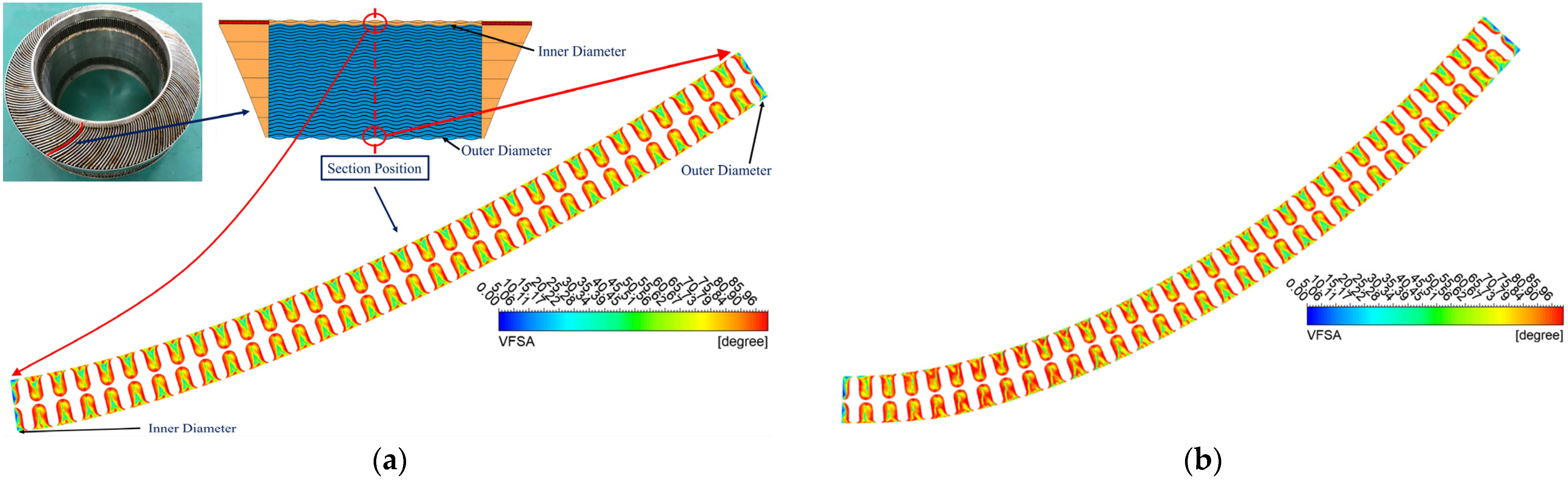
4.4. The Combined Influence of Unit Size and Structural Curvature on the Heat-Transfer and Flow Performance of CW-PSR
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| Nu | Nusselt number |
| f | Fanning friction coefficient |
| Dissipation function | |
| Fs | Convective term |
| ω | Vorticity |
| Re | Reynolds number |
| Pr | Prandtl number |
| k | Curvature |
| A | Amplitude of the longitudinal wave |
| L | Wavelength of the longitudinal wave |
| P | Channel pitch |
| R | Radius of CW channel section |
| W | Width of CW channel section |
| H | Height of CW channel section |
| de | Equivalent diameter |
| Su | Source term for velocity |
| ν | Kinematic viscosity |
| ρ | Density |
| qw | wall heat flux |
| λ | Thermal conductivity |
| Cp | Specific heat at constant pressure |
| u | Velocity |
| Ac | Cross-sectional area |
| S | Wetted perimeter |
| T | Temperature |
| q | Heat transfer quantity |
| μ | dynamic viscosity of fluid |
| μt | turbulent dynamic viscosity |
| c | Specific heat capacity |
| m | Mass flow rate |
| TLMTD | Logarithm mean temperature difference |
| dA | Microelement area |
| dV | Microelement volumn |
| Subscript | |
| c | Cold side |
| h | Hot side |
| s | Solid |
| a | Air |
| g | Gas |
| w | Wall |
| n | Normal direction of section |
| i | Number of CW channel section |
| b | Bulk |
| i | Indicator of tensor |
| Acronyms | |
| CW | Cross wavy |
| PSR | Primary surface recuperator |
| MGT | Micro gas turbine |
| TCW | Tracezoidal cross wavy |
| CC | Cross corrugated |
| CU | Cross undulated |
| FSA | Field synergy angle |
| VFSA | Vorticity field synergy angle |
References
- Dessornes, O.; Landais, S.; Valle, R.; Fourmaux, A.; Burguburu, S.; Zwyssig, C.; Kozanecki, Z. Advances in the Development of a Microturbine Engine. J. Eng. Gas Turbines Power 2014, 136, 071201. [Google Scholar] [CrossRef]
- Gang, X.; Yang, T.; Liu, H.; Dong, N.; Ni, M. Recuperators for micro gas turbines: A review. Appl. Energy 2017, 197, 83–99. [Google Scholar]
- Xu, Z.; Lu, Y.; Wang, B.; Zhao, L.; Xiao, Y. Experimental study on the off-design performances of a micro humid air turbine cycle: Thermodynamics, emissions and heat exchange. Energy 2021, 219, 119660. [Google Scholar] [CrossRef]
- Mcdonald, C.F. Low-cost compact primary surface recuperator concept for microturbines. Appl. Therm. Eng. 2000, 20, 471–497. [Google Scholar] [CrossRef]
- Utriainen, E.; Sunden, B. Numerical analysis of a primary surface trapezoidal cross wavy duct. Int. J. Numer. Methods Heat. Fluid. Flow. 2000, 10, 634–648. [Google Scholar] [CrossRef]
- Wang, Q.W.; Liang, H.X.; Luo, L.Q.; Wang, J.W.; Chen, Z.Q. Experimental Investigation on Heat Transfer and Pressure Drop in a Microtubine Recuperator with Cross-Wavy Primary Surface Channels. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, & Air, Reno, NV, USA, 6–9 June 2005. [Google Scholar]
- Du, L.X.; Zeng, M.; Wang, Q.W. A Simplified CFD Model with Multi-Periodic Boundary Conditions for Cross Wavy Channels. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference & Exposition, Vancouver, BC, Canada, 6–10 June 2011. [Google Scholar]
- Du, L.X.; Ma, T.; Zeng, M.; Guo, Z.X.; Wang, Q.W. Numerical Investigations on the Thermohydraulic Performance of Cross-Wavy Channels with Multi-Periodic Boundary Conditions. Numer. Heat Transf. Part A Appl. 2014, 65, 732–749. [Google Scholar] [CrossRef]
- Ma, T.; Du, L.X.; Sun, N.; Zeng, M.; Sunden, B.; Wang, Q.W. Experimental and numerical study on heat transfer and pressure drop performance of Cross-Wavy primary surface channel. Energy Convers. Manag. 2016, 125, 80–90. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, J.; Saranmanduh, B.; Chen, Y.-T.; Wang, Q.-W.; Zeng, M. Numerical study on small-scale longitudinal heat conduction in cross-wavy primary surface heat exchanger. Appl. Therm. Eng. Des. Process. Equip. Econ. 2015, 76, 272–282. [Google Scholar] [CrossRef]
- Xi, W.; Cai, J.; Huai, X. Numerical investigation on fluid-solid coupled heat transfer with variable properties in cross-wavy channels using half-wall thickness multi-periodic boundary conditions. Int. J. Heat Mass Transf. 2018, 122, 1040–1052. [Google Scholar] [CrossRef]
- Giugno, A. Analysis of uncertainties in compact plate-fin recuperators for microturbines. Appl. Therm. Eng. Des. Process. Equip. Econ. 2019, 150, 1243–1251. [Google Scholar] [CrossRef]
- Cai, J.; Huai, X.; Xi, W. An optimal design approach for the annular involute-profile cross wavy primary surface recuperator in microturbine and an application case study. Energy 2018, 153, 80–89. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Chen, F.; Yu, J.Y.; Song, Y.P.; Hu, H.D.; Xu, D.Q.; Jiang, H.D. Numerical study on heat transfer characteristics of heat exchange cell in an annular cross-wavy primary surface recuperator (annular CWPSR). Appl. Therm. Eng. 2022, 216, 119062. [Google Scholar] [CrossRef]
- Johnson, T.R.; Joubert, P.N. The Influence of Vortex Generators on the Drag and Heat Transfer from a Circular Cylinder Normal to an Airstream. J. Heat Transf. Trans. ASME 1969, 91, 91–99. [Google Scholar] [CrossRef]
- Fiebig, D. Vortices and Heat Transfer. Chem. Eng. Res. Des. 1998, 76, 108–123. [Google Scholar] [CrossRef]
- Tiggelbeck, S.; Mitra, N.; Fiebig, M. Flow structure and heat transfer in a channel with multiple longitudinal vortex generators. Exp. Therm. Fluid Sci. 1992, 5, 425–436. [Google Scholar] [CrossRef]
- Biswas, G.; Deb, P.; Biswas, S. Generation of Longitudinal Streamwise Vortices—A Device for Improving Heat Exchanger Design. J. Heat Transf. 1994, 116, 588–597. [Google Scholar] [CrossRef]
- Torii, K.; Nishino, K.; Nakayama, K. Mechanism of Heat Transfer Augmentation by Longitudinal Vortices in a Flat Plate Boundary Layer. In Proceedings of the International Heat Transfer Conference 10, Brighton, UK, 14–18 August 1994. [Google Scholar]
- Fiebig, M.; Valencia, A.; Mitra, N.K. Wing-type vortex generators for fin-and-tube heat exchangers. Exp. Therm. Fluid Sci. 1993, 7, 287–295. [Google Scholar] [CrossRef]
- Fiebig, M.; Valencia, A.; Mitra, N.K. Local heat transfer and flow losses in Fin-and -Tube heat exchangers with vortex generators: A comparison of round and flat tubes. Exp. Therm. Fluid Sci. 1994, 8, 35–45. [Google Scholar] [CrossRef]
- Biswas, G.; Mitra, N.K.; Fiebig, M. Heat transfer enhancement in fin-tube heat exchangers by winglet type vortex generators. Int. J. Heat Mass Transf. 1994, 37, 283–291. [Google Scholar] [CrossRef]
- Zeng, M.; Tang, L.H.; Lin, M.; Wang, Q.W. Optimization of heat exchangers with vortex-generator fin by Taguchi method. Appl. Therm. Eng. 2010, 30, 1775–1783. [Google Scholar] [CrossRef]
- Lu, J.; Zhuang, D.; Wang, Y.; Ding, G. Effects of vortex generator on subcooled flow boiling characteristics in micro-channel. Int. J. Heat Mass Transf. 2023, 216, 124572. [Google Scholar] [CrossRef]
- Bagre, N.; Parekh, A.D.; Patel, V.K. “Exergy analysis and Experimental investigation of various vortex tube material with different combination of vortex generators”: Analyse exergétique et étude expérimentale de divers matériaux de tubes vortex avec combinaison différente de générateurs de vortex. Int. J. Refrig. 2023, 150, 113–124. [Google Scholar]
- Shi, X.; Chen, W.; Li, Z.; Chai, X.; Chyu, M.K. Investigation of the heat transfer enhancement and deterioration induced by vortex generators in low Prandtl number sodium-potassium alloy liquid. Int. J. Therm. Sci. 2023, 193, 108456. [Google Scholar] [CrossRef]
- Feng, Z.; Jiang, P.; Zheng, S.; Zhang, Q.; Chen, Z.; Guo, F.; Zhang, J. Experimental and numerical investigations on the effects of insertion-type longitudinal vortex generators on flow and heat transfer characteristics in square minichannels. Energy 2023, 278, 127855. [Google Scholar] [CrossRef]
- Gu, H.; Chen, Y.; Wu, J.; Sunden, B. Performance investigation on twisted elliptical tube heat exchangers with coupling-vortex square tube layout. Int. J. Heat Mass Transf. 2020, 151, 119473. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Tan, Y.; Sun, Z.; Tian, G.; Wang, L. Convective thermal-hydraulic performance in twisted tubes: From the perspective of symmetrical cross-sectional shapes. Int. Commun. Heat Mass Transf. 2023, 147, 106974. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, F.; Yu, J.; Song, Y.; Guo, Z. Design and experiment study of a micro radial-flow turbine for a SOFC-MGT turbine hybrid system. Energy Convers. Manag. 2022, 266, 115861. [Google Scholar] [CrossRef]
- Zhang, L.; Che, D. Turbulence Models for Fluid Flow and Heat Transfer Between Cross-Corrugated Plates. Numer. Heat Transf. Part A Appl. 2011, 60, 410–440. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Li, D.Y.; Wang, B.X. A novel concept for convective heat transfer enhancement. Int. J. Heat Mass Transf. 1998, 41, 2221–2225. [Google Scholar] [CrossRef]
- Xu, Z.P.; Zhang, L.; Liu, C.Y.; Wang, Z.L. Experimental Investigation on Performance for Annular Primary Surface Recuperator of Micro Gas-turbine. J. Power Eng. 2009, 29, 540–543+548. [Google Scholar]
- Jiang, H.; Chen, F.; Yu, J.; Song, Y. Theoretical and numerical study on new evaluation criteria for longitudinal vortex enhanced heat transfer. Int. J. Heat Mass Transf. 2024, 220, 124977. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J. Dendrite net: A white-box module for classification, regression, and system identification. IEEE Trans. Cybern. 2021, 52, 13774–13787. [Google Scholar] [CrossRef] [PubMed]

| Geometric Characteristics | Sizes |
|---|---|
| Lc/Ac | 2.1 |
| Wh/Wc | 1.8 |
| 2H | 2200 μm |
| 2H/P | 2.5 |
| de of air channel | 600 μm |
| de of gas channel | 800 μm |
| Property | Gas | Air |
|---|---|---|
| Density (kg·m−3) | ρg = 1.425 − 1.97 × 10−3T + 9.21 × 10−7T2 | ρa = 1.193 + 10.321exp(−T/335.28) |
| Heat capacity (J kg−1 K−1) | cpg = 1005.3 + 0.03423T + 4.617 × 10−4T2 − 3.205 × 10−7T3 + 6.45 × 10−11T4 | cpa = 921.22 + 0.2359T − 1.922 × 10−5T2 − 2.2396 × 10−22T3 |
| Thermal conductivity (W m−1 K−1) | λg = −1.337 × 10−3 + 9.217 × 10−5T − 1.432 × 10−8T2 + 1.221 × 10−8 T3 − 3.39 × 10−15T4 | λa = 7.028 × 10−3 + 7.862 × 10−5T − 4.15 × 10−8T2 + 1.926 × 10−11T3 + 3.61 × 10−14T4 |
| Kinematic viscosity (m2 s−1) | νg = −5.226 × 10−6 + 3.47 × 10−8T + 1.043 × 10−10T2 − 1.651 × 10−14T3 − 7.89 × 10−30T4 | νa = −2.184 × 10−6 + 1.468 × 10−8T + 1.861 × 10−11T2 + 8.372 × 10−29T3 − 1.31 × 10−32T4 |
| Prandtl number | Prg = 0.766 − 2.186 × 10−4T + 5.59 × 10−8T2 | Pra = 0.729 − 8.902 × 10−5T + 1.17 × 10−7T2 |
| Number | Rc | Rh | H | L | A | k |
|---|---|---|---|---|---|---|
| 1 | 0.1740 | 0.2689 | 1.0913 | 5.3057 | 0.9694 | 0.1398 |
| 2 | 0.1496 | 0.2874 | 1.1661 | 5.1296 | 0.8390 | 0.1772 |
| 3 | 0.2101 | 0.3024 | 1.0503 | 6.0982 | 0.9049 | 0.2656 |
| 4 | 0.2065 | 0.2548 | 0.9978 | 5.0627 | 0.7280 | 0.2617 |
| 5 | 0.1629 | 0.2885 | 1.0454 | 5.5423 | 0.4829 | 0.1140 |
| 6 | 0.1235 | 0.3119 | 1.0939 | 5.7928 | 0.8802 | 0.1832 |
| 7 | 0.1916 | 0.2629 | 1.2541 | 6.2197 | 0.5614 | 0.2127 |
| 8 | 0.2028 | 0.3304 | 1.2530 | 4.9873 | 0.3518 | 0.1851 |
| 9 | 0.2155 | 0.3451 | 1.1733 | 5.7338 | 0.4800 | 0.2342 |
| 10 | 0.1263 | 0.3338 | 1.0705 | 6.3799 | 0.7492 | 0.2257 |
| 11 | 0.1705 | 0.2919 | 1.2314 | 4.6297 | 0.6758 | 0.1568 |
| 12 | 0.1803 | 0.2769 | 1.2370 | 5.6307 | 0.7956 | 0.2031 |
| 13 | 0.1939 | 0.3212 | 1.2108 | 5.1695 | 0.9935 | 0.1040 |
| 14 | 0.1967 | 0.2706 | 1.0527 | 4.9417 | 0.9381 | 0.2929 |
| 15 | 0.1885 | 0.3441 | 1.0559 | 4.8906 | 0.6050 | 0.1276 |
| 16 | 0.1977 | 0.3088 | 1.2676 | 5.9453 | 0.9450 | 0.1194 |
| 17 | 0.1557 | 0.3059 | 1.1510 | 6.4838 | 0.2491 | 0.1721 |
| 18 | 0.1791 | 0.2602 | 1.2292 | 4.7115 | 0.2332 | 0.1489 |
| 19 | 0.1332 | 0.2596 | 0.9121 | 6.0383 | 0.4034 | 0.2081 |
| 20 | 0.1276 | 0.2732 | 1.0872 | 4.8130 | 0.6889 | 0.1671 |
| 21 | 0.2186 | 0.3361 | 1.1536 | 6.4154 | 0.5808 | 0.2837 |
| 22 | 0.1511 | 0.3414 | 1.2429 | 6.1088 | 0.8621 | 0.2735 |
| 23 | 0.1842 | 0.3128 | 1.0665 | 5.2086 | 0.6329 | 0.1069 |
| 24 | 0.2148 | 0.3165 | 1.1678 | 5.8353 | 0.5091 | 0.2587 |
| 25 | 0.1420 | 0.2671 | 1.0436 | 5.4345 | 0.6531 | 0.1509 |
| 26 | 0.1448 | 0.3034 | 1.1886 | 6.1738 | 0.7675 | 0.1951 |
| 27 | 0.1538 | 0.3259 | 1.1935 | 5.0337 | 0.2041 | 0.2213 |
| 28 | 0.2100 | 0.2842 | 1.0710 | 4.5584 | 0.8051 | 0.2783 |
| 29 | 0.1602 | 0.3480 | 1.1301 | 5.6595 | 0.2775 | 0.1921 |
| 30 | 0.1459 | 0.2550 | 0.9472 | 6.2722 | 0.5436 | 0.2895 |
| 31 | 0.1400 | 0.2800 | 1.1289 | 4.7869 | 0.3795 | 0.1605 |
| 32 | 0.1674 | 0.2947 | 1.1387 | 5.2660 | 0.4517 | 0.2506 |
| 33 | 0.1595 | 0.2519 | 0.9743 | 5.8883 | 0.7054 | 0.2359 |
| 34 | 0.1364 | 0.3199 | 1.0093 | 4.5272 | 0.2844 | 0.2187 |
| 35 | 0.1697 | 0.2985 | 1.1194 | 6.3308 | 0.3927 | 0.2470 |
| 36 | 0.1325 | 0.2972 | 1.2005 | 5.9731 | 0.3251 | 0.2449 |
| 37 | 0.1857 | 0.3290 | 1.1828 | 5.5504 | 0.3022 | 0.1429 |
| 38 | 0.1216 | 0.3378 | 0.9625 | 4.6622 | 0.4351 | 0.1234 |
| 39 | 0.1755 | 0.3236 | 1.0078 | 5.3510 | 0.8574 | 0.2992 |
| 40 | 0.2014 | 0.2791 | 1.2202 | 5.4883 | 0.5355 | 0.1341 |
| Number | Nu of Air | Nu of Gas | f of Air | f of Gas |
|---|---|---|---|---|
| 1 | 7.8666 | 4.9554 | 0.0371 | 0.0740 |
| 2 | 7.7735 | 5.2067 | 0.0438 | 0.0601 |
| 3 | 8.8237 | 4.1292 | 0.0275 | 0.0652 |
| 4 | 9.1341 | 3.6950 | 0.0326 | 0.1015 |
| 5 | 9.0206 | 4.1118 | 0.0417 | 0.0723 |
| 6 | 9.5101 | 4.2936 | 0.0622 | 0.0576 |
| 7 | 6.6143 | 5.8025 | 0.0250 | 0.0598 |
| 8 | 7.0984 | 5.2092 | 0.0235 | 0.0459 |
| 9 | 7.7808 | 4.7352 | 0.0222 | 0.0445 |
| 10 | 10.3101 | 3.9002 | 0.0593 | 0.0527 |
| 11 | 7.4989 | 4.7287 | 0.0336 | 0.0601 |
| 12 | 6.9753 | 5.4991 | 0.0282 | 0.0583 |
| 13 | 7.4558 | 5.1285 | 0.0260 | 0.0494 |
| 14 | 8.9443 | 3.8384 | 0.0326 | 0.0854 |
| 15 | 8.9579 | 3.6240 | 0.0329 | 0.0586 |
| 16 | 6.9506 | 5.6791 | 0.0230 | 0.0461 |
| 17 | 8.4820 | 4.9234 | 0.0384 | 0.0529 |
| 18 | 7.1822 | 5.1322 | 0.0314 | 0.0727 |
| 19 | 9.2273 | 3.6737 | 0.0741 | 0.1100 |
| 20 | 8.4454 | 4.4457 | 0.0659 | 0.0790 |
| 21 | 7.9509 | 4.5539 | 0.0220 | 0.0467 |
| 22 | 8.4304 | 5.2276 | 0.0358 | 0.0447 |
| 23 | 8.8171 | 3.9914 | 0.0333 | 0.0636 |
| 24 | 7.7309 | 5.0096 | 0.0227 | 0.0509 |
| 25 | 8.3055 | 4.1877 | 0.0548 | 0.0838 |
| 26 | 8.0453 | 5.5949 | 0.0431 | 0.0474 |
| 27 | 8.1344 | 4.6124 | 0.0383 | 0.0503 |
| 28 | 8.6397 | 3.7039 | 0.0301 | 0.0807 |
| 29 | 8.9397 | 4.3426 | 0.0362 | 0.0465 |
| 30 | 8.8148 | 3.7720 | 0.0694 | 0.1042 |
| 31 | 8.1838 | 4.4985 | 0.0520 | 0.0717 |
| 32 | 7.9669 | 4.6473 | 0.0358 | 0.0616 |
| 33 | 8.5096 | 3.7201 | 0.0495 | 0.1022 |
| 34 | 10.1269 | 3.4423 | 0.0632 | 0.0755 |
| 35 | 8.2886 | 4.7509 | 0.0345 | 0.0583 |
| 36 | 8.0738 | 5.3839 | 0.0496 | 0.0523 |
| 37 | 7.8601 | 4.8540 | 0.0277 | 0.0478 |
| 38 | 10.5213 | 3.0521 | 0.0780 | 0.0739 |
| 39 | 9.5136 | 3.4040 | 0.0381 | 0.0666 |
| 40 | 7.0582 | 5.2982 | 0.0242 | 0.0597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Chen, F.; Huang, C.; Yu, J.; Song, Y.; Zhang, J. Numerical Study of the Influence of Different Bending Shapes on the Heat Transfer Characteristics of Annular Cross Wavy Primary Surface Recuperator (CW-PSR). Energies 2023, 16, 7977. https://doi.org/10.3390/en16247977
Jiang H, Chen F, Huang C, Yu J, Song Y, Zhang J. Numerical Study of the Influence of Different Bending Shapes on the Heat Transfer Characteristics of Annular Cross Wavy Primary Surface Recuperator (CW-PSR). Energies. 2023; 16(24):7977. https://doi.org/10.3390/en16247977
Chicago/Turabian StyleJiang, Huadong, Fu Chen, Chonghai Huang, Jianyang Yu, Yanping Song, and Juanshu Zhang. 2023. "Numerical Study of the Influence of Different Bending Shapes on the Heat Transfer Characteristics of Annular Cross Wavy Primary Surface Recuperator (CW-PSR)" Energies 16, no. 24: 7977. https://doi.org/10.3390/en16247977
APA StyleJiang, H., Chen, F., Huang, C., Yu, J., Song, Y., & Zhang, J. (2023). Numerical Study of the Influence of Different Bending Shapes on the Heat Transfer Characteristics of Annular Cross Wavy Primary Surface Recuperator (CW-PSR). Energies, 16(24), 7977. https://doi.org/10.3390/en16247977






