Acoustic Design Parameter Change of a Pressurized Combustor Leading to Limit Cycle Oscillations
Abstract
1. Introduction
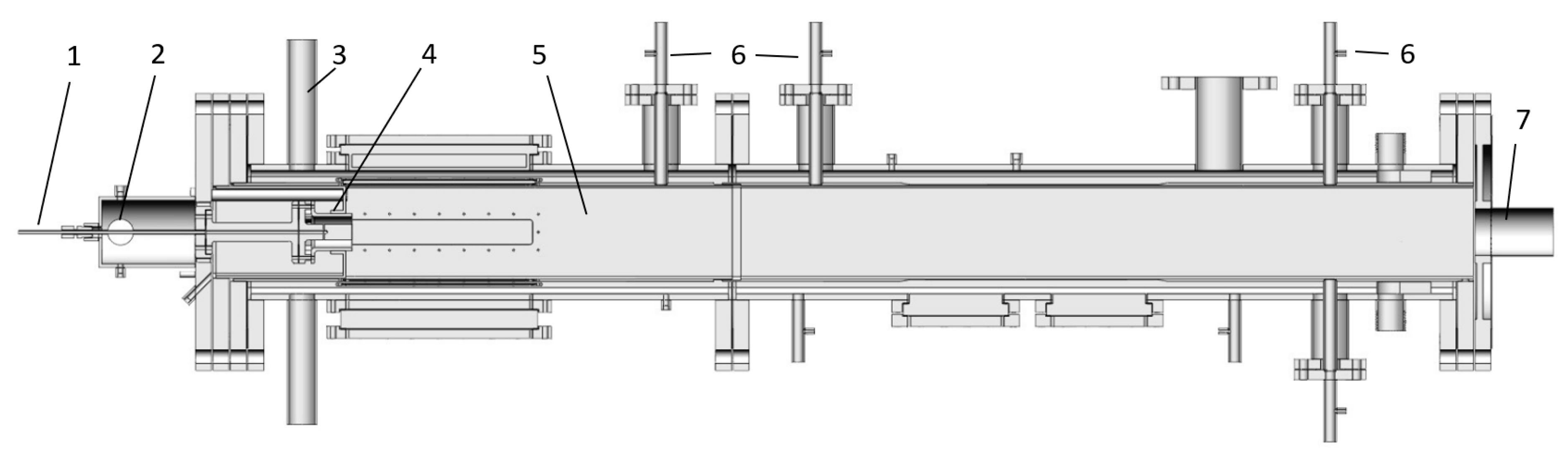
2. Experimental Setup
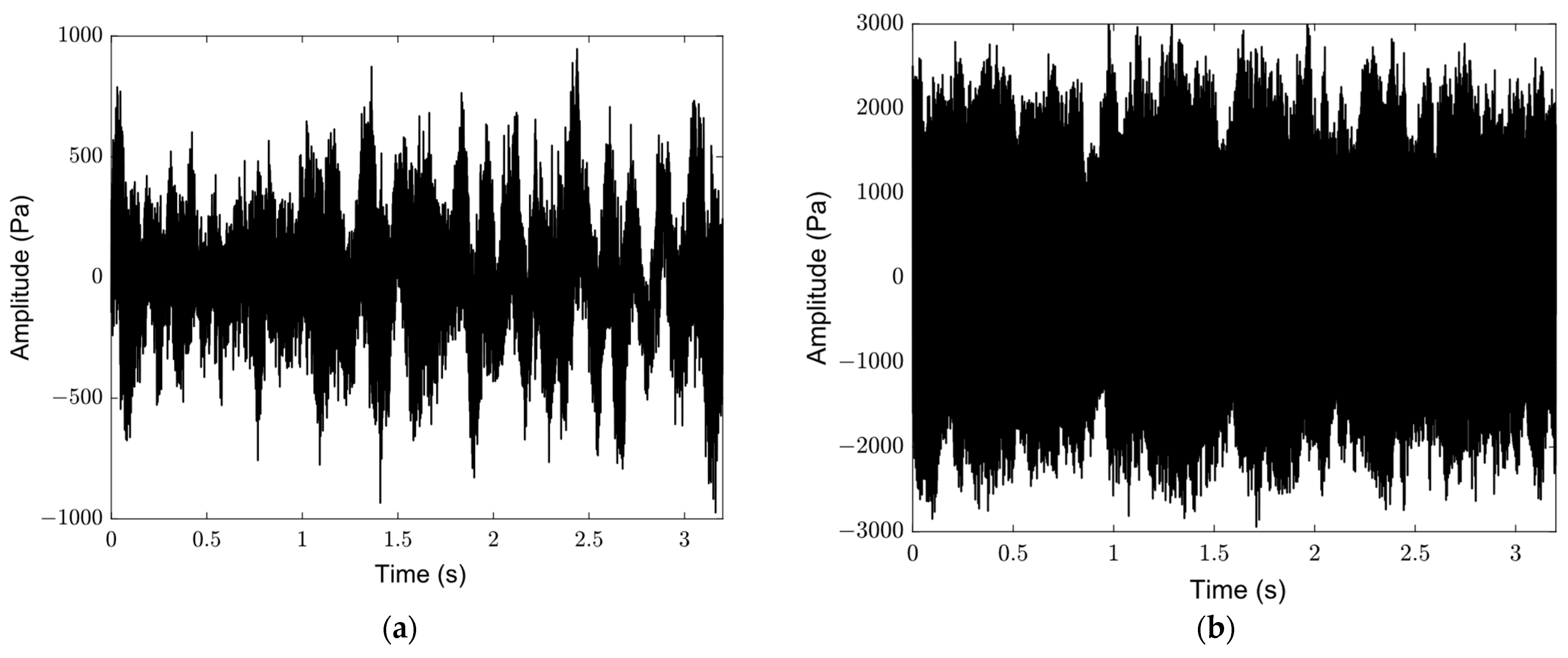
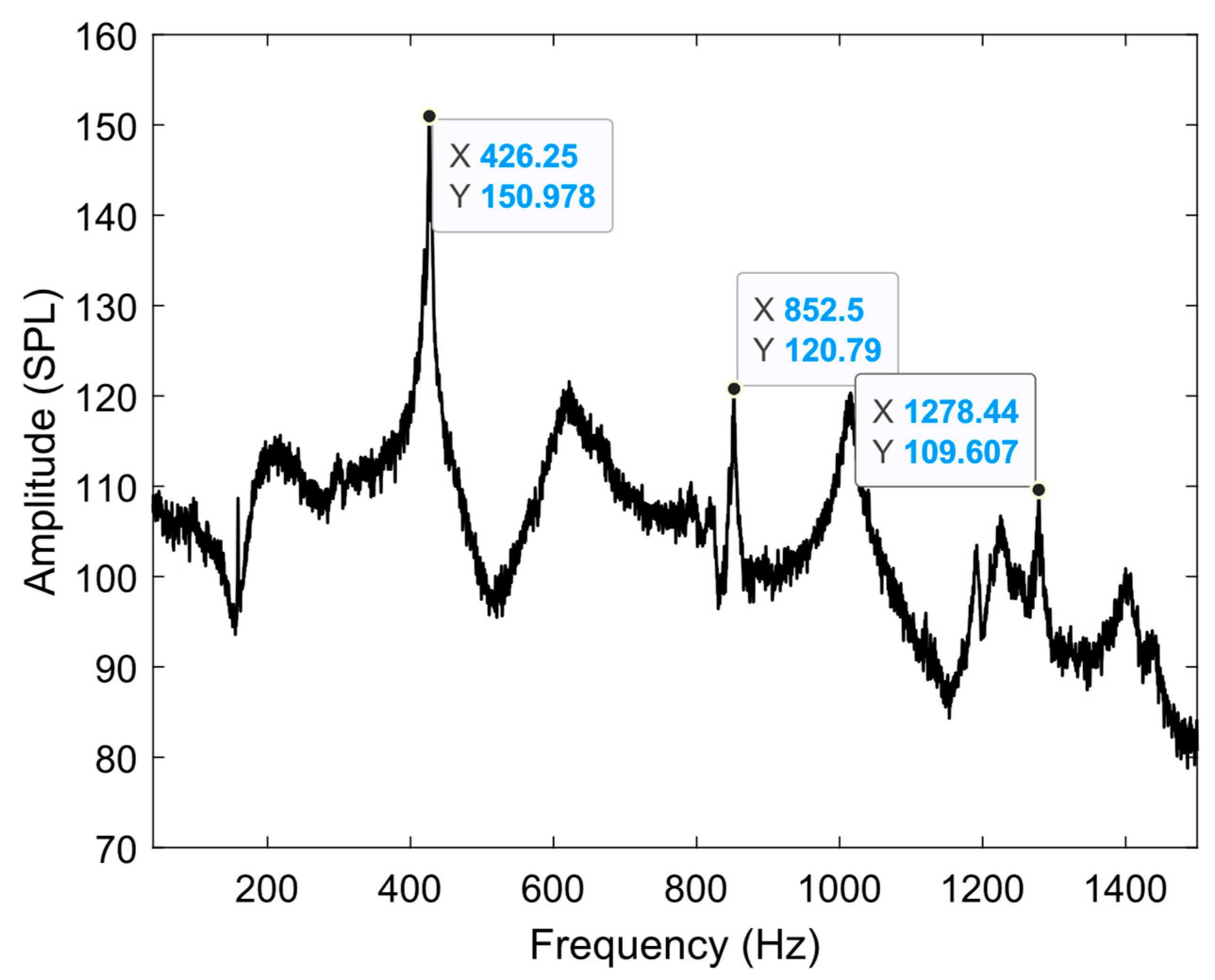
Initial Experimental Observations
3. Acoustic Design Parameter Change of the Combustion Chamber
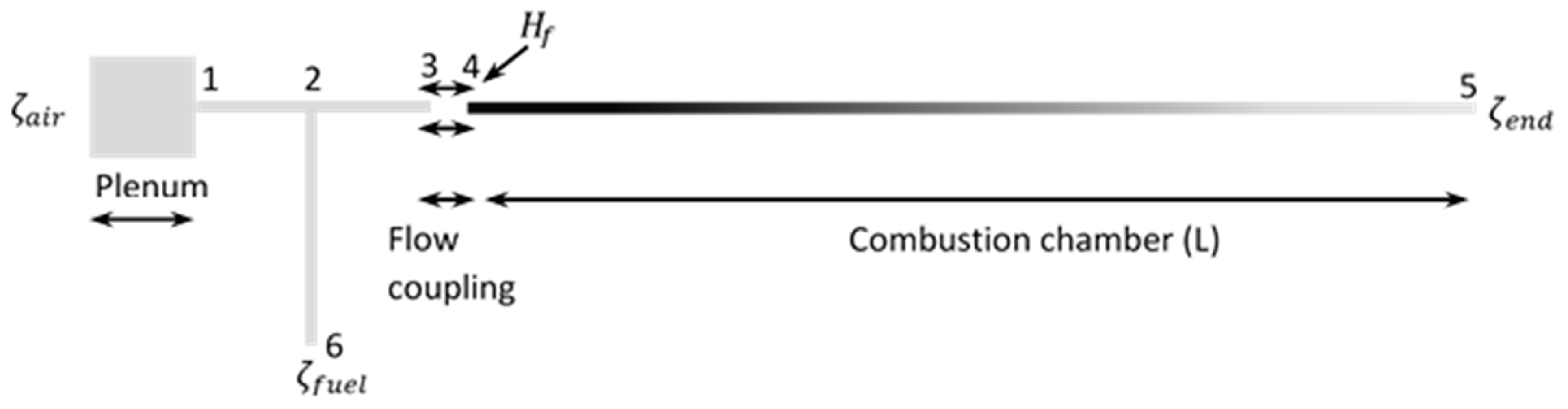
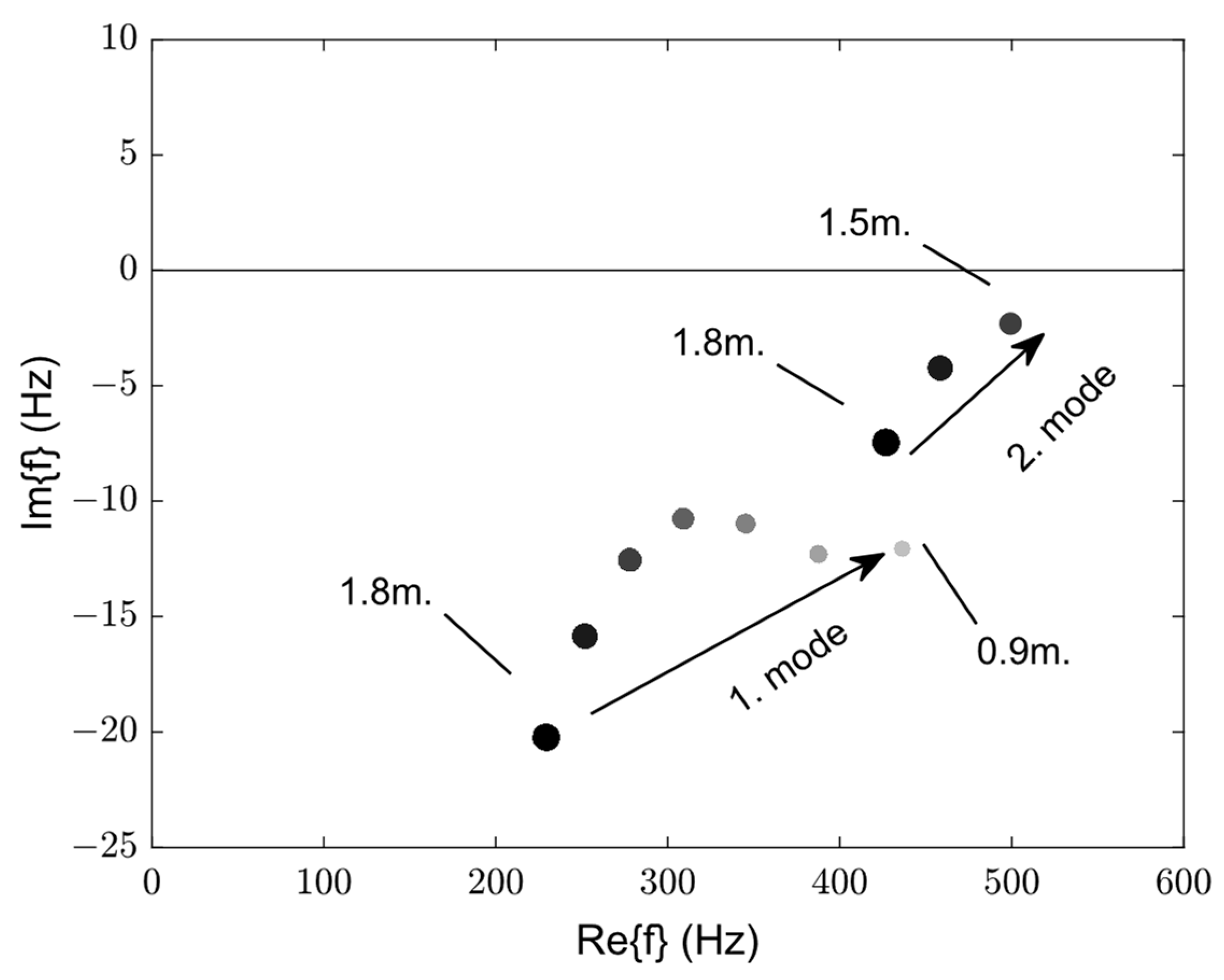
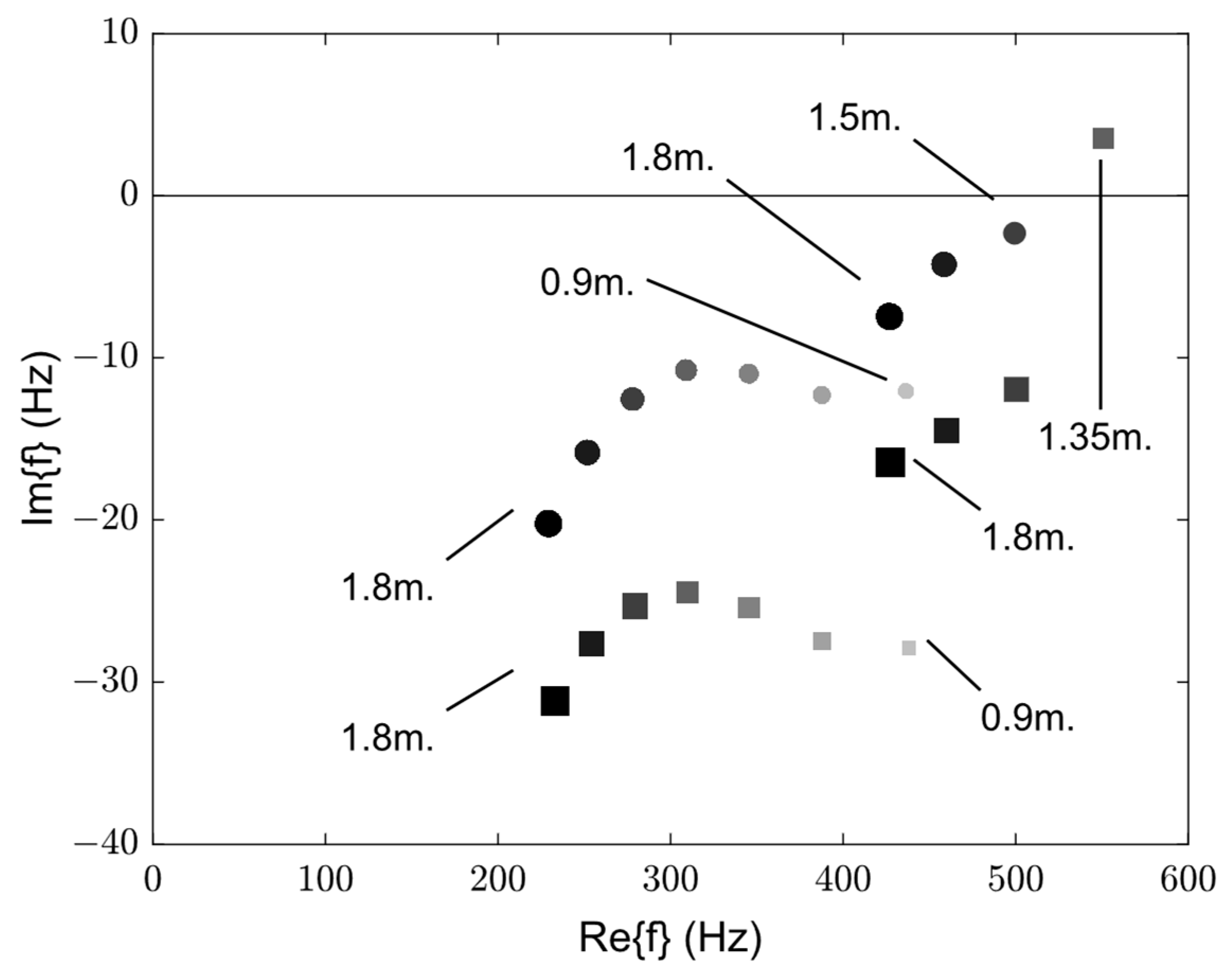
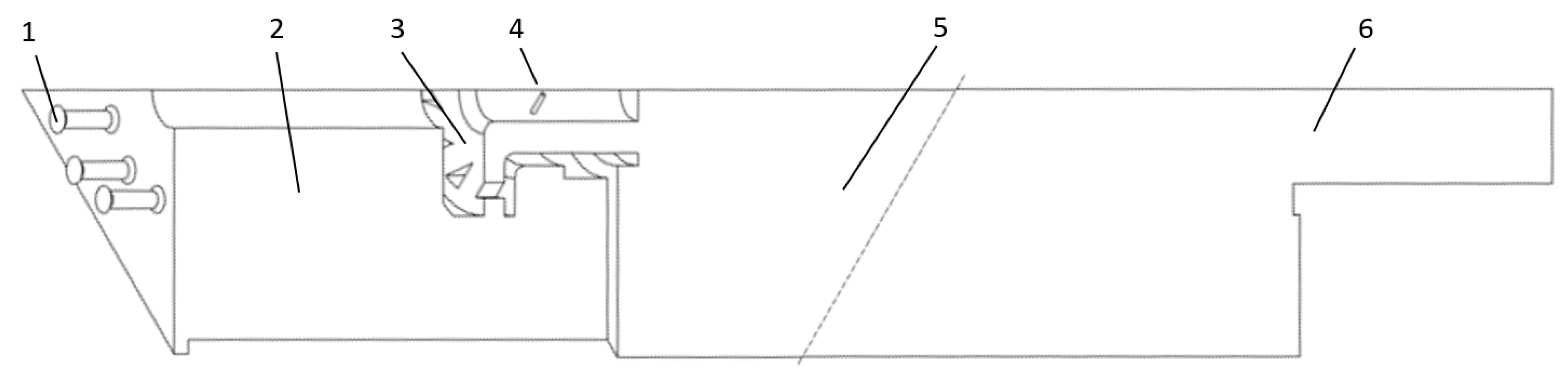
3.1. Changing the Length of the Combustion Chamber
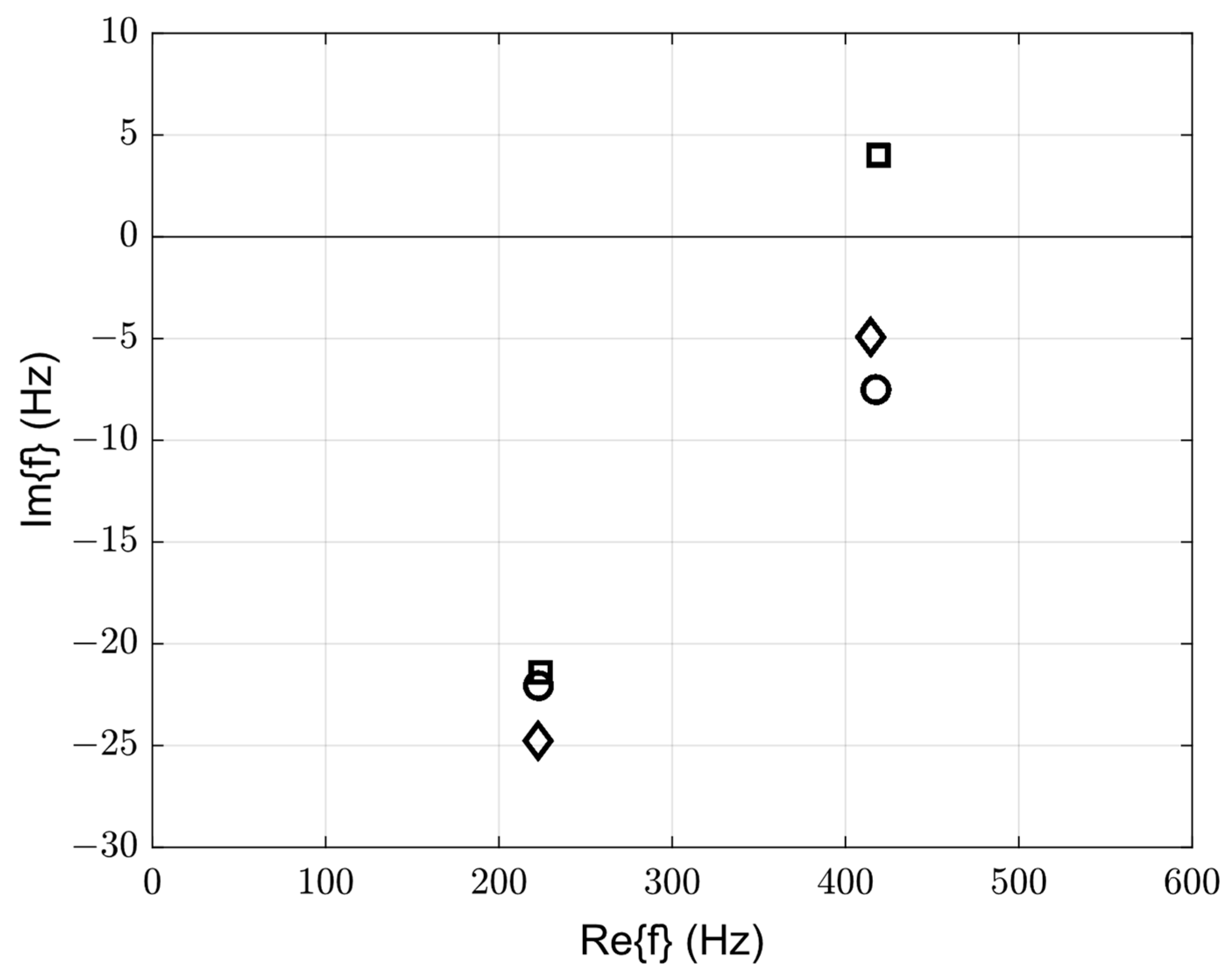
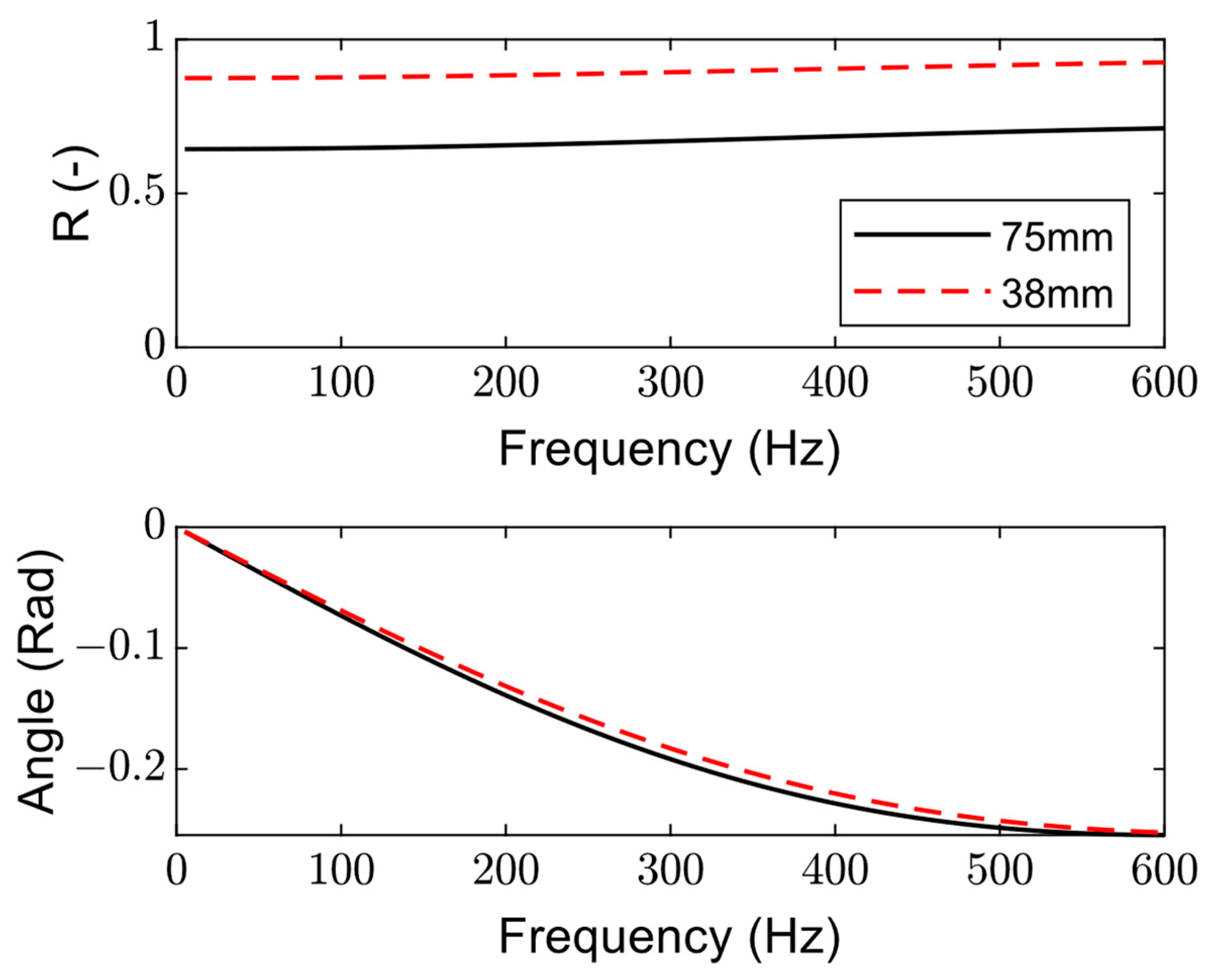
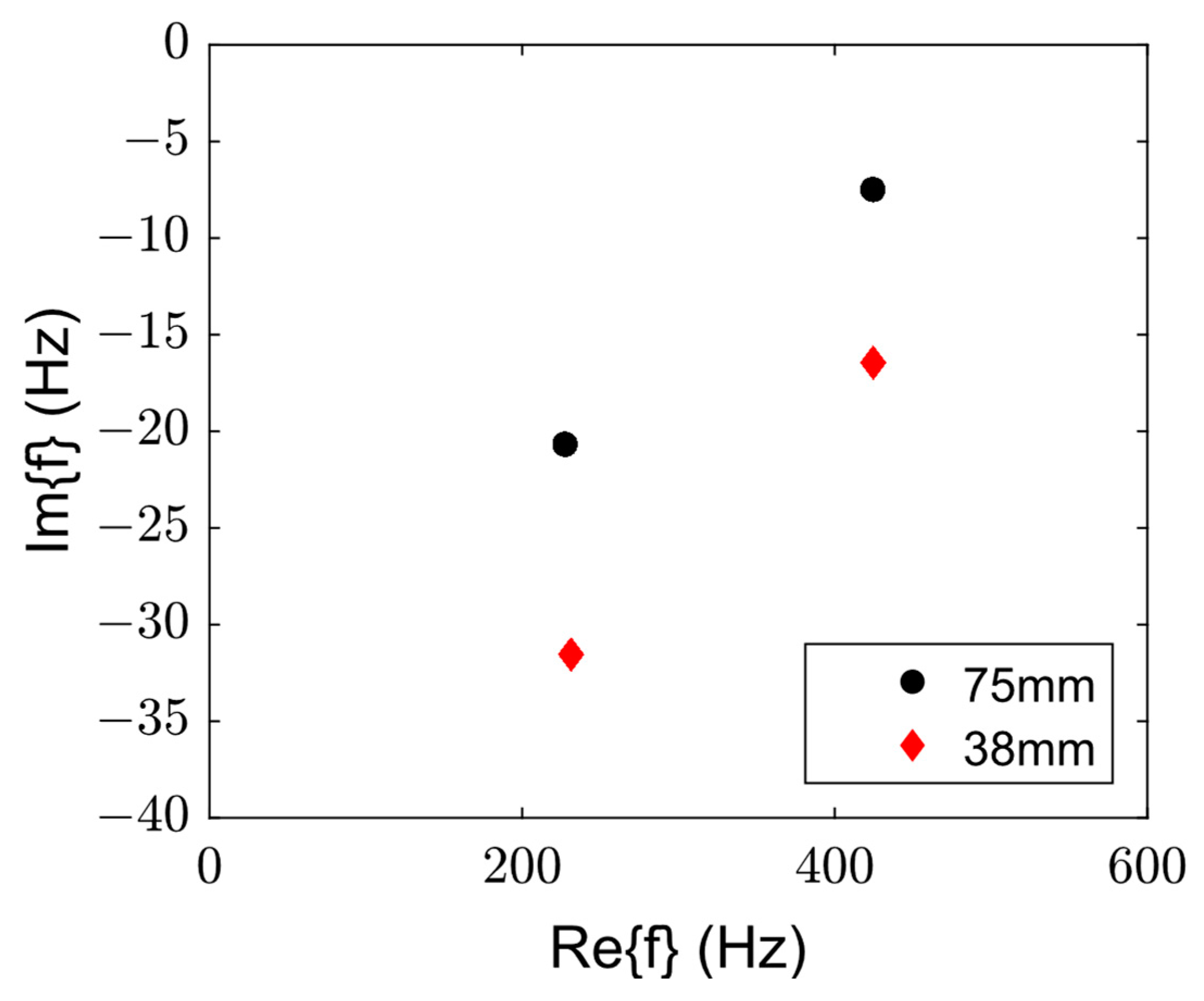
3.2. Changing the Acoustic Boundary Condition
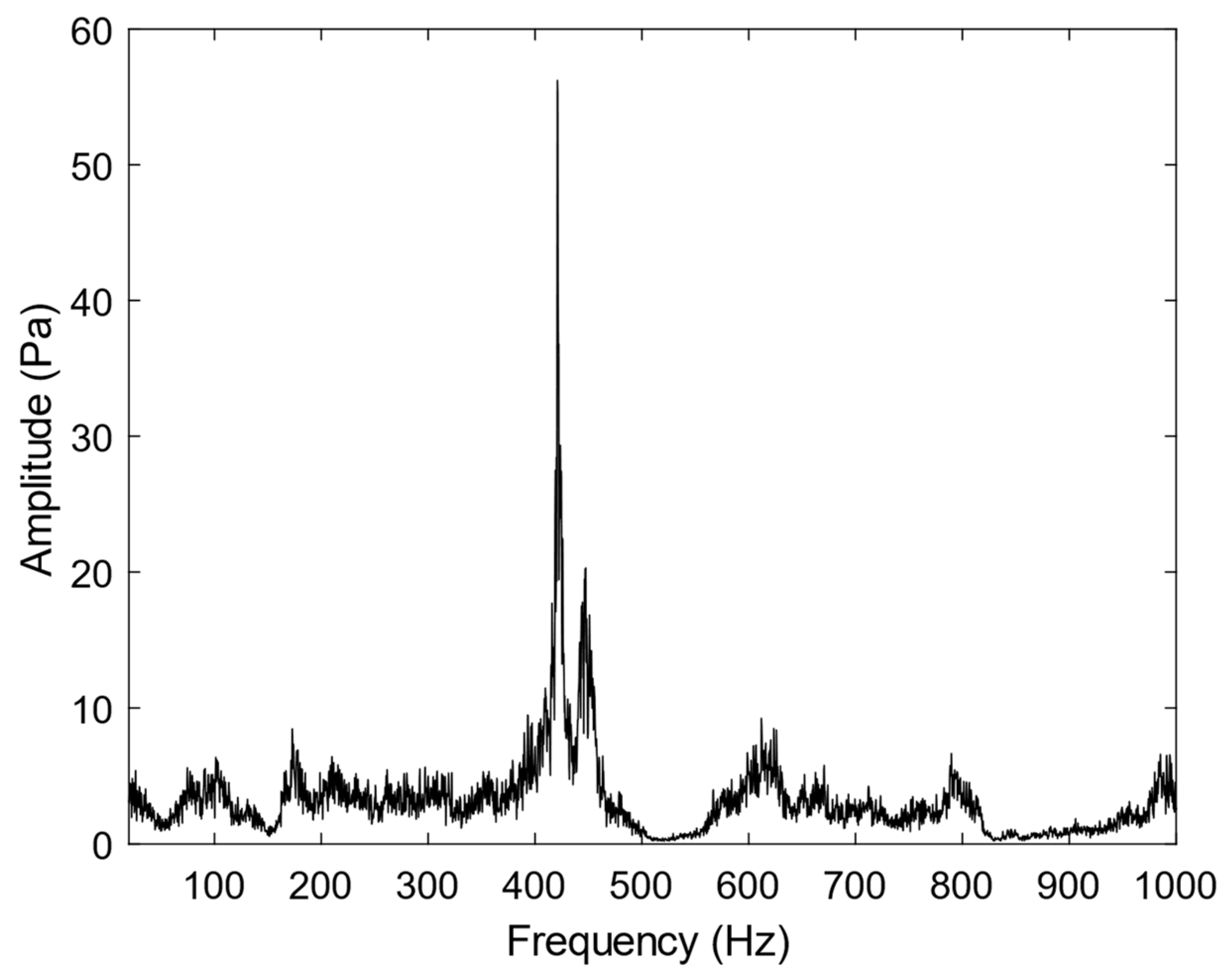
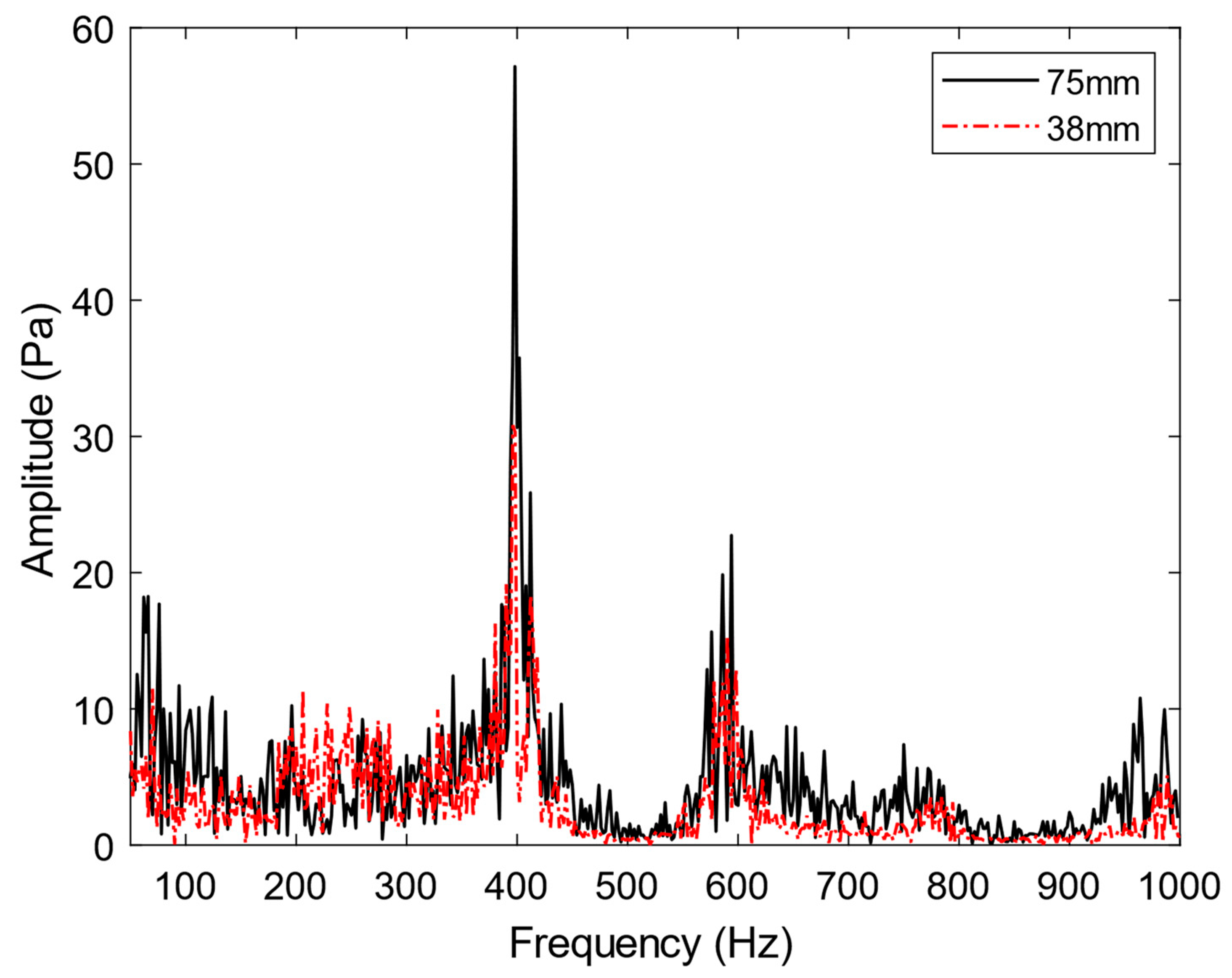
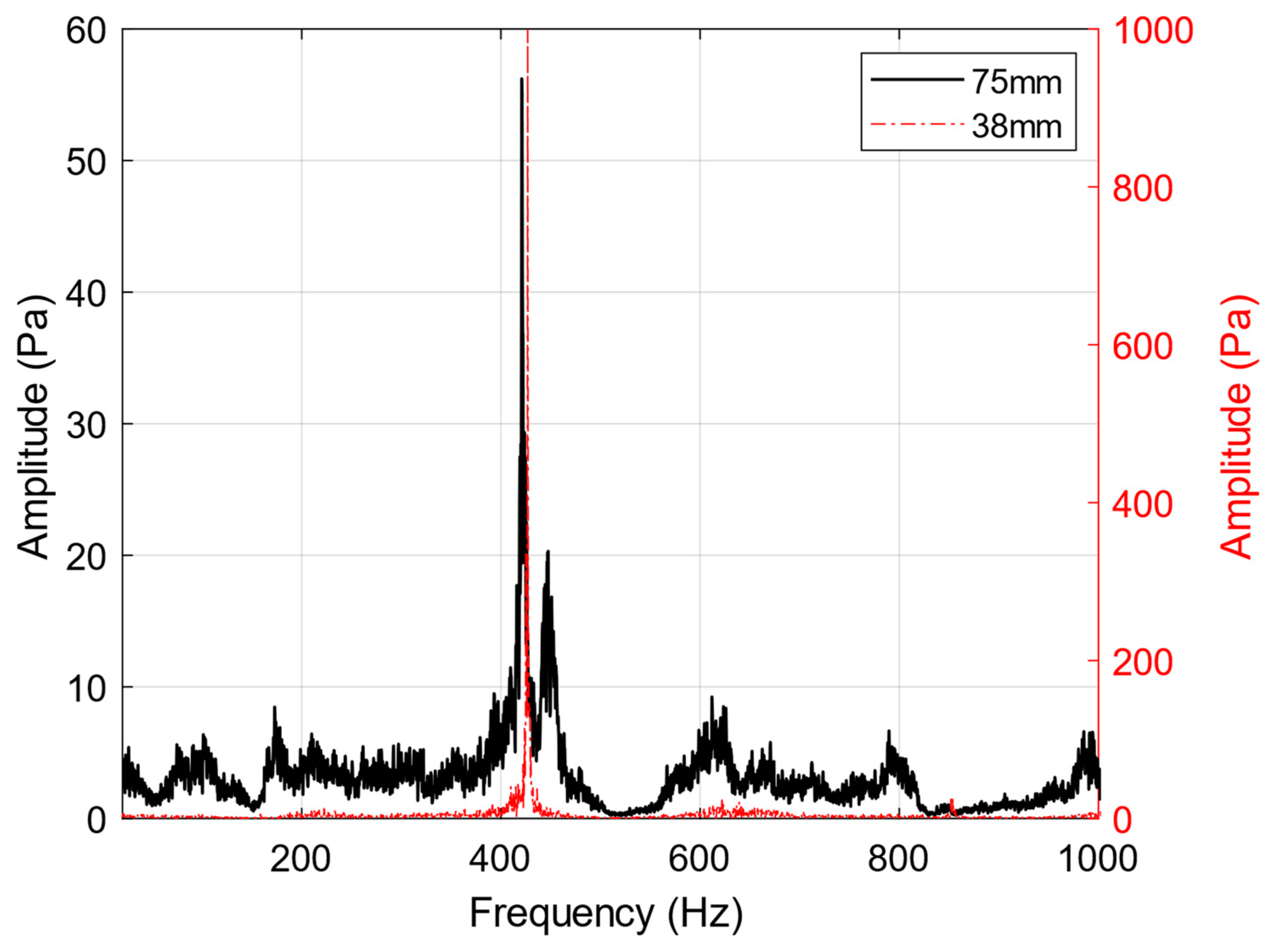
3.3. Experimental Implementation and Observation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Experimental Procedure
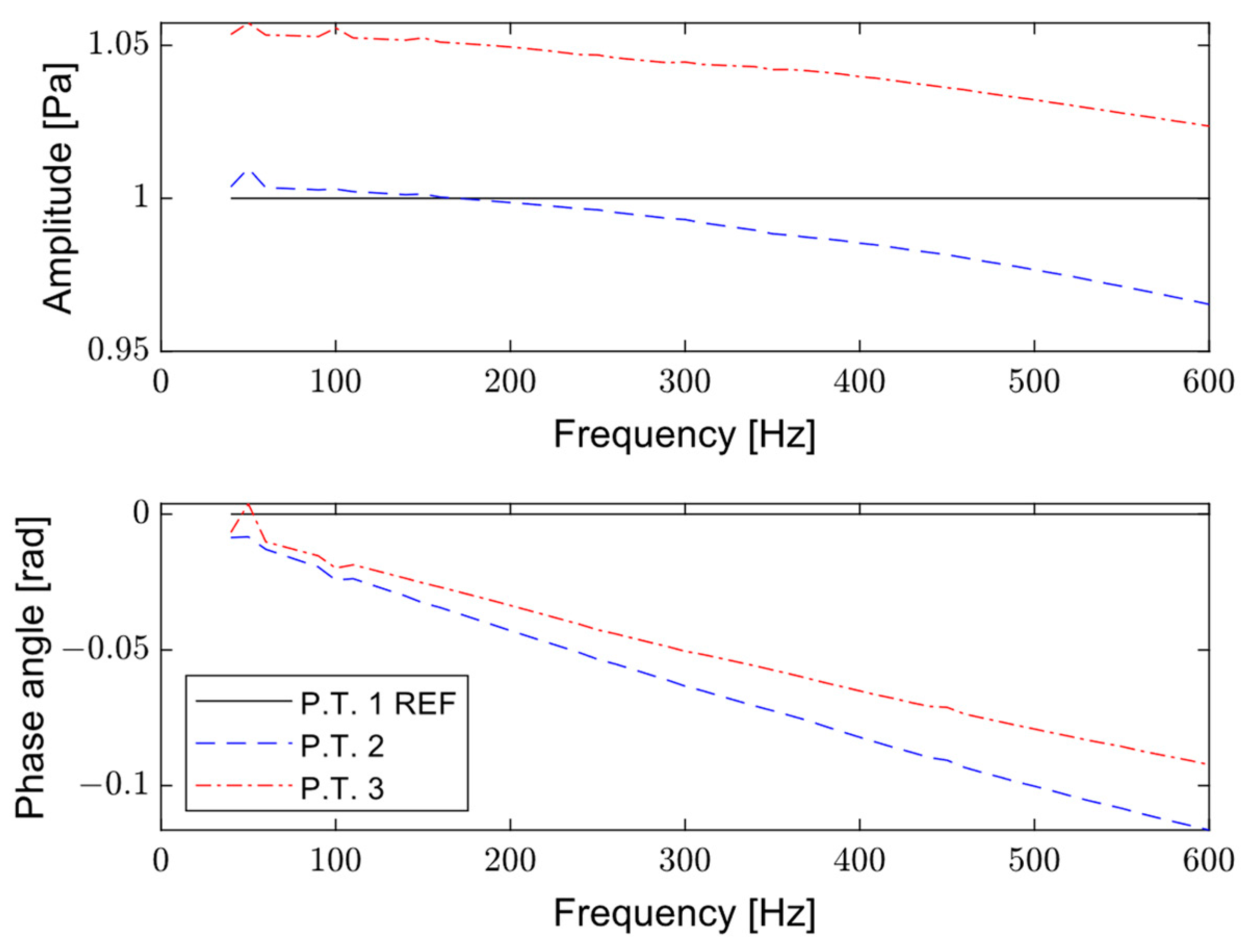
Appendix B. Measured FTF and Parameters for the FTF Fit Models
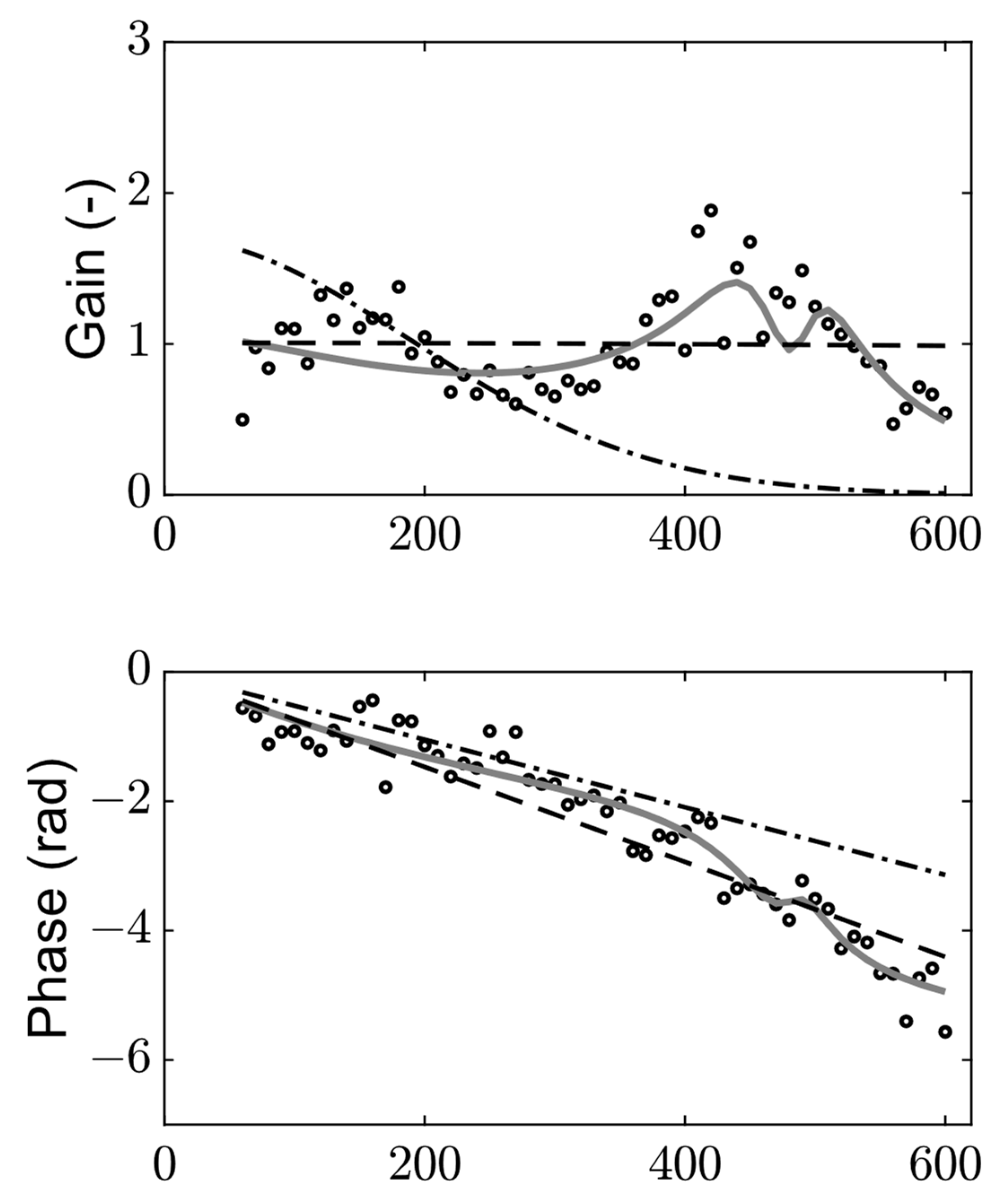
| 1 | |||
| Full fit | |||
| Low pass filter |
Appendix C. Mesh of the Computational Domain
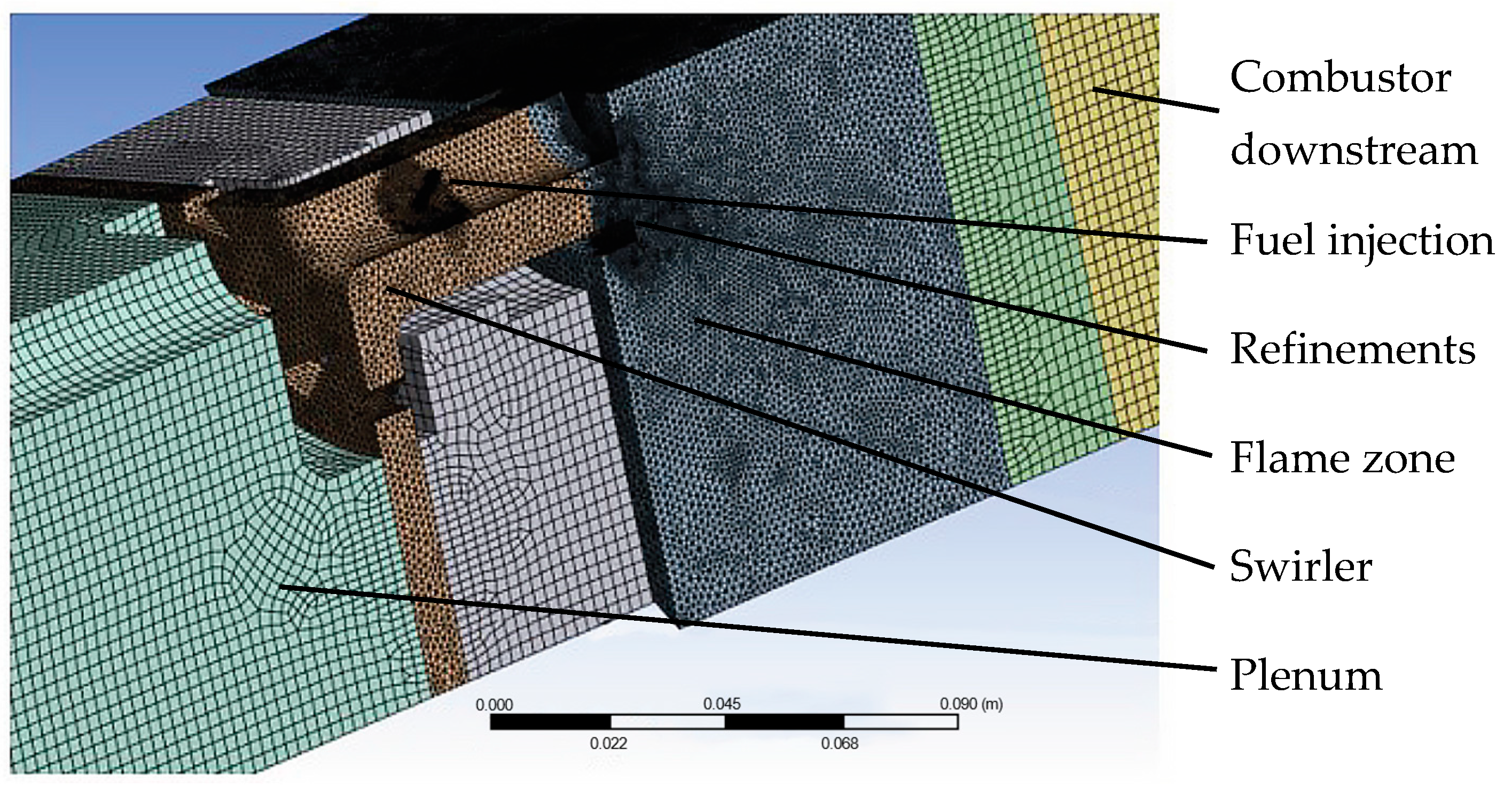
| Contraction diameter | 38 mm | 75 mm |
| Total Number of elements | 1,194,470 | 1,357,395 |
| Total Number of Tetrahedrons | 1,057,682 | 1,202,131 |
| Total Number of Prisms | 5101 | 3052 |
| Total Number of Hexahedrons | 108,588 | 123,538 |
| Total Number of Pyramids | 23,099 | 28,674 |
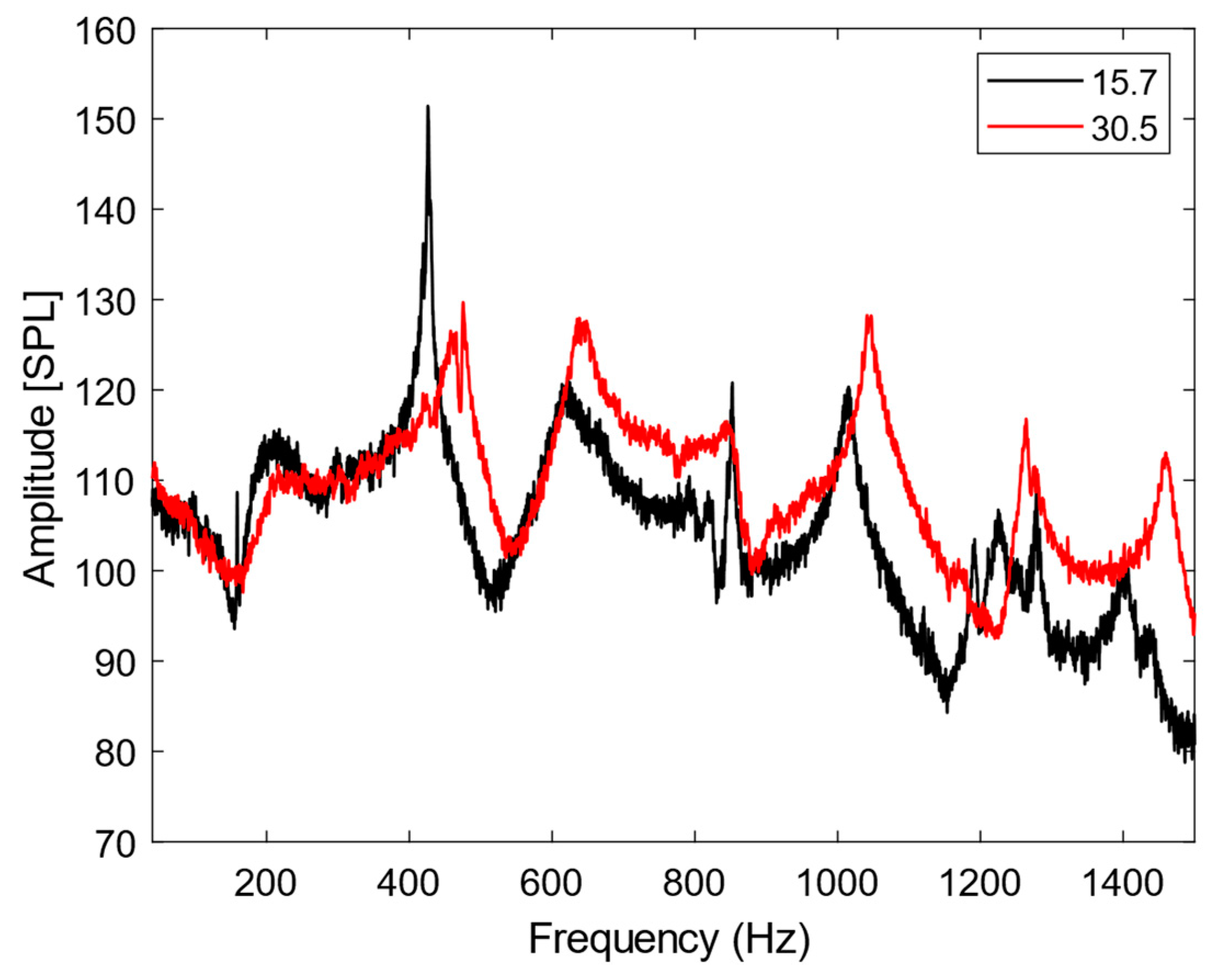
Appendix D. Combustion Test at 3.0 Bar and 250 kW Thermal Power

References
- Lieuwen, T.; Torres, H.; Johnson, C.; Zinn, B.T. A Mechanism of combustion instability in lean premixed gas turbine combustors. J. Eng. Gas Turb. Power Trans. ASME 2001, 123, 182–189. [Google Scholar] [CrossRef]
- Campa, G. Prediction of the Thermoacoustic Combustion Instability in Gas Turbines. Ph.D. Thesis, Politecnico di Bari, Bari, Italy, 2012. [Google Scholar]
- Candel, S. Combustion dynamics and control: Progress and challenges. Proc. Combust. Inst. 2002, 29, 1–28. [Google Scholar] [CrossRef]
- Poinsot, T. Prediction and control of combustion instabilities in real engines. Proc. Combust. Inst. 2017, 36, 1–28. [Google Scholar] [CrossRef]
- Syred, N.; Beér, J. Combustion in swirling flows: A review. Combust. Flame 1974, 23, 143–201. [Google Scholar] [CrossRef]
- Rayleigh, L. The Theory of Sound; Macmillan and Co.: London, UK, 1896; Volume 2. [Google Scholar]
- Poinsot, T.J.; Trouve, A.C.; Veynante, D.P.; Candel, S.M.; Esposito, E.J. Vortex-driven acoustically coupled combustion instabilities. J. Fluid Mech. 1987, 177, 265–292. [Google Scholar] [CrossRef]
- Heckl, M.A. Active control of the noise from a rijke tube. J. Sound Vib. 1988, 124, 117–133. [Google Scholar] [CrossRef]
- Chen, L.S.; Bomberg, S.; Polifke, W. Propagation and generation of acoustic and entropy waves across a moving flame front. Combust. Flame 2016, 166, 170–180. [Google Scholar] [CrossRef]
- Lee, H.J. Combustion Instability Mechanisms in a Lean Premixed Gas Turbine Combustor. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2009. [Google Scholar]
- Kim, D.; Park, S.W. Forced and self-excited oscillations in a natural gas fired lean premixed combustor. Fuel Process. Technol. 2010, 91, 1670–1677. [Google Scholar] [CrossRef]
- Evesque, S.; Dowling, A. Adaptive control of combustion oscillations. In Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998. [Google Scholar]
- Zhang, J.; Ratner, A. Experimental study of the effects of hydrogen addition on the thermoacoustic instability in a variable-length combustor. Int. J. Hydrog. Energy 2021, 46, 16086–16100. [Google Scholar] [CrossRef]
- Paschereit, C.O.; Gutmark, E.; Weisenstein, W. Excitation of thermoacoustic instabilities by interaction of acoustics and unstable swirling flow. AIAA J. 2000, 38, 1025–1034. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, G.; Fang, Y.; Jin, T.; Li, J. Experimental study of the effect of outlet boundary on combustion instabilities in premixed swirling flames. Phys. Fluids 2021, 33, 027106. [Google Scholar] [CrossRef]
- Sahay, A.; Kushwaha, A.; Pawar, S.A.; PR, M.; Dhadphale, J.M.; Sujith, R.I. Mitigation of limit cycle oscillations in a turbulent thermoacoustic system via delayed acoustic self-feedback. Chaos: Interdiscip. J. Nonlinear Sci. 2023, 33, 043118. [Google Scholar] [CrossRef] [PubMed]
- Merk, H. An analysis of unstable combustion of premixed gases. Symp. Int. Combust. 1957, 6, 500–512. [Google Scholar] [CrossRef]
- Dowling, A. The calculation of thermoacoustic oscillations. J. Sound Vib. 1995, 180, 557–581. [Google Scholar] [CrossRef]
- Schuermans, B.B.H.; Polifke, W.; Paschereit, C.O.; van der Linden, J.H. Prediction of Acoustic Pressure Spectra in Combustion Systems Using Swirl Stabilized Gas Turbine Burners. In ASME Turbo Expo 2000: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2000. [Google Scholar]
- Gentemann, A.; Fischer, A.; Evesque, S.; Polifke, W. Acoustic Transfer Matrix Reconstruction and Analysis for Ducts with Sudden Change of Area. In Proceedings of the 9th AIAA/CEAS Aeroacoustics Conference and Exhibit, Hilton Head, SC, USA, 12–14 May 2003. [Google Scholar]
- Kopitz, J.; Polifke, W. CFD-based application of the Nyquist criterion to thermo-acoustic instabilities. J. Comput. Phys. 2008, 227, 6754–6778. [Google Scholar] [CrossRef]
- Polifke, W. System modelling and stability analysis. Lect. Ser. Von Karman Inst. Fluid Dyn. 2007, 9, 7. [Google Scholar]
- Hubbard, S.; Dowling, A.P. Acoustic Resonances of an Industrial Gas Turbine Combustion System. J. Eng. Gas Turbines Power 2000, 123, 766–773. [Google Scholar] [CrossRef]
- Polifke, W.; Poncet, A.; Paschereit, C.; Döbbeling, K. Reconstruction of acoustic transfer matrices by instationary computational fluid dynamics. J. Sound Vib. 2001, 245, 483–510. [Google Scholar] [CrossRef]
- Hobson, D.E.; Fackrell, J.E.; Hewitt, G. Combustion instabilities in industrial gas turbines—Measurements on operating plant and thermoacoustic modeling. J. Eng. Gas Turbines Power 2000, 122, 420–428. [Google Scholar] [CrossRef]
- Van der Eerden, F. Noise Reduction with Coupled Prismatic Tubes. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2000. [Google Scholar]
- Martin, C.E.; Benoit, L.; Sommerer, Y.; Nicoud, F.; Poinsot, T. Large-eddy simulation and acoustic analysis of a swirled staged turbulent combustor. AIAA J. 2006, 44, 741–750. [Google Scholar] [CrossRef]
- Laera, D.; Campa, G.; Camporeale, S.M.; Bertolotto, E.; Rizzo, S.; Bonzani, F.; Ferrante, A.; Saponaro, A. Modelling of Thermoacoustic Combustion Instabilities Phenomena: Application to an Experimental Test Rig. Energy Procedia 2014, 45, 1392–1401. [Google Scholar] [CrossRef]
- Krediet, H.J. Prediction of Limit Cycle Pressure Oscillations in Gas Turbine Combustion Systems Using the Flame Describing Function; University of Twente: Enschede, The Netherlands, 2012. [Google Scholar]
- Hantschk, C.-C.; Vortmeyer, D. Numerical simulation of self-excited thermoacoustic instabilities in a rijke Tube. J. Sound Vib. 1999, 227, 511–522. [Google Scholar] [CrossRef]
- Gövert, S.; Mira, D.; Kok, J.; Vázquez, M.; Houzeaux, G. Turbulent combustion modelling of a confined premixed jet flame including heat loss effects using tabulated chemistry. Appl. Energy 2015, 156, 804–815. [Google Scholar] [CrossRef]
- Kapucu, M.; Kok, J.B.; Alemela, P. Comparison of Two Methods for Flame Transfer Function Measurements: MOOG Valve or Siren and the Impact of Results on the Instability Analysis in a High Pressure Combustor. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2012. [Google Scholar]
- Pozarlik, A. Vibro-Acoustical Instabilities Induced by Combustion Dynamics in Gas Turbine Combustors. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2010. [Google Scholar]
- Van Kampen, J.F. Acoustic Pressure Oscillations Induced by Confined Premixed Natural Gas Flames. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2006. [Google Scholar]
- Kulite Netherlands, Stekon B.V. Meer Duin 64b, 2163 HC Lisse, The Netherlands. Available online: https://kulite.com//assets/media/2022/09/XTE-190-1.pdf (accessed on 26 March 2024).
- Kapucu, M.; Kok, J.B.W. CFD-Based Prediction of Combustion Dynamics and Nonlinear Flame Transfer Functions for a Swirl-Stabilized High-Pressure Combustor. Energies 2023, 16, 2515. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Kapucu, M.; Kok, J.B.W.; Pozarlik, A. Experimental investigation of thermoacoustics and high frequency combustion dynamics with band stop characteristics in a pressurized combustor. Energies 2024, 7, 1680. [Google Scholar] [CrossRef]
- Schuermans, B. Modeling and Control of Thermoacoustic Instabilities. Ph.D. Thesis, Ecole Polytechnique Federale De Lausanne, Lausanne, Switzerland, 2003. [Google Scholar]
- Hoeijmakers, P.M. Flame-Acoustic Coupling in Combustion Instabilities. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2014. [Google Scholar]
- Gonzalez, E.; Lee, J.; Santavicca, D. A study of combustion instabilities driven by flame-vortex interactions. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 11–13 July 2005. [Google Scholar]
- Figura, L.; Lee, J.G.; Quay, B.D.; Santavicca, D.A. The effects of fuel composition on flame structure and combustion dynamics in a lean premixed combustor. In ASME Turbo Expo 2007: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2007. [Google Scholar]
- Marble, F.; Candel, S. Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 1977, 55, 225–243. [Google Scholar] [CrossRef]
- Stow, S.R.; Dowling, A.P.; Hynes, T.P. Reflection of circumferential modes in a choked nozzle. J. Fluid Mech. 2002, 467, 215–239. [Google Scholar] [CrossRef]
- Duran, I.; Moreau, S. Solution of the quasi-one-dimensional linearized Euler equations using flow invariants and the Magnus expansion. J. Fluid Mech. 2013, 723, 190–231. [Google Scholar] [CrossRef]
- Silva, C.F.; Durán, I.; Nicoud, F.; Moreau, S. Boundary conditions for the computation of thermoacoustic modes in combustion chambers. AIAA J. 2014, 52, 1180–1193. [Google Scholar] [CrossRef]
- Durrieu, P.; Hofmans, G.; Ajello, G.; Boot, R.; Aurégan, Y.; Hirschberg, A.; Peters, M.C.A.M. Quasisteady aero-acoustic response of orifices. J. Acoust. Soc. Am. 2001, 110, 1859–1872. [Google Scholar] [CrossRef] [PubMed]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; Acoustic Society of America: New York, NY, USA, 1994. [Google Scholar]
- Ozcan, E. Tuning the self-excited thermo-acoustic oscillations of a gas turbine combustor to Limit Cycle Operations by means of numerical analysis. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2012. [Google Scholar]
- Shahi, M.; Kok, J.B.W.; Pozarlik, A.K.; Casado, J.C.R.; Sponfeldner, T. Sensitivity of the Numerical Prediction of Turbulent Combustion Dynamics in the Limousine Combustor. J. Eng. Gas Turbines Power 2014, 136, 021504. [Google Scholar] [CrossRef]
- Shahi, M. Modeling of Complex Physics & Combustion Dynamics in a Combustor with a Partially Premixed Turbulent Flame. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar]
- van Kampen, J.F.; Kok, J.B.W.; van der Meer, T.H. Efficient retrieval of the thermo-acoustic flame transfer function from a linearized CFD simulation of a turbulent flame. Int. J. Numer. Methods Fluids 2007, 54, 1131–1149. [Google Scholar] [CrossRef]
- Louis, J.J.; Kok, J.B.; Klein, S.A. Modeling and measurements of a 16-kW turbulent nonadiabatic syngas diffusion flame in a cooled cylindrical combustion chamber. Combust. Flame 2001, 125, 1012–1031. [Google Scholar] [CrossRef]
- Keshtiban, I.; Belblidia, F.; Webster, M. Compressible flow solvers for low Mach number flows—A review. Int. J. Numer. Methods Fluids 2004, 23, 77–103. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapucu, M.; Kok, J.B.W.; Pozarlik, A.K. Acoustic Design Parameter Change of a Pressurized Combustor Leading to Limit Cycle Oscillations. Energies 2024, 17, 1885. https://doi.org/10.3390/en17081885
Kapucu M, Kok JBW, Pozarlik AK. Acoustic Design Parameter Change of a Pressurized Combustor Leading to Limit Cycle Oscillations. Energies. 2024; 17(8):1885. https://doi.org/10.3390/en17081885
Chicago/Turabian StyleKapucu, Mehmet, Jim B. W. Kok, and Artur K. Pozarlik. 2024. "Acoustic Design Parameter Change of a Pressurized Combustor Leading to Limit Cycle Oscillations" Energies 17, no. 8: 1885. https://doi.org/10.3390/en17081885
APA StyleKapucu, M., Kok, J. B. W., & Pozarlik, A. K. (2024). Acoustic Design Parameter Change of a Pressurized Combustor Leading to Limit Cycle Oscillations. Energies, 17(8), 1885. https://doi.org/10.3390/en17081885







