Heat Transfer Mechanism of Heat–Cold Alternate Extraction in a Shallow Geothermal Buried Pipe System under Multiple Heat Exchanger Groups
Abstract
:1. Introduction
2. Numerical Model
2.1. Flow Equations in the Pipeline
2.2. Heat Transfer Equations in the Pipeline
2.3. Flow Equations in the Reservoir
2.4. Heat Transfer Equations in the Reservoir
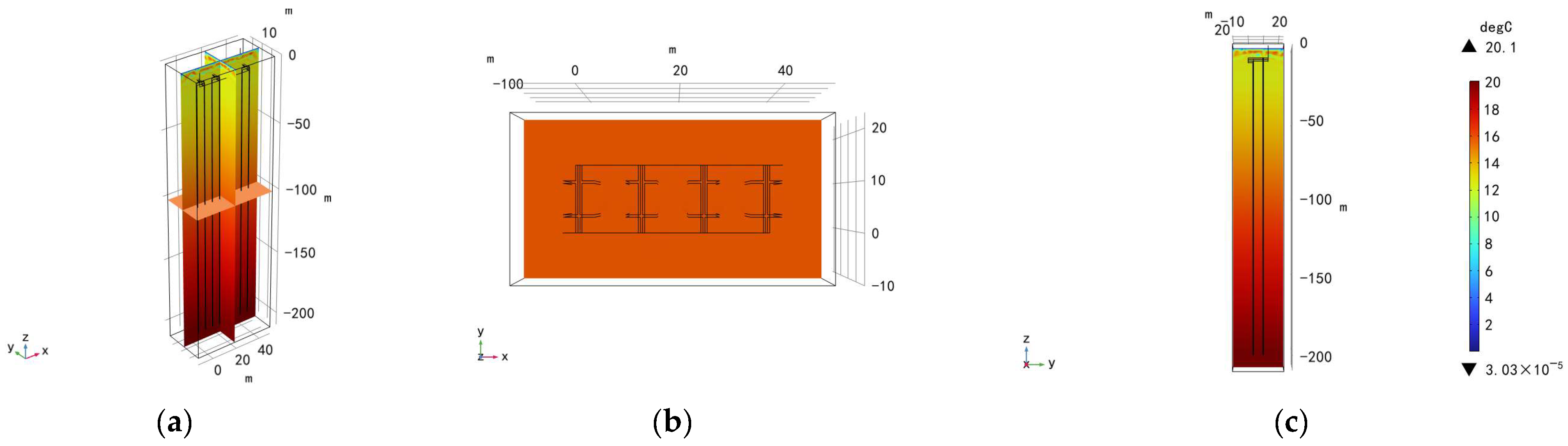
3. Simulation Model Construction
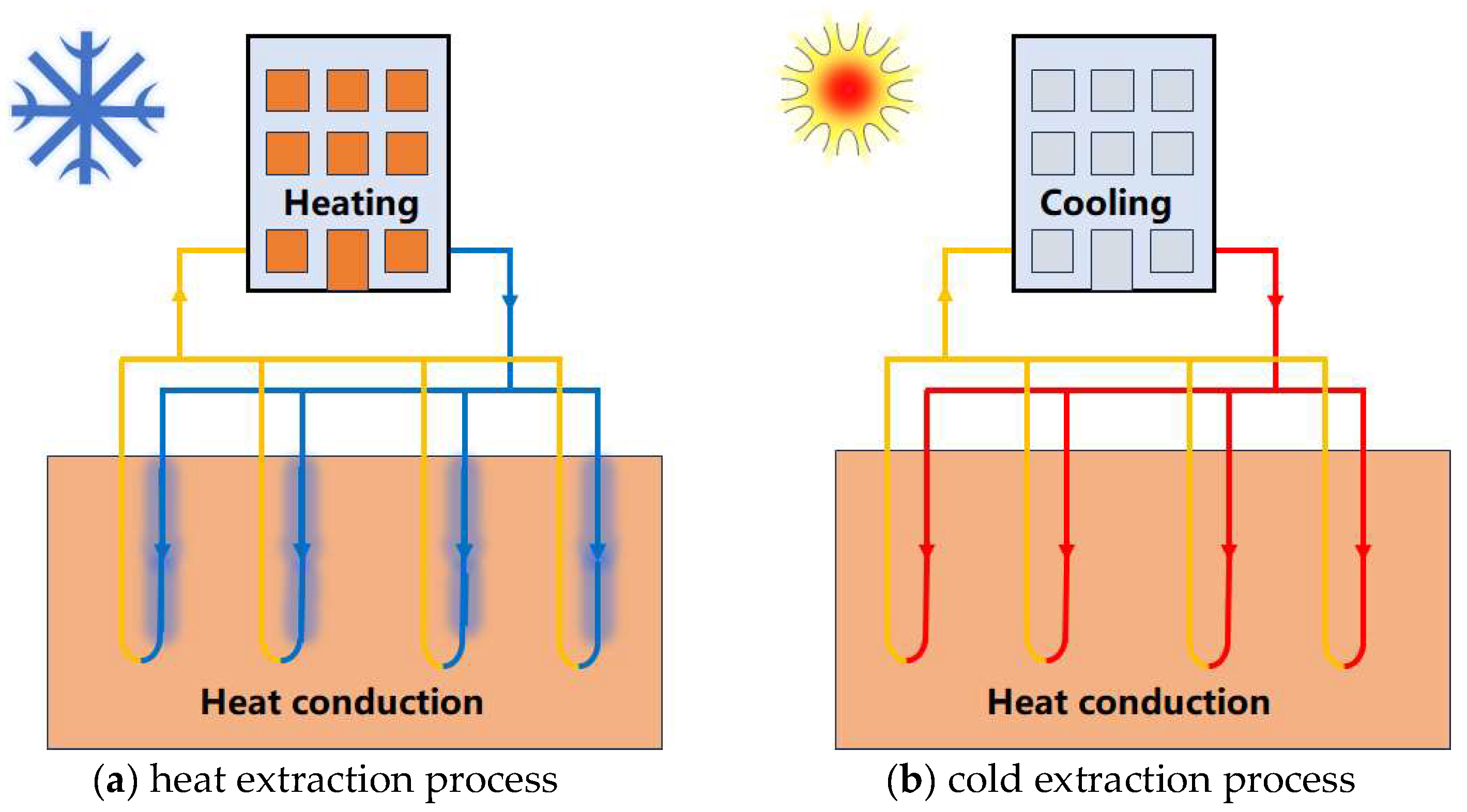
3.1. Heat Transfer Principle of the Shallow Buried Pipe
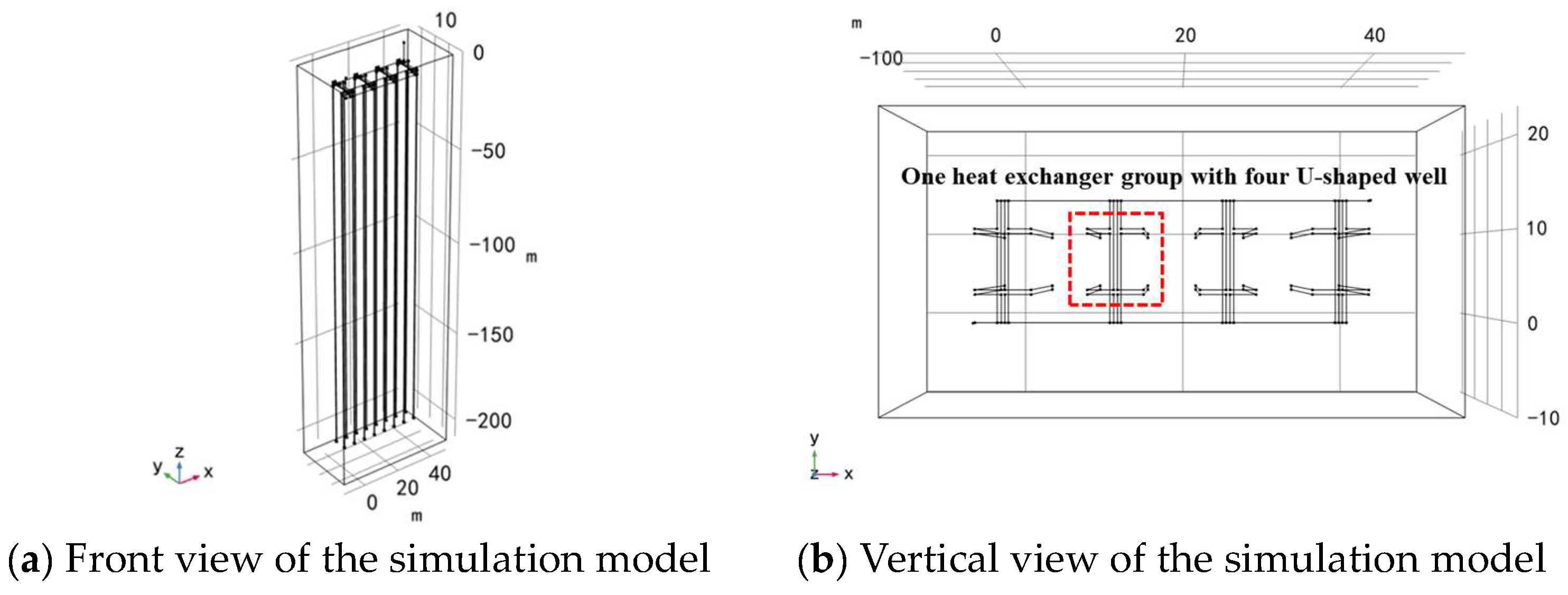
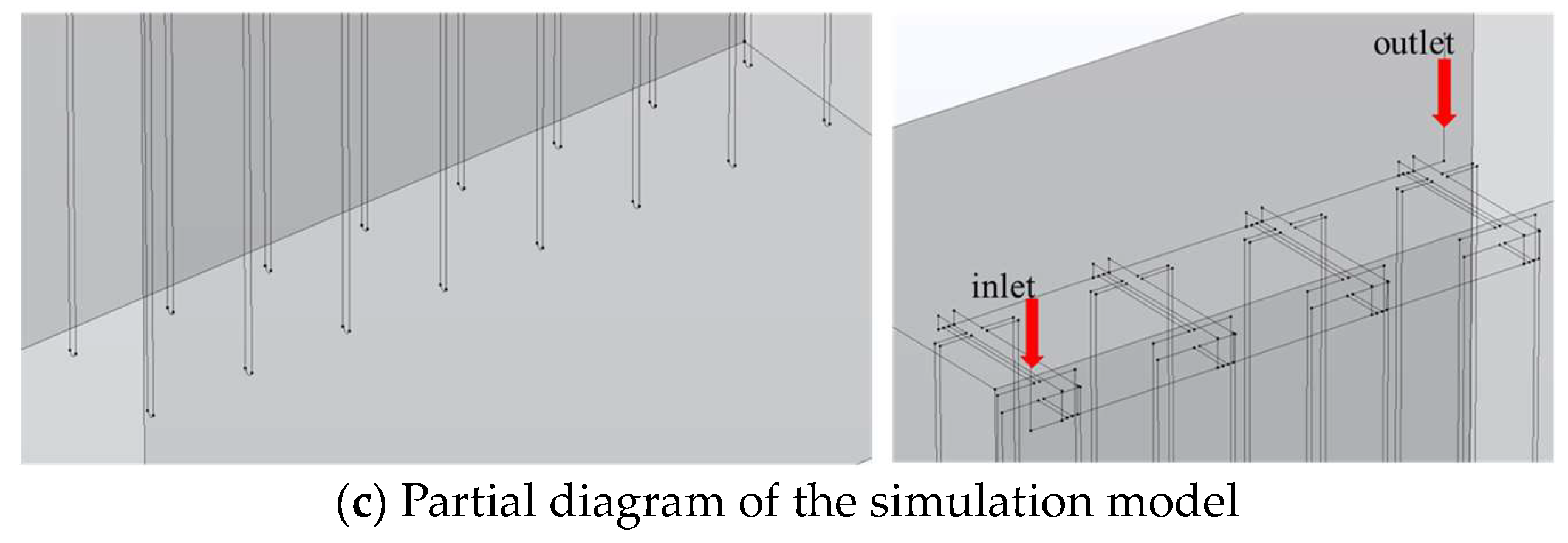
3.2. Model Establishment
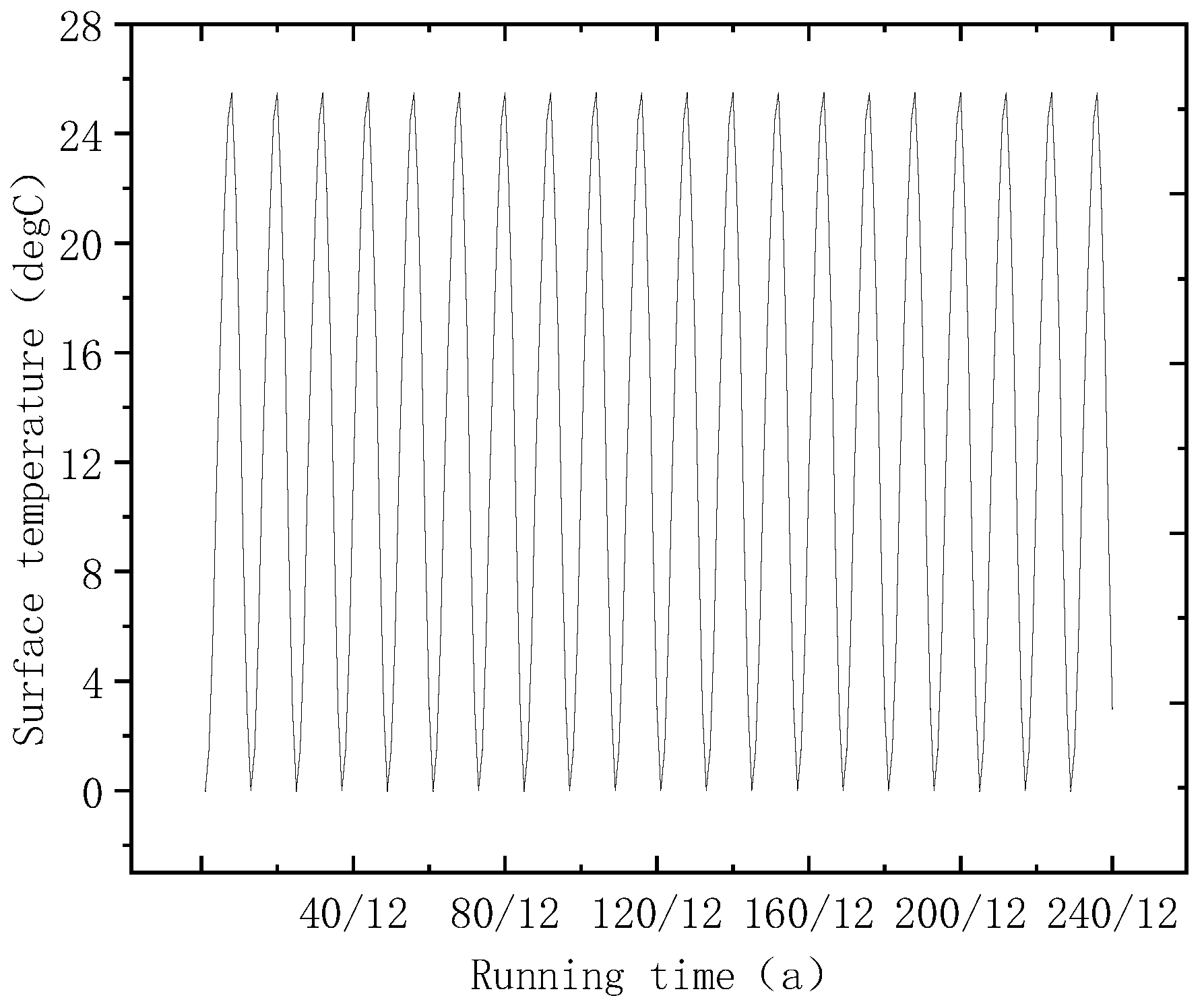
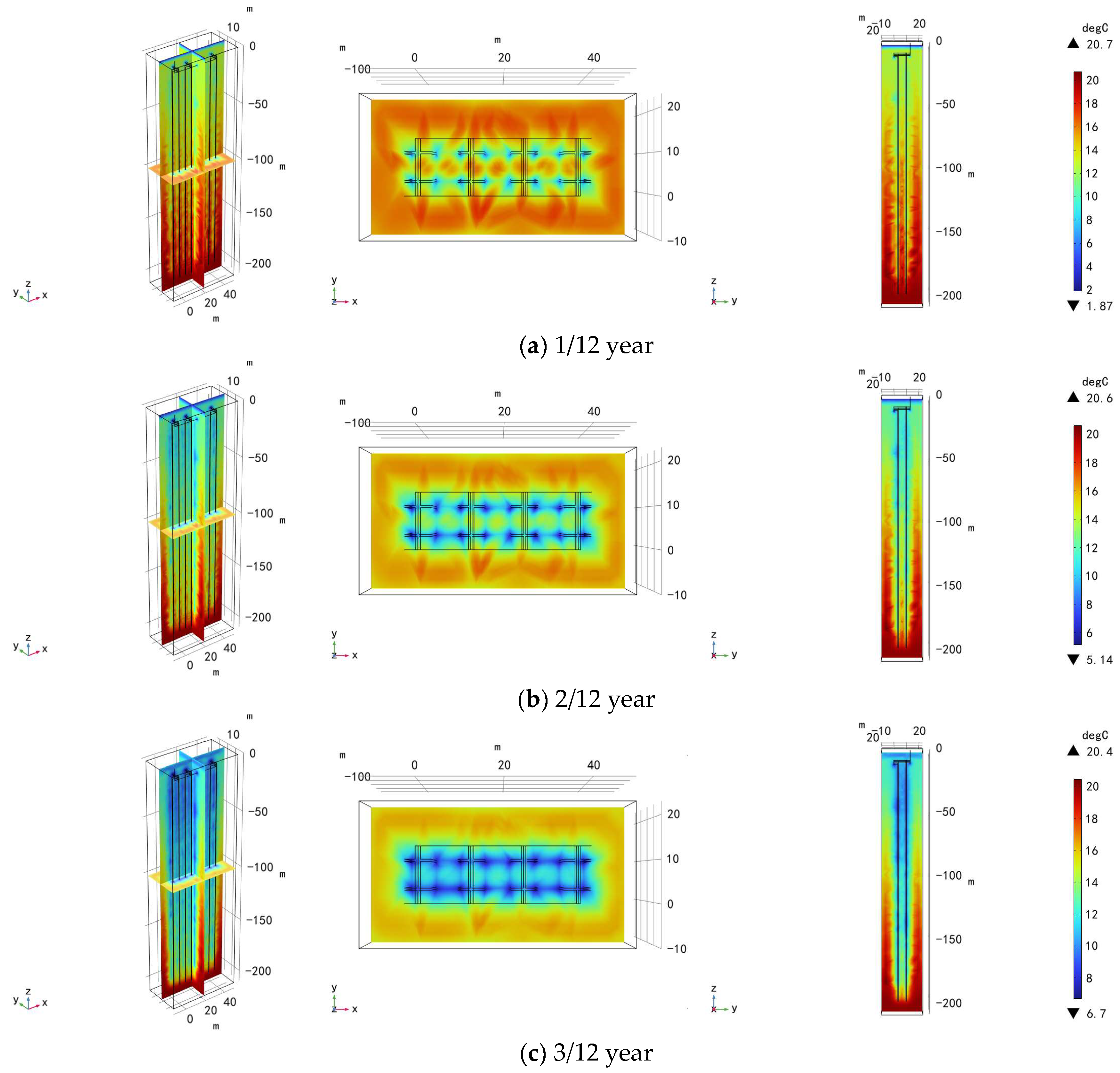
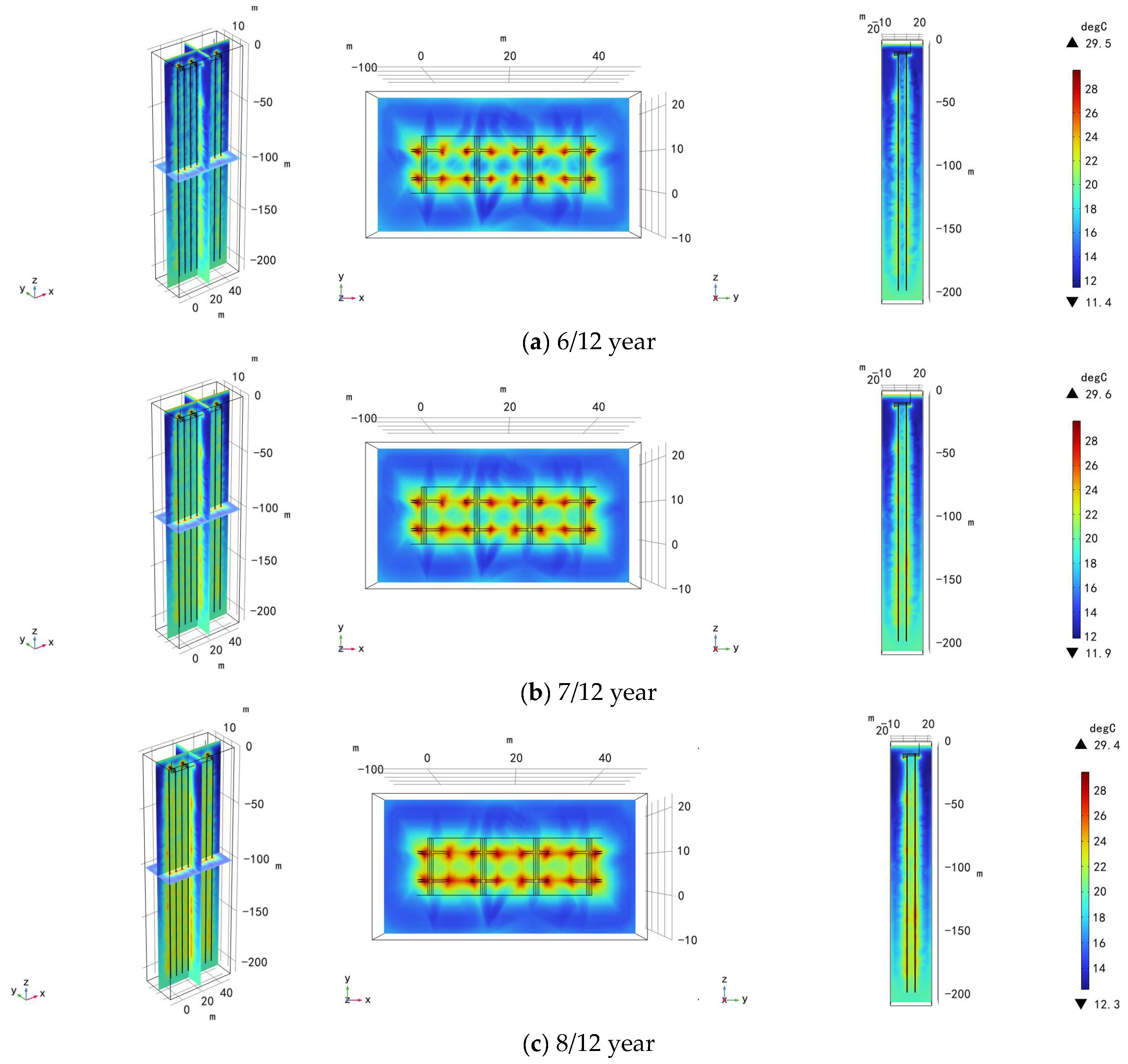
4. The Temperature Field Evolution during the Heat–Cold Alternate Extraction
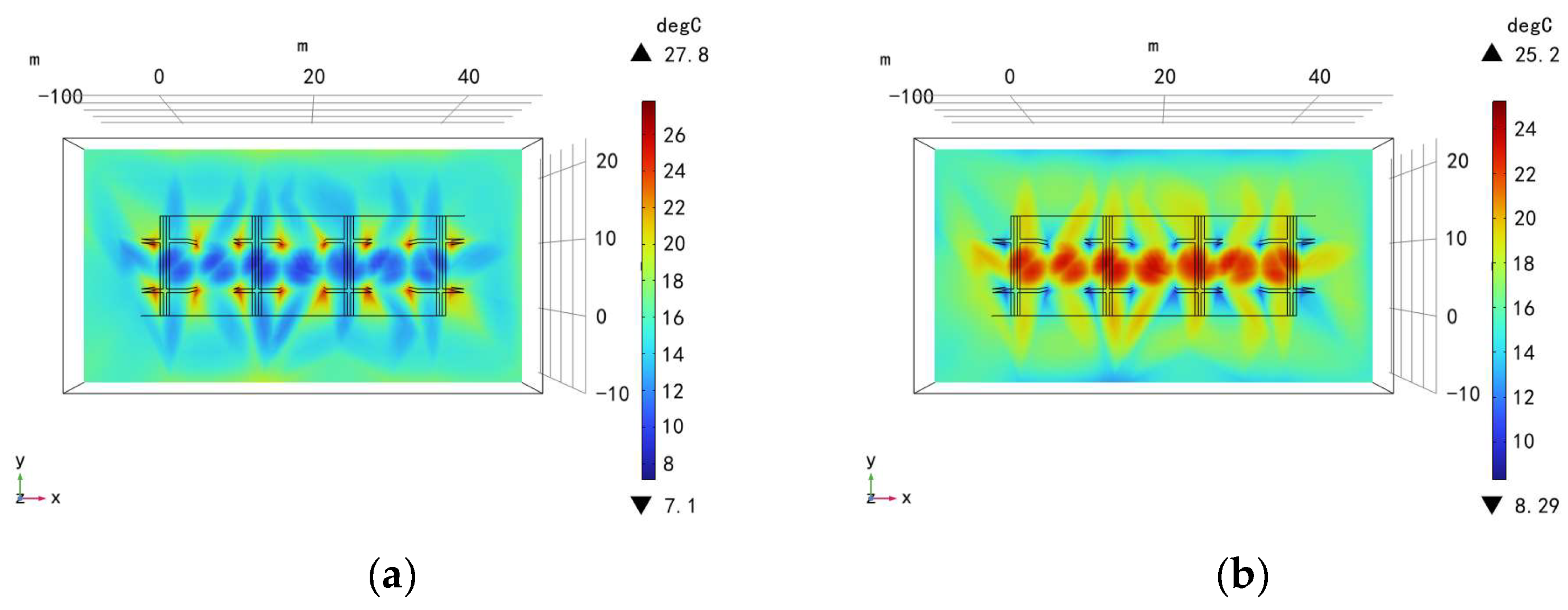
4.1. Temperature Evolution in the Reservoir
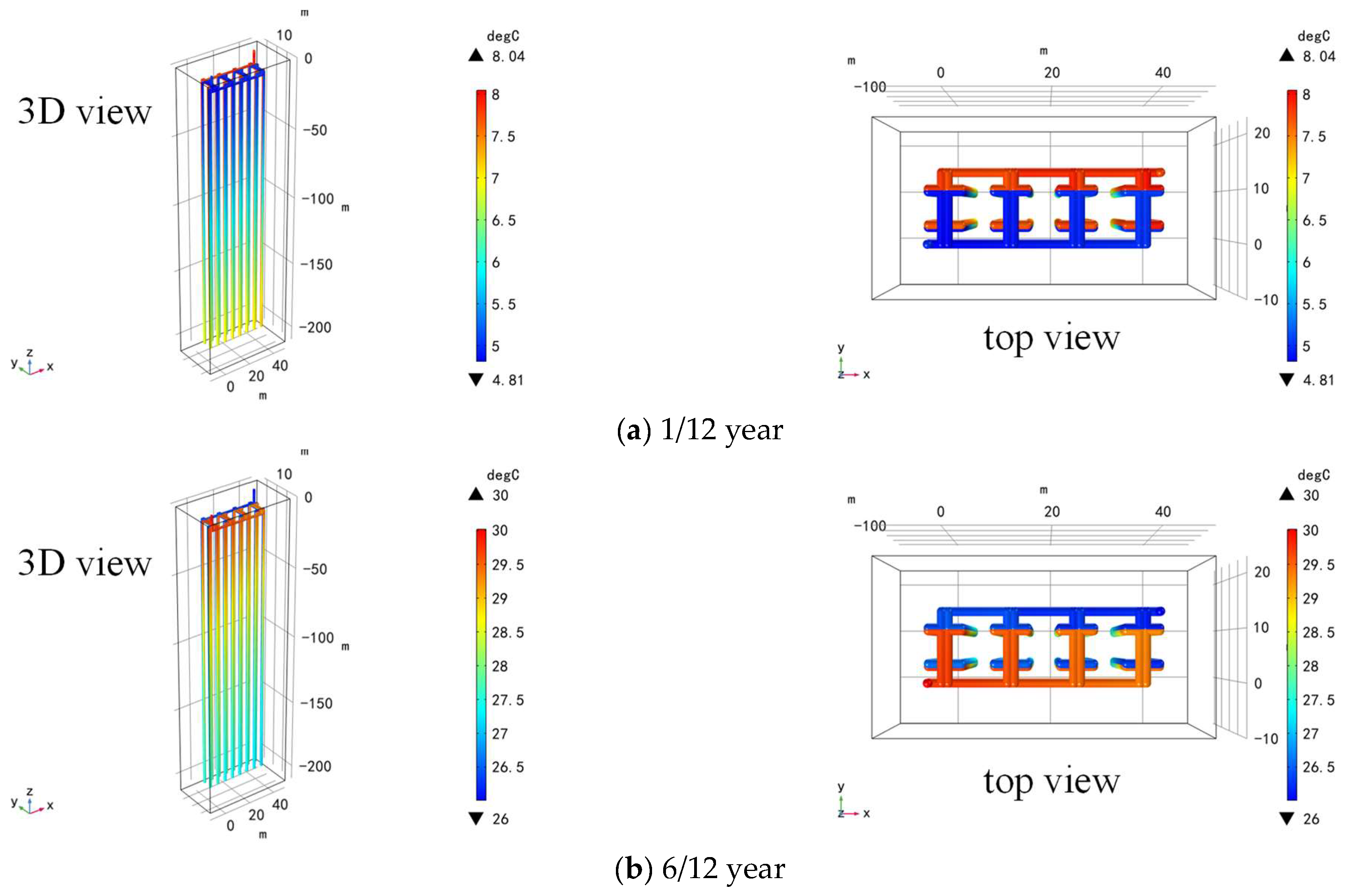
4.2. Temperature Evolution in the Pipeline
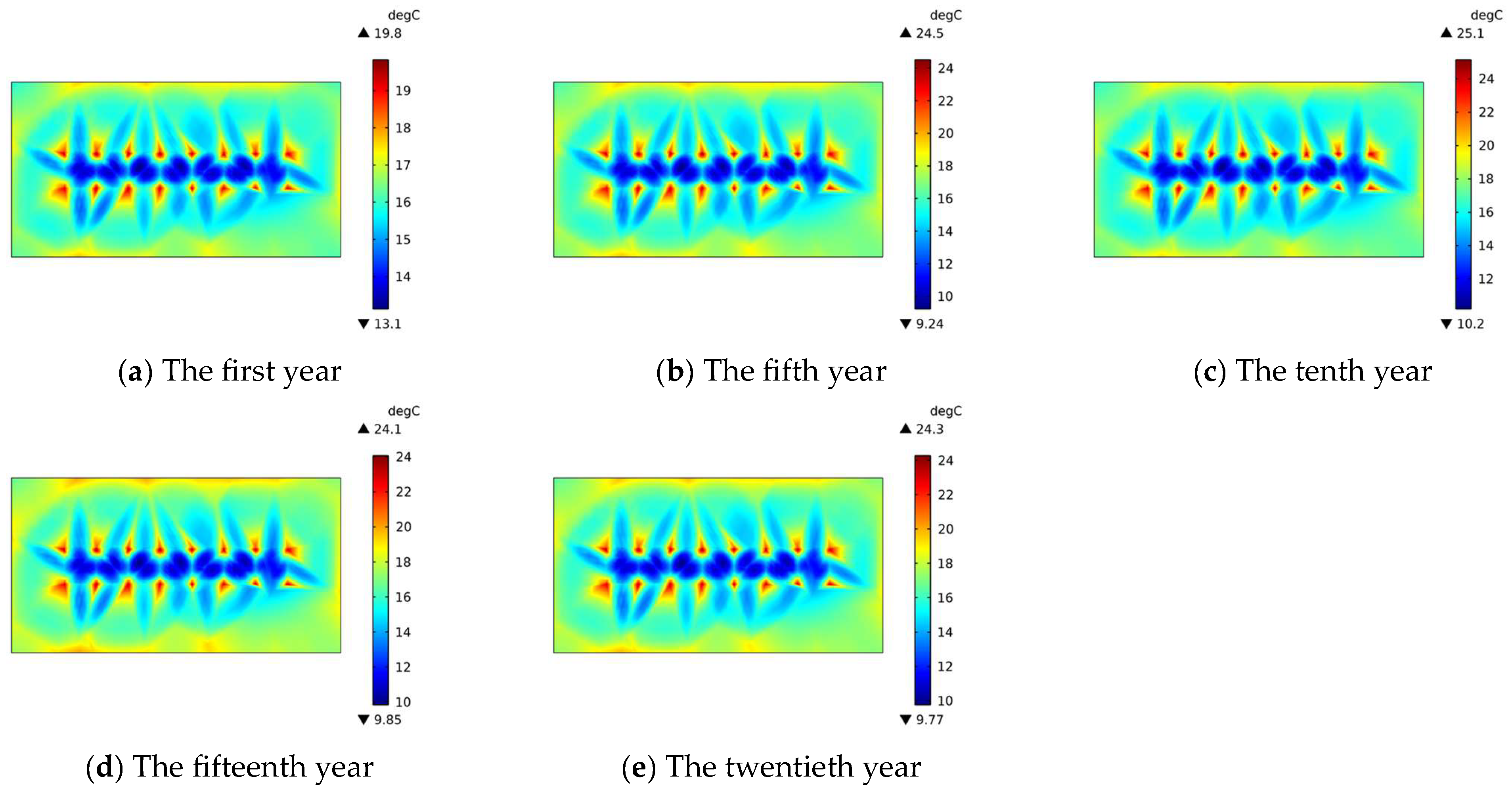
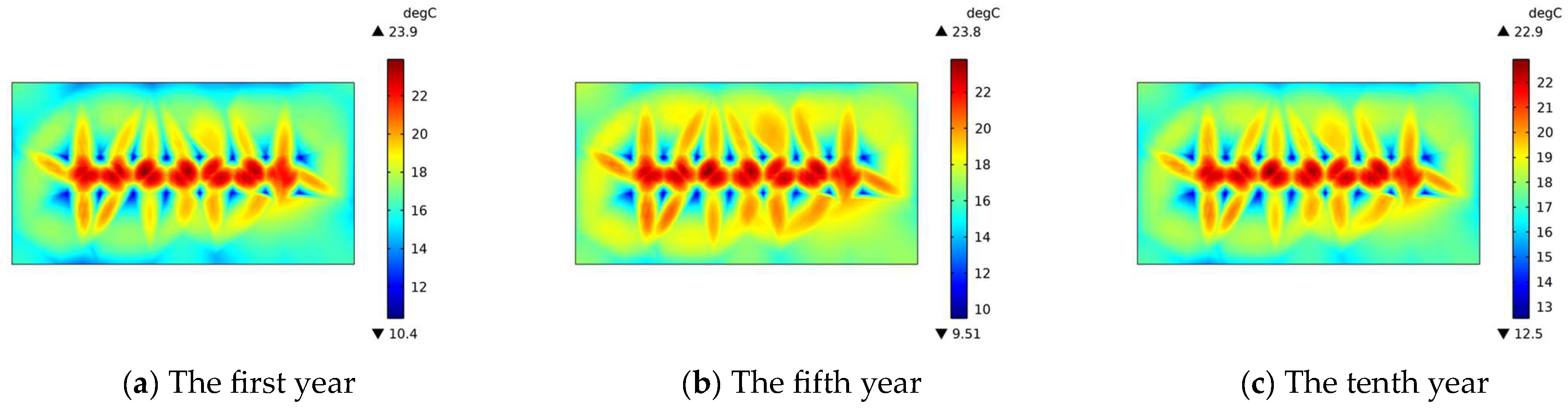
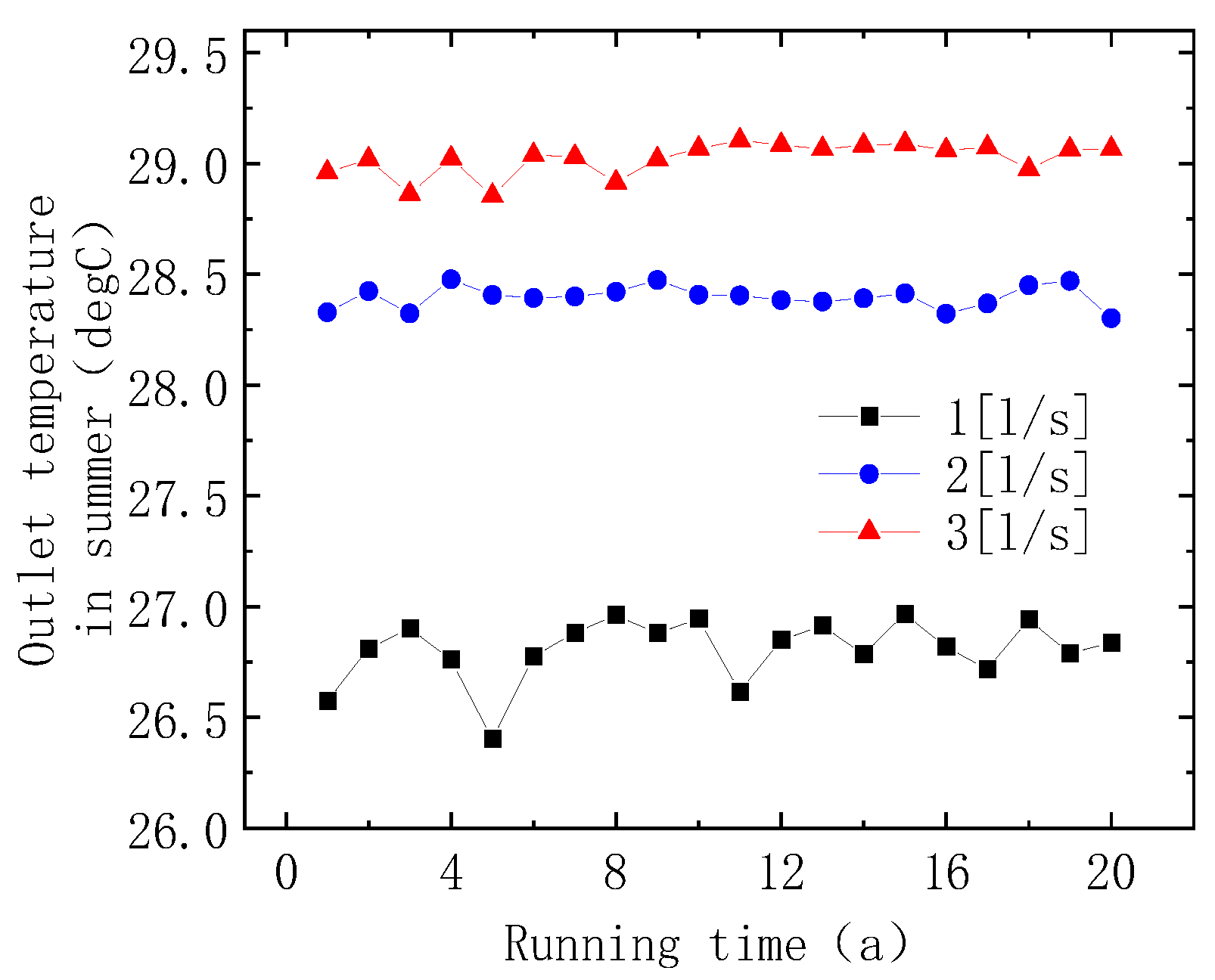
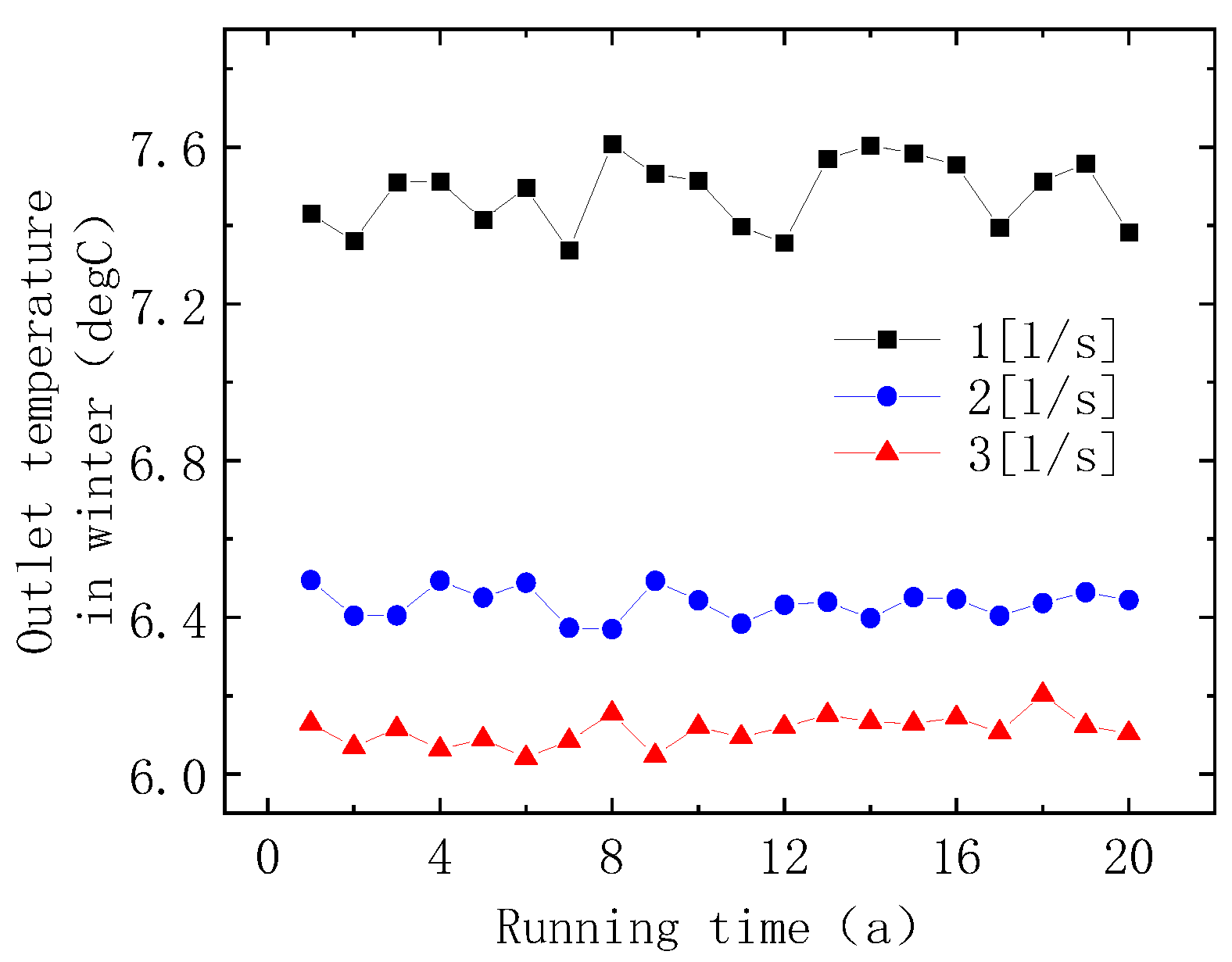
4.3. Temperature Variation with Development Years
5. Sensitivity Analysis
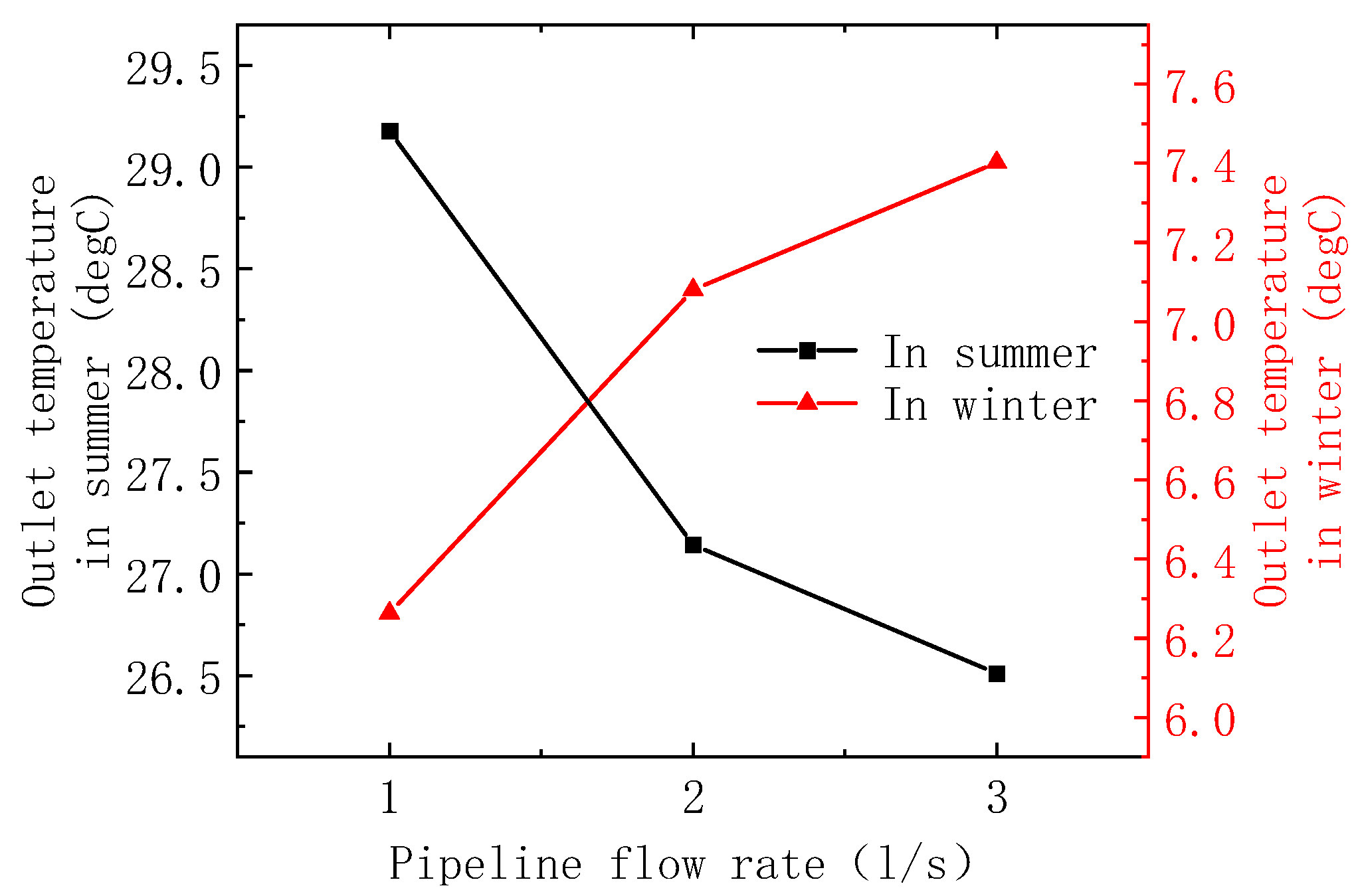
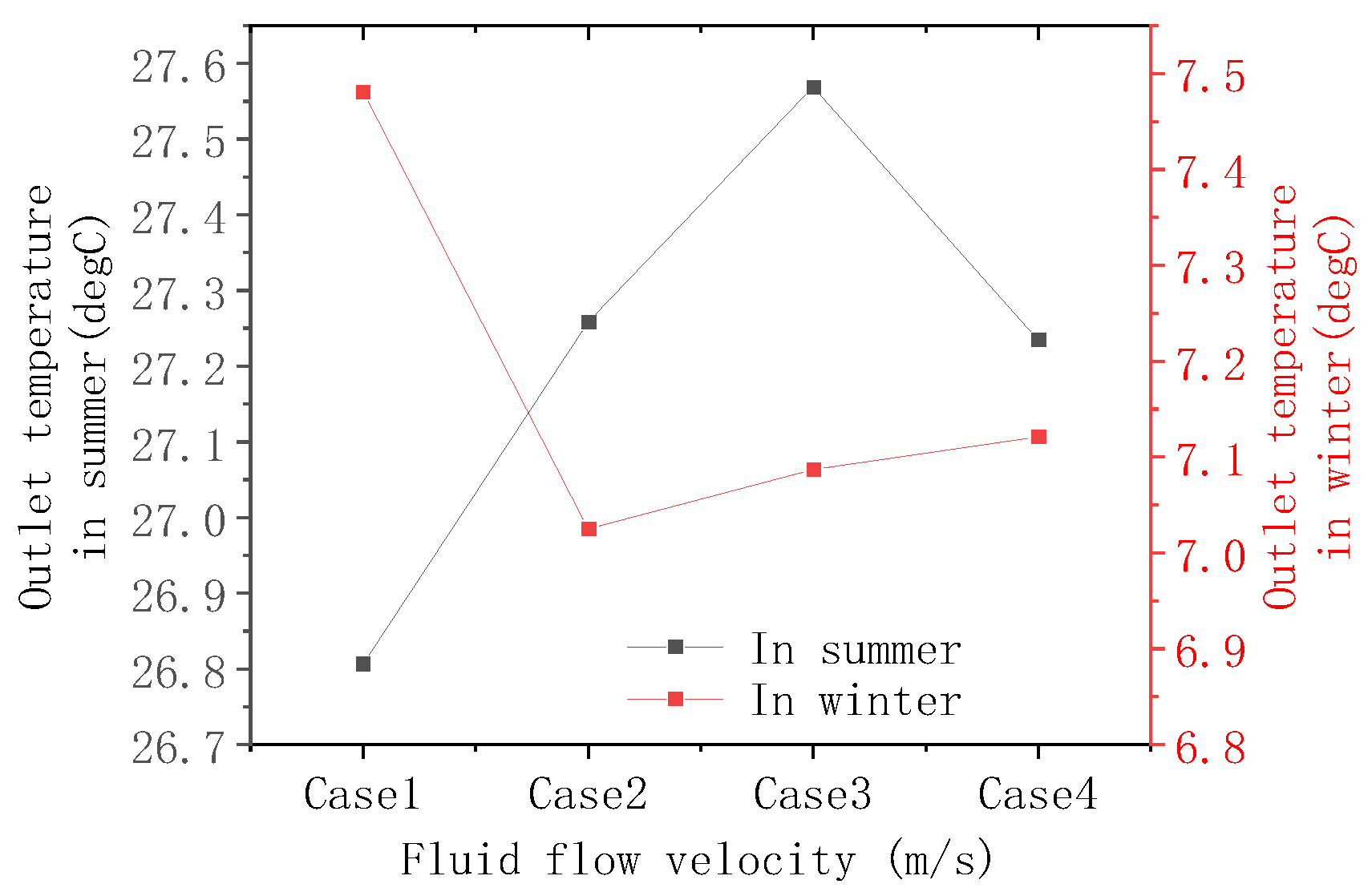
5.1. Effect of Pipeline Flow Rate
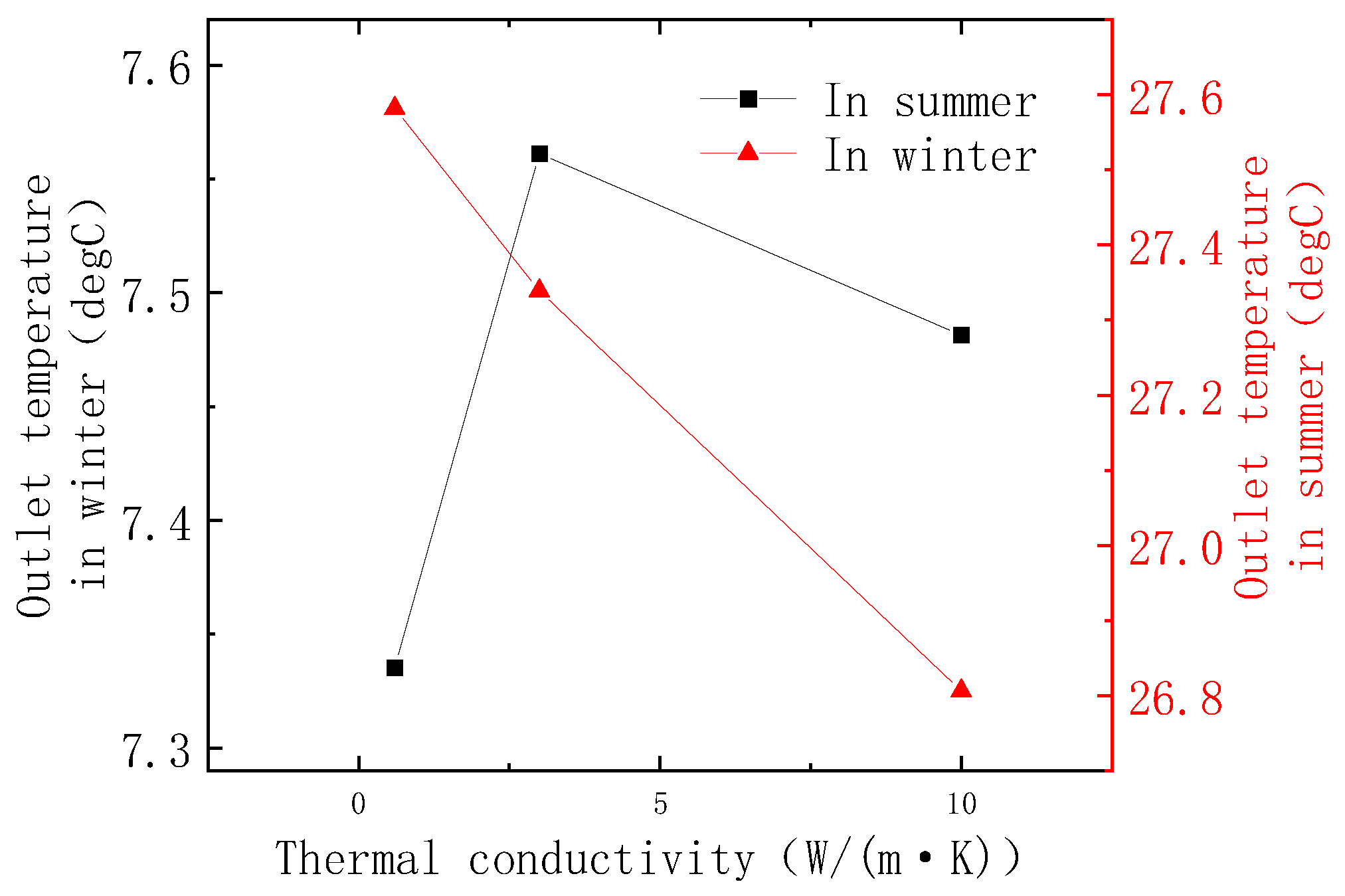
5.2. Effect of Pipeline Wall Thermal Conductivity
5.3. Effect of Heat Injection Duration
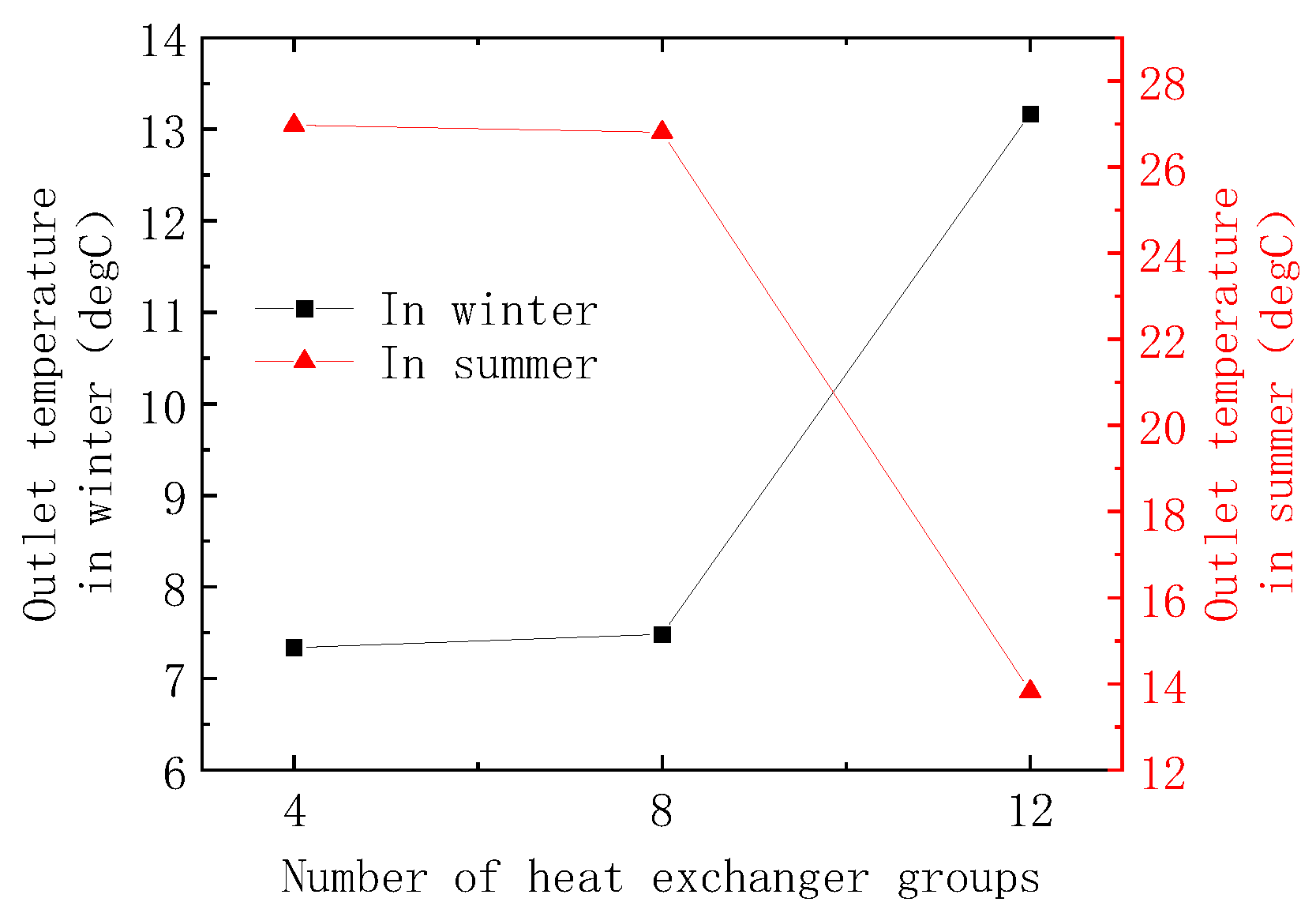
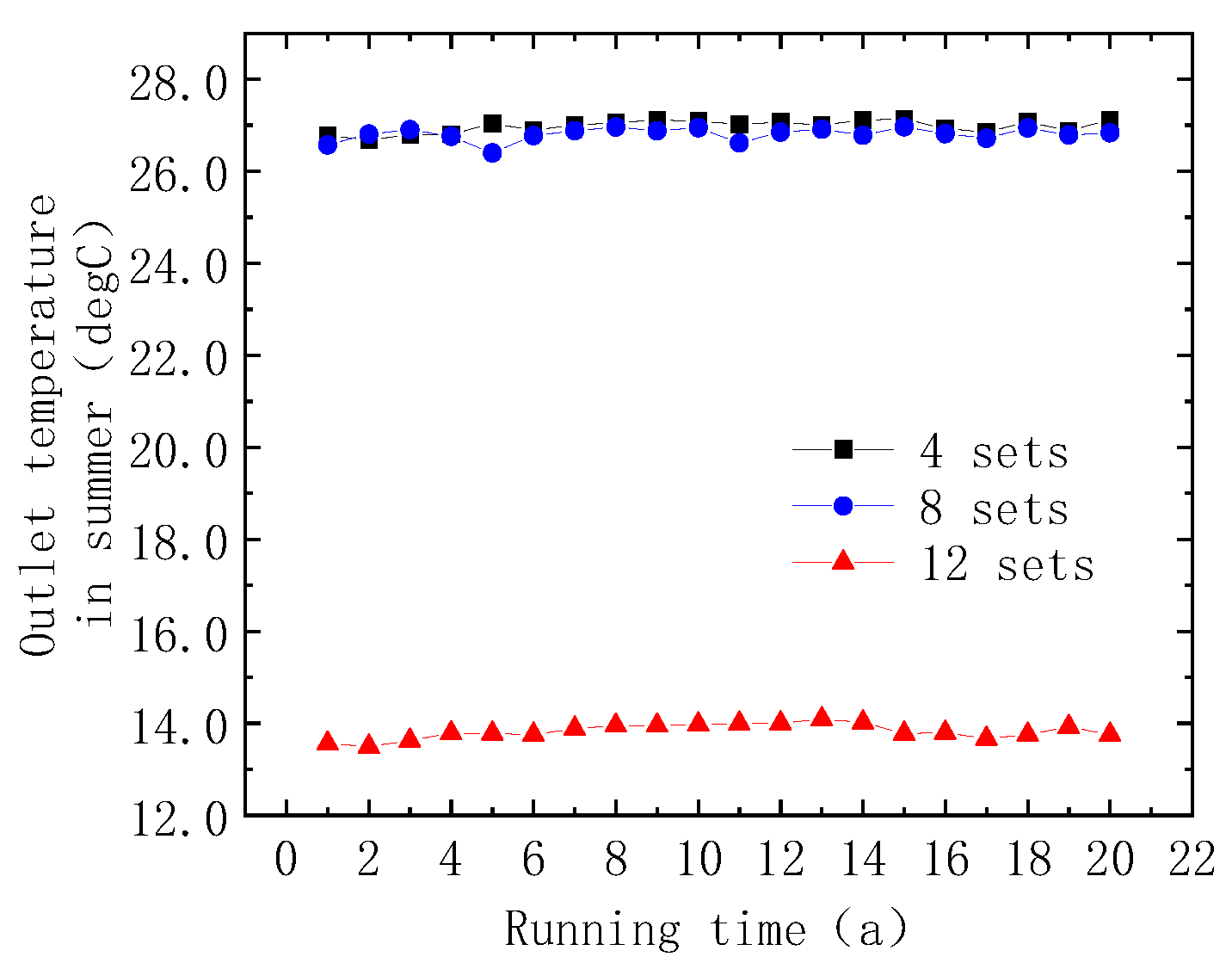
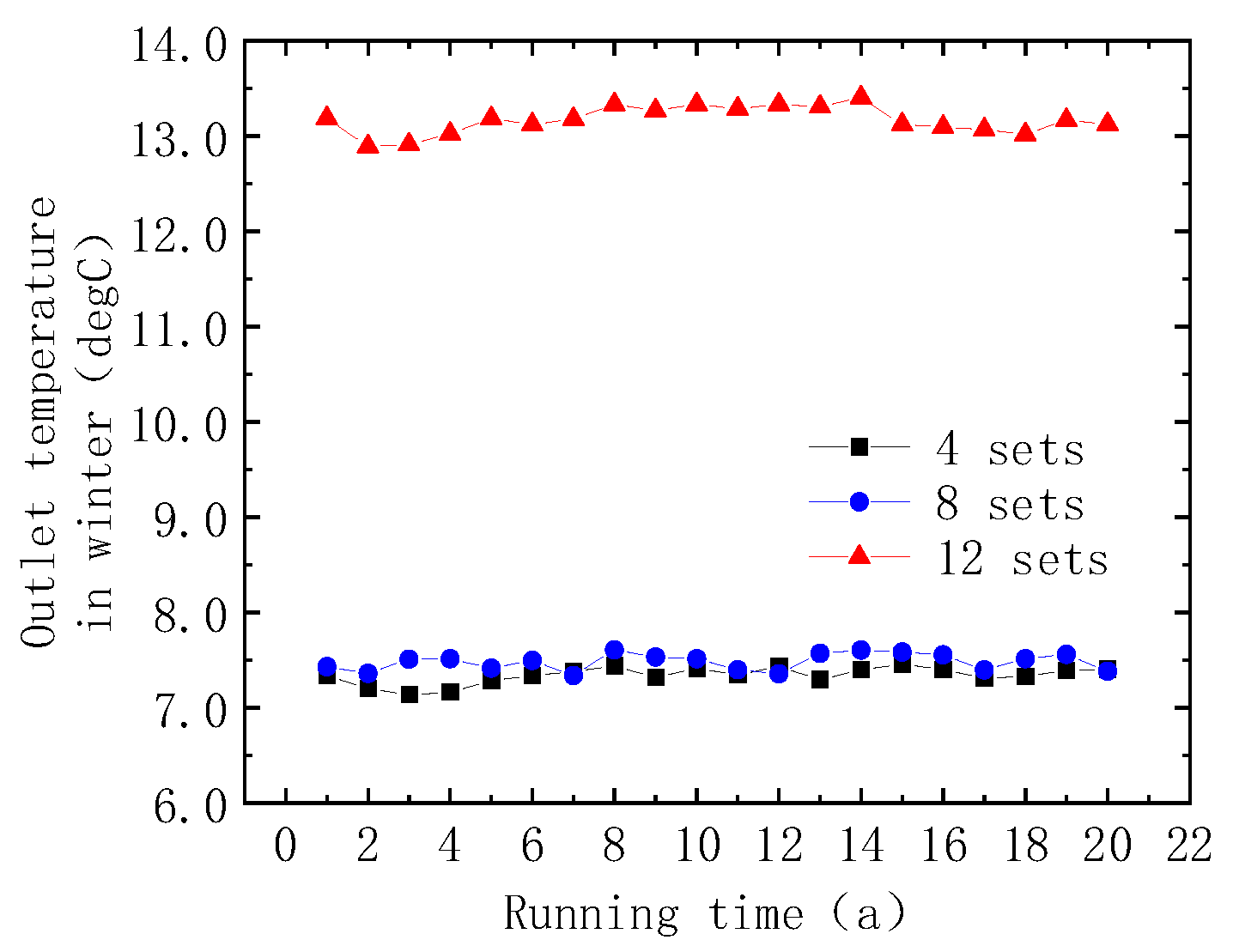
5.4. Effect of the Number of Heat Exchanger Groups
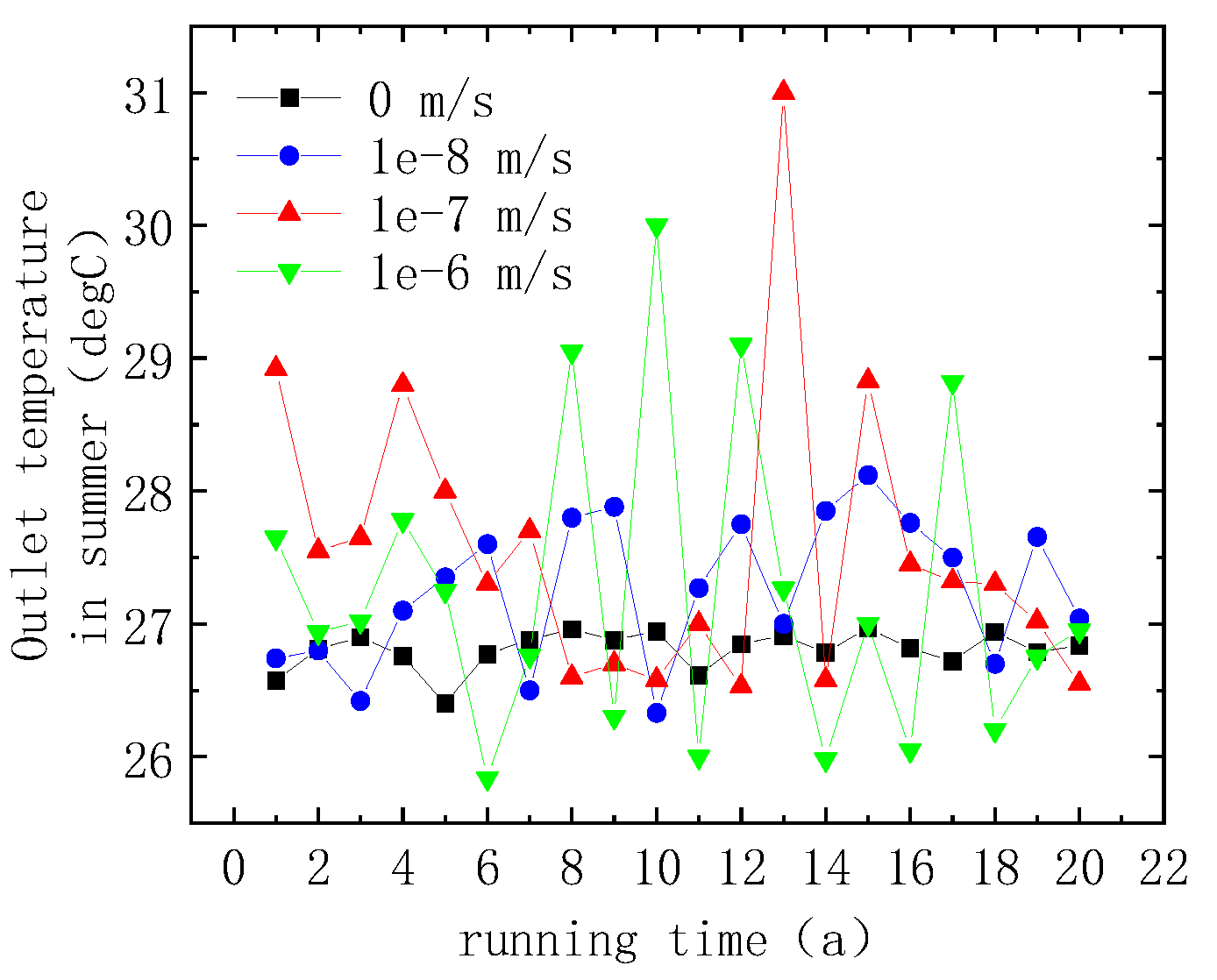
5.5. Effect of Groundwater Flow
6. Conclusions
- (1)
- During the alternating process of heat and cold extraction, the low- or high-temperature zone produced in the previous operating cycle has the promoting effect on the rise or decrease in outlet temperature in the next operating cycle;
- (2)
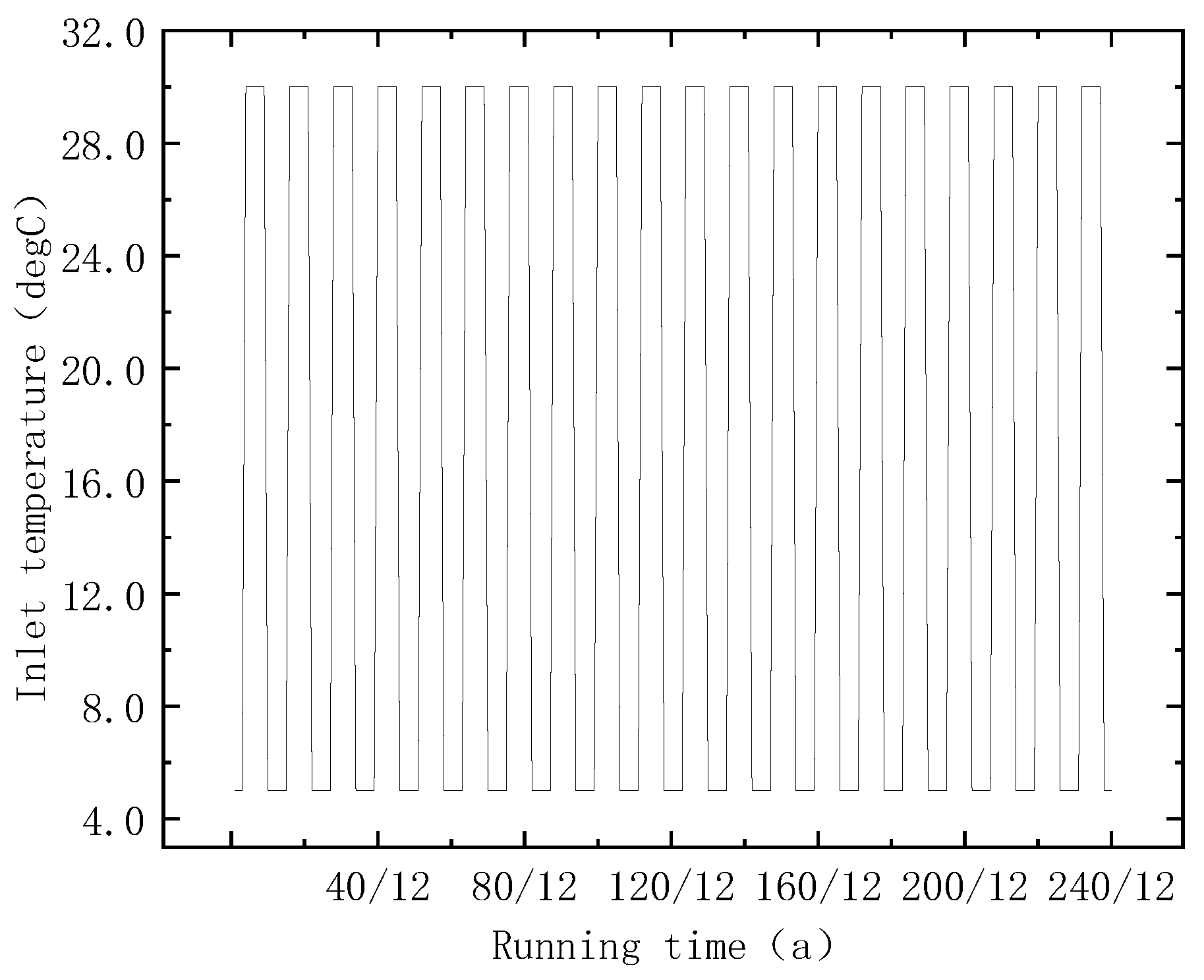
- When the heat extraction (with the injection temperature of 5 °C) and cold extraction (with the injection temperature of 30 °C) duration are consistent each year, it is beneficial to maintain the long-term stable operation for the shallow buried pipe system;
- (3)
- As the pipeline flow rate increases, the heat transfer efficiency of the buried pipe system gradually decreases. When the flow rate increases from 1 l/s to 3 l/s, the heat transfer efficiency in winter and summer decreases by 18.32% and 8.27%, respectively;
- (4)
- The heat transfer efficiency of the SBPS increases with the increase in thermal conductivity in summer, while in winter, the heat transfer efficiency first increases and then decreases with the raise of thermal conductivity. In addition, the operation stability increases with the increase in thermal conductivity;
- (5)
- The cold extraction efficiency in summer decreases with the increase in the heat injection time, while the heat extraction efficiency in winter increases with the increase in the heat injection time. When the heat injection time raises from 4 Ms to 8 Ms, the cold extraction efficiency in summer decreases by 6.59%, and the heat extraction efficiency in winter increases by 16.30%. Therefore, the consistent heat and cold injection time throughout the year is beneficial for the long-term stable operation of the shallow buried pipe system;
- (6)
- As the number of U-shaped tube heat exchanger groups increases, the heat transfer efficiency of the SBPS improves significantly. When the number of heat exchanger groups increases from 4 to 12, the heat transfer efficiency in winter and summer increases by 48.73% and 79.46%, respectively. In addition, as the number of heat exchanger groups increases, the variation pattern of heat transfer stability in cooling and heating condition is different. The stability under cooling conditions in summer increases with the increase in heat exchanger groups, while the stability under heating conditions in winter decreases with the increase in heat exchanger groups;
- (7)
- When there is no groundwater flow in the shallow reservoir, the energy accumulation will play the dominant role, while when the groundwater begins to flow, the energy accumulation effect will be weakened. However, with the increase in the groundwater flow velocity, the recovery ability of the underground temperature field will be enhanced, then the heat transfer efficiency of the SBPS will be improved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.P.; Li, G.; Han, Z.W.; Yang, Z.W.; Bi, W.; Li, X.; Yang, L. Study on the influence of buried pipe fault on the operation of ground source heat pump system. Renew. Energy 2023, 210, 12–25. [Google Scholar] [CrossRef]
- Gigot, V.; Francois, B.; Huysmans, M.; Gerard, P. Monitoring of the thermal plume around a thermally activated borehole heat exchanger and characterization of the ground hydro-geothermal parameters. Renew. Energy 2023, 218, 119250. [Google Scholar] [CrossRef]
- Hou, G.; Taherian, H.; Li, L. A predictive TRNSYS model for long-term operation of a hybrid ground source heat pump system with innovative horizontal buried pipe type. Renew. Energy 2020, 151, 1046–1054. [Google Scholar] [CrossRef]
- De León-Ruiz, J.E.; Beltrán-Chacón, R.; Carvajal-Mariscal, I.; Zacarías, A.; Rodríguez-Maese, R. A data-driven approach to low-enthalpy shallow geothermal energy extraction: A case study on indoor heating for precision agriculture applications. Case Stud. Therm. Eng. 2022, 40, 102578. [Google Scholar] [CrossRef]
- Dalla Santa, G.; Galgaro, A.; Sassi, R.; Cultrera, M.; Scotton, P.; Mueller, J.; Bertermann, D.; Mendrinos, D.; Pasquali, R.; Perego, R.; et al. An updated ground thermal properties database for GSHP applications. Geothermics 2020, 85, 101758. [Google Scholar] [CrossRef]
- Sun, Y.X.; Zhang, X.; Li, X.H.; Cheng, R. Study on the intrinsic mechanisms underlying enhanced geothermal system (EGS) heat transfer performance differences in multi-wells. Energy Convers. Manag 2023, 292, 117361. [Google Scholar] [CrossRef]
- Perego, R.; Dalla Santa, G.; Galgaro, A.; Pera, S. Intensive thermal exploitation from closed and open shallow geothermalsystems at urban scale: Unmanaged conflicts and potential synergies. Geothermics 2022, 103, 102417. [Google Scholar] [CrossRef]
- Li, W.J.; Zhang, W.K.; Li, Z.X.; Yao, H.; Cui, P.; Zhang, F. Investigation of the Heat Transfer Performance of Multi-Borehole Double-Pipe Heat Exchangers in Medium-Shallow Strata. Energies 2022, 15, 134798. [Google Scholar] [CrossRef]
- Galgaro, A.; Dalla Santa, G.; Zarrella, A. First Italian TRT database and significance of the geological settingevaluation in borehole heat exchanger sizing. Geothermics 2021, 94, 102098. [Google Scholar] [CrossRef]
- Kerme, E.D.; Fung, A.S. Heat transfer analysis of single and double U-tube borehole heat exchanger with two independent circuits. J. Energy Storage 2021, 43, 103141. [Google Scholar] [CrossRef]
- Jahanbin, A. Thermal performance of the vertical ground heat exchanger with a novel elliptical single U-tube. Geothermics 2020, 86, 101804. [Google Scholar] [CrossRef]
- Chen, Z.; Lian, X.W.; Tan, J.J.; Xiao, H.; Ma, Q.; Zhuang, Y. Study on heat-exchange efficiency and energy efficiency ratio of a deeply buried pipe energy pile group considering seepage and circulating-medium flow rate. Renew. Energy 2023, 216, 119020. [Google Scholar] [CrossRef]
- Cai, Y. Research on the Influencing Factors of Heat Exchange Capacity of Vertical Buried Tube Heat Exchanger. Master’s Thesis, China University of Geosciences (Beijing), Beijing, China, 2020. (In Chinese). [Google Scholar]
- Li, L.; Fu, Z.; Li, B.; Zhu, Q. Comparison of Thermal Performance for Two Types of ETFP System under Various Operation Schemes. Comput. Model. Eng. 2020, 124, 23–44. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, J.; Li, J.; Shao, J.; Zhang, Q. Numerical study on the heat performance of enhanced coaxial borehole heat exchanger and double U borehole heat exchanger. Appl. Therm. Eng. 2022, 203, 117916. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, J.; Li, T. Applicability of the pipe structure and flow velocity of vertical ground heat exchanger for ground source heat pump. Energy Build. 2016, 117, 109–119. [Google Scholar] [CrossRef]
- Harris, B.E.; Lightstone, M.F.; Reitsma, S.; Cotton, J.S. Analysis of the transient performance of coaxial and u-tube borehole heat exchangers. Geothermics 2022, 101, 102319. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, M.; Zhang, Y. Experimental and numerical investigation of vertical pipe–soil interaction considering pipe velocity. Ships Offshore Struct. 2017, 12, 1112178. [Google Scholar] [CrossRef]
- Jahanbin, A.; Semprini, G.; Pulvirenti, B. Performance evaluation of U-tube borehole heat exchangers employing nanofluids as the heat carrier fluid. Appl. Therm. Eng. 2022, 212, 118625. [Google Scholar] [CrossRef]
- Li, J.; Zheng, J.; Lei, X.D.; Jia, Z.; Liu, A.; Xu, Z. Influence of geologic conditions and buried pipe form on the heat transfer performance of buried pipe heat exchangers. Earth J. 2022, 44, 211–229. (In Chinese) [Google Scholar]
- Ye, W.J.; Dong, X.H.; Yang, G.S.; Chen, Q.; Peng, R.; Liu, K. Effect of moisture content and dry density on thermal parameters of loes. Rock Soil Mech. 2017, 38, 656–662. (In Chinese) [Google Scholar]
- Florides, G.; Christodoulides, P.; Pouloupatis, P. Single and double U-tube ground heat exchangers in multiple-layer substrates. Appl. Energy 2013, 102, 364–373. [Google Scholar] [CrossRef]
- Du, J.; Luo, Z.; Ge, W. Study on the simulation and optimization of the heat transfer scheme in a buried-pipe ground-source heat pump. Arab. J. Geosci. 2020, 13, 437–443. [Google Scholar] [CrossRef]
- Yue, G.F. Numerical simulation study on soil temperature field influenced by GSHP: A case study in Beijing. China Sci. 2017, 12, 1049–1053. (In Chinese) [Google Scholar]
- DiCarlo, A.A. Novel seasonal enhancement of shallow ground source heat pumps. Appl. Therm. Eng. 2021, 186, 116510. [Google Scholar] [CrossRef]
- Wang, L.; Ren, Y.L.; Deng, F.Q.; Zhang, Y.; Qiu, Y. Study on Calculation Method of Heat Exchange Capacity and Thermal Properties of Buried Pipes in the Fractured Rock Mass-Taking a Project in Carbonate Rock Area as an Example. Energies 2023, 16, 020774. [Google Scholar] [CrossRef]
- Fei, Y.C.; Zhou, Y.S.; Zhao, L.Y.; Zhang, Y.C. Effect of compound additives on performance of buried pipe grouting material. J. Donghua Univ. (Nat. Sci.) 2018, 44, 966–972. (In Chinese) [Google Scholar]
- Xu, Y.J.; Huang, X.W.; Fang, Y.; Shu, S.; Zhu, H. Heat transfer characteristics and heat conductivity prediction model of waste steel slag–clay backfill material. Therm. Sci. Eng. Prog. 2023, 46, 102203. [Google Scholar] [CrossRef]
- Song, X.; Jiang, M.; Qin, P. Numerical investigation of the backfilling material thermal conductivity impact on the heat transfer performance of the buried pipe heat exchanger. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 042010. [Google Scholar] [CrossRef]
- Mascarin, L.; Garbin, E.; Di Sipio, E.; Dalla Santa, G.; Bertermann, D.; Artioli, G.; Bernardi, A.; Galgaro, A. Selection of backfill grout for shallow geothermal systems: Materials investigation and thermo-physical analysis. Constr. Build. Mater. 2022, 318, 125832. [Google Scholar] [CrossRef]
- Peng, J.; Li, Q.; Huang, C. A New Environmentally Friendly Utilization of Energy Piles into Geotechnical Engineering in Northern China. Adv. Civ. Eng. 2021, 2021, 4689062. [Google Scholar] [CrossRef]
- Liu, C.; Yu, G.; Jia, S. A Quasi-Three Dimensional Transient Model for Thermal Calculation of Buried Pipe Heat Exchanger Systems. In Proceedings of the International Conference on Computational & Experimental Engineering and Sciences, Tokyo, Japan, 25–28 March 2019; Volume 22, p. 156. [Google Scholar]
- Wang, F.; You, T. Synergetic performance improvement of a novel building integrated photovoltaic/thermal-energy pile system for co-utilization of solar and shallow-geothermal energy. Energy Convers. Manag. 2023, 288, 1117116. [Google Scholar] [CrossRef]
- Chen, G.; Fan, H.; Wang, E.; Shen, H.; Zhang, X.; Wang, Z. Research on the Performance of Solar Energy Buried Pipe Heat Exchanger for Heating Landfill Technology. Sol. Energy 2023, 5, 69–77. [Google Scholar]
- Wei, Y.Q.; Kong, G.Q.; Zhang, J.B.; Yang, Q. Heat transfer efficiency of energy tunnel influenced by inlet temperature, flow rate and pipe spacing. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 072125. [Google Scholar] [CrossRef]
- Naranjo-Mendoza, C.; Oyinlola, M.A.; Wright, A.J.; Greenough, R.M. Experimental study of a domestic solar-assisted ground source heat pump with seasonal underground thermal energy storage through shallow boreholes. Appl. Therm. Eng. 2019, 162, 114218. [Google Scholar] [CrossRef]
- Shi, Y.; Cui, Q.L.; Yang, Z.J.; Song, X.; Liu, Q.; Lin, T. Optimizing the thermal energy storage performance of shallow aquifers based on gray correlation analysis and multi-objective optimization. Nat. Gas Ind. B 2023, 10, 476–489. [Google Scholar] [CrossRef]
- Harjunowibowo, D.; Omer, S.A.; Riffat, S.B. Experimental investigation of a ground-source heat pump system for greenhouse heating–cooling. Int. J. Low-Carbon Technol. 2021, 16, 1529–1541. [Google Scholar] [CrossRef]
- Nagare, R.M.; Mohammed, A.A.; Park, Y.J.; Schincariol, R.A. Modeling shallow ground temperatures around hot buried pipelines in cold regions. Cold Reg. Sci. Technol. 2021, 187, 103295. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Heyns, P. Thermo-structural fatigue and lifetime analysis of a heat exchanger as a feedwater heater in power plant. Eng. Fail. Anal. 2020, 113, 104548. [Google Scholar] [CrossRef]
- Alizadeh, A.; Ghadamian, H.; Aminy, M.; Hoseinzadeh, S.; Sahebi, H.K.; Sohani, A. An experimental investigation on using heat pipe heat exchanger to improve energy performance in gas city gate station. Energy 2022, 252, 123959. [Google Scholar] [CrossRef]
- COMSOL. Multiphysics User’s Guide, Version 6.1; COMSOL Inc.: Burlington, MA, USA, 2023; Available online: https://www.comsol.com (accessed on 1 November 2022).
- Zhang, W.; Wang, C.G.; Guo, T.K.; He, J.; Zhang, L.; Chen, S.; Qu, Z. Study on the cracking mechanism of hydraulic and supercritical CO2 fracturing in hot dry rock under thermal stress. Energy 2021, 221, 119886. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Z.L.; Guo, T.K.; Wang, C.; Li, F.; Qu, Z. The enhanced geothermal system heat mining prediction based on fracture propagation simulation of thermo-hydro-mechanical-damage coupling: Insight from the integrated research of heat mining and supercritical CO2 fracturing. Appl. Therm. Eng. 2022, 215, 118919. [Google Scholar] [CrossRef]
- Dalla Santa, G.; Schincariol, A.R. Effect of thermal-hydrogeological and borehole heat exchanger properties on performance and impact of vertical closed-loop geothermal heat pump systems. Hydrogeol. J. 2014, 22, 189–203. [Google Scholar]



| Project | Value | Unit |
|---|---|---|
| Height of the geometric model | 210 | m |
| Length of the geometric model | 62 | m |
| Width of the geometric model | 33 | m |
| Pipeline diameter | 36 | mm |
| Pipeline flow rate | 1 | l/s |
| Temperature gradient | 0.027 | °C/m |
| Formation thermal conductivity | 1.5 | W/(m·k) |
| Formation permeability | 10 × 10−12 | m2 |
| Thermal conductivity of pipeline | 10 | w/(m·k) |
| Pipeline wall thickness | 0.005 | m |
| Darcy friction coefficient | 1.5 × 10−3 | mm |
| Number of U-shaped tube heat exchanger groups | 4 | group |
| Injection temperature in winter | 5 | °C |
| Injection temperature in summer | 30 | °C |
| Length of U-shaped buried well | 200 | m |
| Distance between each U-shaped buried pipe | 6 | m |
| Pipeline diameter | 36 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhang, W.; Wang, M.; Wang, C.; Wei, Z.; Wang, D.; Zheng, P. Heat Transfer Mechanism of Heat–Cold Alternate Extraction in a Shallow Geothermal Buried Pipe System under Multiple Heat Exchanger Groups. Energies 2023, 16, 8067. https://doi.org/10.3390/en16248067
Shi J, Zhang W, Wang M, Wang C, Wei Z, Wang D, Zheng P. Heat Transfer Mechanism of Heat–Cold Alternate Extraction in a Shallow Geothermal Buried Pipe System under Multiple Heat Exchanger Groups. Energies. 2023; 16(24):8067. https://doi.org/10.3390/en16248067
Chicago/Turabian StyleShi, Jianlong, Wei Zhang, Mingjian Wang, Chunguang Wang, Zhengnan Wei, Dong Wang, and Peng Zheng. 2023. "Heat Transfer Mechanism of Heat–Cold Alternate Extraction in a Shallow Geothermal Buried Pipe System under Multiple Heat Exchanger Groups" Energies 16, no. 24: 8067. https://doi.org/10.3390/en16248067
APA StyleShi, J., Zhang, W., Wang, M., Wang, C., Wei, Z., Wang, D., & Zheng, P. (2023). Heat Transfer Mechanism of Heat–Cold Alternate Extraction in a Shallow Geothermal Buried Pipe System under Multiple Heat Exchanger Groups. Energies, 16(24), 8067. https://doi.org/10.3390/en16248067




