Applying Energy Justice Principles to Renewable Energy Trading and Allocation in Multi-Unit Buildings

Abstract

Although rooftop PV panels and battery energy storage systems have been well established for detached residential buildings, there is still a lack of access to the advantages of onsite renewable energy generation and consumption for residents of multi-unit buildings. To understand the effects of developing distributed renewable energy sources for multi-unit buildings, a new fair energy-sharing model in which different groups of residents can gain benefit from the shared energy systems is proposed. Despite the potential benefits of developing renewable technologies in multi-unit buildings, the energy trading and allocation processes in the buildings can be unfair for some groups of residents. Accordingly, this work studies the main principles of energy justice and analyses how these principles can be applied in the energy trading and allocation processes to achieve fair energy sharing. In addition to fairness and justice, the experimental results show that our method increases the sellers’ profit by 59.7–127% and decreases the buyers’ cost by 8–21%, compared to the baseline methods. Moreover, applying the energy justice principles in the proposed sharing models acts as an efficient incentive for the residents of the multi-unit buildings to invest in the shared distributed renewable energy sources.

1. Introduction

Solar photovoltaic (PV) generation is one of the main technologies for decentralizing and decarbonizing energy systems. To date, PV panels are a settled and approved solution for detached houses, while PV solutions for multi-unit buildings have been relatively limited. Recent studies focus mainly on PV usage in single residential buildings [1] as well as commercial buildings [2,3]. Although distributed renewable energy sources (DRESs) have been widely approved at the residential scale, especially in detached houses, the lack of a legal framework prevents the installation of PV panels and battery energy storage systems (BESSs) in buildings that are composed of several apartment units. The primary reason for the low uptake of sharing DRESs in multi-unit buildings is the lack of regulations to ensure that electricity tax, grid rent, and settlements are in line [4]. Recent studies related to PV panel allocation in multi-unit buildings have focused more on evaluating the technical performance [5] and analyzing the economic and technical feasibility of PV panels in microgrids [6,7]. However, shared DRESs, including PV panels and BESSs, in multi-unit buildings have not been investigated well.

Given that the units of multi-unit buildings are occupied by different groups of residents, e.g., tenants and unit owners with different preferences, the process of sharing energy from shared DRESs between these groups can be unjust and challenging. For instance, from the perspective of investing in shared DRESs, some residents could not afford the investment economically, or there might be a group of residents, such as tenants, who want to enjoy the benefits of shared DRESs for a short period because long-term investment is not affordable for them. In this regard, this study proposes an energy-sharing model that enables efficient, fair, and equitable allocation and distribution of energy, costs, and benefits in multi-unit buildings, considering different groups of residents.

Energy justice provides an effective decision-making tool that helps stakeholders, e.g., consumers and producers, to make more rational energy decisions [8]. In recent years, scholars have reached a joint definition of energy justice in which the costs and benefits of energy services are fairly distributed, and equitable energy decision-making is provided [9]. In general, energy justice addresses the equitable sharing of energy, costs, and benefits and identifies injustices within energy systems [8,9]. Energy justice integrates three different, but interconnected principles that include distributive justice, procedural justice, and recognition justice [10]. Each principle relates to a particular aspect of justice that complements each other. Distributive justice refers to whether all groups share equally in specific services and goods. Procedural justice deals with the equitable participation of stakeholders in decision-making processes. Recognition of justice gives attention to the demands and rights of different groups in society, especially underrepresented or vulnerable groups, to decrease social inequalities [10]. The value of energy justice has not been studied within the concept of energy sharing in multi-unit buildings. Therefore, a set of steps has to be formulated to enable a fair and just energy-sharing system in multi-unit buildings where different groups of residents can participate and gain benefit from the shared DRESs in their building. Applying the principles of energy justice in energy-sharing models removes or reduces barriers to the active participation of end customers (consumers/prosumers) in the future smart and decentralized energy grid.

In this paper, a new fair energy sharing model (FESM) is proposed, which focuses on energy allocation and trading inside different multi-unit buildings, considering energy justice principles. The basis for our definition of FESM is a network behind the meter in which the shared systems (PV panels and BESSs) can be owned by the main owner of a multi-unit building or a group of residents living in the building. Although FESM and community-based microgrids have similarities in their configurations (e.g., both rely on centralized renewable sources), they have an important difference. In community microgrids, shared DRESs are located in front of the meter that are controlled by utility companies (i.e., they are controlled in an aggregate manner) that incur extra costs for the users who use the shared systems (e.g., there will be administrative costs) [11]. Since users of community DRESs do not own DRESs, they are deprived of having access to any of the tax credits and incentives of DRESs. However, in FESM, shared DRESs are installed behind the meter and are not controlled by utility companies; hence, additional costs are eliminated for users. Moreover, users in FESM can own a portion of DRESs and take advantage of the tax benefits.

After allocating shared DRESs and energy to the residents by the energy management operator (EMO) of the buildings, energy trading is enabled in FESM with expected prominent benefits such as cost-savings and carbon footprint reduction. The EMO of the buildings monitors and controls the trading stage and computes the trading price. During the energy trading process, the interests of sellers and buyers are protected, and they are given the opportunity to determine the amount of energy they want to sell and buy based on certain factors, such as priority factors, or after seeing the price. The priority factor is defined as one of the main elements of FESM to retain the fairness and interests of both buyers and sellers during energy trading. Justice and fairness are analyzed in energy allocation and trading processes according to the main principles of energy justice. These analyzes help to understand that justice can be defined differently for each building according to the building conditions (e.g., resident preferences, types of residents, etc.). Moreover, the revenue of the shared DRESs’ users living in the multi-unit buildings are examined under different energy allocation processes. The experimental results show that our method is highly beneficial for all participants as their revenue increases dramatically compared to the baseline methods.

The main contributions of this work are as follows:

• We present a novel fair energy sharing framework FESM plus two different applications of it. In FESM energy demand of buildings is supplied by shared distributed renewable energy sources, including PV panels and battery energy storage systems. FESM is a behind-the-meter network that enables energy allocation and trading inside the buildings.
• To the best of our knowledge, this work is the first to apply the main principles of energy justice, including procedural justice, recognition justice, and distributive justice, in a systematic way in the design of energy allocation and trading processes to create justice and fairness. Moreover, we propose a novel priority factor to prioritize users to secure fair sharing of energy generated by shared DRESs for residents.
• A new and simple pricing mechanism is proposed that increases the profits for sellers and decreases the cost for buyers, and makes the overall operation of the system simple.

The rest of the paper is organized as follows. In the following section, first, we present a brief overview of the shared renewable energy system in multi-unit buildings by discussing the status quo of energy sharing in four countries, including Germany, Austria, France, and Norway. Then, fairness in energy sharing is reviewed, and we discuss how energy justice principles can be applied in an energy-sharing process. The details of the FESM network are presented in Section 3; then, the strategies for energy trading for all participants, such as sellers, buyers, and energy management operators, are summarized in Section 4. Section 5 presents comprehensive experimental results, and the paper is concluded in Section 6.

2. Background

2.1. Shared Renewable Energy Systems

Renewable energy sources have been potentially considered as a practical solution to supply parts of the load in buildings, especially in urban areas [12]. The establishment of more renewable energy communities can increase both the share of renewable energy and flexibility in electricity supply and electricity systems, respectively. Currently, many European countries have not fully considered the particulars of renewable energy communities in their energy support frameworks. However, Germany has the most experience with community energy [13]. In the following, we briefly review the current situation of energy sharing in multi-unit buildings in four countries.

Germany and Austria: In Germany and Austria, shared PV systems can be implemented legally in multi-unit buildings. Germany makes the hardest efforts to increase the uptake of shared PVs in buildings among European countries [12]. In [14], a techno-economic analysis of the self-consumption of rooftop solar panels for different types of buildings in Germany, including multi-unit buildings, is performed. In the course of different projects in Germany, it has been proven that energy generated from PV panels can be successfully shared in buildings under a novel concept called the “Mieterstrommodel” [15]. Under this scheme, landlords or owner communities known as ‘legal suppliers’ may generate energy from rooftop PV panels and sell it to their tenants [16]. Tenants receive the same feed-in tariff compensation for extra energy fed into the grid. However, they receive an extra ‘tenant-electricity surcharge’ for their self-consumed energy [16]. In July 2017, Austria also adopted relevant legislation to enable the uptake of shared PV panels in multi-unit buildings. In Austria, suppliers are also able to supply the energy demand of residents via energy produced by their buildings’ PV panels [12].

France: On 8 November 2019, law no. 2019-1147 was approved in France. It regulates collective electricity self-consumption (In French: autoconsommation collective d’électricité) of energy and climate [17]. In France, users willing to contribute to a collective self-consumption (CSC) operation can establish themselves as an Organizing Moral Person (OMP) responsible for sharing locally produced energy among users. Moreover, each user must be connected to the public distribution network via a meter. The OMP considers the energy sharing ratio equal to the ratio of the total consumption of one household to the consumption of all households. Other sharing ratios among users can be defined by the OMP, and communicated to the distributed system operator (DSO). among users and sends it to the DSO. Each user’s bill is calculated based on the consumption of the household minus the community generation assigned to the household by the supplier, which the user has chosen. CSC communities can be considered platforms for creating innovation in energy sharing. However, community-wide operating rules that adopt consumption practices for single houses, buildings, or neighborhoods are essential for any energy community [17].

Norway: In Norway, customers in detached houses, with both consumption and production behind their connection point, can today utilize their own production without paying grid rent and other fees [18]. However, customers in multi-unit buildings do not enjoy the same benefits. This means that, according to the current regulations, it is not possible for customers in multi-unit buildings who have several measuring points to use their own production without paying grid rent and fees [18]. Recently, a new regulation was proposed by the regulating body, RME [18], which, if approved, will change the rule of sharing energy in buildings. In the RME proposal, different sharing models that can be applied inside the buildings and how energy can be allocated to the residents who joined the sharing solution are discussed. Below, the proposed sharing solutions are reviewed.

• Equal sharing: the simplest way is allocating the production of shared PV panels to residents equally. This means that all residents receive the same share. Although this sharing model is easily managed by network companies, it poses some weaknesses. This model is fair when all building units have the same area, but this is not fair for units with different areas. A larger unit requires more energy than a smaller one.
• Unequal sharing: unequal sharing means that each resident receives different shares of the energy generated by the shared PV panels in the building, e.g., based on the size of the units, the cost that each resident invests in the shared PV panels, etc. In FESM, we focus on the unequal sharing model as a guideline for specializations of the framework that we explore in this paper.
• Dynamic sharing: in this model, residents receive energy based on their consumption at various time slots in a day. This sharing model attempts to maximize the utilization of the energy produced by PV panels in buildings. In this case, the energy is sent back to the grid only for hours, where the total generation exceeds the total consumption in the building. The dynamic share of a resident at a time slot is the ratio of the resident’s consumption to the total consumption of the residents at that time slot.

Legalizing the shared use of PV panels in multi-unit buildings and giving the right to the residents to trade their shared energy with neighbors inside their building benefits the residents (e.g., financial benefits) and the environment (e.g., carbon reduction). To realize that, the above regulations need to be developed with the intention of legalizing energy trading inside multi-unit buildings.

2.2. Fairness in Renewable Energy Sharing

Fairness in energy sharing has been interpreted in different ways in the literature. For example, one study [19] shows that if energy is transparently and equitably shared in a sharing method, then the method is fair. Other studies present different interpretations [20,21,22]. According to [20], fairness is associated with the willingness-to-pay of a prosumer, equal satisfaction is another interpretation of fairness that is supported by Jafari et al. [21], and Lovati et al. [22] proposed a peer-to-peer (P2P) energy trading model in which fairness has been achieved by transparency.

There are several works that use game theoretical approaches to conduct energy sharing in buildings [23,24]. For instance, Cui et al. [25] proposed a non-cooperative game to manage the energy-sharing process, and they believe that energy sharing is fair when all participants gain benefits. A contribution-based and non-pricing energy trading mechanism between microgrids was proposed by Park et al. [26], but they did not show how to calculate the contribution factor. Jadhav et al. [27] extended the work in [26] by proposing a priority factor for buyer microgrids according to their contributions and energy demand. However, prioritizing buyers based on their energy demand makes buyers with the highest demand receive more energy which can be unfair. The authors in [27] also presented an energy trading mechanism based on Nash bargaining theory in which a trading price was computed based on minimizing the total cost of buyer microgrids. In [26,27], only the interests of the buyer microgrids are considered, which makes the energy trading unfair to the seller’s microgrids. In this work, the energy trading method used in [26] is extended in such a way that the benefits of both buyers and sellers are supported in the calculation of the energy trading price. In addition, the priority factor is modified and calculated for both sellers and buyers according to the trading situations.

Some works present different energy-sharing methods and compute a proper fairness index to evaluate the performance of their methods. For example, Long et al. [28] proposed several indexes, including the equality index and participation willingness index, to evaluate their proposed P2P energy trading mechanism, while Chakraborty et al. [29] used the Nash social welfare index for the same purpose. According to the literature, a common framework for evaluating fairness and justice in energy-sharing solutions is missing. Energy justice can be used as an evaluation framework to evaluate fairness in energy-sharing models based on its three main principles. In the following, we will study how justice and fairness can be achieved in energy-sharing systems through the main principles of energy justice.

Recognition justice: This principle of energy justice takes care of different groups of stakeholders, especially vulnerable groups, to have equal access to opportunities and resources in energy systems [9,10]. When recognition justice is considered in designing an energy-sharing model, we have to explore to what extent different groups (e.g., low and high-income groups, tenants, and unit owners) have access to technologies used in the model.

Distributive justice: This principle is about benefit and risk being equitably distributed among stakeholders in energy systems [9,10]. According to this principle, we have to evaluate how cost, profit, DRESs, and energy generated by shared PV panels are distributed among stakeholders (e.g., residents and owners of multi-unit buildings).

Procedural justice: This principle emphasizes that all stakeholders affected by the energy systems have to participate equitably in decision-making [9,10]. In designing an energy-sharing model for multi-unit buildings, we have to focus on how residents can significantly participate in decision-making with transparent procedures.

3. Proposed FESM Framework

We assume a building that has an owner who can be a legal entity such as a person, a company, a municipality, or a cooperative, etc. The energy-sharing model is decided by the owner of the building. The energy-sharing model is the basis for energy allocation and trading. The energy allocation and trading processes in the building are handled by EMO, who could be the owner of the building, a third party, or consortium of residents, etc. The building is comprised of N units denoted by the set $\mathcal{U}=\{1,2,\dots ,N\}$. Each unit has an owner and can be occupied by the owner, called unit-owner, or a tenant. Let $|{\mathcal{U}}_O|=N_O$, where ${\mathcal{U}}_O\subseteq \mathcal{U}$ and $N_O<N$, and $|{\mathcal{U}}_T|=N_T$, where ${\mathcal{U}}_T\subseteq \mathcal{U}-{\mathcal{U}}_O$ and $N_T=N-N_O$, be the sets of unit-owners and tenants, respectively, who live in the building. Each unit is characterized by a set of parameters, such as the area of the unit and the number of members living in the unit, that can be input into the sharing model. The building can be equipped with a number of PV panels that belong to the set $\mathcal{PV}=\{1,\dots ,P\}$. PV panels have an owner that can be the owner of the building, a third party, or a legal entity formed by residents who each own a share. Depending on the sharing model, the residents can lease a share of the PV panels from the owner. Since PV panels may produce more energy than residents need during some time slots in a day, a set of BESSs $\mathcal{B}=\{0,1,\dots ,B\}$ are shared between residents of buildings. Similar to PV panels, each BESS has an owner that can be the owner of the building or a group of residents. Both unit owners and tenants can lease a share of BESSs. Residents can trade their excess energy generated by PV panels inside the building.

In FESM, the allocation process refers to the step where the EMO of the building allocates a fair share of energy generated from PV panels or the energy saved into the shared batteries to the residents of the building. The unequal sharing model proposed by the RME proposal [18] (see Section 2.1) is used for the allocation process in the building. Compared with other sharing models, the unequal sharing model allows the owner of the building to allocate a fair and different share of energy (i.e., $x\%\times Generatio{n}^{PV}$, where $Generatio{n}^{PV}$ is the total generation of PV panels) or capacity of BESSs (i.e., $x\%\times BES{S}^{capacity}$, where $BES{S}^{capacity}$ is the total capacity of BESS) to the residents. The allocated share ($x\%$) can vary between the residents participating in the sharing solution as long as $\sum x=100$, and can be based on different factors, such as the resident’s need or the amount the resident invests in DRESs, etc. In the allocation process, recognition justice will be achieved when all groups of residents, including tenants, unit owners, low-income families, etc., have the opportunity to exploit the building’s DRESs. In the building, a fair share of energy can be allocated to each unit of the building based on factors such as the area of the unit, family members living in the unit, etc. Hence, in this case, distributive justice will be achieved by distributing energy generated by DRESs among the units based on unit characteristics. In other cases, residents can invest in DRESs based on their ability to pay. In this situation, distributive justice is realized by allocating energy to the residents in proportion to the cost that they have invested in DRESs. Moreover, in the energy allocation process, residents can participate in decision-making in which, for example, they can decide whether to invest in DRESs or pay only for their consumption. Therefore, procedural justice will also be fulfilled in the allocation process.

After the allocation step, energy trading takes place in one step, where local energy is traded between the residents of the building. During energy trading, justice is realized so that participants, including sellers, buyers, and the EMO of the building, can participate in decision-making processes (procedural justice), and all groups of residents have the opportunity to participate in energy trading (recognition justice) and gain financial benefit by selling or buying excess energy from DRESs (distributive justice). The following sections discuss the fair energy allocation and trading processes within the proposed framework for two different multi-unit buildings, i.e., Building A and B, illustrating two different approaches to applying the principles of energy justice. These two approaches will be experimentally compared with regard to distributive justice, recognition justice, and procedural justice.

3.1. Building A

Building A has an owner who is a person. This building consistents of $N_A$ units identified by the set ${\mathcal{U}}_A$ such that ${\mathcal{U}}_A\subseteq \mathcal{U}$, ${\mathcal{U}}_A=N_A$, and $N_{O,A}$ and $N_{A,T}$ of the units, where $N_{A,O}<N_A$ and $N_{A,T}=N_A-N_{A,O}$, are occupied by unit-owners and tenants, respectively. Building A is equipped with P rooftop PV panels and B BESSs funded by the owner of the building. The EMO of Building A is the building owner who allocates a fair share of DRESs and energy generated by the PV panels to each unit of the building. After the allocation process, energy trading managed by the EMO of the building takes place in one step, where the local surplus energy is traded between the building occupants. The possible ways of allocating energy in Building A are discussed in the following.

Energy allocation: In building A, the EMO of the building allocates a certain share of PV panels and BESSs to each unit of the building, giving all residents the opportunity to enjoy the benefits of shared DRESs in their building. The allocation process in Building A is based on the unequal sharing model [18]. In this regard, the EMO of the building allocates $x_i\%$ of PV panels (i.e., $x_i\%P{V}^{area,A}$) and BESSs (i.e., $x_i\%BES{S}^{capacity,A}$ ), where $x_i$ is based on the area of unit i and the number of family members living in the unit. The PV panel share ($P{V}_i^{share,A}$) and BESS share ($BES{S}_i^{share,A}$) for the ith unit in Building A are computed as follows:

$$P{V}_i^{share,A}=(\alpha \frac{Uni{t}_i^{area,A}}{Uni{t}^{area,total,A}}+(1-\alpha )\frac{Member{s}_i^A}{Member{s}^{total,A}})P{V}^{area,A},\forall i\in {\mathcal{U}}_A$$

(1)

$$BES{S}_i^{share,A}=BES{S}^{capacity,A}(\alpha \frac{Uni{t}_i^{area,A}}{Uni{t}^{area,total,A}}+(1-\alpha )\frac{Member{s}_i^A}{Member{s}^{total,A}}),\forall i\in {\mathcal{U}}_A$$

(2)

where $P{V}^{area,A}$ and $Uni{t}_i^{area,A}$ are the total area of the PV panels and the area of the ith unit in Building A, respectively. $Member{s}_i^A$ and $Member{s}_i^{total,A}$ are the number of members who live in unit i and the total number of residents living in Building A, respectively. In the above equations, $\alpha$ is a weight factor that gives importance to the number of family members living in a unit and the area of the unit while allocating PV panels and BESSs. In this work, the value of $\alpha$ is set to 0.5 to give equal importance to both numbers of family members and the area of the unit. In Equation (2), $BES{S}^{capacity,A}$ is the total capacity of the building’s battery.

If the shared PV panels in building A generate $G_i^{PV,A}$ amount of energy at time slot t, unit i will receive $E_i^{allocated,A}$ share of energy according to the following equation:

$$E_{i,t}^{allocated,A}=P{V}_i^{share,A}{G}_i^{PV,A},\forall i\in {\mathcal{U}}_A$$

(3)

In Building A, residents can decide whether to lease their share or just pay for their consumption. The latter is most suitable for temporary residents, such as tenants or residents who cannot afford the lease cost. leasing PV panels/BESSs allows residents to sell the remaining energy from their share; otherwise, the remaining energy belongs to the building owner. The lease cost for a resident who leases a share of a PV panel is computed as a certain percentage of the benefit that the resident gain by using the PV panel. The percentage value is defined by the building owner and should not be set too high to avoid loss of benefit. Hence, the value is set to 10%.

3.2. Building B

Similar to Building A, Building B has an owner who is a person and acts as the EMO of the building. We assume that Building B does not possess PV panels and BESSs. Hence, a group of or all building residents decide to install PV panels on the roof of the building with the permission of the building owner. In this case, residents who cooperate to buy PV panels or BESSs are considered owners of PV panels or BESS, respectively. Building B has $N_B$ units; let $|{\mathcal{U}}_B|=N_B$, where ${\mathcal{U}}_B\subseteq \mathcal{U}$, be the set of the units. In the building, there are $N_{B,O}$ and $N_{B,T}$ units, where $N_{B,O}<N_B$ and $N_{B,T}=N_B-N_{B,O}$, that are occupied by unit-owners and tenants.

Energy allocation: In Building B, $n_{pv-o}$ of unit-owners buy PV panels for the building. Let ${\mathcal{U}}_{B,O}$ be the set of such unit-owners such that $|{\mathcal{U}}_{B,O}|=n_{pv-o}$, where $n_{pv-o}\le N_{B,O}$. A number of those unit-owners (i.e., $m_{pv-o}$ of $n_{pv-o}$, where $m_{pv-o}\le n_{pv-o}$) live in the building, and the rest (i.e., $n_{pv-o}-m_{pv-o}=N_{B,T}$) rent their units. In this building, the EMO of the building defines an ownership concept to distribute energy to unit-owner i, where $i\in {\mathcal{U}}_{B,O}$, based on the size of the unit owner’s investment in PV panels. Given that the ownership factor varies for each unit-owner i, the EMO of the building follows the unequal sharing model [18] for allocating the energy generation of the PV panels in the building. The ownership factor ($Ownershi{p}_i^{PV,B}$) for the ith unit-owner who owns a share of PV panels and lives in Building B, where $i\in {\mathcal{U}}_{B,O}$, is equal to the ratio of the cost ($C{t}_i^{PV,B}$) that is invested by the unit-owner to the total cost ($C{t}^{PV,total,B}$), and can be written as follows:

$$Ownershi{p}_i^{PV,B}=\frac{C{t}_i^{PV,B}}{C{t}^{PV,total,B}},\forall i\in {\mathcal{U}}_{B,O},$$

(4)

In addition, the amount of energy $E_i^{allocated,B}$ that the ith unit-owner in Building B will receive is computed as follows:

$$E_{i,t}^{allocated,B}=Ownershi{p}_i^B{G}_t^{PV,B},\forall i\in {\mathcal{U}}_{B,O},$$

(5)

where $G_t^{PV,B}$ is the amount of energy generated by the PV panels in Building B at time slot t.

The investment cost ($Cos{t}_i^{investment,B}$) of unit-owner i per day in Building B is given by the following Equation.

$$Cos{t}_i^{investment,B}=\frac{C{t}_i^{PV,B}}{Paybac{k}^B}$$

(6)

where $Paybac{k}^B$ is the period of time it will take the unit-owner i to pay off the total cost of the PV panel share. Similar to Building A, the lease cost for the tenant who leases a share of PV panels from their unit owner is a certain percentage of the tenant’s benefit and is set to 10%.

Residents of Building B can also contribute to buying BESSs for the building. Let us assume there are $n_{b-o}$ unit-owners who pay for a share of BESSs, and $|{\mathcal{U}}_{B,b-o}|=n_{b-o}$, where $n_{b-o}\le N_{B,O}$, is the set of such unit-owners. The ownership factor $Ownershi{p}_j^{battery,B}$ for the jth unit-owner who owns a share of BESSs, where $j\in {\mathcal{U}}_{B,b-o}$, is computed as follows:

$$Ownershi{p}_j^{battery,B}=\frac{C{t}_j^{battery,B}}{C{t}^{battery,total,B}},\forall j\in {\mathcal{U}}_{B,b-o},$$

(7)

In addition, the share of BESS $BES{S}_j^{share,B}$ that is allocated to the jth unit-owner in Building B is:

$$BES{S}_j^{share,B}=Ownershi{p}_j^{battery,B}BES{S}^{capacity,B},\forall j\in {\mathcal{U}}_{B,b-o},$$

(8)

Generally speaking, residents can charge their share of the battery. If some residents have available capacity in the battery, they can allow other residents to use their capacity at a specific time slot in a day until an agreed-upon time.

Regarding investing in PV panels and BESSs, there are some situations that should be taken into consideration. In Building B, unit owners who do not live in the building and own a share of PV panels or BESSs can lease a part of their share to their tenant. In this case, tenants benefit from energy generated by PV panels by paying for their energy consumption or a fee in excess of their housing rent. In the latter case, tenants can sell the excess energy from their share of PV panels. There might be residents who do not have the opportunity to use PV panels/BESSs in the building. Examples can be tenants whose unit-owners do not invest in PV panels/BESSs, residents who cannot afford the investment cost, residents who just moved into the building and want to own a share of PV panels and there is no available space on the roof of the building for installing PV panels, etc. This issue of fairness is outside the scope of this paper.

3.3. Overview of Fair Local Energy Trading in FESM

Regardless of the group of the building, the EMO of the building has the duty to fulfill the energy demand of all residents. The residents with extra and lack of energy are considered sellers and buyers, respectively. A non-cooperative game takes place between buyers and sellers separately to adjust their energy demand through the game. 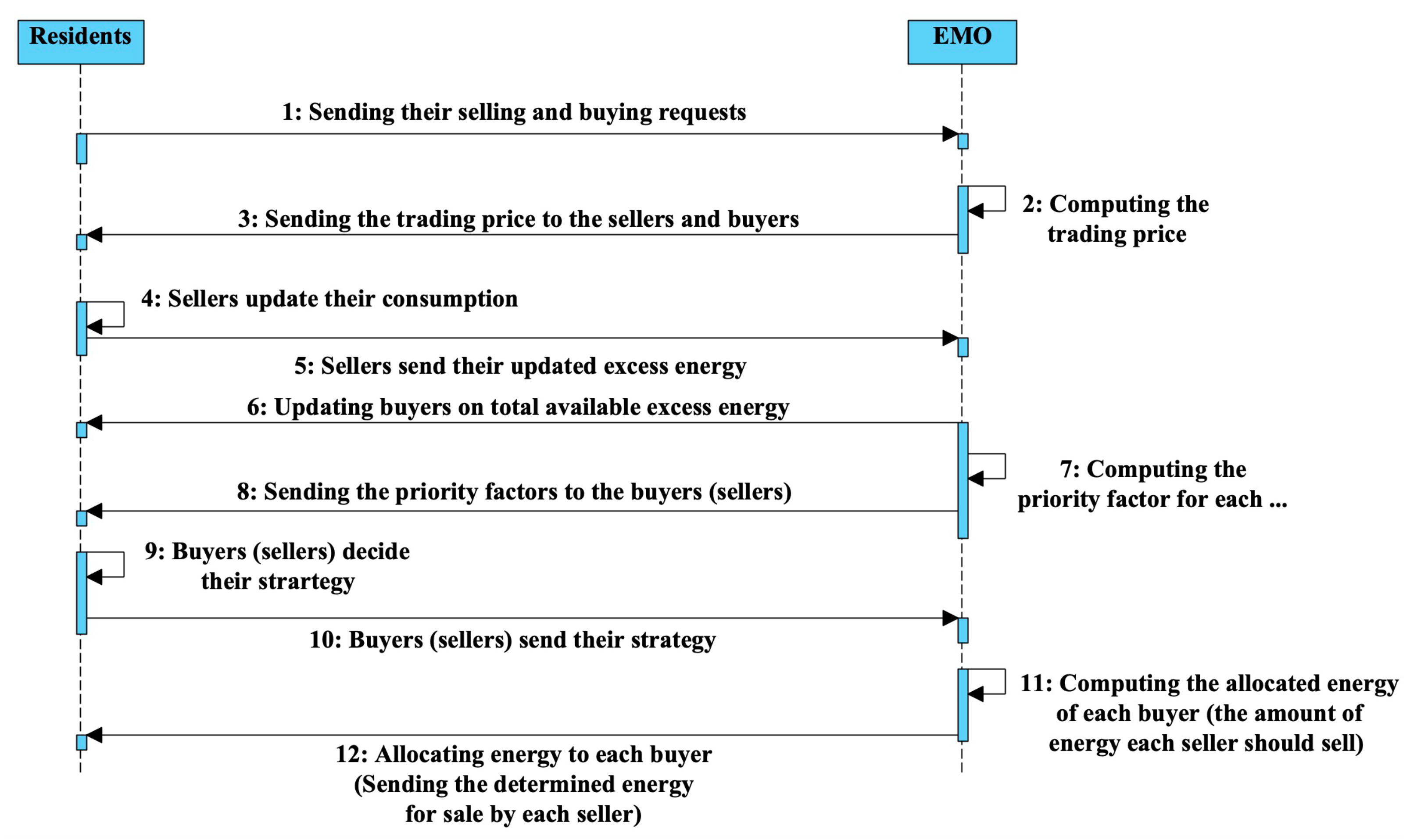In contrast to cooperative energy trading games in which participants try to maximize social benefit via cooperation based on a particular agreement, in non-cooperative games, participants compete to maximize their own financial benefits (i.e., sellers and buyers compete to maximize their benefits and minimize their costs, respectively) [30]. Hence, defining the energy trading price is important in effective energy trading and fair distribution of profit. In this paper, it is assumed energy trading takes place inside the building as depicted in Figure 1.

As seen from Figure 1, first, residents send their selling and buying requests to the EMO of the building. The EMO of the building then decides the trading price in a way that benefits sellers and buyers. The trading price should be bound by the grid buying and selling prices. By considering this, both sellers and buyers prefer to trade energy in the building rather than in the main grid. When seeing the trading price, each seller is allowed to decide its strategy by adjusting its consumption to maximize its own benefit. The sellers then update the EMO on their excess energy, and the buyers are notified by the EMO. In the next step, the EMO calculates the priority factor for each buyer or seller depending on the situation (i.e., buyers are prioritized when the total energy demand of buyers is higher than the total excess energy, and sellers are prioritized in the opposite situation). The EMO considers the priority factor for the purpose of obtaining a fair and stable energy trading system. The priority factor of a buyer/seller is calculated based on the number of times the buyer/seller contributed as seller and buyer in the previous energy trading steps until now, the ownership factor of the buyer, the number of family members of the buyer, the area of the buyer’s unit, and the amount of energy the seller want to sell. In this trading model, a participant with a higher priority factor can trade more energy than other participants. The priority factors are sent by the EMO to the corresponding buyers or sellers. Depending on the situation, the buyer (seller) decides on how much energy to buy (sell) to maximize its benefits based on the buyer’s (seller’s) priority factor and the updated total excess energy available in the building (the total energy demand of buyers). After receiving the strategies, the EMO allocates a specific amount of energy to each buyer (seller) based on the buyer’s (seller’s) strategy, the priority factor of the buyer (seller), and the total energy demand (excess energy). If, after the trading process, there is still excess energy in the building, the energy is fed into the main grid, typically based on a pre-set feed-in tariff, or if there is still unsatisfied demand, it is fulfilled by the main grid at market price.

3.4. The Proposed Energy Trading Model

In this section, the proposed local energy trading inside the building is described in detail.

Let $C_{i,t}$ denote the energy demand of the ith resident at time slot t. Moreover, resident i can have a share in BESSs and $E_{i,t}^{saved}$ of energy saved in the battery during a given time interval of the day. After allocating energy to all residents based on their share of PV panels or ownership factors, if $E_{i,t}^{allocated}+E_{i,t}^{saved}<C_{i,t}$, the resident i needs to buy energy from sellers inside the building. Let ${\mathcal{R}}_t^b$ be the set of residents who act as buyers at time slot t. If $E_{i,t}^{allocated}+E_{i,t}^{saved}>C_{i,t}$ for some residents in the building, then these residents are considered sellers. Let ${\mathcal{R}}_t^s$ be the set of such sellers in the building at time slot t.

In the first stage, buyers send their buying demand to the EMO of the building. The energy demand of buyer $i\in {\mathcal{R}}_{b,t}$ is given by:

$$D_{i,t}=|(E_{i,t}^{allocated}+E_{i,t}^{saved})-C_{i,t}|,\forall i\in {\mathcal{R}}_t^b.$$

(9)

and the total energy demand of all buyers in the building at time slot t is

$$D_t^{total}=\sum _{i\in {\mathcal{R}}_t^b}{D}_{i,t}$$

(10)

The excess energy of the ith seller after fulfilling its essential needs is equal to its minimum consumption at time slot t, i.e., $C_{i,t}={Con{s}_{i,t}}^{min}$, is

$$E_{i,t}^{excess}=(E_{i,t}^{allocated}+E_{i,t}^{saved})-Con{s}_{i,t}^{min},\forall i\in {\mathcal{R}}_t^s$$

(11)

and the total excess energy from solar panels at time slot t is given by

$$E_t^{excess,total}=\sum _{i\in {\mathcal{R}}_t^s}{E}_{i,t}^{excess}.$$

(12)

According to Step 4 in Figure 1, sellers have the opportunity to manage their energy consumption. This means that the seller $i\in {\mathcal{R}}_{s,t}$ intends to adjust its consumption $Con{s}_{i,t}$ s.t. $Con{s}_{i,t}\ge Con{s}_{i,t}^{min}$ and sells its surplus energy ($(E_{i,t}^{allocated}+E_{i,t}^{saved})-Con{s}_{i,t}$) to the neighboring buyers via the proposed energy trading model. In this regard, the updated excess energy of the ith seller after settling its energy consumption is as follows:

$$E_{i,t}^{exces{s}^{*}}=(E_{i,t}^{allocated}+E_{i,t}^{saved})-Con{s}_{i,t},\forall i\in {\mathcal{R}}_t^s$$

(13)

and consequently, the total excess energy available in the building at time slot t is updated as follows:

$$E_t^{exces{s}^{*},total}=\sum _{i\in {\mathcal{R}}_t^s}{E}_{i,t}^{exces{s}^{*}}.$$

(14)

Following that, available energy in the building is traded between participants. Finally, after energy trading is completed, if there are still residents with unsatisfied demand, the energy demand is purchased from the main grid via the EMO of the building. In contrast, the EMO sells the extra energy to the main grid.

4. Players Strategies in Energy Trading

In this section, the strategies of the participants, including the EMO of the building, buyers, and sellers, in the proposed fair energy trading model are discussed. In the model, the purpose of each seller is to maximize its utility by adjusting its consumption after knowing the trading price determined by the EMO of the building. Furthermore, each seller attempts to sell as much of its excess energy as possible when the total excess energy is more than the total energy demand in the building. Buyers’ goal is to gain as much energy as possible by setting their strategy to meet their own energy demands. At the same time, the EMO of the building tries to maximize the welfare of the building.

4.1. Buyers Strategies

Buyers intend to gain as much energy as possible from the local energy market via the EMO of the building, bounded by their energy demand. To this end, buyers participate in a non-cooperative game where they decide their strategy to request a certain amount of energy from the EMO. Thereafter, the EMO allocates energy to each buyer according to their strategy, priority, and the total amount of excess energy available in the building. To allocate energy fairly to each buyer, the priority factor is used to prioritize buyers. The priority factor is also used as an incentive factor to encourage local energy trading.

4.1.1. Priority Factor for Buyers

While determining the priority for a buyer in the energy trading step, three factors are considered:

• Total previous contributions of the buyer as seller or buyer
• Number of family members of the buyer
• Area of the buyer’s unit (m²)

Thus, the priority factor $P{r}_{i,t}^b$ of the ith buyer at time slot t is calculated as follows:

$$\begin{array}{c}\hfill P{r}_{i,t}^b=\frac{\left(\beta C_{i,t}^s\right)+C_{i,t}^b}{C_t^{total}}+\frac{Uni{t}_i^{area}}{Uni{t}^{area,total}}+\frac{Member{s}_i}{Member{s}^{total}},\forall i\in {\mathcal{R}}_t^b\end{array}$$

(15)

The first part of Equation (15) refers to the contribution factor, Here, $C_{i,t}^s$ and $C_{i,t}^b$ are the number of times the buyer contributed as seller and buyer, respectively, until the present time slot t, and $C_t^{total}$ is the total contribution as seller and buyer by the buyers until the present time slot t. Here, $\beta$ is a scaling factor such that when $\beta >1$, more importance is given to the past contributions made as sellers, which will encourage participants to consume less and save energy to act as sellers in the future. In general, the contribution factor motivates participants to trade among themselves instead of trading with the main grid. The second and third parts of the equation are the number of family members for a particular buyer i and the area of the buyer’s unit (m²), respectively, which indicate that the priority factor should be a function of the number of family members and the area of the unit. $Member{s}^{total}$ and $Uni{t}^{area,total}$ are the total number of family members of all buyers and the total area of all buyer units who live in the building.

4.1.2. Utility of Buyers

In this section, the utility function of buyer i$U_{i,t}^b$, living in the building at time slot t, which is always a non-negative function, is defined. The utility of buyer i is computed based on the priority factor of the buyer and the ratio between the strategy of the buyer to the energy allocated by the EMO of the building (i.e., $\frac{A{E}_{i,t}^b}{S_{i,t}^b}$). There are some assumptions regarding the utility of the buyer that must be taken into consideration. The first assumption is that $U_{i,t}^b$ must be a strictly increasing function of $\frac{A{E}_{i,t}^b}{S_{i,t}^b}$, which means fulfillment increases by the ratio between the amount of energy that is allocated to the buyer and the required energy of the buyer as its strategy. Second, the utility function must be a concave function of $A{E}_{i,t}^b$, i.e., as the allocated energy increases, the increasing rate of satisfaction decreases. Since the EMO of the building allocates more energy to buyers who have high priority, the utility function must be proportional to the priority factor considering a weight ($\theta >0$) factor for the priority. The weight factor ($\theta$), which is a dynamic value selected by the EMO of the building, gives importance to the priority during energy trading. Therefore, the utility function of buyer i ($U_{i,t}^b$) is computed using a modified version of the function given in [26]:

$$U_{i,t}^b={\left(P{r}_{i,t}^b\right)}^{\theta }log(1+\frac{A{E}_{i,t}^b}{S_{i,t}^b}),\forall i\in {\mathcal{R}}_t^b$$

(16)

where $P{r}_{i,t}^b$ is the priority factor of the ith buyer at time slot t. $A{E}_{i,t}^b$ and $S_{i,t}^b$ are the energy allocated to buyer i by the EMO of the building and the demand strategy of the ith buyer at time slot t, respectively.

Each buyer demands a different amount of energy; however, the buyer desires to obtain as much energy as possible, bounded by the initial demand of the buyer (e.g., the buyer i should decide its strategy from $[0,D_{i,t}]$). Accordingly, buyers participate in a non-cooperative game using Algorithm A1 in Appendix A to ask for a certain portion of excess energy available from the EMO of the building. Algorithm A1 gives the optimal strategy ($S_{i,t}^b$) for each buyer i participating in the game at time slot t. The existence and uniqueness of the Nash equilibrium solution of the game have been proven in [26]. The utility function of all buyers $U\left(S^b\right)$ is defined as follows [27]:

$$\begin{array}{cc}\hfill & U\left(S^b\right)=\underset{A{E}^b}{argmax}\left[\sum _{i\in {\mathcal{R}}_t^b}{\left(P{r}_{i,t}^b\right)}^{\beta }log(1+\frac{A{E}_{i,t}^b}{S_{i,t}^b})\right]\hfill \\ \hfill & s.t.0\le A{E}_{i,t}^b\le S_{i,t}^b,\forall i\in {\mathcal{R}}_t^b\hfill \\ \hfill & \sum _{i\in {\mathcal{R}}_t^b}A{E}_{i,t}^b\le E_{i,t}^{exces{s}^{*}}.\hfill \end{array}$$

(17)

where $S_{i,t}^b$ is the strategy of the ith buyer at time slot t. A non-cooperative game is used to formulate competition among buyers.

Algorithm A2 in Appendix B provides the optimal solution of the problem in Equation (17), which is a revised version of the famous water-filling problem [31]. According to the water-filling problem [26], there are N tanks, and any two tanks are connected by a pipe. Let $M=\{1,2,\dots ,N\}$ be the set of all the tanks, $\{{\left(P{r}_1^b\right)}^{\beta },{\left(P{r}_2^b\right)}^{\beta },\dots ,{\left(P{r}_N^b\right)}^{\beta }\}$ be the set of tank widths, and $\{\frac{S_1^b}{{\left(P{r}_1^b\right)}^{\beta }},\frac{S_2^b}{{\left(P{r}_2^b\right)}^{\beta }},\dots ,\frac{S_N^b}{{\left(P{r}_N^b\right)}^{\beta }}\}$ be the set of tank heights. It is assumed that tank i has to be on the base of height $\frac{S_i^b}{{\left(P{r}_i^b\right)}^{\beta }}$ for all $i\in M$. The total volume of the water that is used to fill the set of tanks is $E_{i,t}^{exces{s}^{*}}$. Therefore, tank i is filled by pouring $A{E}_{i,t}^b$ volume of water which is the optimal solution for tank i.

4.2. Sellers Strategies

It is assumed that sellers are interested in selling their excess energy to buyers at an appropriate price rather than selling them to the main grid at a lower price. Each seller i gains a payoff by trading its excess energy ($(E_{i,t}^{allocated}+E_{i,t}^{saved})-Con{s}_{i,t}$) with neighbouring buyers and also by managing its consumption $Con{s}_{i,t}$ subject to $Con{s}_{i,t}\ge Con{s}_{i,t}^{min}$ after seeing the trading price $P^{tr}$. The payoff of the ith seller ($U_{i,t}^s$) at time slot t is defined as follows:

$$\begin{array}{cc}\hfill & U_{i,t}^s=r_{i,t}ln(1+Con{s}_{i,t})+P_t^{tr}((E_{i,t}^{allocated}+E_{i,t}^{saved})-Con{s}_{i,t}),\hfill \\ \hfill & (E_{i,t}^{allocated}+E_{i,t}^{saved})-Con{s}_{i,t}>0,\forall i\in {\mathcal{R}}_t^s\hfill \end{array}$$

(18)

The above equation is inspired by the utility function in [32]. The first part of the equation expresses the utility that is achieved by seller i through consuming $Con{s}_{i,t}$ amount of energy, where $r_{i,t}>0$ is the preference parameter of the seller at time slot t. A seller with high $r_{i,t}$ is more interested in consuming more of its energy to maximize its utility. The second part of the equation represents the profit that the ith seller achieves by selling its excess energy to neighboring buyers at trading price $P_t^{tr}$, which is calculated by the EMO of the building. Each seller i has the objective of maximizing its utility by adjusting its own energy consumption $Con{s}_{i,t}$. Therefore, the objective of the seller i at time slot t is as follows:

$$\begin{array}{cc}\hfill & \underset{Con{s}_{i,t}}{max}\left(U_{i,t}^s\right)\hfill \\ \hfill & s.t.Con{s}_{i,t}\ge Con{s}_{i,t}^{min},\forall i\in {\mathcal{R}}_t^s\hfill \end{array}$$

(19)

The objective in Equation (21) can be achieved by computing the first-order derivative of (15), which is:

$$\frac{r_{i,t}}{1+Con{s}_{i,t}}-P_t^{tr}=0$$

(20)

and hence Equation (21) is achieved by further solving Equation (20):

$$Con{s}_{i,t}=\frac{r_{i,t}}{P_t^{tr}}-1$$

(21)

According to Equation (21), each seller’s decision on its energy consumption is affected by the trading price, which is set by the EMO of the building. It can also be observed that the seller’s consumption and the trading price are inversely proportional to each other, which means that sellers are encouraged to reduce their energy consumption and sell more energy when the trading price is high and vice-versa. It is important to note that $r_{i,t}$ should be large enough in such a way that Equation (21) is always positive for all $Con{s}_{i,t}\ge Con{s}_{i,t}^{min}$. Moreover, the lease cost or the investment cost of the seller is subtracted from the total utility of the seller at the end of the day.

We also study the situation where the total excess energy at each trading stage is more than the total energy demand. In this case, after the sellers adjust their consumption, they can also decide their strategy (i.e., demand for selling energy) by participating in a non-cooperative game to sell as much energy as possible to the local energy market, limited by their available excess energy. Similar to Algorithms A1 and A3 uses a non-cooperative game among sellers when the total excess energy is more than the total demand of buyers. In Algorithm A3 in Appendix C, each seller chooses its strategy based on some important factors, such as the seller’s priority factor and its updated excess energy. The EMO of the building then uses Algorithm A4 in Appendix D to decide on how much energy each seller should sell based on the seller’s priority factor, the amount of the seller’s excess energy, and the total demand of buyers.

Priority Factors for Sellers

For each seller i, the EMO of the building calculates the priority factor to prioritize sellers when there is more energy to sell compared to the total energy demand of the buyers. The priority factor of the ith seller relies on the ratio of the number of contributions the seller has made until the present time slot t as a seller ($C_{i,t}^s$) to the total contributions of the sellers and the ratio of the excess energy that the seller intends to sell to the total excess energy in the building. Hence, the following equation is used to calculate the priority factor of the ith seller at time slot t$P{r}_{i,t}^s$:

$$P{r}_{i,t}^s=\frac{C_{i,t}^s}{C_t^{total}}+\frac{E_{i,t}^{exces{s}^{*}}}{{E_t}^{exces{s}^{*},total}},\forall i\in {\mathcal{R}}_t^s$$

(22)

where $C_{i,t}^s$ and $C_t^{total}$ are the number of contributions the seller i has made and the total contributions that have been made by sellers who live in the same building as the seller i. $E_{i,t}^{exces{s}^{*}}$ and ${E_t}^{exces{s}^{*},total}$ are the excess energy that seller i wants to sell energy at and the total excess energy available in the building. When the total excess energy is more than the total energy demand, the utility function of the ith seller is directly proportional to its priority factor and the ratio of the amount of energy decided by the EMO that the seller i can sell and the seller’s strategy. Thus, the utility function of the seller i ($U_{i,t}^s$) at time slot t is defined as follows:

$$U_{i,t}^s={\left(P{r}_{i,t}^s\right)}^{\beta }log(1+\frac{A{E}_{i,t}^s}{S_{i,t}^s}),\forall i\in {\mathcal{R}}_t^s$$

(23)

where $P{r}_{i,t}^s$ is the priority factor of seller i at time slot t. $A{E}_{i,t}^s$ is the amount of energy to be sold by the seller i, and $S_{i,t}^s$ is the selling strategy of the seller i at time slot t.

4.3. Building’s EMO Strategy

The EMO of the building has several roles to maximize the building’s welfare, i.e., the sum of the fulfillment of all buyers and sellers in the building. In this regard, one of the main functions of the EMO is to determine the trading price, $P^{tr}$, for energy trading inside the building. The trading price should be bounded by the grid buying and selling prices, $G^{b,p}$ and $G^{s,p}$, respectively. The EMO should compute the trading price in a way that is at the fulfillment level of buyers and sellers. Hence, the objective of the EMO is defined as follows:

$$\begin{array}{cc}\hfill & \underset{P_t^{tr}}{max}[\frac{1}{C{t}_t^b}+\sum _{i\in {\mathcal{R}}_m}{U}_{i,t}^s]\hfill \\ \hfill & s.t.G^{b,p}\le P_t^{tr}\le G^{s,p}\hfill \end{array}$$

(24)

The above equation expresses the aim to maximize the building’s welfare. According to Equation (24), the satisfaction of sellers and buyers is met by simultaneously maximizing the inverse ratio ($\frac{1}{C{t}_t^b}$) of the total cost of buyers (i.e., minimizing the total cost of buyers) and the total utility of sellers at time slot t.

During energy trading, in addition to the cost of buying energy from neighboring sellers, the total cost of buyers ($C{t}_t^b$) at time slot t also relies on the cost of the remaining energy purchased from the main grid to keep the energy balance, and is calculated as follows:

$$C{t}_t^b=\left\{\begin{array}{c}\left(E_t^{exces{s}^{*},total}{P}_t^{tr}\right)+(D_t^{total}-E_t^{exces{s}^{*},total})G^{s,p},\mathrm{if}{D}_t^{total}\ge E_t^{exces{s}^{*},total}\hfill \\ D_t^{total}{P}_t^{tr},\mathrm{otherwise}\hfill \end{array}\right.$$

(25)

Now, we can use the first-order optimality condition of the EMO’s objective function (i.e., Equation (24)) in the cost function (i.e., Equation (25)) and in the sellers’ utility function to obtain the trading price in trading step. Hence, we have the following equation by using the first-order optimality of Equation (24) in Equations (18) and (25):

$$\frac{\delta \left(\frac{1}{C{t}_t^b}\right)}{\delta P_t^{tr}}+\frac{\delta \left({\displaystyle \sum _{i\in {\mathcal{R}}_m}}{U}_{i,t}^s\right)}{\delta P_t^{tr}}=0$$

(26)

After solving Equation (26); we have

$$\begin{array}{c}\hfill P^{tr}=\left\{\begin{array}{c}\frac{1-(D_t^{total}-E_t^{exces{s}^{*},total})G^{s,p}}{E_t^{exces{s}^{*},total}},\mathrm{if}{D}_t^{total}\ge E_t^{exces{s}^{*},total}\mathrm{and}{P}^{tr}>G^{b,p}\hfill \\ G^{b,p}+\epsilon ,\mathrm{if}{P}^{tr}<G^{b,p}\hfill \end{array}\right.\end{array}$$

(27)

where $\epsilon >0$ is a very small value to keep the trading price $P_t^{tr}$ higher than the grid buying price $G^{b,p}$ at time slot t. The other main function of the EMO to maximize the building’s welfare is to fairly distribute energy generated from the building’s PV panels and energy stored in BESSs among residents. Moreover, the EMO attempts to fairly allocate energy to participants during energy trading to maximize the building’s welfare. Let $U_{i,t}^b\left(A{E}_{i,t}^b\right)$ and $Utilit{y}_{j,t}^s\left(A{E}_{j,t}^s\right)$ be the fulfillment of buyer i when the total demand exceeds the total excess energy and the satisfaction of seller j when the total excess energy is higher than the total energy demand, respectively, from the perspective of the EMO of the building. ${\sum }_{i\in {\mathcal{R}}_t^b}A{E}_i^b$ and ${\sum }_{j\in {\mathcal{R}}_t^s}$ are the social welfare of the system during energy trading. The optimization problem to determine the amount of energy that the seller j should sell ($A{E}_{j,t}^s$ amount of energy) at time slot t is given by

$$\begin{array}{cc}\hfill & \underset{A{E}^s}{max}\left[\sum _{j\in {\mathcal{R}}_t^s}{(P{r}_{j,t}^s)}^{\beta }log(1+\frac{A{E}_{j,t}^s}{S_{j,t}^s})\right]\hfill \\ \hfill & s.t.0\le A{E}_{j,t}^s\le S_{j,t}^s,\forall j\in {\mathcal{R}}_t^s\hfill \\ \hfill & \sum _{j\in {\mathcal{R}}_t^s}A{E}_{j,t}^s\le D_t^{total}\hfill \end{array}$$

(28)

According to Theorem 1 in [26], the optimal amount of energy that should be sold by each seller at time slot t ($A{E}_t^{*,s}=\left\{A{E}_{j,t}^{*,s}\right|j\in {\mathcal{R}}_t^s$), when the total excess energy exceeds the total energy demand is computed as follows:

$$A{E}_{j,t}^{*,s}=\left\{\begin{array}{c}(h{(P{r}_{j,t}^s)}^{\beta }-S_{j,t}^s),\mathrm{if}0<(h{(P{r}_{j,t}^s)}^{\beta }-S_{j,t}^s)<S_{j,t}^s\hfill \\ S_{j,t}^s,\mathrm{if}(h{(P{r}_{j,t}^s)}^{\beta }-S_{j,t}^s)\ge S_{j,t}^s\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(29)

where h is a real number satisfying ${\displaystyle \sum _{j\in {\mathcal{R}}_t^s}}A{E}_{j,t}^s=D_t^{total}$.

Similarly, the optimization problem for allocating energy to buyer i at time slot t is as follows:

$$\begin{array}{cc}\hfill & \underset{A{E}_t^b}{max}\left[\sum _{i\in {\mathcal{R}}_t^b}{(P{r}_{i,t}^b)}^{\beta }log(1+\frac{A{E}_{it}^b}{S_{i,t}^b})\right]\hfill \\ \hfill & s.t.0\le A{E}_{i,t}^b\le S_{i,t}^b,\forall i\in {\mathcal{R}}_t^b\hfill \\ \hfill & \sum _{i\in {\mathcal{R}}_t^b}A{E}_{i,t}^b\le E_t^{exces{s}^{*},total}\hfill \end{array}$$

(30)

By using Theorem 1 in [26], the optimally allocated energy $A{E}^{*,b}=\left\{A{E}_{i,t}^{*,b}\right|i\in {\mathcal{R}}_t^b$}, when the total energy demand exceeds the total excess energy, is given as follows:

$$A{E}_{i,t}^{*,b}=\left\{\begin{array}{c}(h{P{r}_{i,t}^b}^{\beta }-S_{i,t}^b),\mathrm{if}0<(h{(P{r}_{i,t}^b)}^{\beta }-S_{i,t}^b)<S_{i,t}^b\hfill \\ S_{i,t}^b,\mathrm{if}(h{(P{r}_{i,t}^b)}^{\beta }-S_{i,t}^b)\ge S_{i,t}^b\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

(31)

where h is also a real number such that ${\displaystyle \sum _{i\in {\mathcal{R}}_t^b}}A{E}_{i,t}^b=E_t^{exces{s}^{*},total}$.

Problems (28) and (30) are different versions of the water-filling problem [31], and their optimal solutions are given by Algorithms A2 and A4 by performing a modified version of the water-filling algorithm given in [26].

5. Evaluation Results

5.1. Description of the Dataset

Below, two multi-unit buildings with ten units in each building are assumed, which follow the sharing model Building A and Building B, respectively. All units are allocated real household load profiles. To illustrate the potential of the proposed fair energy allocation and trading, data from Austin, Texas [33] is used. Building A is equipped with three PV panels and one BESS. Building B is equipped with two PV panels and one BESS. The capacity of each PV panel is 10 kW and costs about $20,000 [34]. Tesla Powerwall batteries with a usable energy capacity of 13.5 kWh are considered storage systems [35]. The performance of the proposed energy trading model is evaluated from 9 to 19 o’clock each day because there is no solar generation during the early morning and the evening, and the length of the time slot is one hour. The grid selling and buying prices are set to 0.8 cents/kWh and 2.4 cents/kWh, respectively, and the values of $\beta$ and $\alpha$ are set to 1.5 and 0.5. The PV panels’ payback period for Buildings A and B are assumed 12.5 and 10 years, respectively [36]. The proposed model has been developed in the Python programming language. The Gurobi solver [37] is used to solve the involved optimization problems in Pyomo [38].

5.2. Performance Evaluation

5.2.1. Energy Trading Analyses

Data used for allocating energy generated by PV panels to residents at time slot 10 is given in

Table 1. System data for allocating energy generated by PV panels to residents of Buildings A and B at time slot 10 (O: unit-owner, T: tenant).

Building	Type of Residents	PV Share (m2) (Building A) Ownership Factor (Building B)	BESS Share	PV Generation (kWh)
A	[O, O, O, O, O, T, T, T, T, T]	[18.27, 17.55 13.13, 21.98, 11.70, 16.84, 13.84, 7.28, 10.99, 12.42]	[1.71, 1.65, 1.23, 2.06, 1.10, 1.58, 1.30, 0.68, 1.03, 1.16]	18.69
B	[O, O, O, T, T, O, O, O, T, T]	[0.19, 0.18, 0.23, 0.18, 0.08, 0.05, 0.08, 0.03, -, -]	[1.93, 1.93, 1.93, 1.93, -, 1.93, 1.93, 1.93, -, -]	11.23

. The Type of Residents column in the table denotes whether a resident is a unit owner or a tenant. In Building A, Units 1–5 are occupied by the owner of units, and Units 6–10 are occupied by tenants. Units 1–4 and 6–8 of the building lease a share of PV panels and BESSs from the building owner, while Units 5, 9, and 10 pay for their energy consumption. In Building B, Units 1–3 and 6–8 are occupied by their owner, and the rest are occupied by tenants. In this building, the owners of Units 1–5 buy PV panels, separately, while the owners of Units 6–8 cooperate in buying PV panels. The owners of Units 9 and 10 in Building B do not contribute to buying PV panels. All the unit owners in Building B except Units 5, 9, and 10 contribute to paying for a share of the BESS’s cost. The EMO of the building decides the amount of energy to be allocated to the residents of the building utilizing the resident’s share of PV panels or the ownership factor and the total energy generated by the PV panels of the building. After allocating energy to the relevant residents, energy trading takes place. The overall process of our energy trading method during time slot 10 is depicted in

Table 2. The energy trading step in Buildings A and B at time slot 10.

Time Slot (hour)	10
Building	A	B
EA−Cons${}^{\mathit{min}}$	[−2.34, +2.34, −0.64, +3.72, −0.02, +1.22, +0.08, +1.25, +0.32, +0.39]	[−2.18, +2.38, +1.77, +2.61, −0.70, −1.52, −0.22, −0.10, −1.11, −1.22]
Updated excess energy (${\mathit{E}}_{\mathit{i}}^{\mathit{excess}*}$)	[-, 2.34, -, 2.72, -, 1.22, 0.08, 1.25, 0, 0]	[-, 2.38, 1.77, 2.61, -, -, -, -, -, -]
Priority factor	[-, 0.53, -, 0.58, -, 0.40, 0.22, 0.40, -, -, 0.34]	[0.54, -, -, -, 0.45, 0.37, 0.55, 0.28, 0.30, 0.35
Optimal strategy of buyer/seller	[-, 0.74, 0, 0.84, -, 0.48, 0.08, 0.49, -, -, 0.37]	[2.18, -, -, -, 0.70, 1.34, 0.22, 0.10, 1.01, 1.22]
EMO decision	[-, 0.74, 0, 0.84, -, 0.48, 0.08, 0.49, -, -, 0.37]	[2.18, -, -, -, 0.70, 1.34, 0.22, 0.10, 1.01, 1.22]
Final energy demand or excess energy at time slot 10	[0, +1.60, 0, +2.88, 0, +0.74, 0, +0.76, 0, 0, +0.34]	[0, 0, 0, 0, 0, −0.19, 0, 0, −0.10, 0]

.

As can be seen from Table 2, units 1, 3, and 5 of Building A act as buyers because the energy allocated to the units is less than their minimum energy consumption at time slot 10. In contrast, units 2, 4, and 6–10 of the building act as sellers. The EMO of the building has information, such as energy consumption and the selling and buying energy demands of the residents, and preference parameters of the sellers in the building. According to this information, the EMO is able to calculate a trading price in the range [0.8, 2.4] using Equation (27) for the building. Trading prices calculated by the EMO of Buildings A and B are 1.74 and 1.81 Cents/kWh, respectively. By seeing the trading price, several sellers modified their excess energy; for example, units 4, 9, and 10 of Building A decreased their excess energy from 3.72 kWh, 0.32 kWh, and 0.39 kWh to 2.72 kWh, 0 kWh, and 0 kWh, respectively. Therefore, the total excess energy available from residents as sellers in Building A decreases from 9.32 kWh to 7.61 kWh. Given that units 5, 9, and 10 in Building A and unit 5 in Building B pay only for their energy consumption, the rest of their excess energy belongs to the building owner and the unit owner, respectively. To this end, the total energy that goes back to the owner of Buildings A and unit 5 in Building B are 0.71 kWh and 0 kWh, respectively.

It can be observed from Table 2 that the total excess energy available for sale in Building A is higher than the total buying energy demand, while the opposite is true for Building B. Accordingly, the EMO of Buildings A and B calculates a priority factor for each seller and each buyer of their building, respectively. Based on the priority factor, each seller/buyer decides its strategy. Then, the EMO of Building A decides how much energy each seller should sell, and the EMO of Building B allocates an optimal amount of energy to the buyers of the building. By observing the decision of the EMO, sellers and buyers with higher priority sell and buy more energy, respectively. After fulfilling the local demands by the EMO at time slot 10, the total energy required for Building B is 0.29 kWh, and the total excess energy available from Building A is 6.32 kWh.

To emphasize the advantages of our method, we compared our results with the method in [27], called Method 1, and the situation where energy can only be fed into the main grid for a fixed tariff, called Method 2. All three methods follow the energy allocation process performed in each building, while the energy trading process is different in each method. The average utility of sellers after subtracting the lease cost and the investment cost of sellers from their utility throughout the day are illustrated in Figure 2a,c. The average cost of buyers after adding the lease cost and investment cost of buyers to their cost throughout the day is shown in Figure 2b,d. In general, the figure shows that the average revenue of sellers and the average cost of buyers increases and decrease, respectively, when using our method. In comparison with our method, Method 1 only minimizes the total cost of buyers in calculating an energy trading price. Accordingly, the energy trading prices computed in Method 1 (see Figure 3) are mostly close to the grid buying price, which makes sellers prefer consuming the whole or a part of their excess energy rather than selling them at a low price. For this reason, compared to our method, buyers have to buy most of their energy demand from the main grid at a high price, which increases the total cost of buyers in Method 1 (see Figure 2b,d). As can be observed from Figure 3, the trading prices calculated by our method are close to the average feed-in tariff prices. This is due to considering the financial benefits of sellers and buyers in calculating the energy trading price, which encourages sellers to sell their excess energy to their neighbors and supports buyers to buy energy at a lower price than the grid tariff price. Therefore, all sellers and buyers make significant financial benefits when utilizing our method.

5.2.2. Energy Justice Analyses

The proposed framework is specialized into two cases with the aim of analyzing what is fair for each building. This means that fairness in energy sharing can vary from building to building. Analyzing all three principles of energy justice in the design of energy-sharing models in Building A and B helps to understand how design choices can lead to justice. In the following, the energy allocation and trading processes in the buildings are evaluated according to the principles of energy justice.

From the perspective of recognition justice, Buildings A and B support different groups of residents with different preferences to enjoy the benefits of shared DRESs in their building. Given that each unit of Building A has already been allocated a specific share according to its unit characteristics, new residents (i.e., residents who just moved into the building) have the opportunity to use the shared DRESs of the building. Moreover, unit-owners and temporary residents (e.g., tenants) can lease the allocated share of PV panels/BESSs as long as they live in the building (e.g., units 1–4 as unit-owners and units 6–8 as tenants lease a share of PV panels from the owner of Building A), or can pay only for their energy consumption if they do not afford the lease cost (e.g., units 5, 9, and 10 in Building A pay only for their energy consumption). In the case of Building B, the building owner cooperates with the residents of the building by allowing them to install PV panels on the roof of the building. The sharing model in Building B enables residents to participate in the purchase of PV panels/BESSs either alone (e.g., units 1–5 whose owners separately buy a share of PV panels/BESSs) or in collaboration with other units (e.g., units 6, 7, and 8 whose owners collaborate in buying PV panels/BESSs). The sharing model in Building B also considers tenants whose unit owner owns a share of PV panels/BESSs and those tenants who wish to benefit from PV panels/BESSs. In this case, tenants can lease a part of the share from their unit owner (e.g., unit 4 in Building B) or just pay for their energy consumption (e.g., unit 5 in Building B).

From a distributive perspective, it should be seen how energy, profits, and costs are distributed among residents of Buildings A and B using the proposed sharing models. The sharing model of Building A enables the EMO of the building to allocate a specific share of PV panels and/or BESSs to the residents according to their unit characteristics. Accordingly, the amount of energy distributed among residents is based on the cost they pay for leasing the share of PV panels/BESSs or their energy consumption. In this sharing model, residents gain financial profit by participating in energy trading in the building, and the EMO makes financial profit by leasing the share of PV panels/BESSs to each resident, selling energy to the residents who pay for their energy consumption, and selling excess energy available from residents who did not lease PV panels/BESSs share. The sharing model in Building B follows the distribution principle in distributing PV panels/BESSs costs among residents. This means that residents in Building B can either participate in buying PV panels/DRESs considering their ability to pay (e.g., Units 1–5 and Units 6–8 buy PV panels/BESSs separately and together, respectively) or lease a part of the share of PV panels/BESSs from their unit owner (e.g., units 4 lease the share from the unit owner). In this building, energy is distributed among residents according to their ownership factor. In relation to justice in the distribution of profits among residents in Building B, the sharing model in the building supports energy trading in which participants benefit by selling their excess energy available from their share of PV panels/BESSs or buying energy from their neighbors in the building.

With respect to procedural justice, the sharing model in Buildings A and B encourages resident participation in decision-making during energy allocation and trading processes. In the energy allocation process, residents in Building A can participate in decision-making to decide whether to lease the share of PV panels/BESSs from the building owner or pay only for their energy consumption. The residents of Building B can also make a decision on buying PV panels/BESSs separately or in collaboration with their neighbors. The sharing model in Buildings A and B also supports all stakeholders, such as sellers, buyers, and the EMO, in decision-making during energy trading. This means that sellers/buyers are given the opportunity to decide how much energy they should sell/buy to gain more profit. In addition to some factors like unit characteristics which are fixed, sellers/buyers are given the opportunity to increase the chance of selling/buying more energy by participating in previous energy trading in their building (i.e., they can increase their priority by participating in more energy trading). Moreover, the EMO of the building decides on the trading price and allocates energy to participants with the purpose of maximizing their profits.

6. Conclusions

In this paper, a fair energy sharing framework (FESM) is proposed to enable fair and reliable energy allocation and trading in multi-unit buildings. Two different specializations of the framework, referred to as Buildings A and B, that followed different energy-sharing models, are presented. An energy management operator is used for each multi-unit building to coordinate the energy allocation and trading processes among all residents in the building. The processes of energy allocation and trading in our sharing model show that residents receive and trade energy fairly using the characteristics of a unit or ownership factor and priority. To certify fairness between buyers and sellers in all trading stages, this work gives both groups the opportunity to decide on their strategy by participating in a non-cooperative game to increase their financial profit. A simple trading price mechanism is proposed to maximize the profits of sellers and buyers and simplify the trading stages. The efficiency of our method is verified in comparison with the baseline methods on real data from Austin, Texas. The results illustrate high financial profit for sellers and low costs for buyers during the day.

We also analyzed justice in the proposed energy allocation and trading processes for both cases of the framework with respect to the main principles of energy justice. From the recognition justice perspective, justice is achieved when the sharing models ensure the accessibility to the benefits of shared DRESs in the buildings for different groups of residents. For example, recognition justice is realized in the proposed sharing models by giving tenants and low-income families the opportunity to use the DRESs of their building via renting or investing in a share of PV panels/BESSs individually or in cooperation with neighbors or paying for their consumption. Justice as distribution in the sharing models results in fair distribution of cost, benefits, and energy. To reach distributive justice in the proposed sharing models, for example, some factors, such as the unit characteristics, ownership factor, and priority factor, are utilized to perform a fair distribution of energy and benefits among residents during both energy allocation and trading. Procedural justice enables all stakeholders in the sharing model to participate in making decisions on the distribution of cost/benefits, accessing the shared DRESs, etc. Procedural justice is achieved in the proposed sharing models by enabling residents to decide how to use the shared DRESs of their building (i.e., the residents can rent or invest in a share of the DRESs) and their buying or selling strategy. In sum, analyzing the main principles of energy justice in this work is useful in understanding that justice principles have to be applied in the design of energy-sharing models in the first step. These principles can be applied in different ways, and depending on the context or situation justice’s definition can be different. Applying the energy justice principles in the proposed sharing models motivates the residents to use the shared DRESs of their building, which leads to high financial benefits for the building.

Future research could explore how to achieve trust among participants and how much information they should share during energy trading. Future research might also be to develop the proposed framework into an interactive tool for exploring and comparing the effects of different approaches to energy justice. It may also be relevant to study how errors in intraday (<1 h) forecasting of PV power generation may influence the trading results on seller profit and buyer cost.