Insights on the Effects of Magnetic Forces on the Efficiency of Vibration Energy Harvesting Absorbers in Controlling Dynamical Systems
Abstract
:1. Introduction
2. System’s Description and Model Formulation
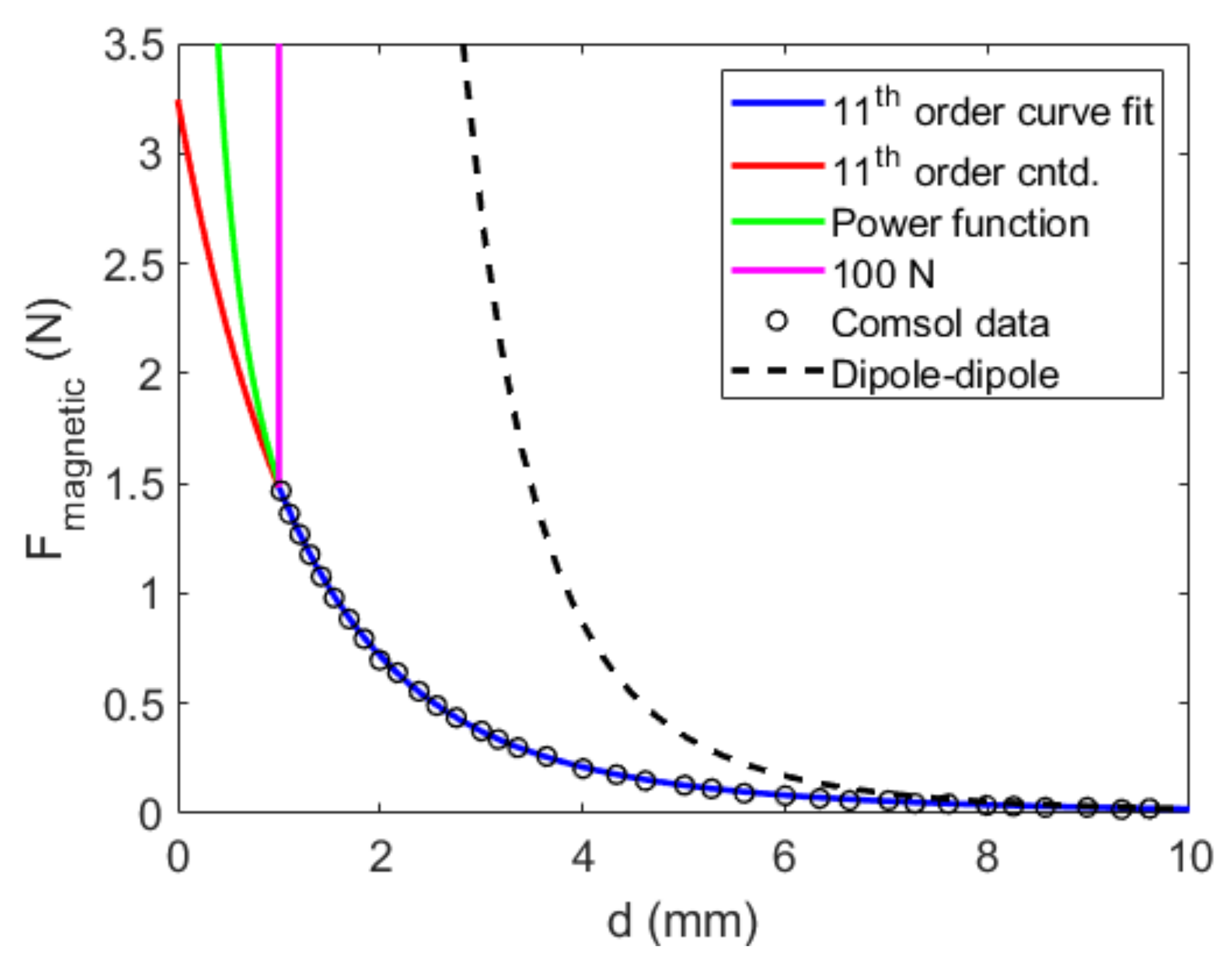
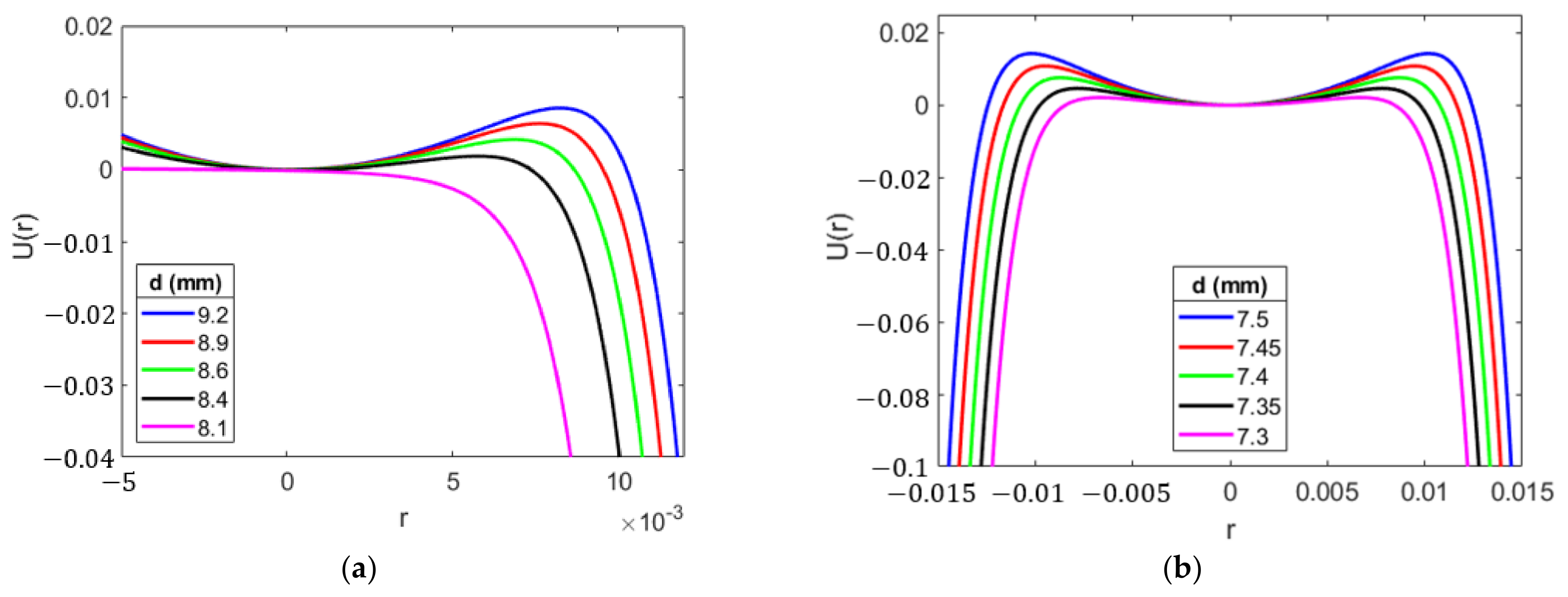
2.1. Magnetic Force Representation
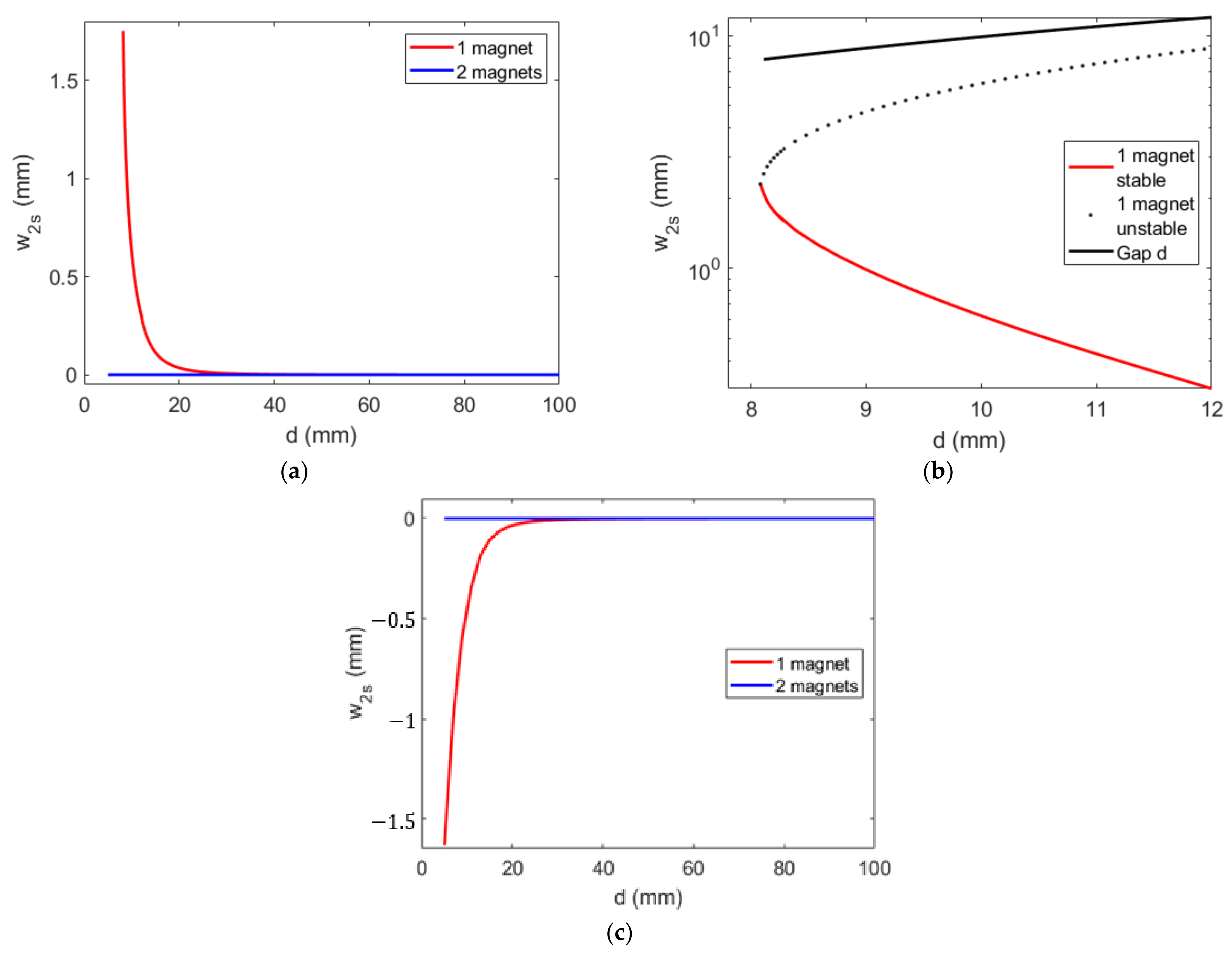
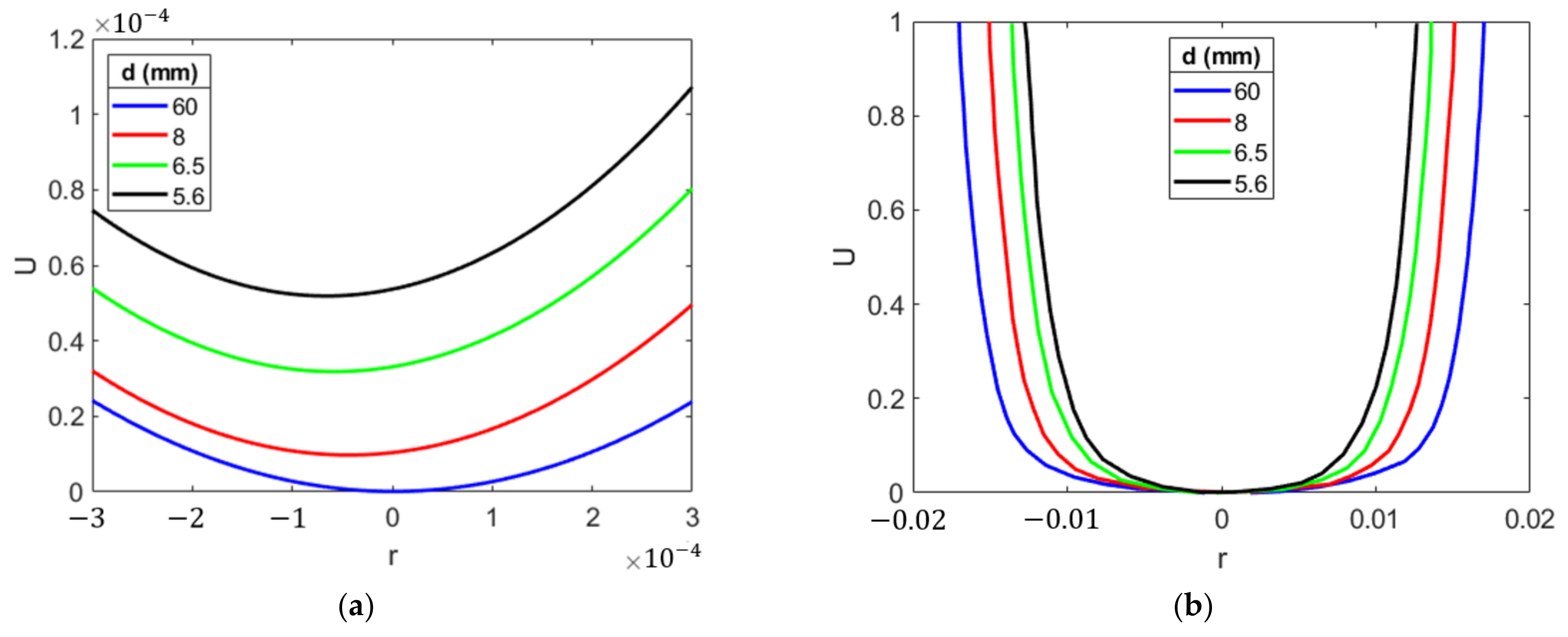
2.2. Magnetic Force Effects on the Absorber’s Static Position and Natural Frequency
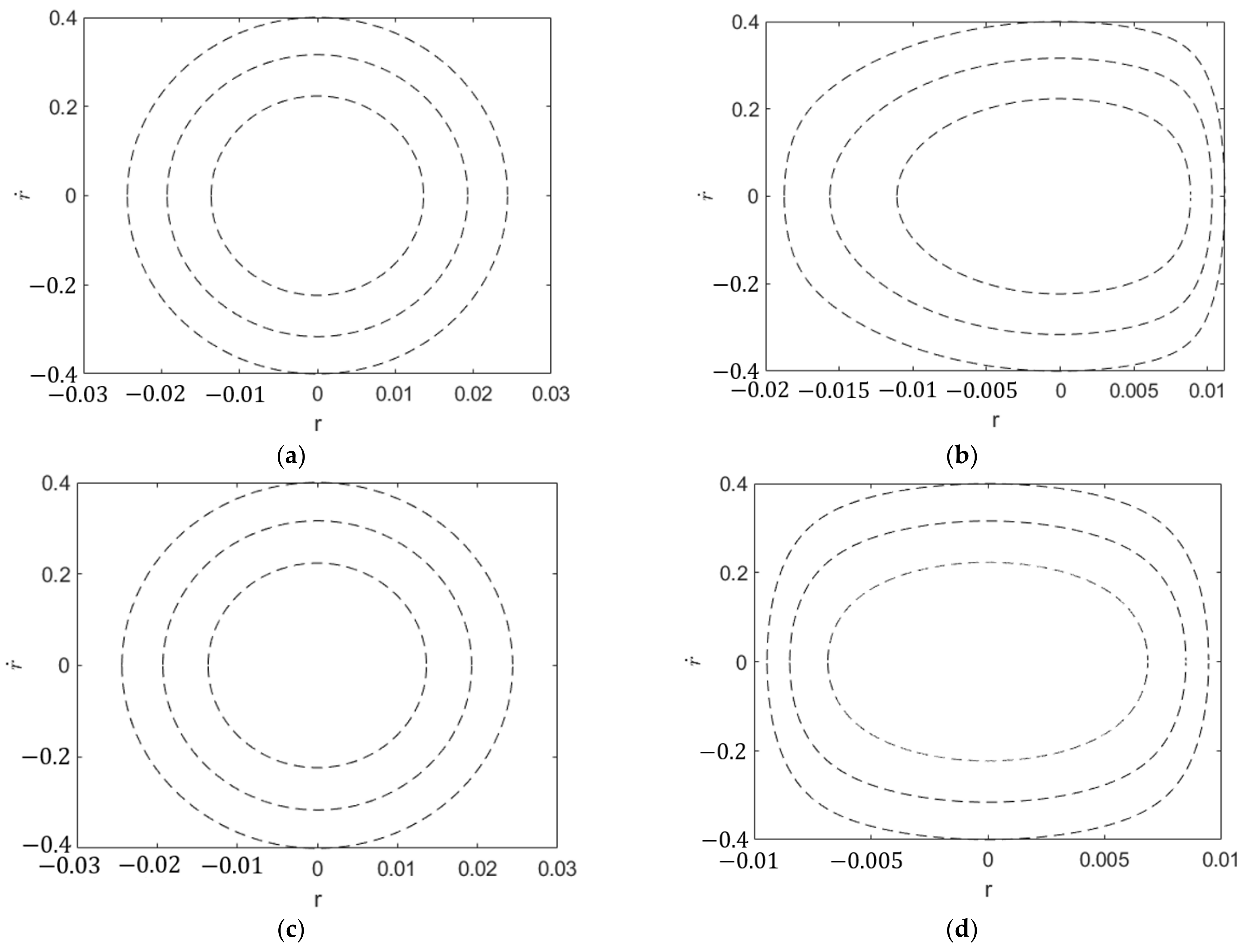
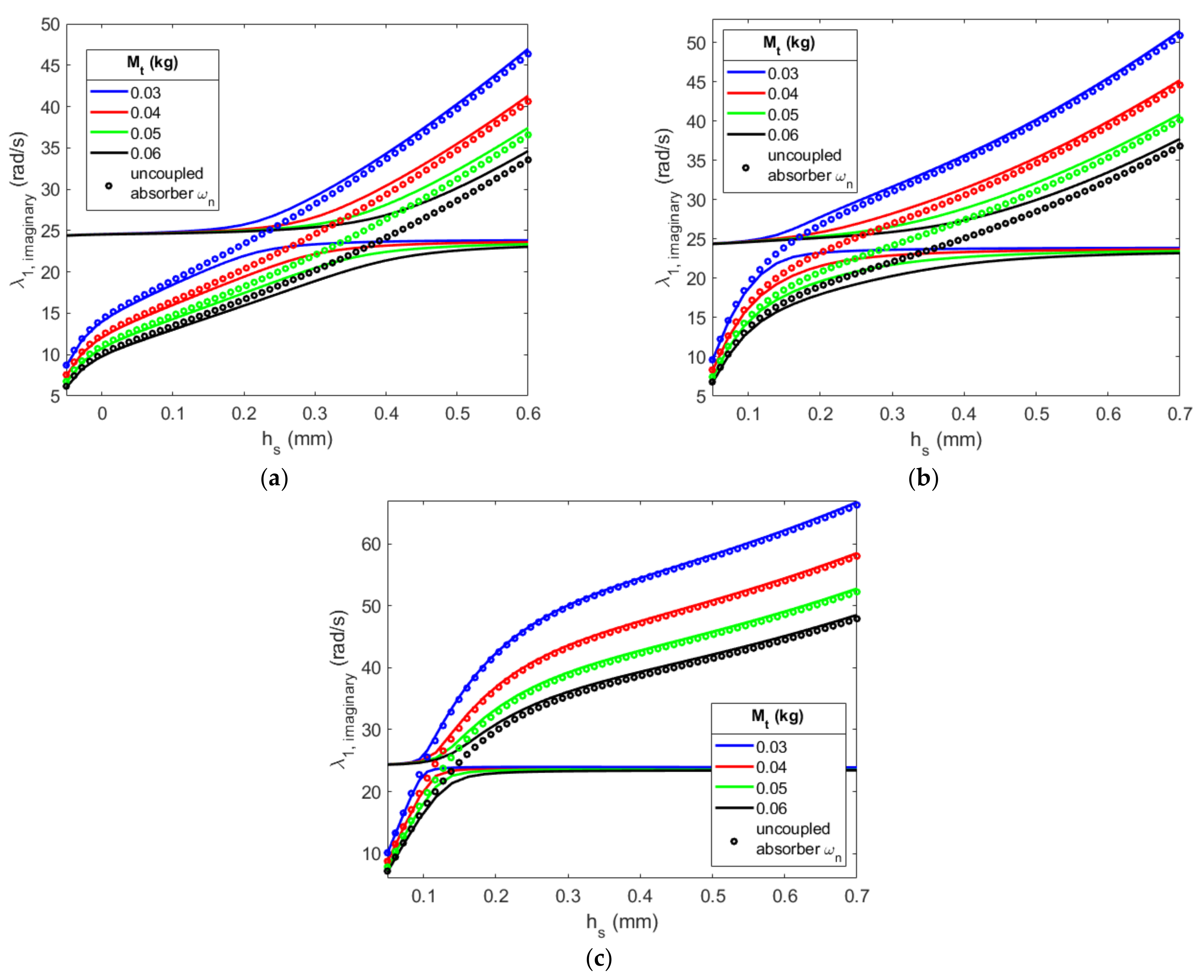
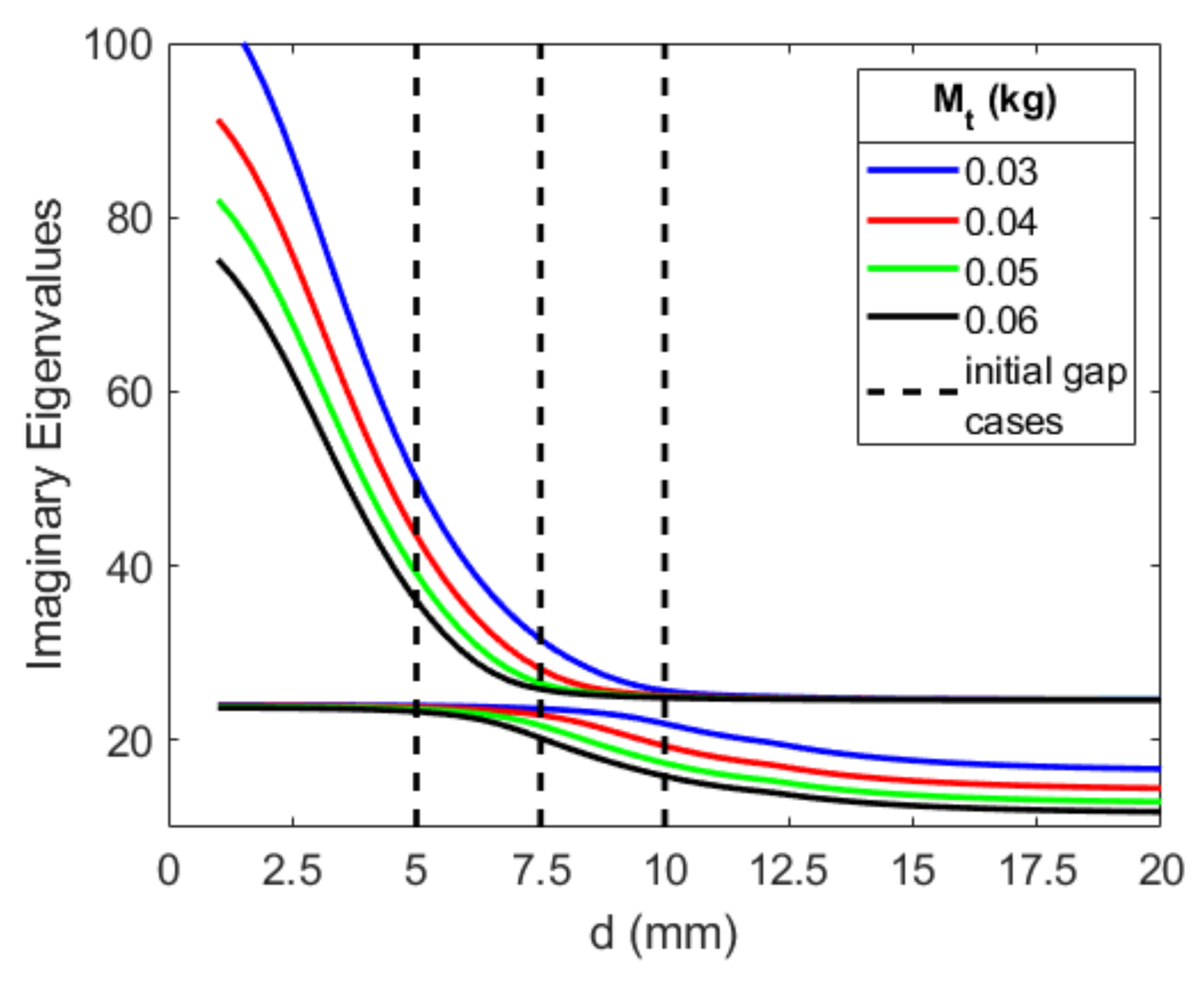
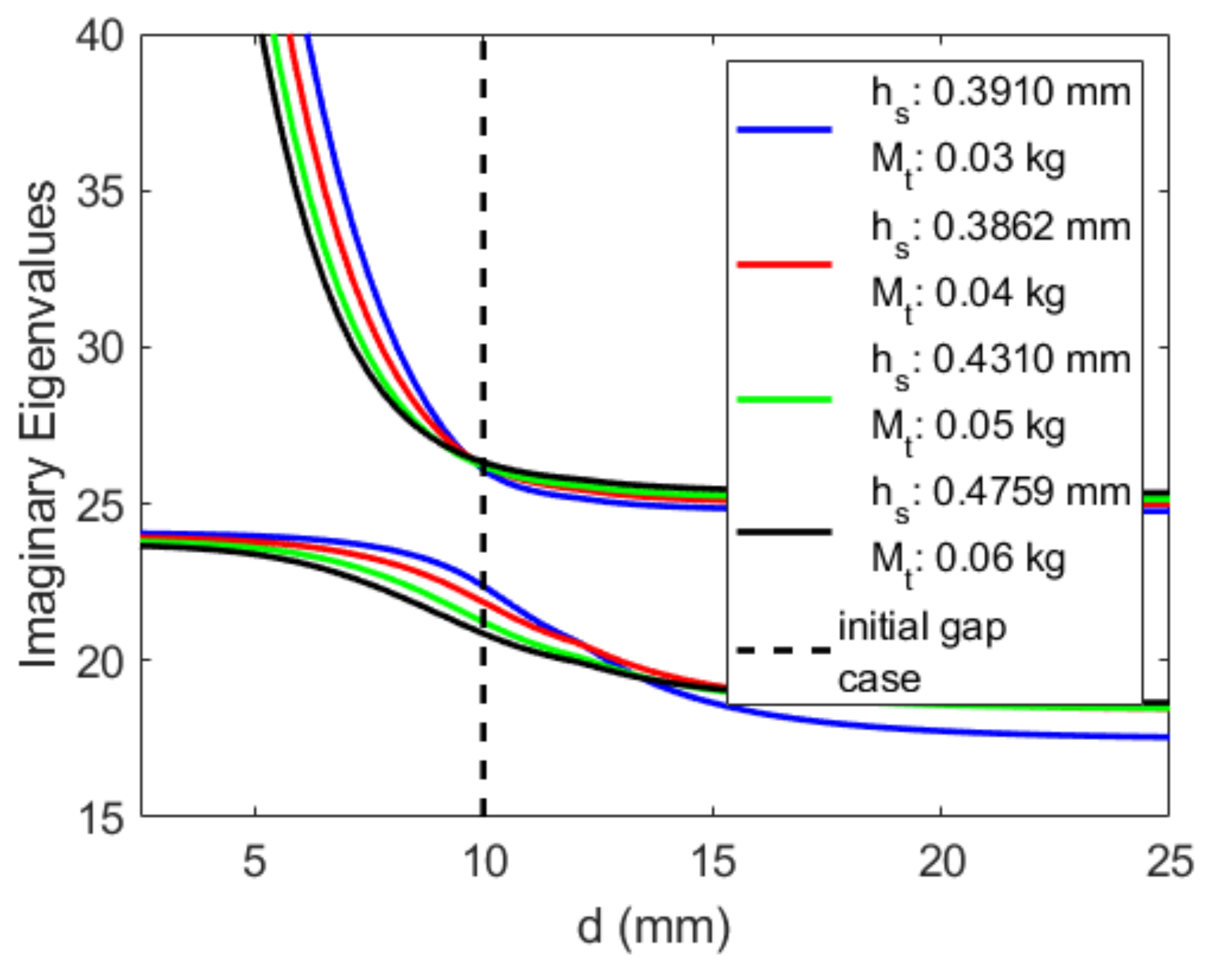
2.3. Effects of the Magnetic Force on the Linear Characteristics of the Coupled System
3. Baseline System’s Effectiveness and Effects of the Magnetic Force
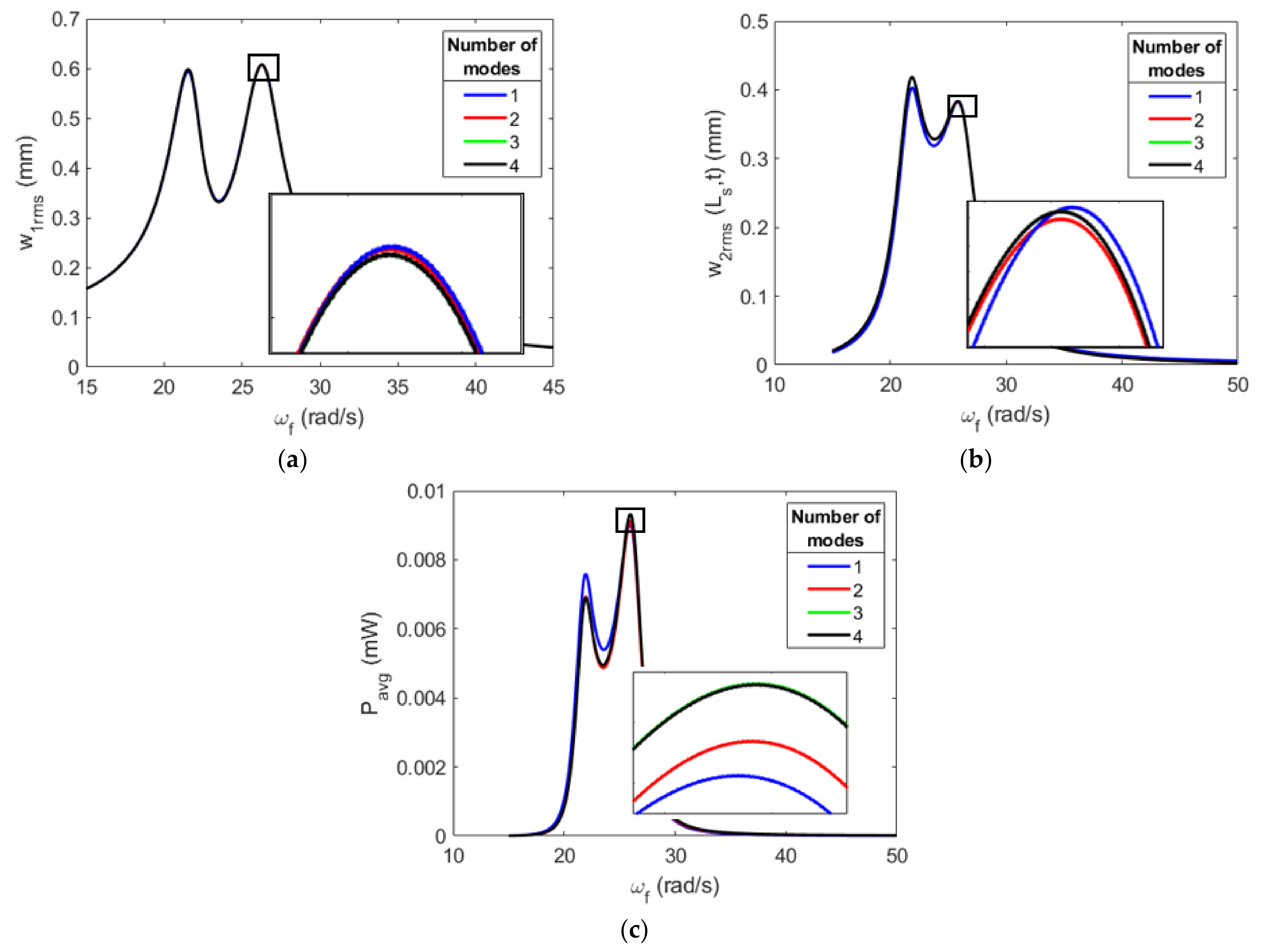
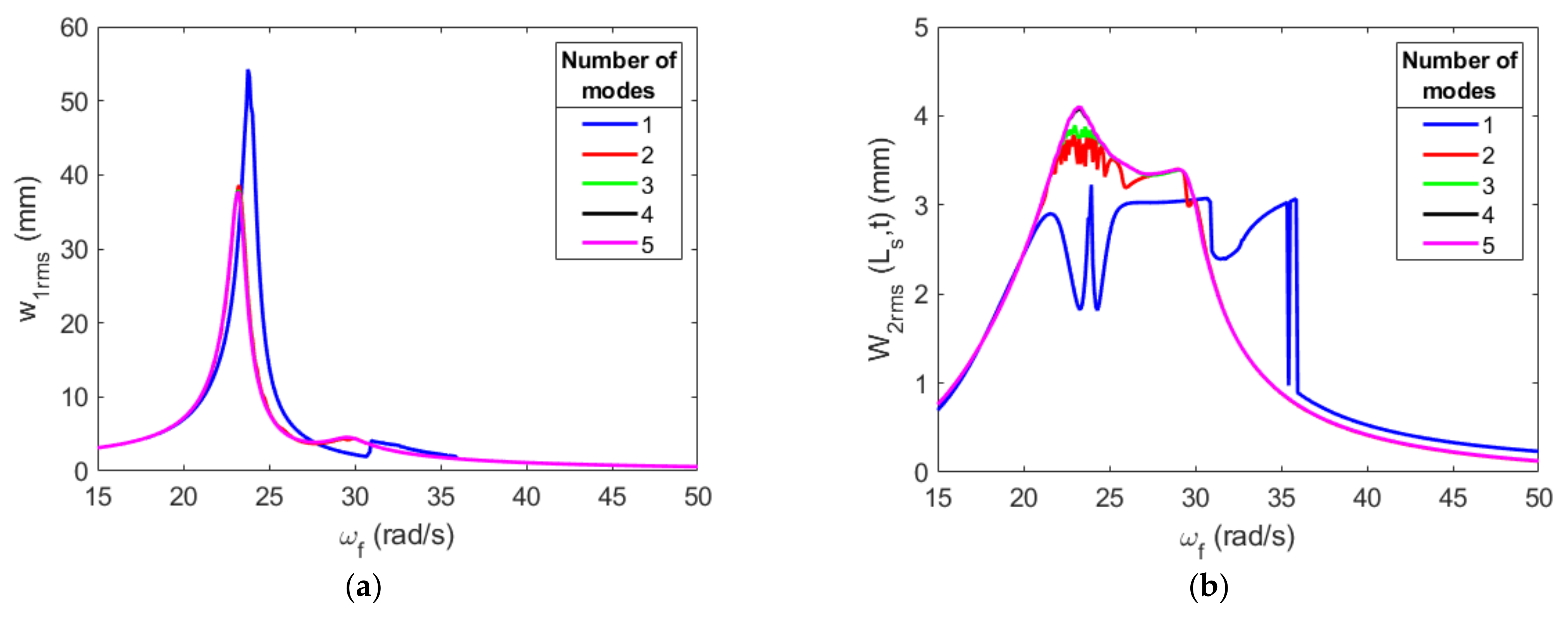
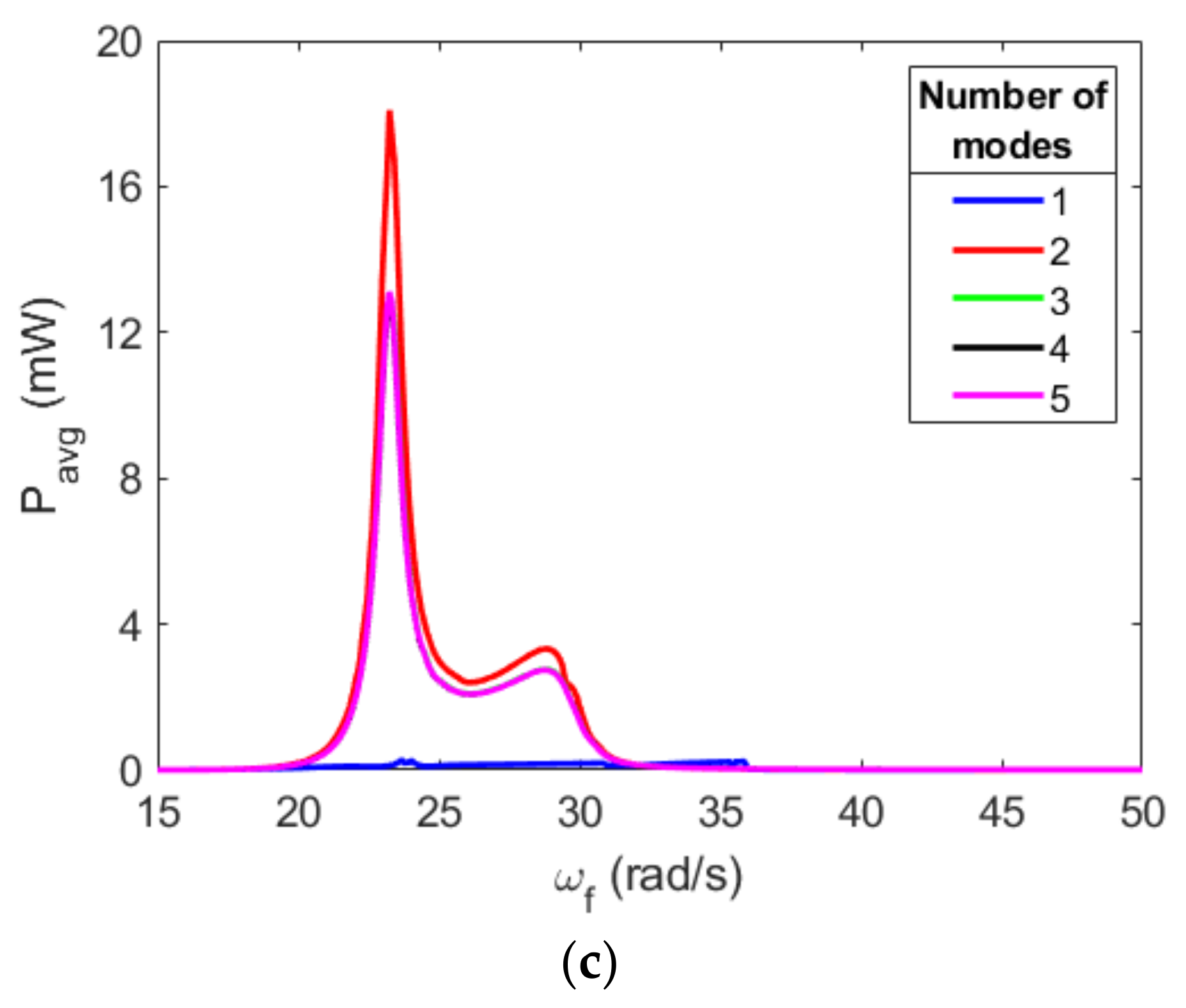
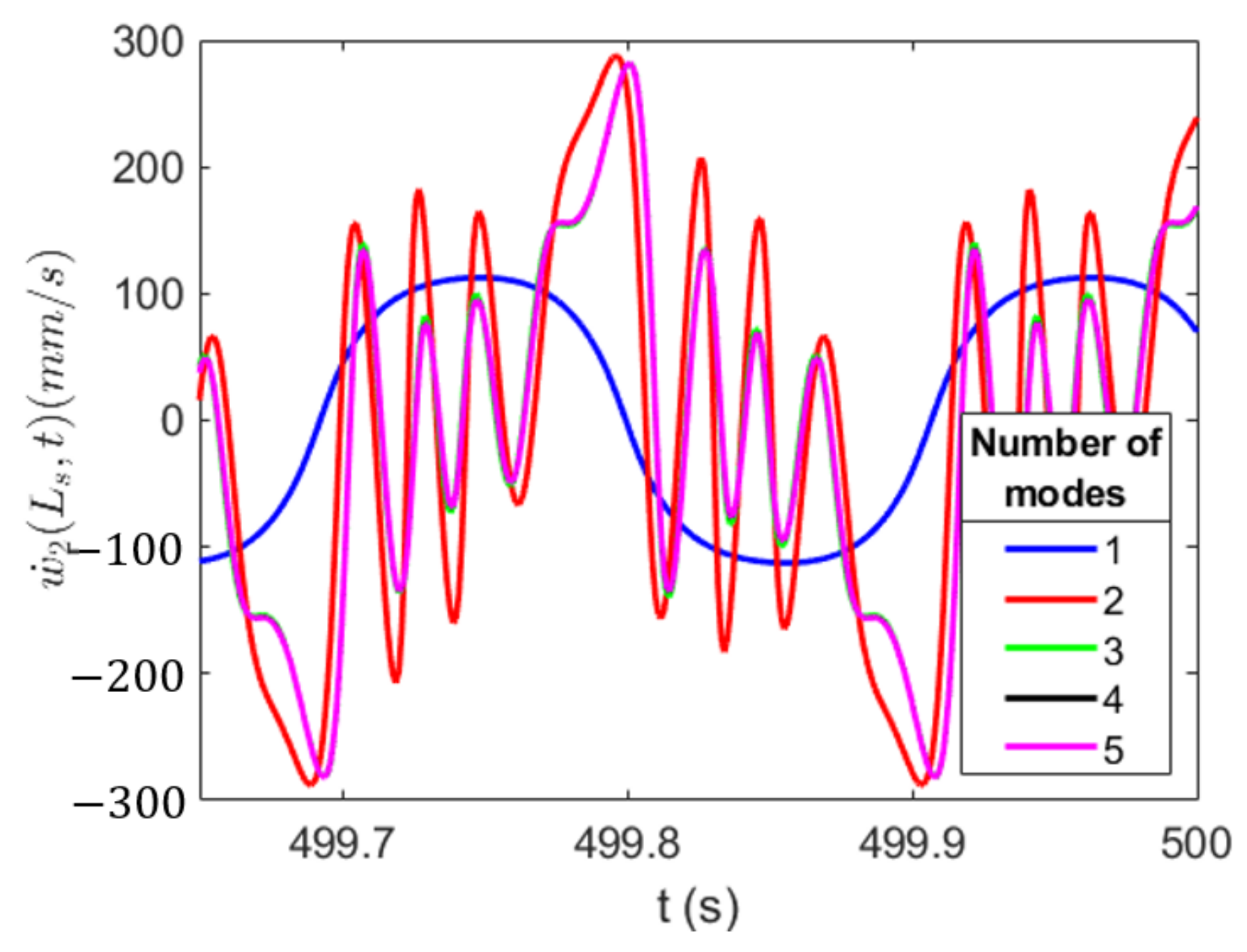
3.1. Investigation of Magnetic Force Representation and Computational Discretization Convergence
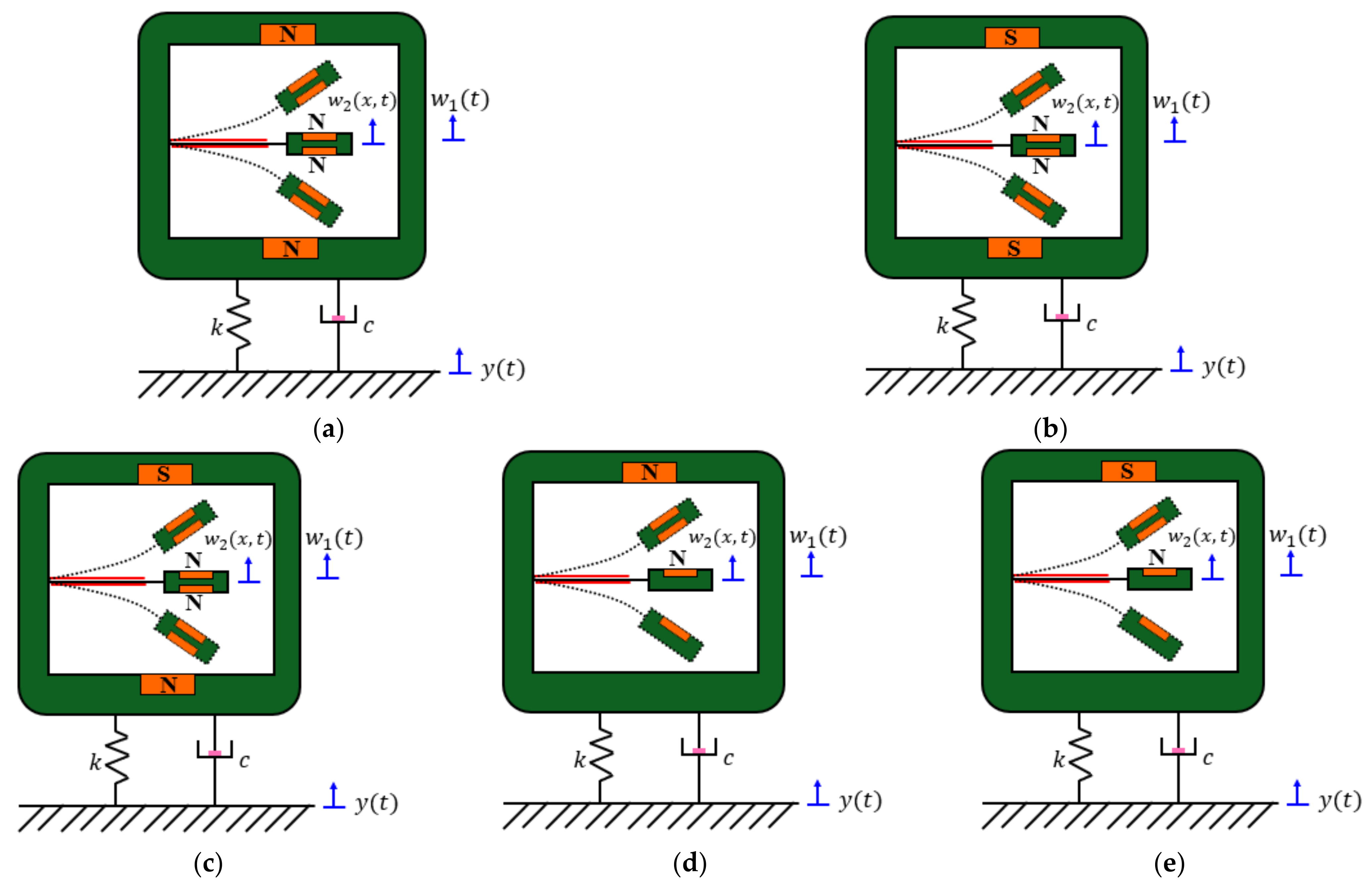
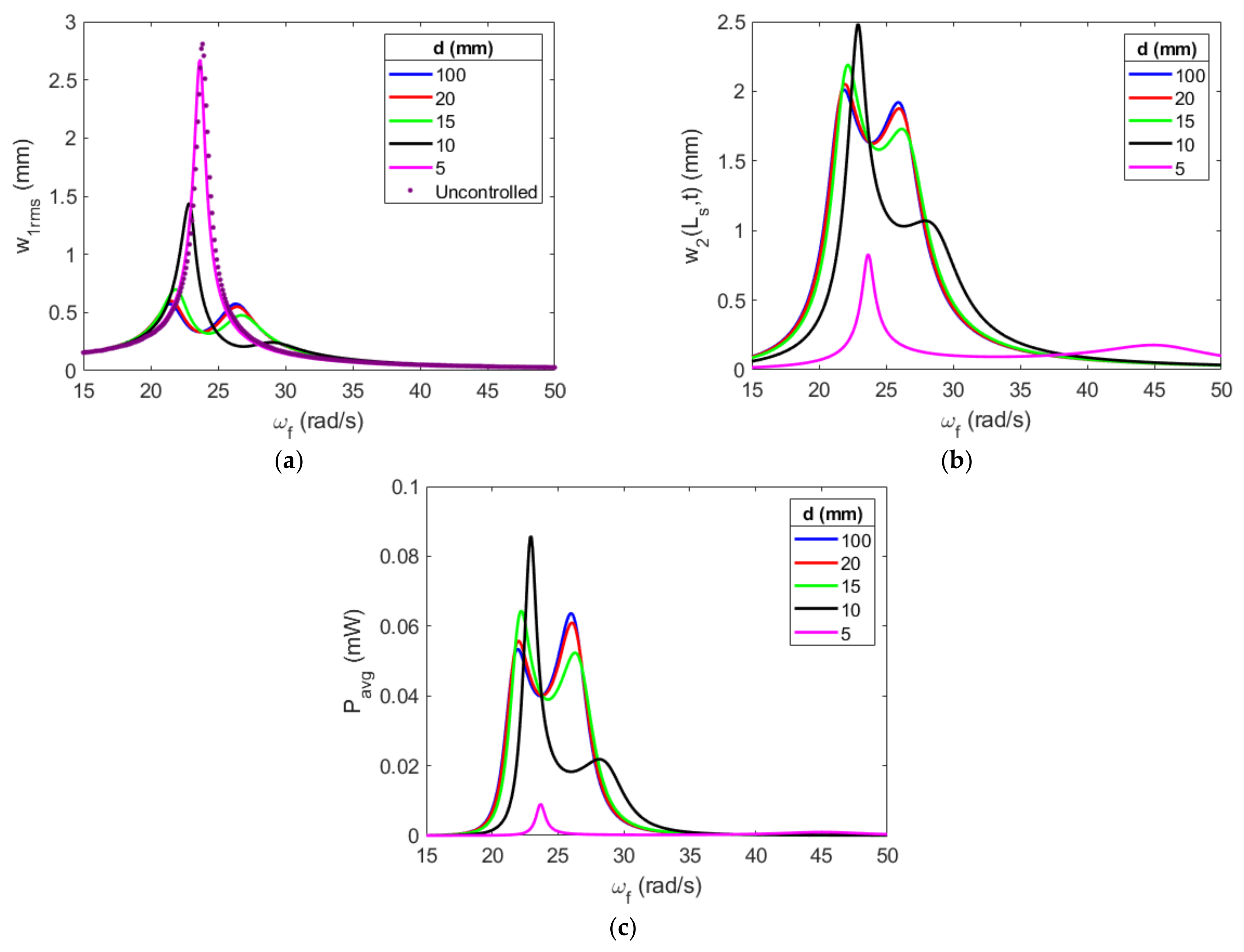
3.2. Attractive Stopper Configurations and System Performance
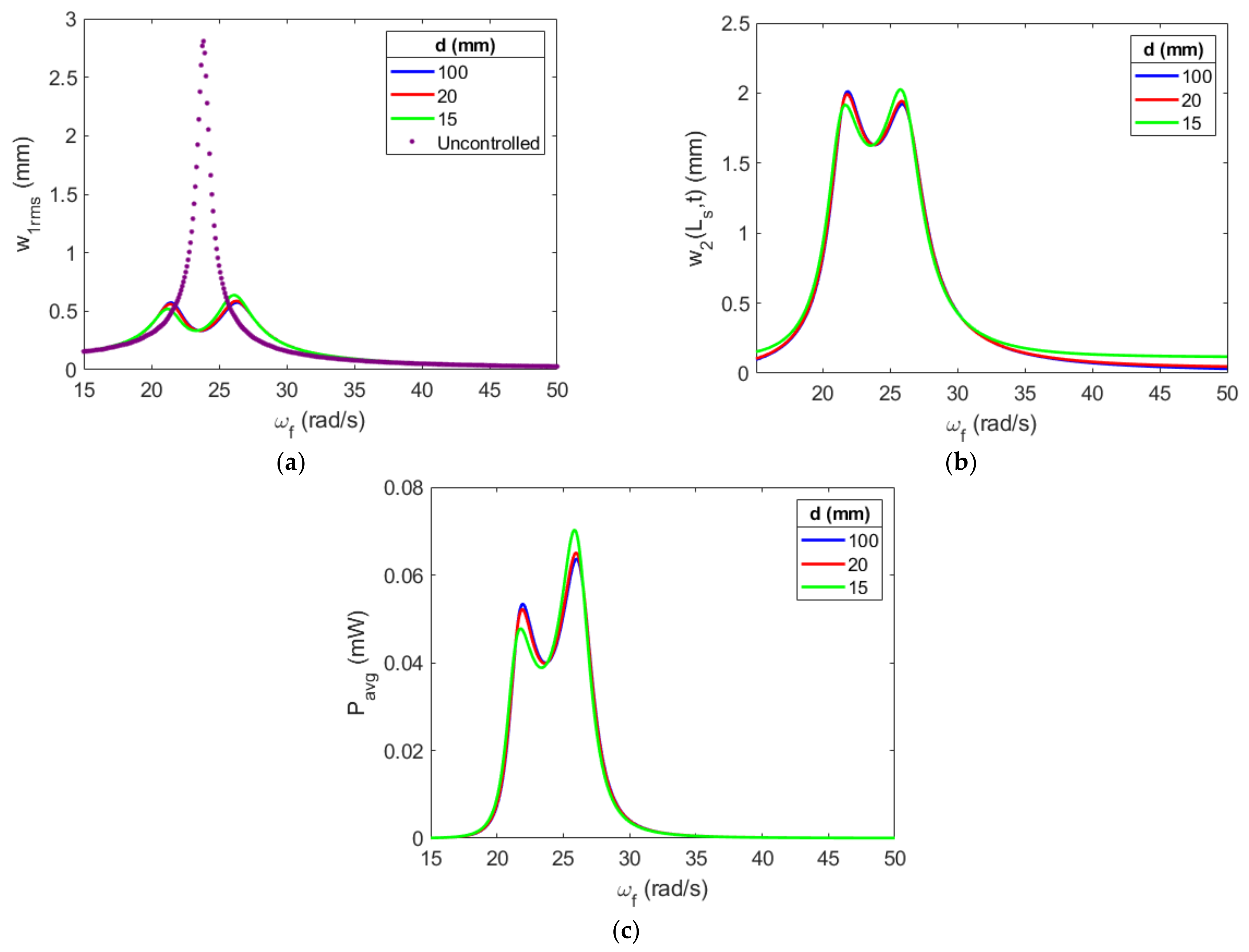
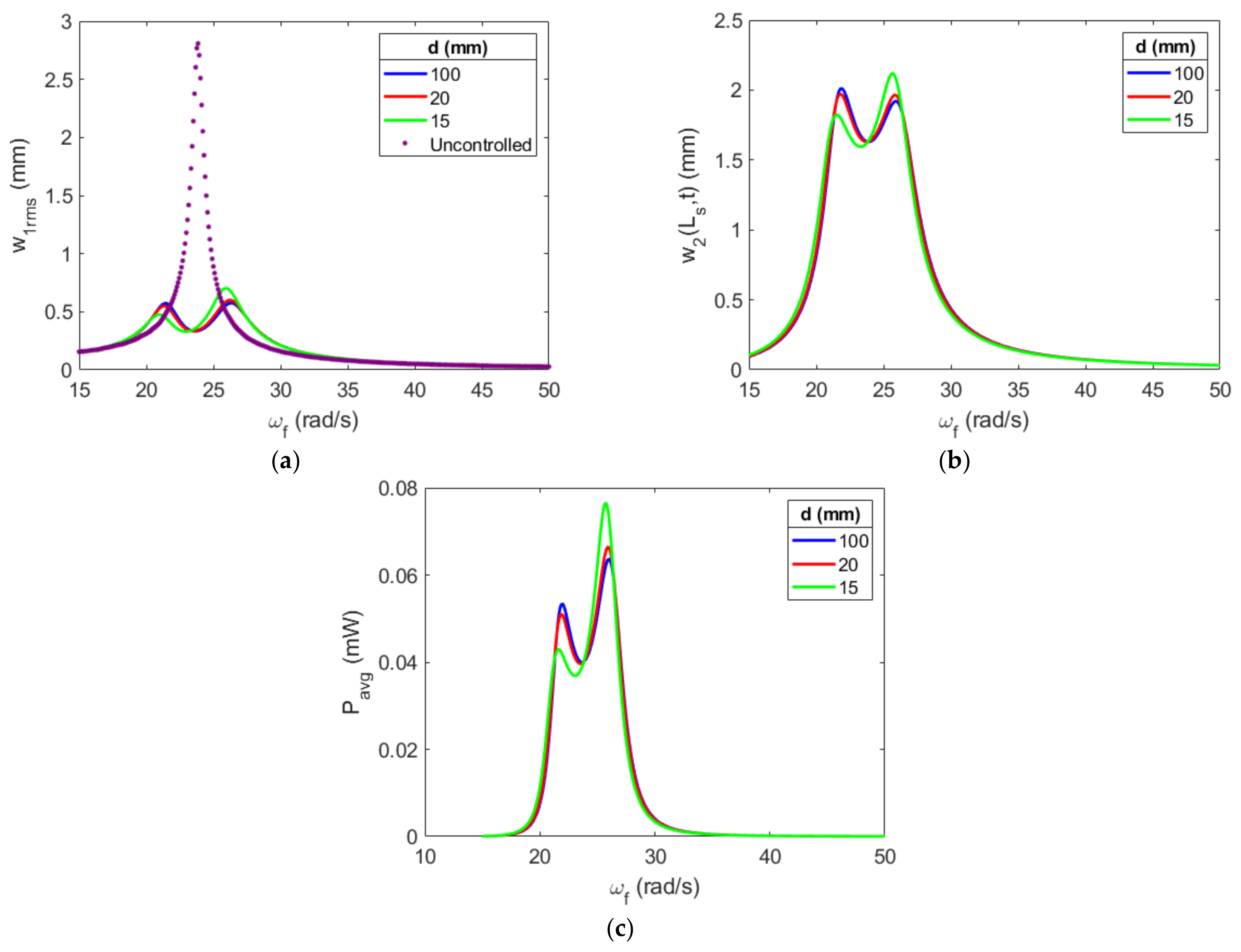
3.3. Repulsive Stopper Configurations
4. Effective Design of Repulsive Magnetic Configurations
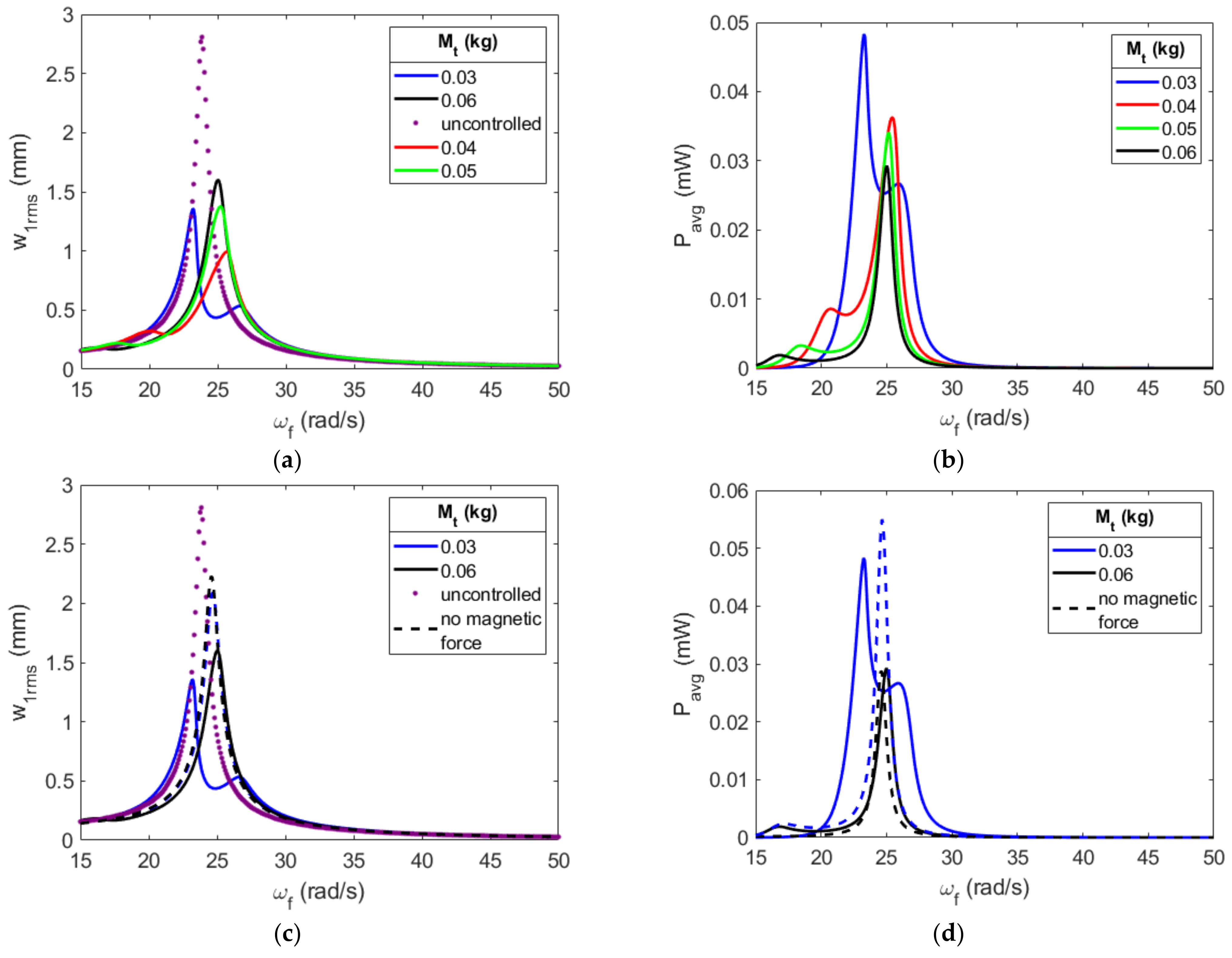
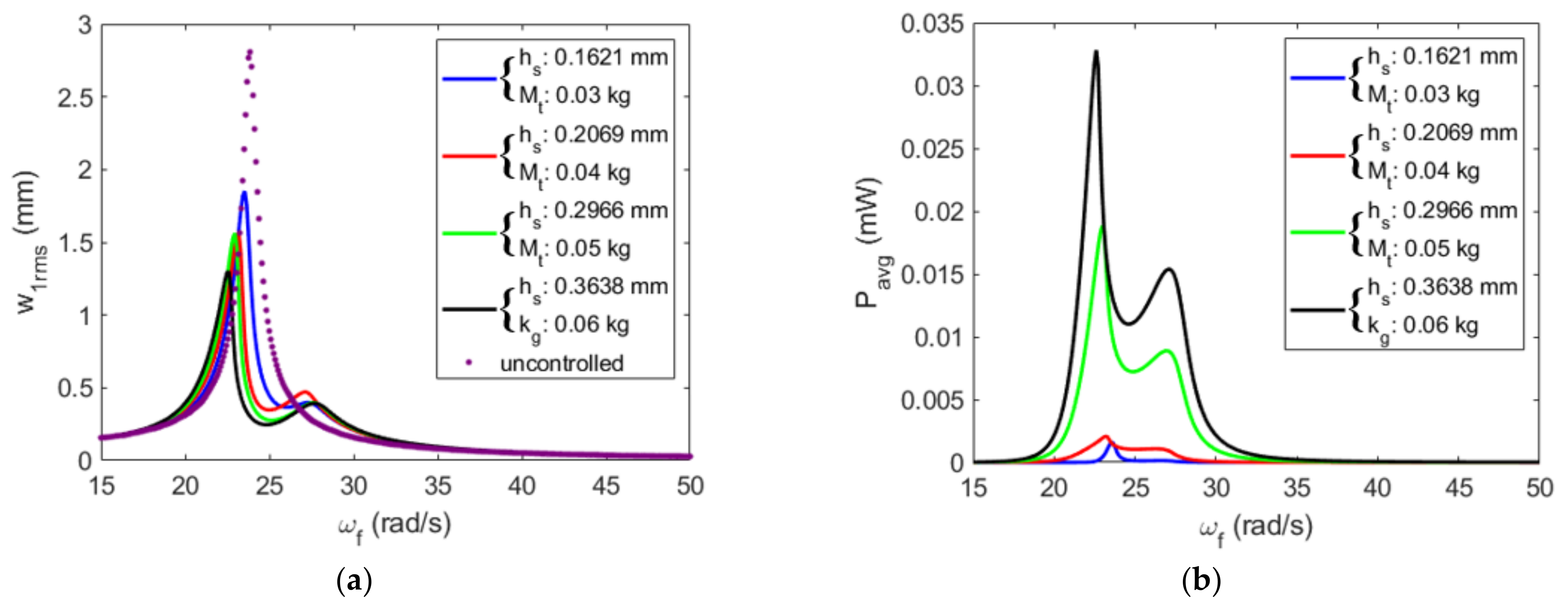
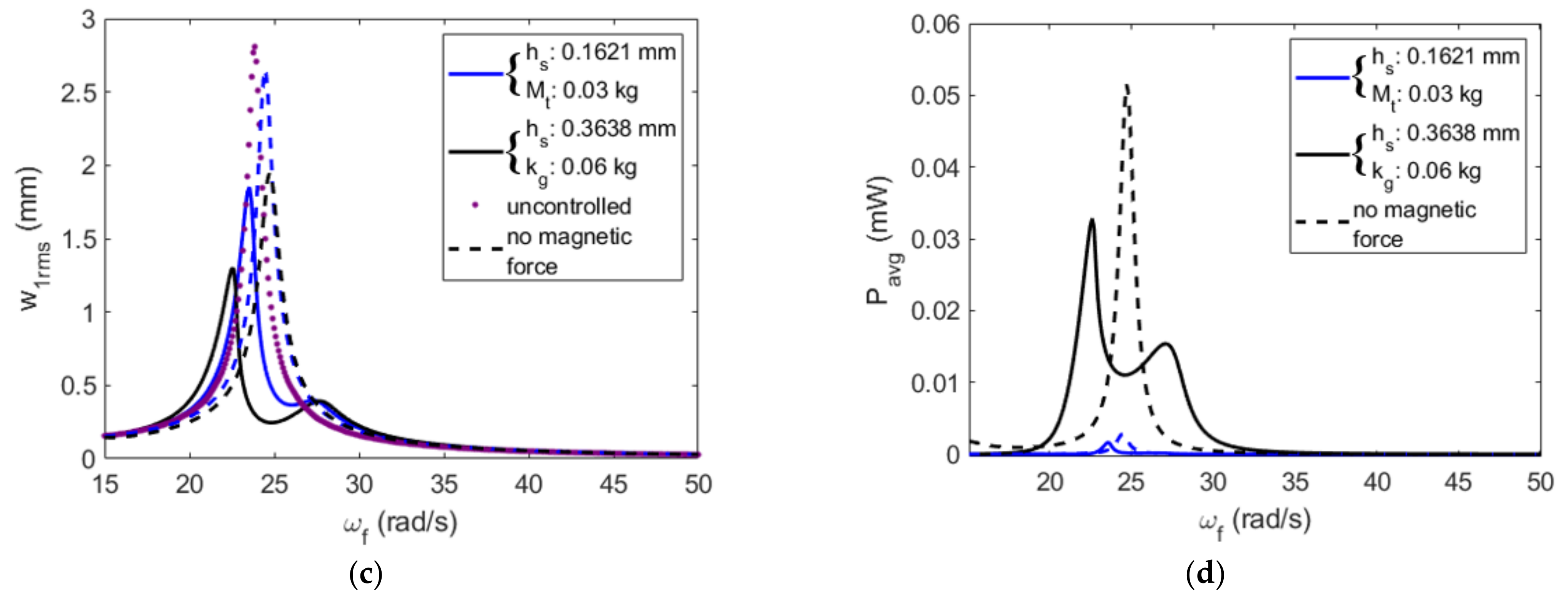
4.1. Effective Design: Absorber’s Tip Mass
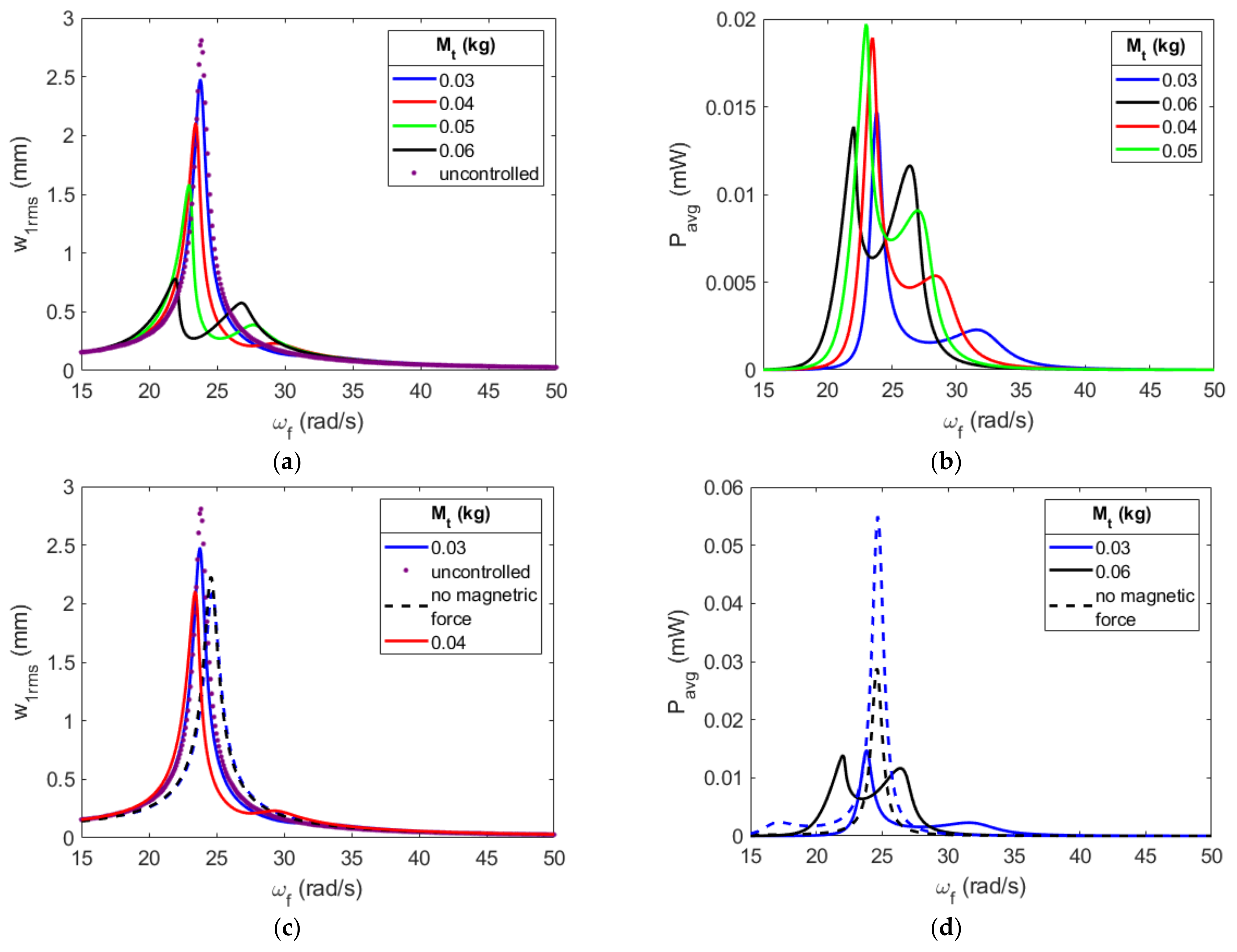
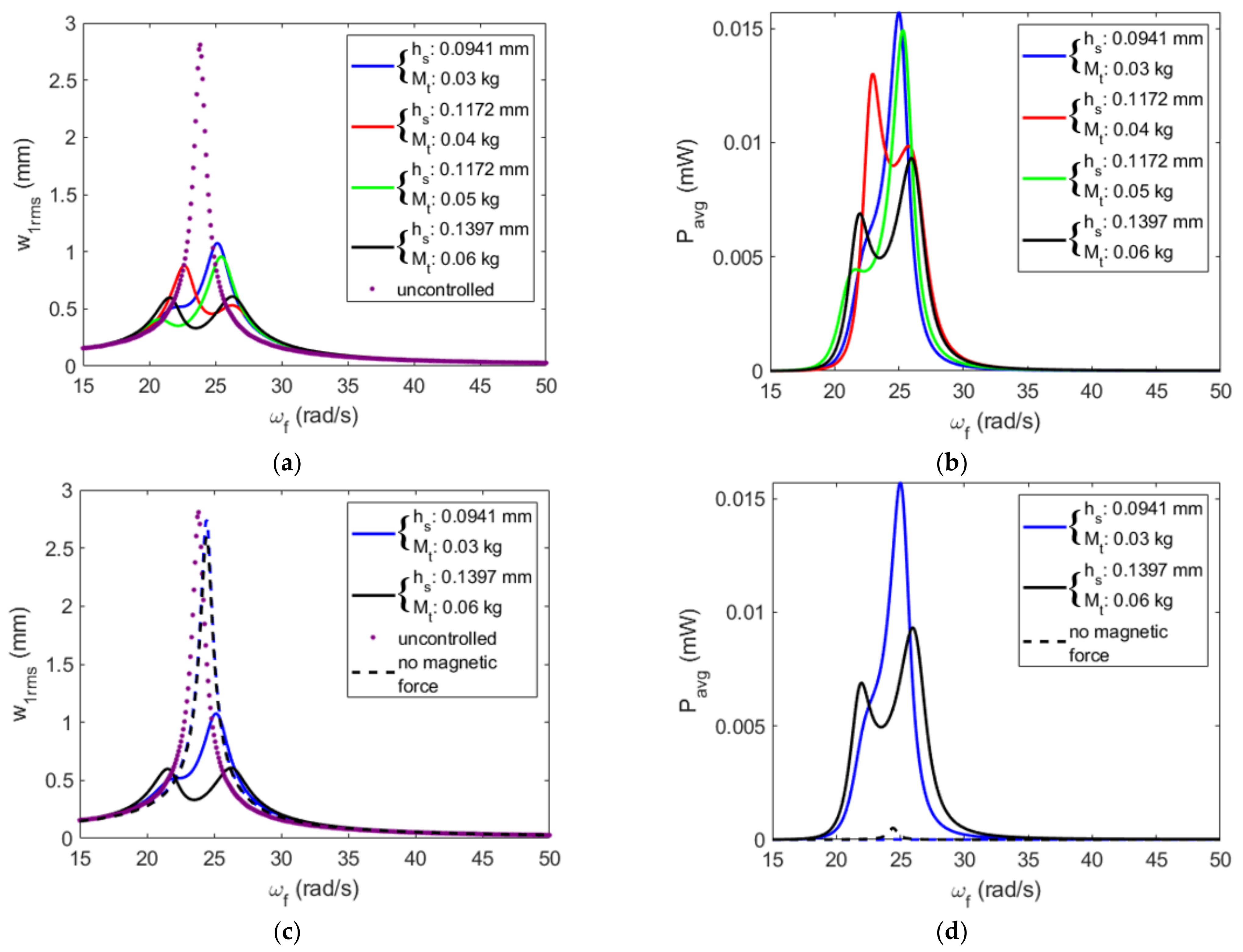
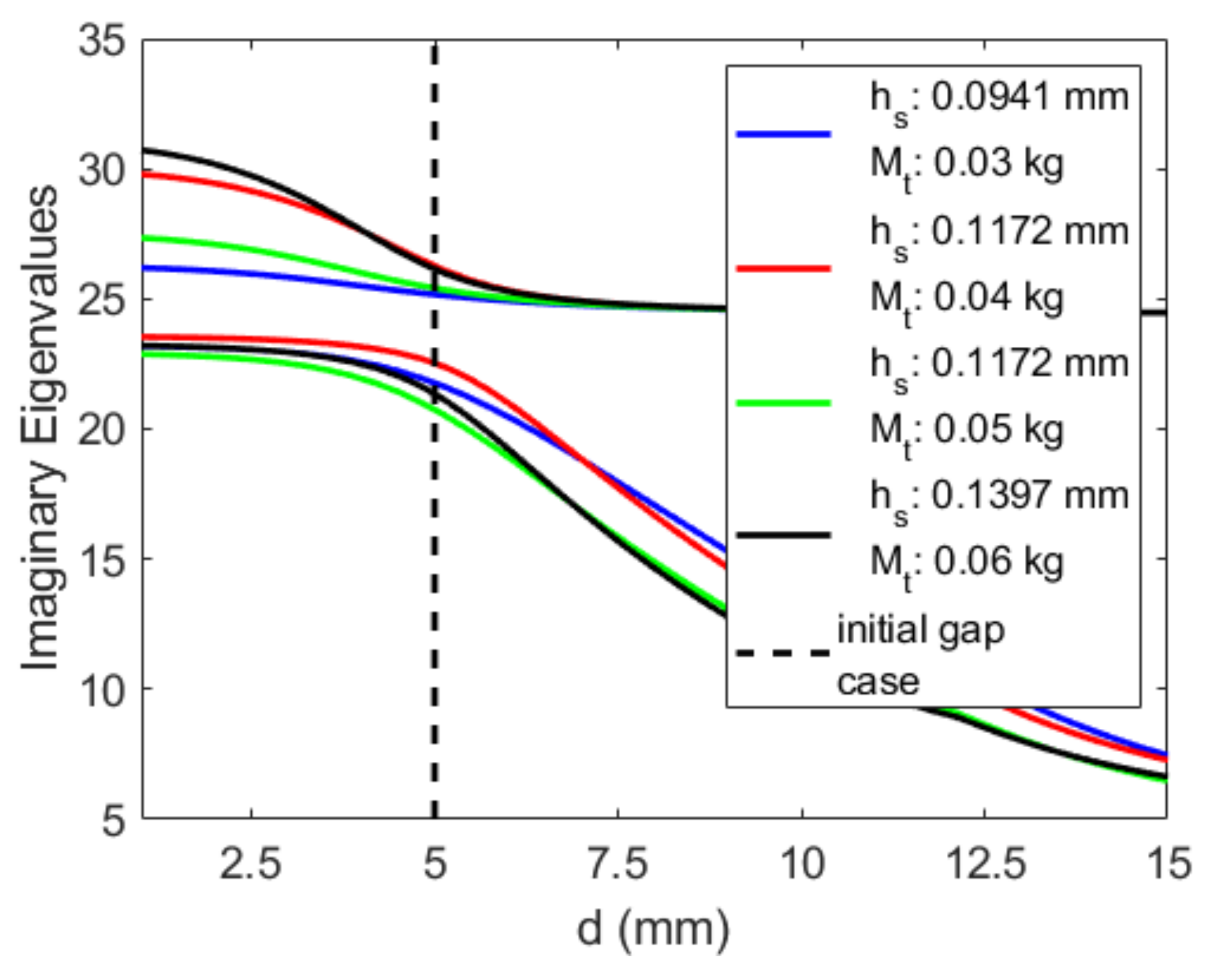
4.2. Effective Design: Absorber’s Substrate Thickness and Tip Mass
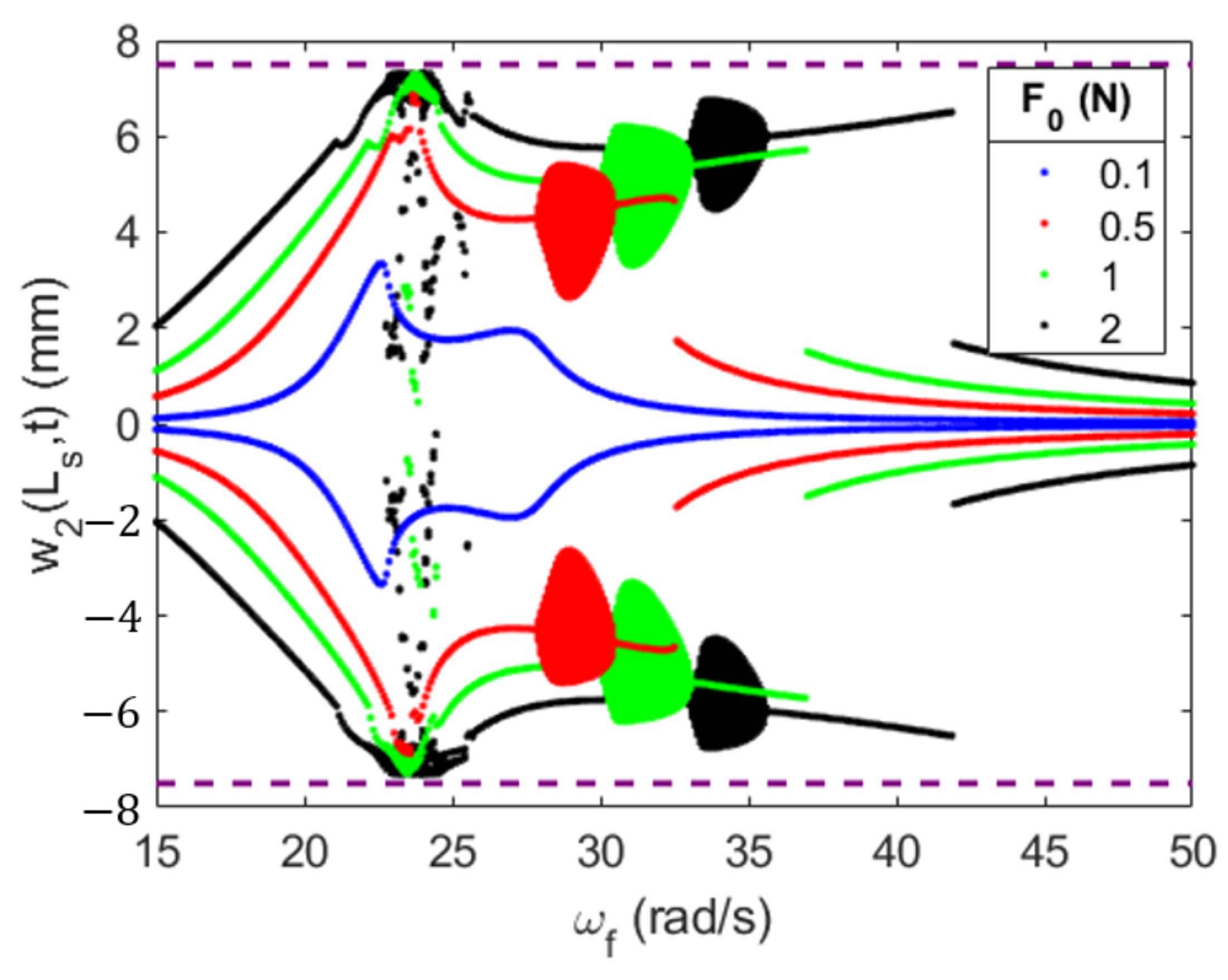
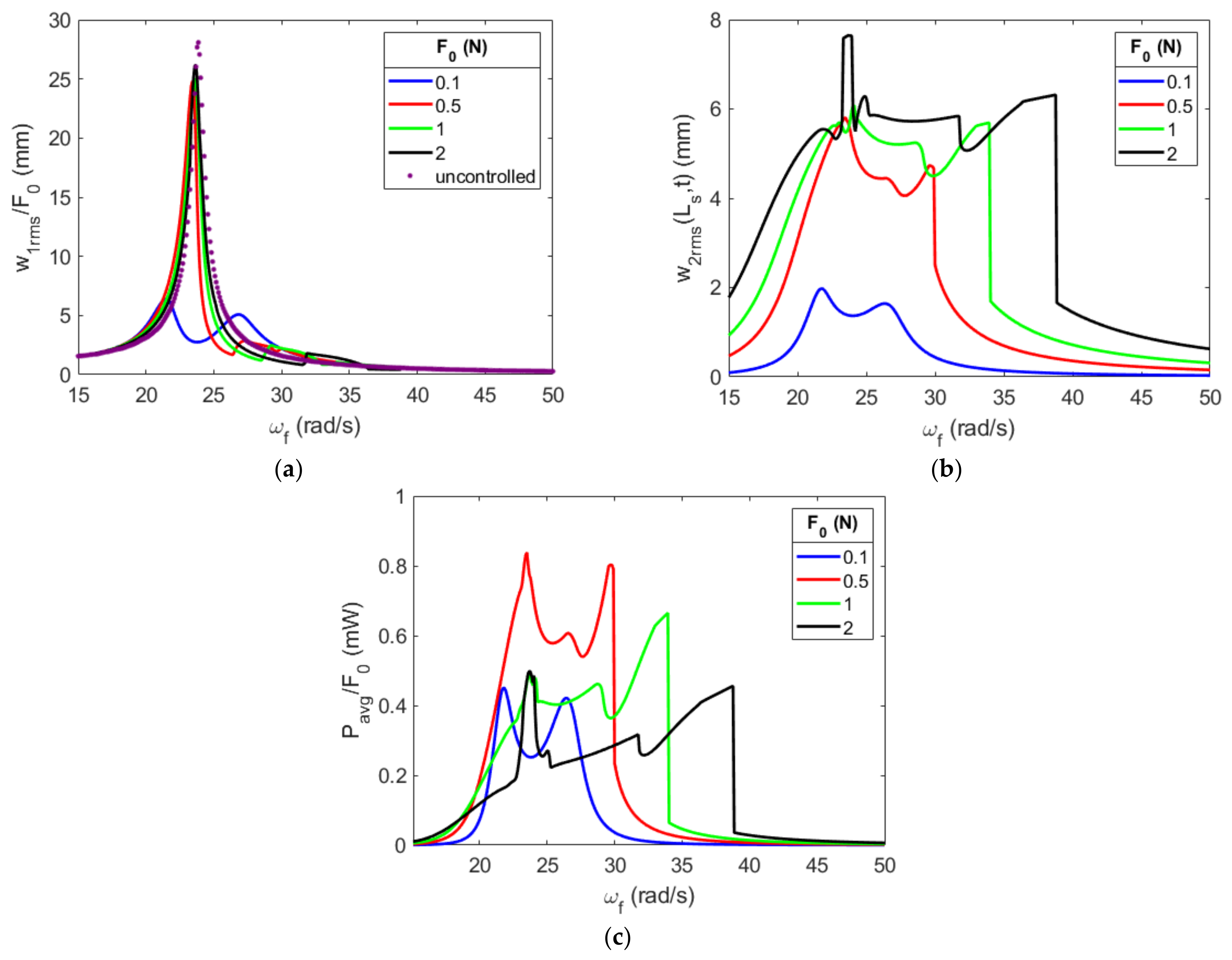
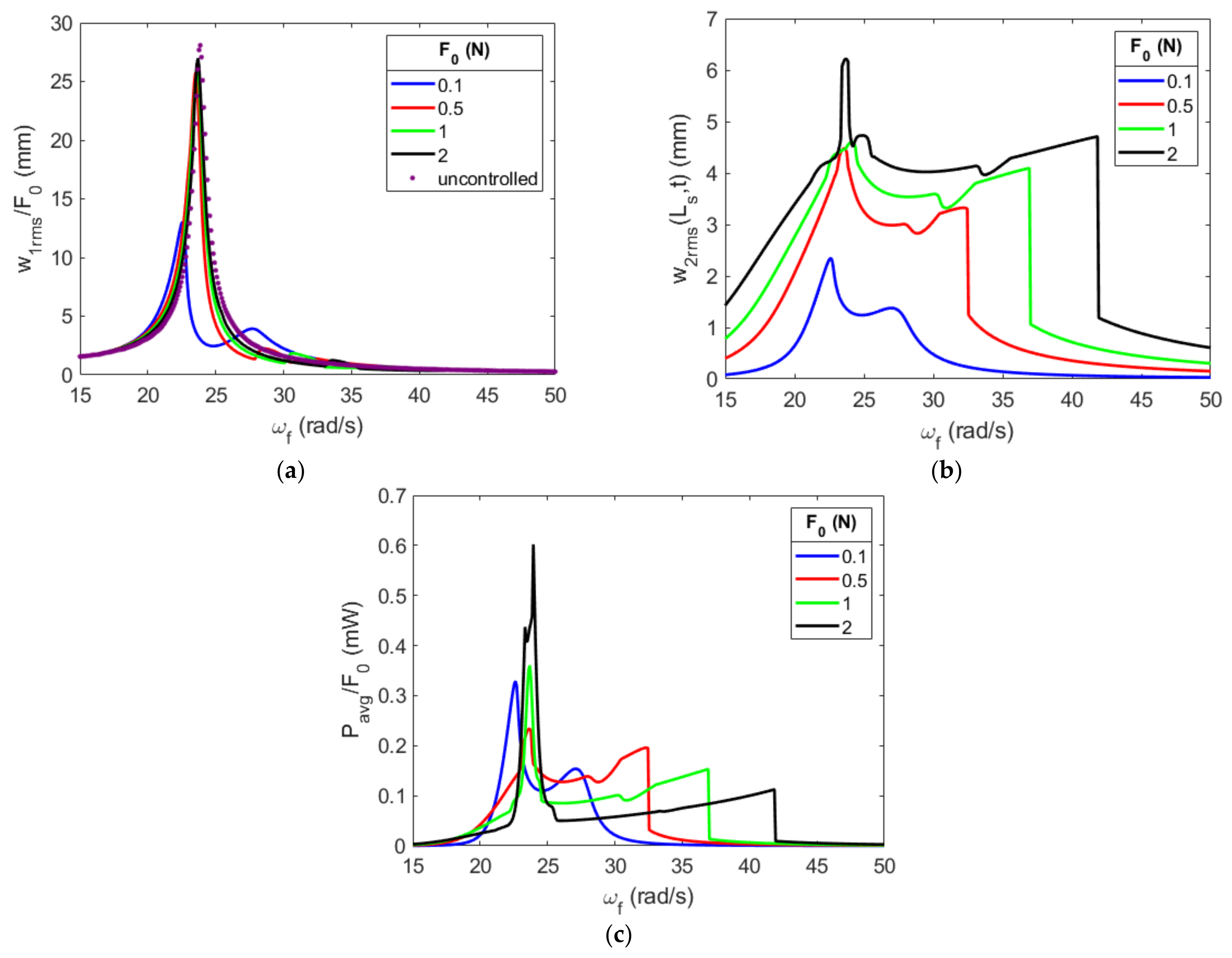
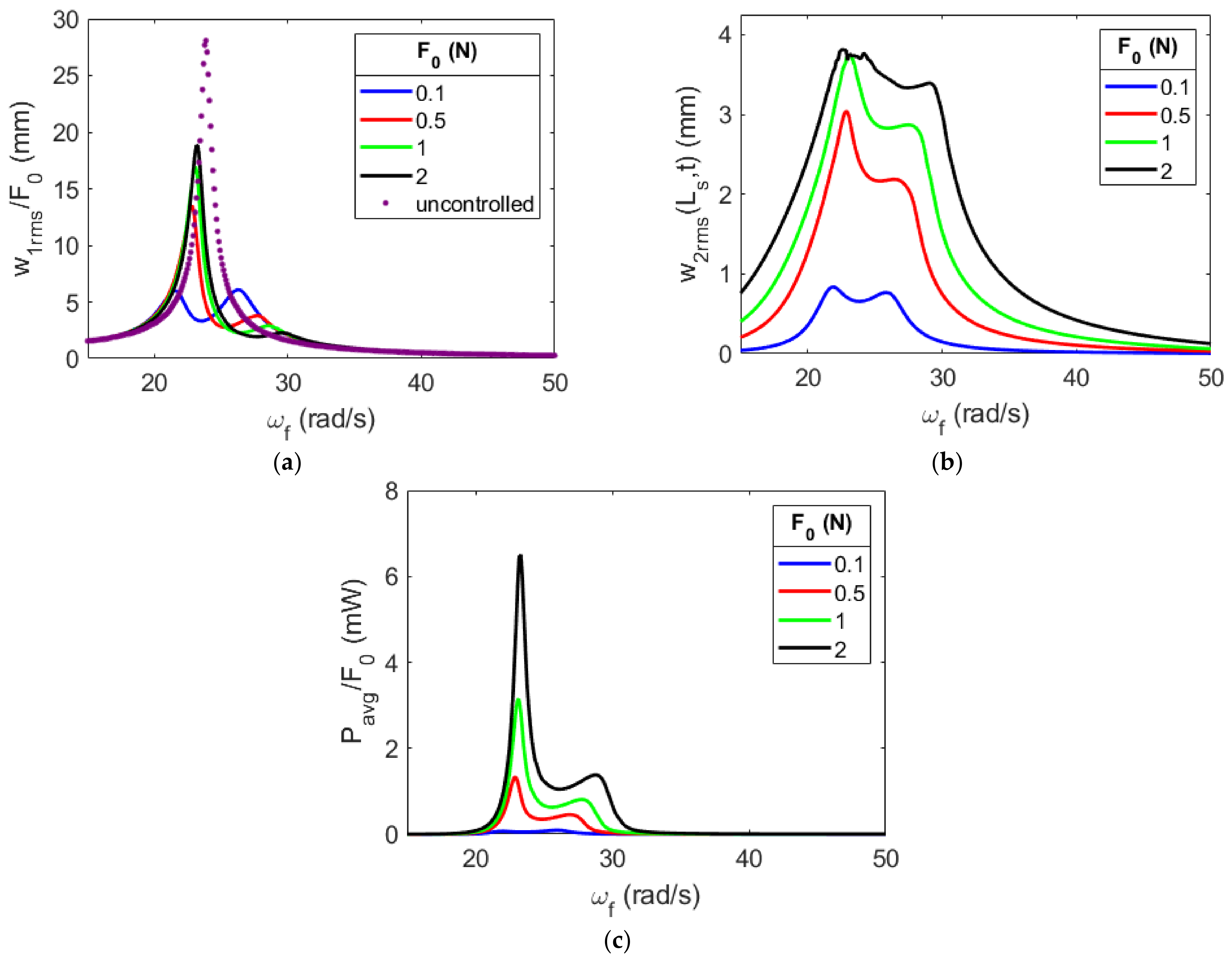
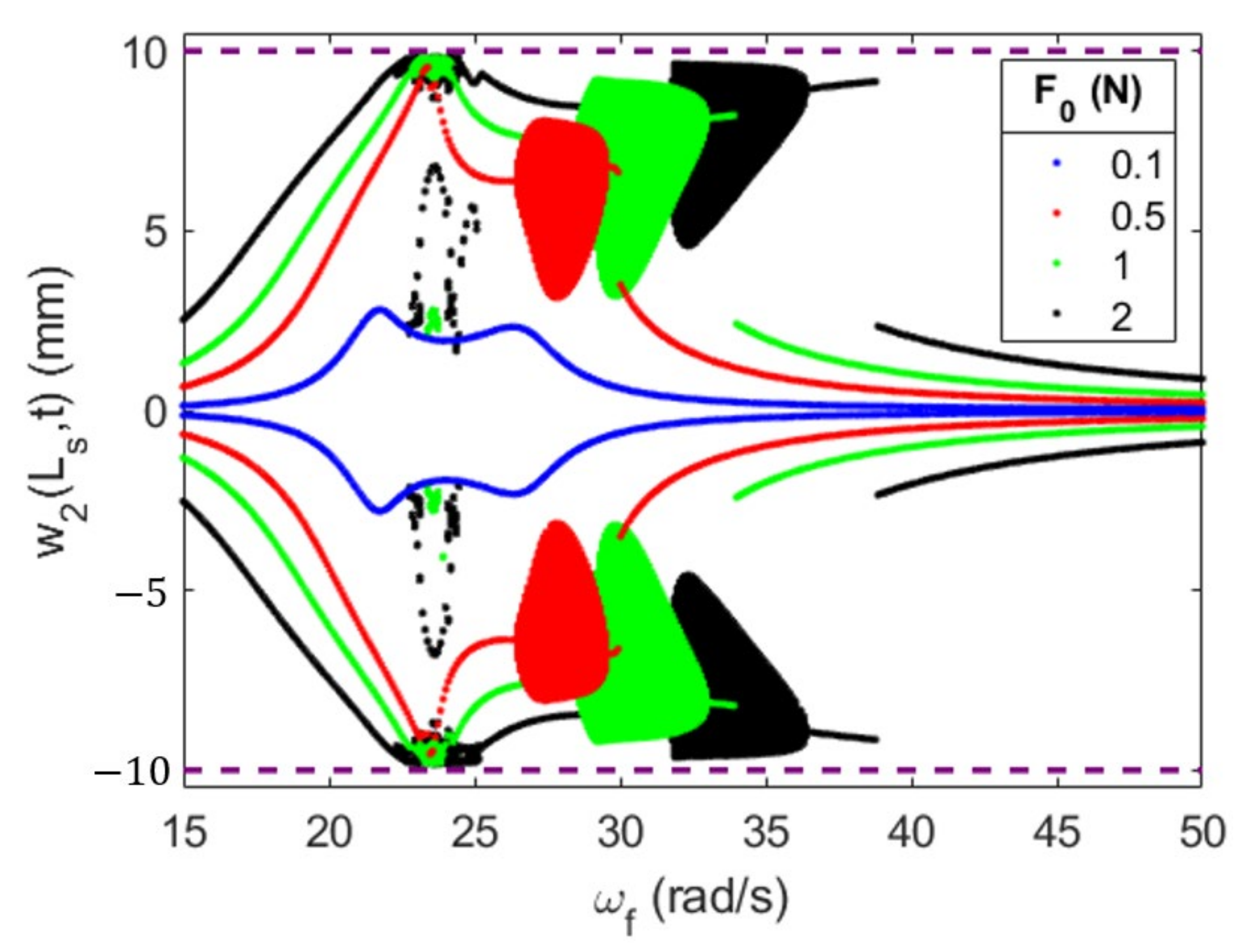
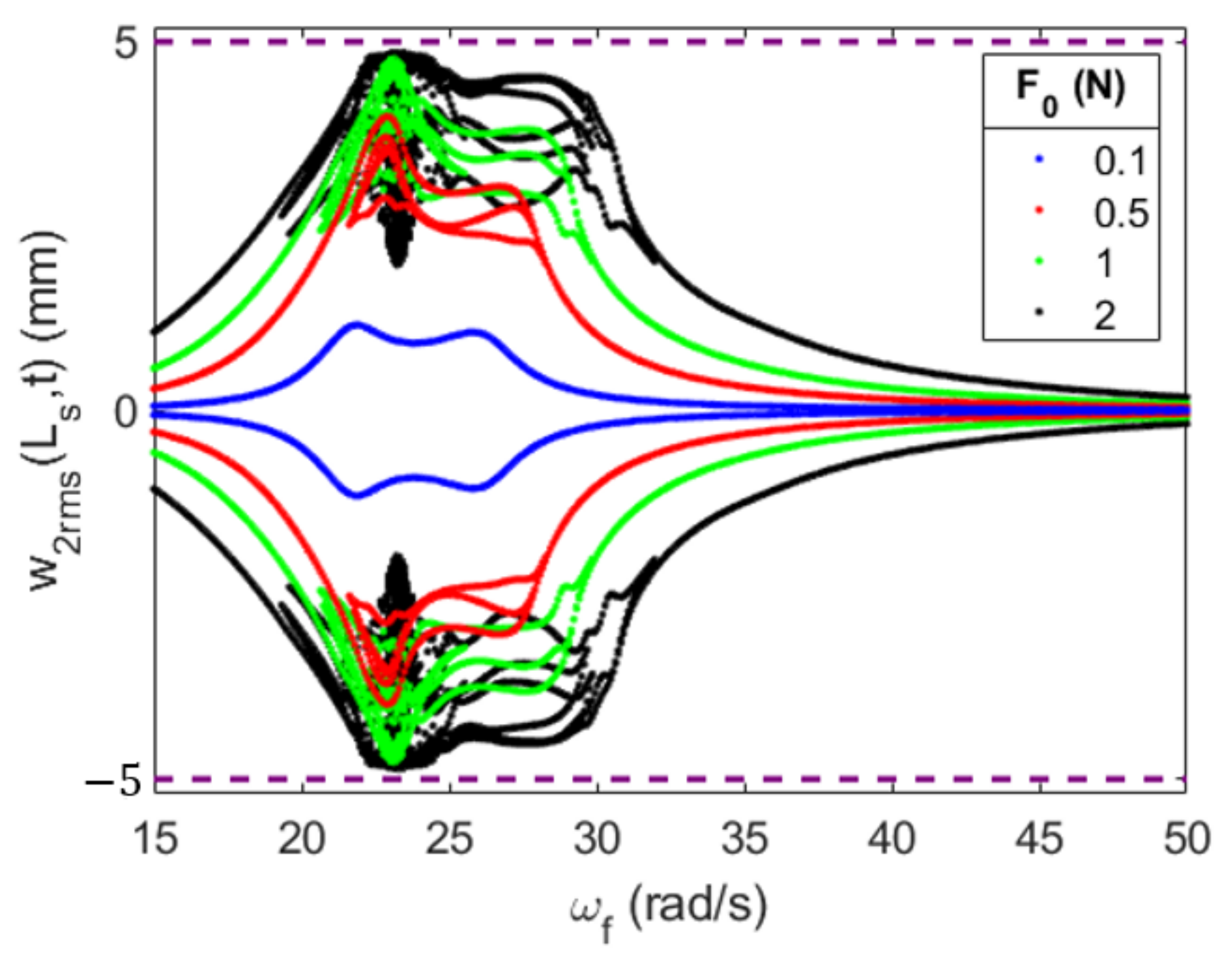
4.3. Effects of the Forcing Amplitude on the System’s Efficiency
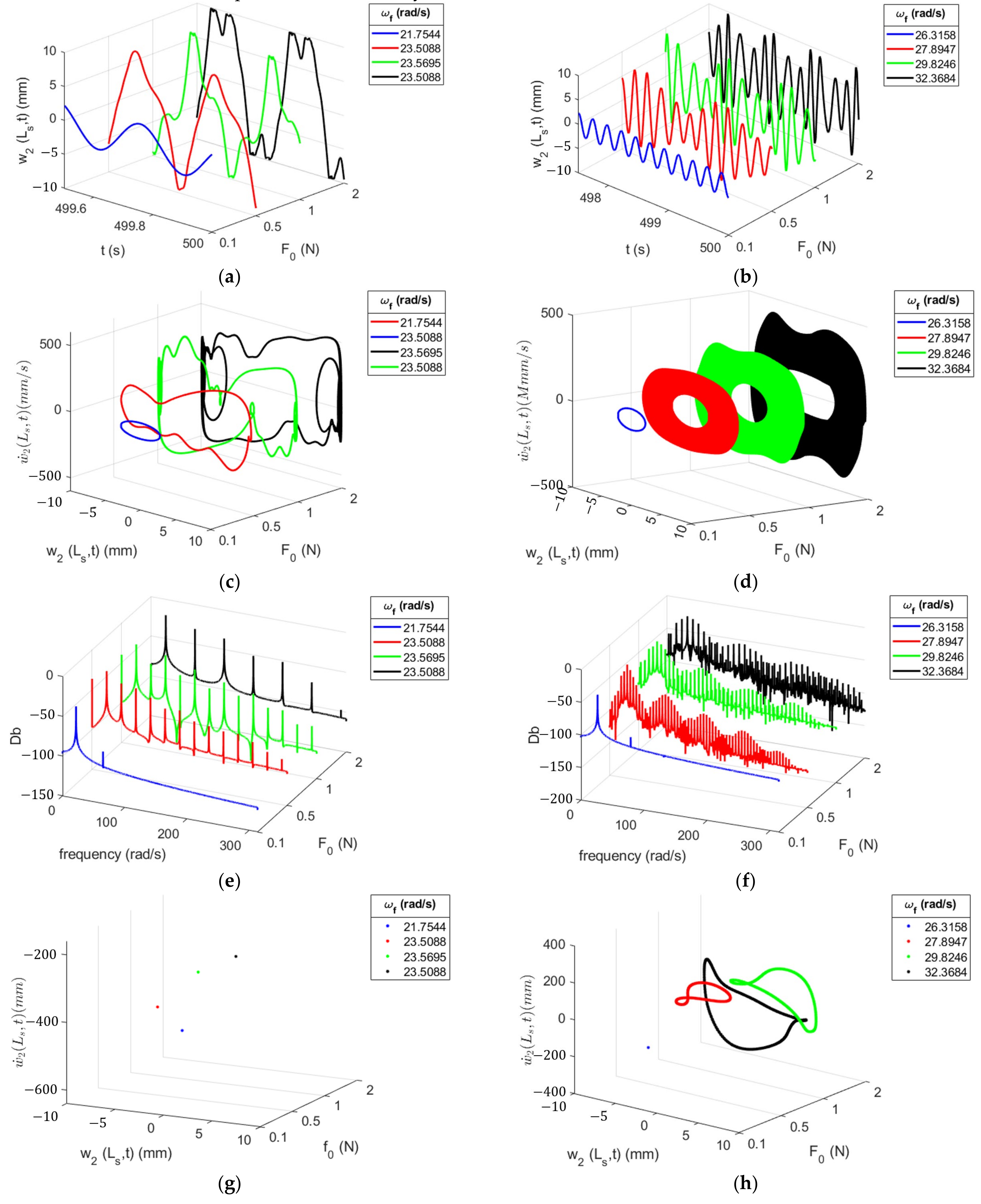
Nonlinear Characterization of the Energy Harvesting Absorber for Varying Forcing Amplitudes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Summary Table of Section 3 Frequency Response
| Config. | Percent of Amplitude Controlled | ||||
|---|---|---|---|---|---|
| Single attractive | 100 | 0.0534 | 0.0636 | 8.42 | 79.5347 |
| 20 | 0.0522 | 0.0651 | 8.42 | 79.0833 | |
| 15 | 0.0477 | 0.0703 | 8.42 | 77.2893 | |
| Double attractive | 100 | 0.0534 | 0.0636 | 8.42 | 79.5345 |
| 20 | 0.0510 | 0.0664 | 8.42 | 78.6168 | |
| 15 | 0.0429 | 0.0765 | 8.42 | 74.9828 | |
| Single repulsive | 100 | 0.0534 | 0.0636 | 8.42 | 79.5350 |
| 20 | 0.0545 | 0.0623 | 8.42 | 79.1360 | |
| 15 | 0.0586 | 0.0580 | 8.42 | 77.6077 | |
| 10 | 0.0762 | 0.0399 | 8.42 | 68.1798 | |
| 5 | 0.0642 | 0.0100 | 8.60 | 30.0985 | |
| Double repulsive | 100 | 0.0540 | 0.0636 | 8.42 | 79.5351 |
| 20 | 0.0558 | 0.0610 | 8.42 | 78.6908 | |
| 15 | 0.0644 | 0.0524 | 8.42 | 75.1193 | |
| 10 | 0.0856 | 0.0218 | 8.68 | 48.9190 | |
| 5 | 0.0090 | 0.0010 | --- | 4.7916 |
Appendix B. Effective Design: Absorber’s Substrate Thickness
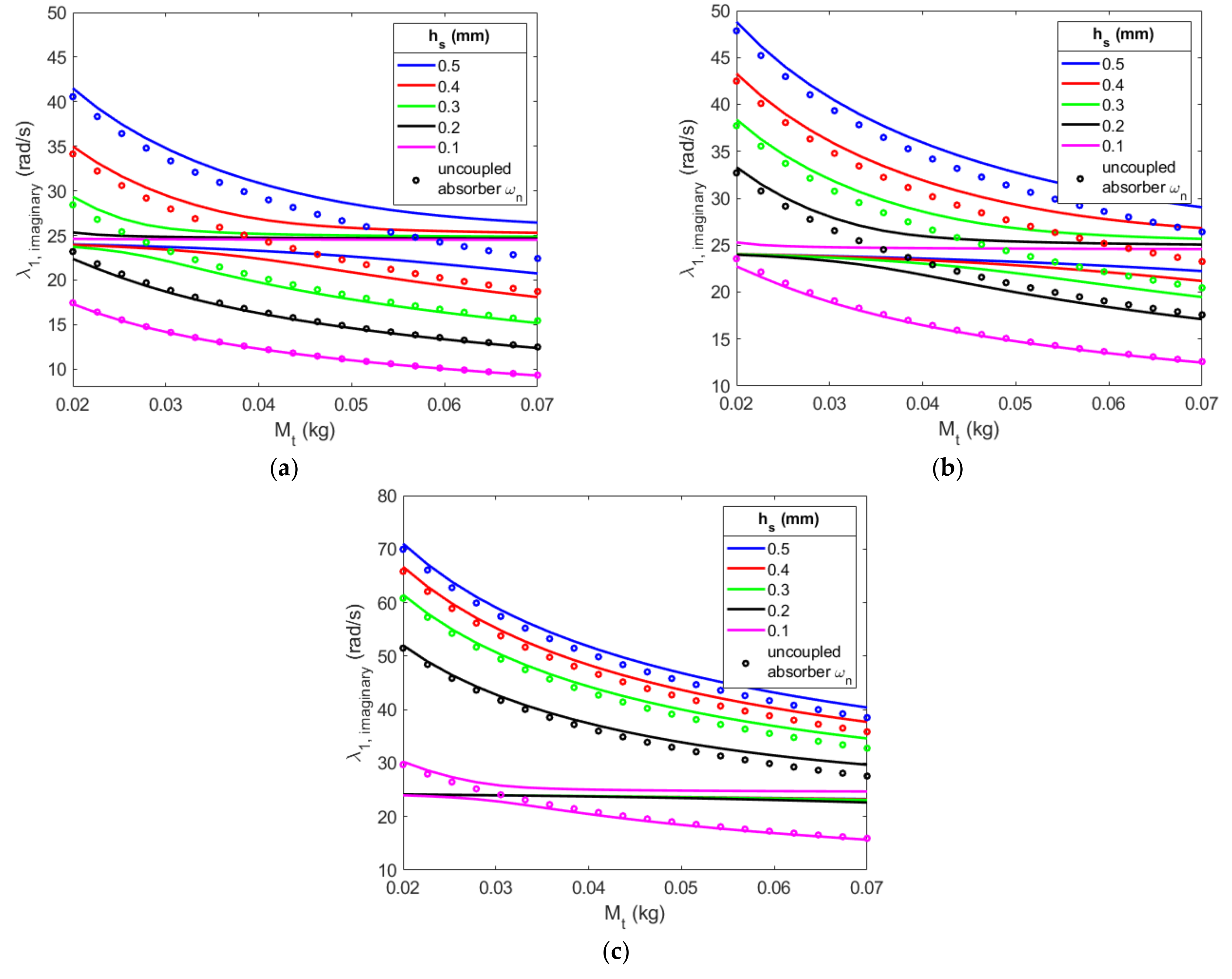
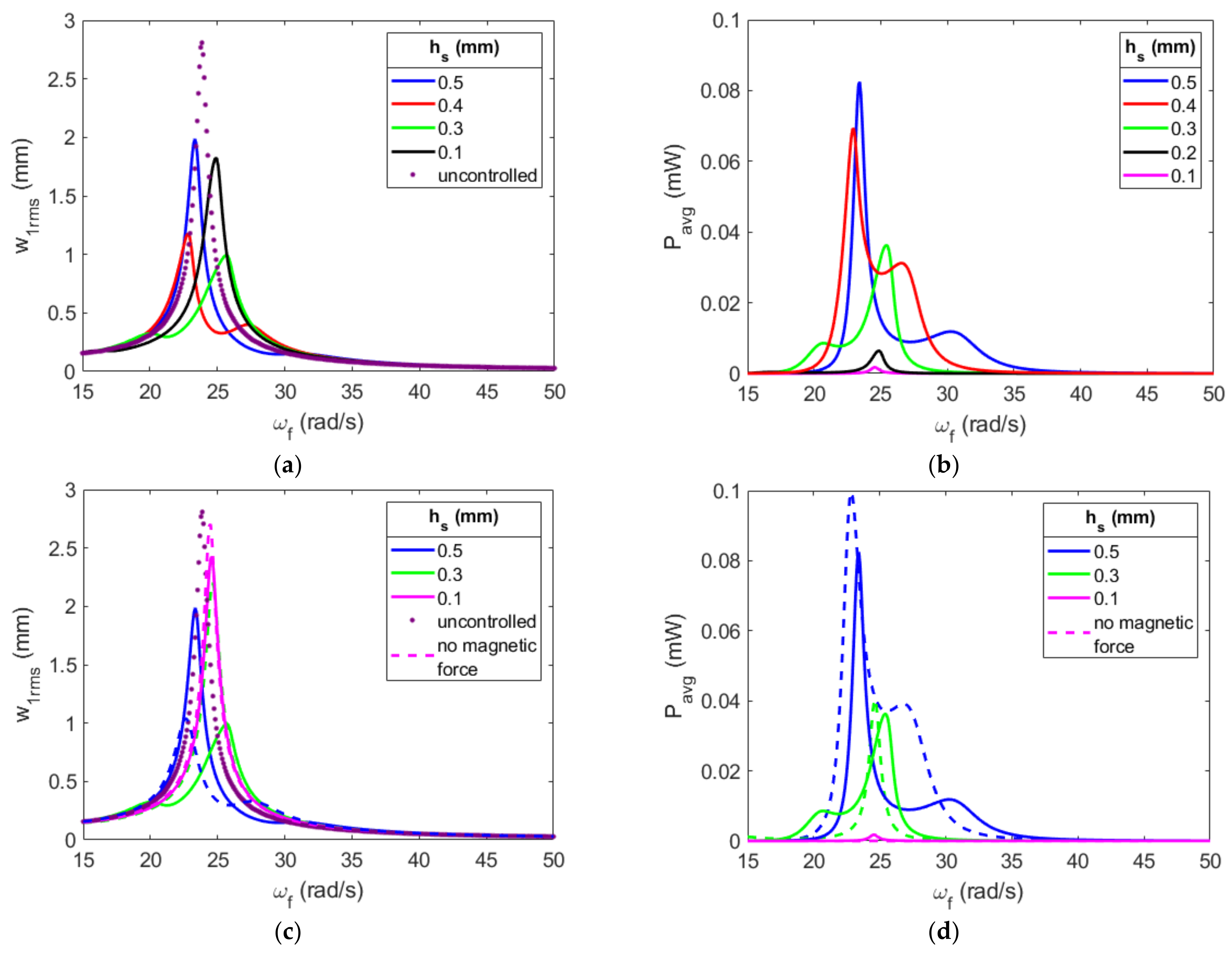
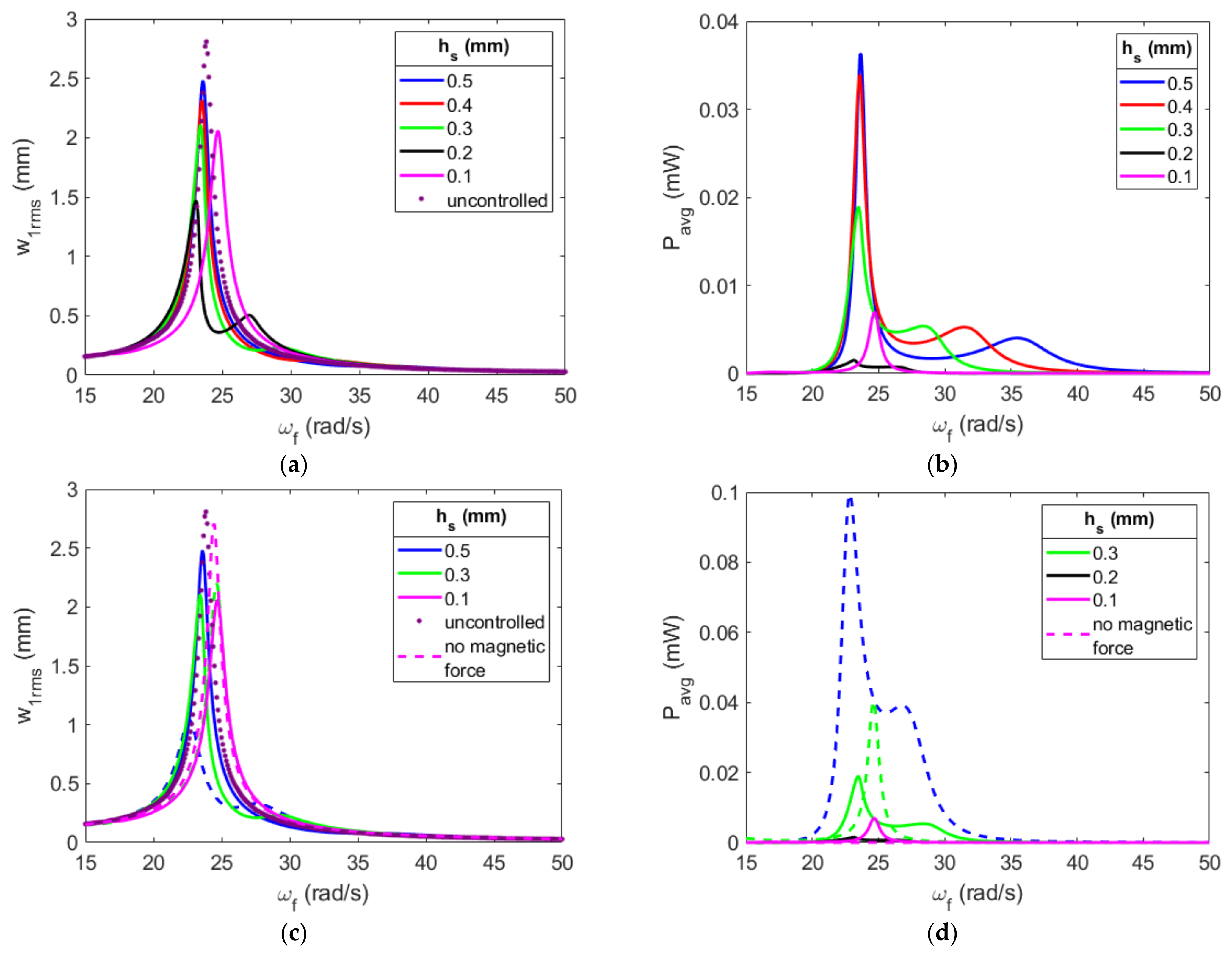

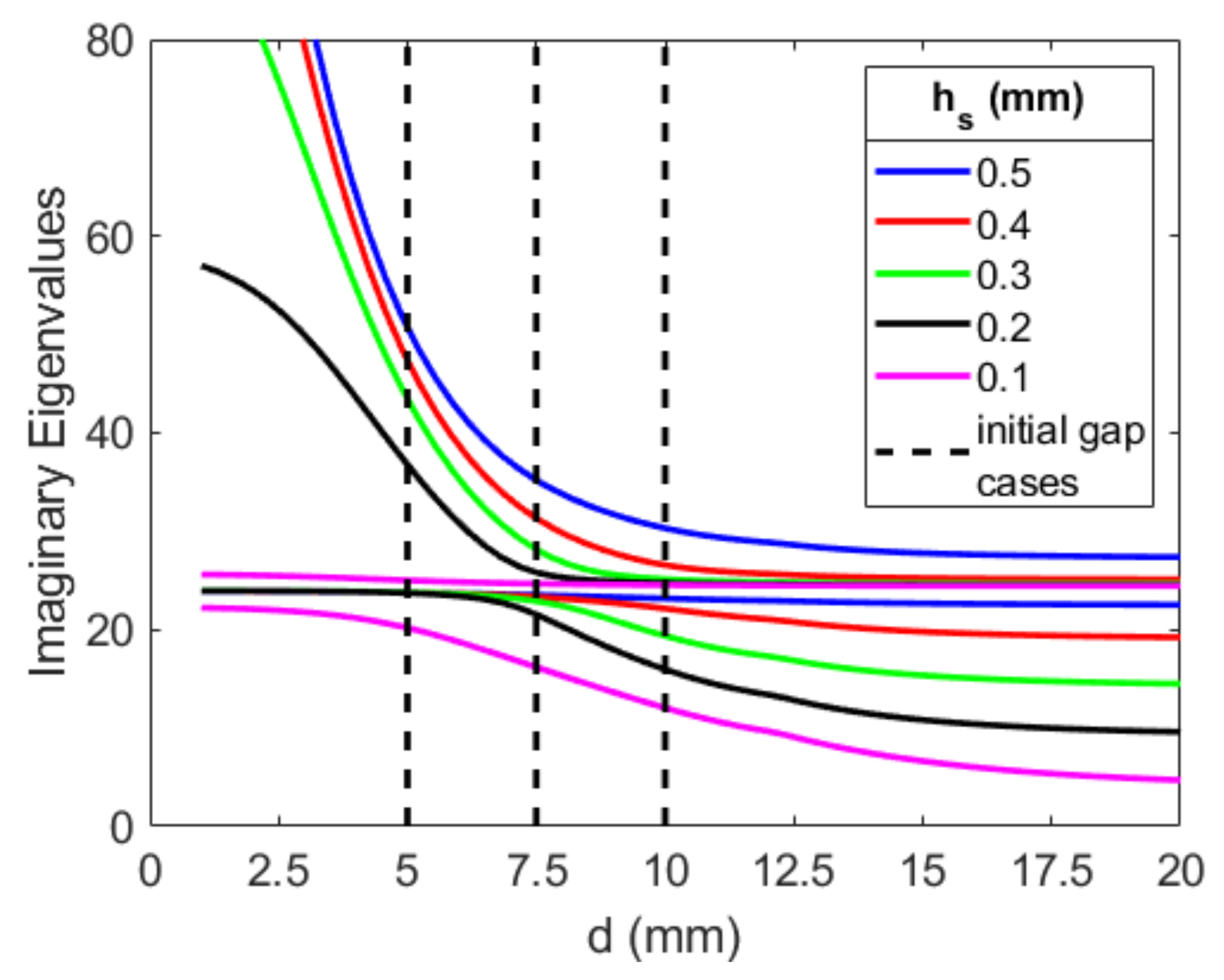
Appendix C. Nonlinear Characterization of Excitation Amplitude’s Effects on the System with a Gap


References
- Kaynia, A.M.; Veneziano, D.; Biggs, J.M. Seismic effectiveness of tuned mass dampers. Am. Soc. Civ. Eng. 1982, 107, 1465–1484. [Google Scholar] [CrossRef]
- Rahimi, F.; Aghayari, R.; Samali, B. Application of Tuned Mass Dampers for Structural Vibration Control: A State-of-the-art Review. Civ. Eng. J. 2020, 6, 1622–1651. [Google Scholar] [CrossRef]
- Thenozhi, S.; Yu, W. Advances in modeling and vibration control of building structures. Annu. Rev. Control. 2013, 37, 346–364. [Google Scholar] [CrossRef]
- Rahman, M.; Ong, Z.C.; Chong, W.T.; Julai, S.; Khoo, S.Y. Performance enhancement of wind turbine systems with vibration control: A review. Renew. Sustain. Energy Rev. 2015, 51, 43–54. [Google Scholar] [CrossRef]
- Yao, J.T.P. Concept of structural control. J. Struct. Div. 1972, 98, 1567–1574. [Google Scholar] [CrossRef]
- Zhang, C.; Ou, J. Control Structure Interaction of Electromagnetic Mass Damper System for Structural Vibration Control. Am. Soc. Civ. Eng. 2008, 134, 428–437. [Google Scholar] [CrossRef]
- Daie, M.; Jalali, A.; Suhatril, M.; Shariati, M.; Khanouki, M.A.; Shariati, A.; Kazemi-Arbat, P. A new finite element investigation on pre-bent steel strips as damper for vibrational control. Int. J. Phys. Sci. 2011, 6, 8044–8050. [Google Scholar]
- Høgsberg, J.; Brodersen, M.L. Hybrid viscous damper with filtered integral force feedback control. J. Vib. Control. 2016, 22, 1645–1656. [Google Scholar] [CrossRef] [Green Version]
- Begdeli, Y.; Kim, D. Damping effects of the passive control devices on structural vibration control: TMD, TLC and TLCD for varying total masses. KSCE J. Civ. Eng. 2016, 20, 301–308. [Google Scholar] [CrossRef]
- Fischer, O. Wind-excited vibrations—Solution by passive dynamic vibration absorbers of different types. J. Wind. Eng. Ind. Aerodyn. 2007, 95, 1028–1039. [Google Scholar] [CrossRef]
- Shu, Z.; Li, S.; Zhang, J.; He, M. Optimum seismic design of a power plant building with pendulum tuned mass damper system by its heavy suspended buckets. Eng. Struct. 2017, 136, 114–132. [Google Scholar] [CrossRef]
- Sun, C.; Jahangiri, V. Bi-directional vibration control of offshore windturbines using 3D pendulum tuned mass damper. Mech. Syst. Signal Process. 2018, 105, 338–360. [Google Scholar] [CrossRef]
- Haxton, R.S.; Barr, A.D.S. The Autoparametric Vibration Absorber. Trans. ASME 1972, 94, 119–125. [Google Scholar] [CrossRef]
- Silva-Navarro, G.; Abundis-Fong, H.F. Passive/Active Autoparametric Cantilever Beam Absorber With Piezoelectric Actuator for a Two-Story Building-Like Structure. J. Vib. Acoust. 2015, 137, 011012. [Google Scholar] [CrossRef]
- Jacquot, R.G.; Foster, J.E. Optimal Cantilever Dynamic Vibration Absorbers. Trans. ASME 1977, 99, 138–141. [Google Scholar] [CrossRef]
- Crovetto, A.; Wang, F.; Hansen, O. Modeling and Optimization of an Electrostatic Energy Harvesting Device. J. Microelectromech. Syst. 2014, 23, 1141–1155. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.U.; Qadir, M.U. State-of-the-art in vibration-based electrostatic energy harvesting. J. Micromech. Microeng. 2016, 26, 103001. [Google Scholar] [CrossRef]
- Palagummi, S.; Yuan, F. An optimal design of a mono-stable vertical diamagnetic levitation based electromagnetic vibration energy harvester. J. Sound Vib. 2015, 342, 330–345. [Google Scholar] [CrossRef]
- Mann, B.; Sims, N. Energy harvesting from the nonlinear oscillations of magnetic levitation. J. Sound Vib. 2009, 319, 515–530. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Gudla, S.; Hassani, F.A.; Heng, C.H.; Lian, Y.; Lee, C. Investigation of the Nonlinear Electromagnetic Energy Harvesters From Hand Shaking. IEEE Sensors J. 2014, 15, 2356–2364. [Google Scholar] [CrossRef]
- Aouali, K.; Kacem, N.; Bouhaddi, N.; Mrabet, E.; Haddar, M. Efficient broadband vibration energy harvesting based on tuned non-linearity and energy localization. Smart Mater. Struct. 2020, 29, 10LT01. [Google Scholar] [CrossRef]
- Anton, S.R.; Sodano, H.A. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, J.H.; Kim, J. A review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Caliò, R.; Rongala, U.B.; Camboni, D.; Milazzo, M.; Stefanini, C.; De Petris, G.; Oddo, C.M. Piezoelectric Energy Harvesting Solutions. Sensors 2014, 14, 4755–4790. [Google Scholar] [CrossRef] [Green Version]
- Toyabur, R.; Salauddin, M.; Cho, H.; Park, J.Y. A multimodal hybrid energy harvester based on piezoelectric-electromagnetic mechanisms for low-frequency ambient vibrations. Energy Convers. Manag. 2018, 168, 454–466. [Google Scholar] [CrossRef]
- Zhao, L.-C.; Zou, H.-X.; Yan, G.; Liu, F.-R.; Tan, T.; Zhang, W.-M.; Peng, Z.-K.; Meng, G. A water-proof magnetically coupled piezoelectric-electromagnetic hybrid wind energy harvester. Appl. Energy 2019, 239, 735–746. [Google Scholar] [CrossRef]
- Mahmoudi, S.; Kacem, N.; Bouhaddi, N. Enhancement of the performance of a hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions. Smart Mater. Struct. 2014, 23, 075024. [Google Scholar] [CrossRef]
- Xia, H.; Chen, R.; Ren, L. Analysis of piezoelectric–electromagnetic hybrid vibration energy harvester under different electrical boundary conditions. Sens. Actuators A Phys. 2015, 234, 87–98. [Google Scholar] [CrossRef]
- Zhao, D.; Liu, S.; Xu, Q.; Sun, W.; Wang, T.; Cheng, Q. Theoretical modelng and analysis of a 2-degree-of-freedom hybrid piezoelectric-electromagnetic vibration energy harvester with a driven beam. J. Intell. Mater. Syst. Struct. 2018, 29, 2465–2476. [Google Scholar] [CrossRef]
- Dai, H.L.; Abdelmoula, H.; Abdelkefi, A.; Wang, L. Towards control of cross-flow-induced vibrations based on energy harvesting. Nonlinear Dyn. 2017, 88, 2329–2346. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Abdelkefi, A. The potential of electrical impedance on the performance of galloping systems for energy harvesting and control applications. J. Sound Vib. 2016, 370, 191–208. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Dai, H.L.; Abdelkefi, A.; Wang, L. Control of base-excited dynamical systems through piezoelectric energy harvesting absorber. Smart Mater. Struct. 2017, 26, 095013. [Google Scholar] [CrossRef]
- McNeil, I.; Abdelkefi, A. Nonlinear modeling and vibration mitigation of combined vortex-induced and base vibrations through energy harvesting absorbers. Commun. Nonlinear Sci. Numer. Simul. 2020, 95, 105655. [Google Scholar] [CrossRef]
- Ali, S.F.; Adhikari, S. Engerry harvesting dynamic vibration absorbers. J. Appl. Mech. 2013, 80, 041004. [Google Scholar] [CrossRef]
- Yan, Z.; Hajj, M.R. Energy harvesting from an autoparametric vibration absorber. Smart Mater. Struct. 2015, 24, 115012. [Google Scholar] [CrossRef]
- Felix, J.L.P.; Balthazar, J.M.; Rocha, R.T.; Tusset, A.M.; Janzen, F.C. On vibration mitigation and energy harvesting of a non-ideal system with autoparametric vibration absorber system. Meccanica 2018, 53, 3177–3188. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Yang, Y.; Soh, C.-K. Improving functionality of vibration energy harvesters using magnets. J. Intell. Mater. Syst. Struct. 2012, 23, 1433–1449. [Google Scholar] [CrossRef]
- Haitao, L.; Qin, W.; Chunbo, L.; Deng, W.; Zhou, Z. Dynamics and coherence resonance of tri-stable energy harvesting system. Smart Mater. Struct. 2015, 25, 015001. [Google Scholar] [CrossRef]
- Kim, P.; Seok, J. A multi-stable eneregy harvester: Dynamic modeling and bifurcation analysis. J. Sound Vib. 2014, 333, 5525–5547. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Liu, S.; Wang, Z. Broadband tristable energy harvester: Modeling and experiment verification. Appl. Energy 2014, 133, 33–39. [Google Scholar] [CrossRef]
- Wang, W.; Cao, J.; Bowen, C.R.; Zhang, Y.; Lin, J. Nonlinear dynamics and performance enhancement of asymmetric potential bistable eneregy harvesters. Nonlinear Dyn. 2018, 94, 1183–1194. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y. A nonlinear piezoelectric energy harvester with magnetic oscillator. Appl. Phys. Lett. 2012, 101, 094102. [Google Scholar] [CrossRef]
- Abdelkefi, A.; Barsallo, N. Comparative modeling of low-frequency piezomagnetoelastic energy harvesters. J. Intell. Mater. Syst. Struct. 2014, 25, 1771–1785. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Zimmerman, S.; Abdelkefi, A. Accurate modeling, comparative analysis, and performance enhancement of broadband piezoelectric energy harvesters with single and dual magnetic forces. Int. J. Non-linear Mech. 2017, 95, 355–363. [Google Scholar] [CrossRef]
- Alvis, T.; Abdelkefi, A. Effectiveness and nonlinear characterization of vibro-impact energy harvesting absorbers in controlling base-excited systems. Smart Mater. Struct. 2021, 30, 095028. [Google Scholar] [CrossRef]
- Alvis, T.; Abdelkefi, A. Effective design of vibro-impact energy harvesting absorbers with asymmetric stoppers. Eur. Phys. J. Spéc. Top. 2022, 231, 1567–1586. [Google Scholar] [CrossRef]
- Upadrashta, D.; Yang, Y.; Tang, L. Material strength consideration in the design optimization of nonlinear energy harvester. J. Intell. Mater. Syst. Struct. 2015, 26, 1980–1994. [Google Scholar] [CrossRef]
- Sezer, N.; Koç, M. A comprehensive review on the state-of-the-art of piezoelectric energy harvesting. Nano Energy 2021, 80, 105567. [Google Scholar] [CrossRef]










| 3.244 | |||||||||||
| Parameter | Parameter’s Symbol | Parameter’s Value |
|---|---|---|
| Young’s modulus of the absorber substrate | ||
| Young’s modulus of the piezoelectric layers | ||
| Height of the substrate | ||
| Height of the piezoelectric layers | ||
| Length of the substrate | ||
| Length of the piezoelectric layers | ||
| Critical length of the tip mass | ||
| Width of the substrate and piezoelectric layers | ||
| Density of the substrate | ||
| Density of the piezoelectric layers | ||
| Tip mass | ||
| Mass of the primary structure | ||
| Damping coefficient of the structure | ||
| Damping ratio of the absorber | ||
| Stiffness of the primary structure | ||
| Piezoelectric strain coefficient | ||
| Piezoelectric permittivity component | ||
| Electric load resistance of the piezoelectric layers |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvis, T.; Mesh, M.; Abdelkefi, A. Insights on the Effects of Magnetic Forces on the Efficiency of Vibration Energy Harvesting Absorbers in Controlling Dynamical Systems. Energies 2023, 16, 1272. https://doi.org/10.3390/en16031272
Alvis T, Mesh M, Abdelkefi A. Insights on the Effects of Magnetic Forces on the Efficiency of Vibration Energy Harvesting Absorbers in Controlling Dynamical Systems. Energies. 2023; 16(3):1272. https://doi.org/10.3390/en16031272
Chicago/Turabian StyleAlvis, Tyler, Mikhail Mesh, and Abdessattar Abdelkefi. 2023. "Insights on the Effects of Magnetic Forces on the Efficiency of Vibration Energy Harvesting Absorbers in Controlling Dynamical Systems" Energies 16, no. 3: 1272. https://doi.org/10.3390/en16031272
APA StyleAlvis, T., Mesh, M., & Abdelkefi, A. (2023). Insights on the Effects of Magnetic Forces on the Efficiency of Vibration Energy Harvesting Absorbers in Controlling Dynamical Systems. Energies, 16(3), 1272. https://doi.org/10.3390/en16031272








