2.2. Comparison between Hydrogeological and Energy Models for BHE Simulation
Numerical modeling is a helpful tool to design a HVAC system and is one of the essential elements of these systems: the ground heat exchanger (BHE). The reproduction of a BHE system was fully validated in MODFLOW/MT3DMS [
25,
35] and in a recent updated version of the software MODFLOW-USG [
32,
33]. The need to validate the same element in TRNSYS, a widely used tool for the dynamic simulation of thermal and electrical energy systems, was high, hence, the reproduction of the same BHE numerical model was carried out in TRNSYS software for the first time in the thesis by Antelmi and Legrenzi [
40].
Different efforts were required by the numerical models, both for the geometry description and the calculation phase. In MODFLOW/MT3DMS, the boundary and internal conditions were applied to reproduce the operation of a BHE coupled to a GSHP, whereas in MODFLOW-USG, a specific package, named the connected linear network (CLN) package, was used for the same purpose of the previous version of the software; the numerical results were similar to those discussed in [
32,
33]. TRNSYS software allows for detailed analyses of the energy performance and comfort conditions related to buildings and systems to be performed. A standard library provides a list of components (“types”) representing common systems and written in the FORTRAN language. User written or non-standard components may also be added due to the modular structure of the code. Among all the types present in the database, the most suitable one was only Type280, based on the TRNVDSTP model. This type was developed by Pahud [
39] and based on the duct storage model (DST) studied by Hellstrom [
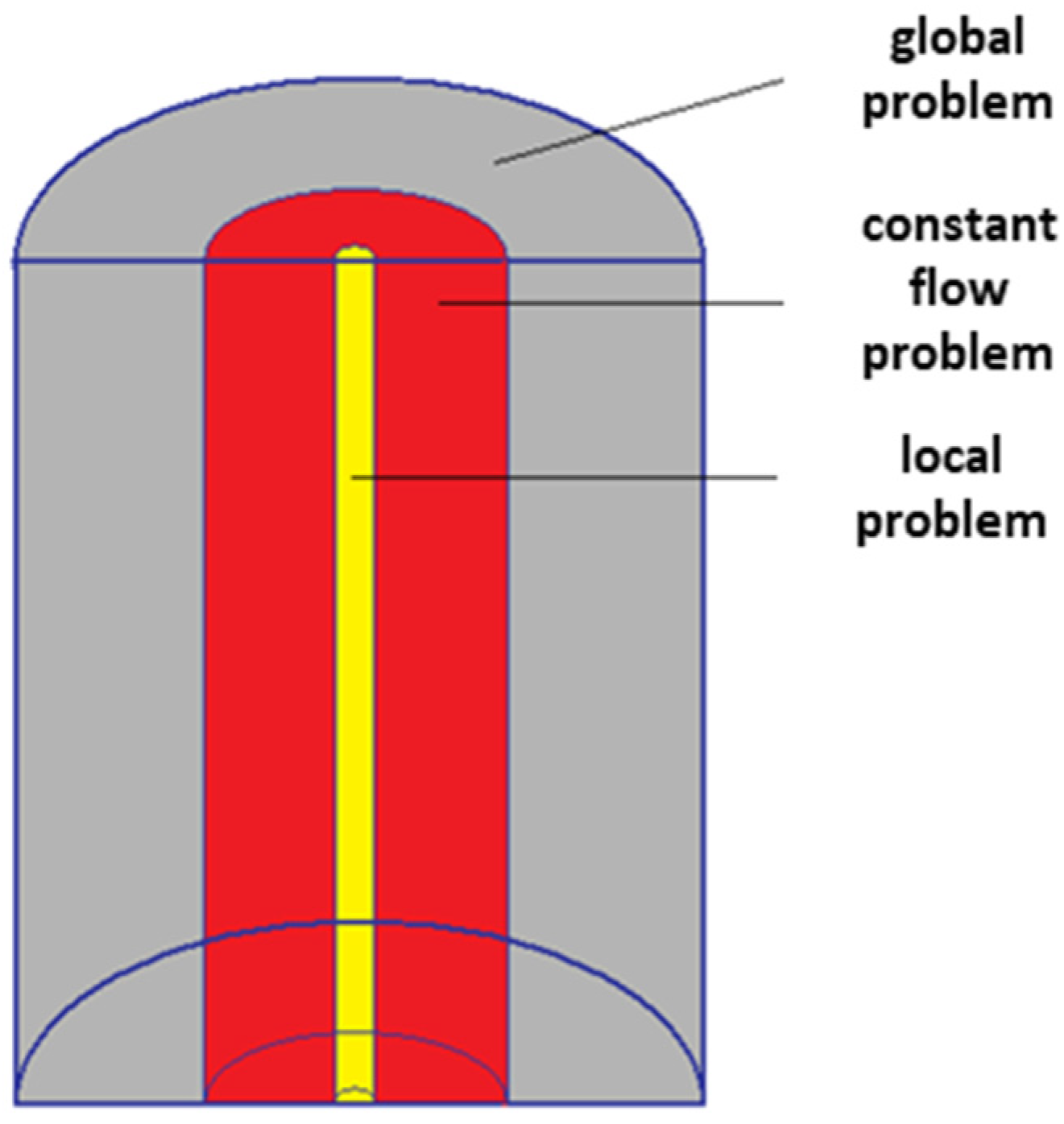
14]. The DST model is the physical model able to reproduce one or more BHE in the same volume of aquifer. The heat carrier fluid is circulated into the U-shape pipe system and a conductive heat transfer is assumed between the heat carrier fluid and the ground. Not only is the heat transferred between the fluid in each pipe and the surrounding ground, but the thermal interaction between the U-pipes is also simulated by modeling the thermal process by overlapping three parts: local, global, and steady-flow problems (
Figure 1). The short-term effects are considered in the local problem, whereas the slow heat redistribution into the storage volume and between the storage boundary and surrounding soil is included in the steady-state and global flow problems [
39]. Local and global problems are solved numerically by finite difference methods; the steady-state flow problem is evaluated analytically, referring to a problem where the heat is locally injected at fixed time intervals in a circular region.
The DST model has been updated over the years and in the latter version, called TRNVDSTP [
39], the possibility to reproduce the groundwater flow effects on heat transfer was taken into account. The heat transferred by forced convection in the storage region is calculated for each layer. It is difficult to achieve an accurate simulation of the influence of the groundwater flow because the calculation procedure assumes a cylindrical geometry around the well, so therefore, the temperature range is not translated in the direction of the groundwater flow. Indeed, the DST model was not initially designed for this purpose.
Through Type280, both the long-term effects of the groundwater flow, which act on the “global problem”, and the short-term effects, which concern the “local problem” are implemented. Regarding the long-term effects, two methods are available to evaluate the heat transferred by forced convection in each layer of the storage subsoil. The first method evaluates the heat convective loss, deriving it from the temperature difference between the temperatures of two cells, placed along the vertical boundary of the storage volume.
The velocity of the thermal plume (v
thermal) is given by:
where C
w is the volumetric heat capacity of the water (J/m
3 K); C
ground is the volumetric heat capacity of the ground layer (J/m
3 K); and u is the groundwater velocity (called Darcy velocity) into the subsoil layer (m/s), given by the product of the hydraulic conductivity of the subsoil layer k (m/s) and hydraulic gradient of the related aquifer i (unitless): u = k⋅i. The hydraulic conductivity is an intrinsic property of ground layers (i.e., for sand, common values are between 10
−4 and 10
−5 m/s, for clay between 10
−7 and 10
−8 m/s), whereas the hydraulic gradient is the ratio between two different levels of water table into the subsoil and the length between these two calculation points. In shallow aquifers, common values of Darcy velocity are between 10
−7 m/s (aquifer consisting of fine materials) and 10
−3 m/s (aquifer consisting of coarse material).
The heat transfer equation is:
where E
conv is the heat amount transferred by forced convection in the storage volume during the time-step Δt (J); S is the transverse storage area involved by the groundwater flow (m
2), evaluated as the product of the storage volume diameter D (m), assumed as cylindrical, and the vertical depth of the storage volume H (m): S = D⋅H; T
mean_out, the average temperature of the cells just outside the storage volume boundary along the depth H (°C); Tmean_in is the average temperature of the cells just inside the storage volume boundary along H (°C); Δt is the time-step for the calculation of the global temperature field in the soil.
In the second method, the heat convective loss is derived from the temperature difference between the average temperature of the ground layers inside the storage volume (T
mean) and the unperturbed temperature of the aquifer (T
g): according to Equation (2), the heat convective loss is evaluated as:
where V is the subsoil volume of the layer within the storage volume (m
3) and E
conv_max is the maximum possible heat amount transferred by forced convection in the storage volume (related to the layer) during the time-step ∆t (J).
The groundwater velocity (Darcy) is a required parameter of Type280 for each subsoil layer; if it is set to zero, the groundwater flow is very low or negligible and any advection phenomenon outside the storage volume is neglected. This condition is rare because in nature, concerning shallow geothermal issues and therefore depths lower than 150 m, an underground water flow is always present. The intensity of this flow (i.e., Darcy velocity) is directly dependent on the lithologies and hydraulic gradients of the area. The influence of the groundwater flow on the exchanged heat of the BHE is evaluated using the Nusselt number, assuming a cylinder buried in a porous medium and run over by the groundwater flow, assumed uniform, and perpendicular to the same cylinder.
An evaluation of the energy extracted or injected from the ground assuming different groundwater flow velocities in TRNSYS was provided in the thesis by Antelmi and Legrenzi [
40]. They compared the exchanged power computed by TRNSYS with those evaluated in MODFLOW/MT3DMS to define which one was in accordance with the experimental data. Assuming identical physical and hydrogeological properties as discussed in [
40,
41], they compared, for the first time, the two software programs in terms of exchanged power, and the results were in disagreement, as shown in
Figure 2.
The extracted (the winter season corresponds to negative values) and injected (summer season, positive values) energies were evaluated as integral of the subtended area of the exchanged power parameter over time: the increase in energies related to the null velocity case for the TRNSYS simulations was equal to 9% (winter) and 14% (summer) whereas the increase in energies for the MODFLOW/MT3DMS simulations was equal to 148% (winter) and 162% (summer) (
Table 1).
Therefore, TRNSYS simulations using Type280 did not reach the energy amount exchanged by MODFLOW/MT3DMS for high groundwater flow velocities and also disagreed with similar literature cases for both the heating and cooling period [
9,
10,
38]; therefore, it is clear that Type280 implemented in TRNSYS version 16 needs some revisions to be applied for the projects where the influence of groundwater flow is present.
2.3. The Creation of Type285
In TRNSYS 18, Type280 has been replaced by Type557 (a non-standard type implemented by TESS company), where users cannot implement a groundwater flow velocity value, but the null value is a default parameter; moreover, no temperature values in the subsoil can be printed out in this version of the type. Therefore, the need to create a new version of Type557 in TRNSYS 18, which is also able to simulate advection effects due to different groundwater flow velocities, is clear.
In the present study, the original FORTRAN code written for Type280 and Type557 was modified: a logarithmic approach was specifically introduced to reproduce the variations in the outlet fluid temperature and exchanged energy by the BHE with the ground due to different groundwater flows. A new numerical model in MODFLOW/MT3DMS with physical and hydrogeological properties and BHE operation defined in [
25] was created. Studying the outlet fluid temperature from the U-pipe allowed them to achieve the exchanged energies. For that specific numerical model, the increase in the exchanged energies can be interpolated with a logarithmic curve in both the heating and cooling periods (
Figure 3) when the Darcy groundwater flow velocity varies from 0 to 10
−5 m/s (0.8 m/d).
The exchanged energy increased up to 86% for the heating period and 69% for the cooling period at the highest groundwater flow velocity simulated.
Starting from the logarithmic shape of the exchanged energies, a multiplying factor for each groundwater flow can be inferred. Specifically, by multiplying the exchanged energy value at null velocity for this coefficient, the logarithmic curve can be reproduced. Obviously, the multiplying factors are constant over time and differ from each other depending on the related velocity, as shown in
Table 2.
Reproducing the multiplying factors for each groundwater flow velocity, the following graph (
Figure 4) is reported.
The values of multiplying factors (
fm) can be calculated according to Equation (4):
where the values 0.1889 and 1.8341 are constants and derived from the curve (
Figure 4); these can be modified in Type285 if the users fit the values with other approximation curves. The definition of the constants and the groundwater Darcy velocity was implemented into the proforma file (see
Appendix A and
Appendix B), whereas the formula was added to the Fortran code of Type557. As soon as the code was compiled, all of the necessary files were created, and Type285 was imported in aa TRNSYS environment as a special non-standard type.
2.4. Numerical Model Implementation
Type285 was implemented in TRNSYS 18 using the same physical and hydrogeological parameters of MODFLOW/MT3DMS, as discussed in [
25,
42] and shown in
Table 3. The main assumptions between the two numerical methods are:
Identical thermal and hydrogeological properties for storage, grout, and aquifer materials.
Unperturbed aquifer temperature equal to 11.8 °C and inferred from the average temperature of North Italy.
One single U-shape pipe, 100 m depth, where 1000 kg/h of water is circulating inside.
The storage volume V is defined by the equation:
where r
st is the radius of the cylindrical storage volume and H is the depth of the BHE. The radius of the storage was achieved by the results of the numerical simulations in MODFLOW/MT3DMS for null velocity (equal to 14.3 m), showing a radial thermal perturbation. The radius of the filling material (usually grout material) was equal to 14 cm (
Table 3), a conventional value of borehole drilling. The value needs to be introduced even if the physical features of the grout material are considered equal to the aquifer ones. This is just an assumption in order to have the same properties in TRNSYS and MODFLOW/MT3DMS justified by the study of the authors in [
35,
43]. The thermal conductivity and volumetric heat capacity of the storage material were equal to the aquifer material properties; therefore, the domain was uniformly homogeneous, consisting of a sandy material (such as in [
25]). The outer and inner radius of the U-shape pipe of the BHE reproduced a real BHE geometry (4 cm diameter). To have the same value in MODFLOW/MT3DMS (that has square geometry grid), a square side of the cell equal to 3.36 cm needed to be set, and this value was inferred by imposing constant total thermal resistances between circular and square geometry (as explained in [
25]). The groundwater flow velocity, calculated as the Darcy velocity, was varied from 0 to 10
−5 m/s to cover all possible velocity ranges in nature.
The above variables refer exclusively to single elements, for example, one U-shape pipe, one subsoil layer etc., but there is also the possibility to subdivide them into different quantities: different cycles are present in the programming code to add the needed quantity of variables and the possibility to assign different characteristics. In detail, four cycles are present: the first to define the number of U-shape pipes, the second for the number of subsoil layers, and the remaining ones for additional output supply and storage volume point.
The heating/cooling operation of a BHE is common for the two numerical approaches: the heating period of the HVAC system is from middle-October to middle-April (winter season), whereas the cooling period is between June and August (summer period); in the remaining periods, the system is turned off.
Table 4 shows the time simulation length and inlet fluid temperature imposed at the top of the U-shape pipe.
2.5. Field Case
To validate Type285, as the numerical simulations of a synthetic case were not exhaustive, new experimental data from a real HVAC system were required. The chance was provided to study the field case presented in Alberti’s study [
3], where physical, hydrogeological, and energy properties were well-described. A real GSHP system consists of five BHEs (single U-pipe), with a depth of 60 m and buried in a heterogeneous aquifer consisting of alluvial materials (gravel and sandy gravel). The application field of this HVAC system is the air-climatization of a post-weaning piglet room at the Veterinary University of Lodi. Since the ventilation rate requirements are very large, as usually occurs in animal housing, the GSHP system was designed to be an air conditioning system equipped with heat recovery from the exhaust air in order to reduce the energy consumption. The heating and cooling generator was a reversible GSHP (heating capacity 14.4 kW at 40/45 °C on the supply side and 3/0 °C on the ground side; cooling capacity 15.9 kW at 10/15 °C on the supply side and 30/35 °C on the ground side). The warm/cold water produced by the heat pump was stored in a 300 L water tank supplying the heating/cooling coil of an air handling unit (AHU) with a nominal ventilation flow rate of 1200 m
3/h. The heat recovery heat exchanger in the AHU had a nominal efficiency equal to 78%. In order to verify the thermo-hygrometric conditions achieved in the piglet room and to measure the energy performance of the GSHP system, a monitoring system was installed to measure the water temperature and flow rate at the heat pump inlet/outlet on the ground and supply sides; the air temperature and relative humidity in several points of the AHU unit and in the piglet room; the air flow rate in the AHU and power consumption by the heat pump; and the AHU. The GSHP system was turned on for a heating period lasting 1 month and the monitoring data were published in [
3].
Therefore, to correctly set Type285 in TRNSYS 18, some parameters were retrieved from Alberti et al [
3] and others were obtained through the enhanced thermal response test discussed in Antelmi’s study [
37]. The complete set of Type285 input data is presented in
Appendix B (
Table A4 and
Table A5).
To exploit the potentiality of Type285, four BHEs (75 m depth) in a square configuration (2 × 2) with a mutual distance of 6 m were implemented. The exchange length meters were equal to the data field, but the number of BHEs was different because this type works better with a square configuration, as discussed below. The unperturbed aquifer temperature was set to be equal to 16.5 °C, coherent with the Lodi shallow aquifer in the autumn period. A Darcy groundwater flow velocity was set to be equal to 1.6∙10
−6 m/s according to the interpreted value through the TRT analysis [
37].
A uniform thermal conductivity of 3.4 W/m K was assigned to the subsoil domain; this is an equivalent value evaluated for different layers of subsoil consisting of gravel, sand, and clay. This value, correctly inside the thermal conductivity interval defined by the literature for these lithologies, was achieved by sensitivity analyses.
Because of this particular operation of the GSHP system, the mass flow rate and inlet fluid temperature values were also assigned as equal to the experimental data discussed in [
3]: the heat pump alternates periods in which the mass flow rate is equal to 0 kg/h to periods with a mass flow rate of 2700 kg/h. The inlet fluid temperature varies according to the heating periods and were enclosed between 5.8 and 17.3 °C.