Noise Spectroscopy: A Tool to Understand the Physics of Solar Cells
Abstract
:1. Introduction
2. Solar Cells: Mechanisms, Structure, Materials, and Characterization
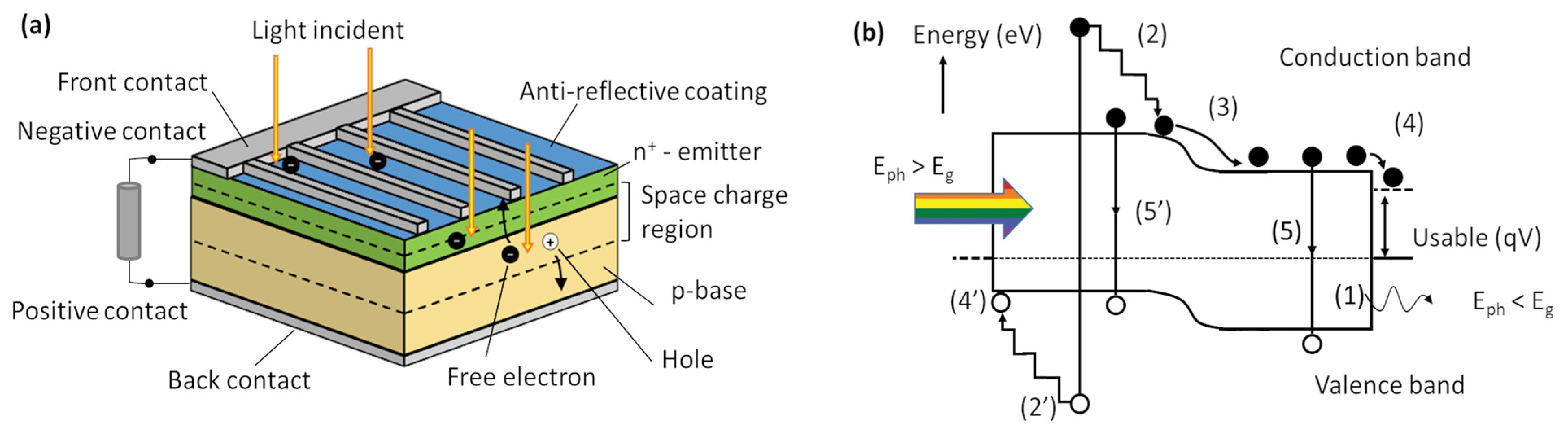
2.1. Silicon-Based Solar Cell
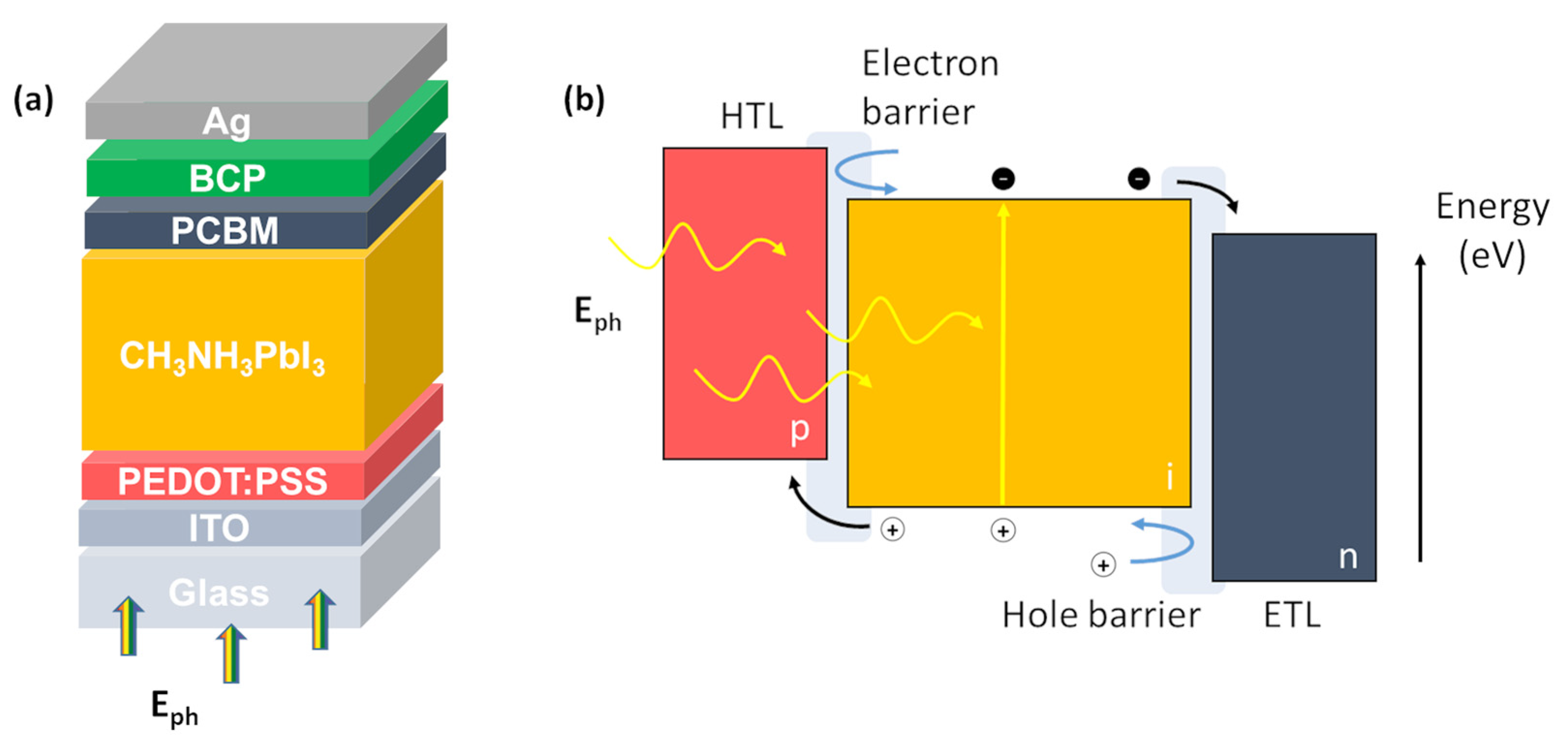
2.2. Polymer: Fullerene-Based Solar Cell
2.3. Perovskite-Based Solar Cell
2.4. Solar Cell Characterization Techniques
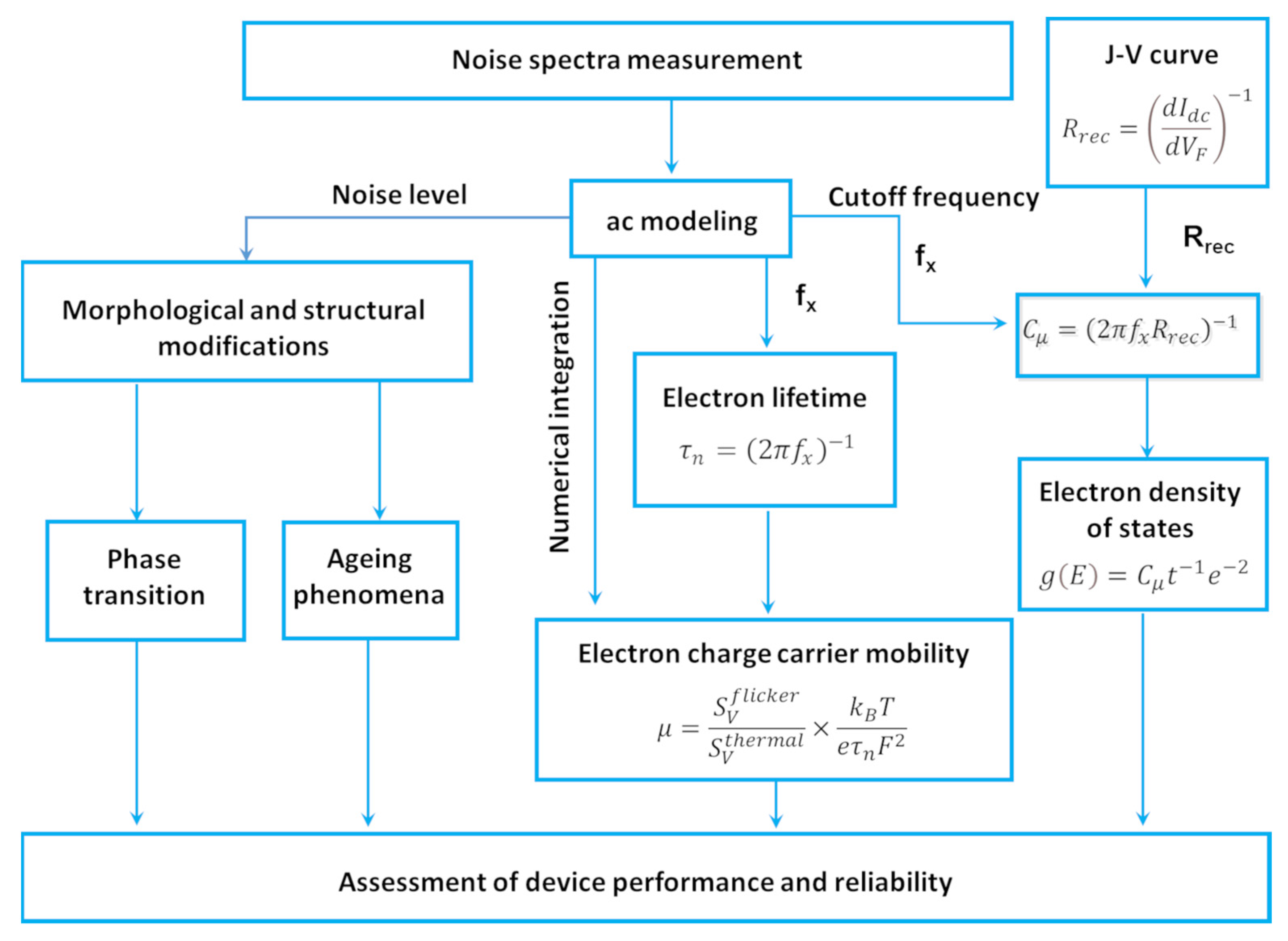
3. Electric Noise Spectroscopy: General Concepts and Measurement Techniques
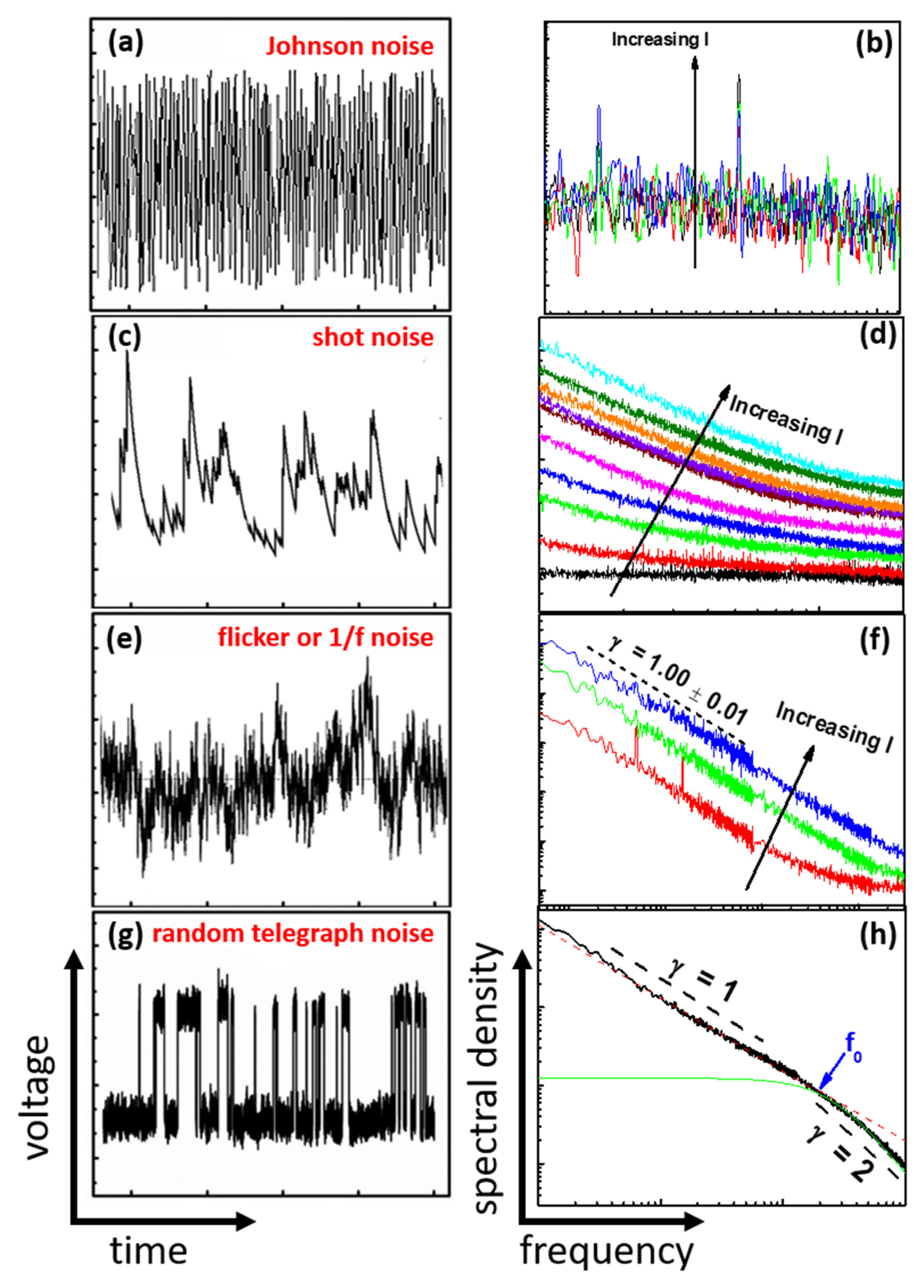
- The electronic noise generated by the thermal agitation of the charge carriers (usually electrons) inside an electrical conductor at equilibrium is the Johnson or thermal noise (Figure 6a). These temperature fluctuation processes are also known as “white noise”, having a voltage-spectral density completely frequency-independent (Figure 6b) and expressed by the following expression:where is the Boltzmann constant, is the system temperature, and is the real part of the system impedance [121,126].
- The electronic noise, which can be modeled by a Poisson process and is originated from the discrete nature of electric charge, is the shot noise (Figure 6c). Similar to temperature fluctuations, current fluctuation processes are also identified as “white noise”, having a voltage-spectral density defined as:where is the electron charge, is the differential resistance of the system, and is the bias current [121,127]. In Figure 6d, the linear current dependence of the shot noise amplitude is shown.
- The electronic noise generated by slow random dynamics is usually known as 1/ or flicker noise (Figure 6e). This is characterized by a frequency spectrum which is inversely proportional to the frequency of the signal (Figure 6f), and is modeled through the Hooge empirical relation as:where is the dc voltage ( in the case of Ohmic compounds), is the frequency, is the normalized Hooge parameter proportional to the noise level amplitude (being the charge carrier density), and is the frequency exponent assuming values in the range from 0.8 to 1.2 [117,121,128].
- The electronic noise consisting of sudden step-like transitions between two or more discrete voltage or current levels (Figure 6g) is the random telegraph noise (RTN). RTN has a spectral density expressed by a Lorentzian type of noise as:where is the Lorentzian noise amplitude and is a cutoff frequency representing the crossover value of the transition from a 1/ to a 1/ behavior (see Figure 6h for details) [121,129].
4. Physical Phenomena and Fluctuation Mechanisms in Solar Cells
- Silicon-based cells (see Figure 2a for a schematic representation). The model of fluctuations, the effect of radiation damage, and evidence of damage from noise are the topics of Section 4.1.
- Organic cells (see Figure 3a for a schematic representation). Physical modeling through the noise, effects of fabrication technology on cell parameters through the noise, and thermal stress effects characterized by noise are the topics of Section 4.2.
- Perovskite-based cells (see Figure 4a for a schematic representation). Physical modeling through the noise, material characterization through the noise, and the correlation between noise and cell efficiency are the topics of Section 4.3.
4.1. Photocurrent Fluctuation Effects in Polycrystalline Silicon-Based Solar Cells
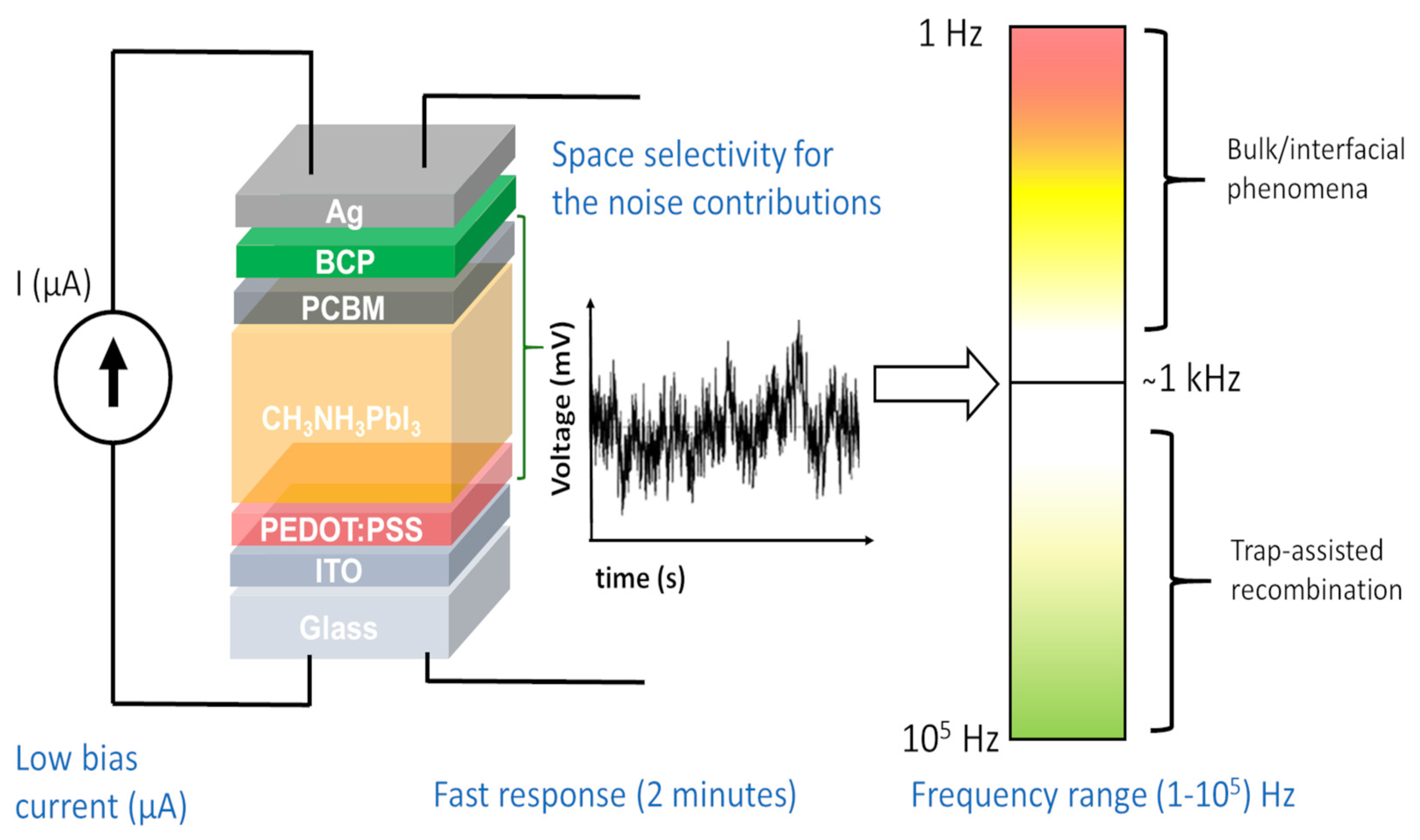
4.2. Physical Modeling and Real-Time Monitoring of Organic Solar Cells through Electric Noise
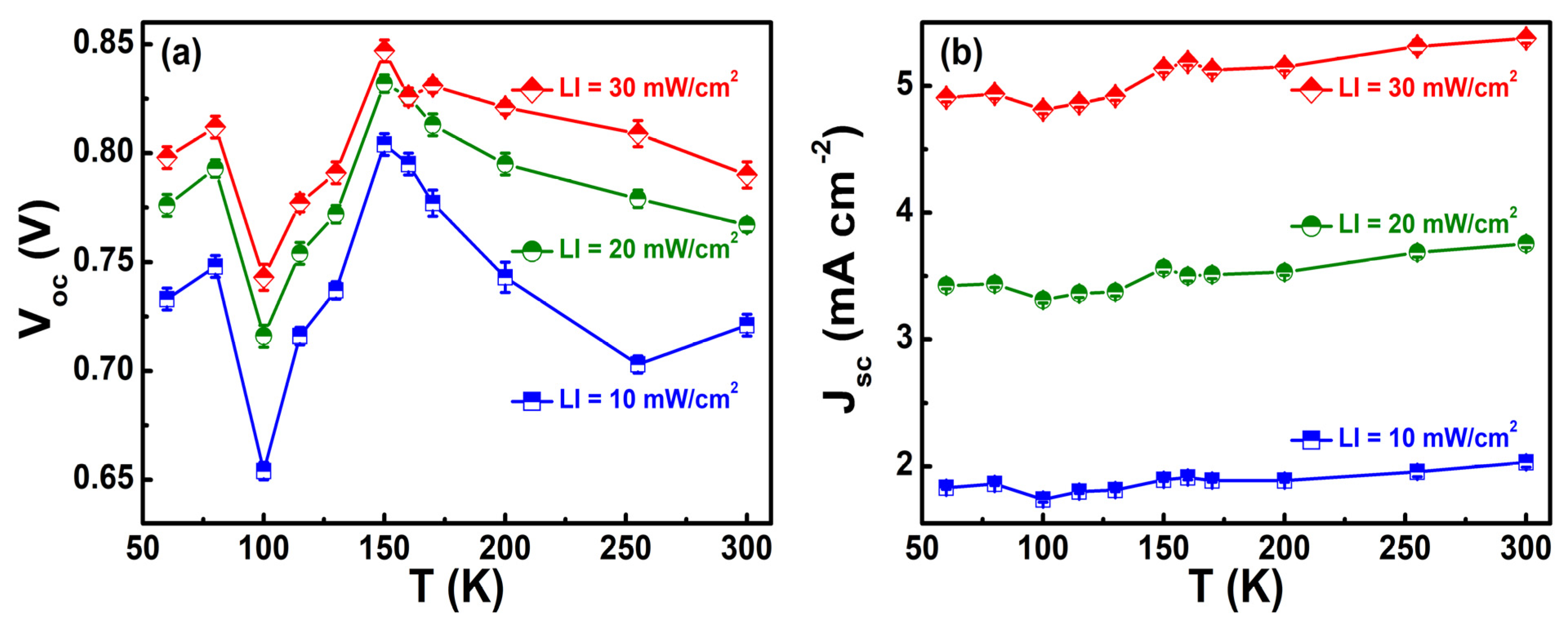
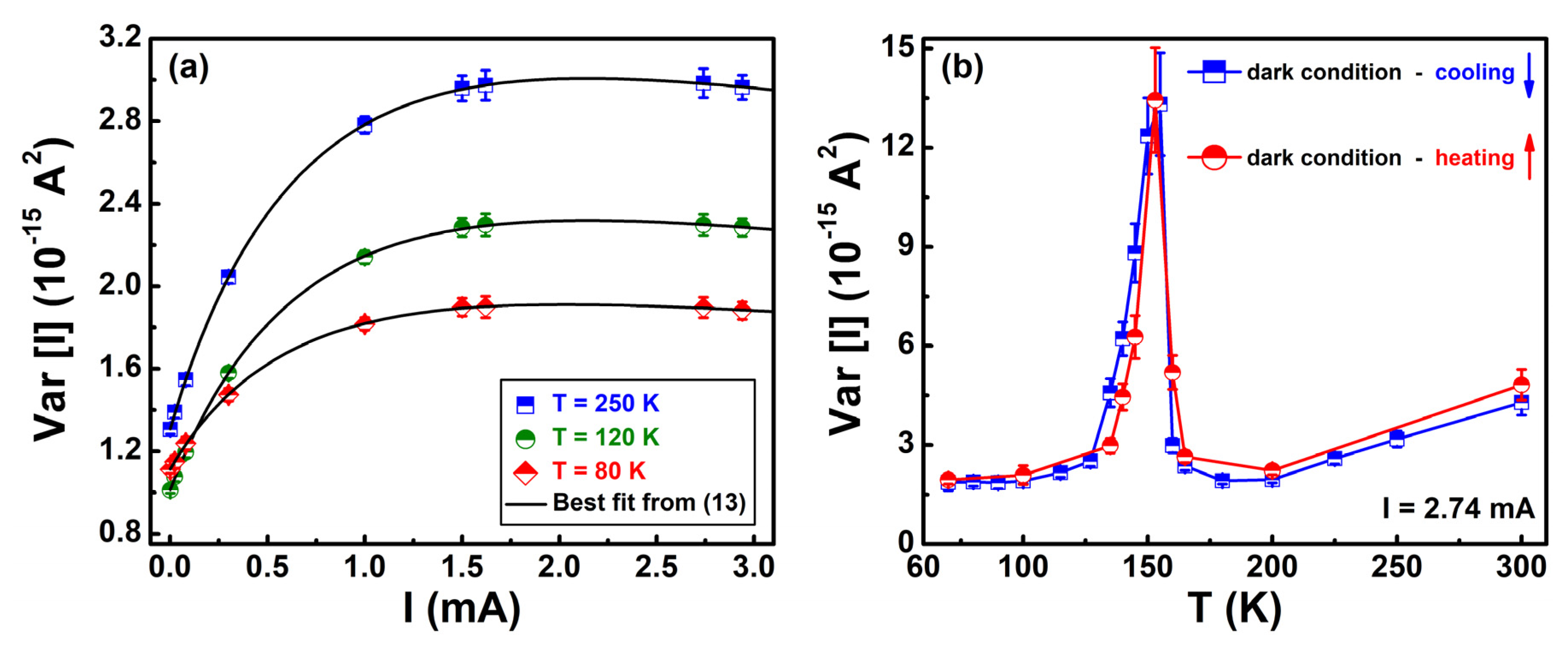
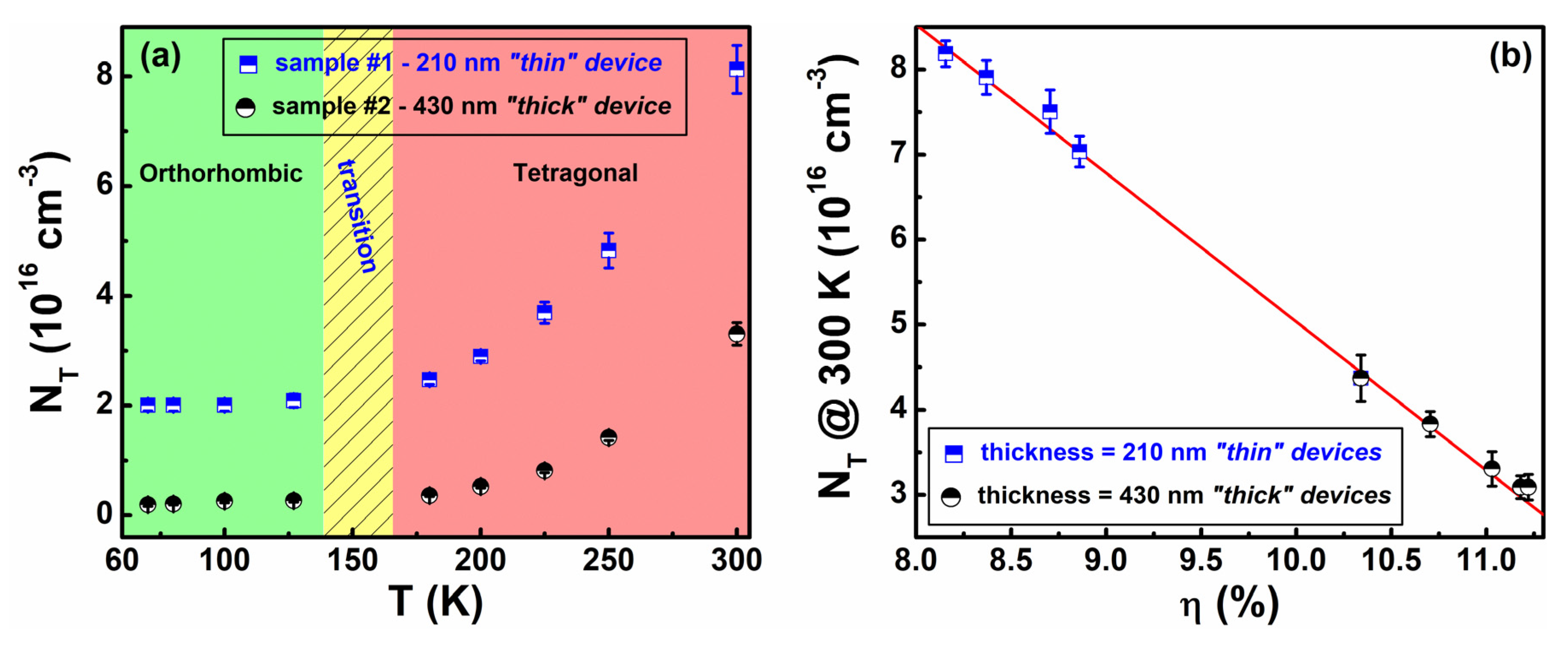
4.3. Material and Efficiency Characterizations of Perovskite Solar Cells by Noise Spectroscopy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. Electricity Market Report—January 2022; IEA: Paris, France, 2022. [Google Scholar]
- Kabeyi, M.J.B.; Olanrewaju, O.A. Sustainable Energy Transition for Renewable and Low Carbon Grid Electricity Generation and Supply. Front. Energy Res. 2022, 9, 743114. [Google Scholar] [CrossRef]
- Becquerel, A.E. Memoire Sur Les Effects d’Electriques Produits Sous l’Influence Des Rayons Solaires. Comptes Rendus L’academie Sci. 1839, 9, 561–567. [Google Scholar]
- IEA. Special Report on Solar PV Global Supply Chains; IEA: Paris, France, 2022. [Google Scholar]
- Vijaya, S.; Landi, G.; Wu, J.J.; Anandan, S. Ni3S4/CoS2 Mixed-Phase Nanocomposite as Counter Electrode for Pt-Free Dye-Sensitized Solar Cells. J. Power Sources 2020, 478, 229068. [Google Scholar] [CrossRef]
- Subbiah, V.; Landi, G.; Wu, J.J.; Anandan, S. MoS2 Coated CoS2 Nanocomposites as Counter Electrodes in Pt-Free Dye-Sensitized Solar Cells. Phys. Chem. Chem. Phys. 2019, 21, 25474–25483. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-H.; Kim, D.-H.; So, J.-H.; Koo, H.-J. Toward Eco-Friendly Dye-Sensitized Solar Cells (DSSCs): Natural Dyes and Aqueous Electrolytes. Energies 2021, 15, 219. [Google Scholar] [CrossRef]
- Yan, J.; Saunders, B.R. Third-Generation Solar Cells: A Review and Comparison of Polymer:Fullerene, Hybrid Polymer and Perovskite Solar Cells. RSC Adv. 2014, 4, 43286–43314. [Google Scholar] [CrossRef] [Green Version]
- Ding, G.; Zheng, Y.; Xiao, X.; Cheng, H.; Zhang, G.; Shi, Y.; Shao, Y. Sustainable Development of Perovskite Solar Cells: Keeping a Balance between Toxicity and Efficiency. J. Mater. Chem. A 2022, 10, 8159–8171. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, N.; Fagerholm, C.; Qiu, M.; Shuai, L.; Egan, R.; Yuan, C. Techno-Economic and Environmental Sustainability of Industrial-Scale Productions of Perovskite Solar Cells. Renew. Sustain. Energy Rev. 2022, 158, 112146. [Google Scholar] [CrossRef]
- Mahapatra, A.; Prochowicz, D.; Tavakoli, M.M.; Trivedi, S.; Kumar, P.; Yadav, P. A Review of Aspects of Additive Engineering in Perovskite Solar Cells. J. Mater. Chem. A 2020, 8, 27–54. [Google Scholar] [CrossRef]
- Trivedi, S.; Prochowicz, D.; Parikh, N.; Mahapatra, A.; Pandey, M.K.; Kalam, A.; Tavakoli, M.M.; Yadav, P. Recent Progress in Growth of Single-Crystal Perovskites for Photovoltaic Applications. ACS Omega 2021, 6, 1030–1042. [Google Scholar] [CrossRef] [PubMed]
- Barone, C.; Landi, G.; De Sio, A.; Neitzert, H.C.; Pagano, S. Thermal Ageing of Bulk Heterojunction Polymer Solar Cells Investigated by Electric Noise Analysis. Sol. Energy Mater. Sol. Cells 2014, 122, 40–45. [Google Scholar] [CrossRef]
- Zhao, J.; Li, Y.; Yang, G.; Jiang, K.; Lin, H.; Ade, H.; Ma, W.; Yan, H. Efficient Organic Solar Cells Processed from Hydrocarbon Solvents. Nat. Energy 2016, 1, 15027. [Google Scholar] [CrossRef]
- Brabec, C.J.; Gowrisanker, S.; Halls, J.J.M.; Laird, D.; Jia, S.; Williams, S.P. Polymer-Fullerene Bulk-Heterojunction Solar Cells. Adv. Mater. 2010, 22, 3839–3856. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Yang, C.; Gong, X.; Lee, K.; Heeger, A.J. Thermally Stable, Efficient Polymer Solar Cells with Nanoscale Control of the Interpenetrating Network Morphology. Adv. Funct. Mater. 2005, 15, 1617–1622. [Google Scholar] [CrossRef]
- Hashemi, S.A.; Ramakrishna, S.; Aberle, A.G. Recent Progress in Flexible-Wearable Solar Cells for Self-Powered Electronic Devices. Energy Environ. Sci. 2020, 13, 685–743. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, J.H.; Shim, T.H.; Park, J.G. Effect of Interface Thickness on Power Conversion Efficiency of Polymer Photovoltaic Cells. Electron. Mater. Lett. 2009, 5, 47–50. [Google Scholar] [CrossRef]
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Hinken, D.; Rauer, M.; Hao, X. Solar Cell Efficiency Tables (Version 60). Prog. Photovolt. Res. Appl. 2022, 30, 687–701. [Google Scholar] [CrossRef]
- Green, M.; Dunlop, E.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Hao, X. Solar Cell Efficiency Tables (Version 57). Prog. Photovoltaics Res. Appl. 2021, 29, 3–15. [Google Scholar] [CrossRef]
- Tromholt, T.; Manceau, M.; Helgesen, M.; Carlé, J.E.; Krebs, F.C. Degradation of Semiconducting Polymers by Concentrated Sunlight. Sol. Energy Mater. Sol. Cells 2011, 95, 1308–1314. [Google Scholar] [CrossRef]
- Yang, S.-S.; Hsieh, Z.-C.; Keshtov, M.L.; Sharma, G.D.; Chen, F.-C. Toward High-Performance Polymer Photovoltaic Devices for Low-Power Indoor Applications. Sol. RRL 2017, 1, 1700174. [Google Scholar] [CrossRef]
- Landi, G.; Granata, V.; Germano, R.; Pagano, S.; Barone, C. Low-Power and Eco-Friendly Temperature Sensor Based on Gelatin Nanocomposite. Nanomaterials 2022, 12, 2227. [Google Scholar] [CrossRef] [PubMed]
- Landi, G.; Neitzert, H.-C. Application of a Bio-Nanocomposite Tissue as an NIR Optical Receiver and a Temperature Sensor. ACS Appl. Electron. Mater. 2021, 3, 2790–2797. [Google Scholar] [CrossRef]
- La Notte, L.; Giordano, L.; Calabrò, E.; Bedini, R.; Colla, G.; Puglisi, G.; Reale, A. Hybrid and Organic Photovoltaics for Greenhouse Applications. Appl. Energy 2020, 278, 115582. [Google Scholar] [CrossRef]
- Fan, R.; Huang, Y.; Wang, L.; Li, L.; Zheng, G.; Zhou, H. The Progress of Interface Design in Perovskite-Based Solar Cells. Adv. Energy Mater. 2016, 6, 1600460. [Google Scholar] [CrossRef]
- Green, M.A.; Ho-Baillie, A.; Snaith, H.J. The Emergence of Perovskite Solar Cells. Nat. Photonics 2014, 8, 506–514. [Google Scholar] [CrossRef]
- Lang, F.; Nickel, N.H.; Bundesmann, J.; Seidel, S.; Denker, A.; Albrecht, S.; Brus, V.V.; Rappich, J.; Rech, B.; Landi, G.; et al. Radiation Hardness and Self-Healing of Perovskite Solar Cells. Adv. Mater. 2016, 28, 8726–8731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, Z.; McElvany, C.L.; Phillips, A.B.; Celik, I.; Krantz, P.W.; Watthage, S.C.; Liyanage, G.K.; Apul, D.; Heben, M.J. A Technoeconomic Analysis of Perovskite Solar Module Manufacturing with Low-Cost Materials and Techniques. Energy Environ. Sci. 2017, 10, 1297–1305. [Google Scholar] [CrossRef]
- Siegler, T.D.; Dawson, A.; Lobaccaro, P.; Ung, D.; Beck, M.E.; Nilsen, G.; Tinker, L.L. The Path to Perovskite Commercialization: A Perspective from the United States Solar Energy Technologies Office. ACS Energy Lett. 2022, 7, 1728–1734. [Google Scholar] [CrossRef]
- Palma, A.L. Laser-Processed Perovskite Solar Cells and Modules. Sol. RRL 2020, 4, 1900432. [Google Scholar] [CrossRef]
- Landi, G.; Neitzert, H.C.; Barone, C.; Mauro, C.; Lang, F.; Albrecht, S.; Rech, B.; Pagano, S. Correlation between Electronic Defect States Distribution and Device Performance of Perovskite Solar Cells. Adv. Sci. 2017, 4, 1700183. [Google Scholar] [CrossRef]
- An, Q.; Paulus, F.; Becker-Koch, D.; Cho, C.; Sun, Q.; Weu, A.; Bitton, S.; Tessler, N.; Vaynzof, Y. Small Grains as Recombination Hot Spots in Perovskite Solar Cells. Matter 2021, 4, 1683–1701. [Google Scholar] [CrossRef]
- Ren, A.; Lai, H.; Hao, X.; Tang, Z.; Xu, H.; Yu Jeco, B.M.F.; Watanabe, K.; Wu, L.; Zhang, J.; Sugiyama, M.; et al. Efficient Perovskite Solar Modules with Minimized Nonradiative Recombination and Local Carrier Transport Losses. Joule 2020, 4, 1263–1277. [Google Scholar] [CrossRef]
- Zhang, D.; Li, D.; Hu, Y.; Mei, A.; Han, H. Degradation Pathways in Perovskite Solar Cells and How to Meet International Standards. Commun. Mater. 2022, 3, 58. [Google Scholar] [CrossRef]
- Long, B.; Zhou, X.; Cao, H.; Chen, R.; He, N.; Chi, L.; Fan, P.; Chen, X. Excellent Stability of Perovskite Solar Cells Encapsulated With Paraffin/Ethylene-Vinyl Acetate/Paraffin Composite Layer. Front. Mater. 2022, 9, 892657. [Google Scholar] [CrossRef]
- Sze, S.M.; Kwok, K. Ng Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Battaglia, C.; Cuevas, A.; De Wolf, S. High-Efficiency Crystalline Silicon Solar Cells: Status and Perspectives. Energy Environ. Sci. 2016, 9, 1552–1576. [Google Scholar] [CrossRef] [Green Version]
- De Wolf, S.; Holovsky, J.; Moon, S.J.; Löper, P.; Niesen, B.; Ledinsky, M.; Haug, F.J.; Yum, J.H.; Ballif, C. Organometallic Halide Perovskites: Sharp Optical Absorption Edge and Its Relation to Photovoltaic Performance. J. Phys. Chem. Lett. 2014, 5, 1035–1039. [Google Scholar] [CrossRef]
- Bhattacharya, S.; John, S. Beyond 30% Conversion Efficiency in Silicon Solar Cells: A Numerical Demonstration. Sci. Rep. 2019, 9, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ITPRV. International Technology Roadmap for Photovoltaic. In ITRPV 2021, 13th ed.; VDMA: Frankfurt, Germany, 2022; p. 53. [Google Scholar]
- Renno, C.; Petito, F.; Landi, G.; Neitzert, H.C. Experimental Characterization of a Concentrating Photovoltaic System Varying the Light Concentration. Energy Convers. Manag. 2017, 138, 119–130. [Google Scholar] [CrossRef]
- Li, J.; Aierken, A.; Liu, Y.; Zhuang, Y.; Yang, X.; Mo, J.H.; Fan, R.K.; Chen, Q.Y.; Zhang, S.Y.; Huang, Y.M.; et al. A Brief Review of High Efficiency III-V Solar Cells for Space Application. Front. Phys. 2021, 8, 1–15. [Google Scholar] [CrossRef]
- Goetzberger, A.; Knobloch, J.; Voß, B. Crystalline Silicon Solar Cells; John Wiley & Sons, Ltd.: Chichester, UK, 2014; ISBN 9781119033769. [Google Scholar]
- Yoshikawa, K.; Kawasaki, H.; Yoshida, W.; Irie, T.; Konishi, K.; Nakano, K.; Uto, T.; Adachi, D.; Kanematsu, M.; Uzu, H.; et al. Silicon Heterojunction Solar Cell with Interdigitated Back Contacts for a Photoconversion Efficiency over 26%. Nat. Energy 2017, 2, 17032. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Wu, Y.; Yang, G.; Mazzarella, L.; Procel-Moya, P.; Tamboli, A.C.; Weber, K.; Boccard, M.; Isabella, O.; et al. High-Efficiency Silicon Heterojunction Solar Cells: Materials, Devices and Applications. Mater. Sci. Eng. R Rep. 2020, 142, 100579. [Google Scholar] [CrossRef]
- Haase, F.; Hollemann, C.; Schäfer, S.; Merkle, A.; Rienäcker, M.; Krügener, J.; Brendel, R.; Peibst, R. Laser Contact Openings for Local Poly-Si-Metal Contacts Enabling 26.1%-Efficient POLO-IBC Solar Cells. Sol. Energy Mater. Sol. Cells 2018, 186, 184–193. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of P-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Green, M.A. Third Generation Photovoltaics: Solar Cells for 2020 and Beyond. Phys. E Low-Dimens. Syst. Nanostruct. 2002, 14, 65–70. [Google Scholar] [CrossRef]
- Tang, C.W. Two-layer Organic Photovoltaic Cell. Appl. Phys. Lett. 1986, 48, 183–185. [Google Scholar] [CrossRef]
- Chamberlain, G.A. Organic Solar Cells: A Review. Sol. Cells 1983, 8, 47–83. [Google Scholar] [CrossRef]
- Halls, J.J.M.; Walsh, C.A.; Greenham, N.C.; Marseglia, E.A.; Friend, R.H.; Moratti, S.C.; Holmes, A.B. Efficient Photodiodes from Interpenetrating Polymer Networks. Nature 1995, 376, 498–500. [Google Scholar] [CrossRef]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer Photovoltaic Cells: Enhanced Efficiencies via a Network of Internal Donor-Acceptor Heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar] [CrossRef] [Green Version]
- Shaheen, S.E.; Brabec, C.J.; Sariciftci, N.S.; Padinger, F.; Fromherz, T.; Hummelen, J.C. 2.5% Efficient Organic Plastic Solar Cells. Appl. Phys. Lett. 2001, 78, 841–843. [Google Scholar] [CrossRef] [Green Version]
- Scharber, M.C.; Sariciftci, N.S. Efficiency of Bulk-Heterojunction Organic Solar Cells. Prog. Polym. Sci. 2013, 38, 1929–1940. [Google Scholar] [CrossRef] [Green Version]
- Service, R.F. Outlook Brightens for Plastic Solar Cells. Science 2011, 332, 293. [Google Scholar] [CrossRef]
- Würfel, U.; Herterich, J.; List, M.; Faisst, J.; Bhuyian, M.F.M.; Schleiermacher, H.-F.; Knupfer, K.T.; Zimmermann, B. A 1 cm2 Organic Solar Cell with 15.2% Certified Efficiency: Detailed Characterization and Identification of Optimization Potential. Sol. RRL 2021, 5, 2000802. [Google Scholar] [CrossRef]
- Gregg, B.A.; Hanna, M.C. Comparing Organic to Inorganic Photovoltaic Cells: Theory, Experiment, and Simulation. J. Appl. Phys. 2003, 93, 3605–3614. [Google Scholar] [CrossRef]
- Street, R.A. Carrier Mobility, Structural Order, and Solar Cell Efficiency of Organic Heterojunction Devices. Appl. Phys. Lett. 2008, 93, 133308. [Google Scholar] [CrossRef]
- De Sio, A.; Madena, T.; Huber, R.; Parisi, J.; Neyshtadt, S.; Deschler, F.; Da Como, E.; Esposito, S.; von Hauff, E. Solvent Additives for Tuning the Photovoltaic Properties of Polymer–Fullerene Solar Cells. Sol. Energy Mater. Sol. Cells 2011, 95, 3536–3542. [Google Scholar] [CrossRef]
- Gao, P.; Grätzel, M.; Nazeeruddin, M.K. Organohalide Lead Perovskites for Photovoltaic Applications. Energy Environ. Sci. 2014, 7, 2448–2463. [Google Scholar] [CrossRef]
- Liu, M.; Johnston, M.B.; Snaith, H.J. Efficient Planar Heterojunction Perovskite Solar Cells by Vapour Deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef] [PubMed]
- Koh, T.M.; Fu, K.; Fang, Y.; Chen, S.; Sum, T.C.; Mathews, N.; Mhaisalkar, S.G.; Boix, P.P.; Baikie, T. Formamidinium-Containing Metal-Halide: An Alternative Material for near-IR Absorption Perovskite Solar Cells. J. Phys. Chem. C 2014, 118, 16458–16462. [Google Scholar] [CrossRef]
- Choi, H.; Jeong, J.; Kim, H.-B.; Kim, S.; Walker, B.; Kim, G.-H.; Kim, J.Y. Cesium-Doped Methylammonium Lead Iodide Perovskite Light Absorber for Hybrid Solar Cells. Nano Energy 2014, 7, 80–85. [Google Scholar] [CrossRef]
- Saliba, M.; Matsui, T.; Domanski, K.; Seo, J.-Y.; Ummadisingu, A.; Zakeeruddin, S.M.; Correa-Baena, J.-P.; Tress, W.R.; Abate, A.; Hagfeldt, A.; et al. Incorporation of Rubidium Cations into Perovskite Solar Cells Improves Photovoltaic Performance. Science 2016, 354, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Jeong, M.; Choi, I.W.; Go, E.M.; Cho, Y.; Kim, M.; Lee, B.; Jeong, S.; Jo, Y.; Choi, H.W.; Lee, J.; et al. Stable Perovskite Solar Cells with Efficiency Exceeding 24.8% and 0.3-V Voltage Loss. Science 2020, 369, 1615–1620. [Google Scholar] [CrossRef] [PubMed]
- Palma, A.L.; Cinà, L.; Busby, Y.; Marsella, A.; Agresti, A.; Pescetelli, S.; Pireaux, J.-J.; Di Carlo, A. Mesoscopic Perovskite Light-Emitting Diodes. ACS Appl. Mater. Interfaces 2016, 8, 26989–26997. [Google Scholar] [CrossRef]
- Dou, L.; Yang, Y.; You, J.; Hong, Z.; Chang, W.-H.; Li, G.; Yang, Y. Solution-Processed Hybrid Perovskite Photodetectors with High Detectivity. Nat. Commun. 2014, 5, 5404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mahapatra, A.; Chavan, R.D.; Tavakoli, M.M.; Kumar, P.; Kalam, A.; Prochowicz, D.; Yadav, P. Revealing the Variation of Photodetectivity in MAPbI3 and MAPb(I0.88Br0.12)3 Single Crystal Based Photodetectors Under Electrical Poling-Induced Polarization. J. Phys. Chem. C 2022, 126, 13458–13466. [Google Scholar] [CrossRef]
- Zhu, H.; Fu, Y.; Meng, F.; Wu, X.; Gong, Z.; Ding, Q.; Gustafsson, M.V.; Trinh, M.T.; Jin, S.; Zhu, X.-Y. Lead Halide Perovskite Nanowire Lasers with Low Lasing Thresholds and High Quality Factors. Nat. Mater. 2015, 14, 636–642. [Google Scholar] [CrossRef] [PubMed]
- Lang, F.; Jošt, M.; Bundesmann, J.; Denker, A.; Albrecht, S.; Landi, G.; Neitzert, H.-C.; Rappich, J.; Nickel, N.H. Efficient Minority Carrier Detrapping Mediating the Radiation Hardness of Triple-Cation Perovskite Solar Cells under Proton Irradiation. Energy Environ. Sci. 2019, 12, 1634–1647. [Google Scholar] [CrossRef]
- Lang, F.; Jošt, M.; Frohna, K.; Köhnen, E.; Al-Ashouri, A.; Bowman, A.R.; Bertram, T.; Morales-Vilches, A.B.; Koushik, D.; Tennyson, E.M.; et al. Proton Radiation Hardness of Perovskite Tandem Photovoltaics. Joule 2020, 4, 1054–1069. [Google Scholar] [CrossRef] [PubMed]
- Seo, J.; Noh, J.H.; Seok, S. Il Rational Strategies for Efficient Perovskite Solar Cells. Acc. Chem. Res. 2016, 49, 562–572. [Google Scholar] [CrossRef]
- Li, G.R.; Gao, X.P. Low-Cost Counter-Electrode Materials for Dye-Sensitized and Perovskite Solar Cells. Adv. Mater. 2020, 32, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhang, S.; Wu, S.; Zhang, W.; Zhu, H.; Xiong, Z.; Zhang, Y.; Chen, W. Effect of BCP Buffer Layer on Eliminating Charge Accumulation for High Performance of Inverted Perovskite Solar Cells. RSC Adv. 2017, 7, 35819–35826. [Google Scholar] [CrossRef] [Green Version]
- Lin, Q.; Armin, A.; Nagiri, R.C.R.; Burn, P.L.; Meredith, P. Electro-Optics of Perovskite Solar Cells. Nat. Photonics 2015, 9, 106–112. [Google Scholar] [CrossRef] [Green Version]
- Jung, H.S.; Park, N.-G. Perovskite Solar Cells: From Materials to Devices. Small 2015, 11, 10–25. [Google Scholar] [CrossRef] [PubMed]
- Ke, W.; Kanatzidis, M.G. Prospects for Low-Toxicity Lead-Free Perovskite Solar Cells. Nat. Commun. 2019, 10, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Yavari, M.; Mazloum-Ardakani, M.; Gholipour, S.; Tavakoli, M.M.; Turren-Cruz, S.H.; Taghavinia, N.; Grätzel, M.; Hagfeldt, A.; Saliba, M. Greener, Nonhalogenated Solvent Systems for Highly Efficient Perovskite Solar Cells. Adv. Energy Mater. 2018, 8, 1–7. [Google Scholar] [CrossRef]
- Chen, Q.; Zhou, H.; Fang, Y.; Stieg, A.Z.; Song, T.-B.; Wang, H.-H.; Xu, X.; Liu, Y.; Lu, S.; You, J.; et al. The Optoelectronic Role of Chlorine in CH3NH3PbI3(Cl)-Based Perovskite Solar Cells. Nat. Commun. 2015, 6, 7269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shao, Y.; Xiao, Z.; Bi, C.; Yuan, Y.; Huang, J. Origin and Elimination of Photocurrent Hysteresis by Fullerene Passivation in CH3NH3PbI3 Planar Heterojunction Solar Cells. Nat. Commun. 2014, 5, 5784. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Higuchi, H.; Negami, T. Largest Highly Efficient 203 × 203 mm2 CH3NH3PbI3 Perovskite Solar Modules. Jpn. J. Appl. Phys. 2018, 57, 08RE11. [Google Scholar] [CrossRef]
- Han, Y.; Meyer, S.; Dkhissi, Y.; Weber, K.; Pringle, J.M.; Bach, U.; Spiccia, L.; Cheng, Y.-B. Degradation Observations of Encapsulated Planar CH3NH3PbI3 Perovskite Solar Cells at High Temperatures and Humidity. J. Mater. Chem. A 2015, 3, 8139–8147. [Google Scholar] [CrossRef]
- Yang, Y.; You, J. Make Perovskite Solar Cells Stable. Nature 2017, 544, 155–156. [Google Scholar] [CrossRef]
- Garcia-Belmonte, G.; Munar, A.; Barea, E.M.; Bisquert, J.; Ugarte, I.; Pacios, R. Charge Carrier Mobility and Lifetime of Organic Bulk Heterojunctions Analyzed by Impedance Spectroscopy. Org. Electron. 2008, 9, 847–851. [Google Scholar] [CrossRef]
- Neukom, M.; Züfle, S.; Jenatsch, S.; Ruhstaller, B. Opto-Electronic Characterization of Third-Generation Solar Cells. Sci. Technol. Adv. Mater. 2018, 19, 291–316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kunst, M.; Beck, G. The Study of Charge Carrier Kinetics in Semiconductors by Microwave Conductivity Measurements. J. Appl. Phys. 1986, 60, 3558–3566. [Google Scholar] [CrossRef]
- Renno, C.; Landi, G.; Petito, F.; Neitzert, H.C. Influence of a Degraded Triple-Junction Solar Cell on the CPV System Performances. Energy Convers. Manag. 2018, 160, 326–340. [Google Scholar] [CrossRef]
- Neitzert, H.C.; Hirsch, W.; Kunst, M. Structural Changes of a -Si:H Films on Crystalline Silicon Substrates during Deposition. Phys. Rev. B 1993, 47, 4080–4083. [Google Scholar] [CrossRef] [PubMed]
- Thiesbrummel, J.; Peña-Camargo, F.; Brinkmann, K.O.; Gutierrez-Partida, E.; Yang, F.; Warby, J.; Albrecht, S.; Neher, D.; Riedl, T.; Snaith, H.J.; et al. Understanding and Minimizing VOC Losses in All-Perovskite Tandem Photovoltaics. Adv. Energy Mater. 2023, 13, 2202674. [Google Scholar] [CrossRef]
- Ghosekar, I.C.; Patil, G.C. Review on Performance Analysis of P3HT:PCBM-Based Bulk Heterojunction Organic Solar Cells. Semicond. Sci. Technol. 2021, 36, 045005. [Google Scholar] [CrossRef]
- Landi, G.; Barone, C.; Mauro, C.; De Sio, A.; Carapella, G.; Neitzert, H.; Pagano, S. Probing Temperature-Dependent Recombination Kinetics in Polymer:Fullerene Solar Cells by Electric Noise Spectroscopy. Energies 2017, 10, 1490. [Google Scholar] [CrossRef] [Green Version]
- Warby, J.; Zu, F.; Zeiske, S.; Gutierrez-Partida, E.; Frohloff, L.; Kahmann, S.; Frohna, K.; Mosconi, E.; Radicchi, E.; Lang, F.; et al. Understanding Performance Limiting Interfacial Recombination in Pin Perovskite Solar Cells. Adv. Energy Mater. 2022, 12, 2103567. [Google Scholar] [CrossRef]
- George, B.M.; Behrends, J.; Schnegg, A.; Schulze, T.F.; Fehr, M.; Korte, L.; Rech, B.; Lips, K.; Rohrmüller, M.; Rauls, E.; et al. Atomic Structure of Interface States in Silicon Heterojunction Solar Cells. Phys. Rev. Lett. 2013, 110, 136803. [Google Scholar] [CrossRef] [PubMed]
- Korte, L.; Conrad, E.; Angermann, H.; Stangl, R.; Schmidt, M. Advances in a-Si:H/c-Si Heterojunction Solar Cell Fabrication and Characterization. Sol. Energy Mater. Sol. Cells 2009, 93, 905–910. [Google Scholar] [CrossRef]
- Levi, D.H.; Teplin, C.W.; Iwaniczko, E.; Yan, Y.; Wang, T.H.; Branz, H.M. Real-Time Spectroscopic Ellipsometry Studies of the Growth of Amorphous and Epitaxial Silicon for Photovoltaic Applications. J. Vac. Sci. Technol. A Vacuum, Surfaces Film. 2006, 24, 1676–1683. [Google Scholar] [CrossRef]
- Jørgensen, M.; Norrman, K.; Krebs, F.C. Stability/Degradation of Polymer Solar Cells. Sol. Energy Mater. Sol. Cells 2008, 92, 686–714. [Google Scholar] [CrossRef]
- Landi, G.; Barone, C.; De Sio, A.; Pagano, S.; Neitzert, H.C. Characterization of Polymer:Fullerene Solar Cells by Low-Frequency Noise Spectroscopy. Appl. Phys. Lett. 2013, 102, 223902. [Google Scholar] [CrossRef]
- Landi, G.; Barone, C.; Pagano, S.; De Sio, A.; Neitzert, H.C. Investigation of the Solvent Influence on Polymer-Fullerene Solar Cells by Low Frequency Noise Spectroscopy. Can. J. Phys. 2014, 92, 879–882. [Google Scholar] [CrossRef]
- Landi, G.; Barone, C.; Mauro, C.; Neitzert, H.C.; Pagano, S. A Noise Model for the Evaluation of Defect States in Solar Cells. Sci. Rep. 2016, 6, 29685. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barone, C.; Lang, F.; Mauro, C.; Landi, G.; Rappich, J.; Nickel, N.H.; Rech, B.; Pagano, S.; Neitzert, H.C. Unravelling the Low-Temperature Metastable State in Perovskite Solar Cells by Noise Spectroscopy. Sci. Rep. 2016, 6, 34675. [Google Scholar] [CrossRef]
- Von Hauff, E.; Klotz, D. Impedance Spectroscopy for Perovskite Solar Cells: Characterisation, Analysis, and Diagnosis. J. Mater. Chem. C 2022, 10, 742–761. [Google Scholar] [CrossRef]
- Luck, K.A.; Sangwan, V.K.; Hartnett, P.E.; Arnold, H.N.; Wasielewski, M.R.; Marks, T.J.; Hersam, M.C. Correlated In Situ Low-Frequency Noise and Impedance Spectroscopy Reveal Recombination Dynamics in Organic Solar Cells Using Fullerene and Non-Fullerene Acceptors. Adv. Funct. Mater. 2017, 27, 1703805. [Google Scholar] [CrossRef] [Green Version]
- Sangwan, V.K.; Zhu, M.; Clark, S.; Luck, K.A.; Marks, T.J.; Kanatzidis, M.G.; Hersam, M.C. Low-Frequency Carrier Kinetics in Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2019, 11, 14166–14174. [Google Scholar] [CrossRef] [Green Version]
- Mahapatra, A.; Parikh, N.; Kumar, P.; Kumar, M.; Prochowicz, D.; Kalam, A.; Tavakoli, M.M.; Yadav, P. Changes in the Electrical Characteristics of Perovskite Solar Cells with Aging Time. Molecules 2020, 25, 2299. [Google Scholar] [CrossRef] [PubMed]
- Landi, G.; Subbiah, V.; Reddy, K.S.; Sorrentino, A.; Sambandam, A.; Ramamurthy, P.C.; Neitzert, H.-C. Evidence of Bipolar Resistive Switching Memory in Perovskite Solar Cell. IEEE J. Electron Devices Soc. 2018, 6, 454–463. [Google Scholar] [CrossRef]
- Landi, G.; Sorrentino, A.; Fedi, F.; Neitzert, H.C.; Iannace, S. Cycle Stability and Dielectric Properties of a New Biodegradable Energy Storage Material. Nano Energy 2015, 17, 348–355. [Google Scholar] [CrossRef]
- Landi, G.; La Notte, L.; Palma, A.L.; Puglisi, G. Electrochemical Performance of Biopolymer-Based Hydrogel Electrolyte for Supercapacitors with Eco-Friendly Binders. Polymers 2022, 14, 4445. [Google Scholar] [CrossRef]
- Landi, G.; La Notte, L.; Palma, A.L.; Sorrentino, A.; Maglione, M.G.; Puglisi, G. A Comparative Evaluation of Sustainable Binders for Environmentally Friendly Carbon-Based Supercapacitors. Nanomaterials 2021, 12, 46. [Google Scholar] [CrossRef] [PubMed]
- Oliviero, M.; Rizvi, R.; Verdolotti, L.; Iannace, S.; Naguib, H.E.; Di Maio, E.; Neitzert, H.C.; Landi, G. Dielectric Properties of Sustainable Nanocomposites Based on Zein Protein and Lignin for Biodegradable Insulators. Adv. Funct. Mater. 2017, 27, 1605142. [Google Scholar] [CrossRef]
- Brus, V.V.; Lang, F.; Bundesmann, J.; Seidel, S.; Denker, A.; Rech, B.; Landi, G.; Neitzert, H.C.; Rappich, J.; Nickel, N.H. Defect Dynamics in Proton Irradiated CH3NH3PbI3 Perovskite Solar Cells. Adv. Electron. Mater. 2017, 3, 1600438. [Google Scholar] [CrossRef] [Green Version]
- Vijaya, S.; Landi, G.; Wu, J.J.; Anandan, S. MoS2 Nanosheets Based Counter Electrodes: An Alternative for Pt-Free Dye-Sensitized Solar Cells. Electrochim. Acta 2019, 294, 134–141. [Google Scholar] [CrossRef]
- Landi, G.; Sorrentino, A.; Iannace, S.; Neitzert, H.C. Differences between Graphene and Graphene Oxide in Gelatin Based Systems for Transient Biodegradable Energy Storage Applications. Nanotechnology 2017, 28, 054005. [Google Scholar] [CrossRef]
- Landi, G.; Fahrner, W.R.; Concilio, S.; Sessa, L.; Neitzert, H.C. Electrical Hole Transport Properties of an Ambipolar Organic Compound With Zn-Atoms on a Crystalline Silicon Heterostructure. IEEE J. Electron Devices Soc. 2014, 2, 179–181. [Google Scholar] [CrossRef]
- Greenbank, W.; Hirsch, L.; Wantz, G.; Chambon, S. Interfacial Thermal Degradation in Inverted Organic Solar Cells. Appl. Phys. Lett. 2015, 107, 263301. [Google Scholar] [CrossRef]
- Hooge, F.N. 1/f Noise Sources. IEEE Trans. Electron Devices 1994, 41, 1926–1935. [Google Scholar] [CrossRef] [Green Version]
- Marinov, O.; Deen, M.J.; Jiménez-Tejada, J.A. Low-Frequency Noise in Downscaled Silicon Transistors: Trends, Theory and Practice. Phys. Rep. 2022, 990, 1–179. [Google Scholar] [CrossRef]
- Davenport, K.; Trinh, C.T.; Hayward, M.; Lips, K.; Rogachev, A. Relaxation Processes in Silicon Heterojunction Solar Cells Probed via Noise Spectroscopy. Sci. Rep. 2021, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Davenport, K.; Zhang, F.; Hayward, M.; Draper, L.; Zhu, K.; Rogachev, A. An Analysis of Carrier Dynamics in Methylammonium Lead Triiodide Perovskite Solar Cells Using Cross Correlation Noise Spectroscopy. Appl. Phys. Lett. 2020, 116, 253902. [Google Scholar] [CrossRef]
- Kogan, S. Electronic Noise and Fluctuations in Solids; Cambridge University Press: Cambridge, UK, 1996; ISBN 9780521460347. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures, 4th ed.; Wiley Blackwell: Hoboken, NJ, USA, 2012; ISBN 9781118032428. [Google Scholar]
- Barone, C.; Pagano, S. What Can Electric Noise Spectroscopy Tell Us on the Physics of Perovskites? Coatings 2021, 11, 96. [Google Scholar] [CrossRef]
- Wiener, N. Generalized Harmonic Analysis. Acta Math. 1930, 55, 117–258. [Google Scholar] [CrossRef]
- Khintchine, A. Korrelationstheorie Der Stationären Stochastischen Prozesse. Math. Ann. 1934, 109, 604–615. [Google Scholar] [CrossRef]
- Johnson, J.B. Thermal Agitation of Electricity in Conductors. Nature 1927, 119, 50–51. [Google Scholar] [CrossRef]
- Schottky, W. Über Spontane Stromschwankungen in Verschiedenen Elektrizitätsleitern. Ann. Phys. 1918, 362, 541–567. [Google Scholar] [CrossRef] [Green Version]
- Dutta, P.; Horn, P.M. Low-Frequency Fluctuations in Solids: 1/f Noise. Rev. Mod. Phys. 1981, 53, 497–516. [Google Scholar] [CrossRef] [Green Version]
- Weissman, M.B. 1/f Noise and Other Slow, Nonexponential Kinetics in Condensed Matter. Rev. Mod. Phys. 1988, 60, 537–571. [Google Scholar] [CrossRef]
- Routoure, J.M.; Wu, S.; Barone, C.; Méchin, L.; Guillet, B. A Low-Noise and Quasi-Ideal DC Current Source Dedicated to Four-Probe Low-Frequency Noise Measurements. IEEE Trans. Instrum. Meas. 2020, 69, 194–200. [Google Scholar] [CrossRef]
- Barone, C.; Galdi, A.; Pagano, S.; Quaranta, O.; Méchin, L.; Routoure, J.-M.; Perna, P. Experimental Technique for Reducing Contact and Background Noise in Voltage Spectral Density Measurements. Rev. Sci. Instrum. 2007, 78, 093905. [Google Scholar] [CrossRef] [PubMed]
- Barone, C.; Pagano, S.; Méchin, L.; Routoure, J.-M.; Orgiani, P.; Maritato, L. Apparent Volume Dependence of 1/f Noise in Thin Film Structures: Role of Contacts. Rev. Sci. Instrum. 2008, 79, 053908. [Google Scholar] [CrossRef] [PubMed]
- Barone, C.; Pagano, S.; Méchin, L.; Guillet, B.; Routoure, J.-M. Comment on “A Case Study on the Scaling of 1/f Noise: La2/3Sr1/3MnO3 Thin Films” [J. Appl. Phys. 113, 094901 (2013)]. J. Appl. Phys. 2014, 115, 116101. [Google Scholar] [CrossRef]
- Barone, C.; Maccagnani, P.; Dinelli, F.; Bertoldo, M.; Capelli, R.; Cocchi, M.; Seri, M.; Pagano, S. Electrical Conduction and Noise Spectroscopy of Sodium-Alginate Gold-Covered Ultrathin Films for Flexible Green Electronics. Sci. Rep. 2022, 12, 9861. [Google Scholar] [CrossRef]
- Barone, C.; Cirillo, C.; Carapella, G.; Granata, V.; Santoro, D.; Attanasio, C.; Pagano, S. Effect of the Substrate on the Electrical Transport and Fluctuation Processes in NbRe and NbReN Ultrathin Films for Superconducting Electronics Applications. Sci. Rep. 2022, 12, 1573. [Google Scholar] [CrossRef]
- Cirillo, C.; Barone, C.; Bradshaw, H.; Urban, F.; Di Bernardo, A.; Mauro, C.; Robinson, J.W.A.; Pagano, S.; Attanasio, C. Magnetotransport and Magnetic Properties of Amorphous NdNi5 Thin Films. Sci. Rep. 2020, 10, 13693. [Google Scholar] [CrossRef] [PubMed]
- Pagano, S.; Martucciello, N.; Enrico, E.; Monticone, E.; Iida, K.; Barone, C. Iron-Based Superconducting Nanowires: Electric Transport and Voltage-Noise Properties. Nanomaterials 2020, 10, 862. [Google Scholar] [CrossRef]
- Barone, C.; Rotzinger, H.; Voss, N.J.; Mauro, C.; Schön, Y.; Ustinov, V.A.; Pagano, S. Current-Resistance Effects Inducing Nonlinear Fluctuation Mechanisms in Granular Aluminum Oxide Nanowires. Nanomaterials 2020, 10, 524. [Google Scholar] [CrossRef] [Green Version]
- Barone, C.; Rotzinger, H.; Mauro, C.; Dorer, D.; Münzberg, J.; Ustinov, A.V.; Pagano, S. Kondo-like Transport and Magnetic Field Effect of Charge Carrier Fluctuations in Granular Aluminum Oxide Thin Films. Sci. Rep. 2018, 8, 13892. [Google Scholar] [CrossRef] [Green Version]
- Barone, C.; Romeo, F.; Pagano, S.; Attanasio, C.; Carapella, G.; Cirillo, C.; Galdi, A.; Grimaldi, G.; Guarino, A.; Leo, A.; et al. Nonequilibrium Fluctuations as a Distinctive Feature of Weak Localization. Sci. Rep. 2015, 5, 10705. [Google Scholar] [CrossRef] [Green Version]
- Schiebel, R.A. A Model for 1/f Noise in Diffusion Current Based on Surface Recombination Velocity Fluctuations and Insulator Trapping. IEEE Trans. Electron Devices 1994, 41, 768–778. [Google Scholar] [CrossRef]
- Kleinpenning, T.G.M. 1f Noise in p-n Diodes. Phys. B+C 1980, 98, 289–299. [Google Scholar] [CrossRef]
- Kleinpenning, T.G.M. 1/ f Noise in p-n Junction Diodes. J. Vac. Sci. Technol. A 1985, 3, 176–182. [Google Scholar] [CrossRef]
- Macku, R.; Koktavy, P. Analysis of Fluctuation Processes in Forward-Biased Solar Cells Using Noise Spectroscopy. Phys. Status Solidi 2010, 207, 2387–2394. [Google Scholar] [CrossRef]
- Anderson, W.W.; Hoffman, H.J. Surface-tunneling-induced 1/ f Noise in Hg1−xCdxTe Photodiodes. J. Vac. Sci. Technol. A Vacuum Surfaces Film. 1983, 1, 1730–1734. [Google Scholar] [CrossRef]
- Hsu, S.T. Surface-State Related 1/f Noise in p-n Junctions and MOS Transistors. Appl. Phys. Lett. 1968, 12, 287. [Google Scholar] [CrossRef]
- van der Ziel, A. Noise in Solid-State Devices and Lasers. Proc. IEEE 1970, 58, 1178–1206. [Google Scholar] [CrossRef]
- Jones, B.K. Electrical Noise as a Measure of Quality and Reliability in Electronic Devices. In Advances in Electronics and Electron Physics; Academic Press: Cambridge, MA, USA, 1993; pp. 201–257. [Google Scholar]
- Chobola, Z. Impulse Noise in Silicon Solar Cells. Microelectronics J. 2001, 32, 707–711. [Google Scholar] [CrossRef]
- Chobola, Z. Noise as a Tool for Non-Destructive Testing of Single-Crystal Silicon Solar Cells. Microelectron. Reliab. 2001, 41, 1947–1952. [Google Scholar] [CrossRef]
- Chobola, Z.; Lunak, M.; Vanek, J.; Barinka, R. Low-Frequency Noise, Microplasma, and Electroluminescence Measurements as Faster Tools to Investigate Quality of Monocrystalline-Silicon Solar Cells. Opt. Eng. 2013, 52, 051203. [Google Scholar] [CrossRef]
- Bag, A.; Mukherjee, C.; Mallik, S.; Maiti, C.K. Low Frequency Noise in Iron Disilicide Hetero-Junction Solar Cells. In Proceedings of the 2012 19th IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits, Singapore, 2–6 July 2012; pp. 1–4. [Google Scholar]
- Jia, X.; He, L. Noise-Based Analysis of the Reliability of Silicon Solar Cells. AIP Adv. 2021, 11, 045206. [Google Scholar] [CrossRef]
- Rein, S.; Glunz, S.W. Electronic Properties of the Metastable Defect in Boron-Doped Czochralski Silicon: Unambiguous Determination by Advanced Lifetime Spectroscopy. Appl. Phys. Lett. 2003, 82, 1054. [Google Scholar] [CrossRef]
- Colina, M.; Morales-Vilches, A.B.; Voz, C.; Martin, I.; Ortega, P.R.; Alcubilla, R. Low Surface Recombination in Silicon-Heterojunction Solar Cells With Rear Laser-Fired Contacts From Aluminum Foils. IEEE J. Photovolt. 2015, 5, 805–811. [Google Scholar] [CrossRef] [Green Version]
- Glunz, S.W.; Rein, S.; Lee, J.Y.; Warta, W. Minority Carrier Lifetime Degradation in Boron-Doped Czochralski Silicon. J. Appl. Phys. 2001, 90, 2397–2404. [Google Scholar] [CrossRef]
- Rein, S.; Rehrl, T.; Warta, W.; Glunz, S.W. Lifetime Spectroscopy for Defect Characterization: Systematic Analysis of the Possibilities and Restrictions. J. Appl. Phys. 2002, 91, 2059–2070. [Google Scholar] [CrossRef]
- Weiss, T.P.; Redinger, A.; Regesch, D.; Mousel, M.; Siebentritt, S. Direct Evaluation of Defect Distributions From Admittance Spectroscopy. IEEE J. Photovolt. 2014, 4, 1665–1670. [Google Scholar] [CrossRef]
- Bertram, T.; Depredurand, V.; Siebentritt, S. Electrical Characterization of Defects in Cu-Rich Grown CuInSe2 Solar Cells. IEEE J. Photovolt. 2016, 6, 546–551. [Google Scholar] [CrossRef] [Green Version]
- Cao, J.; Prince, M.; Kalejs, J.P. Impurity Transients in Multiple Crystal Growth from a Single Crucible for EFG Silicon Octagons. J. Cryst. Growth 1997, 174, 170–175. [Google Scholar] [CrossRef]
- Yang, Y.; Mil’shtein, S.; Borenstein, J.T.; Hanoka, J.I. Deep Levels in Edge-defined, Film-fed Grown Silicon Solar Cells. Appl. Phys. Lett. 1990, 56, 2222–2224. [Google Scholar] [CrossRef]
- Neitzert, H.-C.; Ferrara, M.; Kunst, M.; Denker, A.; Kertész, Z.; Limata, B.; Gialanella, L.; Romano, M. Electroluminescence Efficiency Degradation of Crystalline Silicon Solar Cells after Irradiation with Protons in the Energy Range between 0.8 MeV and 65 MeV. Phys. Status Solidi 2008, 245, 1877–1883. [Google Scholar] [CrossRef]
- Würfel, P.; Würfel, U. Physics of Solar Cells: From Basic Principles to Advanced Concepts; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 9783527408573. [Google Scholar]
- Green, M.A. Intrinsic Concentration, Effective Densities of States, and Effective Mass in Silicon. J. Appl. Phys. 1990, 67, 2944. [Google Scholar] [CrossRef]
- Schmidt, J.; Bothe, K.; Hezel, R. Oxygen-Related Minority-Carrier Trapping Centers in p-Type Czochralski Silicon. Appl. Phys. Lett. 2002, 80, 4395–4397. [Google Scholar] [CrossRef]
- Gogolin, R.; Harder, N.P. Trapping Behavior of Shockley-Read-Hall Recombination Centers in Silicon Solar Cells. J. Appl. Phys. 2013, 114, 064504. [Google Scholar] [CrossRef]
- Landi, G.; Barone, C.; Mauro, C.; Neitzert, H.C.; Pagano, S. Noise Spectroscopy as a Tool for the Characterization of Perovskite, Organic and Silicon Solar Cells. AIP Conf. Proc. 2019, 2082, 020001. [Google Scholar]
- Landi, G.; Barone, C.; Mauro, C.; Pagano, S.; Neitzert, H.C. Evaluation of Silicon, Organic, and Perovskite Solar Cell Reliability with Low-Frequency Noise Spectroscopy. In Proceedings of the 2018 IEEE International Reliability Physics Symposium (IRPS), Burlingame, CA, USA, 11–15 March 2018; Volume 2018, pp. 6C.3-1–6C.3-6. [Google Scholar]
- Ziegler, J.F.; Biersack, J.P. The Stopping and Range of Ions in Matter BT—Treatise on Heavy-Ion Science: Volume 6: Astrophysics, Chemistry, and Condensed Matter. In Treatise on Heavy-Ion Science; Bromley, D.A., Ed.; Springer: Boston, MA, USA, 1985; pp. 93–129. ISBN 978-1-4615-8103-1. [Google Scholar]
- Vasic, A.; Vujisic, M.; Loncar, B.; Osmokrovic, P. Aging of Solar Cells under Working Conditions. J. Optoelectron. Adv. Mater. 2007, 9, 1843–1846. [Google Scholar]
- Ripolles-Sanchis, T.; Guerrero, A.; Bisquert, J.; Garcia-Belmonte, G. Diffusion-Recombination Determines Collected Current and Voltage in Polymer:Fullerene Solar Cells. J. Phys. Chem. C 2012, 116, 16925–16933. [Google Scholar] [CrossRef]
- Perrier, G.; de Bettignies, R.; Berson, S.; Lemaître, N.; Guillerez, S. Impedance Spectrometry of Optimized Standard and Inverted P3HT-PCBM Organic Solar Cells. Sol. Energy Mater. Sol. Cells 2012, 101, 210–216. [Google Scholar] [CrossRef]
- Boix, P.P.; Guerrero, A.; Marchesi, L.F.; Garcia-Belmonte, G.; Bisquert, J. Current-Voltage Characteristics of Bulk Heterojunction Organic Solar Cells: Connection Between Light and Dark Curves. Adv. Energy Mater. 2011, 1, 1073–1078. [Google Scholar] [CrossRef]
- Guerrero, A.; Ripolles-Sanchis, T.; Boix, P.P.; Garcia-Belmonte, G. Series Resistance in Organic Bulk-Heterojunction Solar Devices: Modulating Carrier Transport with Fullerene Electron Traps. Org. Electron. 2012, 13, 2326–2332. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, A.; Marchesi, L.F.; Boix, P.P.; Ruiz-Raga, S.; Ripolles-Sanchis, T.; Garcia-Belmonte, G.; Bisquert, J. How the Charge-Neutrality Level of Interface States Controls Energy Level Alignment in Cathode Contacts of Organic Bulk-Heterojunction Solar Cells. ACS Nano 2012, 6, 3453–3460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bisquert, J.; Garcia-Belmonte, G.; García-Cañadas, J. Effects of the Gaussian Energy Dispersion on the Statistics of Polarons and Bipolarons in Conducting Polymers. J. Chem. Phys. 2004, 120, 6726–6733. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Belmonte, G.; Boix, P.P.; Bisquert, J.; Lenes, M.; Bolink, H.J.; La Rosa, A.; Filippone, S.; Martín, N. Influence of the Intermediate Density-of-States Occupancy on Open-Circuit Voltage of Bulk Heterojunction Solar Cells with Different Fullerene Acceptors. J. Phys. Chem. Lett. 2010, 1, 2566–2571. [Google Scholar] [CrossRef]
- Dennler, G.; Mozer, A.J.; Juška, G.; Pivrikas, A.; Österbacka, R.; Fuchsbauer, A.; Sariciftci, N.S. Charge Carrier Mobility and Lifetime versus Composition of Conjugated Polymer/Fullerene Bulk-Heterojunction Solar Cells. Org. Electron. 2006, 7, 229–234. [Google Scholar] [CrossRef]
- Bertho, S.; Campo, B.; Piersimoni, F.; Spoltore, D.; D’Haen, J.; Lutsen, L.; Maes, W.; Vanderzande, D.; Manca, J. Improved Thermal Stability of Bulk Heterojunctions Based on Side-Chain Functionalized Poly(3-Alkylthiophene) Copolymers and PCBM. Sol. Energy Mater. Sol. Cells 2013, 110, 69–76. [Google Scholar] [CrossRef]
- Lilliu, S.; Agostinelli, T.; Pires, E.; Hampton, M.; Nelson, J.; Macdonald, J.E. Dynamics of Crystallization and Disorder during Annealing of P3HT/PCBM Bulk Heterojunctions. Macromolecules 2011, 44, 2725–2734. [Google Scholar] [CrossRef]
- Tsoi, W.C.; Spencer, S.J.; Yang, L.; Ballantyne, A.M.; Nicholson, P.G.; Turnbull, A.; Shard, A.G.; Murphy, C.E.; Bradley, D.D.C.; Nelson, J.; et al. Effect of Crystallization on the Electronic Energy Levels and Thin Film Morphology of P3HT:PCBM Blends. Macromolecules 2011, 44, 2944–2952. [Google Scholar] [CrossRef]
- Li, G.; Shrotriya, V.; Yao, Y.; Yang, Y. Investigation of Annealing Effects and Film Thickness Dependence of Polymer Solar Cells Based on Poly(3-Hexylthiophene). J. Appl. Phys. 2005, 98, 43704. [Google Scholar] [CrossRef] [Green Version]
- Chandni, U.; Ghosh, A.; Vijaya, H.S.; Mohan, S. Criticality of Tuning in Athermal Phase Transitions. Phys. Rev. Lett. 2009, 102, 25701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barone, C.; Bellingeri, E.; Adamo, M.; Sarnelli, E.; Ferdeghini, C.; Pagano, S. Electric Field Activated Nonlinear 1/f Fluctuations in Fe(Te, Se) Superconductors. Supercond. Sci. Technol. 2013, 26, 075006. [Google Scholar] [CrossRef]
- Bonavolontà, C.; Albonetti, C.; Barra, M.; Valentino, M. Electrical Mobility in Organic Thin-Film Transistors Determined by Noise Spectroscopy. J. Appl. Phys. 2011, 110, 93716. [Google Scholar] [CrossRef]
- Servaites, J.D.; Ratner, M.A.; Marks, T.J. Organic Solar Cells: A New Look at Traditional Models. Energy Environ. Sci. 2011, 4, 4410–4422. [Google Scholar] [CrossRef]
- Chen, F.-C.; Tseng, H.-C.; Ko, C.-J. Solvent Mixtures for Improving Device Efficiency of Polymer Photovoltaic Devices. Appl. Phys. Lett. 2008, 92, 103316. [Google Scholar] [CrossRef]
- Li, L.; Tang, H.; Wu, H.; Lu, G.; Yang, X. Effects of Fullerene Solubility on the Crystallization of Poly(3-Hexylthiophene) and Performance of Photovoltaic Devices. Org. Electron. 2009, 10, 1334–1344. [Google Scholar] [CrossRef]
- Li, L.; Shen, Y.; Campbell, J.C. The Impact of Thermal Annealing Temperature on the Low-Frequency Noise Characteristics of P3HT:PCBM Bulk Heterojunction Organic Solar Cells. Sol. Energy Mater. Sol. Cells 2014, 130, 151–155. [Google Scholar] [CrossRef] [Green Version]
- Vijayan, R.; Azeez, A.; Narayan, K.S. Toward Reliable High Performing Organic Solar Cells: Molecules, Processing, and Monitoring. APL Mater. 2020, 8, 040908. [Google Scholar] [CrossRef] [Green Version]
- Wehrenfennig, C.; Eperon, G.E.; Johnston, M.B.; Snaith, H.J.; Herz, L.M. High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites. Adv. Mater. 2014, 26, 1584–1589. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wehrenfennig, C.; Liu, M.; Snaith, H.J.; Johnston, M.B.; Herz, L.M. Charge-Carrier Dynamics in Vapour-Deposited Films of the Organolead Halide Perovskite CH3NH3PbI3−xClx. Energy Environ. Sci. 2014, 7, 2269–2275. [Google Scholar] [CrossRef]
- Wang, K.L.; Zhou, Y.H.; Lou, Y.H.; Wang, Z.K. Perovskite Indoor Photovoltaics: Opportunity and Challenges. Chem. Sci. 2021, 12, 11936–11954. [Google Scholar] [CrossRef] [PubMed]
- Antonietta Loi, M.; Hummelen, J.C. Perovskites under the Sun. Nat. Mater. 2013, 12, 1087–1089. [Google Scholar] [CrossRef]
- Marchioro, A.; Teuscher, J.; Friedrich, D.; Kunst, M.; van de Krol, R.; Moehl, T.; Grätzel, M.; Moser, J.-E. Unravelling the Mechanism of Photoinduced Charge Transfer Processes in Lead Iodide Perovskite Solar Cells. Nat. Photonics 2014, 8, 250–255. [Google Scholar] [CrossRef] [Green Version]
- Divitini, G.; Cacovich, S.; Matteocci, F.; Cinà, L.; Di Carlo, A.; Ducati, C. In Situ Observation of Heat-Induced Degradation of Perovskite Solar Cells. Nat. Energy 2016, 1, 15012. [Google Scholar] [CrossRef] [Green Version]
- Baikie, T.; Fang, Y.; Kadro, J.M.; Schreyer, M.; Wei, F.; Mhaisalkar, S.G.; Graetzel, M.; White, T.J. Synthesis and Crystal Chemistry of the Hybrid Perovskite (CH3NH3)PbI3 for Solid-State Sensitised Solar Cell Applications. J. Mater. Chem. A 2013, 1, 5628–5641. [Google Scholar] [CrossRef]
- Peña-Camargo, F.; Thiesbrummel, J.; Hempel, H.; Musiienko, A.; Le Corre, V.M.; Diekmann, J.; Warby, J.; Unold, T.; Lang, F.; Neher, D.; et al. Revealing the Doping Density in Perovskite Solar Cells and Its Impact on Device Performance. Appl. Phys. Rev. 2022, 9, 21409. [Google Scholar] [CrossRef]
- Zhang, H.; Qiao, X.; Shen, Y.; Moehl, T.; Zakeeruddin, S.M.; Grätzel, M.; Wang, M. Photovoltaic Behaviour of Lead Methylammonium Triiodide Perovskite Solar Cells down to 80 K. J. Mater. Chem. A 2015, 3, 11762–11767. [Google Scholar] [CrossRef]
- Yin, W.-J.; Shi, T.; Yan, Y. Unusual Defect Physics in CH3NH3PbI3 Perovskite Solar Cell Absorber. Appl. Phys. Lett. 2014, 104, 63903. [Google Scholar] [CrossRef]
- Stranks, S.D.; Burlakov, V.M.; Leijtens, T.; Ball, J.M.; Goriely, A.; Snaith, H.J. Recombination Kinetics in Organic-Inorganic Perovskites: Excitons, Free Charge, and Subgap States. Phys. Rev. Appl. 2014, 2, 034007. [Google Scholar] [CrossRef]
- Shen, Q.; Ng, A.; Ren, Z.; Gokkaya, H.C.; Djurišić, A.B.; Zapien, J.A.; Surya, C. Characterization of Low-Frequency Excess Noise in CH3NH3PbI3 -Based Solar Cells Grown by Solution and Hybrid Chemical Vapor Deposition Techniques. ACS Appl. Mater. Interfaces 2018, 10, 371–380. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Bansode, U.; Ogale, S.; Rahman, A. Understanding the Thermal Degradation Mechanism of Perovskite Solar Cells via Dielectric and Noise Measurements. Nanotechnology 2020, 31, 365403. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Nayak, P.K.; Banerjee, S.; Wang, Z.; Wang, J.T.-W.; Snaith, H.J.; Narayan, K.S. Insights Into the Microscopic and Degradation Processes in Hybrid Perovskite Solar Cells Using Noise Spectroscopy. Sol. RRL 2018, 2, 1700173. [Google Scholar] [CrossRef]



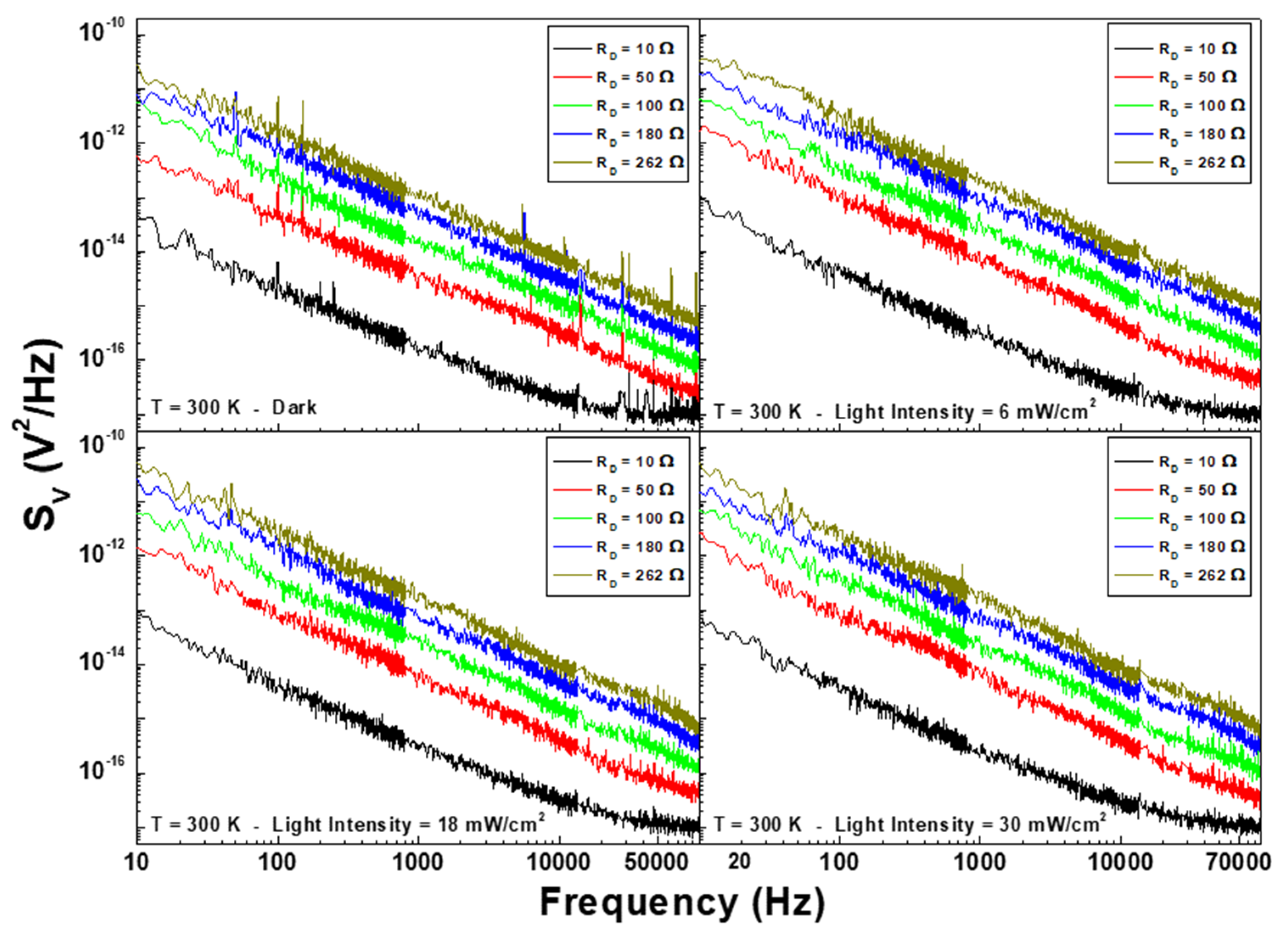
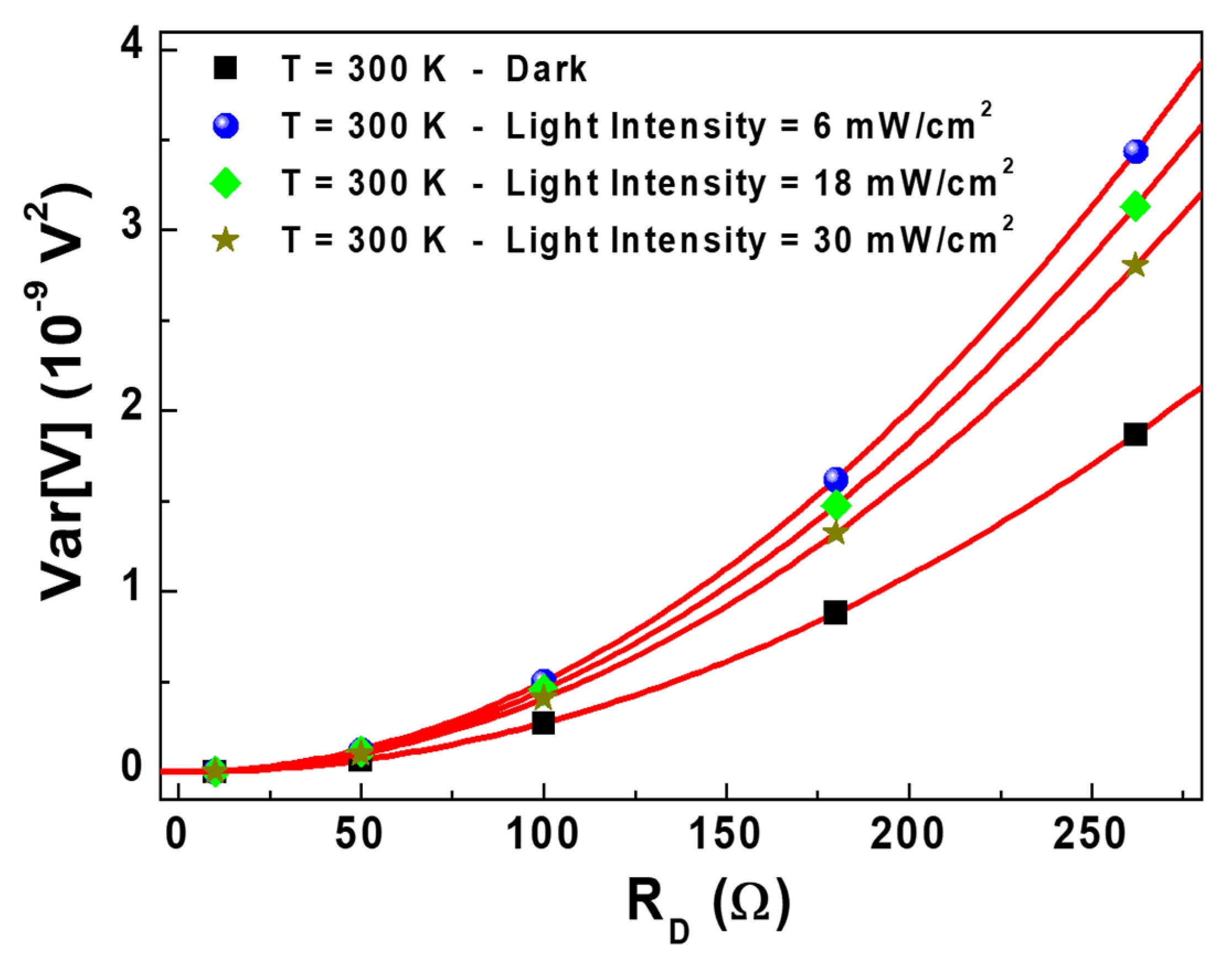

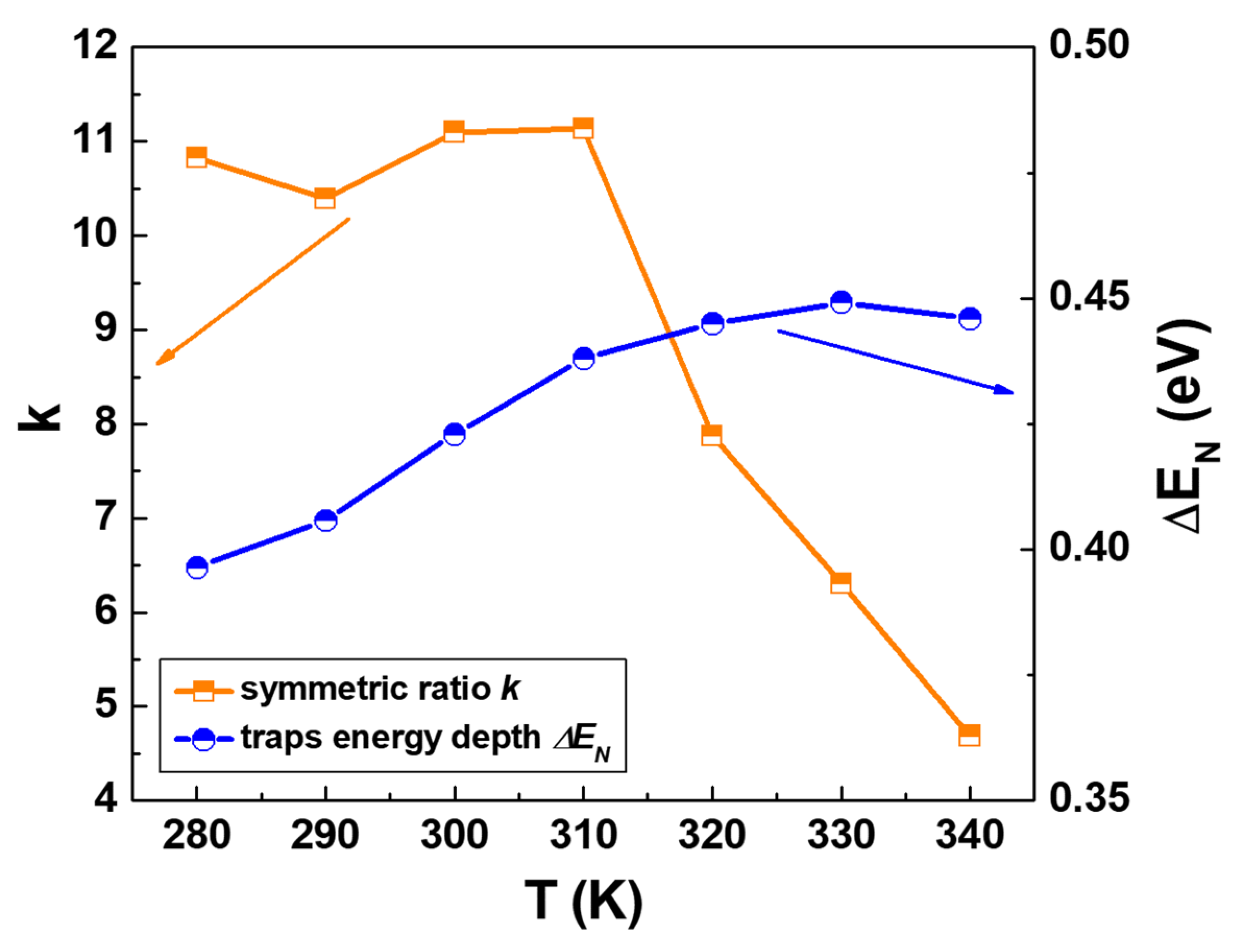
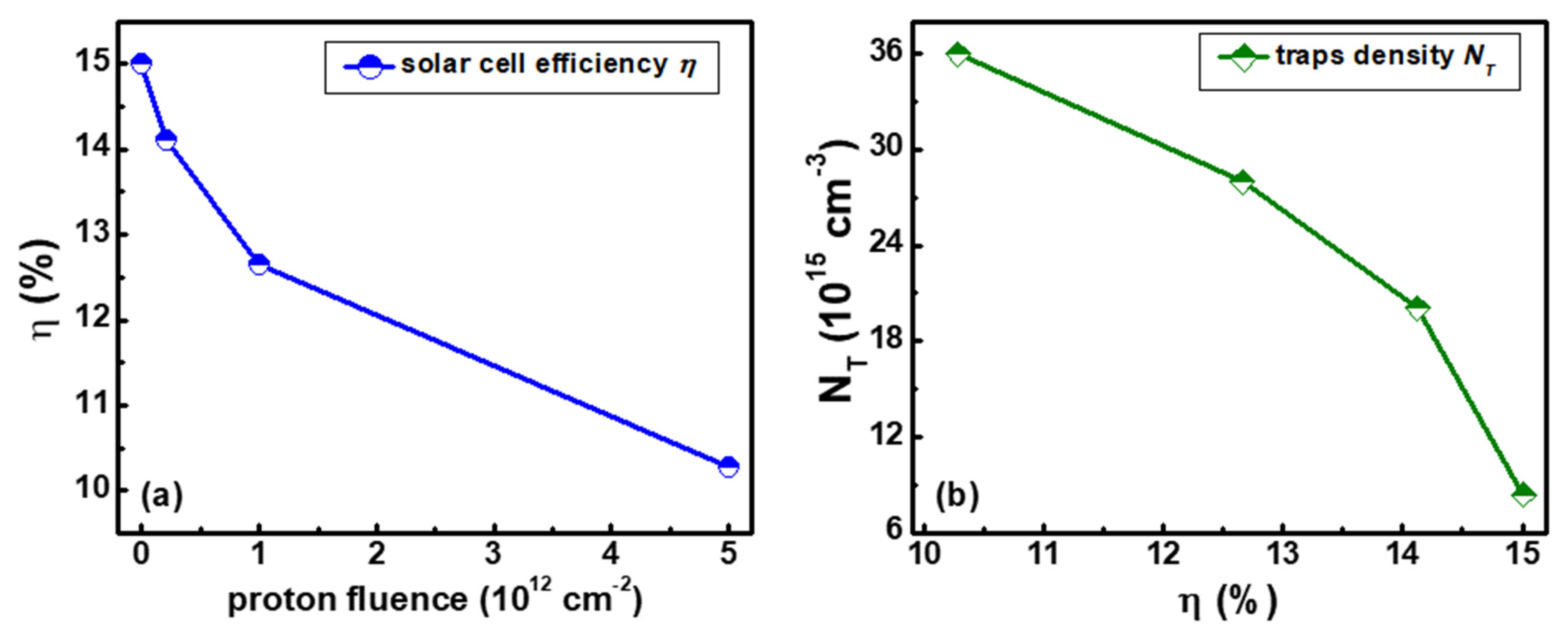
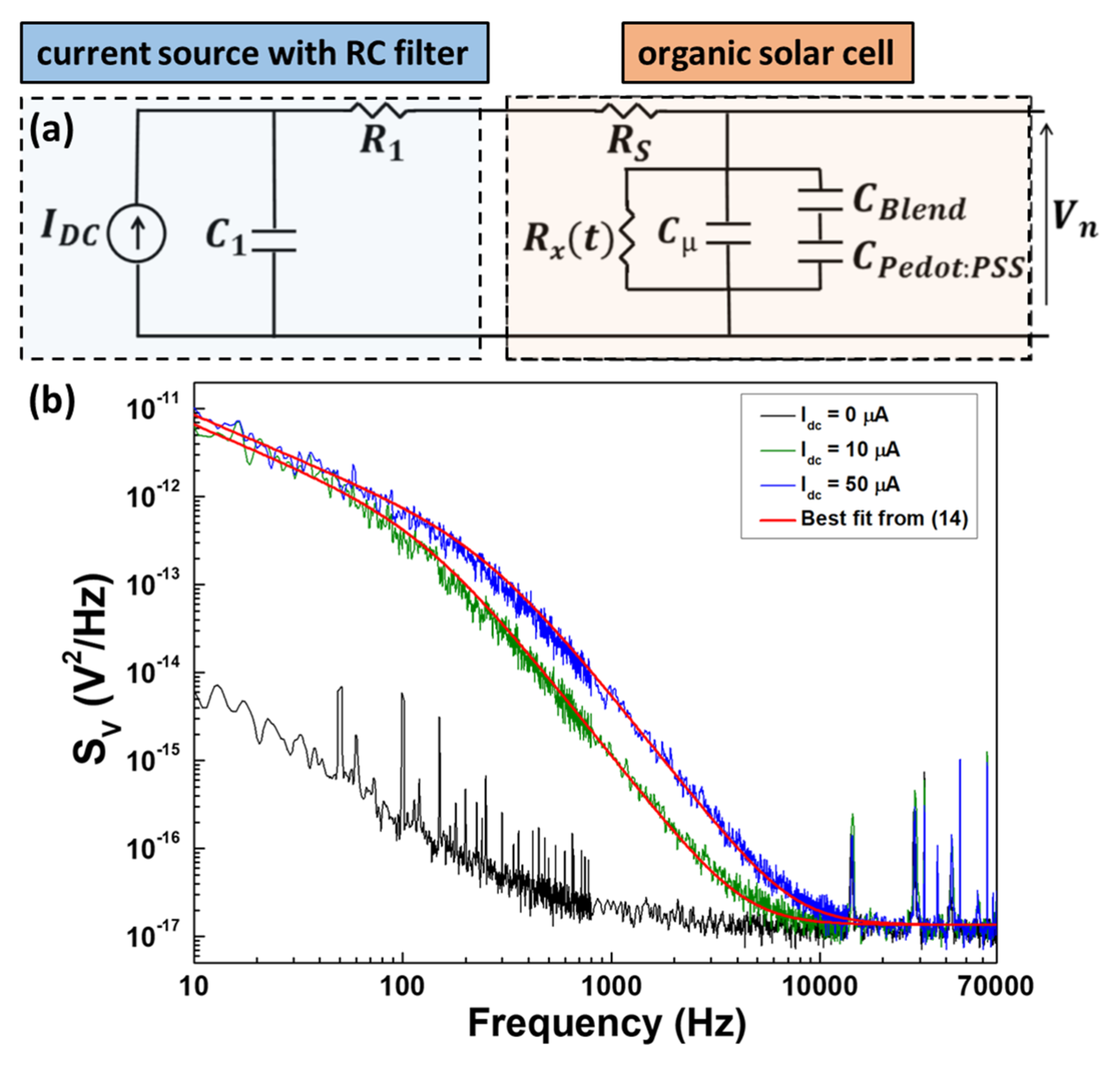
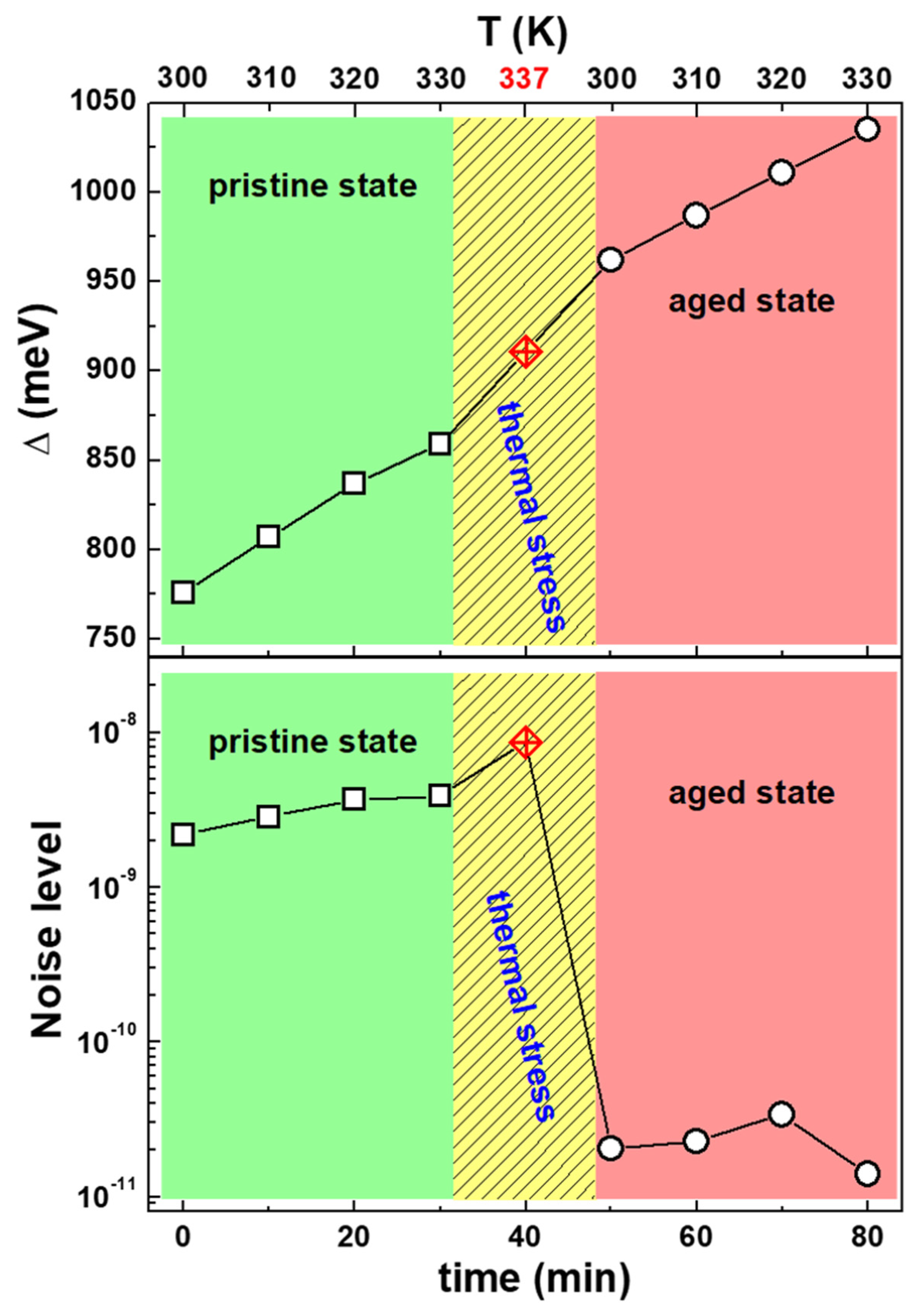
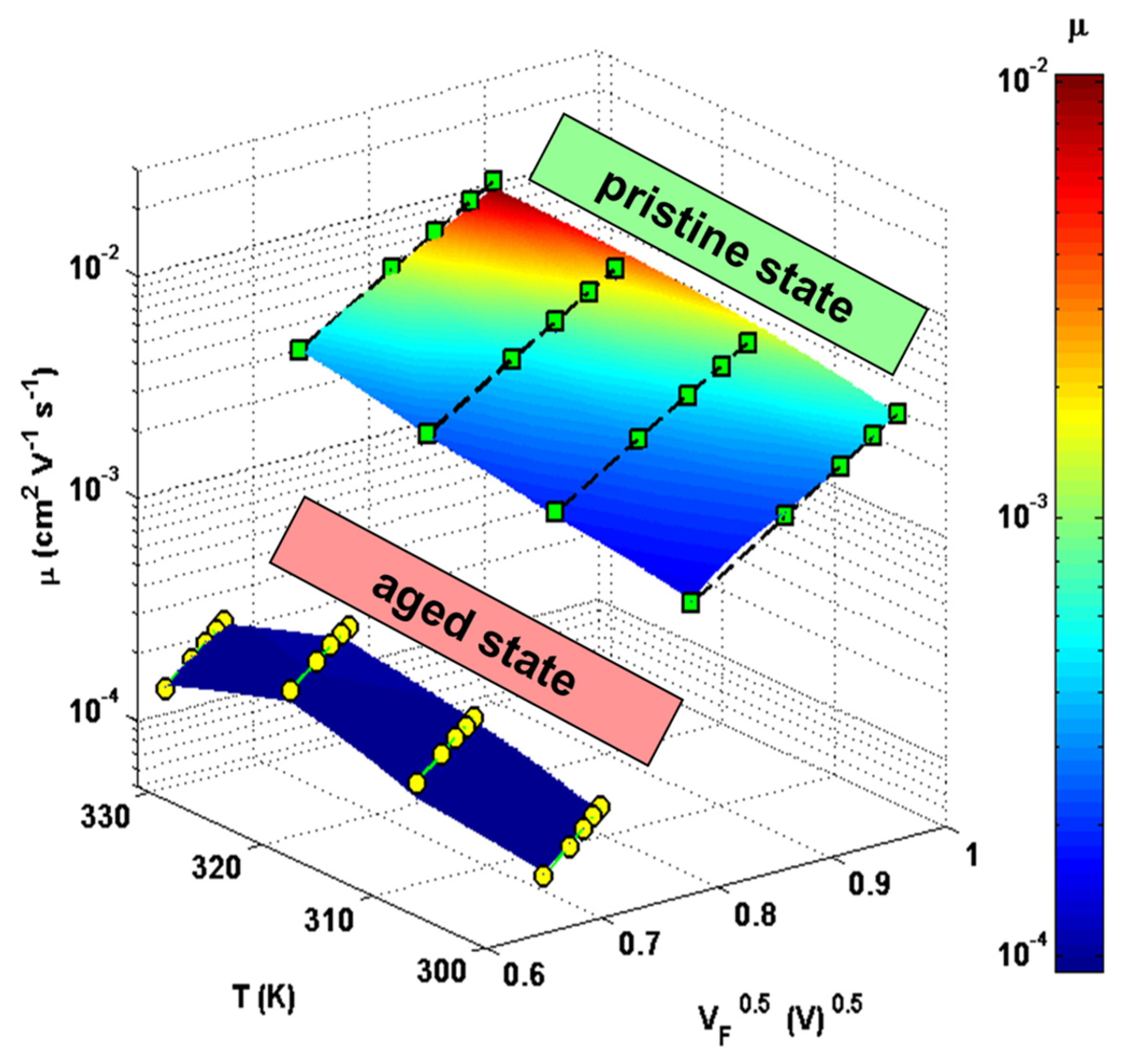

| E (eV) 1 | Cμ (nF⋅cm−2) | g = DOS (eV−1⋅cm−3) | Rrec (kΩ⋅cm2) | τn (ms) |
|---|---|---|---|---|
| 0.58 | 79.5 | 3.47 × 1016 | 10.63 | 0.845 |
| 0.74 | 175 | 5.46 × 1016 | 4.78 | 0.836 |
| 0.83 | 267 | 8.33 × 1016 | 3.04 | 0.811 |
| 0.88 | 297.3 | 9.28 × 1016 | 2.36 | 0.702 |
| 0.92 | 314 | 9.80 × 1016 | 1.93 | 0.606 |
| T (K) 1 | Time (min) | μ0 (cm2⋅V−1⋅s−1) | EGill (meV) |
|---|---|---|---|
| 300 | 0 | 2.68 × 10−6 | 46.88 |
| 310 | 10 | 6.02 × 10−6 | 46.97 |
| 320 | 20 | 11.2 × 10−6 | 46.98 |
| 330 | 30 | 22.9 × 10−6 | 47.02 |
| 337 | breakdown 1 | ||
| 300 | 50 | 1.27 × 10−7 | 64.99 |
| 310 | 60 | 2.41 × 10−7 | 64.95 |
| 320 | 70 | 5.20 × 10−7 | 65.08 |
| 330 | 80 | 5.44 × 10−7 | 65.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Landi, G.; Pagano, S.; Neitzert, H.C.; Mauro, C.; Barone, C. Noise Spectroscopy: A Tool to Understand the Physics of Solar Cells. Energies 2023, 16, 1296. https://doi.org/10.3390/en16031296
Landi G, Pagano S, Neitzert HC, Mauro C, Barone C. Noise Spectroscopy: A Tool to Understand the Physics of Solar Cells. Energies. 2023; 16(3):1296. https://doi.org/10.3390/en16031296
Chicago/Turabian StyleLandi, Giovanni, Sergio Pagano, Heinz Christoph Neitzert, Costantino Mauro, and Carlo Barone. 2023. "Noise Spectroscopy: A Tool to Understand the Physics of Solar Cells" Energies 16, no. 3: 1296. https://doi.org/10.3390/en16031296
APA StyleLandi, G., Pagano, S., Neitzert, H. C., Mauro, C., & Barone, C. (2023). Noise Spectroscopy: A Tool to Understand the Physics of Solar Cells. Energies, 16(3), 1296. https://doi.org/10.3390/en16031296








