An Efficient Variable Step Solar Maximum Power Point Tracking Algorithm
Abstract
:1. Introduction
- A first-order linear Kalman filtering algorithm is employed to pre-process the sensor detection data, which improves the stability and accuracy of the subsequent MPPT control algorithm.
- The calculation method of the step adjustment factor of the traditional variable step conductance increment is improved to increase the efficiency of the photovoltaic system.
- The MQTT protocol is applied to transmit information when the photovoltaic system is in operation, and the corresponding client is designed to remotely monitor the working status of the photovoltaic cells.
2. Photovoltaic Mathematical Model and Output Characteristics Analysis
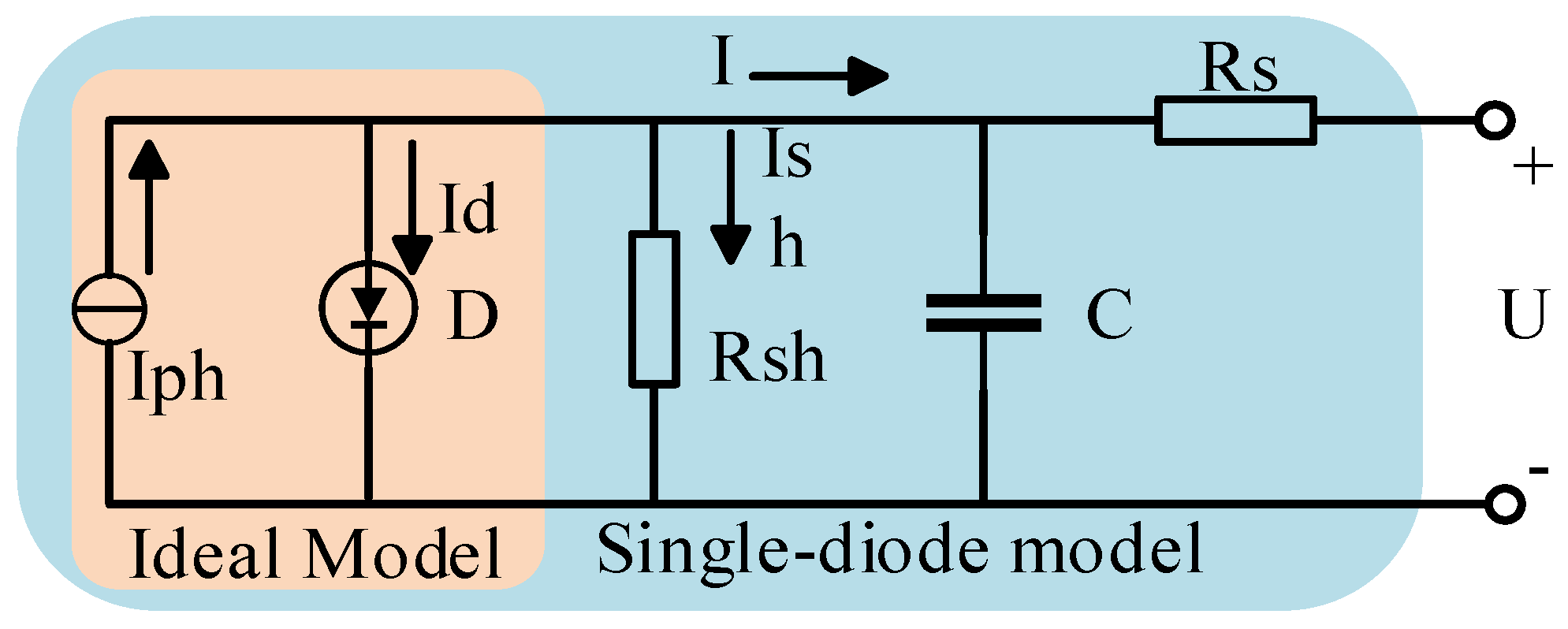
2.1. Photovoltaic Cell Mathematical Modeling and Analysis
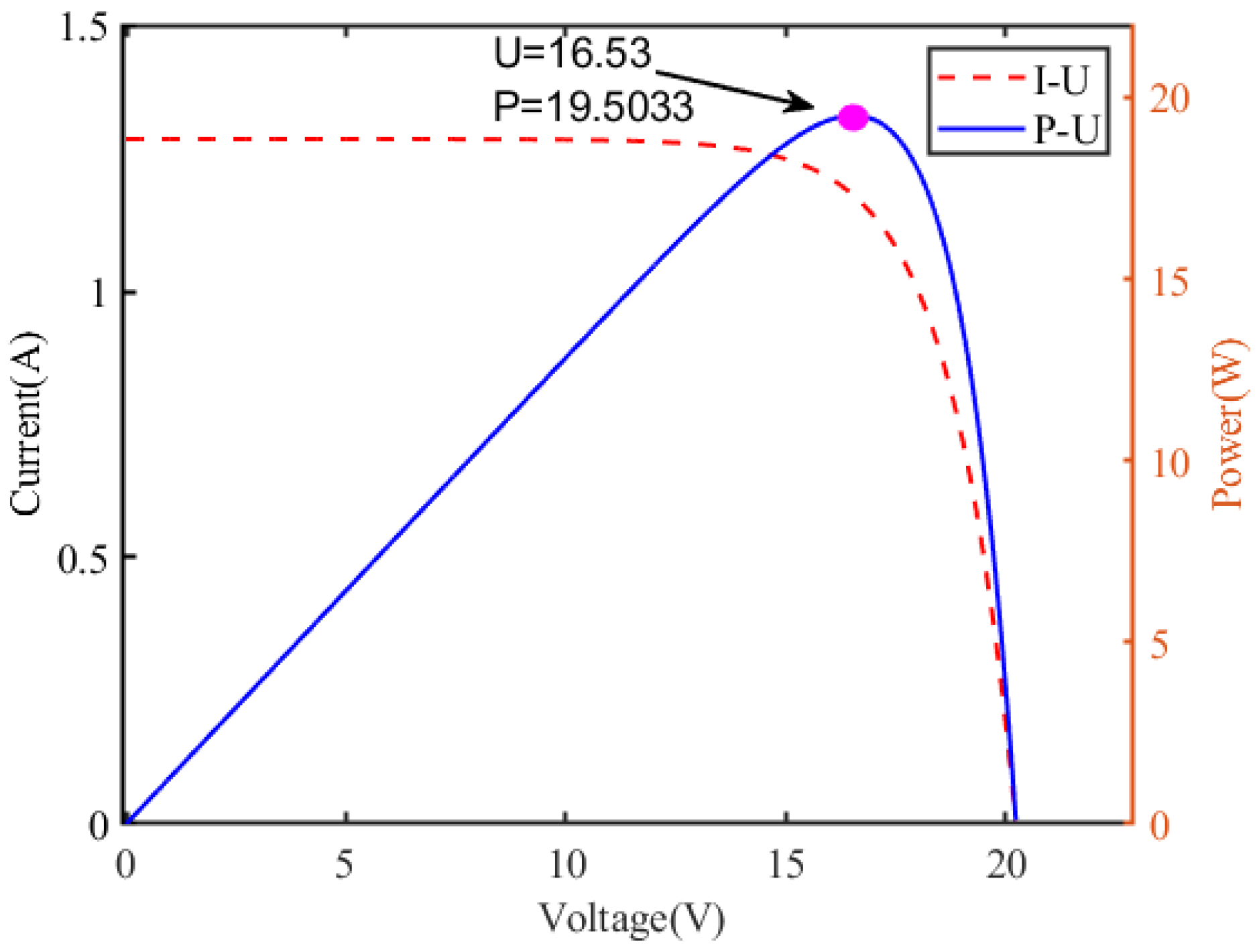
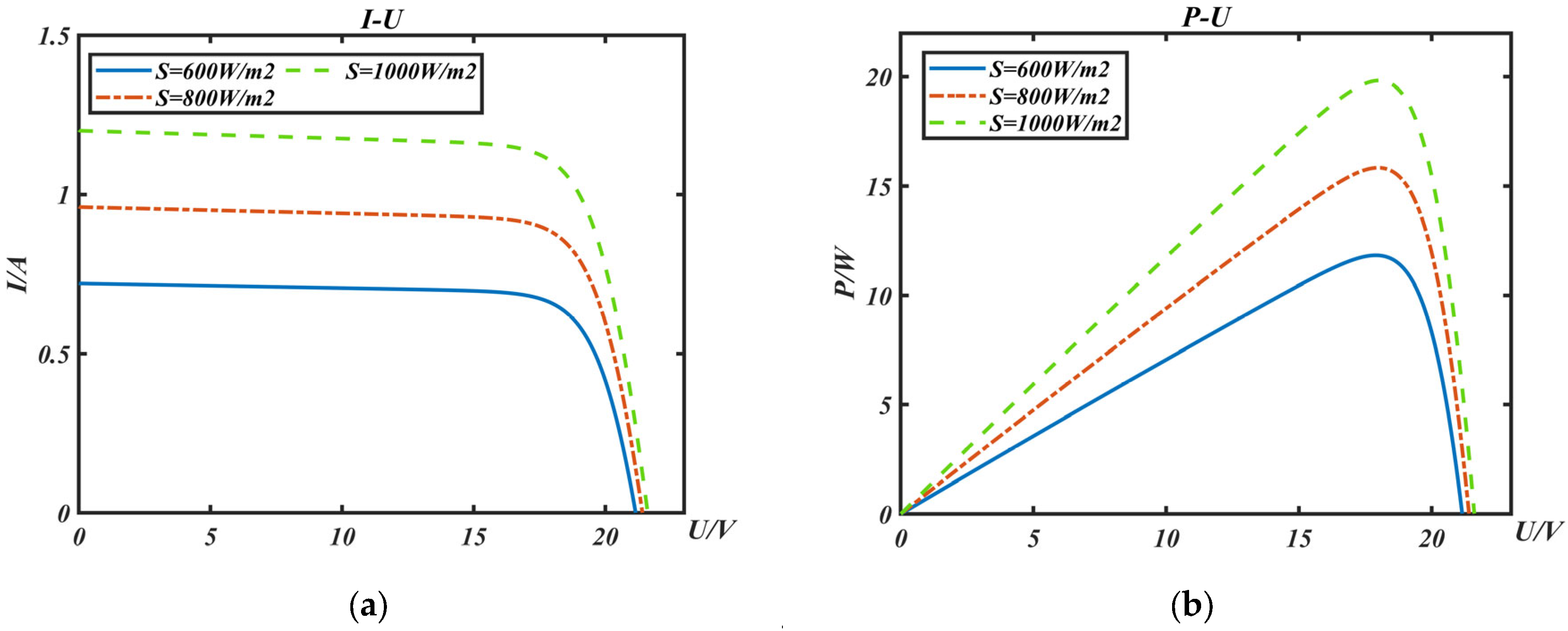
2.2. Photovoltaic Cell Output Characteristics Analysis
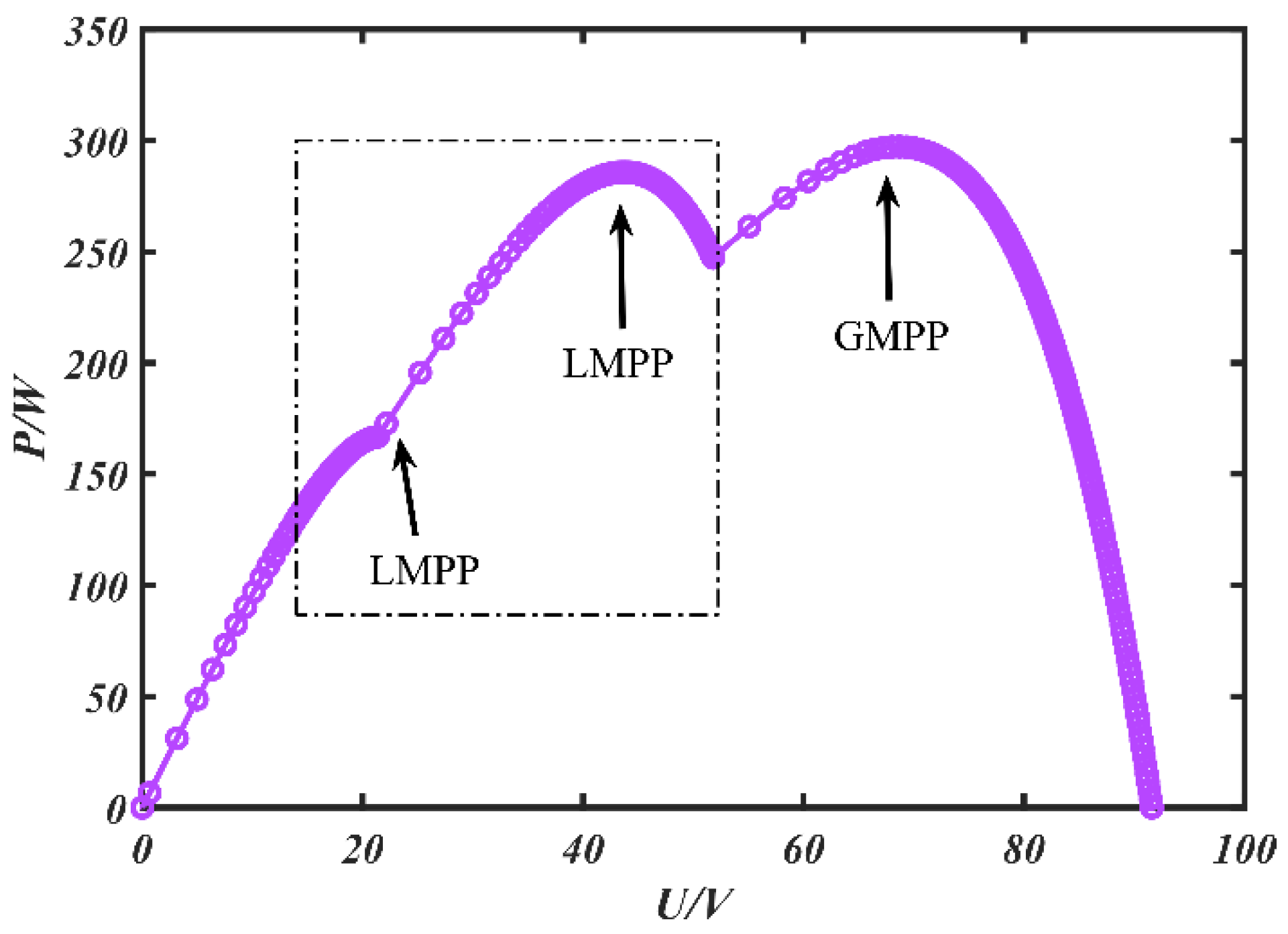
3. MPPT Control Principle Analysis
4. Traditional Conductance Increment Method Analysis
5. Design and Validation of an Improved Three-Stage Variable Step Incremental Conductivity Method
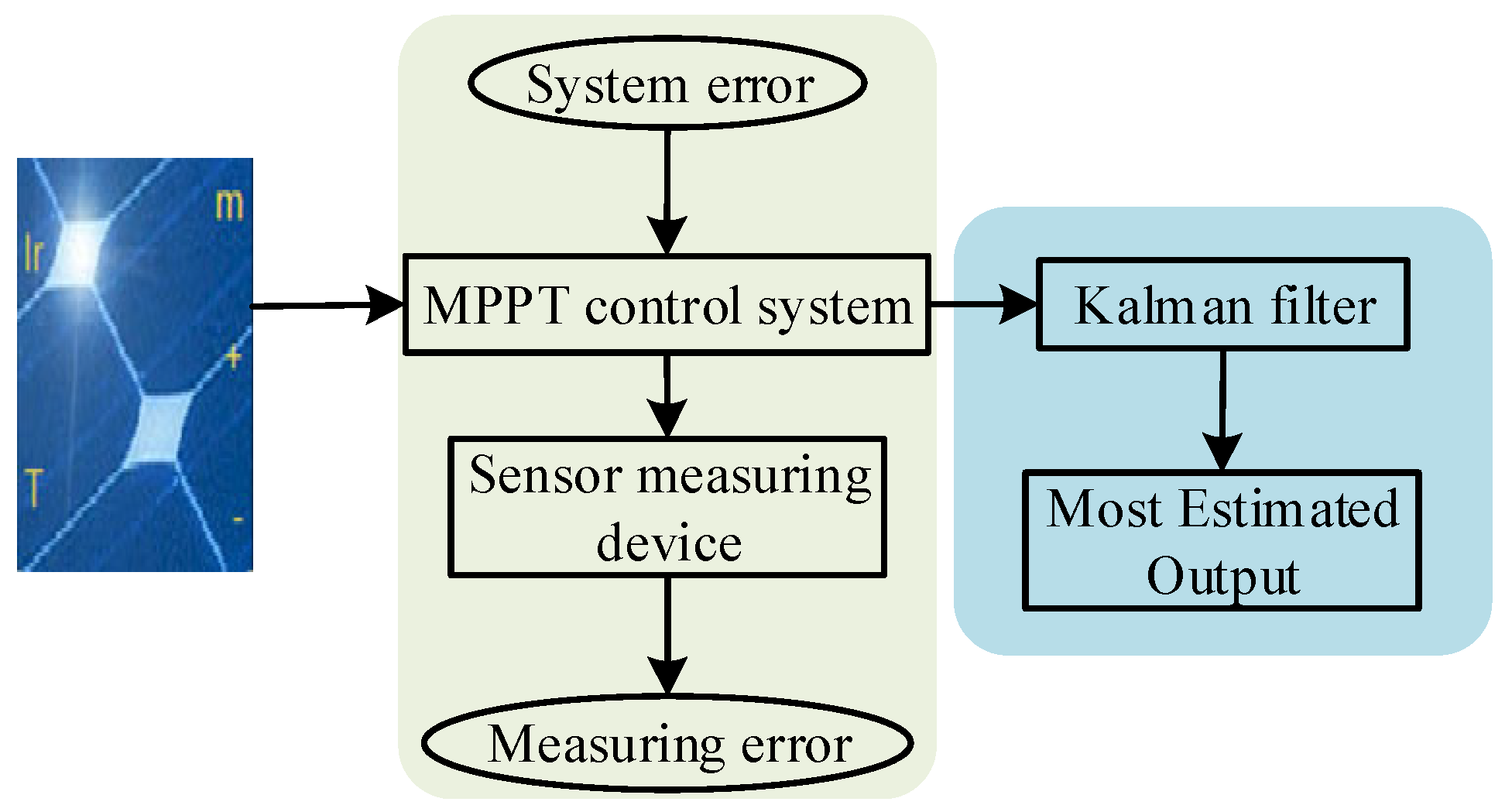
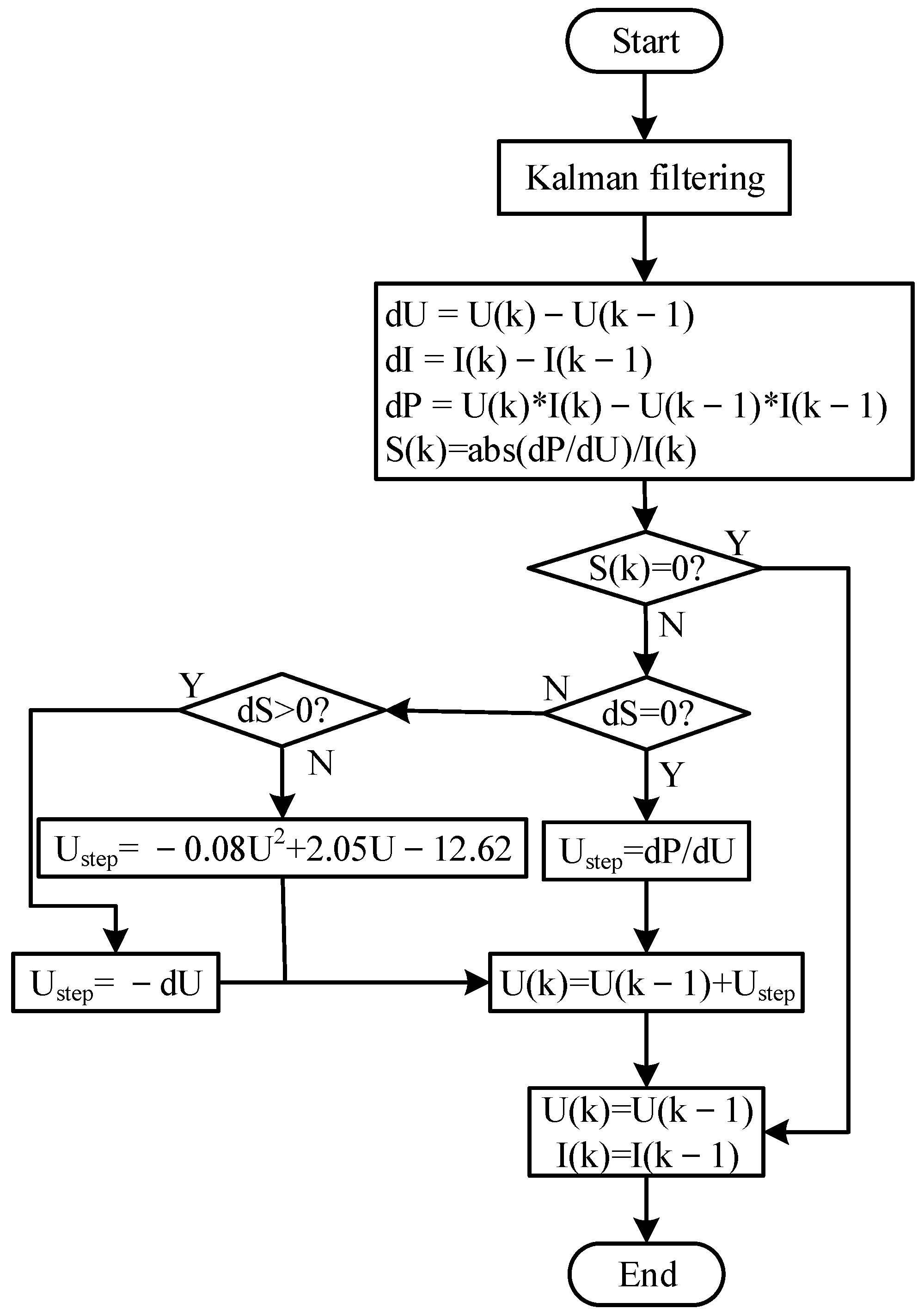
5.1. Principle of Kalman Filter Algorithm
5.2. Processing of Photovoltaic Cell Output Information by Kalman Filtering Algorithm
5.3. Improved MPPT Control Algorithm by Kalman Filter
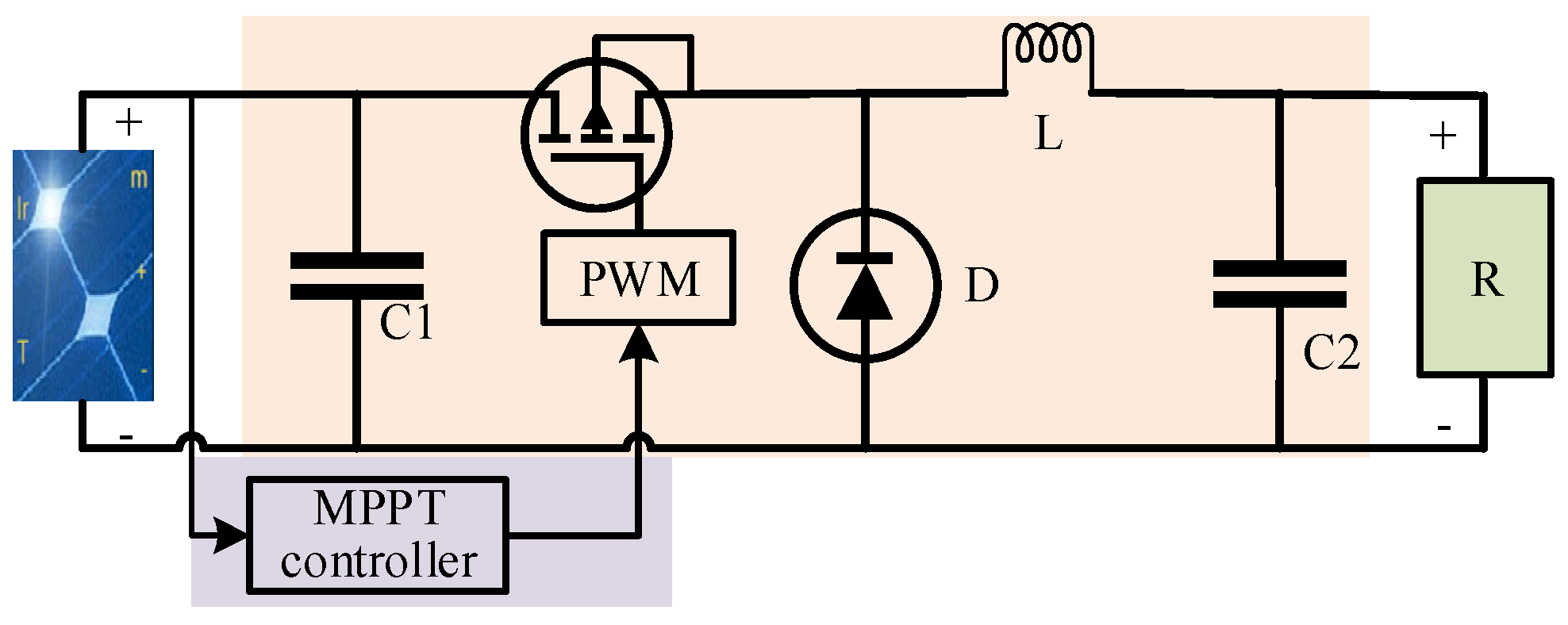
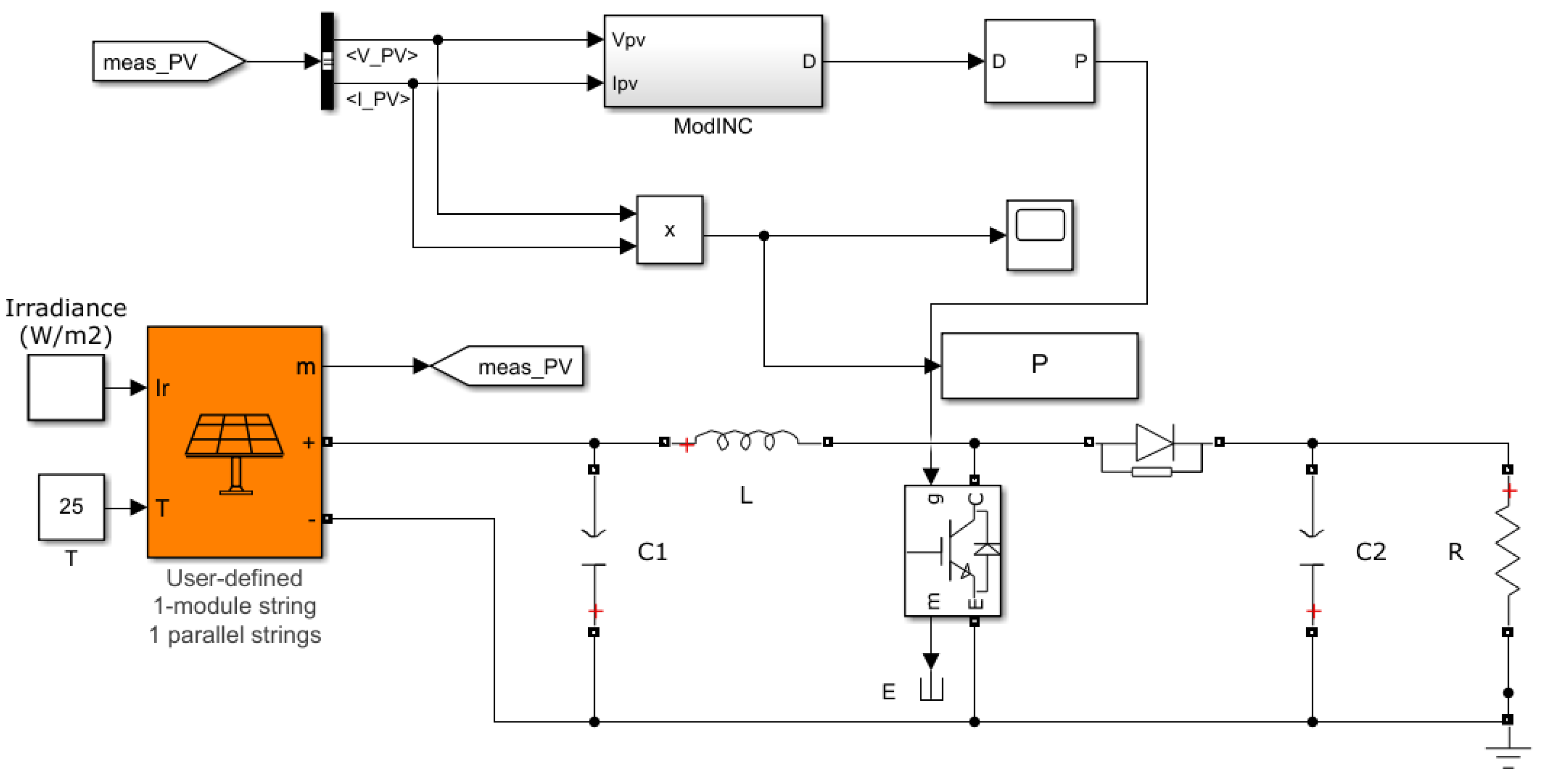
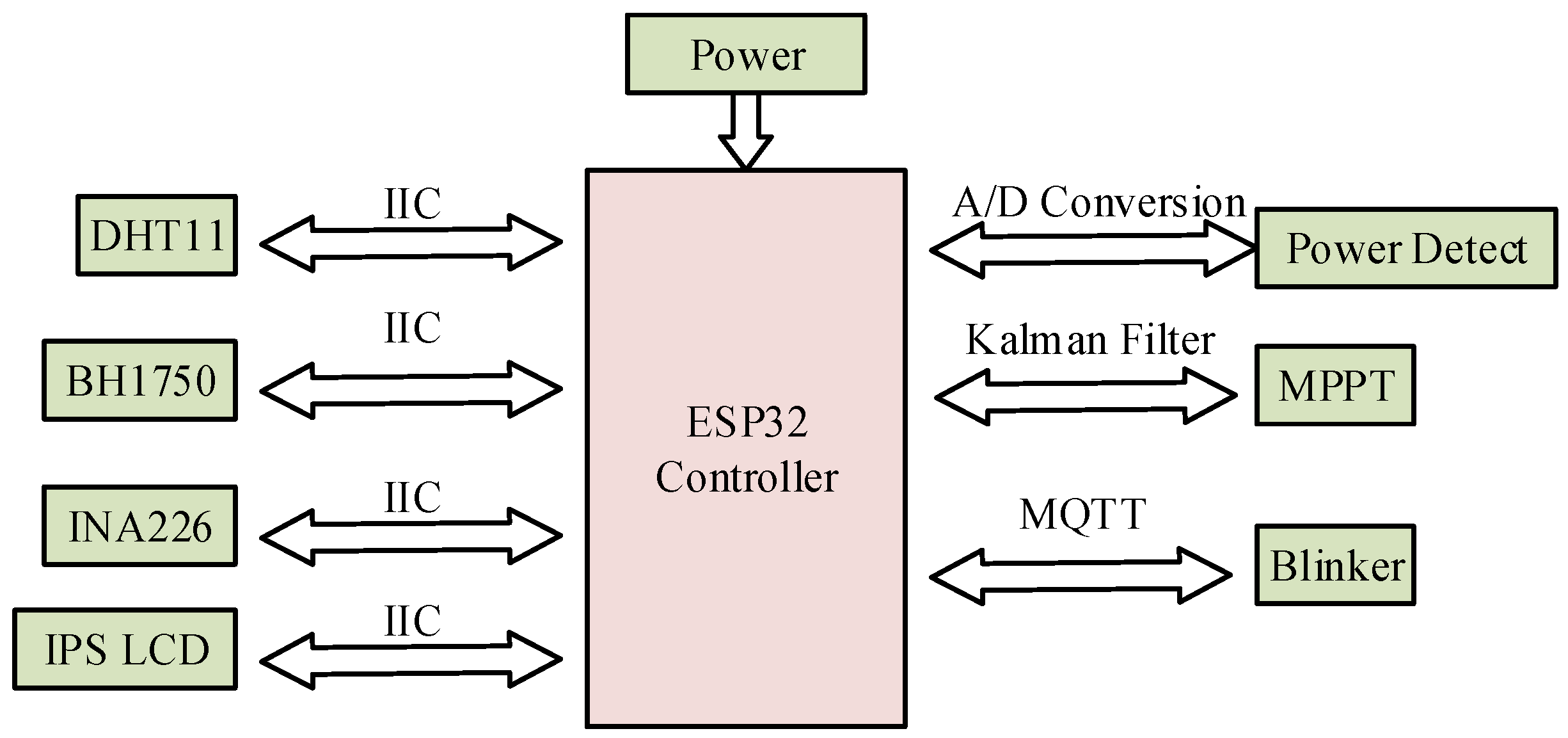
6. Hardware Circuit Design for MPPT Control
6.1. Hardware Circuit Overall Structure
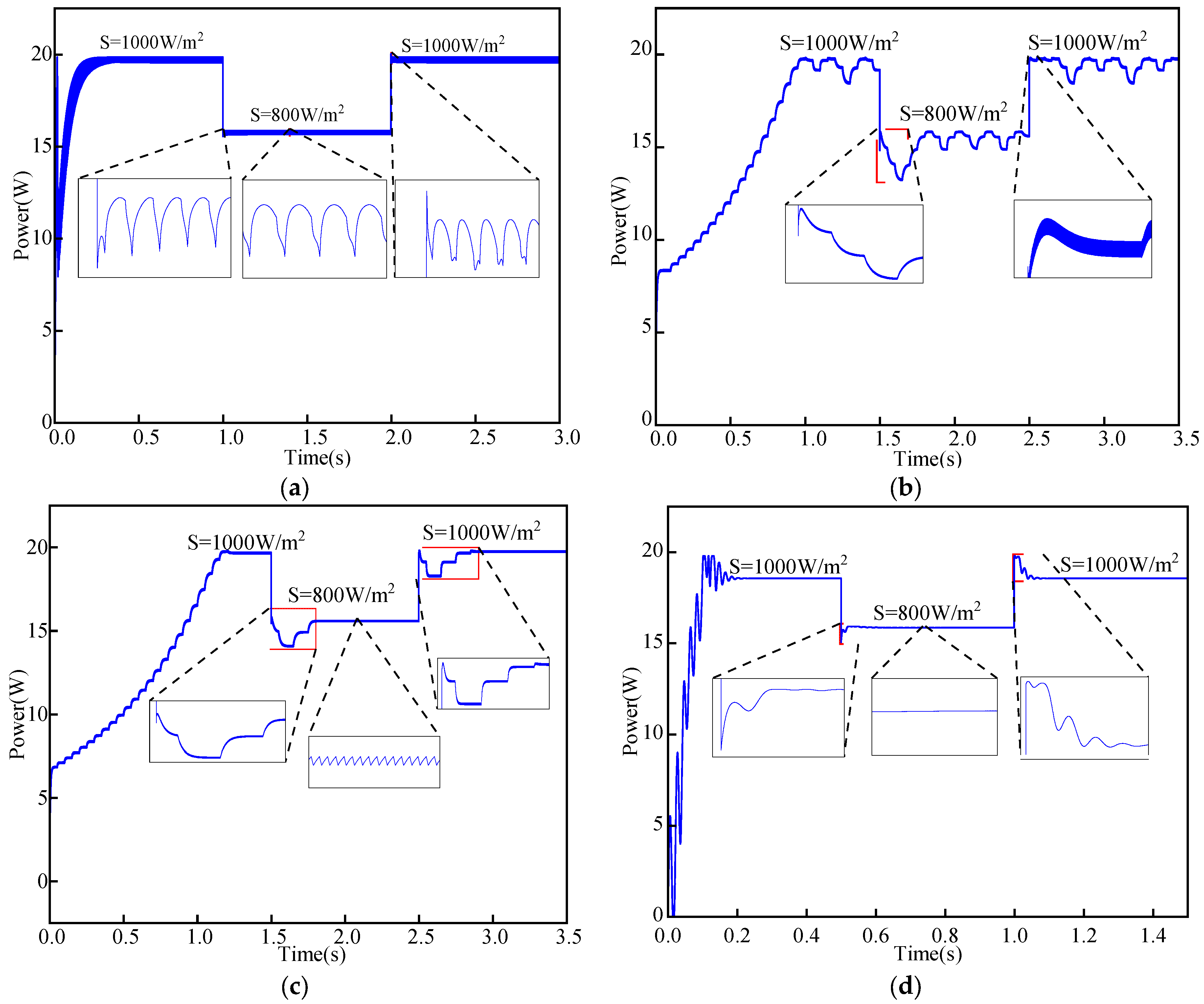
6.2. Analysis of Test Results
7. Conclusions
- (1)
- By examining the effect of environmental elements on the output properties of photovoltaic cells, it can be determined that the temperature has little effect and that the short-circuit current and open-circuit voltage of photovoltaic cells both increase with an increase in light intensity.
- (2)
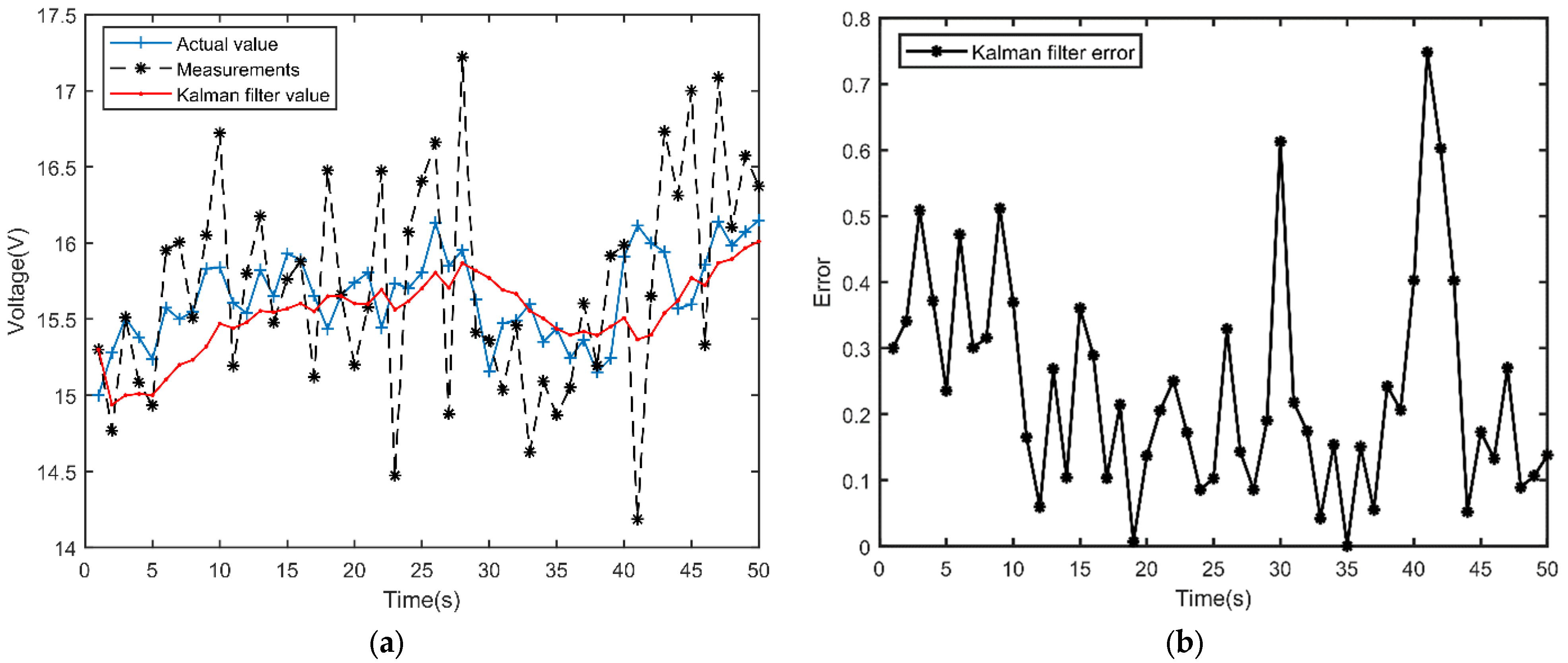
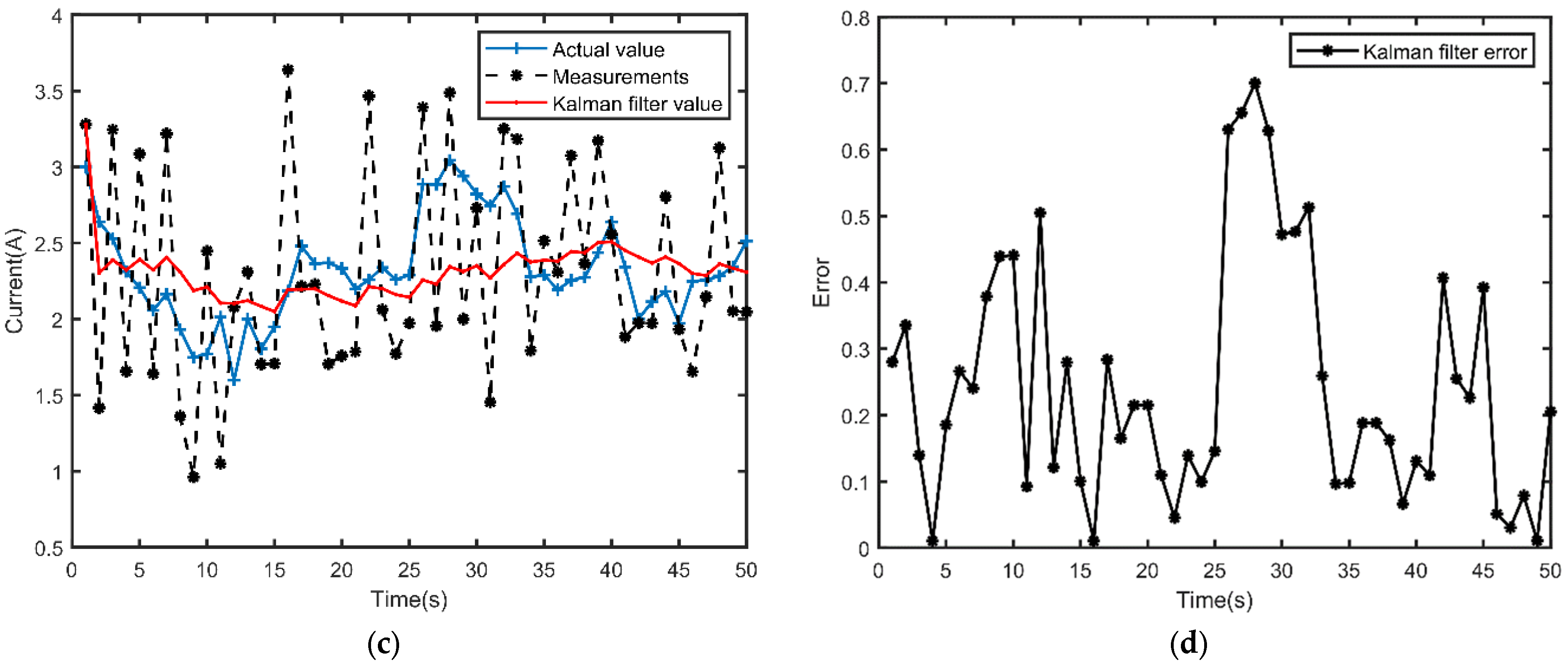
- The measurement error of the sensor can be decreased to 32% by utilizing the Kalman filtering technique to pre-process the output voltage and current of the photovoltaic cells. This significantly increases the steady-state accuracy of the MPPT control.
- (3)
- When Kalman filter parameters were adjusted, it was discovered that the output of the filter is strongly correlated with both the process noise covariance matrix (Q) and the measurement noise covariance matrix (R). When the value of Q increases, the dynamic response of the system becomes faster, but the convergence at stabilization becomes worse. When the value of R increases, the dynamic response of the system slows down, though the convergence stability of the system improves. In the process of parameter adjustment, the values of Q and R cannot be zero at the same time, and the output effect of Kalman filter is only related to the ratio of Q and R.
- (4)
- In calculating the disturbance step based on (24), there is no cyclic judgment condition, which largely improves the calculation speed of MPPT control. After physical testing, the photovoltaic MPPT control system designed in this paper has a tracking accuracy of 99.6% and low fabrication cost and fastest dynamic response time of 0.01 s in comparison to traditional MPPT control algorithms, which can meet the scenario of small power photovoltaic power generation applications.
- (5)
- In practical applications, the solar power system designed in this paper can be applied to street lights, unmanned boats and other scenarios that require power supply in the natural environment. The core of the MPPT control algorithm lies in the calculation of the perturbation step. In this paper, a three-stage perturbation step calculation method is proposed and verified, and the parameters of the perturbation step can be adjusted according to needs to meet particular design applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liao, C.Y.; Subroto, R.K.; Millah, I.S.; Lian, K.L.; Huang, W.T. An Improved Bat Algorithm for More Efficient and Faster Maximum Power Point Tracking for a Photovoltaic System Under Partial Shading Conditions. IEEE Access 2020, 8, 96378–96390. [Google Scholar] [CrossRef]
- Zinatloo-Ajabshir, S.; Morassaei, M.S.; Amiri, O.; Salavati-Niasari, M. Green synthesis of dysprosium stannate nanoparticles using Ficus carica extract as photocatalyst for the degradation of organic pollutants under visible irradiation. Ceram. Int. 2020, 46, 6095–6107. [Google Scholar] [CrossRef]
- Liu, B.; Sharma, M.; Yu, J.; Wang, L.; Shendre, S.; Sharma, A.; Izmir, M.; Delikanli, S.; Altintas, Y.; Dang, C.; et al. Management of electroluminescence from silver-doped colloidal quantum well light-emitting diodes. Cell Rep. Phys. Sci. 2022, 3, 100860. [Google Scholar] [CrossRef]
- Liu, K.C. Review on reliability assessment of smart distribution networks considering distributed renewable energy and energy storage. Electr. Meas. Instrum. 2021, 58, 1–11. [Google Scholar]
- Zhou, D.B. Maximum Power Point Tracking Strategy Based on Modified Variable Step-Size Incremental Conductance Algorithm. Power Syst. Technol. 2015, 39, 1491–1498. [Google Scholar]
- Cai, L. Test System for Power Generation Characteristics of Photovoltaic Modules Based on Real-Time Parameters. Laser Optoelectron. Prog. 2017, 54, 395–401. [Google Scholar]
- Xiao, Y.; Li, S.; Xu, M.; Feng, R. Research on the economy of implementing the MPPT for wind-solar hybrid power generation system: A review. In Proceedings of the 41st Chinese Control Conference, Hefei, China, 25–27 July 2022; pp. 2–7. [Google Scholar]
- Troudi, F.; Jouini, H.; Mami, A.; Ben Khedher, N.; Aich, W.; Boudjemline, A.; Boujelbene, M. Comparative Assessment between Five Control Techniques to Optimize the Maximum Power Point Tracking Procedure for PV Systems. Mathematics 2022, 10, 1080. [Google Scholar] [CrossRef]
- Owusu-Nyarko, I.; Elgenedy, M.A.; Abdelsalam, I.; Ahmed, K.H. Modified Variable Step-Size Incremental Conductance MPPT Technique for Photovoltaic Systems. Electronics 2021, 10, 2331. [Google Scholar] [CrossRef]
- Zhang, D. Research on photovoltaic maximum power point tracking strategy based on improved conductance increment method. J. Sol. Energy 2022, 43, 82–90. [Google Scholar]
- Hannachi, M.; Elbeji, O.; Benhamed, M.; Sbita, L. Comparative study of four MPPT for a wind power system. Wind. Eng. 2021, 45, 1613–1622. [Google Scholar] [CrossRef]
- Kumar, N.; Hussain, I.; Singh, B.; Panigrahi, B.K. Self-Adaptive Incremental Conductance Algorithm for Swift and Ripple-Free Maximum Power Harvesting from PV Array. IEEE Trans. Ind. Inform. 2018, 14, 2031–2041. [Google Scholar] [CrossRef]
- Li, X.; Xu, J. Maximum power point tracking control for grid-connected photovoltaic power generation system. Comput. Simul. 2019, 36, 117–121. [Google Scholar]
- Xu, J.; Wang, H. The hybrid control Maximum Power Point Tracking (MPPT) strategy based on incremental conductance method and improved particle swarm optimization algorithm. Renew. Energy Resour. 2019, 37, 824–831. [Google Scholar]
- Sheikh Ahmadi, S.H.; Karami, M.; Gholami, M.; Mirzaei, R. Improving MPPT Performance in PV Systems Based on Integrating the Incremental Conductance and Particle Swarm Optimization Methods. Iran. Sci. Technol. Trans. Electr. Eng. 2022, 46, 27–39. [Google Scholar] [CrossRef]
- Mi, D.; Hu, J.; Jian, Y. An improved slime mould algorithm based MPPT strategy for multi-peak photovoltaic system. Control Theory Appl. 2022, 39, 1–9. [Google Scholar]
- Ali, Z.M.; Alquthami, T.; Alkhalaf, S.; Norouzi, H.; Dadfar, S.; Suzuki, K. Novel hybrid improved bat algorithm and fuzzy system based MPPT for photovoltaic under variable atmospheric conditions. Sustain. Energy Technol. Assess. 2022, 52, 102156–102179. [Google Scholar] [CrossRef]
- Liu, C.; Sun, Y. Tracking Strategy of Maximum Power Point Based on Three-Stage Variable Step-Size Incremental Conductance Algorithm. Laser Optoelectron. Prog. 2018, 55, 420–426. [Google Scholar]
- Cui, Z. Research progress and prospects of photocatalytic devices with perovskite ferroelectric semiconductors. J. Phys. 2020, 69, 51–83. [Google Scholar] [CrossRef]
- Sabaripandiyan, D.; Sait, H.H.; Aarthi, G. A Novel Hybrid MPPT Control Strategy for Isolated Solar PV Power System. Intell. Autom. Soft Comput. 2022, 32, 1055–1070. [Google Scholar] [CrossRef]
- Senthilkumar, S.; Mohan, V.; Mangaiyarkarasi, S.P.; Karthikeyan, M. Analysis of Single-Diode PV Model and Optimized MPPT Model for Different Environmental Conditions. Int. Trans. Electr. Energy Syst. 2022, 2022, 4980843. [Google Scholar] [CrossRef]
- Annapoorani, S.; Jayaparvathy, R. Modified Seagull Optimization Algorithm based MPPT for augmented performance of Photovoltaic solar energy systems. Automatika 2022, 63, 286601. [Google Scholar]
- Sarwar, S.; Hafeez, M.A.; Javed, M.Y.; Asghar, A.B.; Ejsmont, K. A Horse Herd Optimization Algorithm (HOA)-Based MPPT Technique under Partial and Complex Partial Shading Conditions. Energies 2022, 15, 1880. [Google Scholar] [CrossRef]
- Zhang, J. Research on MPPT Algorithm of Photovoltaic Power Generation System Based on LabVIEW. J. Taiyuan Univ. Technol. 2018, 49, 477–482. [Google Scholar]
- Rui, Z.; Bo, Y.; Nuo, C. Arithmetic optimization algorithm based MPPT technique for centralized TEG systems under different temperature gradients. Energy Rep. 2022, 8, 2424–2433. [Google Scholar]
- Cao, D. Improved Ant Colony Optimization Algorithm for Multi-object Routing in Energy Harvesting Wireless Sensor Networks. J. Chin. Comput. Syst. 2021, 42, 1115–1120. [Google Scholar]
- Boghdady, T.A.; Kotb, Y.E.; Aljumah, A.; Sayed, M.M. Comparative Study of Optimal PV Array Configurations and MPPT under Partial Shading with Fast Dynamical Change of Hybrid Load. Sustainability 2022, 14, 2937. [Google Scholar] [CrossRef]
- Liang, C. Photovoltaic multi peak MPPT control based on Improved Particle Swarm Optimization. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 21–23 May 2022; pp. 389–394. [Google Scholar]
- Hussaian, B.C.; Matcha, M. A new design of transformerless, non-isolated, high step-up DC-DC converter with hybrid fuzzy logic MPPT controller. Int. J. Circuit Theory Appl. 2021, 50, 302–321. [Google Scholar]
- Guo, C. Fuzzy control based variable step conductance increment method for maximum power point tracking strategy. Mod. Electron. Tech. 2022, 45, 145–151. [Google Scholar]
- Pires, V.F.; Cordeiro, A.; Foito, D.; Silva, J.F. Control transition mode from voltage control to MPPT for PV generators in isolated DC microgrids. Int. J. Electr. Power Energy Syst. 2022, 137, 107876–107895. [Google Scholar] [CrossRef]
- Touhami, G.; Sliman, L.; Zohra, A.F.; Abdelkader, H.; Khalil, D. Extraction of Maximum Power of Organic Photovoltaic Generator Using MPPT Technique. Appl. Mech. Mater. 2022, 905, 1–6. [Google Scholar] [CrossRef]
- Villegas-Mier, C.G.; Rodriguez-Resendiz, J.; Álvarez-Alvarado, J.M.; Rodriguez-Resendiz, H.; Herrera-Navarro, A.M.; Rodríguez-Abreo, O. Artificial Neural Networks in MPPT Algorithms for Optimization of Photovoltaic Power Systems: A Review. Micromachines 2021, 12, 1260. [Google Scholar] [CrossRef] [PubMed]
- Pradhan, C.; Senapati, M.K.; Ntiakoh, N.K.; Calay, R.K. Roach Infestation Optimization MPPT Algorithm for Solar Photovoltaic System. Electronics 2022, 11, 927. [Google Scholar] [CrossRef]
- Sousa, S.M.; Gusman, L.S.; Lopes TA, S.; Pereira, H.A.; Callegari, J.M.S. MPPT algorithm in single loop current-mode control applied to dc–dc converters with input current source characteristics. Int. J. Electr. Power Energy Syst. 2022, 138, 107909–107927. [Google Scholar] [CrossRef]
- Awan, M.M.A.; Javed, M.Y.; Asghar, A.B.; Ejsmont, K. Performance Optimization of a Ten Check MPPT Algorithm for an Off-Grid Solar Photovoltaic System. Energies 2022, 15, 2104. [Google Scholar] [CrossRef]
- Li, S. Research on Internet of Things Acquisition System in Greenhouse Based on the Improved Kalman Data Fusion Algorithm. Chin. J. Sens. Actuators 2022, 35, 558–564. [Google Scholar]
- Dong, Z. A new state monitoring method for IoT sensor based on Kalman filter algorithm. Int. J. Auton. Adapt. Commun. Syst. 2021, 13, 448–463. [Google Scholar] [CrossRef]
- Wang, E.; Xiao, L.; Han, X.; Tan, B.; Luo, L. Design of an Agile Training System Based on Wireless Mesh Network. IEEE Access 2022, 529, 84302–84316. [Google Scholar] [CrossRef]
- Tan, B.; Wang, E.; Cao, K.; Xiao, L.; Luo, L. Study and Design of Distributed Badminton Agility Training and Test System. Appl. Sci. 2023, 13, 1113. [Google Scholar] [CrossRef]
- Zhang, Z. Design of home intelligent elderly care monitoring system. Mod. Electron. Tech. 2022, 45, 171–176. [Google Scholar]
- Peng, D.C. Basic Principle and Application of Kalman Filter. Softw. Guide 2009, 8, 32–34. [Google Scholar]
- Osman, H.H.; Ismail, I.A.; Morsy, E.; Hawidi, H.M. Implementing the Kalman Filter Algorithm in Parallel Form: Denoising Sound Wave as a Case Study. Recent Adv. Comput. Sci. Commun. 2021, 14, 2828–2835. [Google Scholar] [CrossRef]
- Liu, F. Kalman filter based method for processing small noisy sample data. J. Shanghai Univ. (Nat. Sci. Ed.) 2022, 28, 427–439. [Google Scholar]
- Yuan, S.; Shengyuan, Y.; Yanxia, S. A Wind Speed Prediction Model Based on ARIMA and Improved Kalman Filter Algorithm. J. Phys. Conf. Ser. 2020, 1650, 032095. [Google Scholar] [CrossRef]
- Tan, B.; You, W.; Tian, S.; Xiao, T.; Wang, M.; Zheng, B.; Luo, L. Soil Nitrogen Detection Based on Random Forest Algorithm and Near-Infrared Spectroscopy. Sensors 2022, 22, 8013. [Google Scholar] [CrossRef] [PubMed]
- Tan, B.; You, W.; Huang, C.; Xiao, T.; Tian, S.; Luo, L.; Xiong, N. An Intelligent Near-Infrared Diffuse Reflectance Spectroscopy Scheme for the Non-Destructive Testing of the Sugar Content in Cherry Tomato Fruit. Electronics 2022, 11, 3504. [Google Scholar] [CrossRef]
- Cai, Z.D.; Xu, J.Y.; Sun, X.Y.; Di Quan, L. SOC Estimation of Modular Lithium Battery Pack Based on Adaptive Kalman Filter Algorithm. J. Phys. Conf. Ser. 2019, 1345, 1. [Google Scholar] [CrossRef]
- You, D.; Liu, P.; Shang, W.; Zhang, Y.; Kang, Y.; Xiong, J. An Improved Unscented Kalman Filter Algorithm for Radar Azimuth Mutation. Int. J. Aerosp. Eng. 2020, 2020, 8863286. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Ji, Y.; Zhang, Z.; Cao, R.; Chen, B.; Li, H.; Yin, Y. Agricultural machinery GNSS/IMU-integrated navigation based on fuzzy adaptive finite impulse response Kalman filtering algorithm. Comput. Electron. Agric. 2021, 191, 106524–106543. [Google Scholar] [CrossRef]








| Symbol | Quantity | Units |
|---|---|---|
| tref | Ambient temperature under STC | °C |
| Sref | Light intensity under STC | W/m2 |
| Isc | Short Circuit Current | A |
| Uoc | Open Circuit Voltage | V |
| a | 0.00255 | °C |
| b | 0.5 | \ |
| c | 0.00288 | °C |
| Symbol | Quantity |
|---|---|
| A | State shift matrix |
| B | Input control matrix |
| H | Observational model matrix |
| Pk | Error covariance matrix |
| Q | Process noise covariance matrix |
| R | Measurement noise covariance matrix |
| I | Unit matrix |
| K | Kalman gain |
| - | represents the priori value |
| ^ | represents the estimated value |
| Parameters | Values |
|---|---|
| Maximum Power | 19.8 W |
| Open circuit voltage (Voc) | 21.6 V |
| Short-circuit current (Isc) | 1.2 A |
| Voltage at maximum power point (Vmp) | 18 V |
| Current at maximum power point (Imp) | 1.1 A |
| Filter Capacitor (C) | 47 uF |
| Load resistance (R) | 1 K |
| Power Inductor (L) | 6.8 uH |
| Response Time | |||
|---|---|---|---|
| MPPT Algorithms | Start-up time | Light reduction | Light increase |
| Constant voltage method | 0.1 | 0.005 | 0.004 |
| Perturbation observation method | 1.02 | 0.25 | 0.19 |
| Constant step conductance increment method | 1.2 | 0.28 | 0.35 |
| Improved MPPT algorithms | 0.12 | 0.01 | 0.06 |
| MPPT Algorithms | 800 W/m2 | 1000 W/m2 | Tracking Accuracy |
|---|---|---|---|
| Constant voltage method | 15.76 | 19.69 | 96.5% |
| Perturbation observation method | 15.35 | 19.08 | 86.7% |
| Constant step conductance increment method | 15.59 | 19.77 | 97.5% |
| Improved MPPT algorithms | 15.85 | 19.78 | 99.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Y.; Chen, Z.; Cheng, H.; Wang, E.; Tan, B. An Efficient Variable Step Solar Maximum Power Point Tracking Algorithm. Energies 2023, 16, 1299. https://doi.org/10.3390/en16031299
Meng Y, Chen Z, Cheng H, Wang E, Tan B. An Efficient Variable Step Solar Maximum Power Point Tracking Algorithm. Energies. 2023; 16(3):1299. https://doi.org/10.3390/en16031299
Chicago/Turabian StyleMeng, Yang, Zunliang Chen, Hui Cheng, Enpu Wang, and Baohua Tan. 2023. "An Efficient Variable Step Solar Maximum Power Point Tracking Algorithm" Energies 16, no. 3: 1299. https://doi.org/10.3390/en16031299
APA StyleMeng, Y., Chen, Z., Cheng, H., Wang, E., & Tan, B. (2023). An Efficient Variable Step Solar Maximum Power Point Tracking Algorithm. Energies, 16(3), 1299. https://doi.org/10.3390/en16031299






