Enhanced Control Designs to Abate Frequency Oscillations in Compensated Power System
Abstract
:1. Introduction
2. System Modeling
3. Control Design
3.1. Particle Swarm Optimization
- Position (x): It determines the location of the ith member in the tth run of the algorithm.
- Velocity (v): It gives the direction and length of the ith member in the tth run of the algorithm.
- Personal best (): is the ith particle’s best location up to this point.
3.2. Fuzzy Logic Controller
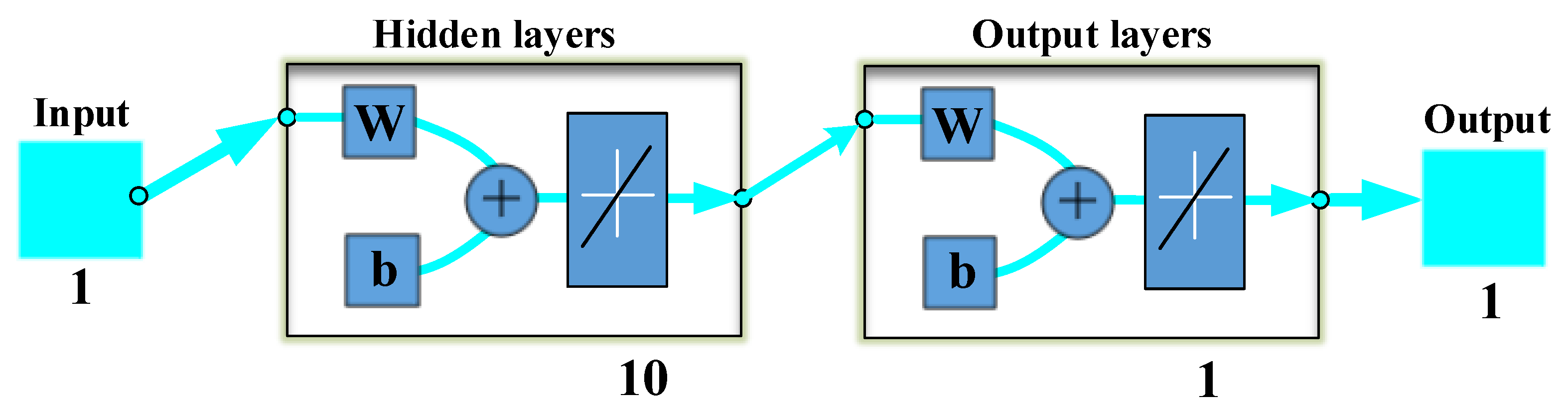
3.3. Neural Network
- Input layer: These input layers/nodes receive information from the outside world and pass it to a hidden layer.
- Hidden layers: These sets of neurons perform all the computation on input data. Each hidden layer is specialized to produce a particular output for purposeful results.
- Output layers: There can be single or multiple nodes in an output layer. These receive hidden layers and perform the calculation via its neurons, and then, the output is computed.
4. Results
4.1. Case 1: Two-Area Power System with Solar Alone
4.2. Case 2: Two-Area Power System with EV Alone
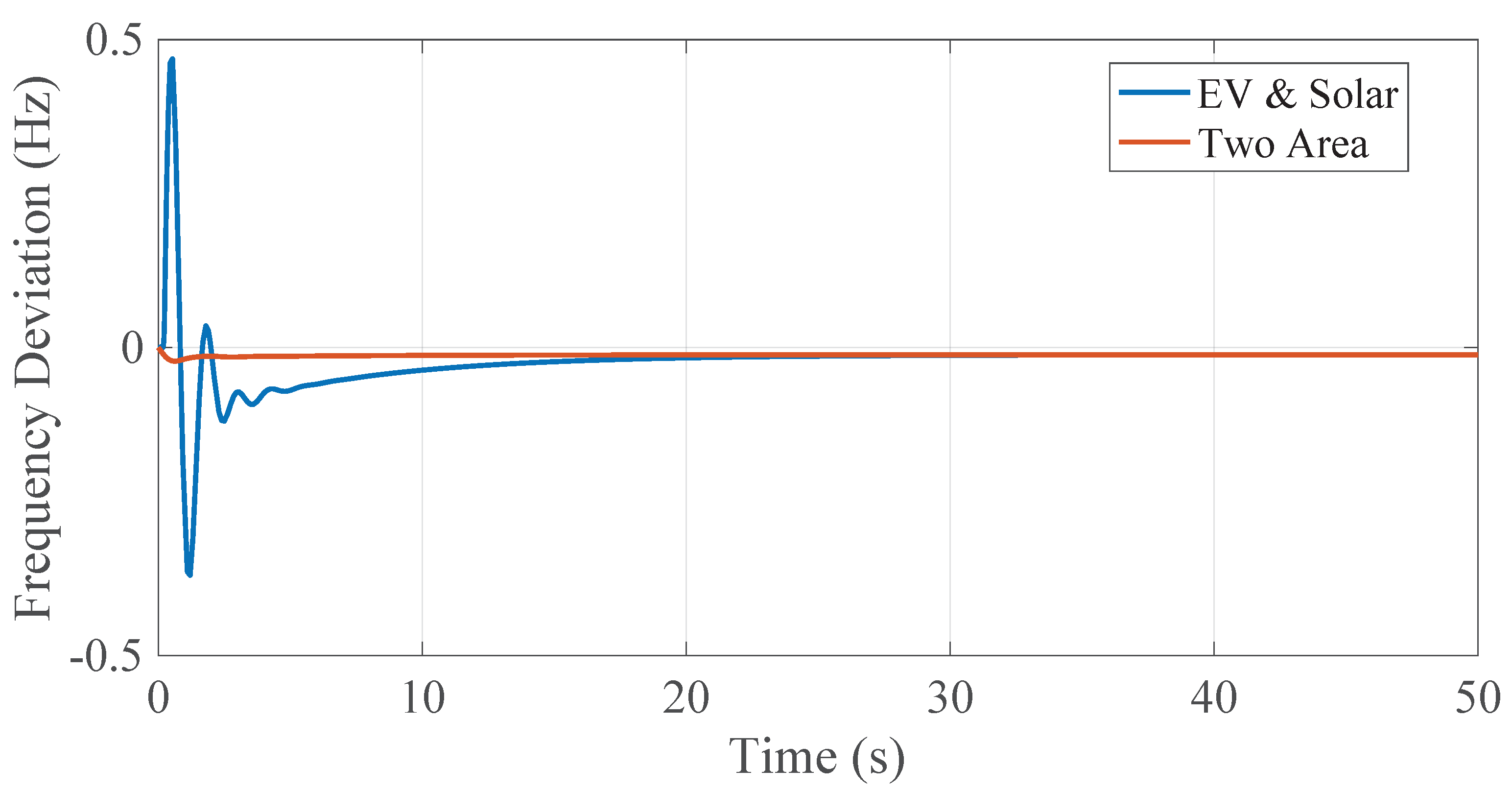
4.3. Case 3: Two-Area Power System with Solar and EV
4.3.1. SSSC Based System
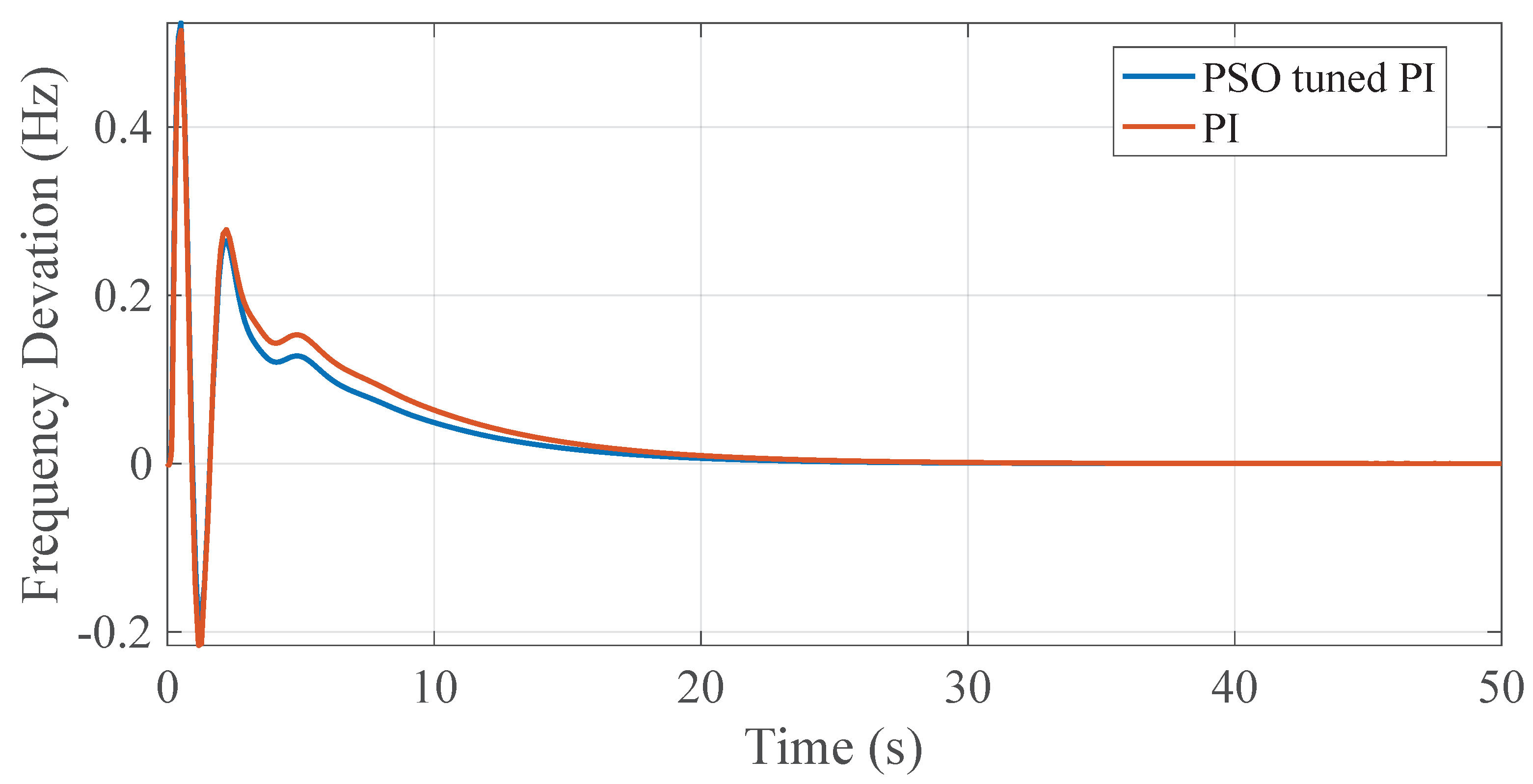
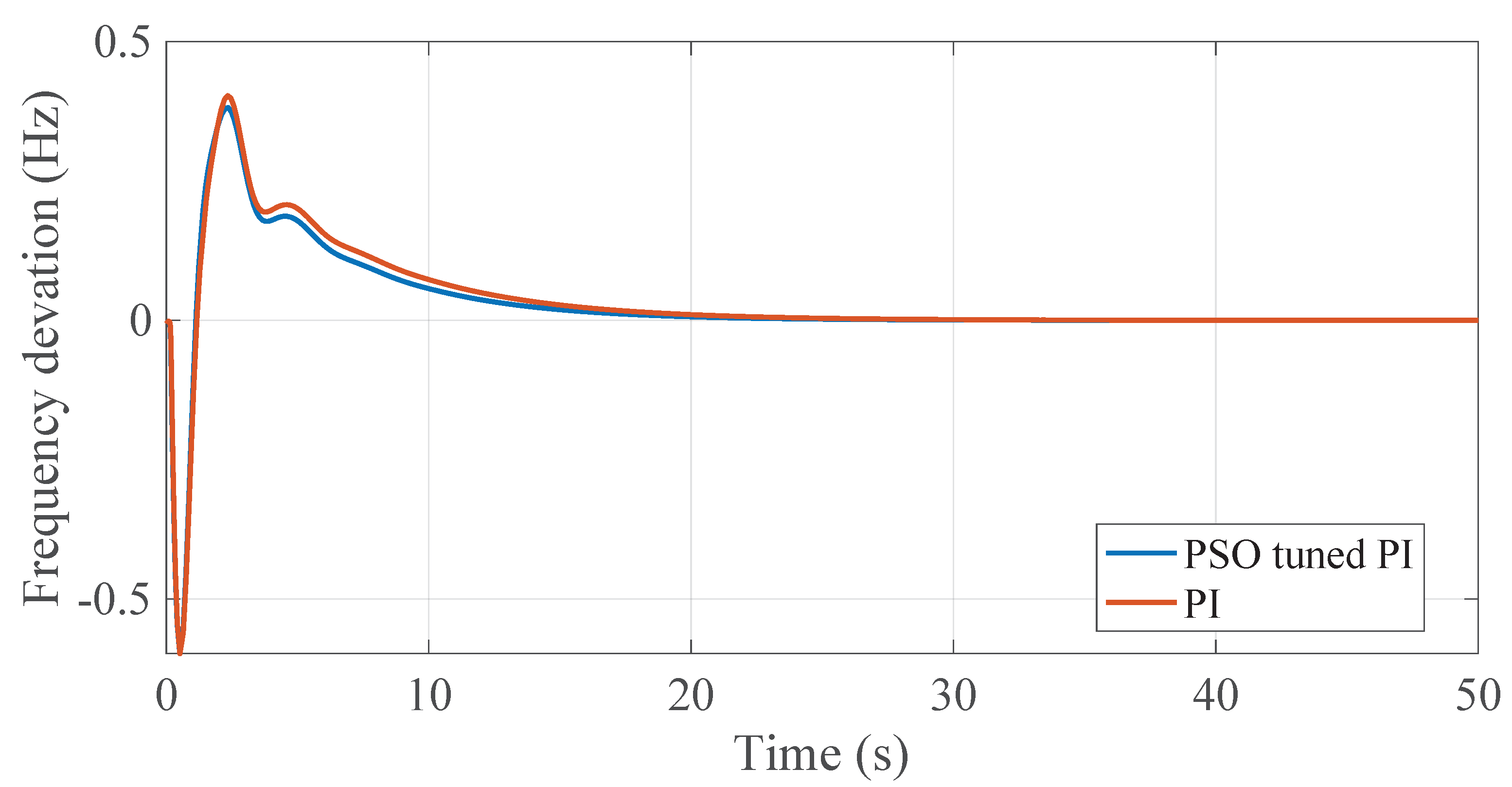
4.3.2. PSO-Tuned PI and Conventional PI
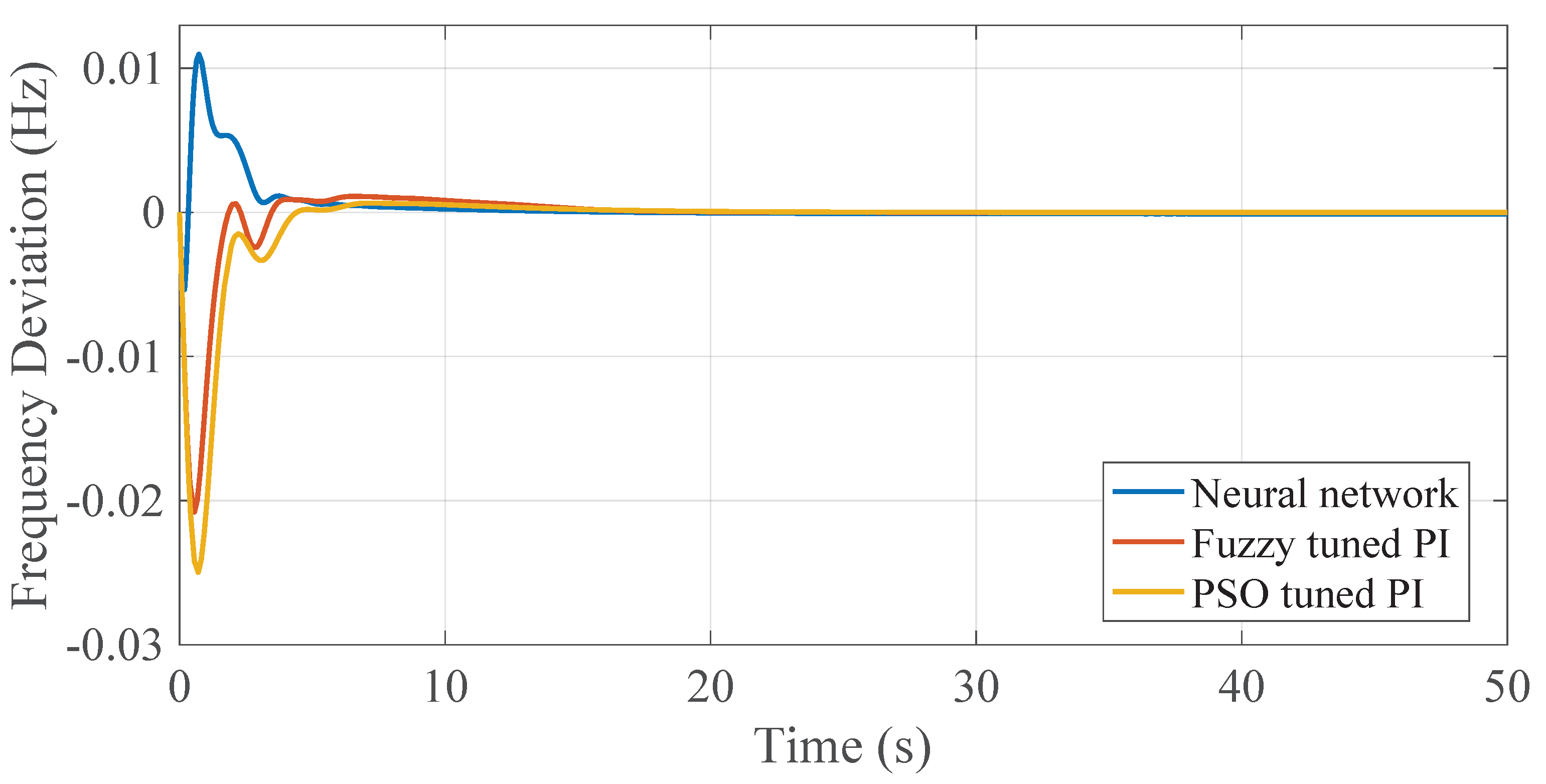
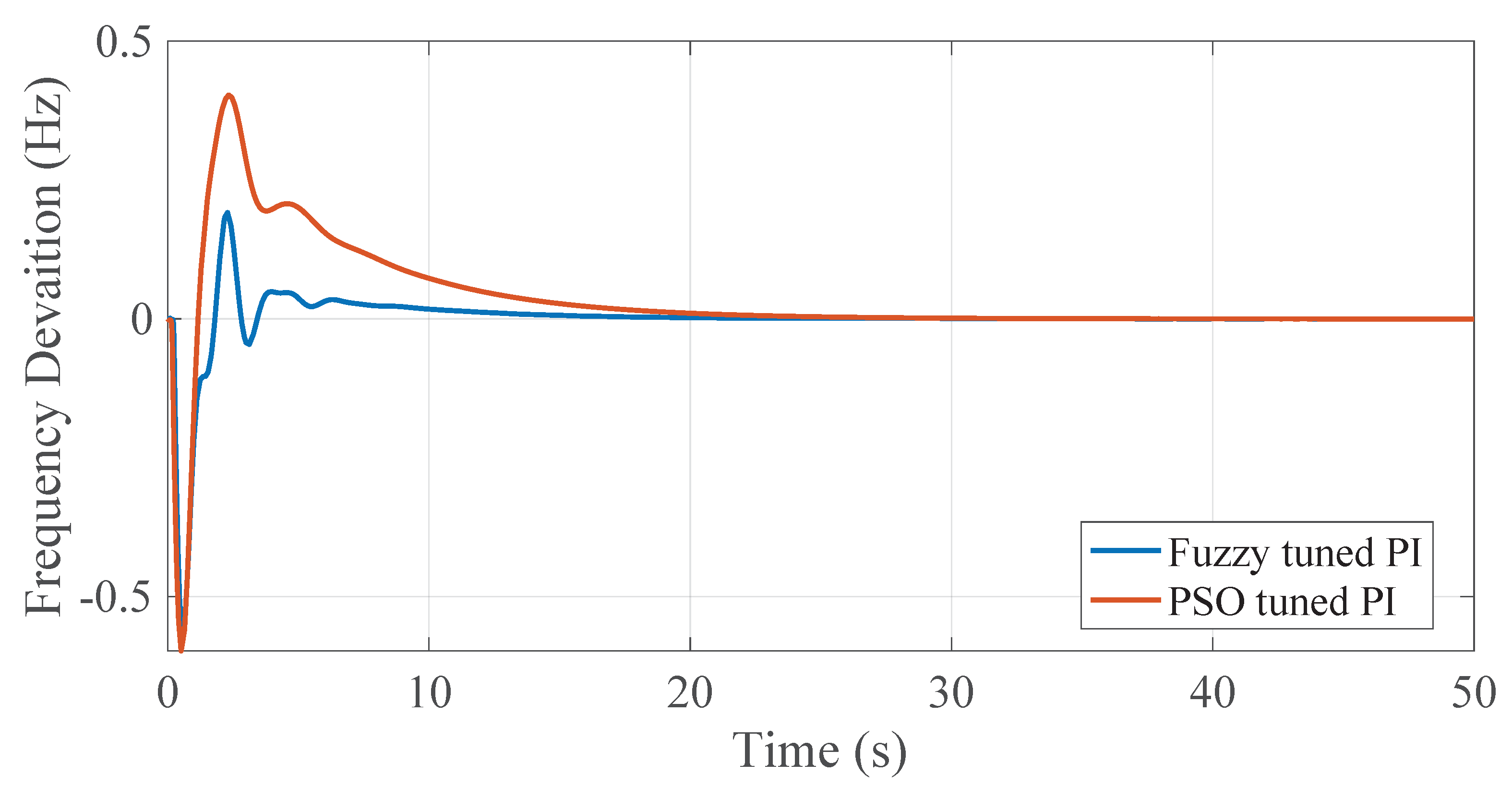
4.3.3. Comparative Analysis of Fuzzy-Tuned PI and PSO-Tuned PI
4.3.4. Fuzzy-Tuned PI and Neural Network
4.4. Comparison between Neural Network, Fuzzy-Tuned PI and PSO-Tuned PI
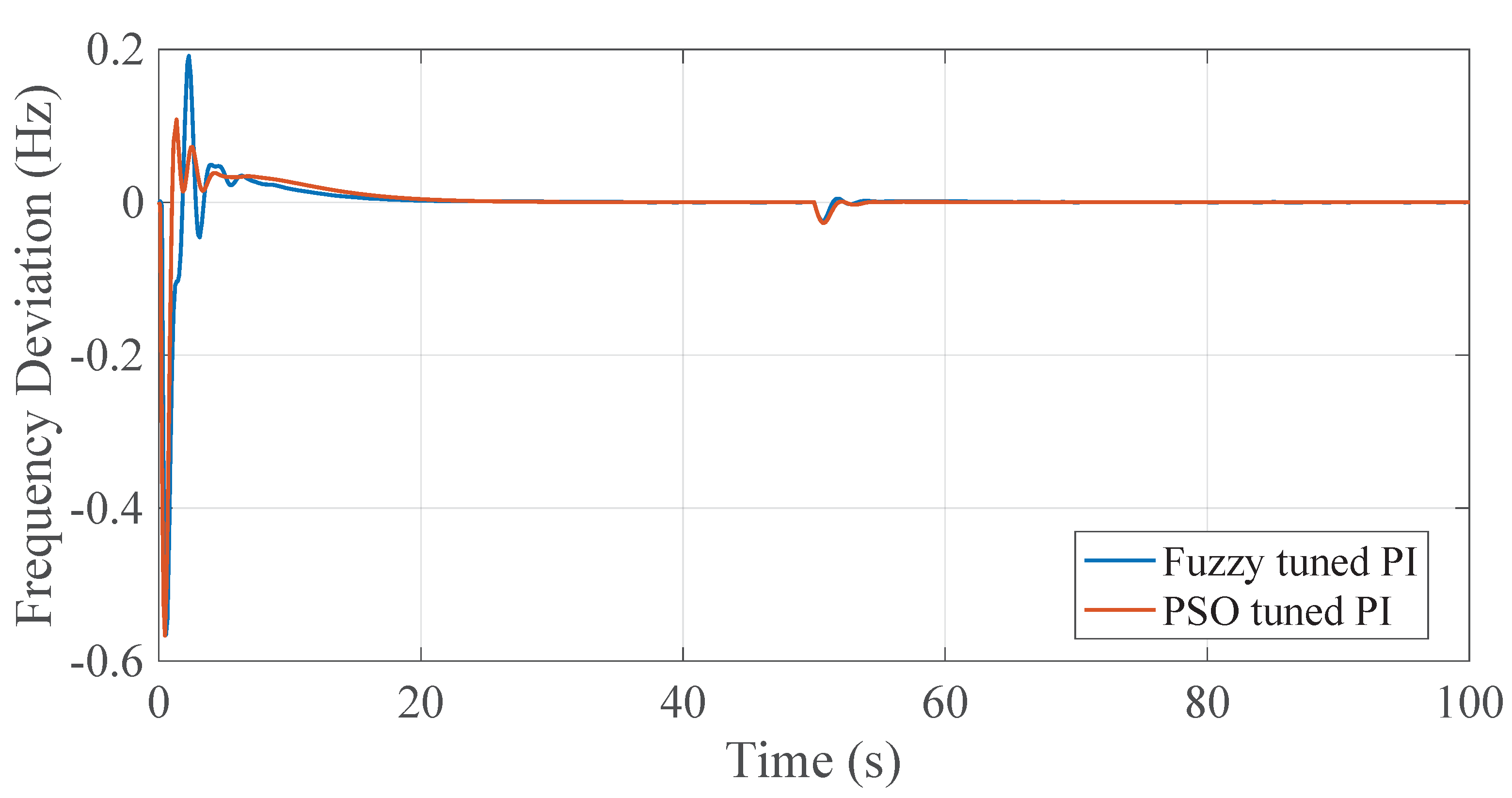
4.5. Disturbance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ACE | Area control error |
| AGC | Automatic generation control |
| DB | Dead band |
| EV | Electrical vehicle |
| FACTS | Flexible AC transmission system |
| FLC | Fuzzy logic controller |
| LFC | Load frequency control |
| NN | Neural network |
| PI | Proportional Integral |
| PSO | Particle swarm optimization |
| PV | Photovoltaic |
| SOC | State of charge |
| SSSC | Static synchronous series compensator |
| Symbols | |
| b | bias linked to neuron |
| k | iteration number |
| Derivative component | |
| integral component | |
| Proportional component | |
| inputs to neural network | |
| Acceleration constants | |
| random values whose values lie between 0 and 1 | |
| Velocity of ith particle | |
| W | Weighted input |
| w | Inertia weight factor |
| Position of ith particle |
References
- Kothari, D.P.; Nagrath, I.J. Modern Power System Analysis; McGraw Hill: New York, NY, USA, 2003. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Bevrani, H. Robust Power System Control; Springer International Pulbishing: Cham, Switzerland, 2014. [Google Scholar]
- Umrao, R.; Kumar, S.; Mohan, M.; Chaturvedi, D.K. Load Frequency Control methodologies for power system. In Proceedings of the 2nd International Conference on Power, Control and Embedded Systems, Allahabad, India, 17–19 December 2012; pp. 1–10. [Google Scholar]
- Guven, A.F.; Samy, M.M. Performance Analysis of Autonomous Green Energy System Based on Multi and Hybrid Metaheuristic Optimization Approaches. Energy Convers. Manag. J. 2022, 269, 116058. [Google Scholar] [CrossRef]
- Saadat, H. Power System Analysis; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Rajan, R.; Fernandez, F.M. Impact of Increased Penetration of Photovoltaic Sources on Small-Signal Stability of Hybrid and Multi-area Power Systems. In Proceedings of the 2019 Innovations in Power and Advanced Computing Technologies (i-PACT), Vellore, India, 22–23 March 2019; pp. 1–6. [Google Scholar]
- Barakat, S.; Emam, A.; Samy, M.M. Investigating grid-connected green power systems’ energy storage solutions in the event of frequent blackouts. Energy Rep. 2022, 10, 5177–5191. [Google Scholar] [CrossRef]
- Arora, K.; Kumar, A.; Kamboj, V.K. Automatic Generation Control and Load Frequency Control: A Comprehensive Review; Springer: Berlin/Heidelberg, Germany, 2019; Volume 553, pp. 449–456. [Google Scholar]
- Alhelou, H.H.; Hamedani-Golshan, M.E.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies 2018, 11, 2497. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-Y.; Kim, H.-M.; Kim, S.-K.; Jeon, J.-H.; Choi, H.-K. Designing an Energy Storage System Fuzzy PID Controller for Microgrid Islanded Operation. Energies 2011, 4, 1443–1460. [Google Scholar] [CrossRef] [Green Version]
- Syan, S.; Biswal, G.R. Frequency control of an isolated hydro power plant using artificial intelligence. In Proceedings of the IEEE Workshop on Computational Intelligence: Theories, Applications and Future Directions (WCI), Kanpur, India, 14–17 December 2015; pp. 1–5. [Google Scholar]
- Al-Majidi, S.D.; Kh. AL-Nussairi, M.; Mohammed, A.J.; Dakhil, A.M.; Abbod, M.F.; Al-Raweshidy, H.S. Design of a Load Frequency Controller Based on an Optimal Neural Network. Energies 2022, 15, 6223. [Google Scholar] [CrossRef]
- Samy, M.M.; Almamlook, R.E.; Elkhouly, H.I.; Barakat, S.T. Design Decision-Making and Optimal Design of Green Energy System Based on Statistical Methods and Artificial Neural Network Approaches. Sustain. Cites Soc. J. 2022, 84, 104015. [Google Scholar] [CrossRef]
- Verma, R.; Pal, S. Intelligent Automatic Generation Control of Two-Area Hydrothermal Power System Using ANN and Fuzzy Logic. In Proceedings of the 2013 International Conference on Communication Systems and Network Technologies, Tiruchengode, India, 4–6 July 2013; pp. 552–556. [Google Scholar]
- Mokhtara, C.; Negrou, B.; Settou, N.; Settou, B.; Samy, M.M. Design Optimization of Off-grid Hybrid Renewable Energy Systems Considering the Effects of Building Energy Performance and Climate Change: Case Study of Algeria Energy. Energy 2021, 219, 119605. [Google Scholar] [CrossRef]
- FatiGüven, A.; Yörükeren, N.; Samy, M.M. Design optimization of a stand-alone green energy system of university campus based on Jaya-Harmony Search and Ant Colony Optimization algorithms approaches. Energy 2022, 253, 124089. [Google Scholar]
- Kouba, N.E.Y.; Menaa, M.; Hasni, M.; Boudour, M. Load Frequency Control in multi-area power system based on Fuzzy Logic-PID Controller. In Proceedings of the IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 17–19 August 2015; pp. 1–6. [Google Scholar]
- Balamurugan, C.R. Three area power system load frequency control using fuzzy logic controller. Int. J. Appl. Power Eng. 2018, 7, 18–26. [Google Scholar] [CrossRef]
- Yang, J.; Zeng, Z.; Tang, Y.; Yan, J.; He, H.; Wu, Y. Load Frequency Control in Isolated Micro-Grids with Electrical Vehicles Based on Multivariable Generalized Predictive Theory. Energies 2015, 8, 2145–2164. [Google Scholar] [CrossRef]
- Ranjan, M.; Shanka, R. A literature survey on load frequency control considering renewable energy integration in power system: Recent trends and future prospects. J. Energy Storage 2022, 45, 103717. [Google Scholar] [CrossRef]
- Debbarma, S.; Dutta, A. Utilizing Electric Vehicles for LFC in Restructured Power Systems Using Fractional Order Controller. IEEE Trans. Smart Grid 2017, 8, 2554–2564. [Google Scholar] [CrossRef]
- Liu, H.; Huang, K.; Yang, Y.; Wei, H.; Ma, S. Real-time vehicle-to-grid control for frequency regulation with high frequency regulating signal. Prot. Control Mod. Power Syst. 2018, 3, 1–8. [Google Scholar] [CrossRef]
- Liu, F.; Song, Y.H.; Ma, J.; Mei, S.; Lu, Q. Optimal load-frequency control in restructured power systems. IET Proc. Gener. Transm. Distrib. 2003, 150, 87–95. [Google Scholar] [CrossRef]
- Samy, M.M.; Emam, A.; Tag-Eldin, E.; Barakat, S. Exploring energy storage methods for grid-connected clean power plants in case of repetitive outages. J. Energy Storage 2022, 54, 5177–5191. [Google Scholar] [CrossRef]
- Sumarmad, K.A.A.; Sulaiman, N.; Wahab, N.I.A.; Hizam, H. Energy Management and Voltage Control in Microgrids Using Artificial Neural Networks, PID, and Fuzzy Logic Controllers. Energies 2022, 15, 303. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. PSS and TCSC Damping Controller Coordinated Design Using GSA. Energy Procedia 2012, 14, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping Controller Design for Power System Oscillations Using Hybrid GA-SQP. Int. Rev. Electr. Eng. 2012, 6, 888–896. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Optimal location of PSS using improved PSO with chaotic sequence. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Kuantan, Malaysia, 21–22 June 2011; pp. 253–258. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A. Optimization and Coordination of Damping Controls for Optimal Oscillations Damping in Multi-Machine Power System. Int. Rev. Electr. Eng. 2011, 6, 1984–1993. [Google Scholar]
- Divya, K.C.; Rao, P.S.N. A simulation model for AGC studies of hydro-hydro systems. Int. J. Electr. Power Energy Syst. 2005, 27, 335–342. [Google Scholar] [CrossRef]
- Sabahi, K.; Sharifi, A.; Aliyari Shoorehdeli, M.; Teshnehlab, M.; Aliasghary, M. Load frequency control in interconnected power system using multi-objective PID controller. In Proceedings of the 2008 IEEE Conference on Soft Computing in Industrial Applications. International Conference on Control, Muroran, Japan, 25–27 June 2008; pp. 217–221. [Google Scholar]
- Mover, W.G.P.; Supply, E. Hydraulic turbine and turbine control models for system dynamic studies. IEEE Trans. Power Syst. 1992, 7, 167–179. [Google Scholar]
- IEEE Power Energy Society. Dynamic Models for Turbine Governors in Power System Studies; Technical Report PES-TR1i; IEEE Power Energy Society: New York, NY, USA, 2013. [Google Scholar]
- Prakash, S.; Sinha, S.K. Four area Load Frequency Control of interconnected hydro-thermal power system by Intelligent PID control technique. In Proceedings of the Students Conference on Engineering and Systems, Allahabad, India, 16–18 March 2012; pp. 1–6. [Google Scholar]
- Farooq, Z.; Rahman, A.; Lone, S.A. Load frequency control of multi-source electrical power system integrated with solar-thermal and electric vehicle. Int. Trans. Electr. Energy Syst. 2021, 31, e12918. [Google Scholar] [CrossRef]
- Izadkhast, S.; Garcia-Gonzalez, P.; Frías, P. An aggregate model of plug-in electric vehicles including distribution network characteristics for primary frequency control. IEEE Trans. Power Syst. 2015, 30, 2987–2998. [Google Scholar] [CrossRef]
- Prasad, B.; Prasad, C.D.; Kumar, G.P. Effect of load parameters variations on AGC of single area thermal power system in presence of integral and PSO-PID controllers. In Proceedings of the 2015 Conference on Power, Control, Communication and Computational Technologies for Sustainable Growth (PCCCTSG), Kurnool, India, 11–12 December 2015; pp. 64–688. [Google Scholar]
- Rao, R.N.; Reddy, P.K. PSO based tuning of PID controller for a Load frequency control in two area power system. Int. J. Eng. Res. Appl. 2015, 1, 1499–1505. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Ghatuari, I.; Mishra, N.; Sahu, B.K. Performance analysis of automatic generation control of a two area interconnected thermal system with nonlinear governor using PSO and DE algorithm. In Proceedings of the International Conference on Energy Efficient Technologies for Sustainability, Nagercoil, India, 10–12 April 2013; pp. 1262–1266. [Google Scholar]
- Sreenath, A.; Atre, Y.R.; Patil, D.R. Two area load frequency control with fuzzy gain scheduling of PI controller. In Proceedings of the First International Conference on Emerging Trends in Engineering and Technology, Nagpur, India, 16–18 July 2008. [Google Scholar]
- Jain, S.K.; Bhargava, A.; Pal, R.K. Three area power system load frequency control using fuzzy logic controller. In Proceedings of the 2015 International Conference on Computer, Communication and Control (IC4), Indore, India, 10–12 September 2015; pp. 1–6. [Google Scholar]
- Kamarposhti, M.A.; Shokouhandeh, H.; Alipur, M.; Colak, I.; Zare, H.; Eguchi, K. Optimal Designing of Fuzzy-PID Controller in the Load-Frequency Control Loop of Hydro-Thermal Power System Connected to Wind Farm by HVDC Lines. IEEE Access 2022, 10, 63812–63822. [Google Scholar] [CrossRef]
- Yousuf, V.; Ahmad, A. Optimal design and application of fuzzy logic equipped control in STATCOM to abate SSR oscillations. Int. J. Circuit Theory Appl. 2021, 49, 4070–4087. [Google Scholar] [CrossRef]
- Lone, A.H.; Yousuf, V.; Prakash, S.; Bazaz, M.A. Load Frequency Control of Two Area Interconnected Power System using SSSC with PID, Fuzzy and Neural Network Based Controllers. In Proceedings of the 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 108–113. [Google Scholar]
- Prakash, S.; Sinha, S.K. Application of artificial intelligence in load frequency control of interconnected power system. Int. J. Eng. Sci. Technol. 2011, 3, 264–275. [Google Scholar] [CrossRef]


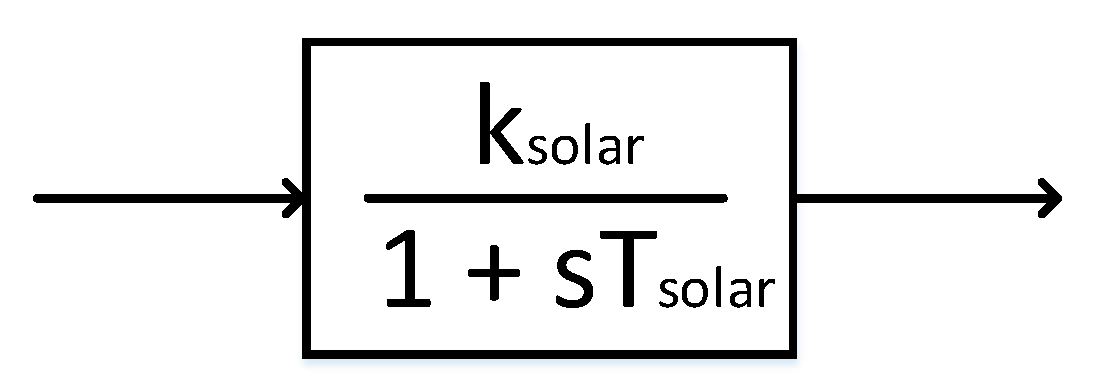



















| Parameters | Values | |
|---|---|---|
| Area 1 | K, , , | 1, 1, 120, 0.0866 0.08 s, 0.3 s, 20 s, 0.425, −2.4 |
| Area 2 | 1, 1, 120 0.08 s, 0.3 s, 20 s, 5 s, 10 s 0.425, −2.4 | |
| SSSC | 0.2035 0.03 s | |
| Electrical Vehicle | 0.24, 1 1 s 1000 | |
| Solar | 1.8 1.8 s |
| A,B | VS | S | Z | B | VB |
|---|---|---|---|---|---|
| VS | S | S | M | M | VB |
| S | S | M | M | VB | VB |
| Z | M | M | VB | VB | VVB |
| B | M | VB | VB | VVB | VVB |
| VB | VB | VB | VVB | VVB | S |
| Controller | Settling Time (s) | Maximum Overshoot/ Undershoot (Hz) | SSD | |||
|---|---|---|---|---|---|---|
| Area 1 | Area 2 | Area 1 | Area 2 | Area 1 | Area 2 | |
| Uncompensated | 31 | 25 | 0.022 | 0.022 | 0.013 | 0.013 |
| Proportional-Integal | 28 | 28 | 0.0008 | 0.001 | 0 | 0 |
| PSO | 19 | 15 | 0.00065 | 0.0025 | 0 | 0 |
| Neural Network | 8 | 7 | 0.0005 | 0.0012 | 0 | 0 |
| FLC | 18 | 14 | 0.0012 | 0.005 | 0 | 0 |
| Controller | Settling Time (s) | Maximum Overshoot/Undershoot (Hz) | ||
|---|---|---|---|---|
| Area 1 | Area 2 | Area 1 | Area 2 | |
| PSO | 23 | 22 | 0.5 | 0.6 |
| FLC | 18 | 16 | 0.58 | 0.6 |
| Neural Network | 8 | 7 | 0.58 | 0.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousuf, S.; Yousuf, V.; Gupta, N.; Alharbi, T.; Alrumayh, O. Enhanced Control Designs to Abate Frequency Oscillations in Compensated Power System. Energies 2023, 16, 2308. https://doi.org/10.3390/en16052308
Yousuf S, Yousuf V, Gupta N, Alharbi T, Alrumayh O. Enhanced Control Designs to Abate Frequency Oscillations in Compensated Power System. Energies. 2023; 16(5):2308. https://doi.org/10.3390/en16052308
Chicago/Turabian StyleYousuf, Saqib, Viqar Yousuf, Neeraj Gupta, Talal Alharbi, and Omar Alrumayh. 2023. "Enhanced Control Designs to Abate Frequency Oscillations in Compensated Power System" Energies 16, no. 5: 2308. https://doi.org/10.3390/en16052308









