Optimal Scheduling Strategy of Regional Power System Dominated by Renewable Energy Considering Physical and Virtual Shared Energy Storage
Abstract
:1. Introduction
1.1. The Background of the Global Energy Industry Revolution and the Demand for ES
1.2. Research Status of Optimal Scheduling Considering ES
1.2.1. Overview of Optimal Scheduling and Planning of ES in Power Systems
1.2.2. Overview of Optimal Scheduling Considering the Carbon Trading Mechanisms
1.3. Research Background, Significance, and Task Summary
2. Operational Characteristics Modeling of PVSES
2.1. Operational Characteristics Modeling of Physical SES (PSES)
- A.
- The constraint of PSES charging and discharging power
- B.
- The constraint of PSES charging and discharging status
- C.
- The constraint of PSES electricity storage
- D.
- Dynamic balance constraint of PSES electricity storage
- E.
- Consistency constraint of stored energy state of charge
2.2. Operational Characteristics Modeling of Virtual SES (VSES)
- A.
- Priced-based DR
- B.
- Incentive DR
3. Carbon Trading Mechanism Considering the Reward and Penalty Ladder Carbon Price (RPLCP)
3.1. Carbon Emission Trading Mode
3.2. CETIM Considering Reward and Penalty Ladder Carbon Price (RPLCP)
4. Optimal Scheduling Model for RPSDRE Considering Battery PSES and DR VSES
4.1. Objective Function of Optimal Scheduling Model for RPSDRE Considering Battery PSES and DR VSES
4.2. Constraints of Optimal Scheduling Model for RPSDRE Considering Battery PSES and DR VSES
- A.
- Power balance constraints
- B.
- Charge and discharge power constraints of VSES
- C.
- Renewable energy power output constraints
- D.
- Network power flow constraints
4.3. Algorithm Flow of Optimal Scheduling for RPSDRE Considering PVSES
5. Results and Discussion
5.1. Introduction of the Lankao RPSDRE
5.2. Analysis of Lankao RPSDRE
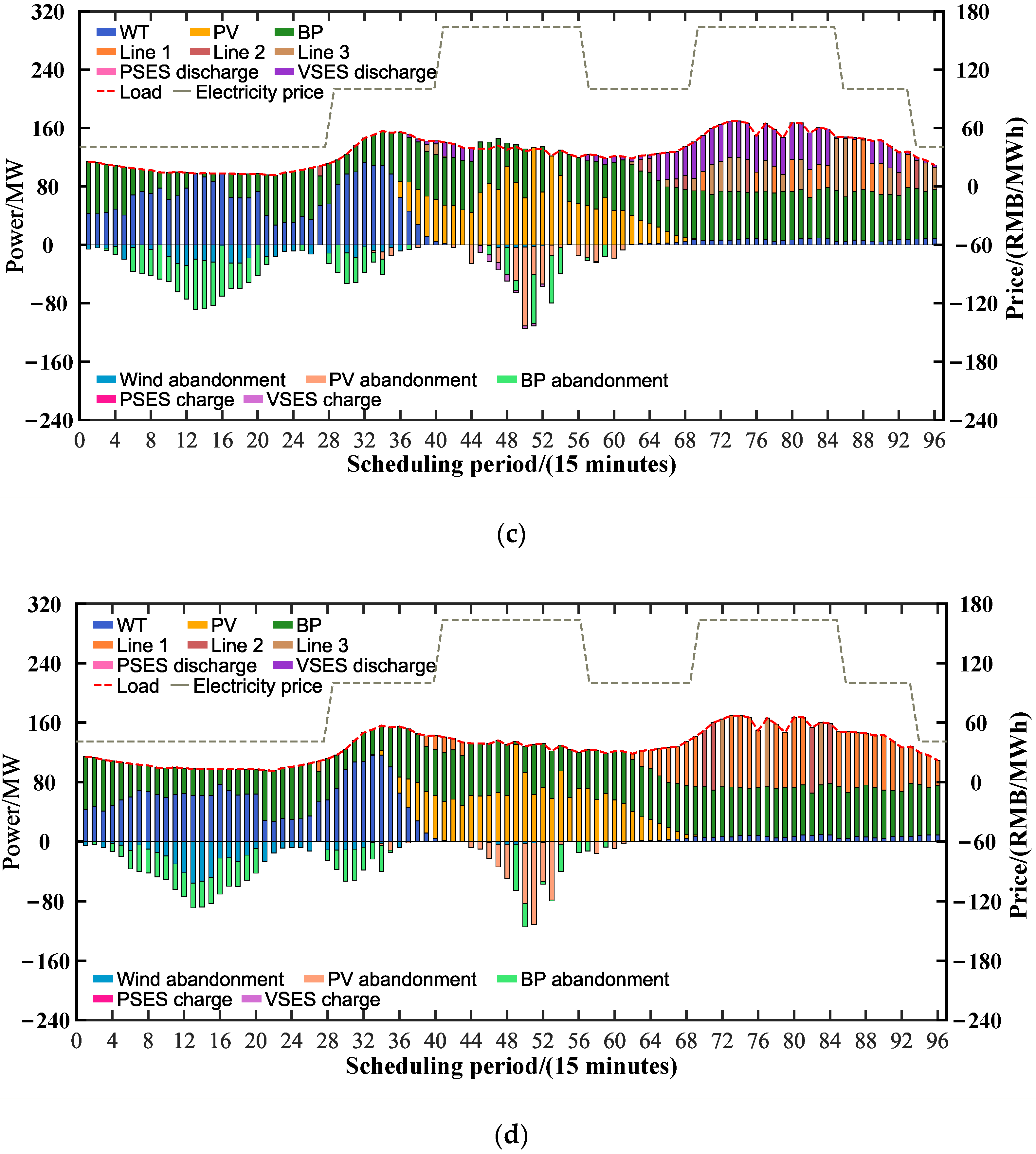
5.2.1. Analysis of Optimal Scheduling for RPSDRE in Different ES Operation Modes
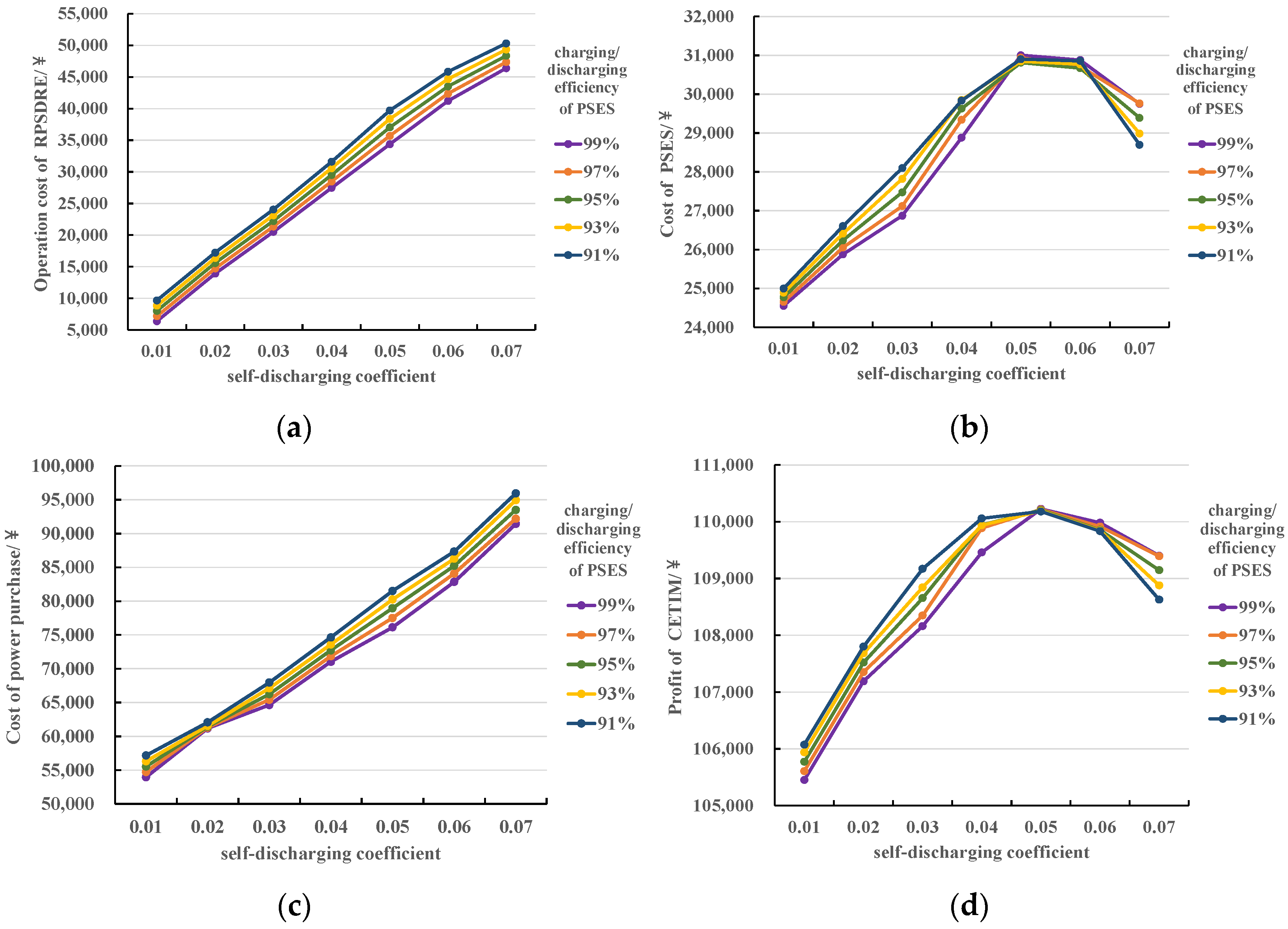
5.2.2. Sensitivity Analysis of Optimal Scheduling for RPSDRE Considering the Degradation of Battery PSES
5.2.3. Comparison among Four Kinds of Optimal Scheduling Strategies for RPSDRE
- M-RPLCP: M-PRLCP refers to the proposed scheduling strategy with the objective function considering the CETIM with the RPLCP;
- M-FCP: M-FCP refers to the scheduling strategy with the objective function considering the CETIM with a fixed carbon price [29];
- M-PLCP: M-PCP refers to the scheduling strategy with the objective function considering the CETIM with a penalty ladder carbon price [30];
- M-NON: M-NON refers to the scheduling strategy without considering the objective function of the CETIM [35].
| Scheduling Strategies for RPSDRE | F (CNY) | fpur (CNY) | fress (CNY) | fvess (CNY) | Carbon Emission (t) | Renewable Energy Consumption Rate (%) |
|---|---|---|---|---|---|---|
| M-RPLCP | 21,353.12 | 65,426.07 | 27,120.49 | 37,154.86 | −1946.96 | 97.42 |
| M-FCP | 57,421.07 | 65,509.94 | 26,541.11 | 36,926.62 | −1933.96 | 96.77 |
| M-PLCP | 38,069.91 | 65,426.07 | 26,487.63 | 37,154.86 | −1936.14 | 96.88 |
| M-NON | 128,326.44 | 64,808.09 | 26,049.40 | 37,468.94 | −1913.72 | 95.77 |
6. Conclusions
- The steady-state optimal scheduling strategy on the hour-level time scale is proposed in this paper and the frequency restoration reserves, frequency containment reserves, and inertial response of battery energy storage systems on the time scale of minutes or seconds have yet to be analyzed, which will be studied in further researches.
- With the upgrading of renewable energy utilization technology, the types and installed capacity of renewable energy power generation are changing rapidly, and waste-to-energy has become an avenue to achieve the disposal of waste and the production of electric energy. Thus, the coordination of waste-to-energy and energy storage could be analyzed in future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A. Abbreviations | |
| PSDRE | power system dominated by renewable energy |
| RPSDRE | regional PSDRE |
| WT | wind turbine |
| PV | photovoltaic |
| BP | biomass power |
| DR | demand response |
| ES | energy storage |
| SES | shared energy storage |
| PSES | physical SES |
| VSES | virtual SES |
| PVSES | physical and virtual SES |
| RPLCP | reward and penalty ladder carbon price |
| TCETM | total carbon emission trading mode |
| CEITM | carbon emission intensity trading mode |
| B. Decision Variables | |
| / | charging and discharging power of PSES j at period t |
| / | charging and discharging states of PSES j at period t |
| / | storage capacity of PSES j at period t/t-1 |
| / | load power and its variation of price-based DR k at period t |
| / | electricity price and its variation of price-based DR k at period t |
| load power after the response of price-based DR k at period t | |
| electricity price after the response of price-based DR k at period t | |
| response power of incentive DR k at period t | |
| / | charging and discharging power of VSES j at period t |
| // / | power of WT m/PV n/BP p/system’s load s in RPSDRE at period t |
| / | charging and discharging states of VSES k at period t |
| transmission power between node a and node b in RPSDRE at period t | |
| / | power of electricity source node and load node at period t |
| C. Input Parameters | |
| / | maximum charging and discharging power of PSES j |
| / | minimum and maximum storage capacity of PSES j |
| // | self-discharging coefficient, and charging and discharging efficiency of PSES j |
| / | storage electricity of PSES j at the beginning/end of the scheduling period |
| (u = v, u = 1, 2, …, T, v = 1, 2, …, T) | self-elastic coefficient |
| (u ≠ v, u = 1, 2, …, T, v = 1, 2, …, T) | mutual-elastic coefficient |
| load power before the response of price-based DR k at period t | |
| electricity price before the response of price-based DR k at period t | |
| / | start/end time of incentive DR |
| contracted capacity of incentive DR k | |
| unit price of the power purchase from line i at period t | |
| / | unit price of charging/discharging of PSES j at period t |
| / | unit price of charging/discharging of VSES k at period t |
| Nline/Nress/Nvess | number of power purchase lines from the superior power grid/PSES/VSES in RPSDRE |
| Nload/Nwind/Nsun/Nbio | number of system’s load nodes/WT/PV/BP in RPSDRE |
| / | maximum charge and discharge proportion of DR VSES |
| load forecast power of DR VSES k at period t | |
| / | upper and lower limits of PV power output |
| / | upper and lower limits of WT power output |
| / | upper and lower limits of BP power output |
| maximum transmission power between node a and node b | |
| /// | impedance of node between a and / node between b and / node between a and / node between b and / node between a and b |
| baseline of carbon emission intensity | |
| unit carbon emission | |
| / | number of segments in reward/penalty carbon price |
| percentage increase in the carbon price | |
| D. Indices and Sets | |
| elasticity coefficient matrix of electricity price and load power | |
| scheduling interval | |
| / | node sets of power source and load in RPSDRE |
| T | numbers of scheduling periods |
References
- Ding, Y.; Zhao, J.; Liu, J.W.; Zhou, J.Z.; Cheng, L.; Zhao, J.; Shao, Z.; Çağatay, I.; Pan, B.J.; Li, X.N.; et al. A review of China’s municipal solid waste (MSW) and comparison with international regions: Management and technologies in treatment and resource utilization. J. Clean. Prod. 2021, 293, 126144.1–1226144.20. [Google Scholar] [CrossRef]
- Ramin, B.N.; Darioush, N.; Reza, G.; Payam, A. Switchable capacitor bank coordination and dynamic network reconfiguration for improving operation of distribution network integrated with renewable energy resources. J. Mod. Power Syst. Clean Energy 2022, 10, 637–646. [Google Scholar]
- Zhou, Z.H.; Shi, L.B.; Chen, Y.X. An optimal over-frequency generator tripping strategy for regional power grid with high penetration level of renewable energy. J. Mod. Power Syst. Clean Energy 2022, 9, 1007–1017. [Google Scholar] [CrossRef]
- Budiman, F.N.; Anwari, M.; Milyani, A.H.; Bouchekara, H.R.E.H.; Rawa, M.; Firmansyah, R.; Seedahmed, M.M.A. Stochastic optimization for the scheduling of a grid-connected microgrid with a hybrid energy storage system considering multiple uncertainties. Energy Rep. 2022, 8, 7444–7456. [Google Scholar] [CrossRef]
- Ju, L.W.; Yin, Z.; Yang, S.B.; Zhou, Q.Q.; Lu, X.L.; Tan, Z.F. Bi-level electricity-carbon collaborative transaction optimal model for the rural electricity retailers integrating distributed energy resources by virtual power plant. Energy Rep. 2022, 8, 9871–9888. [Google Scholar] [CrossRef]
- Yan, Y.M.; Shang, W.L.; Yan, J.; Liao, Q.; Wang, B.H.; Song, H.B.; Liu, Y.Q. Logistic and scheduling optimization of the mobilized and distributed battery in urban energy systems. Resour. Conserv. Recycl. 2022, 189, 106608. [Google Scholar] [CrossRef]
- Marinko, B.; Toni, V.; Tin, B.; Vedrana, J.S. Optimal allocation of renewable energy sources and battery storage systems considering energy management system optimization based on fuzzy inference. Energies 2022, 15, 6884. [Google Scholar]
- Liu, F.; Muhammad, S.P.; Fazal, A.; Khawaja, A.M.; Majid, H.; Li, B. Optimal energy management system of IoT-enabled large building considering electric vehicle scheduling, distributed resources, and demand response schemes. Sensors 2022, 22, 7448. [Google Scholar] [CrossRef]
- Ren, H.; Ma, Z.J.; Tse, C.F.N.; Sun, Y.J. Optimal control of solar-powered electric bus networks with improved renewable energy on-site consumption and reduced grid dependence. Appl. Energy 2022, 323, 119643. [Google Scholar] [CrossRef]
- Abdul, R.; Mahmoud, K.; Muhammad, K. Data-driven optimal battery storage sizing for grid-connected hybrid distributed generations considering solar and wind uncertainty. Sustainability 2022, 14, 11002. [Google Scholar] [CrossRef]
- Qiu, W.Q.; Chen, C.M.; Zhang, Z.; Wang, Y.C.; Lin, Z.Z.; Yang, L. Pricing model of reactive power services of shared energy storage considering baseline power for renewable energy accommodation. Energy Rep. 2022, 8, 427–436. [Google Scholar] [CrossRef]
- Nathaniel, T.; Mahnoosh, A. An online scheduling algorithm for a community energy storage system. IEEE Trans. Smart Grid 2022, 13, 4651–4664. [Google Scholar]
- Chen, C.M.; Li, Y.; Qiu, W.Q.; Liu, C.; Zhang, Q.; Li, Z.Y.; Lin, Z.Z.; Yang, L. Cooperative game based day-ahead scheduling for local integrated energy systems with shared energy storage. IEEE Trans. Sustain. Energy 2022, 13, 1994–2011. [Google Scholar] [CrossRef]
- Wang, Y.C.; Jin, J.F.; Liu, H.F.; Zhang, Z.; Liu, S.Y.; Ma, J.E.; Gong, C.; Zheng, Y.F.; Lin, Z.Z.; Yang, L. The optimal emergency demand response (EDR) mechanism for rural power grid considering consumers’ satisfaction. Energy Rep. 2022, 7, 118–125. [Google Scholar] [CrossRef]
- Hamza, A.; Park, W.; Glick, M.; Kim, Y. Two-Stage stochastic optimization for operating a renewable-based microgrid. Appl. Energy 2022, 325, 119848. [Google Scholar]
- Li, Y.C.; Wang, J.K.; Zhang, Y.; Han, Y.H. Day-ahead scheduling strategy for integrated heating and power system with high wind power penetration and integrated demand response: A hybrid stochastic/interval approach. Energy 2022, 253, 124189. [Google Scholar] [CrossRef]
- Wu, D.; Wang, Y.C.; Li, L.; Lu, P.F.; Liu, S.Y.; Dai, C.; Pan, Y.Z.; Zhang, Z.; Lin, Z.Z.; Yang, L. Demand response ability evaluation based on seasonal and trend decomposition using LOESS and S–G filtering algorithms. Energy Rep. 2022, 8, 292–299. [Google Scholar] [CrossRef]
- Chen, C.M.; Wu, X.G.; Ma, J.E.; Chen, Y.G.; Liu, S.Y.; Wu, X.H.; Ji, Q.F.; Ye, J.Y.; Yang, L.; Lin, Z.Z. Optimal low-carbon scheduling of integrated local energy system considering oxygen-enriched combustion plant and generalized energy storages. IET Renew. Power Gener. 2022, 16, 671–687. [Google Scholar] [CrossRef]
- Çağatay, I.; Jasmine, S.L.L. Optimal energy management and operations planning in seaports with smart grid while harnessing renewable energy under uncertainty. Omega 2021, 103, 102445. [Google Scholar]
- Çağatay, I.; Jasmine, S.L.L. A review of energy efficiency in ports: Operational strategies, technologies and energy management systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar]
- Ma, M.T.; Huang, H.J.; Song, X.L.; Feniosky, P.M.; Zhang, Z.; Chen, J. Optimal sizing and operations of shared energy storage systems in distribution networks: A bi-level programming approach. Appl. Energy 2022, 307, 118170. [Google Scholar] [CrossRef]
- Li, X.L.; Liu, Y.S.; Yan, Y.W. Optimal scheduling of regional integrated energy system based on cloud energy storage. In Proceedings of the 2022 25th International Conference on Electrical Machines and Systems (ICEMS), Chiang Mai, Thailand, 29 November–2 December 2022; pp. 1–6. [Google Scholar]
- Qiu, W.Q.; Zhou, S.; Yang, Y.; Lv, X.Y.; Lv, T.; Chen, Y.G.; Huang, Y.; Zhang, K.M.; Yu, H.F.; Wang, Y.C.; et al. Application prospect, development status and key technologies of shared energy storage toward renewable energy accommodation scenario in the context of China. Energies 2023, 16, 731. [Google Scholar] [CrossRef]
- Qiu, W.Q.; Jiang, X.Y.; Lin, Z.Z.; Li, L.Y.; Pei, Y.; Tao, Y.B. A contract-based, decentralized and privacy-preserving computation scheme of evaluation indices of shared energy storage market for renewable energy accommodation. IEEE Trans. Ind. Appl. 2022, 99, 1–17. [Google Scholar] [CrossRef]
- Fan, W.; Tan, Z.F.; Li, F.Q.; Zhang, A.M.; Ju, L.W.; Wang, Y.W.; Gejirifu, D. A two-stage optimal scheduling model of integrated energy system based on CVaR theory implementing integrated demand response. Energy 2022, 263, 125783. [Google Scholar] [CrossRef]
- Home-Ortiz, J.M.; Melgar-Dominguez, O.D.; Javadi, M.S.; Gough, M.B.; Sanches Mantovani, J.R.; Catalão, J.P.S. A strategy to enhance the distribution systems recoverability via the simultaneous coordination of planning actions and operational resources. Int. J. Electr. Power Energy Syst. 2023, 147, 108863. [Google Scholar] [CrossRef]
- Ren, L.; Peng, D.G.; Wang, D.H.; Li, J.F.; Zhao, H.R. Multi-objective optimal dispatching of virtual power plants considering source-load uncertainty in V2G mode. Front. Energy Res. 2023, 10, 983743. [Google Scholar] [CrossRef]
- Li, Q.F.; Zhao, Y.H.; Yang, Y.W.; Zhang, L.T.; Chen, J. Demand-response-oriented load aggregation scheduling optimization strategy for inverter air conditioner. Energies 2023, 16, 337. [Google Scholar] [CrossRef]
- Liu, X.O. Research on bidding strategy of virtual power plant considering carbon-electricity integrated market mechanism. Int. J. Electr. Power Energy Syst. 2022, 137, 107891. [Google Scholar] [CrossRef]
- Zhu, G.; Gao, Y.; Sun, H. Optimization scheduling of a wind-photovoltaic-gas-electric vehicles community-integrated energy system considering uncertainty and carbon emissions reduction. Sustain. Energy Grids Netw. 2023, 33, 100973. [Google Scholar] [CrossRef]
- Wang, B.W.; Sun, H.B.; Song, X.S. Optimal dispatching modeling of regional power-heat-gas interconnection based on multi-type load adjustability. Front. Energy Res. 2022, 10, 931890. [Google Scholar] [CrossRef]
- Ullah, Z.; Mirjat, N.H. Modelling and analysis of virtual power plants interactive operational characteristics in distribution systems. IET Energy Convers. Econ. 2022, 3, 11–19. [Google Scholar] [CrossRef]
- Zhang, T.H.; Qiu, W.Q.; Zhang, Z.; Lin, Z.Z.; Ding, Y.; Wang, Y.T.; Wang, L.F.; Yang, L. Optimal bidding strategy and profit allocation method for shared energy storage-assisted VPP in joint energy and regulation markets. Appl. Energy 2022, 329, 120158. [Google Scholar] [CrossRef]
- Hayat, M.; Shahnia, F.; Shafiullah, G.; Wen, F.S. Energy self-sufficiency and network support through photovoltaic and energy storage systems owned by private investors in a residential complex. IET Energy Convers. Econ. 2020, 1, 45–47. [Google Scholar] [CrossRef]
- Chen, Y.G.; Chen, C.M.; Ma, J.E.; Qiu, W.Q.; Liu, S.Y.; Lin, Z.Z.; Qian, M.H.; Zhu, L.Z.; Zhao, D.W. Multi-objective optimization strategy of multi-sources power system operation based on fuzzy chance constraint programming and improved analytic hierarchy process. Energy Rep. 2021, 7, 268–274. [Google Scholar] [CrossRef]
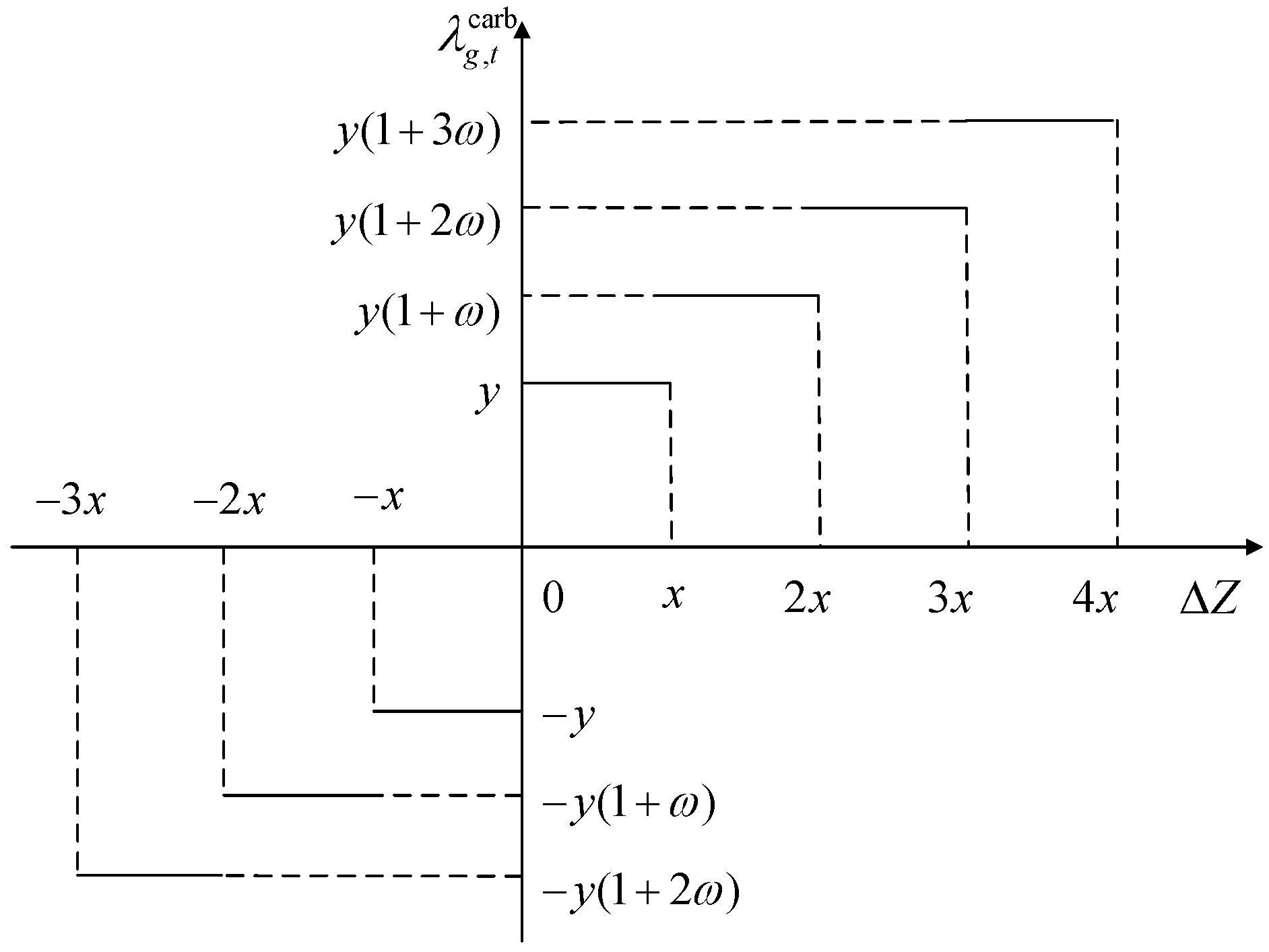

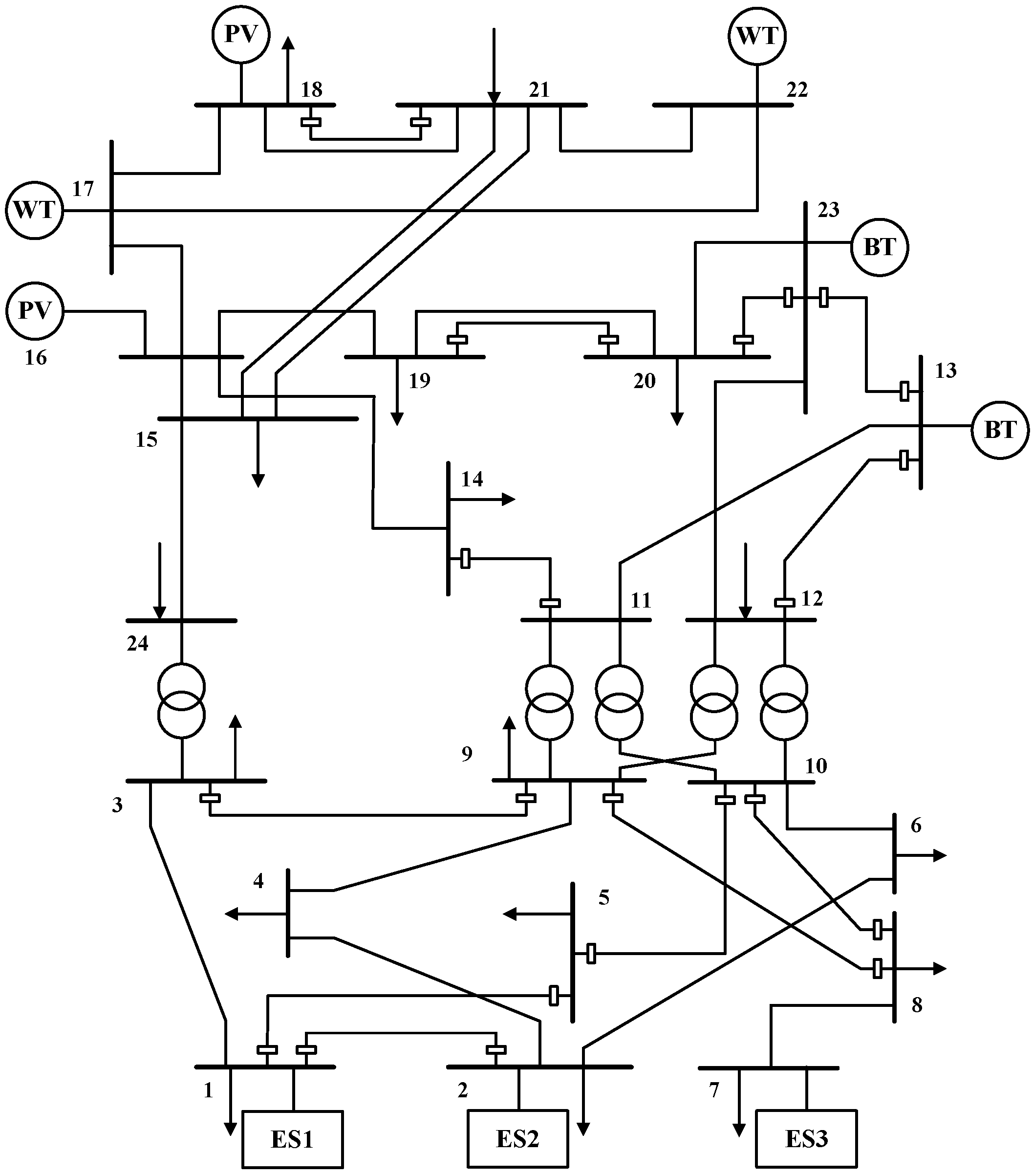

| ES | Node | |||||||
|---|---|---|---|---|---|---|---|---|
| ES 1 | 1 | 20 | 20 | 25 | 300 | 0.01 | 0.93 | 0.93 |
| ES 2 | 2 | 50 | 50 | 25 | 400 | 0.03 | 0.97 | 0.97 |
| ES 3 | 7 | 30 | 30 | 25 | 200 | 0.02 | 0.95 | 0.95 |
| Parameters | |||||
|---|---|---|---|---|---|
| Parameters of DR | 69 | 84 | 0.3 | 0.3 | 20 |
| Scheduling Period | (CNY/MWh) | (CNY/MWh) | (CNY/MWh) | (CNY/MWh) | (CNY/MWh) |
|---|---|---|---|---|---|
| 1–28 and 93–96 | 41 | 10 | 10 | 30 | 30 |
| 29–40 and 57–68 and 85–92 | 100 | 10 | 10 | 30 | 30 |
| 41–56 and 69–84 | 164 | 10 | 10 | 30 | 30 |
| ES Operation Mode | F (CNY) | fpur (CNY) | fress (CNY) | fvess (CNY) |
|---|---|---|---|---|
| PSES and VSES joint-participation | 137,912 | 79,653 | 21,033 | 37,226 |
| only PSES participation | 259,770 | 234,547 | 25,223 | 0 |
| only VSES participation | 195,799 | 157,155 | 0 | 38,644 |
| without PSES and VSES participation | 327,622 | 327,622 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Z.; Liu, J.; Zhang, Y.; Chen, Y.; Zhang, K.; Liu, C.; Yang, M.; Yin, S.; Qiu, W.; Lin, Z.; et al. Optimal Scheduling Strategy of Regional Power System Dominated by Renewable Energy Considering Physical and Virtual Shared Energy Storage. Energies 2023, 16, 2506. https://doi.org/10.3390/en16052506
Chai Z, Liu J, Zhang Y, Chen Y, Zhang K, Liu C, Yang M, Yin S, Qiu W, Lin Z, et al. Optimal Scheduling Strategy of Regional Power System Dominated by Renewable Energy Considering Physical and Virtual Shared Energy Storage. Energies. 2023; 16(5):2506. https://doi.org/10.3390/en16052506
Chicago/Turabian StyleChai, Zhe, Junhui Liu, Yihan Zhang, Yuge Chen, Kunming Zhang, Chang Liu, Meng Yang, Shuo Yin, Weiqiang Qiu, Zhenzhi Lin, and et al. 2023. "Optimal Scheduling Strategy of Regional Power System Dominated by Renewable Energy Considering Physical and Virtual Shared Energy Storage" Energies 16, no. 5: 2506. https://doi.org/10.3390/en16052506
APA StyleChai, Z., Liu, J., Zhang, Y., Chen, Y., Zhang, K., Liu, C., Yang, M., Yin, S., Qiu, W., Lin, Z., & Yang, L. (2023). Optimal Scheduling Strategy of Regional Power System Dominated by Renewable Energy Considering Physical and Virtual Shared Energy Storage. Energies, 16(5), 2506. https://doi.org/10.3390/en16052506






