Optimal Selection of Capacitors for a Low Energy Storage Quadratic Boost Converter (LES-QBC)
Abstract
:1. Introduction
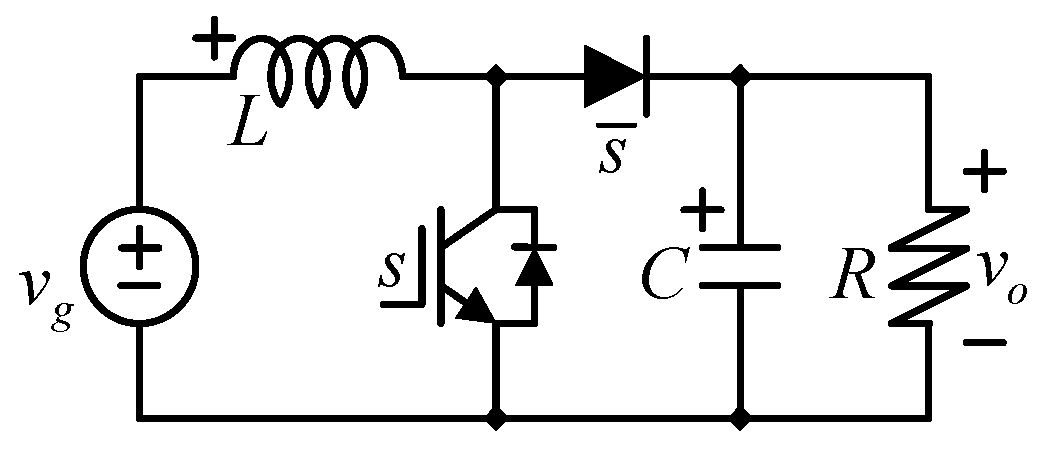
2. The Low Energy Storage Quadratic Boost Converter (LES-QBC)
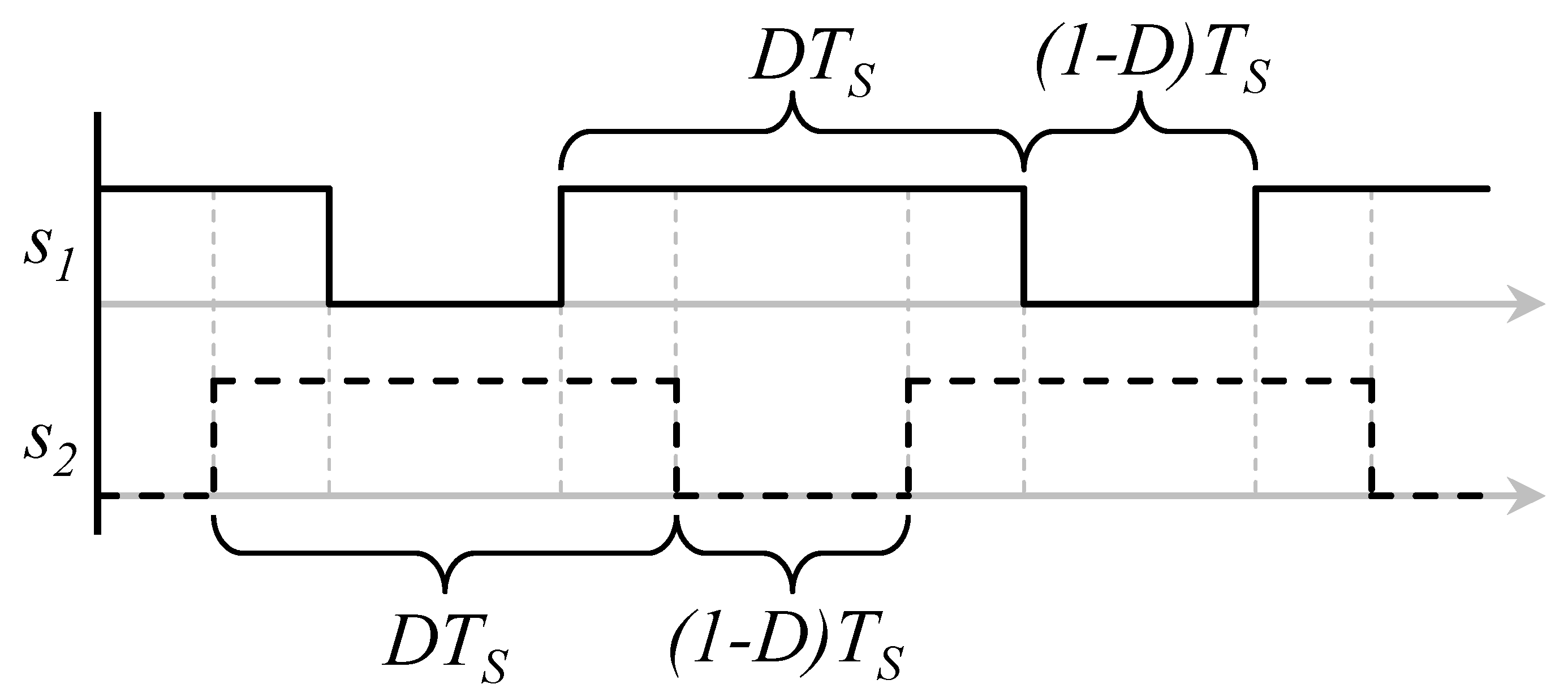
The Duty Ratio
3. Mathematical Model of the LES-QBC
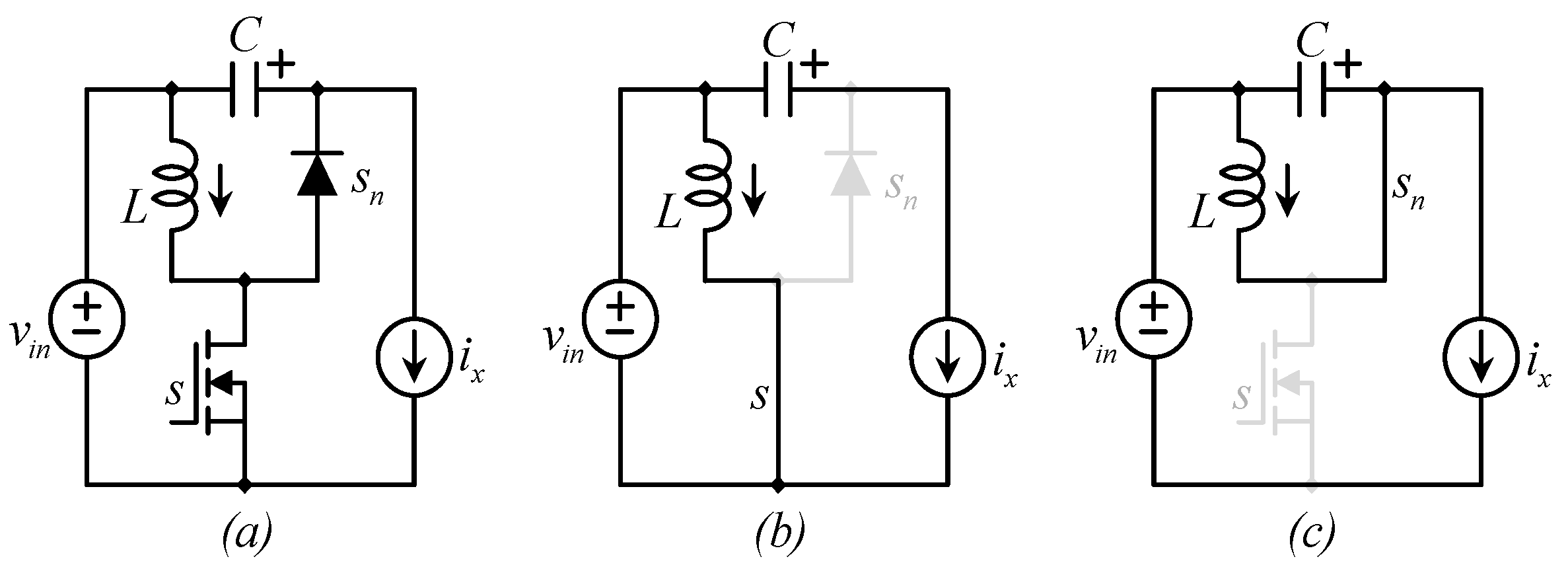
3.1. A Single Power Stage
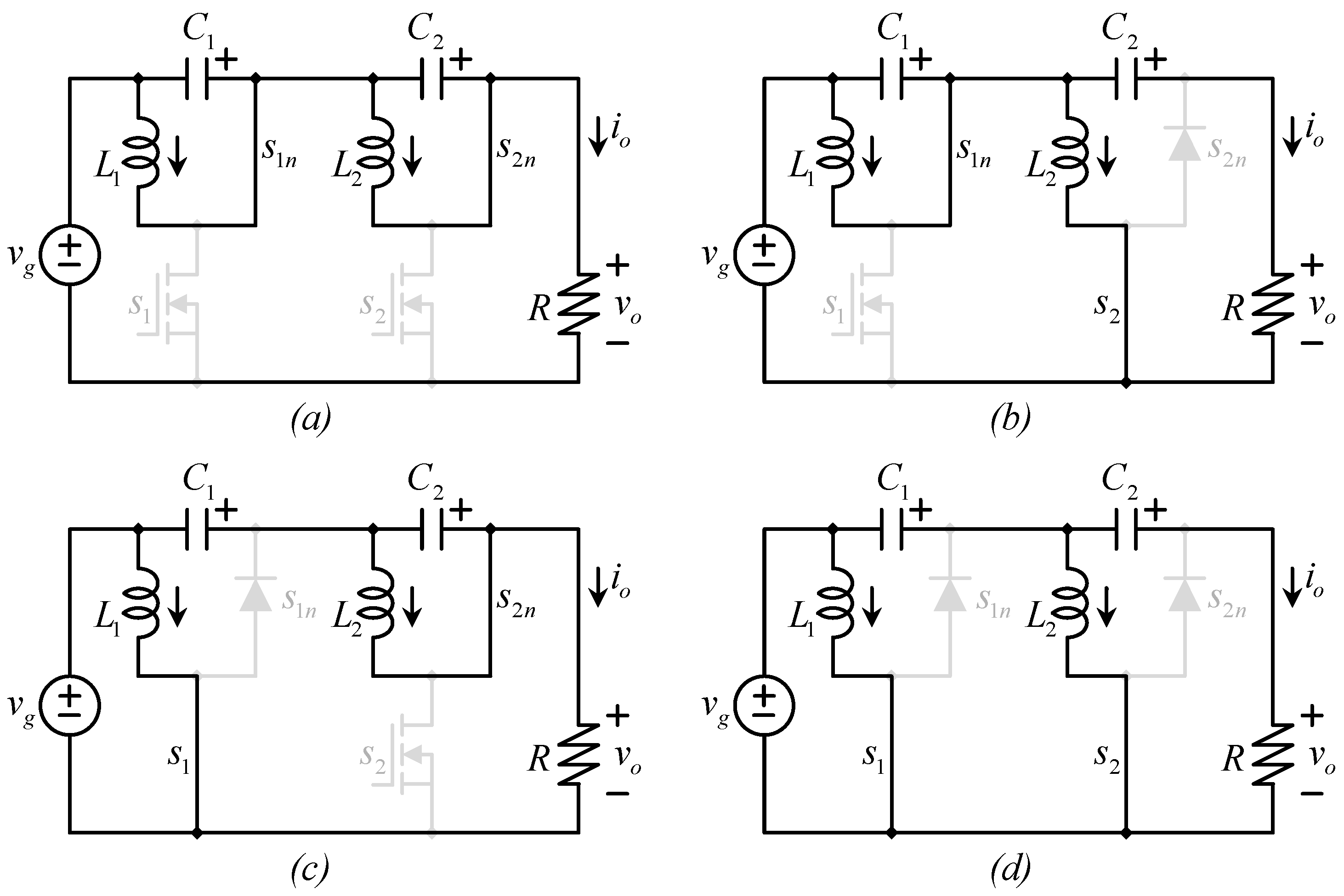
3.2. The LES-QBC
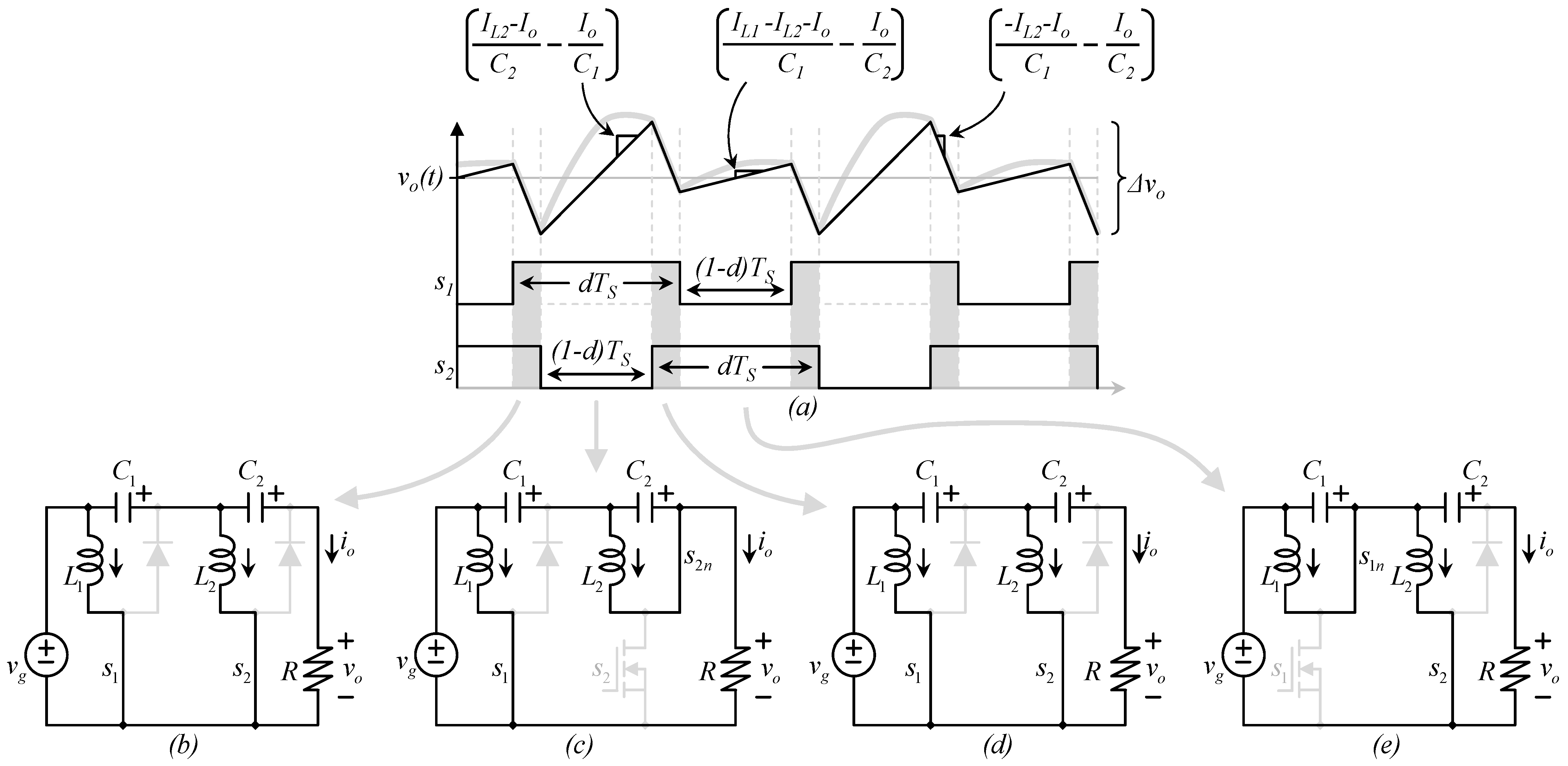
3.3. The Equivalent Circuits of the Real (Composed) Converter
3.4. Calculating the Voltage Ripple at the Output Port
4. The Particle Swarm Optimization (PSO) Algorithm
4.1. Particle Swarm Optimization
4.2. Initialization
4.3. Update Velocity
4.4. New Particle Generation
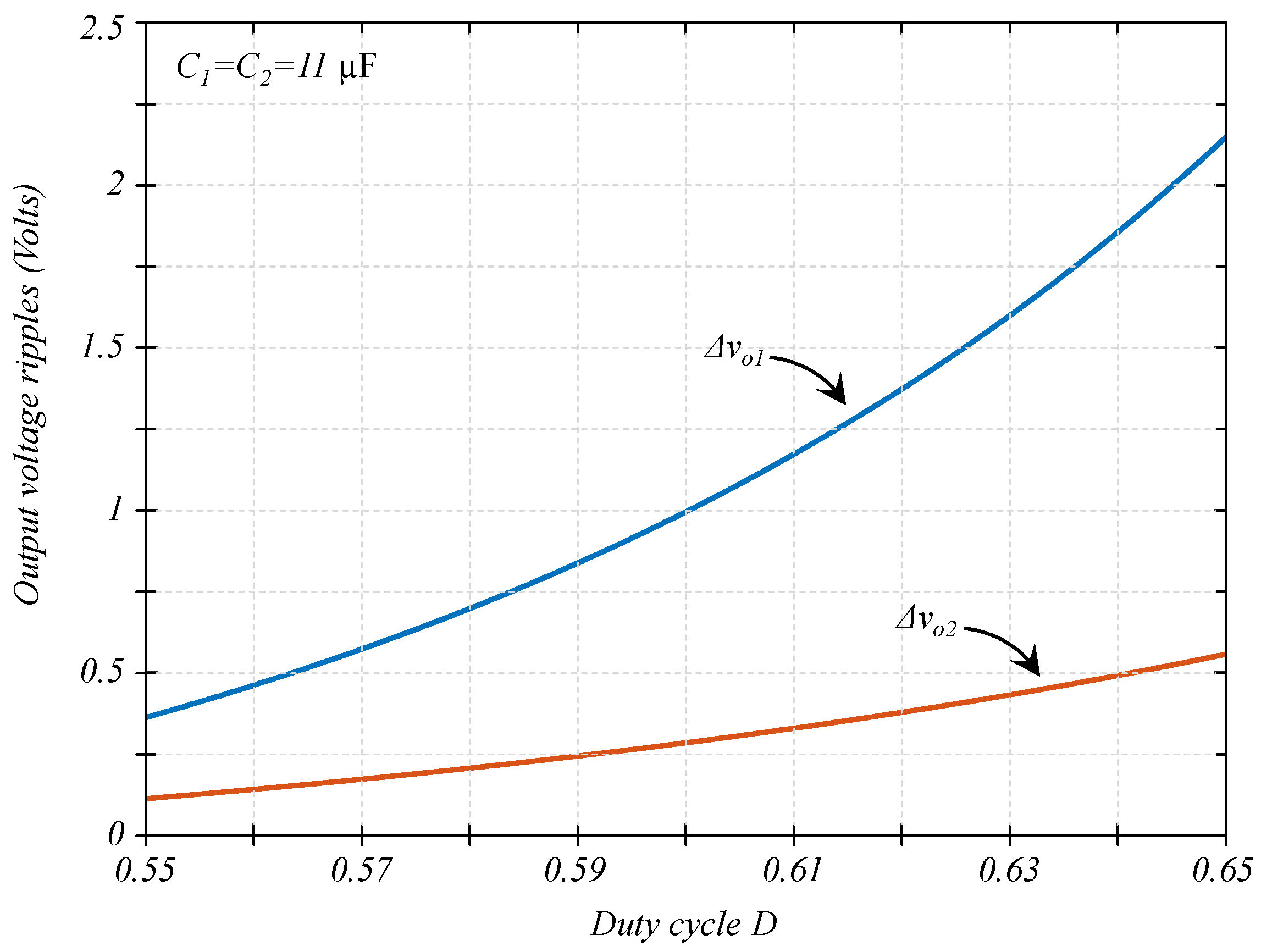
5. Numerical Example
The Problem from the Optimization Point of View
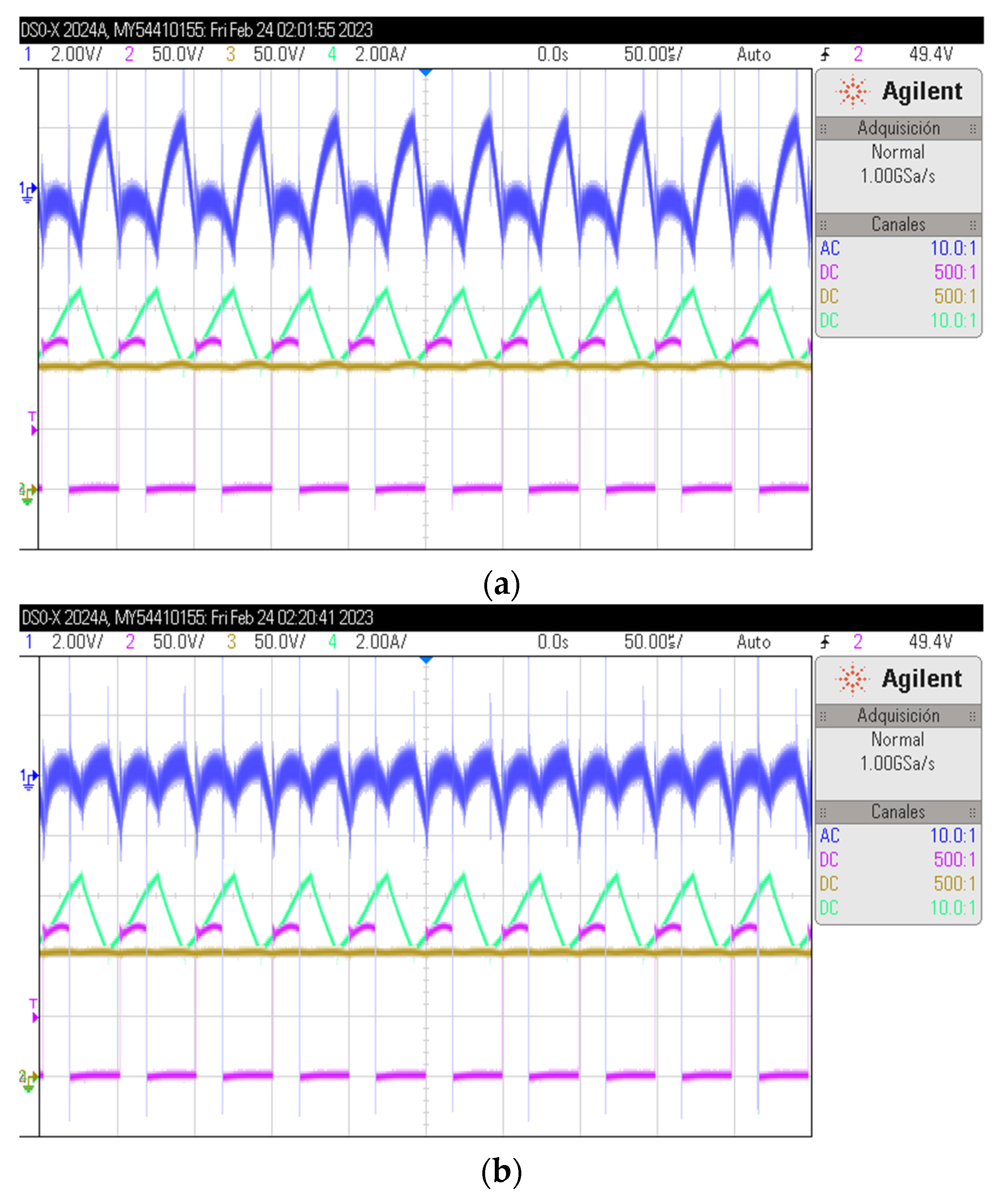
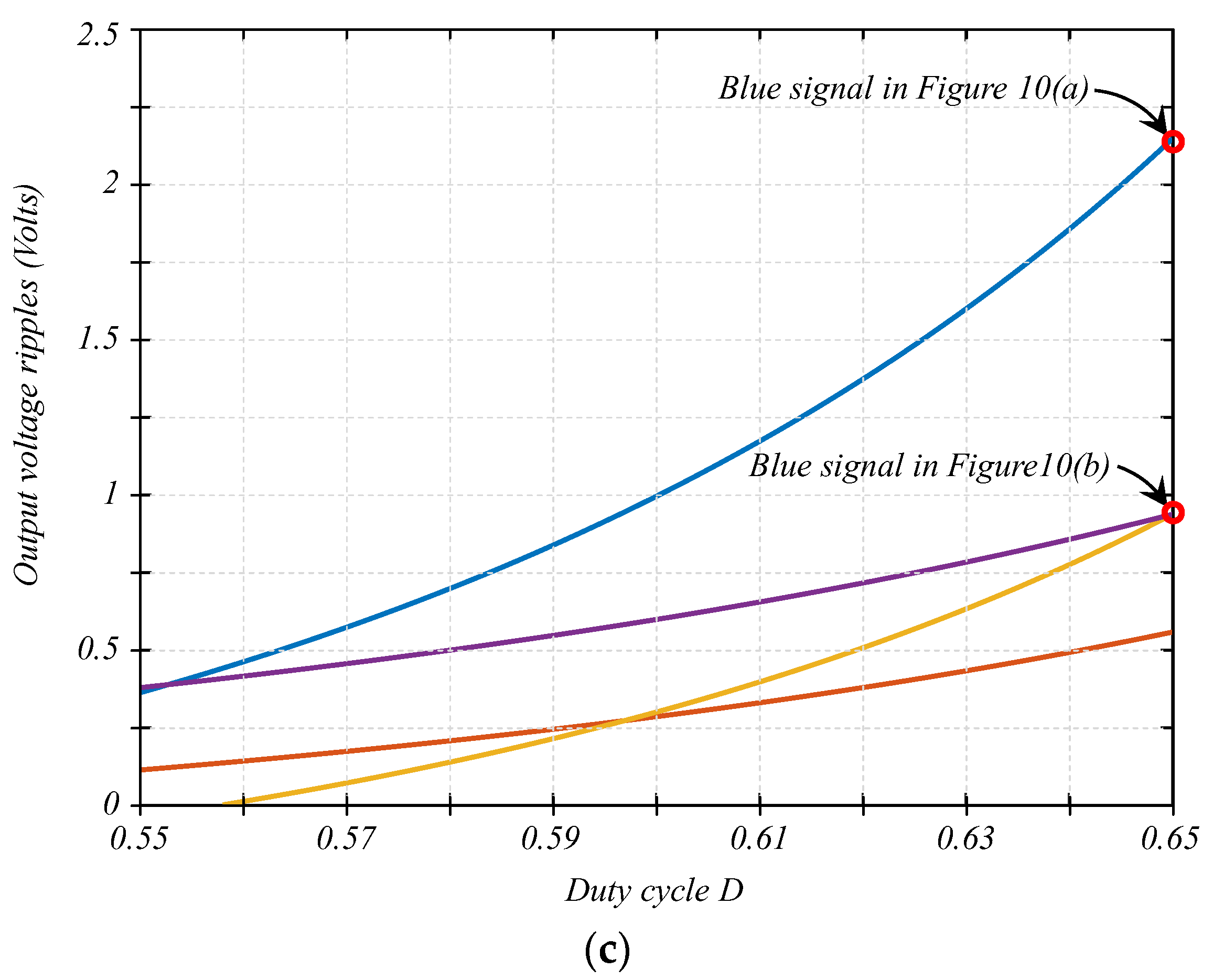
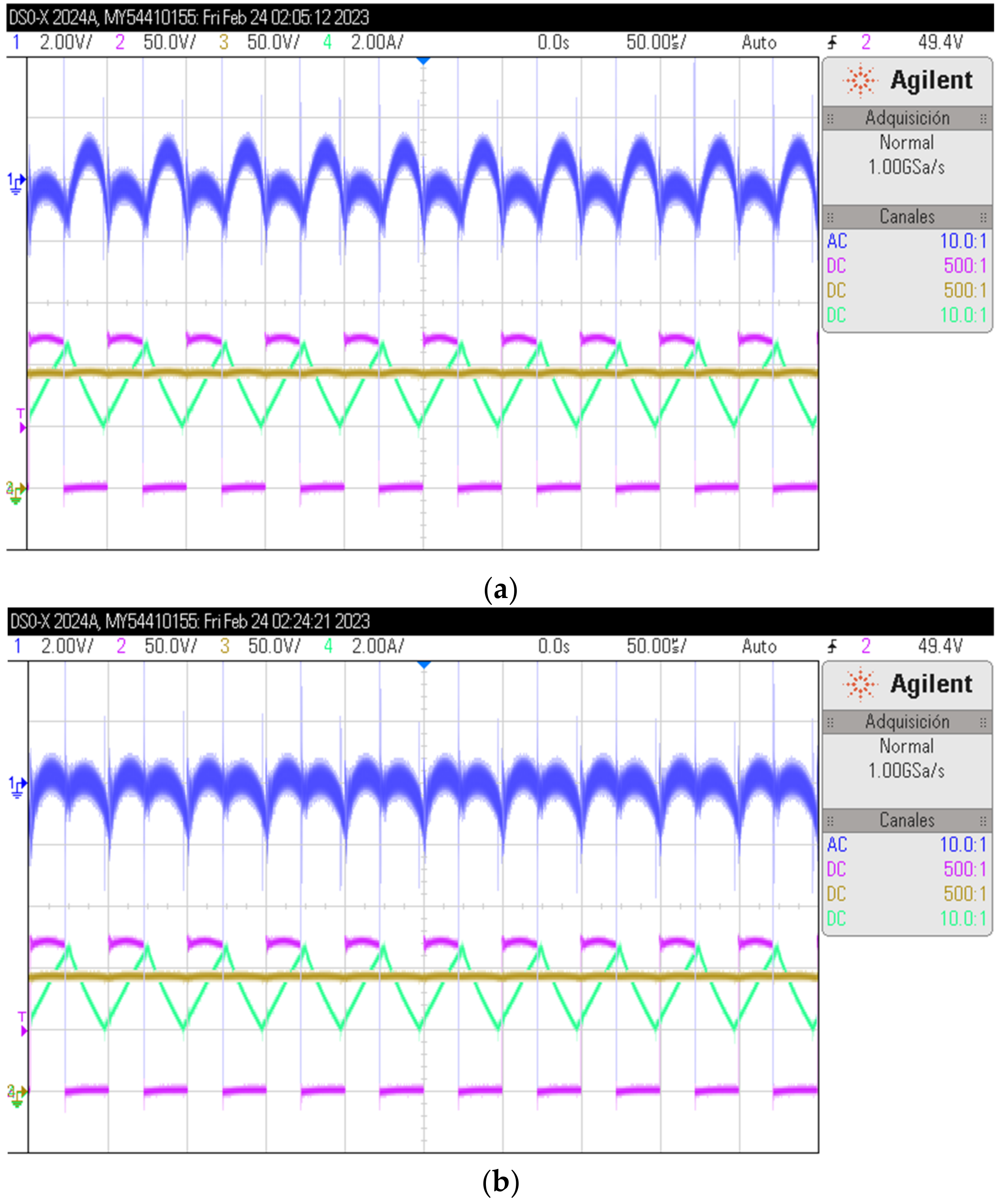
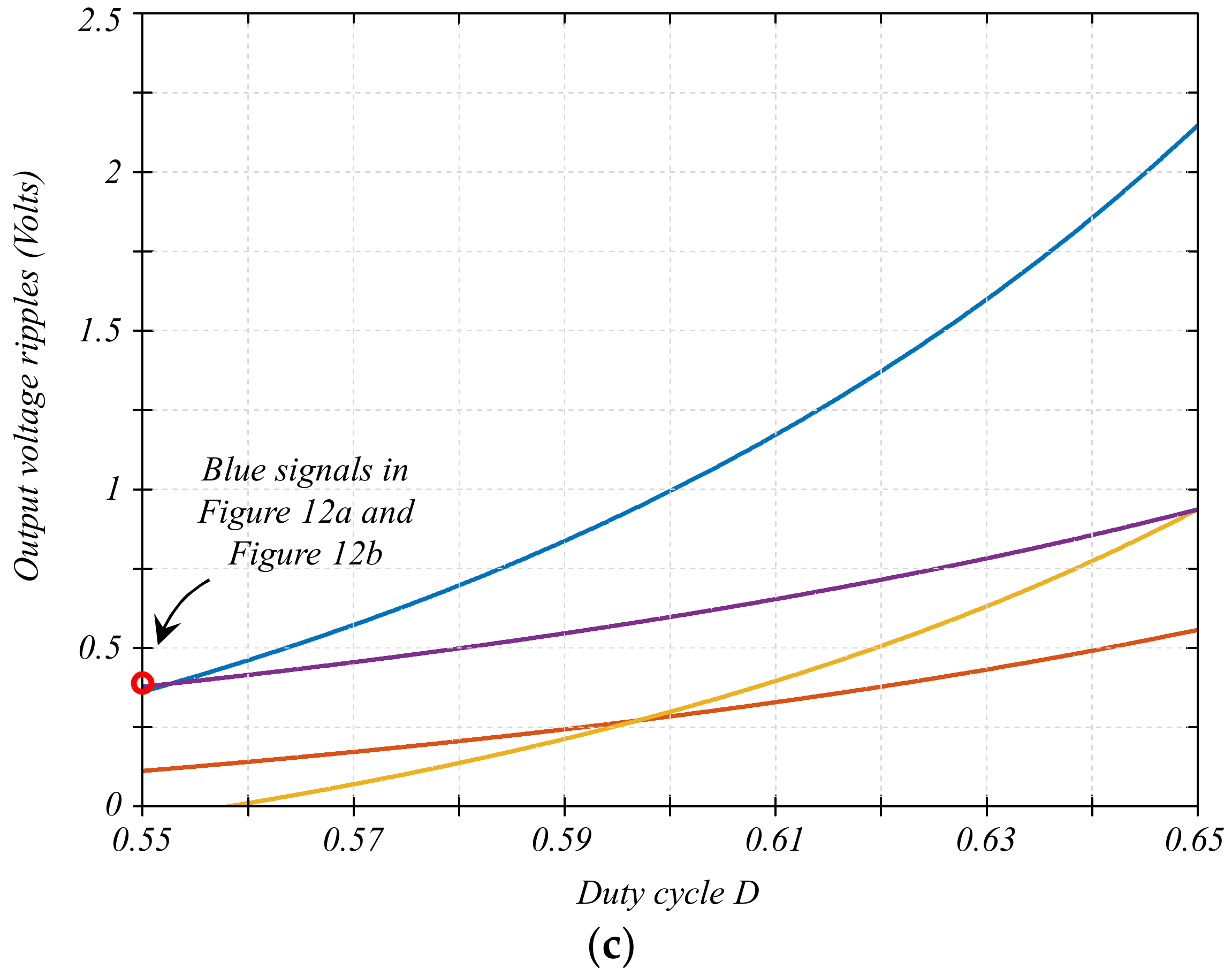
6. The Solution and Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rashid, M. Power Electronics: Circuits, Devices and Applications, 3rd ed.; Prentice Hall: London, UK, 2004; p. 762. [Google Scholar]
- Undeland, M.N.; Robbins, W.P.; Mohan, N. Power Electronics in Converters, Applications, and Design, 3rd ed.; John Whiley & Sons: Hoboken, NJ, USA, 1995; p. 763. [Google Scholar]
- Khan, S.; Rahman, K.; Tariq, M.; Hameed, S.; Alamri, B.; Babu, T.S. Solid-State Transformers: Fundamentals, Topologies, Applications, and Future Challenges. Sustainability 2022, 14, 319. [Google Scholar] [CrossRef]
- Narayanaswamy, J.; Mandava, S. Non-Isolated Multiport Converter for Renewable Energy Sources: A Comprehensive Review. Energies 2023, 16, 1834. [Google Scholar] [CrossRef]
- Saadaoui, A.; Ouassaid, M.; Maaroufi, M. Overview of Integration of Power Electronic Topologies and Advanced Control Techniques of Ultra-Fast EV Charging Stations in Standalone Microgrids. Energies 2023, 16, 1031. [Google Scholar] [CrossRef]
- Rafiq, U.; Murtaza, A.F.; Sher, H.A.; Gandini, D. Design and Analysis of a Novel High-Gain DC-DC Boost Converter with Low Component Count. Electronics 2021, 10, 1761. [Google Scholar] [CrossRef]
- Mohammadzadeh Shahir, F.; Gheisarnejad, M.; Khooban, M.-H. A New Transformer-Less Structure for a Boost DC-DC Converter with Suitable Voltage Stress. Automation 2021, 2, 220–237. [Google Scholar] [CrossRef]
- de Carvalho, M.R.S.; Neto, R.C.; Barbosa, E.J.; Limongi, L.R.; Bradaschia, F.; Cavalcanti, M.C. An Overview of Voltage Boosting Techniques and Step-Up DC-DC Converters Topologies for PV Applications. Energies 2021, 14, 8230. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics; Springer: New York, NY, USA, 2001. [Google Scholar]
- Lenk, R. Practical Design of Power Supplies; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Rosas-Caro, J.C.; Ramirez, J.M.; Peng, F.Z.; Valderrabano, A. A DC-DC multilevel boost converter. IET Power Electron. 2010, 3, 129–137. [Google Scholar] [CrossRef]
- Rosas-Caro, J.C.; Mayo-Maldonado, J.C.; Valdez-Resendiz, J.E.; Alejo-Reyes, A.; Beltran-Carbajal, F.; López-Santos, O. An Overview of Non-Isolated Hybrid Switched-Capacitor Step-Up DC–DC Converters. Appl. Sci. 2022, 12, 8554. [Google Scholar] [CrossRef]
- Haider, Z.; Ulasyar, A.; Khattak, A.; Zad, H.S.; Mohammad, A.; Alahmadi, A.A.; Ullah, N. Development and Analysis of a Novel High-Gain CUK Converter Using Voltage-Multiplier Units. Electronics 2022, 11, 2766. [Google Scholar] [CrossRef]
- Zaid, M.; Malick, I.H.; Ashraf, I.; Tariq, M.; Alamri, B.; Rodrigues, E.M.G. A Nonisolated Transformerless High-Gain DC–DC Converter for Renewable Energy Applications. Electronics 2022, 11, 2014. [Google Scholar] [CrossRef]
- Jana, A.S.; Lin, C.-H.; Kao, T.-H.; Chang, C.-H. A High Gain Modified Quadratic Boost DC-DC Converter with Voltage Stress Half of Output Voltage. Appl. Sci. 2022, 12, 4914. [Google Scholar] [CrossRef]
- Zaid, M.; Lin, C.-H.; Khan, S.; Ahmad, J.; Tariq, M.; Mahmood, A.; Sarwar, A.; Alamri, B.; Alahmadi, A. A Family of Transformerless Quadratic Boost High Gain DC-DC Converters. Energies 2021, 14, 4372. [Google Scholar] [CrossRef]
- Loera-Palomo, R.; Morales-Saldaña, J.A.; Rivero, M.; Álvarez-Macías, C.; Hernández-Jacobo, C.A. Noncascading Quadratic Buck-Boost Converter for Photovoltaic Applications. Micromachines 2021, 12, 984. [Google Scholar] [CrossRef] [PubMed]
- Bhavani, S.; Sivaprakasam, A. Dual Mode Symmetrical Proportional Resonant Controlled Quadratic Boost Converter for PMSM-Drive. Symmetry 2023, 15, 147. [Google Scholar] [CrossRef]
- Luo, F.L.; Ye, H. Positive output cascade boost converters. IEE Proc. Electr. Power Appl. 2004, 151, 590–606. [Google Scholar] [CrossRef]
- Ortiz-Lopez, M.G.; Leyva-Ramos, J.; Carbajal-Gutierrez, E.E.; Morales-Saldaña, J.A. Modelling and analysis of switch-mode cascade converters with a single active switch. IET Power Electron. 2008, 1, 478–487. [Google Scholar] [CrossRef]
- Leyva-Ramos, J.; Lopez-cruz, J.M.; Ortiz-lopez, M.G.; Diaz-Saldierna, L.H. Switching regulator using a high step-up voltage converter for fuel-cell modules. IET Power Electron. 2013, 6, 1626–1633. [Google Scholar] [CrossRef]
- Lopez-Santos, O.; Martinez-Salamero, L.; Garcia, G.; Valderrama-Blavi, H.; Sierra-Polanco, T. Robust sliding mode control design for a voltage-regulated quadratic boost converter. IEEE Trans. Power Electron. 2015, 30, 2313–2327. [Google Scholar] [CrossRef]
- Jiang, W.; Chincholkar, S.H.; Chan, C. Modified voltage-mode controller for the quadratic boost converter with improved output performance. IET Power Electron. 2018, 11, 2222–2231. [Google Scholar] [CrossRef]
- Ye, Y.M.; Cheng, K.W.E. Quadratic boost converter with low buffer capacitor stress. IET Power Electron. 2014, 7, 1162–1170. [Google Scholar] [CrossRef]
- Loera-Palomo, R.; Morales-Saldaña, J.A. Family of quadratic step-up dc–dc converters based on non-cascading structures. IET Power Electron. 2015, 8, 793–801. [Google Scholar] [CrossRef]
- Lopez-Santos, O.; Mayo-Maldonado, J.C.; Rosas-Caro, J.C.; Valdez-Resendiz, J.E.; Zambrano-Prada, D.A.; Ruiz-Martinez, O.F. Quadratic boost converter with low-output voltage ripple. IET Power Electron. 2020, 13, 1605–1612. [Google Scholar] [CrossRef]
- López-Santos, O.; Varón, N.L.; Rosas-Caro, J.C.; Mayo-Maldonado, J.C.; Valdez-Reséndiz, J.E. Detailed Modeling of the Low Energy Storage Quadratic Boost Converter. IEEE Trans. Power Electron. 2022, 37, 1885–1904. [Google Scholar]
- Ponniran, A.; Orikawa, K.; Itoh, J.-I. Minimum flying capacitor for N-level capacitor DC/DC boost converter. In Proceedings of the 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 1289–1296. [Google Scholar] [CrossRef]
- Drofenik, U.; Laimer, G.; Kolar, J.W. Theoretical converter power density limits for forced convection cooling. In Proceedings of the International Conference Power Electronics, Intelligent Motion, Power Quality, Nurnberg, Germany, 7–9 June 2005. [Google Scholar]
- Obara, H.; Sato, Y. Selection criteria of capacitors for flying capacitor converters. IEEJ J. Ind. Appl. 2015, 4, 105–106. [Google Scholar] [CrossRef]
- Yang, X.-S. Engineering Optimization; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solis-Rodriguez, J.; Rosas-Caro, J.C.; Alejo-Reyes, A.; Valdez-Resendiz, J.E. Optimal Selection of Capacitors for a Low Energy Storage Quadratic Boost Converter (LES-QBC). Energies 2023, 16, 2510. https://doi.org/10.3390/en16062510
Solis-Rodriguez J, Rosas-Caro JC, Alejo-Reyes A, Valdez-Resendiz JE. Optimal Selection of Capacitors for a Low Energy Storage Quadratic Boost Converter (LES-QBC). Energies. 2023; 16(6):2510. https://doi.org/10.3390/en16062510
Chicago/Turabian StyleSolis-Rodriguez, Jose, Julio C. Rosas-Caro, Avelina Alejo-Reyes, and Jesus E. Valdez-Resendiz. 2023. "Optimal Selection of Capacitors for a Low Energy Storage Quadratic Boost Converter (LES-QBC)" Energies 16, no. 6: 2510. https://doi.org/10.3390/en16062510
APA StyleSolis-Rodriguez, J., Rosas-Caro, J. C., Alejo-Reyes, A., & Valdez-Resendiz, J. E. (2023). Optimal Selection of Capacitors for a Low Energy Storage Quadratic Boost Converter (LES-QBC). Energies, 16(6), 2510. https://doi.org/10.3390/en16062510









