Coupled Electromagnetic–Thermal Modelling of Dynamic Performance for Modular SPM Machines
Abstract
:1. Introduction
2. Dynamic Performance Analysis
2.1. Without EM–Thermal Coupling
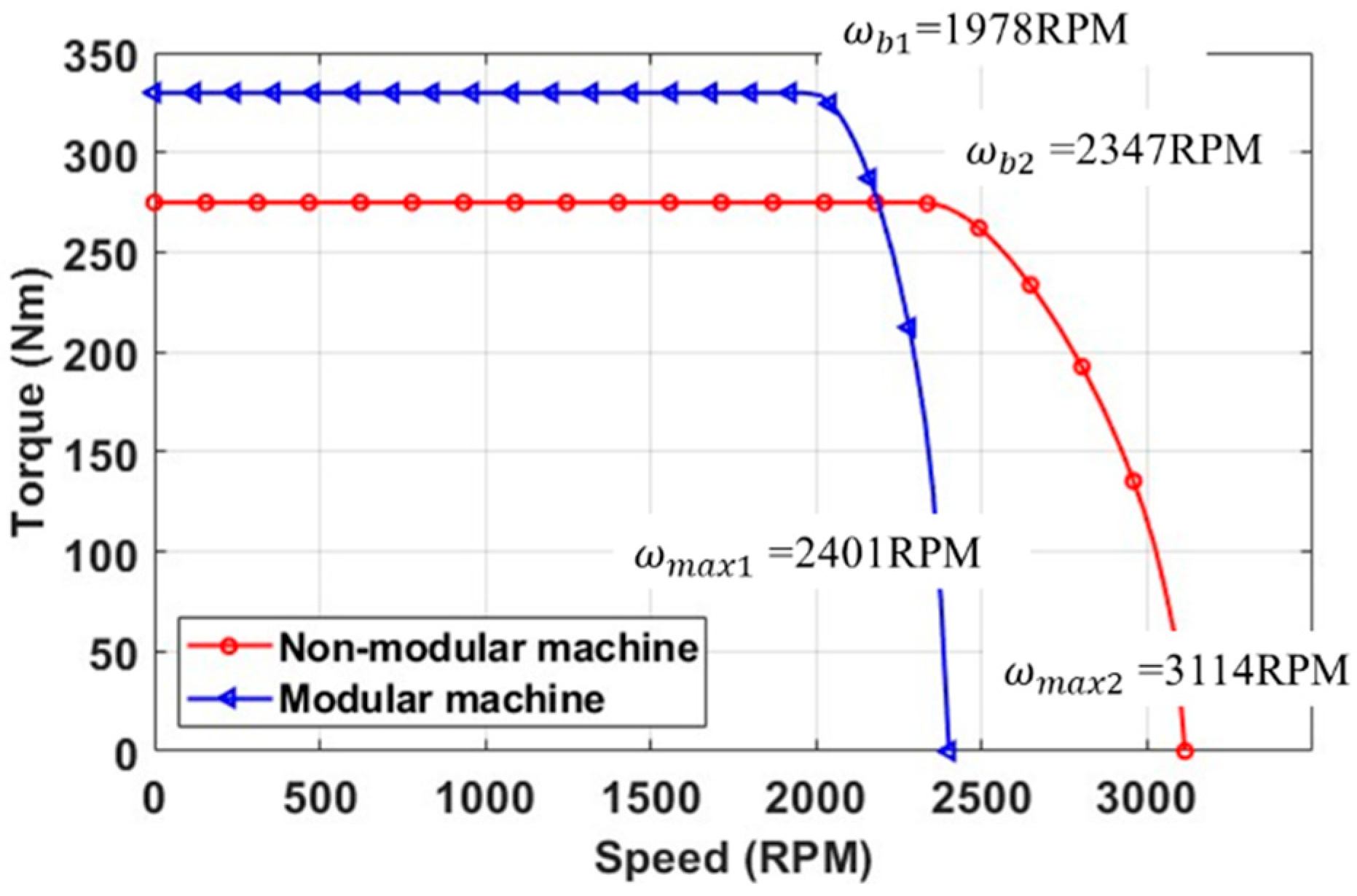
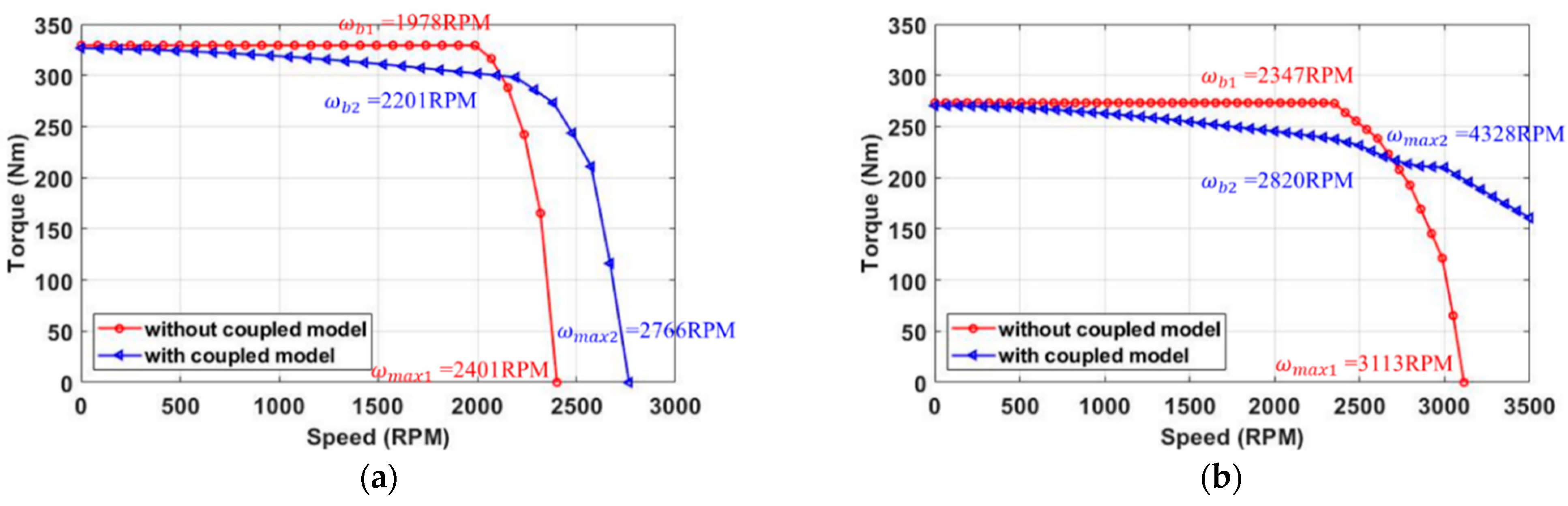
2.1.1. Torque Speed Curve
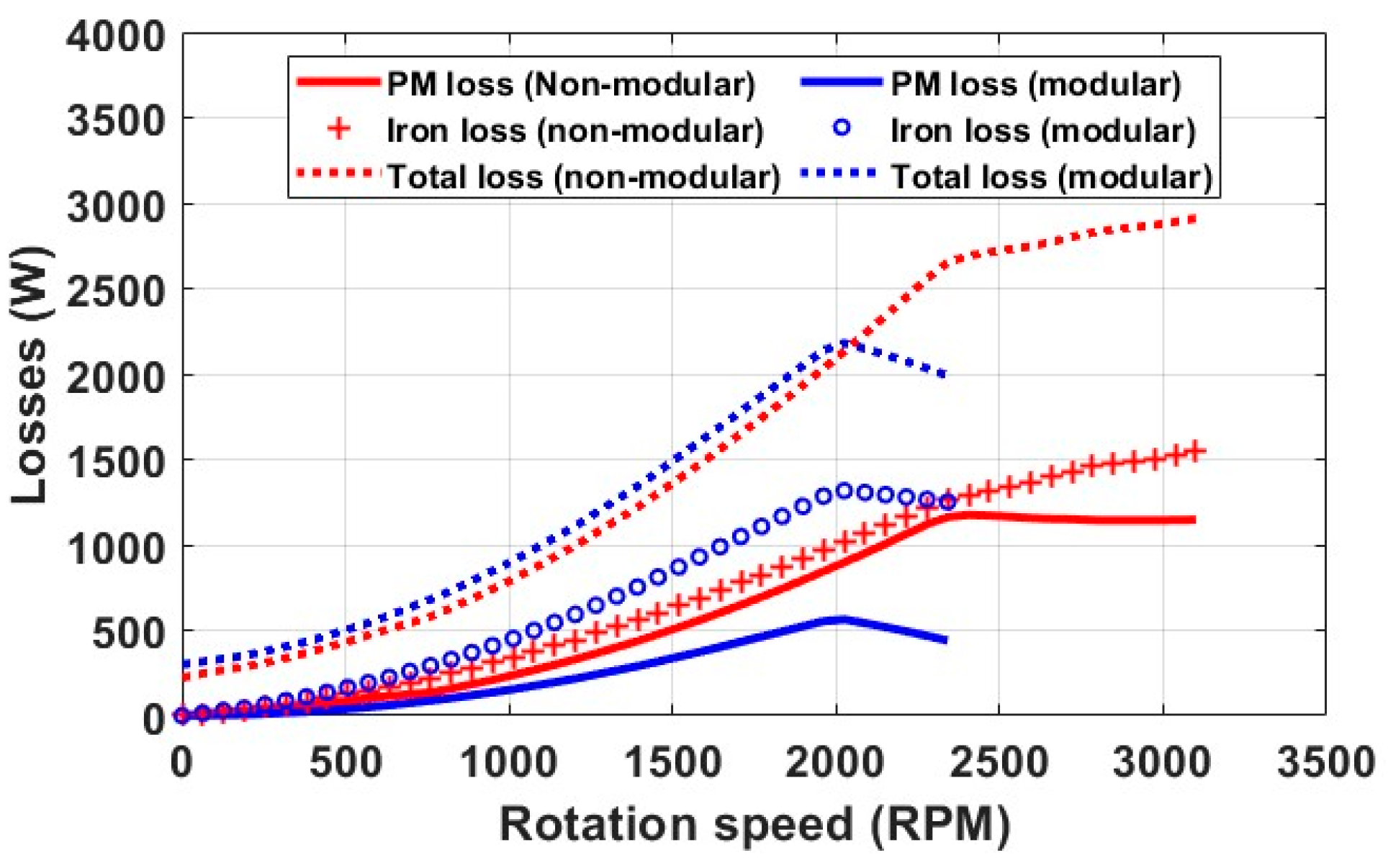
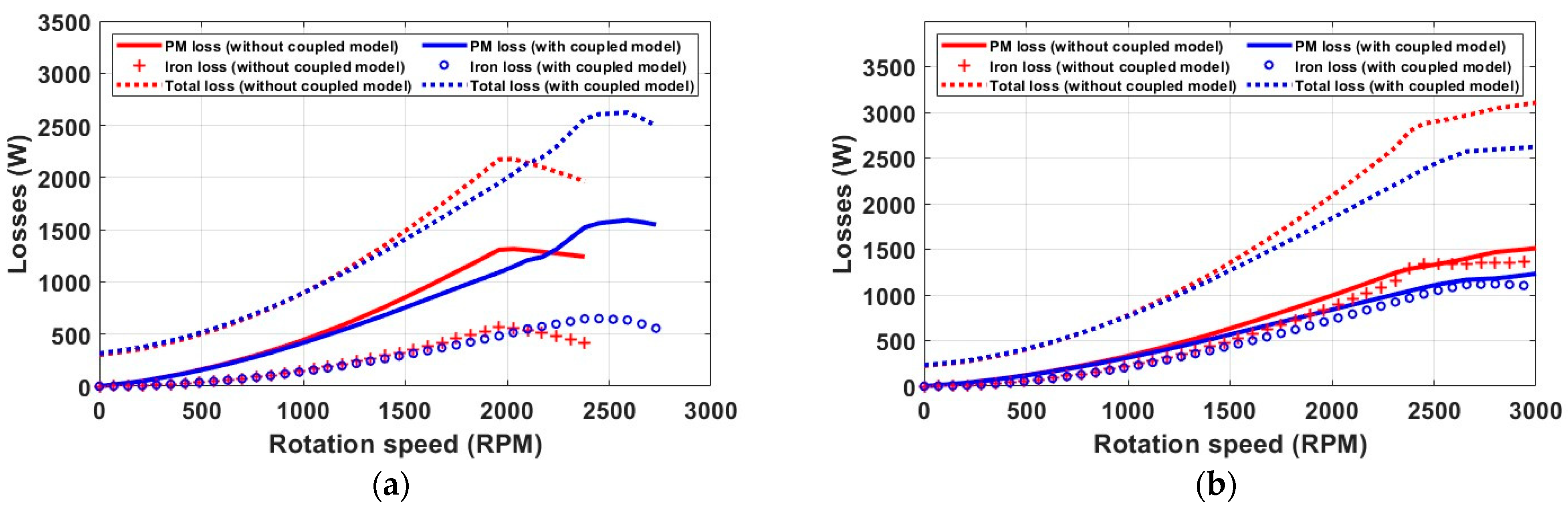
2.1.2. Losses Speed Curve
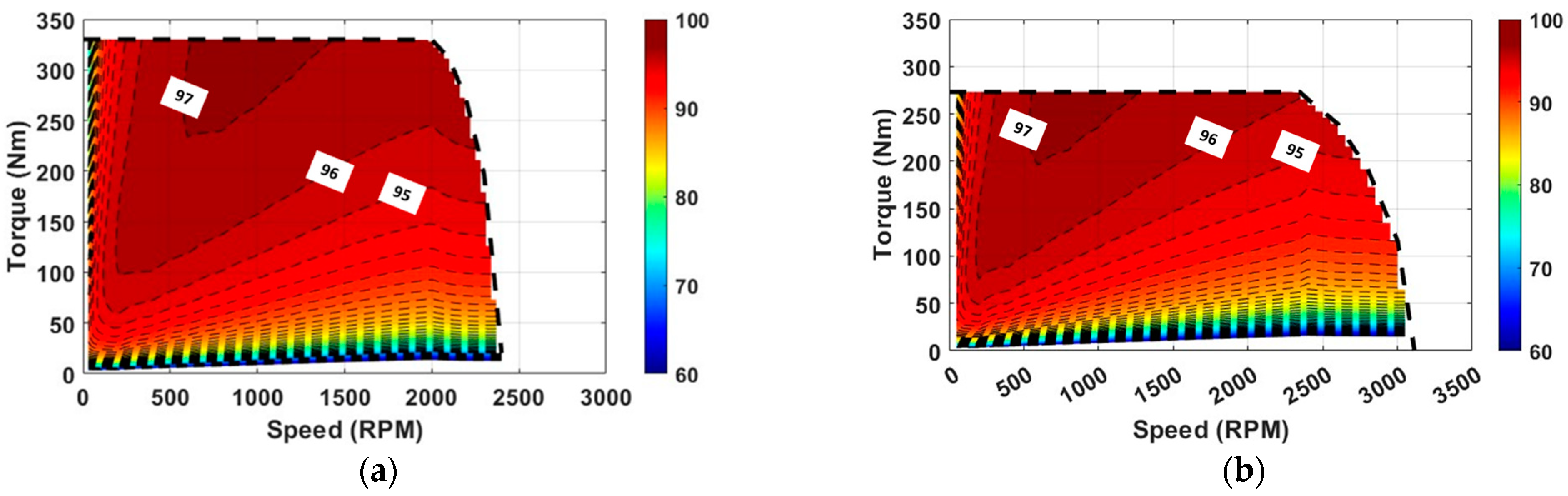
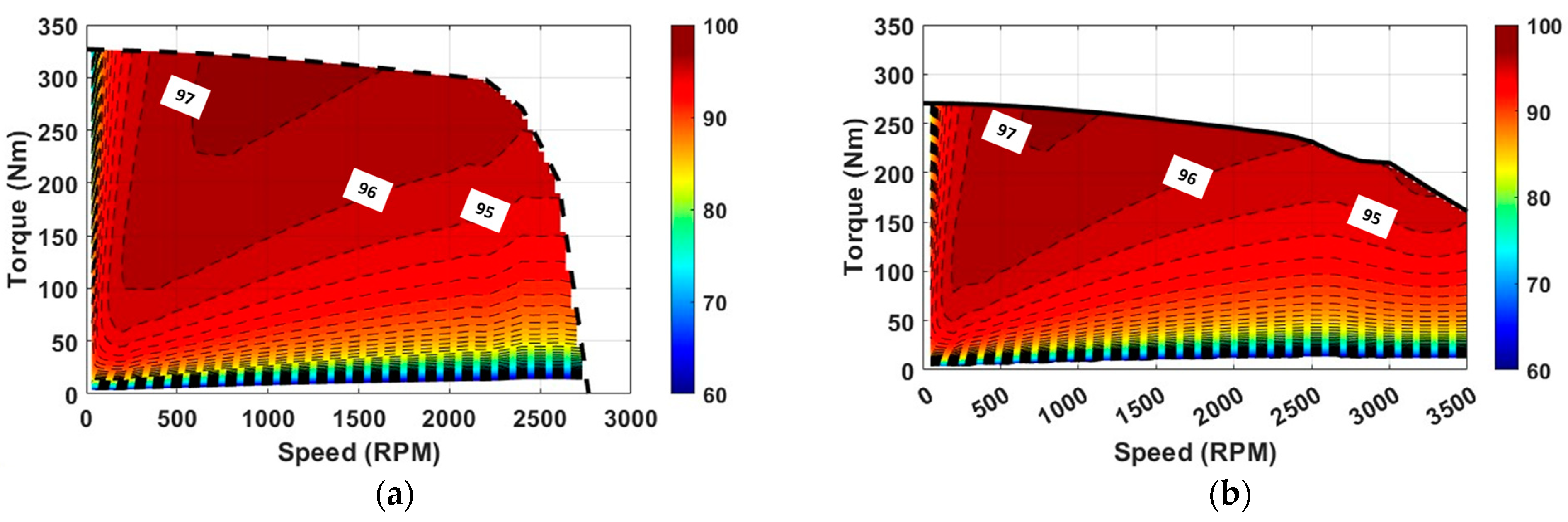
2.1.3. Efficiency Map
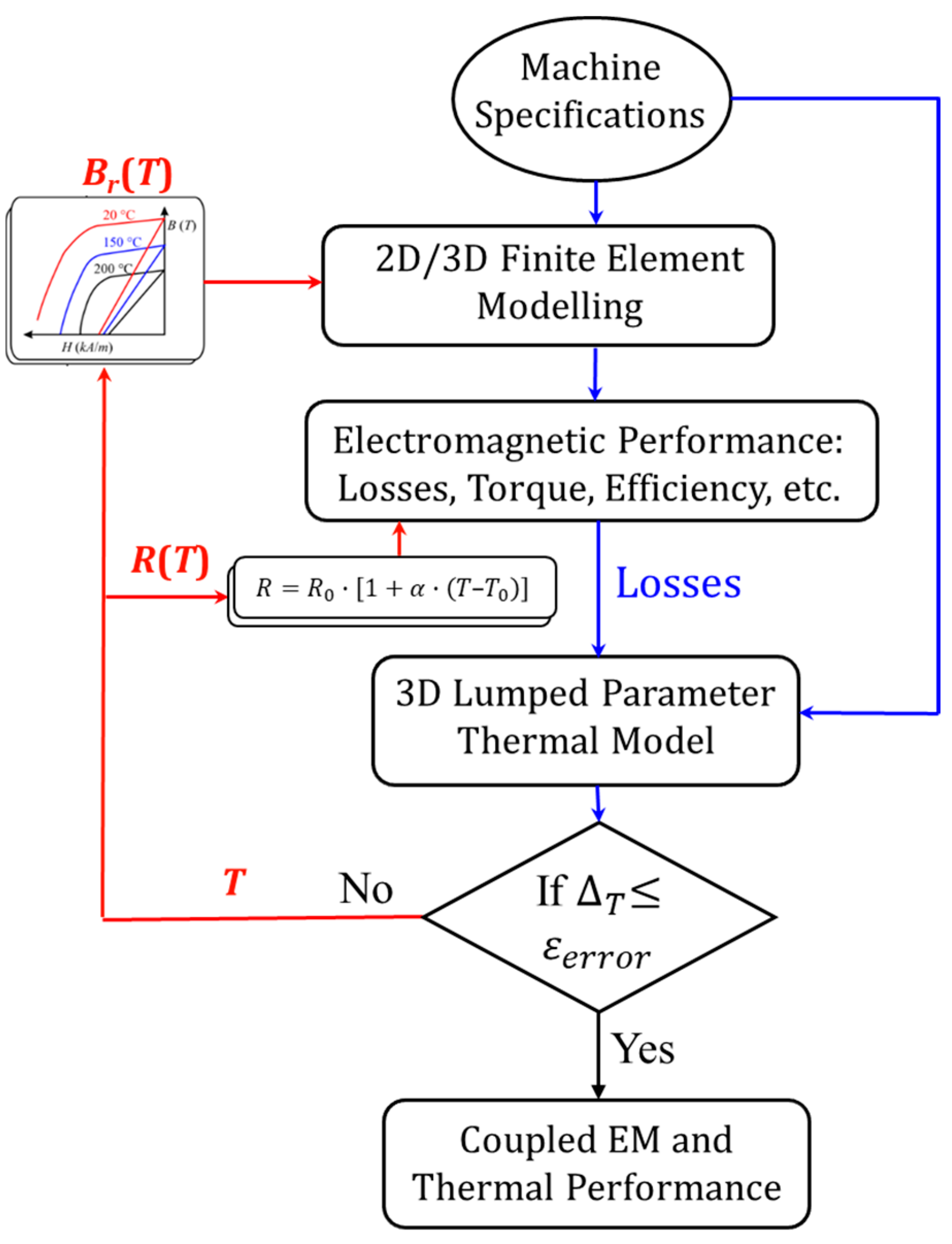
2.2. With EM–Thermal Coupling
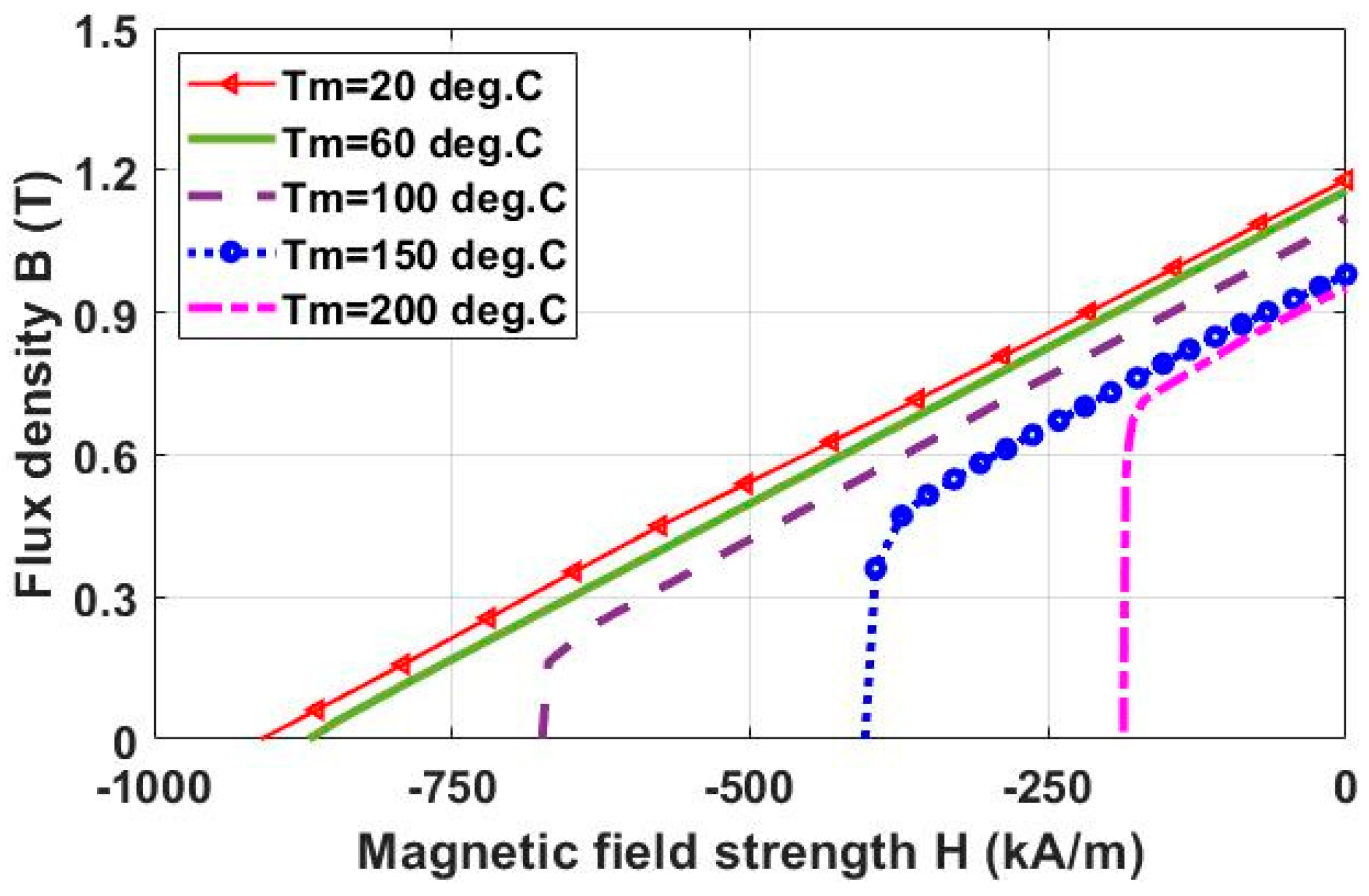
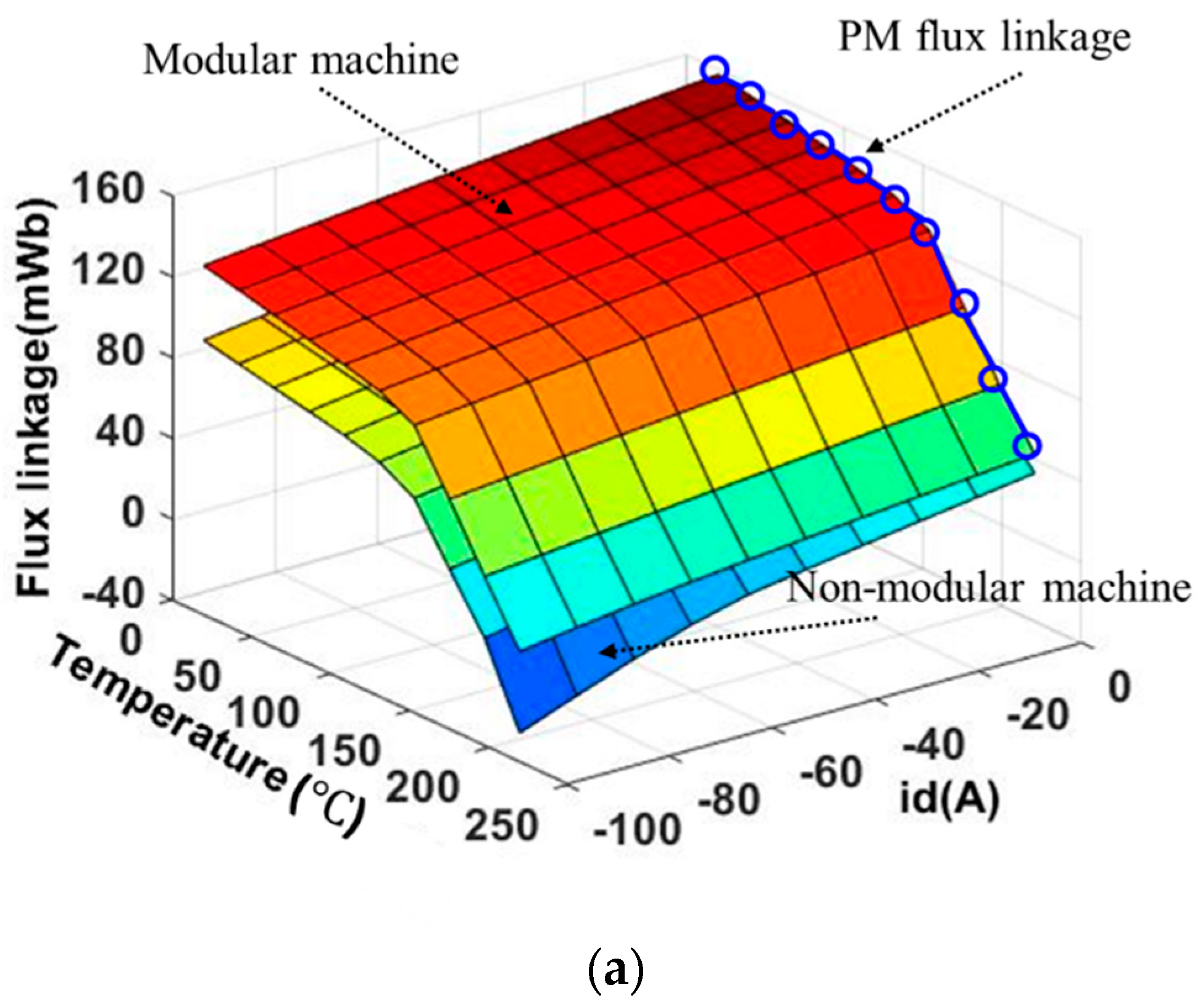
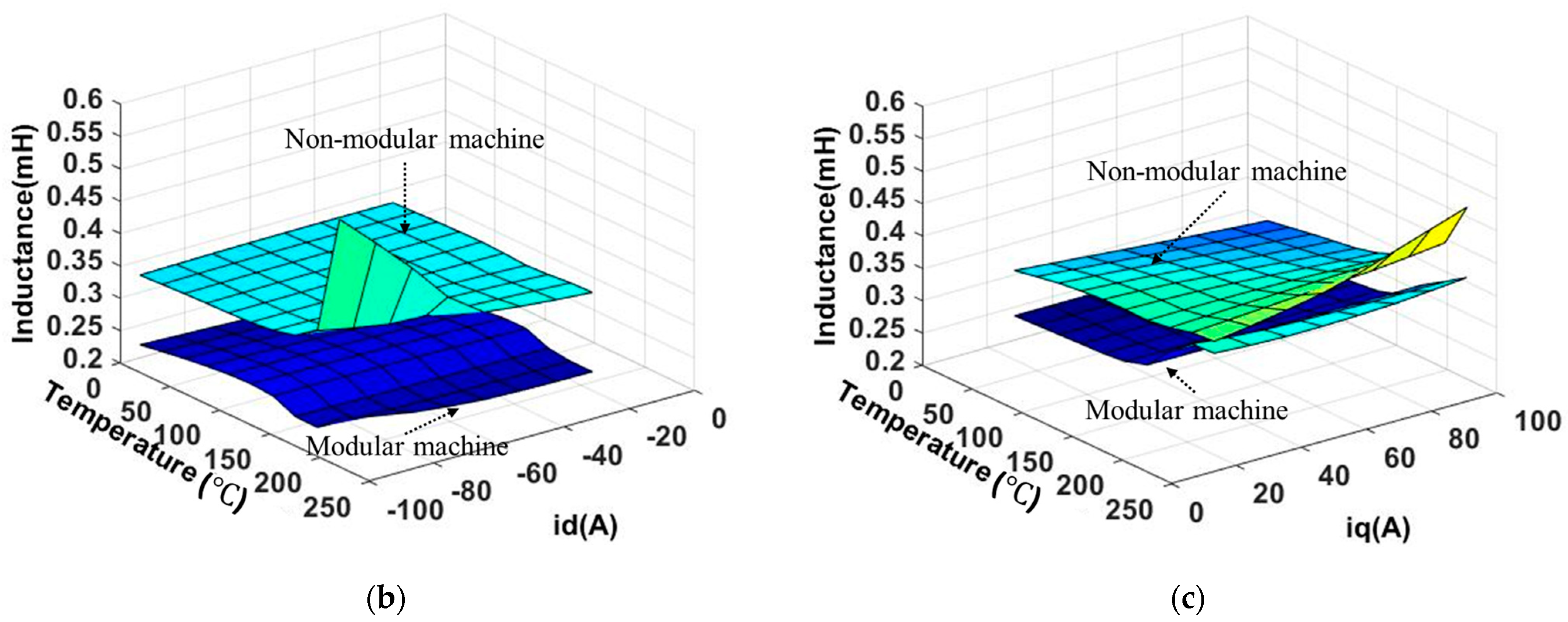
2.2.1. Temperature-Dependent PM Flux Linkage and Inductance
- (a)
- The electrical resistivity of the PM and iron core are independent of temperature variation. This is safe as when temperature increases within a limited range, the increase in resistivity of the PM and iron core can be largely negligible [19].
- (b)
- The investigated machines are designed for the direction control of helicopters that do not require continuous operation. Hence, the duty ratio of 0.2 for the investigated machines has been adopted, and one cycle lasts for 4000 s.
- (c)
- The allowable convergence error () is set to be 0.5% in this paper.
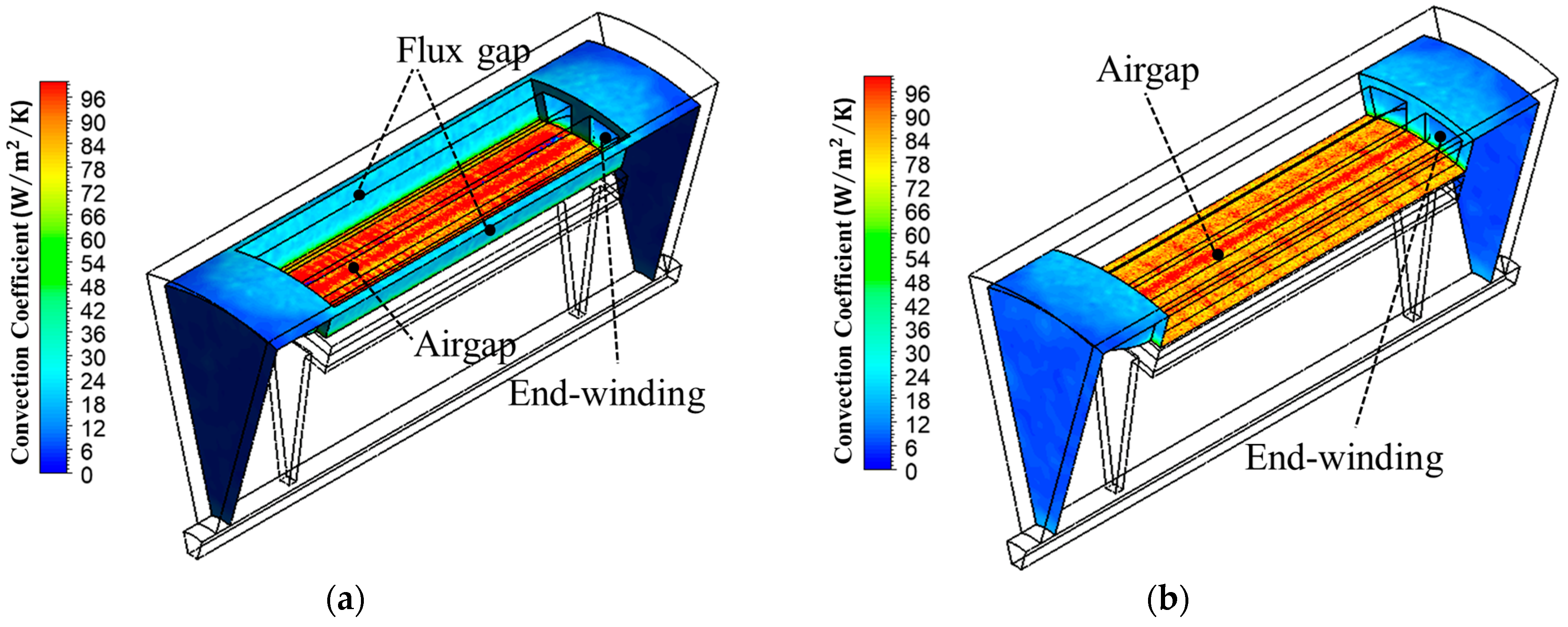
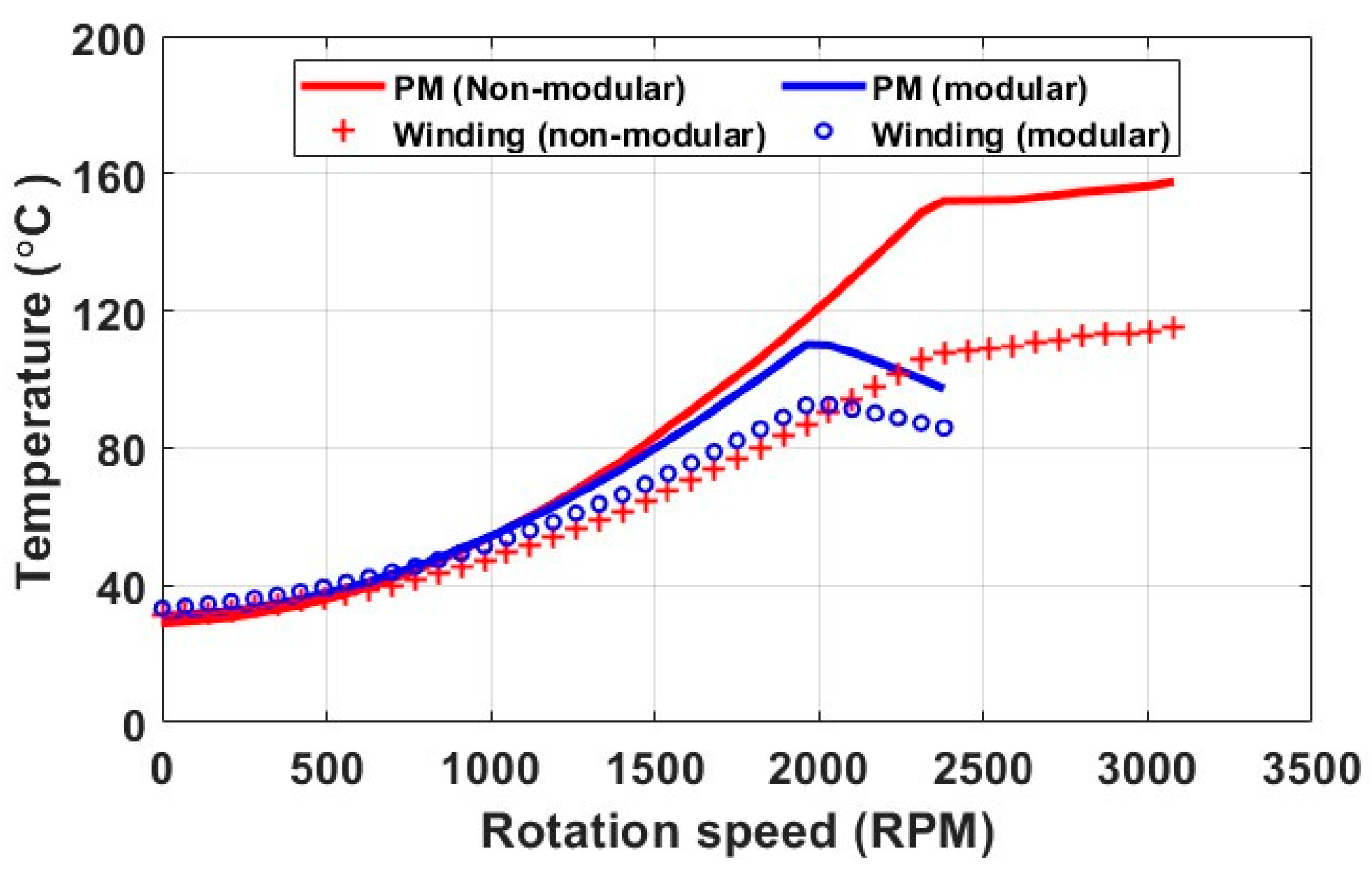
2.2.2. Temperature Speed Curve
2.2.3. Dynamic Performance
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

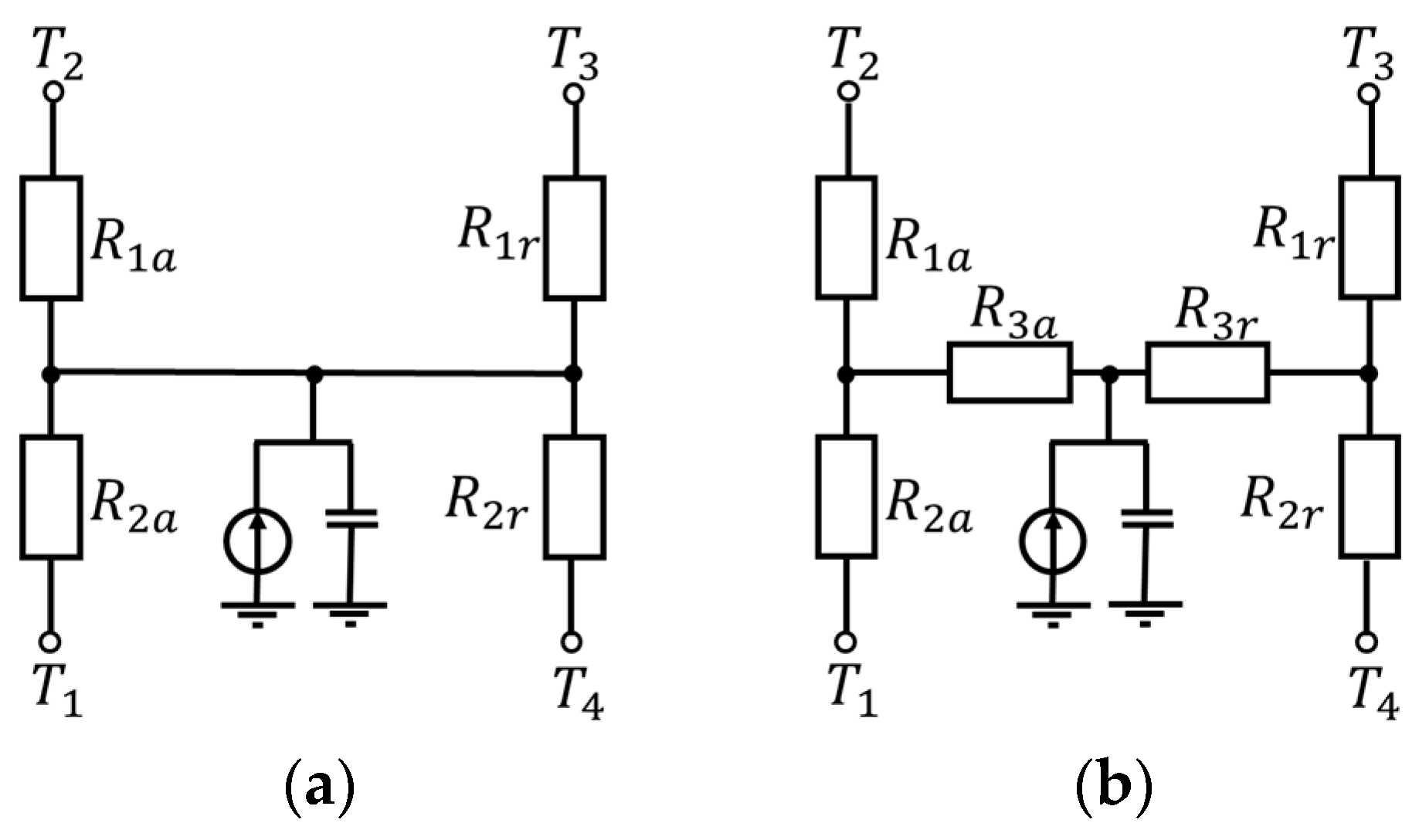
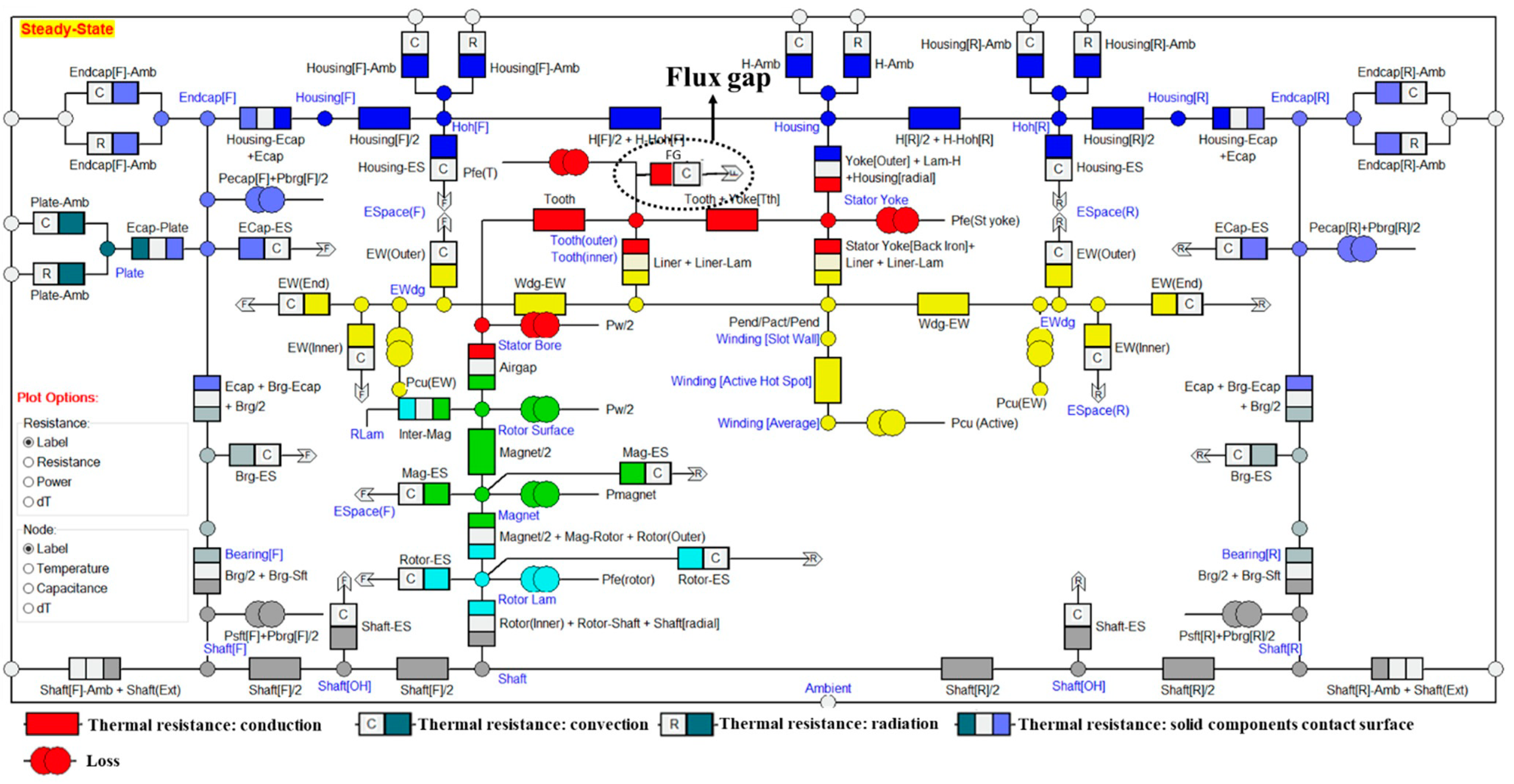
References
- Gerada, C.; Galea, M.; Kladas, A. Electrical Machines for Aerospace Applications. In Proceedings of the 2015 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Torino, Italy, 26–27 March 2015; pp. 79–84. [Google Scholar]
- Galea, M.; Xu, Z.; Tighe, C.; Hamiti, T.; Gerada, C.; Pickering, S. Development of an Aircraft Wheel Actuator for Green Taxiing. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 2492–2498. [Google Scholar]
- Ishak, D.; Zhu, Z.Q.; Howe, D. Permanent Magnet Brushless Machines with Unequal Tooth Widths and Similar Slot and Pole Numbers. In Proceedings of the 2004 IEEE Industry Applications Conference, 39th IAS Annual Meeting, Seattle, WA, USA, 3–7 October 2004; pp. 1055–1061. [Google Scholar]
- Tapia, J.A.; Leonardi, F.; Lipo, T.A. Consequent-pole permanent-magnet machine with extended field-weakening capability. IEEE Trans. Ind. Appl. 2003, 39, 1704–1709. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Zhu, Z. Analytical modeling of modular and unequal tooth width surface-mounted permanent magnet machines. IEEE Trans. Magn. 2015, 51, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Ren, B.; Zhu, Z.; Foster, M.; Stone, D. Demagnetization withstand capability enhancement of surface mounted PM machines using stator modularity. IEEE Trans. Ind. Appl. 2017, 54, 1302–1311. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Li, G.J.; Zhu, Z.Q.; Ren, B.; Chong, Y.C.; Michon, M. Demagnetization Analysis of Modular SPM Machine Based on Coupled Electromagnetic–Thermal Modelling. Energies 2022, 16, 131. [Google Scholar] [CrossRef]
- Li, G.J.; Liang, X.B.; Zhu, Z.Q.; Ojeda, J.; Gabsi, M. Vibrations and Acoustic Noise Analyses of Modular SPM Machines. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 5567–5573. [Google Scholar]
- Zhou, R.; Li, G.J.; Zhang, K.; Zhu, Z.; Foster, M.; Stone, D. Performance Investigation of Consequent-Pole PM Machines with E-core and C-core Modular Stators. IEEE Trans. Energy Convers. 2020, 36, 1169–1179. [Google Scholar] [CrossRef]
- Taras, P.; Li, G.J.; Zhu, Z.Q. Comparative study of fault-tolerant switched-flux permanent-magnet machines. IEEE Trans. Ind. Electron. 2016, 64, 1939–1948. [Google Scholar] [CrossRef]
- Chen, Z.; Spooner, E. A modular, permanent-magnet generator for variable speed wind turbines. In Proceedings of the Seventh International Conference on Electrical Machines and Drives, Durham, UK, 11–13 September 1995; pp. 453–457. [Google Scholar]
- Zhang, W.; Li, G.J.; Zhu, Z.Q.; Ren, B.; Michon, M. Optimization of Modular SPM Machines Considering Stator Modularity. In Proceedings of the International Electric Machines and Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021. [Google Scholar]
- Joo, D.; Cho, J.H.; Woo, K.; Kim, B.-T.; Kim, D.K. Electromagnetic field and thermal linked analysis of interior permanent-magnet synchronous motor for agricultural electric vehicle. IEEE Trans. Magn. 2011, 47, 4242–4245. [Google Scholar] [CrossRef]
- Zhou, P.; Lin, D.; Xiao, Y.; Lambert, N.; Rahman, M. Temperature-dependent demagnetization model of permanent magnets for finite element analysis. IEEE Trans. Magn. 2012, 48, 1031–1034. [Google Scholar] [CrossRef]
- Dellinger, J.H. The Temperature Coefficient of Resistance of Copper; US Government Printing Office: Washington, DC, USA, 1911. [Google Scholar]
- Jiang, W.; Jahns, T.M. Development of Efficient Electromagnetic-Thermal Coupled Model of Electric Machines Based on Finite Element Analysis. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 816–823. [Google Scholar]
- Shi, Y.; Wang, J.; Wang, B. Electromagnetic-thermal coupled simulation under various fault conditions of a triple redundant 9-phase PMASynRM. IEEE Trans. Ind. Appl. 2019, 56, 128–137. [Google Scholar] [CrossRef]
- Ruoho, S.; Santa-Nokki, T.; Kolehmainen, J.; Arkkio, A. Modeling magnet length in 2-D finite-element analysis of electric machines. IEEE Trans. Magn. 2009, 45, 3114–3120. [Google Scholar] [CrossRef]
- Wu, K.; Yao, Y.; Klik, I. Electrical and magnetic properties of NdFeB films. Appl. Surf. Sci. 1997, 113, 174–177. [Google Scholar] [CrossRef]
- Micallef, C. End Winding Cooling in Electric Machines; University of Nottingham: Nottingham, UK, 2006. [Google Scholar]
- Sebastian, T. Temperature effects on torque production and efficiency of PM motors using NdFeB magnets. IEEE Trans. Ind. Appl. 1995, 31, 353–357. [Google Scholar] [CrossRef]
- Nerg, J.; Rilla, M.; Pyrhonen, J. Thermal analysis of radial-flux electrical machines with a high power density. IEEE Trans. Ind. Electron. 2008, 55, 3543–3554. [Google Scholar] [CrossRef]
- Gerling, D.; Dajaku, G. Novel Lumped-Parameter Thermal Model for Electrical Systems. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005; p. 10. [Google Scholar]
- El-Refaie, A.M.; Harris, N.C.; Jahns, T.M.; Rahman, K.M. Thermal analysis of multibarrier interior PM synchronous machine using lumped parameter model. IEEE Trans. Energy Convers. 2004, 19, 303–309. [Google Scholar] [CrossRef] [Green Version]
- Roberts, D. The Application of an Induction Motor Thermal Model to Motor Protection and Other Functions. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 1989. [Google Scholar]
- Mezani, S.; Takorabet, N.; Laporte, B. A combined electromagnetic and thermal analysis of induction motors. IEEE Trans. Magn. 2005, 41, 1572–1575. [Google Scholar] [CrossRef]
- Liu, Z.; Howe, D.; Mellor, P.; Jenkins, M. Thermal Analysis of Permanent Magnet Machines. In Proceedings of the 1993 Sixth International Conference on Electrical Machines and Drives (Conf. Publ. No. 376), Oxford, UK, 8–10 September 1993; pp. 359–364. [Google Scholar]
- Simpson, N.; Wrobel, R.; Mellor, P.H. Estimation of equivalent thermal parameters of impregnated electrical windings. IEEE Trans. Ind. Appl. 2013, 49, 2505–2515. [Google Scholar] [CrossRef]
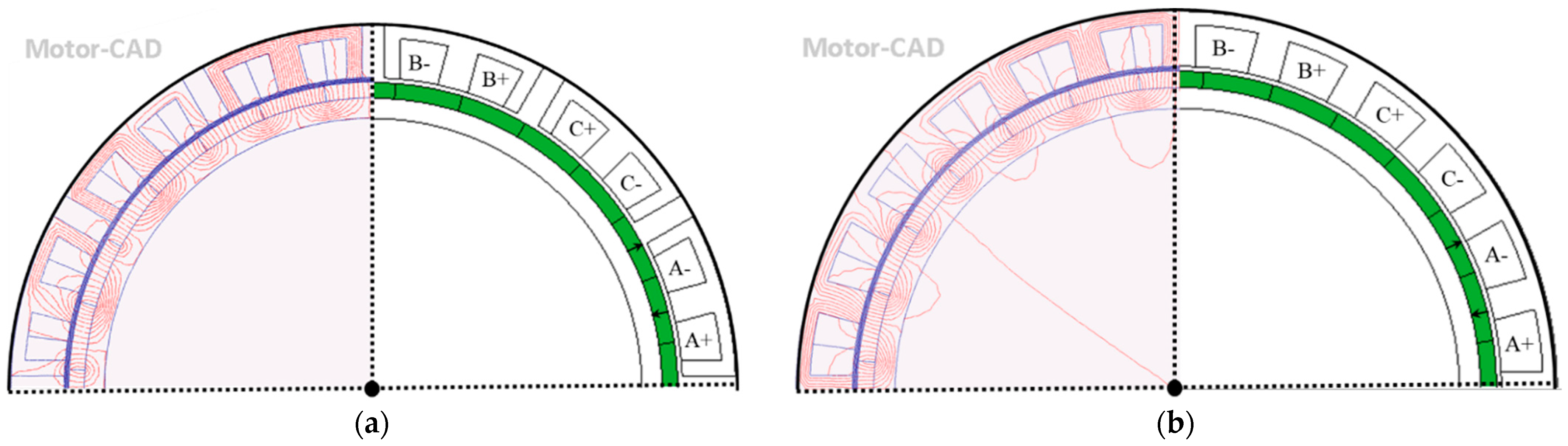
| Slot number | 24 | Rotor outer radius (mm) | 129.4 |
| Pole number | 28 | Rotor yoke thickness (mm) | 8.6 |
| Stator outer radius (mm) | 154 | Stack length (mm) | 210 |
| Stator yoke height (mm) | 5.6 | DC voltage (V) | 800 |
| Tooth width (mm) | 13.2 | Rated phase current () | 100 |
| Flux gap width (mm) | 10 | Number of turns per coil | 10 |
| Airgap length (mm) | 2 | Rate speed (rpm) | 1500 |
| Magnet thickness (mm) | 6.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Li, G.-J.; Zhu, Z.-Q.; Ren, B.; Chong, Y.C. Coupled Electromagnetic–Thermal Modelling of Dynamic Performance for Modular SPM Machines. Energies 2023, 16, 2516. https://doi.org/10.3390/en16062516
Zhang W, Li G-J, Zhu Z-Q, Ren B, Chong YC. Coupled Electromagnetic–Thermal Modelling of Dynamic Performance for Modular SPM Machines. Energies. 2023; 16(6):2516. https://doi.org/10.3390/en16062516
Chicago/Turabian StyleZhang, Wei, Guang-Jin Li, Zi-Qiang Zhu, Bo Ren, and Yew Chuan Chong. 2023. "Coupled Electromagnetic–Thermal Modelling of Dynamic Performance for Modular SPM Machines" Energies 16, no. 6: 2516. https://doi.org/10.3390/en16062516
APA StyleZhang, W., Li, G.-J., Zhu, Z.-Q., Ren, B., & Chong, Y. C. (2023). Coupled Electromagnetic–Thermal Modelling of Dynamic Performance for Modular SPM Machines. Energies, 16(6), 2516. https://doi.org/10.3390/en16062516








