Open-Source Energy, Entropy, and Exergy 0D Heat Release Model for Internal Combustion Engines
Abstract
1. Introduction
2. Model Equations
2.1. Conservation of Mass
2.2. Combustion
Expanded Combustion
2.3. Conservation of Energy
2.4. Conservation of Entropy
2.5. Exergy
3. Experimental Setup
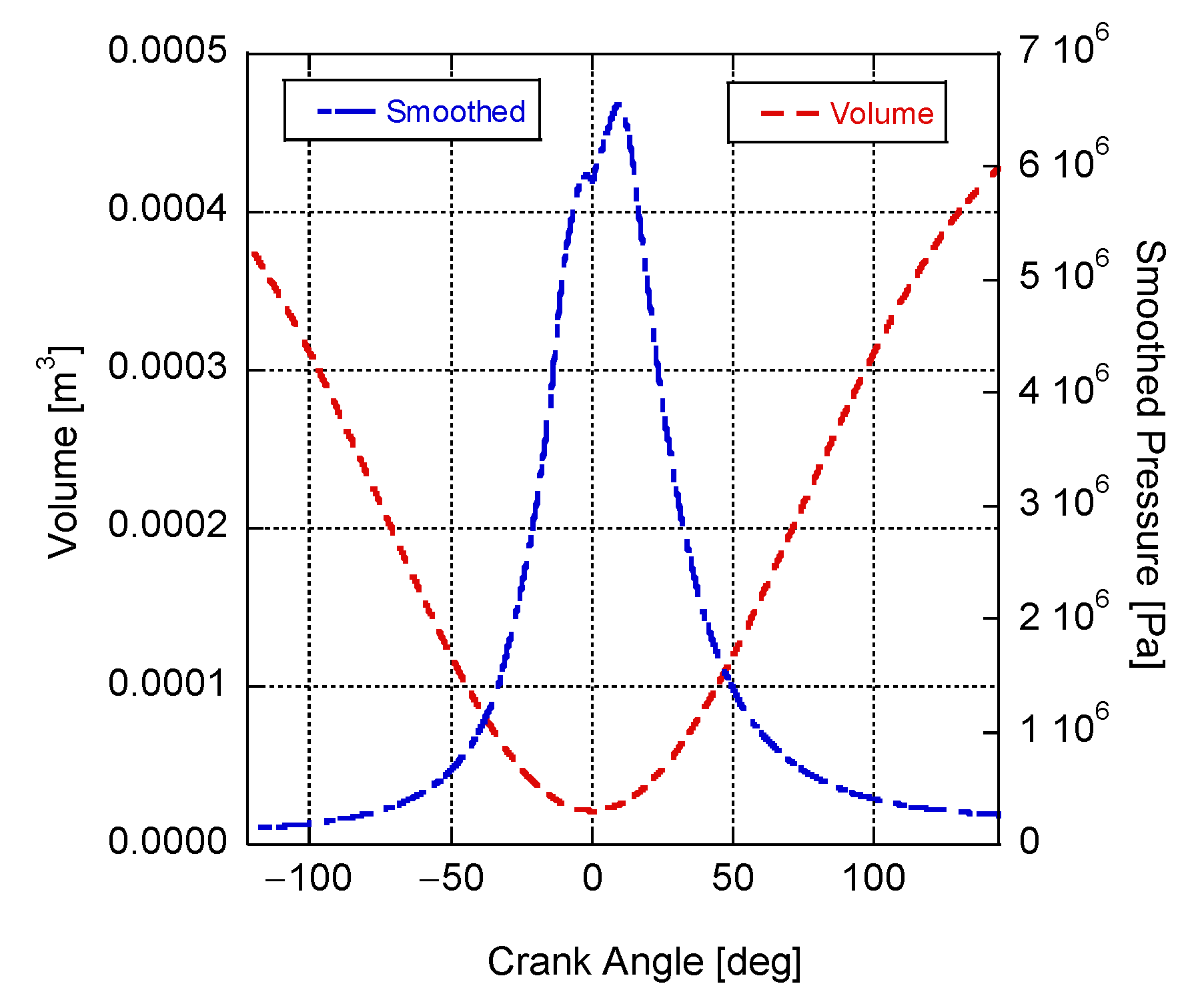
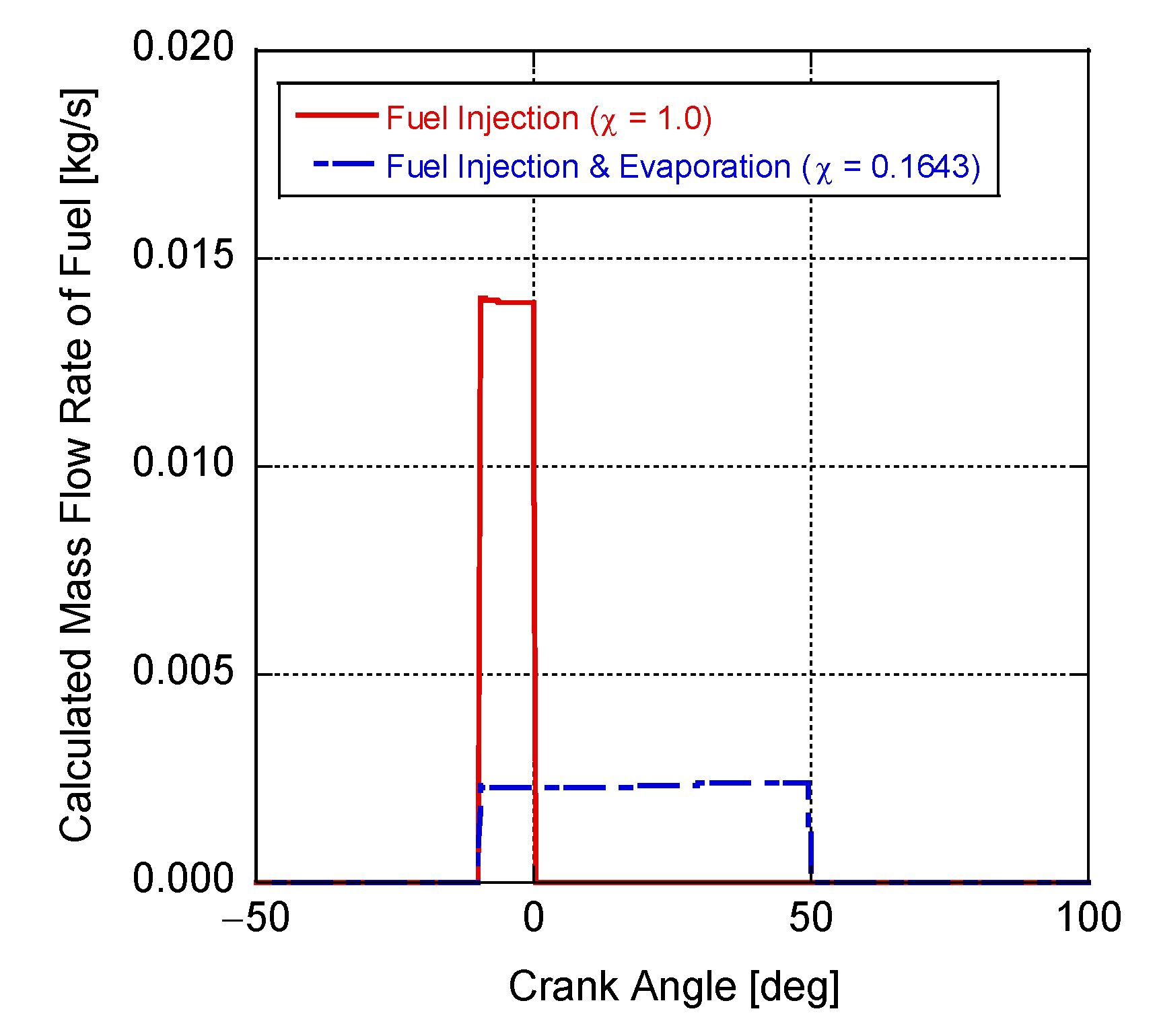
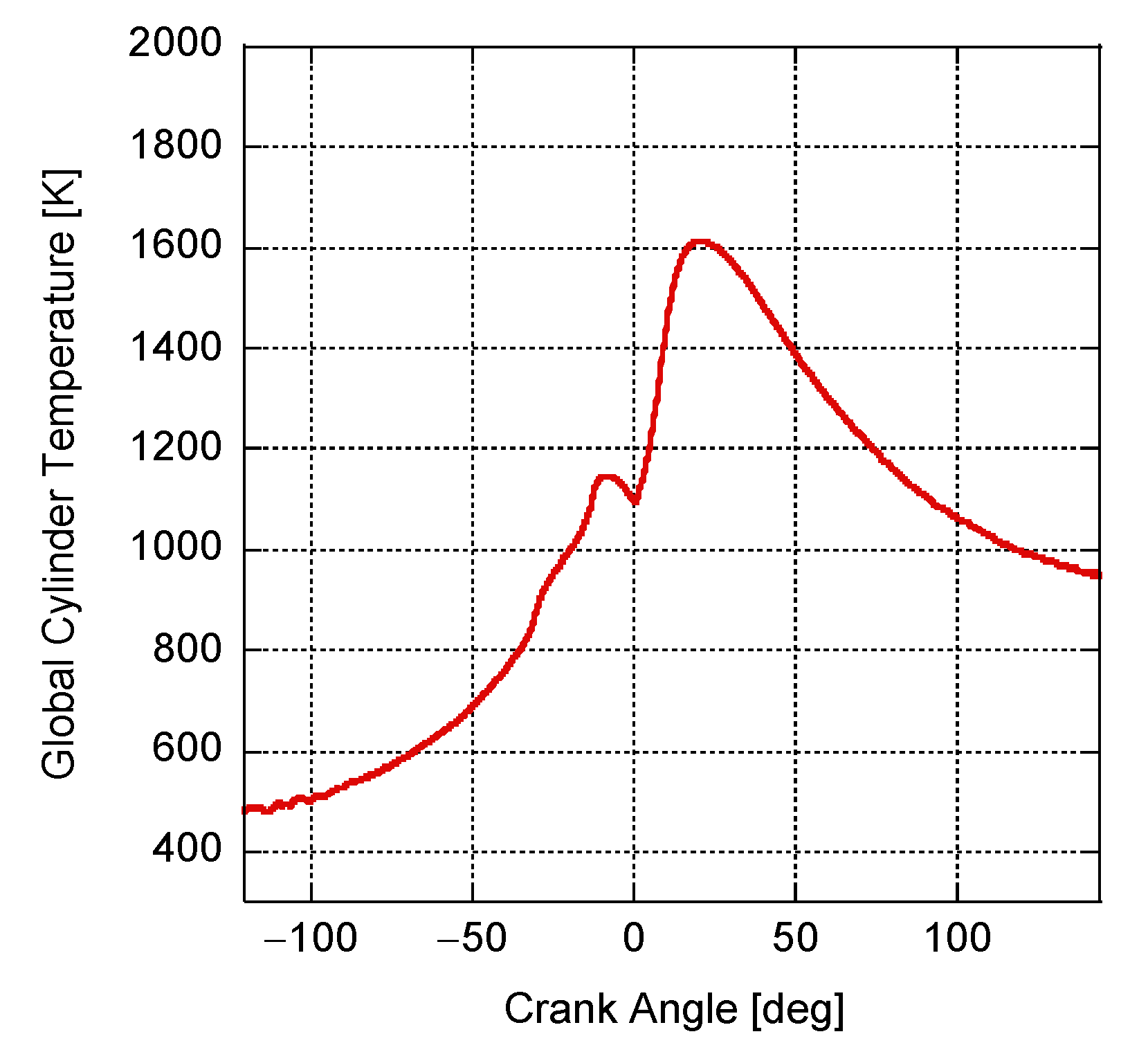
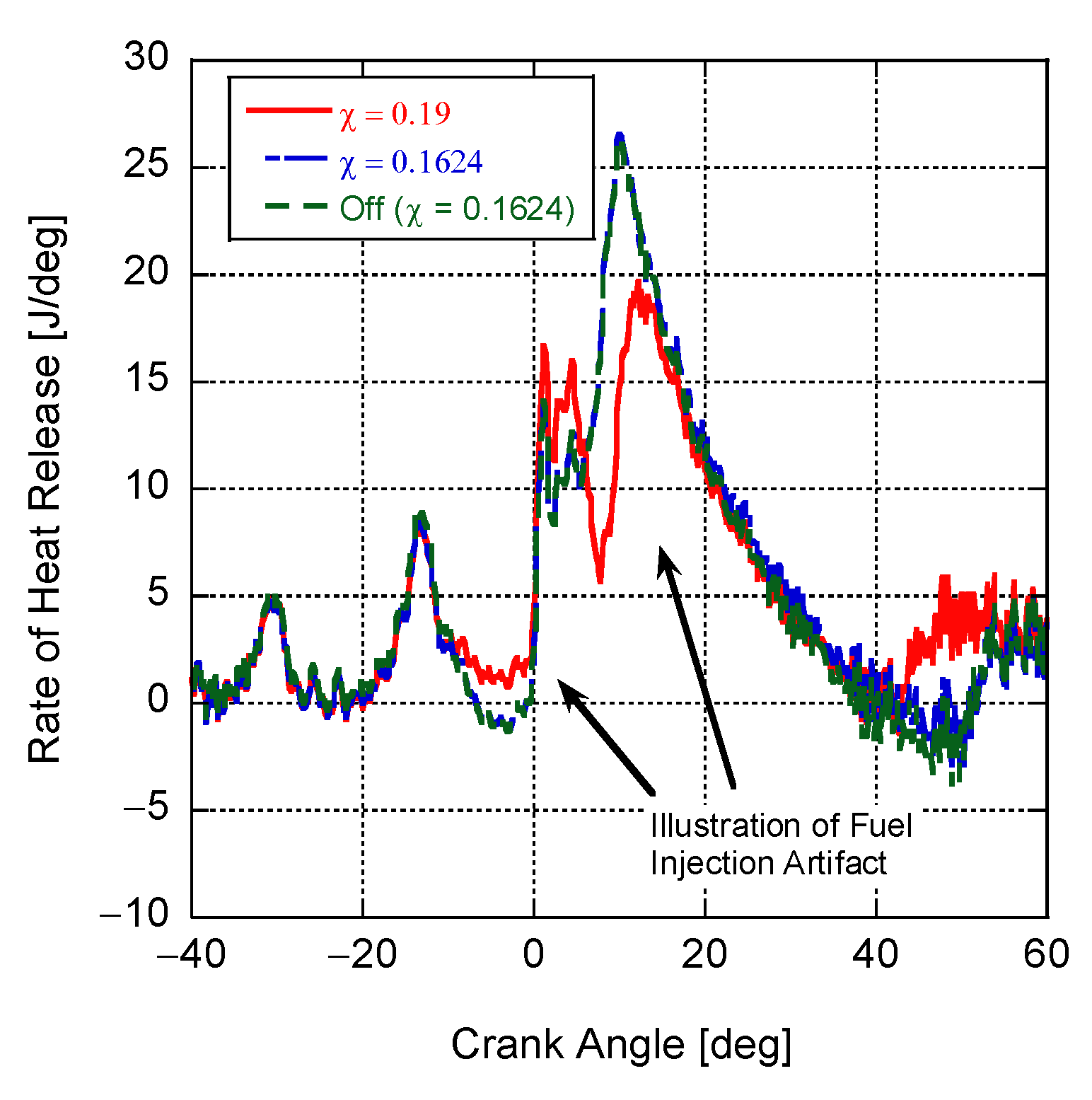
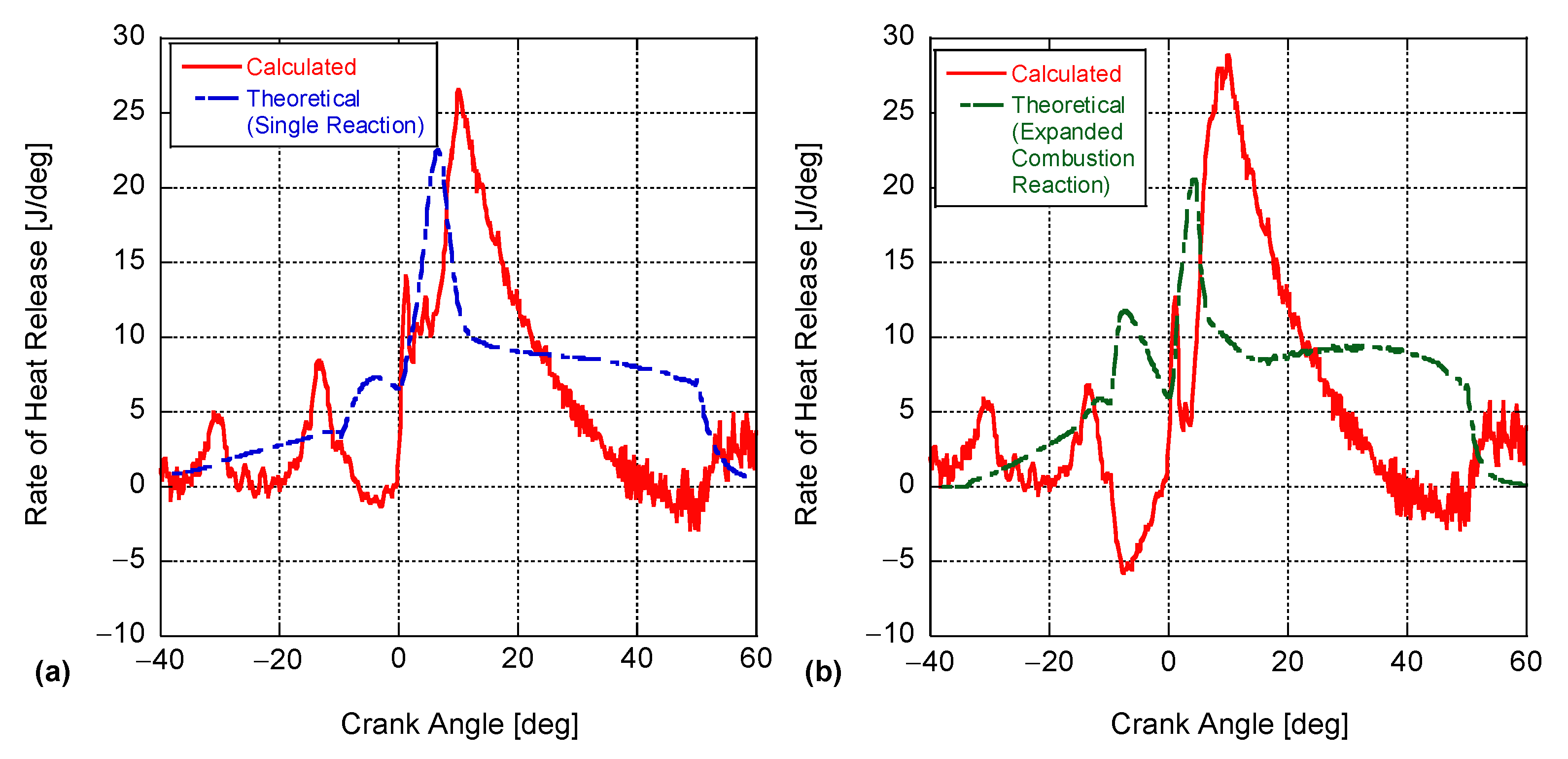
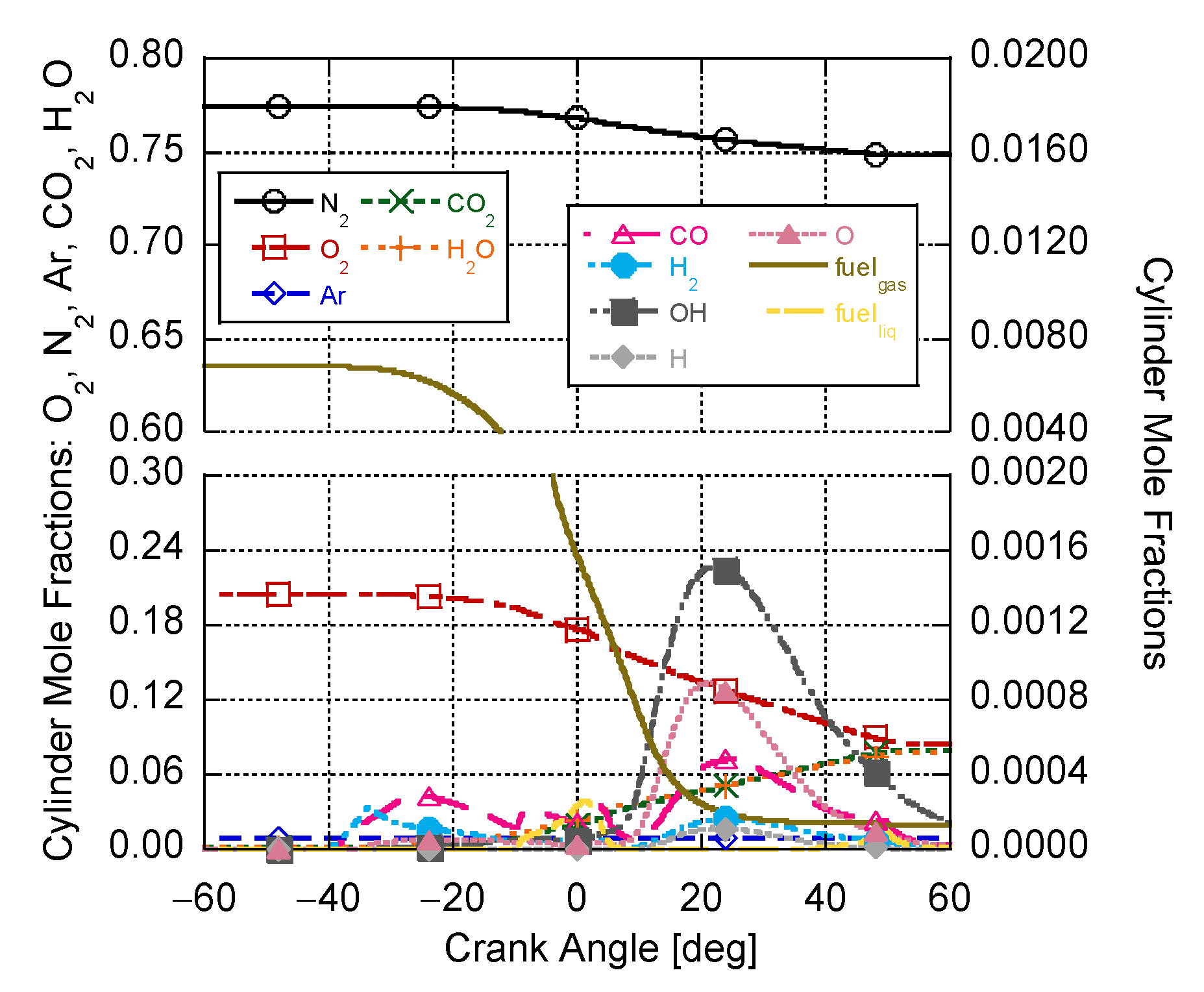
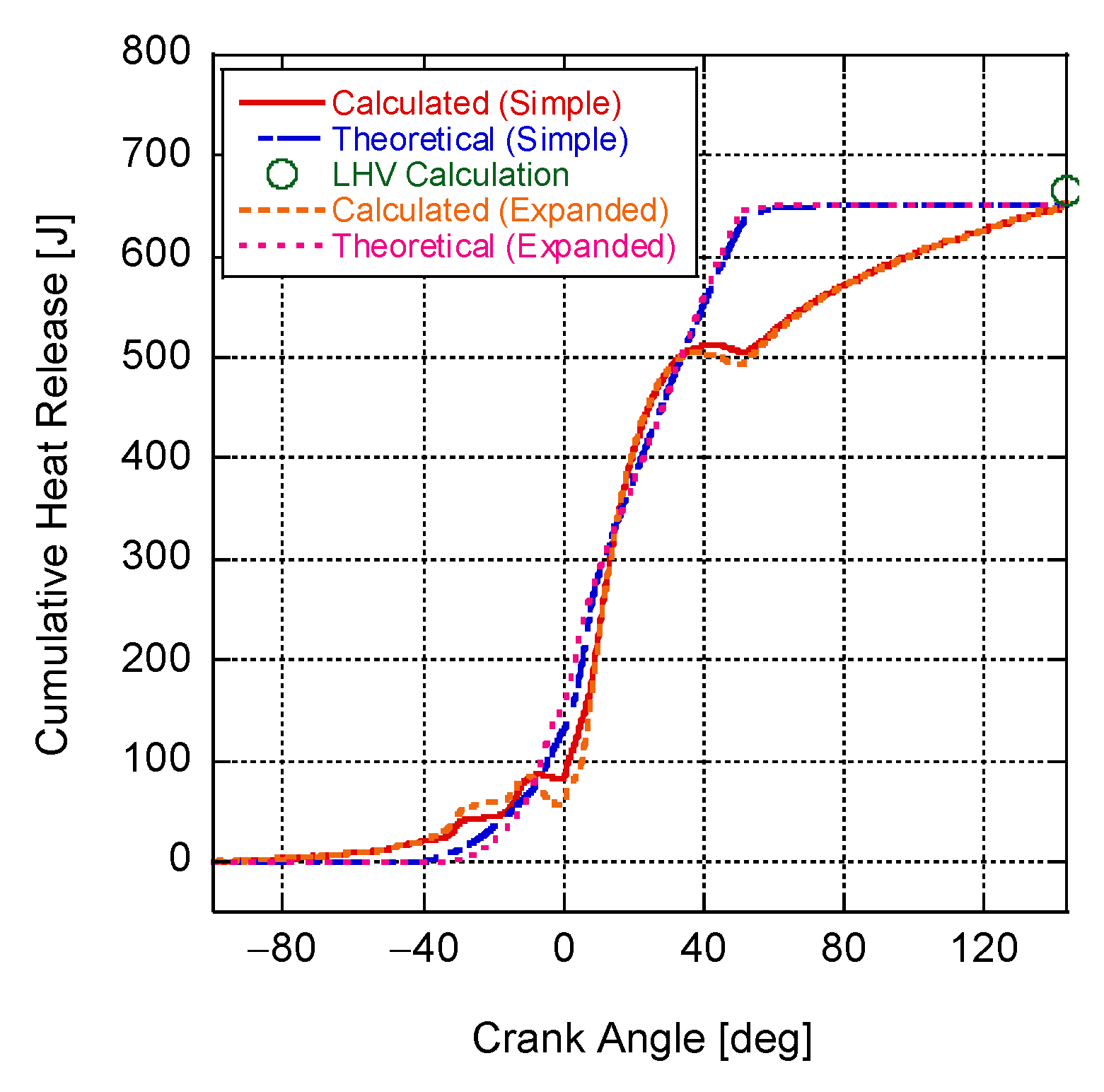
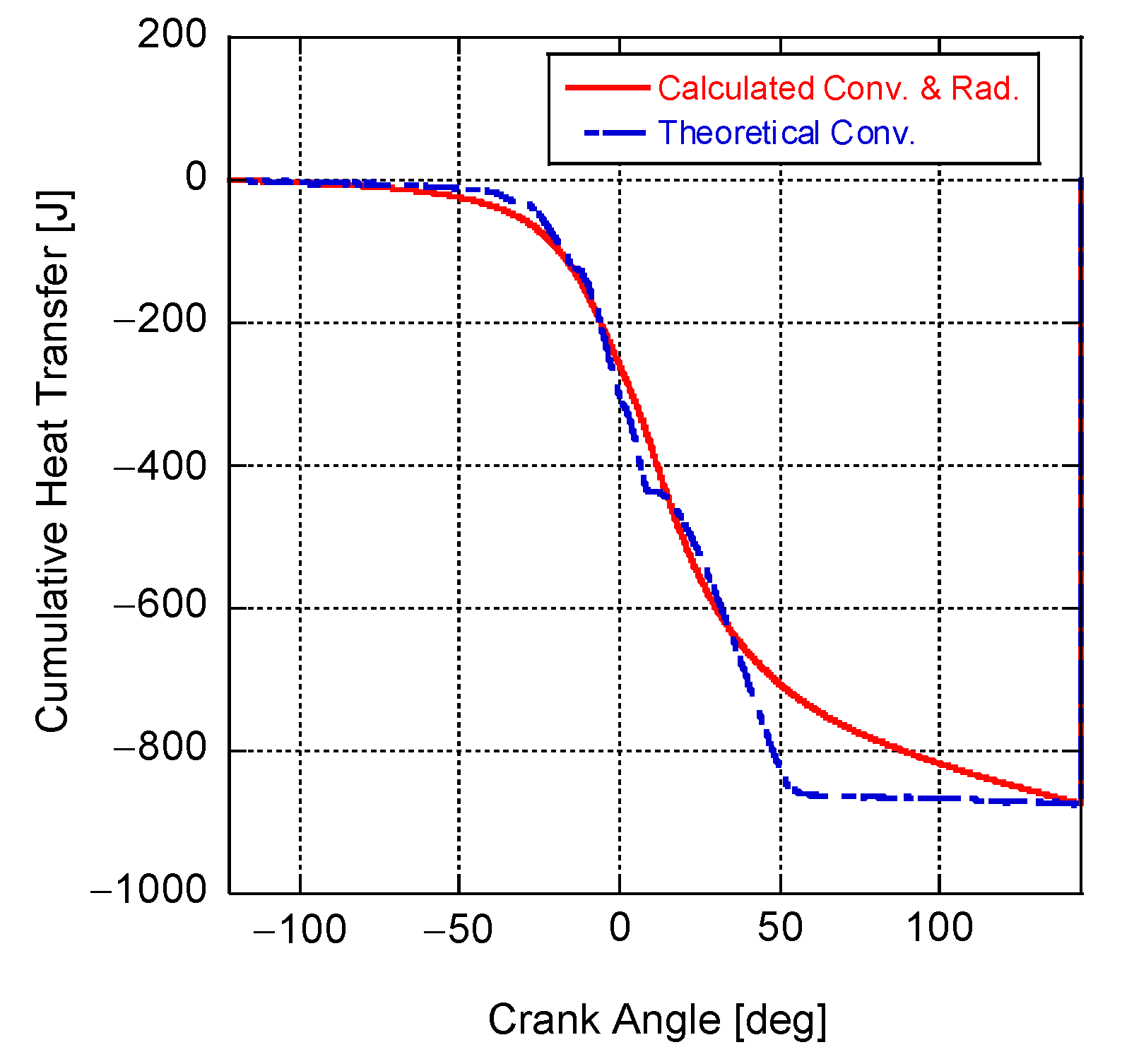
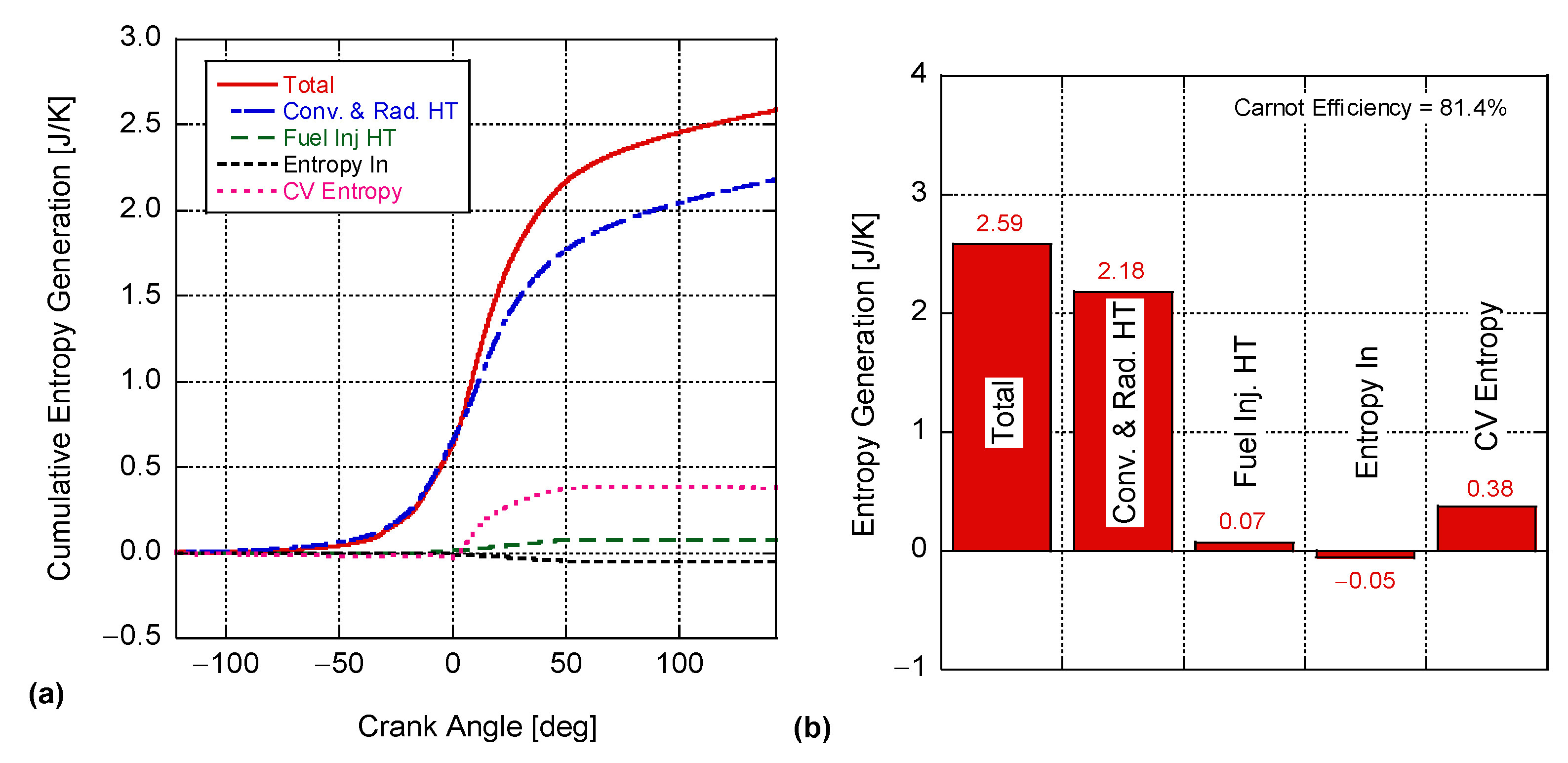
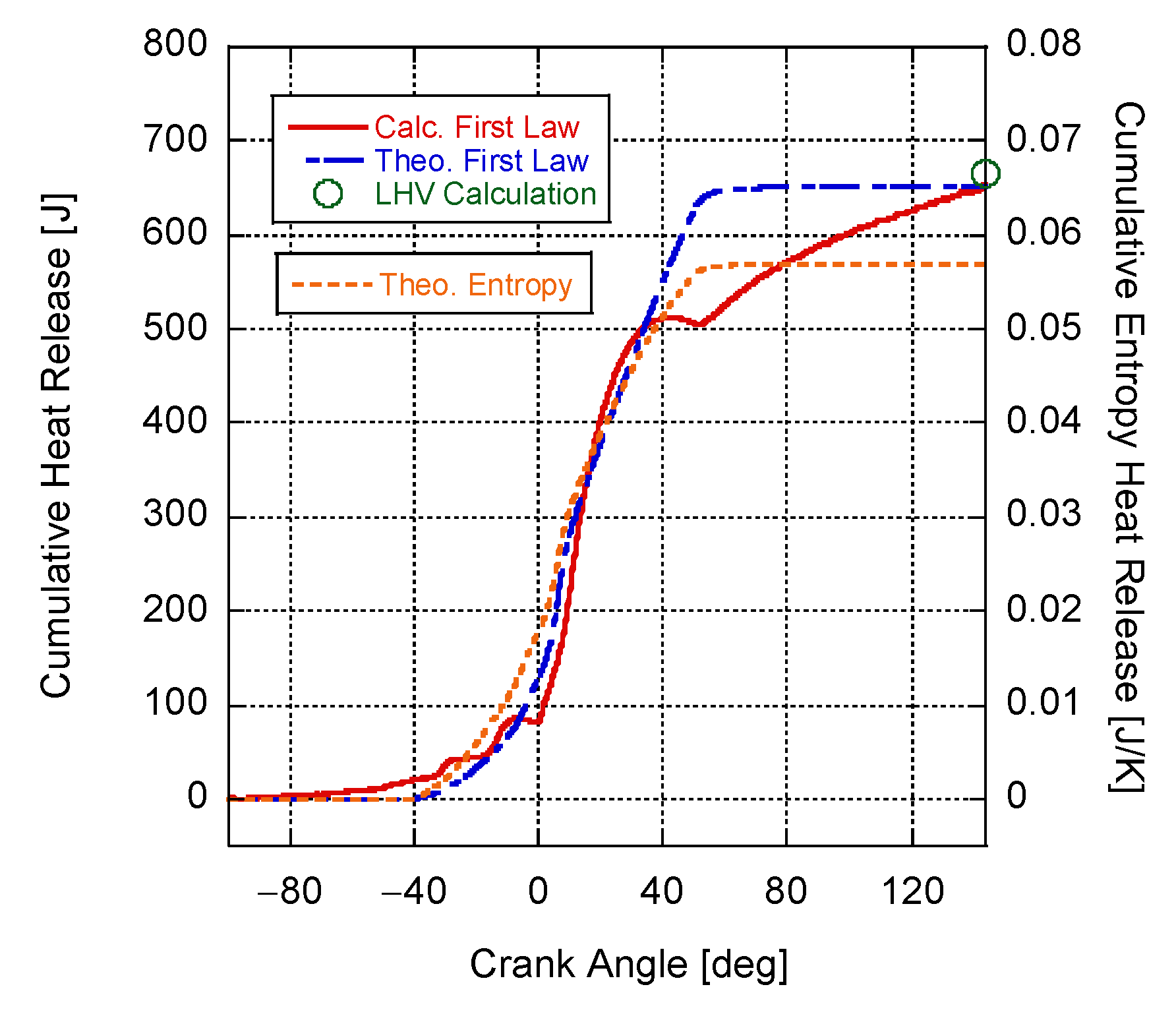
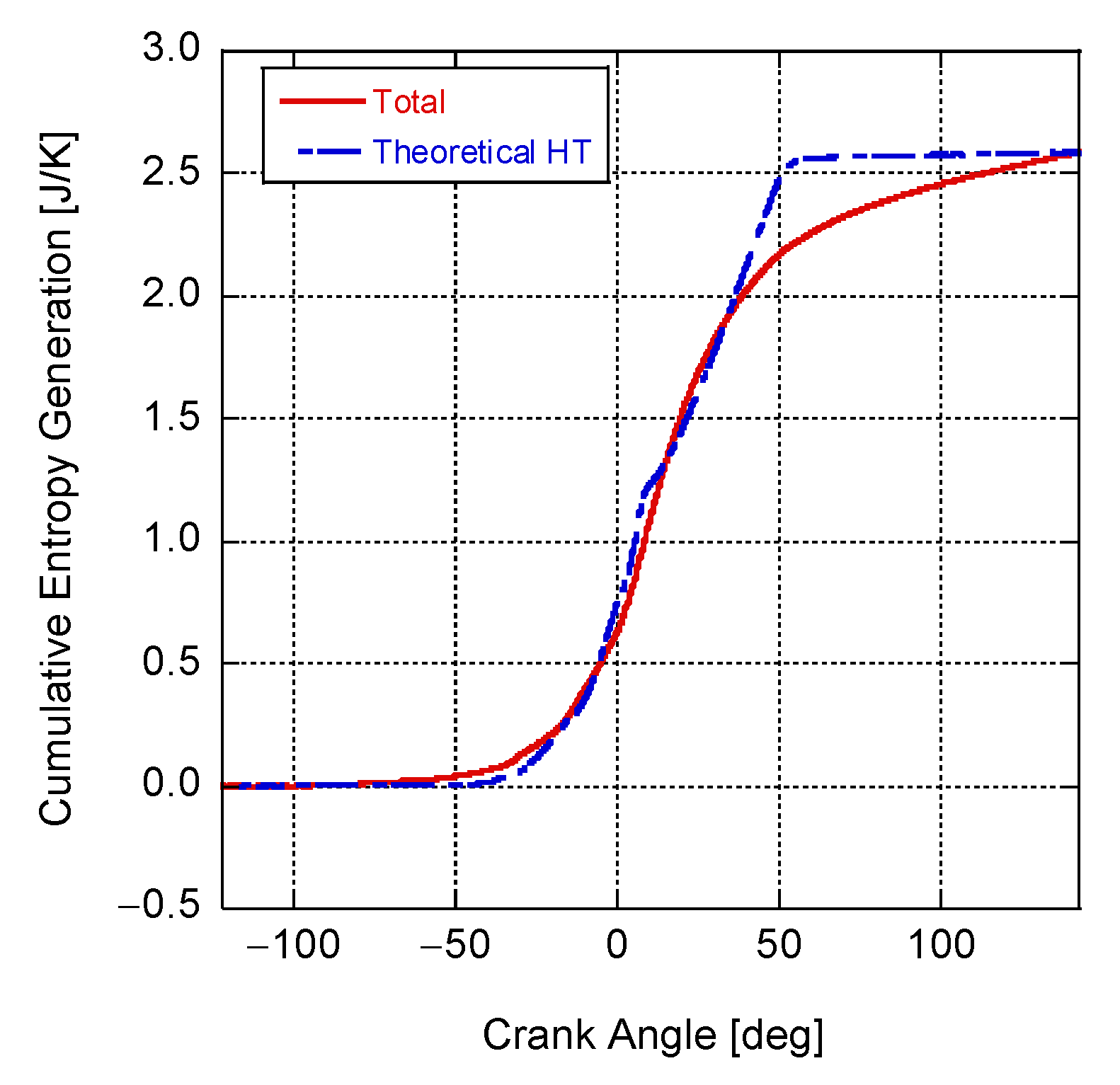
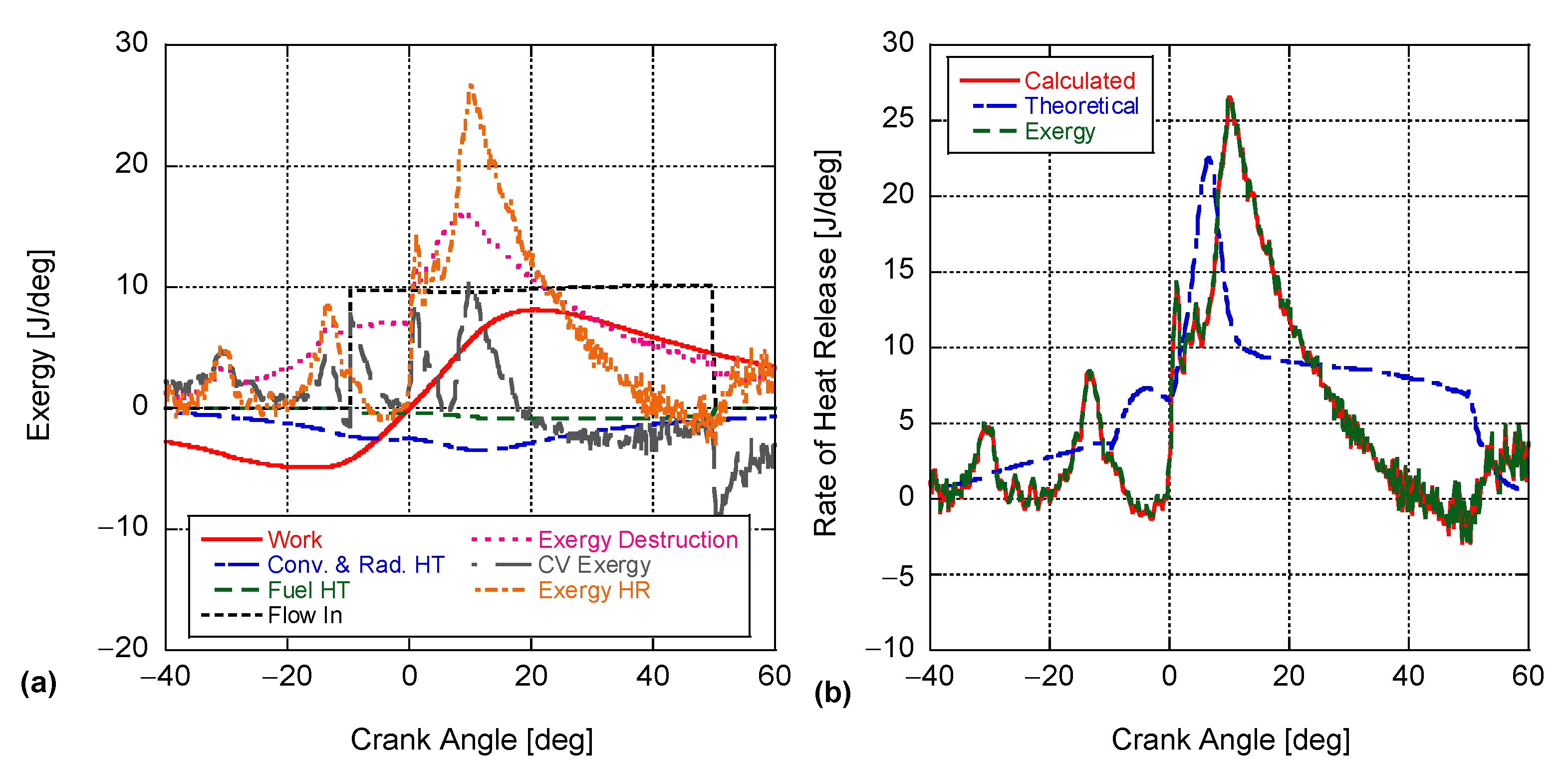
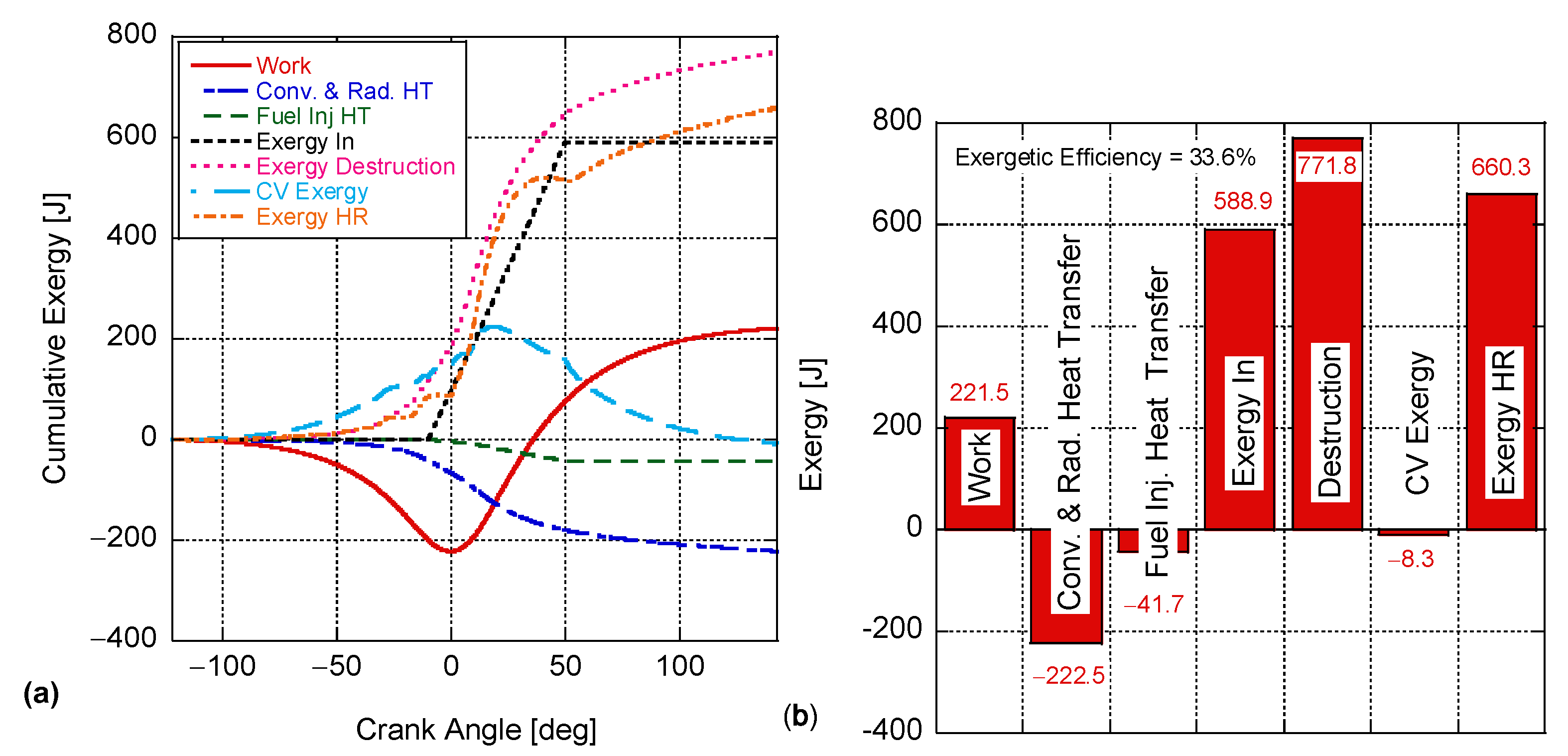
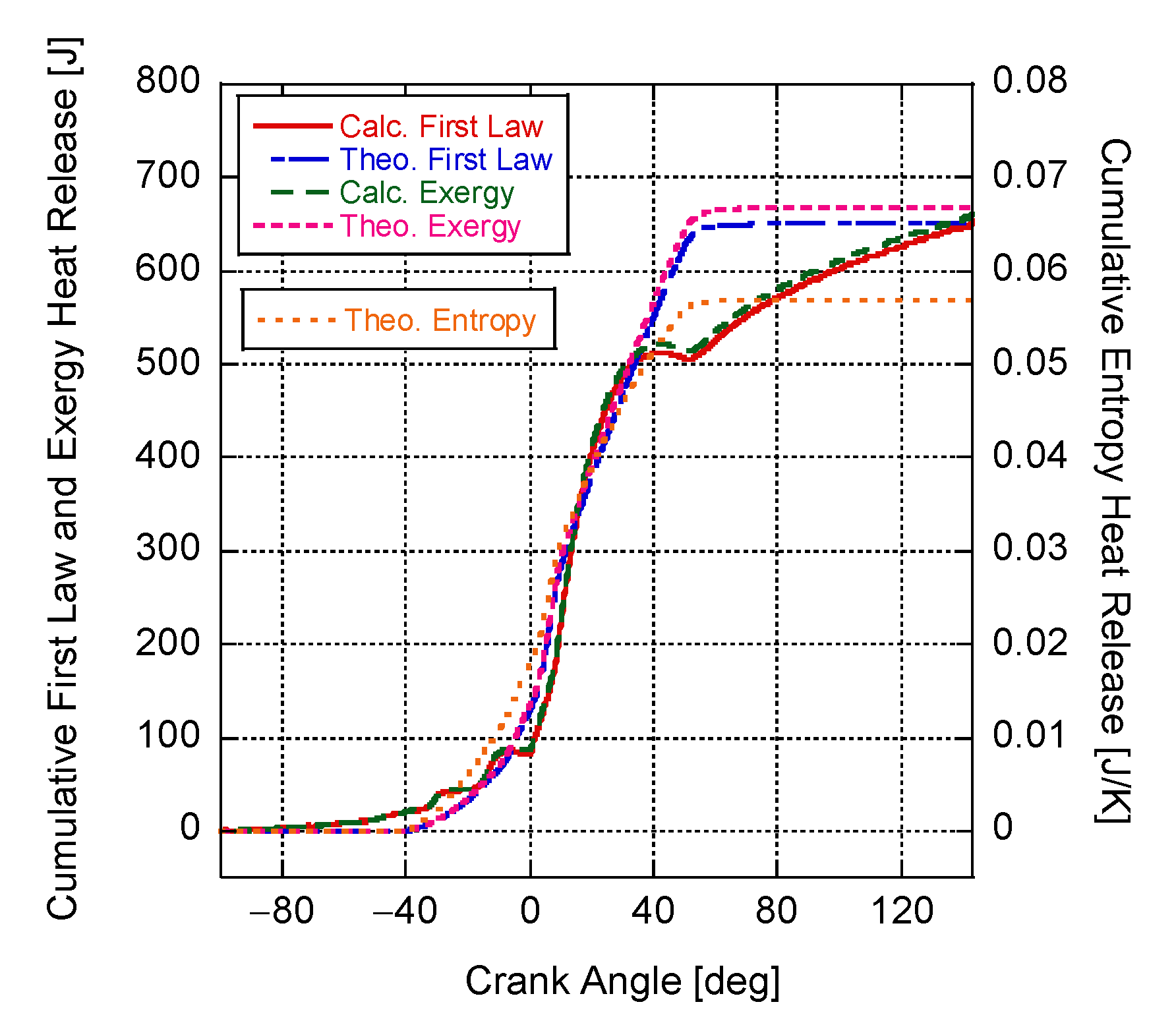
4. Results and Discussion
5. Recommendations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameter | Description | Units |
| Nozzle hole area | m3 | |
| Combustion surface area | m2 | |
| Wall emissivity | - | |
| Cylinder bore | m | |
| Connecting rod length | m | |
| Coefficient of discharge | - | |
| Specific heat of liquid fuel | J/(kg K) | |
| Constant pressure specific heat, vaporized fuel | J/(kg K) | |
| Constant volume specific heat | J/(kg K) | |
| Exergy change in the control volume | W | |
| Total change in specific internal energy | W/kg | |
| Theoretical exergy heat release over time | W | |
| Change in mass within the control volume | kg/s | |
| Mass burn rate of the added gases | kg/s | |
| Mass burn rate of the added liquid fuel | kg/s | |
| Time rate of change of direct injected liquid fuel | kg/s | |
| Change in mixture molecular weight with time | gm/(mol s) | |
| Difference between cylinder and nozzle pressure | Pa | |
| Rate of in-cylinder pressure change | Pa/s | |
| Time rate of change in the total heat transfer into the system through its boundary | W | |
| Rate of change in theoretical heat release | W | |
| Gross rate of heat release | W | |
| Convective heat transfer | W | |
| Rate of heat transfer from the walls and piston | W | |
| Change in mixture gas constant with time | W/(kg K) | |
| Change in gas constant with changing species mass fractions | J/(kg K) | |
| Change in specific entropy | W/(kg K) | |
| Change in entropy within the control volume | W/K | |
| Theoretical entropy heat release expression | W/K | |
| Rate of change in temperature | K | |
| Change in crank angle | deg/s | |
| Change in the specific internal energy of the system | W/kg | |
| Time rate of change in the total energy of the mass contained in the system | W | |
| Time rate of change in cylinder volume | m3/s | |
| Power | W | |
| Change in species mole fractions with time | 1/s | |
| Change in species mass fractions over time | 1/s | |
| Change in mass fractions of ith species over time | 1/s | |
| Chemical energy | J/kg | |
| Flow exergy in or out of the system | J/kg | |
| Emissivity | - | |
| Combustion efficiency | - | |
| Gaseous fuel combustion efficiency | - | |
| Liquid fuel combustion efficiency | - | |
| Residual mass fraction | - | |
| Convective heat transfer coefficient | ||
| Enthalpy of fuel | J/kg | |
| Fuel enthalpy change going from liquid to vapor | J/kg | |
| Enthalpy of mass entering (or leaving) the system | J/kg | |
| Ratio of specific heats | - | |
| Arrhenius pre-exponential | m3/(kg s) | |
| Molecular weight of argon | gm/mol | |
| Mass of the burned gases | kg | |
| Molecular weight of carbon dioxide | gm/mol | |
| Total mass inside the control volume | kg | |
| Mass of port-fuel injected gaseous fuel | kg | |
| Molecular weight of gaseous fuel | gm/mol | |
| . | Total gaseous fuel mass | kg |
| ss of direct injected liquid fuel | kg | |
| Total injected liquid fuel mass | kg | |
| Molecular weight of water | gm/mol | |
| Mass at inlet valve close | kg | |
| Averaged mixture molecular weight | gm/mol | |
| Molecular weight of nitrogen | gm/mol | |
| Molecular weight of oxygen | gm/mol | |
| Residual mass | kg | |
| Mass of the unburned gases | kg | |
| Mass flow exiting the system through the control boundary | kg/s | |
| Mass flow rate of fuel | kg/s | |
| Mass flow rate entering the system through the system boundary | kg/s | |
| Number of moles of recirculated exhaust gas | - | |
| Number of holes | - | |
| Number of injectors | - | |
| Engine speed | rpm | |
| Total molar change in argon (in the burned zone) | mol/s | |
| Total molar change in argon (in the unburned zone) | mol/s | |
| Total molar change in burned carbon dioxide | mol/s | |
| Total molar change in the unburned carbon dioxide | mol/s | |
| Burn rate of gaseous fuel in molar format | mol/s | |
| Burn rate of liquid fuel in molar format | mol/s | |
| Total molar change in water (in the burned zone) | mol/s | |
| Total molar change in water (in the unburned zone) | mol/s | |
| Total molar change in water (in the burned zone) | mol/s | |
| Total molar change in nitrogen (in the unburned zone) | mol/s | |
| Total molar change in unburned oxygen | mol/s | |
| Nusselt number | - | |
| In-cylinder pressure | Pa | |
| Standard state exergy pressure | Pa | |
| Measured pressure in the control volume | Pa | |
| Exhaust pressure | Pa | |
| Intake pressure | Pa | |
| In-cylinder pressure at IVC | Pa | |
| Reference pressure | Pa | |
| Change in specific internal energy with pressure | J/(kg Pa) | |
| Change in specific internal energy with temperature | J/(kg K) | |
| Change in specific internal energy with changing species mass fractions | J/kg | |
| Change in specific internal energy with pressure | J/(kg Pa) | |
| Change in specific internal energy with temperature | J/(kg K) | |
| Change in specific internal energy with changing species mass fractions | J/kg | |
| Prandtl number | - | |
| Total heat transfer | J | |
| Lower heating value of gaseous fuel | J/kg | |
| Lower heating value of liquid fuel | J/kg | |
| Crank arm length | m | |
| Averaged gas constant of the burned zone | J/(kg K) | |
| Compression ratio | - | |
| Mixture-averaged gas constant | J/(kg K) | |
| Gaseous fuel’s gas constant | J/(kg K) | |
| Liquid fuel’s gas constant | J/(kg K) | |
| Gas constant | J/(kg K) | |
| Universal gas constant | J/(mol K) | |
| Averaged gas constant of the unburned zone | J/(kg K) | |
| Reynolds number | - | |
| Control volume density | kg/m3 | |
| Injected liquid fuel density | kg/m3 | |
| Standard state entropy | J/(kg K) | |
| Specific entropy of liquid fuel | J/(kg K) | |
| Molar entropy of the ith species | J/(mol K) | |
| Standard state entropy | J/(mol K) | |
| Entropy generation | W/K | |
| Standard state exergy temperature | K | |
| Burned zone temperature | K | |
| Temperature of the control volume | K | |
| Exhaust gas temperature | K | |
| Gaseous fuel temperature | K | |
| Temperature of injected liquid fuel | K | |
| Temperature of injected liquid fuel (or injector) | K | |
| Intake temperature | K | |
| In-cylinder temperature at IVC | K | |
| Temperature of the unburned zone | K | |
| Vaporization temperature of fuel | K | |
| Wall temperature | K | |
| Specific internal energy of the system | J/kg | |
| Standard state internal energy | J/kg | |
| Internal energy in the burned zone | J | |
| Total internal energy in the cylinder at each time step | J | |
| Internal energy of the gaseous fuel | J | |
| Internal energy of the liquid fuel | J | |
| Specific internal energy of ith species | J/kg | |
| Internal energy in the unburned zone | J | |
| Specific volume | m3/kg | |
| Standard state specific volume | m3/kg | |
| Piston bowl volume | m3 | |
| Clearance volume | m3 | |
| Calculated volume | m3 | |
| Cylinder volume at IVC | m3 | |
| Mass fraction of the corresponding fuel in the control volume | - | |
| Species mass fraction of the ith species | - | |
| Mass fraction of oxygen in the control volume | - | |
Subscripts
| Text | Description |
| CV | Control volume |
| a | Number of carbon atoms in gaseous fuel |
| b | Burned |
| b | Number of hydrogen atoms in gaseous fuel |
| c | Number of oxygen atoms in liquid fuel |
| d | Number of nitrogen atoms in liquid fuel |
| EGR | Exhaust gas recirculation |
| ex | Exiting (the control volume) |
| exh | Exhaust |
| f | Fuel |
| fa | Gaseous fuel |
| fl | Liquid fuel |
| g | Gaseous fuel (goes with and ) |
| HR | Heat release |
| HT | Heat transfer |
| in | Entering (the control volume) |
| int | Intake |
| IVC | Inlet valve close |
| p | Liquid fuel (goes with and ) |
| res | Residual |
| u | Unburned |
| w | Number of carbon atoms in liquid fuel |
| x | Number of hydrogen atoms in liquid fuel |
| y | Number of oxygen atoms in liquid fuel |
| z | Number of nitrogen atoms in liquid fuel |
Greek Symbols
| Symbol | Description |
| Residual term | |
| EGR term | |
| Tuning parameter to slow down the liquid fuel preparation process | |
| Efficiency | |
| Stefan–Boltzmann constant (W/m2 K4) | |
| Crank angle | |
| Number of liquid fuel moles | |
| Number of moles of unburned gases |
Abbreviations
| Abbreviation | Full Form |
| 0D | Zero-dimensional |
| ATDC | After top dead center |
| BTDC | Before top dead center |
| CI | Compression ignition |
| DME | Di-methyl ether |
| ECU | Engine control unit |
| EGR | Exhaust gas recirculation |
| ESR | Energy substitution rate |
| HCCI | Homogeneous charge compression ignition |
| HR | Heat release |
| HT | Heat transfer |
| HTC | Low-temperature combustion |
| ICE | Internal combustion engine |
| IVC | Intake valve closing |
| LHV | Lower heating value |
| LTC | Low-temperature combustion |
| PCCI | Pre-mixed charge compression ignition |
| RCCI | Reactivity controlled compression ignition |
| RHR | Rate of heat release |
| ULSD | Ultra-low sulfur diesel |
Chemical Species
| Species | Chemical Name |
| Ar | Argon |
| C | Carbon atoms |
| CO | Carbon monoxide |
| CO2 | Carbon dioxide |
| H | Hydrogen atoms |
| H2O | Water |
| N | Nitrogen atoms |
| N2 | Nitrogen atoms |
| O | Oxygen atoms |
| O2 | Oxygen |
| OH | Hydroxyl |
References
- Heywood, J.B. Internal Combustion Engine Fundamentals, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2018. [Google Scholar]
- Gatowski, J.A.; Balles, E.N.; Chun, K.M.; Nelson, F.E.; Ekchian, J.A.; Heywood, J.B. Heat Release Analysis of Engine Pressure Data. SAE Trans. 1984, 93, 961–977. [Google Scholar] [CrossRef]
- Abbaszadehmosayebi, G.; Ganippa, L. Characterising Wiebe Equation for Heat Release Analysis based on Combustion Burn Factor (Ci). Fuel 2014, 119, 301–307. [Google Scholar] [CrossRef]
- Mattson, J.M.S.; Depcik, C. Emissions-Calibrated Equilibrium Heat Release Model for Direct Injection Compression Ignition Engines. Fuel 2014, 117, 1096–1110. [Google Scholar] [CrossRef]
- Mangus, M.; Kiani, F.; Mattson, J.; Tabakh, D.; Petka, J.; Depcik, C.; Peltier, E.; Stagg-Williams, S. Investigating the Compression Ignition Combustion of Multiple Biodiesel/ULSD (Ultra-Low Sulfur Diesel) Blends via Common-Rail Injection. Energy 2015, 89, 932–945. [Google Scholar] [CrossRef]
- Rakopoulos, D.C. Heat Release Analysis of Combustion in Heavy-Duty Turbocharged Diesel Engine Operating on Blends of Diesel Fuel with Cottonseed or Sunflower Oils and Their Bio-diesel. Fuel 2012, 96, 524–534. [Google Scholar] [CrossRef]
- Egnell, R. The Influence of EGR on Heat Release Rate and NO Formation in a DI Diesel Engine; SAE Technical Paper 2000-01-1807; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Langness, C.; Mattson, J.; Depcik, C. Moderate Substitution of Varying Compressed Natural Gas Constituents for Assisted Diesel Combustion. Combust. Sci. Technol. 2017, 189, 1354–1372. [Google Scholar] [CrossRef]
- Mattson, J.; Langness, C.; Niles, B.; Depcik, C. Usage of glycerin-derived, hydrogen-rich syngas augmented by soybean biodiesel to power a biodiesel production facility. Int. J. Hydrogen Energy 2016, 41, 17132–17144. [Google Scholar] [CrossRef]
- Mattson, J.M.S.; Langness, C.; Depcik, C. An Analysis of Dual-Fuel Combustion of Diesel with Compressed Natural Gas in a Single-Cylinder Engine; SAE Technical Paper 2018-01-0248; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Ortiz-Soto, E.A.; Lavoie, G.A.; Martz, J.B.; Wooldridge, M.S.; Assanis, D.N. Enhanced Heat Release Analysis for Advanced Multi-Mode Combustion Engine Experiments. Appl. Energy 2014, 136, 465–479. [Google Scholar] [CrossRef]
- Sitaraman, R.; Batool, S.; Borhan, H.; Velni, J.M.; Naber, J.D.; Shahbakhti, M. Data-Driven Model Learning and Control of RCCI Engines based on Heat Release Rate. IFAC-PapersOnLine 2022, 55, 608–614. [Google Scholar] [CrossRef]
- Catania, A.E.; Misul, D.; Mittica, A.; Spessa, E. A Refined Two-Zone Heat Release Model for Combustion Analysis in SI Engines. JSME Int. J. Ser. B 2003, 46, 75–85. [Google Scholar] [CrossRef]
- Gu, J.; Song, Y.; Wang, Y.; Meng, W.; Shi, L.; Deng, K. Prediction of heat release and NOx emissions for direct-injection diesel engines using an innovative zero-dimensional multi-phase combustion model. Fuel 2022, 329, 125438. [Google Scholar] [CrossRef]
- Li, R.C.; Zhu, G.G.; Men, Y. A two-zone reaction-based combustion model for a spark-ignition engine. Int. J. Engine Res. 2021, 22, 109–124. [Google Scholar] [CrossRef]
- DelVescovo, D.A.; Kokjohn, S.L.; Reitz, R.D. A Methodology for Studying the Relationship Between Heat Release Profile and Fuel Stratification in Advanced Compression Ignition Engines. Front. Mech. Eng. 2020, 6, 28. [Google Scholar] [CrossRef]
- Abbaszadehmosayebi, G.; Ganippa, L. Determination of Specific Heat Ratio and Error Analysis for Engine Heat Release Calculations. Appl. Energy 2014, 122, 143–150. [Google Scholar] [CrossRef]
- Gainey, B.; Longtin, J.P.; Lawler, B. A Guide to Uncertainty Quantification for Experimental Engine Research and Heat Release Analysis. SAE Int. J. Engines 2019, 12, 509–523. [Google Scholar] [CrossRef]
- Oppenheim, A.K.; Barton, J.E.; Kuhl, A.L.; Johnson, W.P. Refinement of Heat Release Analysis; SAE Technical Paper Series; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1997. [Google Scholar] [CrossRef]
- Sen, A.K.; Litak, G.; Finney, C.E.A.; Daw, C.S.; Wagner, R.M. Analysis of Heat Release Dynamics in an Internal Combustion Engine Using Multifractals and Wavelets. Appl. Energy 2010, 87, 1736–1743. [Google Scholar] [CrossRef]
- Timoney, D.J. Problems with Heat Release Analysis in D.I. Diesels; SAE Technical Paper 870270; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1987. [Google Scholar] [CrossRef]
- Jafarmadar, S. Three-Dimensional Modeling and Exergy Analysis in Combustion Chambers of an Indirect Injection Diesel Engine. Fuel 2013, 107, 439–447. [Google Scholar] [CrossRef]
- Mattson, J.; Reznicek, E.; Depcik, C. Second Law Heat Release Modeling of a Compression Ignition Engine Fueled with Blends of Palm Biodiesel. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015; Volume 6B. [Google Scholar] [CrossRef]
- Ramos da Costa, Y.J.; Barbosa de Lima, A.G.; Bezerra Filho, C.R.; de Araujo Lima, L. Energetic and Exergetic Analyses of a Dual-Fuel Diesel Engine. Renew. Sustain. Energy Rev. 2012, 16, 4651–4660. [Google Scholar] [CrossRef]
- Mattson, J.; Langness, C.; Depcik, C. Exergy Analysis of Dual-Fuel Operation with Diesel and Moderate Amounts of Compressed Natural Gas in a Single-Cylinder Engine. Combust. Sci. Technol. 2017, 190, 471–489. [Google Scholar] [CrossRef]
- Mattson, J.M.S. Modeling of Compression Ignition Engines for Advanced Engine Operation and Alternative Fuels by the Second Law of Thermodynamics. Ph.D. Thesis of Philosophy, Department of Mechanical Engineering, University of Kansas, Lawrence, KS, USA, 2019. [Google Scholar]
- Eaton, J.W. GNU Octave. 2023. Available online: https://octave.org/ (accessed on 4 March 2023).
- Depcik, C. Open-Source Energy, Entropy, and Exergy 0-D Heat Release Model for Internal Combustion Engines. Available online: https://github.com/depcik/heat-release (accessed on 4 March 2023).
- De Renzis, E.; Mariani, V.; Bianchi, G.M.; Cazzoli, G.; Falfari, S.; Antetomaso, C.; Irimescu, A. Implementation of a Multi-Zone Numerical Blow-by Model and Its Integration with CFD Simulations for Estimating Collateral Mass and Heat Fluxes in Optical Engines. Energies 2021, 14, 8566. [Google Scholar] [CrossRef]
- Stiesch, G.; Merker, G.P. A Phenomenological Model for Accurate and Time Efficient Prediction of Heat Release and Exhaust Emissions in Direct-Injection Diesel Engines; SAE Technical Paper 1999-01-1535; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1999. [Google Scholar] [CrossRef]
- Assanis, D.; Filipi, Z.; Fiveland, S.B.; Syrimis, M. A Methodology for Cycle-By-Cycle Transient Heat Release Analysis in a Turbocharged Direct-Injection Diesel Engine; SAE Technical Paper 2000-01-1185; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Li, J.; Yang, S.; Yang, J.; Rao, S.; Zeng, Q.; Li, F.; Chen, Y.; Xia, Q.; Li, K. Heat transfer for a single deformed evaporating droplet in the internal combustion engine. Phys. Lett. A 2021, 411, 127555. [Google Scholar] [CrossRef]
- Nishida, K.; Hiroyasu, H. Simplified Three-Dimensional Modeling of Mixture Formation and Combustion in a D.I. Diesel Engine; SAE Technical Paper 890269; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1989. [Google Scholar] [CrossRef]
- Alam, S.S.; Depcik, C. Verification and Validation of a Homogeneous Reaction Kinetics Model Using a Detailed H2-O2 Reaction Mechanism Versus Chemkin and Cantera. In Proceedings of the ASME 2019 International Mechanical Engineering Congress and Exposition, Salt Lake City, UT, USA, 11–14 November 2019. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; William, C.; et al. GRI-MECH 3.0. Available online: http://combustion.berkeley.edu/gri-mech/version30/text30.html (accessed on 30 January 2022).
- Burke, M.P.; Chaos, M.; Ju, Y.; Dryer, F.L.; Klippenstein, S.J. Comprehensive H2/O2 kinetic model for high-pressure combustion. Int. J. Chem. Kinet. 2012, 44, 444–474. [Google Scholar] [CrossRef]
- Li, J.; Zhao, Z.; Kazakov, A.; Chaos, M.; Dryer, F.L.; Scire, J.J., Jr. A comprehensive kinetic mechanism for CO, CH2O, and CH3OH combustion. Int. J. Chem. Kinet. 2007, 39, 109–136. [Google Scholar] [CrossRef]
- Woschni, G. Universally Applicable Equation for the Instantaneous Heat Transfer Coefficient in the Internal Combustion Engine; SAE Paper 670931; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1967. [Google Scholar] [CrossRef]
- Hohenberg, G.F. Advanced Approaches for Heat Transfer Calculations; SAE Paper 790825; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1979. [Google Scholar] [CrossRef]
- Depcik, C.; Alam, S.S.; Madani, S.; Ahlgren, N.; McDaniel, E.; Burugupally, S.P.; Hobeck, J. Determination of a Heat Transfer Correlation for Small Internal Combustion Engines. Submitt. Appl. Therm. Eng. 2023. [Google Scholar]
- Kee, R.J.; Rupley, F.M.; Meeks, E.; Miller, J.A. Chemkin-III: A Fortran Chemical Kinetics Package for the Analysis of Gas-Phase Chemical and Plasma Kinetics; SAND96-8216; Sandia National Laboratories: Albuquerque, NM, USA, 1996. [Google Scholar]
- Langness, C.; Mangus, M.; Depcik, C. Construction, Instrumentation, and Implementation of a Low Cost, Single-Cylinder Compression Ignition Engine Test Cell; SAE Technical Paper 2014-01-0673; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 2014. [Google Scholar] [CrossRef]
- Syrimis, M.; Shigahara, K.; Assanis, D.N. Correlation Between Knock Intensity and Heat Transfer Under Light and Heavy Knocking Conditions in a Spark Ignition Engine. SAE Trans. 1996, 105, 592–605. [Google Scholar] [CrossRef]
- Puzinauskas, P.V. Examination of Methods Used to Characterize Engine Knock; SAE Technical Paper 920808; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1992. [Google Scholar] [CrossRef]
- Checkel, M.D.; Dale, J.D. Testing a Third Derivative Knock Indicator on a Production Engine; SAE Technical Paper; Society of Automotive Engineering, Inc.: Warrendale, PA, USA, 1986. [Google Scholar] [CrossRef]
- Theinnoi, K.; Suksompong, P.; Temwutthikun, W. Engine Performance of Dual Fuel Operation with In-cylinder Injected Diesel Fuels and In-Port Injected DME. Energy Procedia 2017, 142, 461–467. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Xiao, F.; Li, D. Combustion and emission characteristics of a diesel engine with DME as port premixing fuel under different injection timing. Energy Convers. Manag. 2014, 77, 52–60. [Google Scholar] [CrossRef]
- Deng, S.; Zhao, P.; Zhu, D.; Law, C.K. NTC-affected ignition and low-temperature flames in nonpremixed DME/air counterflow. Combust. Flame 2014, 161, 1993–1997. [Google Scholar] [CrossRef]
- Krisman, A.; Hawkes, E.R.; Talei, M.; Bhagatwala, A.; Chen, J.H. Polybrachial structures in dimethyl ether edge-flames at negative temperature coefficient conditions. Proc. Combust. Inst. 2015, 35, 999–1006. [Google Scholar] [CrossRef]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. 2023. Available online: https://www.cantera.org (accessed on 1 March 2023).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Depcik, C.; Mattson, J.; Alam, S.S. Open-Source Energy, Entropy, and Exergy 0D Heat Release Model for Internal Combustion Engines. Energies 2023, 16, 2514. https://doi.org/10.3390/en16062514
Depcik C, Mattson J, Alam SS. Open-Source Energy, Entropy, and Exergy 0D Heat Release Model for Internal Combustion Engines. Energies. 2023; 16(6):2514. https://doi.org/10.3390/en16062514
Chicago/Turabian StyleDepcik, Christopher, Jonathan Mattson, and Shah Saud Alam. 2023. "Open-Source Energy, Entropy, and Exergy 0D Heat Release Model for Internal Combustion Engines" Energies 16, no. 6: 2514. https://doi.org/10.3390/en16062514
APA StyleDepcik, C., Mattson, J., & Alam, S. S. (2023). Open-Source Energy, Entropy, and Exergy 0D Heat Release Model for Internal Combustion Engines. Energies, 16(6), 2514. https://doi.org/10.3390/en16062514




