Research on Production Performance Prediction Model of Horizontal Wells Completed with AICDs in Bottom Water Reservoirs
Abstract
:1. Introduction
2. Integrated Coupled Mathematical Model
2.1. Flow Assumptions
2.2. Reservoir Simulation
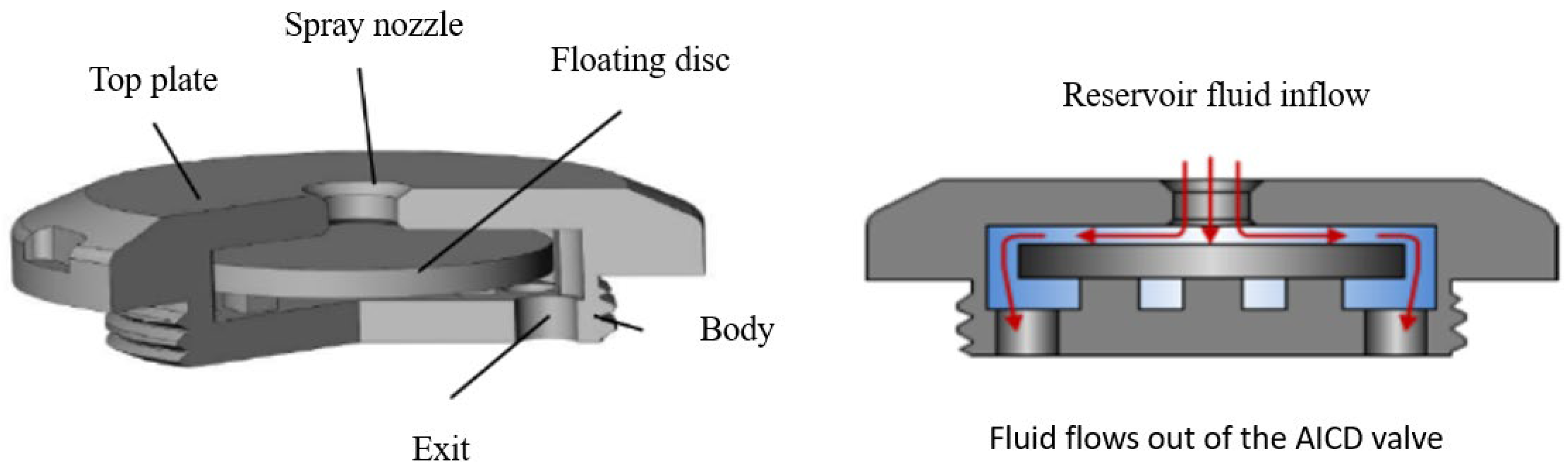
2.3. Flow Performance Model of AICD
- (1)
- Perform parameter fitting on the characteristic curve of pure water (100% water content)—in this case, the AICD coefficient K is equal to the AICD control constant aAICD—to obtain aAICD.
- (2)
- Using different viscosity exponents y, the experimental data of different water contents are fitted by Formulas (12)–(15), and the y with the highest fitting degree is selected. Finally, a characteristic curve model suitable for floating disc AICD is obtained.
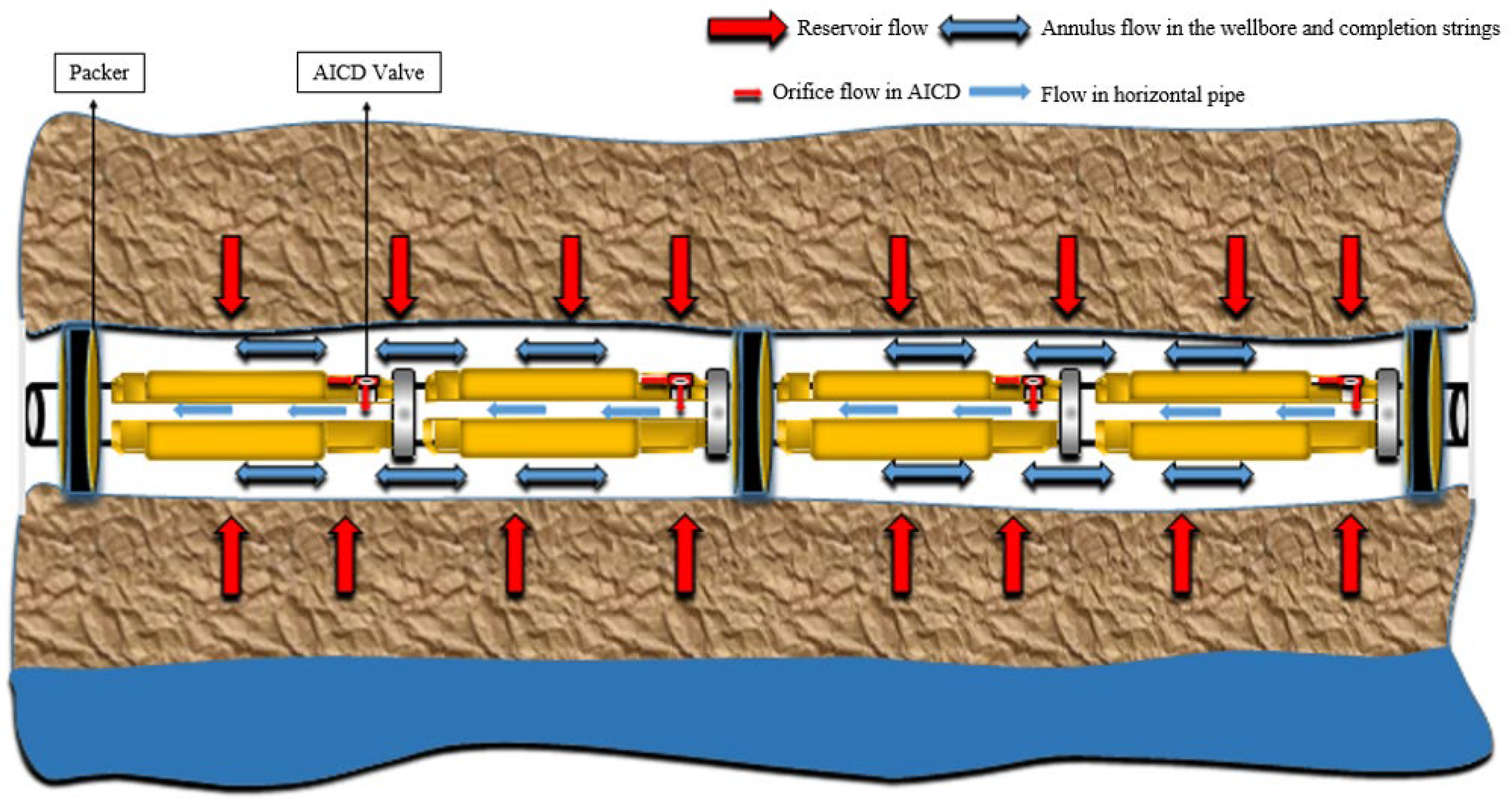
2.4. Flow Model in Horizontal Wellbore
2.5. Model Coupling
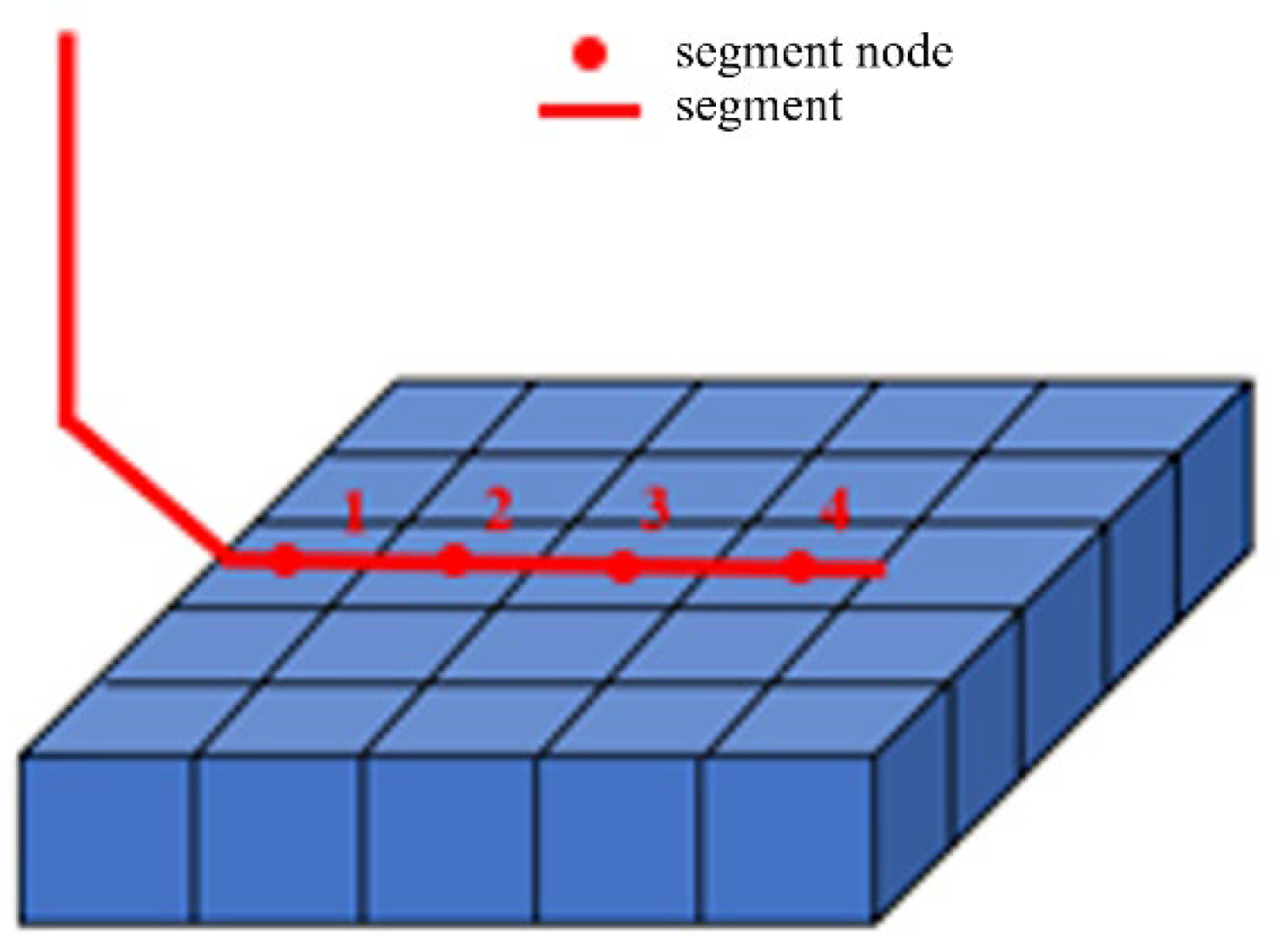
- (1)
- Assume that the packer splits the horizontal well into n segments with m AICDs in each segment.
- (2)
- For each well segment, assume a series of annular pressures and calculate the oil and water inflow for each segment using the reservoir pressure, saturation, permeability, and well index for that time step.
- (3)
- Using the flow performance model of AICD, calculate the bottom hole flow pressure corresponding to a series of annular pressures and obtain the relationship between bottom hole flow pressure and oil and water inflow for each well segment.
- (4)
- Superimpose the production of n segments with the same bottom hole flow pressure to obtain the relationship between total fluid production and bottom hole flow pressure.
- (5)
- Obtain the corresponding bottom hole flow pressure from step (4) and the annular pressure of each well section from step (3) according to the horizontal well production allocation.
- (6)
- Input the annular pressure of each well segment from step (5) into the reservoir model as bottom hole flow pressure in an explicit form and calculate the oil and water inflow at that time step.
3. Optimization of the Position of Packers
3.1. Optimization Methods
- (1)
- Determine the permeability corresponding to each horizontal well segment.
- (2)
- Calculate the Ai, T, and Ci values for all adjacent horizontal well segments.
- (3)
- Obtain the order of importance of each packer sorted by Ri.
- (4)
- Determine the optimal number of packers and optimal position of every packer based on the order of importance of each packer and the actual operating experience.
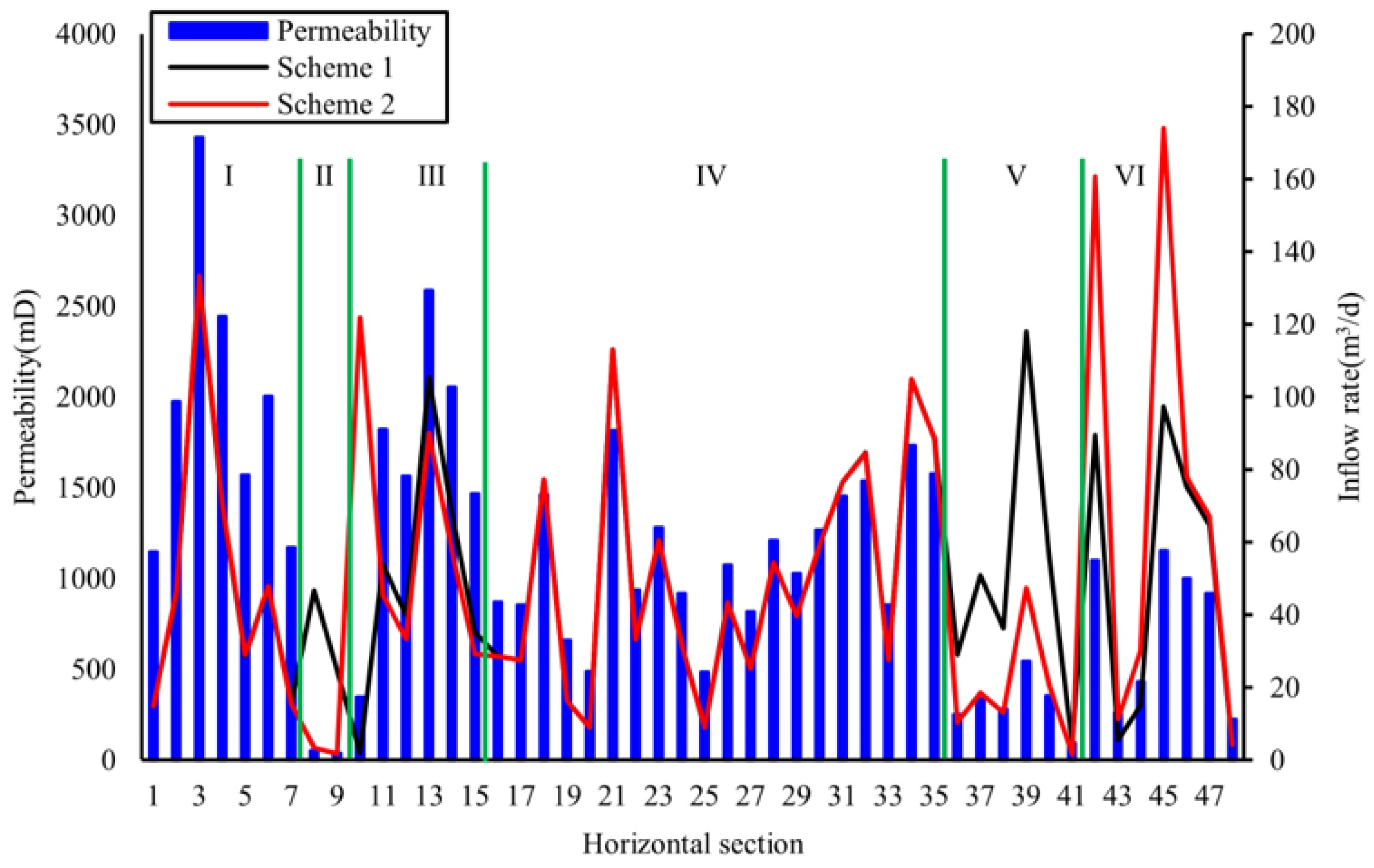
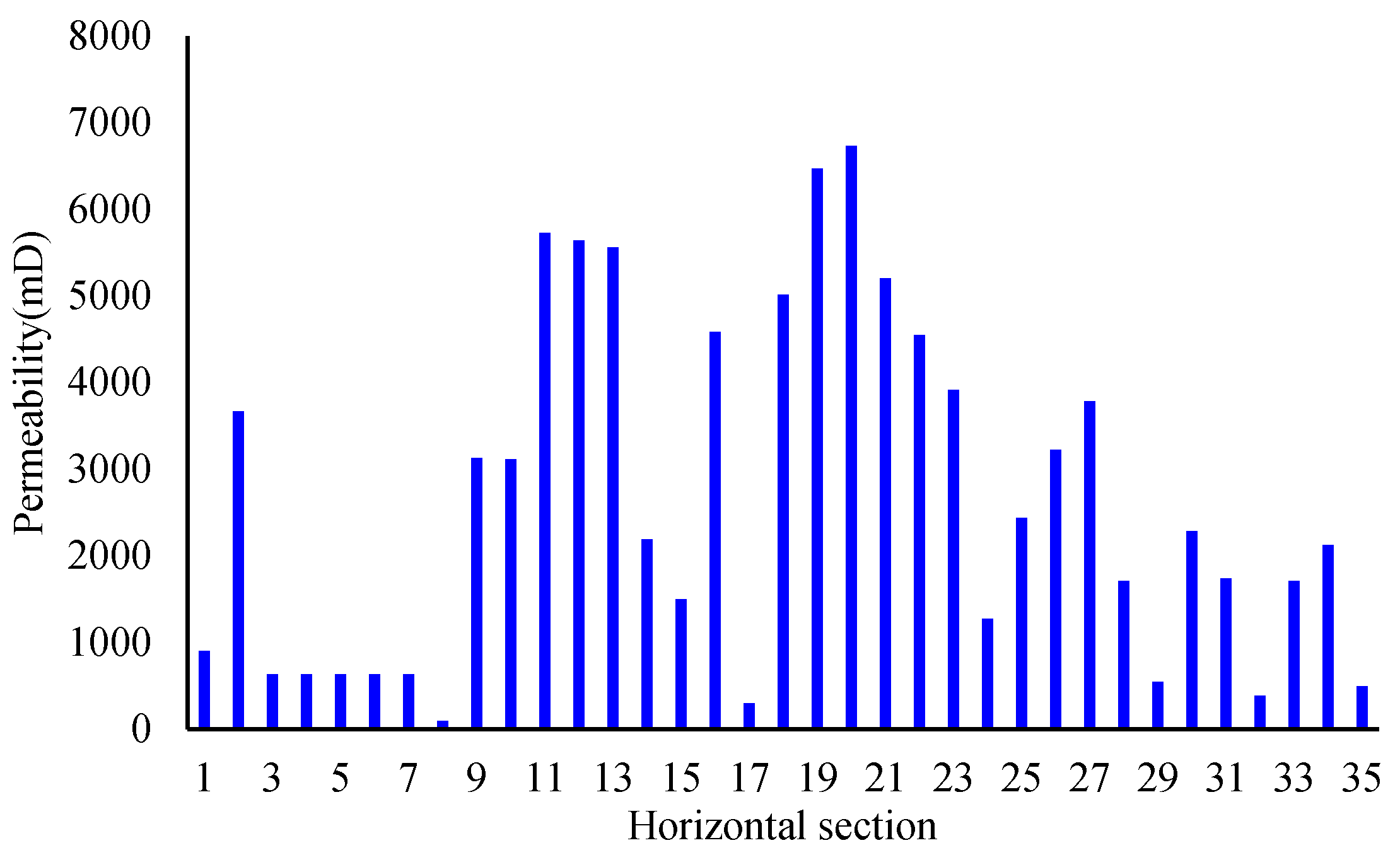
3.2. Optimization Example
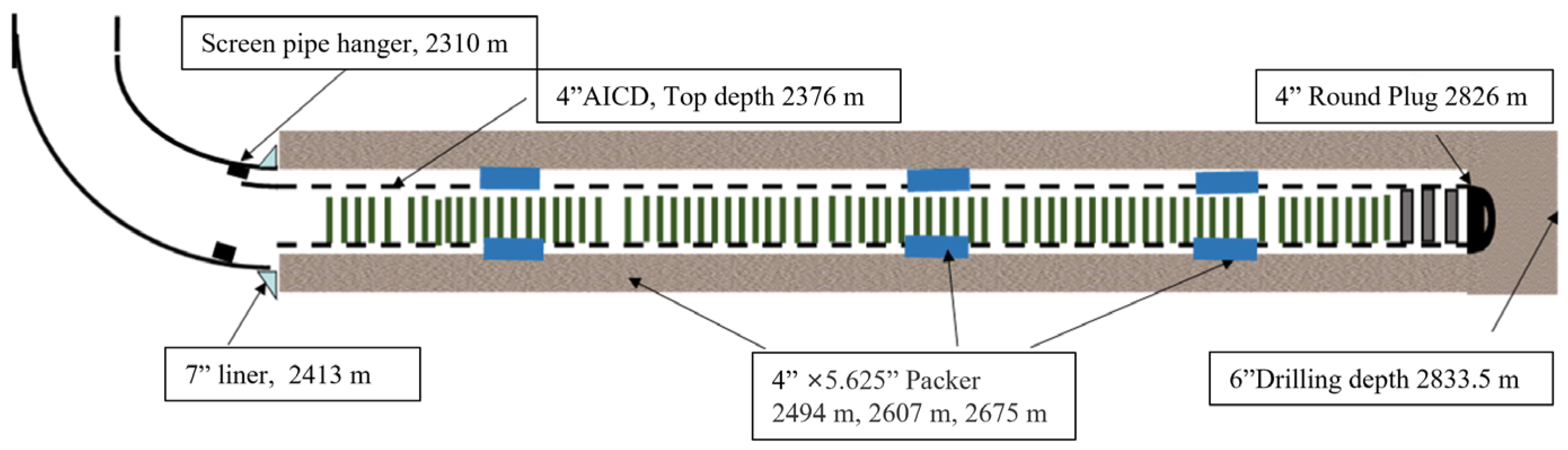
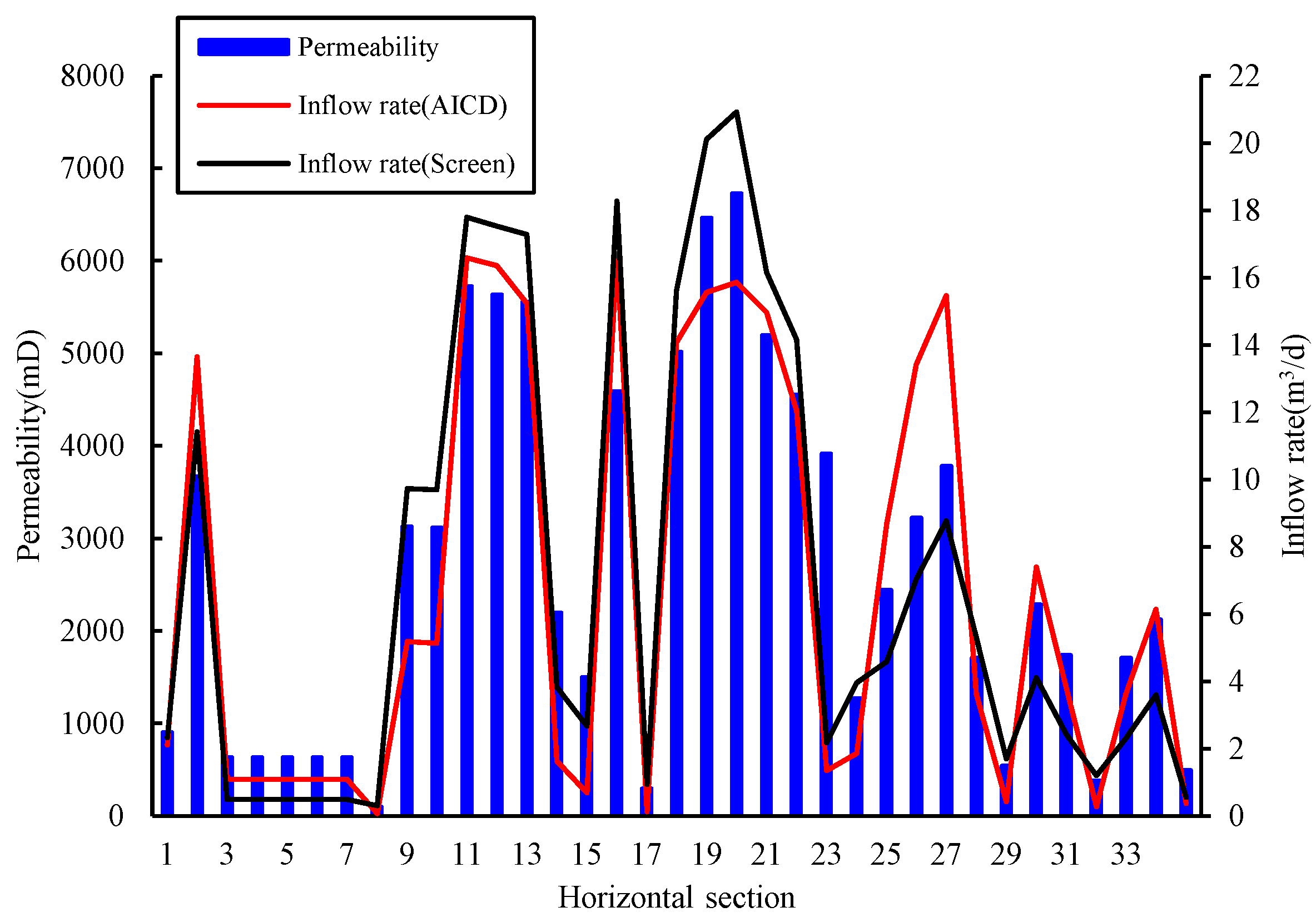
4. Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.; Yang, Z.; He, D.; Wei, Y.; Li, J.; Jia, A.; Chen, J.; Zhao, Q.; Li, Y.; Li, J.; et al. Theory, technology and prospects of conventional and unconventional natural gas. Pet. Explor. Dev. 2018, 45, 604–618. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Gao, S.; Liu, H.; Ye, L.; Wu, H.; Zhu, W.; An, W. Well network optimization and recovery evaluation of tight sandstone gas reservoirs. J. Pet. Sci. Eng. 2020, 196, 107705. [Google Scholar] [CrossRef]
- Meng, D.; Jia, A.; Ji, G.; He, D. Water and gas distribution and its controlling factors of large scale tight sand gas fields: A case study of western Sulige gas field, Ordos Basin, NW China. Pet. Explor. Dev. 2016, 43, 663–671. [Google Scholar] [CrossRef]
- He, D.H.; Bai, B.F. Gas-liquid two phaseflow with high GVF through a horizontal V-Cone throttle device. Int. J. Multiph. Flow 2017, 91, 51–62. [Google Scholar]
- Madsen, T. 2 The Troll Oil Development: One Billion Barrels of Oil Reserves Created Through Advanced Well Technology. In Proceedings of the 15th World Petroleum Congress, Beijing, China, 12–16 October 1997. [Google Scholar]
- Prakasa, B.; Muradov, K.; Davies, D. Rapid Design of an Inflow Control Device Completion in Heterogeneous Clastic Reservoirs Using Type Curves. In Proceedings of the SPE Offshore Europe Conference and Exhibition, Aberdeen, Scotland, UK, 5–8 September 2015. [Google Scholar]
- Shang, B.; Liu, Y.; Meng, X.; Bai, J.; Wu, H.; Yu, F.; Mu, M.; Li, Y. New-Type Water Controlling Technology for Improving Production Performance of Offshore Heavy-Oil Reservoir with Active Bottom Water. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 28 September–2 October 2020. [Google Scholar]
- Michael, F.; Liang, Z.; Least, B. The Theory of a Fluidic Diode Autonomous Inflow Control Device. In Proceedings of the SPE Middle East Intelligent Energy Conference and Exhibition, Manama, Bahrain, 28–30 October October 2013. [Google Scholar]
- Brandon, L.; Stephen, G.; Russell, B.; Adam, U.; Wileman, A. Autonomous ICD Single Phase Testing. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 8–10 October 2012. [Google Scholar]
- Brandon, L.; Stephen, G.; Angel, W.; Ufford, A. Fluidic Diode Autonomous Inflow Control Device Range 3B—Oil, Water, and Gas Flow Performance Testing. In Proceedings of the SPE Kuwait Oil and Gas Show and Conference, Kuwait City, Kuwait, 7–10 October 2013. [Google Scholar]
- Least, B.; Greci, S.; Huffer, R.; Rajan, R.V.; Golbeck, H. Steam Flow Tests for Comparing Performance of Nozzle, Tube, and Fluidic Diode Autonomous ICDs in SAGD Wells. In Proceedings of the SPE Heavy Oil Conference-Canada, Calgary, AB, Canada, 10–12 June 2014. [Google Scholar]
- Greci, S.; Least, B.; Tayloe, G. Testing Results: Erosion Testing Confirms the Reliability of the Fluidic Diode Type Autonomous Inflow Control Device. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 10–13 November 2014. [Google Scholar]
- Corona, G.; Fripp, M.; Yin, W. Fluidic Diode Autonomous ICD Multiphase Performance in Light-Oil Reservoirs. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Manama, Bahrain, 18–21 March 2017. [Google Scholar]
- Pedroso, C.A.; Rocha, P.; Araujo, Z. Successful AICD Application to Reduce Water Production in a Heavy Oil Greenfield. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–5 October 2022. [Google Scholar]
- Rodolfo, O. Study of the Horizontal Wellbore and Reservoir Coupling. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Youngs, B.; Neylon, K.; Anthony Holmes, J. Recent Advances in Modeling Well Inflow Control Devices In Reservoir Simulation. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 7–9 December 2009. [Google Scholar]
- Thornton, K.; Jorquera, R.; Soliman, M.Y. Optimization of Inflow Control Device Placement and Mechanical Conformance Decisions Using a New Coupled Well-Intervention Simulator. In Proceedings of the Abu Dhabi International Petroleum Conference and Exhibition, Abu Dhabi, United Arab Emirates, 11–14 November 2012. [Google Scholar]
- Eltazy, E.; Khafiz, M.; David, D.; Grebenkin, I. Autonomous Inflow Control Valves—Their Modelling and “Added Value”. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- MoradiDowlatabad, M.; Zarei, F.; Akbari, M. The Improvement of Production Profile While Managing Reservoir Uncertainties with Inflow Control Devices Completions. In Proceedings of the SPE Bergen One Day Seminar, Bergen, Norway, 22 April 2015. [Google Scholar]
- Zhao, F.K. The Study on Development Law and Effective Drive Strategy of Horizontal Well in Bottom Water Reservoir; China University of Petroleum (East China): Dongying, China, 2018. [Google Scholar]
- Guo, D.L.; Liu, C.Q. Two-Phase Flow in a Horizontal Well Penetrating a Naturally Fractured Reservoir Under Bottom Water Drive. Pet. Explor. Dev. 1995, 22, 44–46+101–102. [Google Scholar]
- Mathiesen, V.; Aakre, H.; Werswick, B.; Elseth, G. The Autonomous RCP Valve—New Technology for Inflow Control in Horizontal Wells. In Proceedings of the SPE Offshore Europe Oil and Gas Conference and Exhibition, Aberdeen, UK, 6–8 September 2011. [Google Scholar]
- Zhu, C.M.; Liu, G.Z.; Li, X.B. Experimental Study on Water Control Performance of New AICD. China Pet. Mach. 2019, 47, 79–86. [Google Scholar]
- Wang, X.Q.; Wang, Z.H.; Wei, J.G. Investigation of variable mass flow in horizontal well with perforation completion coupling reservoir. J. Hydrodyn. 2005, 3, 326–331. [Google Scholar]
- Sapian, N.F.A.; Tusimin, F.; Mei, S.C.M.; Wang, A.G.J.; Ali, N.A.W.; Madzidah, A.; Ghonim, E.O.; Awid, A.; Hasbullah, N.; Nazim, N.O.M. Maximizing Production Recovery Through Autonomous Inflow Device AICD Configuration in Challenging Long Horizontal Open-Hole Oil Producer with High Gas-Oil-Ratio and Un-Even Fluid Contacts. In Proceedings of the IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition, Bangkok, Thailand, 9–10 August 2022. [Google Scholar]
- Zhang, N.; Li, H.; Dong, W.; Cui, X.; Tan, Y. The optimal model of water control completion based on source function and network model. J. Pet. Sci. Eng. 2022, 213, 110398. [Google Scholar] [CrossRef]

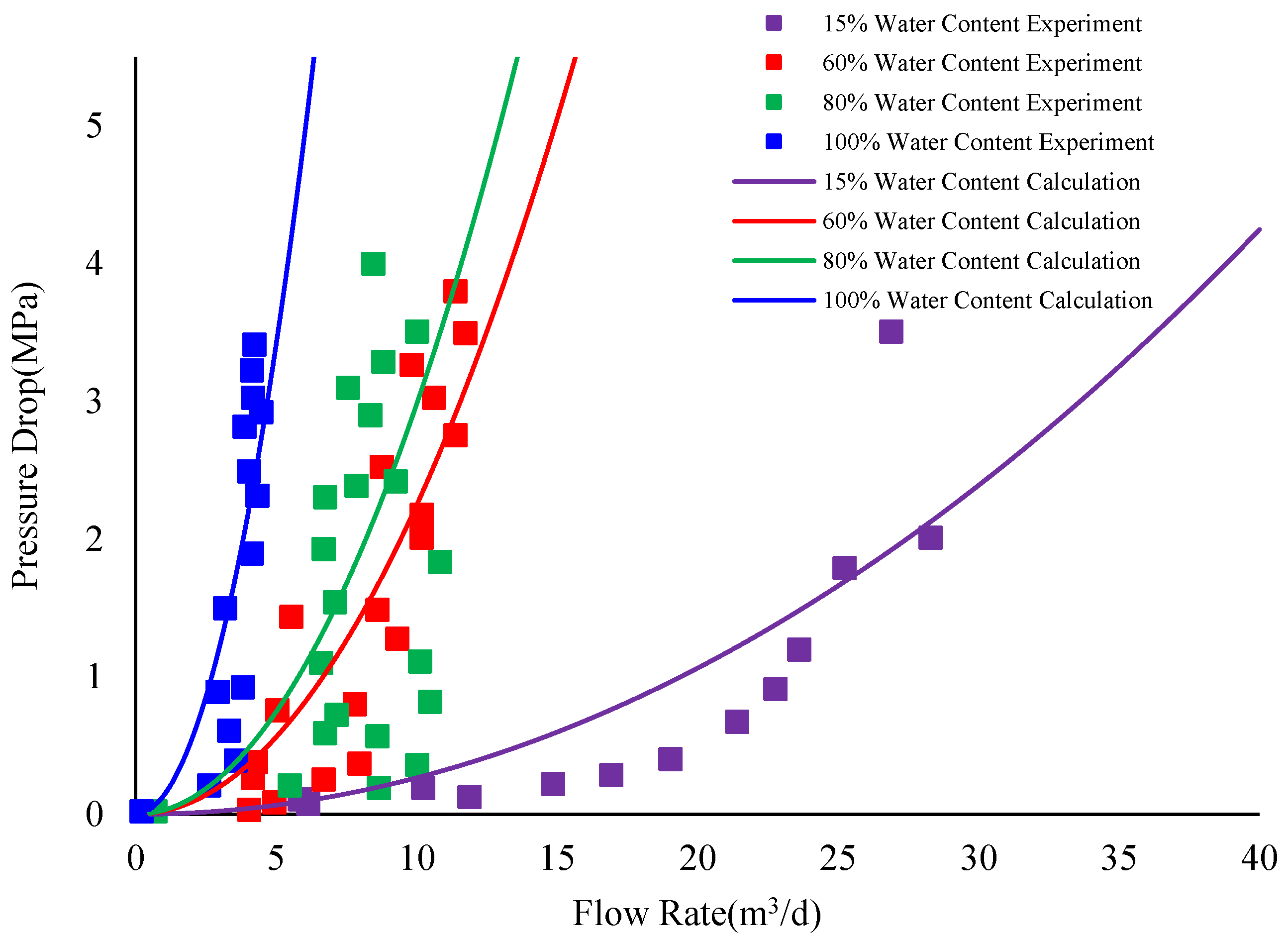



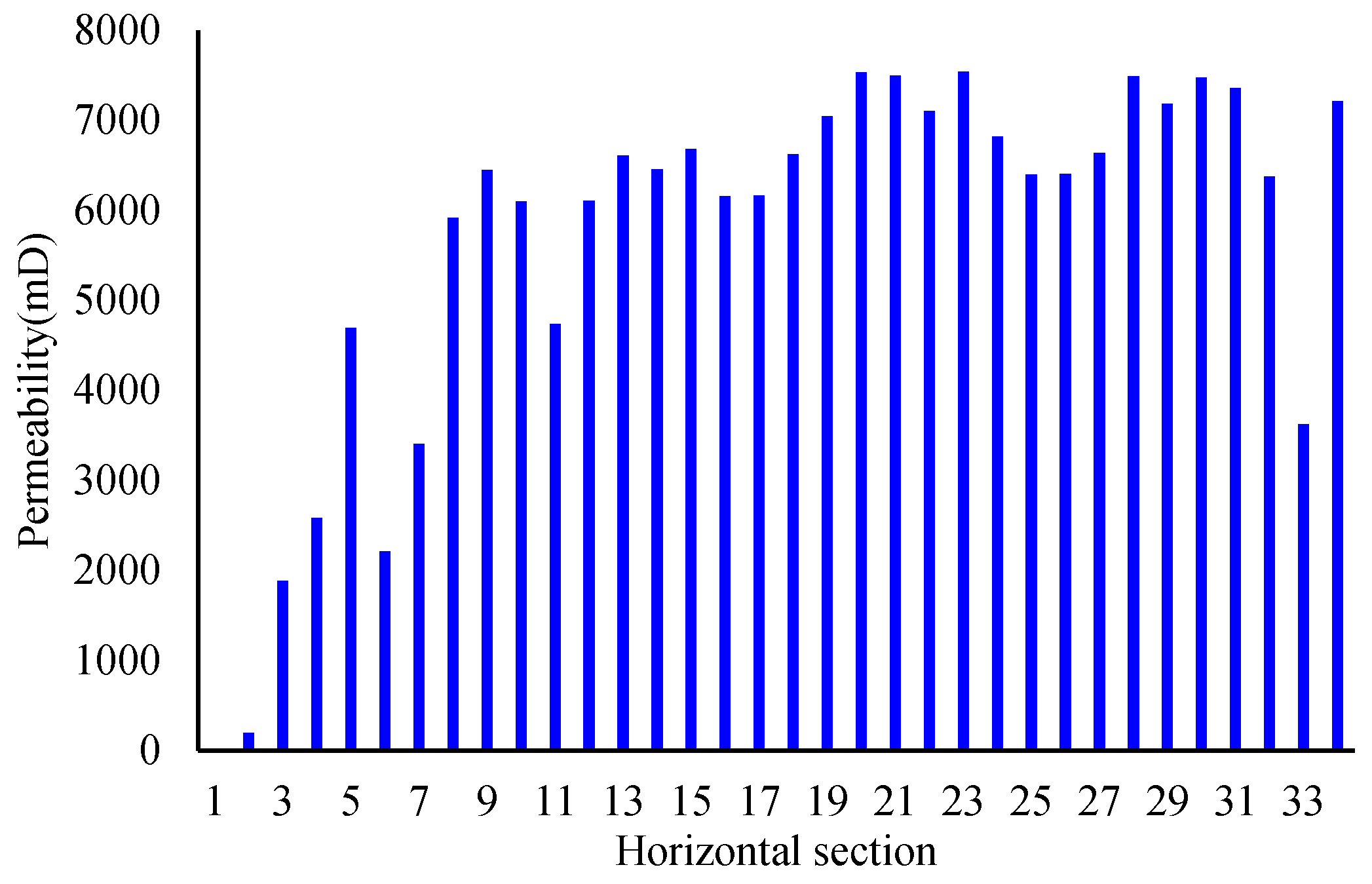
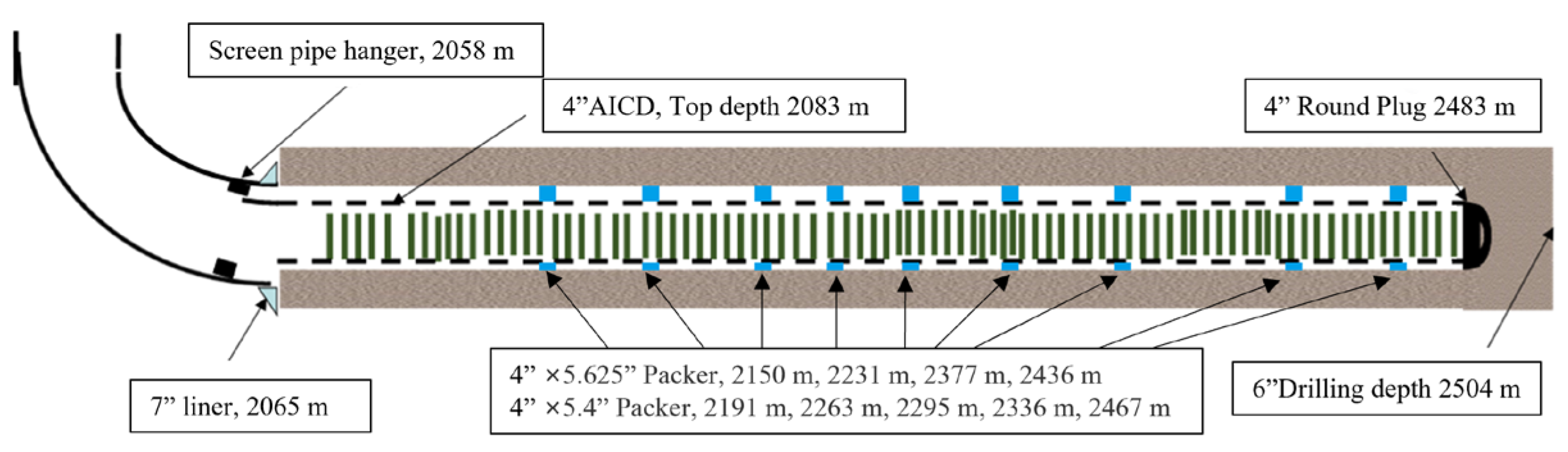

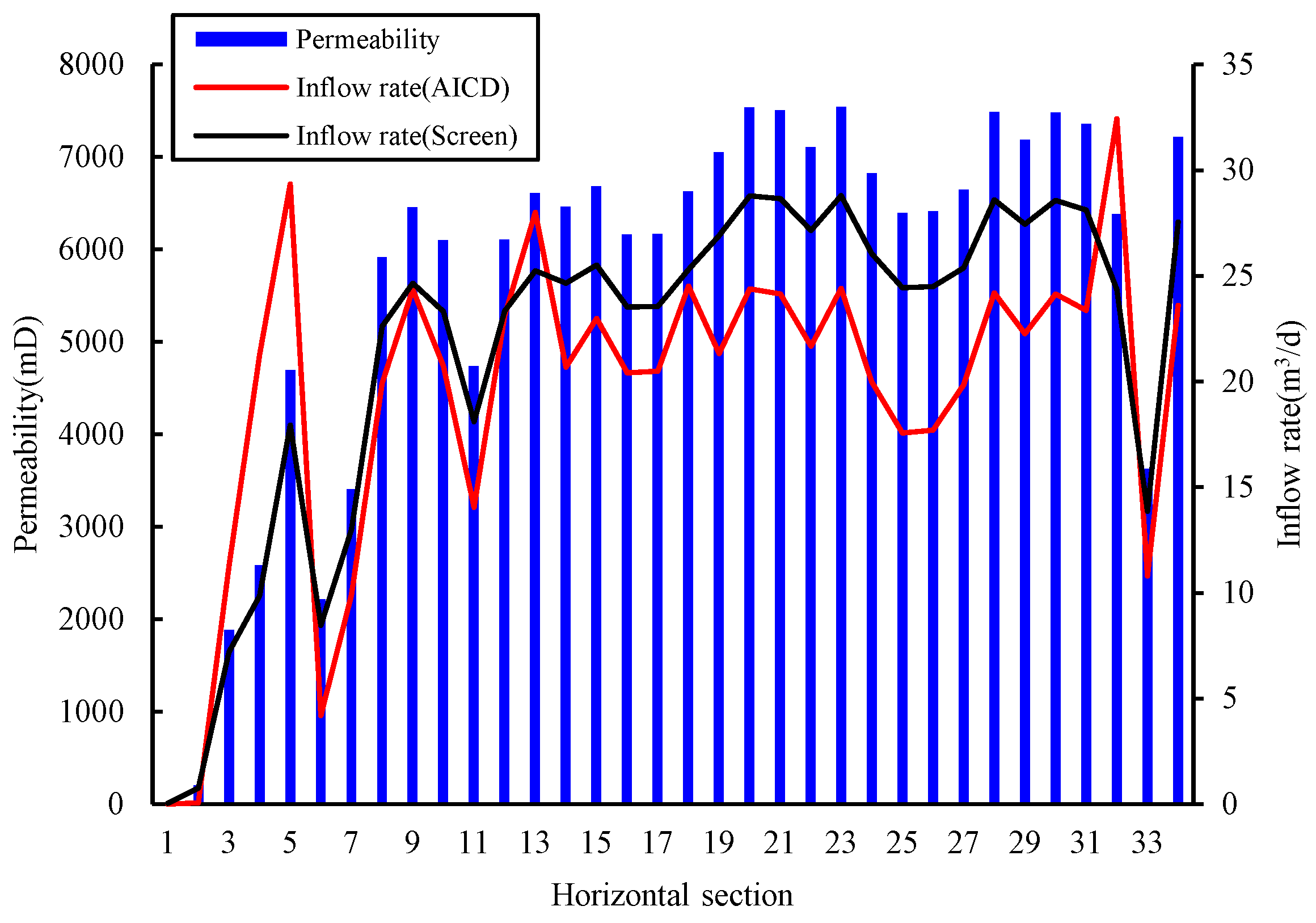
| Water Content | y | aAICD |
|---|---|---|
| 15% | −12.46 | 10.22 |
| 60% | −6.268 | 10.22 |
| 80% | −5.324 | 10.22 |
| 100% | −3.98 | 10.22 |
| a | b |
|---|---|
| −4.525 | −0.5361 |
| Parameters | Values |
|---|---|
| Porosity, % | 23.4 |
| Stratigraphic pressure, MPa | 15.06 |
| Saturation pressure, MPa | 0.4 |
| Stratigraphic temperature, °C | 74.09 |
| Crude oil density, g/cm3 | 0.941 |
| Crude oil viscosity, mPa·s | 353.5 |
| Parameters | Values |
|---|---|
| Porosity, % | 27.9 |
| Stratigraphic pressure, MPa | 16.57 |
| Saturation pressure, MPa | 8.5 |
| Stratigraphic temperature, °C | 74.85 |
| Crude oil density, g/cm3 | 0.941 |
| Crude oil viscosity, mPa·s | 353.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; An, Y.; Huo, R. Research on Production Performance Prediction Model of Horizontal Wells Completed with AICDs in Bottom Water Reservoirs. Energies 2023, 16, 2602. https://doi.org/10.3390/en16062602
Zhang N, An Y, Huo R. Research on Production Performance Prediction Model of Horizontal Wells Completed with AICDs in Bottom Water Reservoirs. Energies. 2023; 16(6):2602. https://doi.org/10.3390/en16062602
Chicago/Turabian StyleZhang, Ning, Yongsheng An, and Runshi Huo. 2023. "Research on Production Performance Prediction Model of Horizontal Wells Completed with AICDs in Bottom Water Reservoirs" Energies 16, no. 6: 2602. https://doi.org/10.3390/en16062602




