Influence of the Reward Function on the Selection of Reinforcement Learning Agents for Hybrid Electric Vehicles Real-Time Control
Abstract
:1. Introduction
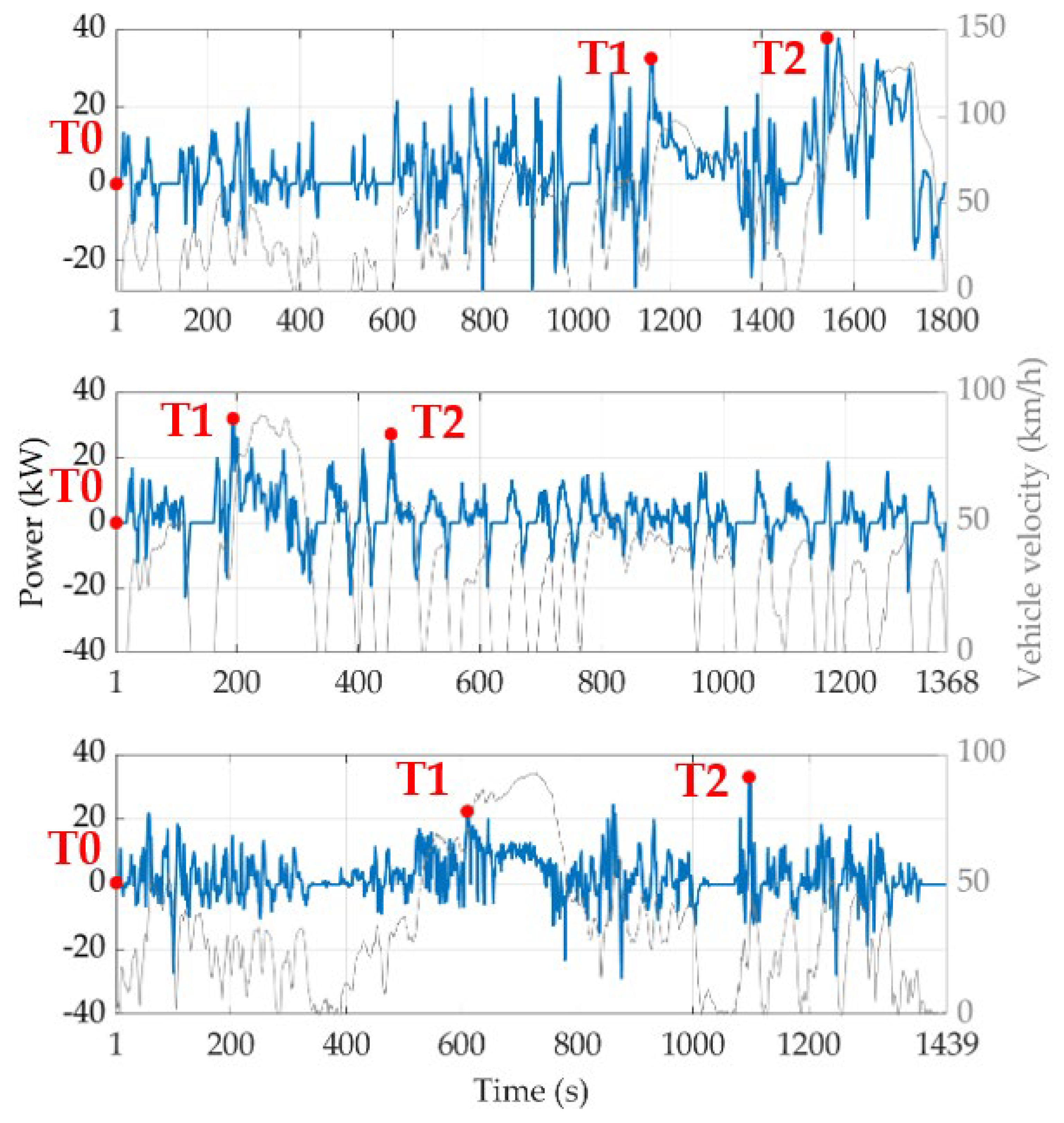
- An approach to evaluate the meaningful stages of the driving missions for an appropriate assessment of the RL agent learning process;
- An assessment of the change in the performances achieved by different RL agents trained on different regulatory driving cycles with two distinct reward functions;
- A detailed analysis of the potential carried by the selected agent when tested on real-world driving conditions.
2. Vehicle Model and Control Framework
2.1. Vehicle
2.2. Environment
2.3. Agent
| Algorithm 1 DQN and DDQN |
| Initialize Q-network and target network with random weights for each episode do for each environment step do Collect observation and select action Execute and collect next observation and reward Store tuple in memory replay buffer Sample tuple from memory buffer Compute loss function of the Q-network: for DQN for DDQN Perform gradient descent to update Every steps the is updated end for end for |
3. Reinforcement Learning for the Energy Management of Hybrid Powertrains
3.1. Observation
3.2. Action
3.3. Reward
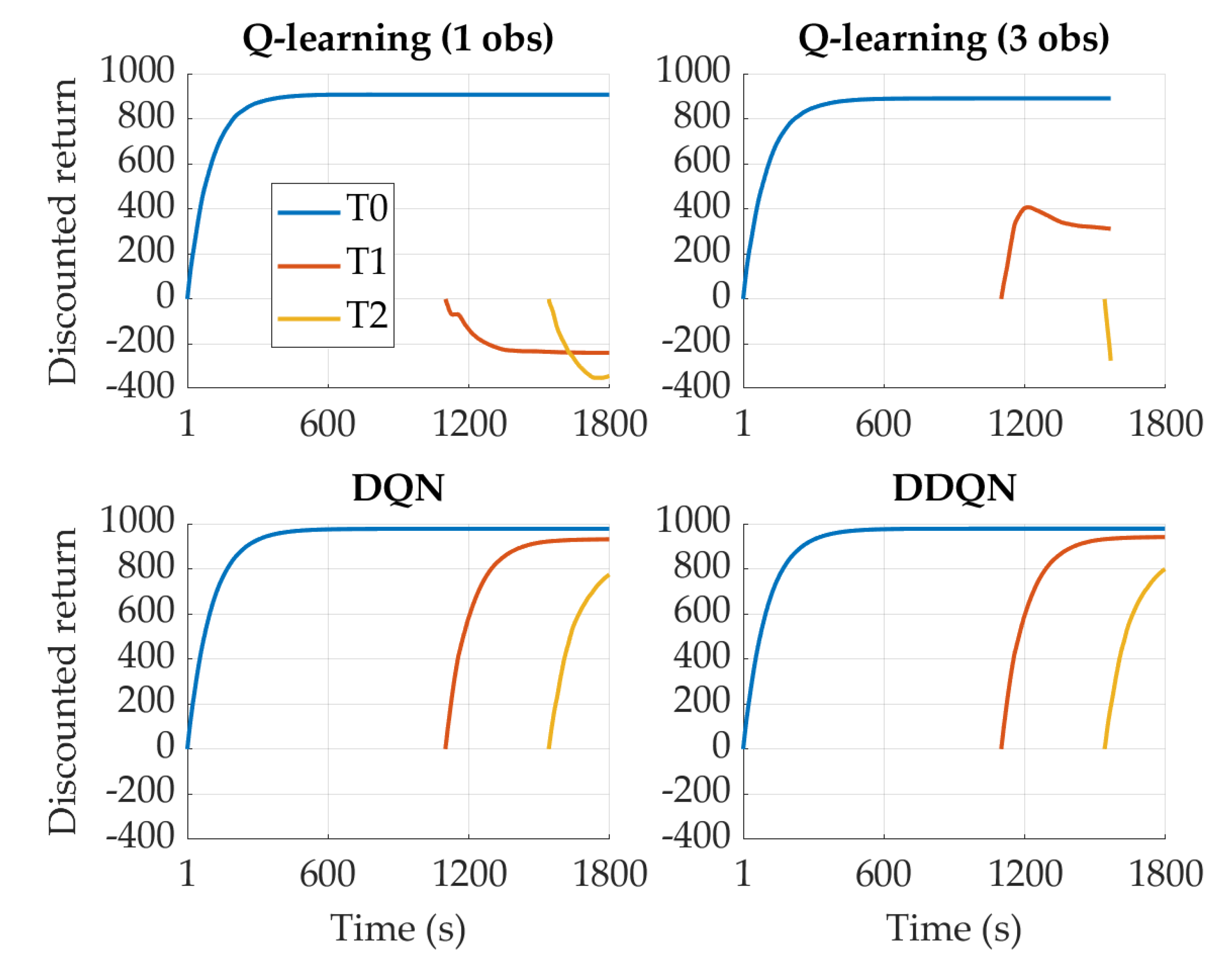
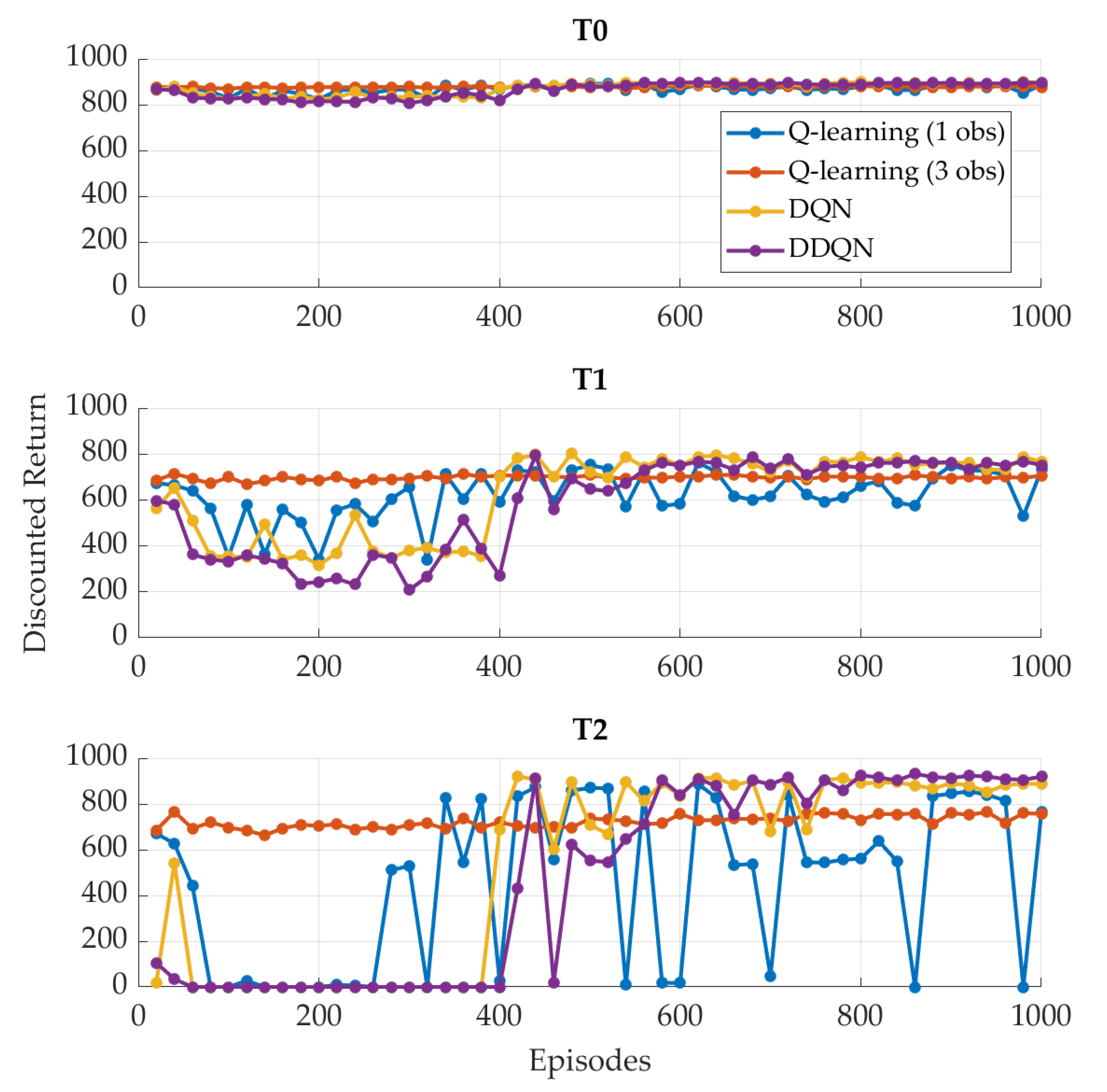
4. Results
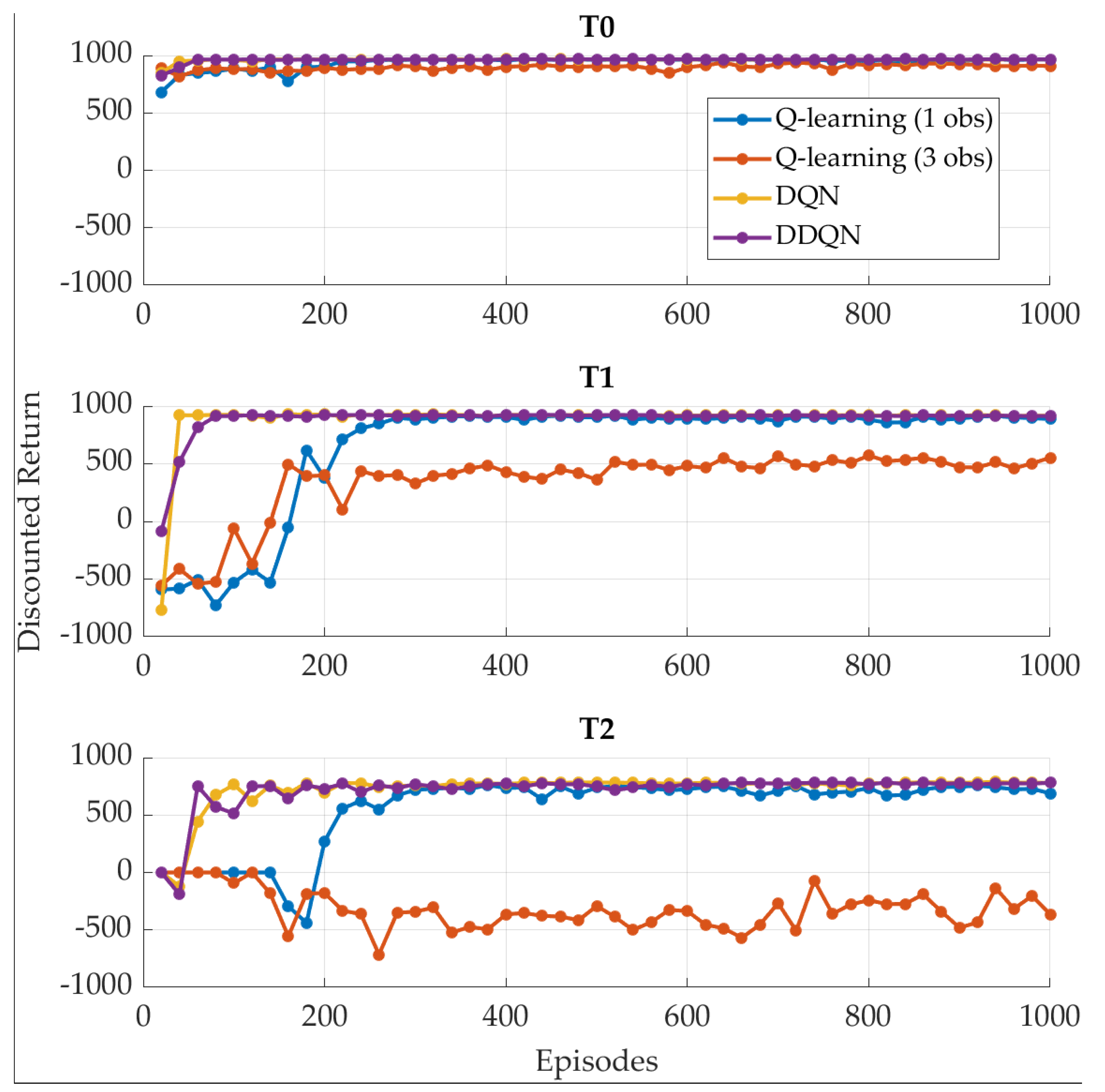
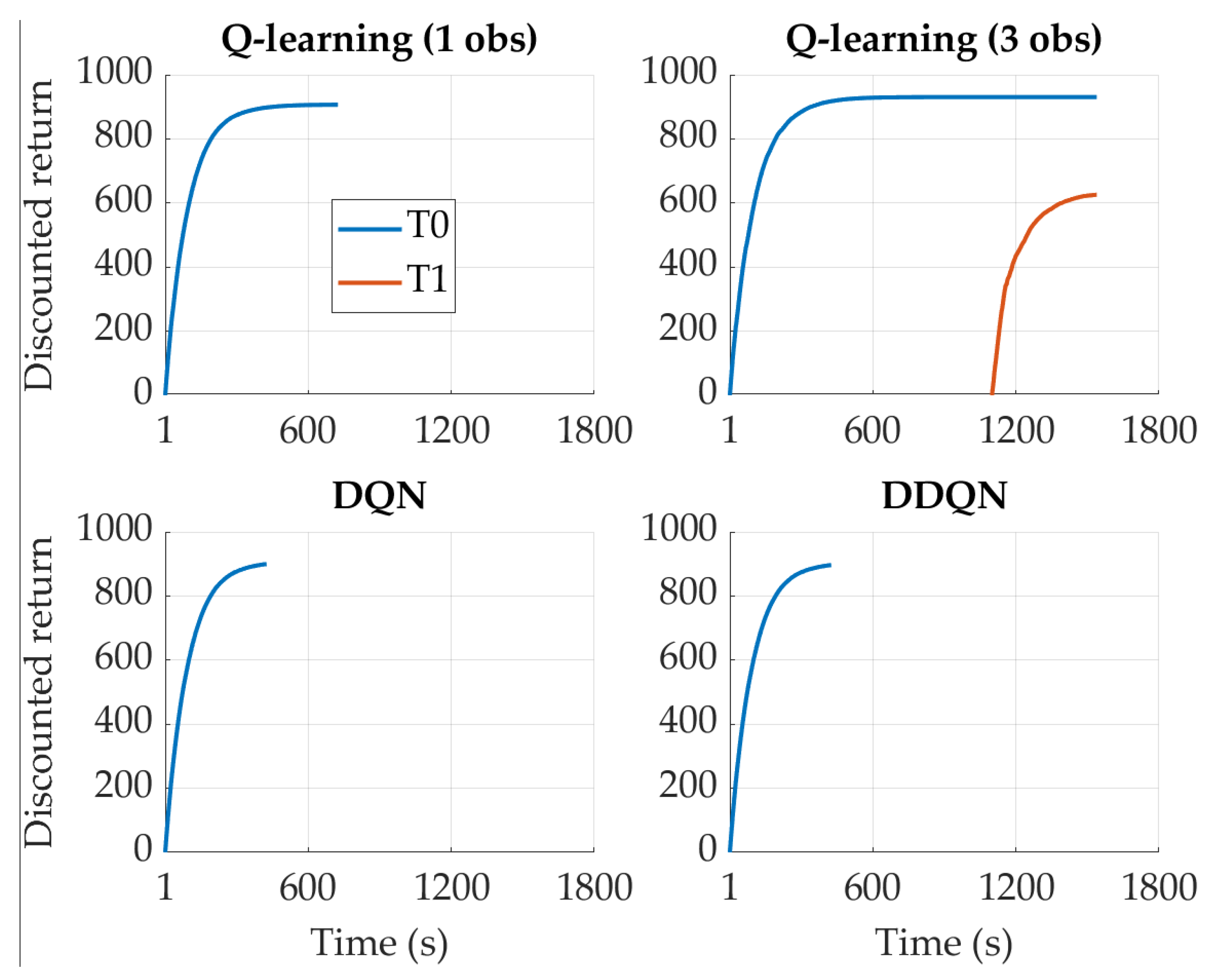
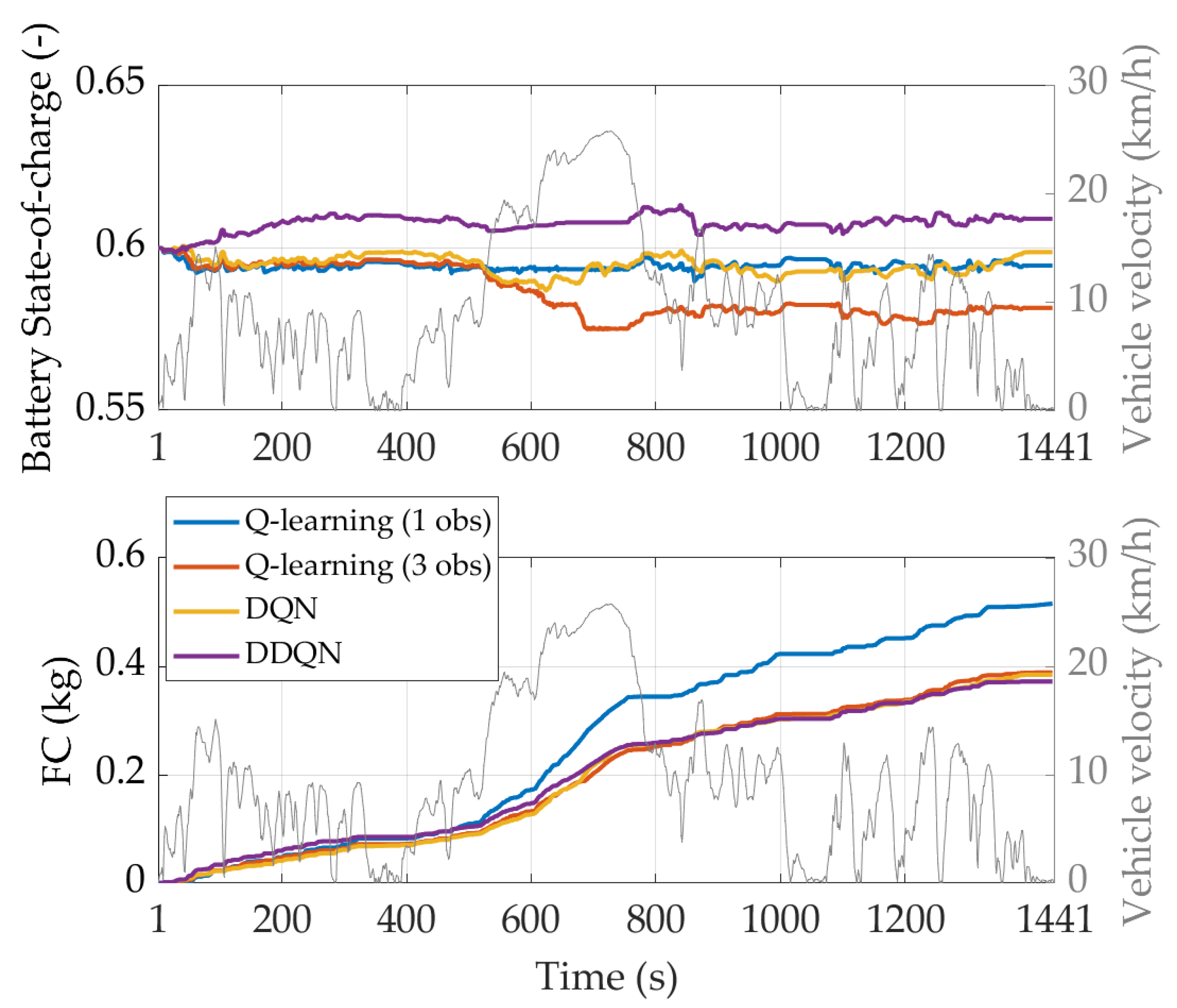
4.1. SOC-Oriented Reward
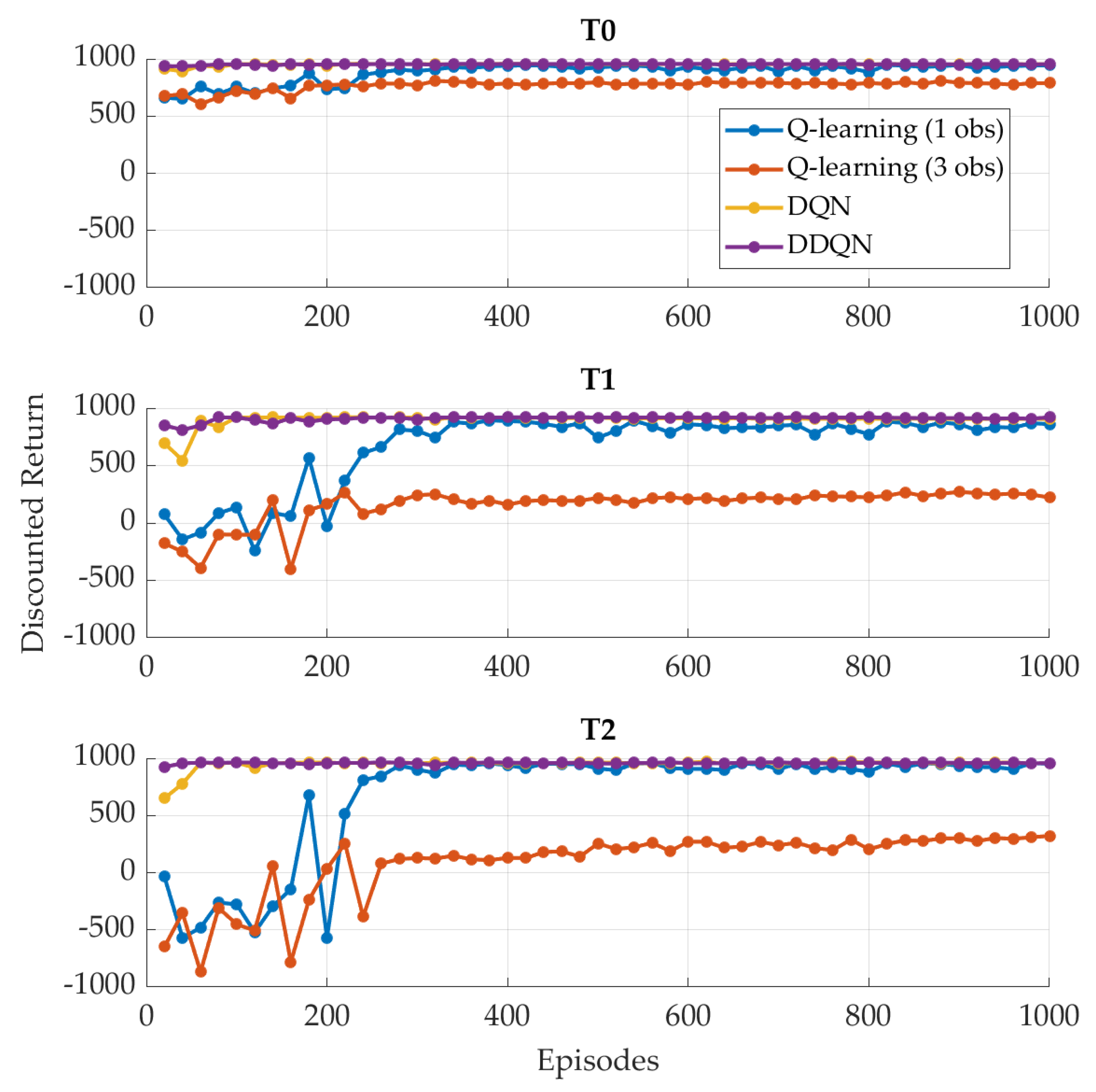
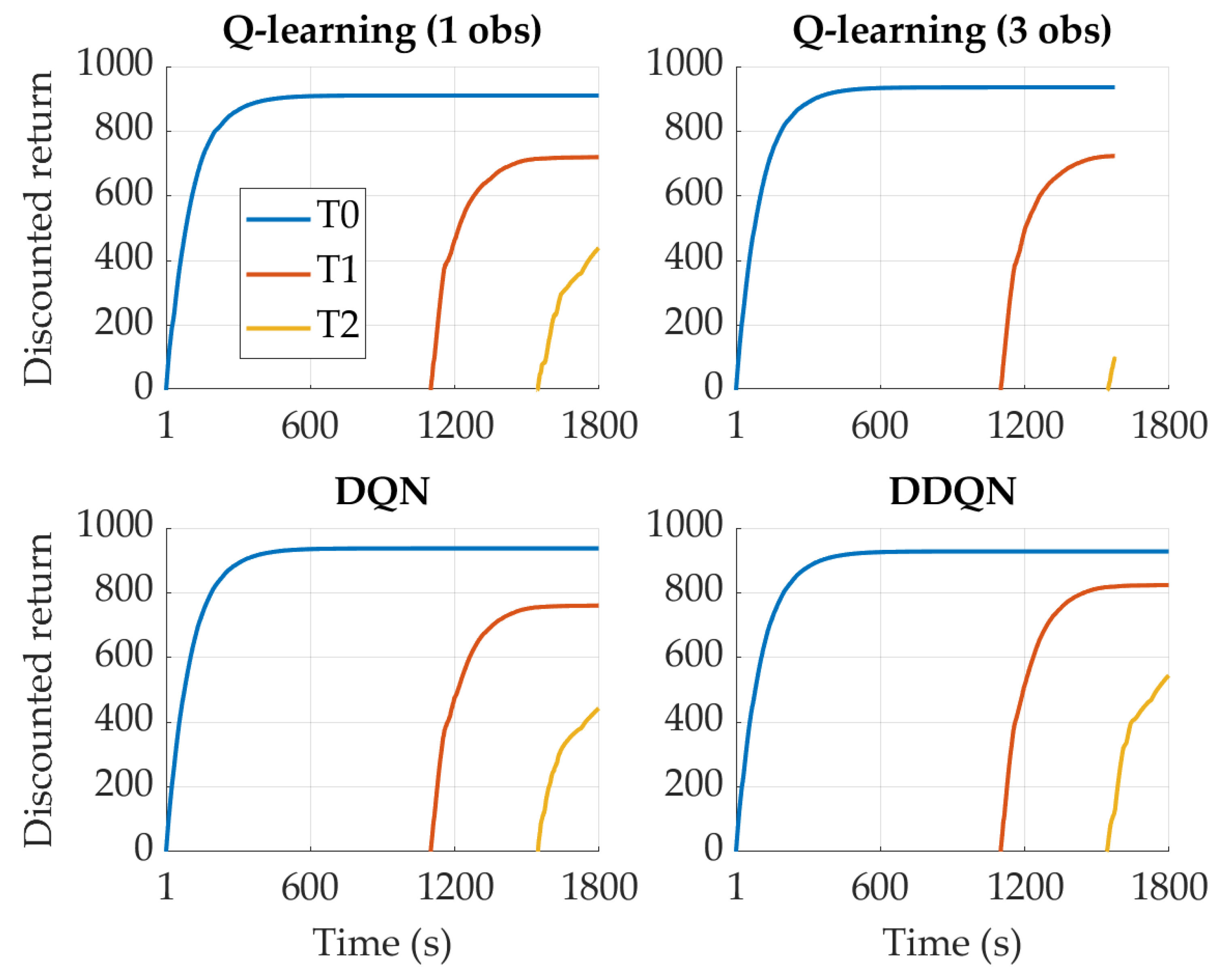
4.2. FC-Oriented Reward
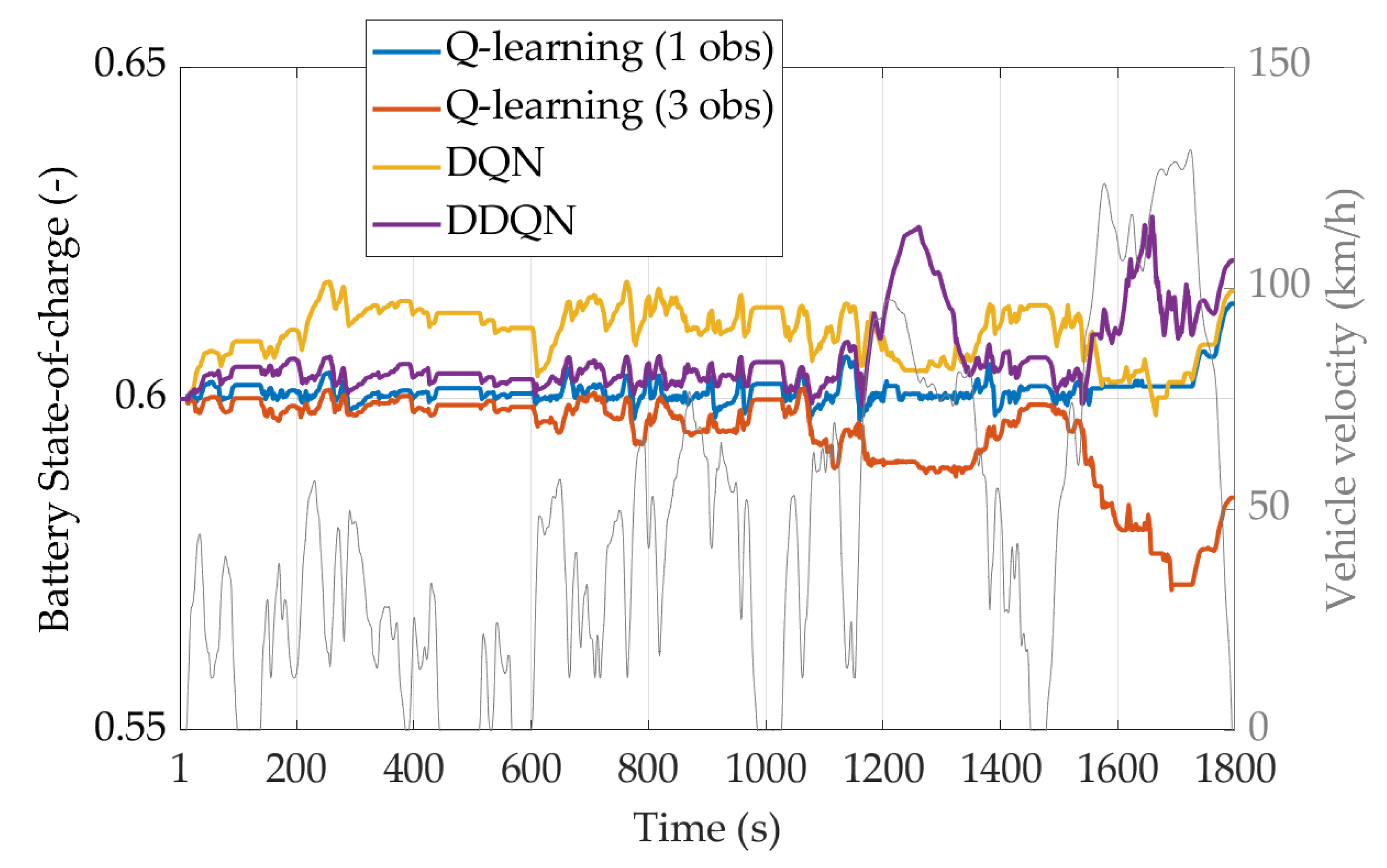
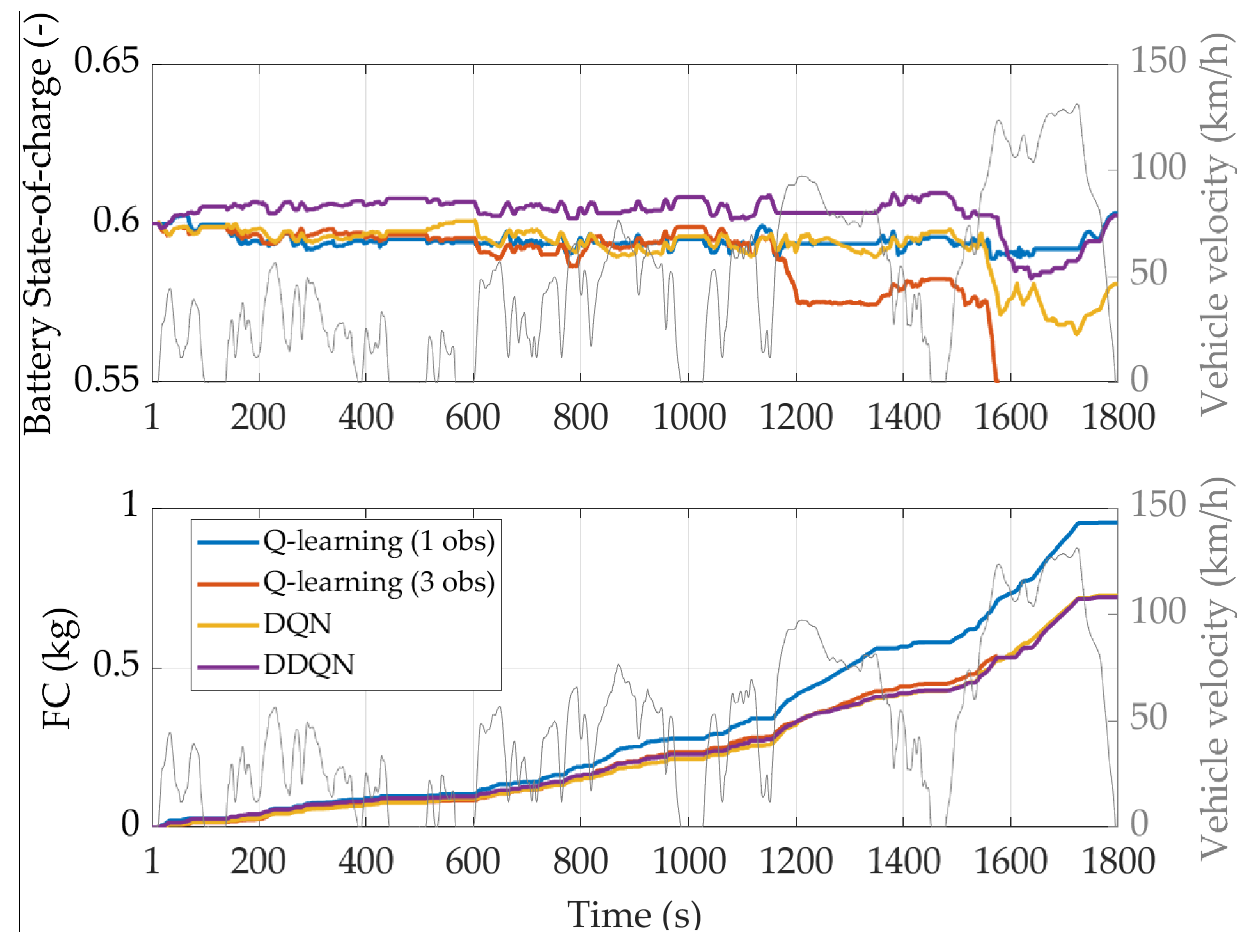
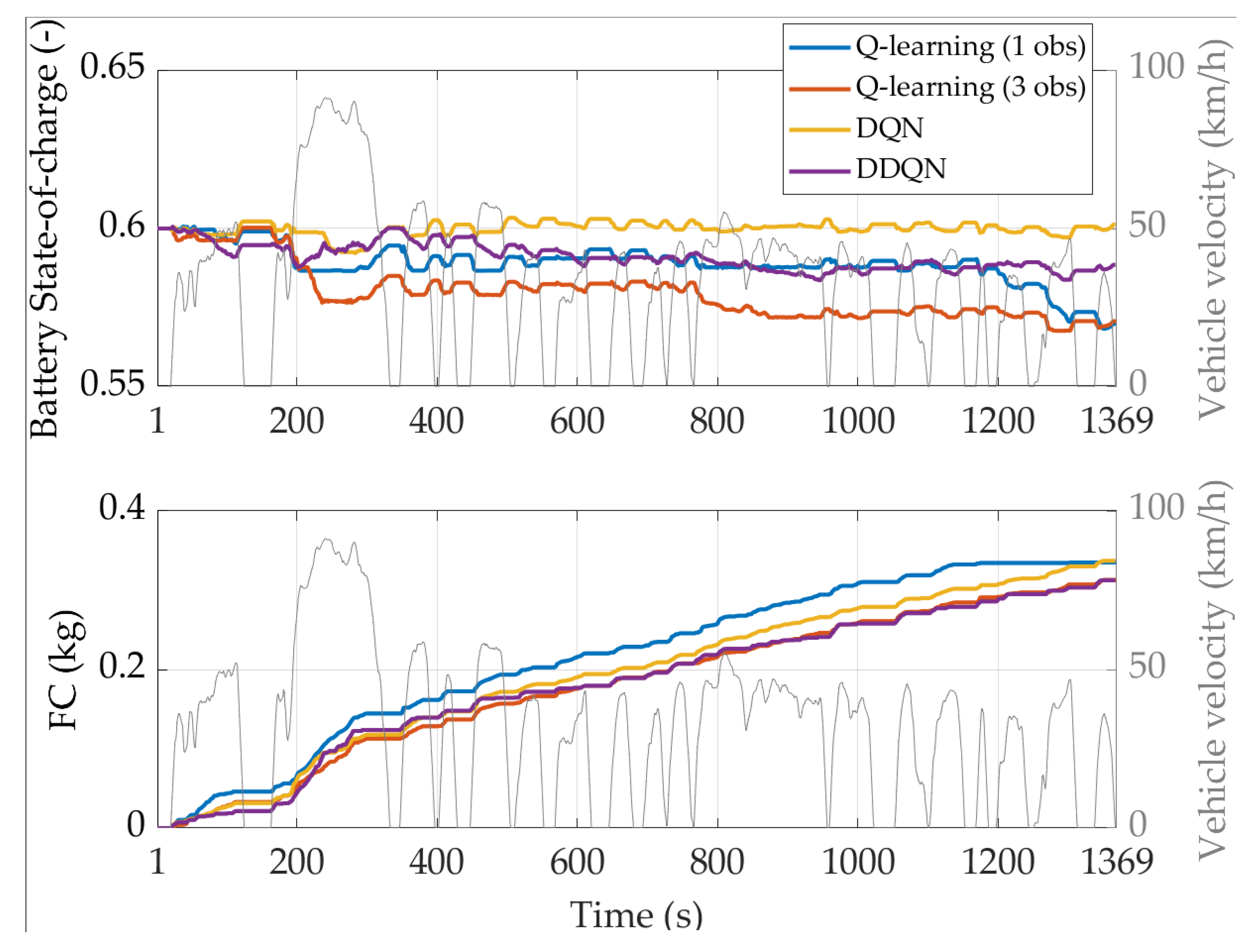
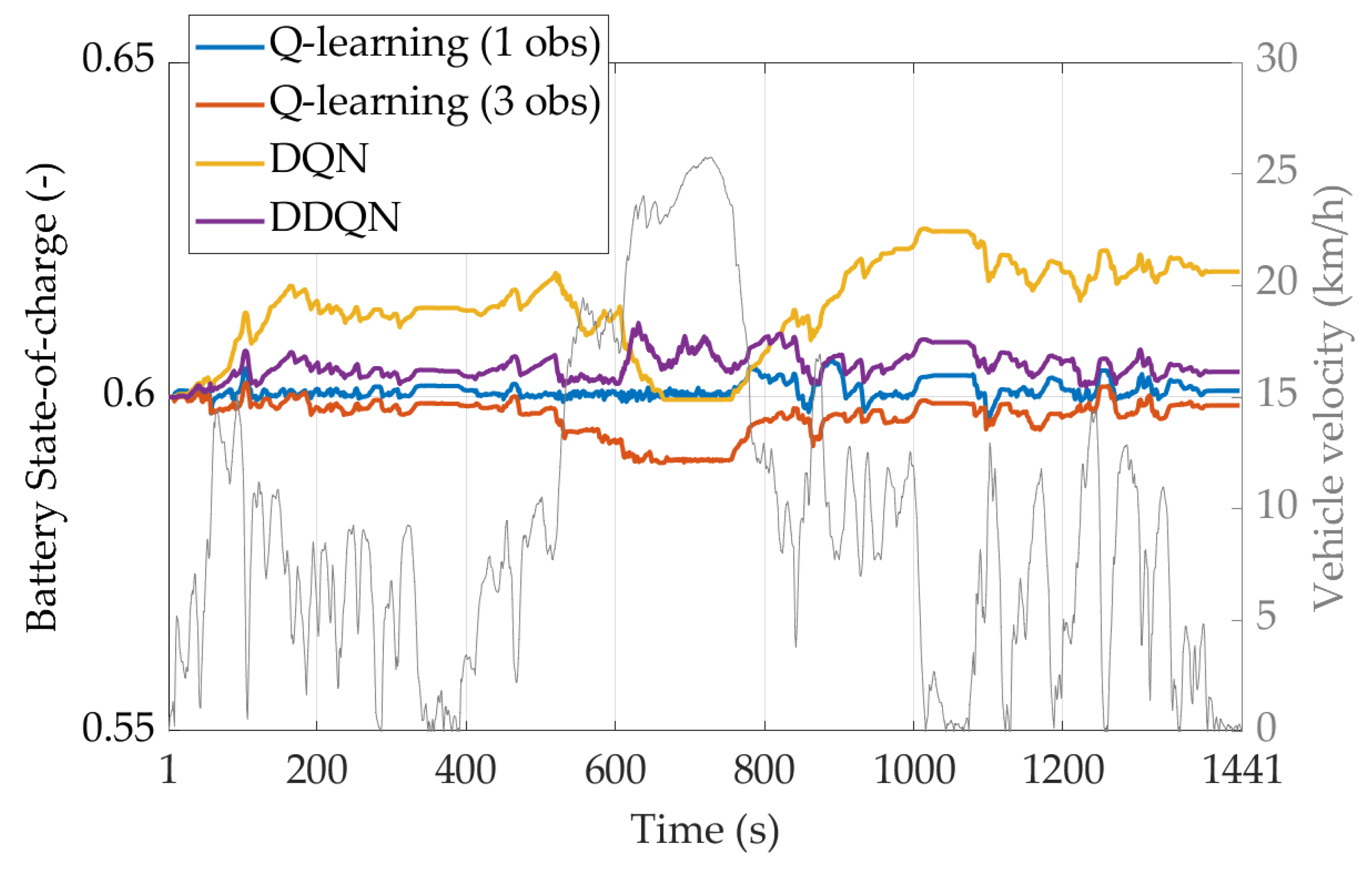
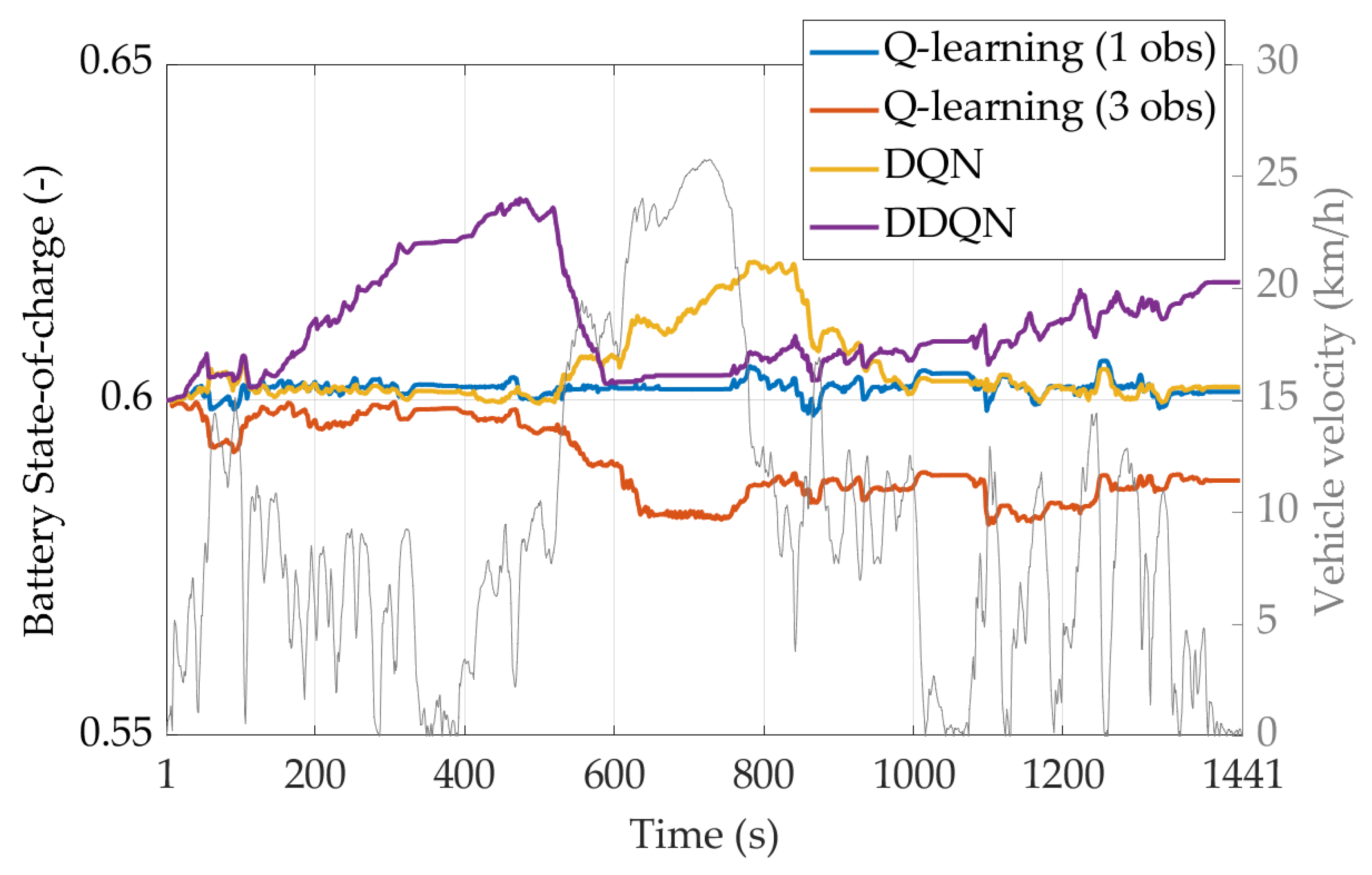
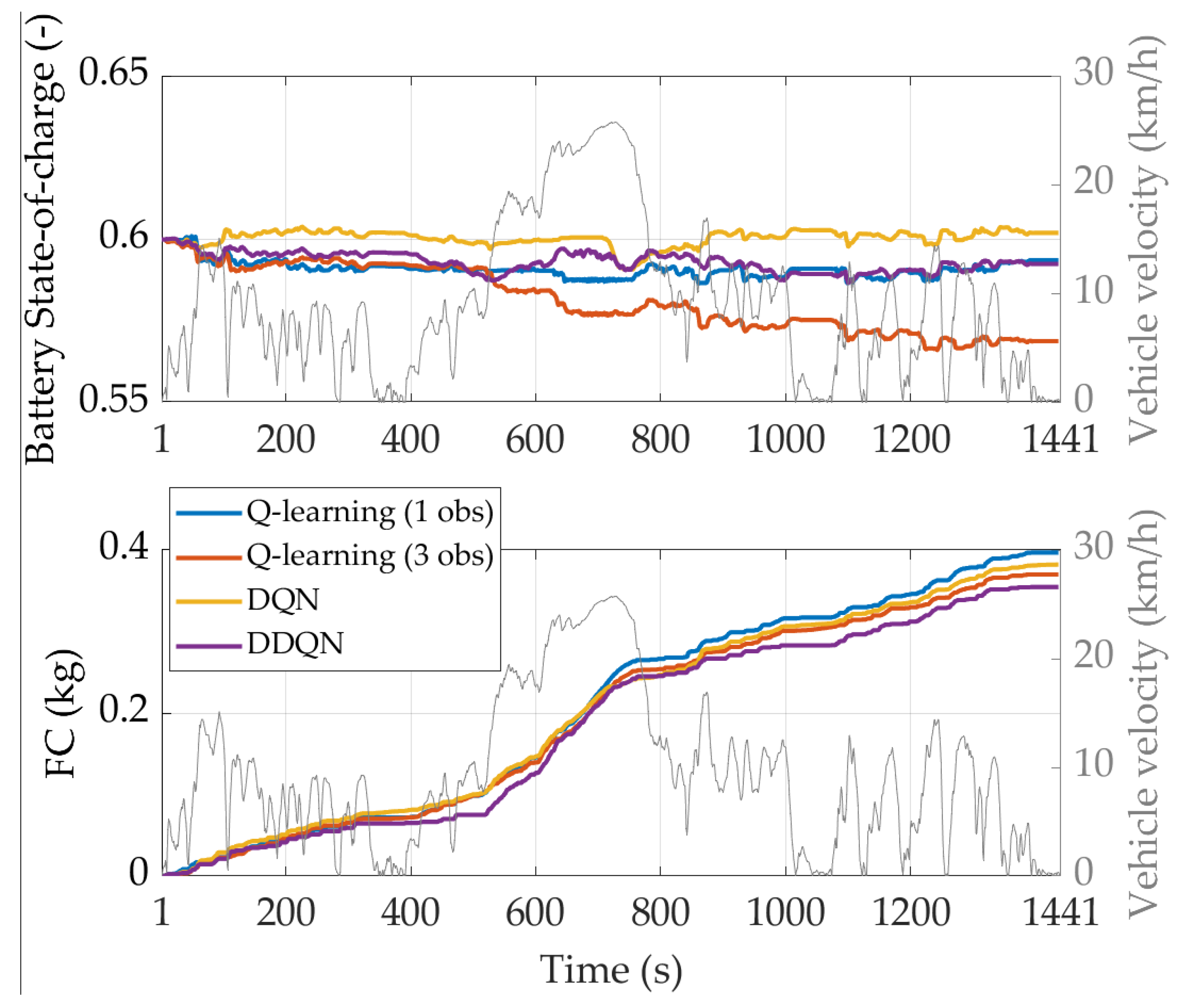
4.3. Testing Reinforcement Learning Agents on a Real-World Driving Mission
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ehsani, M.; Gao, Y.; Longo, S.; Ebrahimi, K. Modern Electric, Hybrid Electric, and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kebriaei, M.; Niasar, A.H.; Asaei, B. Hybrid electric vehicles: An overview. In Proceedings of the 2015 International Conference on Connected Vehicles and Expo (ICCVE), Shenzhen, China, 19–23 October 2015; pp. 299–305. [Google Scholar] [CrossRef]
- Biswas, A.; Emadi, A. Energy management systems for electrified powertrains: State-of-the-art review and future trends. IEEE Trans. Veh. Technol. 2019, 68, 6453–6467. [Google Scholar] [CrossRef]
- Banvait, H.; Anwar, S.; Chen, Y. A Rule-Based Energy Management Strategy for Plug- in Hybrid Electric Vehicle (PHEV). In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; IEEE: New York, NY, USA, 2009; pp. 3938–3943. [Google Scholar]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; He, H.; Ji, J. Model predictive control power management strategies for HEVs: A review. J. Power Sources 2017, 341, 91–106. [Google Scholar] [CrossRef]
- Ganesh, A.H.; Xu, B. A review of reinforcement learning based energy management systems for electrified powertrains: Progress, challenge, and potential solution. Renew. Sustain. Energy Rev. 2022, 154, 111833. [Google Scholar] [CrossRef]
- Cioffi, R.; Travaglioni, M.; Piscitelli, G.; Petrillo, A.; De Felice, F. Artificial intelligence and machine learning applications in smart production: Progress, trends, and directions. Sustainability 2020, 12, 492. [Google Scholar] [CrossRef]
- Hu, X.; Liu, T.; Qi, X.; Barth, M. Reinforcement Learning for Hybrid and Plug-In Hybrid Electric Vehicle Energy Management: Recent Advances and Prospects. IEEE Ind. Electron. Mag. 2019, 13, 16–25. [Google Scholar] [CrossRef]
- Liu, T.; Hu, X.; Li, S.E.; Cao, D. Reinforcement Learning Optimized Look-Ahead Energy Management of a Parallel Hybrid Electric Vehicle. IEEE ASME Trans. Mechatron. 2017, 22, 1497–1507. [Google Scholar] [CrossRef]
- Xu, B.; Rathod, D.; Zhang, D.; Yebi, A.; Zhang, X.; Li, X.; Filipi, Z. Parametric study on reinforcement learning optimized energy management strategy for a hybrid electric vehicle. Appl. Energy 2020, 259, 114200. [Google Scholar] [CrossRef]
- Xu, B.; Tang, X.; Hu, X.; Lin, X.; Li, H.; Rathod, D.; Wang, Z. Q-Learning-Based Supervisory Control Adaptability Investigation for Hybrid Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6797–6806. [Google Scholar] [CrossRef]
- Xu, B.; Malmir, F.; Rathod, D.; Filipi, Z. Real-Time reinforcement learning optimized energy management for a 48V mild hybrid electric vehicle. SAE Tech. Pap. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Xu, K.; Zahid, T.; Qin, F.; Li, C. Energy management strategy for a hybrid electric vehicle based on deep reinforcement learning. Appl. Sci. 2018, 8, 187. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, J.; Tang, X. Multi-objective control and energy management strategy based on deep Q-network for parallel hybrid electric vehicles. Int. J. Veh. Perform. 2022, 8, 371–386. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Han, X.; He, H.; Wu, J.; Peng, J.; Li, Y. Energy management based on reinforcement learning with double deep Q-learning for a hybrid electric tracked vehicle. Appl. Energy 2019, 254, 113708. [Google Scholar] [CrossRef]
- Liu, T.; Wang, B.; Yang, C. Online Markov Chain-based energy management for a hybrid tracked vehicle with speedy Q-learning. Energy 2018, 160, 544–555. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Peng, J.; Zhang, H.; He, H. Deep reinforcement learning of energy management with continuous control strategy and traffic information for a series-parallel plug-in hybrid electric bus. Appl. Energy 2019, 247, 454–466. [Google Scholar] [CrossRef]
- Tan, H.; Zhang, H.; Peng, J.; Jiang, Z.; Wu, Y. Energy management of hybrid electric bus based on deep reinforcement learning in continuous state and action space. Energy Convers. Manag. 2019, 195, 548–560. [Google Scholar] [CrossRef]
- Biswas, A.; Anselma, P.G.; Emadi, A. Real-Time Optimal Energy Management of Multimode Hybrid Electric Powertrain with Online Trainable Asynchronous Advantage Actor—Critic Algorithm. IEEE Trans. Transp. Electrif. 2022, 8, 2676–2694. [Google Scholar] [CrossRef]
- Li, Y.; Tao, J.; Xie, L.; Zhang, R.; Ma, L.; Qiao, Z. Enhanced Q-learning for real-time hybrid electric vehicle energy management with deterministic rule. Meas. Control 2020, 53, 1493–1503. [Google Scholar] [CrossRef]
- Maino, C.; Mastropietro, A.; Sorrentino, L.; Busto, E.; Misul, D.; Spessa, E. Project and Development of a Reinforcement Learning Based Control Algorithm for Hybrid Electric Vehicles. Appl. Sci. 2022, 12, 812. [Google Scholar] [CrossRef]
- Joshi, A. Review of Vehicle Engine Efficiency and Emissions. SAE Tech. Pap. 2021, 2, 2479–2507. [Google Scholar] [CrossRef]
- EPA, United States Environmental Protection Agency. Emission Standards Reference Guide. EPA Federal Test Procedure (FTP). Available online: https://www.epa.gov/emission-standards-reference-guide/epa-federal-test-procedure-ftp (accessed on 29 January 2023).
- Fusco, G.; Bracci, A.; Caligiuri, T.; Colombaroni, C.; Isaenko, N. Experimental analyses and clustering of travel choice behaviours by floating car big data in a large urban area. IET Intell. Transp. Syst. 2018, 12, 270–278. [Google Scholar] [CrossRef]
- Puterman, M. Markov Decision Processes; John Wiley and Sons: New York, NY, USA, 1994. [Google Scholar]
- Fechert, R.; Lorenz, A.; Liessner, R.; Bäker, B. Using Deep Reinforcement Learning for Hybrid Electric Vehicle Energy Management under Consideration of Dynamic Emission Models. SAE Tech. Pap. 2020, 58, 1–13. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Watkins, C.J.C.H.; Dayan, P. Q-Learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Silver, D. Playing Atari with Deep Reinforcement Learning. Available online: https://arxiv.org/abs/1312.5602 (accessed on 29 January 2023).
- Fan, J.; Wang, Z. A Theoretical Analysis of Deep Q-Learning. Available online: https://arxiv.org/abs/1901.00137v3 (accessed on 29 January 2023).
- Fujimoto, S.; Van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. Available online: http://arxiv.org/abs/1802.09477 (accessed on 29 January 2023).
- Van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. Available online: http://arxiv.org/abs/1509.06461 (accessed on 29 January 2023).
- Sciarretta, A.; Guzzella, L. Control of hybrid electric vehicles. IEEE Control Syst. Mag. 2007, 27, 60–70. [Google Scholar] [CrossRef]
- Maino, C.; Misul, D.; Musa, A.; Spessa, E. Optimal mesh discretization of the dynamic programming for hybrid electric vehicles. Appl. Energy 2021, 292, 116920. [Google Scholar] [CrossRef]



| General Specifications | |
|---|---|
| Vehicle class | Passenger car |
| Kerb weight (kg) | 750 |
| Vehicle mass (w/pwt components) | 1200 |
| Transmission | 6-gears |
| Internal Combustion Engine | |
| Fuel type | Gasoline |
| Maximum power (kW (@ rpm)) | 88 (@ 5500) |
| Maximum torque (Nm (@ rpm)) | 180 (@ 1750–4000) |
| Rotational speed range (rpm) | 0–6250 |
| Motor-Generator | |
| Maximum power (kW (@ rpm)) | 70 (@ 6000) |
| Maximum torque (Nm (@ rpm)) | 154 (@ 0–4000) |
| Rotational speed range (rpm) | 0–13,500 |
| Battery | |
| Peak power (kW) | 74 |
| Energy content (kWh) | 6.1 |
| AC/DC converter efficiency (-) | 0.95 |
| Hyperparameters | Values |
|---|---|
| Training episodes | 1000 |
| Discount factor | 0.99 |
| Learning rate (Q-learning) | 0.9 |
| Learning rate (DNNs) | 2 × 10−4 |
| Exploration rate @ = 1 | 0.8 |
| Minimum exploration rate @ = 1 | 0.05 |
| Update frequency of target network | 6000 |
| Mini-batch size | 32 |
| Experience replay memory size | 100,000 |
| Number of hidden layers (DNNs) | 1 |
| Neurons in the hidden layers (DNNs) | 64 |
| Reward coefficient | 10 |
| Reward coefficient (SOC-oriented) | −1000 |
| Reward coefficient (FC-oriented) | −3000 |
| Reward coefficient (SOC-oriented) | −1000 |
| Reward coefficient (FC-oriented) | −150 |
| Reward penalty | −100 |
| Agent | ||||
|---|---|---|---|---|
| WLTC | ||||
| Q-learning (1 obs) | 822 | 0.614 | 822 | - |
| Q-learning (3 obs) | 815 | 0.585 | 836 | −1.66 |
| DQN | 845 | 0.616 | 845 | −2.77 |
| DDQN | 863 | 0.620 | 863 | −4.93 |
| FTP-75 | ||||
| Q-learning (1 obs) | 368 | 0.604 | 368 | - |
| Q-learning (3 obs) | 376 | 0.589 | 392 | −2.20 |
| DQN | 363 | 0.602 | 363 | 1.52 |
| DDQN | 362 | 0.609 | 362 | 1.77 |
| Agent | ||||
|---|---|---|---|---|
| WLTC | ||||
| Q-learning (1 obs) | 954 | 0.603 | 954 | - |
| Q-learning (3 obs) | - | - | - | - |
| DQN | 726 | 0.580 | 753 | 21.07 |
| DDQN | 721 | 0.602 | 721 | 24.41 |
| FTP-75 | ||||
| Q-learning (1 obs) | 335 | 0.570 | 378 | - |
| Q-learning (3 obs) | 313 | 0.571 | 355 | 6.08 |
| DQN | 337 | 0.601 | 337 | 10.85 |
| DDQN | 313 | 0.589 | 329 | 12.96 |
| Agent | ||||
|---|---|---|---|---|
| Train WLTC—Test RDM | ||||
| Q-learning (1 obs) | 436 | 0.601 | 436 | - |
| Q-learning (3 obs) | 447 | 0.599 | 448 | −2.75 |
| DQN | 463 | 0.619 | 463 | −6.19 |
| DDQN | 407 | 0.604 | 407 | 6.65 |
| Train FTP-75—Test RDM | ||||
| Q-learning (1 obs) | 394 | 0.601 | 394 | - |
| Q-learning (3 obs) | 416 | 0.588 | 433 | −9.90 |
| DQN | 404 | 0.602 | 404 | −2.54 |
| DDQN | 459 | 0.617 | 459 | −16.50 |
| Agent | ||||
|---|---|---|---|---|
| Train WLTC—Test RDM | ||||
| Q-learning (1 obs) | 516 | 0.595 | 523 | - |
| Q-learning (3 obs) | 388 | 0.582 | 414 | 20.84 |
| DQN | 384 | 0.599 | 385 | 26.39 |
| DDQN | 372 | 0.602 | 372 | 28.87 |
| Train FTP-75—Test RDM | ||||
| Q-learning (1 obs) | 397 | 0.594 | 406 | - |
| Q-learning (3 obs) | 370 | 0.569 | 415 | −2.22 |
| DQN | 382 | 0.602 | 382 | 5.91 |
| DDQN | 354 | 0.592 | 366 | 9.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acquarone, M.; Maino, C.; Misul, D.; Spessa, E.; Mastropietro, A.; Sorrentino, L.; Busto, E. Influence of the Reward Function on the Selection of Reinforcement Learning Agents for Hybrid Electric Vehicles Real-Time Control. Energies 2023, 16, 2749. https://doi.org/10.3390/en16062749
Acquarone M, Maino C, Misul D, Spessa E, Mastropietro A, Sorrentino L, Busto E. Influence of the Reward Function on the Selection of Reinforcement Learning Agents for Hybrid Electric Vehicles Real-Time Control. Energies. 2023; 16(6):2749. https://doi.org/10.3390/en16062749
Chicago/Turabian StyleAcquarone, Matteo, Claudio Maino, Daniela Misul, Ezio Spessa, Antonio Mastropietro, Luca Sorrentino, and Enrico Busto. 2023. "Influence of the Reward Function on the Selection of Reinforcement Learning Agents for Hybrid Electric Vehicles Real-Time Control" Energies 16, no. 6: 2749. https://doi.org/10.3390/en16062749
APA StyleAcquarone, M., Maino, C., Misul, D., Spessa, E., Mastropietro, A., Sorrentino, L., & Busto, E. (2023). Influence of the Reward Function on the Selection of Reinforcement Learning Agents for Hybrid Electric Vehicles Real-Time Control. Energies, 16(6), 2749. https://doi.org/10.3390/en16062749









