Molecular Dynamics Method for Supercritical CO₂ Heat Transfer: A Review

Abstract

This paper reviews molecular dynamics (MD) concepts on heat transfer analysis of supercritical CO₂, and highlights the major parameters that can affect the accuracy of respective thermal coefficients. Subsequently, the prime aspects of construction, transfer identification, and thermal performance are organized according to their challenges and prospective solutions associated with the mutability of supercritical CO₂ properties. Likewise, the characteristics of bound force field schemes and thermal relaxation approaches are discussed on a case-by-case basis. Both convective and diffusive states of trans- and supercritical CO₂ are debated, given their magnitude effects on molecular interactions. Following the scarcity of literature on similar enquiries, this paper recommended a future series of studies on molecular dynamics models in a large region of supercriticality and phase-interactions for coupled heat and mass transfer systems. This review recognizes that the foremost undertaking is to ascertain the thermo-hydraulic identity of supercritical CO₂ for process feasibility of developed technology.

1. Introduction

With growing awareness of dual coercions of Ozone Depletion (ODP) and global warming, emergent activities have been heading for the endorsing of environmentally benign refrigerants. Accordingly, Carbon Dioxide (CO₂) was subjected to in-depth scrutiny to be adopted as a Holy Grail fluid in vital fields, much like energy conversion systems [1,2,3,4,5], solar energy [6,7], and soil remediation [8,9,10]. Under supercritical conditions, CO₂ can possess certain key properties that allow the exhibition of desirable thermodynamic characteristics compared to major industrial fluids [11,12,13]. This is linked to the uniqueness of its thermal conductivity, viscosity, and specific heat capacity, which displayed remarkable evolutions near the so-called “near-critical region” [14,15].

Since its integration in heavy industry at the 19th century to promote the efficiency of vapor compression cycles [16], CO₂ research was focused on trans-critical heating cycles without apparent success, as the latter have showed unbalanced performances [16,17,18]. Instead of that, the heat transfer process at a supercritical state has shown a particular interest in heat exchangers and microchannel devices [19,20], during which the energy transfer process can occur along a critical isobar [21,22,23]. Nevertheless, the identification of radical changes in CO₂ properties through these devices still remains a challenging issue [24].

To this end, the pioneer works of Gharagheizi et al. [25] and Su et al. [26] showed the crucial role of thermal conductivity and viscosity in characterizing the ability of supercritical fluids to effectively enhance heat transfer with reduced shear stress, relative to its effects on the cost of heating systems. That being said, the estimation of a broad law for these properties remains a tough enquiry [27]. When broad experiments were performed to quantify the critical heat transfer fluctuations and related interfacial process according to such key properties, only reflective replies were projected. This is linked to difficulties associated with observing the corresponding phase change, alongside the reaction rates at a supercritical environment [28,29]. Considering this scarcity of knowledge, molecular dynamics (MD) approaches were applied as aforementioned parameters that can be accurately manipulated by bridging nano- to macro-thermodynamics [30,31].

Stimulated by the first principle of quantum mechanics (i.e., FPQM) for potentiality of inter-atomic energy, the relevance of MD modeling was unbounded at both spatial and temporal scales, with less statistical noise when tuning many parameters simultaneously without being subject to large instabilities [32,33]. In addition to equilibrium and non-equilibrium molecular dynamics (i.e., EMD, NEMD, respectively), the transfer properties in sub- and supercritical regions can be estimated based on molecular structuration [34]. This is particularly functional with the EMD approach through statistics-based functions, which are known as Green–Kubo relations [35]. Otherwise, and with the NEMD approach, both the momentum and the position of each atom would be strongly required during the heat transfer mechanism, to the point that the corresponding transfer properties would have to be calculated with Fourier and Newton’s laws [36]. Of course, both EMD and NEMD approaches may reveal advantages and disadvantages when it comes to illuminating the heat transfer properties of supercritical CO₂; however, the lack of a thorough evaluation of the applicability of each of these techniques has broadened the criterion for DM selection beyond the scope of research experiments [37,38,39].

Since potentiality is crucial in MD simulations, the pioneering model of Murthy, Singer, and McDonald (named, MSM) has been commonly considered as a basic criterion for the MD actuary. Accordingly, a large series of potential models much like the Zhu–Robinson model in 1989 [40], Geiger–Ladanyi–Chapin model in 1990 [41], Palmer–Garret model in 1993 [42], Harris–Yung model (named, EPM2) in 1995 [43], Destrigneville–Brodholt–Wood model in 1996 [44], Errington model in 1999 [45], and Potoff and Siepmann model (namely, TraPPE) in 2001 [46] were pertinently successors. These models have shared a similar molecular structure of O-C-O atoms with short-range interactions. However, among those, only the Harris–Yung model was widely adopted in tremendous research following its excellent performance in predicting vapor–liquid coexistence curves [43]. Nonetheless, the aforementioned models were promoted according to the subcritical state of CO₂, and tended to be relatively deviated to the supercritical region.

Likewise from the perspective of power engineering, Zhang and Duan [47] recommended one of main models to optimize the MD potentiality based on MSM principal. Their developed model has successfully reproduced some experimental data on heat transfer according to MD temperatures of about 240 to 473 (K). Additionally, Merker et al. [48] proposed an equilibrium model to predict the vapor pressure and the vaporization enthalpy, simultaneously, which cannot be achieved from aforementioned models. Although the idea of a flexible model can be traced back to 1990s [49,50], a thorough flexible model on the intercalation mechanisms of supercritical mixtures was mainly developed in 2012 by Cygan et al. [51] in combination with Clay force field [52]. When reaching 2015, Zhong et al. [36] made a rigid-flexible amendment on MSM, EPM2, and TraPPE models to be employed for the heat transfer mechanism of regular and supercritical CO₂. To date, and by end of 2022, Liu et al. [53,54] expanded the literature confines by proposing an optimized set of MD parameters on the basis EPM2 model to improve the applicability of molecular dynamics near the critical region.

Once the focus is merely shifted to CO₂, the prime immersion of molecular dynamics has served to infer the thermal conductivity identity with no close relationship to applied energy nor to heat transfer reservoir conditions [54]. Until now, and to our knowledge, there is no in-depth comparison between the above-mentioned potentials in terms of their contribution to heat transfer characteristics at supercritical states. Accordingly, it is of great interest to evaluate such MD potentials through a careful comparison between their theoretical aspect and practical use, as well as the identification of their transfer aspect and thermal performance relative to the major challenges associated with the mutability of supercritical CO₂. Similarly, it is crucial to highlight the major role of force field and thermal relaxation models for supercritical mixtures’ heat transfer mechanism to accent the energy engineering of the day.

To do so, a state-of-the-art on force field and molecular models is deeply discussed in Section 2 of this review where the basics of transportation properties are underlined. Then, an overview of thermal conductivity and thermal diffusivity coefficients is developed in Section 3 to assess the performance of each MD approach on computing these parameters under supercritical conditions, with particular attention to regions beyond the applicability of existing predictive models. To close, some major challenges on supercritical prospects are put forward in Section 4 based on case studies. This review particularly sheds the light on the adequate MD algorithms that can show efficiency and validity with linear and nonlinear heat transfer theories, and carefully exhibit the current gaps that need to be addressed in the future for advanced energy engineering.

2. Key Developments in Force Field

As the interaction potential is fundamental for both MD and Monto-Carlo (MC) simulations, these latter are inferred from quantum chemistry simulations [47,48]. However, the lack of potential functionality remains an obstacle to advanced MD simulations. When the focus is devoted to the CO₂ molecule, for which the structure (O-C-O) is thought to be linear with 180°, the MD length of C-O bond is taken as 116 (pm), that is, between the C-O double bond (i.e., 124 pm) and the C-O triple bond (i.e., 113 pm), indicating the three-bond characteristics of the carbon–oxygen bond for simulations [55].

Based on that structure, a series of spatial models was increasingly developed [56]. One can mention the simplest spherical model [57] that fully ignored the inner interactions of CO₂ molecule. Likewise, the site–site model that grows into a prevalent model following its accuracy [40,41,42,43,44,45,46,58]. Given the complexity of MD scenarios according to such spatial models, the developed potential of CO₂ does not necessarily allow for the simulation of mixtures. Hence, the recent research has focused on general force fields that can predict interactions between assorted molecules [47,48,49,50,51,52,53,54,55,56,57,58,59]. However, the general force fields can only be adopted to a specific range of temperatures and pressures, with dissimilar performances in predicting CO₂ properties. Subsequently, a series of CO₂ force fields are abridged in this section with a focus on detailed inter-molecular interactions and potential functionality [47,48,49,50,51,52,53,54,55,56,57,58,59].

2.1. MD Potentials

Through a literature survey, several potential models have been traced from the spherical model that simplified the CO₂ molecule to a single sphere. Accordingly, the Belonoshko et al. [57] model displayed the shortest range of interactions that should be taken into consideration through MD simulations. Although this model brought a convenience in terms of computation and efficiency of adjustment, its overview was restricted, with no connection to microstructure information. In earlier 2012, Avendano et al. [60] applied the concept of “top-down” for the growth of a single-site coarse-grained molecular potential for CO₂. Hence, the proposed SAFT-γ force field by Avendano et al. [60] was competitive with aforementioned models.

Until now, the prevalent choice for CO₂ molecule is the site-site interaction model, while the MSM model is considered as a pioneer model for Molecular Dynamics. The latter has shown a significant predictability of various properties compared to that of spherical models [38,39]. Among all of site-site potentials, the elementary EPM2 was the renowned MD model due to its superior performance near the vapor–liquid coexistence curves. To this end, Zhang and Duan [47] optimized this molecular potential model with established MD techniques and histogram-reweighting grand canonical Monte Carlo simulations. Likewise, Zhu et al. [61] developed a fully flexible model with a linear equilibrium shape on the basis of the Zhang and Duan [47] strategy. In order to describe the interactions between CO₂ and silicate materials, Cygan et al. [51] proposed a flexible CO₂ model that can certify the vibration of C-O bond. This model is considered to be potential when evaluating the vibrational state of CO₂ in the clay inter-layer with cooperation of CLAY force field (i.e., CLAYFF).

Indeed, Zhang and Duan [47] provided the assessment on these models in terms of density, volume, and vapor–liquid coexistence curves (see Figure 1 and Figure 2 for instance). According to their data, it was found that the MSM model had a good prediction ability for only gas–liquid equilibrium problems. Meanwhile, there is still a lot of room for improvements in term of predicting the volume properties of liquids. Subsequently, several potential models were developed according to MSM principal. Among them, the EPM2 model can deliver a high accuracy when the deal is on phase equilibrium problems and MD feasibility near the critical region. Nevertheless, the EPM2 model is less accurate than the MSM model in terms of predicting the volume properties of the CO₂ molecule. As the TraPPE model may not predict phase behaviors, literature predictions have shown that Errington’s model [45] can be trusted in case of high densities. However, the abnormal high saturated vapor densities near a critical line have restricted its application with supercritical region.

In all aforementioned models, the O-C-O bond angle remains rigid at 180°, with Liu et al. [53,54] adjusting the bond angle of CO₂ according to EPM2 model to promote the phase equilibrium portability and MD proficiency. Then, the asymmetry behavior around the pseudo-line bridge was revealed using an updated set of CO₂ parameters according to leading parameters for the Liquid Simulations All Atom (OPLS-AA) force field.

Indeed, the formal function of aforementioned models can be displayed in terms of short-range interactions and coulombic interactions. One can write the following [62,63]:

$$u\left(1,2\right)={{\displaystyle \sum }}_{i\in \left\{1\right\}}^M{{\displaystyle \sum }}_{j\in \left\{2\right\}}^N{u}_{short}\left(r_{ij}\right)+{{\displaystyle \sum }}_{i\in \left\{1\right\}}^M{{\displaystyle \sum }}_{j\in \left\{2\right\}}^N\frac{q_i{q}_j}{r_{ij}}$$

(1)

where r_ij refers to distance between atoms i and j, and q_i, q_j are designated partials at atom centers. For MSM, EPM2, TraPPE models, and the adjusted model of Zhang and Duan [47], the short-range interactions are computed according to Lennard–Jones (L-J) function. One can write the following [62,63]:

$$u_{short}^{LJ}\left(r_{ij}\right)=4{\epsilon }_{ij}^{kl}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]$$

(2)

Inconsistently, the Errington adopted the complex function of Buckingham ponential-6 potential. One can write the following [62,63]:

$$u_{short}^{{\mathit{exp}}^{-6}}\left(r_{ij}\right)=\frac{{\epsilon }_{ij}}{1-6/\alpha }\left[\frac{6}{\alpha }\mathit{exp}\left(\alpha \left[1-\frac{r_{ij}}{r_m}\right]\right)-{\left(\frac{r_m}{r_{ij}}\right)}^6\right]$$

(3)

Apart from potential models used during MD simulations of pure CO₂ system, the potential of other components (e.g., silica and oil molecules in displacement systems) are also queried [64,65]. As displayed in

Table 1. Related case works that used diverse potentials for MD of CO₂ molecules and L-J fluids [64,65,66,67,68,69,70,71].

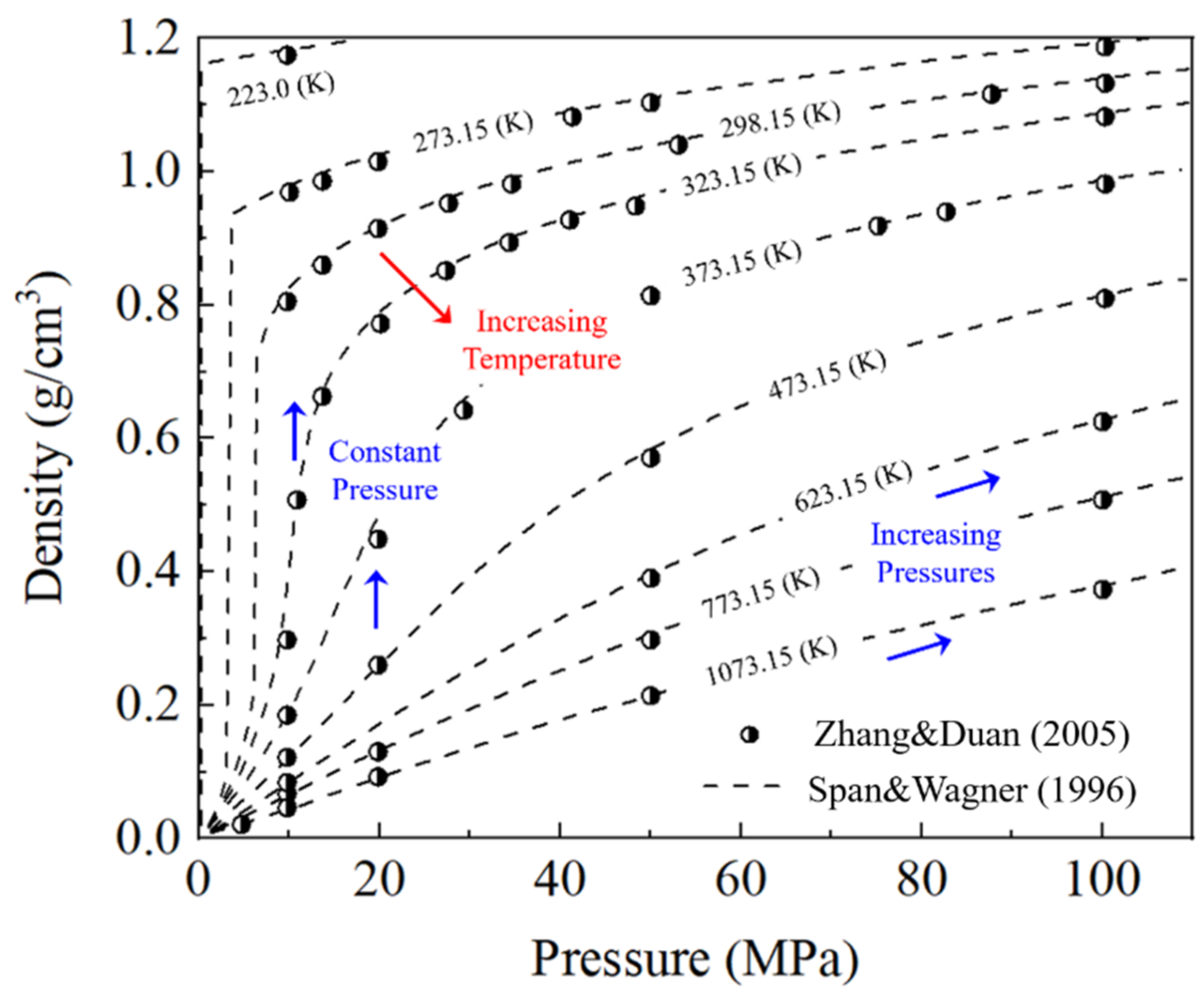
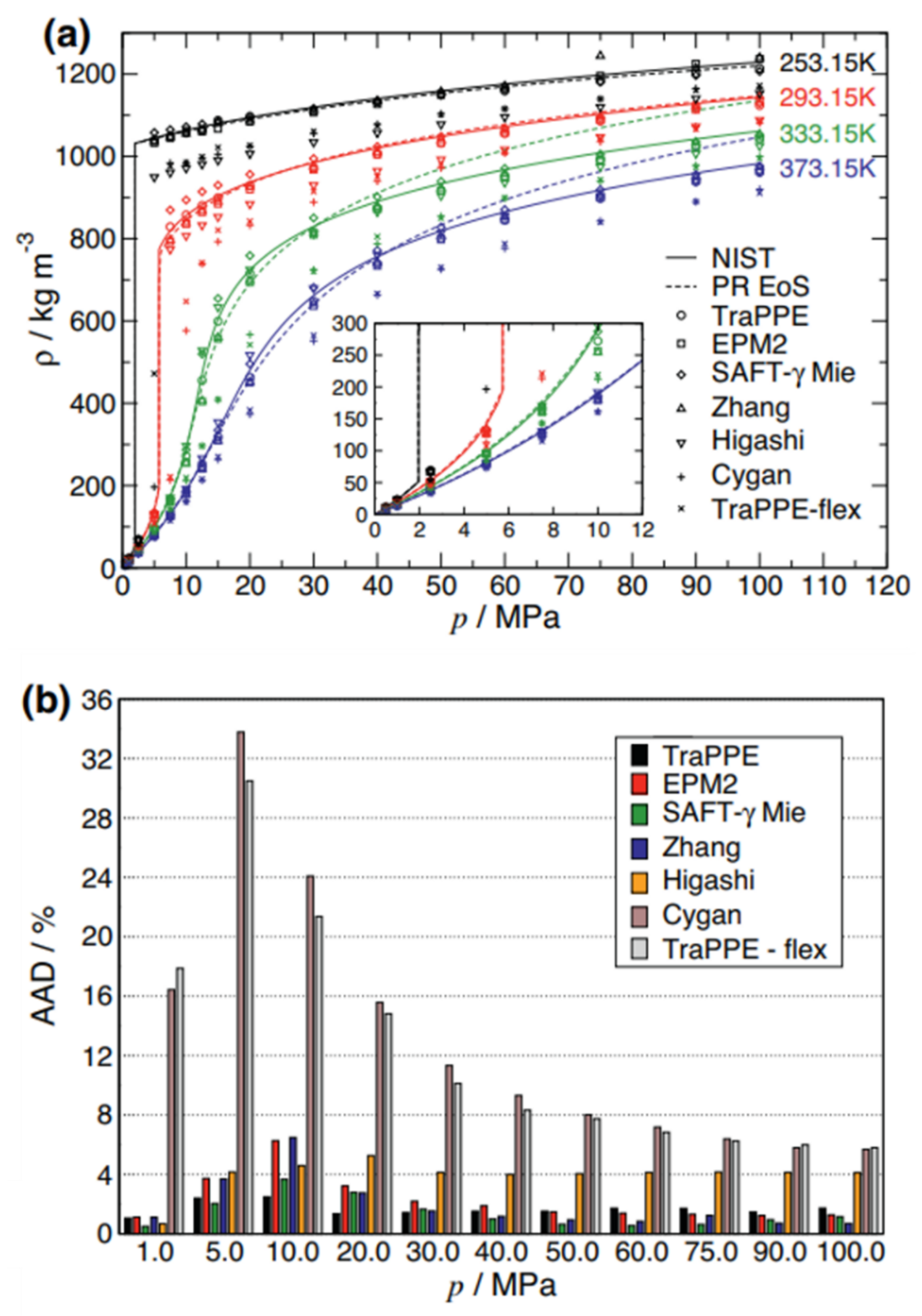
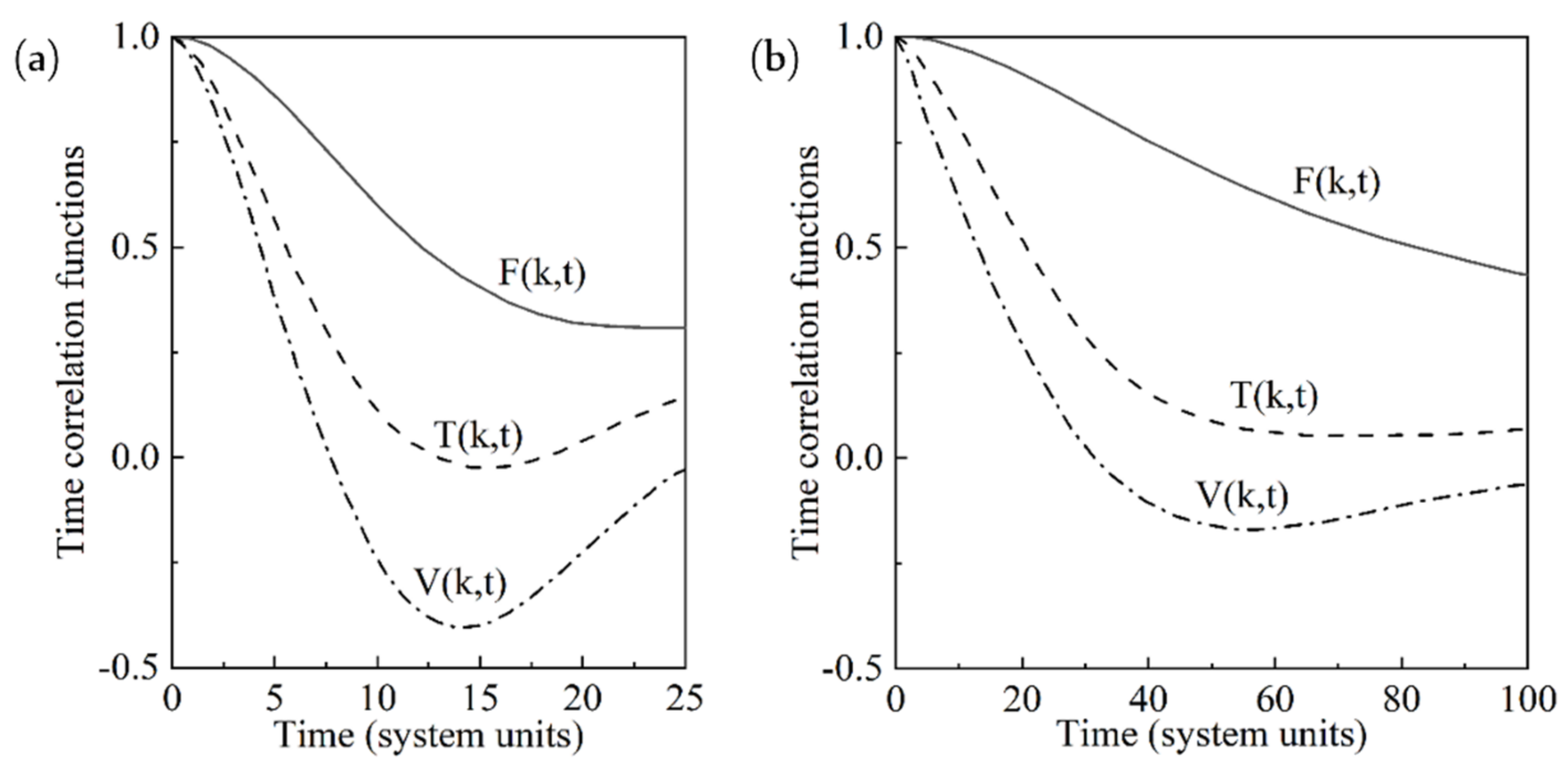
Reference	MD Technology			Key Findings and Observations	Knowledge Gap
	MD Cell	Fluid	Potentials
Tsuji et al. [64]	3D	CO2/H2O/ Silica	EPM2 (CO2)/ SPC/E (H2O)/ (silica)	Interfacial tension changes with wettability of CO2/brine and CO2/H2O/Silica systems.	Large-scale T/p effects on interfacial tension property with experimental validation.
Fang et al. [65]	3D	CO2/Oil/ Silica	EPM2 (CO2)/ OPLS-AA/ CLAYFF	Detachment order of oil and gases from silica surface during injection process of CO2.	Microscopic interaction mechanism between oil and CO2 at reliable reservoirs conditions.
Adams and Siavosh-Haghighi [66]	3D	CO2	EPM2	Diverse response of density and related low-variation zones according to a large series of governing parameters.	Local density enhancement to be solute-induced in the near-critical regime with inhomogeneity degree.
Hamanaka [67]	2D	L-J	-	Thermodynamic characters in near-critical fluids by predicting steady-state density and temperature profiles.	Gas–liquid interface reaction to applied heat flow where latent heat transport is critical at convection mode.
Raabe et al. [68]	3D	Refrigerant/ CO2	AMBER	Comparison of force field simulations with experimental basis at subcritical conditions.	Large-scale experimental data near critical point for validity of chosen force field.
Vaz et al. [69]	3D	Ketone/ CO2	OPLS-AA (ketone)/ EPM2 (CO2)	Mass transfer process of ketones in supercritical CO2 environment.	Mechanism of local interactions that can play a role in the dynamics of the system.
Hafskjold [70]	3D	L-J	-	Supercritical temperature-pressure wave coupling transfer process.	Thermodynamic states far from critical point with no projection to sCO2 heat transfer.
Mahdavi et al. [71]	3D	Al2O3/ CO2	COMPASS/ COMB	Effect of aluminum oxide structure on rheology of supercritical CO2 with self-diffusion coefficient.	Rheology far from critical point conditions with no projection to sCO2 heat transfer characteristics near critical region.

, all atom force field are adopted to describe the interactions between CO₂ and other molecules. In order to better inform the readers, only a series of commonly adopted force fields are gathered for the sake of illustrations of case studies attached.

Coming to the COMPASS model (Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies) [72,73] for simulation of organic/inorganic molecules and polymers, the potential parameters usually acquire empirical techniques. Likewise, the potential of COMPASS can be divided into valence terms, named diagonal/off-diagonal cross-coupling terms and nonbond interaction terms. Apart from these factors, cross-coupling including bond-bond, bond-angle and bond-torsion are crucial for predicting vibration frequencies and structural variations associated with conformational changes. However, such a force field ignores the in-depth details on electron-electron and electron-nucleon interactions, while the focus is devoted to the atomic level.

To this end, Mahdavi et al. [71] employed the COMPASS model to provide properties of supercritical CO₂/Al₂O₃ mixture, as shown in Figure 3. Both viscosity and self-diffusion are emphasized at high temperatures (350 to 410 (K)) and pressures (up to 200 (bar)), which are real working conditions used for enhanced oil recovery. It is worth mentioning that COMB force field is similarly employed in this research to describe the charge transfer between CO₂ and Al₂O₃. Detailed settings can be referred to in the research of Allen et al. [74].

When the focus is on the CHARMM model (i.e., Chemistry at HARvard Macromolecular Mechanics) [75], the total energy is developed as a pure function between internal coordinate and pairwise nonbond interaction terms. Roughly stated, CHARMM mainly consists of six parts: (i) internal energy, including bond potential, bond angle potential, dihedral angle (i.e., torsion), potential and improper torsions; (ii) nonbonded interactions, including constant dielectric, distance-dependent dielectric (i.e., linear), shifted dielectric, electrostatics by groups, and extended electrostatics; (iii) hydrogen bonding; (iv) water–water interactions; (v) constraints; (vi) user energy. Such a force field model is considered to provide a simple form for ignorance of cross-coupling terms [75].

At the same degree, Jorgensen et al. [76] developed improved potentials for OPLS-AA force field based on OPLS-UA, which is considered as being suitable to simulate only organic small molecule and protein aggregation phase. The Jorgensen et al. [76] model may derive parameters for both torsion and non-bonded energetics, while the bond stretching parameter and the angle bindings are mainly provided from the AMBER-AA force field.

By the end of 2022, Liu et al. [53,54] carried on in-depth MD investigation on CO₂ phase equilibrium in the near-critical region (see Figure 4 and Figure 5). The predictability performance of CHARMM and OPLS-AA force field for VLE properties are compared and optimized. Accordingly, the OPLS-AA force field is judged suitable for near-critical predictions within ±10(%) of error range, where 468 (kg/m³) CO₂ is heated between 304.2 to 350 (K) at pressure values up to 10.0 (MPa). Liu et al. [53,54] also designed the heat capacity of supercritical CO_2, which has a same order of magnitude as literature database. These results indicated the great prospect of optimized CO₂ potential parameters in CO₂ heat transfer analysis using coupled CHARMM and OPLS-AA force fields.

In the following, the CLAYFF model is settled to simulate hydrated and multi-components, along with their interfaces with aqueous solutions. The interatomic potentials of simple hydrated compounds result from incorporating structures and spectroscopical data. Particularly, water and hydroxyl behaviors are defined by a flexible single-point charge (SPC)-based water model, and the metal–oxygen interactions consist of an L-J function and a coulombic term with partial charges [71]. The predictions of Cygan et al. [52] have demonstrated the prospect in investigating fluid interfaces with clays and additional complex systems, and highlight the structure of inorganic materials. Likewise, the CLAYFF model has shown promise to be evolved in broadly effective force fields for simulations of fluid-inorganic materials interfaces. Following SPC, CLAYFF can provide a simpler form than CHARMM force field since the total energy is contributed by the coulombic interactions (e.g., electrostatic), Van der Waals term, and bonded interactions.

In the field of carbon sequestration and enhanced oil recovery, CLAYFF force field was widely employed to describe silica surfaces. Thus, Tsuji et al. [64] adopted EPM2, SPC/E, and CLAYFF when describing CO₂, H₂O, and silica properties, respectively. The computed interfacial tension at 2 to 45 (MPa) and with 296 to 398 (K) were successfully performed. The predictions of Tsuji et al. [64] proved the applicability of this set of setting in CO₂-H₂O-Silica systems. Similar settings were applied as the research of Fang et al. [65]. Meanwhile, the detachment sequency of oil and gases from silica surfaces was simulated at T/p conditions (353–393 (K) and 10–50 (MPa)), respectively.

To increase the precision of MD predictions, inter-molecular interactions should be deeply described. However, the number of computed interactions may straightly affect the efficiency of MD; thus, it is significant to achieve a desirable balance between the MD accuracy and the MD efficiency. To this end, several commonly used forcefields are summarized in

Table 2. Potentiality of different force fields in molecular dynamics of CO₂ molecule [52,71,72,73,74,75,76].

Scheme	Bond	Angle	Bond-Bond	Bond-Angle	Bond-Torsion	Dihedral Angle	Coulomb Force	vdW	Electron Transfer
COMPASS	√	√	√	√	√	√	√	√
COMB	√	√							√
CHARMM	√	√			√	√	√	√
CLAYFF	√	√					√	√
OPLS-AA	√	√			√	√	√	√

COMPASS: Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies, Sun. [72,73]; COMB: Charge Optimization Many Body, Allen et al. [74]; CHARMM: Chemistry at HARvard Macromolecular Mechanics, Brooks et al. [75]; CLAYFF: CLAY force field, Cygan et al. [52]; OPLS-AA: Optimized Parameters for Liquid Simulations All Atom, Jorgensen et al. [76].

for the sake of illustration, where various kinds of intermolecular interactions are compared.

2.2. Comparison Criteria for Force Fields

Through the development of CO₂ potentiality, the recovery of vapor–liquid coexistence curves is of great interest, which urges the good prediction in density and pressure terms. According to Aimoli et al. [59], although the flexible model of Cygan [51] is more similar to real molecules, since the marginal nonlinearity of CO₂ is projected under supercritical conditions, it performs more poorly than rigid models. The obtained predictions of Tsuji et al. [64] with flexible molecules also displayed a larger uncertainty compared to rigid models. Among other rigid models, the density results provided by Zhang and Duan [47] are slightly accurate as the pressure increases in the range of 1 to 100 (MPa). This thought corresponds to the data given in the previous figure of the Zhang and Duan model [47] (i.e., Figure 1 and Figure 2), which provided better predictions.

Although Merker et al. [48] claimed that the Zhang and Duan model has deviations in the calculation of vapor pressure and saturated vapor density, the Zhang and Duan model was generally recommended by Aimoli et al. [59] to simulate supercritical CO₂. Indeed, the Zhang and Duan model was employed by Fomin and Ryzhov [77], and the response functions of CO₂ in its supercritical state were calculated. Then, the widow line was fixed in optimum locations. The predictions of Tsuji et al. [64] approved the accuracy of the Zhang and Duan model in the near-critical region and its prospect to study of supercritical CO₂ heat transfer mechanism.

Even though some minor differences can be obtained from Zhang and Duan predictions, the tested models have shown equivalent precision, except when near the critical point. Indeed, a similar pattern can be observed for compressibility and isobar heat transport, respectively (see Figure 6 for instance). These kinds of deviations are comparable to those observed in experiments of Velasco et al. [78], even though C_v deviations from NIST values may appear significant following the reduced range of axis. However, in all cases, the critical improvement in property estimation can be denoted using MD models and cubic Peng–Robinson EoS formulation.

2.3. Future Problems in Force Fields Development

Generally speaking, the focus of MD was devoted to identify a kinetic behavior of CO₂ in its supercritical region, while in-depth investigation on the identity of supercritical CO₂ heat transfer is intermittent, especially near the critical point. This can result from the poor predictability of thermal properties of CO₂ in critical region. Plenty of efforts have been devoted to the improvement of current CO₂ molecular models [50,51,52,53,54,55,56,57,58,59,60,61,62], and most of them depend on Monte Carlo and basic statistical methods. Thus, recently, the rapid development of data science enables the rapid growth of machine-learning-assisted researches. Unlike the conventional development of force fields suggesting that most parameters come from quantum chemistry calculations or experiments, machine learning techniques are able to offer a data-driven scheme that bypasses the physics [79]. With the plentiful data accumulated in the thermal science community, machine learning methods are nowadays believed to produce potentials with higher accuracy and better stability to study MD heat transfer identity at supercritical region.

3. Molecular Dynamics Method in Supercritical Heat Transfer

This part seeks to classify the major circumstances where molecular dynamics models are appropriate in terms of heat transfer, in addition to their mechanisms and limitations when dealing with single and/or coupled molecules. Accordingly, principals of MD thermal relaxation, thermal conductivity, thermal convection, and supercritical mixtures are deeply discussed for the applied industry as follows.

3.1. Thermal Relaxation Process

Near to the critical line, a thermal relaxation may provide unpredictable heat transfer instabilities at MD simulations, which could reveal dissimilar effects [80,81]. Indeed, and when approaching the critical line (also known in bidimensional as critical point) located at a density number n_critical and a T_critical, the CO₂ compressibility may become larger and associated with the unusual values of thermodynamics properties, leading to a reliable behavior with thermodynamics theory [81]. In this situation, both hydro- and thermos-dynamic descriptions become inadequate due to the existence of unknown fluctuations [82]. Hence, an original path for MD simulations arose to compare the computed fluctuation spectrum with that generated from well-known hydrodynamics, given the prime values of heat transfer coefficients.

As displayed by Luo et al. [83], the major difficulty in performing MD simulations on heat transfer behavior near a critical point stems from large-scale fluctuations and slow thermal relaxations in the used MD cell. Thus, MD predictions may require large system sizes with long-time trajectories. Meanwhile, this conjunction has not been confirmed through the previous works of Lennard–Jones on liquid–gas coexistence curves [83,84,85]. This was assisted by another study on two-phase flow that accented the temperature dependence of liquid–vapor interfacial thickness [86] in which the finite size of MD and/or MC simulations comes from the non-deep definition of a critical point [85,86].

Roughly stated, MC predictions have clearly certified the existence of significant fluctuations with relatively large length scales, with a larger value of isothermal compressibility obtained near T_critical [85,86]. Nevertheless, it is not that informal to provide an accurate value of a compressibility that is derived from these fluctuations since the evaluation approach depends firmly on molecule size [76]. Therefore, Luo et al. [82] accomplished their MD simulations on a highly compressible CO₂ that contains interacting particles, specific heats, isothermal compressibility, and speed of sound using collective rates relevant to thermal fluctuations. Likewise, the mutability of properties was defined according to the equilibrium time-correlation functions (named, TCFs) [82], which contain a burst information on near equilibrium relaxations. Together in MD predictions, a self-diffusion, a thermal conductivity, and a bulk and a shear viscosity were computed [77,78,79,80,81,82]. For instance, the relaxation of thermal fluctuations, usually dominated by a slow entropy diffusion mode, was found to be propagated according to the fast acoustic modes near the critical density and temperature (i.e., n_critical and T_critical), making the heat transfer behavior quicker as shown through data of Luo et al. [82].

When the equilibrium thermal fluctuations of energy, pressure, and density of supercritical CO₂ can be computed by MD potentials, the specific heat at constant volume c_v and the isothermal compressibility K_T, besides the pressure gradient (∂p/∂T)_v, can be deduced from these fluctuations as follows [82,83,84,85,86,87]:

$$c_v=\frac{1}{k_{B}N{T}^2}{\left[{〈\widehat{E}〉}^2-〈{\widehat{E}}^2〉\right]}_{NVT}$$

(4)

$$K_T=\frac{V}{k_{B}NT}\underset{k\to 0,t\to 0}{lim}F\left(k,t\right)$$

(5)

$${\left(\frac{\partial p}{\partial T}\right)}_v=\frac{1}{k_B{T}^2}\langle (\widehat{U}-\langle \widehat{U}\rangle ){\left(\widehat{p}-〈\widehat{p}〉\right)\rangle }_{NVT}+k_{B}n$$

(6)

where E and U are the total and potential energy, respectively, and F(k, t) is the number of density for TCF functions.

Indeed, the identity of the local density F(k, t) for TCF functions, besides the longitudinal current V(k, t) and the local temperature T(k, t), should be taken into considerations when processing in MD simulations. Thus, the identity of these latter is expressed as follows [82,83,84,85,86,87]:

$$F\left(k,t\right)=\frac{1}{N}〈{{\displaystyle \sum }}_{i=1}^N,e^{ik·r_i\left(0\right)},{{\displaystyle \sum }}_{j=1}^N,e^{-ik·r_j\left(t\right)}〉$$

(7)

$$V\left(k,t\right)=\frac{k}{N}·〈{{\displaystyle \sum }}_{i=1}^N,v_i,e^{ik·r_i\left(0\right)},{{\displaystyle \sum }}_{j=1}^N,v_j,e^{-ik·r_j\left(t\right)}〉·k$$

(8)

Hence, the local instantaneous temperature is implicitly defined based on local equilibrium assumptions as follows [82,83,84,85,86,87]:

$$\delta e={\left(\frac{\partial e}{\partial n}\right)}_T\delta n+{\left(\frac{\partial e}{\partial T}\right)}_n\delta T$$

(9)

where δ stands for fluctuation and e stands for energy density, as far as the partial derivatives are defined as equilibrium derivatives.

Through a k space, this implicit definition can be adjusted as follows [82,83,84,85,86,87]:

$$N{c}_v\widehat{T}\left(k,t\right)={{\displaystyle \sum }}_{i=1}^N\left[\frac{1}{2}\left(m{v}_i^2\left(t\right)+{{\displaystyle \sum }}_{j\ne 1}^N{\varphi }_{ij}\left(t\right)\right)-{\left(\frac{\partial e}{\partial n}\right)}_T\right]e^{-ik·r_i\left(t\right)}$$

(10)

where (∂e/∂n)_T can be explicitly computed as [82,83,84,85,86,87]:

$${\left(\frac{\partial e}{\partial n}\right)}_T=-\frac{T}{n}\left[{\left(\frac{\partial p}{\partial T}\right)}_V+h\right]$$

(11)

with h as enthalpy density.

From the aforementioned quantities, the specific heat per particle can be obtained at a constant pressure C_p and a speed of sound c_s as [82,83,84,85,86,87]:

$$C_p-C_v=-T{\left(\frac{\partial p}{\partial T}\right)}_v^2{\left(\frac{\partial V}{\partial p}\right)}_T$$

(12)

$$c_s={\left[\frac{C_p}{C_{v}m}{\left(\frac{\partial p}{\partial n}\right)}_T\right]}^{\frac{1}{2}}$$

(13)

Following a known linear Navier–Stokes hydrodynamics equations and a values of equilibrium static fluctuations, the hydrodynamics limit (k―>0) of TCF functions can be identified using the Landau–Placzek formula as [82,83,84,85,86,87] follows:

$$\frac{F\left(k,t\right)}{F\left(k,0\right)}=\left(\frac{\gamma -1}{\gamma }\right)e^{-D_r·k^2\left(t\right)}+\left(\frac{1}{\gamma }\right)e^{-\Gamma ·k^2\left(t\right)}\left[\mathit{cos}\left(c_s{k}_{\left(t\right)}\right)+b_{\left(k\right)}\mathit{sin}\left(c_s{k}_{\left(t\right)}\right)\right]$$

(14a)

$$\frac{V\left(k,t\right)}{V\left(k,0\right)}=\frac{e^{-\Gamma ·k^2\left(t\right)}\left\{\left(c_{s}k\right)\left[\mathit{cos}\left(c_s{k}_{\left(t\right)}\right)+b_{\left(k\right)}\mathit{sin}\left(c_s{k}_{\left(t\right)}\right)\right]-\left(2\Gamma k^2\right)\left[\mathit{sin}\left(c_s{k}_{\left(t\right)}\right)-b_{\left(k\right)}\mathit{cos}\left(c_s{k}_{\left(t\right)}\right)\right]\right\}}{\left(c_{s}k\right)+\left(2\Gamma k^2{b}_{\left(k\right)}\right)}$$

(14b)

$$\frac{T\left(k,t\right)}{T\left(k,0\right)}=\left(\frac{1}{\gamma }\right)e^{-D_T·k^2\left(t\right)}+\left(\frac{\gamma -1}{\gamma }\right)e^{-\Gamma ·k^2\left(t\right)}\left[\mathit{cos}\left(c_s{k}_{\left(t\right)}\right)+\frac{k}{c_s}\left[\Gamma -D_T\left(\gamma +1\right)\right]\mathit{sin}\left(c_s{k}_{\left(t\right)}\right)\right]$$

(14c)

with:

$$\left\{\begin{array}{l}\gamma =C_p/C_V,\\ D_T=\lambda /n{C}_p,\\ \Gamma =\frac{1}{2}\left[\left(\gamma -1\right)D_T+\eta /mn\right],\\ b_{\left(k\right)}=\frac{k}{c_s}\left[\Gamma +D_T\left(\gamma -1\right)\right],\end{array}\right.$$

(14d)

The specific heats ratio γ, thermal diffusivity D_T, sound attenuation coefficient Γ, and speed of sound c_s, can be evaluated either by fitting theoretical solutions (i.e., Equation (14a–c) to generated functions or relying on MD simulations. One can mention the thermal conductivity λ and the viscosity η that should be computed according to the well-known Green–Kubo formulas [35].

Indeed, the behavior of T(k, t) at regular or supercritical conditions could be critically dissimilar. Quoted for Luo et al. [82], the T(k, t) for supercritical fluids decays to less than 10% with acoustic time scales, with the absence of thermal-diffusion-related slowing down in the temperature relaxation possibly caused by the small values of the pre-factor (1/γ) during the diffusion (see Figure 7 for instance).

When the divergence in MD predictions can only be expected through thermodynamics boundaries, it is problematic to provide accurate deductions on the basis of a few hundred particles, even though this can display unusual behaviors at supercritical regions that are understood as that of high compressible fluids [59]. Likewise, for the most part temperature relaxation is driven by isentropic acoustic modes, which are dissimilar to usual liquid-like behaviors where the temperature is purely diffusive, even though the density can be driven by sound waves [81].

3.2. Principals on Thermophysical Properties

Since the focus of this review is devoted to heat transfer mechanism of sCO₂, the control of thermophysical parameters that are linked to heat transfer aspect is of great interest. Accordingly, the MD identity of thermal conductivity is primely developed over the rest of parameters. Meanwhile, MD thermophysical properties may come from the energy and location data of each atom in a used MD cell, which is different from CFD principal. At a conventional statistical thermodynamic, the transfer property is mainly defined as the response of a heat flux driven by external forces [88]. Then, an explicit heat flux expression can be developed according to the particle transport as follows [69]:

$$J=-\lambda \left(\nabla \phi \right)$$

(15)

Similar to Fourier Law, if a thermal gradient is developed in an MD cell, heat flux could be generated until equilibrium of temperature, when thermal conductivity is employed to depict the ability of MD heat transfer [88]. Consequently, the transfer properties would be linked to a non-equilibrium process that can be demonstrated from a non-equilibrium MD approach [88,89]. This can also be computed using the equilibrium molecular simulations, as far as the existing local fluctuations in a microscale system are well thought out [89].

Following the hypothesis of Onsager [90], the regression from a local microscale equilibrium can mainly be governed by a macroscale transportation law, due to the macroscopic reflection of transfer micro-reversibility [90]. Thus, heat transfer properties of a supercritical CO₂ can be thoroughly simulated through EMD rather than NEMD. It is important to mention how remarkable the Onsager regression hypothesis is for a neighborhood of equilibrium state in recognizing the linear response of a generalized flux [91]. Therefore, the initial outline in district equilibrium state should be primarily identified during the equilibrium molecular simulations. Based on this theory, Green–Kubo relations can be developed much like a time autocorrelation function as follows [35]:

$$\lambda ={{\displaystyle \int }}_0^{\infty }⟨J\left(t\right)J\left(0\right)⟩dt$$

(16)

where ⟨J(t) J(0)⟩ denotes the autocorrelation function from generalized heat flux. Roughly stated, the autocorrelation function can reflect the proximity of the correlation of an instantaneous parameter to its initial scale at t = 0 [35,89,90]. Compared to the non-equilibrium MD approach, the determination of an autocorrelation function requires no empirical parameters, but it continuously rises with low efficiency [35].

3.2.1. T/P Relationship

In MD simulations, temperature and pressure are two dissimilar but coupled parameters to highlight the identity of the fluid properties. According to the equipartition theory, the temperature of a group of atoms could be linked to the kinetic energy as follows [91]:

$$KE=\left(\frac{DOF}{2}\right)N{k}_{b}T$$

(17)

where KE is the main kinetic energy of a group of atoms, DOF is the overall degree of freedom for these atoms, k_b is the well-known constant of Boltzmann, and T is the absolute temperature used in MD simulations.

Following this criterion, the temperature of a group of atoms is proportional to kinetic energy, which is lawful in most systems with a wide range of temperatures [91]. However, the temperature in fluid dynamics principals is often overestimated. Thus, in order to eliminate such errors from this factor, the adopted kinetic energy should be referenced from the center of the mass system where the overall partial flow velocity is removed. To do so, the pressure of a group of atoms would be identified as follows [91]:

$$P=\left(\frac{N{k}_{b}T}{V}\right)+\frac{1}{V·DOF}{{\displaystyle \sum }}_{i=1}^N{\overrightarrow{r}}_i.{\overrightarrow{f}}_i$$

(18)

where N is the number of atoms used in MD cell, and V is the corresponding volume. The second term of Equation (18) is the derivative gradient (−∂U/∂V) that can be computed for all pairwise, as well as two- to many-bodied, alongside the long-range interactions [91]. Herein, ${\overrightarrow{r}}_i$ and ${\overrightarrow{f}}_i$ are the position and force vector of each atom i in MD system.

As developed in the aforementioned equation, the pressure of a group of atoms consists of two general terms, much like an ideal gas pressure term and a virial correction term. Roughly stated, the intermolecular interactions at low densities are neglectable through the pressure calculations [92,93]. Likewise, and with high density cases, the influence of intermolecular interactions is significant. Indeed, it is worth noting that DOF values are equals to 2 and 3 for single atoms in bi- and tri-dimensional cases, respectively. However, the consequences of the bond stretching and the angle stretching should be taken into consideration when the deal is with supercritical fluid [93].

3.2.2. Thermal Conductivity

Figuring the thermal conductivity of supercritical CO₂ is one of tough challenges in Molecular Dynamics since the corresponding design is much more sensitive to energy of the treated system and can be affected by the used molecular structure [94]. When the non-equilibrium MD is used, two approaches can be proposed to establish the non-equilibrium process in similar MD system:

(i)

The first approach follows the generation of a heat flux by setting temperature gradients. Then, the simulated system can be set as constant temperature to maintain a constant thermal gradient. Consequently, the NEMD based on this approach is considered a conventional model [95].

(ii)

The second approach provide a thermal gradient following a constant heat flux for non-equilibrium process. Thus, the approach is identified as a reverse NEMD model (i.e., RNEMD) [96].

According the first approach, and for the one-gradient NEMD model, the MD region far away from the heat source and the heat sink could be used to evaluate the thermal gradient; thus, the thermal conductivity is based on the following equality [94,95,96]:

$$\lambda =-\frac{q}{A\left(\frac{\partial T}{\partial x}\right)}$$

(19)

When upgraded to the two-gradient NEMD, both sides of MD cell are defined as a heat source, and can be activated simultaneously. Consequently, heat flux can be transported in two opposite directions, providing the definition of thermal conductivity as follows [94,95,96]:

$$\lambda =-\frac{q}{2A{\left(\frac{\partial T}{\partial x}\right)}_{average}}$$

(20)

During the RNEMD model, an external heat flux is used when the thermal gradient is generated accordingly. Indeed, one can mention that the temperature is simulated according to kinetic energy of supercritical molecules used, as follows [94,95,96]:

$$T_{MD}=-\frac{2}{3N{k}_b}{{\displaystyle \sum }}_i\frac{P_i^3}{2m_i}$$

(21)

Although this temperature was mainly used in MD simulations, the application in a non-equilibrium state has several confines [97]. To this end, Jepps et al. [98] highlighted a microscopic expression based on a statistical theory, when Jackson et al. [99] adopted this expression to predict thermal conductivity of L-J fluids. Their data are compared to those derived by conventional expression, and the conventional expression failed to describe the kinetic temperature, especially at low densities [89,99]. However, limited works have focused on this challenging issue when the temperatures in NEMD are mainly linked to conventional issues. Hence, describing temperature gradients in the NEMD model has much room to be further debated. Moreover, the flexibility of Fourier law near the critical point should also be rethought due to its effects on the critical singularity of thermal conductivity.

It is important to mention that the relaxation time and the required time to generate a stable gradient are a meter of concern. Hence, two majors should be well examined, as follows:

(i)

The thermal conductivity based on NEMD predictions should be extended to supercritical region more than that in the sub-critical;

(ii)

The uniform condition to control the number of atoms in MD predictions far from the empirical database so as to remove the non-adequality of equilibrium that may result, and the waste of computational resource while practicing.

On the other side, both the thermal conductivity and the heat flux can be computed using the equilibrium MD model. Then, the Green–Kubo relationship is commonly adopted as displays Equations (22) and (23) [98,99]:

$$\lambda =\frac{V}{3k_b{T}^2}{{\displaystyle \int }}_0^{\infty }⟨J\left(t\right)J\left(0\right)⟩dt$$

(22)

$$J=\frac{1}{V}\left[{{\displaystyle \sum }}_i{\overrightarrow{v}}_i{e}_i+\frac{1}{2}{{\displaystyle \sum }}_i\left({\overrightarrow{f}}_{ij}{.}_i{\overrightarrow{v}}_i\right){\overrightarrow{r}}_{ij}\right]$$

(23)

While browsing the literature, two main factors could affect the accuracy of MD conductivity: (i) one to mention the selected force field, then (ii) the density of the studied system. Aimoli et al. [59] provided an assessment between rigid and flexible force fields of supercritical CO₂, and concluded the fact that considering the molecule flexibility cannot improve the accuracy of predictions. Meanwhile, the consideration of vibrational principal with a rigid model can expand the MD performance as stated by Liang et al. [100] and Nieto–Draghi et al. [63] due to the combination between the Green–Kubo equilibrium and the vibrational energy as follows [100,101]:

$$\lambda ={\lambda }_{GK}+\rho D{c}_v^{vib}$$

(24)

where this contribution could be related to density, the self-diffusion, and the vibration contribution to heat capacity. Most of these studies have targeted narrow temperatures and pressures, while the experimental data on thermal conductivity of supercritical CO₂ are also available at huge temperatures and pressures up to 1000 (K) and 200 (MPa), respectively. Thus, it is crucial to develop a further MD predictive model for accurate thermal conductivity.

In this context, Trinh et al. [102] reported the MD thermal conductivities of CO₂ in temperatures of about 300–1000 (K) with pressures up to 200 (MPa) (Figure 8). Three MD models were used, namely MSM, EPM2, and TraPPE, besides two flexible models (see

Table 3. Parameters of potential models used in CO₂ Molecular dynamics [102,103].

Models	εC (K)	σC (Å)	εO (K)	σO (Å)	qC (e)	qO (e)	dC-O (Å)
MSM	29.00	2.79	83.10	3.01	0.60	−0.30	1.16
EPM2	28.13	2.76	80.51	3.03	0.65	−0.33	1.15
TraPPE	27.00	2.80	79.00	3.05	0.70	−0.35	1.16
EPM2_Flex 1	ks = 10,739 (kJ/mol·Å2), kb = 10,739 (kJ/mol·rad2)
EPM2_Flex 2	km = 2015.75 (kJ/mol·Å2), α = 2.35, kb = 10,739 (kJ/mol·rad2)

ε, σ: energy and length parameters in L-J potential respectively; q: charge designated on atoms; d: length of C–O bond, k_s, k_m, k_b: force constants describing bond stretching, morse potential, and angle bending, respectively.

for instance) while comparing the sort-out conductivities with those of National Institute of Standards and Technology database (i.e., NIST) [103,104]. The models differed in their bond lengths of C–O and in their values of L-J potential, as well as in their partial charges used. One can mention how remarkable these models are in providing an excellent equation of state of supercritical CO₂ at low and high temperatures. Likewise, TraPPE model may predict the thermal conductivity with a discrepancy of less than 5% in a wide range of pressures compared to the rest of adopted models [102]. Indeed, the underestimation of experimental predictions by all rigid models is probably due to a lack of optimization of force fields at similar boundaries. Hence, and in view of significance of the properties of CO₂, such a lack should be restored by updating MD principals [102].

While the connection between molecular dynamics and macroscopic transfer parameters remains a challenge, the current literature has reflected rare data on such enquiries when the deal is on supercritical CO₂. Once an intermittent heat transfer process in the narrow sense may occur in MD predictions, this part of the review moderately engages the L-J and similar supercritical fluids. Accordingly, Bresme and Armstrong [104] employed two methods to calculate the local thermal conductivities of L-J fluids from boundary-driven non-equilibrium MD simulations. Their local equilibrium idea comes from the main hypotheses on non-equilibrium thermodynamics. Thus, Bresme and Armstrong [104] displayed how to extract thermal conductivities from analysis of local gradients, and compared the NEMD results with those of equilibrium Green–Kubo computations. The Green–Kubo equilibrium simulations were performed in several cubic boxes that contain 2500 molecules. A typical Green–Kubo NVE simulation could involve 5 × 10⁷ steps to certify the good statistics on autocorrelation function, simultaneously. It is important to mention that Green–Kubo and NEMD simulations were performed using LAMMPS force field [104].

It is worth mentioning that predictions near the thermostats should be avoidedsince the curvature of the thermal gradient can be affected by thermostat gradient [104]. Likewise, the thermal conductivity obtained from NEMD simulations may approve the numerical accuracy of Green–Kubo equilibrium. This result may support the local equilibrium hypothesis for transfer characteristics of supercritical CO₂ [104]. Furthermore, the amplitude of the temperature fluctuation in EMD simulation is significantly dependent on the size of simulated MD cell; thus, the size effect of thermal conductivity at critical point should be treated with care [102,103].

3.3. Thermal Convection

Indeed, what matters the most is not to focus entirely on the identity of thermal conductivity, but to focus on the principle of thermal convection that can be reflected from the MD box of atoms. However, the lack of data on supercritical CO₂ has oriented this section to proceed with L-J and similar supercritical fluids for the sake of clarification. Briefly put, the calculations based on the above cited theories can be performed in a space of waved vectors and fluctuations. To account for an enhanced heat transfer at small temperature gradients (∂T/∂z), the critical fluctuations at significant densities should be convicted in the same (or opposite) direction as imposed temperature gradients. Then, the velocity of developed clusters can be given with a length of order ξ as follows [105]:

$$v_{\xi }\sim {\left(\xi /{\xi }_0\right)}^{\beta /v+1-\dot{\eta }\frac{D_T}{T}\frac{dT}{dz}}$$

(25)

with β being the critical exponent. The entropy of the liquid-like zones is minor compared to that of gas-like, where the entropy and the density fluctuations have similar sizes according to the critical isochore as follows [105]:

$$\left\{\begin{array}{l}n{\xi }^d{\delta }_s\sim {\xi }^{d-\frac{\beta }{v}}\\ {\xi }^{d-\beta /v}\sim {\left(T/T_c-1\right)}^{\beta }\end{array}\right.$$

(26)

thus, it gives rise to a conduction behavior [105]. During their lifetimes, the developed clusters can move only over ξ, as follows [105]:

$$v_{\xi }{T}_{\xi }\sim \frac{\Delta n}{n}{\left(\xi /{\xi }_0\right)}^{\beta /v}\left({\xi }^2/L\right)$$

(27)

where ∆n is the ratio (α_p L dT/dz) that defines the difference between densities at the boundaries of the MD cell. This distance is shorter compared to the cell length L, which is much longer than ξ. Hence, it should be tough to unmistakably perceive the cluster motion experimentally, or numerically, as demonstrated in Ohara works [106,107].

To this end, Hamanaka et al. [67] performed a bi-dimensional simulation of supercritical fluids near to the gas–liquid critical point. Based on their temperature and density profiles, the computed thermal conductivity exhibited a critical singularity according to the mode-coupling theory. Following the momentum and heat flux distributions at constant densities, it was found that the liquid-like clusters (i.e., entropy-poor) moved toward the warmer boundary, when the gas-like regions (i.e., entropy-rich) moved toward the cold boundary (see Figure 9 for instance). This counter flow resulted from the critical enhancement of thermal conductivity [67]. It is worth mentioning that the distance of cluster convection was very short, and was not inconsistent with the density increase near the cold limit [67].

In a similar context, Hafskjold [70] was processed with heat transfer of L-J/spline fluid and supercritical fluid through a sudden change of heat flux on one side of MD cell boundaries (see Figure 10 for instance). The changed boundary was fixed at a very high temperature of around 7.5 times the critical value. Hence, a thermal shock wave was recorded synchronously with a developed pressure wave. These coupled T/p shock waves were linked to the thermal instantaneous explosion in the fluid cavity, which disturbed the stability of Fourier’s law, accordingly. The corresponding heat transfer was investigated in a Eulerian framework using non-equilibrium molecular dynamics simulations [70]. However, the exhausted flux used as a boundary condition provided doubts regarding the reported data, as one cannot distinguish between the “wave process” of parameters in similar regions.

When the focus is devoted to the supercritical pseudo-boiling phenomenon and two-phase-like models, MD simulations have been of great interest. One can mention Tamba et al. [108] observations on the interface-like structure during heat transfer in supercritical fluids near the critical point. Their molecular dynamics investigation was performed at supercritical pressures that reproduced a similar structure of normal liquid–vapor interface at subcritical pressure. The findings have led readers to think that an abnormal convection could be observed slightly above the critical line, which has been mentioned latter as boiling-like behavior [108,109]. In addition to this, a particular attention was paid to the transition from subcritical boiling to supercritical free convection.

In early 2005, Zhang et al. [110] provided the relationship between the supercritical CO₂ structure and density changes using a new modified empirical potential model. Pair correlation functions for supercritical CO₂ were calculated along with the isotherm functions. Different trends of change in pair correlation functions have indicated that the gas-like state may occur at low densities, while the liquid-like state may occur at high densities, along with an isotherm [110].

In early 2021, Xu et al. [111,112] showed similar bubble-like structures in the supercritical region with an MD simulation on Argon. The onset pseudo-boiling temperature T⁻ and the termination pseudo-boiling temperature T⁺ were evaluated using the neighbor molecules method, as well as radial distribution functions (named, RDF). A further explanation was given by Xu et al. [111,112] on why the term “bubble-like” was reasonably denoted in the supercritical domain by making a straight link with sub-critical zone. However, the MD results provided more “transient voids” rather than “bubbles” [113].

3.4. Supercritical Mixtures

Except for being employed as a working fluid in heat exchangers, supercritical CO₂ can also work in combination with other materials and molecules as a promising zero-pollution mixture fluid. The thermal behavior of combined molecules is of great value for leading industrial systems. One can mention the supercritical H₂O/CO₂/H₂ mixtures that is adopted for power generation system with coal gasification [113,114]. This mixture can be oxidized with H₂ to be converted to H₂O in oxidation reactors. The generated heat can be used for gasification reactor and feed water preheater. After the expedition of the oxidation reaction, the supercritical H₂O/CO₂ mixture can drive a turbine to generate electricity with high efficiency [113,114]. The exhaust H₂O and CO₂ are then separated using a H₂O circulation and CO₂ storage system. Such a mixture can provide a stable performance at high temperatures and pressures, much like 600–650 (°C) and 25 (MPa), with a high efficiency compared to solo supercritical H₂O in similar conventional systems [114,115].

However, the PVT properties of supercritical mixtures are required to design and optimize the thermodynamic systems that are based on the supercritical gasification process. The adoption of theoretical models remains difficult to expand similar experimental data and critically unreached because of the compressibility of the mixture under extreme circumstances. Thus, a common theoretical models of PVT properties were divided into cubic equation of state models, thermodynamic perturbation models, perturbed hard chain models and others, for which MD simulations can be easily executed with high accuracy [43,114]. Among these models, the P-Robinson equation of state (i.e., PR-EOS) is widely used to predict MD-PVT properties, following its high accuracy for thermodynamic properties [115].

In that context, Yang et al. [116] carried out MD simulations on PVT properties of H₂O/H₂ and H₂O/CO₂/H₂ mixtures in near-critical and supercritical regions, using the Peng-Robinson equation of state. During the implementation of the force field models, the L-J potential is adopted as follows [116]:

$$u_{ij}={{\displaystyle \sum }}_{k=1}^M{{\displaystyle \sum }}_{l=1}^N\left\{4{\epsilon }_{ij}^{kl}\left[{\left(\frac{{\sigma }_{ij}^{kl}}{r_{ij}^{kl}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}^{kl}}{r_{ij}^{kl}}\right)}^6\right]+\frac{q_i^k{q}_j^l}{4\pi {\epsilon }_0{r}_{ij}^{kl}}\right\}$$

(28)

where u_ij refers to the interaction potential energy between molecules i and j, and ε and σ are the interaction parameters of L-J potential that highlight the energy and scale parameters, respectively. The term r refers to the distance between atom k and atom l, and q_i and q_j are the quantity of electric charge of atom k and l, respectively. Herein, ε₀ denotes the dielectric constant used for force field model.

To compare the results with pure supercritical CO₂ outcomes, Yang et al. [116] adopted the EMP2 model, that is, an improved EPM model. As the EPM2 model use the geometric mean combining rule for interactions between unlike atoms of CO₂, the geometric mean of Yang et al. [116] for ε and σ are adopted to show the cross-interactions between unlike L-J sites of supercritical CO₂ molecules, when the geometric mean of ε and the arithmetic mean of σ are used to compute the L-J interactions in any other cases as [116,117]:

$${\epsilon }_{ij}^{kl}={\left({\epsilon }_i^k{\epsilon }_j^l\right)}^{\frac{1}{2}}$$

(29)

$$\left\{\begin{array}{l}{\sigma }_{ij}^{kl}={\left({\sigma }_i^k{\sigma }_j^l\right)}^{\frac{1}{2}}\mathit{for}k,l=C_{C{O}_2},O_{C{O}_2}\mathit{through}EPM2\mathit{mod}el,\\ {\sigma }_{ij}^{kl}=\frac{1}{2}\left({\sigma }_i^k+{\sigma }_j^l\right)\mathit{elsewhere},\end{array}\right.$$

(30)

The analysis of Yang et al. [116] has approved the effectiveness of the MD approach on triphasic mixtures much like H₂O/CO₂/H₂ to match the experimental data with high accuracy, compared to the solo employment of Peng–Robinson equation of state in near-critical and supercritical regions of pure H₂O. Their MD simulations provided insight on the mechanism of mixtures, for which the Peng–Robinson equation of state provided limitations (see Figure 11 for instance). However, the experimental validation is still needed to approve such MD predictions with a large scale of supercritical water coal gasification [116].

A few years later, Chen et al. [118] investigated the question of whether supercritical H₂O/CO₂ mixtures have similar forced convection heat transfer behaviors with pure supercritical fluids. The supercritical H₂O/CO₂ mixtures were expanded to more general mixtures, with one component being H₂O and the other having lower critical temperature and pressure than H₂O. Such general mixtures have similar heat transfer behavior with supercritical H₂O for temperatures and pressures above the critical point of H₂O, as for this condition both H₂O and CO₂ are supercritical and miscible with each other.

To highlight the heat transfer mechanism in such systems, the convection heat transfer coefficients of the supercritical mixtures were simulated using 20(%) CO₂ mass fraction. This mixture was used at 25 (MPa) and 550–700 (°C), flowing upward in a circular tube with 26 (mm) inner diameters. Hence, the diffusion of supercritical H₂O/CO₂ mixture was investigated using the simple-point-charge extension (SPCE) force field model. The interactions between molecules were computed using the summation of the L-J and Coulomb interactions. Then, MD simulations were accomplished at a large-scale atomic/molecular massively parallel simulator (LAMMPS) [119] and visual molecular dynamics (VMD) [120].

The remarkable Chen et al. [118] simulations on mean heat transfer rate were compared to the Jackson heat transfer correlation (Equation (31)) [99], that is, a general correlation for pure supercritical fluids, and for which the discrepancy was below 15(%). Accordingly, Chen et al. [118] evidenced the fact that Jackson correlation is able to predict the forced convection heat transfer coefficients of such supercritical H₂O/CO₂ mixtures for a system of 25 (MPa) and 600 (°C) to 650 (°C), as [118]:

$$\mathrm{N}{\mathrm{u}}_{\mathrm{b}}=0.0183\hspace{0.17em}{\mathrm{Re}}_{\mathrm{b}}^{0.82}\hspace{0.17em}{\mathrm{Pr}}_{\mathrm{b}}^{0.5}\hspace{0.17em}{\left(\frac{{\mathsf{\rho }}_{\mathrm{w}}}{{\mathsf{\rho }}_{\mathrm{b}}}\right)}^{0.3}\hspace{0.17em}\hspace{0.17em}{\left(\frac{{\mathrm{C}}_{\mathrm{p}}}{{\mathrm{C}}_{\mathrm{p}\mathrm{b}}}\right)}^n$$

(31)

where n is calculated according to the following conditions [99]:

$$\left\{\begin{array}{l}n=0.4 for \left(T_b<T_w<T_{pc}\right), and for \left(1.2T_{pc}<T_b<T_w\right),\\ n=0.4+0.2\left(\frac{T_w}{T_{pc}}-1\right) for \left(T_b<T_{pc}<T_w\right),\\ n=0.4+0.2\left(\frac{T_w}{T_{pc}}-1\right)\left(1-5\left(\frac{T_p}{T_{pc}}-1\right)\right) for \left(T_{pc}<T_b<1.2T_{pc}\right) and T_b<T_w,\end{array}\right.$$

(32)

3.5. Supercritical Models and Chemical Application

Supercritical CO₂ in a chemical aspect has garnered much interest in the past decade. This is linked to its remarkable power to identify some multifaceted principals, much like the extractions, purifications, separations, crystal growth, reactions, and fractionations of different compounds [121,122,123]. Due to its supercritical state, CO₂ was able to extract fatty vegetable oils [123], acid esters [124], and antioxidants in food engineering industries, and it can be used for solvation of solid compounds like phenazopyridine, propranolol and methyl salicylate in pharmaceutical processes [125,126] (see

Table 4. Major chemical compounds cooperated by supercritical CO₂ in MD simulations [125,126,127,128].

Chemical Compounds	Tc (K)	Pc (bar)	Ω	vs (cm3/mol)	Refs.
Triphenylene	1013.6	29.28	0.492	175	[125]
Benzoin	853.52	26.6	0.599	162	[126]
Mandelic acid	903.79	34.73	0.645	117	[126]
Propyl 4-hydroxybenzoate	815.92	31.3	0.722	131.6	[126]
Hexamethylbenzene	758	24.4	0.515	152.7	[126]
Henanthrene	882.65	31.72	0.437	182	[126]
Anthracene	869.15	30.8	0.353	142.6	[126]
Carbazole	899.1	32.65	0.496	151.5	[126]
Fluorene	826.4	29.5	0.406	139.3	[126]
Fyrene	936	25.7	0.509	158.5	[126]
O-hydroxy benzoic acid	739	51.8	0.832	95.7	[126]
1-0ctadecanol	777	13.4	0.863	333	[126]
Phenazopyridine	1148.4	27.56	0.735	160.3	[127]
Propranolol	958.5	22	1.061	214.3	[127]
Methimazole	731.7	60.75	0.442	162.1	[127]
Benzoic acid	752	45.6	0.62	92.51	[128]
Acenaphthene	803.15	31	0.38	126.19	[128]
Perylene	863	8.68	0.915	201.85	[128]
Methyl salicylate	700	40.7	0.631	130	[128]
Fluoranthene	905	26.1	0.587	161.55	[128]
Phenol	692.2	60.5	0.45	89	[128]
p-chloropheno	724.75	53.61	0.456	101.4	[128]
2,4-dichlorophenol	718.38	53.04	0.608	117.9	[128]
2.6-dichlorogheno	718.38	53.04	0.608	117.9	[128]
2,4,6-trichlorophenol	745.96	51.52	0.522	132.6	[128]

[125,126,127,128]).

Accordingly, various Peng–-Robinson equations of state associated with mixing rules have been led models to be used in such field of interest due to its relatively high computational accuracy for thermodynamic properties and chemical laws. Among the researchers who focused on such an approach are Kurnik and Reid in early 1982 [129], Kosal and Holder in 1987 [129,130], Cortesi et al. in 1999 [131], and Goodarznia and Esmaeilzadeh in 2002 [132], where their developed thermodynamic model was mainly founded on cubic equations of state with conventional mixing rules [133]. However, mixing rules are judged inaccurate in simulations if these latter are not escorted with Gibbs energy models, following the facts that the behavior of traditional parameter equations of state is ambiguous near the critical region where the deal is with non-ideal mixtures that may involve polar and quadrupolar composites [134,135] due to the necessity of going into microscale dynamics using molecular simulations [135].

Indeed, resultant data on C-H-O molecules by MD emphasizes the intermolecular potentials at low to moderate T/p values for phase equilibrium and shock wave statistics. However, it is extremely difficult to describe the particular limits of pressures and temperatures for straight use of MD with molecular fluid species. The fluid could be intrinsically unstable, and may dissociate into other molecular or induce a phase change [134,135]. In that case, one cannot treat molecules as materials. Likewise, if the species provides phase transformation, the potentiality of interactions could possibly go wrong, due to significant structural modifications [134,135].

To date, and following the field of oil extraction, the gas flooding technology proved to be effective for the improvement of recovery rates. As a promising medium for injection, the displacement process of CO₂ in porous channel is essential to its performance; thus, we denote Fang et al. [136], who successively simulated the MD displacement of CO₂/N₂ flooding (see Figure 12). The synergistic effect of CO₂ slug and N₂ slug was larger than single-phase injection, and even better than mixture gas flooding. Thus, the CO₂ slug is recommended as a front slug for a better displacement efficiency [136].

4. Conclusions

Through this review, a particular attention was devoted to molecular dynamics (MD) on heat transfer of supercritical CO₂ and the applications for energy aspects. For MD development, the attention has been devoted to algorithms that revealed efficient and pertinent linear and nonlinear heat transfer theories.

(i)

Major force fields development has been summarized and compared. Based on recovery of vapor-liquid coexistence curves, the applicability of the model has been justified, while flexible-bond models provided larger uncertainties near the critical point;

(ii)

The predictions near the thermostats should be avoided since the curvature of the thermal gradient can be affected by thermostat gradient. Likewise, the thermal conductivity obtained from NEMD simulations can approve the numerical accuracy of the Green–Kubo equilibrium. This may support the local equilibrium hypothesis for transfer characteristics of supercritical CO₂. Meanwhile, the amplitude of temperature fluctuation in EMD simulation was significantly dependent on the size of simulated MD cell; thus, the size effect should be treated with care near the critical point;

(iii)

On the other hand, the thermal behavior of combined molecules is still under debate. Supercritical mixtures may only provide similar heat transfer behavior with solo supercritical fluids above the critical line.

Still, one ongoing issue is the involvement of potential approaches to obtain thermal conductivity, while the corresponding micro- and nano-scale findings seek more validation by bench-scale measurements. Likewise, there is a lack of broad comparison between the MD potentials themselves in terms of their contribution to the supercritical heat transfer mechanism. It is also crucial to emphasize the role of force field and thermal relaxation models in predicting heat transfer of supercritical mixtures to accentuate the advanced energy engineering. In addition, new approaches such as linking artificial intelligence with molecular dynamics upshots may help expand the current limitations.