Abstract
In this article, we investigate the effect of different energy variables on economic growth of several oil-importing EU member states. Three periods from 2000 to 2020 were investigated. Three different types of regression models were constructed via the gretl software. Namely, the OLS, FE, and SE approaches to panel data analysis were investigated. The FE approach was chosen as the final one. The results suggest the importance of the consumption of both oil and renewable energy on economic growth. Crises of certain periods also had a noteworthy effect as well.
1. Introduction
The topic of oil importation to EU member states has always been a hot topic. And in light of recent events and sanctions on Russia, more and more attention is being paid to the effect that changes in the levels of energy consumption may have on the economy.
In this work, we aim to investigate the potential effect that different energy variables may have on the economic growth of several EU members states that are commonly identified as oil importers. Some of the variables chosen by us were influenced by past literature [1,2,3,4,5,6,7,8,9], which will be discussed in the next section. The main variable is GDP (in current USD). The explanatory variables are: oil price per barrel (USD), oil consumption, coal consumption, renewable energy consumption and, where appropriate, time dummies for significant shifts in GDP. All consumption variables are measured in exajoules. The chosen countries have been member states since 2000, and have not left the EU during the period from 2000 to 2020. The list of countries is as follows: Germany, France, Austria, Belgium, Romania, Spain, Portugal, Finland, Netherlands, and Sweden.
Based on obtained data for the period from 2000 to 2020, we created a panel data set. For this data set, we investigated the application of OLS, FE, and SE approaches [10,11,12,13,14,15,16,17] to regression. The results for all periods will be shown in a later section. Periods were chosen for the analysis: 2006–2013, 2014–2020, and 2006–2020. Models were constructed for all time periods. Further tests were also conducted for the final chosen model type.
Next, the main theoretical approaches taken will be discussed. This part will cover the general forms of econometric models being reviewed.
The analyzed articles allow us to find out the contribution of production to sustainable growth and development. For example, research [18] has identified the place of responsible production and consumption in many goals of sustainable development and growth. The study [19] allowed us to clarify the relationship between existing estimates and the need for transformations in panel data models in order to minimize errors. The AMT model presented in study [20] provides significant efficiency for sustainable and lean production, which is a practical help in making decisions on the choice of sustainable growth models.
The development of economic and mathematical tools for assessing the level of investment attractiveness on the example of oil companies is an important component, because the oil industry is a driver of the economic development of any country. The mathematical methods presented in article [21] make it possible to identify metrics and variables that characterize sustainable development trends on the example of oil companies and take them into account in further analysis.
After this, models for different time periods will be constructed. The most important information on chosen data and variables will also be discussed. Based on the tests conducted automatically by the gretl software, we will explain our final choice for the modeling approach.
As we get closer to the end, we turn to the final version of the model for our research. Yet again, all three periods will be covered. The results of the regression, as well as their interpretation, will be reviewed in this part.
Finally, we will turn to the conclusion for this research. Our findings for different periods will be summarized once again. Based on them, we will also mention the potential ways that information obtained in this research can be used in economic, social, and political scenarios.
In each of the studies, the authors focused on a specific aspect of the problem. For example, in study [10], the authors identified CO2 as a central element of economic value. The study [11] focused on the volume of electricity generation. The study [12] is devoted to the impact of the life cycle on sustainable development in the field of clean and affordable energy.
Thus, a distinctive feature of this study is that previous studies have identified various indicators that affect the sustainable development of the analyzed countries. Our study reaches the results, clarifies the previously identified observations, and, on the basis of research methods, allows us to more accurately calculate the model that illustrates the impact of our results on economic growth.
Hypothesis 1.
Countries of EU must pay more attention to the area of renewable energy and the way it can be implemented in order to enforce the GDP growth in these countries.
2. Materials and Methods
As our data covers dynamics for different variables for different countries. Over a period of time, we can confidently say that we are dealing with Panel Data. Therefore, the choice of models must also be appropriate. We limited ourselves to three main types, mainly: the Pooling (or Ordinary) regression (or Ordinary Regression) approach, the Fixed Effects (or “within”) approach and the Random Effects approach. Their theoretical forms can be seen below:
Ordinary Linear Regression (OR) or Pooling regression:
(independent and identically distributed), where —coefficient vector (the same for all objects); —the same (for all objects).
Fixed effects model (FE) or “within”:
where is the coefficient vector with individual effect for each object, interpreted as a nonrandom constant; —the same (for all objects).
Random effect model (RE):
where is an individual effect for each object, interpreted as a random variable that maintains a constant value for all ; —the same (for all objects).
2.1. Building Models, Modelling, Testing Models
The article attempts to find out how much social, environmental, and human-centric indicators [22,23] affect the sustainability of economic development of the economy. How universal the GDP indicator is and whether its use is justified in making economic decisions was one of our considerations. Does it accurately reflect people’s well-being? Long-term policies based on the GDP criterion are irrational to measure a country’s overall progress. To assess a country’s progress, the use of a GDP indicator is not sufficient. After extensive review, the authors found that GDP was intentionally designed to measure only economic activity, which cannot be equated with social or human well-being [24].
The analyzed studies, in particular [25], assess how renewable energy sources interact with international trade and environmental quality in the analyzed countries from 2001 to 2018 years. The results show that renewable energy is strongly and positively linked to international trade. In addition, the results show that the consumption of renewable energy has a positive effect on the quality of the environment. In addition, the results provide a theoretical framework for the formulation of clean and sustainable development policies to understand the role of renewable energy in stimulating international trade, which maintains a balance between eco-environmental sustainability at the macro and micro levels.
The data for energy variables was taken from BP’s Statistical Review of World Energy 2021 [26]—being the latest one available. The data for GDP was taken from the World Bank and are shown in Figure 1.
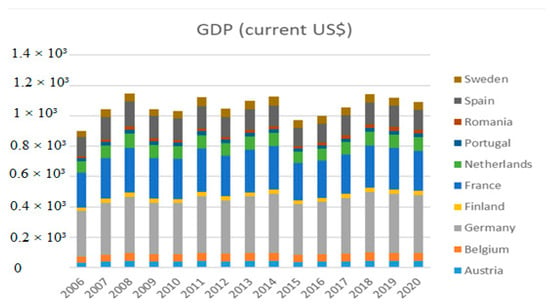
Figure 1.
Data for GDP.
Below, the dynamics for GDP can be seen: In general, we observe similar dynamics for the reviewed member states. Germany seems to be the biggest one in terms of consumption, with Spain and France following behind it. Noteworthy changes can be associated with economic crises, such as the 2008 recession, or with oil-related shocks. We also see an increase in terms of the usage of renewable energy. However, it seems that coal is being gradually phased out.
As stated previously, three periods were chosen: 2006–2013, 2014–2020, and 2006–2020.
Our dependent variable is GDP, as it is the most common measure of economic growth. Our exogenous variables are:
- Crude oil price per barrel.
- Crude oil consumption (exajouls).
- Coal consumption (exajouls).
- Renewable energy consumption (exajouls).
- Time dummy variable.
The first two were chosen to show the impact of oil consumption on economic growth. Coal consumption was added to show the effect of another type of fossil fuel. Renewable energy consumption was investigated, as it is very much the alternative to oil. Time dummies were added to account for crises and other major shifts. Initially, we also considered the inclusion of data on nuclear energy and natural gas consumption. However, the data on the former was missing for several countries, while the latter had troubling levels of correlation with other explanatory variables.
The Pooled regression model, Pooled weighted regression model, Fixed Effects, and Random Effects models were built for early 2000s, and they were compared with each other for accuracy and adequacy. The decision was made in favor of Fixed Effects model.
The main conclusions derived from this model are the following: it is important to mention that there was a multi-caliber in oil consumption between models of 2000–2008 and 2006–2020. This was due to the fact that the price of oil had rebounded strongly since 2005–2006, which did not have a negative impact on GDP. We believe that this situation caused multicollinearity in our model—this was a characteristic feature of the period 2000–2008, since, in the subsequent period 2006–2020, there was no such effect in this indicator.
Thus, start with testing the Pooled regression model [27] for EU countries for the period 2006–2013 period:
Pooled regression model was built, and some important tests were made (Figure 2):
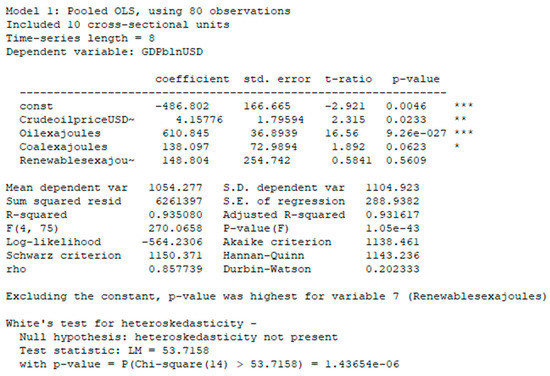
Figure 2.
Pooled regression model.
We see that R2 = 0.9316, which means that 93.16% of changes in the GDP level were explained by the changes in exogenous variables [28] (Crude oil price, Oil, Coal, and Renewables) within the linear regression model.
shows us whether is random. We compared the value of the statistic with the critical value of the corresponding Fisher distribution at a significance level of 1% (Figure 3):

Figure 3.
Compare the value of the statistic with the critical value of the corresponding Fisher distribution at a significance level of 1%.
, which means that was not formed under the influence of random variables, and the quality of the specification model was high.
Now then tested our model for heteroscedasticity (Figure 4).
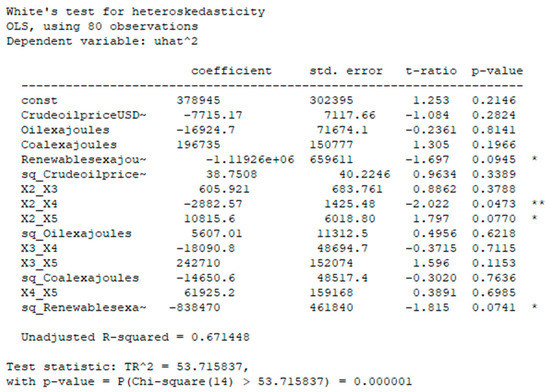
Figure 4.
Testing the model for heteroscedasticity.
There was heteroscedasticity in the model. The most significant variable was Renewables. We built a weighted least squares model to remove heteroscedasticity.
The Pooled weighted regression model then looked as it does in Figure 5.
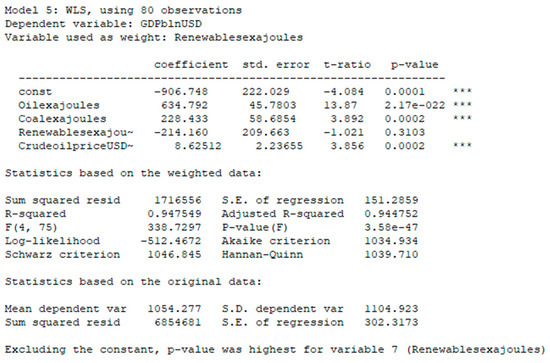
Figure 5.
Testing Pooled regression models.
R2 = 0.9448, which means that 94.48% of changes in the GDP level were explained by the changes in exogenous variables within the linear regression model.
p-value (F) = 3.58 × 10−47—the value was also very small, which means that R2 was not formed under the influence of random variables, and the quality of the specification model was high [29].
In the Pooled regression model, rho = 0.86, which was close to 1, which means there was a huge chance of having individual effects.
Now then compared Fixed Effects model with Pooled regression model (Figure 6).
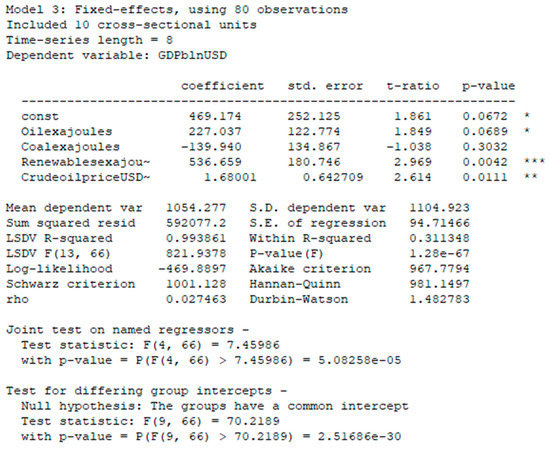
Figure 6.
Compare Fixed Effects and Pooled regression models.
We tested the Fixed Effects model using the Joint test on named regressors. p-value = 5.08258 × 10−5—the value was very small compared with the alpha value, so we chose the Fixed effects model from these two models.
Next, we checked the 3rd premise of the Gauss–Markov theorem—the presence of autocorrelation. We performed the Durbin–Watson statistic test with the 5% significance level. We obtained the critical values and The DW statistic was 1.4827. As we see, there was an autocorrelation. However, it will be explained further.
Now let’s check our model for adequacy, for this we calculate , :
Now, let us consider the Stochastic Effects model (Figure 7).

Figure 7.
Breusch–Pagan test, followed by the Hausman tests.
We looked through the Breusch–Pagan test and then the Hausman tests.
Using the results of Breusch–Pagan test [30] we compared the Pooled regression model with the Stochastic Effects model (Pooled vs. SE). p-value = 7.75515 × 10−40 < alpha value, respectively; from the two models, we chose the Stochastic Effects model.
Let us compare the Stochastic Effects model with the Fixed Effects model using the Houseman test: p-value = 0.00791073, which was also less than the alpha value, respectively. We selected the Fixed Effects model from these two models.
In the end, it turns out that, for the period 2006–2013, the Fixed Effects model corresponded best. Testing on the adequacy for the Fixed Effects model are shown. (Figure 8).
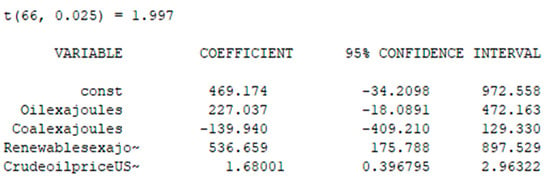
Figure 8.
Testing on adequacy for the Fixed Effects model.
Now we check our model for adequacy. For this purpose, we calculate , : based on Equations (4) and (5).
Since , and our forecast GDP = 586.8418 lay in this interval, our model was adequate, which means that the fourth premise of the Gauss–Markov theorem was satisfied, and the coefficients of the model were unbiased, consistent, and efficient.
We began analysis with the Pooled regression model for countries included in European Union for the period from 2014 to 2020.
We considered the influence of oil prices, oil, gas, coal, nuclear energy, and renewables consumption on economic growth of mentioned countries, specifically on GDP.
Build Pooled regression model and implement appropriate tests (Figure 9).
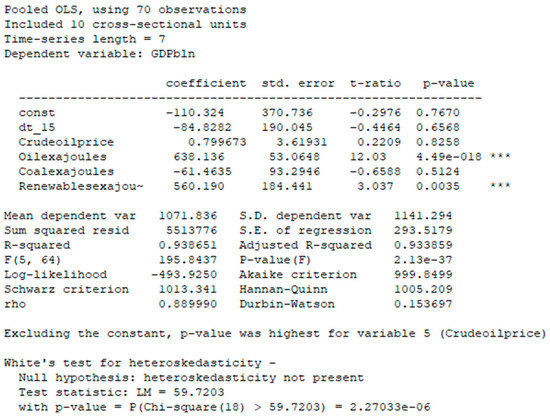
Figure 9.
Output statistics for Pooled regression model in period 2014–2020.
To understand how well GDP is explained by given indicators, we should look at R-squared modified—0.9386. It means that 93.86% of changes in GDP volume were explained by changes in oil prices, consumption of oil, gas, coal, nuclear energy, and renewables [31].
It was assumed that the equation of model contained a random perturbation, which means that the formula contained randomness. That is why we looked at p-value (F). It was equal to 2.13 × 10−63 (less than 2.36, see Figure 10), which means that R2 was not random, it was not formed under the influence of random variables, and the quality of the model specification was high.

Figure 10.
Critical value for Fisher test.
The next step is testing the model for heteroscedasticity (investigate the second hypothesis of the Gauss–Markov theory). It is obvious that there was no heteroscedasticity in the model, the second premise was fulfilled, the residuals of the model were homoscedastic, and the coefficients of the model were not biased, consistent, and efficient (Figure 11).
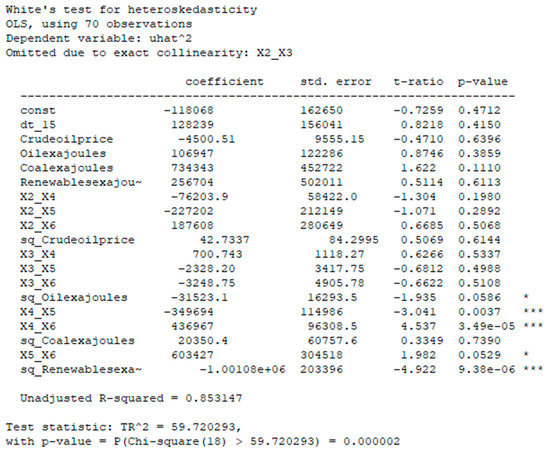
Figure 11.
White’s test.
In the Pooled regression model, the rho = 0.89 parameter was quite close to 1, so we still checked for the presence of individual effects, and we needed to consider other models.
Let us compare the Fixed Effects and Pooled regression models (Figure 12).
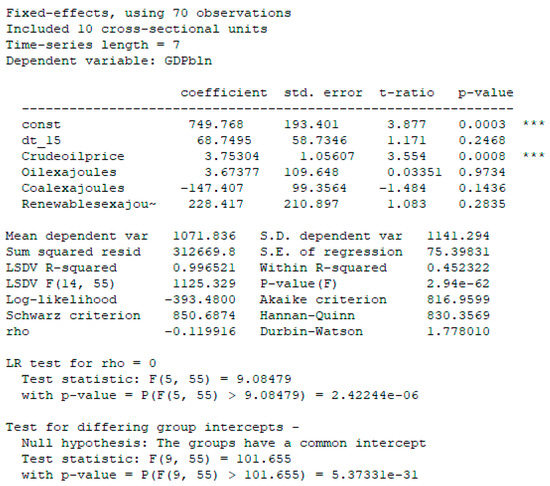
Figure 12.
Model with Fixed Effects.
We tested the Fixed Effects model by Joint test. p-value = P(F(5,55)) = 2.422 × 10−6—the value was very small, so we chose the Fixed effects model from two models (Pooled regression model and Model with Fixed Effects). We also conducted the Durbin–Watson test. Stat. Darbin–Watson = 1.77. The value was low, so we needed to find critical values according to the Darbin–Watson test:
5% critical values for Durbin–Watson test:
n = 70, k = 6
dL = 1.43
dU = 1.80
It turns out that the value did not fall into the dU interval, but was quite close to the critical value. Presumably, there was no autocorrelation in the model. It was probably necessary to introduce an additional variable that had an impact on our dependent variable GDP [32]. Nevertheless we first looked at the Random Effects model (see Figure 13).
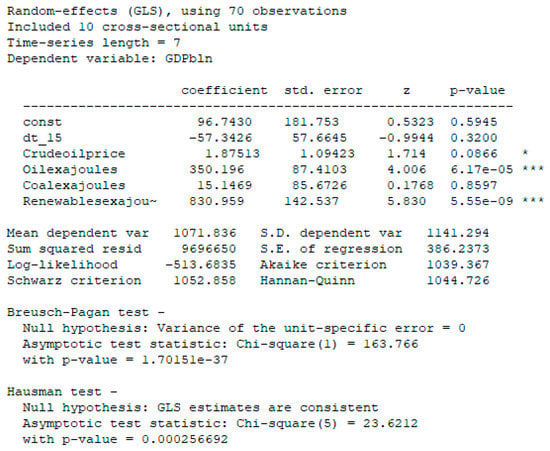
Figure 13.
Random Effects model.
Let us test the model using the Brish–Pegan Test and the Hausman test [33].
Let us compare the random effects model with the united regressions model (Pooled) based on the Brish–Pegan test. p-value = 1.7015 × 10−37 < 0.01, respectively. We chose the Stochastic Effects model from two mentioned models [34].
Let us compare the Stochastic Effects model with the Fixed Effects model using the Hausman test: p-value = 0.00026. It was less than alpha (0.01), respectively. We chose the Fixed Effects model from two models. Taking into account that the Fixed Effects model corresponded for the period 2000–2020 and for the period that we recently considered (2014–2020) too, we can state with full confidence that the Fixed Effects model is the most effective for forecasting.
2.2. Analysis of the Model Received
LSDV R-squared and R-squared in limits take high values. A total of 45% of changes in GDP were explained by changes in independent variables under Fixed Effects model [35].
p-value was extremely small = 2.94 × 10−62. So, the value of R-squared was not random, and the quality of the model specification was high.
2.3. Simulation Results and Their Discussion
As Fixed Effect was our choice for the model, the following equation was created to illustrate the effects that our chosen variables had on GDP (Figure 14).
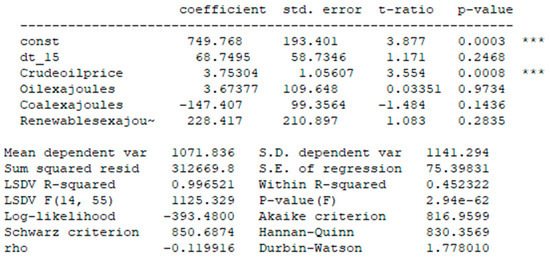 where:
where:

Figure 14.
Equation effects that our chosen variables had on GDP.
GDPit = 749.77 + 3.75*OilPriceit + 3.7*Oil(ex)it − 147.4*Coal(ex)it + 228.4*Renewables(ex)it + 68.8*dt15it + eit
- Oilprice—Crude oil price.
- Oil(ex)—oil consumption (exajoules).
- Coal(ex)—coal consumption (exajoules).
- Renewables (ex)—renewable energy consumption (exajoules).
- Dt15—time dummy variable (for 2020 COVID pandemic).
In order to understand the significance of the explanatory variables, gretl automatically performs the t-test and shows its results, which can be seen next to the variables in the table for the FE model.
The regression results suggest that all explanatory variables, with the exception of coal consumption, were significant on the 1% level, with time dummy being another exception (significant on the 10% level instead). The conclusion that can be drawn is that, while renewable energy does have a significant effect on economic growth, oil dynamics still play an important role in the economic wellbeing of the selected states. Coefficients for both of them, respectively, had a positive sign. Moreover, due to the phase-out of coal consumption, its importance similarly diminished, and its coefficient was negative. The results for the time dummy also indicate that the the COVID-19 pandemic did have a significant effect on GDP. However, it is interesting to observe that the effect was positive. This may be associated with a greater shift towards renewable energy during the pandemic [36,37].
In order to check the adequacy of the model, prerequisites for the Gauss–Markov theorem were checked.
Prerequisite 1: Multicollinearity.
Correlation matrix for the variables (with the exception of the time dummy) can be seen in Figure 15.
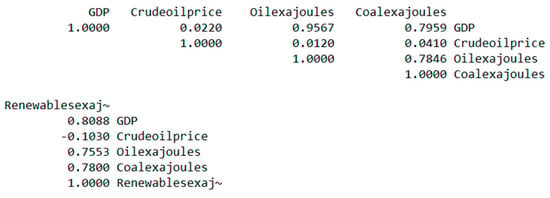
Figure 15.
Correlation matrix for the variables.
As can be seen, while there are some cases of correlation over 0,75, there were no dramatically high values for correlation between exogenous variables. Moreover, given that the signs of coefficients for other periods were the same, we can conclude that there was no multicollinearity present here.
Prerequisite 2: homoskedasticity.
According to the Wald test [38] for heteroskedasticity, we can reject the H0 that the units have a common error variance. Thus, we had heteroskedasticity in the residuals, which fulfilled this premise of the Gauss–Markov theorem.
Prerequisite 3: autocorrelation.
Gretl [39] automatically gives out the test values for the Darbin–Watson statistic. In this case, dW = 1.778, dL = 1.43, and dU = 1.7672. Accordingly, a table for acceptable values can be seen in Figure 16.

Figure 16.
Acceptable values.
As can be seen, our given value lay in the “green zone”, indicating the absence of autocorrelation. This means that the residuals were free from autocorrelation, and the coefficients of the model were not biased, consistent, and efficient.
In order to test for adequacy (Figure 17), the prediction interval was constructed based on the confidence interval for the coefficients:
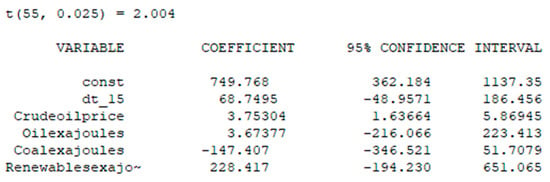
Figure 17.
Test for adequacy.
Now, let us check our model for adequacy; for this, we calculate , : Now we check our model for adequacy. For this purpose, we calculate , : based on Equations (4) and (5).
Since , , and our forecast GDP = 541 lay in this interval, our model was adequate, which means that the fourth premise of the Gauss–Markov theorem was satisfied. and the coefficients of the model were not biased, consistent, and efficient.
Thus, we see that the economy of countries exporting oil depends on oil and non-oil factors only by 32%, which means that it is not surprising that we missed a significant variable, and, because of which, we have autocorrelation and heteroscedasticity in the model. It can be concluded that the economy of the studied countries, among other things, depends on such factors as: unemployment, population, level of education, investment, etc.
Conclusions for the model:
- In the period from 2014 to 2020, alternative energy played a higher role, and therefore it was a significant variable. At the same time, the volatility of oil prices and its consumption were still important for the economic growth of countries.
- Changes in oil prices, consumption of oil, and renewables positively influenced the value of GDP of given countries (Austria, Belgium, Germany, Finland, France, Netherlands, Portugal, Romania, Spain, Sweden).
The negative value for the variable “Gas Consumption” can be explained by the fact that the increase in gas prices from 2014 to 2020 was a consequence of the increase in the costs of its extraction and processing. That is, in principle, the increase in gas consumption could not lead to an increase in the country’s GDP, but on the contrary, it led to a decrease in GDP.
2006–2020 period:
In articles [40,41,42,43], the authors investigated the relationship between the unemployment rate and oil prices, oil price uncertainty, and interest rates. The paper used the method of autoregressive distributed lag (ARDL). A fully modified conventional least squares regression (FMOLS) was also applied to find optimal estimates of long-term coefficients for regressions. All these tests were conducted in Sweden, Norway, Denmark, and Finland based on monthly data from January 2008 to February 2020. The relationship was found for Sweden, Norway, and Denmark. Long-term FMOLS regression coefficients have shown that an increase in oil prices leads to an increase in the unemployment rate in Sweden and Denmark. All countries, with the exception of Denmark, showed evidence of a causal relationship between oil prices and unemployment, thus indicating a strong relationship between these two variables.
Firstly, we built a Pooled regression model and made some important tests (Figure 18):
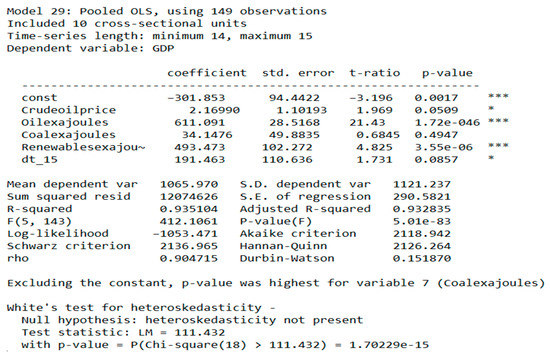
Figure 18.
Pooled regression model. For 2006–2020 period.
The adjusted R-squared was quite high, with low p-value of F, thus indicating that it was not formed due to random chance. The rho criterion was also close to 1, thus indicating a presence of significant individual effects.
Next, we looked at panel models (Figure 19) and compared them against OLS and each other.
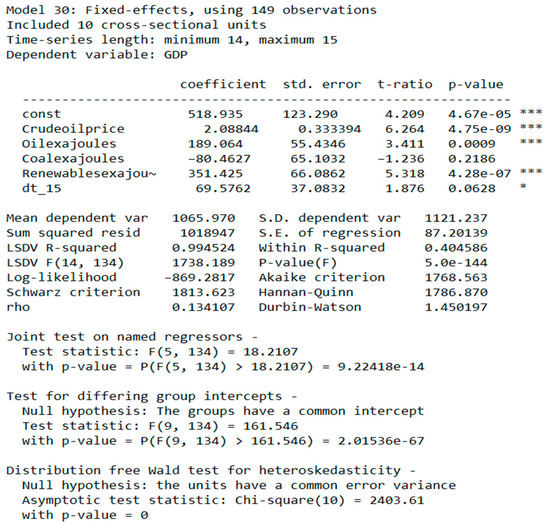
Figure 19.
Panel models.
If we are to look at the joint test on named regressors (Figure 20), we can see that its p-value was very close to 0. This means that the FE approach was preferable to OR.
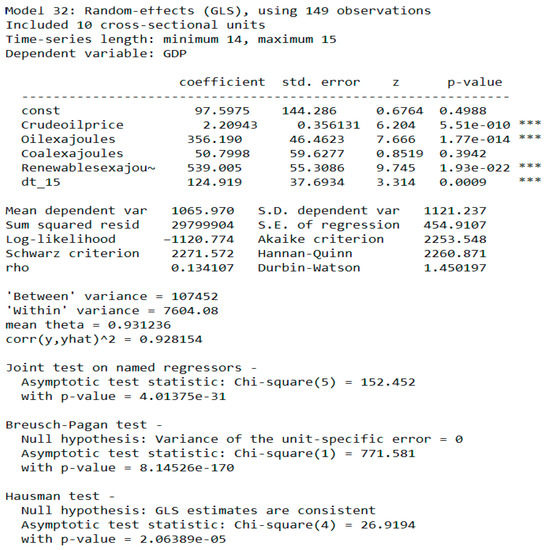
Figure 20.
Joint test on named regressors.
The p-value in case of the Breusch–Pagan was very close to 0, which means that we could choose the RE model over the OR. In case of the Hasusman test, the p-value was similarly low. This, on the other hand, signified that we choose the FE approach.
As can be seen, according to the results of the tests, the FE approach was the best one in this case. Therefore, it was used as the final modelling choice.
3. Simulation Results
Since FE is our choice for the model, the following equation was created to illustrate the effects that our chosen variables have on GDP:
where:
- Oilprice—Crude oil price.
- Oil(ex)—oil consumption (exajoules).
- Coal(ex)—coal consumption (exajoules).
- Renewables (ex)—renewable energy consumption (exajoules).
- Dt15—time dummy variable (for 2020 COVID pandemic).
In order to understand the significance of the explanatory variables, gretl automatically performs the t-test and shows its results, which could be seen next to the variables in the table for the FE model.
The regression results suggest that all explanatory variables, with the exception of coal consumption, were significant on the 1% level, with time dummy being another exception (significant on the 10% level instead).
The conclusion that can be drawn is that, while renewable energy does have a significant effect on economic growth, oil dynamics still play an important role in the economic well-being of the selected states. Coefficients for both of them, respectively, had a positive sign. Moreover, due to the phase-out of coal consumption, its importance has similarly diminished, and its coefficient was negative. The results for the time dummy also indicate that the COVID-19 pandemic did have a significant effect on GDP. However, it is interesting to observe that the effect was positive. This may be associated with a greater shift towards renewable energy during the pandemic.
In order to check the adequacy of the model, the prerequisites for the Gauss–Markov theorem were checked.
Prerequisite 1—Multicollinearity.
In Figure 21, a correlation matrix for the variables (with the exception of the time dummy) can be seen.
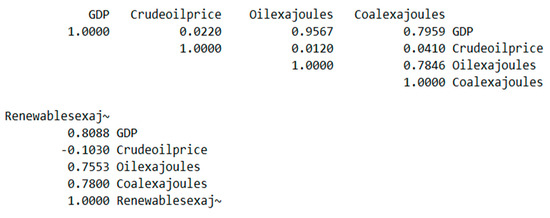
Figure 21.
Correlation matrix for the variables for 2006–2020 period.
As can be seen, while there were some cases of correlations over 0.75, there were no dramatically high values for correlations between exogenous variables. Moreover, as the signs of coefficients for other periods were the same, we can conclude that there was no multicollinearity present here.
Prerequisite 2—homoskedasticity.
According to the Wald test for heteroskedasticity, we could reject the H0 that the units had a common error variance. Thus, we had heteroskedasticity in the residuals, which fulfilled this premise of the Gauss–Markov theorem.
Prerequisite 3—autocorrelation.
Gretl automatically gives out the test values for the Darbin–Watson statistic. In this case, DW = 1.450197, dL = 1.6635, and dU = 1.8020. Accordingly, a table for acceptable values can be seen in Figure 22.

Figure 22.
Test values for the Darbin–Watson statistic.
As can be seen, our given value lay in the “red zone”, thus indicating the presence of autocorrelation. However, this can be explained by the fact that we are only looking at the variables from the energy sectors. It is only to be expected that some significant variables (such as consumption and net trade, for example) are to be omitted.
In order to test for adequacy, the prediction interval was constructed based on the confidence interval for the coefficients (Figure 23).
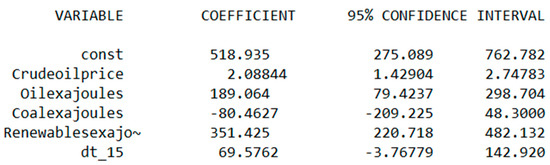
Figure 23.
Confidence interval for the coefficients.
The minimum value for the GDP in this case was 3,898,729, while the maximum was 1,298,872,633. The real value (GDP for Sweden in 2020) was 54,122 bln USD. As the real value fell within the obtained interval, we can conclude that the model was adequate.
4. Discussion
We took an approach to solving the question that was raised at the beginning of the work: how oil prices, consumption of oil, coal, and renewable energy sources affect the GDP of the main EU oil and gas importing countries differs in the utmost accuracy of conclusions compared to other methods of assessing such a relationship.
In this article, several models for estimating the relationship between independent variables and a dependent variable (the GDP of European countries) were analyzed. The analysis has shown that the best model for identifying the correct relationship is a model with Fixed Effects.
The advantage of the model is that the model with Fixed Effects is as close to reality as possible. It is worth noting two important details that make it so accurate:
The second premise requires that the values of regressors related to different objects are independent of each other. However, it is important to emphasize that it admits the existence of a relationship between the values of regressors related to the same object, but different points in time: for example, it admits that xi3 can be correlated with xi2, and that, in turn, can be correlated with xi1. In other words, the future values of the regressor for a given object may depend on its past values. This is a realistic assumption. For example, oil consumption in this region today is probably related to its consumption in the past. Similarly, oil prices in Europe today are likely to affect the future European oil price.
The fourth premise requires that the regressor be exogenous in the sense that it should not be associated with a random error of the model. However, it admits the existence of a correlation between the value of the regressor xit and the fixed effect µi. This is also a realistic premise. As part of our example about energy consumption, the cultural characteristics of a given region (which are precisely characterized by its fixed effect) can influence the decision to change the price of this energy source (that is, the value of xit).
This study made an attempt to take into account the most significant factors influencing sustainable growth within the macro level. The use of mathematical tools made it possible not only to increase the accuracy of the conclusions compared to other methods, but also to identify its fixed effects in each analyzed period, which increases the accuracy of the models that describe the impact of the variables we have chosen on the GDP and sustainable growth of countries. At the same time, it should be noted that the unsustainable development of the global economy imposes its effect on the development model.
5. Conclusions and Recommendations
To sum it up, there were observed three periods of GDP growth and other variables influencing those periods. In all of these time periods, the best model for evaluating the significance of factors in GDP growth became the Fixed Effects model. The results of analysis were approximately the same: renewable energy did have a significant effect on economic growth, while oil dynamics still played an important role in the economic well-being of the selected states. Coefficients for both of them, respectively, had a positive sign [44,45].
Nevertheless, the only difference in these time intervals is the following fact: It is important to mention that there was a multi-caliber in oil consumption between models of 2000–2008 and 2006–2020. This is due to the fact that the price of oil rebounded strongly since 2005–2006, which did not have a negative impact on GDP. We believe that this situation caused multicollinearity in our model—this was a characteristic feature of the period 2000–2008, since, in the subsequent period 2006–2020, there was no such effect in this indicator.
In conclusion, we can say that the value of renewable energy has increased significantly over the years. It is not surprising that many countries, especially ones from the EU, are pushing for it. Our recommendation is that they stay the course. More attention must be paid to the area of renewable energy, as well as the ways that it can be implemented.
On the other hand, oil still has a significant impact on the economy of many states. Thus, while renewable energy is good for the future, the shift from fossil fuels to alternative sources of energy must be gradual, so as to escape major ramifications that such sharp hits may have. Coal is of much lesser importance, so it is advisable to move away from it.
In the future, this analysis could be expanded to provide a more detailed description of the effect of specific types of renewable energy, as well as the effect on nuclear energy.
Author Contributions
Conceptualization, A.B.; methodology, A.Y.; software, A.B.; formal analysis, A.A.; writing—original draft preparation, M.M.; writing—review and editing, M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burcu, O. Nuclear Energy-Economic Growth Nexus in OECD Countries: A Panel Data Analysis. Int. J. Econ. Perspect. 2017, 11, 138–154. [Google Scholar]
- Dynan, K.; Sheiner, L. GDP as a Measure of Economic Well–being. In Hutchins Center Working Paper 43; The Brookings Institution: Washington, DC, USA, 2018; p. 4. [Google Scholar]
- Rehman Khan, Z.Y.; Belhadi, A.M. Investigating the effects of renewable energy on international trade and environmental quality. J. Environ. Manag. 2020, 272, 15. [Google Scholar]
- Raduzzi, R. The macroeconomics outcome of oil shocks in the small Eurozone economies. World Econ. 2019, 43, 191–211. [Google Scholar] [CrossRef]
- Rafindadi, A. Impacts of renewable energy consumption on the German economic growth: Evidence from combined cointegration test. Renew. Sustain. Energy Rev. 2017, 75, 1130–1141. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Kutepov, I.E.; Vygodchikova, I.Y. Quantifying chaos of curvilinear beam via exponents. Commun. Non-Linear Sci. Numer. Simul. 2015, 27, 81–92. [Google Scholar] [CrossRef]
- Vazquez, P.V. Estimation of the potential effects of offshore wind on the Spanish economy. Renew. Energy 2017, 111, 815–824. [Google Scholar] [CrossRef]
- Baldoni, E.; Coderoni, S.; di Giuseppe, E.; D’orazio, M.; Esposti, R.; Maracchini, G. A software tool for a stochastic life cycle assessment and costing of buildings’ energy efficiency measures. Sustainability 2021, 13, 7975. [Google Scholar] [CrossRef]
- Borodin, A.; Zaitsev, V.; Mamedov, Z.F.; Panaedova, G.; Kulikov, A. Mechanisms for Tax Regulation of CO2-Equivalent Emissions. Energies 2022, 15, 7111. [Google Scholar] [CrossRef]
- Tong, D.; Zhang, Q.; Zheng, Y.; Caldeira, K.; Shearer, C.; Hong, C.; Qin, Y.; Davis, S.J. Committed Emissions from Existing Energy Infrastructure Jeopardize 1.5 °C Climate Target. Nature 2019, 572, 373–377. [Google Scholar] [CrossRef]
- Sobamowo, G.M.; Ojolo, S.J. Techno-economic analysis of biomass energy utilization through gasification technology for sustainable energy production and economic development in Nigeria. Energy 2018, 2018, 4860252. [Google Scholar] [CrossRef]
- Levi-Oguike, J.; Sandoval, D.; Ntagwirumugara, E. A Comparative Life Cycle Investment Analysis for Biopower Diffusion in Rural Nigeria. Sustainability 2022, 14, 1423. [Google Scholar] [CrossRef]
- Breusch, T.S.; Pagan, A.R. A Simple Test for Heteroscedasticity and Random Coefficient Variation. Econometrica 1979, 47, 1287–1294. [Google Scholar] [CrossRef]
- Subbotin, Y.; Shevaldin, V. On one method of constructing local parabolic splines with additional nodes. Proc. Inst. Math. Mech. Ural. Branch Russ. Acad. Sci. 2019, 25, 205–219. [Google Scholar]
- Halunga, A.; Orme, C.; Yamagata, T. A Heteroskedasticity Robust Breusch-Pagan Test for Contemporaneous Correlation in Dynamic Panel Data Models. J. Econom. 2017, 198, 209–230. [Google Scholar] [CrossRef]
- Tao, L.; Chen, Y.; Liu, X.; Wang, X. An integrated multiple criteria decision making model applying axiomatic fuzzy set theory. Appl. Math. Model. 2012, 36, 5046–5058. [Google Scholar] [CrossRef]
- Büscher, C.; Ufer, U. The (Un)availability of Human Activities for Social Intervention: Reflecting on Social Mechanisms in Technology Assessment and Sustainable Development Research. Sustainability 2022, 14, 1394. [Google Scholar] [CrossRef]
- Powell, D.J.; Romero, D.; Gaiardelli, P. New and Renewed Manufacturing Paradigms for Sustainable Production. Sustainability 2022, 14, 1279. [Google Scholar] [CrossRef]
- Arellano, M.; Bover, O. Another look at the instrumental variables estimation of error components models. J. Econom. 1995, 68, 29–51. [Google Scholar] [CrossRef]
- Lu, T. A Fuzzy Network DEA Approach to the Selection of Advanced Manufacturing Technology. Sustainability 2021, 13, 4236. [Google Scholar] [CrossRef]
- Mamedov, Z.F.; Qurbanov, S.H.; Streltsova, E.; Borodin, A.; Yakovenko, I.; Aliev, A. Mathematical models for assessing the investment attractiveness of oil companies. SOCAR Proc. 2021, 4, 102–114. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, Z.; Niu, G. Introduction to the Popular Open Source Statistical Software (OSSS); Open Source Software for Statistical Analysis of Big Data; Bryant University: Smithfield, RI, USA, 2020. [Google Scholar]
- Borodin, A.; Panaedova, G.; Ilyina, I.; Harputlu, M.; Kiseleva, N. Overview of the Russian Oil and Petroleum Products Market in Crisis Conditions: Economic Aspects, Technology and Problems. Energies 2023, 16, 1614. [Google Scholar] [CrossRef]
- Kisswani, A.; Kisswani, K. Modeling the employment–oil price nexus: A non-linear cointegration analysis for the U.S. market. J. Int. Trade Econ. Dev. 2019, 28, 1–17. [Google Scholar] [CrossRef]
- Fatima, T.; Mentel, G.; Doğan, B.; Hashim, Z.; Shahzad, U. Investigating the role of export product diversifcation for renewable, and non-renewable energy consumption in GCC (gulf cooperation council) countries: Does the Kuznets hypothesis exist? Environ. Dev. Sustain. 2022, 24, 8397–8417. [Google Scholar] [CrossRef] [PubMed]
- Alzaid, A.; Al-Osh, M.A. First-Order Integer-Valued Autoregressive (INAR (1)) Process: Distributional and Regression Properties. Stat. Neerl. 1988, 42, 53–61. [Google Scholar] [CrossRef]
- Brown, R.P.C.; Carmignani, F.; Fayad, G. Migrants’ remittances and financial development: Macro- and micro-level evidence of a perverse relationship. World Econ. 2013, 36, 636–660. [Google Scholar] [CrossRef]
- Steutel, F.W.; van Harn, K. Discrete Analogues of Self-Decomposability and Stability. Ann. Probab. 1979, 7, 893–899. [Google Scholar] [CrossRef]
- Lima, V.; Souza, T.; Cribari-Neto, F.; Fernandes, G. Heteroskedasticity-robust inference in linear regressions. Comm. Statist. Simulation Comput. 2009, 39, 194–206. [Google Scholar] [CrossRef]
- Sovacool, B.K.; Schmid, P.; Stirling, A.; Walter, G.; MacKerron, G. Differences in carbon emissions reduction between countries pursuing renewable electricity versus nuclear power. Nat. Energy 2020, 5, 928–935. [Google Scholar] [CrossRef]
- Değirmen, S.; Saltık, Ö. Could Nuclear Energy Production and Economic Growth Relationship for Developed Countries Be an Incentive for Developing Ones?: A Panel ARDL Evidence Including Cointegration Analysis; GELISIM-UWE 2019 Special Issue, İstanbul Gelişim Üniversitesi Sosyal Bilimler Dergisi; Mersin University: Mersin, Turkey, 2019; pp. 1–28. [Google Scholar] [CrossRef]
- Hausman, J.A. Specification Tests in Econometrics. Econometrica 1978, 46, 1251–1271. [Google Scholar] [CrossRef]
- Greene, W. Fixed and Random Effects in Stochastic Frontier Models. J. Product. Anal. 2005, 23, 7–32. Available online: http://www.jstor.org/stable/41770178 (accessed on 8 February 2023). [CrossRef]
- deHaan, E. Using and Interpreting Fixed Effects Models. 2021. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3699777 (accessed on 8 February 2023).
- Lepore, D.; Micozzi, A.; Spigarelli, F. Industry 4.0 Accelerating Sustainable Manufacturing in the COVID-19 Era: Assessing the Readiness and Responsiveness of Italian Regions. Sustainability 2021, 13, 2670. [Google Scholar] [CrossRef]
- Basu, A.; Mandal, A.; Mart´ın, N.; Pardo, L. Generalized Wald-type tests based on minimum density power divergence estimators. Statistics 2016, 50, 1–26. [Google Scholar] [CrossRef]
- Borodin, A.; Mityushina, I.; Harputlu, M.; Kiseleva, N.; Kulikov, A. Factor Analysis of the Efficiency of Russian Oil and Gas Companies. Int. J. Energy Econ. Policy 2023, 13, 172–188. [Google Scholar] [CrossRef]
- Lee, C. Adkins, Using gretl for Monte Carlo experiments. J. Appl. Econom. 2010, 5, 880–885. [Google Scholar]
- Segarra-Blasco, A.; Teruel, M.; Cattaruzzo, S. The economic reaction to non-pharmaceutical interventions during Covid-19. Econ. Anal. Policy 2021, 72, 592–608. [Google Scholar] [CrossRef]
- COVID-19. European Centre for Disease Prevention and Control. Published 2021. Available online: https://www.ecdc.europa.eu/en (accessed on 14 January 2022).
- Hale, T.; Angrist, N.; Goldszmidt, R.; Kira, B.; Petherick, A.; Phillips, T. A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker). Nat. Hum. Behav. 2021, 5, 529–538. [Google Scholar] [CrossRef]
- Claeson, M.; Hanson, S. COVID-19 and the Swedish enigma. Lancet 2021, 397, 259–261. [Google Scholar] [CrossRef]
- Olagnier, D.; Mogensen, T.H. The COVID-19 pandemic in Denmark: Big lessons from a small country. Cytokine Growth Factor Rev. 2020, 53, 10–12. [Google Scholar] [CrossRef]
- Mamedov, Z.F.; Qurbanov, S.H.; Streltsova, E.; Borodin, A.; Yakovenko, I.; Aliev, A. Assessment of the potential for sustainable development of electric power enterprises: Approaches, models, technologies. SOCAR Proc. 2022, 2, 15–27. [Google Scholar] [CrossRef]
- Borodin, A.; Natocheeva, N.; Khominich, I.; Kulikov, A.; Shchegolevatykh, N. The Impact of the Business Environment on the Effectiveness of the Implementation of the Financial Strategy of the Oil and Gas Company. Int. J. Energy Econ. Policy 2021, 11, 13–21. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).