A Model Predictive Control Approach for Heliostat Field Power Regulatory Aiming Strategy under Varying Cloud Shadowing Conditions
Abstract
1. Introduction
2. Materials and Methods
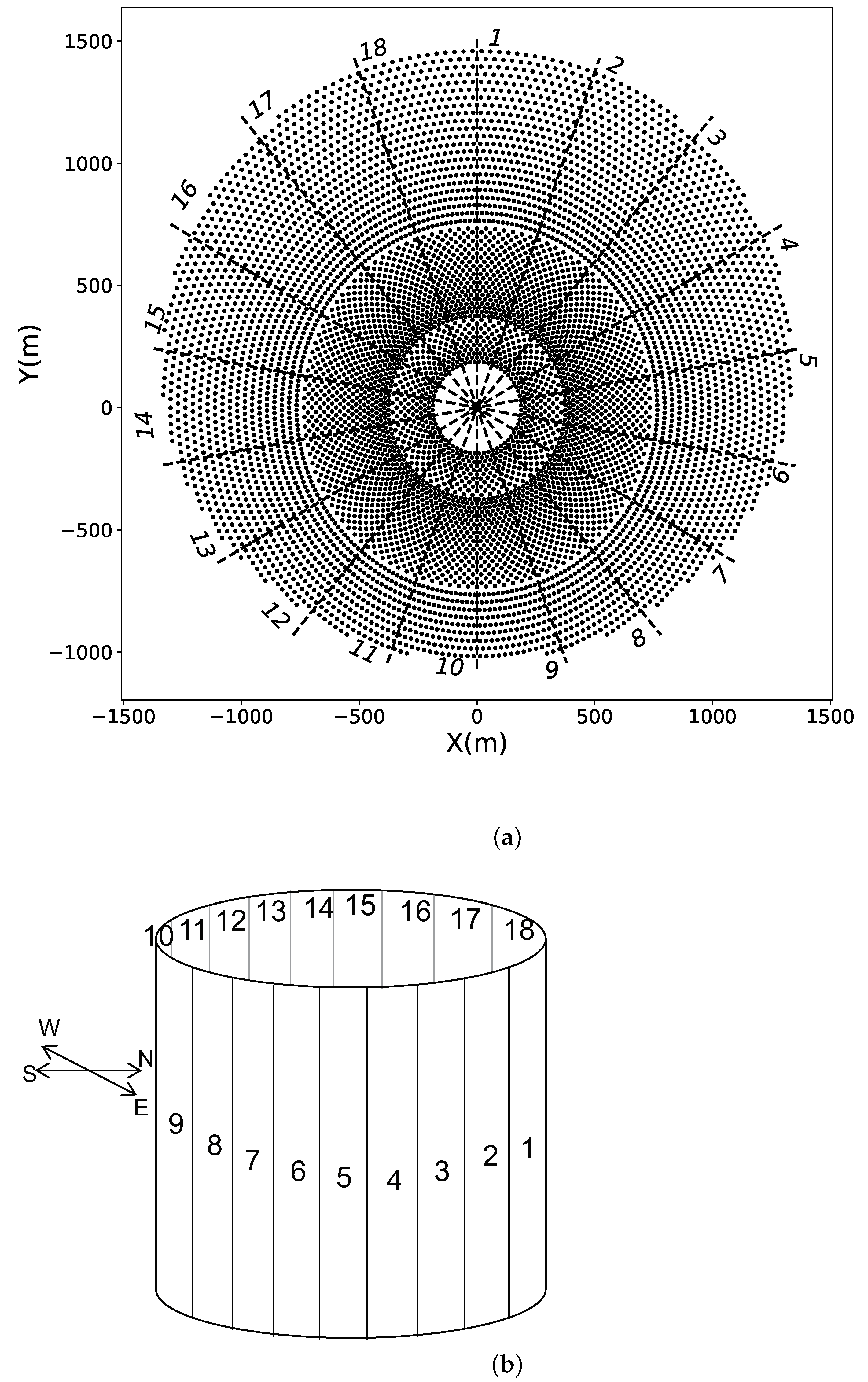
2.1. Problem Description
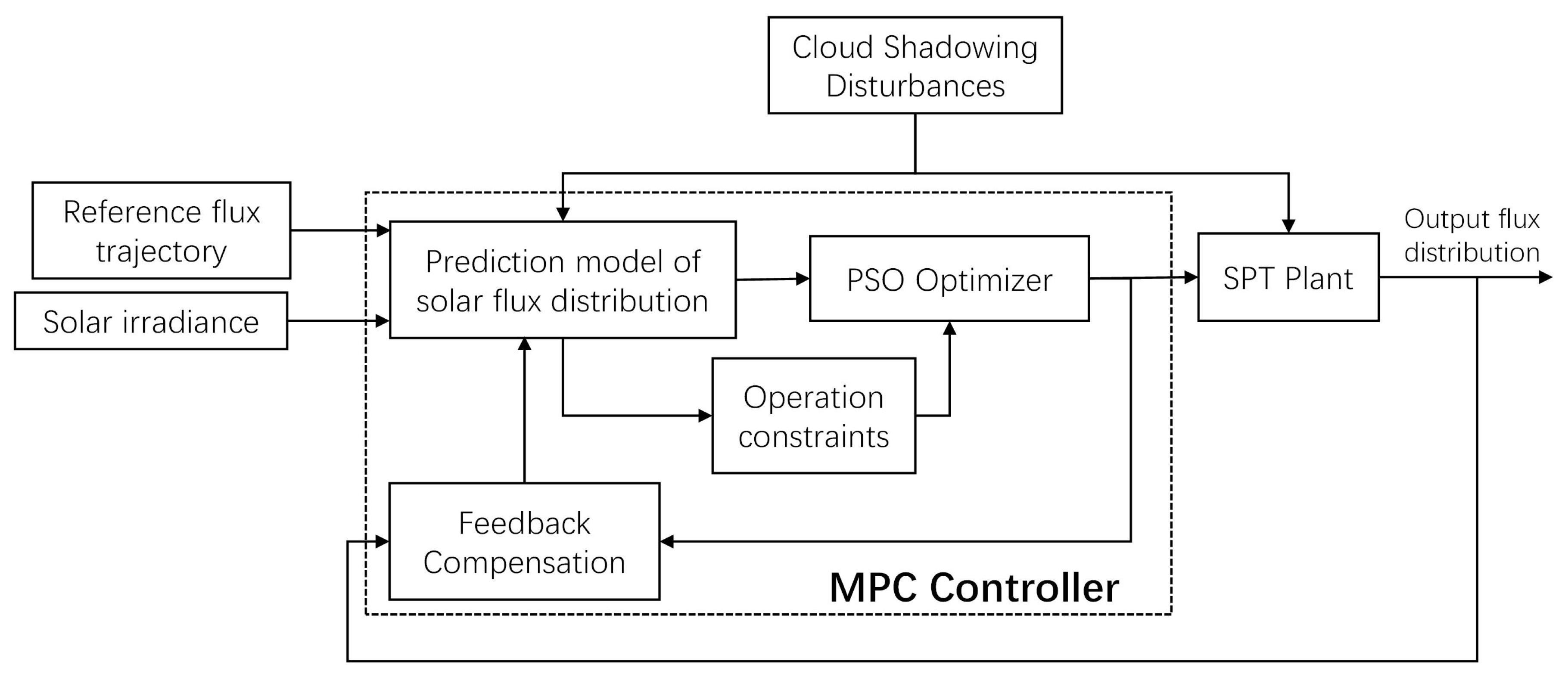
2.2. MPC Formulation
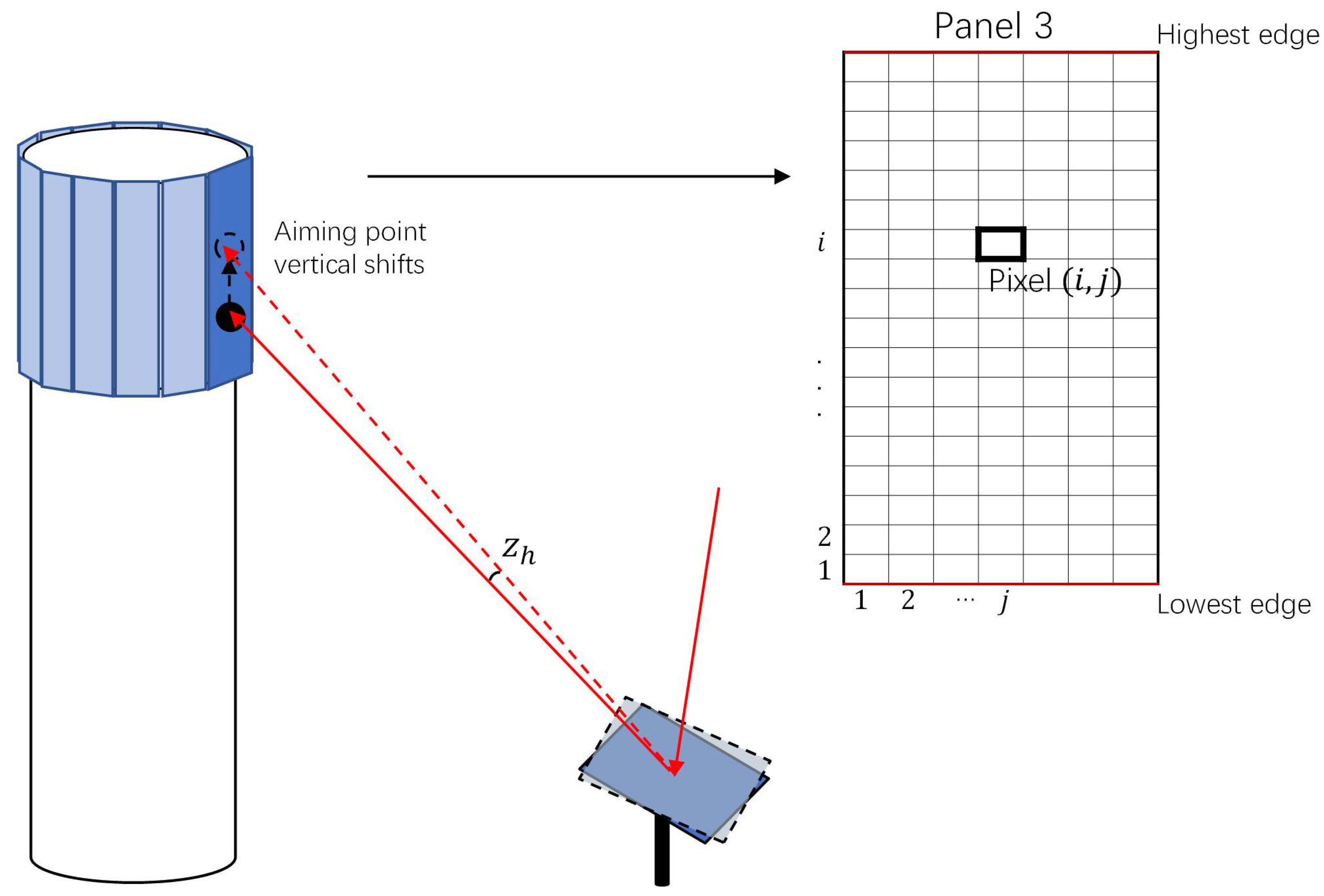
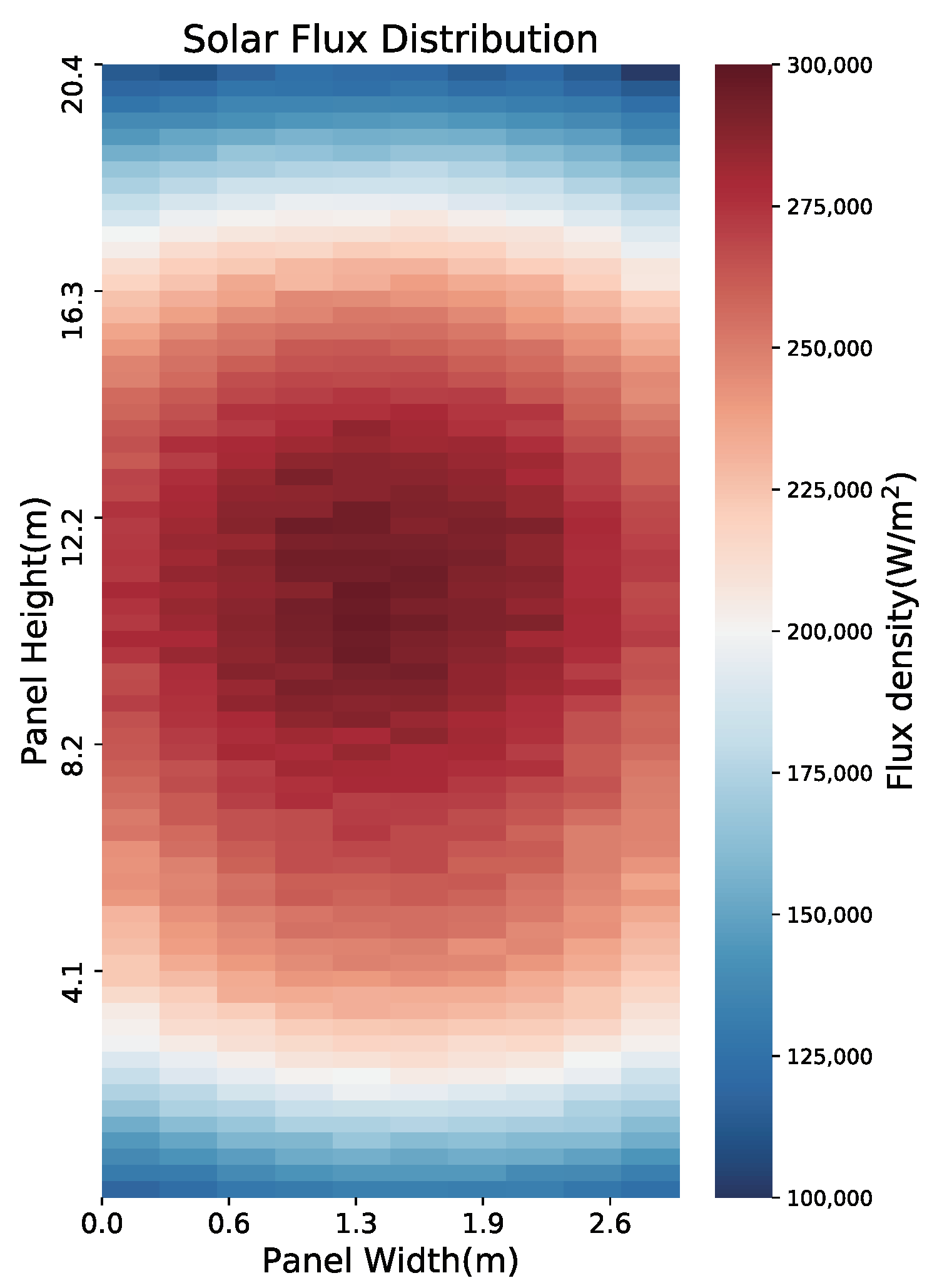
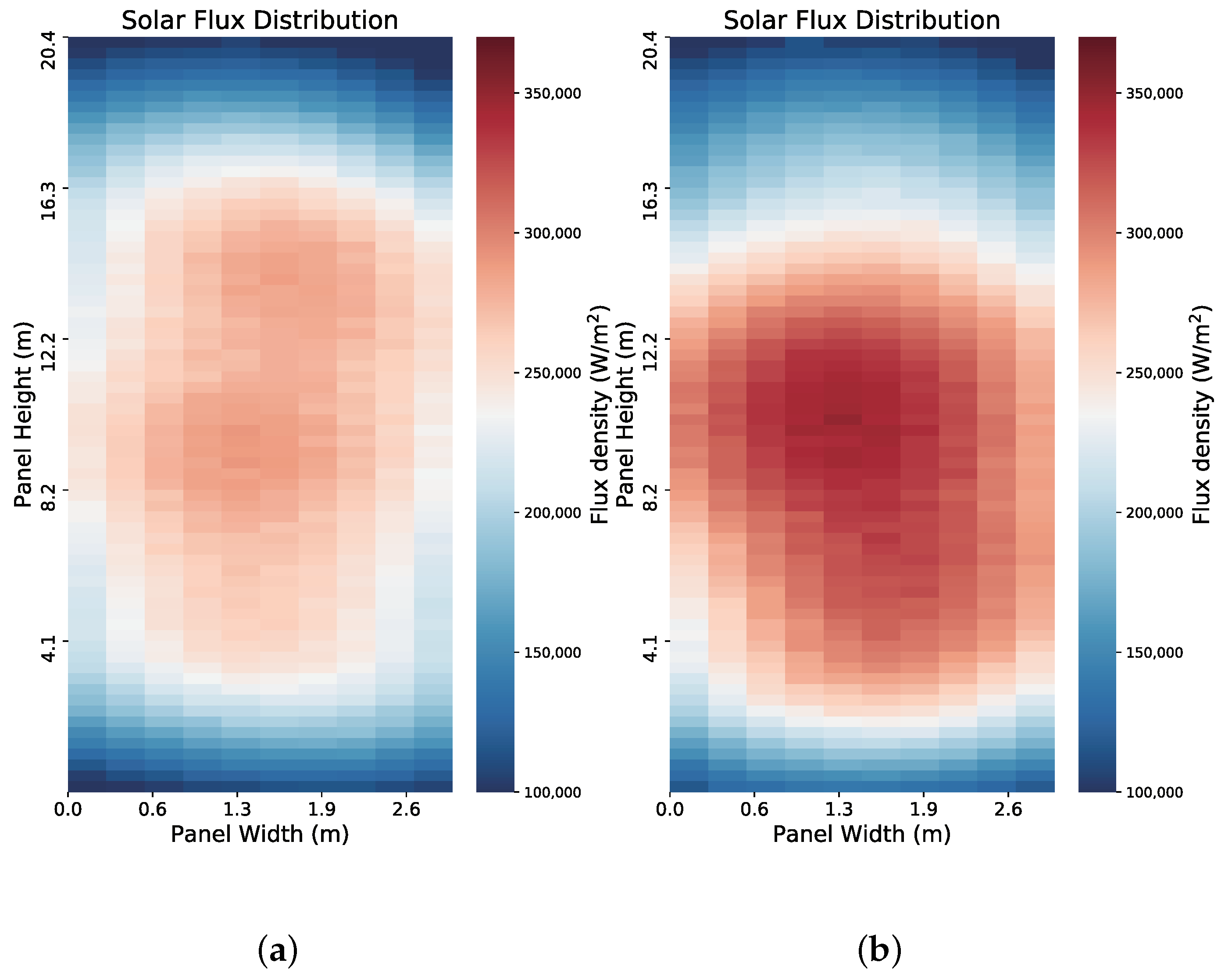
2.3. Solar Flux Distribution Calculation
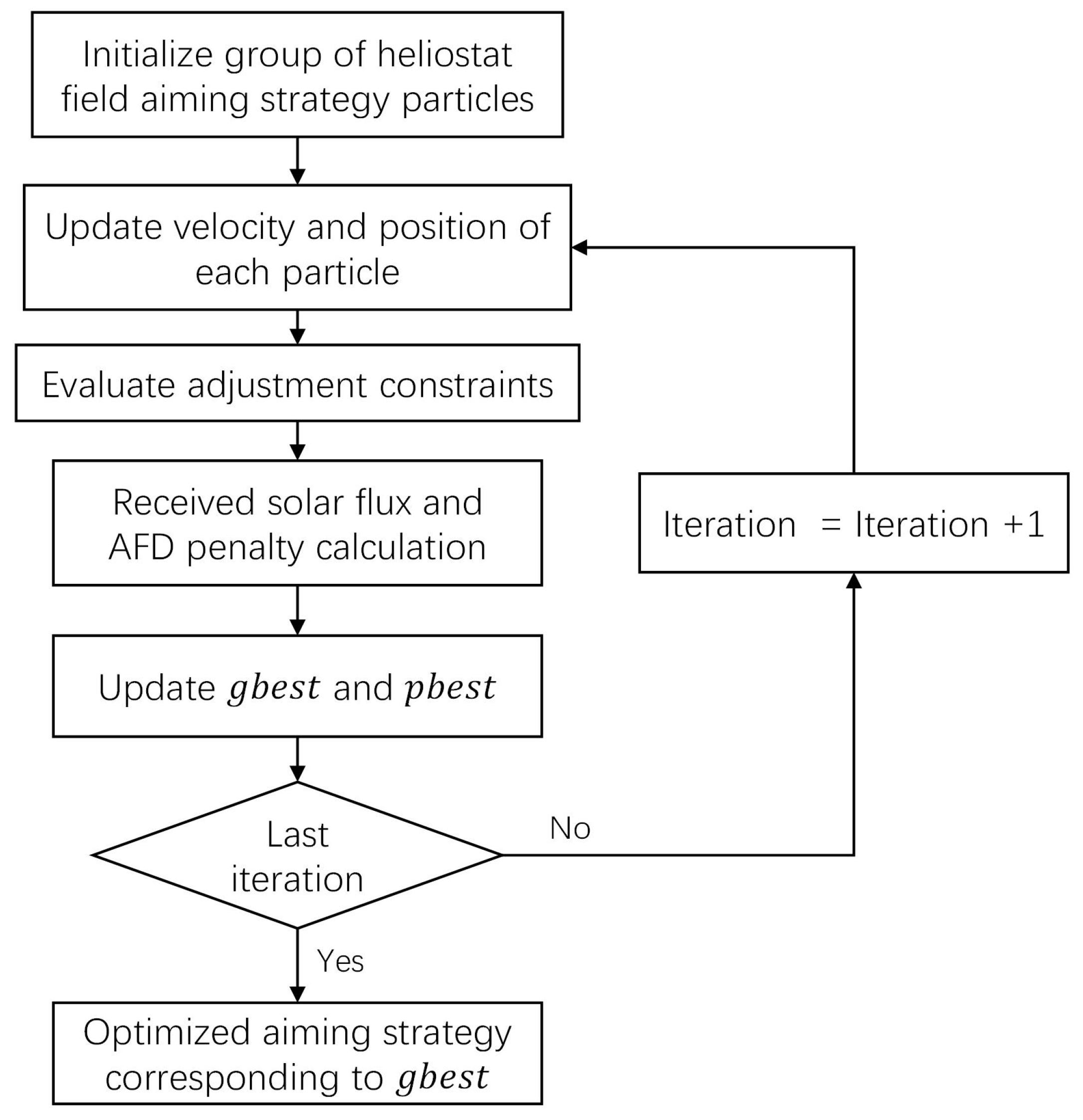
2.4. Particle Swarm Optimization Algorithm
2.5. Feedback Compensation
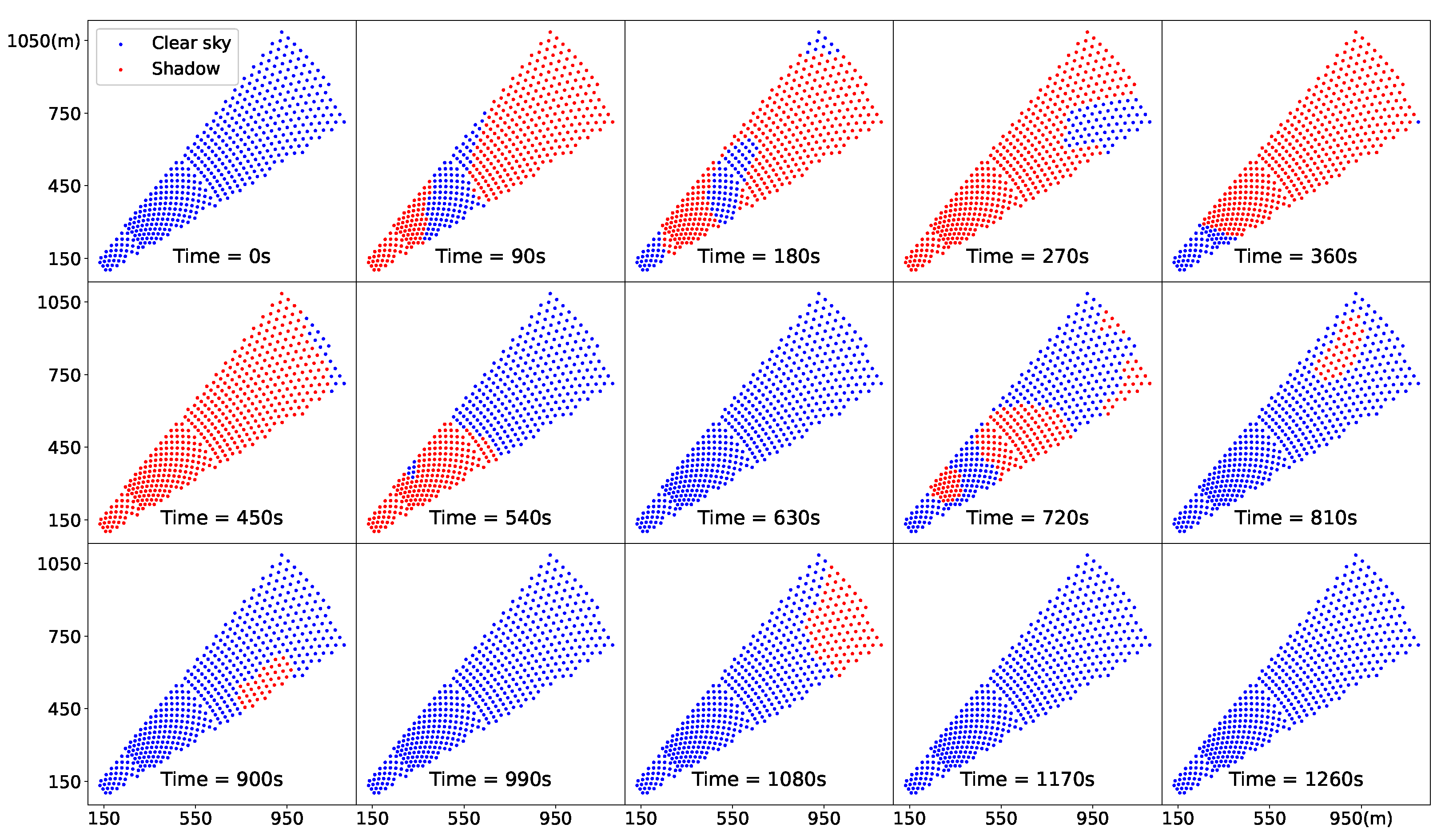
3. Experiments and Results
3.1. Methods in Comparison
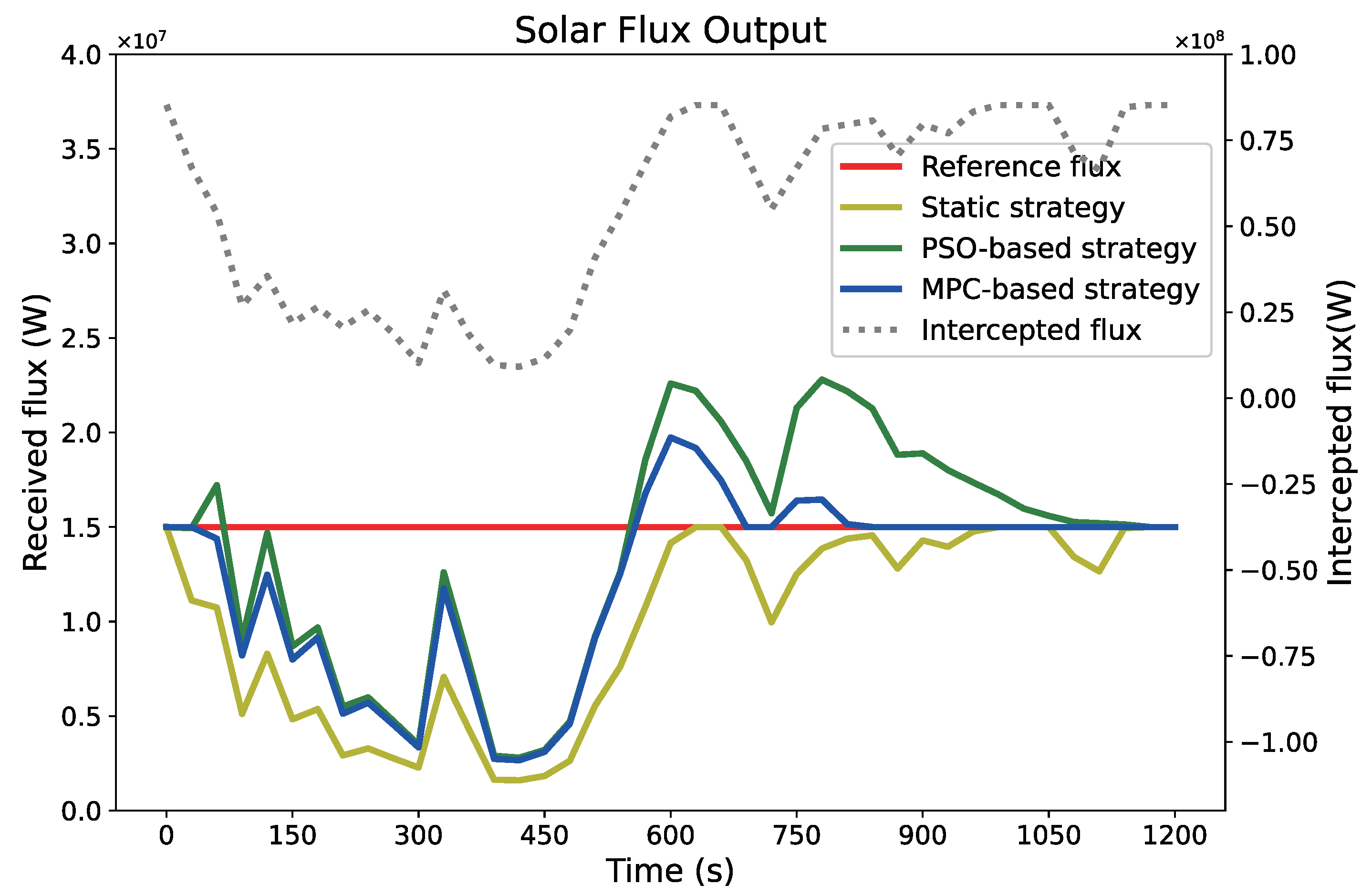
3.2. Single Case Study
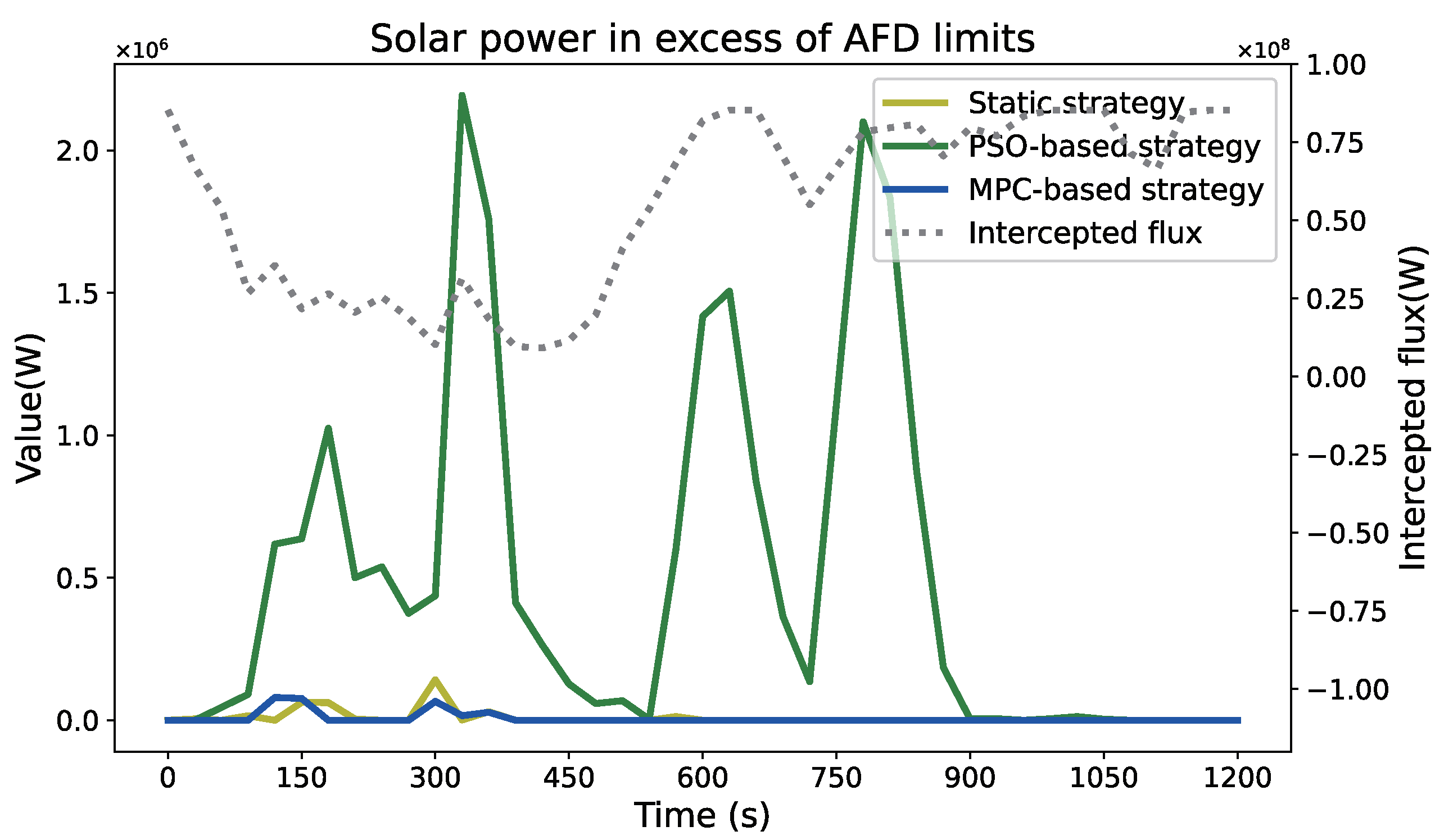
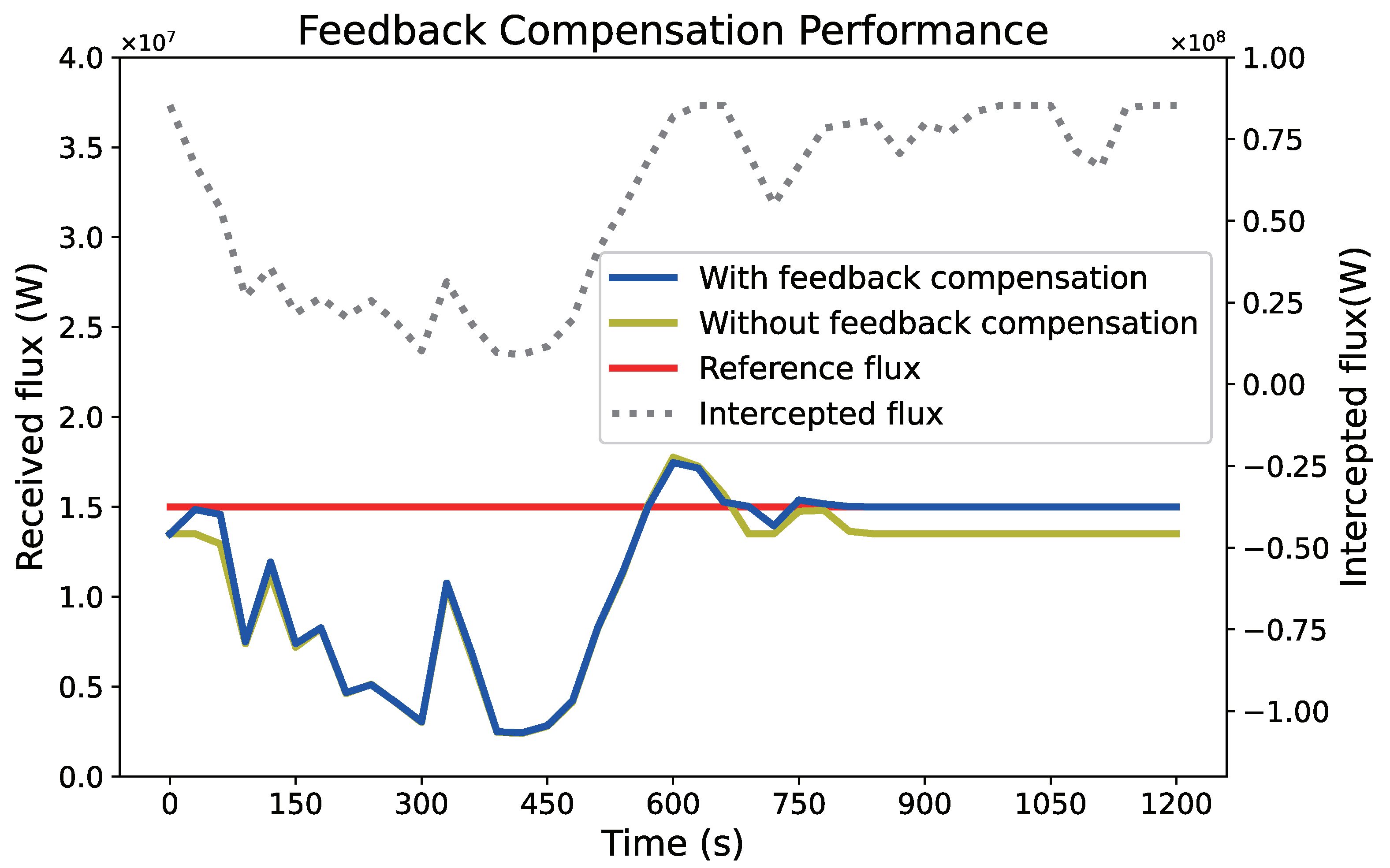
3.3. Feedback Compensation Performance
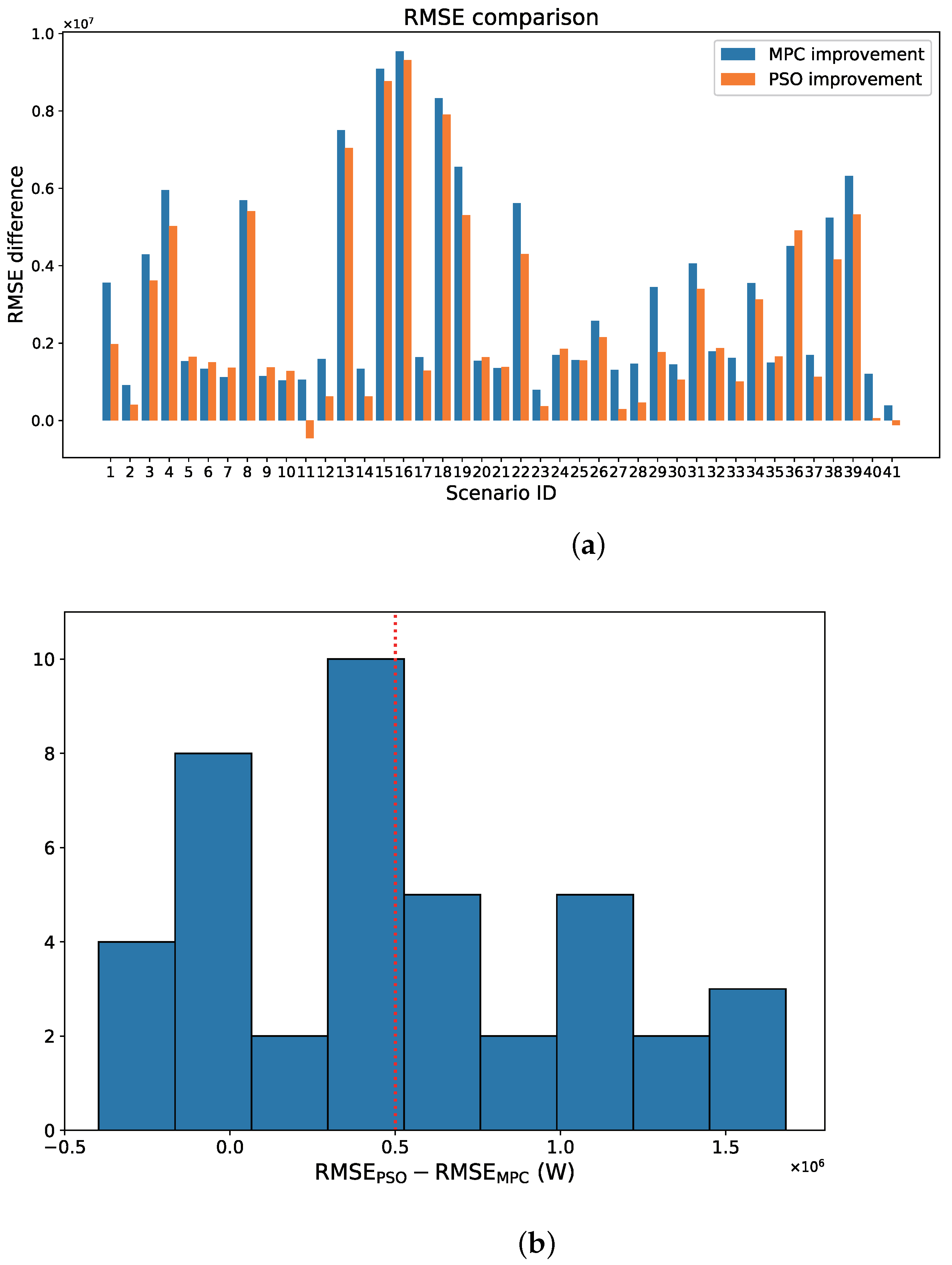
3.4. Real World Performance Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SPT | Solar Power Tower |
| MCRT | Monte Carlo Ray Tracing |
| AFD | Allowable Flux Density |
| MPC | Model Predictive Control |
| RMSE | Root Mean Square Error |
| CSP | Concentrated Solar Power |
| HTF | Heat Transfer Fluid |
| PSO | Particle Swarm Optimization |
References
- McGlade, C.; Ekins, P. The geographical distribution of fossil fuels unused when limiting global warming to 2 C. Nature 2015, 517, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.L.; Baeyens, J.; Degrève, J.; Cacères, G. Concentrated solar power plants: Review and design methodology. Renew. Sustain. Energy Rev. 2013, 22, 466–481. [Google Scholar] [CrossRef]
- Wang, L.; Gueymard, C.A.; Bilal, M.; Lin, A.; Wei, J.; Zhang, M.; Yang, X.; Qin, W. Constructing a gridded direct normal irradiance dataset in China during 1981–2014. Renew. Sustain. Energy Rev. 2020, 131, 110004. [Google Scholar]
- Reddy, V.S.; Kaushik, S.C.; Ranjan, K.R.; Tyagi, S.K. State-of-the-art of solar thermal power plants—A review. Renew. Sustain. Energy Rev. 2013, 27, 258–273. [Google Scholar] [CrossRef]
- Li, Y.; Liao, S.; Rao, Z.; Liu, G. A dynamic assessment based feasibility study of concentrating solar power in China. Renew. Energy 2014, 69, 34–42. [Google Scholar] [CrossRef]
- Behar, O.; Khellaf, A.; Mohammedi, K. A review of studies on central receiver solar thermal power plants. Renew. Sustain. Energy Rev. 2013, 23, 12–39. [Google Scholar] [CrossRef]
- Crespi, F.; Toscani, A.; Zani, P.; Sánchez, D.; Manzolini, G. Effect of passing clouds on the dynamic performance of a CSP tower receiver with molten salt heat storage. Appl. Energy 2018, 229, 224–235. [Google Scholar] [CrossRef]
- Li, L.; Coventry, J.; Bader, R.; Pye, J.; Lipiński, W. Optics of solar central receiver systems: A review. Opt. Express 2016, 24, A985. [Google Scholar] [CrossRef]
- Blanc, P.; Espinar, B.; Geuder, N.; Gueymard, C.; Meyer, R.; Pitz-Paal, R.; Reinhardt, B.; Renné, D.; Sengupta, M.; Wald, L.; et al. Direct normal irradiance related definitions and applications: The circumsolar issue. Sol. Energy 2014, 110, 561–577. [Google Scholar] [CrossRef]
- Bone, V.; Pidgeon, J.; Kearney, M.; Veeraragavan, A. Intra-hour direct normal irradiance forecasting through adaptive clear-sky modelling and cloud tracking. Sol. Energy 2018, 159, 852–867. [Google Scholar] [CrossRef]
- Prasad, A.A.; Taylor, R.A.; Kay, M. Assessment of direct normal irradiance and cloud connections using satellite data over Australia. Appl. Energy 2015, 143, 301–311. [Google Scholar] [CrossRef]
- Binotti, M.; De Giorgi, P.; Sanchez, D.; Manzolini, G. Comparison of different strategies for heliostats aiming point in cavity and external tower receivers. J. Sol. Energy Eng. 2016, 138, 021008. [Google Scholar] [CrossRef]
- Collado, F.J.; Guallar, J. A two-parameter aiming strategy to reduce and flatten the flux map in solar power tower plants. Sol. Energy 2019, 188, 185–189. [Google Scholar] [CrossRef]
- Kuhnke, S.; Richter, P.; Kepp, F.; Cumpston, J.; Koster, A.M.; Büsing, C. Robust optimal aiming strategies in central receiver systems. Renew. Energy 2020, 152, 198–207. [Google Scholar] [CrossRef]
- García-Martín, F.J.; Berenguel, M.; Valverde, A.; Camacho, E.F. Heuristic knowledge-based heliostat field control for the optimization of the temperature distribution in a volumetric receiver. Sol. Energy 1999, 66, 355–369. [Google Scholar] [CrossRef]
- Salomé, A.; Chhel, F.; Flamant, G.; Ferrière, A.; Thiery, F. Control of the flux distribution on a solar tower receiver using an optimized aiming point strategy: Application to THEMIS solar tower. Sol. Energy 2013, 94, 352–366. [Google Scholar] [CrossRef]
- Cruz, N.C.; Álvarez, J.D.; Redondo, J.L.; Berenguel, M.; Ortigosa, P.M.; Klempous, R. Control and optimal management of a heliostat field for solar power tower systems. In Proceedings of the 2019 IEEE 23rd International Conference on Intelligent Engineering Systems (INES), Godollo, Hungary, 25–27 April 2019; pp. 271–274. [Google Scholar]
- García, J.; Barraza, R.; Too, Y.C.S.; Padilla, R.V.; Acosta, D.; Estay, D.; Valdivia, P. Aiming clusters of heliostats over solar receivers for distributing heat flux using one variable per group. Renew. Energy 2020, 160, 584–596. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhao, Y. An Optimal Scheduling of the Heliostat Field in a Solar Tower Power Plant. In Computer Aided Chemical Engineering; Kravanja, Z., Bogataj, M., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 38, pp. 1021–1026. [Google Scholar]
- Fernandez, N.; Street, A.; Montenon, A.; Maussion, P. A scheduling optimization model for sun tracking of an autonomous heliostat. In Proceedings of the 2013 IEEE Grenoble Conference PowerTech, POWERTECH 2013, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- García, J.; Too, Y.C.S.; Padilla, R.V.; Beath, A.; Kim, J.S.; Sanjuan, M.E. Dynamic performance of an aiming control methodology for solar central receivers due to cloud disturbances. Renew. Energy 2018, 121, 355–367. [Google Scholar] [CrossRef]
- Too, Y.C.S.; García, J.; Padilla, R.V.; Kim, J.S.; Sanjuan, M. A transient optical-thermal model with dynamic matrix controller for solar central receivers. Appl. Therm. Eng. 2019, 154, 686–698. [Google Scholar] [CrossRef]
- Ashley, T.; Carrizosa, E.; Fernández-Cara, E. Optimisation of aiming strategies in Solar Power Tower plants. Energy 2017, 137, 285–291. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Pula, R.A. Methods of photovoltaic fault detection and classification: A review. Energy Rep. 2022, 8, 5898–5929. [Google Scholar] [CrossRef]
- Dhanraj, J.A.; Mostafaeipour, A.; Velmurugan, K.; Techato, K.; Chaurasiya, P.K.; Solomon, J.M.; Gopalan, A.; Phoungthong, K. An effective evaluation on fault detection in solar panels. Energies 2021, 14, 7770. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Determination of maximum solar power under shading and converter faults—A prerequisite for failure-tolerant power management systems. Simul. Model. Pract. Theory 2016, 62, 14–30. [Google Scholar] [CrossRef]
- Speetzen, N.; Richter, P. Dynamic aiming strategy for central receiver systems. Renew. Energy 2021, 180, 55–67. [Google Scholar] [CrossRef]
- Ni, D.; Sun, Y. A Deep Learning Based Forecast Method For Regional Cloud Map; Patent pending; Zhejiang University: Hangzhou, China, 2021. [Google Scholar]
- Sánchez-González, A.; Rodríguez-Sánchez, M.R.; Santana, D. Aiming strategy model based on allowable flux densities for molten salt central receivers. Sol. Energy 2017, 157, 1130–1144. [Google Scholar] [CrossRef]
- Collado, F.J.; Guallar, J. Fast and reliable flux map on cylindrical receivers. Sol. Energy 2018, 169, 556–564. [Google Scholar] [CrossRef]
- Richalet, J.; Rault, A.; Testud, J.L.; Papon, J. Model algorithmic control of industrial processes. Ifac Proc. Vol. 1977, 10, 103–120. [Google Scholar] [CrossRef]
- Rawlings, J.B. Tutorial overview of model predictive control. IEEE Control Syst. Mag. 2000, 20, 38–52. [Google Scholar]
- Fernandez-Camacho, E.; Bordons-Alba, C. Model Predictive Control in the Process Industry; Springer: London, UK, 1995. [Google Scholar]
- Solar Plant Simulation Tool. Available online: https://www.meso-star.com/projects/solstice/solstice.html (accessed on 21 March 2023).
- Caliot, C.; Benoit, H.; Guillot, E.; Sans, J.L.; Ferriere, A.; Flamant, G.; Coustet, C.; Piaud, B. Validation of a Monte Carlo integral formulation applied to solar facility simulations and use of sensitivities. J. Sol. Energy Eng. Trans. Asme 2015, 137, 2. [Google Scholar] [CrossRef]
- Delatorre, J.; Baud, G.; Bézian, J.J.; Blanco, S.; Caliot, C.; Cornet, J.F.; Coustet, C.; Dauchet, J.; El Hafi, M.; Eymet, V.; et al. Monte Carlo advances and concentrated solar applications. Sol. Energy 2014, 103, 653–681. [Google Scholar] [CrossRef]
- Zeng, Z.; Ni, D.; Xiao, G. Real-time heliostat field aiming strategy optimization based on reinforcement learning. Appl. Energy 2022, 307, 118224. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-international conference on neural networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95 Sixth International Symposium on Micro Machine and Human Science, Aichi, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle swarm optimization method for constrained optimization problems. Intell.-Technol. -Theory Appl. New Trends Intell. Technol. 2002, 76, 214–220. [Google Scholar]
- Collado, F.J.; Guallar, J. Quick design of regular heliostat fields for commercial solar tower power plants. Energy 2019, 178, 115–125. [Google Scholar] [CrossRef]
- Relloso, S.; Gutiérrez, Y. SENER molten salt tower technology. Ouarzazate NOOR III case. In Proceedings of the AIP Conference Proceedings, Antalya, Turkey, 12–15 May 2017; AIP Publishing LLC: Melville, NY, USA, 2017; Volume 1850, p. 30041. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Ni, D. A Model Predictive Control Approach for Heliostat Field Power Regulatory Aiming Strategy under Varying Cloud Shadowing Conditions. Energies 2023, 16, 2997. https://doi.org/10.3390/en16072997
Zhu R, Ni D. A Model Predictive Control Approach for Heliostat Field Power Regulatory Aiming Strategy under Varying Cloud Shadowing Conditions. Energies. 2023; 16(7):2997. https://doi.org/10.3390/en16072997
Chicago/Turabian StyleZhu, Ruidi, and Dong Ni. 2023. "A Model Predictive Control Approach for Heliostat Field Power Regulatory Aiming Strategy under Varying Cloud Shadowing Conditions" Energies 16, no. 7: 2997. https://doi.org/10.3390/en16072997
APA StyleZhu, R., & Ni, D. (2023). A Model Predictive Control Approach for Heliostat Field Power Regulatory Aiming Strategy under Varying Cloud Shadowing Conditions. Energies, 16(7), 2997. https://doi.org/10.3390/en16072997






