A Triple Boost Seven-Level Common Ground Transformerless Inverter Topology for Grid-Connected Photovoltaic Applications
Abstract
:1. Introduction
- (i).
- Single-phase single-stage 7L CG-type inverter that can diminish the leakage current.
- (ii).
- The voltage gain is 3.
- (iii).
- The voltage stress of capacitors is even, i.e., equal to the input voltage, Vin.
- (iv).
- The MBV is equal to 2/3 of the output voltage.
- (v).
- Capacitors are self-balanced.
- (vi).
- The proposed topology is capable of reactive power support.
2. Proposed 7LCG-TL Inverter
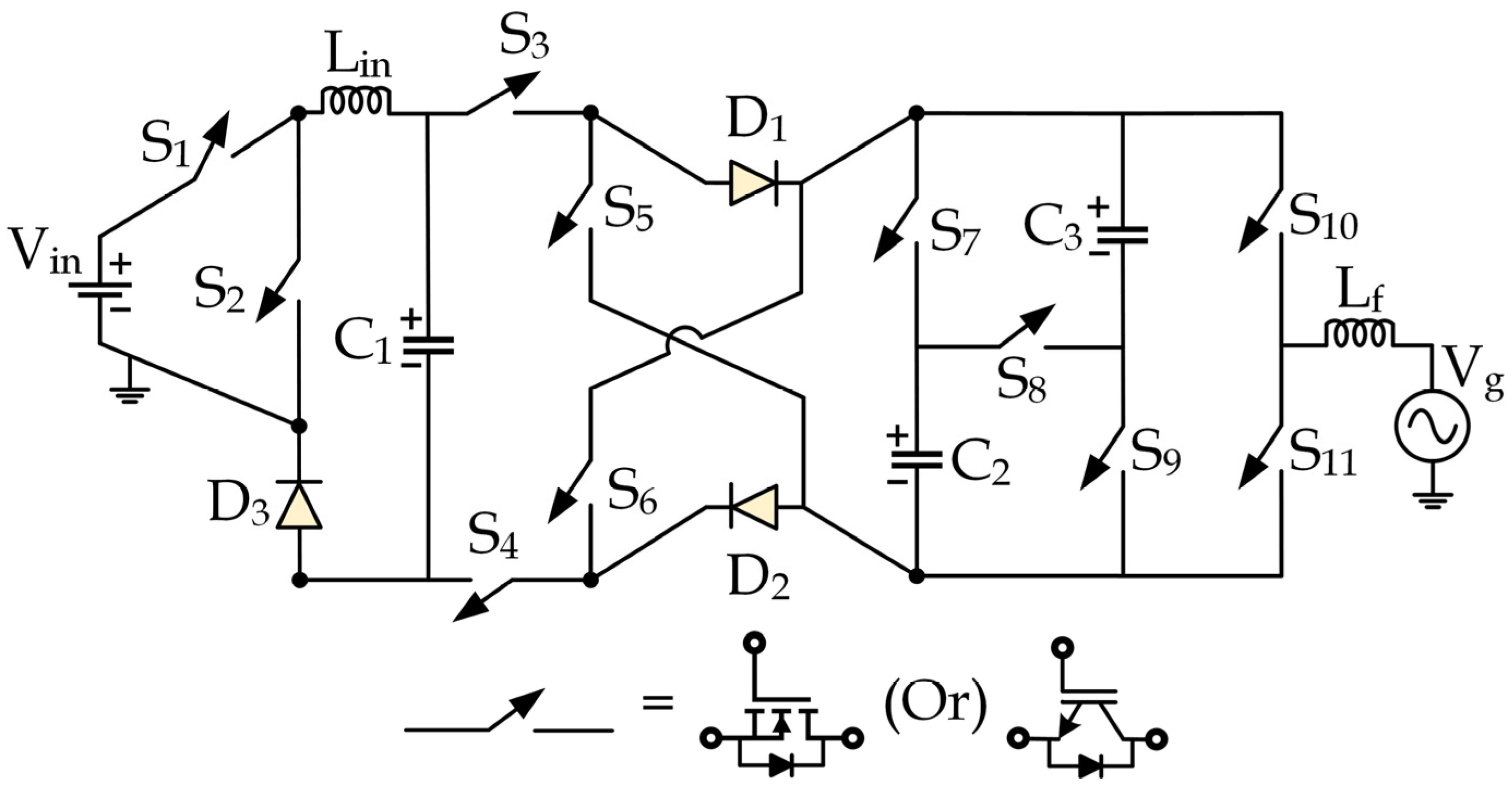
2.1. Description of 7LCG-TL Inverter
2.2. Description of Modes of Operation
2.2.1. Maximum Positive Output Voltage Level (+3Vin)
2.2.2. Second Positive Output Voltage Level (+2Vin)
2.2.3. First Positive Output Voltage Level (+Vin)
2.2.4. Zero Output Voltage Level (0)
2.2.5. First Negative Output Voltage Level (−Vin)
2.2.6. Second Negative Output Voltage Level (−2Vin)
2.2.7. Maximum Negative Output Voltage Level (−3Vin)
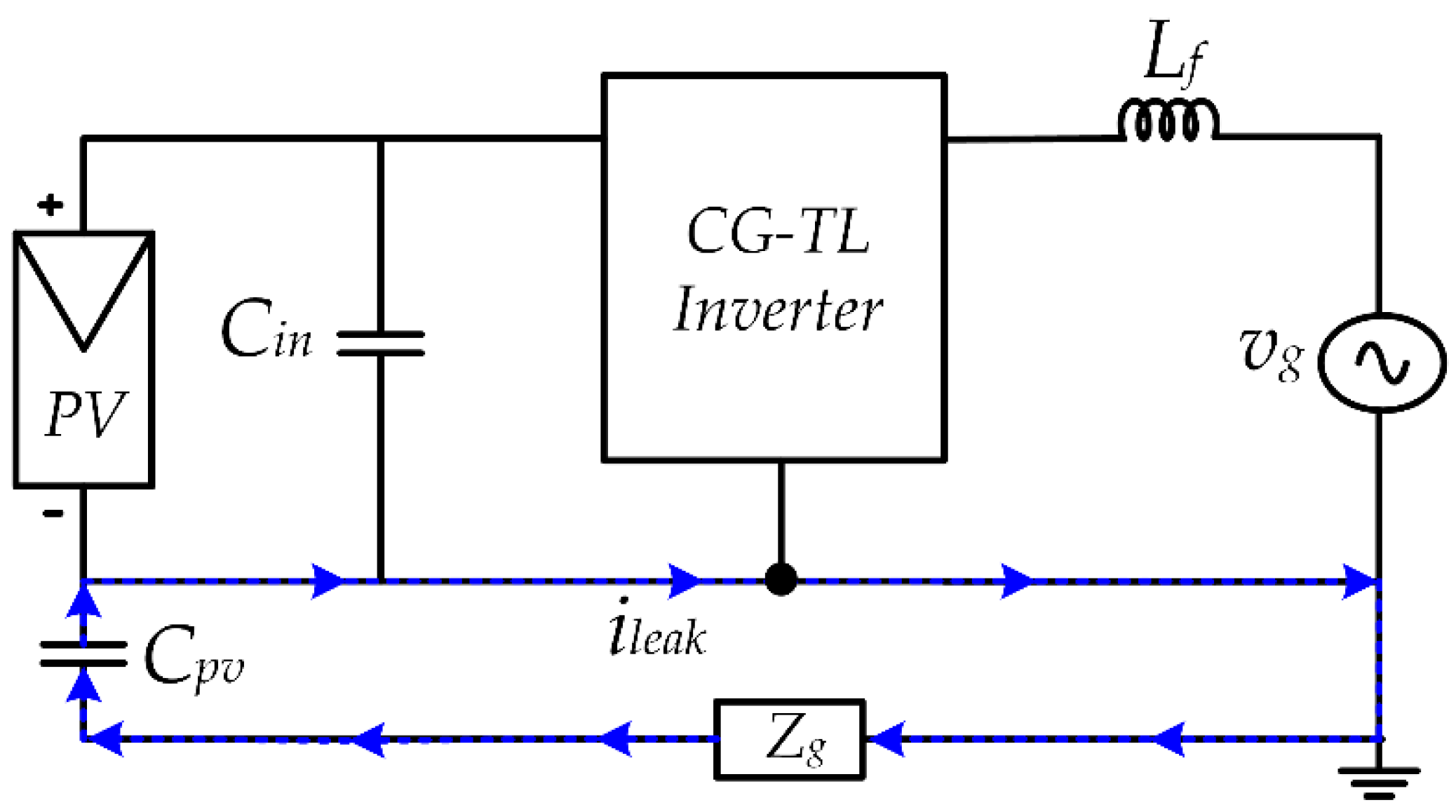
2.3. Common Mode Analysis
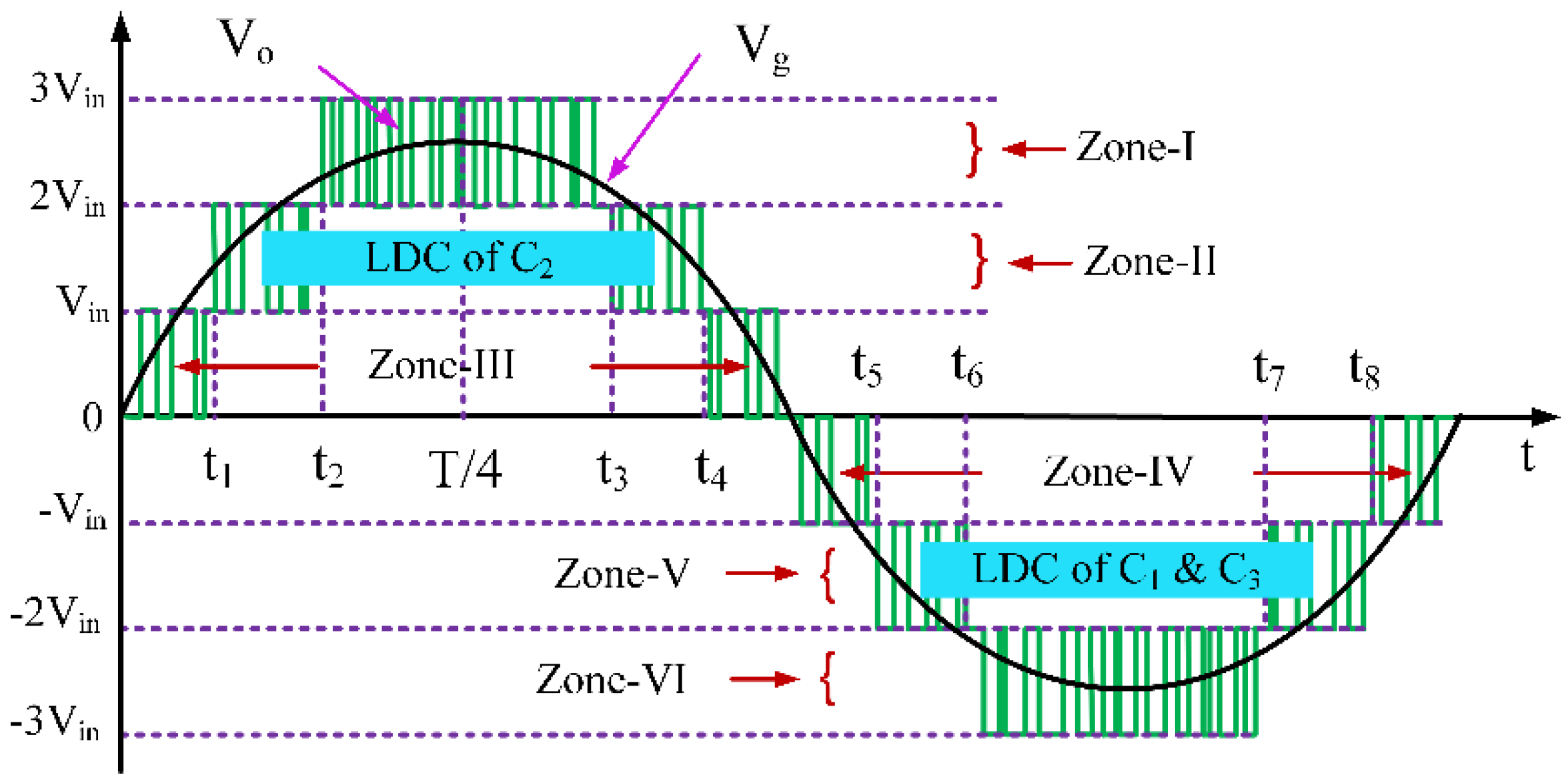
3. Calculation of Duty Cycle of Switches
3.1. Zone-I
3.2. Zone-II
3.3. Zone-III
4. Design of Passive Elements
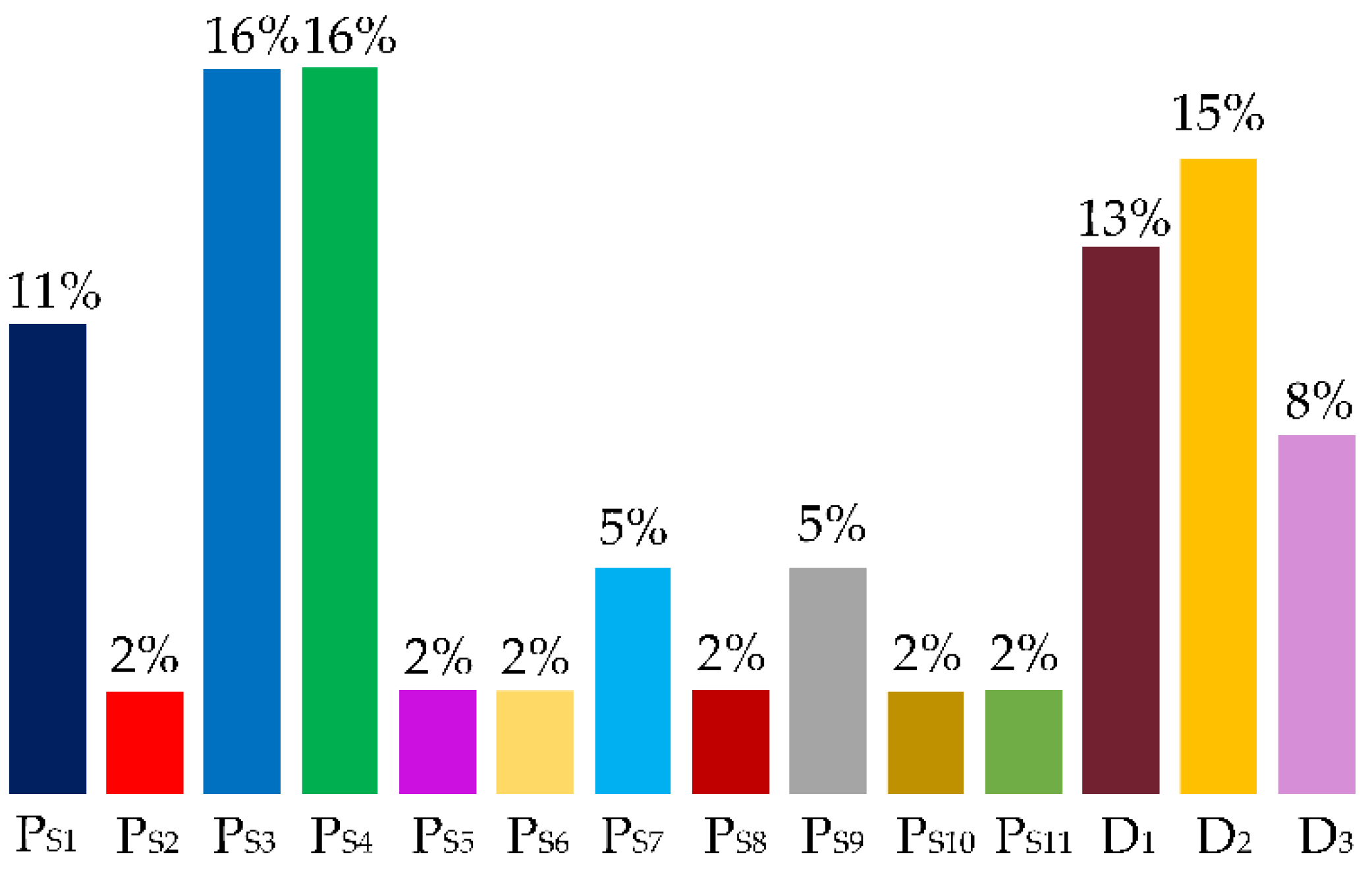
5. Power Loss Analysis
5.1. During the Time Interval
5.2. During the Time Interval
5.3. During the Time Interval
6. Result and Discussion
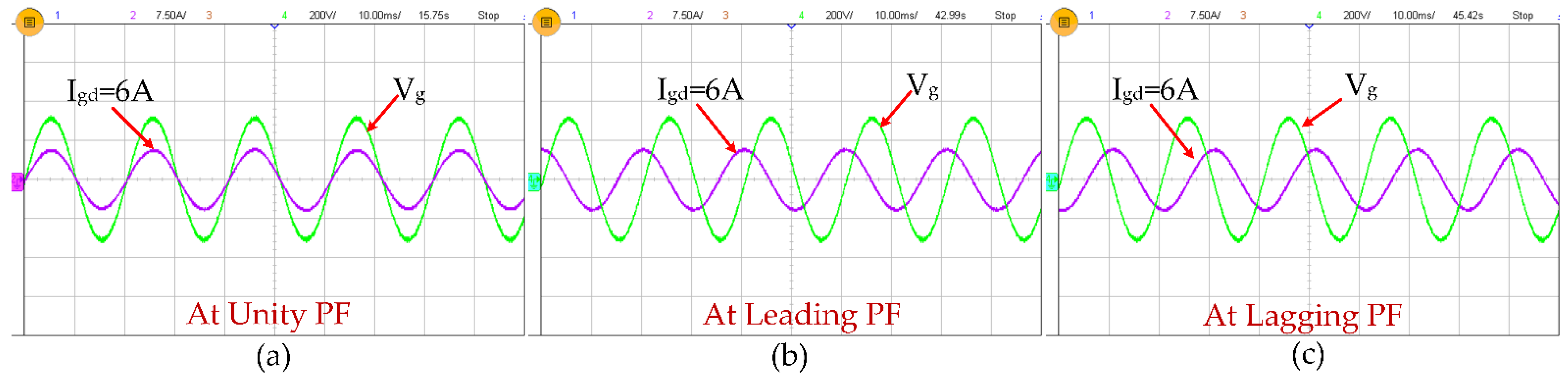
6.1. Simulation Results
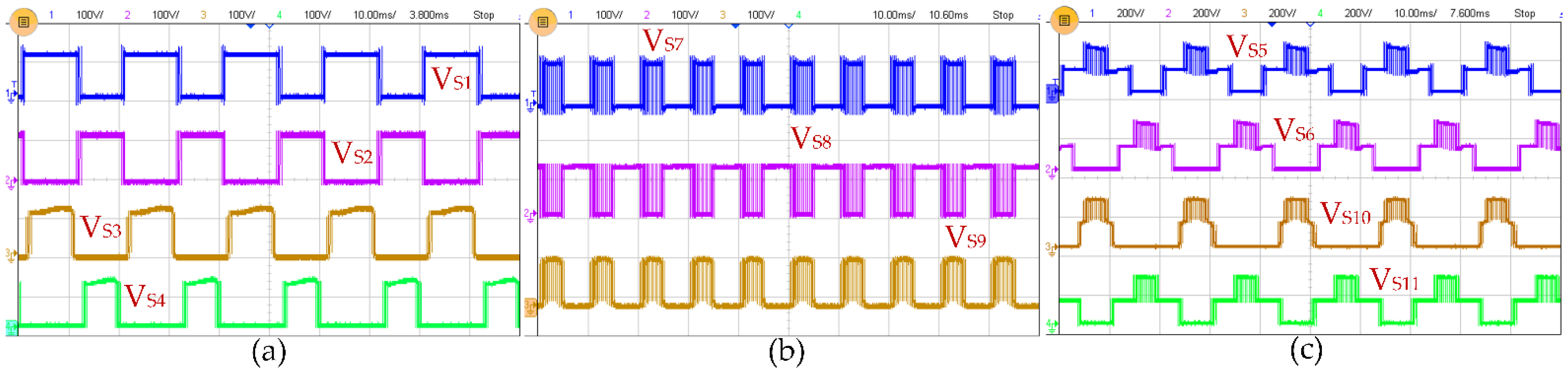
6.2. Experimental Results
7. Comparative Study
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CG | Common Ground | is (1,2,3…11) | Current stress of switches S1,2,3…11 |
| GC-PV | Grid-connected photo voltaic system | d1, d2, and d3 | Duty cycle for the operation Zones I, II and III |
| SC | Switched Capacitor | Maximum value of the inverter output voltage | |
| 7LCG-TL | Seven-Level Common Ground-Transformerless | Inductor current and capacitor voltage ripple | |
| C1, C2 and C3 | Capacitors | MBV | Maximum blocking voltage |
| VC1, VC2, VC3 | Voltage across capacitors C1, C2 and C3 | TSV | Total standing voltage |
| Vin, and Vo | Input and Output voltage | LDC | Longest discharge period |
| Grid voltage and current | Conduction and switching loss of switch S10 | ||
| Peak value of grid voltage and current | RMS value of the switch current | ||
| RMS value of grid current in Zone I, II and III | Power loss of switches S(1,1…11) | ||
| Capacitor charging current of C1, C2 and C3. | Filter inductor |
References
- Subramaniam, U.; Bhaskar, S.M.; Almakhles, D.J.; Padmanaban, S.; Leonowicz, Z. Investigations on EMI Mitigation Techniques: Intent to Reduce Grid-Tied PV Inverter Common Mode Current and Voltage. Energies 2019, 12, 3395. [Google Scholar] [CrossRef] [Green Version]
- Bayrak, G.; Ghaderi, D.; Subramaniam, U. Leakage current repression and real-time spectrum analysis with chirp Z-transform for a novel high-efficiency PV-based inverter applicable in micro-grids. Electr. Eng. 2020, 102, 2041–2057. [Google Scholar] [CrossRef]
- Sunddararaj, S.P.; Rangarajan, S.S.; Nallusamy, S.; Subramaniam, U.; Collins, E.R.; Senjyu, T. Design of Novel HG-SIQBC-Fed Multilevel Inverter for Standalone Microgrid Applications. Appl. Sci. 2022, 12, 9347. [Google Scholar] [CrossRef]
- Ghoudelbourk, S.; Azar, A.T.; Dib, D.; Omeiri, A. Selectivee harmonic elimination strategy in the multilevel inverters for grid connected photovoltaic system. Int. J. Adv. Intell. Paradig. 2020, 15, 317–339. [Google Scholar] [CrossRef]
- Sandeep, N.; Sathik, M.J.; Yaragatti, U.R.; Krishnasamy, V.; Verma, A.K.; Pota, H.R. Common-Ground-Type Five-Level Transformerless Inverter Topology with Full DC-Bus Utilization. IEEE Trans. Ind. Appl. 2020, 56, 4071–4080. [Google Scholar] [CrossRef]
- Gubía, E.; Sanchis, P.; Ursúa, A.; López, J.; Marroyo, L. Ground currents in single-phase transformerless photovoltaic systems. Prog. Photovolt Res. Appl. 2007, 15, 629–650. [Google Scholar] [CrossRef]
- Duong, T.D.; Nguyen, M.K.; Tran, T.T.; Vo, D.V.; Lim, Y.C.; Choi, J.H. Topology Review of Three-Phase Two-Level Transformerless Photovoltaic Inverters for Common-Mode Voltage Reduction. Energies 2022, 15, 3106. [Google Scholar] [CrossRef]
- Vosoughi Kurdkandi, N.; Ghavipanjeh Marangalu, M.; Husev, O.; Aghaie, A.; Islam, M.R.; Siwakoti, Y.; Muttaqi, K.; Hosseini, S.H. A New Seven-Level Transformer-Less Grid-Tied Inverter with Leakage Current Limitation and Voltage Boosting Feature. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 4, 228–241. [Google Scholar] [CrossRef]
- Kibria, M.F.; Elsanabary, A.; Tey, K.S.; Mubin, M.; Mekhilef, S. A Comparative Review on Single Phase Transformerless Inverter Topologies for Grid-Connected Photovoltaic Systems. Energies 2023, 16, 1363. [Google Scholar] [CrossRef]
- Das, C.K.; Annamalai, K.; Tirumala, S.V. A Quasi Z-Source Based Five-Level PV Inverter with Leakage Current Reduction. IEEE Trans. Ind. Appl. 2021, 58, 400–412. [Google Scholar] [CrossRef]
- Mishra, S.; Adda, R.; Joshi, A. Inverse Watkins–Johnson Topology-Based Inverter. IEEE Trans. Power Electron. 2012, 27, 1066–1070. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Le, T.-V.; Park, S.-J.; Lim, Y.-C. A Class of Quasi-Switched Boost Inverters. IEEE Trans. Ind. Electron. 2015, 62, 1526–1536. [Google Scholar] [CrossRef]
- Barath, J.N.; Soundarrajan, A.; Stepenko, S.; Husev, O.; Vinnikov, D.; Nguyen, M.-K. Topological Review of Quasi-Switched Boost Inverters. Electronics 2021, 10, 1485. [Google Scholar] [CrossRef]
- Gaafar, M.A.; Orabi, M.; Ibrahim, A.; Kennel, R.; Abdelrahem, M. Common-Ground Photovoltaic Inverters for Leakage Current Mitigation: Comparative Review. Appl. Sci. 2021, 11, 11266. [Google Scholar] [CrossRef]
- Jahan, H.K.; Kurdkandi, N.V.; Abapour, M.; Zare, K.; Hosseini, S.H.; Yang, Y.; Blaabjerg, F. Common-Ground-Type Single-Source High Step-up Cascaded Multilevel Inverter for Transformerless PV Applications. Mathematics 2020, 8, 1716. [Google Scholar] [CrossRef]
- Siwakoti, Y.P.; Blaabjerg, F. Common-Ground-Type Transformerless Inverters for Single-Phase Solar Photovoltaic Systems. IEEE Trans. Ind. Electron. 2018, 65, 2100–2111. [Google Scholar] [CrossRef]
- Ardashir, J.F.; Sabahi, M.; Hosseini, S.H.; Blaabjerg, F.; Babaei, E.; Gharehpetian, G.B. A Single-Phase Transformerless Inverter with Charge Pump Circuit Concept for Grid-Tied PV Applications. IEEE Trans. Ind. Electron. 2017, 64, 5403–5415. [Google Scholar] [CrossRef]
- Grigoletto, F.B. Five-Level Transformerless Inverter for Single-Phase Solar Photovoltaic Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3411–3422. [Google Scholar] [CrossRef]
- Grigoletto, F.B. Multilevel Common-Ground Transformerless Inverter for Photovoltaic Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 831–842. [Google Scholar] [CrossRef]
- Kadam, A.; Shukla, A. A Multilevel Transformerless Inverter Employing Ground Connection Between PV Negative Terminal and Grid Neutral Point. IEEE Trans. Ind. Electron. 2017, 64, 8897–8907. [Google Scholar] [CrossRef]
- Pandurengan, G.N.; Krishnasamy, V.; Mohamed, J.S.; Almakhles, D.; Engineering, E.; Nadu, T.; Arabia, S.; Nadu, T.; Arabia, S. Five-Level Transformerless Common Ground Type Inverter with Reduced Device Count. Inf. MIDEM-J. Microelectron. Electron. Compon. Mater. 2022, 51, 71–82. [Google Scholar] [CrossRef]
- Vosoughi, N.; Hosseini, S.H.; Sabahi, M. A New Transformer-Less Five-Level Grid-Tied Inverter for Photovoltaic Applications. IEEE Trans. Energy Convers. 2020, 35, 106–118. [Google Scholar] [CrossRef]
- Anand, V.; Singh, V.; Ali, J.S.M. Dual Boost Five-Level Switched-Capacitor Inverter with Common Ground. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 556–560. [Google Scholar] [CrossRef]
- Kumari, S.; Verma, A.; Sandeep, N.; Yaragatti, U.; Pota, H. A Five-Level Transformer-Less Inverter with Self-Voltage Balancing and Boosting Ability. IEEE Trans. Ind. Appl. 2021, 57, 6237–6245. [Google Scholar] [CrossRef]
- Kumari, S.; Verma, A.K.; Sandeep, N.; Yaragatti, U.R.; Pota, H.R. Multilevel common-ground inverter with voltage boosting for PV applications. IET Power Electron. 2021, 14, 901–911. [Google Scholar] [CrossRef]
- Kumari, S.; Sandeep, N.; Verma, A.; Yaragatti, U.R.; Pota, H. Design and Implementation of Transformer-Less Common-Ground Inverter With Reduced Components. IEEE Trans. Ind. Appl. 2022, 9994, 1–10. [Google Scholar] [CrossRef]
- Marangalu, M.G.; Hosseini, S.H.; Kurdkandi, N.V.; Khoshkbar-Sadigh, A. A New Five-Level Switched-Capacitor-Based Transformer-Less Common-Grounded Grid-Tied Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2022. [Google Scholar] [CrossRef]
- Sathik, M.J.; Almakhles, D.J. Common Ground Type Five Level Inverter with Voltage Boosting for PV Applications. Sci. Rep. 2022, 12, 2–11. [Google Scholar] [CrossRef]
- Mohamed Ali, J.S.; Hota, A.; Sandeep, N.; Almakhles, D.J. A Single-Stage Common Ground-Type Transformerless Five-Level Inverter Topology. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 837–845. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Farhangi, M.; Aguilera, R.P.; Lee, S.S.; Blaabjerg, F.; Siwakoti, Y.P. Common-Ground Grid-Connected Five-Level Transformerless Inverter With Integrated Dynamic Voltage Boosting Feature. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6661–6672. [Google Scholar] [CrossRef]
- Almakhles, D.J.; Sathik, M.J. Single—Phase Transformerless Nine—Level Inverter with Voltage Boosting Ability for PV Fed AC Microgrid Applications. Sci. Rep. 2022, 12, 13442. [Google Scholar] [CrossRef]
- Gopinath, N.P.; Vijayakumar, K. Common Ground Nine-Level Boost Inverter for Grid-Connected PV Applications. Front. Energy Res. 2022, 10, 922786. [Google Scholar] [CrossRef]
- Chen, M.; Yang, Y.; Loh, P.C.; Blaabjerg, F. A Single-Source Nine-Level Boost Inverter with a Low Switch Count. IEEE Trans. Ind. Electron. 2022, 69, 2644–2658. [Google Scholar] [CrossRef]
- Kurdkandi, N.V.; Marangalu, M.G.; Mohammadsalehian, S.; Tarzamni, H.; Siwakoti, Y.P.; Islam, M.R.; Muttaqi, K.M. A New Six-Level Transformer-Less Grid-Connected Solar Photovoltaic Inverter with Less Leakage Current. IEEE Access 2022, 10, 63736–63753. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Li, J. A Single-Phase Step-Up Seven-Level Inverter with a Simple Implementation Method for Level-Shifted Modulation Schemes. IEEE Access 2019, 7, 146552–146565. [Google Scholar] [CrossRef]
- Shahsavar, T.H.; Babaei, E.; Sabahi, M.; khoshkbar-Sadigh, A. A New Boost Type Single Source Seven-Level Switched-Capacitor Based Inverter with Reduced Current Stress over the Components. Comput. Electr. Eng. 2022, 101, 108160. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, X.; Zeng, J. A Seven-Level Inverter With Self-Balancing and Low-Voltage Stress. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 685–696. [Google Scholar] [CrossRef]
- Lee, S.S.; Member, S.; Lee, K.; Member, S. Dual-T-Type Seven-Level Boost Active-Neutral-Point-Clamped Inverter. IEEE Trans. Power Electron. 2019, 34, 6031–6035. [Google Scholar] [CrossRef]
- Sathik, M.J.; Sandeep, N.; Blaabjerg, F. High Gain Active Neutral Point Clamped Seven-Level Self-Voltage Balancing Inverter. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2567–2571. [Google Scholar] [CrossRef]
- Kakar, S.; Arif, M.; Ayob, S.M.; Nordin, N.; Mekhilef, S.; Seyedmahmoudian, M.; Stojcevski, A. An Improved Seven-Level Switched-Capacitor-Based Neutral-Point Clamped Inverter. Front. Energy Res. 2022, 10, 1–10. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Y.; Zeng, J.; Liu, J. Low-Voltage Stress Seven-Level Inverter Based on Symmetrical Capacitors. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3033–3044. [Google Scholar] [CrossRef]
- Agarwal, R.; Gupta, K.K.; Singh, S. Switched capacitors-based single-phase seven-level photovoltaic inverter with self-voltage balancing. Electr. Eng. 2022, 104, 3107–3117. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, W.; Naderi Zarnaghi, Y.; Vosoughi Kurdkandi, N.; Zhang, C. A New Boost Switched Capacitor Seven-Level Grid-Tied Inverter. IET Power Electron. 2021, 14, 268–279. [Google Scholar] [CrossRef]
- He, L.; Sun, J.; Lin, Z.; Cheng, B. Capacitor-Voltage Self-Balance Seven-Level Inverter with Unequal Amplitude Carrier-Based APODPWM. IEEE Trans. Power Electron. 2021, 36, 14002–14013. [Google Scholar] [CrossRef]
- Chen, M. Novel Cascaded Seven-Level Inverter With Embedded Voltage Boosting for Renewable Energy Applications. CPSS Trans. Power Electron. Appl. 2022, 7, 58–70. [Google Scholar] [CrossRef]
- Roy, T.; Tesfay, M.W.; Nayak, B.; Panigrahi, C.K. A 7-Level Switched Capacitor Multilevel Inverter with Reduced Switches and Voltage Stresses. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3587–3591. [Google Scholar] [CrossRef]
- Grigoletto, F.B.; de Vilhena Moura, P.H.; Chaves, D.B.; Vilaverde, J.D.S. Step-Up Seven-Level Common-Ground Transformerless Inverter. In Proceedings of the 2021 14th IEEE International Conference on Industry Applications (INDUSCON), São Paulo, Brazil, 15–18 August 2021; pp. 716–722. [Google Scholar] [CrossRef]
- Barzegarkhoo, R.; Farhangi, M.; Lee, S.S.; Aguilera, R.P.; Siwakoti, Y.P. A Novel Seven-Level Switched-Boost Common-Ground Inverter with Single-Stage Dynamic Voltage Boosting Gain. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 873–877. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Mekhilef, S.; Shah, N.M.; Ali, J.S.M.; Blaabjerg, F. A New Switched Capacitor 7L Inverter with Triple Voltage Gain and Low Voltage Stress. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1294–1298. [Google Scholar] [CrossRef]


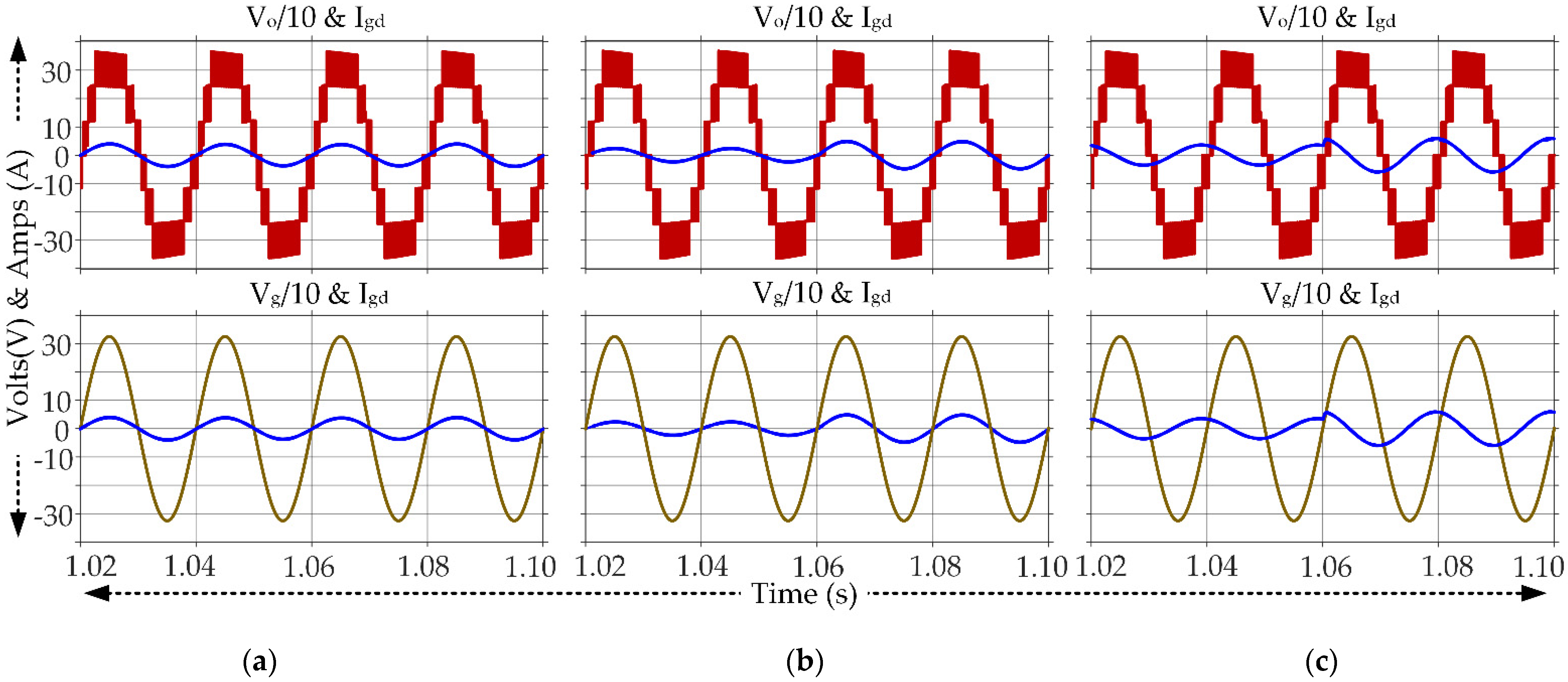

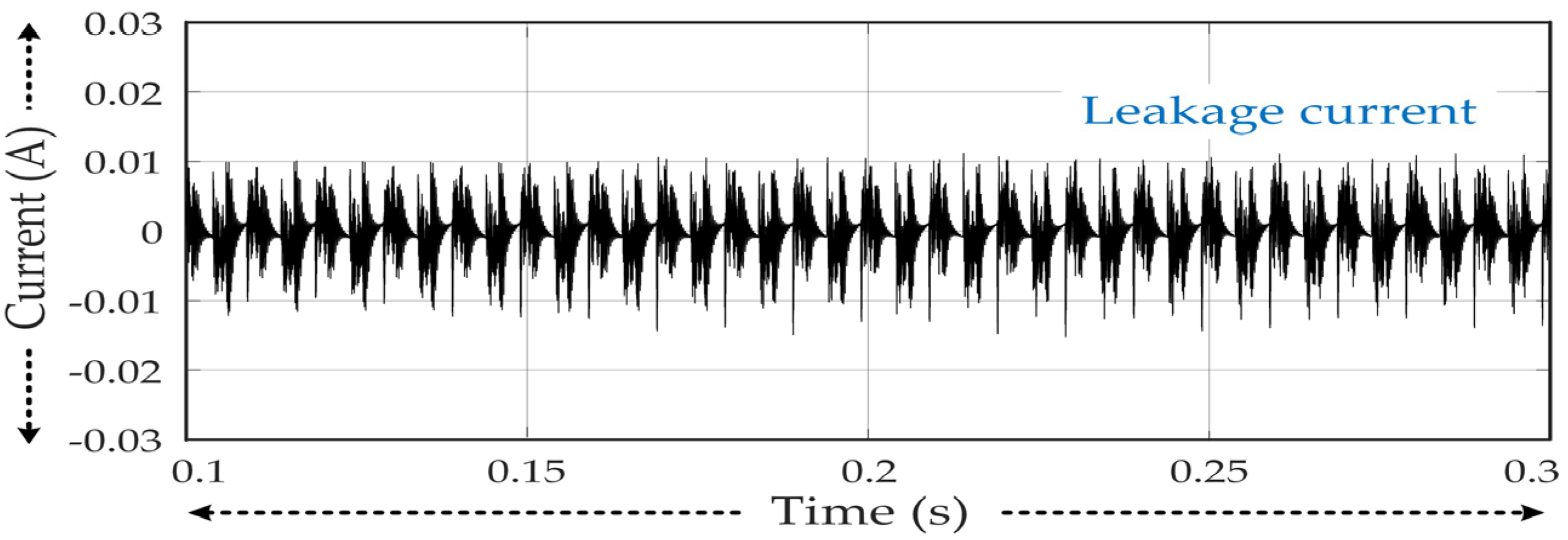
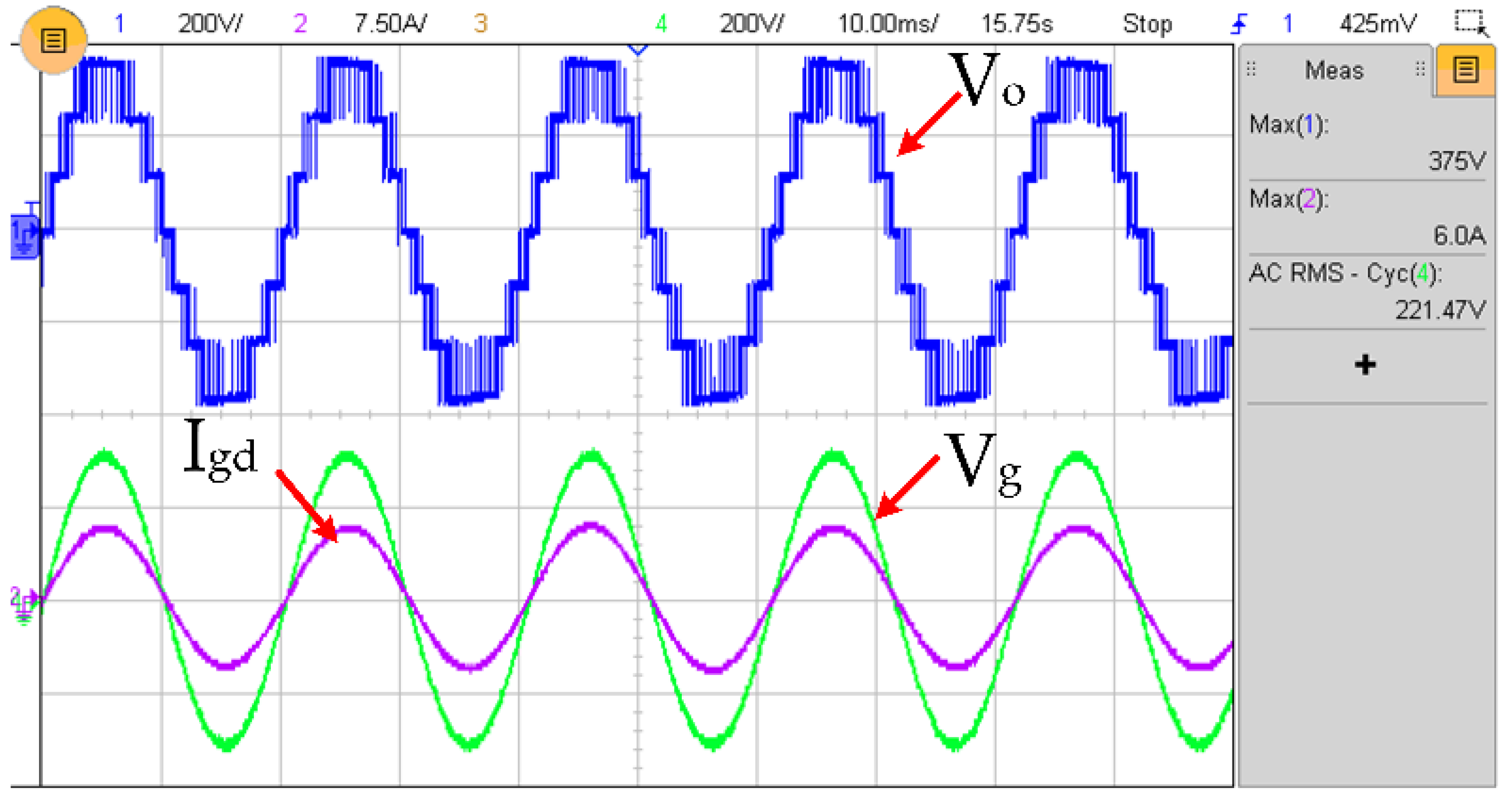
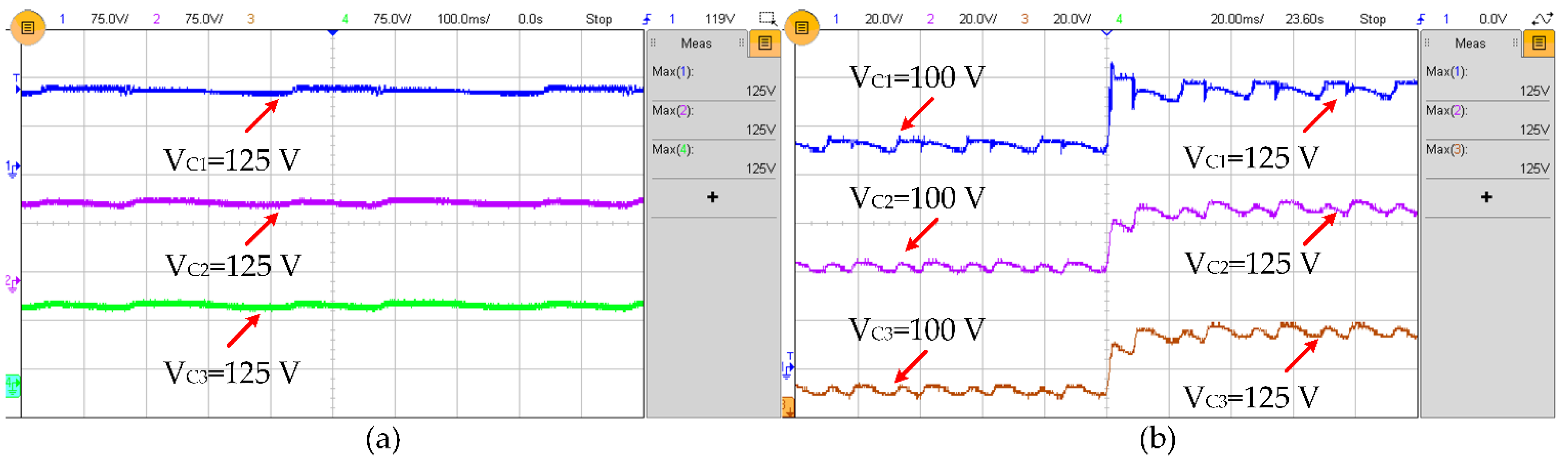



| Level | Status of Switches | Status of Capacitors | Output Voltage | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | C1 | C2 | C3 | ||
| +3 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | C | D | D | +3Vin |
| +2 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | C | D | - | +2Vin |
| +1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | C | C | C | +1Vin |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | C | C | C | 0 |
| −1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | C | D | - | −Vin |
| −2 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | D | - | D | −2Vin |
| −3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | D | D | D | −3Vin |
| Voltage Level | Voltage Stress of Switches | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | |
| +3 | 0 | 0 | 0 | 0 | 0 | ||||||
| +2 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| +1 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| −1 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| −2 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| −3 | 0 | 0 | 0 | 0 | 0 | ||||||
| Output Power (W) | PS1 | PS2 | PS3 | PS4 | PS5 | PS6 | PS7 | PS8 | PS9 | PS10 | PS11 | PD1 | PD2 | PD3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 545 | 1.300 | 0.280 | 1.785 | 1.794 | 0.193 | 0.229 | 0.601 | 0.249 | 0.599 | 0.300 | 0.194 | 1.565 | 1.883 | 1.027 |
| 625 | 1.881 | 0.380 | 2.724 | 2.727 | 0.274 | 0.315 | 0.895 | 0.352 | 0.895 | 0.393 | 0.274 | 2.484 | 2.944 | 1.460 |
| 780 | 2.669 | 0.558 | 4.026 | 3.996 | 0.382 | 0.447 | 1.281 | 0.484 | 1.281 | 0.585 | 0.379 | 3.170 | 3.689 | 2.054 |
| 935 | 3.728 | 0.815 | 5.754 | 5.662 | 0.530 | 0.635 | 1.795 | 0.663 | 1.792 | 0.870 | 0.522 | 4.340 | 5.045 | 2.850 |
| Device | Specification |
|---|---|
| IGBT switches | SKM75GB063D, 600 V/75 A |
| Capacitors C1, C2, and C3 | SAMWHA HK, 1000 uF/450 V |
| Diodes D1, D2, and D3 | RHRG3060-F085, 600 V/30 A |
| Inductor Lf | Ferrite core, 2.6 mH |
| Gate Driver | TLP250-IC |
| Digital Controller | TMS320F28379D |
| Input Voltage (Vin) | 125 V |
| Output Voltage (Vo) | 375 V |
| Output power (W) | 935 W |
| Grid Voltage | 220 V (RMS) |
| Switching Frequency | 20 kHz |
| Local Grid Frequency | 50 Hz |
| Topology | A | B | C | D | F | G | H | I | J | K | L | M | N (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [37] | 10 | 8 | 0 | 3 | Vin | 5.3 | 1:1.5 | 1 | 0.67 | No | Yes | No | NR |
| [38] | 10 | 8 | 0 | 4 | Vin | 7.3 | 1:1.5 | 2 | 1.33 | No | Yes | No | 97.4@1.3 kW |
| [39] | 10 | 9 | 0 | 3 | Vin | 6 | 1:1.5 | 1 | 0.67 | No | Yes | No | 96@1 kW, |
| [35] | 9 | 9 | 1 | 2 | Vin | 5.7 | 1:3 | 3 | 1 | Yes | Yes | No | 92.81@150 W |
| [36] | 10 | 9 | 1 | 1 | 2Vin | 7.33 | 1:3 | 3 | 1 | Yes | Yes | No | 96.68@210 W |
| [44] | 12 | 12 | 0 | 4 | Vin | 5.5 | 1:4 | 4 | 1 | No | Yes | No | 97.62@200 W |
| [40] | 12 | 11 | 4 | 4 | 0.5Vin | 8 | 1:1.5 | 2 | 1.33 | No | Yes | No | 97.5@1.3 kW |
| [45] | 12 | 10 | 4 | 4 | 2Vin | 7.3 | 1:3 | 4 | 1.33 | No | Yes | No | 94.9@500 W |
| [41] | 10 | 8 | 0 | 2 | 0.5Vin | 5.3 | 1:1.5 | 1 | 0.67 | No | Yes | No | 97.6@400 W |
| [42] | 9 | 9 | 0 | 4 | 0.5Vin | 5.3 | 1:1.5 | 1 | 0.67 | No | Yes | No | NR |
| [49] | 12 | 11 | 0 | 2 | Vin | 5.3 | 1:3 | 2 | 0.67 | No | Yes | No | 95@1 kW |
| [46] | 9 | 9 | 2 | 3 | Vin | 5.7 | 1:3 | 3 | 1 | No | Yes | No | 93.1@313 W |
| [43] | 10 | 8 | 0 | 4 | 0.5Vin | 5.7 | 1:1.5 | 1 | 0.67 | No | Yes | No | NR |
| [47] | 8 | 8 | 4 | 3 | 2Vin | 5.3 | 1:3 | 3 | 1 | No | No | Yes | NR |
| [48] | 10 | 10 | 0 | 3 | Vin | 6.8 | 1:2 | 2 | 1 | No | No | Yes | NR |
| Proposed | 11 | 11 | 3 | 3 | Vin | 5 | 1:3 | 2 | 0.67 | No | No | Yes | 96.5@935 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gopinath, N.P.; Vijayakumar, K.; Mohd Ali, J.S.; Raghupathi, K.; Selvam, S. A Triple Boost Seven-Level Common Ground Transformerless Inverter Topology for Grid-Connected Photovoltaic Applications. Energies 2023, 16, 3428. https://doi.org/10.3390/en16083428
Gopinath NP, Vijayakumar K, Mohd Ali JS, Raghupathi K, Selvam S. A Triple Boost Seven-Level Common Ground Transformerless Inverter Topology for Grid-Connected Photovoltaic Applications. Energies. 2023; 16(8):3428. https://doi.org/10.3390/en16083428
Chicago/Turabian StyleGopinath, Narayanan Pandurangan, Krishnasamy Vijayakumar, Jagabar Sathik Mohd Ali, Kumutha Raghupathi, and Sivakumar Selvam. 2023. "A Triple Boost Seven-Level Common Ground Transformerless Inverter Topology for Grid-Connected Photovoltaic Applications" Energies 16, no. 8: 3428. https://doi.org/10.3390/en16083428
APA StyleGopinath, N. P., Vijayakumar, K., Mohd Ali, J. S., Raghupathi, K., & Selvam, S. (2023). A Triple Boost Seven-Level Common Ground Transformerless Inverter Topology for Grid-Connected Photovoltaic Applications. Energies, 16(8), 3428. https://doi.org/10.3390/en16083428







