Modeling and Control of Modular Multilevel Matrix Converter for Low-Frequency AC Transmission
Abstract
:1. Introduction
- (1)
- The mathematical model of the M3C is derived based on the extended MMC topology and the multiple αβ0 and dq transformations. The dual-loop controllers are designed according to the derived mathematical model.
- (2)
- A reduced switching frequency SM voltage balancing method based on the NLC is proposed. According to state sorting and incremental switching, this optimized SM voltage balancing method can avoid unnecessary switching.
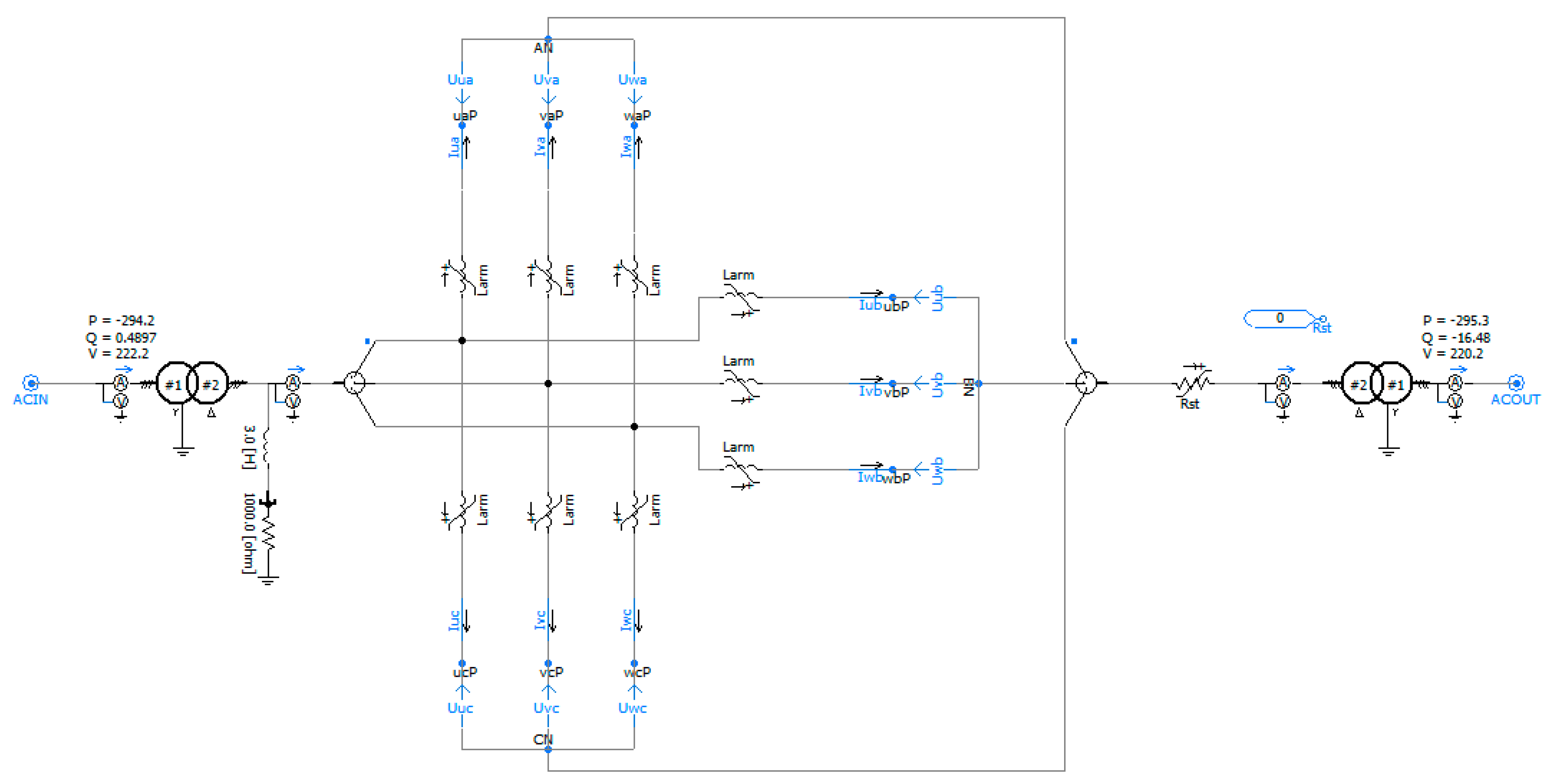
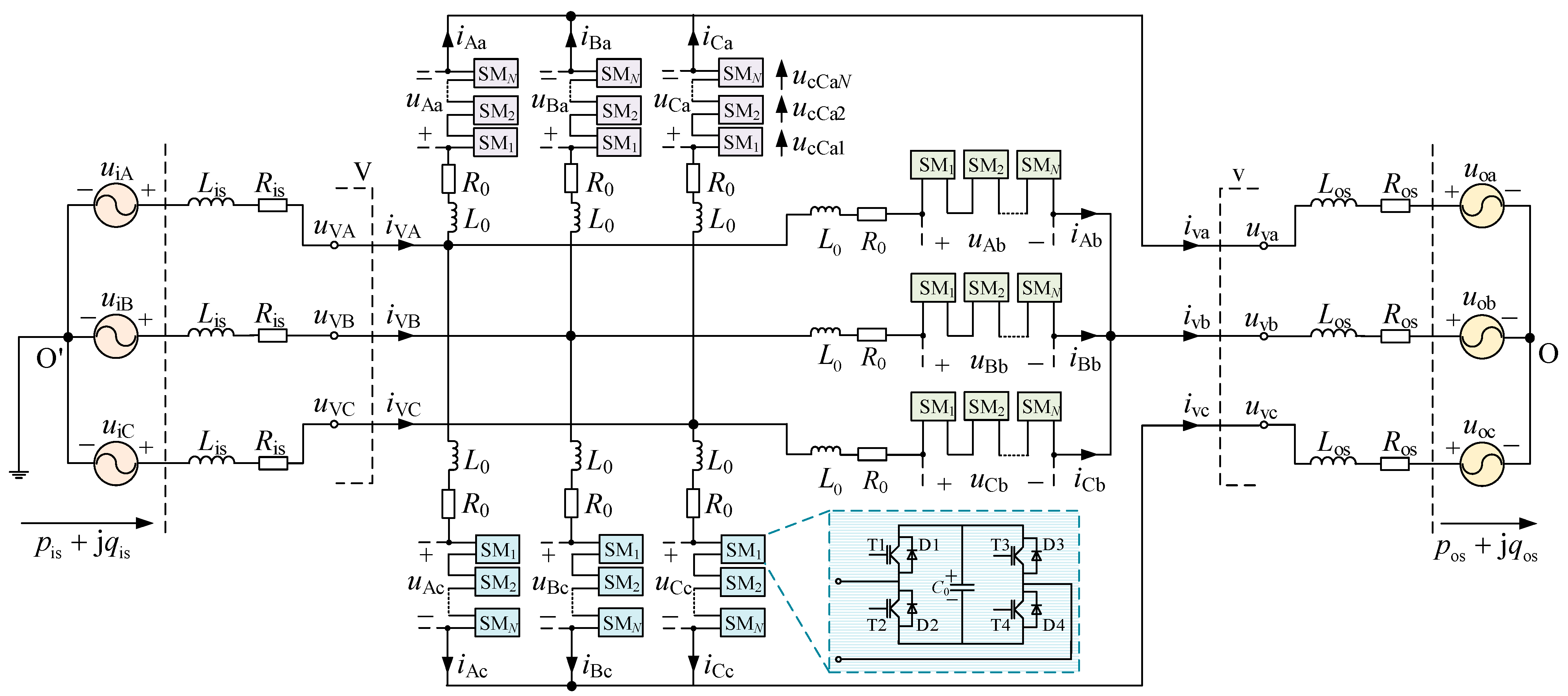
2. Basic Structure and Mathematical Model of M3C
3. Inner Loop Controller
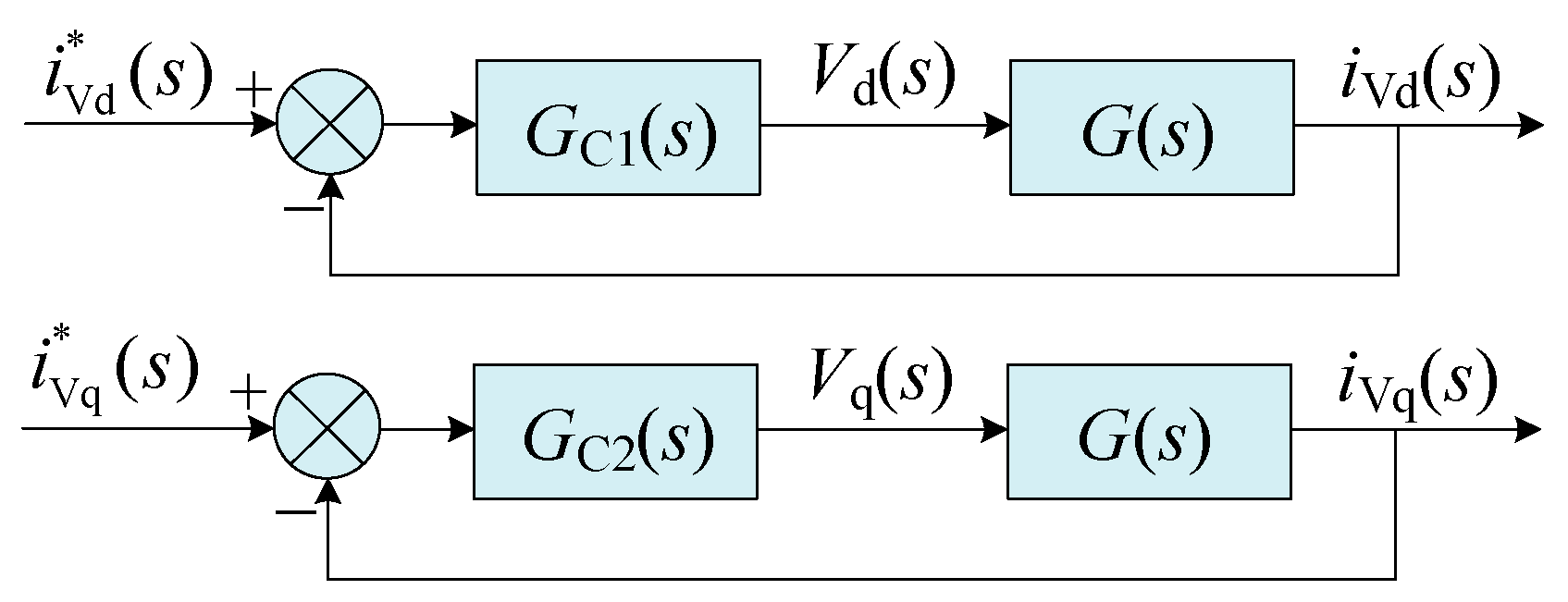
3.1. Current Tracking Controller
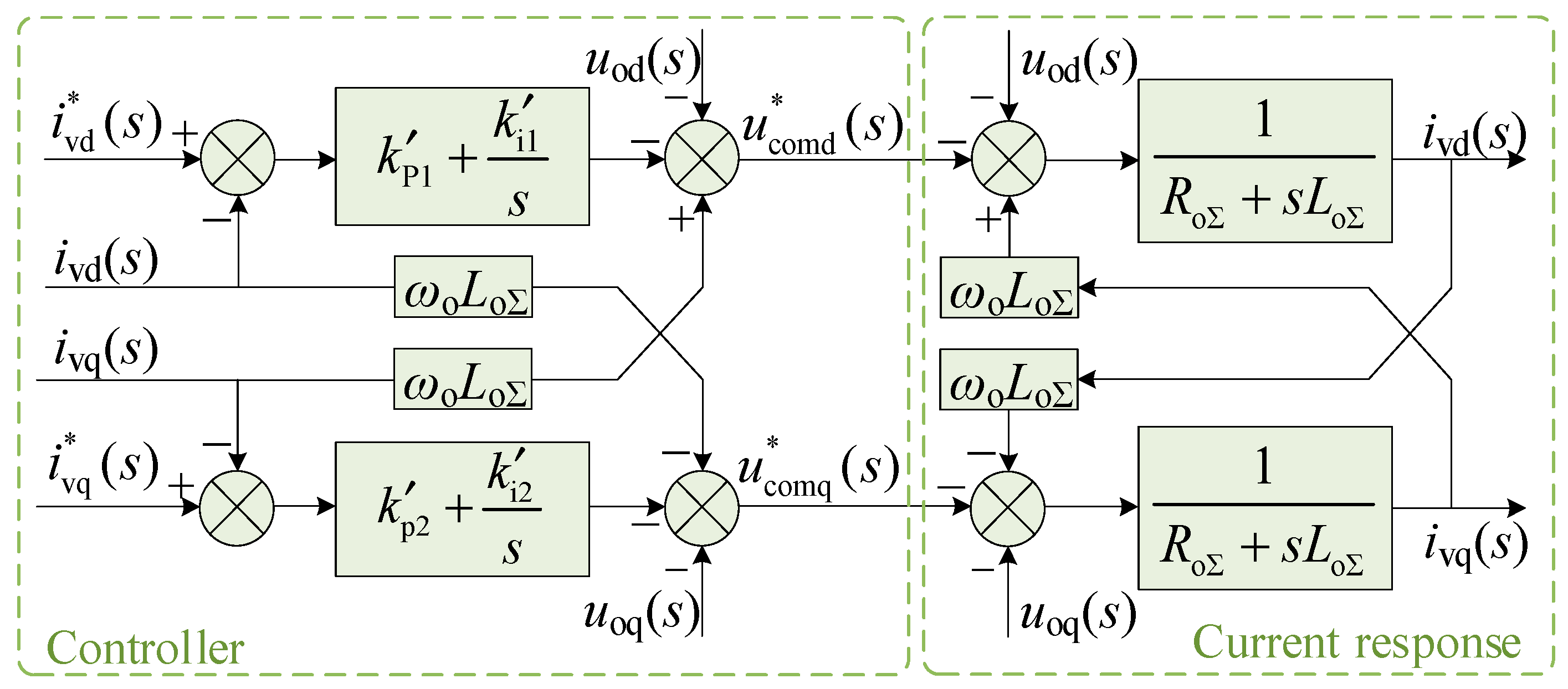
3.2. Circulating Current Suppressing Controller
3.3. Calculation of Arm Voltage References
4. SM Voltage Balancing Method
4.1. Operating Characteristics of FBSM
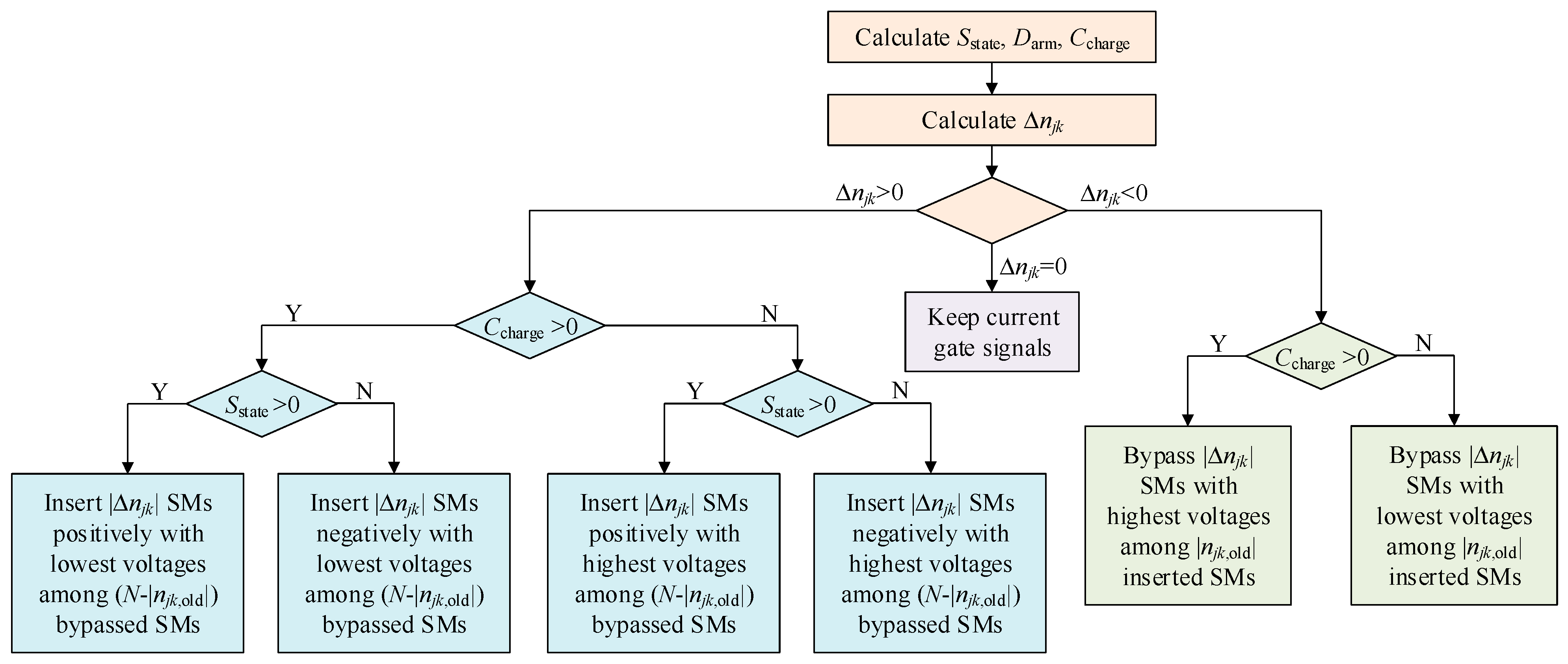
4.2. Switching Strategy of SM
- When the arm current charges the capacitors (Cchange = 1), njk SMs with the lowest capacitor voltages are inserted positively or negatively according to Sstate and the other SMs are bypassed.
- When the arm current discharges the capacitors (Cchange = −1), njk SMs with the highest capacitor voltages are inserted positively or negatively according to Sstate and the other SMs are bypassed.
- If Δnjk = 0, SMs in arm jk have no switching operation at the current control moment and directly wait for the next control moment.
- If Δnjk > 0, the number of the inserted SMs should be increased. Then, if Cchange = 1, Δnjk SMs with the lowest voltage are inserted; if Cchange = −1, Δnjk SMs with the highest voltage are inserted. Sstate determines whether the insertion is positive or negative.
- If Δnjk < 0, the number of the inserted SMs should be decreased. Then, if Cchange = 1, Δnjk SMs with the highest voltage are bypassed, and if Cchange = −1, Δnjk SMs with the lowest voltage are bypassed.
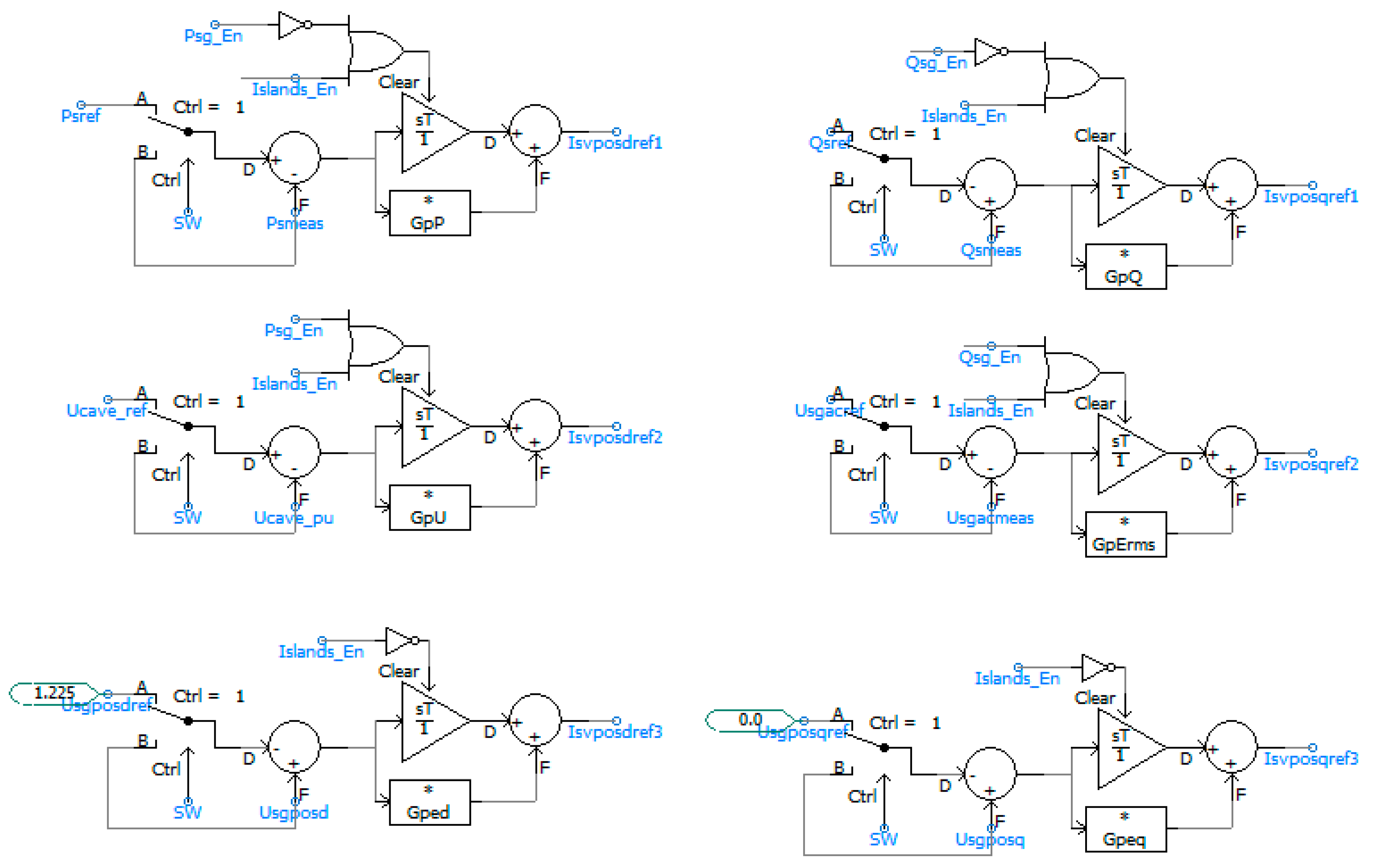
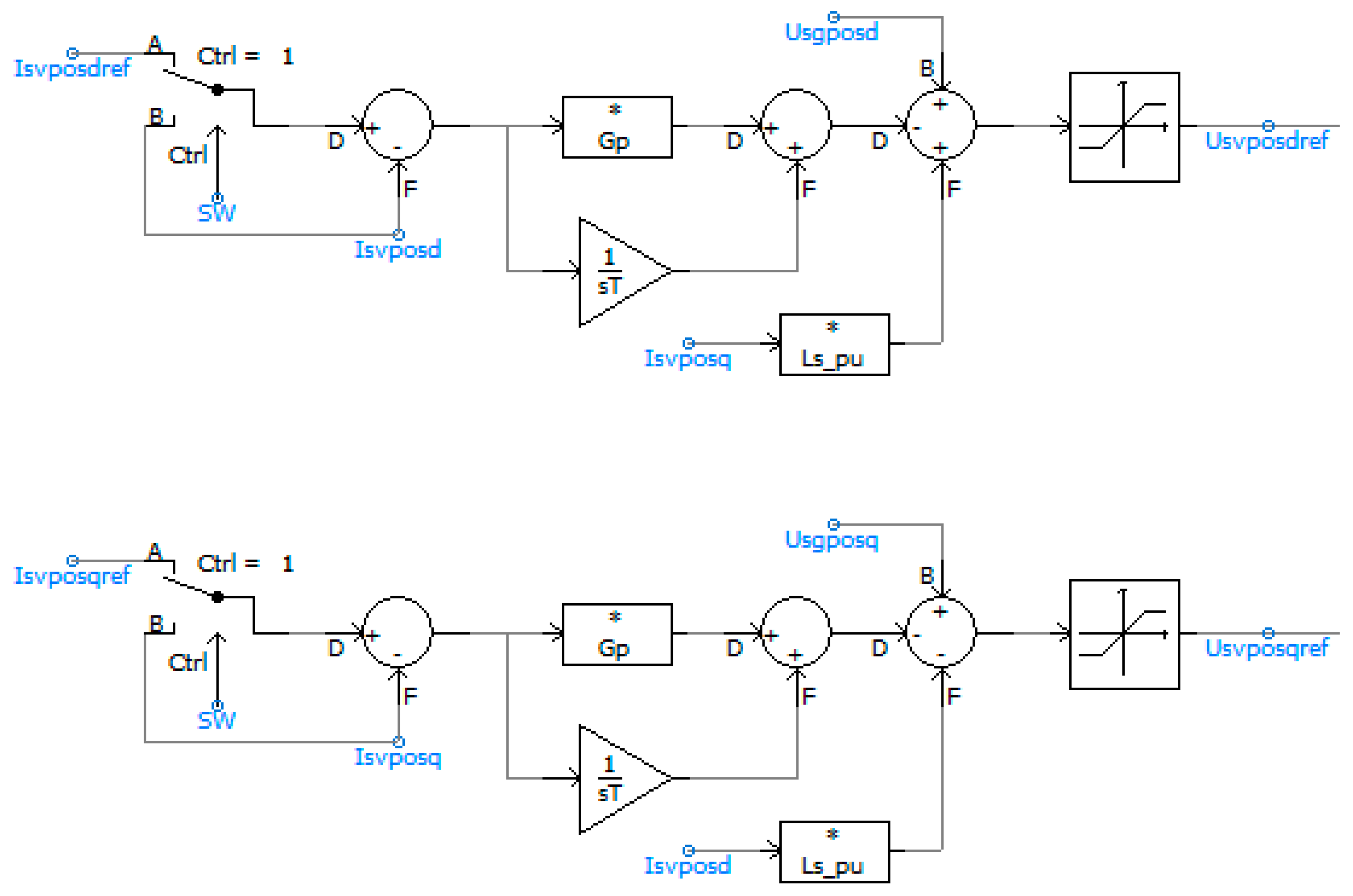
5. Outer Loop Controller
5.1. Outer Loop Controller on Input Side
- (1)
- PLL is no longer needed because the frequency of the offshore system is given, i.e., the electrical angle is completely determined and the rotating speed of the dq reference frame is fixed.
- (2)
- Define the space vector of the AC bus voltage on the input side as uis. The outer loop controller on the input side is used for keeping the amplitude of uis unchanged and keeping uis aligned with the d-axis. In other words, the constant amplitude of uis means that the voltage amplitude of the input side AC bus is constant; the alignment of uis with the d-axis means that the voltage frequency of the input side AC bus equals the rated frequency.
5.2. Outer Loop Controller on the Output Side
- (1)
- The reference of the active power control is the average capacitor voltage of all SMs Uc,ave*; from the perspective of energy balance, this side behaves as a power balance station.
- (2)
- Either the reactive power Qos* or the AC voltage amplitude Uom* on the output side is the reference of the reactive power control.
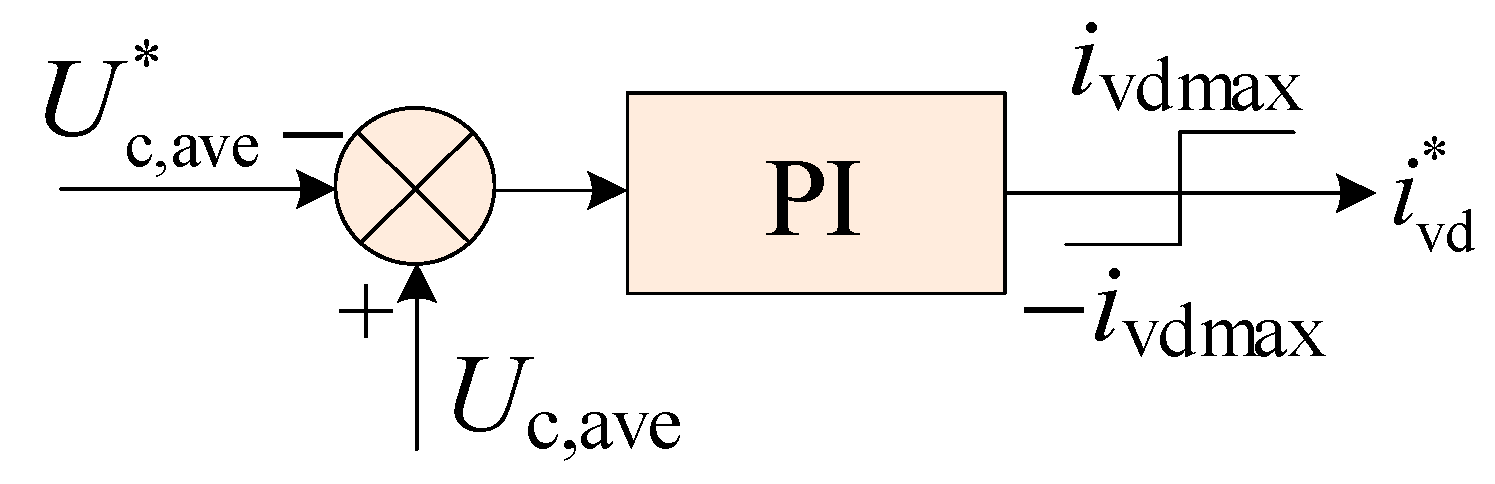
5.2.1. Active Power Control Loop
5.2.2. Reactive Power Control Loop
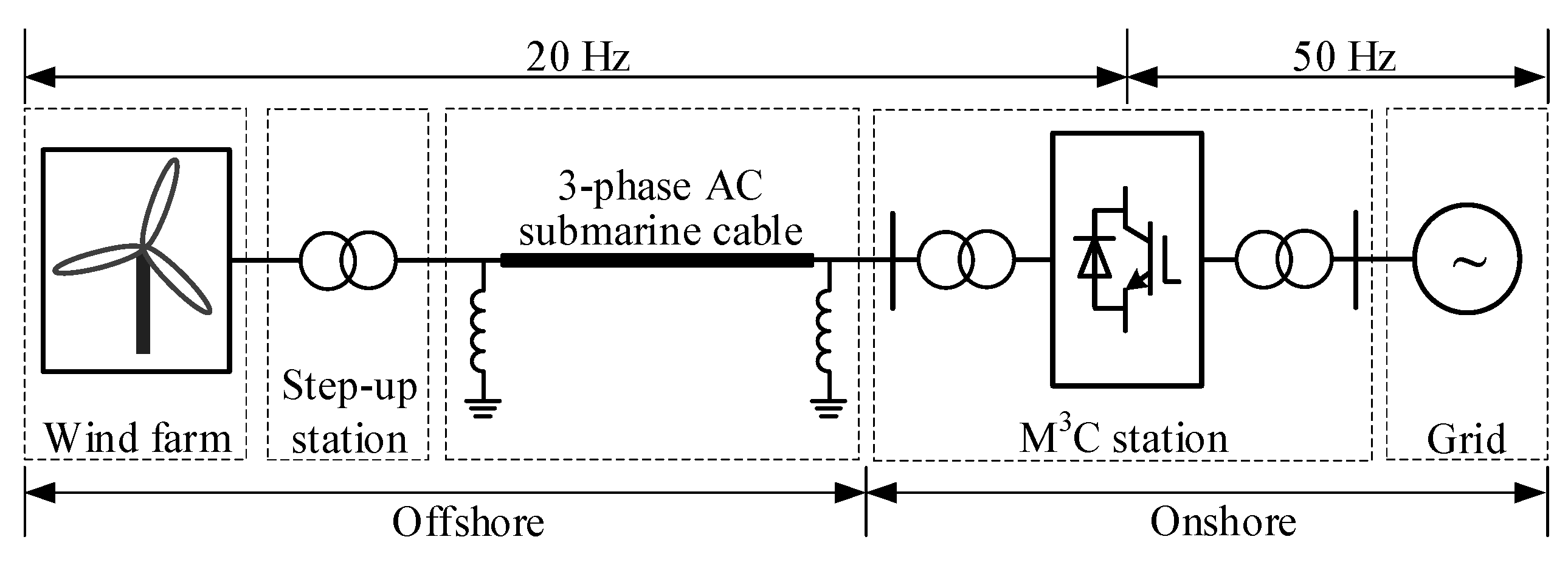
6. Case Study
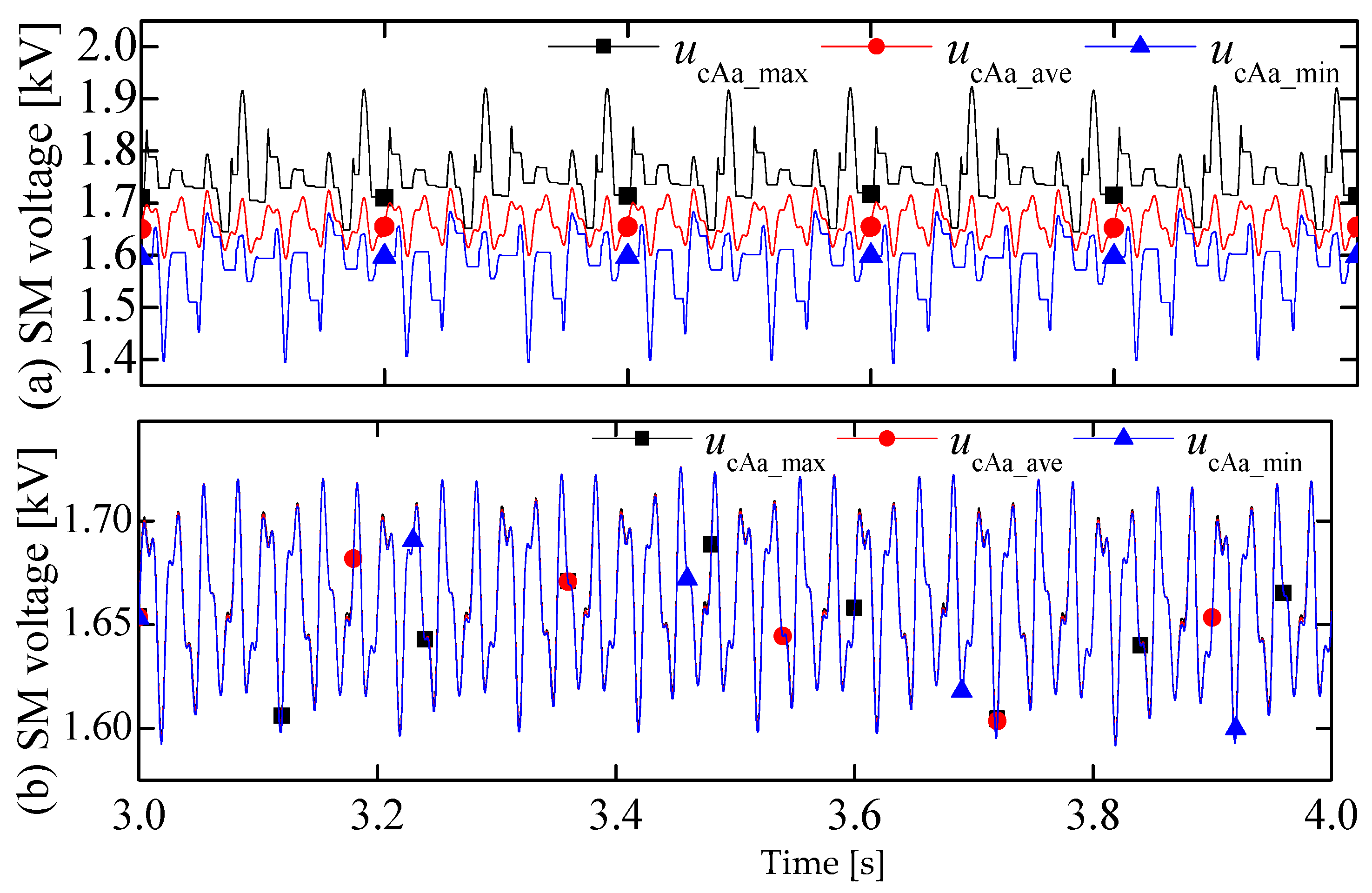
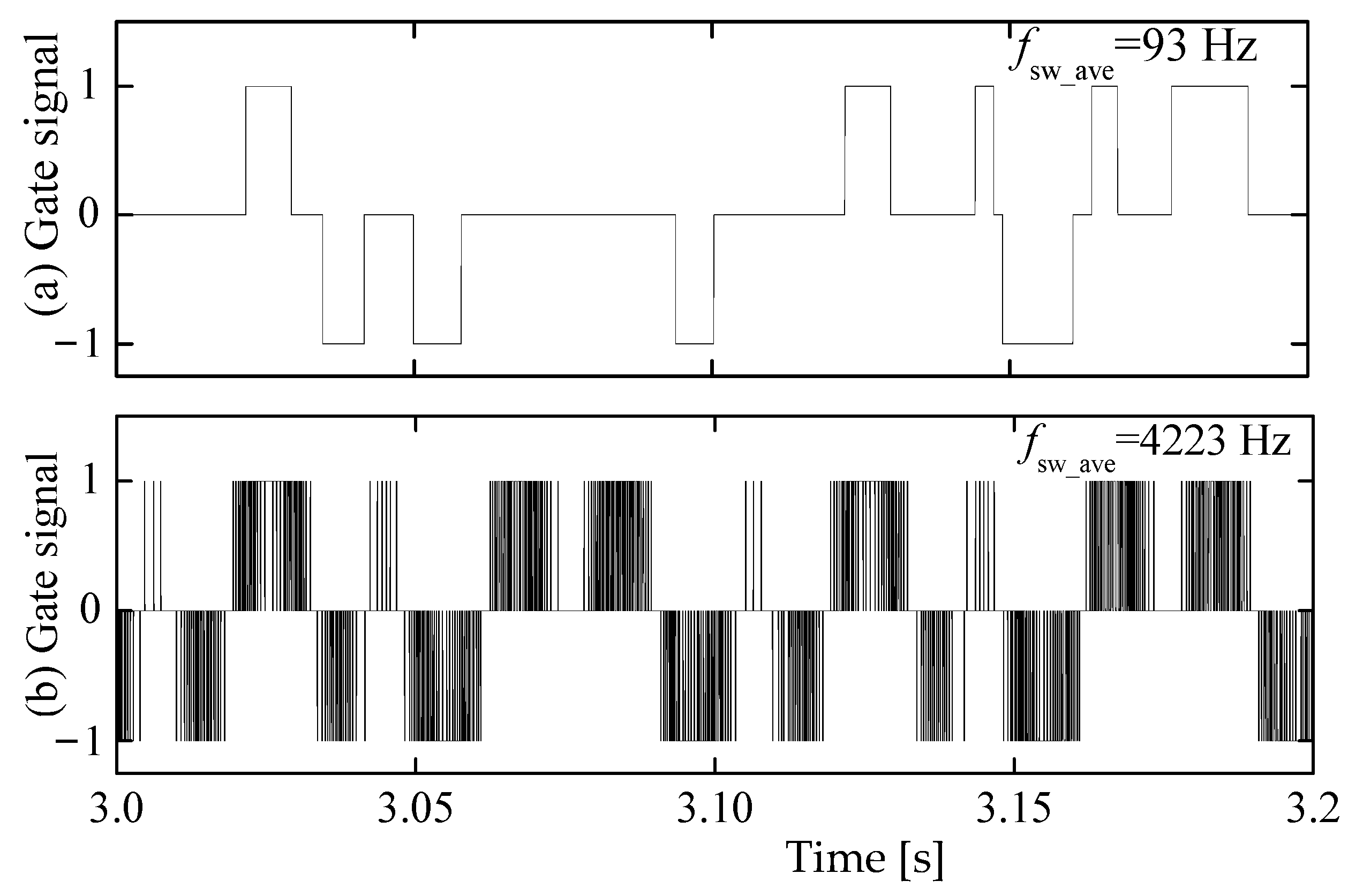
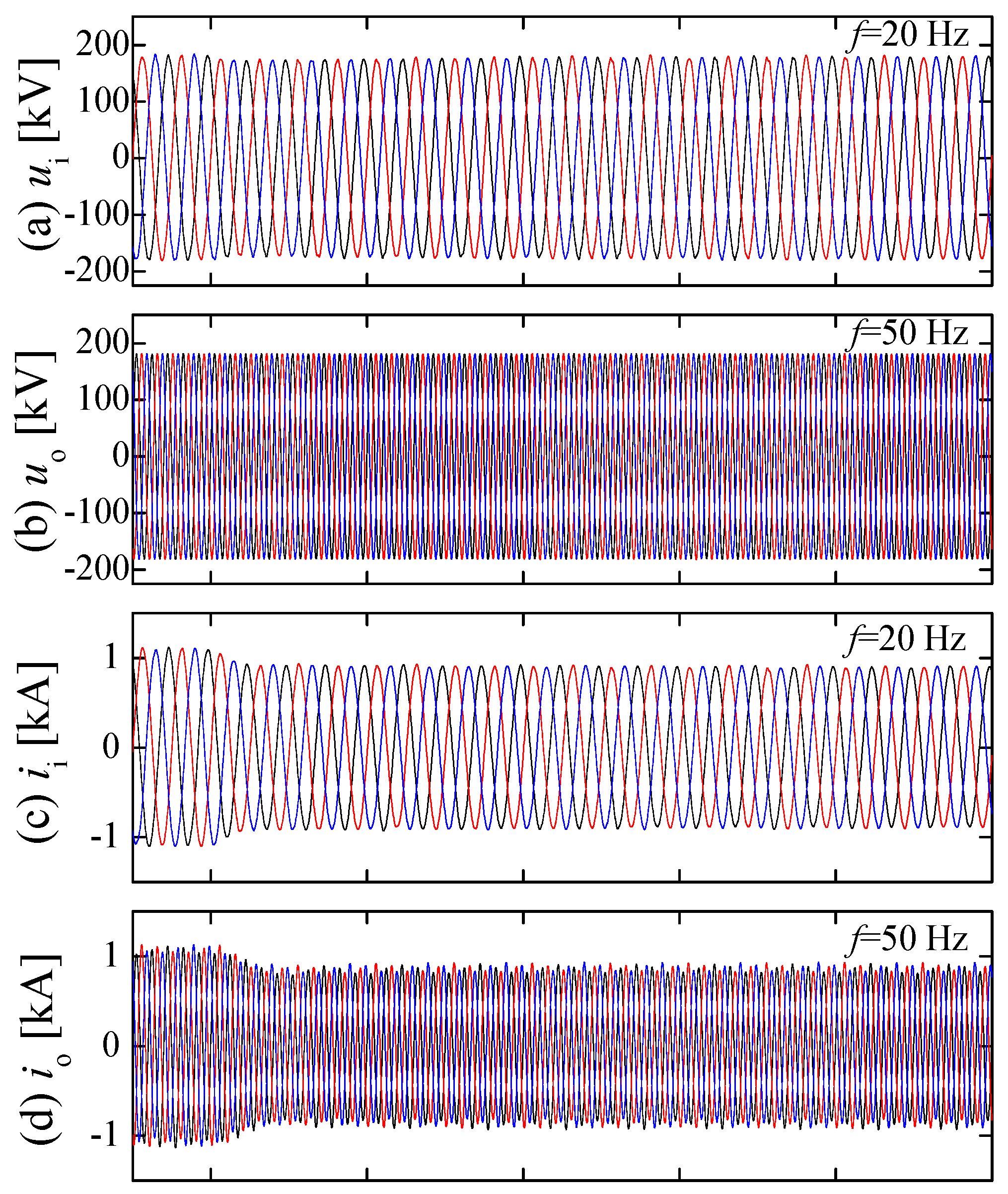
6.1. Characteristics of Reduced Switching Frequency SM Voltage Balancing Method
- (1)
- The SM capacitor voltage should keep balanced, i.e., the average voltage of all SM capacitors does not deviate too much from the rated value.
- (2)
- The maximum SM capacitor voltage should be within the upper limit voltage of the SM capacitor (usually 1.2 times the rated SM voltage).
6.2. Wind Speed Fluctuation
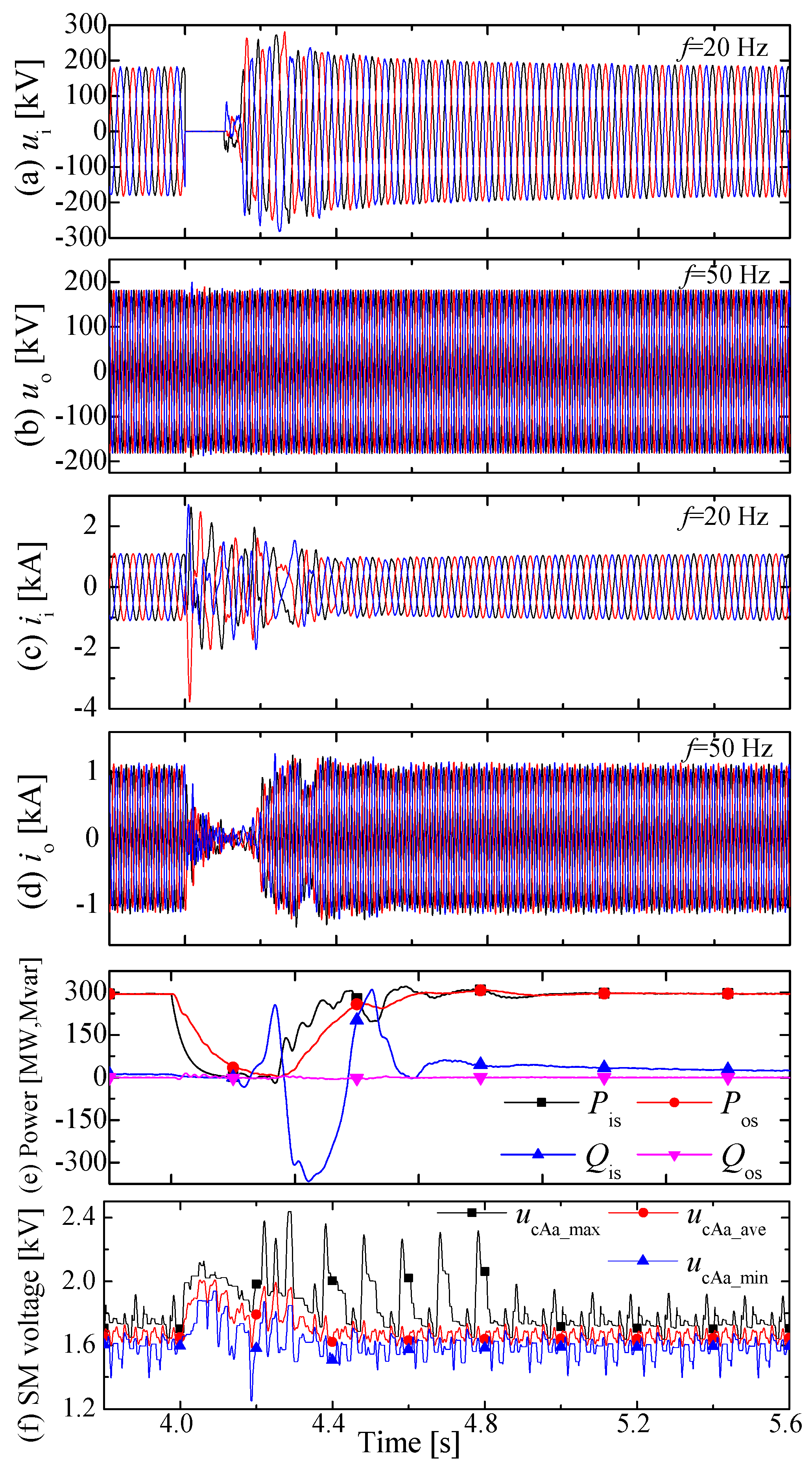
6.3. Offshore Side Fault
7. Conclusions
- (1)
- The ninth order mathematical model of the M3C is derived based on the extended MMC topology and the multiple αβ0 and dq transformations, making the M3C equivalent to two decoupled MMCs on the input side and the output side. The detailed equations of the current tracking controller are deduced in the dq reference frame and the circulating current suppressing controller is designed in the αβ0 reference frame. The outer loop controller is proposed for the scenario of offshore wind power LFAC integration based on M3C.
- (2)
- A reduced switching frequency SM voltage balancing method of the M3C is proposed based on three characteristic variables and the NLC, which not only meet the requirements of SM capacitor voltage balance but also immensely reduce switching frequency. Simulation results in PSCAD/EMTDC verify the availability of the proposed control strategy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Apostolaki-Iosifidou, E.; Mccormack, R.; Kempton, W.; Mccoy, P.; Ozkan, D. Transmission design and analysis for large-scale offshore wind energy development. IEEE Power Energy Technol. Syst. J. 2019, 6, 22–31. [Google Scholar] [CrossRef]
- Erlich, I.; Shewarega, F.; Feltes, C.; Koch, F.W.; Fortmann, J. Offshore wind power generation technologies. Proc. IEEE 2013, 101, 891–905. [Google Scholar] [CrossRef]
- Bresesti, P.; Kling, W.L.; Hendriks, R.L.; Vailati, R. HVDC connection of offshore wind farms to the transmission system. IEEE Trans. Energy Convers. 2007, 22, 37–43. [Google Scholar] [CrossRef]
- Rusk, A.; Rathsman, B.G.; Glimstedt, U. The HVDC Power Transmission from Swedish Mainland to the Swedish Island of Gotland; CIGRE Report No. 406; CIGRE: Paris, France, 1950. [Google Scholar]
- Adamson, C.; Hingorani, N.G. High Voltage Direct Current Power Transmission; Garrway Limited: London, UK, 1960. [Google Scholar]
- Chen, H.; Johnson, M.H.; Aliprantis, D.C. Low-frequency AC transmission for offshore wind power. IEEE Trans. Power Deliv. 2013, 28, 2236–2244. [Google Scholar] [CrossRef]
- Qin, N.; You, S.; Xu, Z.; Akhmatov, V. Offshore wind farm connection with low frequency AC transmission technology. In Proceedings of the IEEE Power and Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Erickson, R.W.; Al-Naseem, O.A. A new family of matrix converters. In Proceedings of the 27th Annual Conference of the IEEE Industrial Electronics Society, Denver, CO, USA, 29 November–2 December 2001; pp. 1515–1520. [Google Scholar]
- Luo, J.; Zhang, X.; Xue, Y.; Gu, K.; Wu, F. Harmonic analysis of modular multilevel matrix converter for fractional frequency transmission system. IEEE Trans. Power Deliv. 2020, 35, 1209–1219. [Google Scholar] [CrossRef]
- Kawamura, W.; Akagi, H. Control of the modular multilevel cascade converter based on triple-star bridge-cells (MMCC-TSBC) for motor drives. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3506–3513. [Google Scholar]
- Kawamura, W.; Hagiwara, M.; Akagi, H. Control and experiment of a modular multilevel cascade converter based on triple-star bridge cells. IEEE Trans. Ind. Appl. 2014, 50, 3536–3548. [Google Scholar] [CrossRef]
- Nakamori, T.; Sayed, M.; Hayashi, Y.; Takeshita, T.; Hamada, S.; Hirao, K. Independent control of input current, output voltage, and capacitor voltage balancing for a modular matrix converter. IEEE Trans. Ind. Appl. 2015, 51, 4623–4633. [Google Scholar] [CrossRef]
- Diaz, M.; Cardenas, R.; Espinoza, M.; Hackl, C.; Rojas, F.; Clare, J.; Wheeler, P. Vector control of a modular multilevel matrix converter operating over the full output-frequency range. IEEE Trans. Ind. Electron. 2019, 66, 5102–5114. [Google Scholar] [CrossRef]
- Perez, M.; Rodriguez, J.; Pontt, J.; Kouro, S. Power distribution in hybrid multi-cell converter with nearest level modulation. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vigo, Spain, 4–7 June 2007; pp. 736–741. [Google Scholar]
- Miura, Y.; Mizutani, T.; Ito, M.; Ise, T. Modular multilevel matrix converter for low frequency ac transmission. In Proceedings of the 10th International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 22–25 April 2013; pp. 1079–1084. [Google Scholar]
- Ma, J.; Dahidah, M.; Pickert, V.; Yu, J. Modular multilevel matrix converter for offshore low frequency AC transmission system. In Proceedings of the 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 768–774. [Google Scholar]
- Al-Tameemi, M.; Liu, J.; Bevrani, H.; Ise, T. A dual VSG-based M3C control scheme for frequency regulation support of a remote AC grid via low-frequency ac transmission system. IEEE Access 2020, 8, 66085–66094. [Google Scholar] [CrossRef]
- Glinka, M.; Marquardt, R. A new AC/AC multilevel converter family. IEEE Trans. Ind. Electron. 2005, 52, 662–669. [Google Scholar] [CrossRef]
- Rohner, S.; Bernet, S.; Hiller, M.; Sommer, R. Modulation, losses, and semiconductor requirements of modular multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2633–2642. [Google Scholar] [CrossRef]
- Tu, Q.; Xu, Z.; Xu, L. Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters. IEEE Trans. Power Deliv. 2011, 26, 2009–2017. [Google Scholar]
- Qin, J.; Saeedifard, M. Reduced switching-frequency voltage-balancing strategies for modular multilevel HVDC converters. IEEE Trans. Power Deliv. 2013, 28, 2403–2410. [Google Scholar] [CrossRef]
- Li, Z.; Gao, F.; Xu, F.; Ma, X.; Chu, Z.; Wang, P.; Gou, R.; Li, Y. Power module capacitor voltage balancing method for a ±350-kV/1000-MW modular multilevel converter. IEEE Trans. Power Electron. 2016, 31, 3977–3984. [Google Scholar] [CrossRef]
- Geng, Z.; Han, M.; Xia, C.; Kou, L. A switching times reassignment-based voltage balancing strategy for submodule capacitors in modular multilevel HVDC converters. IEEE Trans. Power Deliv. 2022, 37, 1215–1225. [Google Scholar] [CrossRef]
- Wang, W.; Wang, M. The application of M3C based on optimized sorting in fractional frequency transmission system. In Proceedings of the IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1430–1434. [Google Scholar]
- White, D.C.; Woodson, H.H. Electromechanical Energy Conversion, 1st ed.; The MIT Press: Cambridge, MA, USA, 1968. [Google Scholar]

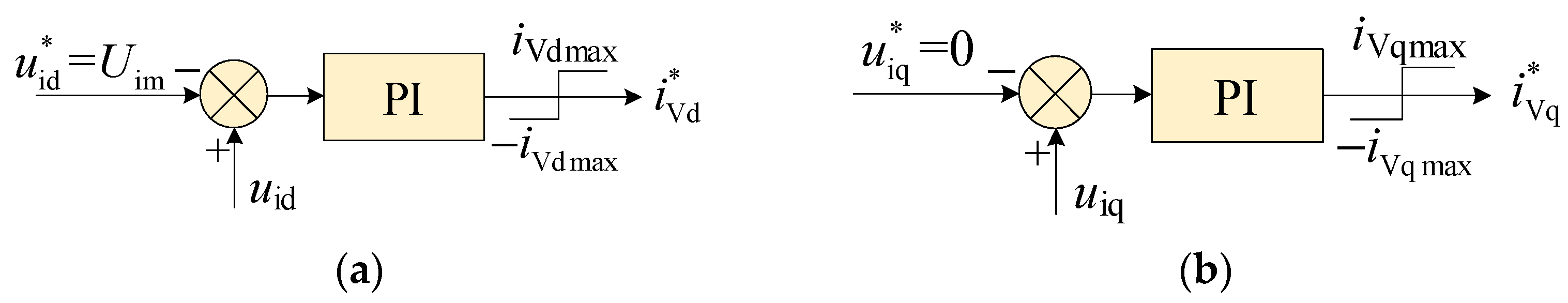


| States | T1 | T2 | T3 | T4 | usm | Arm Current Direction | Capacitor Current Direction |
|---|---|---|---|---|---|---|---|
| Positively inserted | on | off | off | on | +Uc | Positive | Positive |
| Negative | Negative | ||||||
| Negatively inserted | off | on | on | off | −Uc | Positive | Negative |
| Negative | Positive | ||||||
| Bypassed | on | off | on | off | 0 | Positive | --- |
| off | on | off | on | Negative | |||
| Blocked | off | off | off | off | +Uc | Positive | Positive |
| −Uc | Negative | Positive |
| Items | Parameters | Values |
|---|---|---|
| M3C | Transformer rated capacity | 330 MVA |
| Transformer rated ratio | 220 kV/97.5 kV | |
| Transformer leakage inductance | 0.15 p.u. | |
| M3C rated power | 300 MW | |
| Number of SMs per arm | 111 | |
| Rated SM capacitor voltage | 1.66 kV | |
| SM capacitance | 18000 μF | |
| Input-side rated frequency | 20 Hz | |
| Output-side rated frequency | 50 Hz | |
| Submarine cable | Line resistance | 26.8 mΩ/km |
| Line inductance | 0.395 mH/km | |
| Line capacitance | 0.167 μF/km | |
| Length | 100 km | |
| High-voltage reactor capacity | 2 × 35 Mvar | |
| Boosting transformer | Rated capacity | 330 MVA |
| Rated ratio | 220 kV/35 kV | |
| Leakage inductance | 0.105 p.u. | |
| Aggregated wind turbine | Rated power | 300 MW |
| Rated AC voltage | 35 kV |
| Method Type | Algorithm Complexity | Maximum SM Voltage Ripple | Average Switching Frequency |
|---|---|---|---|
| SM voltage balancing method based on sorting all capacitors’ voltages | Higher | 1.04 p.u. | 4223 Hz * |
| Reduced switching frequency SM voltage balancing method based on state sorting and incremental switching | Lower | 1.17 p.u. | 93 Hz * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Jin, Y.; Xu, Z. Modeling and Control of Modular Multilevel Matrix Converter for Low-Frequency AC Transmission. Energies 2023, 16, 3474. https://doi.org/10.3390/en16083474
Zhang Z, Jin Y, Xu Z. Modeling and Control of Modular Multilevel Matrix Converter for Low-Frequency AC Transmission. Energies. 2023; 16(8):3474. https://doi.org/10.3390/en16083474
Chicago/Turabian StyleZhang, Zheren, Yanqiu Jin, and Zheng Xu. 2023. "Modeling and Control of Modular Multilevel Matrix Converter for Low-Frequency AC Transmission" Energies 16, no. 8: 3474. https://doi.org/10.3390/en16083474
APA StyleZhang, Z., Jin, Y., & Xu, Z. (2023). Modeling and Control of Modular Multilevel Matrix Converter for Low-Frequency AC Transmission. Energies, 16(8), 3474. https://doi.org/10.3390/en16083474








