A Hybrid Deep Reinforcement Learning and Optimal Control Architecture for Autonomous Highway Driving
Abstract
1. Introduction
- We propose a novel and innovative hybrid hierarchical decision-making and motion planning control architecture for autonomous vehicles driving in unknown and uncertain non-trivial highway scenarios, which combines the DRL theory for the decision-making layer with the optimal NMPC control theory for the motion-planning task;
- The proposed hybrid architecture solves the problem of autonomous highway driving in a unified fashion by simplifying the overall decision process. Indeed, the decision-making task is demanded to a high-level layer, which only selects the proper route to follow, while the lower-layer computes an optimized and smooth driving profile compliant with vehicle dynamics. Therefore, different from other solutions dealing with both tasks via fully-AI methods, our approach requires fewer data for the training;
- Unlike the automotive technical literature, where vehicle behavior is modeled according to car-following scenarios and lane-change maneuvers via IDM, MOBIL, or their combination, here the motion planning layer is designed by exploiting NMPC theory, which enables the prediction of vehicle future behavior. This allows optimizing safety and comfort requirements, also taking input and state constraints into account;
- The proposed hierarchical architecture is validated in a high-detailed co-simulation platform and a comparison analysis w.r.t. to well-known benchmark IDM solution is provided, in order to better disclose the benefits of the proposed solution.
2. Related Works
3. Hybrid Hierarchical Decision-Making and Motion Planning Control Architecture for Highway Autonomous Driving
3.1. Decision-Making Layer
3.2. Motion Planning Layer
4. Scenario Description and DQN Training Phase
| Algorithm1: DDQN main training loop algorithm. |
 |
| Algorithm2: StepEnvironment(). |
 |
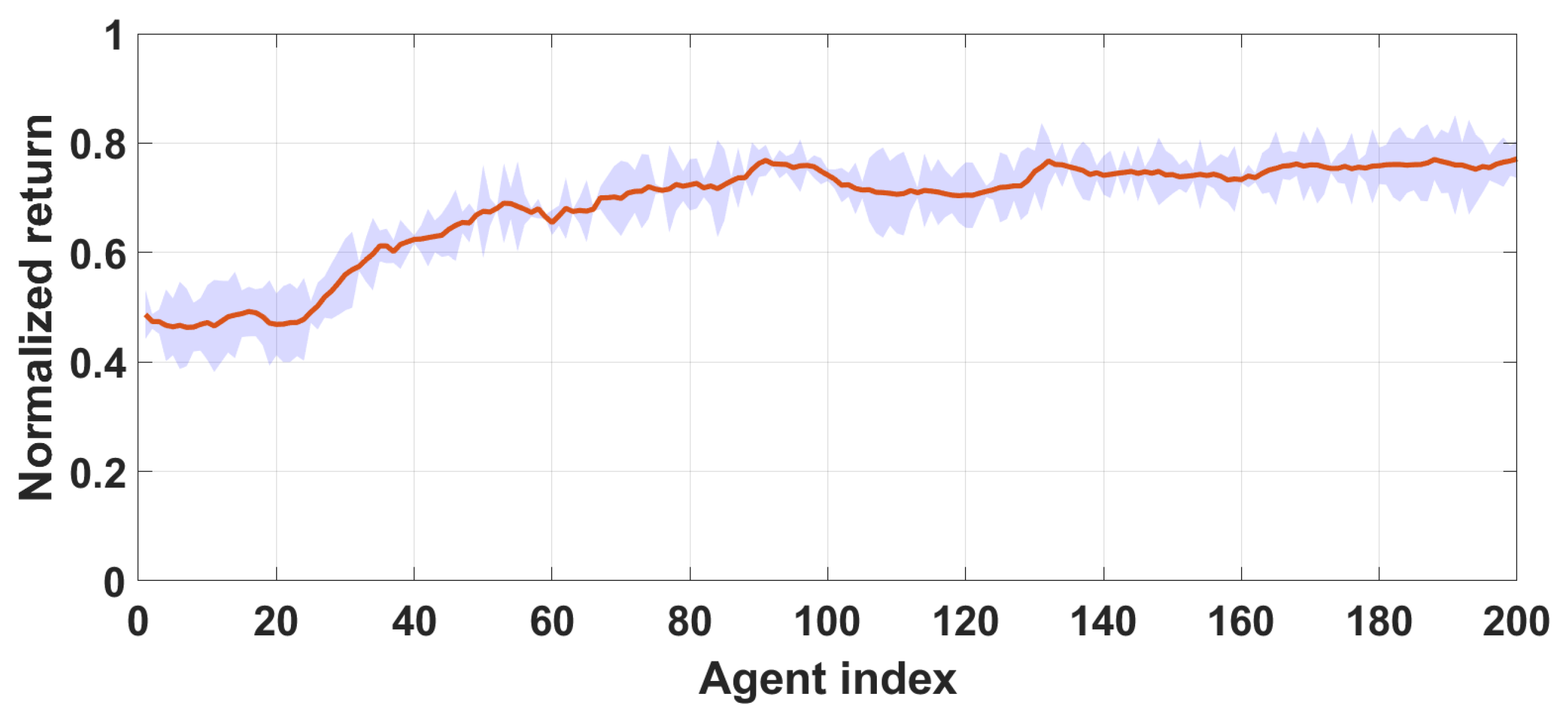
Training Results
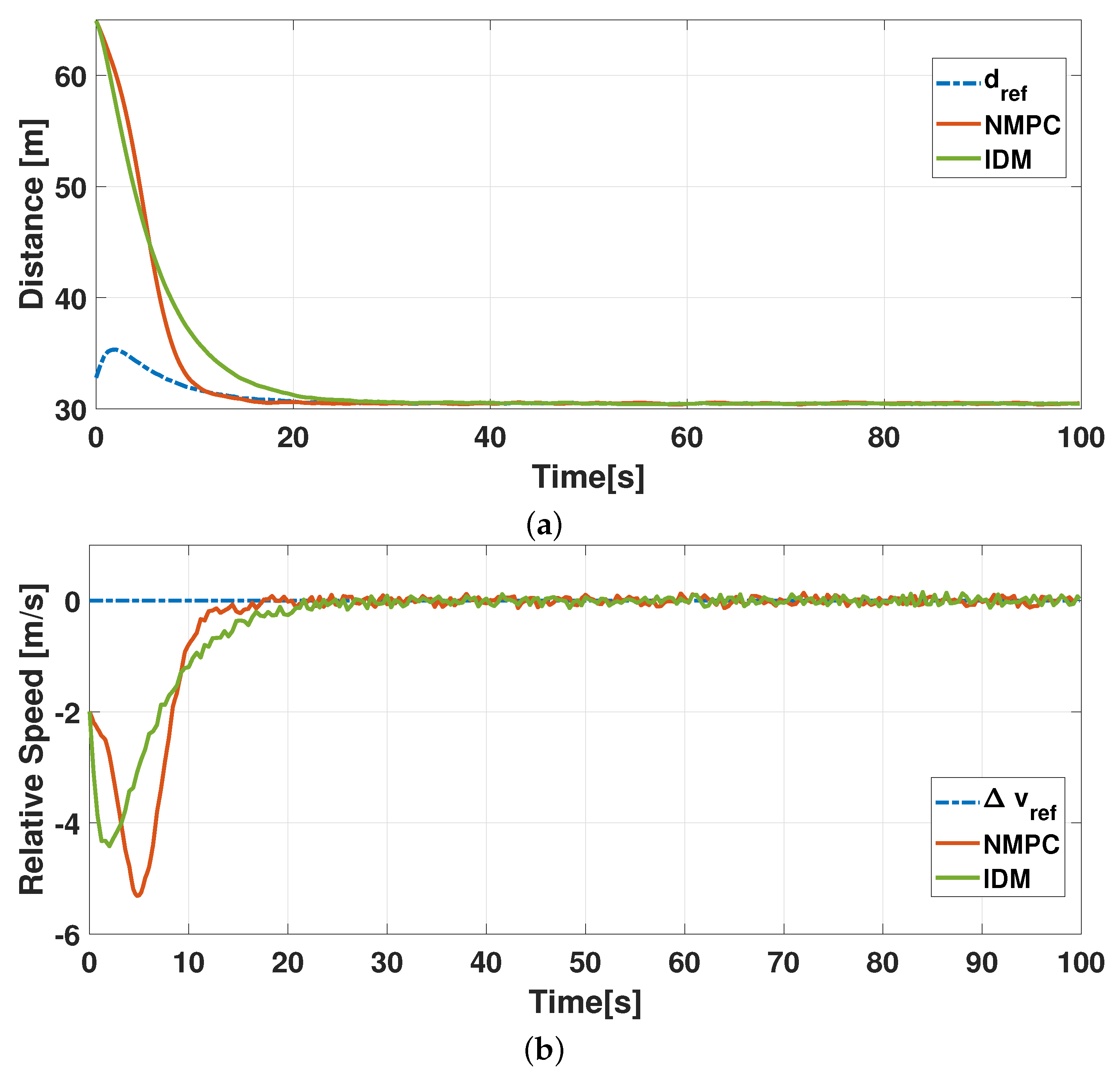
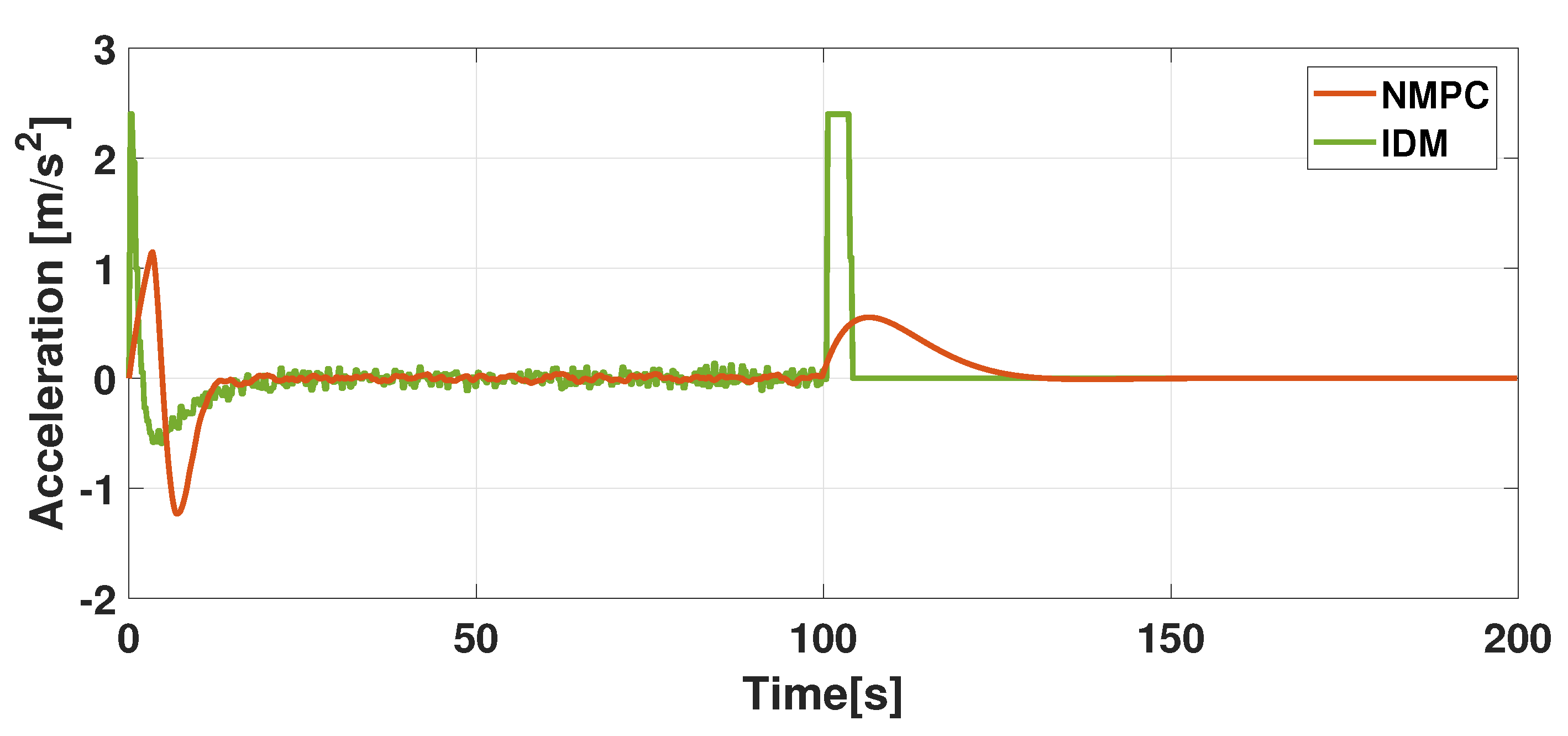
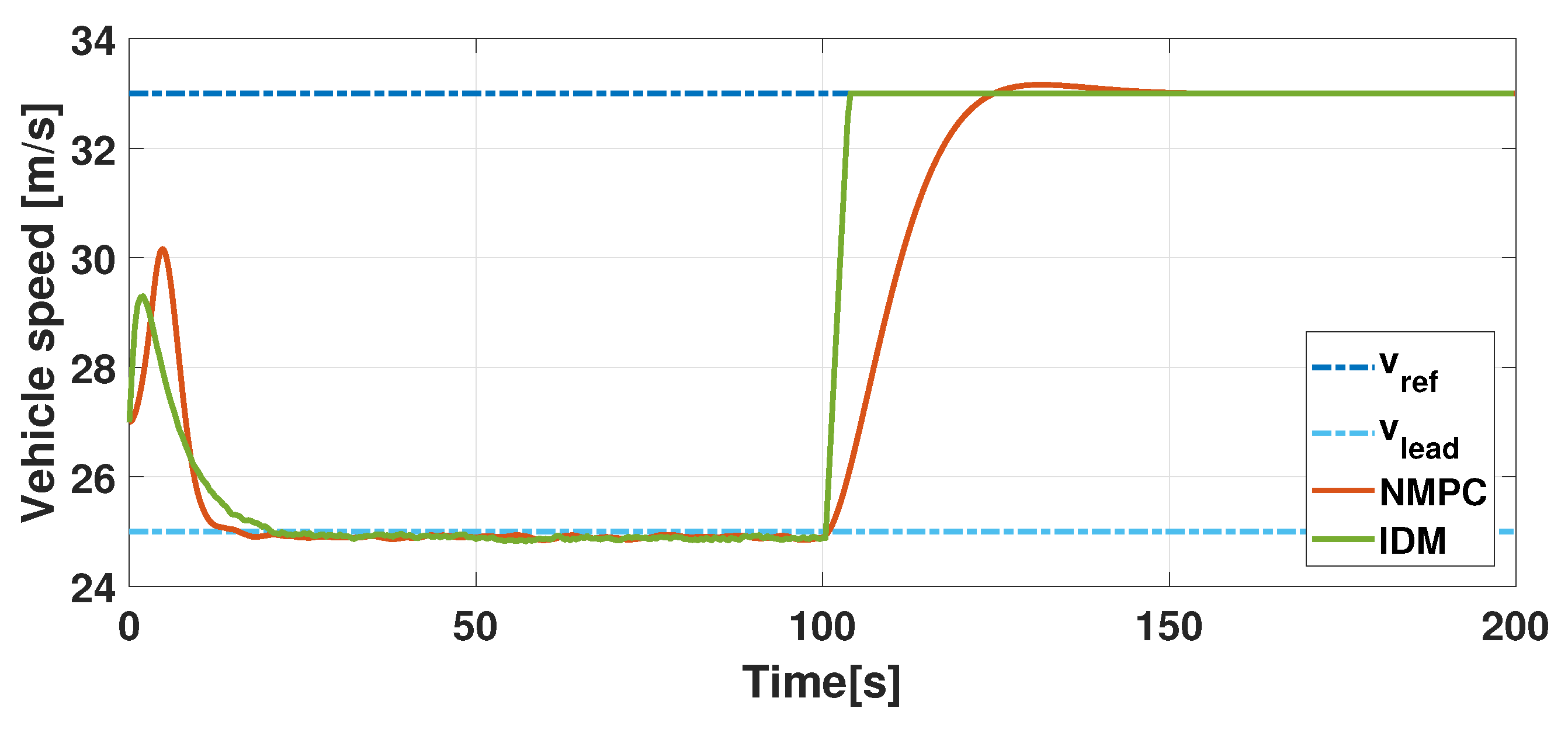
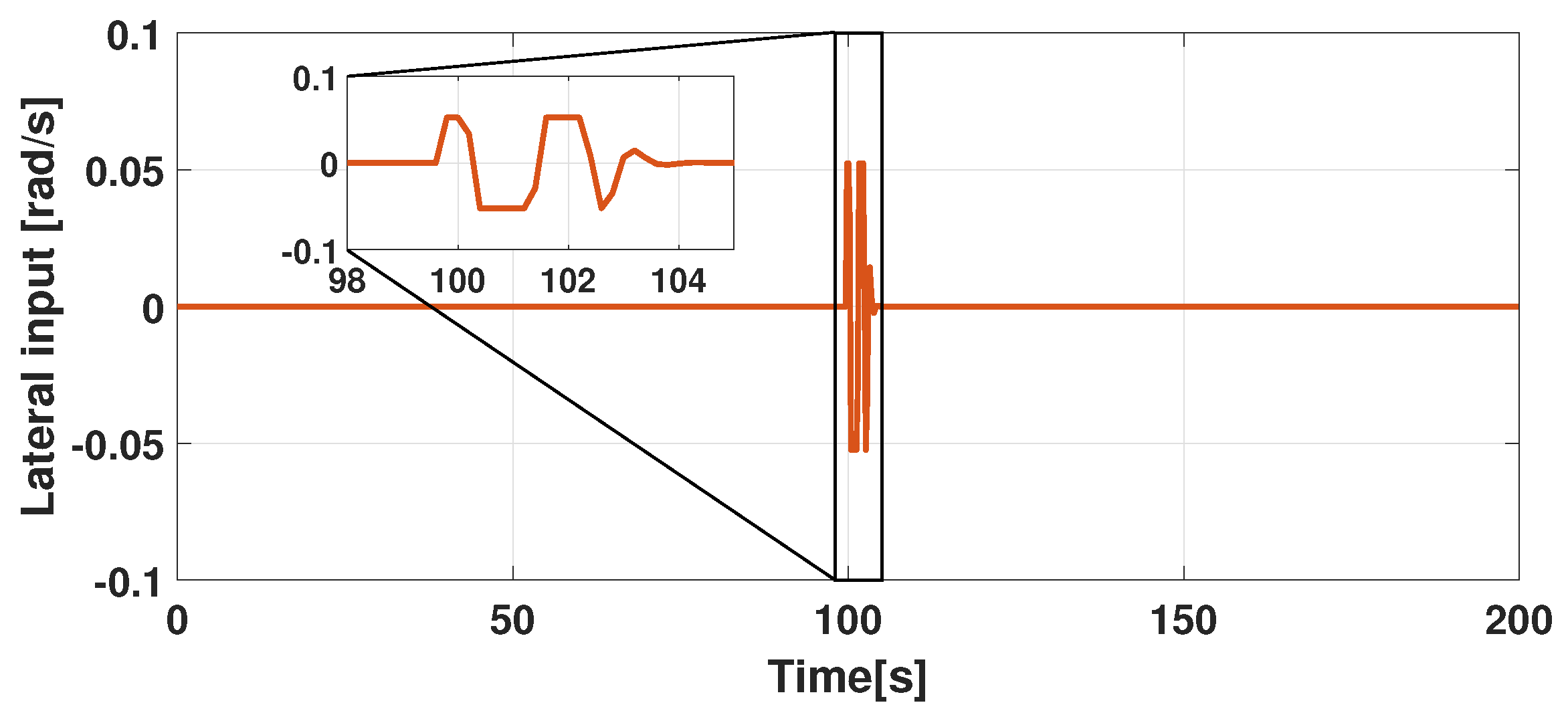
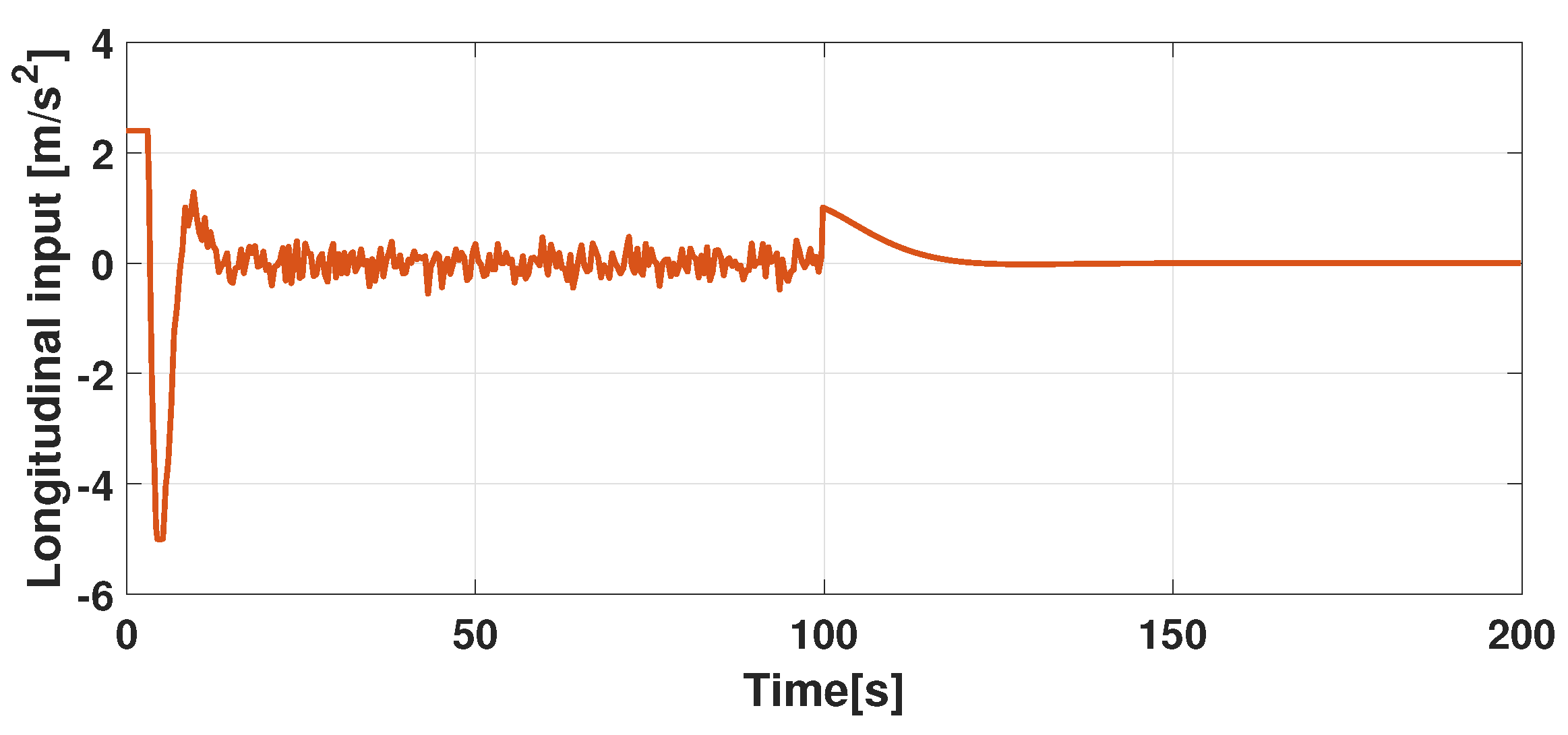
5. Virtual Testing Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rojas-Rueda, D.; Nieuwenhuijsen, M.J.; Khreis, H.; Frumkin, H. Autonomous vehicles and public health. Annu. Rev. Public Health 2020, 41, 329–345. [Google Scholar] [CrossRef] [PubMed]
- Caiazzo, B.; Coppola, A.; Petrillo, A.; Santini, S. Distributed nonlinear model predictive control for connected autonomous electric vehicles platoon with distance-dependent air drag formulation. Energies 2021, 14, 5122. [Google Scholar] [CrossRef]
- Caiazzo, B.; Lui, D.G.; Petrillo, A.; Santini, S. Distributed Double-Layer Control for Coordination of Multi-Platoons approaching road restriction in the presence of IoV communication delays. IEEE Internet Things J. 2021, 9, 4090–4109. [Google Scholar] [CrossRef]
- Coppola, A.; Lui, D.G.; Petrillo, A.; Santini, S. Eco-Driving Control Architecture for Platoons of Uncertain Heterogeneous Nonlinear Connected Autonomous Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24220–24234. [Google Scholar] [CrossRef]
- Coppola, A.; Lui, D.G.; Petrillo, A.; Santini, S. Cooperative Driving of Heterogeneous Uncertain Nonlinear Connected and Autonomous Vehicles via Distributed Switching Robust PID-like Control. Inf. Sci. 2023, 625, 277–298. [Google Scholar] [CrossRef]
- Liu, W.; Hua, M.; Deng, Z.; Huang, Y.; Hu, C.; Song, S.; Gao, L.; Liu, C.; Xiong, L.; Xia, X. A Systematic Survey of Control Techniques and Applications: From Autonomous Vehicles to Connected and Automated Vehicles. arXiv 2023, arXiv:2303.05665. [Google Scholar]
- Zong, W.; Zhang, C.; Wang, Z.; Zhu, J.; Chen, Q. Architecture design and implementation of an autonomous vehicle. IEEE Access 2018, 6, 21956–21970. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, S.; Zhou, Y.; Li, Z. An Integrated Model for Autonomous Speed and Lane Change Decision-Making Based on Deep Reinforcement Learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21848–21860. [Google Scholar] [CrossRef]
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the urban challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
- Kyprianou, G.; Doitsidis, L.; Chatzichristofis, S. Towards the Achievement of Path Planning with Multi-robot Systems in Dynamic Environments. J. Intell. Robot. Syst. 2022, 104, 1–18. [Google Scholar]
- Di Vaio, M.; Fiengo, G.; Petrillo, A.; Salvi, A.; Santini, S.; Tufo, M. Cooperative shock waves mitigation in mixed traffic flow environment. IEEE Trans. Intell. Transp. Syst. 2019, 20, 4339–4353. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, Y.; Ogai, H.; Inujima, H.; Tateno, S. Tactical decision-making for autonomous driving using dueling double deep Q network with double attention. IEEE Access 2021, 9, 151983–151992. [Google Scholar] [CrossRef]
- Baierle, I.C.; Sellitto, M.A.; Frozza, R.; Schaefer, J.L.; Habekost, A.F. An artificial intelligence and knowledge-based system to support the decision-making process in sales. S. Afr. J. Ind. Eng. 2019, 30, 17–25. [Google Scholar] [CrossRef]
- Sardjono, W.; Lusia, E.; Utomo, H.; Sukardi, S.; Rahmasari, A.; Regent Montororing, Y.D. Competitive Advantage Model Through Knowledge Management Systems Implementation to Optimize Business Sustainability. In Proceedings of the 2021 The 9th International Conference on Information Technology: IoT and Smart City, Guangzhou, China, 22–25 November 2021; pp. 154–160. [Google Scholar]
- Yu, J.B.; Yu, Y.; Wang, L.N.; Yuan, Z.; Ji, X. The knowledge modeling system of ready-mixed concrete enterprise and artificial intelligence with ANN-GA for manufacturing production. J. Intell. Manuf. 2016, 27, 905–914. [Google Scholar] [CrossRef]
- Li, G.; Yang, Y.; Li, S.; Qu, X.; Lyu, N.; Li, S.E. Decision making of autonomous vehicles in lane change scenarios: Deep reinforcement learning approaches with risk awareness. Transp. Res. Part Emerg. Technol. 2021, 134, 103452. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, X.; Zhang, X.; Qian, L.; Zhou, X. Hierarchical reinforcement learning for autonomous decision making and motion planning of intelligent vehicles. IEEE Access 2020, 8, 209776–209789. [Google Scholar] [CrossRef]
- Liao, J.; Liu, T.; Tang, X.; Mu, X.; Huang, B.; Cao, D. Decision-Making Strategy on Highway for Autonomous Vehicles Using Deep Reinforcement Learning. IEEE Access 2020, 8, 177804–177814. [Google Scholar] [CrossRef]
- Nageshrao, S.; Tseng, H.E.; Filev, D. Autonomous highway driving using deep reinforcement learning. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 2326–2331. [Google Scholar]
- Baheri, A.; Nageshrao, S.; Tseng, H.E.; Kolmanovsky, I.; Girard, A.; Filev, D. Deep reinforcement learning with enhanced safety for autonomous highway driving. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Anchorage, Alaska, USA, 4–7 June 2023; pp. 1550–1555. [Google Scholar]
- Bifulco, G.N.; Coppola, A.; Petrillo, A.; Santini, S. Decentralized cooperative crossing at unsignalized intersections via vehicle-to-vehicle communication in mixed traffic flows. J. Intell. Transp. Syst. 2022. [Google Scholar] [CrossRef]
- Albeaik, S.; Bayen, A.; Chiri, M.T.; Gong, X.; Hayat, A.; Kardous, N.; Keimer, A.; McQuade, S.T.; Piccoli, B.; You, Y. Limitations and improvements of the intelligent driver model (IDM). SIAM J. Appl. Dyn. Syst. 2022, 21, 1862–1892. [Google Scholar] [CrossRef]
- Albaba, B.M.; Yildiz, Y. Driver modeling through deep reinforcement learning and behavioral game theory. IEEE Trans. Control Syst. Technol. 2021, 30, 885–892. [Google Scholar] [CrossRef]
- Erke, S.; Bin, D.; Yiming, N.; Qi, Z.; Liang, X.; Dawei, Z. An improved A-Star based path planning algorithm for autonomous land vehicles. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420962263. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T.; Erwinski, K. Energy efficient local path planning algorithm based on predictive artificial potential field. IEEE Access 2022, 10, 39729–39742. [Google Scholar] [CrossRef]
- Spanogiannopoulos, S.; Zweiri, Y.; Seneviratne, L. Sampling-based non-holonomic path generation for self-driving cars. J. Intell. Robot. Syst. 2022, 104, 1–17. [Google Scholar]
- Lee, K.; Kum, D. Collision avoidance/mitigation system: Motion planning of autonomous vehicle via predictive occupancy map. IEEE Access 2019, 7, 52846–52857. [Google Scholar] [CrossRef]
- Wang, H.; Huang, Y.; Khajepour, A.; Zhang, Y.; Rasekhipour, Y.; Cao, D. Crash mitigation in motion planning for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3313–3323. [Google Scholar] [CrossRef]
- Li, G.; Yang, Y.; Zhang, T.; Qu, X.; Cao, D.; Cheng, B.; Li, K. Risk assessment based collision avoidance decision-making for autonomous vehicles in multi-scenarios. Transp. Res. Part Emerg. Technol. 2021, 122, 102820. [Google Scholar] [CrossRef]
- Xu, X.; Zuo, L.; Li, X.; Qian, L.; Ren, J.; Sun, Z. A reinforcement learning approach to autonomous decision making of intelligent vehicles on highways. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 50, 3884–3897. [Google Scholar] [CrossRef]
- Celemin, C.; Ruiz-del Solar, J. An interactive framework for learning continuous actions policies based on corrective feedback. J. Intell. Robot. Syst. 2019, 95, 77–97. [Google Scholar] [CrossRef]
- Matsuo, Y.; LeCun, Y.; Sahani, M.; Precup, D.; Silver, D.; Sugiyama, M.; Uchibe, E.; Morimoto, J. Deep learning, reinforcement learning, and world models. Neural Netw. 2022, 152, 267–275. [Google Scholar] [CrossRef]
- Candeli, A.; De Tommasi, G.; Lui, D.G.; Mele, A.; Santini, S.; Tartaglione, G. A Deep Deterministic Policy Gradient Learning Approach to Missile Autopilot Design. IEEE Access 2022, 10, 19685–19696. [Google Scholar] [CrossRef]
- Basile, G.; Lui, D.G.; Petrillo, A.; Santini, S. Deep Deterministic Policy Gradient-based Virtual Coupling Control For High-Speed Train Convoys. In Proceedings of the 2022 IEEE International Conference on Networking, Sensing and Control (ICNSC), Shanghai, China, 15–18 December 2022; pp. 1–6. [Google Scholar]
- Gu, S.; Lillicrap, T.; Sutskever, I.; Levine, S. Continuous deep q-learning with model-based acceleration. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2829–2838. [Google Scholar]
- Rodriguez-Ramos, A.; Sampedro, C.; Bavle, H.; De La Puente, P.; Campoy, P. A deep reinforcement learning strategy for UAV autonomous landing on a moving platform. J. Intell. Robot. Syst. 2019, 93, 351–366. [Google Scholar] [CrossRef]
- Wang, P.; Chan, C.Y.; de La Fortelle, A. A reinforcement learning based approach for automated lane change maneuvers. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Suzhou, China, 26–30 June 2018; pp. 1379–1384. [Google Scholar]
- Moghadam, M.; Elkaim, G.H. A hierarchical architecture for sequential decision-making in autonomous driving using deep reinforcement learning. arXiv 2019, arXiv:1906.08464. [Google Scholar]
- Lubars, J.; Gupta, H.; Chinchali, S.; Li, L.; Raja, A.; Srikant, R.; Wu, X. Combining reinforcement learning with model predictive control for on-ramp merging. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 942–947. [Google Scholar]
- Zanon, M.; Gros, S. Safe reinforcement learning using robust MPC. IEEE Trans. Autom. Control 2020, 66, 3638–3652. [Google Scholar] [CrossRef]
- Zheng, Y.; Ding, W.; Ran, B.; Qu, X.; Zhang, Y. Coordinated decisions of discretionary lane change between connected and automated vehicles on freeways: A game theory-based lane change strategy. IET Intell. Transp. Syst. 2020, 14, 1864–1870. [Google Scholar] [CrossRef]
- Yavas, U.; Kumbasar, T.; Ure, N.K. A new approach for tactical decision making in lane changing: Sample efficient deep Q learning with a safety feedback reward. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1156–1161. [Google Scholar]
- Sheng, Z.; Liu, L.; Xue, S.; Zhao, D.; Jiang, M.; Li, D. A Cooperation-Aware Lane Change Method for Autonomous Vehicles. arXiv 2022, arXiv:2201.10746. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Polack, P.; Altché, F.; Novel, B.; de La Fortelle, A. The kinematic bicycle model: A consistent model for planning feasible trajectories for autonomous vehicles? In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 812–818. [Google Scholar] [CrossRef]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated vehicle sideslip angle estimation considering signal measurement characteristic. IEEE Sens. J. 2021, 21, 21675–21687. [Google Scholar] [CrossRef]
- Xia, X.; Hashemi, E.; Xiong, L.; Khajepour, A. Autonomous Vehicle Kinematics and Dynamics Synthesis for Sideslip Angle Estimation Based on Consensus Kalman Filter. IEEE Trans. Control Syst. Technol. 2022, 31, 179–192. [Google Scholar] [CrossRef]
- Xiong, L.; Xia, X.; Lu, Y.; Liu, W.; Gao, L.; Song, S.; Yu, Z. IMU-based automated vehicle body sideslip angle and attitude estimation aided by GNSS using parallel adaptive Kalman filters. IEEE Trans. Veh. Technol. 2020, 69, 10668–10680. [Google Scholar] [CrossRef]
- Liu, W.; Xiong, L.; Xia, X.; Lu, Y.; Gao, L.; Song, S. Vision-aided intelligent vehicle sideslip angle estimation based on a dynamic model. IET Intell. Transp. Syst. 2020, 14, 1183–1189. [Google Scholar] [CrossRef]
- Borrelli, F.; Falcone, P.; Keviczky, T.; Asgari, J.; Hrovat, D. MPC-based approach to active steering for autonomous vehicle systems. Int. J. Veh. Auton. Syst. 2005, 3, 265–291. [Google Scholar] [CrossRef]
- Teng, S.; Deng, P.; Li, Y.; Li, B.; Hu, X.; Xuanyuan, Z.; Chen, L.; Ai, Y.; Li, L.; Wang, F.Y. Path Planning for Autonomous Driving: The State of the Art and Perspectives. arXiv 2023, arXiv:2303.09824. [Google Scholar]
- Hoel, C.J.; Wolff, K.; Laine, L. Automated speed and lane change decision making using deep reinforcement learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2148–2155. [Google Scholar]
- Domahidi, A.; Jerez, J.; FORCES Professional. Embotech AG, 2014–2019. Available online: https://embotech.com/FORCES-Pro (accessed on 6 March 2023).
- Lei, L.; Liu, T.; Zheng, K.; Hanzo, L. Deep reinforcement learning aided platoon control relying on V2X information. IEEE Trans. Veh. Technol. 2022, 71, 5811–5826. [Google Scholar] [CrossRef]
- Gao, C.; Yan, J.; Zhou, S.; Varshney, P.K.; Liu, H. Long short-term memory-based deep recurrent neural networks for target tracking. Inf. Sci. 2019, 502, 279–296. [Google Scholar] [CrossRef]





| State | Description |
|---|---|
| Ego vehicle speed | |
| Longitudinal distance of Ego Vehicle w.r.t. the j-th vehicle | |
| Lateral distance of Ego Vehicle w.r.t. the j-th vehicle | |
| Relative velocity of Ego Vehicle w.r.t. the j-th vehicle | |
| Action | Description |
| Changing Lane to the left | |
| Lane Keeping | |
| Changing Lane to the right | |
| Acceleration manoeuvre | |
| Braking manoeuvre |
| Parameter | Value |
|---|---|
| Sampling Time, | 0.2 [s] |
| Prediction Horizon, T | 4 [s] |
| Front axle-C.o.G. distance, | 1.2 [m] |
| Rear axle-C.o.G. distance, | 1.6 [m] |
| Power-train time constant, | 5 [s] |
| Lane width, | 3.6 [m] |
| Minimum reference distance, | 3 [m] |
| Tracking weights, | 50, 50, 30, 30, 20 |
| Effort weights, | 10, 1 |
| Headway time increments, | 0.1 [s] |
| Lateral error constraints, | −5.4, 5.4 [m] |
| Angular error constraints, | −0.35, 0.35 [rad] |
| Steering constraints, | −0.35, 0.35 [rad] |
| Steering rate constraints, | −0.035, 0.035 [rad/s] |
| Distance constraint, | 2 [m] |
| Velocity constraint, | 35 [m/s] |
| Acceleration constraints, | −5, 2.4 [m/s2] |
| Acceleration command constraints, | −5, 2.4 [m/s2] |
| Parameter | Value |
|---|---|
| Number of training episodes, | 60,000 |
| Number of steps per episode, | 500 |
| Sampling Time, | 0.2 |
| Replay Memory size, | 500,000 |
| Mini-batch size, | 32 |
| Discount factor, | 0.99 |
| Learning rate, | 0.0005 |
| Initial exploration constant, | 1 |
| Final exploration constant, | 0.1 |
| Exploration decay, | 2.3026 |
| Target Network update frequency, | 20,000 |
| Input neurons, | 19 |
| Number of dense layers, | 2 |
| Number of neurons for dense layers, | 128 |
| Output neurons, | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albarella, N.; Lui, D.G.; Petrillo, A.; Santini, S. A Hybrid Deep Reinforcement Learning and Optimal Control Architecture for Autonomous Highway Driving. Energies 2023, 16, 3490. https://doi.org/10.3390/en16083490
Albarella N, Lui DG, Petrillo A, Santini S. A Hybrid Deep Reinforcement Learning and Optimal Control Architecture for Autonomous Highway Driving. Energies. 2023; 16(8):3490. https://doi.org/10.3390/en16083490
Chicago/Turabian StyleAlbarella, Nicola, Dario Giuseppe Lui, Alberto Petrillo, and Stefania Santini. 2023. "A Hybrid Deep Reinforcement Learning and Optimal Control Architecture for Autonomous Highway Driving" Energies 16, no. 8: 3490. https://doi.org/10.3390/en16083490
APA StyleAlbarella, N., Lui, D. G., Petrillo, A., & Santini, S. (2023). A Hybrid Deep Reinforcement Learning and Optimal Control Architecture for Autonomous Highway Driving. Energies, 16(8), 3490. https://doi.org/10.3390/en16083490









