Design, Implementation and Test of a Novel Cylindrical Permanent Magnet DC Linear Motor

Abstract

Electric motors that convert electrical energy into motion are one of the basic components of automation systems. In these systems, either linear or circular motion is needed. Linear motion can be obtained either from motors that generate circular motion with the help of ancillary equipment or directly by the means of a linear motor. Obtaining linear motion from motors that produce rotary motion leads to additional costs and reduced efficiency. Linear motors, on the other hand, eliminate the need for conversion mechanisms. Despite this advantage, linear motors have some disadvantages, such as length limitation and low force/current ratio. In this study, a novel Cylindrical Direct Current Linear Motor (CDCLM) with high force/current ratio and no length limitation (long stroke) has been developed. Analyses of the developed motor has been performed with an analytical method. In addition, detailed numerical analyses have been carried out in an Ansys-Maxwell environment. A prototype of the designed DC linear motor has been implemented in a laboratory environment and experimental analyses have been carried out. The results of analytical, numerical and experimental analyses have been compared.

1. Introduction

The need for both linear and circular motion in automation systems is inevitable [1,2]. While rotational motion is produced directly by conventional rotational motors, linear motion is obtained in two ways: directly and indirectly by means of additional equipment. Linear motors are machines that produce the linear motion directly. To obtain linear motion from a rotary motion machine is possible with the help of auxiliary systems, such as belts, gears, etc. The mechanisms used for motion conversion bring additional costs and losses. Therefore, linear machines are used in systems that require linear motion to take advantages of the benefits offered in industrial applications [3,4,5]. Linear motors are preferred in systems such as automation applications, CNC machines, missile guidance systems, conveyor systems, crane systems and magnetic levitation, especially maglev trains [6].

As linear motors can be produced from a rotary motor which has been cut along a radial plane, these motors are similar to a rotary machine, and any rotational motor that produces rotational motion can be converted into a linear motor [5,7]. In the last century, design, control and test of linear motors with many different geometric structures has been carried out. As an early study, a DC linear motor was designed as a reluctance motor in 1917 and used as a launcher. If this machine is considered as a magnetic launcher, then the first DC linear motor that directly generates linear motion was produced by Ratcliff and Griffiths in 1964 as a wound field DC linear motor. DC linear motors that were developed from 1964 until the 1970s, when strong magnets were discovered, were field-wound motors. Permanent magnet DC linear motors have been developed since 1970. Basak used a ferrite permanent magnet instead of field windings for the first time in 1975 [4,8,9].

With the use of stronger magnets, the design, development, analysis, modeling and control of linear motors in different geometries has been carried out until today [10]. Both analytical and numerical analyses of linear motors designed in different geometric shapes have been performed and the results of these analyses have been compared in [11]. PID, fuzzy-PID [9,12], genetic algorithms (GA) [13], and response surface methodology [14] methods have been used for determining parameters of linear motors so as to be able to control them.

Generally speaking, there are two types of linear motors: AC linear motor and DC linear motor. In the historical development process, many linear motors have been developed in different topologies such as AC, DC, synchronous, asynchronous, and permanent magnet [15], and these topologies in different structures can be categorized according to brush condition, material of core, or geometric shape. Additionally, according to their geometric shape, linear machines are classified as flat, single sided, double-sided, U-channel and cylindrical motor [16].

In a Cylindrical Direct Current Linear Motor (CDCLM), the core and the moving part are geometrically tubular. Simply, the cylindrical linear motors can be developed by rotating the stator of single- or double-sided linear motors about a linear axis [17]. Among the various configurations, cylindrical linear motors are preferred in applications in which dynamic performance and reliability are important due to their high force/current ratio [18]. This situation encourages researchers to design and develop new cylindrical motors. A novel sort of the brushed DC linear motors, which was designed as the first tubular DC linear motor with wound field two pole, was developed by Green and Paul in 1969 [19]. Yao et al. have developed a modular motor that can be used in vehicle suspension, produces high thrust force and has a robust mover structure by combining a tubular linear motor and a vernier motor [20]. Zou et al. designed a new permanent magnet homopolar tubular linear motor that generates 60 N thrust force with 67% efficiency, and performed its analysis and optimization [21]. Consolo et al. developed a tubular linear motor with a long stroke and high thrust force, and carried out analytical and numerical analyses of this motor [22]. Alberto et al. designed a tubular linear motor with a small radius for biomedical applications, also performing numerical analysis by using finite elements. Moreover, position and force control parameters were determined with MATLAB/Simulink interface [23]. Birbilen and Lazoğlu developed a miniature tubular linear motor that can be used in linear compressor applications. The permanent magnets are placed within a Halbach array in a motor designed to be slotless [24].

Many advantages of linear motors can be listed, such as producing linear motion directly without the need for additional equipment, low maintenance cost [25,26], high efficiency, improved reliability and compact structure [27]. However, there are also some disadvantages. Especially important parameters that needs to be improved are low force/current ratio and length limitation. These two issues have been solved considerably with the DC linear motor developed in a study conducted in recent years [1,2]. High power/current ratio has been achieved in the motor, which is designed as double-sided. Thanks to developed brush-collector system, it can be designed in the desired stroke.

In this study, a novel cylindrical DC linear motor has been developed by changing the geometric shape of the previously designed double-sided DC linear motor in [1]. Windings of the formerly manufactured motor are wound on a rectangular cross-sectional core. As the magnets that produce magnetic field are placed in double side of the windings in this study, the thrust force is generated only these areas [1]. With the newly developed topology, the motor is redesigned by winding the coils on a cylindrical core. The permanent magnets that create the magnetic field are arc magnets, and since the magnets have the same geometric structure as the windings, almost all parts of each winding remain in the magnetic field. Thus, a DC motor with a higher force-current ratio has been produced by generating force in more areas. Consequently, in this study the designed CDCLM has higher force/current ratio (thrust), a long stroke, and no requirement for additional electronic circuits when fabricated to be longer. The performance of the CDCLM has been analyzed analytically with given equations in this paper, numerically using a finite-element method (FEM), and experimentally in a laboratory setup via a loadcell, and the obtained values have been compared. A nomenclature of all parameters and variables used throughout the paper is given in the following.

2. Configuration of CDCLM

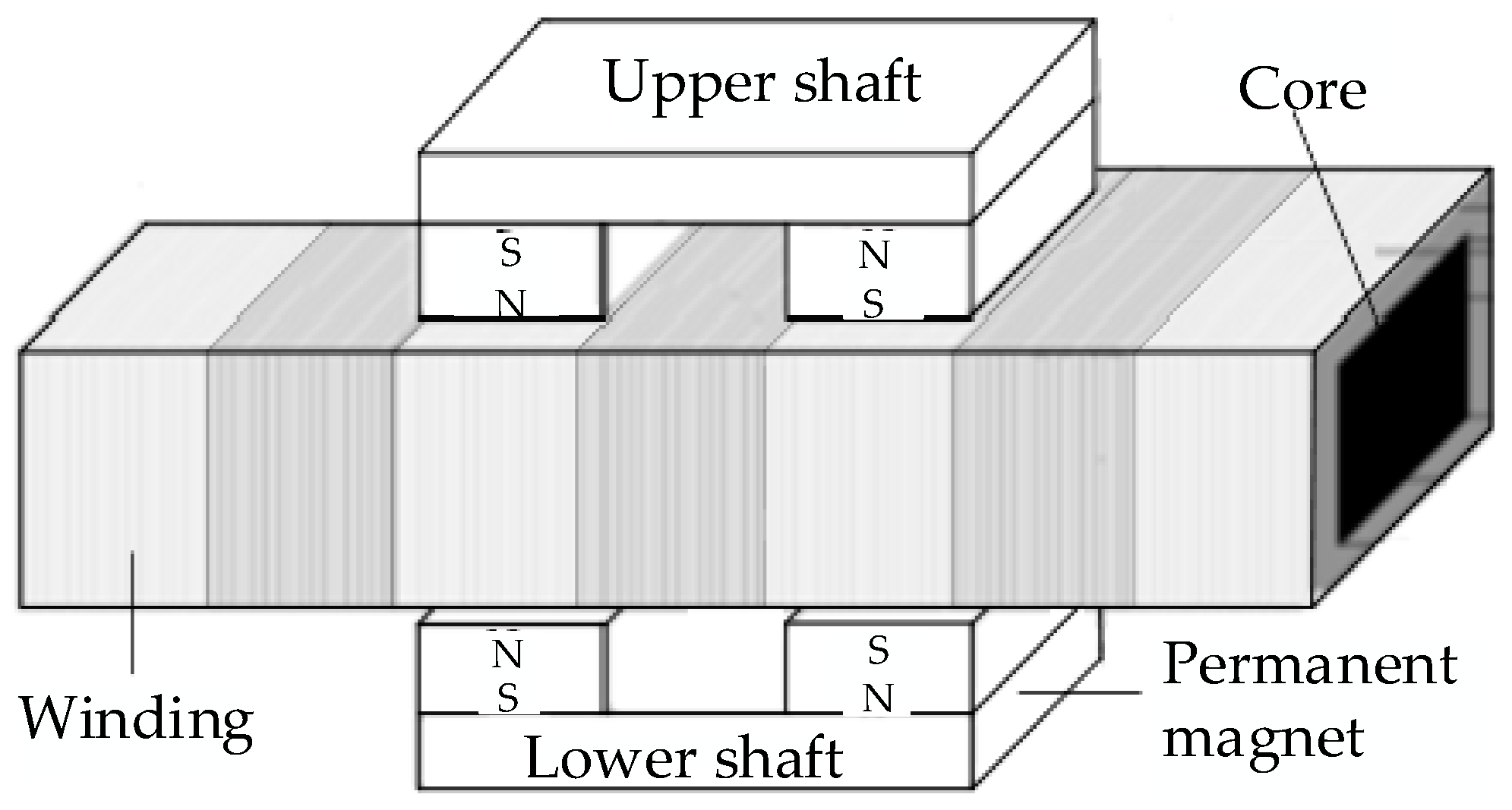
The permanent magnet DC linear motor fabricated in this study has brought an important solution to the length limitation problem without the need for additional control circuits. Moreover, the developed motor has a high force/current ratio. As shown in Figure 1, when the topology of the motor is examined, there are two parts in the moving unit (forcer), the upper and the lower shaft. Two neodymium (NdFeB)-type permanent magnets are placed on the inner surface of each shaft, and the moving unit—made of 1010 low carbon mild steel material—carries 4 magnets in total. The coils wound on the core have the same length as the magnets. With the help of the developed brush collector mechanism, only the windings under the magnets are energized. Thus, the other coils will not be energized, and the coils that have completed their task will cool down until they are energized again.

The permanent magnets are placed on only two sides of the windings, which are wound on a rectangular core made of 1010 type mild steel material [1]. No force is produced in the two areas outside the magnetic field according to Ampere’s law.

The armature and magnetic field unit of the motor with the topology given in Figure 1 has been redesigned as cylindrical in order to create force in the two areas outside the magnetic field as well. Thus, a novel CDCLM has been developed, which has no stroke limitation, has higher force current ratio, and does not require additional control circuits when fabricated with a longer stroke. Thanks to these advantages, this study offers an important solution to the problems of stroke limitation, low force-current ratio and complex circuit usage. The 3D geometric structure of the developed CDCLM is given in Figure 2. Its cross-sectional view is also given in Figure 3. Values of the parameters of the CDCLM are given in

Table 1. Values of the parameter of the CDCLM.

Parameter	Value (mm)
Radius of core, rc	25
Total layer length of winding	8
Length of air gap, lg	12
Inner radius of the magnet, ri	37
Outer radius of the magnet, ro	62
Thickness of the magnet, wm	50
Length of the magnet, lm	25
Inner radius of yoke, ry	62
Outer radius of yoke, rk	82
Length of yoke, ly	150

.

The CDCLM consists of two main units, a moving and a stationary part as shown in Figure 2 and Figure 3. The moving part, which is produced from 1010 low carbon mild steel material and is the magnetic field unit of the motor, consists of two shafts, right and left, carrying 4 arc NdFeB type permanent magnets in total. Permanent magnets have an inner radius of 37 mm, an outer radius of 62 mm, a length of 25 mm and a thickness of 20 mm. The magnets have been placed on the inner surfaces of right and left yoke as SN–NS and NS–SN, opposite to each other. The moving part (forcer) consists of two separate parts: right and left yoke. The inner radius of each piece is 62 mm, the outer radius is 82 mm, the height is 20 mm and the length is 150 mm. Eight brushes are placed on the underside of the moving part, which will move synchronously with this part, and a total of four linear bearings are placed on the moving part to reduce friction. Also, the linear bearings for the horizontal motion assembly are mounted on horizontal guide shafts. The stationary part consists of windings and a 50 mm diameter core made of 1010 low carbon mild steel. The windings are wound of enamel-coated copper wire with a diameter of 0.55 mm, 1000 turns, in total 14 layers. There is a total of 20 windings with a length of 50 mm, in which each coil length is the same as the permanent magnets. Coils are energized via the brush-collector system as shown in the Figure 4, and the winding terminals are connected to the collectors through the groove on the shaft. The insulating brush holder moves with the moving part and can be designed with four or eight brushes. The collector length is the same as the winding at 50 mm. Thus, the coil will be energized as long as it is in the magnetic field, and de-energized when it is outside of the magnetic field. As a result, energy conservation and cooling of the coils is provided by turning off the supply when they are not under the magnetic field effect.

3. Analytical Analysis

The magnetic circuit of the motor shown in Figure 5 is important in calculating the generated force by the CDCLM. When the array of the permanent magnets in the magnetic circuit is examined, two symmetrical magnetic circuits are formed, each of which completes its circuit through the left or right yoke, the air gap and the core. Since the magnetic flux created in both of the magnetic circuits given in Figure 5 is in the same direction in the core, the total magnetic flux passing through the core is equal to the sum of the magnetic flux produced in two circuits. Right-left yoke and core are made of 1010 low carbon mild steel and its magnetic permeability (µ) is considered infinite.

The magnetic flux generated in each of the circuits can be calculated with the equations as follow:

$$\mathrm{\Phi }=B_m{A}_m=q{B}_g{A}_g$$

(1)

$$B_m=\frac{A_g}{A_m}{B}_g$$

(2)

where B_m is the magnetic flux density of the magnet, B_g denotes the flux density in the air gap, A_m represents the surface area of the magnet, A_g is the air gap surface area and q depicts the leakage factor. The flux density in the air gap can be expressed as:

$$B_g={\mu }_0{H}_g$$

(3)

where µ₀ is the permeability of vacuum. Substituting Equation (3) into Equation (2) yields:

$$B_g=\frac{A_g}{A_m}{\mu }_0{H}_g$$

(4)

The B–H curve of NdFeB type permanent magnets to be used in the designed motor is given in Figure 6. As shown in Figure 6, the changes in the curve are linear. Using the curve, the magnetic flux density at the operating point can be determined. The calculation of magnetic flux density in DC linear motors is highly important for the analysis of the force produced by this type of motors.

In Figure 6, B_r is remanent flux density in Tesla (T) (catalog value), B_Q denotes the magnetic flux density at the operating point (Q) in Tesla (T), H_c represents the coercive force in (kA/m) and H_Q stands for the magnetic field intensity of the permanent magnet at operating point (Q) in (kA/m). Ampere’s law is widely used in the analysis of magnetic circuits.

Ampere’s law is given by:

$$⨖\overrightarrow{H}\overrightarrow{dl}=\int \overrightarrow{J}dA$$

(5)

Ampere’s law can be rewritten using the magnetomotive force. The magnetomotive force (MMF), which was generated when current i is passed through a coil with N windings, can be written as follows:

$$F_m=Ni$$

(6)

Unit of magnetomotive force is ampere-turns (At), and Ampere’s Law can be written as:

$$F_m={\displaystyle ⨖\overrightarrow{H}\overrightarrow{dl}}$$

(7)

and:

$${\displaystyle \sum Ni={\displaystyle ⨖\overrightarrow{H}\overrightarrow{dl}}}$$

(8)

Magnetomotive force is produced by the permanent magnet, and there is no winding in the permanent magnet, so number of turns is equal to zero (N = 0), and number of turns times current is equal to zero (Ni = 0). Equation (8) can be rewritten as:

$$0=H_m{l}_m+H_g{l}_g$$

(9)

$$H_g=-\frac{l_m}{l_g}{H}_m$$

(10)

where H_m is the magnetic field density of the permanent magnet, H_g represents the magnetic flux intensity in the air gap, l_m denotes the length of the magnet, l_g stands for length of the air gap.

By substituting Equation (10) into Equation (4), the load line equation is obtained.

$$B_m=-\frac{{\mu }_0{A}_g{l}_m}{A_m{l}_g}{H}_m$$

(11)

where µ₀ = 4π × 10⁻⁷ H/m is the magnetic permeability of vacuum. The B_Q and H_Q values, which are the B and H values at the operating point on the load and demagnetization curves of the magnet, are obtained by determining the point of intersections on the load curve obtained by Equation (11) and the demagnetization curve. At the intersection point, the magnetic field intensity of the magnet (H_Q) and the magnetic field density (B_Q) can be expressed by Equation (12) and Equation (13) respectively.

$$H_Q=-\frac{B_r}{\frac{B_r}{H_c}+{\mu }_0\frac{A_g}{A_m}\frac{l_m}{l_g}}$$

(12)

$$B_Q=\frac{B_r}{H_c}{H}_Q+B_r$$

(13)

By considering the losses, the magnetic flux density in the air gap can be written as:

$$B_{gQ}=-\frac{B_Q}{q}$$

(14)

By considering the physical structure of the magnets used in the developed motor, the magnet area, A_m and the air gap area, A_g can be calculated by using [28,29,30]. The uniform cross-sectional area of the permanent magnet used in this study and the cross-sectional area of the air gap are shown in Figure 7. The magnetic flux (Φ), which was generated by the arc permanent magnet, flows to the S pole by starting from N pole of magnet and passing through the air gap.

In Figure 7, w_m is thickness of the permanent magnet, r_i stands for inner radius of the permanent magnet, l_g is length of air gap and l_m depicts length of the magnet.

The differential surface vector in cylindrical coordinate system for calculate of cross-sectional area of the arc permanent magnet can be expressed as:

$$ds=rd\varnothing dz$$

(15)

The integral can be written as:

$${\displaystyle {\mathsf{\int }}_{S}Ads={\displaystyle \underset{0}{\overset{w_m}{\mathsf{\int }}}{\displaystyle \underset{0}{\overset{\pi }{\mathsf{\int }}}{r}_{i}d\varnothing dz}}}$$

(16)

and:

$$A=\pi r_i{w}_m$$

(17)

If the magnetic material surfaces on opposite sides of the air gap are in parallel and the same, the cross-sectional area of the air gap can be expressed as:

$$A_g=(a+l_g)(b+l_g)$$

(18)

The cross sectional area of the air gap of the CDCLM can be written as:

$$A_g=\pi (r_i+l_g)(w_m+l_g)$$

(19)

Substituting the values into Equation (19) and performing the calculations, it can be obtained thus:

$$A_g=9539\times {10}^{-6}{\mathrm{m}}^2$$

The permanent magnet surface area is calculated by using Equation (17) and is obtained as:

$$A_m=5809\times {10}^{-6}{\mathrm{m}}^2$$

Magnetic flux losses can be calculated as:

$$q=\frac{A_g}{A_m}$$

(20)

Substituting the values of A_m and A_g into Equation (20), value of leakage factor, q is obtained as 1.64. The magnetic field intensity of the permanent magnet at operating point, H_Q and magnetic flux density of the permanent magnet at operating point, B_Q value is calculated by using Equations (12) and (13) respectively. Considering the losses, the magnetic flux density, B_gQ value in the air gap is calculated by using Equation (14). As a result of the calculations, the H_Q value is 209.103 A/m, the B_Q value equals 0.888 T and the B_gQ value is obtained as 0.541 T.

After calculating the magnetic flux density in the air gap, the generated force can be analyzed. When a current is passed through a conducting wire (such as copper), the wire is pushed by a magnetic field that affected it according to Lorentz Force Law. The thrust produced by the magnetic field is a vector perpendicular to the plane formed by the current and magnetic flux density vectors. Lorentz’s Law as a vector can expressed as:

$$\overrightarrow{F}=i(\overrightarrow{l}X\overrightarrow{B})$$

(21)

where F is the force (in Newton, N) in armature, i represents the current flowing through the conductor (in Ampere, A), l stands for the length of the conductor (in meter, m), and B depicts the magnetic flux density (in Tesla, T). The conductor wire length (l) of the multilayer winding can be calculated by the average of the coil length per layer or by the average of the smallest layer radius and the largest layer radius of coil. The mean coil length (l) for each winding in the magnetic field produced by the magnet was obtained as 92.002 mm. Considering number of turns in coil the force equation can be arranged as:

$$F=BlIN\sin \theta$$

(22)

The magnetic field vector is perpendicular to the current vector, therefore sinθ is equal to 1, and the force equation can be simplified as:

$$F=BlIN$$

(23)

The force generated by each magnet is calculated as:

$$F=49.772iN$$

and overall force is obtained as:

$$F=49.772N$$

$$F=199i=KiN$$

where K is the static force/current ratio. In DC linear motors, the equation F = KI is widely used to express the static force obtained at constant current. The static force/current ratio, K of the CDCLM is calculated as 199 N/A by using Equation (23). In other words, for each one ampere of current applied to the windings, a force of 199 N/A has been produced in the moving unit of the motor.

4. Magnetic Analysis of CDCLM

In addition to the analytical analysis of the CDCLM, numerical analyses were also carried out in computer environment. The analyses were fulfilled by creating a 3D model of the CDCLM in the Maxwell-Ansys software, version 19.2. These analyses were performed by considering dimensions given in Table 1. In Figure 8, the magnetic flux density distribution of the CDCLM obtained as a result of the analysis performed in Maxwell-Ansys software is given.

As shown in Figure 8, while color changes from blue to red, the magnetic flux density increases. The highest magnetic flux density is 2.13 T while the lowest magnetic flux density is 6.9 mT. The highest magnetic flux density is shown on the core with red color. The reason for this is that the magnetic fluxes of two symmetrical magnetic circuits complete their circuits in the same direction through the core as shown in Figure 5. Compared to the core, the magnetic flux density passing through the right and left yoke is less. However, the magnetic flux density is less in the areas that are not in the magnetic field, such as fifth winding shown in Figure 5.

Another point to be noted is the magnetic saturation point of the materials used as core and yoke. In this study, SAE 1010 low carbon steel is used as magnetic material. SAE 1010 low carbon steel B–H curve is given in Figure 9. According to the B–H curve, the saturated magnetic flux density of mild steel material is approximately 2 T. As shown in Figure 8, suitable material was chosen for the core and left-right yoke in this study, since the maximum magnetic flux density is 2.13 T.

Vectorial magnetic flux density variation of the CDCLM, i.e., the direction of the magnetic flux, is given in Figure 10. In permanent magnets, the magnetic flux direction is from the N pole to the S pole. As shown in Figure 5, magnetic field lines in permanent magnets are in the r-direction. Thus, the magnetic field lines formed in the r-direction complete their path along the z-axis through the core and yokes. The highest magnetic flux density is shown in red and measured as 2.13 T in the core.

The magnetic field created by the permanent magnets completes its path in the −z direction through the left-right yokes and in the +z direction through the core, since the direction of magnetic flux in a permanent magnet is from the N pole to the S pole.

It is very important to determine the magnetic flux density in different areas of the CDCLM for the core and yoke materials being used. Besides this, it is necessary to calculate the magnetic flux in the air gap to decide the value of thrust. Considering the losses, the magnetic flux density in the air gap can be calculated by using Equation (14). Considering the surface area of the permanent magnet opposite to the air gap and the air gap surface area, the air gap magnetic flux density is calculated as 0.541 T analytically. As a result of the analysis conducted in Maxwell-Ansys environment the magnetic field density is determined as 0.562 T numerically. As a result, it is seen that the values calculated in both analyses are very close to each other with a difference of 3.8 percent, in other words, the difference between two analyses 2.1 mT.

The magnetic flux density distribution in the air gap along the z-axis, which is the movement direction of the armature, is given in Figure 11. Radius of the air gap, r_g is 32 mm. When the graphs are examined, it has been shown that the distribution is homogeneous. The magnetic field is produced in the areas of 0–50 mm and 100–150 mm interval, and the magnetic flux distribution is homogeneous in these areas. In the area of the 50–100 mm interval, there is no magnetic field and the distribution is not immediately zero due to the leakage flux.

5. Experimental Validation

A prototype of the DC linear motor, whose analytical and numerical analyses were performed in the previous sections, was produced as shown in Figure 12 in a laboratory environment with the dimensions specified in Table 1. The coils under the magnets of the prototype motor are supplied by the 24 V DC power supply. The produced force, force/current ratio, and static force coefficient, K, are some of the important parameters of DC linear motors to be investigated.

In the CDCLM developed, while the static force coefficient, K, was calculated as 199 N/A by using Equation (23), it was obtained numerically as 203 N/A in the computer environment. As a result of the experimental analysis of the produced CDCLM in the laboratory environment, the force/current ratio was measured as 193 N/A. In order to determine the force/current ratio produced by the motor, the moving unit was fixed in the starting position of one of the windings wound on the core and the produced force was measured with the loadcell by increasing the current variable in 0.1 A intervals. The changes in the resistance of the loadcell were amplified with loadcell amplifier (HX711) and transferred to the computer environment with Arduino uno. The variations of force values obtained from analytical, numerical and experimental analyses with respect to current are shown in Figure 13.

It is remarkable that approximately 97% agreement is observed between experimental and theoretical force values. Small ripples in the measured force curve are due to static friction force and loadcell sensitivity.

One of the important advantages of the produced motor is the developed brush collector system. The number of brushes used determines the variation of the force produced depending on the location. As seen in Figure 14, the value of the force produced by using 8 brushes in experimental measurements is constant with small fluctuations according to the location. As the position of the moving unit changes, since the number of active conductors (N) opposite to the permanent magnet do not change, the generated force remains constant. The force measurement with respect to the position was carried out statically via a loadcell by sliding the position of the moving unit at intervals of 0.1 mm.

Mean of the static force value in position between 0 mm and 150 mm is measured as 192 N/A. It has been observed that there is striking similarity (with 3% difference) between experimental and analytical results. In the experimental analysis, the highest static force is measured as 195.3 N/A at 16 mm and the lowest value is measured as 187.4 N/A at 50 mm.

Another experiment has been implemented for simulation and experimental results comparison of time variations of position and velocity. For simulation, a MATLAB/Simulink model of the motor shown in Figure 15 has been used with the parameter values given in Table 1. Experiments are implemented by using a 5 kΩ Opkon RTL linear potentiometer for position measurement, shown in Figure 16. Figure 17 and Figure 18 show a comparison of time variations of position and velocity, respectively, for simulation and experiments.

As it can be seen from Figure 17 and Figure 18, simulation and experiment results are in good agreement. The total displacement is around 300 mm in 1 s. Figure 18 shows that the velocity variations settle at 1 s, and average velocity is 305 mm/s. Percentage overshoot is 4.5%. The ripples after 1 s is due to the distance between two coils created by the insulation materials.

A comparison of the obtained results to the pertinent available literature yields interesting results. The basic comparison criterion is the force developed for unit current. For the same kind of motors, 2.67 N force is produced for 1 A current in [31], 27 N in [32], 1 N in [33], 7.8 N in [34], less than 1 N in [35], and 24 N in [36]. A very recent study [37] reports generation of 27 N force per ampere. On that basis, 199 N force developed for 1 A current in this study is a considerable improvement for this kind of motor.

To provide a quantitative information on the dynamic behavior of the designed and implemented motor, time variation of the motor current is also given in Figure 19. At the very beginning, the current reaches 1.5 A and then it settles with an average of 0.5 A at no-load test. Since a copper conductor of 0.55 mm diameter is used, its maximum current capacity is 3 A at steady-state, which is also the maximum current of the motor. Accordingly, the maximum force of the motor 579.6 N and the maximum velocity is 474 mm/s for this maximum current value.

6. Conclusions

In this study, a novel cylindrical DC linear motor, which has a high static force current ratio, no stroke limitation, and does not require complex control circuits when manufactured to be longer thanks to its brush collector mechanism, has been designed and a prototype has been implemented in a laboratory environment. The magnetic flux density in the air gap and the generated force were calculated by analytical and numerical analyses carried out during the design phase. Numerical analyses are performed in Maxwell-Ansys environment. An experimental static force analysis of the CDCLM has been carried out. Force and current values were transferred to the computer environment via loadcell and current sensor, respectively. It has been clearly shown that the experimental and theoretical results are in good agreement. When the analysis results are considered, this motor offers an important solution to the low force-current ratio, which is a significant disadvantage of DC linear motors. This machine, which can be designed as both brushed and brushless, can be used to develop new DC linear motors with different characteristics by using different lengths of permanent magnets and armature windings.