Discharge Characteristics and Numerical Simulation of the Oil–Gas Surface under DC Voltage
Abstract
:1. Introduction
2. Materials and Methods
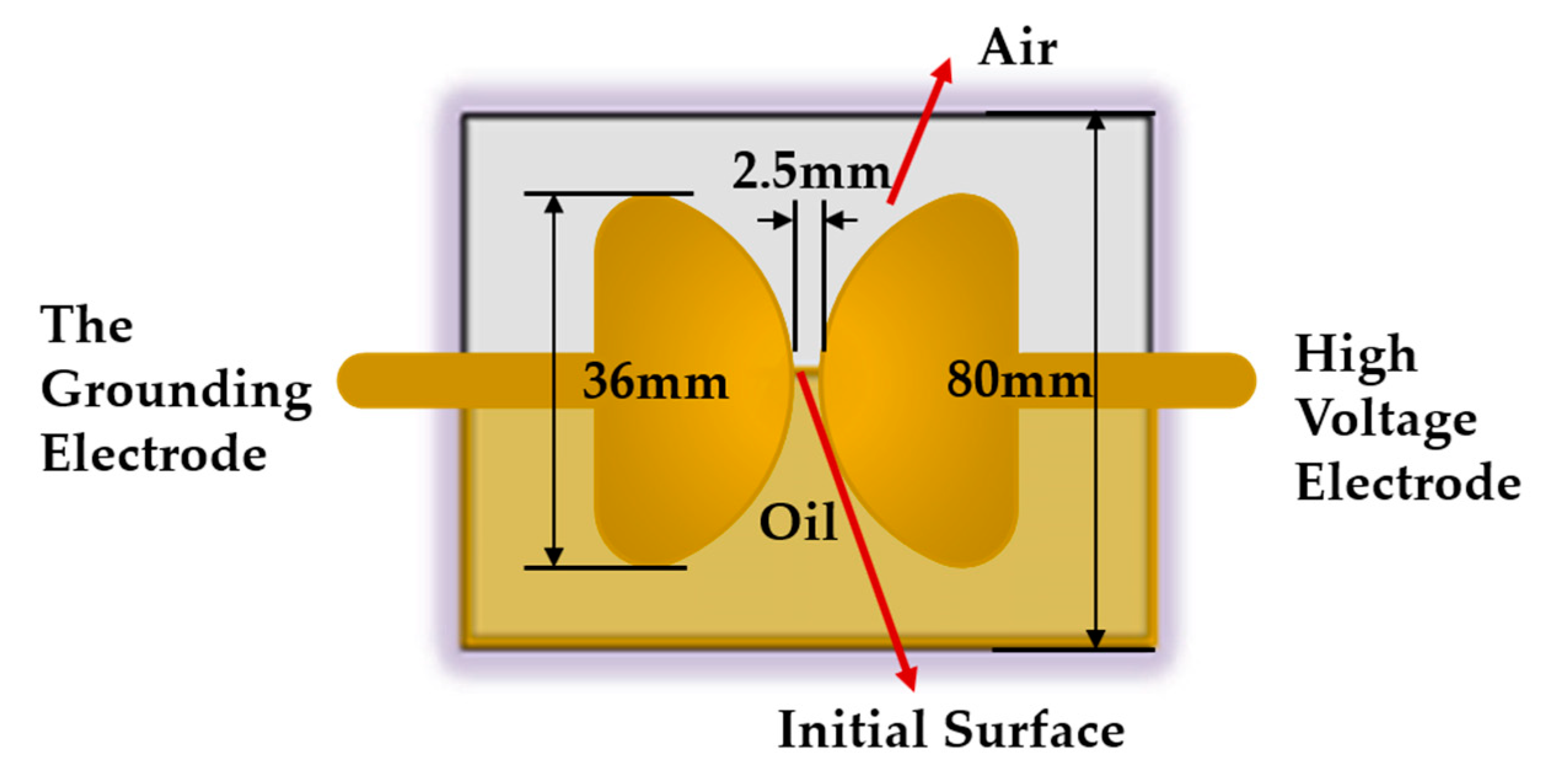
2.1. Sample Preparation
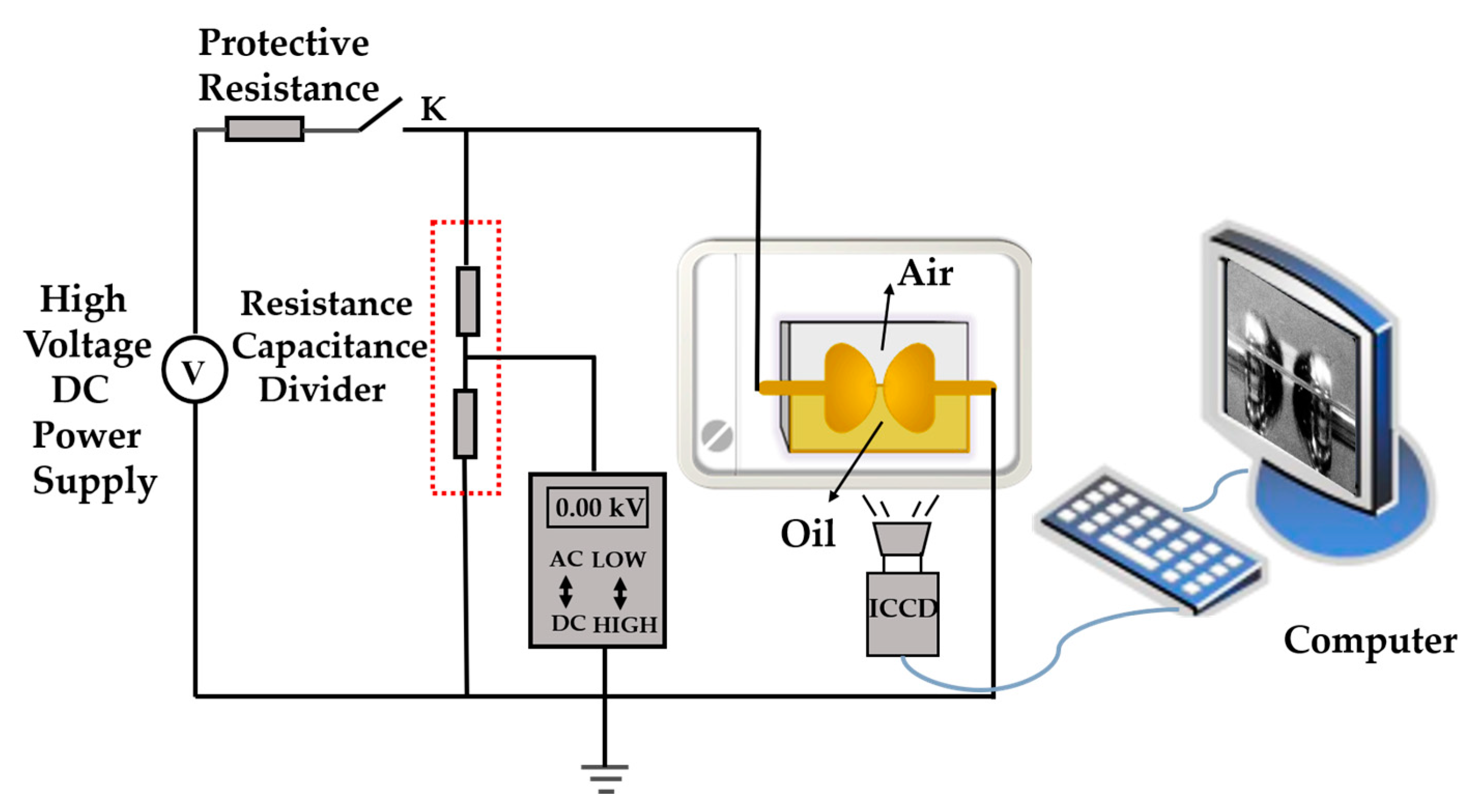
2.2. Test Platform
2.3. Simulation Model
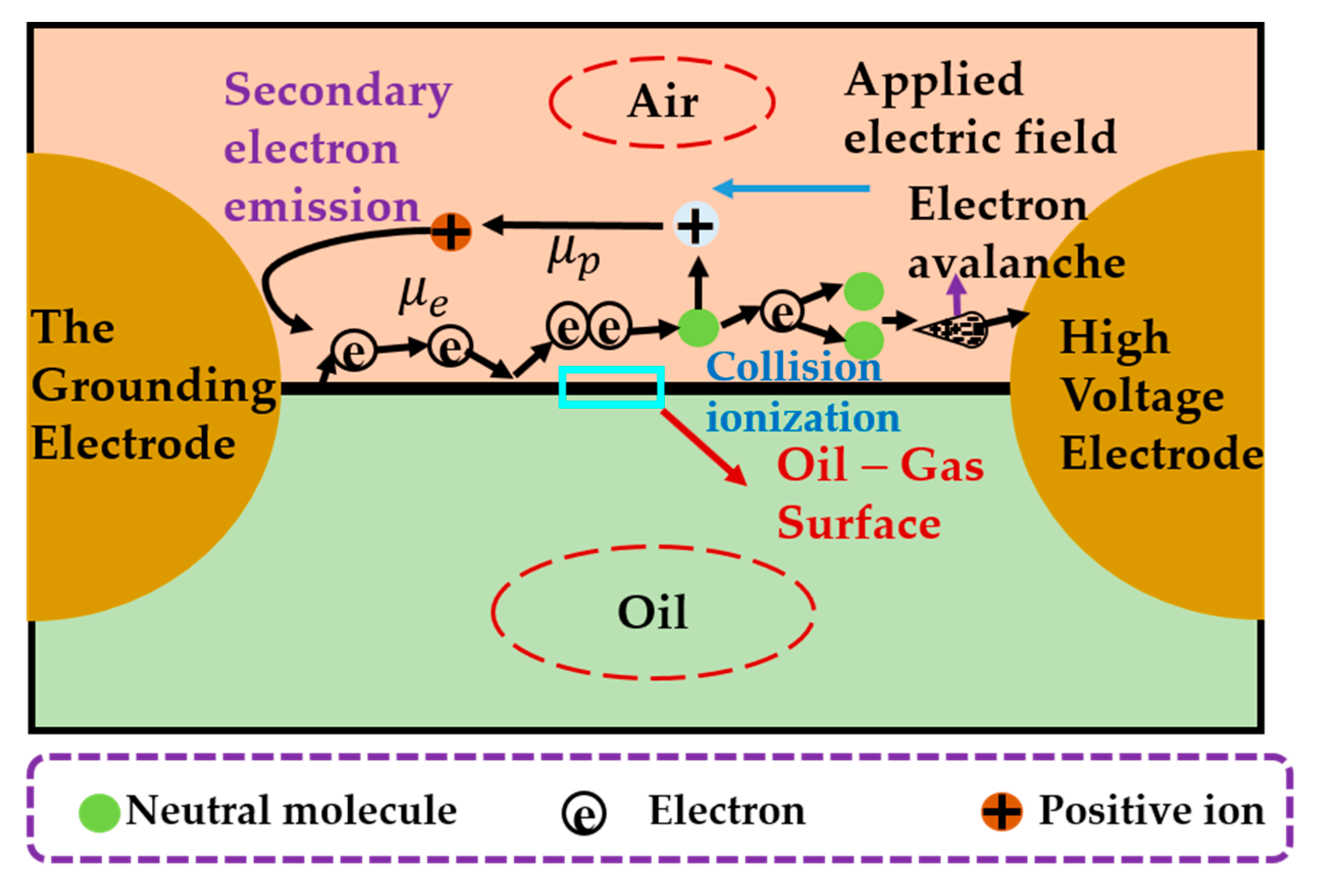
2.3.1. Streamer Discharge Model
2.3.2. Gas–Liquid Two-Phase Flow Model
3. Test Results and Analysis
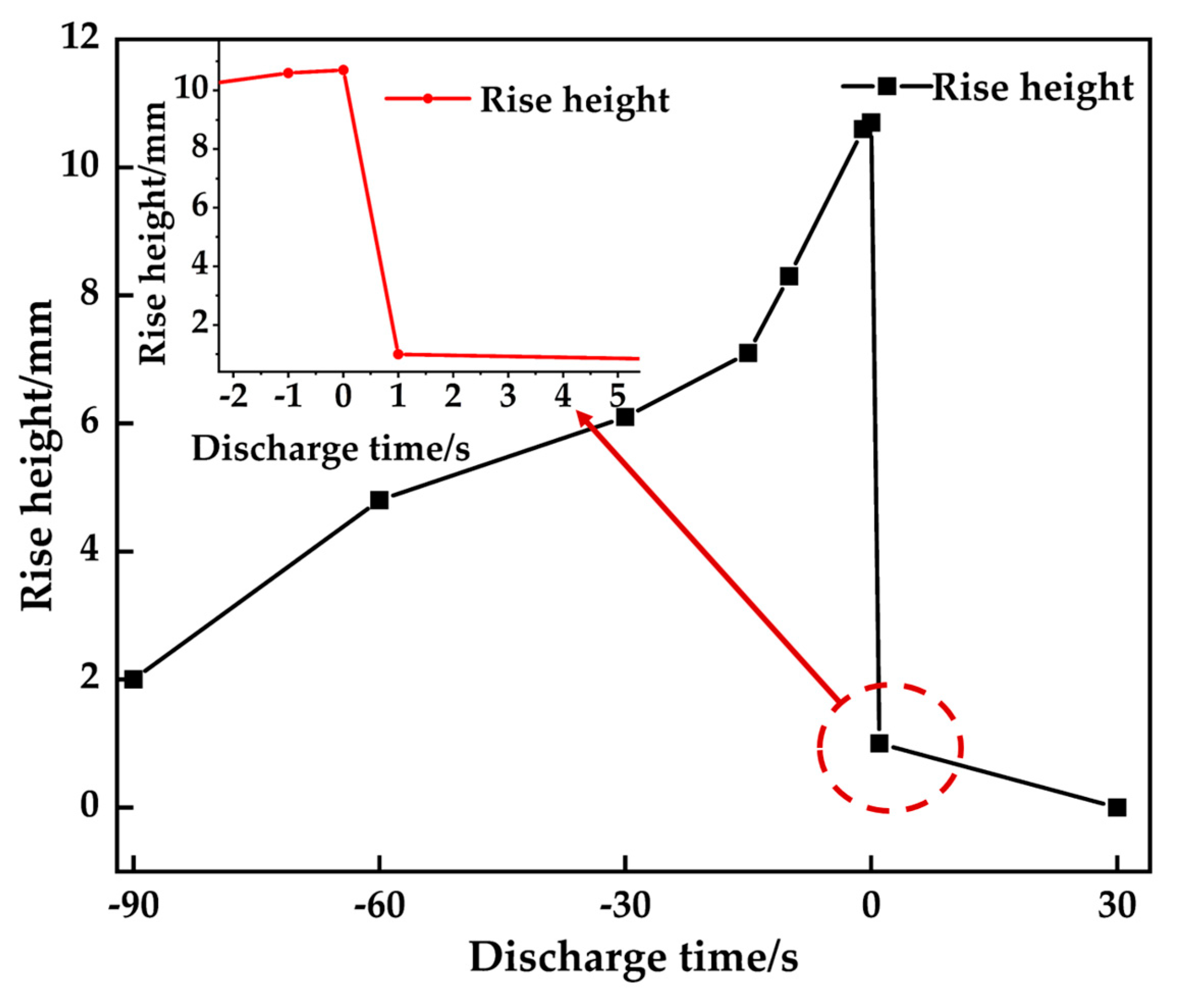
3.1. Initiation and Development of the Oil–Gas Surface Discharge
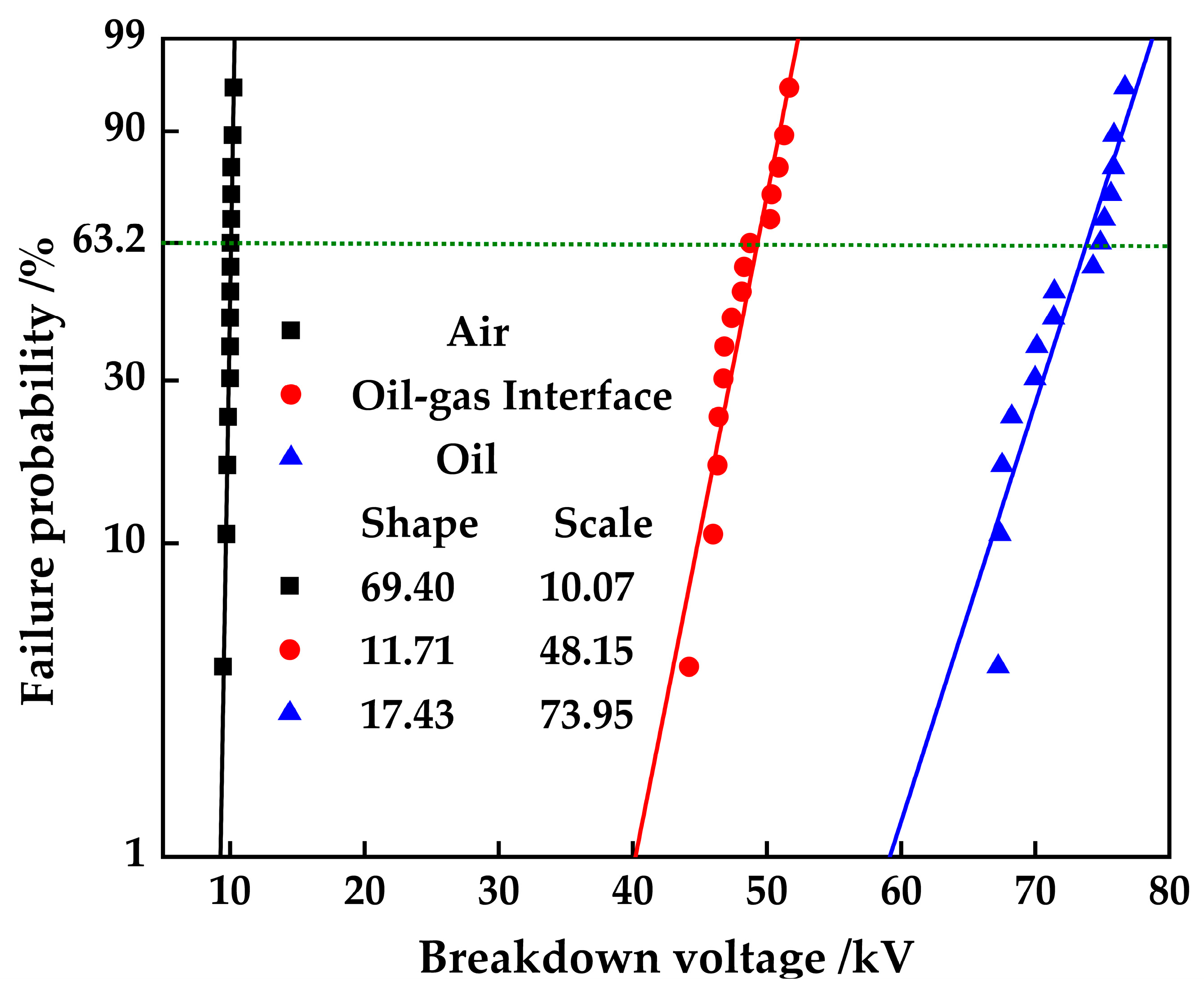
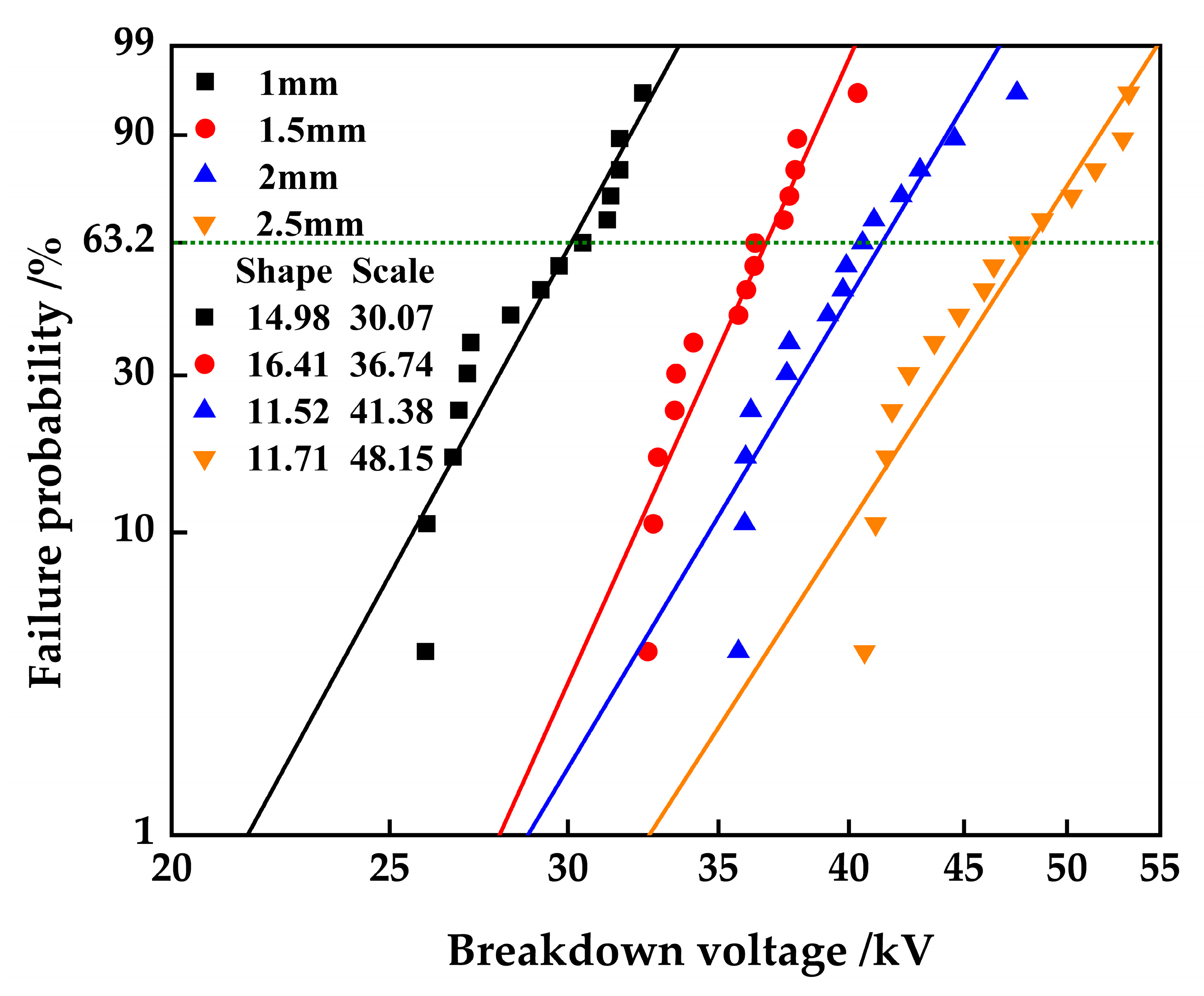
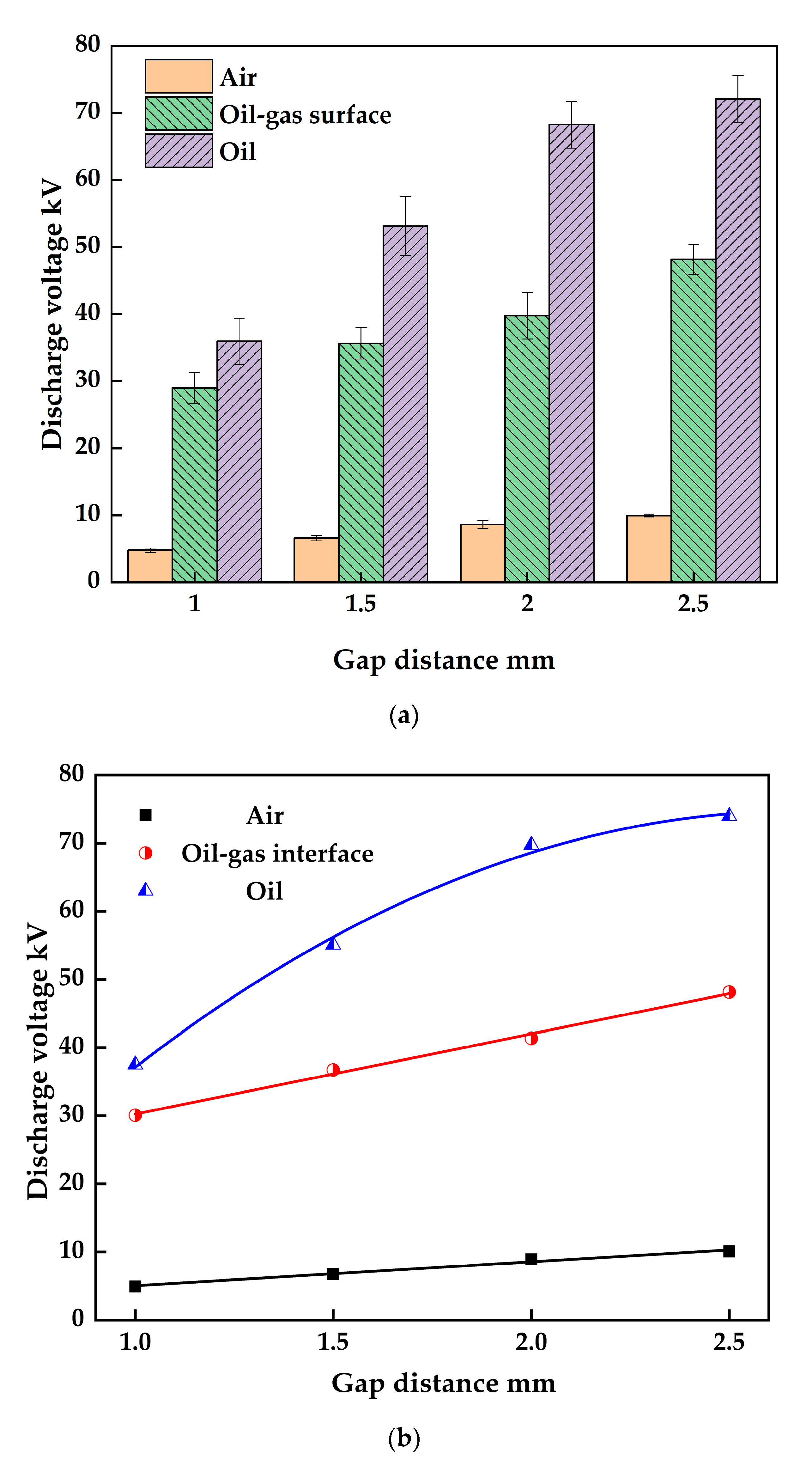
3.2. Discharge Voltage Distribution at Oil–Gas Surface
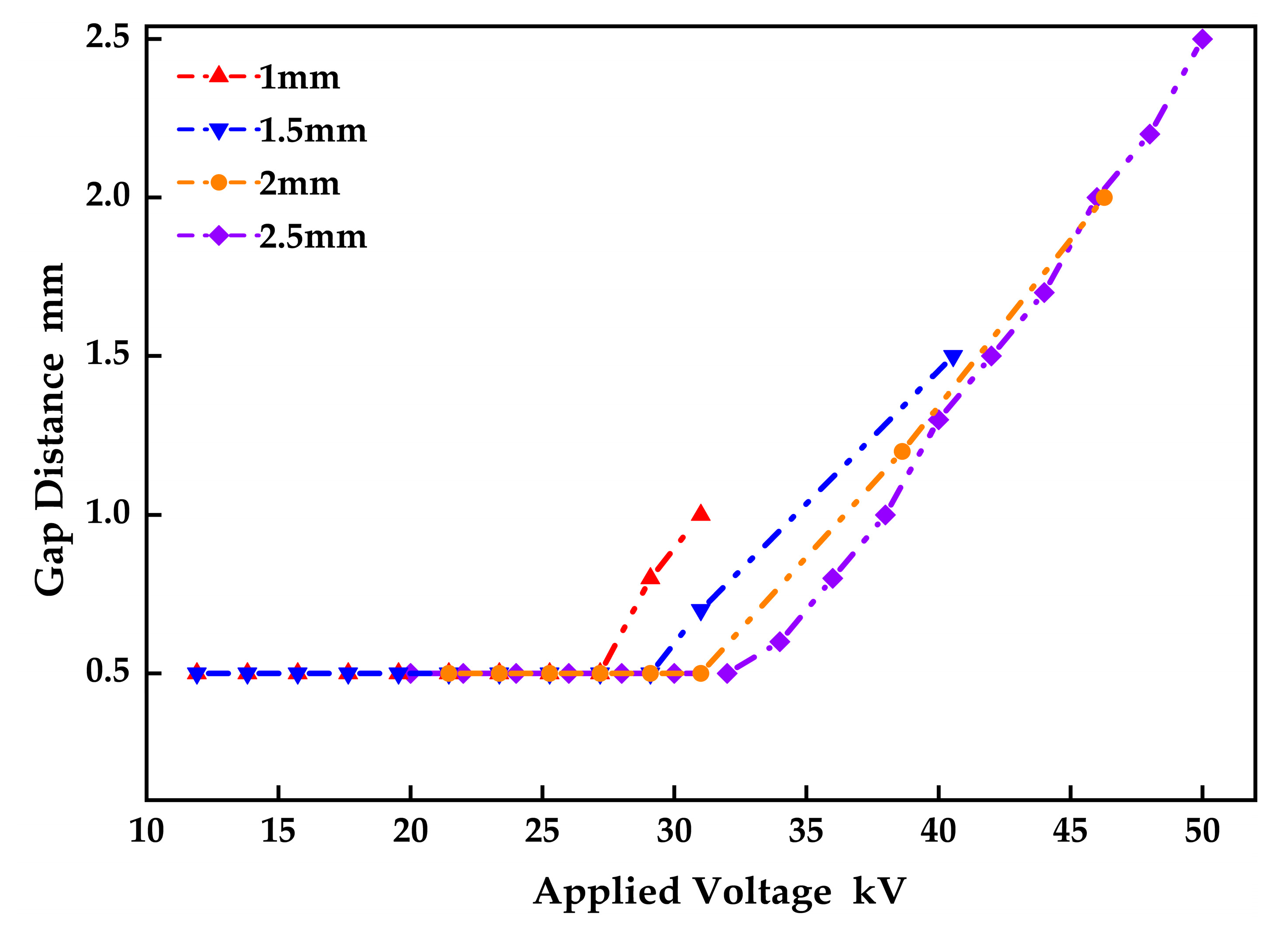
3.3. Effect of Gap Distance on Discharge Voltage at Oil–Gas Surface
4. Simulation Results and Analysis
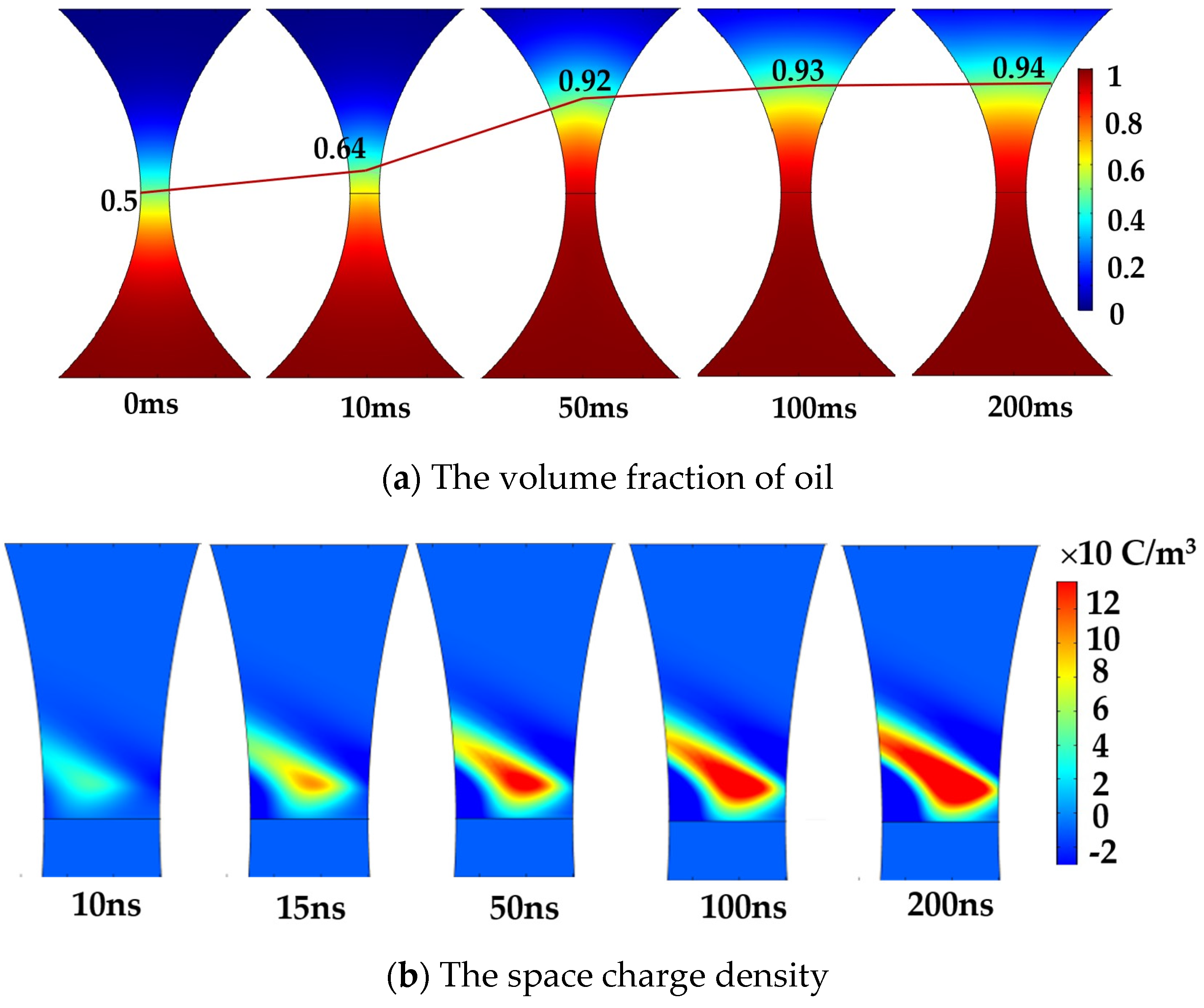
4.1. Development of Oil–Gas Surface Discharge Streamer
4.2. The Influence of Gap Distance on Streamer Development
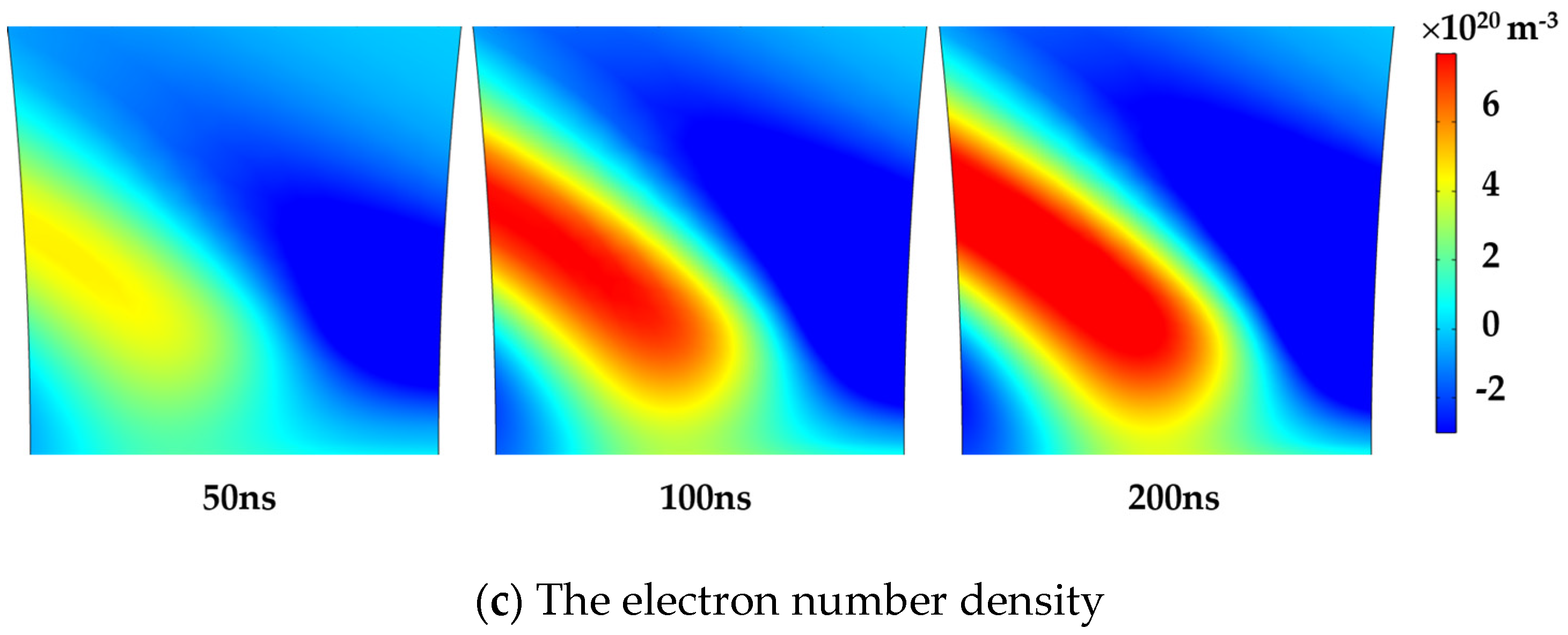
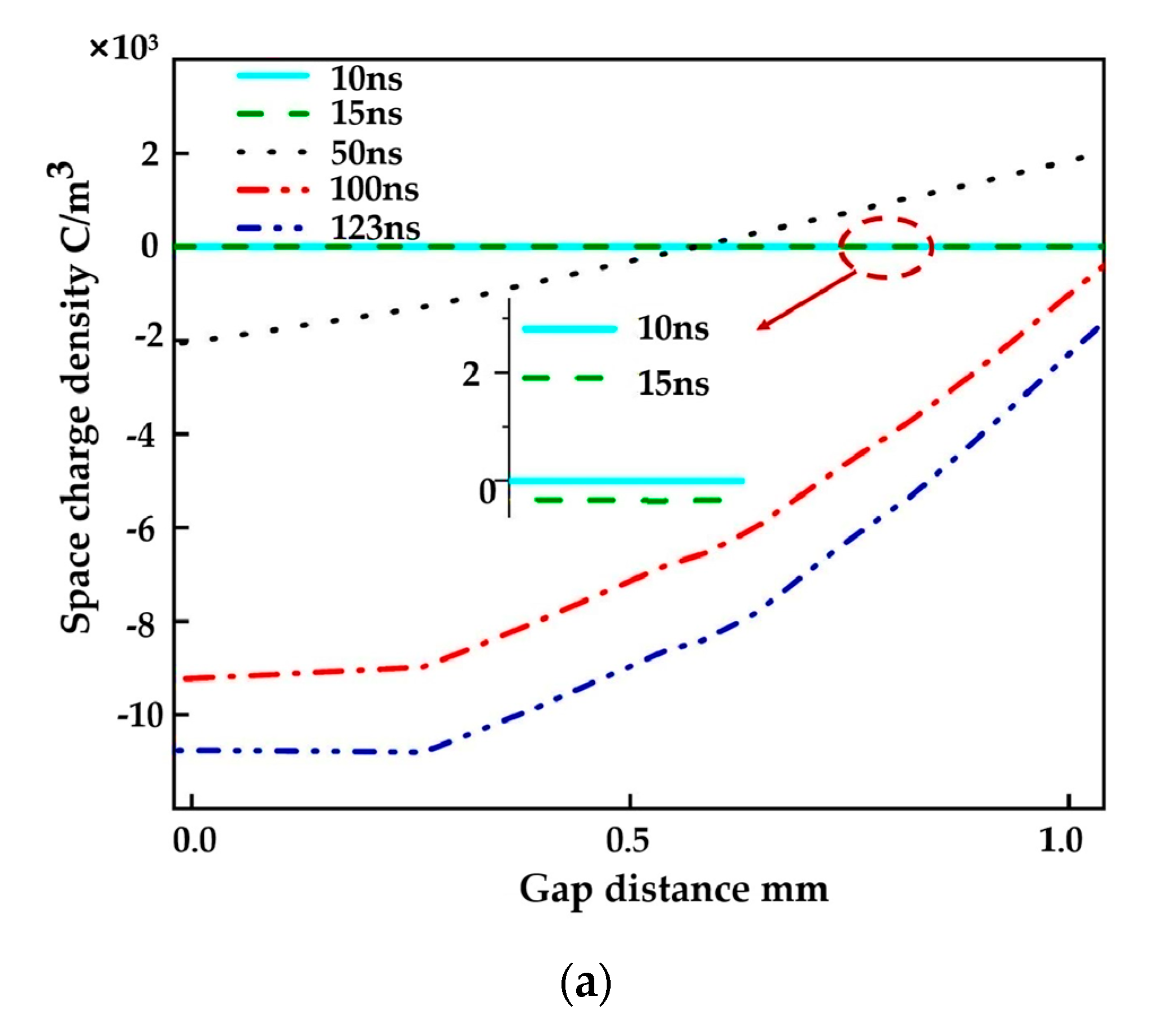
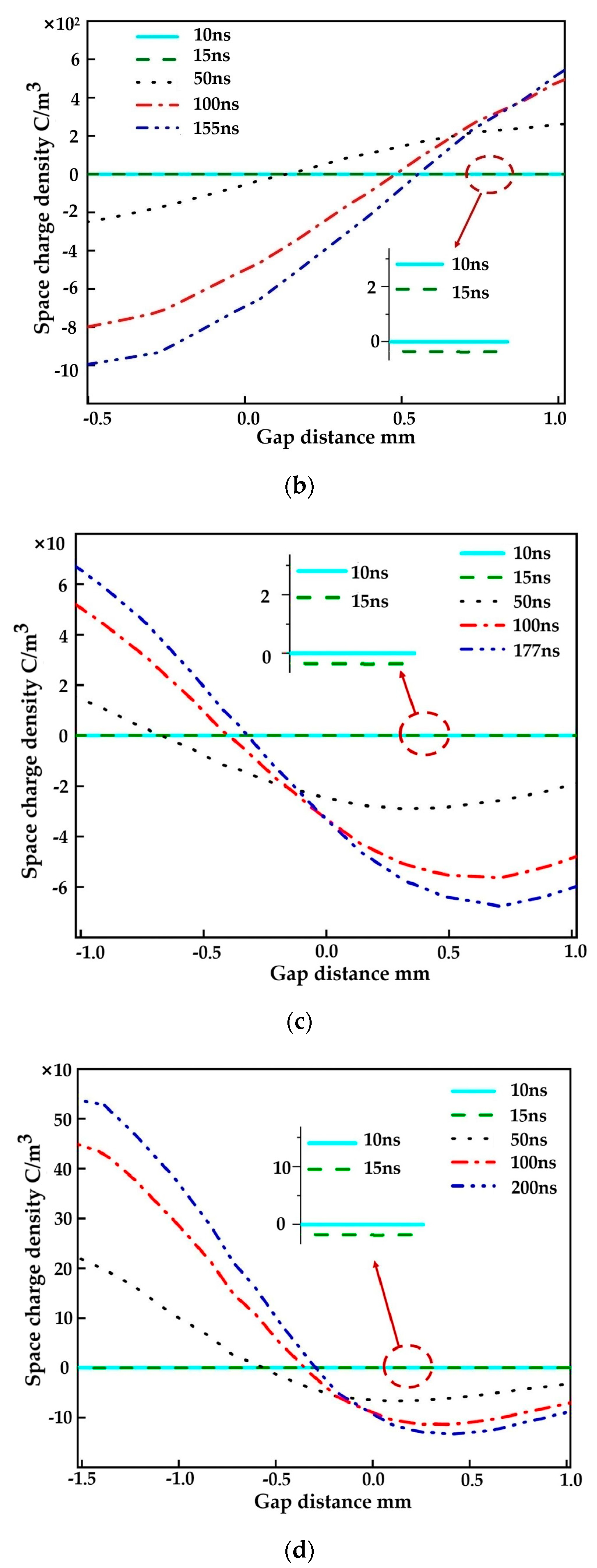
4.3. Effect of Gap Distance on Charge Distribution
4.4. Influence of Gap Distance on Velocity
5. Conclusions
- (1)
- The oil–gas surface discharge starts at the surface and develops towards the air side. The discharge voltage is higher than the air gap discharge voltage.
- (2)
- Oil–gas surface discharge is a typical streamer process. The streamer form is a cathode streamer. It is triggered by the electron emission at the junction of oil, electrode, and gas. Finally, a penetrating conductive channel forms above the initial surface.
- (3)
- As the gap distance increases from 1 mm to 2.5 mm, the average velocity of streamer development increases from 8.13 km/s to 12.5 km/s, an increase of 53.8%. Because the gap distance increases, more gas molecules will be ionized, accelerating the space charge generation.
- (4)
- The electric field strength in the gap can affect the discharge form of the oil–gas surface. If the gap distance increases from 1 mm to 2.5 mm, the discharge voltage will increase by 60%, and the form of the surface discharge streamer will change from the anode streamer to the cathode streamer.
- (5)
- Regarding the content and conclusions of this study, it is found that there are still many aspects that need to be improved. Therefore, future research should delve into the factors affecting oil–gas surface discharge, such as voltage form, gas components, and long gap distance on oil–gas surface discharge.
- (6)
- The study of oil–gas surface discharge in oil-immersed power equipment has significant practical and theoretical significance. It can provide a theoretical basis and technical support for the diagnosis and prediction of faults in power equipment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rafiq, M.; Shafique, M.; Azam, A.; Ateeq, M. The impacts of nanotechnology on the improvement of liquid insulation of transformers: Emerging trends and challenges. J. Mol. Liq. 2020, 302, 112482. [Google Scholar] [CrossRef]
- Li, W.; Wang, J.; Luo, W.H. Analysis and suggestions on the sudden fault of transformer caused by 750 kV bushing defect. High Volt. Appl. 2016, 52, 216–220. [Google Scholar]
- Cigre, J.T.F. 12/14 10-01: Service Performance of HVDC Converter Transformers and Oil-cooled Smoothing Reactors. Electra 1994, 155, 7–32. [Google Scholar]
- Jin, F.B.; Zhou, Y.X.; Huang, M. Influence of DC Voltage Component on Surface Discharge Process of Oil Paper Insulation in AC/DC Composite Electric Field. High Volt. Eng. 2015, 41, 3082–3090. [Google Scholar]
- Zhang, L.; Chen, J.N.; Zhou, Y.X. Progress in the theoretical model and numerical simulation of space charge dynamics in polymer insulation. Chin. J. Electr. Eng. 2022, 42, 3037–3055. [Google Scholar]
- Zhou, Y.X.; Zhao, Y.Z.; Chen, J.N. Flashover characteristics and numerical simulation of oil-paper insulation under dc voltage. Insul. Mater. 2021, 54, 64–72. [Google Scholar]
- Ou, Y.X.; Zhou, Q.; Li, X.F. Analysis of microstructure and electrical performance of oil-immersed insulating paper under different AC and DC composite voltage. Chin. J. Electr. Eng. 2019, 39, 7394–7404. [Google Scholar]
- Jin, F.B.; Zhou, Y.X.; Huang, J.W. Effect of temperature on surface discharge characteristics of oil-paper insulation under AC/DC composite electric field. High Volt. Eng. 2017, 43, 931–939. [Google Scholar]
- Huang, X.; Zhou, Y.X.; Gesang, Q.Z. Construction of Nanocellulose Sandwich-structured Insulating Paper and Its Enhancement for Mechanical and Electrical Properties. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1127–1135. [Google Scholar] [CrossRef]
- Zhang, P.N.; Li, L.; Cheng, Z.G. Simulation and Test Comparison of Core Vibration of Shunt Reactor and Transformer Models. J. Electr. Technol. 2018, 33, 5273–5281. [Google Scholar]
- Cv, L.; Chen, W.G.; Du, J.C. Characteristics of Air Gap Discharge in Vegetable Oil-paper Insulation. J. Electr. Technol. 2018, 33, 618–626. [Google Scholar]
- Zaghdoudi, M.; Lallemand, M. Study of the behavior of a bubble in an electric field: Steady shape and local fluid motion. Int. J. Therm. Sci. 2000, 39, 39–52. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Tang, J.; Pan, C.; Luo, X.Y. Simulation of bubble dynamics and electric field distribution in flowing transformer oil. High Volt. Eng. 2020, 46, 2004–2012. [Google Scholar]
- Chen, F.; Peng, Y.; Song, Y.Z. Experimental visualization of a single bubble in an electric field. J. Sci. Technol. 2007, 47, 722–725. [Google Scholar]
- Morrow, R.; Lowke, J.J. Streamer propagation in the air. J. Appl. Phys. 1997, 30, 61–627. [Google Scholar] [CrossRef]
- Jadidian, J.; Zahn, M.; Lavesson, N. Effects of impulse voltage polarity, peak amplitude, and rise time on streamers initiated from a needle electrode in transformer oil. IEEE Trans. Plasma Sci. 2012, 40, 909–918. [Google Scholar] [CrossRef]
- Lewis, T.J. Basic electrical processes in dielectric liquids. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 630–643. [Google Scholar] [CrossRef]
- Tobazeon, R. Pre-breakdown phenomena in dielectric liquids. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 1132–1147. [Google Scholar] [CrossRef]
- Chen, P.; Chen, G. Numerical Modeling of Partial Discharges in a Solid Dielectric-bounded Cavity: A Review. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 981–1000. [Google Scholar]
- Meek, J.M.; Craggs, J.D. (Eds.) Electrical Breakdown of Gases; John Wiley & Sons: Chichester, UK, 1978. [Google Scholar]
- Zhang, Y.H.; Ma, Q.S. Transmission technique of repetition pulse and intense current electron-beam. Acta Phys. Sin. 2005, 54, 3111–3115. [Google Scholar] [CrossRef]
- Masala, G. Positive streamer propagation in large oil gaps: Electrical properties of streamers. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 371–381. [Google Scholar] [CrossRef]
- Lundgaard, L.; Linhjell, D.; Berg, G. Propagation of positive and negative streamers in oil with and without pressboard surfaces. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 388–395. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. Positive streamer between parallel plate electrodes in atmospheric pressure air. J. Appl. Phys. 1997, 30, 441–450. [Google Scholar] [CrossRef]
- Harada, M.; Ohga, Y.; Watanabe, I. Ionization energies for solvated polycyclic aromatic hydrocarbons. Chem. Phys. Lett. 1999, 303, 489–492. [Google Scholar] [CrossRef]
- Shao, X.J.; Ma, Y.; Li, Y.X.; Zhang, G.J. One-dimensional simulation of low-pressure xenon dielectric barrier discharge. Acta Phys. Sin. 2010, 59, 8747–8754. [Google Scholar] [CrossRef]
- Smalø, H.S.; Hestad, Ø.; Ingebrigtsen, S.; Åstrand, P.O. Field dependence on the molecular ionization potential and excitation energies compared to conductivity models for insulation materials at high electric fields. J. Appl. Phys. 2011, 109, 073306. [Google Scholar] [CrossRef]
- Korobeynikov, S.M.; Ridel, A.V.; Medvedev, D.A. Registration and simulation of partial discharges in free bubbles at AC voltage. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1035–1042. [Google Scholar] [CrossRef]
- Sun, A.; Huo, C.; Zhuang, J. Formation mechanism of streamer discharges in liquids: A review. High Volt. 2016, 1, 74–80. [Google Scholar] [CrossRef]
- Ha, J.; Liu, L.F.; He, S.J. The Mechanism of Electrode Spacing Effect on Cavity Cathode Self Pulsing Discharge Film. High Volt. Eng. 2021, 47, 796–804. [Google Scholar]
- Devins, J.C.; Rzad, S.J.; Schwabe, R.J. Breakdown and pre-breakdown phenomena in liquids. J. Appl. Phys. 1981, 52, 4531–4545. [Google Scholar] [CrossRef]
- Zener, C. A theory of the electrical breakdown of solid dielectrics. Proc. R. Soc. A 1934, 145, 523–529. [Google Scholar]
- Jadidian, J.; Zahn, M. Charge transport analysis in two-phase composite dielectric systems. IEEE Trans. Plasma Sci. 2013, 41, 2464–2474. [Google Scholar] [CrossRef]
- Tobazeon, R.; Filippini, J.C.; Marteau, C. on the measurement of the conductivity of highly insulating liquids. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 1000–1004. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, M.; Wang, Y.; Yan, P. Simulation of two-phase flow discharge in transformer oil under nanosecond pulse. Intense Laser Part. Beam 2020, 32, 63–67. [Google Scholar]
- Mahjour, S.K. Evaluation of unsupervised machine learning frameworks to select representative geological realizations for uncertainty quantification. J. Petrol. Sci. Eng. 2022, 209, 109822. [Google Scholar] [CrossRef]
- Ahmadi, S. Proposing a modified mechanism for determination of hydrocarbons dynamic viscosity, using artificial neural network. Petrol. Sci. Technol. 2020, 38, 699–705. [Google Scholar] [CrossRef]
- Soltanmohammadi, R. Insights into Multi-Phase Flow Pattern Characteristics and Petrophysical Properties in Heterogeneous Porous Media. EarthDoc 2021, 2021, 1–5. [Google Scholar]
- Shao, T.; Sun, G.S.; Yan, P. Calculation of escape process of high energy fast electrons under nanosecond pulse. J. Phys. 2006, 11, 5964–5968. [Google Scholar]
- Fujita, H.; Kanazawa, S.; Ohtani, K. Initiation process and propagation mechanism of positive streamer discharge in water. J. Appl. Phys. 2014, 116, 213–301. [Google Scholar] [CrossRef]
- Xiang, C.M.; Zhou, Q.; Li, J. Gas production characteristics of vegetable insulating oils under thermal decomposition based on molecular dynamic simulation. High Volt. Eng. 2018, 44, 3595–3603. [Google Scholar]


| Name | Symbol | Numerical Value |
|---|---|---|
| Intermolecular distance/m | a | 3.0 × 10−10 |
| Ionization energy/eV | ∆ | 7.5 |
| Number of ionizable molecules/m−3 | n0 | 1 × 10−25 |
| Recombination of positive and negative ions/m3/s | Rpn | 1.64 × 10−17 |
| Positive ion and electron recombination/m3/s | Rpe | 1.64 × 10−17 |
| Mobility of positive ions/m2/(V·s) | μm,cp | 1 × 10−9 |
| Negative ion mobility/m2/(V·s) | μm,cn | 1 × 10−9 |
| Electronic mobility/m2/(V·s) | μm,ce | 1 × 10−4 |
| Electron adsorption time constant/ns | Ta | 200 |
| Name | Symbol | Numerical Value |
|---|---|---|
| Collision ionization coefficient/m−1 | α0 | 25 |
| Mobility of positive ions/m2/(V·s) | μm,cp | 1 × 10−7 |
| Negative ion mobility/m2/(V·s) | μm,cn | 1 × 10−7 |
| Electronic mobility/m2/(V·s) | μm,ce | 1 × 10−2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Yang, X.; Li, Y.; Jiang, G.; Chen, J. Discharge Characteristics and Numerical Simulation of the Oil–Gas Surface under DC Voltage. Energies 2023, 16, 3558. https://doi.org/10.3390/en16083558
Zhou Y, Yang X, Li Y, Jiang G, Chen J. Discharge Characteristics and Numerical Simulation of the Oil–Gas Surface under DC Voltage. Energies. 2023; 16(8):3558. https://doi.org/10.3390/en16083558
Chicago/Turabian StyleZhou, Yuanxiang, Xiaojing Yang, Yuhang Li, Guiming Jiang, and Jianning Chen. 2023. "Discharge Characteristics and Numerical Simulation of the Oil–Gas Surface under DC Voltage" Energies 16, no. 8: 3558. https://doi.org/10.3390/en16083558
APA StyleZhou, Y., Yang, X., Li, Y., Jiang, G., & Chen, J. (2023). Discharge Characteristics and Numerical Simulation of the Oil–Gas Surface under DC Voltage. Energies, 16(8), 3558. https://doi.org/10.3390/en16083558






