Pore Structure and Fractal Characteristics of Coal-Measure Sedimentary Rocks Using Nuclear Magnetic Resonance (NMR) and Mercury Intrusion Porosimetry (MIP)
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. MIP Measurements
2.3. NMR Measurements
3. Results
3.1. TOC and Mineralogical Compositions
3.2. Petrophysical Properties
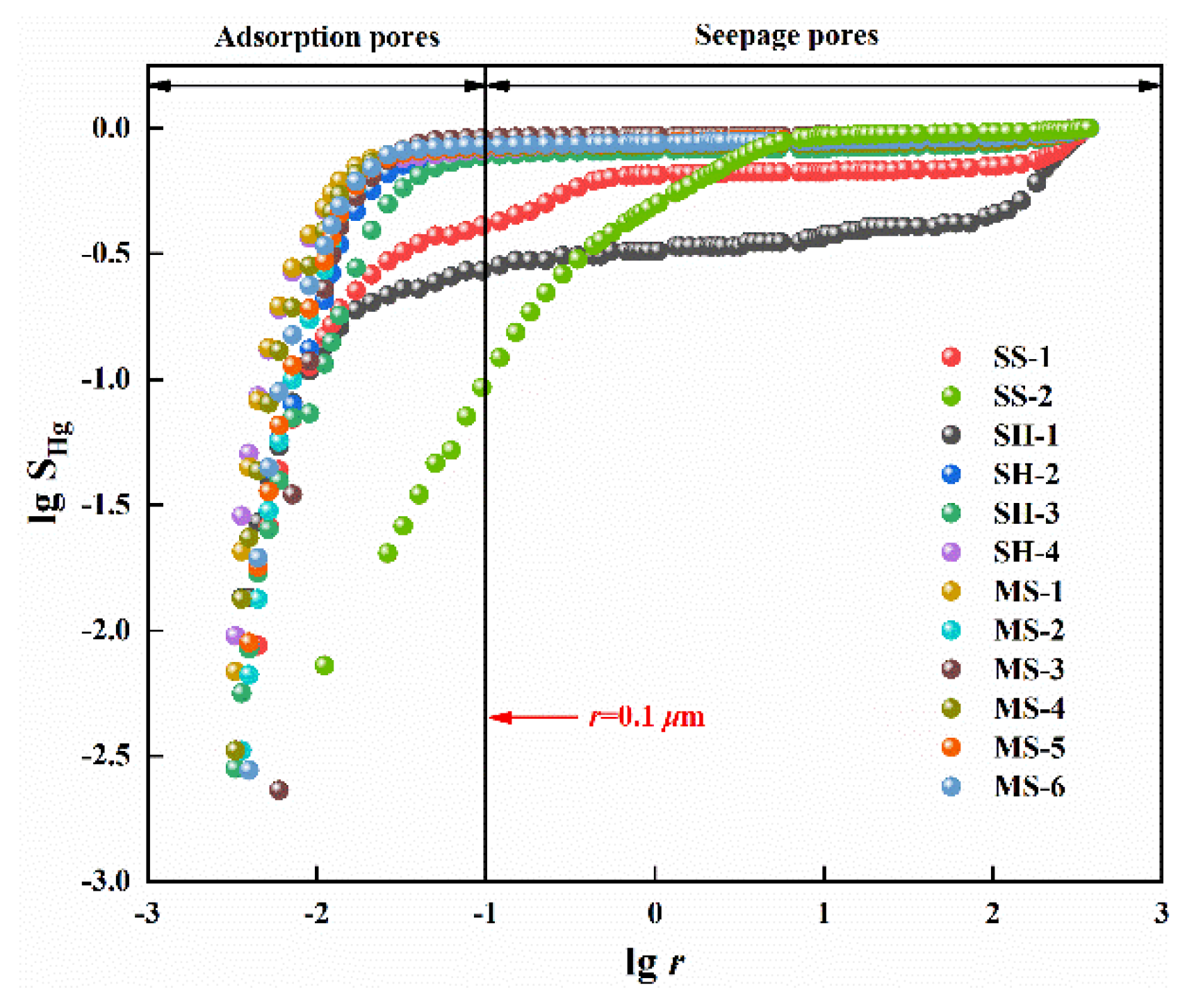
3.3. Pore Size Distributions (PSDs) Determined by MIP
3.4. T2 Distributions and PSD Determined by NMR
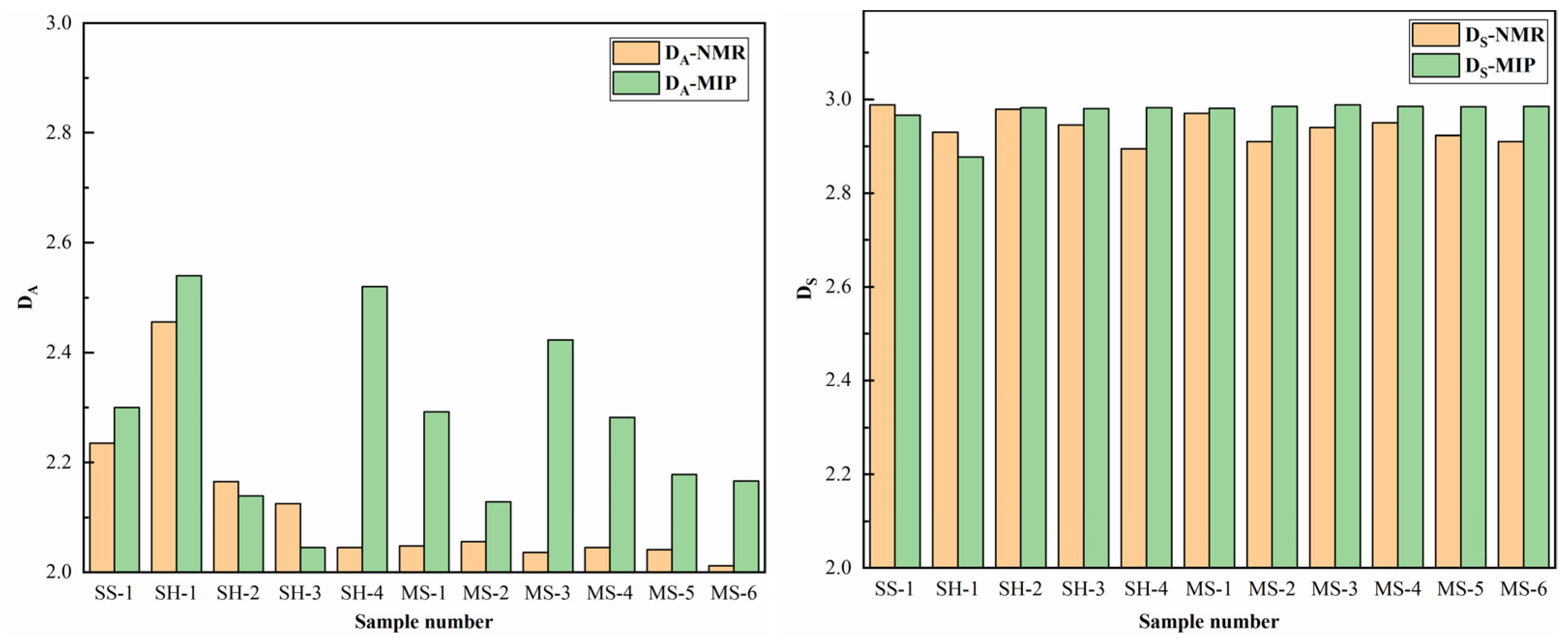
3.5. Fractal Dimension Calculated Using MIP
3.6. Fractal Dimension Calculation Using NMR
4. Discussion
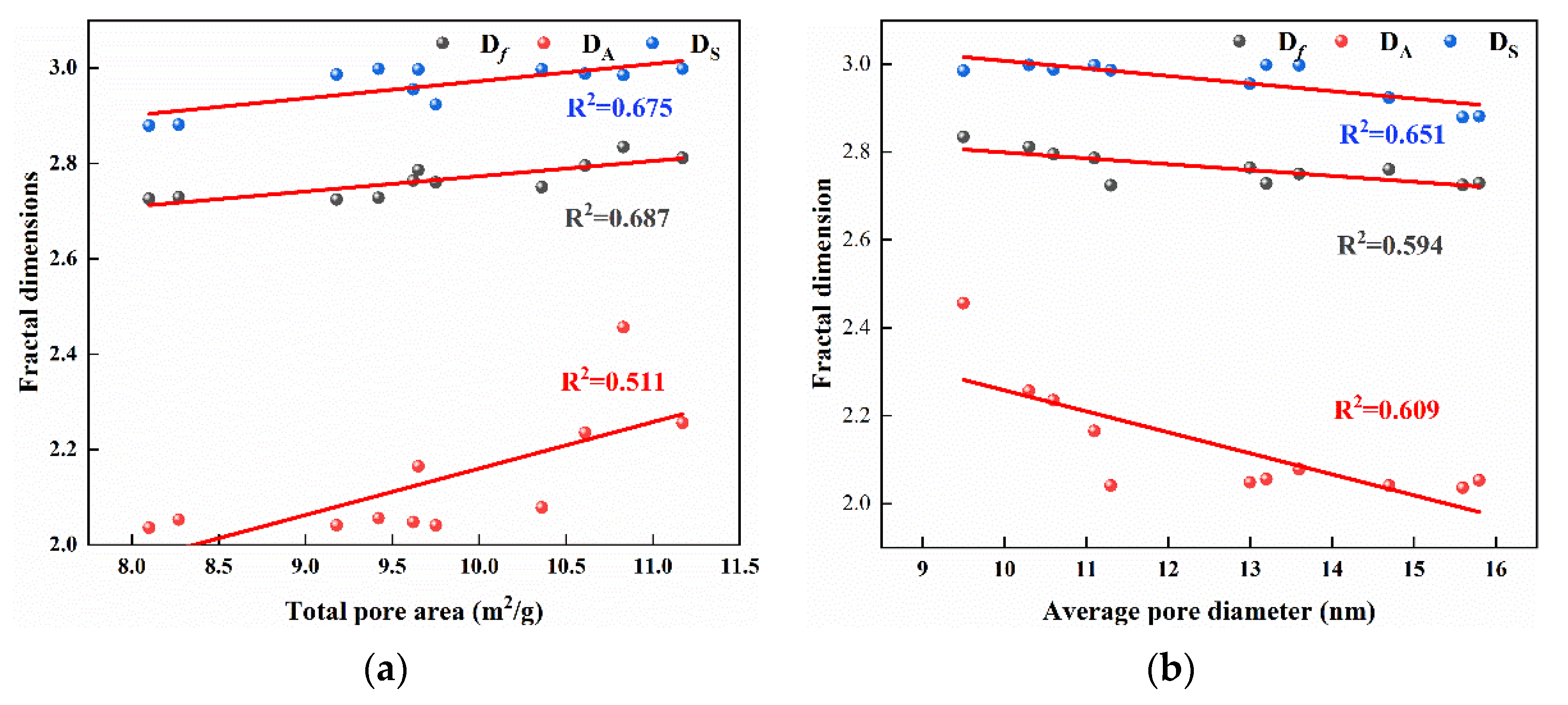
4.1. Correlation between Physical Properties and Multifractal Dimensions
4.2. Correlation between Minerals and Multifractal Dimensions
4.3. Fractal Dimension Mathematical Model
5. Conclusions
- (1)
- The investigated samples are dominated by clay minerals and quartz, with TOC contents ranging from 0.03% to 10.81%. The main composition of clay minerals is kaolinite and chlorite.
- (2)
- The pore structure features of the investigated samples reveal obvious deviations. All the PSD curves are unimodal distributions. The sandstone (SS-1), mudstone, and shale are mainly with nanopores of 0.01–1 μm, while the sandstone (SS-2) is dominated by mesopores and macropores of 1–100 μm.
- (3)
- The pore structures of the investigated samples show prominent multipartite characteristics using MIP and NMR tests. Multifractal dimensions can better characterize the heterogeneity of rock samples, in which DA reflects the surface structure of micropores, while DS represents the pore structure of macropores.
- (4)
- Multifractal dimensions are affected by many factors, in which DA is greatly influenced by the pore surface features and mineral components and DS by average pore diameters. Moreover, the multivariate linear regression model of adsorption pores and seepage pores were established, respectively, which has a better correlation effect on the multifractal dimensions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, C.N.; Yang, Z.; Tao, S.Z.; Yuan, X.J.; Zhu, R.K.; Hou, L.H.; Wu, S.T.; Sun, L.; Zhang, G.S.; Bai, B.; et al. Continuous hydrocarbon accumulation over a large area as a distinguishing characteristic of unconventional petroleum: The Ordos Basin, North-Central China. Earth-Sci. Rev. 2013, 126, 358–369. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Cheng, H. Gas Adsorption Characterization of Pore Structure of Organic-rich Shale: Insights into Contribution of Organic Matter to Shale Pore Network. Nat. Resour. Res. 2021, 30, 2377–2395. [Google Scholar] [CrossRef]
- Xu, S.; Hu, E.; Li, X.; Xu, Y. Quantitative Analysis of Pore Structure and Its Impact on Methane Adsorption Capacity of Coal. Nat. Resour. Res. 2020, 30, 605–620. [Google Scholar] [CrossRef]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Hammes, U. Spectrum of pore types and networks in mudrocks and a descriptive classification for matrix-related mudrock pores. Aapg. Bull. 2012, 96, 1071–1098. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Solano, N.; Bustin, R.M.; Bustin, A.M.M.; Chalmers, G.R.L.; He, L.; Melnichenko, Y.B.; Radliński, A.P.; Blach, T.P. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar] [CrossRef]
- Jiang, J.; Yang, W.; Cheng, Y.; Zhao, K.; Zheng, S. Pore structure characterization of coal particles via MIP, N2 and CO2 adsorption: Effect of coalification on nanopores evolution. Powder Technol. 2019, 354, 136–148. [Google Scholar] [CrossRef]
- Yang, X.; Guo, S. Comparative analysis of shale pore size characterization methods. Pet. Sci. Technol. 2020, 38, 793–799. [Google Scholar] [CrossRef]
- Shi, X.; Xu, H.; Che, M.; Xiao, C.; Ni, H.; Gao, Q. Investigations of fracture behavior and pore structure change in pulse fracturing for cement block. Int. J. Rock. Mech. Min. Sci. 2023, 166, 105366. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, Y.; Yuan, L.; Xu, Q. Impact of nanopore structure on coal strength: A study based on synchrotron radiation nano-CT. Results Phys. 2020, 17, 103029. [Google Scholar] [CrossRef]
- Liu, S.; Huang, Z. Exploration of microstructure characteristics and mechanical behaviors of thermal-damaged argillaceous sandstone via LF-NMR and µ-CT technologies. Geomech. Geophys. Geo 2023, 9, 27. [Google Scholar] [CrossRef]
- Zhang, N.; Zhao, F.; Guo, P.; Li, J.; Gong, W.; Guo, Z.; Sun, X. Nanoscale Pore Structure Characterization and Permeability of Mudrocks and Fine-Grained Sandstones in Coal Reservoirs by Scanning Electron Microscopy, Mercury Intrusion Porosimetry, and Low-Field Nuclear Magnetic Resonance. Geofluids 2018, 2018, 2905141. [Google Scholar] [CrossRef]
- He, J.; Ding, W.; Li, A.; Sun, Y.; Dai, P.; Yin, S.; Chen, E.; Gu, Y. Quantitative microporosity evaluation using mercury injection and digital image analysis in tight carbonate rocks: A case study from the Ordovician in the Tazhong Palaeouplift, Tarim Basin, NW China. J. Nat. Gas. Sci. Eng. 2016, 34, 627–644. [Google Scholar] [CrossRef]
- Yang, R.; He, S.; Yi, J.; Hu, Q. Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi shale from Jiaoshiba area, Sichuan Basin: Investigations using FE-SEM, gas adsorption and helium pycnometry. Mar. Pet. Geol. 2016, 70, 27–45. [Google Scholar] [CrossRef]
- Fu, H.; Yan, D.; Yao, C.; Su, X.; Wang, X.; Wang, H.; Li, Y. Pore Structure and Multi-Scale Fractal Characteristics of Adsorbed Pores in Marine Shale: A Case Study of the Lower Silurian Longmaxi Shale in the Sichuan Basin, China. J. Earth Sci. 2022, 33, 1278–1290. [Google Scholar] [CrossRef]
- Song, Z.; Liu, G.; Yang, W.; Zou, H.; Sun, M.; Wang, X. Multi-fractal distribution analysis for pore structure characterization of tight sandstone—A case study of the Upper Paleozoic tight formations in the Longdong District, Ordos Basin. Mar. Pet. Geol. 2018, 92, 842–854. [Google Scholar] [CrossRef]
- Wang, T.; Tian, F.; Deng, Z.; Hu, H.; Xie, Z.; Liu, D. The Pore Structure of Marine to Continental Transitional Shales in the Permian Shanxi Formation on the East Margin of the Ordos Basin, China. Geofluids 2022, 2022, 5601862. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, S.; Zhao, F.; Sun, X.; He, M. Characterization of the Pore Structure and Fluid Movability of Coal-Measure Sedimentary Rocks by Nuclear Magnetic Resonance (NMR). ACS Omega 2021, 6, 22831–22839. [Google Scholar] [CrossRef]
- Wu, B.; Xie, R.; Wang, X.; Wang, T.; Yue, W. Characterization of pore structure of tight sandstone reservoirs based on fractal analysis of NMR echo data. J. Nat. Gas Sci. Eng. 2020, 81, 103483. [Google Scholar] [CrossRef]
- Li, Z.; Shen, X.; Qi, Z.; Hu, R. Study on the pore structure and fractal characteristics of marine and continental shale based on mercury porosimetry, N2 adsorption and NMR methods. J. Nat. Gas Sci. Eng. 2018, 53, 12–21. [Google Scholar] [CrossRef]
- Al-Yaseri, A.Z.; Lebedev, M.; Vogt, S.J.; Johns, M.L.; Barifcani, A.; Iglauer, S. Pore-scale analysis of formation damage in Bentheimer sandstone with in-situ NMR and micro-computed tomography experiments. J. Pet. Sci. Eng. 2015, 129, 48–57. [Google Scholar] [CrossRef]
- Xie, R.; Wu, Y.; Liu, K.; Liu, M.; Xiao, L. De-noising methods for NMR logging echo signals based on wavelet transform. J. Geophys. Eng. 2014, 11, 035003. [Google Scholar] [CrossRef]
- Xie, W.; Yin, Q.; Zeng, J.; Wang, G.; Feng, C.; Zhang, P. Fractal-Based Approaches to Pore Structure Investigation and Water Saturation Prediction from NMR Measurements: A Case Study of the Gas-Bearing Tight Sandstone Reservoir in Nanpu Sag. Fractal Fract. 2023, 7, 273. [Google Scholar] [CrossRef]
- Guo, X.; Huang, Z.; Zhao, L.; Han, W.; Ding, C.; Sun, X.; Yan, R.; Zhang, T.; Yang, X.; Wang, R. Pore structure and multi-fractal analysis of tight sandstone using MIP, NMR and NMRC methods: A case study from the Kuqa depression, China. J. Pet. Sci. Eng. 2019, 178, 544–558. [Google Scholar] [CrossRef]
- Wang, G.; Han, D.; Qin, X.; Liu, Z.; Liu, J. A comprehensive method for studying pore structure and seepage characteristics of coal mass based on 3D CT reconstruction and NMR. Fuel 2020, 281, 118735. [Google Scholar] [CrossRef]
- Wang, J.; Cao, Y.; Liu, K.; Gao, Y.; Qin, Z. Fractal characteristics of the pore structures of fine-grained, mixed sedimentary rocks from the Jimsar Sag, Junggar Basin: Implications for lacustrine tight oil accumulations. J. Pet. Sci. Eng. 2019, 182, 106363. [Google Scholar] [CrossRef]
- Ramia, M.E.; Martín, C.A. Sedimentary rock porosity studied by electromagnetic techniques: Nuclear magnetic resonance and dielectric permittivity. Appl. Phys. A 2014, 118, 769–777. [Google Scholar] [CrossRef]
- Gao, H.; Li, H. Determination of movable fluid percentage and movable fluid porosity in ultra-low permeability sandstone using nuclear magnetic resonance (NMR) technique. J. Pet. Sci. Eng. 2015, 133, 258–267. [Google Scholar] [CrossRef]
- Li, X.; Kang, Y.; Haghighi, M. Investigation of pore size distributions of coals with different structures by nuclear magnetic resonance (NMR) and mercury intrusion porosimetry (MIP). Measurement 2018, 116, 122–128. [Google Scholar] [CrossRef]
- Wang, F.; Yang, K.; Cai, J. Fractal characterization of tight oil reservoir pore structure using nuclear magnetic resonance and mercury intrusion porosimetry. Fractals 2018, 26, 1840017. [Google Scholar] [CrossRef]
- Wang, F.; Yang, K.; You, J.; Lei, X. Analysis of pore size distribution and fractal dimension in tight sandstone with mercury intrusion porosimetry. Results Phys. 2019, 13, 102283. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, S.; Wang, J.; Hu, Q.; Wang, M.; Chao, J. Applying Fractal Theory to Characterize the Pore Structure of Lacustrine Shale from the Zhanhua Depression in Bohai Bay Basin, Eastern China. Energy Fuels 2018, 32, 7539–7556. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G. Fractal analysis of tight gas sandstones using high-pressure mercury intrusion techniques. J. Nat. Gas Sci. Eng. 2015, 24, 185–196. [Google Scholar] [CrossRef]
- Turlapati, V.Y.; Prusty, B.K.; Bakshi, T. Detailed Pore Structure Study of Damodar Valley and Upper Assam Basin Shales Using Fractal Analysis. Energy Fuels 2020, 34, 14001–14011. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Wei, Q.; Sun, K.; Zhang, G.; Wang, F. Characterization of Full-Sized Pore Structure and Fractal Characteristics of Marine–Continental Transitional Longtan Formation Shale of Sichuan Basin, South China. Energy Fuels 2017, 31, 10490–10504. [Google Scholar] [CrossRef]
- Zhou, L.; Kang, Z. Fractal characterization of pores in shales using NMR: A case study from the Lower Cambrian Niutitang Formation in the Middle Yangtze Platform, Southwest China. J. Nat. Gas Sci. Eng. 2016, 35, 860–872. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Che, Y.; Tang, D.; Tang, S.; Huang, W. Petrophysical characterization of coals by low-field nuclear magnetic resonance (NMR). Fuel 2010, 89, 1371–1380. [Google Scholar] [CrossRef]
- Fan, X.; Wang, G.; Li, Y.; Dai, Q.; Linghu, S.; Duan, C.; Zhang, C.; Zhang, F. Pore structure evaluation of tight reservoirs in the mixed siliciclastic-carbonate sediments using fractal analysis of NMR experiments and logs. Mar. Pet. Geol. 2019, 109, 484–493. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, G.; Dong, Y.; Danesh, N.N.; Chen, Z.; Zhang, T. Comparison of low-field NMR and microfocus X-ray computed tomography in fractal characterization of pores in artificial cores. Fuel 2017, 210, 217–226. [Google Scholar] [CrossRef]
- ISO/WD 19990:2023; Natural Stones—Determination of Water Absorption, Density, Porosity, and Bulk Specific Gravity. International Organization for Standardization: Geneva, Switzerland, 2023.
- ISO 10370:2014; Petroleum Products—Determination of Carbon Residue—Micro Method. International Organization for Standardization: Geneva, Switzerland, 2014.
- ISO 14689:2017; Geotechnical Investigation and Testing—Identification, Description and Classification of Rock. Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 15901-1:2016; Evaluation of Pore Size Distribution and Porosity of Solid Materials by Mercury Porosimetry and Gas Adsorption—Part 1: Mercury Porosimetry. International Organization for Standardization: Geneva, Switzerland, 2016.
- Lai, J.; Wang, G.; Fan, Z.; Chen, J.; Wang, S.; Zhou, Z.; Fan, X. Insight into the Pore Structure of Tight Sandstones Using NMR and HPMI Measurements. Energy Fuels 2016, 30, 10200–10214. [Google Scholar] [CrossRef]
- Zhang, P.; Lu, S.; Li, J.; Chen, C.; Xue, H.; Zhang, J. Petrophysical characterization of oil-bearing shales by low-field nuclear magnetic resonance (NMR). Mar. Pet. Geol. 2018, 89, 775–785. [Google Scholar] [CrossRef]
- ASTM E2977-14; Standard Practice For Measuring and Reporting Performance Of Fourier-Transform Nuclear Magnetic Resonance (FT-NMR) Spectrometers For Liquid Samples. American Society for Testing and Materials: West Conshohocken, PA, USA, 2014.
- Cheng, M.; Li, C.; Zhou, L.; Feng, L.; Algeo, T.J.; Zhang, F.; Romaniello, S.; Jin, C.; Ling, H.; Jiang, S. Transient deep-water oxygenation in the early Cambrian Nanhua Basin, South China. Geochim. Cosmochim. Acta 2017, 210, 42–58. [Google Scholar] [CrossRef]
- Ge, X.; Fan, Y.; Zhu, X.; Li, R. Determination of nuclear magnetic resonance T-2 cutoff value based on multifractal theory—An application in sandstone with complex pore structure. Geophysics 2015, 80, D11–D21. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Lu, S.; Zhang, P.; Cai, J.; Zhao, J.; Li, W. Microdistribution and mobility of water in gas shale: A theoretical and experimental study. Mar. Pet. Geol. 2019, 102, 496–507. [Google Scholar] [CrossRef]
- Shao, X.; Pang, X.; Li, H.; Zhang, X. Fractal Analysis of Pore Network in Tight Gas Sandstones Using NMR Method: A Case Study from the Ordos Basin, China. Energy Fuels 2017, 31, 10358–10368. [Google Scholar] [CrossRef]
- Ji, W.; Song, Y.; Jiang, Z.; Meng, M.; Liu, Q.; Chen, L.; Wang, P.; Gao, F.; Huang, H. Fractal characteristics of nano-pores in the Lower Silurian Longmaxi shales from the Upper Yangtze Platform, south China. Mar. Pet. Geol. 2016, 78, 88–98. [Google Scholar] [CrossRef]






| Sample No. | Lithology | Petrographic Characteristics |
|---|---|---|
| SS-1 | sandstone | Caesious sandstone with good gradation and fine psephicity of grains |
| SS-2 | Grey–white fine sandstone with good gradation of detrital grains | |
| SH-1 | shale | Brown laminar shale with noticeable rhyolitic structure |
| SH-2 | Dark-grey laminated silty shale | |
| SH-3 | Grey laminated silty shale | |
| SH-4 | Brown laminated silty shale | |
| MS-1 | mudstone | Gray massive mudstone |
| MS-2 | Gray massive mudstone | |
| MS-3 | Yellow–gray massive mudstone | |
| MS-4 | Gray massive mudstone | |
| MS-5 | Dark-gray massive mudstone | |
| MS-6 | Gray massive mudstone |
| Sample No. | TOC (%) | Minerals (%) | Clay Minerals (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Clay Minerals | Quartz | K-Feldspar | Plagioclase | Kaolinite | Chlorite | Illite | I/S | %S | ||
| SS-1 | 0.03 | 30 | 43 | 8 | 19 | 77 | 9 | 4 | 10 | 30 |
| SS-2 | 0.06 | 12 | 54 | 11 | 17 | 89 | 6 | 3 | 2 | 25 |
| SH-1 | 10.81 | 26 | 52 | 5 | 13 | 60 | 10 | 7 | 23 | 25 |
| SH-2 | 5.18 | 34 | 24 | 3 | 6 | 55 | 23 | 11 | 11 | 25 |
| SH-3 | 2.92 | 43 | 41 | 4 | 12 | 49 | 20 | 9 | 22 | 25 |
| SH-4 | 3.29 | 25 | 16 | 1 | 2 | 46 | 23 | 13 | 18 | 25 |
| MS-1 | 1.73 | 55 | 35 | 3 | 7 | 34 | 26 | 14 | 26 | 20 |
| MS-2 | 0.84 | 49 | 35 | 4 | 12 | 44 | 25 | 12 | 19 | 25 |
| MS-3 | 0.62 | 42 | 39 | 4 | 12 | 45 | 26 | 10 | 19 | 25 |
| MS-4 | 0.73 | 50 | 38 | 3 | 9 | 39 | 25 | 13 | 23 | 25 |
| MS-5 | 1.08 | 47 | 37 | 4 | 12 | 45 | 23 | 13 | 19 | 25 |
| MS-6 | 1.21 | 44 | 41 | 3 | 12 | 44 | 25 | 12 | 19 | 25 |
| Sample No. | Density (g/cm3) | Total Porosity φ (%) | Permeability K (mD) | Total Pore Area (m2/g) | Average Pore Diameter (nm) |
|---|---|---|---|---|---|
| SS-1 | 2.57 | 3.70 | 0.0046 | 10.61 | 10.60 |
| SS-2 | 2.17 | 17.50 | 2.4133 | 5.20 | 230.40 |
| SH-1 | 2.53 | 1.40 | 0.0003 | 10.83 | 9.5 |
| SH-2 | 2.64 | 6.30 | 0.0006 | 9.65 | 11.1 |
| SH-3 | 2.36 | 8.20 | 0.0015 | 9.18 | 11.3 |
| SH-4 | 2.51 | 13.40 | 0.0028 | 11.17 | 10.3 |
| MS-1 | 2.44 | 4.70 | 0.0018 | 9.62 | 13 |
| MS-2 | 2.46 | 5.80 | 0.0048 | 9.42 | 13.2 |
| MS-3 | 2.40 | 6.40 | 0.0008 | 8.1 | 15.6 |
| MS-4 | 2.40 | 7.70 | 0.0017 | 10.36 | 13.6 |
| MS-5 | 2.40 | 8.30 | 0.0012 | 9.75 | 14.7 |
| MS-6 | 2.37 | 10.20 | 0.0026 | 8.27 | 15.8 |
| Sample No. | Semaphore Amplitude/a.u. | |||||
|---|---|---|---|---|---|---|
| Adsorption Pores | Seepage Pores | |||||
| R ≤ 0.1 μm | Proportion/% | 0.1 μr < r ≤ 1 μm | Proportion/% | R > 1 μm | Proportion/% | |
| SS-1 | 1724.89 | 78.93% | 256.98 | 11.76% | 203.38 | 9.31% |
| SS-2 | 127.32 | 1.11% | 3562.99 | 30.98% | 7811.42 | 67.92% |
| SH-1 | 1008.98 | 82.14% | 63.92 | 5.20% | 155.51 | 12.66% |
| SH-2 | 2440.47 | 53.63% | 2047.11 | 44.99% | 62.64 | 1.38% |
| SH-3 | 2208.56 | 49.31% | 1992.96 | 44.50% | 277 | 6.19% |
| SH-4 | 6739.31 | 56.14% | 5166.55 | 43.04% | 98.14 | 0.82% |
| MS-1 | 3167.79 | 45.49% | 3796.23 | 54.51% | 0 | 0.00% |
| MS-2 | 3800.55 | 77.68% | 1033.72 | 21.13% | 58.47 | 1.20% |
| MS-3 | 2947.82 | 44.62% | 3638.8 | 55.08% | 19.36 | 0.29% |
| MS-4 | 3073.61 | 43.69% | 3891.42 | 55.32% | 69.54 | 0.99% |
| MS-5 | 3305.6 | 48.37% | 3528.63 | 51.63% | 0 | 0.00% |
| MS-6 | 2793.11 | 38.87% | 4392.15 | 61.13% | 0 | 0.00% |
| Sample No. | Porosity φ (%) | Permeability K (mD) | TOC (%) | Df | Correlation Coefficient | DA (r ≤ 0.1 μm) | Correlation Coefficient | DS (r > 0.1 μm) | Correlation Coefficient |
|---|---|---|---|---|---|---|---|---|---|
| SS-1 | 3.70 | 0.0046 | 0.03 | 2.821 | 0.391 | 2.301 | 0.773 | 2.966 | 0.758 |
| SS-2 | 17.50 | 2.4133 | 0.06 | 2.507 | 0.766 | / | / | / | / |
| SH-1 | 1.40 | 0.0003 | 10.81 | 2.771 | 0.425 | 2.54 | 0.563 | 2.877 | 0.694 |
| SH-2 | 6.30 | 0.0006 | 5.18 | 2.793 | 0.423 | 2.139 | 0.871 | 2.979 | 0.94 |
| SH-3 | 8.20 | 0.0015 | 2.92 | 2.724 | 0.48 | 2.045 | 0.913 | 2.945 | 0.758 |
| SH-4 | 13.40 | 0.0028 | 3.29 | 2.663 | 0.391 | 2.52 | 0.841 | 2.895 | 0.929 |
| MS-1 | 4.70 | 0.0018 | 1.73 | 2.764 | 0.425 | 2.292 | 0.877 | 2.97 | 0.998 |
| MS-2 | 5.80 | 0.0048 | 0.84 | 2.682 | 0.436 | 2.128 | 0.889 | 2.91 | 0.833 |
| MS-3 | 6.40 | 0.0008 | 0.62 | 2.725 | 0.451 | 2.423 | 0.887 | 2.94 | 0.998 |
| MS-4 | 7.70 | 0.0017 | 0.73 | 2.753 | 0.44 | 2.282 | 0.889 | 2.95 | 0.765 |
| MS-5 | 8.30 | 0.0012 | 1.08 | 2.762 | 0.435 | 2.178 | 0.888 | 2.923 | 0.998 |
| MS-6 | 10.20 | 0.0026 | 1.21 | 2.683 | 0.446 | 2.166 | 0.88 | 2.91 | 0.905 |
| Sample No. | Porosity φ (%) | Permeability K (mD) | TOC (%) | Df | Correlation Coefficient | DA (T2 ≤ 1 ms) | Correlation Coefficient | DS (T2 > 1 ms) | Correlation Coefficient |
|---|---|---|---|---|---|---|---|---|---|
| SS-1 | 3.70 | 0.0046 | 0.03 | 2.795 | 0.425 | 2.235 | 0.84 | 2.988 | 0.812 |
| SS-2 | 17.50 | 2.4133 | 0.06 | 2.507 | 0.766 | / | / | / | / |
| SH-1 | 1.40 | 0.0003 | 10.81 | 2.834 | 0.391 | 2.456 | 0.773 | 2.985 | 0.817 |
| SH-2 | 6.30 | 0.0006 | 5.18 | 2.786 | 0.423 | 2.165 | 0.871 | 2.997 | 0.45 |
| SH-3 | 8.20 | 0.0015 | 2.92 | 2.724 | 0.48 | 2.041 | 0.913 | 2.986 | 0.509 |
| SH-4 | 13.40 | 0.0028 | 3.29 | 2.811 | 0.391 | 2.256 | 0.841 | 2.998 | 0.794 |
| MS-1 | 4.70 | 0.0018 | 1.73 | 2.764 | 0.425 | 2.048 | 0.877 | 2.955 | 0.793 |
| MS-2 | 5.80 | 0.0048 | 0.84 | 2.728 | 0.436 | 2.056 | 0.889 | 2.998 | 0.33 |
| MS-3 | 6.40 | 0.0008 | 0.62 | 2.725 | 0.451 | 2.036 | 0.887 | 2.879 | 0.905 |
| MS-4 | 7.70 | 0.0017 | 0.73 | 2.75 | 0.44 | 2.078 | 0.889 | 2.997 | 0.41 |
| MS-5 | 8.30 | 0.0012 | 1.08 | 2.76 | 0.435 | 2.041 | 0.888 | 2.923 | 0.89 |
| MS-6 | 10.20 | 0.0026 | 1.21 | 2.729 | 0.446 | 2.053 | 0.88 | 2.881 | 0.88 |
| Model | R2 | F | a | S | r | TOC | Clay Minerals | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beta | t | Beta | t | Beta | t | Beta | t | ||||
| DA | 0.981 | 31.454 | 1.648 | 0.413 | 2.877 | 0.274 | 1.530 | 0.578 | 3.642 | −0.390 | −2.906 |
| DS | 0.933 | 8.371 | 3.148 | 0.282 | 1.068 | −1.154 | −3.491 | −0.474 | −1.622 | 0.302 | 1.221 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Wang, S.; Xun, X.; Wang, H.; Sun, X.; He, M. Pore Structure and Fractal Characteristics of Coal-Measure Sedimentary Rocks Using Nuclear Magnetic Resonance (NMR) and Mercury Intrusion Porosimetry (MIP). Energies 2023, 16, 3812. https://doi.org/10.3390/en16093812
Zhang N, Wang S, Xun X, Wang H, Sun X, He M. Pore Structure and Fractal Characteristics of Coal-Measure Sedimentary Rocks Using Nuclear Magnetic Resonance (NMR) and Mercury Intrusion Porosimetry (MIP). Energies. 2023; 16(9):3812. https://doi.org/10.3390/en16093812
Chicago/Turabian StyleZhang, Na, Shuaidong Wang, Xingjian Xun, Huayao Wang, Xiaoming Sun, and Manchao He. 2023. "Pore Structure and Fractal Characteristics of Coal-Measure Sedimentary Rocks Using Nuclear Magnetic Resonance (NMR) and Mercury Intrusion Porosimetry (MIP)" Energies 16, no. 9: 3812. https://doi.org/10.3390/en16093812
APA StyleZhang, N., Wang, S., Xun, X., Wang, H., Sun, X., & He, M. (2023). Pore Structure and Fractal Characteristics of Coal-Measure Sedimentary Rocks Using Nuclear Magnetic Resonance (NMR) and Mercury Intrusion Porosimetry (MIP). Energies, 16(9), 3812. https://doi.org/10.3390/en16093812






