An ECMS Based on Model Prediction Control for Series Hybrid Electric Mine Trucks
Abstract
:1. Introduction
2. Problem Description and Formulation
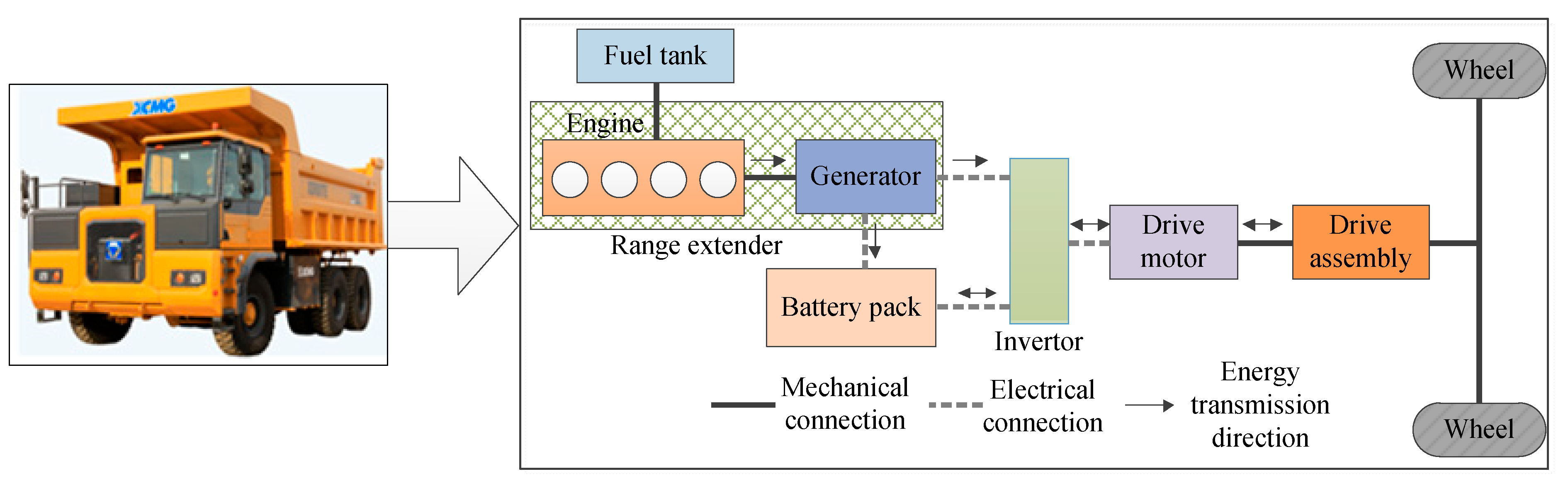
2.1. Dynamics Model
2.2. Fuel Consumption Optimization Problem
3. On-Line Speed Prediction
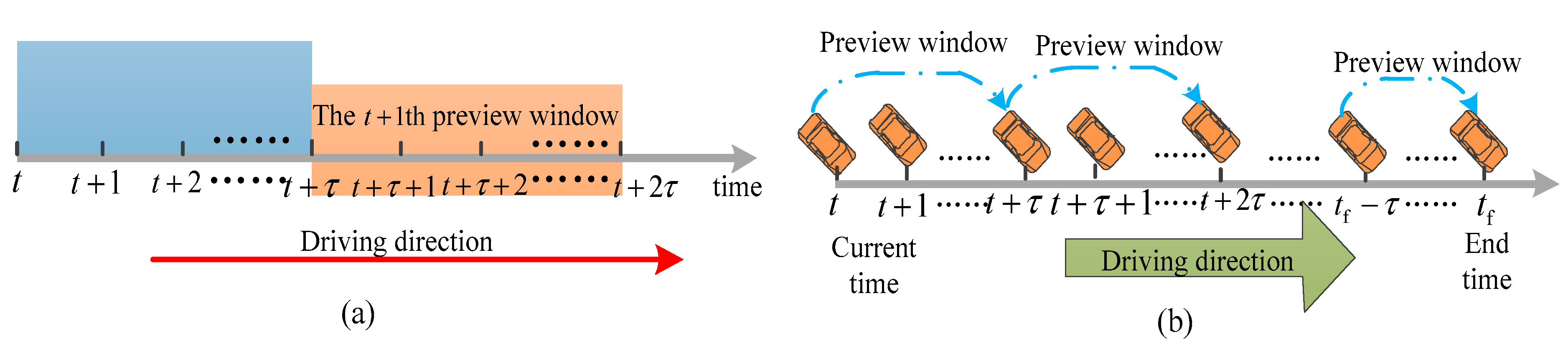
3.1. Vehicle Speed Prediction Problem
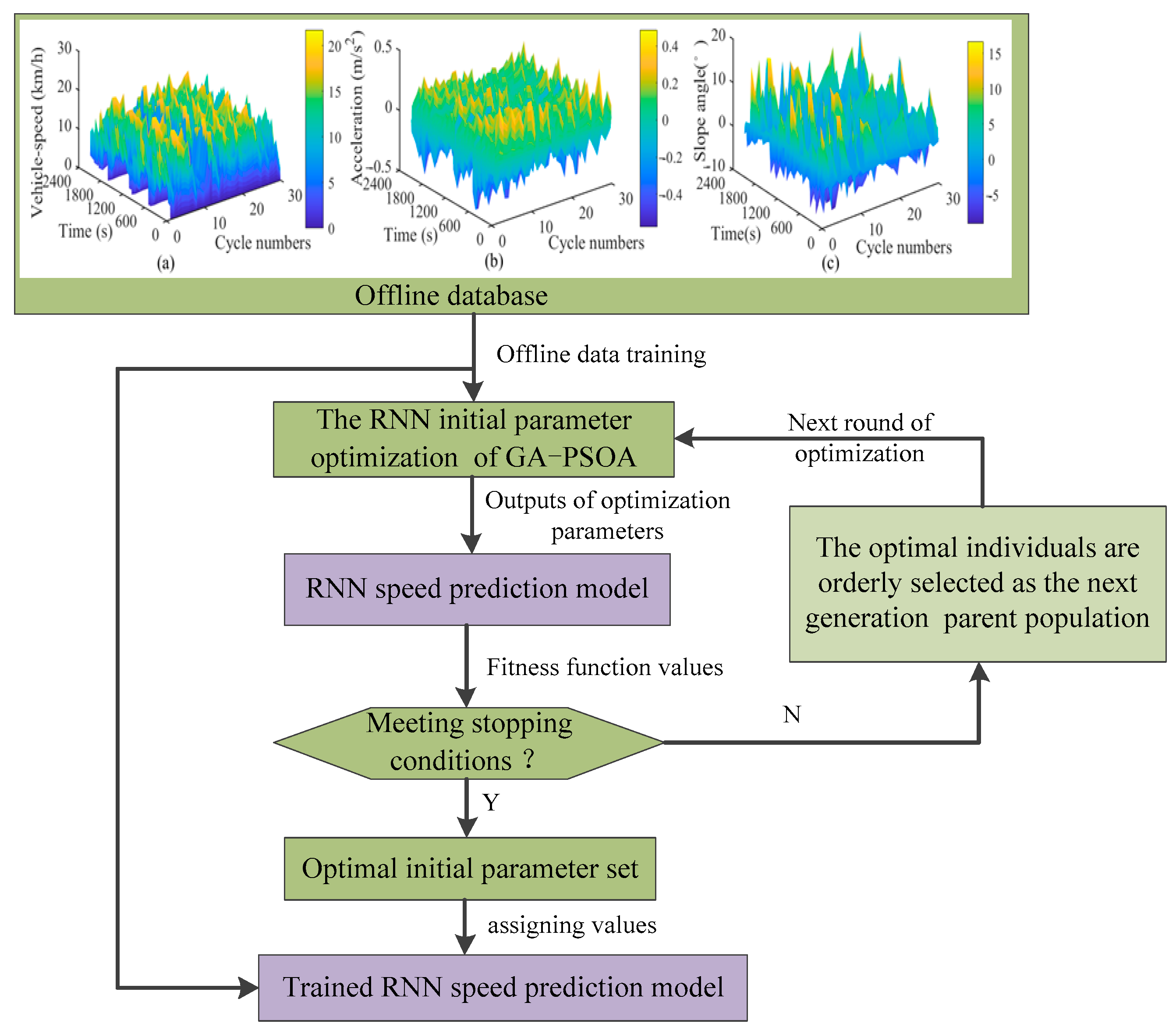
3.2. Speed Prediction Model Based on RNN
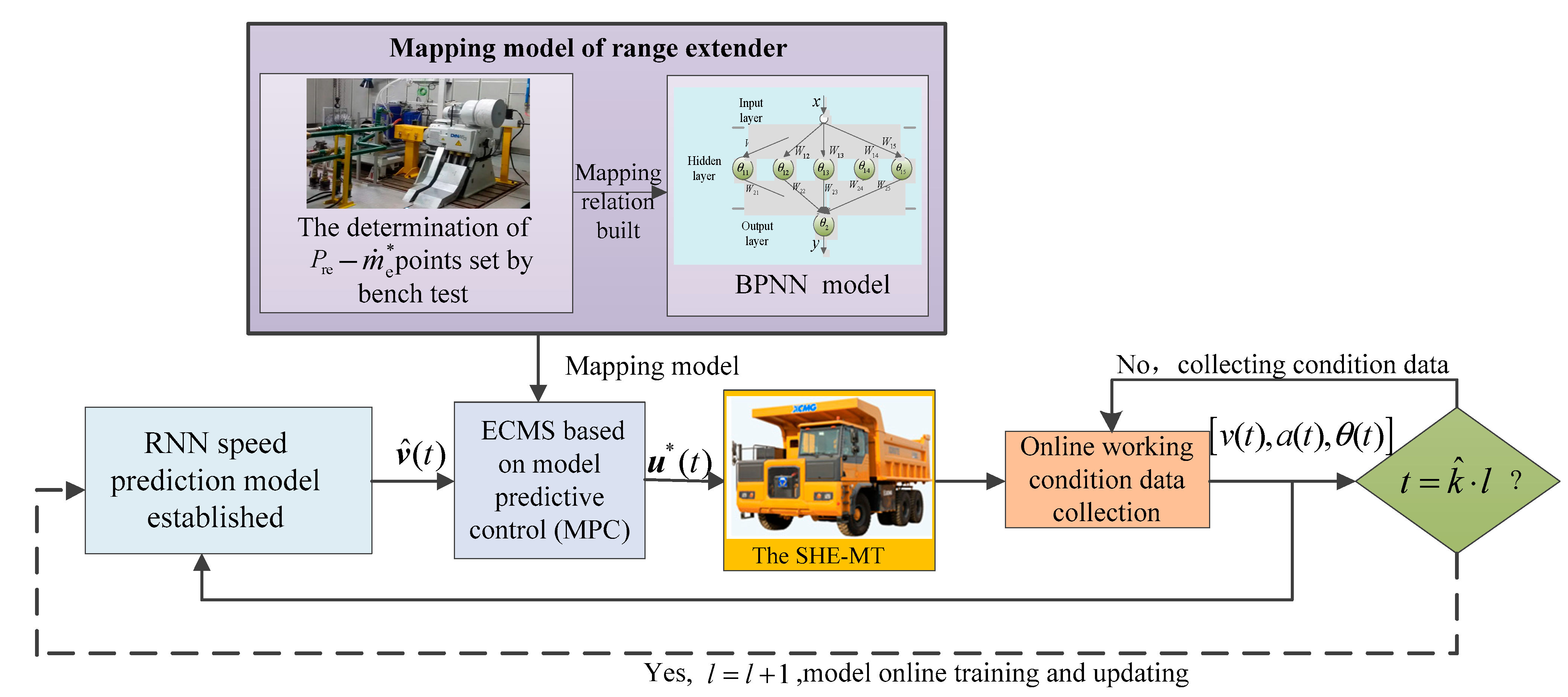
4. ECMS Based on Model Predictive Control
4.1. − Mapping Model
4.2. The Realization Process of ECMS-MPC
| Algorithm 1: The solution on the basis of PSOA. |
| // Step 1: The initialization of parameters: , , , , and of (22) in [14]; , in [14],; // Step 2: Fitness function determination: Executing (9); // Initializing fitness function // Step 3: Initializing individual and population: = 1; // Generating population for = 1,, // Generating individual of PSOA Conducting (17) in [14]; // Encoding individual Conducting (9); // Calculating fitness value end for Conducting (17) in [14]; // Generating the population as the parent population of PSOA Fitness values of individuals; // Step 4: Reforming child population on the basis of PSOA: ; // PSOA’s population regeneration for = 1, , // Reforming child population for PSOA Conducting (22) in [14]; // Updating individual Conducting (9); // Calculating Fitness end for Conducting (17) in [14]; Fitness values of individuals; // Step 5: Generating new parent population of PSOA: ; // Updating Selecting the individuals with smaller fitness values sequentially to form a population from ; // Forming the new parent population // Step 6: Judging stopping conditions: Choosing the optimal individual in ; if // Satisfying stopping conditions Going back ; // Outputting Producing Step 7; else Returning to Step 4; // Forming new population end if // Step 7: Taking as . |
5. Results and Discussion
5.1. Experimental Setup
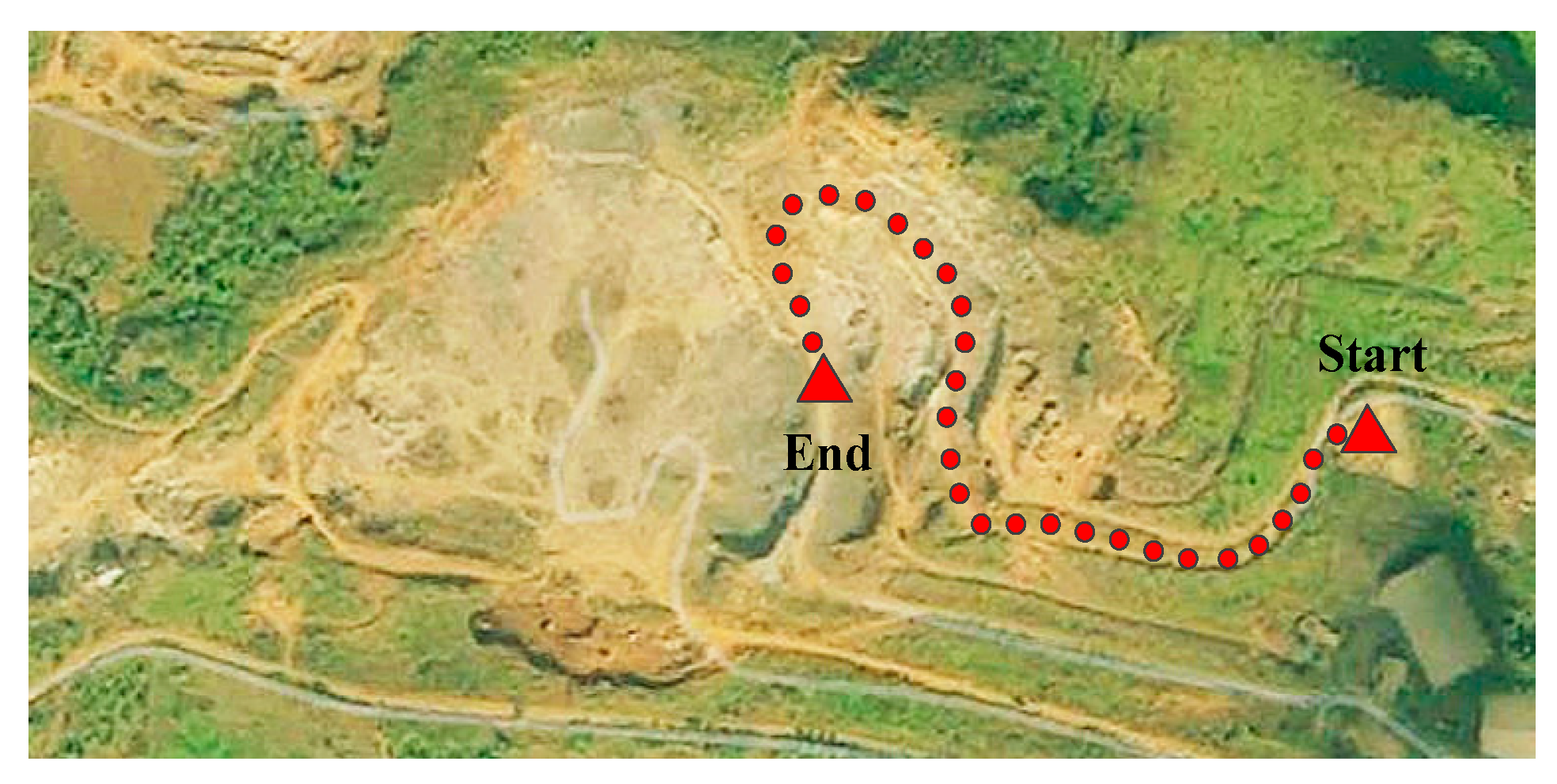
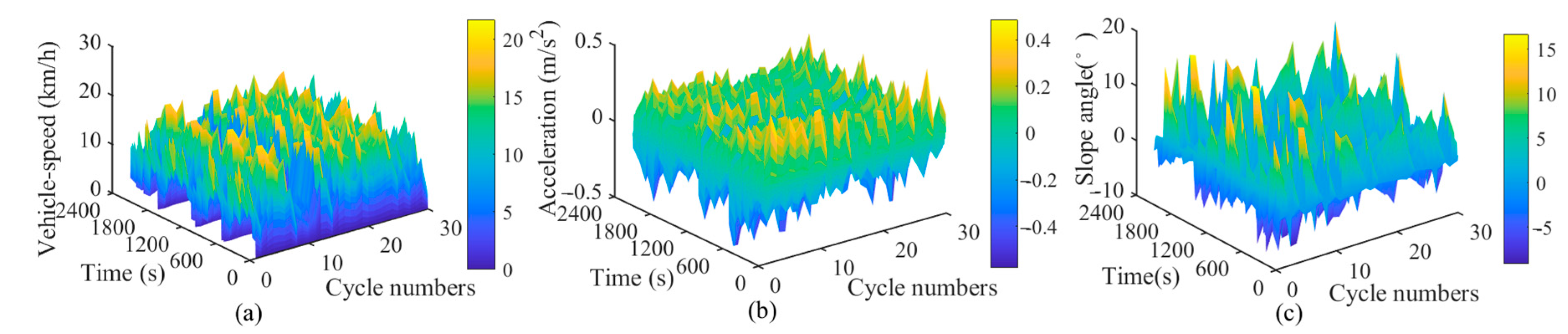
5.1.1. Cycle Selection
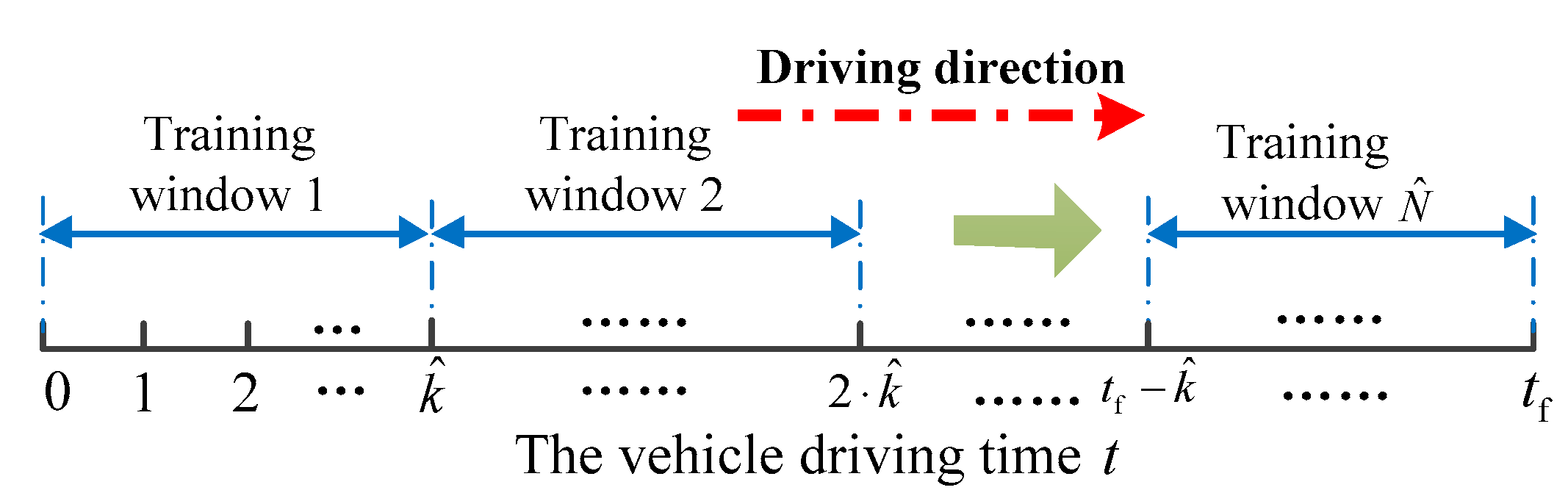
5.1.2. Model Training Parameters
5.1.3. Simulation Platform Establishment
5.1.4. Error Evaluation Methods
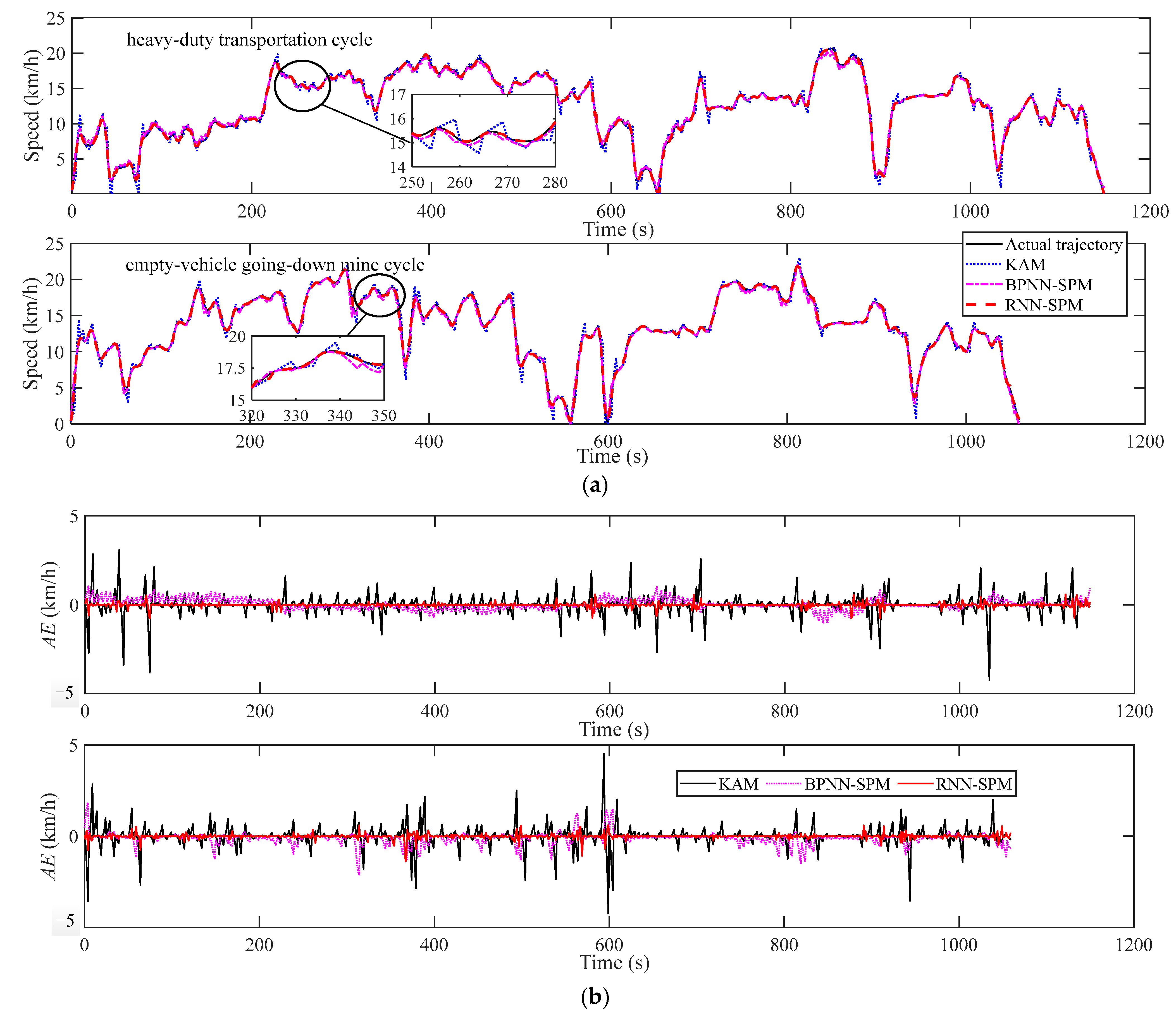
5.2. Analysis of the Speed Prediction
5.2.1. The Initial Parameter Setting
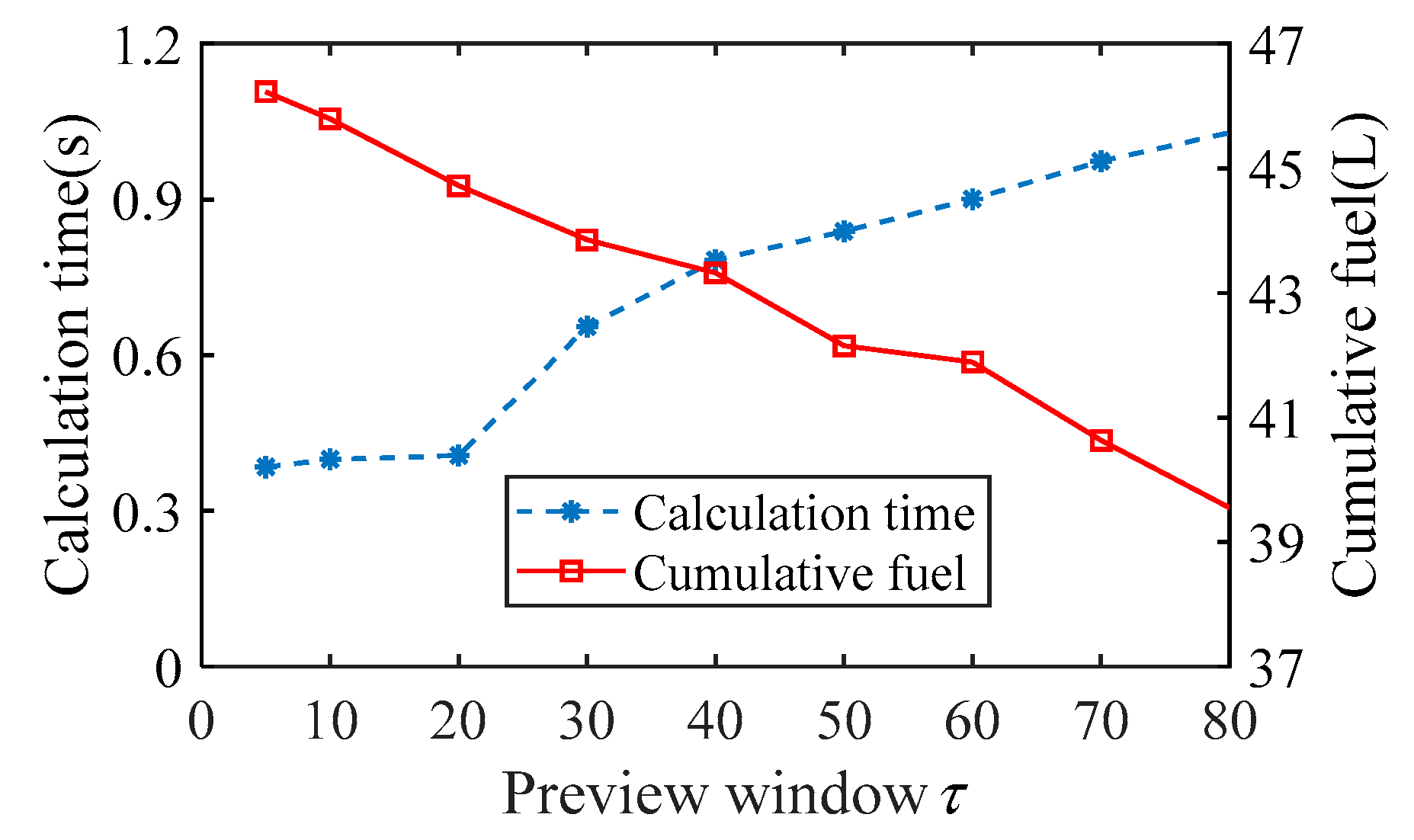
5.2.2. Selection of τ and
5.2.3. Speed Prediction Analysis
5.3. Performance Analysis of EMS
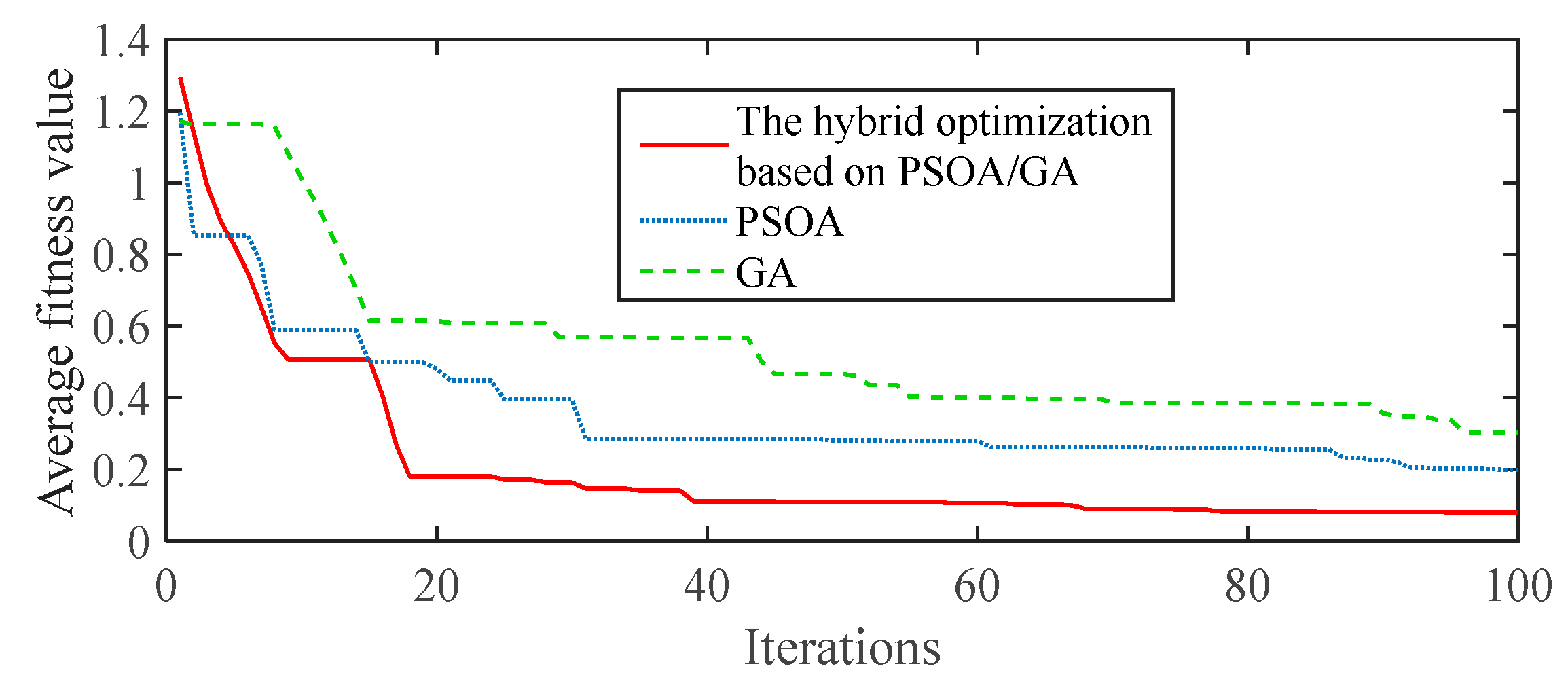
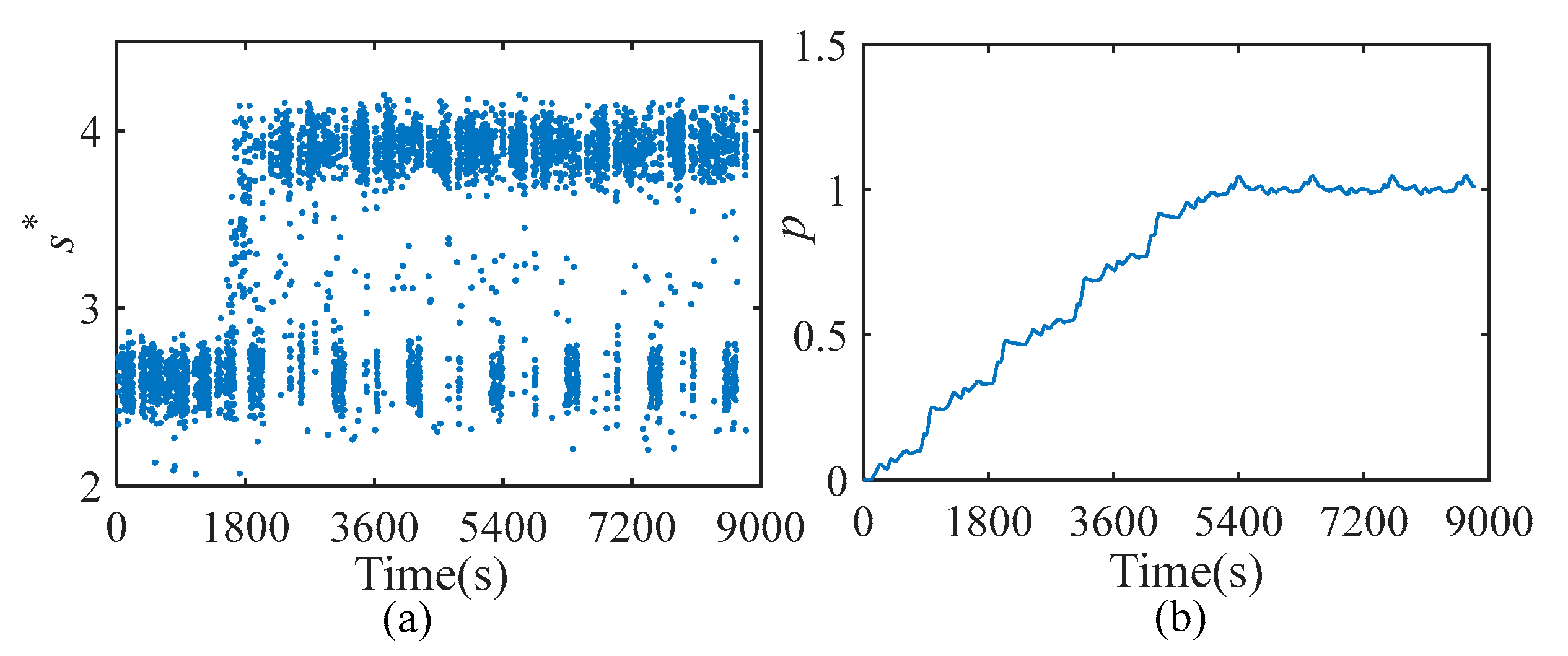
5.3.1. Parameter Determination of the ECMS-MPC
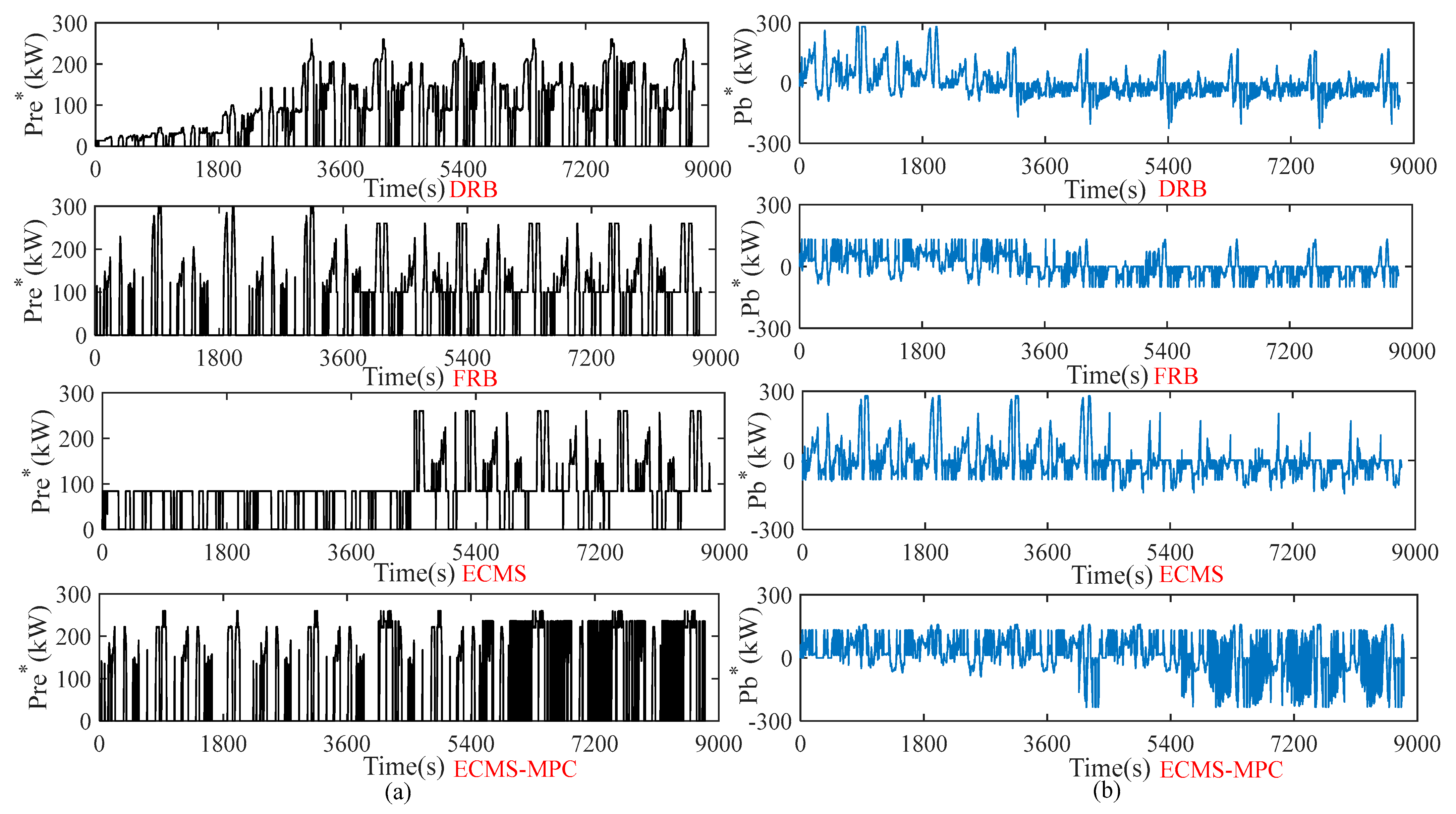
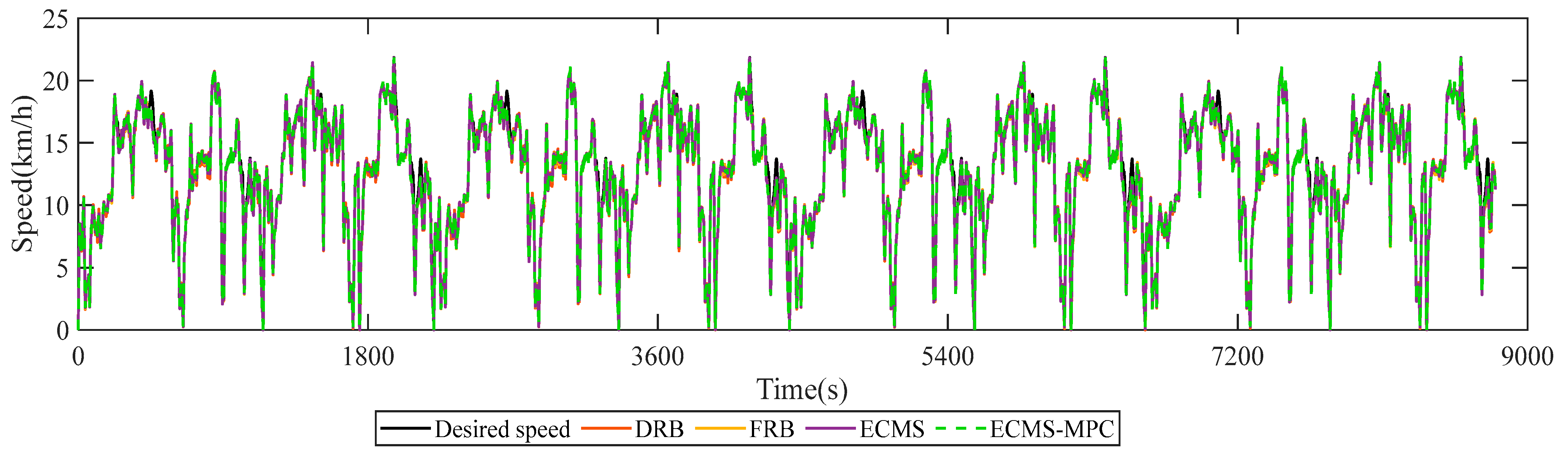
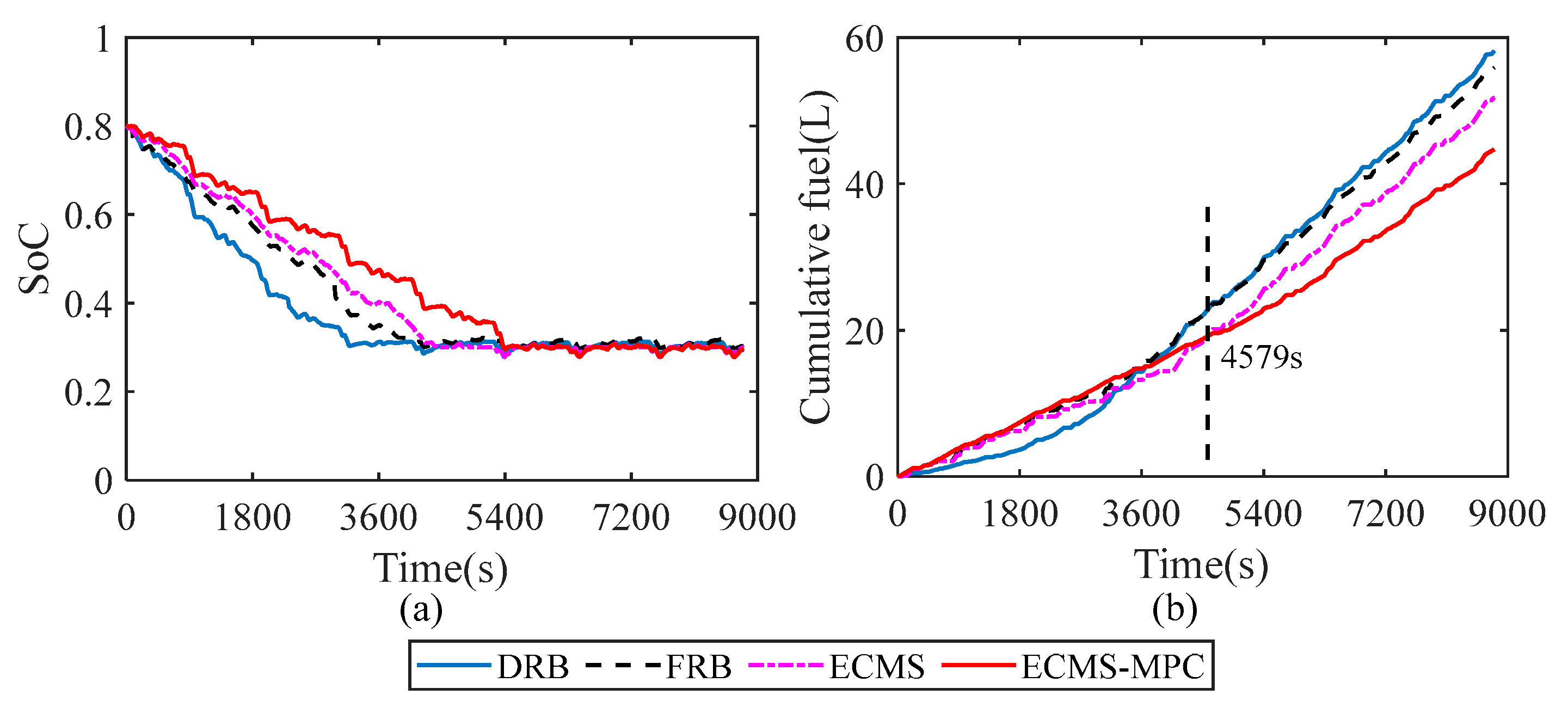
5.3.2. Performance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECMS | equivalent consumption minimization strategy | |
| SHE-MTs | series hybrid electric mine trucks | |
| RNN | recurrent neural network | |
| GA | genetic algorithm | |
| PSOA | particle swarm optimization algorithm | |
| MPC | model predictive control | |
| EF | equivalent factor | |
| ECMS-MPC | ECMS based on MPC | |
| EMSs | energy management strategies | |
| RB | rule-based | |
| CDCS | charge-sustaining | |
| DRB | deterministic RB | |
| FRB | fuzzy RB | |
| SoC | state of charge | |
| PMP | Pontryagin’s minimum principle | |
| DP | dynamic programming | |
| BPNN | backpropagation neural network | |
| − | power —optimal fuel consumption | |
| HIL | hardware-in-loop | |
| VCU | vehicle control unit | |
| KAM | kinematics analysis method | |
| BPNN-SPM | BPNN speed prediction method | |
| RNN-SPM | RNN speed prediction method based on GA-PSOA | |
| ICE-MT | internal combustion engine mine truck | |
| Variables and Its Unit | ||
| Variables | Name | Unit |
| demand torque of the wheel | Nm | |
| speed of the wheel | r/min | |
| power of the wheel | kW | |
| discrete time | s | |
| vehicle mass | kg | |
| g | gravity acceleration | m/s2 |
| θ | slope angle | ° |
| rolling resistance coefficient | – | |
| δ | rotational mass conversion coefficient | – |
| α | acceleration | m/s2 |
| CD | air resistance coefficient | – |
| A | frontal area | m2 |
| air density | kg/m3 | |
| v | vehicle speed | m/s |
| rwh | wheel radius | m |
| output power of the range extender | kW | |
| electric power of the generator | kW | |
| engine fuel consumption rate | g/kwh | |
| torque of the range extender | Nm | |
| speed of the range extender | r/min | |
| output mechanical power of the engine | kW | |
| output torque of the engine | Nm | |
| output speed of the engine | r/min | |
| fuel consumption of the range extender | g | |
| voltage of the generator | V | |
| current of the generator | A | |
| input torque of the generator | Nm | |
| input speed of the generator | r/min | |
| mechanical transmission efficiency between the engine and generator | – | |
| generating efficiency of the generator | – | |
| efficiency of the range extender | – | |
| terminal voltage of the battery back | V | |
| internal resistance of the battery back | ohm | |
| capacity of the battery back | Ah | |
| output electric power of the battery pack | kW | |
| loop current of the battery pack | A | |
| charging efficiency of the battery pack | – | |
| discharging efficiency of the battery pack | – | |
| output mechanical power | kW | |
| output torque of the driving motor | Nm | |
| output speed of the driving motor | r/min | |
| voltage of the driving motor | V | |
| current of the driving motor | A | |
| converting efficiency of driving motor between the mechanical and electric energy | – | |
| driving efficiency of the drive assembly | – | |
| speed ratio of the drive assembly | – | |
| total fuel consumption of whole trip | g | |
| equivalent fuel consumption ratio | g/s | |
| fuel calorific value | J/g | |
| start moment of driving condition | s | |
| end moment of driving condition | s | |
| EF | – | |
| penalty factor | – | |
| preview window size | – | |
| optimal control sequence at discrete time t | – | |
| optimal power combination of the range extender and battery pack at each discrete moment | – | |
| optimal power of range extender | kW | |
| optimal power of battery pack | kW | |
References
- He, X.; Jiang, Y. Review of hybrid electric systems for construction machinery. Autom. Constr. 2018, 92, 286–296. [Google Scholar] [CrossRef]
- Tong, Z.-M.; Miao, J.-Z.; Li, Y.-S.; Tong, S.-G.; Zhang, Q.; Tan, G.-R. Development of electric construction machinery in China: A review of key technologies and future directions. J. Zhejiang Univ. Sci. 2021, 22, 245–264. [Google Scholar] [CrossRef]
- Liu, T.; Yu, H.; Guo, H.; Qin, Y.; Zou, Y. Online Energy Management for Multimode Plug-In Hybrid Electric Vehicles. IEEE Trans. Ind. Inform. 2019, 15, 4352–4361. [Google Scholar] [CrossRef]
- Buccoliero, G.; Anselma, P.G.; Bonab, S.A.; Belingardi, G.; Emadi, A. A New Energy Management Strategy for Multimode Power-Split Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 69, 172–181. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Li, W.; Shang, F.; Zhan, J. Hybrid-Trip-Model-Based Energy Management of a PHEV With Computation-Optimized Dynamic Programming. IEEE Trans. Veh. Technol. 2017, 67, 338–353. [Google Scholar] [CrossRef]
- Hofman, T.; Steinbuch, M.; Van Druten, R.; Serrarens, A. Rule-based energy management strategies for hybrid vehicles. Int. J. Electr. Hybrid Veh. 2007, 1, 71. [Google Scholar] [CrossRef]
- Zulkifli, S.A.; Saad, N.; Aziz, A.R.A. Deterministic and fuzzy logic control of through-the-road split-parallel hybrid electric vehicle. In Proceedings of the 2016 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 15–17 December 2016; pp. 169–174. [Google Scholar] [CrossRef]
- Chen, J.; Xu, C.; Wu, C.; Xu, W. Adaptive Fuzzy Logic Control of Fuel-Cell-Battery Hybrid Systems for Electric Vehicles. IEEE Trans. Ind. Inform. 2016, 14, 292–300. [Google Scholar] [CrossRef]
- Jalil, N.; Kheir, N.A.; Salman, M. Rule-based energy management strategy for a series hybrid vehicle. In Proceedings of the American Control Conference, Albuquerque, NM, USA, 6 June 1997; Volume 1, pp. 689–693. [Google Scholar]
- Wen, Q.; Wang, F.; Xu, B.; Sun, Z. Improving the Fuel Efficiency of Compact Wheel Loader with a Series Hydraulic Hybrid Powertrain. IEEE Trans. Veh. Technol. 2020, 69, 10700–10709. [Google Scholar] [CrossRef]
- Zhao, D.; Zhang, Z.; Li, T.; Lan, H.; Zhang, M.; Dong, Y. Fuzzy logic control strategy of series hybrid power loader. J. Jilin Univ. Eng. Technol. Ed. 2014, 44, 1334–1341. [Google Scholar] [CrossRef]
- Wu, J.; Ruan, J.; Zhang, N.; Walker, P.D. An Optimized Real-Time Energy Management Strategy for the Power-Split Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2018, 27, 1194–1202. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Zhan, J.; Shang, F. Heuristic Dynamic Programming Based Online Energy Management Strategy for Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2019, 68, 4479–4493. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Zhan, J.; Shang, F. An On-Line Energy Management Strategy Based on Trip Condition Prediction for Commuter Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 3767–3781. [Google Scholar] [CrossRef]
- Paganelli, G.; Guerra, T.M.; Delprat, S.; Santin, J.-J.; Delhom, M.; Combes, E. Simulation and assessment of power control strategies for a parallel hybrid car. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2000, 214, 705–717. [Google Scholar] [CrossRef]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal Control of Parallel Hybrid Electric Vehicles. IEEE Trans. Control Syst. Technol. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- Sezer, V.; Gokasan, M.; Bogosyan, S. A Novel ECMS and Combined Cost Map Approach for High-Efficiency Series Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2011, 60, 3557–3570. [Google Scholar] [CrossRef]
- Zhang, Y.; Chu, L.; Fu, Z.; Xu, N.; Guo, C.; Zhang, X.; Chen, Z.; Wang, P. Optimal energy management strategy for parallel plug-in hybrid electric vehicle based on driving behavior analysis and real time traffic information prediction. Mechatronics 2017, 46, 177–192. [Google Scholar] [CrossRef]
- Li, L.; You, S.; Yang, C.; Yan, B.; Song, J.; Chen, Z. Driving-behavior-aware stochastic model predictive control for plug-in hybrid electric buses. Appl. Energy 2016, 162, 868–879. [Google Scholar] [CrossRef]
- Han, J.; Shu, H.; Tang, X.; Lin, X.; Liu, C.; Hu, X. Predictive energy management for plug-in hybrid electric vehicles considering electric motor thermal dynamics. Energy Convers. Manag. 2021, 251, 115022. [Google Scholar] [CrossRef]
- Nilsson, T.; Fröberg, A.; Åslund, J. Predictive control of a diesel electric wheel loader powertrain. Control Eng. Pract. 2015, 41, 47–56. [Google Scholar] [CrossRef]
- Xie, S.; He, H.; Peng, J. An energy management strategy based on stochastic model predictive control for plug-in hybrid electric buses. Appl. Energy 2017, 196, 279–288. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Liu, T.; Hu, X.; Hu, W.; Zou, Y. A Heuristic Planning Reinforcement Learning-Based Energy Management for Power-Split Plug-in Hybrid Electric Vehicles. IEEE Trans. Ind. Inform. 2019, 15, 6436–6445. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Peng, J.; Zhang, H.; He, H. Deep reinforcement learning of energy management with continuous control strategy and traffic information for a series-parallel plug-in hybrid electric bus. Appl. Energy 2019, 247, 454–466. [Google Scholar] [CrossRef]
- Sun, C.; Sun, F.; He, H. Investigating adaptive-ECMS with velocity forecast ability for hybrid electric vehicles. Appl. Energy 2017, 185, 1644–1653. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Qin, D.; Li, G.; Chen, Z. Research on Equivalent Factor Boundary of Equivalent Consumption Minimization Strategy for PHEVs. IEEE Trans. Veh. Technol. 2020, 69, 6011–6024. [Google Scholar] [CrossRef]
- Gu, B.; Rizzoni, G. An Adaptive Algorithm for Hybrid Electric Vehicle Energy Management Based on Driving Pattern Recognition. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; pp. 249–258. [Google Scholar] [CrossRef]
- Guo, H.; Sun, Q.; Wang, C.; Wang, Q.; Lu, S. A systematic design and optimization method of transmission system and power management for a plug-in hybrid electric vehicle. Energy 2018, 148, 1006–1017. [Google Scholar] [CrossRef]
- Kazemi, H.; Fallah, Y.P.; Nix, A.; Wayne, S. Predictive AECMS by Utilization of Intelligent Transportation Systems for Hybrid Electric Vehicle Powertrain Control. IEEE Trans. Intell. Veh. 2017, 2, 75–84. [Google Scholar] [CrossRef]
- Richalet, J.; Abu El Ata-Doss, S.; Delineau, L.; Estival, J.; Butler, H. Model based predictive control of exotic systems. In Proceedings of the IFAC Symposia Series-Proceedings of a Triennial World Congress, Tallinn, Finland, August 1990; pp. 249–256. [Google Scholar] [CrossRef]
- Fu, K.S. Learning control systems and intelligent control systems. An intersection of artificial intelligence and automatic control. IEEE Trans. Autom. Control 1971, 16, 70–72. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, L.; Sun, X.; Jin, Z.; Xue, M. ECMS-MPC Energy Management Strategy for Plug-In Hybrid Electric Buses Considering Motor Temperature Rise Effect. IEEE Trans. Transp. Electrif. 2022, 9, 210–221. [Google Scholar] [CrossRef]
- Xie, H.; Tian, G.; Du, G.; Huang, Y.; Chen, H.; Zheng, X.; Luan, T.H. A Hybrid Method Combining Markov Prediction and Fuzzy Classification for Driving Condition Recognition. IEEE Trans. Veh. Technol. 2018, 67, 10411–10424. [Google Scholar] [CrossRef]
- Vadamalu, R.S.; Beidl, C. Explicit MPC PHEV energy management using Markov chain based predictor: Development and validation at Engine-In-The-Loop testbed. In Proceedings of the 2016 European Control Conference, ECC 2016, Aalborg, Denmark, 29 June–1 July 2016; pp. 453–458. [Google Scholar] [CrossRef]
- Levin, E. A recurrent neural network: Limitations and training. Neural Netw. 1990, 3, 641–650. [Google Scholar] [CrossRef]
- Bao, X.; Sun, Z.; Sharma, N. A recurrent neural network based MPC for a hybrid neuroprosthesis system. In Proceedings of the 2017 IEEE 56th Annual Conf. on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 4715–4720. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M. Neural Network Design; China Machine Press: Beijing, China, 2002. [Google Scholar]
- Michalewicz, Z.; Vignaux, G.A.; Hobbs, M. A Nonstandard Genetic Algorithm for the Nonlinear Transportation Problem. ORSA J. Comput. 1991, 3, 307–316. [Google Scholar] [CrossRef]
- Yu, Z.; Dawei, M.; Meilan, Z.; Dengke, L. Management Strategy Based on Genetic Algorithm Optimization for PHEV. Int. J. Control Autom. 2014, 7, 399–408. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Zhang, W.; Hao, Z.; Zhu, J.; Du, T.; Hao, H. BP neural network model for short-time traffic flow forecasting based on trans-formed grey wolf optimizer algorithm. Transp. Syst. Eng. Inf. 2020, 20, 196–203. [Google Scholar] [CrossRef]
- Yang, Z.-L.; Guo, X.-Q.; Chen, Z.-M.; Huang, Y.-F.; Zhang, Y.-J. RNN-Stega: Linguistic Steganography Based on Recurrent Neural Networks. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1280–1295. [Google Scholar] [CrossRef]
- Wang, D.; Zou, Y.; Tao, Y.; Wang, B. Password guessing based on recurrent neural networks and generative adversarial net-works. Jisuanji Xuebao/Chin. J. Comput. 2021, 44, 1519–1534. [Google Scholar] [CrossRef]
- Chen, F.-C. Back-propagation neural networks for nonlinear self-tuning adaptive control. IEEE Control Syst. Mag. 1990, 10, 44–48. [Google Scholar] [CrossRef]






| Type | Description |
|---|---|
| Vehicle body | id = 0.9; ρf = 0.02; |
| Engine | 2100 rpm@1695 Nm |
| Motor | 3500 rpm@3000 Nm |
| Generator | 2200 rpm@2000 Nm |
| Battery | Cah = 300 Ah; Ub = 600 V; Rb = 0.2 ohm; idis = ich = 0.96 |
| Other |
| Parameters | Initial Values | ||||
|---|---|---|---|---|---|
| −1.62 | −2.30 | −1.69 | 0.31 | 1.00 | |
| 2.40 | 1.13 | 0.80 | 0.82 | 1.76 | |
| −1.91 | −0.61 | 0.09 | −2.61 | 1.72 | |
| W | −3.32 | −0.76 | −1.68 | −1.42 | −3.87 |
| −2.23 | 0.84 | 1.80 | −0.22 | −2.46 | |
| −2.16 | −0.23 | 1.15 | −2.20 | −1.14 | |
| 1.84 | 2.80 | 1.30 | 0.86 | −1.63 | |
| 0.25 | −1.44 | −2.95 | 1.72 | 2.85 | |
| V | −1.39 | −1.63 | −1.17 | 2.76 | 3.17 |
| 0.34 | −1.86 | 1.30 | 1.37 | −2.36 | |
| Cycle | Prediction Methods | MAE | RMSE | MRE |
|---|---|---|---|---|
| Heavy-duty transportation cycle | KAM | 0.2611 | 0.0153 | 0.0381 |
| BPNN-SPM | 0.2143 | 0.0085 | 0.0316 | |
| RNN-SPM | 0.06 | 0.0041 | 0.0095 | |
| Empty-vehicle going-down-mine cycle | KAM | 0.2647 | 0.0167 | 0.0480 |
| BPNN-SPM | 0.2016 | 0.0108 | 0.0351 | |
| RNN-SPM | 0.0618 | 0.0045 | 0.0105 |
| EMSs | ICE-MT | DRB | FRB | ECMS | ECMS-MPC |
|---|---|---|---|---|---|
| Initial SoC | - | 0.8 | 0.8 | 0.8 | 0.8 |
| Final SoC | - | 0.3 | 0.3 | 0.3 | 0.3 |
| Fuel (L) | 72.55 | 58.19 | 55.87 | 51.78 | 44.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liang, Y.; Chen, Z.; Yang, H. An ECMS Based on Model Prediction Control for Series Hybrid Electric Mine Trucks. Energies 2023, 16, 3942. https://doi.org/10.3390/en16093942
Liu J, Liang Y, Chen Z, Yang H. An ECMS Based on Model Prediction Control for Series Hybrid Electric Mine Trucks. Energies. 2023; 16(9):3942. https://doi.org/10.3390/en16093942
Chicago/Turabian StyleLiu, Jichao, Yanyan Liang, Zheng Chen, and Hai Yang. 2023. "An ECMS Based on Model Prediction Control for Series Hybrid Electric Mine Trucks" Energies 16, no. 9: 3942. https://doi.org/10.3390/en16093942
APA StyleLiu, J., Liang, Y., Chen, Z., & Yang, H. (2023). An ECMS Based on Model Prediction Control for Series Hybrid Electric Mine Trucks. Energies, 16(9), 3942. https://doi.org/10.3390/en16093942







